Optimization of material thickness distribution in single and double partition panels for maximized sound insulation

Abstract

In this work, we propose a method to optimize the material thickness distribution of partition panels for maximized sound insulation while constraining material usage. A framework is developed to couple structural optimization with diffuse field sound transmission loss (STL) predictions based on deterministic-statistical energy analysis (Det-SEA). The methodology can handle the design of both single panels, including a single mechanical plate, and double panels, in which two mechanical plates are separated by an air cavity. Three formulations of the optimization problem are developed and compared in terms of final obtained performance and computational cost. In the first formulation, the resonance dips in the STL are suppressed by pushing the panel eigenfrequencies as far away as possible from the target frequency. In the second and the third formulations, the diffuse STL of the panel is directly maximized respectively at the target frequency and in a frequency band around the target frequency. The practical advantages of the method are investigated for different target frequencies in the audible range and for relevant design cases, such as the suppression of the STL dip located around the critical frequency of single panels and around the mass–spring–mass resonance frequency of double panels. For single panels, all three different formulations lead to significant insulation improvements, with no big differences in the final obtained performance. For double panels instead, we show that simply suppressing the resonance dips with the first formulation does not lead to adequate insulation improvements, but a direct maximization of STL is needed.

1 Introduction

Achieving sufficient levels of sound insulation is necessary to provide quiet and comfortable living and working environments, e.g. in buildings (Osipov et al. 1997) or transport systems (Koval 1976; Van Genechten et al. 2011; Jung et al. 2019). For this reason, single and double partition panels are frequently used to separate rooms and to enclose noisy machines. However, common single and double panels are often acoustically deficient in specific frequency ranges, where they exhibit poor effectiveness against tonal noises, e.g. due to rotating machines. Single panels exhibit low sound insulation around the critical frequency, at which the wave speed in the panel coincides with the speed of sound in air (coincidence phenomenon) (Rindel 2018). Furthermore, the sound insulation of single panels scales with mass, and a significant amount of material may be needed to guarantee adequate comfort levels (Fahy and Gardonio 2007). In double panels, two plates separated by a cavity are employed, leading to higher sound insulation and a higher increase of insulation over frequency. However, double panels typically suffer from reduced sound insulation at low frequencies due to the mass–spring–mass resonance effect (Rindel 2018).

Novel design strategies for acoustic partitions are therefore emerging to achieve higher sound insulation while limiting the amount of used material. For example, vibroacoustic metamaterial solutions are based on attaching local resonators to a host panel, and create a sound insulation peak at the resonance frequency of the resonators (Vazquez Torre et al. 2021; Giannini et al. 2023). Also, structural and topology optimization (Bendsøe and Sigmund 2004), originally proposed to design structures with maximum stiffness and limited mass (Bendsøe and Sigmund 1999), have recently been proposed for obtaining optimized lightweight designs in different engineering domains. These include structural dynamics with control of structural response (Ma et al. 1995; Tcherniak 2002) and of structural eigenfrequencies (Giannini et al. 2020a, 2021a, b), acoustics (Du and Olhoff 2007; Dühring et al. 2008), wave propagation (Dahl et al. 2008; Van hoorickx et al. 2016), and vibroacoustics (Yoon et al. 2007; Dilgen et al. 2019), with some attention given to noise control (Du and Olhoff 2010; Wang et al. 2017).

One of the main challenges of structural optimization for vibroacoustics is that the employed prediction model needs to be both sufficiently accurate and computationally efficient. In most of the examples found in the literature, both the mechanical and acoustic domains are modeled deterministically. The use of full finite element models (Kook 2019; Jensen 2019), with discretized mechanical and acoustic domains, usually comes with high computational costs. Different degrees of simplification to reduce computational costs have been proposed, e.g. high-frequency approximations in which the acoustic pressure is computed by multiplying the interface velocity with the characteristic impedance of air (Du and Yang 2015), and finite element - elementary radiator approaches, where the acoustic pressure field is found by superposing the effects of elementary radiators distributed on a vibrating surface (Jung et al. 2017, 2022). In the design of partition panels with maximized sound insulation, a specific challenge is to account for diffuse incident sound fields. When using fully deterministic models, the sound transmission loss (STL) can be maximized separately for different angles of incident, or by integration of the response to plane incident sound waves over the incidence angles (Cool et al. 2024). As an alternative to fully deterministic models, an approach based on the hybrid deterministic-statistical energy analysis (Det-SEA) method has been proposed (Reynders et al. 2014; Reynders and Van hoorickx 2023). In this case, the partition panel is modeled in full detail, while the surrounding sound fields are inherently modeled as diffuse. This enables efficient and accurate predictions of diffuse STL, by rigorously considering the interaction between the finite structure and the diffuse sound fields through the diffuse field reciprocity relationship.

In this paper, a methodology is developed to optimize the material thickness distribution of partition panels for maximum diffuse STL, while constraining the maximum mass. In other words, optimized material thickness topologies are designed for maximum sound insulation without exceeding the maximum material usage. The designed panels with non-uniform thickness distribution can be fabricated by additive manufacturing, molding, or milling processes. Some preliminary results for the design of simple single panels have been published in Van den Wyngaert et al. (2019) and Giannini et al. (2021). We here offer a generalized framework to couple Det-SEA vibracoustic modeling with structural optimization, which for the first time handles also the more complex design of double panels. In addition, the sensitivity analysis for the design of both single and double panels is presented in full detail.

Three formulations of the optimization problem are developed and compared in terms of final obtained performance and computational costs, pointing out their level of effectiveness in the different design cases. In the first formulation, the resonance dips in the STL are suppressed by pushing the panel eigenfrequencies as far away as possible from a given target frequency. In the second formulation, the diffuse STL of the panel at the target frequency is maximized. In the third formulation, the diffuse STL is maximized over a frequency band around the target frequency. The practical advantages of the developed method are demonstrated for different target frequencies in the audible range and for relevant showcases, such as the suppression of the STL dips located at the critical frequency of single panels and at the mass–spring–mass resonance frequency of double panels.

The paper is organized as follows. Section 2 describes the Det-SEA vibroacoustic model of single and double panels. Section 3 discusses the formulation of the optimization problem, i.e. the chosen design variables, objective function and constraints, along with the solution procedure. The optimized layouts and their vibroacoustic performance are discussed in Sect. 4. Section 5 contains conclusions and remarks.

2 Vibroacoustic model

In this Section, we describe the approach followed to model the panel and to efficiently compute its diffuse STL, which is based on the hybrid Deterministic-Statistical Energy Analysis (Det-SEA) framework. We first present the mechanical model of the panel, and then we discuss the coupling with the diffuse model of the surrounding sound fields for STL computations.

2.1 Deterministic model of the panel

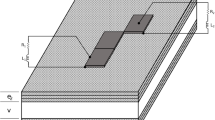
The present work considers both single panels (Fig. 1a), consisting of one single mechanical plate, and double panels (Fig. 1b), consisting of two mechanical plates (plate 1 and plate 2), separated by an air cavity. In what follows, the models of the mechanical plates and of the air cavity are discussed, along with their coupling in the case of double panels.

2.1.1 Model of the mechanical plates

Fig. 1

Layout of (a) single and (b) double panels

For both single and double panels, each mechanical plate is discretized by plate finite elements (cf. Fig. 1) and modeled as simply supported on its four edges. The equations of motion of the pth mechanical plate ($p=1$ for single panels and $p=1,2$ for double panels) in the frequency domain can be written as:

$$\begin{aligned} \boldsymbol{D}_p \boldsymbol{u}_{p} = \left[ - \omega^2 \boldsymbol{M}_p + \boldsymbol{K}_p (1 + \mathrm{i}\eta_{p}) \right] \boldsymbol{u}_{p} = \boldsymbol{f}_p \end{aligned}$$

(1)

where $\varvec{u}_{p}$ are the degrees of freedom of the plate corresponding to the finite element discretization, $\boldsymbol{M}_p$ and $\boldsymbol{K}_p$ are the associated mass and stiffness matrices, $\boldsymbol{D}_p$ is the dynamic stiffness matrix, $\mathrm{i} := \sqrt{-1}$ is the imaginary unit, and $\eta _{p}$ denotes the damping loss factor of the plate. The vector $\varvec{f}_p$ contains the external loads, e.g. the fluid loading onto the plate due to the acoustic pressure in the surrounding acoustic space. In what follows, discretizations by Kirchhoff and Mindlin plate finite elements are considered. Through-thickness effects, such as dilatational propagating waves and thickness resonances (Hopkins 2007) are therefore not modeled here. In case these effects are of interest in the audible range, e.g. for thick walls, volume finite element model discretizations e.g. by hexahedral elements can be adopted (Reynders et al. 2014).

The eigenfrequencies $\omega _{p,k}$ and the mode shapes $\varvec{\phi }_{p,k}$ of the pth plate are found by solving the following undamped eigenvalue problem:

$$\begin{aligned} (-\omega _{p}^2 \varvec{M}_p+\varvec{K}_p) \varvec{\phi }_{p}=\varvec{0} \end{aligned}$$

(2)

and the eigenfrequencies in Hz are found as $f_{p}=\omega _{p}/2\pi$.

The equations of motion in Eq. (1) are projected onto a set of basis functions $\varvec{\Phi }_{p} = \left[ \varvec{\phi }_{p,1},..., \varvec{\phi }_{p,{n_p}}\right]$ consisting of the first $n_p$ mass-normalized mode shapes computed from Eq. (2), in order to reduce the size of the model. By approximating $\varvec{u}_{p} \approx \varvec{\Phi }_{p} \varvec{q}_{p}$ through the modal coordinates $\varvec{q}_{p}$, we therefore obtain:

$$\begin{aligned}{} & {} \varvec{D}_{\text{m},p}\varvec{q}_{p} = \left[ - \omega ^2 \varvec{M}_{\text{m},p} + \varvec{K}_{\text{m},p} (1 + \text{i}\eta _{p}) \right] \varvec{q}_{p}\nonumber \\{} & {} =\varvec{f}_{\text{m},p} \end{aligned}$$

(3)

where $\varvec{D}_{\text{m},p}$ is the modal dynamic stiffness matrix of the plate, $\varvec{M}_{\text{m},p} = \varvec{\Phi }_{p}^T \varvec{M}_{p} \varvec{\Phi }_{p} = \varvec{I}$, $\varvec{K}_{\text{m},p} = \varvec{\Phi }_{p}^T \varvec{K}_{p} \varvec{\Phi }_{p} = {{\,\text{diag}\,}}\left( \omega _{p,1}^2, \omega _{p,2}^2,..., \omega _{p,n_p}^2 \right)$ are the modal mass and stiffness matrices, $\varvec{I}$ is the identity matrix, and $\varvec{f}_{\text{m},p} = \varvec{\Phi }_{p}^T \varvec{f}_p$ is the vector of modal loads.

2.1.2 Model of the air cavity

Following what was proposed in Van den Wyngaert et al. (2018), the air cavity present in double panels is studied by approximating the associated pressure field $p_\text{cav}(\varvec{x},\omega )$, at spatial location $\varvec{x} = (x,y,z)$ and frequency $\omega$, using a set of basis functions $\phi _{\text{cav},k}(\varvec{x})$, such that $p_\text{cav}(\varvec{x},\omega ) \approx \sum _{k=1}^{n_\text{cav}} \phi _{\text{cav},k}(\varvec{x}) q_{\text{cav},k}(\omega )$ where $q_{\text{cav},k}(\omega )$ are the modal coordinates of the cavity. The basis functions are chosen as the first $n_\text{cav}$ analytically computed and normalized mode shapes of the decoupled, hard-walled, rectangular cuboid cavity. The kth mode shape of the cavity is computed as:

$$\begin{aligned} \phi _{\text{cav},k}(\varvec{x}) = a_k \cos \left( \frac{m_k \pi x}{L_\text{x}}\right) \cos \left( \frac{n_k \pi y}{L_\text{y}}\right) \cos \left( \frac{p_k \pi z}{L_\text{z}}\right) \end{aligned}$$

(4)

where $L_\text{x}$,$L_\text{y}$ are the in-plane dimensions of the plates and the cavity, $L_\text{z}$ is the cavity depth (cf. Fig. 1), $m_k \in \mathbb {N}_0$, $n_k \in \mathbb {N}_0$ and $p_k \in \mathbb {N}_0$ are the number of half wavelengths in the x-, y- and z-coordinate directions. The normalization constants satisfy

$$\begin{aligned} & a_k= {} \frac{c_\text{a}\gamma (m_k)\gamma (n_k)\gamma (p_k)}{\sqrt{L_\text{x} L_\text{y} L_\text{z}}} \\ &\text{with:} \quad \gamma (s)= {} {\left\{ \begin{array}{ll} \begin{aligned} \sqrt{2} \quad &{} \text {if } s\ne 0 \\ 1\quad &{} \text {if } s=0 \end{aligned} \end{array}\right. } \end{aligned}$$

(5)

where $c_\text{a}$ = 343 m/s is the speed of sound in air. The angular natural frequency corresponding to mode k equals:

$$\begin{aligned} \omega _{\text{cav},k} = c_\text{a} \sqrt{\left( \frac{m_k \pi }{L_\text{x}}\right) ^2 + \left( \frac{n_k \pi }{L_\text{y}}\right) ^2 + \left( \frac{p_k \pi }{L_\text{z}}\right) ^2} \end{aligned}$$

(6)

The presence of absorbents or metal studs in the cavity has not been considered in the model, but can be added, e.g. following Van den Wyngaert et al. (2018).

2.1.3 Model of the double panel

The equations of motion of the double panel are derived by coupling the two plates and the air cavity through the loads on the plates due to the sound pressure in the cavity, and the loads on the cavity due to the displacement of the plates:

$$\begin{aligned}{} & {} \begin{bmatrix} \varvec{D}_{\text{m},1} &{}\varvec{0} &{}\varvec{L}_{\text{f,m},1} \\ \varvec{0} &{}\varvec{D}_{\text{m},2} &{}\varvec{L}_{\text{f,m},2} \\ \varvec{L}_{\text{s,m},1} &{}\varvec{L}_{\text{s,m},2} &{}\varvec{D}_\text{cav} \end{bmatrix} \begin{Bmatrix} \varvec{q}_{1} \\ \varvec{q}_{2} \\ \varvec{q}_\text{cav} \end{Bmatrix} = \begin{Bmatrix} \varvec{f}_{\text{m},1} \\ \varvec{f}_{\text{m},2} \\ \varvec{0} \end{Bmatrix}\nonumber \\{} & {} \Rightarrow \qquad \varvec{D}_\text{d} \varvec{q} = \varvec{f} \end{aligned}$$

(7)

where $\varvec{D}_{\text{m},1}$ and $\varvec{D}_{\text{m},2}$ are the modal dynamic stiffness matrices of the plates as defined in Sect. 2.1.1, and $\varvec{D}_\text{cav}$ is the modal dynamic stiffness matrix of the air cavity. In particular, $\varvec{D}_\text{cav}$ is a diagonal matrix with entries:

$$\begin{aligned} D_{\text{cav},kk} = -\omega ^2 + \omega _{\text{cav},k}^2 (1 + \text{i}\eta _{\text{cav},k}) \end{aligned}$$

(8)

where $\eta _{\text{cav},k}$ denotes the damping loss factor of cavity mode k. We here consider an empty cavity and determine the modal loss factor from $\eta _{\text{cav},k} = \frac{4.4 \pi }{\omega _{\text{cav},k} T_\text{cav}}$, for a chosen reverberation time $T_\text{cav}$ = 2 s.

In Eq. (7), the interaction matrices $\varvec{L}_{\text{f,m},p}$ express the loading on the modes of the pth plate due to the cavity pressure $p_\text{cav}(\varvec{x},\omega )$ (Van den Wyngaert et al. 2018). The load on the transversal degree of freedom of kth node of the plate can be expressed as:

$$\begin{aligned} \begin{aligned} f_{p,k,\text{cav}} (\omega ) & = -\int _{\Gamma _{p}} U_{p,k}(\varvec{x}) p_\text{cav} (\varvec{x},\omega )\text{d}\varvec{x}\\& \approx -\sum _{l=1}^{n_\text{cav}} L_{\text{f}p,kl} q_{\text{cav},l} (\omega )\end{aligned} \\ \text {with: } \quad L_{\text{f}p,kl} = \int _{\Gamma _{p}} U_{p,k}(\varvec{x}) \phi _{\text{cav},l} (\varvec{x}) \text{d}\varvec{x} \end{aligned}$$

(9)

where the function $U_{p,k}(\varvec{x})$ has a unitary value at the kth node of the plate, is zero at the other nodes and in-between the nodes follows the interpolation provided by the shape functions of the plate elements. The integral in Eq. (9) is computed over the interface surface area $\Gamma _{p}$ between the plate and the cavity. Equation (9) leads to the matrices $\varvec{L}_{\text{f},p}$, which can be projected onto the modal basis of the plates as $\varvec{L}_{\text{f,m},p} = \varvec{\Phi }_{p}^T \varvec{L}_{\text{f},p}$.

The interaction matrices $\varvec{L}_{\text{s,m},p}$ in Eq. (7) express the loading on the modes of the cavity, due to the modal displacements of the plate. The load on the kth mode of the cavity, due to the transversal displacement of the pth plate $u_{p}(\varvec{x}, \omega ) \approx \sum _k U_{p,k}(\varvec{x}) u_{p,k}(\omega )$ (Van den Wyngaert et al. 2018), can be expressed as:

$$\begin{aligned}f_{\text{cav},k,p} &= -\rho _\text{a} \omega ^2 \int _{\Gamma _{p}} \phi _{\text{cav},k}(\varvec{x})u_{p}(\varvec{x},\omega ) \text{d}\varvec{x} \\ &\approx -\sum _{l=1}^{n_1} L_{\text{s}p,kl} u_{p,l}(\omega ) \\ &\text {with: } \quad L_{\text{s}p,kl} = \rho _\text{a} \omega ^2 L_{\text{f}p,lk} \end{aligned}$$

(10)

with $\rho _\text{a}$ = 1.20 kg/m$^3$ being the density of air. Equation (10) leads to the matrices $\varvec{L}_{\text{s},p}$, which can be projected onto the modal basis of the plates as $\varvec{L}_{\text{s,m},p} = \varvec{L}_{\text{s},p} \varvec{\Phi }_{p}$.

When considering homogenous equations of motion, the eigenfrequencies and the mode shapes of the double panel can be found by solving the following eigenvalue problem:

$$\begin{aligned} \left( \varvec{K}_\text{d} - \omega _\text{d}^2 \varvec{M}_\text{d} \right) \varvec{\phi }_\text{d} = \varvec{0} \\ \begin{aligned} \text {with:} \quad &\varvec{K}_\text{d} = \begin{bmatrix} \varvec{K}_\text{m,1} &{}\varvec{0} &{}\varvec{L}_{\text{f,m},1} \\ \varvec{0} &{}\varvec{K}_\text{m,2} &{}\varvec{L}_{\text{f,m},2} \\ \varvec{0} &{}\varvec{0} &{}\varvec{K}_\mathrm {m,\text{cav}} \end{bmatrix},\\&\varvec{M}_\text{d} = \begin{bmatrix} \varvec{M}_\text{m,1} &{}\varvec{0} &{}\varvec{0} \\ \varvec{0} &{}\varvec{M}_\text{m,2} &{}\varvec{0} \\ -\rho _\text{a}\varvec{L}_{\text{f,m},1}^T &{}-\rho _\text{a}\varvec{L}_{\text{f,m},2}^T &{}\varvec{M}_\mathrm {m,\text{cav}} \end{bmatrix} \end{aligned} \end{aligned}$$

(11)

where $\varvec{M}_\mathrm {m,\text{cav}} = \varvec{I}$, $\varvec{K}_\mathrm {m,\text{cav}} = {{\,\text{diag}\,}}\left( \omega _{\text{cav},1}^2, \omega _{\text{cav},2}^2,..., \omega _{\text{cav},n_\text{cav}}^2 \right)$ are the modal mass and stiffness matrices of the cavity. In general, the stiffness and mass matrices $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$ of the double panel are nonsymmetric, and therefore each eigenvalue $\omega _{\text{d},k}^2$ will be associated with a left eigenvector $\varvec{\phi }_{\text{d},k,\text{L}}$ and a right eigenvector $\varvec{\phi }_{\text{d},k,\text{R}}$.

2.2 Diffuse STL computations based on the hybrid Det-SEA modeling framework

Fig. 2

Scheme of the transmission suite (room–panel–room) model: two possible realizations of the random ensemble of rooms are represented

A complete description of diffuse STL computations based on the Det-SEA framework can be found in dedicated literature (Reynders et al. 2014; Shorter and Langley 2005a, b; Decraene et al. 2018; Sound transmission 2016). In what follows, we introduce the main relations that will be employed further on in this paper, based on the summary provided in Reynders and Van hoorickx (2023).

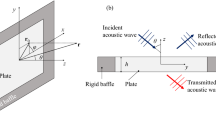
The airborne sound insulation of the partition panel depends on the properties of the panel itself, but also on the nature of the incident sound field at the source side and of the radiated sound field at the receiver side. Referring to Fig. 2, we here consider an indoor setting in which the panel is interposed between two rooms, i.e. a source room (room 1) and a receiver room (room 2). In such indoor setting, the sound fields in rooms 1 and 2 are conventionally approximated as diffuse, i.e. the incident sound field consists of incoherent plane waves coming from all possible directions and carrying the same energy, and the radiated sound field equals that of an acoustic halfspace. A diffuse field is by definition a random field, representing not just a nominal situation, but the sound field of a conceptual random ensemble of rooms with the same modal density and total absorption, yet otherwise any possible arrangement of boundaries and small objects that have a wave scattering effect. The employed Det-SEA model therefore accurately represents the average insulation performance of the finite-sized panel across a random ensemble of rooms.

The STL R across the partition panel is determined by the sound transmission coefficient $\tau$, which is the ratio between the power flow from the source room to the receiver room $P_{\text{in}}^{(1\rightarrow 2)}$ and the incident sound power on the panel in the source room $P_{\text{inc}}^{(1)}$:

$$\begin{aligned} R(\omega ):= - 10 \log \tau (\omega ), \qquad \text {with:} \quad \tau = \frac{P_{\text{in}}^{(1\rightarrow 2)}(\omega )}{P_{\text{inc}}^{(1)}(\omega )} \end{aligned}$$

(12)

where $\omega$ is the angular frequency. A quantity related to the transmission coefficient is the coupling loss factor $\eta _{12}$ between the source and the receiver rooms, which is defined as:

$$\begin{aligned} \eta _{12}(\omega ):=\frac{P_{\text{in}}^{(1\rightarrow 2)}(\omega )}{\omega E_1(\omega )} \end{aligned}$$

(13)

If the source room carries a diffuse sound field, the ensemble mean of the incident power relates to the total energy of the room (Lyon and DeJong 1995):

$$\begin{aligned} \hat{P}_{\text{inc}}^{(1)} (\omega ) = \frac{c L_\text{x} L_\text{y}}{4V_1}\hat{E}_1(\omega ) \end{aligned}$$

(14)

where the hat denotes the mean across the diffuse random field ensemble, c denotes the sound speed, $L_\text{x}$, $L_\text{y}$ are the planar dimensions of the wall, and $V_1$ the volume of the source room ($V_1$ = $V_2$ = 87 m$^3$ have been considered).

In the diffuse model of the rooms, the sound fields are decomposed into a direct field and a reverberant field. The direct field is deterministic and describes waves traveling away from the panel, due to its vibration. The reverberant field is random and represents reflected and scattered waves traveling back to the panel. The equations of motion of the rth room (r = 1,2) can be written as:

$$\begin{aligned} \varvec{D}_{r,p} \varvec{u}_{p} = \left( \varvec{D}_{\text{dir},r,p} + \varvec{D}_{\text{rev},r,p} \right) \varvec{u}_{p} = \varvec{f}_{r,p} \end{aligned}$$

(15)

where the dynamic stiffness matrix $\varvec{D}_{r,p}$ of the room describes the relationship between the displacements of the pth plate $\varvec{u}_p$ and the forces $\varvec{f}_{r,p}$ at the interface between the plate and the room. $\varvec{D}_{r,p}$ has been decomposed into a deterministic direct field dynamic stiffness matrix $\varvec{D}_{\text{dir},r,p}$ and a random reverberant field dynamic stiffness matrix $\varvec{D}_{\text{rev},r,p}$. In particular, the deterministic direct field dynamic stiffness matrix is the one of an acoustic halfspace, which can be computed numerically via the Rayleigh integral, e.g. using a wavelet discretization of the baffled interface (Langley 2007).

Equation (15) can be projected onto the modal basis of the single or double panel by approximating $\varvec{u}_{p} \approx \varvec{\Phi }_{p} \varvec{q}_{p}$, and therefore:

$$\begin{aligned} \varvec{D}_{\text{m},r,p} \varvec{q}_{p} = \left( \varvec{D}_{\text{dir,m},r,p} + \varvec{D}_{\text{rev,m},r,p} \right) \varvec{q}_{p} = \varvec{f}_{\text{m},r,p} \end{aligned}$$

(16)

where $\varvec{D}_{\text{m},r,p} = \varvec{\Phi }_{p}^T \varvec{D}_{r,p} \varvec{\Phi }_{p}$ is the direct field dynamic stiffness matrix expressed in modal coordinates, and $\varvec{f}_{\text{m},r,p} = \varvec{\Phi }_{p}^T \varvec{f}_{r,p}$ is the vector of interface modal loads.

The equations of motion of the room-wall-system are therefore:

$$\begin{aligned} & \left( \varvec{D}_\text{tot} + \varvec{D}'_{\text{rev},1} + \varvec{D}'_{\text{rev},2}\right) \varvec{q} = \varvec{f} \\ &\text { with:} \quad \varvec{D}_\text{tot} = \varvec{D}_{0} + \varvec{D}'_{\text{dir},1} + \varvec{D}'_{\text{dir},2} \end{aligned}$$

(17)

where $\varvec{D}_{0}$ is the dynamic stiffness matrix of the in-vacuo panel, i.e. for single panels $\varvec{D}_{0} = \varvec{D}_{\text{m},1}$ and for double panels $\varvec{D}_{0} = \varvec{D}_\text{d}$, while $\varvec{D}'_{\text{dir},1}$, $\varvec{D}'_{\text{dir},2}$, $\varvec{D}'_{\text{rev},1}$, $\varvec{D}'_{\text{rev},2}$ are the (expanded) direct field and reverberant field dynamic stiffness matrices, expressed in terms of the reduced panel coordinate vector.

Considering that the diffuse reverberant dynamic stiffness matrices have zero mean, and invoking the diffuse field reciprocity relationship (Shorter and Langley 2005b), it can be proven that the expected value $\hat{P}_\text{in}^{(1\rightarrow 2)}$ of the sound power flow from the source room to the receiver room is (Reynders and Van hoorickx 2023):

$$\begin{aligned} \hat{P}_\text{in}^{(1\rightarrow 2)} = \frac{2\hat{E}_1}{\pi \omega n_1} \sum _{rs} \text{Im}(\varvec{D}'_{\text{dir},2})_{rs} (\varvec{D}_\text{tot}^{-1} \text{Im}(\varvec{D}'_{\text{dir},1}) \varvec{D}_\text{tot}^{-H})_{rs} \end{aligned}$$

(18)

where $n_1$ is the modal density of the source room, i.e. the expected number of modes per unit radial bandwidth (Lyon and DeJong 1995).

Combining the previous equations leads to:

$$\begin{aligned} \tau= & {} \frac{4 V_1 \omega }{L_\text{x} L_\text{y} c_\text{a}} \eta _{12}, \quad \text {with:} \nonumber \\{} & {} \eta _{12} = \frac{2}{\pi \omega n_1} \sum _{rs} \text{Im}(\varvec{D}'_{\text{dir},2})_{rs} (\varvec{D}_\text{tot}^{-1} \text{Im}(\varvec{D}'_{\text{dir},1}) \varvec{D}_\text{tot}^{-\text{H}})_{rs} \end{aligned}$$

(19)

3 Optimization of the material thickness distribution

3.1 Design variables

Once the modeling strategy for the computation of the panel eigenfrequencies and the STL has been established, a set of design variables is chosen in order to describe the material thickness distribution to be optimized.

The thickness distribution within each plate area is described by considering a design variable $\gamma _e \in [0,1]$ for each finite element e. The set of design variables $\varvec{\gamma }$ is used to scale the thickness of the elements. The framework is similar to density-based topology optimization (Bendsøe and Sigmund 2004), in which the design variables are used to scale the material properties between void ($\gamma _e=0$) and solid ($\gamma _e=1$). In density-based topology optimization intermediate values are usually penalized in order to ensure all elements are void or solid in the final design. In the present work instead, no penalization is used, such that also the intermediate thickness values within the given range are allowed.

A convolution filter is applied to the set of design variables $\varvec{\gamma }$ (Wang et al. 2011), in order to avoid mesh dependence of the solution and convergence to checkerboard layouts. The filtered design variables are obtained as:

$$\begin{aligned} \tilde{\gamma }_e=\frac{\sum _{j\in \mathbb {N}_{s,e}}w(\varvec{x}_j) A_j \gamma _{e,j}}{\sum _{j\in \mathbb {N}_{s,e}} w(\varvec{x}_j) A_j} \end{aligned}$$

(20)

where $A_j$ is the area of the jth element and $\mathbb {N}_{s,e}$ is the set of elements with centers lying within a circle with radius $r_\text{min}$ centered on the centroid of element e, and belonging to the same plate. The linear weighting function $w(\varvec{x_j})$ is given as:

$$\begin{aligned} w(\varvec{x}_j)=r_\text{min}-\mid \varvec{x}_j-\varvec{x}_e\mid \end{aligned}$$

(21)

where $\varvec{x}_j=(x_j,y_j)$ and $\varvec{x}_e=(x_e,y_e)$ are the centroid coordinates of elements j and e.

The filtered design variables are used to scale the element thicknesses between a minimum value $t_\text{min}$ and a maximum value $t_\text{max}$:

$$\begin{aligned} t_e=t_\text{min}+(t_\text{max}-t_\text{min}) \tilde{\gamma }_e \end{aligned}$$

(22)

The element matrices are then scaled according to the element thickness. In what follows, both Kirchhoff and Mindlin plate finite elements are considered, whose stiffness and mass matrices are the combination of a term proportional to the thickness and a term proportional to the third power of the thickness (Bathe 1996):

$$\begin{aligned} \begin{aligned}&\varvec{K}_e (t_e)=\varvec{K}_{e,1}(t=1) t_e + \varvec{K}_{e,3}(t=1) t_e^3 \\&\varvec{M}_e (t_e)= \varvec{M}_{e,1} (t=1) t_e + \varvec{M}_{e,3} (t=1) t_e^3 \end{aligned} \end{aligned}$$

(23)

It can be noted that no artificial interpolation (e.g., like SIMP (Bendsøe and Sigmund 1999) or RAMP (Pedersen 2000) in topology optimization) of material properties is employed in this work. Instead, the considered scaling of the stiffness and mass matrices accurately follows the finite element formulation. The scaled element matrices are finally assembled to find the global plate stiffness and mass matrices $\varvec{K}_p$ and $\varvec{M}_p$ used in Eq. (1).

3.2 Formulation of the optimization problem

Three formulations of the thickness optimization problem are proposed in order to improve the vibroacoustic performance of the panel around a given target frequency. The three formulations consider three different objective functions, which are separately maximized while constraining material usage. The first formulation simply focuses on controlling the panel eigenfrequencies, while the second and the third formulations maximize the panel STL respectively at the target frequency and in a surrounding frequency band.

3.2.1 Widest frequency band without eigenfrequencies around the target frequency (F1)

In the first formulation (F1), the goal is to control the in-vacuo eigenfrequencies of the panel. The material thickness distribution is optimized to maximize the width of the frequency band without structural eigenfrequencies around a given target frequency $f_\text{c}$. The aim of this formulation is to keep a low model complexity (only an in-vacuo model of the panel is needed, with no acoustic coupling), while still improving the vibroacoustic performance against tonal noises by indirectly avoiding resonance STL dips around the target frequency.

For (F1), the following objective function and constraints are considered:

$$\begin{aligned}& \max_{\boldsymbol{\gamma},\beta} && \beta \\& \text{subject to}&& \beta \leq d_{f_i} = \frac{\left|f_i - f_\mathrm{c}\right|}{f_\mathrm{c}} \qquad \forall i \\& && t_{\mathrm{avg},p} = \frac{\sum_{e_p} t_{e_p} A_{e_p}}{\sum_{e_p} A_{e_p}} \leq \overline{t} = \frac{t_\mathrm{min}+t_\mathrm{max}}{2} \qquad \forall p\end{aligned}$$

(24)

The formulation in Eq. (24) aims at maximizing the minimum normalized distance $d_{f_i} = \frac{\left|{f_i - f_\text{c}}\right|}{f_\text{c}}$ between the eigenfrequencies $f_i$ and the target frequency $f_\text{c}$. The corresponding max-min problem is treated by introducing an additional design variable $\beta$, which is maximized while imposing that $\beta$ is lower than all the considered normalized distances. A further constraint is imposed to set the maximum material usage, by prescribing that for each plate the average thickness $t_{\text{avg},p}$ computed over the elements of the plate (index $e_p$) should not exceed the mean value between $t_\text{min}$ and $t_\text{max}$. The computation of the eigenfrequencies follows Eq. (2) for single plates, where the simple finite element model of the in-vacuo mechanical plate is considered. For double plates, we instead compute the eigenfrequencies through Eq. (11), when considering the coupled plate-cavity-plate system.

3.2.2 Maximum STL at the target frequency (F2)

In the second formulation (F2), we directly focus on maximizing the STL at the target frequency $f_\text{c}$. In this case, the modeling complexity increases with respect to (F1) (acoustic coupling is now needed), but the computational cost is kept low by solving for the STL only at one single target frequency. The formulated optimization problem is, therefore:

$$\begin{aligned}& \max_{\boldsymbol{\gamma}} & & R(f_\mathrm{c}) \\& \text{subject to}& & t_{\mathrm{avg},p} = \frac{\sum_{e_p} t_{e_p} A_{e_p}}{\sum_{e_p} A_{e_p}} \leq \overline{t} = \frac{t_\mathrm{min}+t_\mathrm{max}}{2} \qquad \forall p\end{aligned}$$

(25)

where the STL computation has been discussed in Sect. 2.2, and the same constraints as (F1) on the maximum material usage have been introduced.

3.2.3 Maximum STL around the target frequency (F3)

In the third formulation (F3), we maximize an averaged measure $R_\text{avg}(f_\text{c})$ of the STL in a frequency band $\Omega _f$ around the target frequency $f_c$. In this case, we aim at achieving a broader frequency band with improved STL, in order to increase the robustness against variations of the tonal noise frequency and modeling approximations. However, the computational cost of (F3) is expected to be higher than (F1) and (F2): in order to compute the average STL, the values of the STL for multiple frequencies need to be computed.

(F3) is formulated as:

$$\begin{aligned}& \max_{\boldsymbol{\gamma}} & & R_\mathrm{avg}(f_\mathrm{c}) = -10 \log \left( \frac{1}{n_f} \sum_{\omega_j \in \Omega_f} 10^{\left( L(\omega_j)-R(\omega_j)\right) / 10} \right)\\& \text{subject to}& & t_{\mathrm{avg},p} = \frac{\sum_{e_p} t_{e_p} A_{e_p}}{\sum_{e_p} A_{e_p}} \leq \overline{t} = \frac{t_\mathrm{min}+t_\mathrm{max}}{2} \quad \forall p\end{aligned}$$

(26)

$R_\text{avg}(f_\text{c})$ is obtained by discretizing the frequency band by $n_f$ frequencies $\omega _j$ and computing the corresponding energetic mean of the STL. In the computation of $R_\text{avg}(f_\text{c})$, spectral adaptation terms $L(\omega _j)$ can be introduced to account for different spectra of noise sources and for the fact that the sensitivity of human hearing is frequency-dependent as, e.g. proposed in ISO 717-1 (2020). Also, in (F3) the same constraints on material usage as in (F1) (Eq. (24)) and (F2) (Eq. (25)) are considered.

In particular, in the following examples, no specific adaptation terms are introduced, i.e. $\forall j: L(\omega _j)$ = 0 dB, and the considered frequency bands are 1/3 octave bands which are discretized by $n_f$=16 points that are equidistant on a logarithmic axis.

3.3 Solution of the problem

The optimization problems formulated in Eqs. (24), (25), (26) are solved through the Method of Moving Asymptotes (MMA) (Svanberg 1987), which is a gradient-based optimizer searching for local optimality. In order to iteratively update the designs until convergence, the sensitivities of objective function and constraints with respect to changes in the design variables are needed. We here compute the sensitivities analytically, using an adjoint method when needed, since a significant number of design variables is considered.

The expressions of the sensitivities of objective functions and constraints can be derived analytically once the sensitivities of eigenfrequencies and coupling loss factor are known. The sensitivities of the eigenfrequencies, needed to compute the sensitivities of the constraints in (F1) (Eq. (24)), can be found in Bendsøe and Sigmund (2004) and are briefly recalled in Appendix A. The sensitivities of the coupling loss factor, needed to compute the sensitivities of the objective functions in (F2) (Eq. (25)) and (F3) (Eq. (26)), are also derived in Appendix A.

The local optimum found by MMA generally depends on the choice of the initial guess. Numerical experiments have therefore been performed in order to identify guidelines for this choice. It has been found that satisfying solutions are obtained by choosing a uniform initial guess with a somewhat higher thickness than the maximum average one $\overline{t} = \frac{t_\text{min}+t_\text{max}}{2}$ set by the constraint on material usage (cf. Eqs. (24), (25), (26)). Therefore, uniform initial guesses with thickness equal to $t_\text{min} + 0.7 (t_\text{max} - t_\text{min})$ are used in the following examples. For the presented design examples we have used the following MMA parameters: $a_0$ = 1, $a_\text{i}$ = 0, $c_\text{i}$ = 1000, $d_\text{i}$ = 0, whose nomenclature and explanation are provided in Svanberg (2002). The optimization parameters have been chosen based on exhaustive numerical experiments. The optimization is run for 500 steps, after which the convergence of the objective function is also assessed visually.

The thickness optimization algorithm, along with the needed FEM and Det-SEA solvers, is implemented in MATLAB: eigenvalue problems are solved by ARPACK (as ”eigs”), applying an implicitly restarted Lanczos method (IRLM), whereas matrix inversions are considered by applying LU decomposition (as ”$\backslash$”). At each optimization step, the amount of computed modes $n_p$ (p = 1,2) and $n_\text{cav}$, for the plates and the cavity respectively, is such that we retain all the modes with a natural frequency that is lower than twice the frequency of the analysis.

4 Optimization results and discussion

Table 1 Material and geometrical properties of the considered single PMMA panels and double glazing panels

4.1 Single panel

As a first case, we consider the design of a single polymethyl methacrylate (PMMA) panel. Table 1 lists the material properties (mass density $\rho$, Young modulus E, Poisson ration $\nu$, damping loss factor $\eta$), along with the panel dimensions and the range of variation for thickness $[t_\text{min},t_\text{max}]$. The considered 1 m $\times$ 1 m panel is discretized by 50 $\times$ 50 linear Mindlin plate finite elements, and the filter radius $r_\text{min}$ is set to twice the dimension of one single element. We also note that, due to the varying thickness, the designed panel will be translucent but not fully transparent.

Fig. 3

Sound STL of a uniform single PMMA panel with constant thickness equal to $\overline{t}$ = 37.5 mm. At the critical frequency $f_\text{crit}$, the wavelength $\lambda _\text{air}$ of the incident sound waves in air coincides with the wavelength $\lambda _\text{B}$ of free bending waves in the panel, and a band with reduced STL appears

The single panel is optimized following the three problem formulations outlined in Sect. 3.2. Two different target frequencies are considered, i.e. $f_\text{c}$ = 500 Hz as an example of a mid-frequency tonal noise (coming, e.g. from compressor machines (Ku et al. 2019)), and $f_\text{c} = f_\text{crit}$ as the critical frequency of the uniform panel having a thickness equal to $\overline{t} = \frac{t_\text{min}+t_\text{max}}{2}$ = 37.5 mm. The critical frequency is defined as the frequency at which the speed and the wavelength of the incident sound waves coincide with the speed and the wavelength of free bending waves in the panel (Rindel 2018), creating a resonance phenomenon:

$$\begin{aligned} f_\text{crit} = \frac{c_\text{a}^2}{2\pi }\sqrt{\frac{\rho \overline{t}}{\overline{D}}}, \end{aligned}$$

(27)

where $\overline{D} = \frac{E \overline{t}^3}{12(1-\nu ^2)}$ is the bending stiffness of the uniform panel. High radiation efficiency and sound transmission are observed around the critical frequency: as shown in Fig. 3, the STL reduces around $f_\text{crit}$ = 862 Hz, while at higher frequencies it follows the stiffness-controlled trend with an average increase of 18 dB/octave (Fahy and Gardonio 2007).

Fig. 4

Optimized single panel layouts

The optimized layouts for the chosen target frequencies are shown in Fig. 4. It can be observed that, as the target frequency increases, finer details in the optimized design are needed to control higher order modes. This follows the reducing bending wavelength, which is known to impose a required finite length-scale to the design (Sigmund and Jensen 2003). The resolution of the optimization process, i.e. the minimum admissible size of the design features, is strictly related to the filter radius (Wang et al. 2011). Therefore, a filter radius that is too big can inhibit well-performing designs with fine enough features. In our designs, the chosen filter radius is significantly smaller than the minimum bending wavelength in the panel $\lambda _\text{min}(t_\text{min})=2\pi \left( \frac{E t_\text{min}^2}{12 \rho \omega ^2 (1-\nu ^2)} \right) ^{1/4}$, in order to allow for the creation of both sub-wavelength and supra-wavelength features in the control of the modes of interest.

Table 2 Comparison between the different optimized single panel layouts in terms of obtained objective functions

The convergence histories of the objective functions for the different design cases are plotted in Fig. 5. The algorithm is run for 500 iteration, however we can see that convergence is generally achieved in around 100 iterations. The details of the convergence history for the layout optimized with formulation (F2) for $f_\text{c}$ = 500 Hz is shown in Fig. 6. The performances of the optimized layouts in terms of final objective functions $\min _i d_{f_i}$, $R(f_\text{c})$, $R_\text{avg}(f_\text{c})$ are listed in Table 2, while the corresponding STL curves are shown in Fig. 7. A comparison with the uniform panel having constant thickness equal to $\overline{t}$ is also provided, in order to assess the vibroacoustic advantages introduced by optimizing panels with non-uniform thickness distribution.

Fig. 5

Convergence history of the single panel optimization for (a) $f_\text{c}$ = 500 Hz (b) $f_\text{c}$ = $f_\text{crit}$ = 862 Hz

Fig. 6

Convergence history of the single panel layout: optimization with (F2) for $f_\text{c}$ = 500 Hz

Fig. 7

STL of the single panel optimized for (a) $f_\text{c}$ = 500 Hz and (b) $f_\text{c}$ = $f_\text{crit}$ = 862 Hz

In general, for the same total amount of used material and mass, a non-uniform thickness distribution leads to superior sound insulation properties around the target frequency. We see that for this design case all the three employed formulations boil down to a similar design strategy, as the algorithm creates bands without structural eigenfrequencies around the target frequency, allowing for higher STL by pushing away the STL dips related to mechanical resonances. For this reason, similar insulation performances in terms of $R(f_\text{c})$ and $R_\text{avg}(f_\text{c})$ are obtained when using the different problem formulations, and the optimization always leads to layouts without eigenfrequencies in a band wider than a 1/3-octave band, for both $f_\text{c}$ = 500 Hz and $f_\text{c}$ = $f_\text{crit}$. However, we still see how the maximum distance of the closest eigenfrequency is achieved when using formulation (F1). $R(f_\text{c})$ and $R_\text{avg}(f_\text{c})$ are instead maximum when using (F2) and (F3). Around $f_\text{c}$ = 500 Hz, the uniform panel presents already a STL peak and a band without structural resonances, but optimizing non-uniform thickness distributions leads to increases in $R(f_\text{c})$ and $R_\text{avg}(f_\text{c})$ by about 4 dB and about 5 dB respectively. When considering $f_\text{c}$ = $f_\text{crit}$, the uniform panel presents a coincidence STL dip, and the optimization leads to higher increases in $R(f_\text{c})$ and $R_\text{avg}(f_\text{c})$ by about 10 dB. For both $f_\text{c}$ = 500 Hz and $f_\text{c}$ = $f_\text{crit}$, we can see that the improvements in sound insulation are mainly localized in the targeted frequency band: a relatively pronounced STL dip is obtained at immediately higher frequencies, and for further increase in frequency the behaviour of non-uniform panels becomes again similar to the one of the uniform layout.

Table 3 Single panel optimization: average computational time per iteration for the different formulations of the optimization problem

The computational costs associated with the different problem formulations are reported in Table 3, in terms of the average computational time of one single optimization iteration, when using a Intel(R) Core(TM) i7-9850 H CPU (2.60GHz). We can see how (F3) is associated to the highest computational cost, which is about 5 to 6 times the one of (F2) and about 2 to 3 times the one of (F1). However, as discussed above, for this design case the highest computational cost of (F3) does not lead to a significant improvement in the vibroacoustic performances of the panel.

4.2 Double panel

The second considered case is related to the design of translucent double glazings with non-uniform material distribution. The material properties, panel dimensions and thickness ranges are again shown in Table 1. Since in this case the maximum thickness is low with respect to the in-plane dimensions of the panels (1.25 m $\times$ 1.5 m), a mesh of 50 $\times$ 60 linear Kirchhoff plate finite elements is used. The filter radius $r_\text{min}$ is again set as twice the dimension of one element.

In this case, the baseline uniform double panel (denoted as a 4-12-6 glazing) consists of plates with constant thickness equal to 4 mm and 6 mm, and separated by a 12 mm cavity. The target frequencies for the optimization are $f_\text{c}$ = 500 Hz and $f_\text{c}$ = $f_\text{msm}$, where $f_\text{msm}$ is the mass–spring–mass resonance frequency of the equivalent infinite-sized double panel. This frequency is characterized by a surrounding band with low STL, with both plates vibrating quasi-rigidly in anti-phase and the air cavity being compressed as a spring. For uniform panels with constant thicknesses $t_1$ and $t_2$, the mass–spring–mass resonance frequency can be estimated as (Rindel 2018):

$$\begin{aligned} f_\text{msm} = \frac{c_a}{2\pi }\sqrt{\frac{\rho _\text{a}}{L_z}\left( \frac{1}{\rho t_1}+\frac{1}{\rho t_2}\right) } \end{aligned}$$

(28)

Fig. 8

Sound STL of a uniform 4-12-6 double glazing. At the mass–spring–mass resonance frequency $f_\text{msm}$, the two plates vibrate quasi-rigidly in anti-phase and the air cavity is compressed as a spring

Similarly to the critical frequency of single panels discussed in Sect. 4.1, around the mass–spring–mass resonance frequency of double panels a reduction in STL is observed. Figure 8 shows the STL of the uniform finite-sized 4-12-6 glazing, and highlights the mass–spring–mass resonance frequency, around which a band with reduced STL appears. The objective of the design is to obtain a non-uniform double panel with superior vibroacoustic behavior around $f_\text{c}$ = 500 Hz and $f_\text{c}$ = $f_\text{msm}$ = 223 Hz, when keeping the same maximum plate masses as the uniform 4-12-6 glazing panel.

Fig. 9

Optimized double panel layouts

Fig. 10

Convergence history of the double panel optimization for (a) $f_\text{c}$ = $f_\text{msm}$ = 223 Hz (b) $f_\text{c}$ = 500 Hz

Table 4 Comparison between the different optimized double panel layouts in terms of obtained objective functions

The optimized double panel layouts when using the three formulations of the problem are shown in Fig. 9, while the associated convergence histories of the objective functions are shown in Fig. 10. Similarly to the single panel optimization, we see that layouts with finer details are optimized when targeting higher frequencies, in order to control the behaviour of higher order modes.

Fig. 11

TL of the double panel optimized for (a) $f_\text{c}$ = $f_\text{msm}$ = 223 Hz (b) $f_\text{c}$ = 500 Hz

Table 5 Double panel optimization: average computational time per iteration for the different formulations of the optimization problem

The final values of the objective functions corresponding to the optimized double panel layouts are shown in Table 4, while the corresponding STL curves compared with the uniform 4-12-6 glazing are shown in Fig. 11. The computational costs associated to each problem formulation are reported in Table 5. For both $f_\text{c}$ = $f_\text{msm}$ and $f_\text{c}$ = 500 Hz, we can see how maximizing the width of the frequency band without eigenfrequencies (formulation (F1)) has the lowest computational cost and successfully suppresses resonance dips around the target frequency, but does not lead to an adequate increase of the STL. Despite the creation of a STL peak, pronounced resonance dips remain still close to $f_\text{c}$, leading to insulation performances in terms of $R(f_\text{c})$ and $R_\text{avg}(f_\text{c})$ that can be still lower than the uniform double glazing. A direct maximization of the STL at the target frequency (formulation (F2)) comes with a slight increase of the computational cost and allows to achieve a clear and pronounced peak in the STL, with increases in $R(f_\text{c})$ with respect to the uniform panel of about 12 dB and about 7 dB for $f_\text{c}$ = $f_\text{msm}$ and $f_\text{c}$ = 500 Hz respectively. However, the presence of close and pronounced STL dips still limits broader band insulation improvements in terms of $R_\text{avg}(f_\text{c})$. When directly maximizing broader band insulation (formulation (F3)), the important increase in computational costs is paid off by the significant improvements achieved in broadband sound insulation. In the targeted band the STL curve shows in fact a plateau at increased values, and the overlapped modal behaviour has no pronounced STL dips: this is probably due to the low degree of coupling between the two plates in the corresponding mode shapes of the double panel. The final increase in $R_\text{avg}(f_\text{c})$ obtained with formulation (F3) are of about 8 dB for $f_\text{c}$ = $f_\text{msm}$, with an effective suppression of the low STL region due to mass–spring–mass resonance effects, and of about 4 dB for $f_\text{c}$ = 500 Hz.

5 Conclusions

In this paper, an approach has been proposed to optimize the material thickness distribution in partition panels, with the aim of maximizing sound insulation around a given target frequency while constraining material usage. First, a framework has been developed to couple structural optimization with deterministic-statistical energy analysis modeling, which provides accurate diffuse sound transmission loss (STL) predictions and reduces the computational costs with respect to fully deterministic models. The framework can handle both the simpler design of single panels, including a single mechanical plate, and the more complex design of double panels, in which two mechanical plates are separated by an air cavity. The sensitivity analysis for both cases has been also presented.

Subsequently, three formulations of the optimization problem have been developed and compared, i.e. (F1) pushing the panel eigenfrequencies away from the target frequency, (F2) maximizing the STL at the target frequency, and (F3) maximizing the STL in a frequency band around the target frequency. The practical advantages offered by the proposed approach have been demonstrated by considering different target frequencies in the audible range and for relevant showcases. In particular, sound insulation improvements have been targeted at 500 Hz and in correspondence with the STL dips present at the critical frequency of the single panel and at the mass–spring–mass resonance frequency of the double panel.

In the design of single panels, the layouts optimized with the three formulations have shown similar STL improvements, outperforming corresponding uniform panels with equal mass by about 4 to 10 dB around the target frequency. In this case, the different formulations of the problem boil down to a similar design strategy, in which the STL dips associated with structural resonances are pushed far away from the target frequency. However, in the design of double panels, results have shown how simply suppressing the resonance dips as for (F1) is not enough to adequately improve the sound insulation properties, due to the high modal density of the panel. A direct maximization of the STL through (F2) or (F3) is instead needed, with a possible increase of computational costs and modeling complexity. In these cases, the STL of a uniform panel with the same mass has been outperformed by about 4 to 12 dB at the target frequency, and to effectively suppress the STL dip due to the mass–spring–mass resonance.

Appendix A: Sensitivity analysis of panel eigenfrequencies and coupling loss factor

In this Appendix, the expression of the sensitivities of the panel eigenfrequencies and of the coupling loss factor with respect to changes in the design variables are presented. Also, some details regarding the computation of the needed sensitivities of the system matrices are discussed.

1.1 A.1: Sensitivity analysis of the panel eigenfrequencies

In single panels, the sensitivities of the squared eigenfrequencies can be found as:

$$\begin{aligned} \frac{\partial \omega _{p,k}^2}{\partial \tilde{\gamma }_e} = \varvec{\phi }_{p,k}^T \left( \frac{\partial \varvec{K}_{p}}{\partial \tilde{\gamma }_e}-\omega _{p,k}^2 \frac{\partial \varvec{K}_{p}}{\partial \tilde{\gamma }_e} \right) \varvec{\phi }_{p,k} \end{aligned}$$

(A1)

while for double panels:

$$\begin{aligned} \frac{\partial \omega ^2_{\text{d},k}}{\partial \tilde{\gamma }_e} = \varvec{\phi }_{\text{d},k,\text{L}}^\text{T} \left( \frac{\partial \varvec{K}_\text{d}}{\partial \tilde{\gamma }_e} - \omega ^2_k \frac{\partial \varvec{M}_\text{d}}{\partial \tilde{\gamma }_e}\right) \varvec{\phi }_{\text{d},k,\text{R}} \end{aligned}$$

(A2)

The (filtered) design variables $\tilde{\gamma }_e$ directly influence only the stiffness and mass matrices of the mechanical plates $\varvec{K}_p$ and $\varvec{M}_p$, while the sensitivities of stiffness and mass matrices of the double panel $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$ can be computed from the sensitivities of $\varvec{K}_p$ and $\varvec{M}_p$, as discussed in Appendix A.3. Similarly to what was done in Giannini et al. (2021a), the multiplicity of the eigenfrequencies has not been considered in the sensitivity analysis. Despite the fact that this choice may disturb the convergence for formulation (F1), the employed optimization algorithm has demonstrated to be robust enough to obtain adequate designs.

1.2 A.2: Adjoint sensitivity analysis of the coupling loss factor

The sensitivities of the coupling loss factor $\eta _{12}$ with respect to a design variable $\tilde{\gamma }_e$ can be written as:

$$\begin{aligned} & \frac{\partial \eta _{12}}{\partial \tilde{\gamma }_e} = \frac{2}{\pi \omega n_1} \frac{\partial \phi }{\partial \tilde{\gamma }_e} \\ &\text {with: } \quad \phi = \sum _{rs} \text{Im}(\varvec{D}'_{\text{dir},2})_{rs}(\varvec{D}_\text{tot}^{-1}\text{Im}(\varvec{D}'_{\text{dir},1})\varvec{D}_\text{tot}^{-\text{H}})_{rs} \end{aligned}$$

(A3)

By considering the following property of the element-wise product:

$$\begin{aligned} \sum _{rs} \varvec{A}_{rs}(\varvec{B}\varvec{C})_{rs} = \sum _{rs} (\varvec{A}\varvec{C}^\text{T})_{rs}\varvec{B}_{rs} \end{aligned}$$

(A4)

the term $\phi$ can be rewritten as:

$$\begin{aligned} \begin{aligned} \phi&= \sum _{rs} \text{Im}(\varvec{D}'_{\text{dir},2})_{rs}(\varvec{D}_\text{tot}^{-1}\text{Im}(\varvec{D}'_{\text{dir},1})\varvec{D}_\text{tot}^{-\text{H}})_{rs} \\&= \sum _{rs} (\text{Im}(\varvec{D}'_{\text{dir},2}){{\,\text{conj}\,}}(\varvec{D}_\text{tot}^{-1}))_{rs}(\varvec{D}_\text{tot}^{-1}\text{Im}(\varvec{D}'_{\text{dir},1}))_{rs} \\&= \sum _{rs} \varvec{X}^\text{T}_{rs}\varvec{Y}_{rs} = \sum _{rs} \varvec{x}_r^\text{T} \varvec{E}_{sr} \varvec{y}_s \end{aligned} \end{aligned}$$

(A5)

where $\varvec{E}_{sr}$ is a matrix with unitary element in position (s, r) and zeros elsewhere, while $\varvec{x}_r$ and $\varvec{y}_s$ are respectively the rth column of matrix $\varvec{X}$ and the sth column of matrix $\varvec{Y}$. The matrices $\varvec{X}$ and $\varvec{Y}$ are defined such that:

$$\begin{aligned} \varvec{D}_\text{tot}^\text{H} \varvec{X} = \text{Im}(\varvec{D}_{\text{dir},2}^{\prime \text{T}}), \qquad \varvec{D}_\text{tot} \varvec{Y} = \text{Im}(\varvec{D}'_{\text{dir},1}) \end{aligned}$$

(A6)

By separating the contributions of the real and the imaginary parts of $\varvec{X}$ and $\varvec{Y}$, the term $\phi$ can be rewritten as:

$$\begin{aligned} \phi&= \sum _{rs} (\text{Re}(\varvec{x}_r)+\text {i}\text{Im}(\varvec{x}_r))^\text{T} \varvec{E}_{sr} (\text{Re}(\varvec{y}_s)+\text {i}\text{Im}(\varvec{y}_s)) \\ & = \sum _{rs} \left( \text{Re}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Re}(\varvec{y}_s) - \text{Im}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Im}(\varvec{y}_s) \right) \\ & \quad + \text{i} \left( \text{Re}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Im}(\varvec{y}_s) + \text{Im}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Re}(\varvec{y}_s) \right) \\&= \sum _{rs} \left( \text{Re}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Re}(\varvec{y}_s) - \text{Im}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}\text{Im}(\varvec{y}_s) \right) \end{aligned}$$

(A7)

where we have considered that $\phi$ is real-valued and therefore its imaginary part is null.

By introducing the real and the imaginary parts of $\varvec{D}_\text{tot}$ and $\varvec{D}_\text{tot}^\text{H}$, the first equality in Eq. (A6) can be rewritten as:

$$\begin{aligned} \begin{aligned}&\left( \text{Re}(\varvec{D}_\text{tot}^\text{H})+ \text{i} \text{Im}(\varvec{D}_\text{tot}^\text{H}) \right) \left( \text{Re}(\varvec{X})+ \text{i} \text{Im}(\varvec{X}) \right) = \text{Im}(\varvec{D}_{\text{dir},2}^{\prime \text{T}}) + \varvec{0}\text{i} \\&\Rightarrow \left( \text{Re}(\varvec{D}_\text{tot}^\text{H})\text{Re}(\varvec{X}) - \text{Im}(\varvec{D}_\text{tot}^\text{H})\text{Im}(\varvec{X})\right) \\& \quad + \text{i} \left( \text{Re}(\varvec{D}_\text{tot}^\text{H})\text{Im}(\varvec{X}) + \text{Im}(\varvec{D}_\text{tot}^\text{H})\text{Re}(\varvec{X})\right) = \text{Im}(\varvec{D}_{\text{dir},2}^{\prime \text{T}}) + \varvec{0}\text{i}\\&\Rightarrow \forall r: \left( \text{Re}(\varvec{D}_\text{tot}^\text{H}) \text{Re}(\varvec{x}_r) - \text{Im}(\varvec{D}_\text{tot}^\text{H}) \text{Im}(\varvec{x}_r)\right) \\& \quad+ \text{i} \left( \text{Re}(\varvec{D}_\text{tot}^\text{H}) \text{Im}(\varvec{x}_r) + \text{Im}(\varvec{D}_\text{tot}^\text{H}) \text{Re}(\varvec{x}_r)\right) = \text{Im}(\varvec{d}_{2,r}) + \varvec{0}\text{i}\\ \end{aligned} \end{aligned}$$

(A8)

The second equality in Eq. (A6) can be rewritten as:

$$\begin{aligned} \begin{aligned}&\left( \text{Re}(\varvec{D}_\text{tot})+ \text{i} \text{Im}(\varvec{D}_\text{tot}) \right) \left( \text{Re}(\varvec{Y})+ \text{i} \text{Im}(\varvec{Y}) \right) = \text{Im}(\varvec{D}'_{\text{dir},1}) + \varvec{0} \text{i}\\&\Rightarrow \left( \text{Re}(\varvec{D}_\text{tot})\text{Re}(\varvec{Y}) - \text{Im}(\varvec{D}_\text{tot})\text{Im}(\varvec{Y})\right) + \\& \quad+ \text{i} \left( \text{Re}(\varvec{D}_\text{tot})\text{Im}(\varvec{Y}) + \text{Im}(\varvec{D}_\text{tot})\text{Re}(\varvec{Y})\right) = \text{Im}(\varvec{D}'_{\text{dir},1}) + \varvec{0}\text{i}\\&\Rightarrow \forall s:\left( \text{Re}(\varvec{D}_\text{tot}) \text{Re}(\varvec{y}_s) - \text{Im}(\varvec{D}_\text{tot}) \text{Im}(\varvec{y}_s)\right) \\& \quad+ \text{i} \left( \text{Re}(\varvec{D}_\text{tot}) \text{Im}(\varvec{y}_s) + \text{Im}(\varvec{D}_\text{tot}) \text{Re}(\varvec{y}_s)\right) = \text{Im}(\varvec{d}_{1,s}) + \varvec{0} \text{i}\\ \end{aligned} \end{aligned}$$

(A9)

where $\text{Im}(\varvec{d}_{2,r})$ and $\text{Im}(\varvec{d}_{1,s})$ are the imaginary parts respectively of the rth column of $\varvec{D}_{\text{dir},2}^{\prime \text{T}}$ and of the sth column of $\varvec{D}'_{\text{dir},1}$.

In order to find the sensitivities of $\phi$, we first define the augmented functional $\tilde{\phi }$, by adding Eqs. (A8) and (A9) to $\phi$ through the Lagrange multipliers $\varvec{\lambda }_{\text{R},r}$, $\varvec{\lambda }_{\text{I},r}$, $\varvec{\mu }_{\text{R},s}$ and $\varvec{\mu }_{\text{I},s}$:

$$\begin{aligned} \begin{aligned} \tilde{\phi } = \phi&+ \sum _r \left[ \varvec{\lambda }_{\text{R},r}^\text{T} \left( \text{Re}(\varvec{D}_\text{tot}^\text{H}) \text{Re}(\varvec{x}_r) - \text{Im}(\varvec{D}_\text{tot}^\text{H}) \text{Im}(\varvec{x}_r) - \text{Im}(\varvec{d}_{2,r}) \right) \right. \\&\left. - \varvec{\lambda }_{\text{I},r}^\text{T} \left( \text{Re}(\varvec{D}_\text{tot}^\text{H}) \text{Im}(\varvec{x}_r) + \text{Im}(\varvec{D}_\text{tot}^\text{H}) \text{Re}(\varvec{x}_r)\right) \right] \\&+ \sum _s \left[ \varvec{\mu }_{\text{R},s}^\text{T} \left( \text{Re}(\varvec{D}_\text{tot}) \text{Re}(\varvec{y}_s) - \text{Im}(\varvec{D}_\text{tot}) \text{Im}(\varvec{y}_s) - \text{Im}(\varvec{d}_{1,s}) \right) \right. \\&\left. - \varvec{\mu }_{\text{I},s}^\text{T} \left( \text{Re}(\varvec{D}_\text{tot}) \text{Im}(\varvec{y}_s) + \text{Im}(\varvec{D}_\text{tot}) \text{Re}(\varvec{y}_s)\right) \right] \end{aligned} \end{aligned}$$

(A10)

The sensitivities with respect to a design variable $\tilde{\gamma }_e$ can be computed by differentiating the previous equation:

$$\begin{aligned} \begin{aligned} \frac{\partial \tilde{\phi }}{\partial \tilde{\gamma }_e} =&\sum _r \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} \frac{\partial \text{Re}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} + \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} \frac{\partial \text{Im}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} \right) \\ +&\sum _s \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} \frac{\partial \text{Re}(\varvec{y}_s)}{\partial \tilde{\gamma }_e} + \frac{\partial \phi }{\partial \text{Im}(\varvec{y}_s)} \frac{\partial \text{Im}(\varvec{y}_s)}{\partial \tilde{\gamma }_e} \right) \\ +&\sum _r \left( \varvec{\lambda }_{\text{R},r}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{x}_r) + \text{Re}(\varvec{D}_\text{tot}^\text{H}) \frac{\partial \text{Re}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} \right. \right. \\&\left. \left. - \frac{\partial \text{Im}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{x}_r) - \text{Im}(\varvec{D}_\text{tot}^\text{H}) \frac{\partial \text{Im}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} \right) \right) \\ -&\sum _r \left( \varvec{\lambda }_{\text{I},r}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{x}_r) + \text{Re}(\varvec{D}_\text{tot}^\text{H}) \frac{\partial \text{Im}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} \right. \right. \\&\left. \left. + \frac{\partial \text{Im}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{x}_r) + \text{Im}(\varvec{D}_\text{tot}^\text{H}) \frac{\partial \text{Re}(\varvec{x}_r)}{\partial \tilde{\gamma }_e} \right) \right) \\ +&\sum _s \left( \varvec{\mu }_{\text{R},s}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{y}_s) + \text{Re}(\varvec{D}_\text{tot}) \frac{\partial \text{Re}(\varvec{y}_s)}{\partial \tilde{\gamma }_e} \right. \right. \\&\left. \left. - \frac{\partial \text{Im}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{y}_s) - \text{Im}(\varvec{D}_\text{tot}) \frac{\partial \text{Im}(\varvec{y}_s)}{\partial \tilde{\gamma }_e} \right) \right) \\ -&\sum _s \left( \varvec{\mu }_{\text{I},s}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{y}_s) + \text{Re}(\varvec{D}_\text{tot}) \frac{\partial \text{Im}(\varvec{y}_s)}{\partial \tilde{\gamma }_e} \right. \right. \\&\left. \left. + \frac{\partial \text{Im}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{y}_s) + \text{Im}(\varvec{D}_\text{tot}) \frac{\partial \text{Re}(\varvec{y}_s)}{\partial \tilde{\gamma }_e}\right) \right) \end{aligned} \end{aligned}$$

(A11)

with:

$$\begin{aligned} \begin{aligned}&\frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} = \sum _s \text{Re}(\varvec{y}_s)^\text{T} \varvec{E}_{sr}^\text{T}, \quad \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} = - \sum _s \text{Im}(\varvec{y}_s)^\text{T} \varvec{E}_{sr}^\text{T} \\&\frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} = \sum _r \text{Re}(\varvec{x}_r)^\text{T} \varvec{E}_{sr}, \quad \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} = - \sum _r \text{Im}(\varvec{x}_r)^\text{T} \varvec{E}_{sr} \end{aligned} \end{aligned}$$

(A12)

In order to eliminate the terms in $\frac{\partial \text{Re}(\varvec{x}_r)}{\partial \tilde{\gamma }_e}$, $\frac{\partial \text{Im}(\varvec{x}_r)}{\partial \tilde{\gamma }_e}$, $\frac{\partial \text{Re}(\varvec{y}_s)}{\partial \tilde{\gamma }_e}$ and $\frac{\partial \text{Im}(\varvec{y}_s)}{\partial \tilde{\gamma }_e}$ from Eq. (A11), we impose:

$$\begin{aligned} \begin{aligned}&\forall r: \varvec{\lambda }_{\text{R},r}^\text{T} \text{Re}(\varvec{D}_\text{tot}^\text{H}) - \varvec{\lambda }_{\text{I},r}^\text{T} \text{Im}(\varvec{D}_\text{tot}^\text{H}) = - \frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} \\& \qquad \varvec{\lambda }_{\text{R},r}^\text{T} \text{Im}(\varvec{D}_\text{tot}^\text{H}) + \varvec{\lambda }_{\text{I},r}^\text{T} \text{Re}(\varvec{D}_\text{tot}^\text{H}) = \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} \\&\forall s: \varvec{\mu }_{\text{R},s}^\text{T} \text{Re}(\varvec{D}_\text{tot}) - \varvec{\mu }_{\text{I},s}^\text{T} \text{Im}(\varvec{D}_\text{tot}) = - \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} \\& \qquad \varvec{\mu }_{\text{R},s}^\text{T} \text{Im}(\varvec{D}_\text{tot}) + \varvec{\mu }_{\text{I},s}^\text{T} \text{Re}(\varvec{D}_\text{tot}) = \frac{\partial \phi }{\partial \text{Im}(\varvec{y}_s)} \end{aligned} \end{aligned}$$

(A13)

Multiplying the second and the fourth equations by the imaginary unit $\text{i}$, and summing them to the first and the third ones respectively, we get:

$$\begin{aligned} \begin{aligned}&\forall r: \varvec{\lambda }_{\text{R},r}^\text{T} \text{Re}(\varvec{D}_\text{tot}^\text{H}) - \varvec{\lambda }_{\text{I},r}^\text{T} \text{Im}(\varvec{D}_\text{tot}^\text{H}) + \text{i} \varvec{\lambda }_{\text{R},r}^\text{T} \text{Im}(\varvec{D}_\text{tot}^\text{H}) + \text{i} \varvec{\lambda }_{\text{I},r}^\text{T} \text{Re}(\varvec{D}_\text{tot}^\text{H}) \\& \qquad= - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} \right) \\&\Rightarrow \left( \varvec{\lambda }_{\text{R},r} + i \varvec{\lambda }_{\text{I},r}\right) ^\text{T}\left( \text{Re}(\varvec{D}_\text{tot}^\text{H}) + \text{i} \text{Im}(\varvec{D}_\text{tot}^\text{H})\right) \\& \qquad= - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} \right) \\&\forall s: \varvec{\mu }_{\text{R},s}^\text{T} \text{Re}(\varvec{D}_\text{tot}) - \varvec{\mu }_{\text{I},s}^\text{T} \text{Im}(\varvec{D}_\text{tot}) + \text{i} \varvec{\mu }_{\text{R},s}^\text{T} \text{Im}(\varvec{D}_\text{tot}) + \text{i} \varvec{\mu }_{\text{I},s}^\text{T} \text{Re}(\varvec{D}_\text{tot}) \\& \qquad = - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{y}_s)} \right) \\&\Rightarrow \left( \varvec{\mu }_{\text{R},s} + \text{i} \varvec{\mu }_{\text{I},s}\right) ^\text{T} \left( \text{Re}(\varvec{D}_\text{tot})+\text{i}\text{Im}(\varvec{D}_\text{tot})\right) \\& \qquad = - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{y}_s)} \right) \end{aligned} \end{aligned}$$

(A14)

From Eq. (A14) we can derive the adjoint problems that allow to computing the multipliers $\varvec{\lambda }_r = \varvec{\lambda }_{\text{R},r} + \text{i} \varvec{\lambda }_{\text{I},r}$ and $\varvec{\mu }_s = \varvec{\mu }_{\text{R},s} + \text{i} \varvec{\mu }_{\text{I},s}$:

$$\begin{aligned} \begin{aligned}&\forall r: \quad {{\,\text{conj}\,}}(\varvec{D}_\text{tot})\varvec{\lambda }_r = - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{x}_r)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{x}_r)} \right) ^\text{T} \\&\forall s: \quad\varvec{D}_\text{tot}^\text{T} \varvec{\mu }_s = - \left( \frac{\partial \phi }{\partial \text{Re}(\varvec{y}_s)} - \text{i} \frac{\partial \phi }{\partial \text{Im}(\varvec{y}_s)} \right) ^\text{T} \\ \end{aligned} \end{aligned}$$

(A15)

The expression of the sensitivities of $\phi$ therefore becomes:

$$\begin{aligned} \begin{aligned} \frac{\partial \tilde{\phi }}{\partial \tilde{\gamma }_e} =&\sum _r \left( \varvec{\lambda }_{\text{R},r}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{x}_r) - \frac{\partial \text{Im}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{x}_r) \right) \right) \\ -&\sum _r \left( \varvec{\lambda }_{\text{I},r}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{x}_r) + \frac{\partial \text{Im}(\varvec{D}_\text{tot}^\text{H})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{x}_r) \right) \right) \\ +&\sum _s \left( \varvec{\mu }_{\text{R},s}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{y}_s) - \frac{\partial \text{Im}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{y}_s) \right) \right) \\ -&\sum _s \left( \varvec{\mu }_{\text{I},s}^\text{T} \left( \frac{\partial \text{Re}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Im}(\varvec{y}_s) + \frac{\partial \text{Im}(\varvec{D}_\text{tot})}{\partial \tilde{\gamma }_e} \text{Re}(\varvec{y}_s) \right) \right) \\ =&\sum _r \text{Re}\left( \varvec{\lambda }_r^\text{T} \frac{\partial \varvec{D}_\text{tot}^\text{H}}{\partial \tilde{\gamma }_e} \varvec{x}_{r}\right) + \sum _s \text{Re}\left( \varvec{\mu }_{s}^\text{T} \frac{\partial \varvec{D}_\text{tot}}{\partial \tilde{\gamma }_e} \varvec{y}_{s}\right) \end{aligned} \end{aligned}$$

(A16)

In Eq. (A16), the sensitivities of the total dynamic stiffness matrix $\varvec{D}_\text{tot}$ can be computed from the sensitivities of the stiffness and mass matrices $\varvec{K}_p$ and $\varvec{M}_p$ of the mechanical plates, as discussed in Appendix A.3.

1.3 A.3: Sensitivities of the system matrices

The sensitivities of the panel eigenfrequencies in Eqs. (A1) and (A2) and of the coupling loss factor in Eq. (A16) involve the sensitivities of the system matrices. The design variables directly influence the stiffness and mass matrices of the mechanical plates $\varvec{K}_p$ and $\varvec{M}_p$, while the sensitivities of $\varvec{D}_\text{tot}$, $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$ can be computed from the sensitivities of $\varvec{K}_p$ and $\varvec{M}_p$.

For single panels, $\varvec{D}_\text{tot}$ can be expressed as:

$$\begin{aligned} \begin{aligned} \boldsymbol{D}_\mathrm{tot} & = \boldsymbol{\Phi}_{1}^T \left(\boldsymbol{D}_{1} + \boldsymbol{D}_{\mathrm{dir},1,1} + \boldsymbol{D}_{\mathrm{dir},2,1} \right) \boldsymbol{\Phi}_{1} \end{aligned} \end{aligned}$$

(A17)

while, for double panels, $\varvec{D}_\text{tot}$ can be expressed as:

$$\begin{aligned} \begin{aligned} \boldsymbol{D}_\mathrm{tot} &= \boldsymbol{\Phi}^T \left( \begin{bmatrix} \boldsymbol{D}_{1} &\boldsymbol{0} &\boldsymbol{L}_{\mathrm{f},1} \\ \boldsymbol{0} & \boldsymbol{D}_{2} &\boldsymbol{L}_{\mathrm{f},2} \\ \boldsymbol{L}_{\mathrm{s},1} &\boldsymbol{L}_{\mathrm{s},2} &\boldsymbol{D}_\mathrm{cav} \end{bmatrix} \right.\\ & + \left. \begin{bmatrix} \boldsymbol{D}_{\mathrm{dir},1,1} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \end{bmatrix} + \begin{bmatrix} \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{D}_{\mathrm{dir},2,2} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \end{bmatrix} \right) \boldsymbol{\Phi} \end{aligned} \end{aligned}$$

(A18)

with $\varvec{\Phi } = {{\,\text{diag}\,}}(\varvec{\Phi }_1, \varvec{\Phi }_2, \varvec{I})$.

The matrices $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$ can be expressed as:

$$\begin{aligned} \begin{aligned}&\varvec{K}_\text{d} = \varvec{\Phi }^T \begin{bmatrix} \varvec{K}_\text{1} &{}\varvec{0} &{}\varvec{L}_{\text{f},1} \\ \varvec{0} &{}\varvec{K}_\text{2} &{}\varvec{L}_{\text{f},2} \\ \varvec{0} &{}\varvec{0} &{}\varvec{K}_\mathrm {\text{cav}} \end{bmatrix} \varvec{\Phi }\\ &\varvec{M}_\text{d} = \varvec{\Phi }^T \begin{bmatrix} \varvec{M}_\text{1} &{}\varvec{0} &{}\varvec{0} \\ \varvec{0} &{}\varvec{M}_\text{2} &{}\varvec{0} \\ -\rho _\text{a}\varvec{L}_{\text{f},1} &{}-\rho _\text{a}\varvec{L}_{\text{f},2} &{}\varvec{M}_\mathrm {\text{cav}} \end{bmatrix} \varvec{\Phi } \end{aligned} \end{aligned}$$

(A19)

When computing the sensitivity of $\varvec{D}_\text{tot}$, $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$, the sensitivities of the (modal) reduction basis $\varvec{\Phi }$ have been neglected as proposed in Haftka and Gürdal (1992) and similarly performed in Giannini et al. (2020b, 2021a). The sensitivities of $\varvec{D}_\text{tot}$, $\varvec{K}_\text{d}$ and $\varvec{M}_\text{d}$ can be therefore expressed as:

$$\begin{aligned} \begin{aligned} & \text{For single panels:} \\ & \frac{\partial\boldsymbol{D}_\mathrm{tot}}{\partial\tilde{\gamma}_e} = \boldsymbol{\Phi}_{1}^T \frac{\partial\boldsymbol{D}_\mathrm{1}}{\partial\tilde{\gamma}_e} \boldsymbol{\Phi}_{1} \\ &\text{For double panels:}\\ & \frac{\partial \boldsymbol{D}_\mathrm{tot}}{\partial \tilde{\gamma}_e} = \boldsymbol{\Phi}^T \begin{bmatrix} \frac{\partial\boldsymbol{D}_\mathrm{1}}{\partial\tilde{\gamma}_e} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} & \frac{\partial\boldsymbol{D}_\mathrm{2}}{\partial\tilde{\gamma}_e} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \end{bmatrix} \boldsymbol{\Phi}^T, \\ & \frac{\partial \boldsymbol{K}_\mathrm{d}}{\partial \tilde{\gamma}_e} = \boldsymbol{\Phi}^T \begin{bmatrix} \frac{\partial\boldsymbol{K}_{1}}{\partial \tilde{\gamma}_e} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} &\frac{\partial\boldsymbol{K}_{2}}{\partial \tilde{\gamma}_e} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \end{bmatrix} \boldsymbol{\Phi}, \\ & \frac{\partial \boldsymbol{M}_\mathrm{d}}{\partial \tilde{\gamma}_e} = \boldsymbol{\Phi}^T \begin{bmatrix} \frac{\partial\boldsymbol{M}_{1}}{\partial \tilde{\gamma}_e} &\boldsymbol{0} &\boldsymbol{0} \\ \boldsymbol{0} &\frac{\partial\boldsymbol{M}_{2}}{\partial \tilde{\gamma}_e} &\boldsymbol{0} \\ \boldsymbol{0} &\boldsymbol{0} &\boldsymbol{0} \end{bmatrix} \boldsymbol{\Phi} \end{aligned} \end{aligned}$$

(A20)