Abstract
We propose a high-performance GPU solver for inverse homogenization problems to design high-resolution 3D microstructures. Central to our solver is a favorable combination of data structures and algorithms, making full use of the parallel computation power of today’s GPUs through a software-level design technology exploration. This solver is demonstrated to optimize homogenized stiffness tensors, such as bulk modulus, shear modulus, and Poisson’s ratio, under the constraint of bounded material volume. Practical high-resolution examples with \(512^3 \approx 134.2\) million finite elements run in less than 40 s per iteration with a peak GPU memory of 9 GB on an NVIDIA GeForce GTX 1080Ti GPU. Besides, our GPU implementation is equipped with an easy-to-use framework with less than 20 lines of code to support various objective functions defined by the homogenized stiffness tensors. Our open-source high-performance implementation is publicly accessible at https://github.com/lavenklau/homo3d.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Microstructure design is fundamental in various applications, such as aerospace and biomedicine. Topology optimization for inverse homogenization problems (IHPs) (Sigmund 1994) is a powerful and effective method to find optimal microstructures. Many methods have been developed for the microstructure topology optimization, such as density-based method (Aage et al. 2015; Groen and Sigmund 2018), isogemetric topology optimization (Gao et al. 2019, 2020), bidirectional evolutionary structural optimization (Huang et al. 2012, 2011), and level set method (Vogiatzis et al. 2017; Li et al. 2018).
We focus on high-resolution periodic 3D microstructure design via the density-based method. High-resolution microstructures expand the search space of multi-scale structures, making their mechanical properties more likely to approach the optimal solution. In addition, a microstructure is periodically arranged in a macro-scale domain behaving like a material under the premise that the length scale of the microstructure is much smaller than that of the macrostructure based on the homogenization theory (Bendsøe and Kikuchi 1988; Suzuki and Kikuchi 1991; Nishiwaki et al. 1998).
We aim to use the parallel computation power of today’s GPUs for time- and memory-efficiently solving large-scale IHPs under periodic boundary conditions with the density representation. However, it is challenging to make full use of the computing resources of GPU to realize the solver. The reasons are twofold. First, since the solver contains multiple steps with different computational profiles, the choice of data structures and algorithms should be considered globally to be suitable for every step. Second, as the GPU memory is limited, the memory usage should be reduced to adapt to high resolution while ensuring accuracy and high efficiency.
Solving large-scale IHPs on the unit cell domain (\(512\times 512\times 512\) elements) with three different objectives: bulk modulus B (a), shear modulus G (b), and Poisson’s ratio r (c). The corresponding volume fractions are 0.3, 0.3 and 0.2, respectively. We show the optimized objective values below models.
The goal of (Wu et al. 2015) is similar with ours, and they propose a high-performance multigrid solver with deep integration of GPU computing for solving compliance minimization problems. However, since what they need to store is different from ours due to different problems, their data structure and multigrid solver are unsuitable for ours. For example, we should store six displacement fields to evaluate the elastic matrix and perform sensitivity analysis, but this storage is a heavy burden for most GPUs. Besides, handling periodic boundary conditions is another difference.
This paper proposes an optimized, easy-to-use, open-source GPU solver for large-scale IHPs with periodic boundary conditions to design high-resolution 3D microstructures. By exploring the software-level design technologies operating at only one GPU, we present a favorable combination of data structures and algorithms to address the computational challenges of the desired solver. Specifically, the mixed floating-point precision representation is deeply integrated into all components of the solver to achieve a favorable trade-off between memory usage, running time, and microstructure quality. The mixed-precision formats under various precisions are tested, and we ultimately find that FP16/FP32 is the most suitable for IHPs. Besides, different types of memory are called properly and reasonably to significantly increase the number of optimizable finite elements on a GPU. We also provide test results to identify these favorable design choices.
We demonstrate the capability and effectiveness of our GPU solver by successfully optimizing the homogenized stiffness tensors, such as bulk modulus, shear modulus, and Poisson’s ratio, under the material volume-bounded constraint (Fig. 1). In practice, our solver consumes less than 40 s for each iteration with a peak GPU memory of 9 GB for high-resolution examples with \(512^3 \approx 134.2\) million finite elements on an NVIDIA GeForce GTX 1080Ti GPU. Besides, we provide an easy-to-use framework for GPU implementation. Specifically, the framework uses less than 20 lines of code to support various objective functions defined by the homogenization stiffness tensor. Code for this paper is at https://github.com/lavenklau/homo3d.
2 Related work
Inverse homogenization problems. Solving IHPs (Sigmund 1994) to optimize the distribution of materials is a powerful method to obtain superior mechanical properties under given load and boundary conditions. Topology optimization is used to solve IHPs with different objectives, such as extreme shear or bulk moduli (Gibiansky and Sigmund 2000), negative Poisson’s ratios (Theocaris et al. 1997; Shan et al. 2015; Morvaridi et al. 2021), and extreme thermal expansion coefficients (Sigmund and Torquato 1997). Although there are several open-source codes for microstructure design (Xia and Breitkopf 2015; Gao et al. 2021), most of them focus on 2D microstructure design. We focus on developing an efficient GPU solver for large-scale IHPs to design 3D microstructures via the density-based method.
High-resolution topology problems. Several acceleration techniques for high-resolution topology problems are available, such as parallel computing (Borrvall and Petersson 2001; Aage et al. 2015), GPU computation (Challis et al. 2014), adaptive mesh refinement (Stainko 2006; De Sturler et al. 2008; Rong et al. 2022). Equipping and solving large-scale equilibrium equations is essential for slowing down the optimization process. Thus, the geometric multigrid solver is used (Briggs et al. 2000; Zhu et al. 2010; McAdams et al. 2011; Zhang et al. 2022). Wu et al. (2015) present a high-performance multigrid solver with deep integration of GPU computing for compliance minimization problems. PETSc (Aage et al. 2015) is a large-scale topology optimization framework, where each iteration takes about 60s on 40 CPUs (240 cores) for a model with \(288^3\) (23.8 million) elements. The state-of-the-art work (Träff et al. 2023) which accelerated topology optimization based on GPU implementation is not designed for solving IHP problems. We focus on using the parallel computation power of today’s GPU and customize data structure and multigrid solver to solve large-scale IHPs of 3D microstructure design. A comparison with Aage et al. (2015) is shown in Fig. 11, and our method shows superiority.
Mixed-precision methods. The IEEE standard provides for different levels of precision by varying the field width, e.g., 16 bits (half precision), 32 bits (single precision) and 64 bits (double precision). Double-precision arithmetic earns more accurate computations by suffering higher memory bandwidth and storage requirements. However, half precision is 4 times speedup for a double precision Haidar et al. (2018) single-precision calculations take 2.5 times faster than the corresponding double-precision calculations (Göddeke and Strzodka 2010). Mixed-precision algorithms are proposed in many works for the trade-off between high efficiency and high precision (Sun et al. 2008; Ben Khalifa et al. 2020; Zhang et al. 2019; Hosseini et al. 2023). Liu et al. (2018) developed a mixed-precision multigrid solver to accelerate the linear elasticity calculation. We use the mixed-precision representation for a trade-off between memory usage, running time, and microstructure quality.
3 Inverse homogenization problem
3.1 Model
The IHP is performed on a unit cell domain \(\varOmega \) = \([0,1]^3\), which is evenly discretized into M elements. Each element is assigned an density variable \(\rho _e\) and a fixed volume \(v_e\). All density variables \(\rho _e (e=1,\cdots ,M)\) form a vector \(\varvec{\rho }\). IHP is formulated as follows:
where the objective \(f(C^H(\varvec{\rho }))\) is a function as the elastic matrix \(C^H(\varvec{\rho })\) to indicate mechanical properties. The displacement field \({\textbf{u}}\) is calculated by solving the equilibrium equation with six load cases \({\textbf{f}}\) for three dimensions. The stiffness matrix \({\textbf{K}}\) is a function of the material properties in the elements. \(|\varOmega |\) is the volume of the unit cell domain \(\varOmega \), V is the prescribed volume fraction, and \(\rho _{min} = 0.001\).
3.2 Homogenization
Homogenization theory is typically used to determine the elastic tensor \(E^H\) of a microstructure (Allaire 2002). The derivation of the homogenized elasticity tensor involves a two-scale asymptotic expansion and boils down to solving the following cell problem :
Here, \(e^{kl}\) with \(k,l\in \{1,2,3\}\) is a unit tensor whose (kl)-th component equals to 1 and other components equal to 0. The operator “ : ” means the double dot product of two tensors. The second equation means \({\textbf{w}}^{kl}\) is a periodic function whose period is \({\textbf{t}}\) with \(t_i=\pm 1, i=0,1,2\). \(\left( \nabla \varvec{\chi }^{kl}\right) \) is the gradient of \(\varvec{\chi }^{kl}\) computed as \([\nabla \varvec{\chi }^{kl}]_{ij}=\frac{\partial \chi ^{kl}_i}{\partial x_j}\). E is the spatially varied elastic tensor of the base material. \(\varepsilon ({\textbf{w}}^{kl})=\frac{1}{2}\left( \nabla {\textbf{w}}^{kl}+(\nabla {\textbf{w}}^{kl})^\top \right) \) is the Cauchy strain tensor of the displacement field \({\textbf{w}}^{kl}\).
After solving this problem, the homogenized elastic tensor is determined as:
For numerical computation, Finite Element Method is used to solve (2) (Andreassen and Andreasen 2014). We first enforce a macro strain on each element and compute the response force \({\textbf{f}}_e^{ij}\):
where \(\varvec{\chi }^{ij}_e\) is the displacement on element e-th vertices corresponding to the unit strain tensor \(e^{ij}\). The global force vector \({\textbf{f}}^{ij}\) is assembled from element force vector \({\textbf{f}}^{ij}_e\). Based on the SIMP approach (Bendsøe 1989), \({\textbf{K}}_e= \rho ^p_e{\textbf{K}}^0\) is the element stiffness matrix, where \({\textbf{K}}^0\) is the element stiffness matrix of the solid element and p is a penalization factor. The global stiffness matrix \({\textbf{K}}\) is assembled from element stiffness matrix \({\textbf{K}}_e\). Then, we achieve the numerical solution \({\textbf{u}}^{ij}\) by solving
After solving (5) for each pair of ij, the homogenized elastic tensor is computed as
where \(i,j,k,l\in \{1,2,3\}\) and \({\textbf{u}}_e^{ij}\) means the components of \({\textbf{u}}^{ij}\) on the element e.
Using the engineering notation with \(11\rightarrow 0\), \(22\rightarrow 1\), \(33\rightarrow 2\), \(12\rightarrow 3\) , \(23\rightarrow 4\) and \(13\rightarrow 5\) , the elasticity tensor, i.e., \(E_{ijkl}^H\) in (7), is rewritten as
The objective \(f(C^H)\) is a user-defined function as the components of \(C^H\). Its gradient is computed as:
where
The sensitivity filtering defined in Andreassen et al. (2011) is adopted by default.
3.3 Optimization model
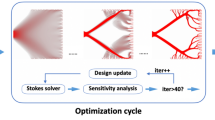
Solver for IHP (1). We solve IHP in an iterative manner. In each iteration, the following four steps are performed:
-
1.
Compute the displacement field \({\textbf{u}}\) by solving (5).
-
2.
Compute the homogenized elastic tensor \(C^H\) via (7) and the objective function \(f(C^H)\).
-
3.
Perform sensitivity analysis, i.e., evaluate the gradient \(\frac{\partial f}{\partial \varvec{\rho }}\) via (8) and (9)
-
4.
Update density \(\varvec{\rho }\) using \(\frac{\partial f}{\partial \varvec{\rho }}\) based on the Optimal Criteria (OC) method (Sigmund 2001).
Multigrid solver. Solving (5) to compute \({\textbf{u}}\) for large-scale problems is time-consuming and memory-intensive. To reduce the time and memory overhead, the multigrid solver is used (Dick et al. 2011; Wu et al. 2015; Liu et al. 2018). The main idea of multigrid is to solve a coarse problem by a global correction of the fine grid solution approximation from time to time to accelerate the convergence.
Our first level grid is the cell domain \(\varOmega \). Then, we recursively divide \(\varOmega \) to construct a hierarchy of coarse grids. To transfer data between grids of levels l and \(l+1\), we use trilinear interpolation and its transpose as the restriction operator, denoted as \(I^{l}_{l+1}\) and \(R^{l+1}_{l}\), respectively. Based on Galerkin rule, the numerical stencil on the level \(l+1\) is determined from the level l as \({\textbf{K}}^{l+1}=R^{l+1}_{l}{\textbf{K}}^{l}I^{l}_{l+1}\). Then, the V-cycle of the multigrid solver, with the Gauss–Seidel relaxation as the smoother, is employed to effectively decrease the residual on the first level grid until convergence. In addition, the coarsening process would be stopped if the subsequent coarsened mesh becomes smaller than \(4 \times 4 \times 4\) while using coarsening ratio of 1 : 2. The pseudocode of the V-cycle is outlined in Algorithm 1.
4 Optimized GPU scheme for solving IHPs
We describe our optimized GPU scheme for solving large-scale IHPs using a GPU-tailored data structure (Sect. 4.1), a dedicated multigrid solver (Sect. 4.2), and an efficient evaluation of the elastic matrix and sensitivity (Sect. 4.3).
4.1 Data structure tailored to solve IHPs
Data for each vertex. For each vertex \({\textbf{v}}\) of each level’s mesh, we store the numerical stencil \({\textbf{K}}_v\), the displacement \({\textbf{u}}_v\), the force \({\textbf{f}}_v\), and the residual \({\textbf{r}}_v\) in the multigrid implementation. The numerical stencil \({\textbf{K}}_v\) consists of 27 matrices of dimension \(3\times 3\), each of which corresponds to one adjacent vertex. The displacement, force, and residual are all vectors with three components, named nodal vectors. From the perspective of implementation, a numerical stencil can be regarded as composed of \(27 \times 3\) nodal vectors. On the first level mesh, the density variable is stored for each element, which is used to assemble the numerical stencil on the fly. To handle different boundary conditions and facilitate the Gauss-Seidel relaxation, a 2-byte flag is stored for each vertex and element on each level’s mesh, named vertex flag and element flag, respectively.
Mixed floating-point precision representations. By employing mixed floating-point precision, a balance between computational accuracy and performance can be achieved. Since a large-scale IHP involves large elements calculation and requires significant memory usage, applying mixed precision can help conserve memory and enable more efficient data storage. The throughput of lower precision format is usually much higher than that of higher precision. Only using the higher precision through the computation leaves the lower precision pipeline underutilized, wasting significant computing resources. Through extensive testing (Table 1), we are pleasantly surprised to find that using mixed floating-point precision (FP16/FP32) can maximize computational efficiency and memory storage under the tolerance relative residual \(r_\mathrm{{rel}} = 10^{-2}\), computed as \(\Vert {\textbf{r}}\Vert _2/\Vert {\textbf{f}}\Vert _2\) (see more discussions about \(r_\mathrm{{rel}}\) in Fig. 5 and Sect. 4.2). The numerical stencils are stored in half-precision (FP16), and the rest vectors are stored in single-precision (FP32).
Memory layouts. Nodal vectors are all stored in the Structure of Array (SoA) format. Namely, the same component of stencil or nodal vector of all vertices is stored together in an array, and different components are stored in different arrays. The numerical stencils are stored in Array of Structure (AoS) format.
Specifically, the eight-color Gauss-Seidel relaxation is used for the parallelization, which partitions the vertices into eight independent subsets and parallelizes the computation within each subset. Our memory layout should provide an efficient memory access pattern for this procedure. Given a vertex with an integer coordinate \((x_0,x_1,x_2)\), it belongs to the subset \((x_0\,\text {mod}\, 2)2^0 + (x_1\,\text {mod}\, 2) 2^1 + (x_2\,\text {mod}\,2) 2^2\). To exploit the high memory bandwidth and leverage the coalesced memory transaction, we use a similar memory layout as (Dick et al. 2011), i.e., the data on the vertices of the same subset are grouped and different subsets are stored in the consecutive memory block.
In most modern GPUs, only the 32-, 64-, or 128-byte segments of device memory that are aligned to multiple of their size can be read or written by memory transactions. To maximize the memory throughput, data should be organized in such a way that the i-th thread of a warp (containing 32 threads) accesses the i-th 32-bit (or 64-bit) word of a 128-byte segment at single (or double) precision. Thus, we add a few “ghost” vertices to supplement each subset so that its number of vertices is a multiple of 32. Then, we can assign one warp to each group of 32 vertices for each subset. Each warp accesses an aligned 128-byte (or 256-byte) segment for single-precision (or double-precision) nodal vectors. Ideally, each warp’s memory access to the same adjacent vertices of the group of 32 vertices is also coalesced as these adjacent vertices are consecutive in another subset’s memory block.
2D illustration for periodic boundary conditions. In the Gauss-Seidel relaxation, the vertices are partitioned into four subsets. Each subset is shown in one color. We use the memory access to the left adjacent vertex (the red solid or dotted arrow) for illustration. For the red dotted arrow, memory access starts from the vertex of the left boundary. Before padding (upper left), memory access from the left boundary vertex is discontinuous (lower left), leading to uncoloasced memory transactions. After padding (upper right), such memory access becomes continuous (lower right); thus, the memory access is coloasced.
Padding layers for periodic boundary conditions. The coarse mesh in the multigrid solver should inherit the periodic feature of the fine mesh. Due to periodic boundary conditions, the vertices on the opposite boundaries are the same. Hence, when restricting residuals or numerical stencils from the fine grid to the coarse grid, the vertices on one side of the boundary should add the transferred data from the neighbor on the other side.
In our GPU implementation, we pad a layer of vertices and elements around the mesh (Fig. 2). Those padded vertices and elements are copies of their periodic equivalents and are updated when their copied vertices or elements change. After the padding, the memory layout is updated to incorporate the padded vertices. Then, the restriction can transfer data from neighbors regardless of periodic boundary conditions. We do not execute computations on the padded vertices or elements and they only provide data to their neighbors. This padding leads to a more efficient memory access pattern (see an example in Fig. 2).
Accessing data in memory. Our grid is highly regular as it is evenly divided from a cube. Given the integer coordinate \((x_0,x_1,x_2)\) of a vertex, the memory location is:
where \(\text {Id} = (x_0\,\text {mod}\, 2)2^0 + (x_1\,\text {mod}\, 2) 2^1 + (x_2\,\text {mod}\,2) 2^2\) is the index of the subset, \(p_\text {base}^\text {Id}\) denotes the start address of the memory block of the subset \(\text {Id}\), \(N^\text {Id}_i,i=0,1,2\) is the number of vertices of the subset \(\text {Id}\) along three axes:
where \(N_i,i=0,1,2\) is the number of elements along three axes, \(O^\text {Id}_i\) is the origin of the subset Id defined as \(O^\text {Id}_0=\text {Id} \,\text {mod}\, 2,O^\text {Id}_1=\lfloor \text {Id} / 2\rfloor \,\text {mod}\, 2,O^\text {Id}_2 =\lfloor \text {Id} / 4\rfloor \).
Since the coordinates of one vertex’s adjacent elements or vertices can be calculated by offsetting the position of itself, we can compute their memory locations easily. Hence, we do not store the topology information, e.g., the index of the adjacent vertex, to reduce a large amount of memory.
Different GPU memory types. In high-resolution problems, the storage for the nodal vectors, e.g., nodal displacements, is enormous. For example, we need about 1.5GB memory for one single-precision nodal displacement field of a grid with a resolution of \(512^3\). Six displacement fields should be stored to evaluate the elastic matrix and perform sensitivity analysis. Besides, they are proper initializations for solving (5) in the next iteration. However, it costs nearly 9GB of memory, which is unaffordable for most GPUs. Thus, our GPU implementation stores them in unified memory that supports oversubscription. It is noteworthy that the previously mentioned 9GB peak memory requirement does not encompass the unified memory. This exclusion stems from the oversubscription feature, allowing, for example, an allocation of 22GB unified memory even when the device memory capacity is only 11GB. Hosts and devices can access unified memory, and the CUDA underlying system manages the physical location of data stored within, whether in host memory or device memory. Intuitively, through the utilization of unified memory, the rest device memory, beyond our allocated portion, serves as a “cache” for data originating from the host memory. We provide methods to reduce the performance loss of unified memory in Sect. 4.3.
Except for these displacement fields, the storage for the nodal vectors of the multigrid solver is allocated and resident on the device memory, which is the same as the density variable, vertex, and element flag. The numerical stencils are also stored in the device memory except for the first level mesh, where we assemble the numerical stencil using densities on the fly. The frequently used data are cached on constant memory, such as the template matrix, pointers to vertices, element data, and grid information like resolution.
An ablation study of the Dirichlet boundary for maximizing the bulk modulus with the resolution of \(128^3\) and the volume ratio of 0.2. The optimizations start from the same initialization. The terms “With” and “W/O” mean the optimization is running with and without enforcing the Dirichlet boundary condition, respectively
4.2 Dedicated multigrid solver
Singular stiffness matrices. Due to the loss of precision caused by the mixed-precision scheme and the high resolutions, the multigrid solver may diverge with a numerical explosion. We find in practice that these situations may be caused by (1) insufficient Dirichlet boundary conditions and (2) no materials at corners during optimization.
During homogenization, the eight corner vertices of the unit cube domain are usually selected as the fixed vertices. This amounts to adding Dirichlet boundary conditions at the eight corner vertices to the cell problem (2) to guarantee a unique solution (see Fig. 3b). Otherwise, the global stiffness matrix becomes singular (see Fig. 3a).
However, as the density field evolves during the optimization, it often tends to be zero near the corners. Accordingly, the solid part gets isolated from the corners. Then, the global stiffness matrix is again becoming singular. To handle such a problem, we remove the component belonging to the numerical stencil’s null space from the restricted residual before solving the system on the coarsest mesh, similar to (Panetta et al. 2015; Zhang et al. 2022). We show an example with the resolution \(128^3\) under the volume fraction 0.3 in Fig. 4.
Enforce macro strain. The response force on the vertex \({\textbf{v}}\) from an enforced macro strain \(e^{kl}\) is:
where \({\textbf{K}}^0_{[i,j]}\) denotes (i, j)-th \(3\times 3\)-block of \({\textbf{K}}_0\), and \(\varvec{\chi }^{i}_{e,v_j}\) is the displacement on vertex \({\textbf{v}}_j\) for the macro strain, where the superscript i is the engineering notation for kl.
To enforce macro strain \(e^{kl}\), we assign one thread for each vertex. Each thread traverses the incident elements of its assigned vertex and accumulates the response force of each element on this vertex. On the vertex \({\textbf{v}}_j\), we have
where \({\textbf{x}}^{v_j} = (x^{v_j}_0,x^{v_j}_1,x^{v_j}_2)\) is the coordinate of the vertex \({\textbf{v}}_j\). Due to the accuracy loss of the half-precision stiffness matrix, the translation of the nodal displacement causes a response force that cannot be ignored numerically. Consequently, the absolute position of \({\textbf{v}}_j\) affects the response force. Hence, we use the relative coordinate of \({\textbf{v}}_j\) in the element rather than the coordinate in the entire grid as \({\textbf{x}}^{v_j}\).
Relaxation and residual update. To implement the eight-color Gauss-Seidel relaxation, we serially launch one computation kernel for each subset of the vertices. The performance bottleneck of the multigrid solver is the Gauss-Seidel relaxation and residual update on the first level mesh. Central to both procedures is to compute \(\textbf{Ku}\) on each vertex \({\textbf{v}}\):
where the subscript e is the incident element of the vertex \({\textbf{v}}\), and \({\textbf{u}}^{v_j,e}\) is the nodal displacement on \(v_j\)-th vertex of element e. The residual is then updated as
We introduce two notations for the relaxation:
where we use \({\textbf{M}}_v\) to denote the modified \([\textbf{Ku}]_v\) and \({\textbf{S}}_v\) to denote the sum of \(3\times 3\) diagonal block of \({\textbf{K}}^0\). Then, the Gauss-Seidel relaxation is performed via the following linear system to update \({\textbf{u}}_v\):
Singular stiffness matrices. We optimize the bulk modulus, and the initial density fields of (a) and (b) are the same. If our multigrid solver does not remove the component belonging to the null space of numerical stencil, it diverges at the 10-st iteration (a). When we remove the component belonging to the null space (b), the optimization achieved numerical convergence
To perform these computations via GPU, we first dispatch eight warps for each group of 32 consecutive vertices. Each warp accumulates the contribution of one incident element in (13) or (15). Then, we compute the total sum by a block reduction.
Comparing the evolution of relative residuals (i.e., \(\Vert {\textbf{r}}\Vert _2/\Vert {\textbf{f}}\Vert _2\)) in a multigrid solver with various precisions (i.e., FP16, FP32, FP64, FP32/FP16, and FP64/FP32) using different density distributions. The average time of per V-cycle for each precision is 31.2 ms, 35.8 ms, 65.5 ms, 33.0 ms, and 65.2 ms, respectively. Left: a random density field is generated by assigning values between 0 and 1. Right: an optimized density field is obtained by bulk modulus optimization for volume ratio 0.2. The solver iterates for 50 and 200 V-cycles, respectively, on a grid resolution of \(128^3\)
To use the computational power of modern GPUs, lower precision representations such as FP32 and FP16 are preferred over FP64 due to their higher throughput and smaller bandwidth requirement. However, a trade-off exists between computational efficiency and accuracy. We explore different combination schemes of precision representations within our multigrid solver (Fig. 5 and Table 1). In Fig. 5, a random initial design leads to a quite good condition number of the stiffness matrix as the density filter smears out all the contrast. However, the condition number of the stiffness matrix becomes larger when the density contrast is obvious shown in the the right side of Fig. 5. It is observed that compared to the single-precision scheme, the mixed-precision scheme achieves a comparable relative residual using less memory. Based on these comparisons, we have identified that the combination of FP32 and FP16 yields the best results within the specified tolerance error.
We also test different \(r_\mathrm{{rel}}\)s of the equilibrium equation in Fig. 6. Again, the structures are almost the same, and the differences in bulk modulus are less than 3%.
Restriction and prolongation. We follow (Dick et al. 2011) to restrict residuals and prolong displacements, except that the index of the adjacent vertex is computed via (10) instead of being loaded from global memory.
Assembling numerical stencils for coarse grids. Since the numerical stencil on the first level is not stored, we assemble the numerical stencil on the second level as follows:
Here, \([{\textbf{K}}_v]_{v_k}\in {\mathbb {R}}^{3\times 3}\) is the numerical stencil of the vertex \({\textbf{v}}\) to its adjacent vertex \({\textbf{v}}_k\) on the second level grid. N(v) is the set of elements on the first level grid covered by the adjacent elements of \({\textbf{v}}\) on the second level. The weight \(w^v_{e,v_i}\) is:
where \((x^{v}_0,x^{v}_1,x^{v}_2)\) and \((x^{e,v_i}_0,x^{e,v_i}_1,x^{e,v_i}_2)\) are the coordinates of \({\textbf{v}}\) and the \(v_i\)-th vertex of the element e, respectively, and d is the length of element on the second level. The weight \(w^{v_k}_{e,v_j}\) is defined in the same way.
In the GPU implementation, we assign one thread to each vertex in the second level. Each thread iterates through its 27 neighboring vertices and accumulates the summands in (17). More specifically, in each loop, the thread accesses the density value in (17) from global memory, computes its power, and then multiplies it by the weights and the \(3\times 3\) block \({\textbf{K}}^0_{[v_i,v_j]}\). The resulting product is then summed into a \(3\times 3\) matrix in local memory, which is written back to global memory at the end of each loop. It is worth noting that, due to the presence of many zero weights in (17), we only perform computations on the first-level elements that are covered by both the incident elements of the assigned vertex and the current looping neighboring vertices in the second level. This excludes many summands with zero weight. If the resolution of the second level grid is high, e.g., the number of elements exceeds \(128^3\), the memory cost is reduced by the non-dyadic coarsening strategy (Wu et al. 2015) that directly transfers the numerical stencil from the first level to the third level.
The numerical stencil on the higher-level grid (e.g., third level, fourth level, etc) is assembled in the same way. Specifically, we use the numerical stencil on the fine grid to assemble the numerical stencil on the coarse grid, e.g., second level for third level. First, our GPU implementation assigns a thread for each vertex on the coarse grid. The thread loops 9 times to compute the 9 entries for all \(3\times 3\) matrices of the numerical stencil. In each loop, the thread loads one of the 9 entries from the numerical stencil of its adjacent vertices on the fine grid and computes the weighted sum. Then, the thread writes the sum back to the global memory.
4.3 Elastic matrix evaluation and sensitivity analysis
Handling unified memory. Evaluating elastic matrix and sensitivity heavily depends on the six displacement fields stored in the unified memory. The performance loss of the unified memory increases the time cost for both operations. We find in practice that the FP32 precision displacement is necessary for numerical stability when solving FEM, whereas the FP16 precision is enough to evaluate the elastic matrix and perform sensitivity analysis. To reduce such performance loss, we first launch a kernel to cast the FP32 precision displacements to FP16 precision and then store them in the memory of the displacement, the residual, and the force on the first level mesh (Fig. 7).
Evaluation. The elastic matrix and sensitivity are evaluated similarly. Eight warps are assigned for each group of 32 consecutive elements. The first 6 warps compute \(\varvec{\chi }_e^{i}-{\textbf{u}}_e^{i}, i\in \{0,1,2,3,4,5\}\) and store it in the shared memory, where \(\varvec{\chi }_e^{i}\) is computed on the fly and \({\textbf{u}}_e^{i}\) is loaded from the memory.
To evaluate the elastic matrix in our GPU implementation, we first split \(\left( \varvec{\chi }_e^{i}-{\textbf{u}}_e^{i}\right) ^\top {\textbf{K}}_e\left( \varvec{\chi }_e^{j}-{\textbf{u}}_e^{j}\right) \) in (7) into 8 summands by dividing \({\textbf{K}}_e\) into eight 3-row blocks, which are dispatched into the eight warps, respectively. Then, a block reduction is performed to get the product in the first warp for each element. Since we aim to sum over all elements according to (7), we do a warp reduction using the warp shuffle operation to compute the sum over the 32 elements in the first warp before writing it to memory. Finally, several parallel reduction kernels are serially launched to compute the sum of the results produced by the last step.
For sensitivity analysis, the split product becomes \(p\rho _e^{p-1}\frac{\partial f}{\partial C^{H}_{ij}}\left( \varvec{\chi }_e^{i}-{\textbf{u}}_e^{i}\right) ^\top {\textbf{K}}^0\left( \varvec{\chi }_e^{j}-{\textbf{u}}_e^{j}\right) \) with a constant coefficient. We do not sum over all the elements as the sensitivity is computed for each element according to (9).
5 An easy-to-use framework
5.1 Setup
Users can clone this framework or fork the current master branch from the GitHub repository (https://github.com/lavenklau/homo3d). The compilation and runtime environment mainly requires CUDA 11, gflags, Eigen3, glm, and OpenVDB. The main classes are listed and explained in the supplementary material.
5.2 Compiling and code invoking
The framework provides a good user interface. After installing the framework, the user can use the following steps to design 3D microstructure:
-
The initialization includes optimization parameters, the design domain, and its resolution:

where
 is a parsed configuration file with command line arguments, including the Young’s modulus and Poisson’s ratio of the base material, grid resolution, volume fraction, initialization type, symmetry requirement, etc.
is a parsed configuration file with command line arguments, including the Young’s modulus and Poisson’s ratio of the base material, grid resolution, volume fraction, initialization type, symmetry requirement, etc. -
Define the material interpolation method based on the SIMP approach (Bendsøe 1989):

where
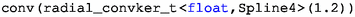 means a convolution operation with the kernel
means a convolution operation with the kernel
 , which is same with the filtering method of (Wu et al. 2015). The periodic filter kernel is discussed in Sect. 6.5.
, which is same with the filtering method of (Wu et al. 2015). The periodic filter kernel is discussed in Sect. 6.5. -
Create an elastic matrix from the design domain
 and the material interpolation method
and the material interpolation method
 :
:

-
Define the objective function \(f(C^H)\), e.g., the following objective is to maximize the bulk modulus:
 (19)
(19)The code is written as

-
Define the optimization process. We create an optimizer and begin the main optimization loop. In each iteration, we evaluate the objective, compute the gradient, and then update the density variable:

where
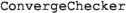 is a class to check convergence,
is a class to check convergence,  is a
function to symmetrize a 3D tensor according to a given symmetry type. In this routine, we do not filter the sensitivity since the density is already filtered.
is a
function to symmetrize a 3D tensor according to a given symmetry type. In this routine, we do not filter the sensitivity since the density is already filtered. -
Output the optimized density field and elastic matrix:

where
 is
a function to prefix the output directory to a given string. The member function
is
a function to prefix the output directory to a given string. The member function  writes the
data of
writes the
data of  to a
OpenVDB file.
to a
OpenVDB file.
Users only need to define  , the material
interpolation method, and the objective function before running the code to solve the IHPs. The outputs contain a microstructure visualization file (
, the material
interpolation method, and the objective function before running the code to solve the IHPs. The outputs contain a microstructure visualization file ( ), an
elastic tensor matrix (
), an
elastic tensor matrix ( ), Users
can use Rhino to visualize
), Users
can use Rhino to visualize  files.
files.
5.3 Extensions
Our framework uses the automatic differentiation (AD) technique (Griewank and Walther 2008) to make it easy to extend our program to optimize various objective and material interpolation methods. Users can modify the code according to their needs by changing expressions with different objectives or constraints and material interpolation methods without repeating the tedious calculation.
Different objectives. For other objective function, such as shear modulus, its expression can be defined accordingly:
We change nothing than the objective from the code of bulk modulus optimization by calling

To design negative Poisson’s ratio materials, Xia and Breitkopf (2015) propose a relaxed form of objective function for 2D problems. Accordingly, we can define a similar objective to design negative Poisson’s ratio materials in 3D:
where \(\beta \in \left( 0,1\right) \) is a user-specified constant and the exponential l is the iteration number. The code is:

where  is a constant in (0, 1) and
is a constant in (0, 1) and  is the iteration number in the main loop of optimization. We also support common mathematical functions, such as exponential and logarithm functions, to define the expression. Several works Radman et al. (2013); Xia and Breitkopf (2015) find that the negative value of Poisson’s ratio can reach -1 when the shear modulus is much larger than its bulk modulus. Accordingly, we can optimize the following objective function to obtain the negative Poisson’s ratio:
is the iteration number in the main loop of optimization. We also support common mathematical functions, such as exponential and logarithm functions, to define the expression. Several works Radman et al. (2013); Xia and Breitkopf (2015) find that the negative value of Poisson’s ratio can reach -1 when the shear modulus is much larger than its bulk modulus. Accordingly, we can optimize the following objective function to obtain the negative Poisson’s ratio:

where \(\eta , \tau , \gamma \) are three parameters. In our experiments, we set \(\eta = 0.6, \tau = -1/E_0^\gamma \), and \(\gamma = 0.5\), where \(E_0\) is the Young’s modulus of solids. We discuss the difference between (21) and (22) in Sect. 6.5.
Different material interpolation methods. For the routine of Sect. 5.2, we support other convolution kernels (e.g., linear convolution kernels) for density filtering. Our program is extensible, and users can define their own convolution kernel. A more direct material interpolation is defined as:

where we only penalize the density variable by the power of 3 without filtering. Accordingly, we should filter the sensitivity before updating the density by  :
:

6 Experiments and applications
For the optimization parameters, the material penalization factor is 3, the filter radius is 2, the maximum iteration number is 300, the iterative step size of density is 0.05, and the damping factor of the OC method is 0.5. The optimization is stopped when the relative change of the objective function is less than 0.0005 for three consecutive iterations. The cubic domain is discretized with 8-node brick elements. The mechanical properties of solids are Young’s modulus \(E_0=1\) and Poisson’s ratio \(\nu = 0.3\).
We optimize three different objectives: bulk modulus (19), shear modulus (20), and negative Poisson’s ratio (21) (Fig. 8). Table 2 summarizes the numerical statistics of all examples. Our solver consumes less than 40 s for each iteration with a peak GPU memory of 9 GB for high-resolution examples with \(512^3 \approx 134.2\) million elements. All experiments are executed on a desktop PC with a 3.6 GHz Intel Core i9-9900K, 32GB of memory, and an NVIDIA GTX 1080Ti graphics card with 11 GB graphics card RAM size.
An ablation study of the symmetry operation targeting at negative Poisson’s ratio (21). Upper row: symmetric initializations. Middle row: without symmetries. Bottom row: with symmetries. The resolution is \(128\times 128\times 128\) and the volume fraction is 20%
6.1 Symmetry
Symmetry is essential for designing isotropic material. We have predefined three symmetry types:
-
 : the reflection symmetry on three planes \(\left\{ x=0.5,y=0.5,z=0.5\right\} \) of the cube domain;
: the reflection symmetry on three planes \(\left\{ x=0.5,y=0.5,z=0.5\right\} \) of the cube domain; -
 : the reflection symmetry on six planes \(\{x=0.5, y=0.5,z=0.5,x+y=0,y+z=0,z+x=0\}\) of the cube domain;
: the reflection symmetry on six planes \(\{x=0.5, y=0.5,z=0.5,x+y=0,y+z=0,z+x=0\}\) of the cube domain; -
 : rotation symmetry means that the structure is invariant under the rotation of \(90^\circ \) around the x, y, z axes that pass through the cube domain’s center, as same under their compositions.
: rotation symmetry means that the structure is invariant under the rotation of \(90^\circ \) around the x, y, z axes that pass through the cube domain’s center, as same under their compositions.
Each symmetry splits the cube into many orbits. To enforce the symmetry, we set the density variables on the same orbit to their average. Figure 9 shows different symmetry results. When the initial value is symmetric, the optimization naturally ensures the symmetry even without reflect3 or rotate3 operation. However, the operation with or without reflect6 shows the most distinct structural difference. Specifically, the result without using reflect6 only possesses reflect3. We conjecture that since more symmetry restrictions exist in reflect6 than reflect3 or rotate3, the numerical and machine errors are enlarged with the optimization, thereby causing the symmetric constraint to be violated. Hence, we add symmetry operations to generate symmetric structures. In the experiments, we use the  symmetry by default.
symmetry by default.
We show different initial density fields (upper row) and optimized results (bottom row) for bulk modulus maximization (a\(_1\))-(a\(_3\)), shear modulus maximization (b\(_1\))-(b\(_3\)), and negative Poisson’s ratio materials (c\(_1\))-(c\(_3\)) with \(128\times 128\times 128\) elements under the volume fraction 10%
6.2 Density initializations
The optimization problem (1) admits a trivial solution, where all the density variables are the predefined volume ratio. Besides, it (1) has numerous local minima. The initial density field greatly influences which local minimum it converges to. Thus, it is necessary to construct various initial density fields to find desired microstructures. Previous work usually constructs initialization artificially and seldom discusses other ways of initialization, while we propose to increase the initialization diversity. Different initial density fields and their corresponding optimizated structures are shown in Fig. 10.
We use trigonometric functions to cover various initial density fields. We first try the following basis functions:
where the integer n determines the size of the initialization space, \({\textbf{x}}\in {\mathbb {R}}^3\) is the coordinate of the element’s center, \({\textbf{R}}_q\in {\mathbb {R}}^{3\times 3}\) is a rotation matrix determined by a normalized quaternion q with 4 random entries. Then, to exploit more initializations, we extend \(T_n\) as: \(Q_n=T_n\cup \left\{ p_1p_2 : p_1,p_2\in T_n\right\} \), where the products of any two items in \(T_n\) are incorporated. \(Q_n\) of each element is different.
To initialize a density field, we first generate a set of random numbers in \([-1,1]\) as weights, whose number is the number of the basis functions in \(Q_n\). Then, for each element, we use the obtained weights to weight the basis functions in \(Q_n\) and then sum them. Finally, we project the sum into \([\rho _{\min },1]\) via a rescaled Sigmoid function \(S(y)=\rho _{\min } + {\widehat{V}}/\left( {1+e^{-k(y-\mu )}}\right) \), where \(k=15\), \({\widehat{V}} = \min (1.5V,1)\), and \(\mu \) is determined by the binary search such that the volume constraint is satisfied after the projection. This projection aims to produce a valid density distribution, i.e., the constraint \(\rho _{min}\le \rho _{e} \le 1\) is satisfied for each element, and make the initialization far from the trivial solution. In Fig. 10, we use different initial density fields for optimization. Different initial density fields lead to different results, which are different local optimal solutions.
6.3 Mixed-precision scheme
To demonstrate the effectiveness of the proposed mixed-precision approach, we test various precision representations under the same configuration (optimization parameters, resolutions, and desktop PC). The statistics are shown in Table 1. A more precise representation of storage yields a smaller residual, albeit at the cost of increased memory consumption and iteration time. The computation time for pure single precision (FP32) is comparable to that of mixed precision (FP32/FP16). However, utilizing mixed precision (FP32/FP16) can lead to a 47% reduction comparing with pure FP32 in memory consumption. In addition, the relative error of different precisions in the final bulk modulus is less than 1.1%. In summary, due to this mixed-precision scheme, we can solve high-resolution examples with \(512^3 \approx 134.2\) million finite elements on only a NVIDIA GeForce GTX 1080Ti GPU.
6.4 Comparison with multi-CPU framework
We implement the multi-CPU framework Aage et al. (2015) and conduct the experiments on a cluster with a total of 9 nodes, each equipped with two Interl Xeon E5-2680 v4 28-core CPUs and 128GB memory connected by Intel OPA. Since we have verified that the relative residual \(10^{-2}\) is acceptable for IHPs (see Fig. 6), the relative residual thresholds for both multi-CPU and our frameworks are set as \(10^{-2}\). In Fig. 11, the same initialization is adopted for these two frameworks. The multi-CPU framework is configured based on the default settings mentioned in Aage et al. (2015) except the residual tolerance. The precision scheme used in Aage et al. (2015) is FP64, whereas we employ the mixed-precision scheme FP32/FP16. The final structures and moduli obtained by both frameworks are very similar. The average time of each iteration for the Multi-CPU framework is around 40.0 s, while our framework achieves a significantly reduced average time cost of 4.4 s.
Optimizing the bulk modules B using different material interpolation methods with a same initial density field and a same filtering radius. Left: we filter the density field via the  convolution kernel, i.e.,
convolution kernel, i.e.,
 .
Middle: we filter the density field by the linear convolution kernel. Right: we do not filter the density but filter sensitivity. The number of iterations are 282 (left), 255 (middle), and 100 (right), respectively
.
Middle: we filter the density field by the linear convolution kernel. Right: we do not filter the density but filter sensitivity. The number of iterations are 282 (left), 255 (middle), and 100 (right), respectively
6.5 Extending our framework
Users can optimize material properties according to their own goals through our framework. To verify the scalability of the framework, we optimize (21) and (22) to achieve the negative Poisson’s ratio structures using different density fields, as shown in Fig. 12. From the results, both objective functions can lead to negative Poisson’s ratios and have their own advantages. It is an interesting future work to design specific initial density fields so that the objective functions can be optimized to get smaller Poisson’s ratios.
In Fig. 13, we test three material interpolation methods for optimizing the bulk modules. The sensitivity filtering of the OC solver is better than density filtering as it has fewer iteration numbers and generates a greater bulk modules.
When the symmetry operation is not enforced, the microstructure is not guaranteed to be well connected. Therefore, we modify the filter kernel to be periodic to improve connectivity (see the zoomed-in views in Fig. 14). When filtering the sensitivity or density of elements near the boundary, the periodic filter kernel encompasses those elements near the opposite boundary as if multiple unit cells are connected along the boundaries.
6.6 Resolution
We test the applications by optimizing bulk modulus (19), shear modulus (20), and negative Poisson’s ratio (21) with three different resolutions \(64\times 64 \times 64\), \(128\times 128 \times 128\), \(256\times 256 \times 256\) in Fig. 15. The increase in computational resolution provided by GPU implementation leads to design improvement. The respective bulk moduli of the optimized results with different resolutions are 0.1111, 0.1124, and 0.1127. The shear moduli of the three structures are 0.0653, 0.0721, and 0.0741, respectively. With the increase in resolution, the results show a clear improvement in values and details. A similar conclusion can be obtained for the negative Poisson’s ratio microstructures in Fig. 15c.
Various resolutions for bulk modulus maximization (a), shear modulus maximization (b), and negative Poisson’s ratio materials (c). Left: \(64\times 64\times 64\). Middle: \(128\times 128\times 128\). Right: \(256\times 256\times 256\). The volume fraction is \(30\%\) for (a & b) and \(20\%\) for (c)
To further validate the effect of resolution on structural properties, we run our optimization on bulk modulus 100 times with different initializations for each resolution, count the resulting bulk modulus, and show the statistics in Fig. 16. The results show that most of the bulk modulus concentrates near the high value when the resolution is high. There are also more outliers as the resolution becomes lower. The lower the resolution, the more likely it is to approach the trivial solution.
The highest achievable resolution using our current setup is \(512^3\). This limitation remains in place, even though the peak memory usage of 9GB does not completely utilize the device memory. This constraint arises due to the need to consider the establishment of a multigrid hierarchy via iterative grid coarsening. Ideally, the resolution of the finest grid should be a multiple of a power of 2 to streamline this process. Failing to meet this condition would necessitate an increase in resolution to generate an adequate number of coarse grid levels, quickly surpassing our memory capacity. As a result, the largest resolution manageable with our current setup appears to be capped at \(512^3\).
6.7 Volume fraction
In Fig. 17, three applications are optimized for volume ratios from 10 to 30%. When the volume ratio is 10%, the results of the bulk modulus and shear modulus optimization are similar to the P surface. With the increase of volume fraction, the structures become diversified. However, with the increase of volume fraction, the structure changes from rod structure to closed wall structure for the negative Poisson’s ratio structures. In Fig. 18, we also compare our optimized results with the Voigt bound (Voigt 1928), which provides a theoretical bound of the shear modulus of anisotropic materials under different volume ratios. Increasing the resolution of the microstructure would be considered in the future to obtain the microstructures closer to the upper limit of the theoretical value.
7 Conclusions
We have proposed an optimized, easy-to-use, open-source GPU solver for large-scale inverse homogenization problems. Through a software-level design technology exploration, a favorable combination of data structures and algorithms, which makes full use of the parallel computation power of today’s GPUs, is developed to realize a time- and memory-efficient GPU solver. Specifically, we use the mixed-precision representation (FP32/FP16) and incorporate padding to handle periodic boundary conditions. Consequently, this new implementation is carried out on a standard computer with only one GPU operating at the software level. Topology optimization for achieving high-resolution 3D microstructures becomes computationally tractable with this solver, as demonstrated by our optimized cells with up to \(512^3\) (134.2 million) elements. Our framework is easy-to-use, and the used automatic differentiation technique enables users to design their own objective functions and material interpolation methods. Code for this paper is publicly available at https://github.com/lavenklau/homo3d.
Future work and limitations Even though our framework is designed to be user-friendly, it needs to modify the source code for specific goals; however, indiscreet modification may produce unexpected compilation or runtime errors. Heavy dependence on the templates makes it harder to track the error. In future work, we would work on providing a better user interface, e.g., encapsulating the framework as a python module that the user could import.
The most time consuming part of our solver is solving the FEM equation which takes several V-cycles. Within our current configuration, overlapped memory access exists between consecutive vertices on their common neighboring vertices or elements. This overlap leads to a wastage of bandwidth, impeding optimal performance. Advanced data structures and access patterns such as block partition Liu et al. (2018) may be designed to potentially achieve further acceleration.
We support a few material interpolation methods and will add more (e.g., RAMP scheme Stolpe and Svanberg (2001)) in future work. Besides, geometry represented by an implicit function will be added later, where the tensor variable becomes the parameters of a set of implicit functions.
References
Aage N, Andreassen E, Lazarov BS (2015) Topology optimization using PETSc: an easy-to-use, fully parallel, open source topology optimization framework. Struct Multidisc Optim 51:565–572
Allaire G (2002) Shape optimization by the homogenization method. Springer, New York
Andreassen E, Andreasen CS (2014) How to determine composite material properties using numerical homogenization. Comput Mater Sci 83:488–495
Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in MATLAB using 88 lines of code. Struct Multidisc Optim 43:1–16
Ben Khalifa D, Martel M, Adjé A (2020) Pop: a tuning assistant for mixed-precision floating-point computations. In: International workshop on formal techniques for safety-critical systems, pp 77–94
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202
Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224
Borrvall T, Petersson J (2001) Large-scale topology optimization in 3d using parallel computing. Comput Methods Appl Mech Eng 190(46–47):6201–6229
Briggs WL, Henson VE, McCormick SF (2000) A multigrid tutorial
Challis VJ, Roberts AP, Grotowski JF (2014) High resolution topology optimization using graphics processing units (GPUs). Struct Multidisc Optim 49(2):315–325
De Sturler E, Paulino GH, Wang S (2008) Topology optimization with adaptive mesh refinement. In: Proceedings of the 6th international conference on computation of shell and spatial structures IASS-IACM, pp 28–31
Dick C, Georgii J, Westermann R (2011) A real-time multigrid finite hexahedra method for elasticity simulation using CUDA. Simul Model Pract Theory 19(2):801–816
Gao J, Xue H, Gao L, Luo Z (2019) Topology optimization for auxetic metamaterials based on isogeometric analysis. Comput Methods Appl Mech Eng 352:211–236
Gao J, Xiao M, Gao L, Yan J, Yan W (2020) Isogeometric topology optimization for computational design of re-entrant and chiral auxetic composites. Comput Methods Appl Mech Eng 362:112876
Gao J, Wang L, Luo Z, Gao L (2021) IgaTop: an implementation of topology optimization for structures using IGA in MATLAB. Struct Multidisc Optim 64(3):1669–1700
Gibiansky LV, Sigmund O (2000) Multiphase composites with extremal bulk modulus. J Mech Phys Solids 48(3):461–498
Göddeke D, Strzodka R (2010) Cyclic reduction tridiagonal solvers on GPUs applied to mixed-precision multigrid. IEEE Trans Parallel Distrib Syst 22(1):22–32
Griewank A, Walther A (2008) Evaluating derivatives, 2nd edn. Society for Industrial and Applied Mathematics
Groen JP, Sigmund O (2018) Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int J Numer Methods Eng 113(8):1148–1163
Haidar A, Tomov S, Dongarra J, Higham NJ (2018) Harnessing GPU tensor cores for fast fp16 arithmetic to speed up mixed-precision iterative refinement solvers. SC18: international conference for high performance computing. Networking, storage and analysis, IEEE, pp 603–613
Hosseini MT, Ghaffari A, Tahaei MS, Rezagholizadeh M, Asgharian M, Nia VP (2023) Towards fine-tuning pre-trained language models with integer forward and backward propagation. Find Assoc Comput Linguist: EACL 2023:1867–1876
Huang X, Radman A, Xie YM (2011) Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput Mater Sci 50(6):1861–1870
Huang X, Xie YM, Jia B, Li Q, Zhou S (2012) Evolutionary topology optimization of periodic composites for extremal magnetic permeability and electrical permittivity. Struct Multidisc Optim 46(3):385–398
Li H, Luo Z, Gao L, Qin Q (2018) Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput Methods Appl Mech Eng 331:536–561
Liu H, Hu Y, Zhu B, Matusik W, Sifakis E (2018) Narrow-band topology optimization on a sparsely populated grid. ACM Trans Gr (TOG) 37(6):1–14
Liu H, Hu Y, Zhu B, Matusik W, Sifakis E (2018) Narrow-band topology optimization on a sparsely populated grid. ACM Trans Gr 37(6):1–14
McAdams A, Zhu Y, Selle A, Empey M, Tamstorf R, Teran J, Sifakis E (2011) Efficient elasticity for character skinning with contact and collisions. In: ACM SIGGRAPH 2011 papers, pp 1–12
Morvaridi M, Carta G, Bosia F, Gliozzi AS, Pugno NM, Misseroni D, Brun M (2021) Hierarchical auxetic and isotropic porous medium with extremely negative Poisson’s ratio. Extreme Mech Lett 48:101405
Nishiwaki S, Frecker MI, Min S, Kikuchi N (1998) Topology optimization of compliant mechanisms using the homogenization method. Int J Numer Methods Eng 42(3):535–559
Panetta J, Zhou Q, Malomo L, Pietroni N, Cignoni P, Zorin D (2015) Elastic textures for additive fabrication. ACM Trans Gr 34(4):1–12
Radman A, Huang X, Xie Y (2013) Topological optimization for the design of microstructures of isotropic cellular materials. Eng Optim 45(11):1331–1348
Rong Y, Zhao ZL, Feng XQ, Xie YM (2022) Structural topology optimization with an adaptive design domain. Comput Methods Appl Mech Eng 389:114382
Shan S, Kang SH, Zhao Z, Fang L, Bertoldi K (2015) Design of planar isotropic negative Poisson’s ratio structures. Extreme Mech Lett 4:96–102
Sigmund O (1994) Materials with prescribed constitutive parameters: an inverse homogenization problem. Int J Solids Struct 31(17):2313–2329
Sigmund O (2001) A 99 line topology optimization code written in MATLAB. Struct Multidisc Optim 21(2):120–127
Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45(6):1037–1067
Stainko R (2006) An adaptive multilevel approach to the minimal compliance problem in topology optimization. Commun Numer Methods Eng 22(2):109–118
Stolpe M, Svanberg K (2001) An alternative interpolation scheme for minimum compliance topology optimization. Struct Multidisc Optim 22(2):116–124
Sun J, Peterson GD, Storaasli OO (2008) High-performance mixed-precision linear solver for FPGAS. IEEE Trans Comput 57(12):1614–1623
Suzuki K, Kikuchi N (1991) A homogenization method for shape and topology optimization. Comput Methods Appl Mech Eng 93(3):291–318
Theocaris P, Stavroulakis G, Panagiotopoulos P (1997) Negative Poisson’s ratios in composites with star-shaped inclusions: a numerical homogenization approach. Arch Appl Mech 67(4):274–286
Träff EA, Rydahl A, Karlsson S, Sigmund O, Aage N (2023) Simple and efficient GPU accelerated topology optimisation: codes and applications. Comput Methods Appl Mech Eng 410:116043
Vogiatzis P, Chen S, Wang X, Li T, Wang L (2017) Topology optimization of multi-material negative Poisson’s ratio metamaterials using a reconciled level set method. Comput-Aided Des 83:15–32
Voigt W (1928) Lehrbuch der kristallphysik (textbook of crystal physics). BG Teubner, Leipzig
Wu J, Dick C, Westermann R (2015) A system for high-resolution topology optimization. IEEE Trans Vis Comput Gr 22(3):1195–1208
Xia L, Breitkopf P (2015) Design of materials using topology optimization and energy-based homogenization approach in MATLAB. Struct Multidisc Optim 52(6):1229–1241
Zhang D, Zhai X, Fu XM, Wang H, Liu L (2022) Large-scale worst-case topology optimization. Comput Gr Forum 41(7)
Zhang H, Chen D, Ko SB (2019) Efficient multiple-precision floating-point fused multiply-add with mixed-precision support. IEEE Trans Comput 68(7):1035–1048
Zhu Y, Sifakis E, Teran J, Brandt A (2010) An efficient multigrid method for the simulation of high-resolution elastic solids. ACM Trans Gr (TOG) 29(2):1–18
Acknowledgements
The authors would like to acknowledge the financial support from the Provincial Natural Science Foundation of Anhui (2208085QA01), the Fundamental Research Funds for the Central Universities (WK0010000075), the National Natural Science Foundation of China (61972368 and 62025207).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
Important details for replication of results have been described in the manuscript. Code for this paper is at https://github.com/lavenklau/homo3d.
Additional information
Responsible Editor: Ole Sigmund.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, D., Zhai, X., Liu, L. et al. An optimized, easy-to-use, open-source GPU solver for large-scale inverse homogenization problems. Struct Multidisc Optim 66, 207 (2023). https://doi.org/10.1007/s00158-023-03657-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-023-03657-y













 is a parsed configuration file with command line arguments, including the Young’s modulus and Poisson’s ratio of the base material, grid resolution, volume fraction, initialization type, symmetry requirement, etc.
is a parsed configuration file with command line arguments, including the Young’s modulus and Poisson’s ratio of the base material, grid resolution, volume fraction, initialization type, symmetry requirement, etc.
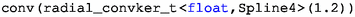 means a convolution operation with the kernel
means a convolution operation with the kernel
 , which is same with the filtering method of (Wu et al.
, which is same with the filtering method of (Wu et al.  and the material interpolation method
and the material interpolation method
 :
:




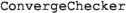 is a class to check convergence,
is a class to check convergence,  is a
function to symmetrize a 3D tensor according to a given symmetry type. In this routine, we do not filter the sensitivity since the density is already filtered.
is a
function to symmetrize a 3D tensor according to a given symmetry type. In this routine, we do not filter the sensitivity since the density is already filtered.
 is
a function to prefix the output directory to a given string. The member function
is
a function to prefix the output directory to a given string. The member function  writes the
data of
writes the
data of  to a
OpenVDB file.
to a
OpenVDB file.

 : the reflection symmetry on three planes
: the reflection symmetry on three planes  : the reflection symmetry on six planes
: the reflection symmetry on six planes  : rotation symmetry means that the structure is invariant under the rotation of
: rotation symmetry means that the structure is invariant under the rotation of 







