1 Introduction

In structural design, safety and cost are the two main contradictory design criteria that have to be met simultaneously by designers. While cost savings can reduce the safety level of structures, improving safety may result in increasing costs (Melchers and Beck 2018). Moreover, uncertainty is the intrinsic characteristic of all engineering systems in real world and can be associated with material properties and physical quantities such as dimensions, manufacturing tolerances, and external loads. Although traditional deterministic design optimization methods can reduce the design costs, they ignore the effects of uncertainty which can result in unreliable structures and even catastrophic failures. Accordingly, reliability-based design optimization (RBDO) methods have been introduced that use structural reliability theory to take the effect of uncertainty into account (Shayanfar et al. 2018). The main objective of this theory is to find the failure probability \({p}_{f}\) based on Limit State Functions (LSF) or performance functions, and can be evaluated as (Liu and Der Kiureghian 1991):

$${P}_{f}=\int \dots {\int }_{G\left({\varvec{X}}\right)\le 0}^{ }{f}_{X}\left({x}_{1},{x}_{2},\dots ,{x}_{n}\right){dx}_{1}\dots {dx}_{n}={\int }_{G\left({\varvec{X}}\right)\le 0}^{ }{f}_{X}({\varvec{X}})dx,$$
(1)

where \({\varvec{X}}={\left[{x}_{1},{x}_{2},\dots ,{x}_{n}\right]}^{T}\) is the vector of random variables, \({f}_{X}({\varvec{X}})\) is the joint probability density function (JPDF) of random variables vector, \(G\left({\varvec{X}}\right)\) is the LSF, and \(G\left({\varvec{X}}\right)\le 0\) indicates failure region. The JPDF of random variables is usually rarely known and evaluating the above-mentioned multi-dimensional integral is also a very daunting task, especially in the case of dealing with highly complicated implicit LSFs. Therefore, the aforementioned computational challenges have led to the development of alternative ways to estimate \({P}_{f}\). These alternatives can be grouped into two main methods: (1) simulation methods such as Monte Carlo simulation (MCS), importance sampling (IS), and Latin hypercube (LHC). (2) approximation methods including first-order reliability methods (FORM) and second-order reliability methods (SORM). In comparison with FORM, SORM has more accuracy, but more computational burden since it requires to calculate second derivates. So, FORM is widely used in RBDO for its effectiveness and less effort. There are two different first-order reliability assessment approaches including the reliability index approach (RIA) and performance measure approach (PMA). While in the former, the algorithm seeks for the most probable failure point (MPFP) on the LSF surface with the minimum distance from the origin, in the latter, the algorithm searches for the minimum performance target point (MPTP) on the target reliability index hypersphere.

In the RIA, the most commonly used algorithm is HL-RF which was first introduced by Hasofer and Lind (Hasofer and Lind 1974) and was further developed by Rackwitz and Flesser with the inclusion of distribution information of random variables (Rackwitz and Flessler 1978). Although this method has a fast convergence rate for linear and some moderately nonlinear LSFs, it can produce periodic oscillation or fail to converge for some simple and highly nonlinear LSFs, which can result in unstable solutions. Therefore, ample studies have been done to circumvent these problems and increase the accuracy and speed of the method. A modified HL-RF that uses a merit function to monitor the convergence of the method was proposed in (Liu and Der Kiureghian 1991). Different merit functions were also developed to determine the step length (Zhang 1994; Santos et al. 2012). Stability transformation method (STM) of chaos feedback control was employed in the chaos control (CC) method for convergence control of FORM (Yang 2010). Despite its higher robustness compared with the HL-RF, CC method is computationally expensive for highly nonlinear problems and converges very slowly due to its small control factor. To alleviate its computational cost, various improved CC methods such as enhanced HL-RF (EHL-RF) (Kang et al. 2011), adaptive chaos control (ACC) (Li et al. 2015), enhanced chaos control (ECC) (Hao et al. 2017), directional stability transformation method (DSTM) (Meng et al. 2017) were proposed in which the control parameter is adaptively chosen between 0 and 1 based on various criteria. Finite-step-length (FSL) iterative algorithm was introduced in (Gong and Yi 2011) that uses a new step length in the direction of the gradient vector. Roudak et al. proposed a generalization of HL-RF and FSL that uses two parameters to eliminate the numerical instability of HL-RF (Roudak et al. 2017). Different methods were introduced to calculate the optimum search direction in each iteration. Keshtegar and Miri adopted the conjugate gradient approach and Wolfe conditions to compute the search direction and step size, respectively, in line (Keshtegar and Miri 2014). Conjugate stability transformation (CSTM) (Keshtegar 2016a, b), chaotic conjugate control (CCC) (Keshtegar 2016a, b), conjugate finite-step-length (CFSL) (Keshtegar 2017a, b) were also developed by Keshtegar et al. to improve the robustness of FORM. Several studies have shown that RIA is less efficient than PMA due to its low numerical efficiency (Lee et al. 2002).

In the PMA, the main idea is the fact that minimizing a complicated function under simple constraints is much easier than minimizing a simple function under complicated constraints (Aoues and Chateauneuf 2010). So, the target reliability level is defined in advance and MPTP is sought on this level. Advanced mean value (AMV) (Wu et al. 1990) uses the steepest decent direction to find MPTP and is the fastest approach for convex problems. However, it cannot perform well for concave and highly nonlinear LSFs, so unstable solutions such as oscillation, bifurcation, and slow convergence may occur. Thus, conjugate mean value (CMV) and hybrid mean value (HMV) were proposed (Youn et al. 2003). Despite the good convergence of the HMV method for convex and slightly nonlinear problems, it fails to converge for highly nonlinear concave LSFs. Enhanced hybrid mean value (EHMV) was proposed further by Youn to increase numerical efficiency (Youn et al. 2005). Meng et al. reduced the computational cost of the CC method by extending the iterative points to the \(\beta\)-hypersphere known as MCC method (Meng et al. 2015). The efficiency of the PMA was improved by the studies of Keshtegar et al. in relaxed PMA (Keshtegar et al. 2016c), modified advanced mean value (MMV) (Keshtegar 2017a, b), and Self-adaptive modified chaos control (SMCC) (Keshtegar et al. 2017c). Hybridized conjugate mean value (HCMV) (Zhu et al. 2021), Dynamical accelerated chaos control (DACC) (Keshtegar et al. 2018a), and Augmented step size adjustment (ASSA) (Hao et al. 2019) are other methods that improved stability and robustness of PMA.

In recent years, various methods have been proposed for solving RBDO problems (Shayanfar et al. 2018). A traditional strategy is a nested two-level approach called the double-loop approach in which, the outer loop is responsible for deterministic constrained optimization (DO), whereas the inner loop, which is responsible for reliability analysis, assesses the value of random variables by computing the failure probability based on predefined limit state functions. Accordingly, either PMA or RIA can be used in this loop. Despite the simplicity of the classic RBDO, the computational costs can be very high since a large number of function evaluations may be needed. Therefore, single-loop and decoupled methods have been proposed for efficiency improvement (Jeong and Park 2017). In single-loop approaches, the reliability analysis is removed by replacing probabilistic constraints with equivalent deterministic constraints. In decoupled methods, reliability analysis is separated from deterministic optimization. Sequential optimization and reliability assessment (SORA) is one of the robust decoupled methods proposed by (Du and Chen 2004) which will be discussed further. It is also worth mentioning that machine learning-based RBDO methods have been developed recently (Li and Wang 2020, 2022). The Kriging method has been employed in various studies to develop surrogate models (Wang and Wang 2013). Surrogate modeling is a special case of supervised machine learning that is trained using a data-driven approach and the idea behind this method is to replace the original computationally expensive model with a cheap easy-to-analysis approximation model to reduce both time and computer runs and increase efficiency. Moreover, time-variant RBDO framework is another area which has been investigated in several studies like (Wang et al. 2021, 2022).

One of the recently developed methods that uses adaptive chaos control factor is proposed by (Roudak et al. 2018). This method that employs the RIA with two internal parameters and a criterion to alter the control parameter during the computation process, exhibits numerical stability and small iteration numbers to reach MPP. However, it suffers from a high number of function evaluations in each iteration to achieve the proper control parameter. Therefore, in this study, it has been tried to reduce the computational burden of this algorithm by introducing novel criteria through two stages in DS-MACC to distinguish the type of function and modify the step length. Furthermore, to improve the numerical efficiency, the idea of SORA is employed in this study to expedite the RBDO process. The proposed algorithm is compared with AMV, HMV, MCC, improved adaptive CC (IACC), and some other recent methods for mathematical and structural reliability analysis and RBDO problems.

The organization of this paper is as follows. RBDO formulation as well as RIA and PMA approaches are illustrated in Sect. 2. IACC method is explained in detail within Sect. 3. In the next two sections, the proposed method is introduced and formulated. Illustrative examples are used to compare aforementioned methods in Sect. 6. Eventually, the conclusion is drawn in last Section.

2 Formulation of the reliability-based design optimization (RBDO)

The mathematical model of the classic two-level RBDO is generally formulated as follows:

$$\begin{gathered} Find\,\,\,\, {\varvec{d}},{\varvec{\mu}}_{{\varvec{X}}} \hfill \\ Minimize\,\, f\left( {{\varvec{d}},{\varvec{X}}} \right) \hfill \\ s.t. \,\,\,\,P_{f} \left( {G_{i} \left( {{\varvec{d}},{\varvec{X}}} \right) \le 0} \right) \le P_{f,i}^{t} \hfill \\ Where \,\,\,\,P_{f,i}^{t} = {\Phi }\left( { - \beta_{t}^{i} } \right), i = 1,2, \ldots ,m \hfill \\ {\varvec{d}}^{L} \le {\varvec{d}} \le {\varvec{d}}^{U} \hfill \\ \end{gathered},$$
(2)

where \({\varvec{d}}\) represents design variables vector with the lower and upper bounds of \({{\varvec{d}}}^{L}\) and \({{\varvec{d}}}^{U}\) for each variable, respectively. \({\varvec{X}}\) is the random variables vector and \({{\varvec{\mu}}}_{{\varvec{X}}}\) contains the mean value of these variables. \(f(.)\) is the objective function, \({G}_{i}\left(.\right)\) is the ith performance function (constraint function) and \(m\) is the number of probabilistic constraints. \({P}_{f}(.)\) and \({P}_{f,i}^{t}\) are the probability of failure and allowable failure probability, respectively. \({\beta }_{i}^{t}\) is the target reliability index of the ith performance function, and \(\Phi \left(.\right)\) stands for the standard normal cumulative distribution function. As mentioned before, to reduce the computational cost of the nested two-level RBDO, sequential optimization and reliability assessment (SORA) was proposed (Du and Chen 2004). In this method, deterministic optimization (DO) and reliability analysis are performed separately as follows. During the first cycle, constrained DO is carried out first to obtain the value of the design variables. Afterward reliability analysis is performed. At this stage, the feasibility of the constraint is checked, and the MPTP corresponding to each constraint is computed. This is the end of the first cycle. To start the next cycle, a shifting vector is needed to move the violated constraints to the feasible zone, and the DO in the next cycle is performed with shifted constraints. This shifting vector is computed based on the MPTP points obtained in the previous cycle as follows:

$${\varvec{s}}_{i}^{k} = {\varvec{\mu}}_{{\varvec{X}}}^{k - 1} - {\varvec{X}}_{{MPTP_{i} }}^{k - 1} ,\,\,\,\,\, i = 1,2, \ldots ,m$$
(3)

In which, \(k\) is the number of the current cycle, and \({{\varvec{\mu}}}_{{\varvec{X}}}^{k-1}\) is the vector of mean values of random design variables drawn during constrained DO of previous cycle \(k-1\). \({\varvec{X}}_{{MPTP_{i} }}^{k - 1}\) is the MPTP computed for the \(i\) th constraint in reliability analysis of previous cycle \(k-1\), and \(m\) is the number of constraints. This should be noted that this vector for unviolated constraints is \(0\). The formulation of SORA is mathematically expressed as:

$$\begin{gathered} Find\,\,\, {\varvec{d}},{\varvec{\mu}}_{{\varvec{X}}} \hfill \\ Minimize\,\,\, f\left( {{\varvec{d}},{\varvec{\mu}}_{{\varvec{X}}} } \right) \hfill \\ s.t. \,\,\,\,\,G_{i} \left( {{\varvec{d}},{\varvec{\mu}}_{{\varvec{X}}} - {\varvec{s}}_{i}^{k} } \right) \ge 0,\,\,\,\, i = 1,2, \ldots ,m \hfill \\ \end{gathered}$$
(4)

Thus, as the aforementioned procedure goes on, the reliability of the optimum design is augmented and the probability of the failure is reduced. Eventually, when the probabilistic constraints are feasible and the convergence condition is met, the algorithm stops. The schematic view of the SORA process in the first and last cycles are illustrated in Fig. 1.

Fig. 1
figure 1

Schematic view of SORA procedure a DO in the first cycle, b Shifting constarints before the last cycle, c Finding the reliable optimum design in the last cycle

Full size image

The probabilistic constraints of the RBDO can be assessed by two alternative approaches of RIA and PMA which have been introduced briefly before. In RIA, the reliability index is obtained by solving the following constrained optimization problem:

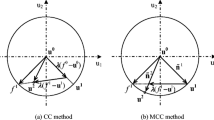
$$\begin{gathered} \mathop {\min }\limits_{u} { }\left| {\left| {\varvec{U}} \right|} \right| \hfill \\ s.t.\,\,\,\,\,{ }G_{i} \left( {\varvec{U}} \right) \le 0 \hfill \\ \end{gathered},$$
(5)

where \({\varvec{U}}\) is the vector of random variables transformed from \(X\)-space to standard normal space (\(U\)-space). In Fig. 2a, the schematic view of this approach for a two-variable LSF can be easily observed. As it is obvious, in RIA, the algorithm tries to find the minimum distance from the origin to the limit state \(G\left({\varvec{U}}\right)=0\). Therefore, the radius of the \(\beta\)-circle varies as the iterations go on until it touches the limit state surface. The distance is called reliability index. Whereas, in PMA, as can be seen in Fig. 2b, the radius of \(\beta\)-circle is constant and equal to the target reliability index \({\beta }^{T}\), and the algorithm searches for MPTP over this circle. PMA can be mathematically expressed as:

$$\begin{gathered} \mathop {\min }\limits_{u} { }G_{i} \left( {\varvec{U}} \right) \hfill \\ s.t.\,\,\,\,\,{ }\left| {\left| {\varvec{U}} \right|} \right| = \beta_{{i{ }}}^{T} \hfill \\ \end{gathered}$$
(6)
Fig. 2
figure 2

Illustration of a RIA and b PMA approaches

Full size image

3 Improved FORM method using adaptive chaos control (IACC)

The process of chaos control method is formulated as follows (Yang and Yi 2009):

$$\left({{\varvec{U}}}_{k+1}^{CC}\right)={{\varvec{U}}}_{k}^{CC}+\lambda {\varvec{C}}\left(f\left({{\varvec{U}}}_{k}\right)-{{\varvec{U}}}_{k}^{CC}\right)\,\,\,\, 0<\lambda <1,$$
(7)

where \({\varvec{C}}\) is the \(n\times n\) dimensional involutory matrix with merely one element in each row. The value of elements in each column is 1 or − 1 and the other ones are 0 in this matrix. So, there are \({2}^{n}n!\) Involutory matrixes can be selected. However, the unit matrix \({\varvec{I}}\) is usually picked as matrix \({\varvec{C}}\). \(\lambda\) is the control factor and is determined based on the eigenvalues of the original system’s Jacobian matrix. \(f\left( {{\varvec{U}}_{k}^{{}} } \right)\) is the next iterative point calculated using steepest descent direction. While a small value for control factor \(\lambda\) can lead to a more robust iterative process, especially for highly nonlinear problems, the computational cost can become very exorbitant. Conversely, a large value of \(\lambda\) can be very efficient, however, the possibility of oscillation or divergence may rise. In the CC method usually, a fixed and relatively small value of \(\lambda\) is selected for the iterative process, which can result in a large number of iterations to reach MPFP. Therefore, efficiency is obviously sacrificed for accuracy especially when a larger value for \(\lambda\) may work. Roudak et al. proposed a method that is RIA-based and employs a varying control parameter \(\lambda\) to improve the efficiency of the CC method (Roudak et al. 2018). In the IACC method, \(\lambda\) is proportional to the rate of convergence and is reduced based on the nonlinearity degree in a specific part of an LSF by considering the change in the direction of the two consecutive gradient vectors. At the onset of the search process of this method, \(\lambda\) is equal to 1 and its reduction is controlled with three parameters \({c}_{1}\), \({c}_{2}\), and \(b\), all of which are between 0 to 1. In the following, the function of these parameters is explained briefly.

Consider this algorithm is performing the kth iteration and wants to find the next iterative point \(({{\varvec{U}}}_{k+1})\). To do so, the last value of \(\lambda\) is first chosen to compute \({{\varvec{U}}}_{k+1}\). Then, \(\nabla {G({\varvec{U}}}_{k+1})\) is calculated at that point. Here, a criterion is utilized for checking the direction of the two gradient vectors in current and prospective iterative points; thus, the cosine of the angle between the aforementioned vectors is computed by the following relation:

$$cos \,{\theta }_{k}=\frac{\nabla {G({\varvec{U}}}_{k}) \nabla {G({\varvec{U}}}_{k+1})}{\left|\nabla {G({\varvec{U}}}_{k})\right|\left|\nabla {G({\varvec{U}}}_{k+1})\right|}$$
(8)

If \(|cos {\theta }_{k}|\) is larger than b, \({{\varvec{U}}}_{k+1}\) is accepted and \(\lambda\) is decreased very slightly as \(\lambda ={c}_{2}\lambda\). If not, \(\lambda ={c}_{1}\lambda\) and \({{\varvec{U}}}_{k+1}\) will be re-calculated using the new reduced value of \(\lambda\) and this continues until the relation expressed in Eq. 8 is larger than b. In the aforementioned study, values of \({c}_{1}\), \({c}_{2}\), and \(b\) are suggested to be 0.9, 0.99, and 0.95, respectively. \({c}_{1}\) is the local sensitivity controller; the closer the value of \({c}_{1}\) is to 1, the more conservative the iterative process will be, since \(\lambda\) is reduced very slowly. When the nonlinearity degree of the LSF is high, this is favored, however, this can lead to a high number of function evaluations. When the angle between two consecutive gradient vectors is sufficiently small, to prevent oscillation, the value of \(\lambda\) is not let to be constant, so \({c}_{2}\) which is very close to unity is used to reduce the control parameter slightly. In addition, the value of \(b\) determines the severity of Eq. 8. A larger value of \(b\) indicates a more limited accepted range for the angle between two successive gradient vectors, consequently, the convergence rate may reduce. Whereas, by a smaller value for \(b\), the process is faster, but the risk of divergence increases.

The above-mentioned method has been successful in reducing the number of iterations and is robust during the iterative process, which will be illustrated in Sect. 6. However, the high number of function evaluations is the main deficiency of this algorithm. Considering a constant fixed value such as \({c}_{1}\) or \({c}_{2}\) for control parameter reduction, especially in first iterations, the computational cost is still high which can reduce the efficiency of the algorithm. Moreover, RIA-based algorithms typically require much more function evaluations. What is more, considering the absolute value of the \(\mathit{cos}{\theta }_{k}\) is not efficient, because in case of highly nonlinear LSFs, this can lead to slow convergence of the algorithm i.e., if \(\mathit{co}s{\theta }_{k}\) is − 0.97, its absolute value is 0.97 which is greater than \(b=0.95\). This means the algorithm should modify the step size with \({c}_{2}\) parameter which is too slow. In Sect. 6, example 7 is a good illustration of this problem which will be discussed further. For this reason, in the next section, these problems are tackled to improve the efficiency of this algorithm.

4 Proposed method

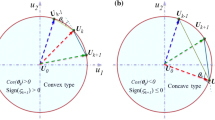
In reliability methods using chaos control, all use a control parameter to prevent chaotic solutions. The important thing is what value should be chosen for this control parameter to reach a balance between the number of function calls and convergence. For instance, a very small value of control parameter λ may be able to converge to MPP but needs thousands of iterations to do so and vice versa. Thus, the value of λ is very effective. Some methods like the MCC method use small and fixed values for this parameter which cannot guarantee convergence and may lead to high computational cost. Some methods use varying values of λ during the process which is more reasonable. In our study, we tried to use the available information at each iteration to find an appropriate value of λ and modify it at each iteration to reach high efficiency and fast convergence. In this section, double-step modified adaptive chaos control (DS-MACC) method is proposed to alleviate the high computational cost of the IACC method. Besides, the proposed method is coupled with SORA to enhance the efficiency and convergence speed of the RBDO. In the first step, two new criteria are introduced to find the intervals in which MPTP may exist. Information required to check the conditions are demonstrated in the following relations:

$$\mathit{cos}\,\,{\theta }_{1}=\frac{{{\varvec{U}}}_{k-1}{{\varvec{U}}}_{k}}{\left|{{\varvec{U}}}_{k-1}\right|\left|{{\varvec{U}}}_{k}\right|}, \mathit{cos}{\theta }_{2}=\frac{{{\varvec{U}}}_{k+1}^{AMV}{{\varvec{U}}}_{k}}{\left|{{\varvec{U}}}_{k+1}^{AMV}\right||{{\varvec{U}}}_{k}|},$$
(9)

where \({\theta }_{1}\) is the angle between the current (\({{\varvec{U}}}_{k}\)) and previous iterative points (\({{\varvec{U}}}_{k-1}\)) which can be seen in Fig. 3. The next relation is the same as Eq. 8 as follows:

Fig. 3
figure 3

Illustration of \({\theta }_{1}\) and \({\theta }_{2}\) for different types of LSFs

Full size image
$$cos\, {\theta }_{k}=\frac{\nabla {G({\varvec{U}}}_{k}) \nabla {G({\varvec{U}}}_{k+1})}{\left|\nabla {G({\varvec{U}}}_{k})\right|\left|\nabla {G({\varvec{U}}}_{k+1})\right|}$$
(10)

To predict the probable location of MPTP, there are 3 different conditions:

1. Steepest descent direction is the direction through which, the value of the performance function decreases at its fastest rate and it also points to the minimum of the performance function. Thus, if the cosine of the angle between the current and previous iterative points is positive (\(cos {\theta }_{k}\ge 0\)), it means that MPTP is located out of the interval of \({{\varvec{U}}}_{k-1}\) and \({{\varvec{U}}}_{k}\). In addition, \({{\varvec{U}}}_{k+1}^{AMV}\) is utilized to find out if the steepest descent direction can be used as \({\varvec{U}}_{k + 1}^{{}}\) or not. In other words, if \(\left|\mathit{cos}{\theta }_{1}\right|\le \left|\mathit{cos}{\theta }_{2}\right|\) or (\({\theta }_{2}<{\theta }_{1}\)) defined in Eq. 9, steepest descent direction is the fastest and most efficient search direction; therefore, AMV method is adopted to calculate the next iterative point using Eq. 11 and the algorithm goes for the next iteration; otherwise, another approach is employed which will be explained further in this section.

$${{{\varvec{U}}}_{k+1}={\varvec{U}}}_{k+1}^{AMV}=-{\beta }_{T}\frac{\nabla G({{\varvec{U}}}_{k})}{\Vert \nabla G({{\varvec{U}}}_{k})\Vert }$$
(11)

To better understand this, consider the following example: \({G}_{1}\left(X\right)=-\mathrm{exp}\left({x}_{1}-7\right)-{x}_{2}+10\) is a convex function with two normally distributed random variables \({x}_{\mathrm{1,2}}\sim N(\mathrm{6,0.8})\), and the target reliability index is set as 3. This performance function is depicted in Fig. 4a. The first two iterative points that are calculated utilizing the steepest descent direction are shown with numbers 1 and 2. At each of them, negative normalized gradient vectors are illustrated with black arrows, and as can be observed, they point out the interval beyond \({{\varvec{U}}}_{1}\) and \({{\varvec{U}}}_{2}\). So, the next probable iterative point is obtained using the AMV method (Eq. 11). At this stage, the second criterion is checked. It can be easily seen that \(\left|\mathit{cos}{\theta }_{1}\right|\le \left|\mathit{cos}{\theta }_{2}\right|\), as a result, AMV method is chosen to calculate\({\varvec{U}}_{k + 1}^{{}}\).

Fig. 4
figure 4

Three different states of iterative histories a 1st state, b 2nd state, c 3rd state

Full size image

2. If \(cos {\theta }_{k}\le 0,\) MPTP is located between \({{\varvec{U}}}_{k}\) and \({{\varvec{U}}}_{k-1}\) and there is no need to check the other condition. Consider \({G}_{6}\left(X\right)=0.2Ln\left[\mathrm{exp}\left[5\left(1+{x}_{1}-{x}_{2}\right)\right]+\mathrm{exp}\left[5\left(5-5{x}_{1}-{x}_{2}\right)\right]\right]\) as an example, which is a concave function having two random variables with normal distributions: \({x}_{\mathrm{1,2}}\sim N(\mathrm{0,1})\), and \({\beta }_{t}\) is 3. This \({G}_{6}\left(x\right)\) is shown in Fig. 4b. Regarding the direction of the negative normalized gradient vectors, it is obvious that MPTP is between \({{\varvec{U}}}_{1}\) and \({{\varvec{U}}}_{2}\). When this occurs, the step length is calculated using \({{\varvec{U}}}_{k-1}\) and \({{\varvec{U}}}_{k}\). For doing so, the augmented step size adjustment (ASSA) method (Hao et al. 2019) is employed which offers one the most efficient step length adjustment processes. ASSA method uses a vector that is depicted in Fig. 5 to calculate the step length \(\lambda\). This vector which is expressed as \({\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}\) is calculated by the following relation (Hao et al. 2019):

Fig. 5
figure 5

Illustration of \(\overrightarrow{ab}\) vector

Full size image
$${\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}=-\frac{\nabla G\left({{\varvec{U}}}_{k}\right)}{\Vert \nabla G\left({{\varvec{U}}}_{k}\right)\Vert } - \frac{{{\varvec{U}}}_{k}}{\Vert {{\varvec{U}}}_{k}\Vert }$$
(12)

As shown in Fig. 5, \({\overrightarrow{ab}}^{k}\) links the endpoint of the normalized direction vector \(a\) to the endpoint of the normalized negative gradient vector \(b\) in the \(k\)th iteration. The step length \({\lambda }^{k}\) is then computed as follows:

$${\lambda }^{k}=\frac{\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}\Vert }{\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k-1}\Vert +\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}\Vert }|\left|{{\varvec{U}}}_{k}-{{\varvec{U}}}_{k-1}\right||$$
(13)

The next iterative point can be obtained by the following relations:

$${{\varvec{U}}}_{k+1}={\beta }^{t}\frac{n({{\varvec{U}}}_{k+1})}{|\left|n({{\varvec{U}}}_{k+1})\right||},\boldsymbol{ }\boldsymbol{ }{\varvec{n}}\left({{\varvec{U}}}_{k+1}\right)={{\varvec{U}}}_{k}+{\lambda }^{k}\frac{{{\varvec{U}}}_{k+1}^{AMV}-{{\varvec{U}}}_{k}}{|\left|{{\varvec{U}}}_{k+1}^{AMV}-{{\varvec{U}}}_{k}\right||}$$
(14)

3. As mentioned before, if \(cos {\theta }_{k}\ge 0,\) MPTP is located out of the interval \({{\varvec{U}}}_{k-1}\) to \({{\varvec{U}}}_{k}\). Additionally, if \(\left|\mathit{cos}{\theta }_{1}\right|>|\mathit{cos}{\theta }_{2}|\), the steepest descent direction may lead to divergence. This can be readily observed via the next example, a highly nonlinear performance function \({G}_{4}\left(X\right)=\mathrm{exp}\left(1.5{x}_{1}^{1.5}-5\right)+\mathrm{exp}\left(1.2{x}_{2}^{2}-15\right)-15\) (Keshtegar et al. 2018c) which is illustrated in Fig. 4c. The random variables are \({x}_{\mathrm{1,2}}\sim N(\mathrm{5,0.8})\) with \({\beta }_{t}=3\). In the corresponding figure, the iterative point \({U}_{3}\) depicts the current iteration and the algorithm wants to find the interval in which, MPTP is located. The negative normalized gradient vectors point out of \({U}_{2}\) and \({U}_{3}\). Furthermore, the location of the iterative point obtained by the AMV method cannot satisfy the second condition and this means the AMV method here, can lead to divergence or bifurcation, so it cannot be employed. Moreover, the direction of the steepest descent directions in points \({U}_{1}\) and \({U}_{3}\), illustrates the MPTP is somewhere between \({{\varvec{U}}}_{1}\) to \({{\varvec{U}}}_{3}\). Generally speaking, \({\lambda }^{k}\) in this state, is computed as:

$${\lambda }^{k}=\frac{\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}\Vert }{\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k-2}\Vert +\Vert {\overrightarrow{{\varvec{a}}{\varvec{b}}}}^{k}\Vert }|\left|{{\varvec{U}}}_{k}-{{\varvec{U}}}_{k-2}\right|||$$
(15)

when either of the second or third states happens, this is the end of the first step in which a trial \({{\varvec{U}}}_{k+1}\) is obtained and needed to be modified in the second step. Based on the criterion introduced in Eq. 16 the cosine of the angle between \(\nabla {G({\varvec{U}}}_{k})\) and \(\nabla {G({\varvec{U}}}_{k+1})\) should be greater than \(b\) which is considered to be 0.7 in this study. If this condition is met, \({{\varvec{U}}}_{k+1}\) is accepted and the next iteration will be performed; otherwise, \({\lambda }^{k}\) is reduced exponentially by Eq. 17 until the aforementioned criterion is satisfied. In Eq. 17, \(t\) is the number of times that the second step is performed until the \(k\)th iteration. So, \(t\) changes only when the second step is adopted. This prevents the step length reduction rate from being either too slow or too fast. If the LSF is highly nonlinear, during the step size modification in initial iterations, the \(t\) parameter causes the step size to reduce slightly, thereby searching the sensitive part of the performance function more efficiently. During the last iterations, the step length is usually very small and thus, less sensitive to the value of \(t\).

$$cos {\theta }_{k}=\frac{\nabla {G({\varvec{U}}}_{k}) \nabla {G({\varvec{U}}}_{k+1})}{\left|\nabla {G({\varvec{U}}}_{k})\right|\left|\nabla {G({\varvec{U}}}_{k+1})\right|}>b=0.7$$
(16)
$${\lambda }^{k}=\mathit{exp}\left(-\frac{t}{10}\right)|\left|{{\varvec{U}}}_{k+1}-{{\varvec{U}}}_{k}\right||$$
(17)

5 The iterative procedure of DS-MACC

Step 1: :

Define a performance function i.e., \(G({\varvec{d}},{\varvec{X}})\), target reliability index \({\beta }_{t}\), \({\varvec{\mu}}\) and \({\varvec{\sigma}}\) of random variables. Set \(k=0\), stopping criterion \(\varepsilon\), and the control parameter \(b\). (here, \(b\) is set as 0.7).

Step 2: :

Transform random variables from X-space to U-space.

Step 3: :

If \(k\le 3,\) then compute the new point based on the AMV method formula in Eq. 11.

Else; start the first step:

  • If \(\left|\mathit{cos}{\theta }_{1}\right|\le \left|\mathit{cos}{\theta }_{2}\right|\) (defined in Eq. 9) and \(cos {\theta }_{k}\ge 0\) (defined in Eq. 10), then compute the new point based on AMV method formula in Eq. 11. Afterward, go to Step 5

  • If \(cos {\theta }_{k}\le 0\), then Compute the trial point \({{\varvec{U}}}_{k+1}\) using Eqs. 12, 13, and 14. Afterward, go to the next step.

  • If \(\left|\mathit{cos}{\theta }_{1}\right|>|\mathit{cos}{\theta }_{2}|\), and \(cos {\theta }_{k}\ge 0\), then Compute the trial point \({{\varvec{U}}}_{k+1}\) using Eqs. 14 and 15. Afterward, go to the next step.

Step 4: :

checking the criterion introduced in Eq. 16 in the second step:

  • While \(cos {\theta }_{k}<b\), modify \({\lambda }^{k}\) using Eq. 17 and recalculate the \({{\varvec{U}}}_{k+1}\) until this criterion is satisfied.

Step 5: :

Check the convergence criterion: If \(\left|\left|{{\varvec{U}}}_{k+1}-{{\varvec{U}}}_{k}\right|\right|/|\left|{{\varvec{U}}}_{k}\right||<\varepsilon\), then stop and finish the process. Otherwise, set \(k=k+1\) and go to Step 3.

The flowchart of the proposed method is shown in Fig 6.

Fig. 6
figure 6

The flowchart of the DS-MACC method

Full size image

6 Illustrative examples and numerical results

In this section, several numerical and structural examples are solved for verifying the proposed method. The numerical results are compared with other methods including AMV, HMV, MCC, IACC, and some other recent methods in terms of the number of iterations and function evaluations for investigating their accuracy and efficiency. For doing so, two sets of examples are considered. The first set deals with seven mathematical and one structural performance functions for reliability analysis. The implementation of the above-mentioned methods in RBDO are illustrated via the second set including five mathematical and structural problems. All methods are coded with MATLAB. For the MCC method, the control parameter \(\lambda\) is set both 0.1 and 0.5. It has to be mentioned that the value of \(\lambda\) will also be different for these methods in RBDO examples. Moreover, \({\varvec{C}}={\varvec{I}}\) for all methods employing the concepts of the CC method. To have a fair comparison, the PMA approach of IACC is also implemented. The convergence criterion for the first set is considered as \(\left|\left|{{\varvec{U}}}_{k+1}-{{\varvec{U}}}_{k}\right|\right|/|\left|{{\varvec{U}}}_{k}\right||<{10}^{-5}\), and for the second set is \(\left|\left|{{\varvec{U}}}_{k+1}-{{\varvec{U}}}_{k}\right|\right|/|\left|{{\varvec{U}}}_{k}\right||<{10}^{-6}\).

6.1 Set I: mathematical and structural examples for reliability analysis

Seven mathematical nonlinear limit state functions are used for comparison and listed in Table 1. The value of the performance functions (\(G({{\varvec{X}}}^{\boldsymbol{*}})\)) and the number of function evaluations, as well as iterations, are provided in Table 2. From this table, it is readily apparent that IACC and DS-MACC can converge to MPTP for all LSFs. However, the number of function evaluations of the proposed method is much less than that of IACC. MCC with \(\lambda =0.1\) has shown to be a robust method in comparison with the other four methods. AMV is the least efficient method among all since it can only reach to MPTP for merely one LSF. MCC with \(\lambda =0.5\) and HMV methods usually have greater computational effort compared with other iterative processes.

Table 1 Limit state functions with their corresponding distribution information
Full size table
Table 2 Numerical results of MPTP search for different methods (iterations/function evaluations)
Full size table

The first performance function, as mentioned before, is a convex function which is weakly nonlinear. AMV, HMV, and the proposed method converge to \({{\varvec{X}}}^{\boldsymbol{*}}\) with the same number of function evaluations because based on the criteria utilized in these methods, they all use the steepest descent direction for the process and act like the AMV method. Although the IACC shows fewer function evaluations compared with the MCC method, its computational cost is still higher since it modifies \(\lambda\) unnecessarily. In the MCC method, the small fixed step size has increased the number of iterations especially when \(\lambda\) is 0.1. The convergence history of example 2 is plotted in Fig. 7. This is a moderately nonlinear performance function, and all the methods except for AMV can find the MPTP. As can be seen from Table 2, DS-MACC method is the most efficient approach for MPTP search and is five times faster than the IACC method. In this example, a small control parameter for the MCC method is more desirable because of the high nonlinearity of LSF near MPTP. For this reason, the MCC method with \(\lambda =0.5\) and HMV are very slow to converge.

Fig. 7
figure 7

Iterative histories of MPTP search for Example 2

Full size image

The third performance function has a large reliability index that augments the challenge of seeking MPTP. From Fig. 8, it is apparent that oscillation occurs in AMV iterative procedure. DS-MACC method provides the best numerical results with 15 function evaluations to find MPTP. This is mainly because it uses the steepest descent direction when it is needed based on the conditions introduced in this study, which expedites the process. In addition, the step length expressed in Eq. 17 can sufficiently narrow the search interval for the second step of the algorithm and this prevents it from unnecessary function calls in the IACC method. IACC has fewer iterations than MCC with \(\lambda =0.1,\), whereas, its number of function evaluations is relatively twofold. MCC (\(\lambda =0.5\)) and HMV also require many iterations to satisfy the convergence criterion and thus, are less efficient.

Fig. 8
figure 8

Iterative histories of MPTP search for Example 3

Full size image

For example 4, iterations are plotted in Fig. 9. It is highly nonlinear with a great curvature around MPTP; a difficult problem for AMV, HMV, MCC methods. It can be viewed that the IACC method can converge to MPTP after 8 iterations, which is the least among all. However, its computational burden is larger than others with 30 function evaluations. MCC (\(\lambda =0.1\)) and the proposed method exhibit acceptable efficiency. Example 5 is a multi-dimensional highly nonlinear LSF with seven random variables. DS-MACC method can accurately reach MPTP with only 15 function calls which is approximately less than one-third of that of the next best result obtained by MCC with 42 function calls. IACC has been able to reduce the number of iterations of the MCC method, but its computational cost is higher. MCC (\(\lambda =0.5\)) and HMV found the MPTP after 169 and 551 iterations, respectively, showing their ineffectiveness. AMV encounters oscillation and fail to converge.

Fig. 9
figure 9

Iterative histories of MPTP search for Example 4

Full size image

Example 6 and 7 are two strictly nonlinear performance functions and their iterative procedures are depicted in Fig. 10 and Fig. 11, respectively. For example 6, only the IACC and DS-MACC method can find MPTP and are the most robust and efficient methods compared to others. Even the small control parameter of MCC (\(\lambda =0.1\)) could not help it to reach the minimum target point. The proposed method has the least number of function calls which is around half of the IACC method’s function calls. This illustrates that DS-MACC method has been successful to improve the numerical instability and efficiency of the IACC method. This happens thanks to the criterion introduced to narrow the search interval iteration by iteration letting the algorithm reduce the step length fewer times than the IACC method. In terms of example 7, both the MCC (\(\lambda =0.1\)) and proposed method demonstrate good efficiency in MPTP search. Conversely, IACC though converge to MPTP, as can be seen in Fig. 11, it shows instabilities and \(\lambda\) reduction is done insufficiently resulting in the high number of function evaluations. This is mainly because it considers the absolute value of the \(cos {\theta }_{k}\) which is not correct and can lead to this kind of iteration history. This problem is successfully tackled in the proposed method. Thus, it can be concluded from the examples above that DS-MACC method is the most efficient and accurate one to find MPTP. MCC (\(\lambda\)=0.1) is also an efficient algorithm for highly nonlinear LSFs due to its small control parameter. However, it may fail to converge for LSFs with severe nonlinearity like example 7. Also, it shows less efficiency for moderately nonlinear or convex performance functions. The IACC is also a robust method that can solve problems with different levels of curvature, but its computational cost can be high.

Fig. 10
figure 10

Iterative histories of MPTP search for Example 6

Full size image
Fig. 11
figure 11

Iterative histories of MPTP search for Example 7

Full size image

Example 8:

To illustrate the efficiency of the proposed method, an explicit performance function with a large number of random variables is considered here which is introduced based on the displacement of the node under load \({P}_{1}({\Delta }_{p1}^{z})\) at the z-direction in the space truss with 24 elements shown in Fig. 12. Finite element method can be used to calculate \({\Delta }_{p1}^{z}\) which should be less than the maximum value of 0.01 m (Keshtegar et al. 2018a).

Fig. 12
figure 12

The space truss structure of Example 8

Full size image
$${{\varvec{G}}}_{8}({{\varvec{X}}}^{\boldsymbol{*}})=0.01-|{\Delta }_{p1}^{z}|$$
(18)

There are 32 independent normal and non-normal random variables in this example. Their description and statistical properties of them are listed in Table 3. The target reliability index is 3.0. From Table 4, it is apparent that the proposed method has superior performance above others including the IACC method. While the Ds-MACC method requires only 650 function calls to converge to MPTP, the IACC and SMCC methods need 1170 and 1366 function evaluations to do so. In addition, HMV, HCC, and MCC methods could not reach the solution because of their instability and inefficiency. This example vividly shows the robustness of the proposed method to reduce the computational burden of structural reliability analysis.

Table 3 Statistics of random variables in Example 8
Full size table
Table 4 Comparison of different methods for Example 8
Full size table

6.2 Set II: mathematical and structural examples for reliability-based design optimization

Example 9:

A weakly nonlinear RBDO example is given as follows (Hao et al. 2019):

$$\begin{gathered} find {\varvec{d}} = \left[ {d_{1} ,d_{2} } \right]^{T} \hfill \\ \min f\left( {\varvec{d}} \right) = d_{1} + d_{2} \hfill \\ S.t. P_{f} \left[ {G_{j} \left( {\varvec{X}} \right) > 0} \right] \le \Phi \left( { - \beta_{t}^{j} } \right), j = 1,2,3 \hfill \\ G_{1} = 1 - \frac{{X_{1}^{2} X_{2} }}{20} \hfill \\ G_{2} = 1 - \frac{{\left( {X_{1} + X_{2} - 5} \right)^{2} }}{30} - \frac{{\left( {X_{1} - X_{2} - 12} \right)^{2} }}{120} \hfill \\ G_{3} = 1 - \frac{80}{{X_{1}^{2} + 8X_{2} + 5}} \hfill \\ 0 \le d_{i} \le 10, X_{i} = N\left( {d_{i} ,0.3} \right) for i = 1,2 \hfill \\ {\varvec{d}}^{0} = \left[ {5,5} \right]^{T} , \beta_{t}^{1} = \beta_{t}^{2} = \beta_{t}^{3} = 3.0 \hfill \\ \end{gathered}$$
(19)

This example involves two independent random variables with normal distribution and three probabilistic constraints. The optimum results obtained by AMV, HMV, MCC, HCC, and ASSA are extracted from literature (Hao et al. 2019) and are shown in Table 5 for comparison. These methods use a double-loop RBDO algorithm to find the optimum. The MCS method with \({10}^{6}\) samples is utilized to validate the reliability level of each probabilistic constraint. Results indicate all methods can find the optima, however, DS-MACC and IACC methods that use the SORA procedure are faster and more efficient to find the optimum design variables and can converge to that point after 212 and 219 function calls, respectively, which is about two third of that of needed for the ASSA method. Moreover, the MCC method with \(\lambda =0.1\) is the most computationally expensive method because of using a very small step size in each iteration. The design variables obtained after the first, second, and last cycles can be seen in Fig. 13. It can be seen that the third constraint is inactive during the process.

Table 5 Comparison of different methods for Example 9
Full size table
Fig. 13
figure 13

Iterative history of Example 9

Full size image

Example 10

A highly nonlinear RBDO example is considered as follows (Keshtegar et al. 2018a):

$$\begin{gathered} find {\varvec{d}} = \left[ {d_{1} ,d_{2} } \right]^{T} \hfill \\ \min f\left( {\varvec{d}} \right) = - \frac{{\left( {d_{1} + d_{2} - 10} \right)^{2} }}{30} - \frac{{\left( {d_{1} - d_{2} + 10} \right)^{2} }}{120} \hfill \\ S.t. P_{f} \left[ {G_{j} \left( {\varvec{X}} \right) > 0} \right] \le \Phi \left( { - \beta_{t}^{j} } \right), j = 1,2,3 \hfill \\ G_{1} = 1 - \frac{{X_{1}^{2} X_{2} }}{20} \hfill \\ G_{2} = - 1 + \left( {Y - 6} \right)^{2} + \left( {Y - 6} \right)^{3} - 0.6\left( {Y - 6} \right)^{4} + Z \hfill \\ Y = 0.9063X_{1} + 0.4226X_{2} , Z = 0.4226X_{1} - 0.9063X_{2} \hfill \\ G_{3} = 1 - \frac{80}{{X_{1}^{2} + 8X_{2} + 5}} \hfill \\ 0 \le d_{i} \le 10, X_{i} = N\left( {d_{i} ,0.3} \right) \,\,\,for i = 1,2 \hfill \\ {\varvec{d}}^{0} = \left[ {5,5} \right]^{T} , \beta_{t}^{1} = \beta_{t}^{2} = \beta_{t}^{3} = 3.0 \hfill \\ \end{gathered}$$
(20)

In this example, the two random variables have normal distribution. Three probabilistic constraints are defined herein. The second constraint is highly nonlinear which is a difficult challenge for methods to deal with. For the aim of comparison, the results of the iterative algorithms are extracted from literature (Keshtegar et al. 2018a). For this example, the MCS method with \({10}^{7}\) samples is employed. The RBDO results for this example are presented in Table 6. Moreover, to compare the performance of the proposed method with kriging-based RBDO methods, the results for hybrid adaptive kriging-based single-loop (HAK-SLA) method are also extracted from literature (Yang et al. 2021) which considered the stopping criterion of \(\varepsilon ={10}^{-3}\) for reliability analysis. Therefore, we also solved this example with the same stopping criterion which is shown in the last row of Table 6. As it is evident, the proposed method shows the fastest convergence rate as it can reach the optimum after 5 cycles and 348 function evaluations. Whereas, the DCC method requires 10 iterations and 567 function calls to do so. The IACC is also more efficient than the DCC method with approximately 100 more function calls than the proposed method. The HCC and MCC need more than 16,000 and 7000 function evaluations, respectively, to converge which is very exorbitant. The AMV and HMV methods cannot make it to satisfy the convergence criterion. The DS-MACC method also works slightly better than the HAK-SLA method with only 5 cycles and 299 function calls while HAK-SLA requires 36 iterations and 308 function evaluations which shows the better performance of the proposed method in comparison with the kriging-based method. In Fig. 14, the first, second, and last cycles of the proposed method’s performance for this example are illustrated. It shows that the first and second probabilistic constraints are the active ones. The high nonlinearity of the second constraint is easily handled by the proposed method with the least number of function calls. This certifies the superior performance of DS-MACC method coupled with the SORA over other methods with nested double-loop RBDO procedure.

Table 6 Comparison of different methods for Example 10
Full size table
Fig. 14
figure 14

Iterative history of Example 10

Full size image

Example 11

The structural diagram of a roof truss subjected to uniform loads is illustrated in Fig. 15 in which, the top and compression bars are made of reinforced concrete members, bottom and tension bars are made of steel. Regarding the structural mechanics’ requirements, the perpendicular deflection \({\Delta }_{C}\) should be less than 0.03. This example is considered in the RBDO problem as follows (Keshtegar et al. 2018a):

$$\begin{gathered} Find {\varvec{d}} = \left[ {A_{c} ,A_{s} } \right]^{T} \hfill \\ min f\left( {\varvec{d}} \right) = 20224A_{s} + 364A_{c} \hfill \\ S.t. P_{f} \left[ {G\left( {\varvec{X}} \right) = 0.03 - \left( {\frac{{ql^{2} }}{2}} \right)\left( {\frac{3.81}{{A_{c} E_{c} }} + \frac{1.13}{{A_{s} E_{s} }}} \right) \le 0} \right] \le {\Phi }\left( { - \beta_{t} } \right) \hfill \\ where\,\, 0.0006 \le A_{s} \le 0.0012, 0.018 \le A_{c} \le 0.063 \hfill \\ \left[ {A_{s} ,A_{c} } \right]^{0} = \left[ {0.001,0.042} \right], \beta_{t} = 3.0 \hfill \\ \end{gathered}$$
(21)
Fig. 15
figure 15

Schematic of the roof truss

Full size image

where \(l\) is the length of truss, \({A}_{c}\), and \({A}_{s}\) are the cross-sectional areas of reinforced concrete and steel bars, respectively. \({E}_{c}\) and \({E}_{s}\) represent the corresponding elastic modulus. This example involves two random design variables, namely \({A}_{s}\) and \({A}_{c}\) with four random variables. The statistical parameters of the random variables can be found in Table 7. The results for the RBDO model of this example are solved by HCC, HDMV, and DCC methods and extracted from (Keshtegar et al. 2018b) and (Keshtegar et al. 2018a) to compare with the IACC and proposed method. In Table 8, the results are indicated. Furthermore, the reliability index for the LSF of this example is computed with \({10}^{7}\) samples using the MCS method. It is observed that all methods are converged accurately to the optimum design point with a high-reliability level with a good agreement with results presented in (Rashki et al. 2014). However, the number of function calls for the proposed method is about thirteen times and three times faster than HCC, HDMV, and DCC methods, respectively. Hence, the IACC is as efficient as DS-MACC method but still requires more function evaluations. It should be mentioned that the DCC method has the highest reliability level among all, while its computational effort is about two times that of the proposed method.

Table 7 Statistics of random variables in Example 11
Full size table
Table 8 Comparison of different methods for Example 11
Full size table

Example 12

A welded beam problem (Cho and Lee 2011) shown in Fig. 16 is given. This problem has four independent normally distributed random variables and five probabilistic constraints. Detailed explanation of this example can be accessed via (Cho and Lee 2011). The RBDO model is defined as follows:

$$\begin{gathered} Find\,\, {\varvec{d}} = \left[ {d_{1} , d_{2} , d_{3} , d_{4} } \right]^{T} \hfill \\ min \,\,f\left( {{\varvec{d}},{\varvec{z}}} \right) = c_{1} d_{1}^{2} d_{2} + c_{2} d_{3} d_{4} \left( {z_{2} + d_{2} } \right) \hfill \\ S.t.\,\, P_{f} \left[ {G_{j} \left( {\varvec{X}} \right) > 0} \right] \le {\Phi }\left( { - \beta_{t}^{j} } \right), j = 1, 2, \ldots ,5 \hfill \\ \end{gathered}$$
(22)
Fig. 16
figure 16

Schematic of the welded beam structure

Full size image

The RBDO results for AMV, HMV, MCC, HCC, and HCMV methods using double-loop strategy are extracted from from (Keshtegar et al. 2018c) and (Zhu et al. 2021), respectively, and summarized in Table 9. All methods can successfully obtain the optimum as 2.5913. The performance of AMV, HMV, and HCC are the same as each other with 1350 function calls. The MCC method requires the highest number of function evaluations to reach the optimal design point. The HCMV method could save about %50 of the computational cost of the HCC method, however, it is still two times and three times slower than the IACC and proposed method, respectively. DS-MACC method could also successfully reduce the number of function calls of the IACC method from 409 to 389. In addition, the SORA procedure needs only four cycles to reach the solution, while the double-loop RBDO needs more than 10 iterations to do so, which shows the high convergence rate of the proposed method.

Table 9 Comparison of different methods for Example 12
Full size table

Example 13

Speed reducer illustrated in Fig. 17 is utilized for engine and propeller rotation with efficient velocity in the light plane (Keshtegar et al. 2018c). This design problem includes seven normal and independent random variables plus eleven probabilistic constraints. The random design variables are gear width \(({X}_{1})\), gear module \(({X}_{2})\), the number of pinion teeth \(({X}_{3})\), distance between bearings \(({X}_{4}, {X}_{5})\), and diameter of each shaft \(({X}_{6}, {X}_{7})\). The RBDO model for this example is expressed in Eq. (22), and more details is accessible in (Keshtegar et al. 2018c):

$$\begin{gathered} Find \,\,\,{\varvec{d}} = \left[ {d_{1} , d_{2} , d_{3} , d_{4} ,d_{5} ,d_{6} , d_{7} } \right]^{T} \hfill \\ min\,\,\, f\left( {\varvec{d}} \right) = 0.7854d_{1} d_{2}^{2} \left( {3.3333d_{3}^{2} + 14.9334d_{3} - 43.0934} \right) - 1.508d_{1} + 7.477\left( {d_{6}^{3} + d_{7}^{3} } \right) + 0.7854\left( {d_{4} d_{6}^{2} + d_{5} d_{7}^{2} } \right) \hfill \\ S.t.\,\,\, P_{f} \left[ {G_{j} \left( {\varvec{X}} \right) > 0} \right] \le {\Phi }\left( { - \beta_{t}^{j} } \right), j = 1, 2, \ldots ,11 \hfill \\ \end{gathered}$$
(23)
Fig. 17
figure 17

Schematic of the speed reducer

Full size image

Table 10 presents the results of the RBDO approaches for this example. Results for the double-loop based AMV, HMV, MCC, HCC, and HCMV are reported from (Zhu et al. 2021). It should be noted that the convergence criterion is considered as \({10}^{-4}\) for this example. From Table 8, while all methods can find the optima, it can be seen that only the HCMV, IACC, and DS-MACC methods can obtain the optimum design variables with less than 1000 function calls. Both the IACC and proposed method are more efficient than others with 184 and 154 function calls, respectively. Moreover, AMV, HMV, and HCC methods have the same efficiency as each other, which shows the constraints are almost convex types. Therefore, DS-MACC method coupled with the double-loop strategy may yield the same result as the AMV method. But, incorporating the SORA approach could reduce the number of function calls from 1147 to 154 for this example. The HCMV method also reduces the function calls by combining their proposed method with sufficient conditions with AMV.

Table 10 Comparison of different methods for Example 13
Full size table

7 Conclusion

In this work, a new double-step PMA based on the improved adaptive chaos control (IACC) method was proposed and integrated with the SORA procedure to alleviate the computational cost of RBDO problems. Usually, the reliability analysis loop is responsible for the largest percentage of computations. So, making this process more efficient is a key to reduce the computational burden. The nonlinearity degree of LSFs can be easily found via the direction of the normalized gradient vector which is utilized in the IACC method. However, the strategy used for step length reduction is not efficient since it does not consider any information related to the type of the LSF. Thus, the computational cost can rise in the case of convex and highly nonlinear LSFs. Regarding this defect, double-step modified adaptive chaos control (DS-MACC) is introduced. In this method, to detect the function type, two novel criteria are considered in the first step. based on the different conditions of these criteria, three states of iterations can happen for each of which, a particular relation for initial step size calculation is proposed which makes the whole process faster because of choosing an efficient step size in advance. During the second step, the initial step length is adaptively modified until the angle between two consecutive steepest descent directions is smaller than a particular value. In addition, to prevent a large number of function evaluations of dealing with highly nonlinear constraints in the double-loop RBDO strategy, the DS-MACC method is linked with SORA.

To evaluate the capability of the proposed method, two sets of problems comprised of mathematical and structural reliability analysis as well as RBDO problems are considered. Results indicate that DS-MACC has been successful to address the inefficiency of IACC and the high computational cost of traditional double-loop approaches. DS-MACC is capable of dealing with highly nonlinear LSFs with a fast convergence rate. It also has a high accuracy to find the MPTP thanks to the double-step strategy integrated in this method besides the criteria introduced to find the intervals in which MPTP may exist. To conclude, the robustness and less computational burden of the proposed method certifies its competitive and reliable performance, especially in the case of dealing with highly nonlinear performance functions.