Topology optimization of frame structures with stress and stability constraints

Abstract

At present, most of the researches on topology optimization focus on continuum structures, but few on frame structures. This paper presents a methodology for topology optimization of frame structures with stress and stability constraints under a prescribed volume. In order to solve the pseudo buckling mode issues and calculation efficiency caused by low-density elements, new smooth penalty functions of the element elastic stiffness matrix and stress stiffness matrix are constructed, and an effective pseudo buckling mode identification measure is adopted to solve the corresponding problems. Moreover, a comprehensive measure, including the stress relaxation and the constraint aggregation method and the varying constraint limit scheme, to deal with stress and stability constraints is proposed. Furthermore, the Heaviside mapping scheme is introduced to obtain a clear solid/empty beam layout. Then, the sensitivities of stress and stability constraints with respect to design variables are given, and the proposed topology optimization problem is solved by the method of moving asymptotes. Finally, several numerical examples are given to demonstrate the feasibility and effectiveness of the proposed approach.

1 Introduction

In the last decades, there have been researches toward to solve topology optimization problem, much of them were devoted to the optimization designs of continuum structures (Sigmund and Maute 2013a; b; Zhu et al. 2021). While frame structures are more common in civil and mechanical engineering applications, in order to seek the best layout of members for frame structures under specific performance, the ground structure approach has been usually implemented in the frame structural topology optimization (FSTO) (Zegard and Paulino 2015; Gao et al. 2017a, b). Using this approach, novel designs, which achieve maximum stiffness frame structures under a prescribed volume constraint, have been developed in recent years (Kim et al. 2016; Shen and Ohsaki 2021). However, without comprehensively considering both strength and stability requirements, the above stiffness related designs might not serve as a good candidate for realistic designs. In view of this, it is indispensable to take stress and stability constraints into consideration to promote FSTO to practical engineering applications.

As for stress-constrained topology optimization, there are three challenge issues to address in stress-constrained topology optimization, i.e., stress singularity, large number of local stress constraints and high non-linearity (Bruggi 2008; París et al. 2009; Le et al. 2010). In the first place, the stress singularity arises in which topology design variables approaches zero due to the discontinuity of local stress constraints. For this matter, some relaxation methods, such as the ε-relaxed approach (Bruggi 2008) and the qp relaxation method (Moon and Yoon 2013), were proposed to avoid the singularity phenomenon. In the next place, a large number of stress points must be constrained due to the local nature of stress constraints, which result in the increase of computational burden. To overcome this problem, the global stress measure, such as the Kreisselmeier–Steinhauser (KS) and P-norm aggregation function, is applied to reduce the computational burden (París et al. 2009; Kiyono et al. 2016). As regards the third issue, the use of global stress measure methods will aggravate the non-linearity of stress constraints and gradients. This problem further leads to the weak control of local stresses and convergence problem, which request an efficient and accurate optimizer (Le et al. 2010; Long et al. 2019). Moreover, some regional or clustered aggregation techniques were put forward to make a trade-off between the global and local stress constraint methods to alleviate this issue (Holmberg et al. 2013). The above stress-constrained topology optimization works are mainly focused on searching the optimal material layout within continuum structures, while there are few researches on frame structures. The cause may be that the stress evaluation of frame structures, the corresponding sensitivity derivation and their programming are more complex than those of continuum structures. Recently, stress-related topology optimization of frame structures has been investigated by some researchers, where the cross-sectional size or area of each beam element are taken as design variables (Zuo et al. 2016; Changizi and Jalalpour 2017; Mitjana et al. 2019; Changizi and Warn 2020). In these studies, the common measure is that a beam element would be removed when the cross-sectional design variable below the threshold value, which may lead the obtained design to be a non-optimal design.

More importantly, without considering stability requirement, the emergence of slender members within frame structures is inevitable during optimization process, which further greatly affect the structural safety. Some studies primarily addressed the local stability issues of truss topology optimization, where the local stability constraints of members are imposed based on the Euler buckling criterion (Guo et al. 2001; Mela 2014). Although the axial stress of each individual member of the optimized structure was controlled to be under the Euler buckling stress capacity, the following two major challenges were posed for FSTO based on the Euler buckling criterion. In the first place, the local stability constraints should be imposed on each member of the ground structure, which give rise to a large number of constraints and further bring in computationally expensive problem. Moreover, there might be some collinearly connected truss members in the final optimized topology, which can be merged into a one longer member in most cases (Guo et al. 2005). While these slender members may increase the potential of local instabilities, and the global stability cannot be ensured furthermore. In view of this, many researchers suggested that the global buckling controls should be considered in truss optimization, and attempted to find optimal truss design under overall structure buckling controls (Jalalpour et al. 2011; Madah and Amir 2017). However, the problem of local instability might not be captured since these structures are modeled by truss elements (Torii et al. 2015). As a result, it is indispensable to incorporate the global stability requirement within FSTO.

Meanwhile, overall structure stability capacity can be as well as examined by solving an eigenvalue problem of the optimized structure. While conducting an eigenvalue analysis within a gradient-based FSTO, two numerical issues could be inevitably encountered. The first one needs to be addressed is the identification of “pseudo buckling modes”, which are caused by the material regions with low relative density variables (Kemmler et al. 2005; Asadpoure et al. 2020). It should be noted that the main contribution in the design performance stems from members with higher relative density variables. Consequently, such a buckling mode which is mainly contributed by members with relatively low relative density variables needs to be identified as “a pseudo buckling mode”, and eliminated at best when determining the critical load factor. To address this issue, referring to the solution measures of “pseudo modes” in dynamic optimization, many researches adopted material penalty models to modify element stiffness and/or mass matrices of elements in low-density regions to eliminate low-order pseudo buckling modes (Munk et al. 2017; Gao et al. 2017b, 2020). Nevertheless, using the aforementioned approaches, there are still many low-order pseudo buckling modes in the optimized structures. Therefore, an efficient pseudo buckling mode identification measure was developed, where the required real buckling modes are identified by using the pseudo modal energy ratios (Li and Khandelwal 2017; Changizi and Jalapour 2018). Meanwhile, in order to improve the buckling resistant performance, the critical buckling load factor often was taken as the objective or a constraint function in FSTO, while a so-called mode transition phenomenon may occur during optimization processes. To address this issue, a so-called bound method was used to transform the original objective function to a set of differentiable constraint functions (Lindgaard and Dahl 2013). Alternately, the multi-order buckling load factor constraints were introduced, where the buckling constraints were formulated as an equivalent one by cooperating with the aggregation function method (Ferrari and Signund 2019; Luo and Zhan 2020; Torii and Faria 2017; Torii et al. 2022).

Most of the aforementioned works concerned FSTO were carried out where either stress or stability requirement was taken into consideration solely, the associative effects of these two requirements on the optimal designs were neglected. Although few attempts are devoted to find the optimal design for frame structure considering both stress and stability constraints, these optimal designs are achieved by mapping from cross-sectional parameters, such as the cross-sectional size or area, to standard members (Changizi and Jalalpour 2017; Mitjana et al. 2019). For one thing, this mapping relationship cannot accurately correspond cross-sectional parameters to standard members, and may further result in several different standard members to one design parameter. For another, these works were constrained to simple frame structures of which the ground structures are formed by only a few dozen of beams or simple planar frame structures. Therefore, an efficient methodology taking into stress and stability requirements simultaneously should be developed to achieve a realistic optimal design.

The main goal of this paper is to present a topology optimization approach able to considering both stress and stability constraints in the design of frame structures under a given volume. In order to address the low-order pseudo buckling mode issues and computational burden problems triggered by low-density elements, a new polynomial interpolation model and an effective pseudo buckling mode identification measure are proposed. Meanwhile, a comprehensive treatment measure, including the stress relaxation and the constraint aggregation and the varying constraint limit scheme, is proposed to deal with stress and stability constraints. Furthermore, the Heaviside mapping scheme is introduced so that the beam layout with clear 0/1 distribution is achieved. Finally, several examples are provided to demonstrate that the proposed method is feasible and effective.

This paper is organized as follows: In Sect. 2, the threshold projection and a polynomial smooth interpolation model are presented. In Sect. 3, a comprehensive treatment measure dealing with the local stress constraints and stability constraints is presented. In Sect. 4, an effective pseudo buckling mode identification measure are proposed to obtain the required real buckling modes. In Sect. 5, the optimization problem of finding the stiffest frame structure with both stress and stability constraints under a given volume is proposed. In Sect. 6, the sensitivities of the objective function and constraints with respect to the design variables are derived. In Sect. 7, several numerical examples are presented to illustrate the feasibility of the proposed method. In Sect. 8, concluding remarks are finally drawn.

2 Threshold projection and material interpolation model

2.1 Threshold projection

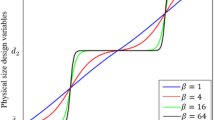
In the past decades, many works attempted to find optimal designs for frame structures under specified performance requirements. While these optimal designs are obtained by rudely removing the members of which the cross-sectional parameters below the threshold, which may result in the non-optimal design. In order to achieve a clear 1/0 (solid/empty) design, many researchers have investigated the suppression methods of intermediate variables (Guest et al. 2011; Wang et al. 2011). Referring to these approaches, the pseudo densities of beam elements are taken as design variables and the smooth Heaviside function is adopted (seeing Eq. (1)) to provide a faster way of computing the 1/0 projection. Then, a design variable field ${\varvec{\rho}}$, and a physical density variable field $\varvec{\overline{\rho }}$ are formed. The physical density variables $\overline{\rho }_{i}$ in Eq. (1) are employed in finite element analyses of structures.

$$\overline{\rho }_{i} = \frac{{\tanh(\beta \eta ) + \tanh (\beta (\rho_{i} - \eta ))}}{\tanh (\beta \eta ) + \tanh (\beta (1 - \eta ))},$$

(1)

where $\beta$ is the Heaviside projection parameter, and the detail of $\beta$ can be found in Wang et al. (2011).

2.2 Material interpolation model

As mentioned in the introduction, pseudo buckling modes are triggered in low-density regions due to the unrealistic high ratios between their local stress stiffnesses with corresponding local elastic stiffnesses, which result in the inaccuracy of structural buckling analyses and the increase of computational burden. To address this issue, a differentiable smooth material interpolation based on the SIMP (Solid Isotropic Material with Penalization) model (seeing Eq. (2)) is adopted to modify both the element elastic and stress stiffness matrices in low-density regions (Lindgaard and Dahl 2013; Munk et al. 2017).

$${\varvec{k}}_{i} = \left( {\overline{\rho }_{\min } { + }\left( {1 - \overline{\rho }_{\min } } \right)\overline{\rho }_{i}^{p} } \right){\varvec{k}}_{i}^{0} ,\quad {\varvec{k}}_{i}^{g} = \overline{\rho }_{i}^{p} {\varvec{k}}_{i}^{g,0},$$

(2)

where $\rho_{i}$ and $\overline{\rho }_{i}$ are the design variable and physical density variable of the ith element, respectively. $\overline{\rho }_{\min }$ is set such that problems with artificial modes are avoided when the element density $\overline{\rho }_{i}$ is around its lower bound value. ${\varvec{k}}_{i}^{0}$ and ${\varvec{k}}_{i}^{g,0}$ are the initial element elastic and stress stiffness matrices of the ith element, respectively. The penalty parameter $p > 1$ is usually used in Eq. (2) to impose penalties on both the stress and elastic stiffness matrices, which can circumvent the pseudo buckling mode issues in low-density regions (Lindgaard and Dahl 2013; Munk et al. 2017).

Whereas a lot of pseudo buckling modes in some iterations cannot be avoided in low-density gathered regions, resulting in the inaccurate evaluation of buckling load factors. In view of this, referring to the measures of “localized modes” in dynamic optimization (Ni et al. 2014), a new smooth polynomial material interpolation (SPLMP) model is constructed, which is given as:

$${\varvec{k}}_{i} = \left( {\left( {1 - \alpha } \right)\overline{\rho }_{i}^{{p_{1} }} { + }\alpha \overline{\rho }_{i}^{{p_{2} }} } \right){\varvec{k}}_{i}^{0} ,\quad {\varvec{k}}_{i}^{g} = {\varvec{k}}_{i}^{g} \left( {\overline{\rho }_{i}^{{p_{3} }} {\varvec{f}}_{i}^{0} } \right) = \overline{\rho }_{i}^{{p_{3} }} {\varvec{k}}_{i}^{g,0},$$

(3)

where $\alpha$ is polynomial interpolation parameters, p₁ and p₂ are corresponding penalty parameters. $\alpha = \frac{1}{16}$, $p_{1} = 5$ and $p_{2} = 2$ are used. ${\varvec{f}}_{i}^{0}$ is the internal force vector of the ith beam element, $p_{3}$ is the corresponding penalty parameter for the internal force vector and $p_{3} = 3$ is used in this paper. The initial stress stiffness matrices ${\varvec{k}}_{i}^{g,0}$ is constructed based on the internal force vector ${\varvec{f}}_{i}^{0}$, and the detail can be found in Cook et al. (2002).

To further illustrate the advantage of the proposed method, the characteristics of the above-mentioned two material interpolation models (SIMP and SPLMP) are investigated here. From Fig. 1, it can be observed that the suitable ratios between stress and elastic stiffness can be obtained by using the SIMP with the increase of the penalty parameter p. However, when a much higher penalty parameter p is applied in the SIMP, the non-convexity of the optimization problem increases and the oscillation of optimization process might be encountered, which may lead to convergent to local minima. Therefore, the penalty parameter p has to be determined carefully and p = 3 is usually used to ensure good convergence to a good 0/1 solution (Sigmund and Maute 2013a, b; Lindgaard and Dahl 2013; Munk et al. 2017). Furthermore, as shown in Fig. 1, compared with the SIMP model, between penalty function ratio for stress and elastic stiffness, especially in the low-density regions, shows better matching by using the SPLMP model.

Fig. 1

Ratio between penalty function ratio for stress and elastic stiffness by using SIMP and the proposed smooth polynomial material interpolation model

3 Stress and stability constraints

In this section, the space-frame structural analyses including stress and linear buckling analysis are briefly described in which all structural members are modeled by hollow cylindrical beam elements, but the approach can be generalized to other cross-sections. Based on the frame structural analysis, stress and stability constraints are formulated to satisfy the corresponding design requirements within FSTO.

Meanwhile, as described in Sect. 2, each beam is assigned with a topology variable to represent whether the beam exists, and the size or other cross-sectional parameters are not included in the optimal beam layout. This idea apparently shares the strong mathematical similarities to those researches on continuum topology optimization (Gao et al. 2017b, 2020; Ferrari and Sigmund 2019; Dalklint et al. 2021). Despite that the continuum topology optimization can achieve free-form optimal design, but has difficulty in generating beam-column structures that are easy for construction. As a result, the proposed approach which cooperating the measures on continuum topology optimization within FSTO can provide an efficient way to achieve an innovative design for frame structures. That is to say, the stress relaxation and aggregation constraint measures (Le et al. 2010; Long et al. 2019), as well as the smooth approximation measures concerned with buckling constraints (Dalklint et al. 2021; Torii et al. 2022), can also be applied to FSTO in this paper.

3.1 Stress constraints

In the finite element analysis of beam element, the strain ${\varvec{\varepsilon}}$ at a point on the cross-section of beam element can be expressed as:

$$\varvec{\varepsilon} = \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{xy} } \\ {\varepsilon_{xz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u^{\prime} - yv^{\prime\prime} - zw^{\prime\prime}} \\ { - z\theta_{x}^{\prime } } \\ {y\theta_{x}^{\prime } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & { - y} \hfill & { - z} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - z} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & y \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {u^{\prime}} \hfill \\ {v^{\prime\prime}} \hfill \\ {w^{\prime\prime}} \hfill \\ {\theta_{x}^{\prime } } \hfill \\ \end{array} } \right],$$

(4)

where $\left( {x,y,z} \right)$ is the position of the point in the local coordinate system.$\varepsilon_{xx}$ is the axial strain along x axis, $\varepsilon_{xy}$ and $\varepsilon_{xz}$ are the shear strain on the cross-section. $u$ and $\theta_{x}$ are the axial displacement and torsion angle, respectively. $v$ and $w$ are the lateral displacements along y and z directions, respectively. The superscript ′represents first-order derivative operator with respect to x.

Meanwhile, the displacement vector of any cross-section of the beam element can be determined by interpolation of nodal displacements, which can be expressed as:

$$\left[ {\begin{array}{*{20}l} u \hfill \\ v \hfill \\ w \hfill \\ {\theta_{x} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {{\varvec{N}}_{1} \left( x \right)} \hfill \\ {{\varvec{N}}_{2} \left( x \right)} \hfill \\ {{\varvec{N}}_{3} \left( x \right)} \hfill \\ {{\varvec{N}}_{4} \left( x \right)} \hfill \\ \end{array} } \right]{\varvec{Tu}} ,$$

(5)

where ${\varvec{N}}_{i} \left( x \right),i = 1,2,3,4$ is the shape function matrix, the corresponding construction for the shape function matrix can be found in Cook et al. (2002). ${\varvec{u}}$ is the nodal displacement vector of both ends of the beam element in the global coordinate system, T is the transformation matrix between the local and global coordinate system. According to the expression of the strain and displacement vector, the stress state at the above given point on the cross-section of the beam element can be expressed as:

$$\varvec{\sigma} = \left[ {\begin{array}{*{20}c} {\sigma_{xx} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{{\text{T}}} \varvec{ = D\varepsilon = DBTu},$$

(6)

where D is the elastic matrix and ${\varvec{D}} = \left[ {\begin{array}{*{20}l} E \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & G \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & G \hfill \\ \end{array} } \right]$. E and G are the elastic and shear modulus, respectively. ${\varvec{B}} = \left[ {\begin{array}{*{20}l} 1 \hfill & { - y} \hfill & { - z} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - z} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & y \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\varvec{N}}_{1}^{\prime } \left( x \right)} \hfill \\ {{\varvec{N}}_{2}^{\prime \prime } \left( x \right)} \hfill \\ {{\varvec{N}}_{3}^{\prime \prime } \left( x \right)} \hfill \\ {{\varvec{N}}_{4}^{\prime } \left( x \right)} \hfill \\ \end{array} } \right]$ is the strain–displacement matrix. The superscript ^T represents the matrix transpose operator.

In this paper, the von Mises yield criterion is used to predict the onset of yielding of materials, and the general form of the von Mises yield criterion can be written as:

$$\sigma^{vm} = \sqrt {\sigma_{xx}^{2} + 3(\tau_{xy}^{2} + \tau_{xz}^{2} )} = \sqrt {{\varvec{\sigma}}^{{\text{T}}} \varvec{\Lambda \sigma }},$$

(7)

where $\sigma^{vm}$ is the von Mises stress of the given point on the cross-section. A is a constant matrix and ${\varvec{\varLambda}}= \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 3 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 3 \hfill \\ \end{array} } \right]$.

Considering the local nature of stresses, it is necessary to determine some stress evaluation points to obtain the maximum von Mises stress value of a beam element, and the selected stress evaluation points in this paper are shown by red dots in Fig. 2. Then, stress constraints are applied on the evaluation points of each beam element within FSTO, which can be mathematically formulated as:

$$\frac{{\sigma_{i,k}^{vm,l} }}{{\overline{\sigma }}} \le 1,i = 1,2, \ldots ,n_{e} ,k = 1,2, \ldots ,12,l = 1,2, \ldots ,n_{l},$$

(8)

where $\sigma_{i,k}^{vm}$ is the von Mises stress of the kth evaluation point of the ith beam element in the structure under the lth loading case, $n_{e}$ is the total number of beam elements in the ground structure, $\overline{\sigma }$ is the yield strength of material.

Fig. 2

Stress evaluation points on the cross-section of a beam element

In order to address the stress singular difficulty, the qp-parametrization scheme from with different penalization for stress and yield strength is adopted to implement stress relaxation. As a result, stress constraints Eq. (8) can be reformulated as:

$$\frac{{\overline{\rho }_{i}^{{p_{s} }} \sigma_{i,k}^{vm,l} }}{{\overline{\rho }_{i}^{q} \overline{\sigma }}} = \overline{\rho }_{i}^{{p_{s} - q}} \frac{{\sigma_{i,k}^{vm,l} }}{{\overline{\sigma }}} \le 1,$$

(9)

where p_s and q are two independent penalty parameters of stress and yield strength, respectively. Here, given that the internal force and stress are closely related (Cook et al. 2002), the penalization for these two terms had better to be consistent. Therefore, p_s = p₃ and q = 2.5 are used in this paper (Moon and Yoon 2013).

To address the large number of local stress constraints, the aggregation over the local stress constraints is performed to form a global stress aggregate constraint for the structure under the lth loading case, i.e.,

$$\left( {\sum\limits_{i = 1}^{Q} {\sum\limits_{k = 1}^{12} {\left( {\overline{\rho }_{i}^{{p_{3} - q}} \frac{{\sigma_{i,k}^{vm,l} }}{{\overline{\sigma }}}} \right)^{{p_{a} }} } } } \right)^{{\frac{1}{{p_{a} }}}} \le 1,$$

(10)

where $p_{n}$ is the aggregation parameter, and $p_{a} = 6$ is used in this paper (París et al. 2009; Le et al. 2010).

3.2 Critical load factor constraints

In elastic global stability analyses, an equilibrium state is considered to be unstable if the tangent stiffness matrix of the structure becomes singular. Therefore, the buckling load factor can be found by solving the following eigenvalue problem (Changizi and Jalalpour 2018):

$$\left( {{\varvec{K}} + \lambda_{i}^{l} {\varvec{K}}^{g,l} } \right)\varvec{\varphi }_{i}^{l} = {\mathbf{0}},i = 1,2, \ldots ,N,l = 1,2, \ldots ,n_{l},$$

(11)

where ${\varvec{K}}$ is are the global elastic and stress stiffness matrix and ${\varvec{K}}^{g,l}$ are the global stress stiffness matrix under the lth loading case. The eigenvalue $\lambda_{i}^{l}$ and eigenvector $\varvec{\varphi }_{i}^{l}$ in Eq. (11) are the ith buckling load factor and its buckling mode for the structure under the lth loading case, respectively. $N$ is the total degrees of freedom (DOF) of the structure. The smallest eigenvalue $\lambda_{1}^{l}$ is defined as the structural critical buckling load factor for the structure under the lth loading case, the better buckling resistant performance is achieved with the increase of $\lambda_{1}^{l}$. For the purpose of achieve a buckling resistant design, a stability constraint concerned with the critical buckling load factor is introduced to the optimization problem, which can be expressed as:

$$\mathop {\min }\limits_{{\lambda_{i} \in {\varvec{R}}_{\lambda } }} \left| {\lambda_{i}^{l} } \right| = \left| {\lambda_{1}^{l} } \right| \ge \lambda^{*} > 0,l = 1,2, \ldots ,n_{l},$$

(12)

where $\lambda^{*}$ is the lower bound of $\left| {\lambda_{1}^{l} } \right|$, which means that the design is achieved when the absolute value of the buckling load factor is greater than $\lambda^{*}$. ${\varvec{R}}_{\lambda }$ is the set including all valid buckling load factors.

For Eq. (12), the minimum operator is not always differentiable, to address this issue, several studies suggested to employ some smooth approximation, such as P-norm and KS aggregation functions, to replace the non-smooth minimum operator. However, this direct aggregation approach may lead to numerical problems such as slow convergence and poor solutions during the optimization process. Aimed at such problems, Torii et al. (2015)

advocated that the regularization of multi-order critical load factors cooperated with the P-norm aggregation approach are employed to overcome non-smooth minimum operator. Furthermore, Torii et al. (2022) recently have presented a useful discussion on the subject, with some comparisons between p-norm and KS regularization and advice for choosing the value of the aggregation parameter. Referring to these works, the stability constraints can be transformed as an equivalent continuously-differentiable function for each loading case (Luo and Zhan 2020; Torii et al. 2022), which can be expressed as:

$$\left( {\sum\limits_{{i = 1,\lambda_{i} \in {\mathbf{R}}_{\lambda } }}^{{n_{\lambda } }} {\left( {\lambda^{*} \mu_{i}^{l} } \right)^{{p_{a} }} } } \right)^{{\frac{1}{{p_{a} }}}} \le 1,$$

(13)

where $\mu_{i}^{l} = \frac{1}{{\lambda_{i}^{l} }}$ is the reciprocal of the ith buckling load factor $\lambda_{i}^{l}$ under the lth loading case, $n_{\lambda }$ is the number of specified buckling constraints.

4 The identification and deletion measure of pseudo buckling modes

However, a few of pseudo buckling modes cannot be completely eliminated by using the polynomial material interpolation model described in Sect. 2. Therefore, a methodology to identify pseudo buckling modes is introduced in the buckling load factor calculation. In this approach (Li and Khandelwal 2017; Changizi and Jalalpour 2018), the buckling modes are firstly classified into low-energy or high-energy modes. To this end, each node j in the ground structure is assigned a normalized design variable $\chi_{j}$, and $\chi_{j}$ can be mathematically expressed as:

$$\chi_{j} = \frac{{\sum\nolimits_{{k \in {\varvec{nb}}}} {\overline{\rho }_{k} } }}{{n_{e} \sum\limits_{i = 1}^{{n_{e} }} {\overline{\rho }_{i} } }},$$

(14)

where nb is the set of all beams connected to the jth node. $\overline{\rho }_{k}$ is the physical variable of the kth element in the set nb. Next, the jth node is categorized as a low normalized node when the corresponding normalized design variable $\chi_{j}$ is less than $t\sum\nolimits_{j = 1}^{n} {\eta_{j} }$, where t is the selected threshold parameter, and n is the total number of the nodes in the structure. Otherwise the jth nodes is assigned to set with a high normalized volume. These two sets ${\varvec{n}}_{{\varvec{l}}}$ and ${\varvec{n}}_{{\varvec{h}}}$ with low and high normalized volumes, respectively, can be written as

$${\varvec{n}}_{{\varvec{l}}} = \left\{ {j\left| {\chi_{j} < t\sum\limits_{j = 1}^{n} {\chi_{j} } } \right.} \right\},\quad {\varvec{n}}_{{\varvec{h}}} = \left\{ {j\left| {\chi_{j} > t\sum\limits_{j = 1}^{n} {\chi_{j} } } \right.} \right\}.$$

(15)

Then, for the ith buckling mode, the buckling eigenvector $\varvec{\varphi }_{i}$ can be divided into an assembly of two vectors $\varvec{\varphi }_{il}$ and $\varvec{\varphi }_{ih}$, where $\varvec{\varphi }_{il}$ and $\varvec{\varphi }_{ih}$ are comprised of the components of DOF of nodes in the sets ${\varvec{n}}_{{\varvec{l}}}$ and ${\varvec{n}}_{{\varvec{h}}}$, respectively. Then, the modal strain energy ratio $r_{i}$ associated with the ith eigenmode is defined as $r_{i} = \frac{{\varvec{\varphi }_{il}^{{\text{T}}} \varvec{K\varphi }_{i} }}{{\varvec{\varphi }_{i}^{{\text{T}}} \varvec{K\varphi }_{i} }}$.

Then the ith buckling mode is identified as the pseudo buckling mode when the modal strain energy ratio $r_{i} \ge t$ (Li and Khandelwal 2017). And ${\varvec{R}}_{\lambda }$ is the set of that collects the buckling load factors associated with the required real buckling modes when $r_{i} \le t$.

5 Optimization problem with stress and stability constraints

In this paper, the well-known ground structure approach is used to form an initial proper meshed frame structure composed of all potential candidate beams (Zegard and Paulino 2015; Gao et al. 2017a, b). Then the optimal design is achieved by eliminating the inefficient beam members of which the corresponding topology variables approaches to the lower bound. Unlike previous studies (Changizi and Jalalpour 2017; Mitjana et al. 2019), the size or other cross-sectional properties of the beam member are not included in the optimization model. Although this is a limitation of the proposed approach, it also provides the advantage of avoiding the need to map cross-sectional parameters to standard members. The corresponding mapping relationship cannot accurately correspond cross-sectional parameters to standard members, and may further result in several different standard members to one design parameter. Following this optimization idea, the optimization problem of finding the stiffest frame structure with both stress and stability constraints under a given volume is investigated in this paper, the optimization model can be expressed as:

$$\left\{ {\begin{array}{*{20}{c}} {{\text{find:}}}&{{\mathbf{\rho }} = {{\left[ {{\rho _1},{\rho _2}, \ldots ,{\rho _Q}} \right]}^{\text{T}}}} \\ {{\text{min:}}}&{{C_{{\text{tol}}}}\left( {\mathbf{\rho }} \right) = \sum\limits_{l = 1}^{{n_l}} {{\kappa _l}{C_l}\left( {{\mathbf{\bar \rho }}\left( {\mathbf{\rho }} \right)} \right) = \sum\limits_{l = 1}^{{n_l}} {{\kappa _l}{{\left( {{{\mathbf{U}}^l}} \right)}^{\text{T}}}{{\mathbf{K}}^e}{{\mathbf{U}}^l}} } } \\ {{\text{s.t.}}}: &{f_s^l\left( {\mathbf{\rho }} \right) = {{\left( {\sum\limits_{t = 1}^{P + Q} {{{\sum\limits_{k = 1}^{12} {\left( {\left( {{{\bar \rho }_t}\left( {{\rho _t}} \right)} \right)_{}^{_{{p_{_3}} - q}}\frac{{\sigma _{t,k}^{vm,l}}}{{\overline \sigma }}} \right)} }^{{p_a}}}} } \right)}^{\frac{1}{{{p_a}}}}} \leqslant 1} \\ {}&{f_\lambda ^l\left( {\mathbf{\rho }} \right) = {{\left( {\sum\limits_{j = 1,j \in {{\mathbf{R}}_\lambda }}^{{n_\lambda }} {{{\left( {{\lambda ^*}\mu _j^l} \right)}^{{p_a}}}} } \right)}^{\frac{1}{{{p_a}}}}} \leqslant 1} \\ {}&{{f_v}\left( {\mathbf{\rho }} \right) = \sum\limits_{i = 1}^Q {{{\bar \rho }_i}\left( {{\rho _i}} \right){V_i}/{V^0} \leqslant {V^*}/{V^0}} } \\ {}&{{K^e}{{\mathbf{U}}^l} = {F^l}} \\ {}&{{\rho _{\min }}\; \leqslant {\rho _i} \leqslant 1,i = 1,2, \ldots ,Q} \end{array}} \right.$$

(16)

where $\rho_{i}$ is the topology design variable of the ith beam element and $\rho_{\min }$ is the lower bound of topology design variables. ${\mathbf{U}}^{l}$ is the structural displacement vector under the lth external load ${\varvec{F}}^{l}$. P is the total number of non-designable beam elements in the ground structure, Q is the total number of designable beam elements in the ground structure. $V_{i}$ are the volume of the ith beam element, $V^{0}$ and $V^{*}$ denote the initial and prescribed volume of the ground structure, respectively. The superscript ^l represents the corresponding variables under the lth loading case, and $n_{l}$ is the number of loading cases. $C_{\rm tol}$ is the combined compliance, $\kappa_{l}$ is a corresponding adaptive weighting coefficient, and ${\kappa _l} = \left| {{C_1}\left( {{{{\mathbf{\bar \rho }}}^{\left( {k - 1} \right)}}\left( {\mathbf{\rho }} \right)} \right)} \right|/\left| {{C_l}\left( {{{{\mathbf{\bar \rho }}}^{\left( {k - 1} \right)}}\left( {\mathbf{\rho }} \right)} \right)} \right|$.

In order to prevent the structural performance from fluctuating dramatically during the optimization process, a varying limit scheme is adopted here to ensure the smooth change of the topologies during optimization process (Rong et al. 2021). Therefore, the topology optimization model (16) at the kth iterative step can be formulated as:

$$\left\{ {\begin{array}{*{20}{c}} {{\text{find:}}}&{{\mathbf{\rho }} = {{\left[ {{\rho _1},{\rho _2}, \ldots ,{\rho _Q}} \right]}^{\text{T}}}} \\ {{\text{min:}}}&{{C_{tol}}\left( {\mathbf{\rho }} \right) = \sum\limits_{l = 1}^{{n_l}} {{\kappa _l}{C_l}\left( {{\mathbf{\bar \rho }}\left( {\mathbf{\rho }} \right)} \right) = \sum\limits_{l = 1}^{{n_l}} {{\kappa _l}\left( {{{\mathbf{U}}^l}} \right)_{}^{\text{T}}{{\mathbf{K}}^e}{{\mathbf{U}}^l}} } } \\ {{\text{s.t.}}}:&{f_s^l\left( {\mathbf{\rho }} \right) = {{\left( {\sum\limits_{t = 1}^{P + Q} {{{\sum\limits_{k = 1}^{12} {\left( {\left( {{{\bar \rho }_t}\left( {{\rho _t}} \right)} \right)_{}^{_{{p_{_3}} - q}}\frac{{\sigma _{t,k}^{vm,l}}}{{\overline \sigma }}} \right)} }^{{p_a}}}} } \right)}^{\frac{1}{{{p_a}}}}} \leqslant f_{s,\left( k \right)}^{l.U}} \\ {}&{f_\lambda ^l\left( {\mathbf{\rho }} \right) = {{\left( {\sum\limits_{j = 1,j \in {{\mathbf{R}}_\lambda }}^{{n_\lambda }} {{{\left( {{\lambda ^*}\mu _j^l} \right)}^{{p_a}}}} } \right)}^{\frac{1}{{{p_a}}}}} \leqslant f_{s,\left( k \right)}^{l.U}} \\ {}&{f_v^{}\left( {\mathbf{\rho }} \right) = \sum\limits_{i = 1}^Q {{{\bar \rho }_i}\left( {{\rho _i}} \right){A_i}{L_i}/{V^0} \leqslant V_{(k)}^U/{V^0}} } \\ {}&{{K^e}{{\mathbf{U}}^l} = {F^l}} \\ {}&{{\rho _{\min }}\; \leqslant {\rho _i} \leqslant 1,i = 1,2, \ldots ,Q} \end{array}} \right.$$

(17)

where $f_{s,\left( k \right)}^{l.U}$, $f_{\lambda ,\left( k \right)}^{l.U}$ and $V_{(k)}^{U}$ are the varying constraint limits of stress and stability aggregate constraints and volume of the optimized structure under the lth loading case at the kth iterative step, respectively. The concrete expressions for these three terms are presented in Eqs. (18a)–(18c), respectively.

$$f_{s,\left( k \right)}^{l.U} = \left\{ \begin{gathered} \max\,\left( {f_{{s,\left( {k - 1} \right)}}^{l.U} \,\left( {1 - \delta } \right)\;,1} \right),\quad f_{{s,\left( {k - 1} \right)}}^{l.U} \ge \quad 1 \hfill \\ \min\,\left( {f_{{s,\left( {k - 1} \right)}}^{l.U} \,\left( {1 + \delta } \right)\;,1} \right),\quad \;f_{{s,\left( {k - 1} \right)}}^{l.U} < 1 \hfill \\ \end{gathered} \right.$$

(18a)

$$f_{\lambda ,\left( k \right)}^{l.U} = \left\{ \begin{gathered} \max\left( {f_{{\lambda ,\left( {k - 1} \right)}}^{l.U} \left( {1 - \delta } \right)\;,1} \right)\,,\quad f_{{\lambda ,\left( {k - 1} \right)}}^{l.U} \ge \quad 1 \hfill \\ \min\,\left( {f_{{\lambda ,\left( {k - 1} \right)}}^{l.U} \left( {1 + \delta } \right)\;,1} \right),\quad \;f_{{\lambda ,\left( {k - 1} \right)}}^{l.U} < 1 \hfill \\ \end{gathered} \right.$$

(18b)

$$V_{(k)}^{U} = \left\{ \begin{gathered} \max\,\left( {V_{(k - 1)}^{U} \left( {\,1 - \delta } \right)\,\;,V^{*} } \right),\quad V_{(k - 1)}^{U} \ge \quad V^{*} \hfill \\ \min\,\,\left( {V_{(k - 1)}^{U} \left( {\,1 + \delta } \right)\,\;,V^{*} } \right),\quad \;V_{(k - 1)}^{U} < V^{*} \hfill \\ \end{gathered} \right.$$

(18c)

where $f_{{s,\left( {k - 1} \right)}}^{l.U}$, $f_{{\lambda ,\left( {k - 1} \right)}}^{l.U}$ and $V_{(k - 1)}^{U}$ are the varying constraint limits of stress and stability aggregate constraints and volume of the optimized structure under the lth loading case at the (k − 1)th iterative step, respectively. $\delta$ is the varying parameter, and $\delta = 0.01$ is used in this paper (Rong et al. 2021).

6 Sensitivity analyses

Considering the large number of topology design variables, the topology optimization model (17) can be solved efficiently by using the gradient-based optimizers. Therefore, the sensitivities of the objective and constraint functions are required to obtain the optimized results. And the derivative of any performance function of the structure with respect to the design variable $\rho_{i}$ can be formulated as

$$\frac{{\partial f({\varvec{\rho}})}}{{\partial \rho_{i} }} = \frac{{\partial f({\varvec{\rho}})}}{{\partial \overline{\rho }_{i} }}\frac{{\partial \overline{\rho }_{i} }}{{\partial \rho_{i} }} = \frac{{\beta \left( {1 - \left( {\tanh (\beta (\overline{\rho }_{i} - \eta ))} \right)^{2} } \right)}}{\tanh (\beta \eta ) + \tanh (\beta (1 - \eta ))}\frac{{\partial f({\varvec{\rho}})}}{{\partial \overline{\rho }_{i} }}$$

(19)

Meanwhile, as shown in optimization model (17), the combined compliance $C_{\rm tol}$ and the volume constraint $f_{v} \left( {{\varvec{\uprho}}} \right)$ are the explicit functions with respect to the physical density variable $\overline{\rho }_{i}$, which can easily be obtained.

6.1 Sensitivity analyses of stress aggregate constraint function

Although the actual expressions of the stress formulas associated with continuum and frame structures are not exactly the same, the general forms of von Mises yield criterion and stress constraints (seeing in Eqs. (6)–(9)) are almost identical in both cases. Therefore, the derivation procedure of the sensitivities of the stress aggregate constraint function can refer to the related studies (Le et al. 2010; Long et al. 2019). Then from the expression of the von Mises stress Eq. (6), the derivative of the von Mises stress with respect to the physical density variable $\overline{\rho }_{i}$ can be expressed as:

$$\frac{{\partial \sigma_{t,k}^{vm,l} }}{{\partial \overline{\rho }_{i} }} = \frac{1}{{\sigma_{t,k}^{vm,l} }}\left( {{\mathbf{DB}}_{t,k} {\mathbf{T}}_{t} {\mathbf{u}}_{t}^{e,l} } \right)^{T} {{\varvec{\Lambda}}}\left( {{\mathbf{DB}}_{t,k} {\mathbf{T}}_{t} \frac{{\partial {\mathbf{u}}_{t}^{e,l} }}{{\partial \overline{\rho }_{i} }}} \right),$$

(20)

where ${\mathbf{u}}_{t}^{e,l}$ is the nodal displacement vector of the tth element for the ground structure under the lth loading case, and ${\mathbf{u}}_{t}^{e,l} = {{\varvec{\Gamma}}}_{t} {\mathbf{U}}^{l}$. Wherein ${\mathbf{U}}^{l}$ the structural nodal displacement vector ${\mathbf{U}}^{l}$ under the lth loading case and ${{\varvec{\Gamma}}}_{t}$ is the position matrix associated with the degrees of freedom of the tth beam element in the ground structure. Therefore, for the derivative of the structural nodal displacement vector ${\varvec{U}}^{l}$ under the lth loading case, it has

$$\frac{{\partial {\varvec{u}}_{t}^{e,l} }}{{\partial \overline{\rho }_{i} }} = -{\varvec{\varGamma}}_{t} \left( {\varvec{K}} \right)^{ - 1} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}{\varvec{U}}^{l}$$

(21)

Substituting Eq. (21) into Eq. (20), then Eq. (20) can be transformed as

$$\frac{{\partial \sigma_{t,k}^{vm,l} }}{{\partial \overline{\rho }_{i} }} = - \frac{1}{{\sigma_{t,k}^{vm,l} }}\left( {{\mathbf{DB}}_{t,k} {\mathbf{T}}_{t} {\mathbf{u}}_{t}^{e,l} } \right)^{T} {{\varvec{\Lambda}}}\left( {{\mathbf{DB}}_{t,k} {\mathbf{T}}_{t} {{\varvec{\Gamma}}}_{t} \left( {\varvec{K}} \right)^{ - 1} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}{\varvec{U}}^{l} } \right)$$

(22)

Meanwhile, the derivative of stress aggregate constraint function in optimization model Eq. (17) can be derived as

$$\frac{{\partial f_s^l\left( {\mathbf{\rho }} \right)}}{{\partial {{\bar \rho }_i}}} = \frac{{f_s^l{{\left( {\mathbf{\rho }} \right)}^{1 - {p_a}}}}}{{\bar \sigma }}\sum\limits_{t = 1}^{P + Q} {{{\sum\limits_{k = 1}^{12} {\left( {\frac{{{{\bar \rho }_t}^{_{{p_3} - q}}\sigma _{t,k}^{vm,l}}}{{\bar \sigma }}} \right)} }^{{p_a} - 1}}} \left( {\left( {{p_3} - q} \right){{\bar \rho }_t}^{{p_3} - q - 1}\sigma _{t,k}^{vm,l} + {{\bar \rho }_t}^{{p_3} - q}\frac{{\partial \sigma _{t,k}^{vm,l}}}{{\partial {{\bar \rho }_i}}}} \right)$$

(23)

In this paper, the adjoint method is employed order to reduce the computational complexity. Then, the adjoint vector ${\varvec{\gamma}}^{l}$ under the lth loading case is defined according to the following adjoint equation:

$${\varvec{K}}^{e} {\varvec{\gamma}}^{l} = \frac{{f_{s}^{l} \left( {{\varvec{\uprho}}} \right)^{{1 - p_{a} }} }}{{\overline{\sigma }}}\sum\limits_{t = 1}^{P + Q} {\sum\limits_{k = 1}^{12} {\left( {\frac{{\overline{\rho }_{t}^{{_{{p_{{_{3} }} - q}} }} \sigma_{t,k}^{vm,l} }}{{\overline{\sigma }}}} \right)}^{{p_{a} - 1}} } \left( {\overline{\rho }_{t}^{{p_{3} - q}} \frac{1}{{\sigma_{t,k}^{vm,l} }}\left( {{\varvec{DB}}_{t,k} {\varvec{T}}_{t} {\varvec{u}}_{t}^{e,l} } \right)^{{\text{T}}} \varvec{\Lambda DB}_{t,k} {\varvec{T}}_{t}{\varvec{\varGamma}}_{t} } \right)$$

(24)

Substituting the defined adjoint vector ${\varvec{\gamma}}^{l}$ into Eq. (23) yields the derivative of the stress aggregate constraint function under the lth loading case as

$$\frac{{\partial f_{s}^{l} \left( {{\varvec{\uprho}}} \right)}}{{\partial \overline{\rho }_{i} }} = \frac{{f_{s}^{l} \left( {{\varvec{\uprho}}} \right)^{{1 - p_{a} }} }}{{\overline{\sigma }}}\sum\limits_{t = 1}^{P + Q} {\sum\limits_{k = 1}^{12} {\left( {\frac{{\overline{\rho }_{t}^{{_{{p_{{_{3} }} - q}} }} \sigma_{t,k}^{vm,l} }}{{\overline{\sigma }}}} \right)}^{{p_{a} - 1}} } \left( {p_{3} - q} \right)\overline{\rho }_{t}^{{p_{3} - q - 1}} \sigma_{t,k}^{vm,l} - \left( {{\varvec{\gamma}}^{l} } \right)^{{\text{T}}} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}{\varvec{U}}^{l}$$

(25)

where $\frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}$ is the assembly of the ith element-level stiffness matrix $\frac{{\partial {\varvec{k}}_{i} }}{{\partial \overline{\rho }_{i} }}$, and according to Eq. (3), $\frac{{\partial {\varvec{k}}_{i} }}{{\partial \overline{\rho }_{i} }}$ can be expressed as

$$\frac{{\partial {\varvec{k}}_{i} }}{{\partial \overline{\rho }_{i} }} = \left( {\left( {1{ - }\alpha } \right)p_{1} \overline{\rho }_{i}^{{p_{1} - 1}} { + }\alpha \overline{\rho }_{i}^{{p_{2} - 1}} } \right){\varvec{k}}_{i}^{0}$$

(26)

6.2 Sensitivity analyses of stability constraint function

Many attempts have been devoted to solve the buckling or vibration frequency related optimization, the eigenvalue sensitivity derivation was an essential step and has been proven to be credible in these studies (Torii and Faria 2017; Changizi and Jalalpour 2018; Ferrari and Sigmund 2019). Referring to these studies, the eigenvalue sensitivities can be derived by taking the derivatives of Eq. (11) with respect to physical density variable $\overline{\rho }_{i}$, and yields

$$\left( {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial \overline{\rho }_{i} }} + \mu_{j}^{l} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }} + \frac{{\partial \mu_{j}^{l} }}{{\partial \overline{\rho }_{i} }}{\varvec{K}}} \right)\varvec{\varphi }_{j}^{l} = 0$$

(27)

In view of the symmetries of stiffness and stress stiffness matrices, and pre-multiplying $\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}}$ on the left side of Eq. (27), then $\frac{{\partial \mu_{j}^{l} }}{{\partial \overline{\rho }_{i} }}$ can be rewritten as

$$\frac{{\partial \mu_{j}^{l} }}{{\partial \overline{\rho }_{i} }} = - \frac{1}{{\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \varvec{K\varphi }_{j}^{l} }}\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial \overline{\rho }_{i} }} + \sum\limits_{b = 1}^{N} {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial u_{b}^{l} }}} \frac{{\partial u_{b}^{l} }}{{\partial \overline{\rho }_{i} }}{ + }\mu_{j}^{l} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}} \right)\varvec{\varphi }_{j}^{l}$$

(28)

Meanwhile, the derivative of stability constraint function with respect to physical density variable $\overline{\rho }_{i}$ in optimization formulation (17) can be expressed as

$$\frac{{\partial f_{\lambda }^{l} }}{{\partial \overline{\rho }_{i} }} = \left( {f_{\lambda }^{l} } \right)^{{1 - p_{a} }} \sum\limits_{{j = 1,j \in {\mathbf{R}}_{\lambda } }}^{{n_{\lambda } }} {\left( {\lambda^{*} \mu_{j}^{l} } \right)^{{p_{a} - 1}} } \lambda^{*} \frac{{\partial \mu_{j}^{l} }}{{\partial \overline{\rho }_{i} }}$$

(29)

Substituting Eq. (28) into Eq. (29), yields:

$$\frac{{\partial f_{\lambda }^{l} }}{{\partial \overline{\rho }_{i} }} = - \left( {f_{\lambda }^{l} } \right)^{{1 - p_{a} }} \sum\limits_{{j = 1,\lambda_{i} \in {\mathbf{R}}_{\lambda } }}^{{n_{\lambda } }} {\frac{{\left( {\lambda^{*} \mu_{j}^{l} } \right)^{{p_{a} - 1}} \lambda^{*} }}{{\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \varvec{K\varphi }_{j}^{l} }}} \left( {\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial \overline{\rho }_{i} }}{ + }\mu_{j}^{l} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}} \right)\varvec{\varphi }_{j}^{l} + \left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \sum\limits_{b = 1}^{N} {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial u_{b}^{l} }}} \frac{{\partial u_{b}^{l} }}{{\partial \overline{\rho }_{i} }}\varvec{\varphi }_{j}^{l} } \right)$$

(30)

Similar to the derivative process of the stress aggregation constraint function, the adjoint method is also employed here to form the adjoint vector ${\varvec{\xi}}^{l}$ for the last term in Eq. (29), which can be formulated as

$$\varvec{K\xi }^{l} = \left( {f_{\lambda }^{l} } \right)^{{1 - p_{n} }} \sum\limits_{{j = 1,\lambda_{j} \in {\mathbf{R}}_{\lambda } }}^{{n_{\lambda } }} {\frac{{\left( {\lambda^{*} \mu_{j}^{l} } \right)^{{p_{n} - 1}} \lambda^{*} }}{{\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \varvec{K\varphi }_{j}^{l} }}} \left( {\sum\limits_{b = 1}^{N} {\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \frac{{\partial {\varvec{K}}^{g,l} }}{{\partial u_{b} }}} \varvec{\varphi }_{j}^{l}{\varvec{\varPsi}}_{b}^{{\text{T}}} } \right)$$

(31)

where ${\varvec{\varPsi}}_{b}$ is an 1 × N unit vector and its bth component is 1, and its other components all are zero. Then, substituting the adjoint vector ${\varvec{\xi}}^{l}$ into Eq. (29), yields:

$$\frac{{\partial f_{\lambda }^{l} }}{{\partial \overline{\rho }_{i} }} = - \left( {f_{\lambda }^{l} } \right)^{{1 - p_{a} }} \sum\limits_{{j = 1,\lambda_{j} \in {\mathbf{R}}_{\lambda } }}^{{n_{\lambda } }} {\frac{{\left( {\lambda^{*} \mu_{j}^{l} } \right)^{{p_{a} - 1}} \lambda^{*} }}{{\left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \varvec{K\varphi }_{j}^{l} }}} \left( {\varvec{\varphi }_{j}^{l} } \right)^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial \overline{\rho }_{i} }}{ + }\mu_{j}^{l} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}} \right)\varvec{\varphi }_{j}^{l} { + }\left( {{\varvec{\xi}}^{l} } \right)^{{\text{T}}} \frac{{\partial {\varvec{K}}}}{{\partial \overline{\rho }_{i} }}{\varvec{U}}^{l}$$

(32)

where $\frac{{\partial {\varvec{K}}^{g,l} }}{{\partial \overline{\rho }_{i} }}$ is the assembly of the sensitivities of the ith element-level stress stiffness matrix $\frac{{\partial {\varvec{k}}_{i}^{g,l} }}{{\partial \overline{\rho }_{i} }}$, and according to Eq. (3), the term $\frac{{\partial {\varvec{k}}_{i}^{g,l} }}{{\partial \overline{\rho }_{i} }}$ can be formulated as

$$\frac{{\partial {\varvec{k}}_{i}^{g,l} }}{{\partial \overline{\rho }_{i} }} = p_{2} \overline{\rho }_{k}^{{p_{2} - 1}} {\varvec{k}}_{i}^{g,l0} + \overline{\rho }_{k}^{{p_{2} }} \frac{{\partial {\varvec{k}}_{i}^{g,l0} }}{{\partial \overline{\rho }_{i} }}$$

(33)

where $\frac{{\partial {\varvec{k}}_{i}^{g,l0} }}{{\partial \overline{\rho }_{i} }}$ is the derivative of the initial stress stiffness matrix of the ith beam element, the construction of $\frac{{\partial {\varvec{k}}_{i}^{g,l0} }}{{\partial \overline{\rho }_{i} }}$ can be found in Mitjana et al. (2019).

7 Numerical examples

In this paper, the ground structure approach is used to generate an initial proper meshed frame structure consisting of all potential beams with rigid connectivity, wherein the potential beams are formed by connecting two different nodes. Then, the frame structural topology optimization is implemented to eliminate the inefficient beams within the ground structure, and the best beam layout with prescribed mechanical performance is obtained by the proposed method. Obviously, the connection level that how far one node can reach to another node has a strong impact on the complexity of the ground structure. Here, a 4 × 4 node meshed ground structure with different connection levels are presented in Fig. 3a–c to illustrate the effect of the connection level.

Fig. 3

Ground structure: a connection level 1; b connection level 2; c connection level 3

With the increase of the connection level, the complexity of the ground structure increases and slender beams generate, resulting in the increase of computational burden and the possibility of local instability. Therefore, it is indispensable to selected a proper connection level to make a trade-off between the complexity of the ground structure and the computational burden. In this section, the connection level lv = 2 is used to determine an optimization space.

Meanwhile, the candidate members in the ground structure are modeled by hollow cylindrical beam elements, and selected from code for design of steel structures of China. In order to ensure the feasibility of optimization space, the cross-sectional properties of candidate members are determined by the mechanical performance of the initial ground structure. The selection criteria are that the ratio between the critical load factor and the corresponding constraint limit should be greater than the prescribed volume ratio, and the ratio between the maximum von Mises stress and the yield strength should be smaller than the prescribed volume ratio. Moreover, referring to the above-mentioned design code, the members are made by Q345B steel materials, then the material properties are set as: the Young’s modulus E = 210 GPa, Poisson’s ratio v = 0.3 and the yield strength $\overline{\sigma } = 345{\text{Mpa}}$.

For all examples in this section, the design variables are updated by MMA algorithm, of which a conservative move-limit 0.08 and other default parameters are used in this paper (Svanberg 1987). As a widely used approach, MMA algorithm has been employed in topology optimization, especially in stress and buckling related problems (Le et al. 2010;  Ferrari and Sigmund 2019; Dalklint et al. 2021), and proven to be credible by these researches. Furthermore, since the entire codes about MMA have been kindly provided by Svanberg, the relevant parameters in the MMA algorithm can be appropriately modified as recommended in the literatures (Guest et al. 2011; Wang et al. 2011). Obviously, the feature of adjustable parameters in the MMA algorithm provides an advantage over the other available packages, such as the MATLAB optimization toolbox. However, users need to determine the appropriate parameters according to the characteristics of the optimization problem and their own experience, which also become its disadvantage. In this paper, the termination criteria are either the change in design variables or the gray level indicator, its flow chart is similar to that of the references (Guest et al. 2011; Wang et al. 2011).

$$\frac{{\left| {{\varvec{\rho}}^{\left( k \right)} - {\varvec{\rho}}^{{\left( {k - 1} \right)}} } \right|}}{{\left| {{\varvec{\rho}}^{\left( k \right)} } \right|}} < \varepsilon_{1}$$

(34)

$$m_{d} = \sum\limits_{i = 1}^{N} {\frac{{4\overline{\rho }_{i} (1 - \overline{\rho }_{i} )}}{N}} \le \varepsilon_{2}$$

(35)

where $m_{d}$ denotes a gray level indicator, $\varepsilon_{1}$ and $\varepsilon_{2}$ are two small positive parameters. $\varepsilon_{1} = 0.001$ and a value of [0.001,0.02] may be selected as $\varepsilon_{2}$.

Many excellent works have been devoted to buckling topology optimization concerned with continuum structures to achieve a buckling resistant design (Gao et al. 2017b, 2020; Ferrari and Sigmund 2019). Since only topology variables are included in the optimization model (Eq. (15)), the employed measures dealing with stability constraints in this paper share the strong mathematical similarities to the corresponding researches (Gao et al. 2017b, 2020). Therefore, a cantilever structure is firstly investigated to show the advantages over the existing continuum topology optimization approach proposed by Gao et al. (2017b). Then the examples concerned with frame structures are studied to demonstrate the effectiveness of the proposed method, for these examples, the stress-constrained optimization problem without stability constraints under a given volume is firstly presented as a reference design. Afterward, the optimized designs with stress and different stability constraints under the same fixed volume are presented, and the buckling performances including the global stability and individual member stability are examined to indicate the feasibility of the proposed method in this paper. Here, the individual member stability can be evaluated by the individual member buckling stress ratio (IMBSR), of which the expression for the ratio can refer to Changizi and Jalalpour (2018) and the individual member stability can be ensured when the maximum value of these ratios is less than 1.

7.1 A cantilever structure

In order to illustrate the advantage of the proposed method over the existing approach (Gao et al. 2017b), the optimized design concerned with the continuum structure only with buckling constraints is firstly investigated in this example. The design domain for the cantilever continuum structure under concentrated load $F = 50\;{\text{KN}}$, which is applied at the upper middle position of the structure, is shown in Fig. 1. The dimensions, boundary conditions as well as the material properties of the structure keep consistent with those in the literature (Gao et al. 2017b). The optimized designs under buckling constraints ($\lambda^{*} = 1$) obtained by employing the measures in this paper and literature (Gao et al. 2017b) are presented in Fig. 4b, c, respectively. And the corresponding compliances for these two optimized designs are $1.47\;{\text{KN}} \; {\text{m}}$ and $1.66\;{\text{KN}} \; {\text{m}}$, respectively. The comparison indicates that the former optimized design possesses better stiffness and has more materials distributed in the compressive zone to achieve buckling resistant performance.

Fig. 4

Cantilever continuum structure: a the design domain; the optimized design obtained by employing the measures in this b paper and c literature (Gao et al. 2017b)

Furthermore, the cantilever frame ground structure composed by 88 beam members is shown in Fig. 5, the dimensions and loading as well as boundary conditions are same as those on continuum structure. As mentioned in the beginning of this section, the type of standard beam member is determined by the mechanical performance of the ground structure, and the inner and outer diameters of cross-section of the beam members are $d_{{{\text{inner}}}} = 4\;{\text{mm}}$ and $d_{{{\text{outer}}}} = 14\;{\text{mm}}$, respectively. The volume fraction $V^{*} = 0.15$ is used in this example, and the initial maximum von Mises stress, critical buckling load factor and compliance of the ground structure are 96.52 MPa, 4.13 and $15.97\;{\text{N}}\;{\text{m}}$, respectively.

Fig. 5

Cantilever frame structure: a the ground structure; b stress-constrained optimized design; optimized design when c $\lambda^{*} = 1$; d $\lambda^{*} = 1.5$

The reference design only considering stress constraints for the cantilever frame ground structure is shown in Fig. 5, the compliance and maximum von Mises stress of this optimized design are $23.39\;{\text{N}} \; {\text{m}}$ and 139.13 MPa, respectively. For comparison, the optimized designs with stress and stability constraints, which correspond to the lower bound $\lambda^{*} = 1$ and $\lambda^{*} = 1.5$, are presented in Fig. 6a, b, respectively. The comparison of these designs indicate that shorter beam members are distributed in the compression zone of the cantilever frame structure to achieve better buckling resistant performances, and the final optimized designs vary with different mechanical performance requirements.

Fig. 6

Comparison for the number of low-order pseudo buckling modes that need to be identified and deleted by using the proposed SPLMP and SIMP model ($\lambda^{*} = 1$)

Within optimization, in order to suppress the low-order pseudo buckling modes and further reduce the computational burden, the identification and deletion measures of pseudo buckling modes in Sect. 4 has to be adopted. Figure 7a, b gives the number of low-order pseudo buckling modes that need to be identified and deleted by using the proposed smooth polynomial material interpolation model and SIMP model, respectively. The comparison shows that more pseudo buckling modes need to be identified and deleted by using SIMP model, and further indicates that the advantage of the proposed smooth polynomial material interpolation model in suppressing the low-order pseudo buckling modes. Moreover, the first two real buckling modes for the optimized design ($\lambda^{*} = 1$) are presented in Fig. 7a, b, respectively, where the thin bars represent the eliminated beam members in the final design. It can be observed that the first two buckling load factors are different and obviously the modal strain energy ratio is mainly contributed by the nodes with high normalized volume (as defined in Sect. 4). These results also indicate that the validity of the measures dealing with stability constraints adopted in this paper.

Fig. 7

Real buckling modes for the optimized design when $\lambda^{*} = 1$: a first mode ($\lambda = 1.0291$); b second mode ($\lambda = 1.1549$)

Meanwhile, the comparison among the critical buckling load factor of the optimized designs with or without stability constraints are shown in Table 1, this result manifest that the need to include stability requirements within FSTO. Also as shown in Table 1, the compliances for the optimized designs with stress and two different stability constraints are $25.94\;{\text{N}}\;{\text{m}}$ and $28.38\;{\text{N}}\;{\text{m}}$, respectively. It can be concluded that the better buckling resistant performances can achieved by compromising the stiffness in the optimized design. Moreover, the iteration processes of the structural mechanical performance for the optimized design when $\lambda^{*} = 1$ are shown in Fig. 8. Obviously, the maximum individual member buckling stress ratio (IMBSR) always less than 1, which implies that the individual member stability can be ensured during the optimization process. The iteration processes in Fig. 6 also indicate that the optimized design can stably converge to the final optimized solutions, and further validate the feasibility and effectiveness of the comprehensive measures concerned with the stress and stability constraints.

Table 1 Mechanical performances of the optimized design for the cantillever frame structure

Table 2 Mechanical performances of the optimized design for the roof structure

Table 3 Mechanical performances of the optimized design for the tower structure under single loading case

Fig. 8

Optimization histories of the roof structure with stress and stability constraints ($\lambda^{*} = 1$): a the compliance and the maximum von Mises stress; b the maximum IMBSR and the critical buckling load factor

7.2 A roof structure

A roof structure under uniformly distributed load $F = 10$ KN/m applied at the top of the structure is shown in Fig. 9, the corresponding ground structure and geometric parameters are also presented in Fig. 9. The ground structure consists of 126 beam members, and those at the top of the roof structure are non-designed members, which are represented by black colors. The designable beam members are represented by blue colors, and the total number of the designable beam elements Q = 108. For the roof structure, the inner and outer diameters of cross-section of the beam members are $d_{{{\text{inner}}}} = 8\;{\text{mm}}$ and $d_{{{\text{outer}}}} = 60\;{\text{mm}}$, respectively. The initial maximum von Mises stress, critical buckling load factor and compliance of the ground structure are 206.91 MPa 10.01 and $4.10\;{\text{KN}}\;{\text{m}}$, respectively. And the volume fraction $V^{*} = 0.3$ is used in this example.

Fig. 9

Ground structure for the roof structure

Figure 10 gives the stress-constrained optimized design for the roof structure, the compliance and maximum von Mises stress of this optimized design is $7.12\;{\text{KN}}\;{\text{m}}$ and 278.46 MPa, respectively. As a contrast, the optimized designs with stress and two different stability constraints are presented in Fig. 11a, b, respectively. The comparison between Figs. 10 and 11 implies that the final optimized designs vary with different mechanical performance requirements, and more beam members are needed in the middle and constraint regions of the roof structure to ensure the stability requirement. Moreover, it is also observed that the optimized design with more beam members distributed at the middle regions of the roof structure to achieve a better buckling resistant performance. The first two buckling modes for the optimized design ($\lambda^{*} = 1$) are presented in Fig. 12a, b, respectively. Obviously, the eliminated beam members have little effect on the modal strain energy ratio (as defined in Sect. 4) and can be seen as real buckling modes.

Fig. 10

Stress-constrained optimized designs for the roof structure

Fig. 11

Optimized designs with stress and stability constraints for the roof structure: a $\lambda^{*} = 1$; b $\lambda^{*} = 1.5$

Fig. 12

Real buckling modes for the optimized design when $\lambda^{*} = 1$: a first mode ($\lambda = 1.1762$); b second mode ($\lambda = 1.4969$)

As shown in Table 2, the critical buckling load factor finally to be 1.1762 and 1.6756 corresponding to the designs with overall structural instability prevention at two levels of $\lambda^{*} = 1$ and $\lambda^{*} = 1.5$, respectively. And the critical buckling load factor for the optimized designs only with stress constraints is 0.8920. These results manifest that both the stress and stability constraints are well controlled during the optimization process, and the great importance of considering the stability requirement within FSTO. What’s more, the results also indicate that the effectiveness of the comprehensive measures concerned with the pseudo buckling modes. At the same time, the compliances for these two optimized designs are $7.32\;{\text{KN}}\;{\text{m}}$ and $7.55\;{\text{KN}}\;{\text{m}}$, respectively. It can be drawn the conclusion that the buckling resistant requirements can be satisfied by compromising the stiffness in the optimized design. During the optimization process, the individual member stability is checked by the individual member buckling stress ratio (IMBSR), of which the maximum value corresponding to the iteration steps are presented in Fig. 13b. The result shows that the individual member stability can be guaranteed throughout the optimization. Also, the iteration processes of the volume fraction and structural mechanical performance, including the compliance, the maximum von Mises stress and the critical buckling load factors when $\lambda^{*} = 1$ are shown in Fig. 8, it’s obvious that the optimized design can stably converge to the final optimized solutions, which implies the feasibility and effectiveness of the proposed method.

Fig. 13

Optimization histories of the roof structure with stress and stability constraints ($\lambda^{*} = 1$): a the compliance and the maximum von Mises stress; b the maximum IMBSR and the critical buckling load factor

7.3 A tall frame tower structure under multiple loading cases

A tall frame tower structure with height of 80 m and consists of 12 layers with a 5 m × 5 m square at the bottom and a regular octagon at the top is shown in Fig. 14a, its construction along the height can be referred to Zegard and Paulino (2015). The ground structure, which consists of 648 beam members, corresponding to different views are presented in Fig. 14b, c, respectively. The ground structure is under two different loading cases where each single force $F = - F{^{\prime}} = 10\;{\text{KN}}$ is applied at the lateral top of the structure is shown in Fig. 14a, and according to the mechanical performance of the ground structure, the cross-sectional inner and outer diameters of each beam member is determined as: $d_{{{\text{inner}}}} = 10\;{\text{mm}}$ and $d_{{{\text{outer}}}} = 89\;{\text{mm}}$, respectively. Due to the symmetry of the ground structure and loading conditions, the initial maximum von Mises stress, critical buckling load factor of the ground structure under two different loading cases are 67.65 MPa and 9.9974, respectively. The combined compliance $C_{{{\text{tol}}}}$ of the ground structure is $1.74\;{\text{KN}}\;{\text{m}}$, and the volume fraction $V^{*} = 0.25$ is used in this example.

Fig. 14

A tall frame tower structure: a ground structure; b front view; c lateral view

The reference design only with stress constraints under the fixed volume is presented in Fig. 15, and the combined compliance and the maximum von Mises stress of its final optimized structure are $4.90\;{\text{KN}}\;{\text{m}}$ and 116.29 MPa, respectively. Figures 16, 17 give the final optimized designs for the tower structure with both stress and different stability constraints under the same volume, respectively. It can be found from the comparison among these optimized designs that shorter beam members and more column beam members are distributed in the bottom and lateral regions of the optimized structures, respectively, to achieve better buckling resistance performance.

Fig. 15

Stress-constrained optimized designs for the tall frame tower structure

Fig. 16

Optimized designs with stress and stability constraints ($\lambda^{*} = 1$) for the tower structure

Fig. 17

Optimized designs with stress and stability constraints ($\lambda^{*} = 1.5$) for the tower structure

The critical buckling load factor of the optimized structure at two different buckling resistant requirements of $\lambda^{*} = 1$ and $\lambda^{*} = 1.5$ are 1.008 and 1.6493, respectively. However, the critical buckling load factor of the optimized structure only with stress constraints is 0.8160, which imply that it is indispensable to consider stability requirement in frame structural topology optimization. As shown in Fig. 18, the maximum individual member buckling stress ratio (IMBSR) keep below the safe value, which indicate that the individual member stability can be ensured throughout the optimization. At the same time, the iteration processes of the structural mechanical performance with stress and stability constraints ($\lambda^{*} = 1$) under single loading case are shown in Fig. 18. Due to the symmetry of the ground structure and loading conditions, the structural performance under the other loading case can be easily obtained. As shown in Table 3, the combined compliances of the final optimized designs under two different stability constraints are $5.03\;{\text{KN}}\;{\text{m}}$ and $7.15\;{\text{KN}}\;{\text{m}}$, respectively. It can be seen that the stiffness of the final optimized structure is reduced with the requirement of better buckling resistance performance. The conclusion from the above analysis can be also drawn that both the stress and stability constraints are well controlled during optimization process, which imply that the effectiveness of the comprehensive measures concerned with pseudo buckling modes and the feasibility of the proposed optimization method.

Fig. 18

Optimization histories of the roof structure with stress and stability constraints ($\lambda^{*} = 1$) under single loading case: a the compliance and the maximum von Mises stress; b the maximum IMBSR and the critical buckling load factor

8 Concluding remarks

This work aims to find the stiffest design with stress and stability requirements for frame structures with hollow beam members, but the proposed approach can be generalized to the design of frame structures with beam members of other cross-sections. Since only topology design variables are included in the optimization problem, the problem studied in this paper share the strong mathematical similarities to the corresponding researches on continuum structures. This is not the usual formulation employed in recent researches, although this is a limitation of the proposed approach, it also provides the advantage of avoiding the need to map cross-sectional parameters to standard members. To demonstrate the feasibility and effectiveness of the proposed method, several numerical examples are designed and the corresponding mechanical performances are examined. The following conclusion can be drawn as follows:

• (1) The employed measures concerned with pseudo buckling mode issues, including the proposed smooth polynomial material interpolation model and the pseudo buckling mode identification measure, are effective in suppressing the low-order pseudo buckling modes and reducing the computational burden.

• (2) The mechanical performances of the optimized design can be well controlled throughout the optimization, which illustrate that the comprehensive measures, which dealing with both stress and stability constraints, are feasible.

• (3) The optimized design obtained by using the proposed method possesses a clear 0/1 beam layout, and stably converge to the final optimized solutions, which imply the effectiveness of the proposed method.

• (4) Despite the proposed method in this paper is suitable for static loading case, the optimized frame design considering more structural behavior requirements, such as earthquake and wind resistance performance constraints, needs further mathematical and scientific developments. Moreover, the construction process requirements, such as the intersecting member constraints and many types of members, should be taken into consideration in further studies.