Layout optimization of structures with distributed self-weight, lumped masses and frictional supports

Abstract

The well-known ‘ground structure’-based truss layout optimization method has recently been extended to allow accurate modelling of distributed self-weight. By incorporating equally stressed catenaries in the ground structure, non-conservative errors caused by neglecting bending effects within members carrying their own weight are eliminated. However, in cases where the self-weight of a structure has a favourable role in supporting the applied loads, solutions that include convoluted arrangements of overlapping elements may often be generated. To address this, an enhanced layout optimization formulation is proposed that explicitly allows inclusion of favourable unstressed masses, such as counterweights. Frictional supports are also modelled and the cost of abutments and anchorages taken account of in the formulation. The efficacy of the proposed methodology is demonstrated through application to benchmark examples and to the conceptual design of a simplified long-span bridge structure, considering both ground anchored and self-anchored alternatives.

1 Introduction

The theory of minimum volume structures was developed by Michell (1904) and Hemp (1973). However, the classical solutions identified by these workers are time consuming and difficult to identify and neglect many real-world considerations. Although Rozvany and Wang (1984) extended classical theory to treat self-weight, due to the additional challenges involved, solutions have only been found for a certain class of structures, which are restricted to be entirely in compression or entirely in tension (Wang and Rozvany 1983).

Numerical methods such as the ‘ground structure’-based truss layout optimization method originally proposed by Dorn et al. (1964) provide significantly more flexibility in identifying new classes of optimal solutions. With the ground structure method optimal truss layouts can be obtained using linear programming. Modern computing hardware and improvements in computational efficiency (e.g. Gilbert and Tyas 2003) have allowed such numerical methods to be used to quickly identify structures that have volumes very close to theoretical values, often within a small fraction of one percent.

These numerical results can also be used to help identify analytically optimal, or near-optimal, solutions. For a pin-supported single span, an arch bridge-type solution was proposed by Hemp (1974), later shown to be optimal in restricted cases by Chan (1975) and Pichugin et al. (2012). For a multiple span structure, a solution was provided by Pichugin et al. (2015), with further studies undertaken by Beghini and Baker (2015).

Numerical methods have been extended to include a range of additional practical considerations. The traditional means of modelling self-weight in ground structure-based layout optimization has been to assume that the weight of a truss member acts directly at the end nodes, e.g. see Bendsøe and Sigmund (1995) and Pritchard et al. (2005). However, this formulation neglects the bending stresses that are generated by the distributed self-weight of any non-vertical member, potentially leading to significantly non-conservative designs, particularly when very long members are involved.

Fairclough et al. (2018) proposed an alternative method of modelling self-weight, whereby self-weight forces are assumed to be distributed continuously along the length of a given member, making use of an equal stress catenary in place of a normal straight member. This means that bending stresses are not induced, thereby allowing accurate solutions to be generated irrespective of the distance spanned. In Fairclough et al. (2018) the method was applied to idealized long-span bridges notionally comprising an infinite number of spans. This allowed new optimized forms to be identified, with these then compared with cable stayed and suspension bridge forms. Significantly, the study indicated that large material savings could be realized using the new forms (e.g. approx. 70% over suspension bridge forms and 40% over cable-stayed bridge forms for 5 km spans in steel). The material savings were found to be largest for the longest spans, due to the higher relative importance of self-weight loading in such cases. This has also been observed in practice; for example, in the case of the 1991-m span Akashi Kaikyo Bridge, the self-weight of the bridge has been reported to account for over 90% of the cross-section of the main suspension cables (Ito 1996). Limits on the ability of a given material to carry its own self-weight when used to construct a bridge of a given form has been recognized as one of two major limiting factors by the designers of both the 1624-m span Great Belt Bridge (Ostenfeld 1996) and of the proposed 3300-m span Messina Bridge (Brancaleoni et al. 2011). Optimization methods capable of identifying structurally efficient forms therefore have the potential to be of great benefit in this field.

In practice, suspension bridges have traditionally been the preferred solution for long spans. In these structures the force at the ends of the main cables are transmitted into the ground; this generally requires constructions of significant mass to provide sufficient anchorage (Gimsing and Georgakis 2011). Self-anchored suspension bridges are possible, but have generally been considered impractical for spans of more than a few hundred metres (Ochsendorf and Billington 1999). Conversely, an ‘outstanding advantage’ (Troitsky 1988) of cable-stayed bridges is that they are usually self-anchored, with no horizontal force transmitted at the ends of the structure. This permits efficient construction using the cantilever method, but also leads to significant compressive forces in the deck. Ground-anchored cable-stayed bridges have also been proposed (Shao et al. 2013), but have rarely been constructed in practice.

These different boundary conditions can cause issues for theoretical comparative studies. To allow fair comparison between suspension and cable-stayed forms, Croll (1997) and Dalton et al. (1997) considered a ground-anchored cable-stayed bridge which gives rise to similar reaction forces as the suspension form. Lewis (2012) extends this to include some consideration of the self-weight of the structure but, as with Croll (1997), the study is limited to classical bridge forms, with parabolic suspension cables and parallel (harp style) cable stays.

Some novel designs for very long spans have been proposed, such as the designs of Lin and Chow (1991) and Starossek (1996), which both utilize a split-pylon concept, based on a ground-anchored suspension form and a self-anchored fan-type cable-stayed form, respectively. Other proposals also address more complex issues, such as out of plane stability (Menn and Billington 1995). However very few bridges of significant span have been constructed using non-traditional forms, with a recent exception being the Yavuz Sultan Selim Bridge that employs a hybrid cable stayed and suspension form for increased stiffness (Virlogeux 2018). This bridge also includes some regions with ground-anchored cable stays (de Ville de Goyet et al. 2018).

When ground-anchored solutions are used, a number of foundation types may be possible, depending on local ground conditions, material availability and other site considerations. Probably the most common is the gravity-type foundation (Gimsing and Georgakis 2011), where a large anchorage block is used such that the frictional force between its base and the ground is sufficient to carry the horizontal loading. An advantage of this configuration is that the mass may largely comprise inexpensive local materials, such as sand (Ostenfeld 1996). Alternatively other configurations may be appropriate, such as direct anchorage into bedrock, if the local conditions allow this.

For more modest bridge spans, counterweights have in some cases been used as a means of generating novel forms. An example is Calatrava’s eye-catching Alamillo Bridge, which balances a cable net against an inclined pylon, obviating the need for back stays. However various workers (e.g. Guest et al. 2013; Croll 2019) have pointed out that in this particular case the resulting form is highly structurally inefficient. Unfortunately the current optimization literature provides little help to engineers wishing to identify efficient gravity-balanced structural forms, whether making use of distributed self-weight elements or explicit lumped masses.

Consideration of scenarios with support types beyond classical fixed pin or pin/roller supports is also rare within the current optimization literature. Rozvany and Sokół (2012) consider support types where reaction forces incur a cost proportional to their magnitude, and, in discussion of this paper (Espí 2013; Sokół and Rozvany 2013), some solutions with frictional foundations are identified. However, these required a priori knowledge of the foundation employed in the optimal solution. Furthermore, self-weight was not considered, which may usefully be employed to provide resistance against horizontal forces, such as via an anchorage block.

To allow for consideration of these differing boundary conditions, the distributed self-weight method presented by Fairclough et al. (2018) is here extended to allow inclusion of the costs of unstressed material, such as in anchorage or abutment structures. This will permit exploration of the potential for material savings in the case of both ground anchored and self-anchored cases, as well as potentially more realistic cases where restraint is provided via friction. The inclusion of unstressed material will also permit investigation of cases where counterweights can be used as part of a structural solution.

This paper is organized as follows: Sect. 2 provides a brief overview of the distributed self-weight formulation for modelling self-weight, with illustrative examples used to demonstrate the mechanisms by which the optimal forms identified may change with span. Section 3 then proposes new formulations that extend the range of boundary conditions that can be treated. These are then applied to the initial design of a bridge-type structure in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Layout optimization with distributed self-weight

2.1 Formulation

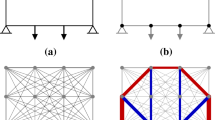
The classical ground structure-based truss layout optimization procedure is shown diagrammatically in Fig. 1a–d. When distributed self-weight is included, each straight line connection between nodes is replaced by a pair of equal strength (i.e. equally stressed) catenary elements (Fig. 1e, f), one to carry compressive forces and the other tensile forces. However, the resulting problem formulation differs from the standard formulation only in the composition of the coefficient matrices such that linear programming can still be used to obtain solutions; thus for a problem comprising n nodes and m potential elements the formulation can be written as:

$$\begin{aligned}&\text{minimize }&V&= \mathbf{c}^\mathrm{T}\mathbf{q}, \end{aligned}$$

(1a)

$$\begin{aligned}&\text{subject to }&\mathbf{Bq}&= \mathbf{f}, \end{aligned}$$

(1b)

$$\begin{aligned}&{\mathbf{q}}&\ge \mathbf{0}, \end{aligned}$$

(1c)

where V is the total volume of all members in the structure. Also $\mathbf{q} = [q_1^+, q_1^-, q_2^+, ..., q_m^-]^\mathrm{T}$ and $q_i^+, q_i^-$ are the tensile and compressive member forces; $\mathbf{f} = [f_1^x, f_1^y, f_2^x, ..., f_n^y]^\mathrm{T}$ is the vector of externally applied forces at each node, $\mathbf{c}=[\frac{l_1}{\sigma _T}, \frac{l_1}{\sigma _C},\frac{l_2}{\sigma _T}, ..., \frac{l_m}{\sigma _C}]^\mathrm{T}$ where $l_i$ is the length of member i and $\sigma _T$ and $\sigma _C$ are the allowable stresses in tension and compression, and $\mathbf{B}$ is a suitable $2n \times 2m$ (for 2D problems) equilibrium matrix.

Fig. 1

Layout optimization stages: a problem specification; b design domain discretized with grid of nodes; c form of ground structure for a problem without self-weight—employing straight truss members connecting each pair of nodes; d resulting optimal solution; e ground structure for a problem with distributed self-weight—employing two equally stressed catenaries connecting each pair of nodes; f resulting optimal solution, comprising tensile members sagging downwards and compressive members arching upwards due to distributed self-weight

Fig. 2

Member with distributed self-weight: a geometry; b end force in the case of a single equally stressed catenary member. Dashed lines correspond to corresponding member without self-weight

It should be noted that when self-weight is considered, members that would, in the non-self-weight formulation, have overlapped and been superfluous should now be explicitly included in the model. Such members are included in the ground structure shown in Fig. 1e, which shows curved elements spanning across two or three nodal divisions (e.g. along the top and bottom edges of the domain). It is evident that, although the end nodes of members may lie on the same straight line, the elements themselves are not coincident¹, and thus more than one element may exist in the optimal solution.

The coefficients in $\mathbf{B}$ and $\mathbf{c}$ are found from the geometry of the catenary member, as shown in Fig. 2. The centreline of any member formed of a given material consists of a section of a ‘catenary of equal strength’ (Routh 1896). This centreline is independent of the magnitude of the load and depends only on the force direction (i.e. tensile or compressive). This leads to two possible members connecting each pair of nodes; these are given by the relations

$$\begin{aligned} \alpha&= C_1 - \kappa x, \end{aligned}$$

(2)

$$\begin{aligned} \kappa y&= \log (\cos ( \alpha )) + C_2, \end{aligned}$$

(3)

where x and y are the coordinates of the centreline, $\alpha$ is the inclination of the centreline at (x, y), $\kappa$ is a signed constant that depends on the strength-to-weight ratio of the material (where $\kappa = \frac{\rho g}{\sigma_T}$ or $\kappa = -\frac{\rho g}{\sigma_C}$, with $\rho g$ the unit weight of the material), which may differ in magnitude in tension and compression, and $C_1$ and $C_2$ are constants of integration.

The coefficients in $\mathbf{c}$ are given by integrating the expression for the area $a = \frac{q\cos \theta }{\sigma \cos \alpha }$ (where $\sigma = \sigma _T$ or $\sigma _C$ as appropriate), between the two end nodes. For a single catenary element, i, this implies

$$\begin{aligned} \mathbf{c}_i = \begin{bmatrix} \frac{\cos \theta _i\left( \tan \alpha _{\rm A}^+-\tan \alpha _{\rm B}^+\right) }{\rho g}&\frac{\cos \theta _i\left( \tan \alpha _{\rm B}^--\tan \alpha _{\rm A}^-\right) }{\rho g} \end{bmatrix}^\mathrm{T} \end{aligned}$$

(4)

where $\alpha ^+_{\rm A}$ and $\alpha ^+_{\rm B}$ and $\alpha ^-_{\rm A}$ and $\alpha ^-_{\rm B}$ are, respectively, the values of $\alpha$ for tensile and compressive scenarios, at points A and B. Also $\theta _i$ is the angle directly between the end nodes, as indicated in Fig. 2.

The coefficients of matrix $\mathbf{B}$ are such that end forces are aligned to the centreline, with the horizontal components being unchanged by the addition of self-weight, as shown in Fig. 2. Therefore for a single member i the relevant coefficients are

$$\begin{aligned} \mathbf{B}_i = \begin{bmatrix}\cos \theta _i &{} -\cos \theta _i \\ \cos \theta _i\tan \alpha _{\rm A}^+ &{} -\cos \theta _i\tan \alpha _{\rm A}^- \\ -\cos \theta _i &{} \cos \theta _i \\ -\cos \theta _i\tan \alpha _{\rm B}^+ &{} \cos \theta _i\tan \alpha _{\rm B}^- \end{bmatrix} \end{aligned}$$

(5)

For full details of the formulation readers are referred to Fairclough et al. (2018).

However, in the case of vertical members, $\alpha _{\rm A} = \alpha _{\rm B} = \frac{\pi }{2}$ and $\tan (\alpha _{\rm A})$ and $\tan (\alpha _{\rm B})$ are undefined. Therefore the coefficients in Eqs. (4) and (5) cannot be directly evaluated. In Fairclough et al. (2018) this was addressed using the force at point A, $q_{\rm A}$, as the optimization variable for vertical elements (only). However, in the interests of consistency, here consistent optimization variables are used for all elements, using coefficients that are derived below.

The force $q_{\rm A}$ is proportional to the area at that point, i.e. $q_{\rm A} = q\frac{\cos \theta }{\cos \alpha _{\rm A}}$. From Eqs. (2) and (2.2) in Fairclough et al. (2018), $\alpha _{\rm A}$ may be written in terms of the horizontal span of the element, $x_{\rm B} - x_{\rm A} = u$, and the vertical span of the element, $y_{\rm B} - y_{\rm A} = w$. In this notation, $\theta = \arctan \frac{w}{u}$. This gives the relationship between q and $q_{\rm A}$ for an inclined member as:

$$\begin{aligned} q_{\rm A} = q \left( \frac{\sqrt{1 + \frac{(e^{\kappa w}-\cos (\kappa u))^2}{\sin ^2(\kappa u)}}}{\sqrt{1 + \frac{w^2}{u^2}}}\right). \end{aligned}$$

(6)

The term in brackets can then be isolated and the limit as $u \rightarrow 0$ is found. This then gives the relationship between q and $q_{\rm A}$ for a vertical member:

$$\begin{aligned} q_{\rm A} = \frac{e^{\kappa w} - 1}{\kappa w} q. \end{aligned}$$

(7)

This relationship can then be used in conjunction with relationships given in (Fairclough et al. 2018, equations 2.10, 2.11, 3.6, 3.7) to obtain coefficients for vertical members using an optimization variable q that is consistent, irrespective of member orientation.

When the self-weight is insignificant, i.e. for short spans or when using very strong materials, members will be almost straight and will have almost constant cross-section. However, as spans increase, the sag of tensile members (or rise of compressive members) will increase gradually. However, small changes in the geometries of individual members can combine to cause significant and abrupt changes in the overall optimal topology of the structure under consideration, as will be demonstrated in the next section.

Once the result of the layout optimization is known, a geometry optimization method based on that developed by He and Gilbert (2015) can be used to further refine the joint positions within the solution; see Fairclough et al. (2018) for further details.

2.2 Illustrative examples

2.2.1 Inclined load example

Fig. 3

Inclined load example: optimal structures in the presence of increasing material unit weight $\rho g$, a structures obtained via layout optimization; b rationalized structures obtained after subsequent geometry optimization step

Fig. 4

Inclined load example: volumes of optimal structures in the presence of increasing material unit weight $\rho g$

Table 1 Cantilever example: forms of optimal structures with restricted and extended design domains

To illustrate how changes in the geometry of individual elements resulting from self-weight effects can lead to substantial changes in overall topology, it is useful to consider a simple example. This consists of a design domain of width L and height 2L, with fixed pin supports at the top corners and a load f applied at an angle $30^\circ$ from the vertical at the bottom right corner. The structure is constructed from a material with limiting strength in tension and compression of $\sigma _0$ and unit weight $\rho g$. The problem comprises a fully connected ground structure comprising six nodes and is solved for various values of $\rho g$, as indicated in Fig. 3a. These solutions are then refined using geometry optimization, generating the structures shown in Fig. 3b. The associated structural volumes are also plotted in Fig. 4.

When the unit weight of the material is small, the elements in the ground structure approximate to straight lines and the problem approaches that considered by (Gilbert and Tyas 2003, Figs. 1 and 2). The longest diagonal member in the solution lies above the line of action of the applied load and a three-member supporting structure is required to ensure equilibrium. During geometry optimization, the member connecting the applied load becomes aligned to the line of action of the applied load but kinks as it passes over the supporting structure, now reduced to a single compression member connecting with the top right support. The thickness of this member reduces as the material unit weight and therefore also the cable sag increases.

When $\rho g$ is increased to $0.1155\frac{\sigma _0}{L}$, the main diagonal member becomes oriented parallel to the applied load at its point of application and as a consequence no secondary support structure is necessary. Also, since the only nodes involved in the solution are located at a support point or at the location of the applied load, there is no opportunity for the geometry optimization step to improve the solution.

As the unit weight $\rho g$ is increased further, the sag of the main structural element brings it below the line of action of the applied load. Therefore, support from above is now required, leading to the addition of a new tension member and to a further change in the optimal topology, thereby illustrating how this can be affected by self-weight effects.

2.2.2 Cantilever example

Fig. 5

Cantilever example: volumes of optimal structures in the presence of increasing material unit weight $\rho g$

The classical Michell cantilever problem now provides the starting point for a study that illustrates the interesting possibilities that become available when self-weight loads are involved.

Consider the cantilever problem originally considered by Hemp (1973) with limiting stress in tension and compression, $\sigma _0$ and material unit weight, $\rho g$. Two design domains are considered: a ‘restricted domain’, lying entirely within one half plane, and an ‘extended domain’, which continues behind the supports. Sample results are shown in Table 1 and Fig. 5.

When self-weight has a small-to-moderate influence, the layouts identified when using the ‘restricted domain’ are very similar to the well-known analytical solution. However, when self-weight effects become more significant, the geometry of the optimal structure changes, with the overall depth of the structure increasing and a larger proportion of the material employed close to the supports.

If the extended design domain is used, no change is observed for small values of the unit weight. However, as the unit weight is increased, a sudden and significant change in the overall topology is evident. The new structure makes use of the back span to provide a counterweight to the applied load, thereby reducing the moment that must be provided by the supports and allowing for an even greater structural depth. However, as the method is based on the assumption that all material should be fully stressed, these counterweights take the form of tall thin members aligned along the leftmost edge of the permitted domain.

Figure 5 shows that the use of this counterweight form gives a lower volume than is possible with the restricted domain, by up to approx. 20%, with the counterweight solution being preferred for cases where the unit weight is greater than approx. $0.48\frac{\sigma _0}{L}$. However, the form of the counterweight in the solution (tall thin members aligned to the leftmost edge) is clearly unsatisfactory from a practical perspective; therefore, in the next section an alternative formulation is proposed that allows unstressed material to be present in the optimal solution. The present problem will be revisited in Sect. 3.1.1, using the improved formulation.

Table 2 Cantilever example revisited: new solutions obtained by explicitly including unstressed counterweights in the problem formulation (problem specification as shown for the ‘extended domain’ in Table 1; counterweights are indicated by filled circles.). Percentage change given in $p_{\rm U} = 0.25p_{\rm S}$ column are relative to the value in $p_{\rm U} = 0.99p_{\rm S}$ column

3 Extended formulations

3.1 Formulation incorporating self-weight of unstressed lumped masses

The layout optimization method can be extended to include unstressed lumped masses via the introduction of an additional variable, $r_j$, at each node to represent the volume of unstressed material at that location. This volume is used to calculate the self-weight from the unstressed material ($\rho g r_j$) for use in the vertical nodal equilibrium constraint and also added to the total volume in the objective function.

Therefore, the linear programming optimization formulation becomes

$$\begin{aligned}&\text{minimize }&V&= \mathbf{c}^\mathrm{T}\mathbf{q} + \mathbf{e}^\mathrm{T}\mathbf{r} \end{aligned}$$

(8a)

$$\begin{aligned}&\text{subject to }&\mathbf{Bq} + \rho g\mathbf{Z r}&= \mathbf{f} \end{aligned}$$

(8b)

$$\begin{aligned}&\mathbf{q,r}\ge \mathbf{0} \end{aligned}$$

(8c)

where $\mathbf{r}$ is a vector of length n, containing the volume of material of the lumped mass at each node and $\mathbf{e}$ is a vector of length n with all elements equal to one. $\mathbf{Z}$ is a $2n\times n$ matrix where $z_{i,j}=\{ ^{ 1 \text{ if } i = 2j}_{0 \text{ if } i \ne 2j }$.

In practice it would be unusual for bulk material to have the same unit cost as material used to form structural members. Thus to address this the formulation can be modified so that the objective is now to minimize the total material cost:

$$\begin{aligned}&\text{minimize }&C&= p_{\rm S}\mathbf{c}^\mathrm{T}\mathbf{q} + p_{\rm U} \mathbf{e}^\mathrm{T} \mathbf{r} \end{aligned}$$

(9a)

$$\begin{aligned}&\text{subject to }&\mathbf{Bq} + \rho g\mathbf{Z r}&= \mathbf{f} \end{aligned}$$

(9b)

$$\begin{aligned}&\mathbf{q,r} \ge \mathbf{0} \end{aligned}$$

(9c)

where C is the total material cost and $p_{\rm S}$ and $p_{\rm U}$ are the costs per unit volume of stressed and unstressed material, respectively.

Note also that the value of $\rho g$ used for the unstressed material need not be the same as that of the stressed material. However, the important quantity for unstressed material used to form counterweights is the cost-to-weight ratio, i.e. $\frac{p_{\rm U}}{\rho g}$. In problem (9), materials with the same cost-to-weight ratio are interchangeable in terms of their effect on the rest of the problem, so that the volume of any such unstressed material located at a node is calculable by simple scaling. However, for the sake of simplicity, herein the unit weight of unstressed material will be assumed to be equal to that of the structural material.

3.1.1 Cantilever example revisited

The problem considered in Sect. 2.2.2 is now revisited, with a view to generating optimal structures with more practical counterweight configurations and also enabling evaluation of the effects of altering the relative cost of the unstressed material forming a counterweight.

Considering the extended domain defined in Table 1, optimal layouts for the same two unit weight values considered previously are presented in Table 2. When $p_{\rm U}$ is almost equal to $p_{\rm S}$, the overall forms obtained are almost exactly the same as before, except that the ‘towers’ of members forming the counterweights previously are now replaced by equivalent unstressed masses.

When the cost of the unstressed material is significantly less than that of the structural members, in order to reduce the quantity of structural material required, it can become advantageous to use one or more larger counterweights, located closer to the supports. Thus although the structures presented in Table 2 generated with $p_{\rm U} = 0.25p_{\rm S}$ have a higher overall volume than those generated with $p_{\rm U} = 0.99p_{\rm S}$, greater proportions of the overall volumes are unstressed, leading to lower overall costs.

3.2 Frictional foundations

In major infrastructure projects large quantities of unstressed material are often employed, for example, to form bridge abutments and anchorages. Since these elements can contribute significantly to the overall cost of construction, it is important to ensure they are represented in the optimization problem.

Here gravity-type anchorages are considered of the sort commonly found in suspension bridges (Gimsing and Georgakis 2011). For the purposes of preliminary design, an anchorage is required to have sufficient weight to ensure that the frictional force required to move it horizontally is sufficiently large. More detailed considerations, such as resistance of the anchorage against overturning, or details of the connection between cables and the anchor block are not considered here.

In the layout optimization problem formulation nodes lying at locations of potential foundations are modelled as resting on a rigid frictional plane. For sake of simplicity, such support planes are here assumed to be horizontal, although inclined planes are considered in Appendix 1. The coefficient of friction between the plane and the unstressed material is denoted as $\mu$. This gives rise to support forces normal and tangential to the support plane, denoted for node j by $t_j$ and $s_j$, respectively, as shown in Fig. 6.

Standard Coulomb sliding friction is assumed, leading to a constraint on $s_j$ and $t_j$ of

$$\begin{aligned} |s_j| \le \mu t_j \end{aligned}$$

(10)

For a scenario involving n nodes, of which k are supported, the linear programming optimization formulation becomes

$$\begin{aligned}&\text{minimize }&C = p_{\rm S}\mathbf{c}^\mathrm{T}\mathbf{q} + p_{\rm U} \mathbf{e}^\mathrm{T}\mathbf{r}&\end{aligned}$$

(11a)

$$\begin{aligned}&\text{subject to }&\mathbf{Bq} + \rho g\mathbf{Z r} + \mathbf{C}\mathbf{s} + \mathbf{D}\mathbf{t}&= \mathbf{f} \end{aligned}$$

(11b)

$$\mathbf{s}\le \mu \mathbf{t}$$

(11c)

$$\mathbf{s}\ge -\mu \mathbf{t}$$

(11d)

$$\mathbf{q,r,t}\ge \mathbf{0}$$

(11e)

where $\mathbf{s} = [s_1, s_2, ..., s_k]^\mathrm{T}$ is a vector of reaction forces at nodes lying on a frictional support plane, acting parallel to this plane and $\mathbf{t} = [t_1, t_2, ..., t_k]^\mathrm{T}$ is a vector of reaction forces at nodes lying on a frictional support plane, acting normal to this plane. $\mathbf{C}$ and $\mathbf{D}$ are $2n \times k$ equilibrium matrices such that for supported node j, equation (11b) becomes

$$\begin{aligned} \mathbf{B}_j\mathbf{q} + \rho g \begin{bmatrix}0\\ 1 \end{bmatrix} r_j + \begin{bmatrix} 1 \\ 0 \end{bmatrix} s_j + \begin{bmatrix} 0 \\ 1 \end{bmatrix} t_j = \begin{bmatrix} f_j^x \\ f_j^y \end{bmatrix} \end{aligned}$$

(12)

where $\mathbf{B}_j$ represents the rows of $\mathbf{B}$ relating to node j. Note that the value of g in the above is taken to be negative, since gravity always acts in a downward direction.

Fig. 6

Reaction and counterweight forces acting at a frictional foundation node

3.2.1 Interpretation of boundary conditions

Formulation (11) requires that $t_j$ be non-negative, i.e. the support plane cannot resist an upwards pull on a node. But such a case can still be considered as the vertical equilibrium constraint in (12) will ensure that the lumped mass, $r_j$, is sufficiently large that the combined action of the member forces and the lumped mass weight acts in a downwards direction (or is zero).

In cases where the cost of unstressed material $p_{\rm U}=0$, an arbitrary amount of load parallel to the plane can be supported at no additional cost, by increasing the volume of unstressed material at that location. This is equivalent to providing a fixed pin support. Similarly, specifying an infinite value of the coefficient of friction $\mu$ will give behaviour identical to that of a fixed pin support, although in this case only if the normal reaction force, $t_j$, is positive.

At the other extreme, if the coefficient of friction $\mu =0$ then it is not possible to carry any horizontal force; this is broadly equivalent to a pin/roller support, although again with the proviso that the normal reaction force, $t_j$, must be positive. If $\mu =0$ and $p_{\rm U} = 0$ then the presence of an upwards reaction is possible at no cost by adding a sufficient quantity of unstressed material.

Other values for $\mu$ and $p_{\rm U}$ will produce intermediate behaviour, allowing a range of alternative design options to be explored. Gimsing and Georgakis (2011) recommend a value for the coefficient of friction $\mu = 0.3$ for preliminary calculations, although values of $\mu = 0.55$ may be attainable in certain ground conditions (Mathur and Molina 2005). Here, larger values are also considered to facilitate exploration of how the optimal designs generated change as conditions tend towards the fixed pin case. A possible physical interpretation of these high $\mu$ values can be found in Appendix 1.

4 Bridge design examples

The proposed method will now be applied to the initial conceptual design of a three-span bridge structure. The idealized scenario considered consists of a main span of length L and two side spans, each of length $\frac{L}{2}$. The maximum height of the structure is also permitted to be up to $\frac{L}{2}$, as shown in Table 3. Also, in this case the limiting stress of the material is taken as 1500MPa in tension and 150MPa in compression, with a unit weight of 0.08 MN/$\hbox{m}^3$.

A uniformly distributed vertical loading is applied across the full length of the bridge, attributable to the dead load of the deck material required to provide a flat traffic surface and loading from the traffic itself. It is assumed that the dead load of the deck material is significantly higher than the traffic loading such that only a single load case needs to be modelled at the preliminary design stage. This can be considered reasonable for very long-span structures. The associated total imposed deck weight load is denoted $W_{\rm D}$.

Exploiting symmetry, only half the domain needs to be modelled, with a total of 100 nodal divisions used across the half domain (nodal spacing = 0.01L). This produces a problem containing 500 nodes and over 12 million potential members, although the use of the adaptive ‘member adding’ method (Gilbert and Tyas 2003) means that only a subset of these need to be explicitly modelled.

Table 3 Bridge with fixed pin vs pin/roller supports: forms of optimized structures for spans of 1, 3, and 5 km. Design domain dimensions are also shown and dash-dotted line represents line of symmetry. Superstructure weight W shown in terms of deck weight W_D

Fig. 7

Bridge with fixed pin vs pin/roller supports: a structural weight (proportional to total cost in this case); b magnitudes of required reaction forces for optimized structures

4.1 Standard support types

Initially, the influence of the support conditions is investigated, considering fixed pin (ground anchored) and pin/roller (self-anchored) support conditions for a range of spans. Results are shown in Table 3 and Fig. 7. (Note that for the purposes of this section the superstructure weight W includes the weights of all cables and pylons, but excludes the loading, including deck weight as previously specified.)

Firstly, from Table 3 it is evident that the support conditions have a huge influence on the forms of the optimal structures identified. Specifically, for the pinned support case a ground-anchored cable-stayed type structure is identified, with additional pylon elements at longer spans to counteract the effects of cable sag. Results are similar to those found by Fairclough et al. (2018), as the symmetry boundary conditions considered therein also allowed horizontal reaction forces of unlimited magnitude to be carried. However, it can be observed that the horizontal reaction force generated at each end of the bridge is very substantial, having a magnitude of over half that of the imposed deck-level load (see Fig. 7b). Resisting such a force in practice would likely be very costly. Additionally, a significant horizontal force begins to develop at the pylon base as the region containing compression members becomes asymmetric; note that this force is in the opposite direction to the force at the adjacent end support and provides an abutment to the central compression ribs.

Table 4 Bridge with pin/roller supports: solutions without and with mid-span arching permitted (arching prevented by disallowing compression members across the line of symmetry)

For comparatively short spans, the use of pin/roller supports leads to identification of an optimal structure resembling a series of tied arches, separated by fan regions over the intermediate supports. However, the geometry of the optimal form changes as the span is increased, with the arch sections reducing in size and the extent of the fan regions over the intermediate supports increasing. The resulting fans are also asymmetrical, with more material placed over the side span to counter-balance loads from the main span. For the L = 5 km case, the structure is 3.7 times heavier than the equivalent structure with fixed pin supports (see Fig. 7a).

Fig. 8

Bridge with frictional supports: a, b total cost when span $L=3$ and 5 km, respectively; c, d structural and total weights for $L=3$ and 5 km, respectively. Results are presented for various ratios of stressed to unstressed costs (p_S vs p_U), and corresponding fixed pin and pin/roller results are also included for comparison

When pin/roller supports are present but arch-type forms are not permitted (e.g. imposed by preventing compressive forces from being transmitted over the symmetry plane) then half wheel-type structures are always identified; at very short spans this increases the weight of the superstructure compared with the self-anchored arch solution by a further 28%, although the penalty reduces with span as indicated in Table 4. The half wheels could be simplified by reducing the number of spokes emanating from the pylon supports; in the extreme case this could result in a single vertical and two horizontal spokes emanating from each pylon support, i.e. a traditional self-anchored cable-stayed bridge. In the weightless case, no vertical reaction forces are present at end supports, as would be the case during construction when employing the balanced cantilever method. However, at longer spans, the fan becomes asymmetric and more self-weight is located over the side spans, resulting in vertical reactions at the end supports.

Table 5 Bridge with frictional supports: optimal forms for selected values of unstressed cost, $p_{\rm U}$ and coefficient of friction, $\mu$ (the dash-dotted line represents the line of symmetry; unstressed mass indicated by filled squares)

4.2 Frictional supports

Partly as a means of exploring the solution space that lies between the fixed pin and pin/roller extremes considered in the previous section, it is of interest to now consider frictional foundations, with the coefficient of friction, $\mu$, varied up to a value of $\mu = 2$. (Although this is a much higher value than usually encountered in the real-world, it is of interest to investigate how results change as $\mu$ increases towards the point at which the supports become fixed pins; an alternative interpretation is provided in Appendix 1.) Results are presented for spans of $L= 3$ km and $L=5$ km for a range of cost values, $p_{\rm U}$, in Table 5 and Fig. 8.

Firstly, from Fig. 8 it is evident that the trends are similar for the 3 and 5 km spans. When $\mu = 0$, the optimal structures generated are the same as the corresponding pin/roller support solutions for any value of $p_{\rm U}$. This is because there is no benefit in placing unstressed material at the end (anchorage) points in this case. For each value of $p_{\rm U}$, a value of $\mu$ can be determined above which a ground-anchored solution becomes preferable; at this point the total and structural costs start to decrease whilst total weight, W, starts to increase (potentially very significantly) as $\mu$ is increased. As the coefficient of friction $\mu$ becomes very large the weight and associated cost of a given structure will tend towards the corresponding solution obtained assuming fixed pin supports, although this may often occur at values of $\mu$ well beyond those achievable in the real world.

When the cost of unstressed counterweight material is comparatively low, only a relatively low value of $\mu$ is required before the optimized solution approaches the corresponding optimized fixed pin solution.

However, when the cost of unstressed counterweight material is comparatively high, after an initial rapid decrease in weight/cost, beyond a certain point further reductions are much slower. This point corresponds to a solution that makes use of the horizontal force from the frictional support at intermediate pylons. As there is a substantial vertical load supported here, significant horizontal forces can be carried without requiring additional unstressed material. This results in a structure with a cable-stayed central span and side spans that are a hybrid of a fan structure emanating from each pylon support and a tied arch form close to the each end of the bridge. This structure differs from those identified using the standard support types and for many values of $p_{\rm U}$ can be observed to be optimal over much of the realistic range of $\mu$. This structure is observed in most solutions for $p_{\rm U} = 0.99p_{\rm S}$ in Table 5.

Table 6 Bridge with mixed supports (end frictional supports and pin/roller at pylon base; span $L =$3 km): optimal forms for various values of unstressed cost, $p_{\rm U}$ and coefficient of friction, $\mu$ (the dash-dotted line represents the line of symmetry; unstressed mass indicated by filled squares)

Fig. 9

Bridge with mixed supports (end frictional supports and pin/roller at pylon base; span $L =$3 km): a total cost and b total and superstructure structural weight. Results are presented for various ratios of stressed to unstressed costs (p_S vs p_U), and corresponding fixed pin and pin/roller support solutions are also included for comparison

For a given ratio of $\frac{p_{\rm U}}{p_{\rm S}}$ a significant juncture is the point at which, for realistic values of $\mu$, a ground-anchored solution becomes most cost effective. Although the optimal forms identified here do not closely resemble traditional bridge forms, the same situation occurs in current practice, with self-anchored structures preferred for shorter spans and ground-anchored forms favoured for long spans.

4.3 Mixed support types

Many of the forms presented in Table 5 benefit from the presence of horizontal restraint at the bases of the intermediate pylons. This is achieved as a significant downwards force is already present at these locations, reducing the need for additional anchorage mass. However, in practice these intermediate points may often be supported by tall, slender piers that cannot provide significant horizontal restraint.

It is therefore of interest to undertake a further study involving frictional end supports but with intermediate support points only allowed to sustain vertical reaction forces, via the use of pin/roller supports; see Table 6 and Fig. 9 for results for $L=3$ km bridge case.

It is evident that the initial rapid reduction in cost and subsequent region of comparative insensitivity to $\mu$ observed in Fig. 8 are no longer present. Instead, the reduction in cost is fairly constant at high values of counterweight cost (e.g. $p_{\rm U} = 0.99p_{\rm S}$), with only minimal change in optimal form. At lower counterweight costs (e.g. $p_{\rm U}=0.25p_{\rm S}$), an abrupt divergence at a critical value of $\mu$ is again observed; at this point the arched sections of the optimal form are replaced by horizontal reaction forces at the anchorage points and little difference is seen in the layout in the vicinity of the intermediate pin/roller supports. The span-to-dip ratio of these cable-stayed structures is low initially, but increases at higher values of $\mu$.

Fig. 10

Simplified bridge designs ($L = 3$ km, $\mu = 0.3$, $p_{\rm U}=0.25p_{\rm S}$): a cable-stayed design with purely vertical support (i.e. self-anchored; span:dip ratio limited to 3.3); b cable-stayed design with frictional supports at anchorages (i.e. ground anchored; optimal span:dip = 3.28); c proposed design supported vertically at intermediate pylons, with frictional supports at anchorages (optimal span:dip = 3.34); d proposed design for frictional supports at both anchorages and intermediate supports (optimal span:dip = 3.43). Relative total material costs, C, are indicated for each bridge design

4.4 Simplified designs

The bridge structures presented thus far have been the produced via layout optimization using a fine nodal grid. Whilst these are useful for benchmarking purposes and for providing an indication of potentially optimal forms for use at the initial conceptual design stage, in the form presented they are clearly far too complex to be considered for a real-world construction project.

Therefore, simplified forms for the $L = 3$ km scenario have been manually identified based on the layouts identified in the preceding sections (see the Electronic Supplementary Material for details). Geometry optimization has then been used to refine the joint positions. Forms have been identified for both the entirely frictional support case (based on the layout shown in Table 5) and for the mixed frictional/roller support case (based on the layout shown in Table 6). The value of $\mu$ has been taken as 0.3 and the value of $p_{\rm U}$ as $0.25p_{\rm S}$.

The resulting structures are shown in Fig. 10c and d. These have costs that are only a few percent higher than the corresponding raw layout optimization solutions, yet are clearly much simpler and more practical. The structure shown in Fig. 10c is similar to the simplified forms obtained by Fairclough et al. (2018), although with asymmetry caused by the boundary conditions. Fairclough et al. (2018) also note a number of real world and proposed designs that bear some resemblance to this form, although none replicate all features. The structure shown in Fig. 10d is even more unusual, consisting of a hybrid arch and split-pylon cable-stayed form, which to the authors knowledge has not been proposed before, but which allows a further substantial reduction in material costs by making use of the available frictional restraint at the supports.

For comparison purposes, two traditional cable-stayed forms comprising vertical pylons are also considered, with geometry optimization used to identify the optimal cable locations. When only vertical support is permitted at the ends of the bridge, a self-anchored cable-stayed bridge is identified. This has an optimal span-dip ratio of 2:1, as it is essentially a rationalized form of the half wheel structure shown in Table 4. However, to allow comparison with the other designs and to better reflect current real-world designs, Fig. 10a shows the form when the height is limited to give a span:dip ratio of 3.3.

When the end supports can support a frictional force, a partially ground-anchored cable-stayed bridge is identified (Fig. 10b); the optimal span:dip for this structure was found to be 3.28. This essentially corresponds to the infinite span bridges considered by Fairclough et al. (2018).

By comparing Fig. 10b and c (which have identical boundary conditions) several beneficial features of the proposed optimal design shown in Fig. 10c can be observed. Firstly, the steeper angle of the stay cables reduces the horizontal force applied to the anchorages, therefore necessitating the use of a smaller unstressed mass. The inclined pylons over the side spans are longer, reducing the horizontal thrust applied to the end anchorages, whilst over the main span inclined pylons of reduced length are used to reduce overall volume.

5 Concluding remarks

A method of modelling distributed self-weight employing equally stressed catenaries has recently been developed for use in the ground structure-based layout optimization procedure. In this contribution the method is extended to incorporate the costs of unstressed material, as, for example, used to form counterweights or anchorage blocks in civil engineering structures. Additionally, a friction-based support type has been implemented that increases the range of applicability of the method. This also allows fairer comparisons to be drawn between ground anchored and self-anchored forms when considering the design of long-span bridges.

As the proposed optimization formulation remains linear, high-resolution layout optimization solutions can be obtained. These provide accurate benchmark solutions and can be used to assess both favourable and unfavourable effects of self-weight. It is also shown that geometry optimization provides a practical means of refining the layouts obtained, allowing simplified versions of the structures to be derived.

The method developed has been applied to the initial concept design of a bridge-type structure consisting of a main span and two shorter side spans. Unlike the multi-span bridges considered in previous studies, this allows comparisons to be drawn between ground anchored and self-anchored bridge types. When other variables are kept constant, self-anchored structures are found to be most cost effective for moderate spans, whilst for longer spans ground-anchored structures become more cost effective. However, it was also found that the optimal design may lie between these two classes of bridges, resulting in a novel hybrid structure that can only be identified using the boundary condition types considered herein.

Appendix 1: Inclined frictional planes

1.1 Appendix 1.1: Formulation with inclined frictional supports

This appendix describes an extension to the proposed formulation to handle cases where a structure is supported on a non-horizontal frictional plane, inclined at an angle of $\psi$ to the horizontal, as shown in Fig. 11.

The equilibrium constraint (11b) can be modified by changing the coefficients of $\mathbf{C}$ and $\mathbf{D}$ such that for a single supported node j, Eq. (11b) becomes

$$\begin{aligned} \mathbf{B}_j\mathbf{q} + \rho g \begin{bmatrix}0\\ 1 \end{bmatrix} r_j + \begin{bmatrix} \cos \psi _j \\ \sin \psi _j \end{bmatrix} s_j + \begin{bmatrix} -\sin \psi _j \\ \cos \psi _j \end{bmatrix} t_j = \begin{bmatrix} f_j^x \\ f_j^y \end{bmatrix} \end{aligned}$$

(13)

where $\mathbf{B}_j$ represents the rows of $\mathbf{B}$ relating to node j and $\psi _j$ is the inclination of the frictional plane at joint j.

Fig. 11

Reaction and counterweight forces acting on a frictional foundation node

1.2 Appendix 1.2: Equivalent values of $\mu$ and $\psi$

Consider a scenario where the frictional force $t_j$ is known to act in one (positive) direction and where the volume of the counterweight, $r_j$, is chosen to ensure the foundation just resists sliding failure. In this case Eq. (11c) effectively becomes an equality constraint and the resultants of $t_j$ and $s_j$ in the x- and y-directions can be written as,

$$\begin{aligned} t_j (\mu \cos \psi + \sin \psi )&= f_x \end{aligned}$$

(14a)

$$\begin{aligned} t_j (\mu \sin \psi + \cos \psi )&= f_y \end{aligned}$$

(14b)

A set of modified values $\mu ^*$ and $\psi ^*$ will produce identical behaviour if they result in the same values of $f_x$ and $f_y$ for some value $t^*_j$. By equating original and modified versions of equation (14) and eliminating $\frac{t_j}{t^*_j}$, a relationship between the original and modified values can be found. After some rearrangement, this may be conveniently stated as,

$$\begin{aligned} \psi ^*+\arctan \mu ^*= \psi +\arctan \mu \end{aligned}$$

(15)

For example, consider an inclined foundation plane with $\psi =20^\circ$ and $\mu =0.4$ where the structure applies a force which pulls a given node uphill; this could be equivalently represented by $\mu ^*\approx 0.9$ on a flat surface ($\psi ^*=0$).

Note, however, that the conditions imposed in deriving this equivalence are somewhat onerous and provide little scope for consideration of alternate loading cases or construction stages. For example, the example considered in the previous paragraph would be equivalent to flat surface $\mu ^*\approx 0.03$ if the direction of the horizontal force was reversed. Additionally, the stability of the slope itself would need to be taken into consideration. For these reasons, Eq. (15) has not been incorporated within the optimization formulation and is instead presented here primarily to provide physical justification for the use of relatively large values of $\mu$ in certain special cases.