1 Introduction

Structural optimization problems consist of finding a vector of design variables which minimizes an objective function and is subject to constraints (Spillers and MacBain 2009). Usually, the objective function is related to the weight or cost of the structure and the constraints correspond to design criteria, such as allowable stresses and displacements. Therefore, in these cases, evaluations of objective functions are simple to perform, while evaluations of constraints many times depend on the application of numerical models to represent the structural behavior.

Application of complex computational models, in an attempt to better represent the real behavior of structures, raised challenges in the field of structural optimization. Usually, such models lead to high computational efforts. For example, a single run of a structural analysis which takes into account the effects of material and geometric nonlinearities may easily demand several minutes of computational time, and many structural analyses are usually necessary to perform an optimization. Therefore, the optimization process must require as few as possible evaluations of the constraints to avoid prohibitive computational costs. If the problem presents many local minima, its solution becomes much more challenging, since application of global optimization procedures, such as metaheuristic optimizations algorithms (Holland 1975; Kennedy and Eberhart 1995; Yang 2005; Atashpaz-Gargari and Lucas 2007; Gonçalves et al. 2015), usually requires too many constraints evaluations.

In the literature, surrogate models, also known as metamodels, have been used to deal with problems that have expensive functions (Zhao et al. 2020; Chunna et al. 2020; Kroetz et al. 2020). These metamodels correspond to an approximation of a function, in the entire design space, based on a small number of sample points. Thus, computationally expensive functions can be replaced by surrogate models which are much faster to be evaluated than the original functions (Forrester et al. 2008). In optimization, many authors proposed to include samples in an adaptive manner, according to metrics that try to identify regions which are important to improve the accuracy of the metamodel. However, the main focus of these studies is related to expensive objective functions, while a more limited number has addressed problems with constraints (Durantin et al. 2016; Qian et al. 2020; Zhang et al. 2018; Wu et al. 2018; Dong et al. 2020; Yang et al. 2020). In addition, studies that apply such approaches to structural problems are even more limited (Parr et al. 2012; Dong et al. 2016; Liu et al. 2017; Li et al. 2017; Dong et al. 2018; Shi et al. 2019).

Usually, these procedures adopt infill sampling criteria based on the concepts of expected improvement, probability of feasibility or model error, and some also apply space reduction strategies. Among the surrogate models applied for this purpose, Kriging (Krige 1951; Jones et al. 1998) can be highlighted due to the great flexibility of the model and the ability to estimate its uncertainty, which may facilitate the identification of important regions, under an optimization point of view.

Lee and Jung (2008) proposes the so-called constraint boundary sampling method (CBS) to build a metamodel that can accurately predict the optimal point while satisfying constraints, where sample points are sequentially located along the constraint boundary by using the mean squared error of the Kriging estimate. Meng et al. (2019) proposes another active learning method, which presents high performance in comparison with CBS. References Lee and Jung (2008) and Meng et al. (2019) both focus on reliability-based design optimization problems.

Dong et al. (2018) present, as an extension of a previous study (Dong et al. 2016), a global optimization approach based on space reduction, where two subspaces of the search space are created, one in the neighborhood of the best solution and the other in a region that covers promising samples, and a multi-start optimization is performed alternately on the subspaces and the global space, to explore the surrogate models and add new samples. Qian et al. (2020) presents an update approach of the Kriging surrogate model when applied to represent constraints. The approach is based on confidence intervals, and tries to assess if the feasibility status of the candidate design can be changed due to the interpolation uncertainty related to the Kriging predictor. In Dong et al. (2020) a discrete constrained optimization method based on Kriging is proposed, where a multi-start optimization is performed to find promising solutions in the continuous design range. After a projection of the solutions to the discrete space takes place, a k-nearest neighbors search strategy is used, in conjunction with the expected improvement criterion, to find supplementary samples.

Although the approaches found in the literature seem promising and have been continually discussed, they usually focus on specific types of optimization problems. Studies that employ surrogate models for the constraints and aim at more general structural optimization problems were not found by the authors of the present paper, and this is one of the main purposes of the method presented herein.

In this context, the present paper proposes a global optimization framework based on surrogate models, for structural problems with computationally expensive constraints. The approach consists of building a single Kriging model for all the constraints from a set of sample points and, in each iteration of the method, adding points to this set only in the regions of the domain that are promising to contain the global optimum. In this way, many unnecessary constraints evaluations are avoided. For this, three search strategies are performed during the optimization process, using the metamodel: a local search, which is based on the farthest apart subset concept and applies a metaheuristic optimization method to look for multiple local minima along the design space; a global search, which is also performed by using a metaheuristic optimization method in an attempt to find the global minima; and a refinement step, which aims to improve the best solution found so far using a gradient-based method. Seven optimization problems from the literature are evaluated, where different types of structures, design variables, objective functions and constraints are addressed.

It is noteworthy that the objective here is not necessarily to obtain the best result in comparison with the results presented in the literature, but rather to find feasible results close to the best, with far fewer constraints evaluations. This may significantly accelerate the solution of large structural optimization problems, leading to viable solutions to practical engineering problems. Moreover, as the objective functions of the problems defined here demand low computational effort, it is not advantageous to replace them by a surrogate model, since the time to determine the parameters of the metamodel could be longer than the time to evaluate the true functions.

The remainder of this paper is organized as follows: Sect. 2 presents the surrogate model considered herein; the proposed global optimization framework is described in Sect. 3; Sect. 4 presents the application of the proposed approach in numerical examples; conclusions about the performance and accuracy of the framework are drawn in Sect. 5.

2 Surrogate model

Surrogate model is a mathematical model constructed based on a limited data set from a computational or physical experiment. Thus, it is possible to use the surrogate model in order to predict the results assumed by the experiment, without performing it (Forrester et al. 2008). In the context of optimization, surrogate models can be used, for example, to replace objective and/or constraint functions, when these functions demand high computational efforts to be evaluated. The main idea is to obtain metamodels sufficiently accurate and with construction and evaluation time considerably shorter than the evaluations of the original functions.

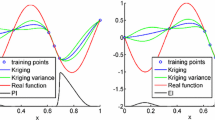
Considering a sampling plan \(\mathbf{X} = \left[ \mathbf{x} ^{(1)}, ..., \mathbf{x} ^{(n)}\right] ^T\) formed by n points of the m-dimensional design space. Each one of these points can be associated with a value of the function \(f(\mathbf{x} )\) to be replaced. In this way, one can calculate the responses vector \(\mathbf{y} = \left[ y^{(1)}, ..., y^{(n)}\right] ^T\), where \(y^{(i)} = f(\mathbf{x} ^{(i)})\), with \(i = 1, ..., {n}\). From these data, it is possible to fit a surrogate model and to obtain predictions \(\hat{y}(\mathbf{x} )\approx f(\mathbf{x} )\) at any point \(\mathbf{x}\) from design space, via metamodel. There are several surrogate models that can be used for this purpose, and Kriging is adopted.

2.1 Kriging

Kriging models can be seen as the realization of a Gaussian process, understood as

$$\begin{aligned} G\left( \mathbf{x} \right) = \mu + Z\left( \mathbf{x} \right) , \end{aligned}$$
(1)

where \(\mu\) is the deterministic part which gives an approximation of the response in the mean (global trend) and \(Z\left( \mathbf{x} \right)\) is a stationary Gaussian process with zero mean (Echard et al. 2011), which represents a local deviation from the model (local trend). \(Z\left( \mathbf{x} \right)\) can be obtained by using the correlation between the local position and its nearby observations (Chunna et al. 2020). The covariance between outputs of the Gaussian process Z is given by

$$\begin{aligned} \text{ Cov }\left[ Z\left( \mathbf{x} ^{(i)}\right) ,Z\left( \mathbf{x} ^{(j)}\right) \right] = \sigma ^2R\left( \mathbf{x} ^{(i)},\mathbf{x} ^{(j)}\right) , \end{aligned}$$
(2)

where \(\sigma ^2\) is the process variance and \(R\left( \mathbf{x} ^{(i)},\mathbf{x} ^{(j)}\right)\) is the correlation function (or basis function) between points \(\mathbf{x} ^{(i)}\) and \(\mathbf{x} ^{(j)}\), with \(i,j = 1, ..., n\) (Bichon 2008). The most commonly used correlation function is Gaussian (Eq. (3)), which is also used herein, where \(\mathbf {\theta } = \left[ \theta _1, ..., \theta _m\right] ^T\) are the unknown parameters of the model.

$$\begin{aligned} R\left( \mathbf{x} ^i,\mathbf{x} ^j\right) = \text{ exp }\left[ -\sum _{l = 1}^{m}\theta _l\left| x_l^{(i)} - x_l^{(j)}\right| ^2\right] \end{aligned}$$
(3)

In Kriging, the unknown parameters \(\mathbf {\theta }\) are usually found by using the Maximum Likelihood Estimate (MLE). More details of the procedure can be obtained in Forrester et al. (2008).

For given \(\mathbf{X}\), \(\mathbf{y}\) and \(\mathbf {\theta }\), \(\hat{\mu }\) and \(\hat{\sigma }\) can be estimated by

$$\begin{aligned} \hat{\mu } = \frac{\mathbf {1}^T\mathbf {R}^{-1}\mathbf {y}}{\mathbf {1}^T\mathbf {R}^{-1}\mathbf {1}}, \ \ \ \hat{\sigma }^2 = \frac{\left( \mathbf {y}-\mathbf {1}\hat{\mu }\right) ^T\mathbf {R}^{-1}\left( \mathbf {y}-\mathbf {1}\hat{\mu }\right) }{n}, \end{aligned}$$
(4)

where \(\mathbf{R}\) is the correlation matrix of all the observed data and \(\mathbf{1}\) is an \(n \times 1\) column vector of ones (Forrester et al. 2008). Therefore, the resulting prediction function and the respective mean squared error (MSE) can be written as in Eqs. (5) and (6), respectively, where \(\mathbf {r}\) is the vector of correlations between the observed data and the new prediction.

$$\begin{aligned}&\hat{y}\left( \mathbf {x}\right) = \hat{\mu } + \mathbf {r}^T\mathbf {R}^{-1}\left( \mathbf {y}-\mathbf {1}\hat{\mu }\right) \end{aligned}$$
(5)
$$\begin{aligned}&s^2\left( \mathbf {x}\right) = \hat{\sigma }^2\left[ 1-\mathbf {r}^T\mathbf {R}^{-1}\mathbf {r} + \frac{\left( 1-\mathbf {1}^T\mathbf {R}^{-1}\mathbf {r}\right) ^2}{\mathbf {1}^T\mathbf {R}^{-1}\mathbf {1}}\right] \end{aligned}$$
(6)

Figure 1 shows an example of a function prediction via Kriging, as well as the estimate of the prediction error.

Fig. 1
figure 1

Example of Kriging metamodel prediction

Full size image

3 Global optimization framework

The optimization problem addressed herein consists of finding the values of the design variables \(\mathbf {x}\) that minimize the objective function \(f(\mathbf {x})\), subject to inequality constraints \(g_i(\mathbf {x}) \le 0\) and to lower and upper bounds of each variable \(x_j\), with \(i = 1, ..., p\) and \(j = 1, ..., m\), where p and m are the numbers of constraints and design variables (or dimension of the design space), respectively. It is considered that objective functions are cheap to evaluate and that constraints require high computational effort, as previously discussed.

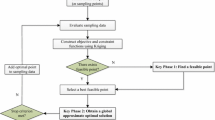
Since the surrogate model is used as an approximation of the constraints, based on sampled points, it is prudent to improve the accuracy of the metamodel during the optimization process, by inserting infill points (IPs) in regions of the design space that may contain the best design. In general, an optimization procedure based on metamodels can be summarized in the following main steps:

  1. (1)

    Determine a sampling plan;

  2. (2)

    Fit a surrogate model to the sampled points;

  3. (3)

    Insert infill points in the sampling plan and go to the step 2. The procedure is performed until a stop criterion is reached.

The approaches adopted in the framework proposed herein are presented in the following sections, with some illustrations of the method when applied in the solution of the Toy problem, adapted from Gramacy et al. (2015). Equations (7), (8) and (9) present the objective function and the constraints of the Toy problem addressed herein. For a better understanding of the framework, Fig. 2 shows the flowchart of the optimization process. All codes are developed in MATLAB (MathWorks 2017) and the Kriging algorithm adopted herein is the one available in Forrester et al. (2008).

$$\begin{aligned}&f(\mathbf {x}) = x_1 + x_2 \end{aligned}$$
(7)
$$\begin{aligned}&g_{1}(\mathbf {x}) = \frac{3}{2} - x_1 - 2x_2 - \frac{1}{2}\text{ sin }\left( 4\pi \left( x_1^2 - 2x_2\right) \right) \end{aligned}$$
(8)
$$\begin{aligned}&g_{2}(\mathbf {x}) = x_1^2 + x_2^2 - \frac{3}{2} \end{aligned}$$
(9)
Fig. 2
figure 2

Flowchart of the framework

Full size image

3.1 Sampling plan

The sampling plan \(\mathbf{X} = \left[ \mathbf{x} ^{(1)}, ..., \mathbf{x} ^{(n)}\right] ^T\) is generated in such a way that the points selected to compose the sample are the points most distant from each other in the design space, ensuring wide coverage of the search space. To do so, \(n_{samp}\) random points are generated uniformly in the design space. Among these points, the one closest to the center of the search space is selected and included in the sampling plan. The next selected point is defined as the farthest apart point from those selected previously. The selection proceeds by the criterion of the maximum Euclidean distance between the points, until the n points which define the initial sampling plan are obtained. The design space used in the framework is normalized, so that the lower and upper bounds correspond to 0 and 1, respectively. Thus, variables with different magnitudes have the same contribution to the distances. Figure 3 shows a sample generated by the proposed procedure for the Toy problem, with \(n = 12\). Note that other procedures could be used to obtain similar initial sampling plans. For example, if Latin Hypercube Sampling (McKay et al. 1979) is employed, aiming at maximizing the minimum distance between points and with a sufficient number of improving iterations, it would lead to similar results.

Fig. 3
figure 3

Sampling plan of Toy problem

Full size image

3.2 Construction of the Kriging model

Here, a single surrogate model is created to represent all constraints of the problem, although different surrogates could be used to represent different constraints or groups of constraints. For this, it is necessary to evaluate the constraints at each sampled point, obtaining the response vector \(\mathbf{g} = \left[ g^{(1)}, ..., g^{(n)}\right] ^T\), where \(g^{(i)} = \text{ max }\left( \left[ g_1(\mathbf{x} ^{(i)}), ..., g_p(\mathbf{x} ^{(i)})\right] \right)\), with \(i = 1, ..., n\), and \(\text{ max }\) is the operator that returns the maximum value among elements. So, the surrogate model is created based on the sampling plan \(\mathbf{X}\) and the respective constraints values \(\mathbf{g}\). The prediction obtained via the metamodel is denoted by \(\hat{g}(\mathbf{x} )\). To fit the parameters \(\mathbf {\theta }\) of the basis function to the data set, the MLE is performed by Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995), which proved to be more accurate and faster than the genetic algorithm (GA) used in Forrester et al. (2008). Other metaheuristic optimization methods could also be employed, but the results obtained via PSO seemed to be good enough for the purposes of this paper.

3.3 Search strategies

Three search strategies used to select infill points are proposed herein. Note that the proposed framework differs from what has been found in the literature because it combines these three different strategies, which have complementary characteristics. As a result, the framework becomes more robust and sometimes faster than other procedures presented in the literature. To avoid further evaluations of the true time-consuming constraints, all of these strategies make use of a surrogate optimization problem, where the constraints are replaced by the prediction function \(\hat{g}(\mathbf{x} )\). The optimum points \(\hat{\mathbf{x }}^*\) found in these optimizations are inserted as infill points in the sampling plan, even if they are classified as infeasible by the true functions. During the entire optimization process, the true constraints are evaluated only once, at each point of the sampling plan. The total number of evaluations of the constraints equals the size of the sampling plan. More details about the strategies are presented below.

3.3.1 Local search and global search

The local search is performed in order to look for multiple local minima over the design space, so that a number of promising regions may be explored. For this, \(n_s\) design subspaces are defined and, in each one of these subspaces, the surrogate optimization problem is solved via a metaheuristic optimization method. Firefly algorithm (FA) (Yang 2005) was chosen to be used herein due to its good performance in structural problems (Gandomi et al. 2011; Miguel and Fadel Miguel 2012; Miguel et al. 2015; Gebremedhen et al. 2020), although other global optimization methods could be employed. The best design \(\hat{\mathbf{x }}^*\) found in each optimization subproblem is taken as an infill point. To generate the design subspaces, first a point in the sampling plan is randomly selected, defining \(\mathbf{x} _{s}^1\). The next points \(\mathbf{x} _{s}^i\), with \(i = 2, ..., n_s\), are chosen based on the farthest apart subset concept, selecting the point from the sampling plan which is the farthest from the already selected points. The lower and upper bounds of the i-th design subspace, defined as \(\mathbf{lb} ^i_{s}\) and \(\mathbf{ub} ^i_{s}\), respectively, are given by

$$\begin{aligned} \mathbf {lb}^i_{s} = \text{ max }\left( \left[ \mathbf {lb}, \left( \mathbf {x}_{s}^i + \mathbf {\bigtriangleup lb}^i - \mathbf {\bigtriangleup ub}^i\right) - \frac{\mathbf {d}}{2}\right] \right) \nonumber \\ \mathbf {ub}^i_{s} = \text{ min }\left( \left[ \mathbf {ub}, \left( \mathbf {x}_{s}^i + \mathbf {\bigtriangleup lb}^i - \mathbf {\bigtriangleup ub}^i\right) + \frac{\mathbf {d}}{2}\right] \right) , \end{aligned}$$
(10)

where all vectors sizes are \(m \times 1\) and each row is associated with a dimension of the design space: \(\mathbf{lb}\) and \(\mathbf{ub}\) are the lower and upper bounds of the problem, respectively, \(\mathbf{d}\) represents the widths of the subspace and \(\mathbf {\bigtriangleup lb}^i\) and \(\mathbf {\bigtriangleup ub}^i\) are calculated by

$$\begin{aligned} \mathbf {\bigtriangleup lb}^i = \text{ max }\left( \left[ \mathbf {0}, \mathbf {lb} - \left( \mathbf {x}_{s}^i - \frac{\mathbf {d}}{2}\right) \right] \right) \nonumber \\ \mathbf {\bigtriangleup ub}^i = \text{ max }\left( \left[ \mathbf {0}, \left( \mathbf {x}_{s}^i + \frac{\mathbf {d}}{2}\right) - \mathbf {ub}\right] \right) . \end{aligned}$$
(11)

In addition, \(\text{ max }\) and \(\text{ min }\) are the operators that return the maximum and minimum value of a row, respectively. All subspaces have the same size, chosen as \(\mathbf{d = (\mathbf{ub} - \mathbf{lb} )/(n_s^{1/m})}\), which result in some superpositions between them if the value of \(\mathbf{d}\) is greater than half the range defined by \(\mathbf{ub}\) and \(\mathbf{lb}\), in any dimension of the problem. The boundaries given by Eqs. (10) and (11) tend to center the subspaces in their respective \(\mathbf{x} _s^i\). However, when these points are close to the bounds, the subspace cannot be centered on them. The subspaces must be relocated so that the upper and lower bounds are not violated. Figure 4 shows two possible sets of subspaces generated from different \(\mathbf{x} _s^1\). It should be noted that, given the random aspect of the selection of the first subspace point and due to the updating of the sampling plan throughout the process, the subspaces change with each iteration of the method, so that different regions of the domain are explored during the optimization process.

Fig. 4
figure 4

Different subspaces obtained with the proposed formulation

Full size image

On the other hand, the global search is employed in an attempt to find the global minima. Here, the surrogate optimization problem is solved considering the entire design space. The optimum point \(\hat{\mathbf{x }}^*\) found in the process is selected as an IP. The optimization is also performed by the Firefly algorithm (FA).

The local and global searches are performed until a stop criteria is reached, which is defined in Sect. 3.4. Although the combination of these strategies has been found to be quite robust in finding the region of the global minimum, one more search strategy is needed to obtain more accurate results in this region, which corresponds to the refinement step.

3.3.2 Refinement

The refinement step corresponds to the solution of the surrogate optimization problem via a gradient-based method, starting from the best design \(\mathbf{x} ^*\) found so far. This point is chosen among those of the sampling plan which are feasible. The optimum point \(\hat{\mathbf{x }}^*\) obtained in the refinement step is also taken as an IP. This procedure is performed several times, until a stop criterion is reached (Sect. 3.4). Similar strategies, when applied alone, can converge to a local minimum, as exemplified in Jones et al. (1998), in which a surrogate model is built for the objective function. However, in this framework, the design space is explored by the previous strategies, so that this step has only the objective of improving the best result found in the region of the global minimum. The gradient-based method adopted herein is the Interior point (Coleman and Li 1996), which is an established method in the literature and is available in MATLAB.

Figure 5 illustrates the Toy problem and the points evaluated by \(g(\mathbf{x} )\) during the solution process, and Fig. 6 shows the behavior of \(\hat{g}(\mathbf{x} )\) in different stages of the framework. In the last iteration of the global search (Fig. 6b), it is possible to observe that most of the IPs were added in two regions of minimums and that in the refinement step (Fig. 6c), the IPs were added only in the region of the global minimum. In addition, the method was able to deal with the fact that, initially (Fig. 6a), the global optimum was considered to be unfeasible by the Kriging model.

Fig. 5
figure 5

Toy problem and the sampled points of the optimization process

Full size image
Fig. 6
figure 6

Search strategies during the optimization process of Toy problem

Full size image

3.4 Stopping criteria and optimal result

The stopping criterion adopted corresponds to the number \(it_{stall}\) of iterations in which the optimum result does not present improvements greater than a given tolerance \(f_{tol}\) between consecutive iterations, also attending to a minimum \(it_{min}\) and maximum \(it_{max}\) number of iterations. After the stopping criterion is achieved, the optimal design \(\mathbf{x} ^*\) is taken as the feasible point of the sampling plan that has the lowest value of the objective function.

4 Numerical examples

The proposed methodology is applied in the solution of seven structural optimization problems. In order to evaluate the performance of the framework, each example is run several times and some metrics such as best and mean results, standard deviation (Std) and mean number of constraint function evaluations (FE) are presented.

The numerical examples are divided in two sections: the first (Sect. 4.1) corresponds to the solution of benchmark examples, and the results of the framework are compared with the results of the literature; the second (Sect. 4.2) presents the solution of examples also taken from the literature, but with modifications in the structural model adopted. In this case, as no results were found in the literature for these examples, they are also solved by other methods from the literature for comparison purposes. The first method is the Firefly algorithm (FA) discussed in Sect.  3.3.1. The second is an adaptive metamodeling-based method described in Forrester et al. (2008), represented herein by KG-GA. In KG-GA, initially a Kriging model is constructed for the constraints, based on a Latin Hypercube sampling plan, and subsequently, the minimums found in successive solutions of the surrogate optimization problem via genetic algorithms are selected as infill points.

Although each one of these approaches has a different main purpose, the objective of these comparisons is to investigate if the proposed method is capable of providing similar results with fewer constraints evaluations, for the problems at hand.

The input data of the framework used in all examples, except when specified otherwise, are given by the following: \(n_{samp} = 1\cdot 10^{6}\); \(n = \text{ min }\left( \left[ 10m \ 150\right] \right)\); \(n_s = \text{ min }\left( \left[ 2m \ 20\right] \right)\); \(it_{stall} = 2\), \(f_{tol} = 0.1\), \(it_{min} = 3\) and \(it_{max} = 12\) for the first stop criterion, related to the global and local searches; \(it_{stall} = \text{ min }\left( \left[ 2m \ 30\right] \right)\), \(f_{tol} = 0.001\), \(it_{min} = \text{ min }\left( \left[ 10m \ 150\right] \right)\) and \(it_{max} = \text{ min }\left( \left[ 20m \ 300\right] \right)\) for the second stop criterion, related to the refinement step. In Sect. 4.1, each example is run 100 times, while the examples in Sect. 4.2 are run only 15 times due to the high computational effort of some of them. It is noteworthy that most of the parameters adopted herein are defined as proportional to the number of dimensions of the optimization problems. For example, the number of subspaces adopted corresponds to twice the number of design variables of the evaluated problem, since preliminary tests indicated that this value is sufficient to adequately cover the design space with subspaces. Such value is limited to 20, in order to avoid prohibitive computational effort in large problems. However, a more rigorous analysis of some of these parameters could be performed in future studies to try to further improve the proposed framework.

4.1 Benchmark problems

4.1.1 Tubular column

The first optimization problem corresponds to a tubular column, illustrated in Fig. 7, addressed by Hsu and Liu (2007), Gandomi et al. (2013) and Rao (2020), which has length \(L = 250\) cm and is under a compressive load \(P = 2500\) kgf. The material has a yield stress \(\sigma _y = 500\) kgf/cm\(^2\) and modulus of elasticity \(E = 0.85\cdot 10^{6}\) kgf/cm\(^2\). The aim is to find the dimensions t and d that minimize the cost of the structure (Eq. (12)) and that meets the constraints of yield stress (Eq. (13)) and buckling stress (Eq. (14)). The lower and upper bounds are, in cm, \(2 \le d \le 14\) and \(0.2 \le t \le 0.8\). Table 1 shows the results obtained herein and some others available in the literature.

Fig. 7
figure 7

Tubular column problem

Full size image
$$\begin{aligned} f(\mathbf{x} ) = 9.82dt + 2d \end{aligned}$$
(12)
$$\begin{aligned} g_{1}(\mathbf{x} ) = \frac{P}{\pi dt \sigma _y}-1 \le 0 \end{aligned}$$
(13)
$$\begin{aligned} g_{2}(\mathbf{x} ) = \frac{8PL^2}{\pi ^3Edt\left( t^2+d^2\right) }-1 \le 0 \end{aligned}$$
(14)
Table 1 Optimal design and statistical results obtained by different methods for Tubular column problem
Full size table

4.1.2 I-beam

The second problem corresponds to a simply supported I-beam, studied by Wang (2003), Gandomi et al. (2013) and Cheng and Prayogo (2014). The problem consists of finding the dimensions of the cross section of the structure, which minimizes the vertical displacement and which meets the constraints of maximum cross-sectional area and of bending stress. Figure 8 shows the structure, where \(L = 200\) cm, \(P = 600\) kN and \(Q = 50\) kN (both loads in the middle of the span), with modulus of elasticity equal to \(2\cdot 10^{4}\) kN/cm\(^2\), maximum allowable bending stress of 6 kN/cm\(^2\) and maximum cross-sectional area of 300 cm\(^2\). The design space is, in cm, \(10 \le h \le 80\), \(10 \le b \le 50\), \(0.9 \le t_w \le 5\) and \(0.9 \le t_f \le 5\). Equation (15) corresponds to the objective function and Eqs. (16) and (17) define the constraints. Due to the order of magnitude of the \(f(\mathbf{x} )\), \(f_{tol} = 0.001\) and \(f_{tol} = 0.00001\) are adopted for the first and second stopping criteria, respectively, and the results achieved are shown in Table 2.

Fig. 8
figure 8

I-beam problem

Full size image
$$\begin{aligned} f(\mathbf{x} ) = \frac{5000}{\frac{t_w \left( h - 2t_f\right) ^3}{12} + \frac{bt_f^3}{6} + 2t_fb\left( \frac{h-t_f}{2}\right) ^2} \end{aligned}$$
(15)
$$\begin{aligned} g_1(\mathbf{x} ) = 2bt_f + t_w\left( h - 2t_f\right) - 300 \le 0 \end{aligned}$$
(16)
$$\begin{aligned}&g_2(\mathbf{x} ) = \frac{180000h}{t_w\left( h - 2t_f\right) ^3 + 2bt_f\left( 4t_f^2 + 3h\left( h - 2t_f\right) \right) } \nonumber \\&\quad + \frac{15000b}{2t_fb^3 + \left( h - 2t_f\right) t_w^3} - 6 \le 0 \end{aligned}$$
(17)
Table 2 Optimal design and statistical results obtained by different methods for I-beam problem
Full size table

4.1.3 10-bar truss

The 10-bar truss problem shown in Fig. 9 is often used as a benchmark example (Wei et al. 2005; Gomes 2011; Wei et al. 2011; Kaveh and Zolghadr 2011; Miguel and Fadel Miguel 2012; Kaveh and Zolghadr 2012; Zuo et al. 2014; Kaveh and Zolghadr 2017; Tejani et al. 2016, 2018; Kumar et al. 2019). The problem consists in finding the cross-sectional areas of the elements that minimize the mass of the structure, taking into account constraints based on the natural frequencies. Thus, 10 areas are considered as design variables, whose design space is 0.645 cm\(^2 \le A_i \le 50\) cm\(^2\), with \(i = 1, ..., 10\). The material has Young modulus equal to \(6.98\cdot 10^{10}\) Pa and density of 2770 kg/m\(^3\). At all free nodes (nodes 1–4) non-structural masses of 454 kg are attached to the truss. The natural frequency constraints are \(f_1 \ge 7\) Hz, \(f_2 \ge 15\) Hz and \(f_3 \ge 20\) Hz. Table 3 shows the results obtained by the framework using \(it_{stall} = 4\) and \(it_{min} = 6\) for the first stop criterion, due to the large number of variables.

Fig. 9
figure 9

10-bar truss problem

Full size image
Table 3 Optimal design and statistical results obtained by different methods for 10-bar truss problem
Full size table

4.1.4 37-bar truss

The fourth problem select, as shown in Fig. 10, is a simply supported bridge studied by several authors (Wei et al. 2005; Gomes 2011; Wei et al. 2011; Kaveh and Zolghadr 2011; Miguel and Fadel Miguel 2012; Kaveh and Zolghadr 2017; Tejani et al. 2016, 2018; Kumar et al. 2019). Similar to the previous example, here the objective is to minimize the mass of the structure subjected to natural frequency constraints. However, in addition to the size variables (cross-sectional area), shape variables (vertical position of the nodes) are also adopted. Lower nodes are considered to be fixed and lower elements (bar 28 to 37) are assumed to have fixed cross-sections of 40 cm\(^2\). Since symmetry of structure about its middle vertical plane is considered, the problem has 14 size variables, whose design space is 1 cm\(^2 \le A_i \le 10\) cm\(^2\), with \(i = 1, ..., 14\), and 5 shape variables, whose design space is 0.1 m \(\le y_j \le 3\) m, with \(j = 3, 5, 7, 9, 11\). The material has Young modulus equal to \(2.1\cdot 10^{11}\) Pa and density of 7800 kg/m\(^3\). In addition, non-structural masses equal to 10 kg are attached at each of the nodes on the lower chord. The natural frequency constraints are \(f_1 \ge 20\) Hz, \(f_2 \ge 40\) Hz and \(f_3 \ge 60\) Hz. As in the previous problem, \(it_{stall} = 4\) and \(it_{min} = 6\) are used to the first stop criterion, due to the large number of variables, while the other parameters are kept as previously defined. Table 4 compares the results of the problem.

Fig. 10
figure 10

37-bar truss problem

Full size image
Table 4 Optimal design and statistical results obtained by different methods for 37-bar truss problem
Full size table

4.1.5 Discussion of results

In all examples, the best and the mean values found by the proposed framework were close to those indicated in the literature, with differences less than 1.92% in relation to the best reference found. On the other hand, the number of constraints evaluations required by the framework was at least 85.73% lower than the number of evaluations employed in the literature. Throughout the runs, the framework tended to provide similar results, as indicated by the small standard deviations observed.

4.2 Problems with nonlinear structural analysis

For each example in this section, two constraint scenarios are considered: scenario 1 corresponds to that taken from the literature, and scenario 2 evaluates a structural model that takes into account material and/or geometric nonlinearities. In both scenarios, the structural analysis is performed using the MASTAN2 software (McGuire et al. 2014; Ziemian and McGuire 2007).

Here, the performance of the framework is also evaluated in relation to the computational time required in the execution of the algorithms. For all examples, a population of 10 individuals and 100 iterations are adopted to the Firefly algorithm as well as to the genetic algorithm of the adaptive metamodeling-based method. For both methods, the number of constraints evaluations is limited to 1000, due to the high computational effort of some examples. In addition, the number of points that define the initial sampling plan of KG-GA is the same of the framework proposed herein.

4.2.1 8-story frame

The example consists of finding the cross-sectional areas of the elements of a frame, which minimize its weight and which meets a displacement constraint. This example has been studied by some authors (Camp et al. 1998; Nanakorn and Meesomklin 2001; Kaveh and Hassani 2009; Schevenels et al. 2014), but among these only Kaveh and Hassani (2009) use continuous variables. Figure 11 shows the frame where the elements are categorized into 8 groups. The lateral displacement at the top of the frame must be less than 2 in (5.08 cm). The material has modulus of elasticity equal to \(29\cdot 10^{3}\) ksi (200 GPa) and density of \(2.83\cdot 10^{-4}\) kip/in\(^3\) (76.8 kN/m\(^3\)). Kaveh and Hassani (2009) disregards the effects of axial internal forces, but here it is considered. The design space adopted is 5 in\(^2\) (32.26 cm\(^2\)) \(\le A_i \le 30\) in\(^2\) (193.55 cm\(^2\)), with \(i = 1, ..., 8\), and the following empirical relationship between the cross-sectional area (A) and the moment of inertia (I) is applied (Kaveh and Hassani 2009):

$$\begin{aligned} I = \left\{ \begin{matrix} 4.592 A^2 \ \ \ \ \ \ \ \ \ \ \ \ &{} \ \ 0 \le A \le 15\\ 4.638 A^2 \ \ \ \ \ \ \ \ \ \ \ \ &{} \ 15 \le A \le 44 \\ 256.229A - 2300 &{} \ \ \ 44 \le A \le 100 \end{matrix}\right. \end{aligned}$$
(18)

While in the first scenario linear structural analyses are performed, geometric nonlinearities are considered in the second scenario. In this situation, the effects of deformations and displacements related to a load increase are included in the formulations of equilibrium equations. Table 5 shows the results obtained in both scenarios.

Fig. 11
figure 11

8-story frame problem

Full size image
Table 5 Optimal design and statistical results obtained by different methods for 8-story frame problem
Full size table

4.2.2 A model of Forth bridge

This example was previously evaluated by Gil and Andreu (2001) and Kaveh and Khayatazad (2013), although some modifications in relation to the number of design variables have been adopted herein, in order to reduce the computational time associated with the solution of the problem. The structure is shown in Fig. 12, where the configuration is symmetrical in relation to the middle vertical plane and the bars are categorized into three groups. The objective is to find the vertical position \(y_i\) of the nodes and the areas of the cross-sections \(A_j\) that minimize the weight of the structure, whose search space is -1.4 m \(\le y_i \le\) 1.4 m and 25 cm\(^2 \le A_j \le\) 100 cm\(^2\), with i = 2, ..., 11 and j = 1, ..., 3. The modulus of elasticity of material is 2.1\(\times\)10\(^{8}\) kN/m\(^2\) and the specific weight of material is 7.8 ton/m\(^3\).

Fig. 12
figure 12

A model of Forth bridge problem

Full size image

In the first scenario, the stress \(\sigma\) of the structural elements cannot exceed the maximum allowable stress \(\sigma _{adm}\) = 25 kN/cm\(^2\). Therefore, the following constraint must be verified for each bar

$$\begin{aligned} g(\mathbf{x} ) = \frac{\sigma (\mathbf{x} )}{\sigma _{adm}} - 1 \le 0. \end{aligned}$$
(19)

In the second scenario, a single constraint is considered, given by

$$\begin{aligned} g(\mathbf{x} ) = \frac{P}{P_{cr}(\mathbf{x} )} - 1 \le 0, \end{aligned}$$
(20)

where P is the applied load and \(P_{cr}(\mathbf{x} )\) is the critical load, which is the maximum load value that the structure can handle before reaching failure. In this scenario, failure may occur due to buckling or yielding of one or more bars. In order to incorporate the possibility of buckling and yielding in the computation of the critical load, it is necessary to impose initial imperfections to each bar of the structure and to perform inelastic and geometrically nonlinear structural analyses. To do so, in this paper the initial imperfections are based on the first vibration mode of the structure, according to Eq. 21, and the materials are assumed to have elastic-perfectly plastic characteristics.

$$\begin{aligned} \mathbf{c} = \mathbf{c} _0 + 0.001\mathbf{u} \end{aligned}$$
(21)

where

\(\mathbf{c} =\) Vector of nodal coordinates after perturbation;

\(\mathbf{c} _0 =\) Vector of inicial nodal coordinates;

\(\mathbf{u} =\) Vector of nodal displacements, according the vibration mode considered in the eigenvalue analysis.

In structural analysis, truss bars are modeled using several frame elements with moment releases at hinged connections. So elements that are connected to hinges are modeled as fixed-hinge frame element, while others are modeled as fixed-fixed elements. For more details about the model the readers are referred to Madah and Amir (2017) and Juliani et al. (2019), since the structural model adopted herein is very similar to the ones described in these references.

Table 6 shows the results, using \(it_{stall} = 4\) and \(it_{min} = 6\) to the first stop criterion, due to the large number of variables, while the other parameters are kept as previously defined.

Table 6 Optimal design and statistical results obtained by different methods for a model of Forth bridge problem
Full size table

4.2.3 120-bar dome truss

The 120-bar space truss was studied by several authors, with different variables, constraints, dimensions and loads (Soh and Yang 1996; Fallahian et al. 2009; Kaveh and Talatahari 2010; Kaveh and Khayatazad 2013; Kumar et al. 2019). Here, the configuration studied is the one presented by Fallahian et al. (2009) (Fig. 13).

Fig. 13
figure 13

120-bar dome truss problem

Full size image

In the first scenario, the allowable stresses \(\sigma _{adm}\) follow the requirements of the AISC ASD (1989) code, calculated by

$$\begin{aligned}&\sigma _{adm} = \left\{ \begin{matrix} 0.6F_y \ \ \ \text {for tensile stress} \\ F_{cr} \ \text {for compression stress} \end{matrix}\right. \end{aligned}$$
(22)
$$\begin{aligned}&F_{cr} = \left\{ \begin{matrix} \left[ \left( 1 - \frac{\lambda _i^2}{2C_c^2}\right) F_y\right] / \left[ \frac{5}{3} + \frac{3\lambda _i}{8C_c} - \frac{\lambda _i^3}{8C_c^3}\right] \ \lambda _i < C_c \\[10pt] 12\pi ^2E/23\lambda _i^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \lambda _i \ge C_c \end{matrix}\right. . \end{aligned}$$
(23)

In these equations, \(C_c = \sqrt{2 \pi ^2 E / Fy}\) is the slenderness ratio dividing the elastic and inelastic buckling regions and \(\lambda _i = kl_i/r_i\) is the member slenderness ratio, where \(F_y\) is the yield stress of steel, E is the modulus of elasticity, k is the effective length factor; \(l_i\) is the member length and \(r_i = 0.4993A_i^{0.6777}\) is the radius of gyration, with \(i = 1, ..., 120\). The vertical loads applied are − 13.49 kips (− 60 kN) at node 1, − 6.744 kips (− 30 kN) ate node 2 through 13 and − 2.248 kips (− 10 kN) at the rest of free nodes. The design variables are the cross-sectional areas of the bars, which are categorized into 7 groups, as shown in Fig. 13, whose design space adopted is 1.2 in\(^2\) (7.74 cm\(^2\)) \(\le A_j \le 10\) in\(^2\) (64.52 cm\(^2\)), with \(j = 1, ..., 7\). The parameters \(F_y = 58\) ksi (400 MPa), \(E = 30450\) ksi (210 GPa), \(k = 1\) are adopted, and the material density is taken equal to 0.288 lb/in\(^{3}\) (7971.81 kg/m\(^{3}\)).

The second scenario is similar to the previous example, where a single constraint based on a critical load is verified as a safety criterion. Table 7 shows the results obtained in both scenarios, where \(it_{stall} = 4\) and \(it_{min} = 6\) was adopted to the first stop criterion, as in the previous example.

Table 7 Optimal design and statistical results obtained by different methods for 120-bar dome truss problem
Full size table

4.2.4 Discussion of results

In all scenarios, the best results in terms of final objective function values were provided by the proposed framework, with means approximately 19% and 7% smaller than the ones provided by FA and KG-GA, respectively. In addition, the number of constraints evaluations required by the framework was at least 47.30% lower, reaching a 73.10% reduction in one case. It is noteworthy that the mean results achieved by the KG-GA with the same number of evaluations performed by the framework are on average 17.80% higher than those of the framework. This indicates a good performance of the proposed method, especially when dealing with complex problems, even in comparison with another metamodel-based method.

Regarding computational time, when simple problems are considered, the running time of Firefly is the lowest, although the standard deviation of its final responses is still very large. However, when nonlinear structural analyses are considered for larger structures, the framework surpasses both FA and KG-GA also in terms of running time. It should be noted the performance of the framework in scenario 2 of the 120-bar dome truss, where the times required by FA and KG-GA were above 2 h and almost 2 h, respectively, while better results were achieved by the framework in about half an hour. This emphasizes the fact that, due to its own computational demands, the framework should be applied only if the evaluations of the constraints are expensive enough.

5 Conclusion

In this paper, an optimization framework based on Kriging was presented to deal with structural problems that have expensive constraints. The main idea is to improve the accuracy of the surrogate model during the optimization process and only in promising regions of the design space. In order to identify these regions in a robust manner, the framework is composed of three search strategies: local search, global search, and refinement step. Seven examples from the literature were evaluated and the results were compared with those obtained by other optimization methods. It was found that the proposed framework achieved results close to the best presented in the literature, with far fewer constraints evaluations. Thus, the approach is found to be promising in reducing the computational effort associated with the solution of expensive constrained structural optimization problems, although as pointed out in other papers from the literature, there is a tendency of loss of efficiency when the dimensionality of the problems increases.