1 Introduction

Reliability-based design optimization (RBDO), which considers the uncertainty of both design variables and system parameters, has been widely used in practical engineering fields (Ho-Huu et al. 2018). In the study of Lv et al. (2016), a reliability optimization of front-end structure design of a vehicle was carried out to reduce passenger injuries and to improve the design reliability. Compared with deterministic optimization, RBDO considers fluctuations in the design variables caused by noise, which improves the failure probability of the structures. However, the traditional double-loop method (DLM) embeds reliability evaluation into the optimization algorithm, and the calculation cost is unacceptable. Therefore, an efficient RBDO method is urgently needed.

At present, research on the efficiency of the RBDO can be divided into two categories: (1) research that establishes a surrogate model to reduce the time of the reliability evaluation and (2) research that adopts efficient optimization strategies, such as the single-loop method and the decoupling method, to reduce the number of constraint evaluations in the reliability assessment.

In practical engineering, implicit functions that require finite element analysis (FEA) and computational fluid dynamics (CFD) are always computationally expensive and time consuming. To solve this problem, a surrogate model can be established to improve the efficiency of the performance function evaluations. Common surrogate models include the radial basis functions (Dai et al. 2011), a chaotic polynomial (Hu and Youn 2011), kriging (Ju et al. 2008), and support vector machine (SVM) (Basudhar and Missoum 2008). Zhang et al. (2017) adopted the response surface (RS) method, the expansion optimal linear estimation (EOLE) method, and the gradient projection method (GPM) to transform a time-dependent reliability problem into a time-independent reliability problem. To further improve the modeling efficiency, various sampling criteria have been proposed. Bichon et al. (2008) developed an efficient global reliability analysis (EGRA) method that selected points with high uncertainty as sample points. Lee et al. (2008) proposed the constraint boundary sampling (CBS) method, which evaluated samples around the limit state constraint boundary. Based on this idea, the sequential sampling (SS) method (Zhao et al. 2009), local adaptive sampling (LAS) method (Chen et al. 2014), and local kriging approximation method based on the MPP (LMPP) (Li et al. 2016), which selects the sample point on the limit state constraint boundaries around the current design point, were proposed to further improve modeling efficiency. Based on the kriging model, Meng et al. (2018, 2019) developed an adaptive directional boundary sampling (ADBS) method and an importance learning function (ILF) to improve the efficiency of kriging model construction. ADBS and ILF were extended to accurately and efficiently solve the RBDO and non-probabilistic reliability-based design optimization (NRBDO) problems with multiple performance functions. In ADBS, the points near the constraint boundary along the descending direction of objective functions were selected with more opportunity. In ILF, the non-probabilistic reliability indexes of different points near the limit state surface were calculated to compare points in terms of importance.

Although the surrogate model can effectively improve the efficiency of RBDO by reducing the calculation time of the performance function, the traditional strategy of the DLM makes the computation expensive. Nested structure is utilized in the optimization process of DLM and reliability assessment is performed after each optimization iteration. Thus, optimization strategies reducing the number of reliability assessments were developed (Liao and Ivan 2014; Wang et al. 2018; Lu et al. 2018; Cho and Lee 2011). The single-loop strategy (Agarwal et al. 2008) uses the Karush-Kuhn-Tucker (KKT) optimality condition corresponding to the probability constraint instead of reliability assessments. Shan and Wang (2008) proposed a novel approach that decomposed RBDO into two independent parts, and a deterministic optimization constrained by the reliable design space (RDS) would be performed only once. However, the error around the saddle point of the performance function increases as the standard deviations of the design variables increase. The decoupling loop strategy sequentially performs optimization design and a reliability assessment by an iterative method to improve efficiency while maintaining almost the same precision. Wu and Wang (1996) used safety-factor-based deterministic constraints instead of the probabilistic constraints to avoid performing an optimization with nested structure. Du and Chen (2003) proposed a sequential optimization and reliability assessment (SORA) method to shift the boundaries of violated constraints (with low reliability) in the feasible direction based on the reliability information obtained in the previous cycles. Liang et al. (2004) developed a single-loop method (SLM) to calculate the RDS based on the derivatives of the optimal design point. Cheng et al. (2006) obtained the optimum design by solving a sequence of subprogramming problems and introduced a new formulation for approximate reliability constraints and its linearization. Huang et al. (2012) proposed an enhanced SORA (ESORA) method that considers constant and varying variances. The gradient of the performance function at MPP is approximated to improve the RBDO efficiency when the performance functions are not all linear. Chen et al. developed an optimal shifting vector (OSV) approach (Chen et al. 2013a) and an adaptive decoupling approach (ADA) (Chen et al. 2013b) to further improve the efficiency of RBDO. Huang et al. (2016) proposed an incremental shifting vector (ISV) approach to obtain the new shifting vector by preserving the shifting vector from the previous steps and computing a shifting vector increment, which made the process of reliability analysis unnecessary.

However, the decoupling methods mentioned above approximate the limit state function based on the MPP or Taylor series expansion. The equivalent deterministic constraints are obtained by translating the whole limit state surface based on the reliability information of optimal design points, which will sometimes introduce errors. In recent years, a moment-based reliability assessment method that requires neither iterations nor the computation of sensitivities was developed. This method consists of two steps: the calculation of statistical moments and the estimation of a probability density function (PDF). The univariate dimension reduction method (UDRM), proposed by Rahman and Xu (2004), calculates statistical moments precisely and rapidly and has promoted the development of moment-based reliability assessment. Several approaches, including the Pearson system (Nagahara 2004), saddlepoint approximations (SA) (Huang and Du 2006), the extended generalized lambda distribution (EGLD) (Acar et al. 2010), and the maximum entropy method (MEM) (Dai et al. 2008), were used to estimate the distribution of a continuous random variable with moments of finite orders. To handle arbitrary probability distribution, Liu et al. (2018) proposed a general framework for the forward and inverse structural uncertainty propagations based on the dimension reduction (DR) method and the derivative lambda probability density function (λ-PDF). The results indicated that the moment methods are generally more accurate and efficient for distribution generation than the first-order reliability method (FORM) and the second-order reliability method (SORM). Due to their advantageous features, the moment methods are alternatives to FORM or SORM when (1) the performance function does not have a derivative; (2) the MPP is hard to identify; (3) there are multiple MPPs; or (4) the probability is close to the median and FORM or SORM cannot provide accurate solutions (Huang and Du 2006). Lee and Jung (2008) proposed a DRM-based MPP method for inverse reliability analysis, and the method is then used for the next design iteration of RBDO to obtain an optimal design. Du (2008) considered the SA for sequential optimization to reduce the nonlinearity caused by a non-normal-to-normal transformation, which did not improve the RBDO accuracy based on the MPP.

While moment-based methods for reliability assessment have been well-developed in recent years, the decoupling strategy for RBDO still focuses on MPP-based methods. The objective of this work is to develop an efficient and accurate decoupling strategy for RBDO based on the moment-based method. In the proposed method, the moment-based reliability assessment method is employed to perform uncertainty analysis; and the corresponding decoupling loop strategy, which includes the calculation of a probabilistic constraint shifting scalar and a local shifting-modified factor, is then developed to obtain the equivalent deterministic constraints corresponding to the probabilistic constraints; an inactive constraint checking criterion is utilized to further improve the efficiency. Three numerical examples and an automobile crashworthiness lightweight design problem are examined to show the effectiveness of the proposed approach. Additionally, the accuracy of PDF estimation methods, i.e., MEM and Edgeworth series expansion, is compared based on the optimization results.

The rest of this article consists of four sections. Section 2 describes the combined reliability assessment method employed in the proposed method. The proposed method is then introduced in detail in Section 3. In Section 4, four RBDO examples are discussed to illustrate and test the approach. Finally, concluding remarks on this new method are provided in Section 5.

2 Essence of the moment method

In this section, the basic procedure of the moment-based method involving UDRM and PDF estimation is mathematically described.

The core of RBDO is its probabilistic constraint defined in (1), which requires reliability assessments of a deterministic constraint based on random variables and parameters. The function prob(⋅) is defined as:

$$ \boldsymbol{prob}\left(g\left(\mathbf{D},\mathbf{X},\mathbf{P}\right)\le 0\right)={\int}_{g\left(\mathbf{D},\mathbf{X},\mathbf{P}\right)\le 0}\cdots \int {f}_{\mathbf{X},\mathbf{P}}\left(\mathbf{X},\mathbf{P}\right)\mathrm{d}\mathbf{X}\mathrm{d}\mathbf{P} $$
(1)

where D, X, and P denote the vector of deterministic design variables, the vector of basic random design variables, and the vector of random parameters, respectively. g(D, X, P) is the performance function, which denotes one of the deterministic constraints; and f(X, P) is the joint PDF of all random variables and parameters. For convenience, we combine all random variables and random parameters as V = [X, P]T = [x1, …, xl, p1, …, pq]T and assume that all random variables are independent and normally distributed. Correlated random variables can be transformed into normal independent random variables by the Rosenblatt transformation (Rosenblatt 1952). The probabilistic constraint is simply expressed as:

$$ \boldsymbol{prob}\left(g\left(\mathbf{D},\mathbf{V}\right)\le 0\right)={\int}_{g\left(\mathbf{D},\mathbf{V}\right)\le 0}\cdots \int {f}_{\mathbf{V}}\left(\mathbf{V}\right)\mathrm{d}\mathbf{V} $$
(2)

The integral operation of the PDF is the key step in calculating the reliability or failure probability of a performance functiong(D, V). We can see that (2) involves a high-dimensional integration with the same dimension as the number of random variables and parameters, which is quite difficult to calculate directly. Analytical methods such as FORM and SORM are efficient in reliability analysis, but the potential error resulting from limit state approximation is not known.

To ensure that RBDO based on a decoupled loop can be employed for more problems in engineering applications, this paper uses statistical moments and PDF estimation to calculate the reliability of the performance function. Therefore, the first four statistical moments based on the UDRM and the PDF calculated via MEM or Edgeworth series expansion are introduced in Section 2.1 and Section 2.2, respectively.

2.1 Univariate dimension reduction method

The UDRM was proposed by Rahman and Xu (2004) to approximate the statistical moments of the performance function, which is affected by the random variables and parameters. The calculation procedure of statistical moments involves an additive decomposition of a multidimensional function into multiple one-dimensional functions, an approximation of response moments by the moments of single random variables or parameters, and a quadrature rule for numerical integration.

In general, considering an n-dimensional, differentiable, real-valued performance function g(V) with random variables V(v1, …vn), the performance function g(V) approximated by multiple one-dimensional functions can be expressed as:

$$ g\left(\mathbf{V}\right)=g\left({v}_1,\dots, {v}_n\right)\cong \sum_{i=1}^n{g}_i-\left(n-1\right)g\left({\mu}_{v_1},\dots, {u}_{v_n}\right) $$
(3)

where \( {g}_i={g}_i\left({\mu}_{v_1},\dots, {\mu}_{v_{i-1}},{v}_i,{\mu}_{v_{i+1}},\dots, {\mu}_{v_n}\right) \) denotes the one-dimensional function with respect to vi. If we define \( {g}_0=g\left({\mu}_{v_1},\dots, {\mu}_{v_n}\right) \), then, the jth origin moment of the performance function, mj, can be calculated as (Zhang et al. 2011):

$$ {m}_j=E\left[{g}^j\left(\mathbf{V}\right)\right]\cong \sum_{k=0}^j{C}_j^kE\left\{{\left[\sum_{i=1}^n{g}_i\right]}^k\right\}\times {\left[\left(1-n\right)\times E\left({g}_0\right)\right]}^{j-k} $$
(4)

where \( {C}_j^k=j!/k!/\left(j-k\right)! \) denotes the binomial coefficients and E(·) denotes the mean function. According to the polynomial theory, the summation \( E{\left[\sum_{i=1}^n{g}_i\right]}^k \) can be further rewritten as:

$$ E{\left[\sum_{i=1}^n{g}_i\right]}^k=\sum_{k_l\ge 0,{k}_1+\dots +{k}_n=k}\left(\begin{array}{c}k\\ {}{k}_1,\dots, {k}_n\end{array}\right)\prod_{1\le i\le n}E\left({g}_i^{k_i}\right) $$
(5)

The one-dimensional integration in (5) can be expressed as:

$$ E\left({g}_i^k\right)=\int {g}^k\left({\mu}_{v_1},\dots, {\mu}_{v_{i-1}},{v}_i,{\mu}_{v_{i+1}},\dots, {\mu}_{v_n}\right){f}_{v_i}(v) dv $$
(6)

where k denotes the order of moments for the one-dimensional random function and \( {f}_{v_i}(v) \) denotes the PDF of vi, which is transformed into a normal distribution.

Finally, the Gauss-Hermite quadrature rule is used to approximate the one-dimensional integration function \( E\left({g}_i^k\right) \). The number of integration points depends on the nonlinearity of the performance function. In this paper, we take six integration points for the exponential function and four integration points for the polynomial function. The computational effort (CE) can be measured by the number of function evaluations and is given by

$$ CE={n}_v\times {n}_g+1 $$
(7)

where nv denotes the number of design variables and ng denotes the number of Gauss integral points.

2.2 PDF estimation method based on statistical moments

The calculation accuracies of the SA, EGLD, Pearson system, and MEM for the PDF of the performance function were compared in Li and Zhang (2011). The results showed that the MEM is the most accurate method in PDF modeling and that it is not sensitive to a moderately low reliability level. Meng et al. (2016) demonstrated that Edgeworth series expansion has the advantages of fast convergence speed and fewer calculations and can estimate a PDF of a complex structure. Therefore, while validating the efficiency of the proposed method, the accuracies of the reliability calculation of the MEM and Edgeworth series expansion method are discussed.

2.2.1 Edgeworth series expansion

Edgeworth series expansion (Barndorff-Nielsen and Cox 1979) is a true asymptotic expansion that can theoretically approximate an arbitrary distribution by using the Gauss basis function. The first four terms can usually obtain a sufficiently high accuracy, and the cumulative distribution function (CDF) is defined as follows:

$$ F(z)\cong \varPhi (z)-\left({\left({u}_{\mathrm{g}}^2\right)}^{-\frac{1}{2}}/6\right){\varPhi}^{(3)}(z)+\frac{1}{24}\left({u}_{\mathrm{g}}^4/{\left({u}_{\mathrm{g}}^2\right)}^2/24-0.125\right){\varPhi}^{(4)}(z)+{\left({\left({u}_{\mathrm{g}}^2\right)}^{-\frac{1}{2}}/72\right)}^2{\varPhi}^{(6)}(z) $$
(8)

where z denotes the value of the performance function; \( {u}_{\mathrm{g}}^k \) denotes the kth center moment of the performance function, which can be calculated by the origin moments; Φ denotes the standard normal CDF; Φ(k)(z) = (−1)k − 1φ(z)Hk − 1(z) denotes the kth derivative of the standard normal CDF; φ denotes the standard normal PDF; and Hk − 1(z) is the Hermite polynomial, and its recursive relation can be expressed as follows:

$$ \left\{\begin{array}{c}{H}_0(z)=1,{H}_1(z)=z\\ {}{H}_n(z)=z{H}_{n-1}(z)-\left(n-1\right){H}_{n-2}(z)\end{array}\right. $$
(9)

2.2.2 Maximum entropy method

The MEM is regarded as the most unbiased estimation of a PDF, which means the most likely PDF from all the PDFs under constraints of the statistical moments (Zellner and Highfield 1988). The PDF is an optimal solution to the optimization problem, which is defined as follows:

$$ {\displaystyle \begin{array}{c}\mathit{\max}\int -f(z)\mathrm{In}f(z)\mathrm{d}z\\ {}\mathrm{s}.\mathrm{t}.\int {z}^if(z)\mathrm{d}z={m}_i,i=0,1,\dots, n\end{array}} $$
(10)

where mi is the ith origin moment and n denotes the number of the given moment constraints, which is defined as 4 in this paper. f(z) stands for the PDF of the performance function determined by the MEM. The method of Lagrangian multipliers is used to solve the above optimization problem. With the Lagrangian multipliers λi, i = 0, …, 4, the Lagrangian function can be expressed as

$$ L=\int -f(z)\boldsymbol{In}f(z)\mathrm{d}z+\sum_{i=0}^4{\lambda}_i\left(\int {z}^if(z)\mathrm{d}z-{m}_i\right) $$
(11)

The analytical expression of f(z) is solved by \( f(z)=\mathit{\exp}\left(-\sum_{t=0}^4{\lambda}_t{z}^t\right) \) based on the necessary conditions for a stationary point for (10). We can obtain the five Lagrangian multipliers by solving the set of nonlinear equations as follows:

$$ \int {z}^{\mathrm{i}}\mathit{\exp}\left(-\sum_{t=0}^4{\lambda}_t{z}^t\right)\mathrm{d}z={m}_{\mathrm{i}},i=0,\dots, 4 $$
(12)

3 Proposed method

It is universally known that different reliability assessment methods correspond to different decoupled loop strategies of RBDO. The accuracy of the RBDO is determined by three factors: (1) the accuracies of the reliability assessment methods used to determine the upper limit of the accuracy of RBDO, (2) the errors introduced by the decoupled loop strategies, and (3) the accuracy of the optimization algorithm. The research described in this paper focuses on the first two points. First, the existing decoupled strategies are all based on FORM. However, the results in the literature show that the moment methods are slightly more accurate than FORM in some cases (Huang and Du 2006; Dai et al. 2008; Acar et al. 2010). Second, the transformation of probabilistic constraints is based on the reliability information of optimal points rather than areas, which will inevitably cause errors. In this paper, a sequential optimization and moment-based reliability assessment (SOMRA), which includes the moment-based reliability assessment method and a corresponding decoupled loop strategy, is proposed. It provides the same results as the conventional nested optimization structure, but it is more efficient.

In the following sections, the SOMRA is described in detail. The optimization framework and the mathematical model of the SOMRA are introduced in Section 3.1. The method for calculating the probabilistic constraint shifting scalar is presented in Section 3.2. A modified factor of the probabilistic constraint shifting scalar is introduced in Section 3.3. In Section 3.4, an inactive constraint checking method is employed to further improve the efficiency. Finally, the flowchart and procedure of the proposed SOMRA are presented in Section 3.5.

3.1 Optimization framework and mathematical model of the SOMRA

The decoupled loop strategy performs deterministic optimization and reliability assessment sequentially to solve the RBDO problems. The well-recognized framework of the decoupled loop strategy is illustrated in Fig. 1. The whole optimization process mainly consists of four parts: initialization, deterministic optimization, reliability assessment, and convergence conditions. The reliability assessment part applies the methods mentioned in Section 2. The deterministic optimization part is the core procedure and is described in detail first; the other three parts will be introduced in subsequent sections.

Fig. 1
figure 1

Frame of the decoupled loop strategy

Full size image

The mathematical model includes the key information of an optimization problem. The main difference between deterministic optimization and probabilistic optimization is reflected in constraint functions. The construction of the appropriate equivalent deterministic constraints is critical during iteration. Corresponding to the feasible design space (FDS) consisting of deterministic constraints, the space as defined by the probabilistic constraints is called an RDS (Shan and Wang 2008). The difference between the FDS and the RDS depends on the reliable information of the design points. Based on the decoupled loop strategy and inverse MPP, Du and Chen (2003) presented the mathematical model of SORA during the iterative process:

$$ {\displaystyle \begin{array}{c} minf\left(\mathbf{D},\boldsymbol{\upmu} \left(\mathbf{V}\right)\right)\\ {}\mathrm{s}.\mathrm{t}.g\left(\mathbf{D},\mathbf{V}-{\mathbf{S}}^k\right)\le 0\end{array}} $$
(13)

where Sk is the estimated difference between the inverse MPP and the reliable design point in cycle k. It is relatively easy to obtain the relationship between the MPP and the mean value of X via deviation. Benefiting from the MPP-based method itself, SORA transforms the probabilistic constraints into deterministic constraints based on the design variables. Actually, the transformation between the probabilistic constraints and equivalent deterministic constraints is a translation of the performance function in the domain of independent variable X, as shown by (13). However, the moment-based reliability assessment cannot provide the MPP directly. It provides the PDF of the performance function, which works well in calculating the difference between FDS and RDS from the perspective of the values of the performance function. In other words, for the limit state equation Z = g(D, X) = 0, we can obtain the deviation between probabilistic constraints and equivalent deterministic constraints from the respective of the dependent variable Z. Thus, the mathematical model of the SOMRA during iteration can be expressed as follows:

$$ {\displaystyle \begin{array}{c} minf\left(\mathbf{D},\boldsymbol{\upmu} \left(\mathbf{V}\right)\right)\\ {}\mathrm{s}.\mathrm{t}.g\left(\mathbf{D},\mathbf{V}\right)+{\lambda}^k\le 0\end{array}} $$
(14)

where λk is the probabilistic constraint shifting scalar, which defines the difference between the deterministic and probabilistic performance functions in cycle k. It is obvious that the transformation of SOMRA is a movement of the performance function in the domain of dependent variable Z. Figure 2a and b illustrate how SORA and the SOMRA transform probabilistic constraints into equivalent deterministic constraints, respectively, by taking a two-dimensional performance function as an example. From Fig. 2b, it is obvious that the SORA class methods approximate the probabilistic constraint by calculating the shifting vector \( \overrightarrow{\mathrm{AB}} \), and the proposed SOMRA approximates the probabilistic constraint by calculating the shifting scalar BC.

Fig. 2
figure 2

Transforming probabilistic constraint to equivalent deterministic constraint. a SORA. b SOMRA

Full size image

3.2 Probabilistic constraint shifting scalar calculation

The PDF and CDF of the performance function are obtained through the MEM or Edgeworth series expansion methods mentioned in Section 2.2. However, the PDF does not strictly follow a normal distribution in most cases, even though the basis function of the method mentioned above is the Gauss function and the random variables are normally distributed. Therefore, the shifting scalar calculated by the required reliability index will cause a large error and divergence of the algorithm. The PDF is then used to inversely calculate the reliability index corresponding to the required reliability of R. At the beginning of optimization cycle k, the reliability index βk is expressed as follows:

$$ {\beta}^k={F}^{-1}(R) $$
(15)

where R denotes the value of the probabilistic constraint and F−1 denotes the inverse function of the CDF of the performance function at the optimal point Vk in the previous cycle k − 1. For the performance function subject to the standard normal distribution, the value of the function is equal to the product of the failure probability corresponding reliability index and the standard deviation. The symbol L is then defined to represent this value, and we obtained the new limit state surface of Z − L = g(D, X) − L = 0. The difference between the SOMRA and SORA class methods is the limit state surface obtained by transforming the performance function from the perspective of the dependent variable (the value of the performance function). When Z = g(D, X) ≤ L is satisfied, the probabilistic constraint is almost satisfied. Therefore, the step length L is a rough estimate of the shifting scalar. With mean \( {\mu}_{g\left(\mathbf{V}\right)}^k \) and standard deviation \( {\sigma}_{g\left(\mathbf{V}\right)}^k \), we determine the step length Lk at the design point Vk:

$$ {L}^k={\sigma}_{g\left(\mathbf{V}\right)}^k\times {\beta}^k $$
(16)

It is found that the skewness of the performance function is not equal to zero in most cases, which means that the mean μk f the performance function at the design point Vk is not equal to g(Vk). However, the optimization process is actually the iterative movement of the design variable V in the feasible region. To locate Vk on the limit state surface of the probabilistic constraint precisely, a compensation value α is added to Lk:

$$ {\alpha}^k={\mu}_{g\left(\mathbf{V}\right)}^k-g\left({\mathbf{V}}^k\right) $$
(17)

By using (16) and (17), the probabilistic constraint shifting scalar λk∗ can be expressed as:

$$ {\lambda}^k\ast ={L}^k+{\alpha}^k $$
(18)

Then, a deterministic optimization and reliability assessment are conducted on the updated optimization model based on the shifting scalar λk∗. λ1∗ in cycle 1 is set equal to zero. The reliability of those violated probabilistic constraints in cycle k − 1 should be improved markedly using the proposed probabilistic constraint shifting scalar. If some probabilistic constraints are still not satisfied, we repeat the procedure cycle by cycle until the objective converges, and the reliability requirement is achieved when the difference in the shifting scalars between two consecutive cycles is small enough.

Thus, similar to SORA, the proposed method accomplishes the transformation from probabilistic constraints to equivalent deterministic constraints. However, the proposed method converges to a different design point than DLM for some numerical examples. Therefore, it is necessary to develop a local modified factor of shifting scalar to improve the accuracy of the proposed strategy, as introduced in Section 3.3.

3.3 Local shifting modified factor calculation

Research shows that the accuracy of the equivalent deterministic boundary of the SORA depends on the nonlinearity around the inverse MPP, but the accuracy of the proposed method depends on the integration of the nonlinearity from the deterministic design point to the corresponding reliable design point, which results in the equivalent deterministic constraints deviating from the actual probabilistic constraints, which the fundamental cause for why SOMRA gives an incorrect result. However, the deviation is difficult to modify because of the basic attribute of the performance function. Some tests show that the limit state surface around the optimal point calculated by SOMRA deviates greatly from the actual limit state surface when the optimal point calculated by SOMRA converges to an erroneous point. For convenience of discussion, we still take a two-dimensional function as an example. Its limit state surface is the cross section of the two-dimensional function with the value of shifting scalar. It is impossible to construct the true limit state surface because the shape of the two-dimensional function is certain and the shifting scalar is the same across the domain. This is the direct cause of deviation.

It is obvious that only the shifting scalar can be modified. Meanwhile, in FORM, the relationship between a point and its MPP can be expressed approximately by explicit formulation. Additionally, the relationship can be utilized to correct the shifting scalar. Therefore, to construct the approximate limit state surface, a modified factor based on MPP is proposed to carry out global correction of a shifting scalar.

By using the method of Lagrange multipliers, Shan and Wang (2008) give:

$$ {v}_i^{u\ast }=-\beta {\left(\partial g/\partial {v}_i^u\right)}_{\ast }/\sqrt{\sum {\left(\partial g/\partial {v}_i^u\right)}_{*}^2},i=1,\dots, n $$
(19)

where * denotes the point on the state limit surface; u denotes the standard normal distribution space; \( {v}_i^{u\ast } \) is the component of the MPP Vu∗; the derivatives \( {\left(\partial g/\partial {v}_{\mathrm{i}}^u\right)}_{\ast } \) are evaluated at the MPP Vu∗; and β is the reliability index. By using the transformation \( {v}_i^u=\left({v}_i-{u}_{v_i}\right)/{\sigma}_{v_i} \), we can transform (19) back to the original design space:

$$ {v}_i\ast ={\mu}_{v_i}-\beta {\sigma}_{v_i}^2{\left(\partial g/\partial {v}_i\right)}_{\ast }/.\sqrt{\sum {\left({\sigma}_{v_i}{\left(\partial g/\partial {v}_i\right)}_{*}\right)}^2} $$
(20)

where vi∗ denotes a component of the point in the original design space corresponding to the MPP in the normalized variable space. We approximate the direction cosine part, \( {\left(\partial g/\partial {v}_i\right)}_{\ast }/\sqrt{\sum {\left({\sigma}_{v_i}{\left(\partial g/\partial {v}_i\right)}_{*}\right)}^2} \), in (20) by evaluating it at the corresponding mean point by substituting (∂g/∂vi)∗ with \( \left(\partial g/\partial {\mu}_{v_i}\right) \). Thus, we have (Shan and Wang 2008):

$$ {v}_i\ast \cong {\mu}_{v_i}-\beta {\sigma}_{v_i}^2\left(\partial g/\partial {\mu}_{v_i}\right)/\sqrt{\sum {\left({\sigma}_{v_i}\left(\partial g/\partial {\mu}_{v_i}\right)\right)}^2} $$
(21)

The difference d between the equivalent deterministic constraint and deterministic constraint can be approximately expressed as:

$$ d\cong g\left({\boldsymbol{\upmu}}_{\mathbf{V}}\right)-g\left(\mathbf{V}\ast \right) $$
(22)

To simplify d, a first-order Taylor series expansion at the point μV is employed to approximate the performance function. By using (21) and (22), d can be rewritten as:

$$ d\cong g\left({\boldsymbol{\upmu}}_{\mathbf{V}}\right)-\left(g\left({\boldsymbol{\upmu}}_{\mathbf{V}}\right)+\sum_{i=1}^n\partial g/\partial {\mu}_{v_i}\times \left({v}_i\ast -{\mu}_{v_i}\right)\right)=\beta \sqrt{\sum {\left({\sigma}_{v_i}\left(\partial g/\partial {\mu}_{v_i}\right)\right)}^2} $$
(23)

The modified factor Fk based on the optimal point Vk in cycle k can be expressed as a proportionality coefficient as follows:

$$ {F}^k=d/{d}^k=\sqrt{\sum {\left({\sigma}_{v_i}\left(\partial g/\partial {\mu}_{v_i}\right)\right)}^2}/\sqrt{\sum {\left({\sigma}_{v_i^k}\left(\partial g/\partial {\mu}_{v_i^k}\right)\right)}^2} $$
(24)

Finally, with the shifting scalar λ∗ calculated in Section 3.2, we obtain the modified probabilistic constraint shifting scalar λk in cycle k:

$$ {\lambda}^k={F}^k\times {\lambda}^k\ast =\sqrt{\sum {\left({\sigma}_{v_i}\left(\partial g/\partial {\mu}_{v_i}\right)\right)}^2}/\sqrt{\sum {\left({\sigma}_{v_i^k}\left(\partial g/\partial {\mu}_{v_i^k}\right)\right)}^2}\times \left({\sigma}_{g\left(\mathbf{V}\right)}^k\times {\beta}^k+\left({\mu}_{g\left(\mathbf{V}\right)}^k-\mathrm{g}\left({\mathbf{V}}^k\right)\right)\right) $$
(25)

With the shifting scalar λ, the construction procedure of the equivalent deterministic constraints considers the performance function around the optimal point rather than the monolithic translation. Because each probabilistic constraint has its own PDF and reliability index, each probabilistic constraint has its own shifting scalar. The stopping criteria for the SOMRA are as follows: (1) the Euclidean norm of the difference of the optimal design points between two consecutive cycles is small enough, and (2) all the reliability requirements are satisfied.

3.4 Inactive constraint checking criterion

It is unnecessary to conduct reliability assessment and to calculate the shifting scalar for inactive probabilistic constraints during the optimization process, as these processes reduce the efficiency. Using the UDRM, we can roughly judge whether the constraints are active. When obtaining the statistical moments, the reliability index \( {\beta}_c^k \) can be expressed as follows:

$$ {\beta}_c^k={\mu}_{g\left(\mathbf{V}\right)}^k/{\sigma}_{g\left(\mathbf{V}\right)}^k $$
(26)

where \( {\mu}_{g\left(\mathbf{V}\right)}^k \) and \( {\sigma}_{g\left(\mathbf{V}\right)}^k \) denote the mean and standard deviation of the performance function, respectively. We can roughly judge whether the probabilistic constraints are active as follows:

  1. 1)

    Inactive when \( {\beta}_c^k-{\beta}_r>\varepsilon \). βr is the required reliability index and ε is a small positive number; we choose ε = 0.3βr.

  2. 2)

    Active when \( {\beta}_c^k-{\beta}_r\le \varepsilon \).

For inactive probabilistic constraints, the procedures for PDF modeling and shifting scalar calculation can be omitted. The statistical moments will be recalculated in each iteration. Thus, the error prediction does not accumulate.

Here, we calculate the probabilistic constraint shifting scalar λ of SOMRA. By using the mathematical model of the SOMRA, the number of reliability assessments will be reduced significantly at the cost of adding several deterministic optimizations.

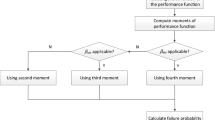
3.5 Flowchart and procedure of the proposed method

The flowchart of the SOMRA method is given in Fig. 3. It consists of five procedures:

  1. 1)

    Definition of the initial design point d0. In cycle k(k ≥ 2), the initial design point is taken as the optimal point of the previous cycle.

  2. 2)

    Computation of the probabilistic constraint shifting scalar λ according to the proposed method. The shifting scalar λ will be used to update the mathematical model. In the first cycle, λ is set as zero.

  3. 3)

    Optimization of the updated mathematical model using sequential quadratic programming (SQP).

  4. 4)

    Reliability assessment using the method introduced in Section 2. When obtaining the mean and standard deviation, inactive constraint checking is carried out to judge whether PDF estimation and shifting scalar calculation are necessary.

  5. 5)

    End RBDO if the convergence conditions are reached; otherwise, go back to step (1).

Fig. 3
figure 3

Flowchart of the SOMRA method

Full size image

4 Applications

In this section, three numerical examples and an engineering application are presented to demonstrate the effectiveness of the SOMRA. For each example, the DLM is based on the performance measurement approach (PMA), and the SORA, the DLM moment-based method, and the SOMRA proposed in this paper are used for optimization. In addition, the optimization results of the DLM based on Monte Carlo simulation (MCS) and the SOMRA based on probabilistic constraints shifting scalar λ∗ are given in the first two examples. The sampling size of MCS is ten million. The result of DLM + MCS as the reference standard and the relative error is expressed as:

$$ \boldsymbol{Relative}\ \boldsymbol{error}=\frac{\left\Vert {\mathbf{X}}_t-\mathbf{X}\right\Vert }{\left\Vert \mathbf{X}\right\Vert}\times 100\% $$
(27)

where X denotes the design variables of the reference standard and Xt denotes the design variables of different methods. SQP is used to solve deterministic optimization problems and PMA. For every example, the optimal solution of the design variables and objective function, the number of reliability assessments, the number of optimizations, and the number of constraint function evaluations are given. Additionally, the actual reliability index of the design results is assessed through MCS with a sampling size of ten million. All program codes are tested in “MATLAB2016a,” and the SQP algorithm is realized by the optimization routine “fmincon.”

4.1 Numerical example 1

Example 1.1 (Bichon et al. 2008) has two random design variables and two probabilistic constraints. All the random variables are statistically independent and have normal distributions as follows:

$$ {\displaystyle \begin{array}{l}\boldsymbol{find}\kern2em \mathbf{d}={\left[{d}_1,{d}_2\right]}^T\\ {}\min \kern1.25em f\left(\mathbf{d}\right)=\frac{{\left({d}_1+{d}_2-8\right)}^2}{30}+\frac{{\left({d}_1-{d}_2-15\right)}^2}{120}\\ {}\begin{array}{l}\mathrm{s}.\mathrm{t}.\kern2em P\left({g}_i\left(\mathbf{X}\right)\le 0\right)\ge \varPhi \left({\beta}_i\right),i=1,2,3\\ {}\boldsymbol{where}\kern0.75em \begin{array}{l}{g}_1\left(\mathbf{X}\right)=\frac{5-\exp \left(0.8{X}_1-1.5\right)-\exp \left(0.7{X}_2-0.2\right)}{10}\\ {}{g}_2\left(\mathbf{X}\right)=\frac{{\left({X}_1+{X}_2+4.5\right)}^2}{120}+\frac{{\left({X}_1-{X}_2-2.5\right)}^2}{30}-2.3\\ {}\begin{array}{l}0\le {d}_1\le 4,0\le {d}_2\le 5,{X}_i\sim N\left({d}_i,{0.3}^2\right),i=1,2,3\\ {}{\beta}_1={\beta}_2={\beta}_3=2,{d}^{(0)}={\left[3,3\right]}^T\end{array}\end{array}\end{array}\end{array}} $$

The optimization results are shown in Table 1. This problem has only one active constraint g1. Clearly, the optimization result of the SOMRA converges to the same point as the DLM for the moment-based reliability assessment method, which significantly reduces the number of reliability assessments. The result of the shifting scalar λ∗ causes a large error as predicted, which means that the modified factor F of the shifting scalar does work. However, the SORA gives the same result as DLM + PMA, although there is no correction of the shifting vector in the optimization process of SORA. In summary, compared with MCS, the accuracies of all the methods are acceptable based on the results of the objective function and reliability indexes, excluding the SOMRA based on the shifting scalar λ∗. The SOMRA based on MEM provides the best design point with a slightly lower efficiency than SORA.

Table 1 Summary of the optimization results for numerical example 1.11
Full size table

Figure 4 is presented to further demonstrate the effectiveness of the SOMRA with the PDF estimation method of the MEM. The black dashed line and red solid line denote the limit state surface of the deterministic constraints and the equivalent deterministic constraints with different shifting scalars, respectively. For convenience of discussion, we define the RDS calculated by different reliability assessment methods as the calculation RDS (CRDS), which is the limit state surface of probabilistic constraints. The blue dashed-dotted line denotes the CRDS of different reliability assessment methods, which consists of points meeting the probabilistic requirements after sequential testing in the FDS. The optimal design points of the different methods are also shown in Fig. 4.

Fig. 4
figure 4

Limit state functions of numerical example 1.1. a Shifting scalar λ∗ in the last cycle. b Shifting scalar λ∗ at the point d2. c Shifting scalar λ in the last cycle. d Result of SORA

Full size image

Figure 4a shows the optimization result with the shifting scalar λ∗. As the distance from the optimal point increases, the deviation from the limit state surface of the equivalent deterministic constraint to the CRDS boundaries increases, leading to a poor result. Figure 4b shows the limit state surface of the equivalent deterministic constraint using the actual optimal point calculated by DLM + MEM as the iteration point. When the boundaries of the equivalent deterministic constraint exactly include the reliable optimal point P2, the optimal point P4 based on the equivalent deterministic constraint is out of the CRDS, meaning that P4 is unreliable. In the next cycle, the limit state surface of the equivalent deterministic constraint will be smaller based on the reliability information of P4, and the real reliable optimal point P4 will be discarded. Figure 4c shows the result of the shifting scalar λ corrected by the modified factor F. It is observed that the limit state surface of the equivalent deterministic constraint around the optimal design point has a significant improvement in the fitting accuracy of the CRDS. The small deviation between the SOMRA and moment-based DLM further demonstrates the effectiveness and necessity of the modified factor F. Figure 4d shows the SORA result. Although there is no correction of the shifting vector in the SORA, the limit state surface of the equivalent deterministic constraint fits CRDS well. The SORA and DLM + PMA converge to almost the same optimal design point; however, convergence occurs only when the nonlinearity of limit state surface around the optimal point is sufficiently low.

The convergence history of the objective function is depicted in Fig. 5. The results are given by the strategies of the MEM-based SOMRA and DLM. Notably, in the DLM, iteration requires computations because of the reliability assessment. However, in the SOMRA, one reliability assessment follows one optimization, and only six reliability assessments are performed in this example.

Fig. 5
figure 5

Convergence history of the object of example Example 1.1

Full size image

To illustrate the necessity of the modified factor in the decoupled loop strategies, the objective function in example 1.1 is adjusted slightly by substituting f(d) = (d1 − 3.7)2 + (d2 − 4)2 with f(d) = (d1 − 3)2 + (d2 − 4)2. The new optimization example 1.2 is expressed as:

$$ {\displaystyle \begin{array}{l}\boldsymbol{find}\kern2em \mathbf{d}={\left[{d}_1,{d}_2\right]}^T\\ {}\min \kern1.25em f\left(\mathbf{d}\right)={\left({d}_1-3\right)}^2+{\left({d}_2-4\right)}^2\\ {}\begin{array}{l}\mathrm{s}.\mathrm{t}.\kern2em P\left({g}_i\left(\mathbf{X}\right)\ge 0\right)\le \varPhi \left({\beta}_i\right),i=1,2\\ {}\boldsymbol{where}\kern0.75em \begin{array}{l}{g}_1\left(\mathbf{X}\right)=-{X}_1\mathit{\sin}\left(4{X}_1\right)-1.1{X}_2\mathit{\sin}\left(2{X}_2\right)\\ {}{g}_2\left(\mathbf{X}\right)={X}_1+{X}_2-3\\ {}\begin{array}{l}0\le {d}_1\le \mathrm{3.7,0}\le {d}_2\le 4,{X}_i\sim N\left({d}_i,{0.1}^2\right),i=1,2\\ {}{\beta}_1={\beta}_2=2,{d}^{(0)}={\left[\mathrm{2.5,2.5}\right]}^T\end{array}\end{array}\end{array}\end{array}} $$

Table 2 shows the optimization results of numerical example 1.2. The result of the SOMRA with shifting scalar λ is given, and the SOMRA exhibits good consistency of convergence. Moment-based RBDO methods give more accurate results than those of MPP-based RBDO methods in this numerical example. The result of the PDF estimation method of MEM is slightly more accurate than that of the Edgeworth series expansion. The result of SORA is not given because of non-convergence.

Table 2 Summary of the optimization results for numerical example 1.2
Full size table

Figure 6a shows the limit state surface of the MEM-based SOMRA in the last cycle. The limit state surface of the equivalent deterministic constraint g1 fits well with CRDS around the optimal design point; thus, the SOMRA has a good consistency of convergence. Similar to the shifting scalar λ∗, the optimal design point of DLM + PMA is considered to be the optimal design point, and the limit state surface of the equivalent deterministic constraint of the SORA is given in Fig. 6b. Clearly, the contour of the equivalent deterministic constraint around the optimal design point deviates from CRDS. The optimal design point of DLM + PMA has two MPPs, which are located on the left and right side of the saddle point on the limit state surface of the deterministic constraint. The inverse MPP on the right side is selected to construct the shifting vector in the SORA. The optimal design point in such a situation is out of CRDS and on the left side of the result of DLM + PMA, and the inverse MPP calculated by PMA is on the left side of the saddle point of the deterministic constraint. In the next cycle, the inverse MPP will be on the right side of the saddle point, causing the optimization to oscillate until the maximum number of iterations is reached.

Fig. 6
figure 6

Limit state functions of numerical example 1.2. a Result of SOMRA. b Result of SORA

Full size image

Taking the points on the limit state surface of deterministic constraints as the MPP, the corresponding design points can be obtained by using (20) under the assumption of a first-order Taylor series expansion. The reliability indexes of constraints g1 and g2 are both set to 2. Figure 7a shows the result of the limit state surface based on the inverse calculation of the MPP. The equivalent deterministic constraints fit the CRDS well, except, in the areas around the saddle point denoted by a rectangular box. Figure 7b is the local magnification of Fig. 7a around the saddle point. Point D has two MPPs of points DMPP1 and DMPP2on both sides of the saddle point of the limit state surface of the deterministic constraint. The noticeable deviation between the equivalent deterministic constraint and CRDS occurs when the deterministic constraints have saddle points at which the first derivative of the constraint equals zero. The points in the inverted triangle region constructed by the red solid line above have a corresponding MPP of reliability index equal to 2 on the limit state surface of deterministic constraint, but they do not fulfill the required probability. When the optimal point is located on the limit state surface between DMPP1 and DMPP2 in the first cycle, the SORA will not converge or provide a misleading result. Existing SORA class methods do not provide a solution distinguishable from the MPP candidates. The region that results in non-convergence increases with the standard deviation of the random variables, the second derivative of the limit state surface of the performance function, and the reliability index.

Fig. 7
figure 7

Limit state surface. a The result of limit state surface based on the inverse calculation of the MPP. b Local magnification of the rectangular box

Full size image

To illustrate the effectiveness of the SOMRA in different distribution types, the numerical example 1.3 with design variable of uniform distribution is performed. In this example, when calculating the statistic moment, the Gauss-Hermite quadrature is replaced by the Gauss-Legendre quadrature according to PDF of uniform distribution. Example 1.3 is expressed as follows.

$$ {\displaystyle \begin{array}{l}\boldsymbol{find}\kern2em \mathbf{d}={\left[{d}_1,{d}_2\right]}^T\\ {}\min \kern1.25em f\left(\mathbf{d}\right)=\left({d}_1-3.7\right)+{\left({d}_4-4\right)}^2\\ {}\begin{array}{l}\mathrm{s}.\mathrm{t}.\kern2em P\left({g}_i\left(\mathbf{X}\right)\ge 0\right)\le \varPhi \left({\beta}_i\right),i=1,2\\ {}\boldsymbol{where}\kern0.75em \begin{array}{l}{g}_1\left(\mathbf{X}\right)={X}_1\mathit{\sin}\left(4{X}_1\right)-1.1{X}_2\mathit{\sin}\left(2{X}_2\right)\\ {}{g}_2\left(\mathbf{X}\right)={X}_1+{X}_2-3\\ {}\begin{array}{l}0\le {d}_1\le \mathrm{3.7,0}\le {d}_2\le 4,{X}_i\sim \mathrm{U}\left({d}_i-0.1,{d}_i+0.1\right),i=1,2\\ {}{\beta}_1={\beta}_2=2,{d}^{(0)}={\left[\mathrm{2.5,2.5}\right]}^T\end{array}\end{array}\end{array}\end{array}} $$

Table 3 shows the optimization results of numerical example 1.3. The result of the SOMRA with shifting scalar λ is given. All the methods give satisfactory results. The methods of DLM + PMA and SORA have good consistency that there is little difference between the results of them. And the SOMRA is more efficient with acceptable accuracy. Therefore, the convergence performance of SOMRA is good for design variables with uniform distribution.

Table 3 Summary of the optimization results for numerical example 1.3
Full size table

4.2 Numerical example 2

This example has two random design variables and three probabilistic constraints. All the random variables are statistically independent and have normal distributions as follows:

$$ {\displaystyle \begin{array}{l}\boldsymbol{find}\kern2em \mathbf{d}={\left[{d}_1,{d}_2\right]}^T\\ {}\min \kern1.25em f\left(\mathbf{d}\right)=\frac{{\left({d}_1+{d}_2-8\right)}^2}{30}+\frac{{\left({d}_1-{d}_2-15\right)}^2}{120}\\ {}\begin{array}{l}\mathrm{s}.\mathrm{t}.\kern2em P\left({g}_i\left(\mathbf{X}\right)\le 0\right)\ge \varPhi \left({\beta}_i\right),i=1,2,3\\ {}\boldsymbol{where}\kern0.75em \begin{array}{l}{g}_1\left(\mathbf{X}\right)=\frac{5-\mathit{\exp}\left(0.8{X}_1-1.5\right)-\mathit{\exp}\left(0.7{X}_2-0.2\right)}{10}\\ {}{g}_2\left(\mathbf{X}\right)=0.5\times {\left({X}_1-1\right)}^2+{X}_2-5\\ {}\begin{array}{l}{g}_3\left(\mathbf{X}\right)=\frac{{\left({X}_1+{X}_2+4.5\right)}^2}{120}+\frac{{\left({X}_1-{X}_2-2.5\right)}^2}{30}-2.3\\ {}0\le {d}_1\le 4,0\le {d}_2\le 5,{X}_i\sim N\left({d}_i,{0.3}^2\right),i=1,2,3\\ {}{\beta}_1={\beta}_2={\beta}_3=2,{d}^{(0)}={\left[3,3\right]}^T\end{array}\end{array}\end{array}\end{array}} $$

The optimization results are shown in Table 4. Some of the conclusions are similar to those of numerical example 1.1. The difference is that the convergence of the shifting scalar λ∗ is worse for example 2. With the same number of reliability assessments, UDRM+MEM is more accurate than UDRM+Edgeworth, although the result of UDRM+Edgeworth is acceptable. However, although SORA gives the optimal solution in the CRDS among the reliability methods based on the MPP, the accuracy of the solution is the worst because the accuracies of the reliability methods are low.

Table 4 Summary of the optimization results for numerical example 2
Full size table

Figure 8a and b show the boundary of the constraint in the last cycle with the shifting scalars λ and λ*, respectively. There is an interesting phenomenon in which the shifting scalars λ∗ and λ of the SOMRA obtain the same results. The optimal design points are located at the intersection of the limit state surface of equivalent deterministic constraints g1 and g2. The equivalent deterministic constraints calculated by shifting scalar λ fit the CRDS better than those of shifting scalar λ∗. Unlike numerical example 1, the number of active constraints is equal to that of the design variables in example 2. That is, the optimal point is determined by the intersection of the limit state surface of the active equivalent deterministic constraints. The intersection converges to the optimal design point resulting from the gradient algorithm. However, oscillation occurs during the convergence process due to the low accuracy of the limit state surface calculated by shifting scalar λ∗, and the efficiency of optimization decreases. The convergence history of the objective function is depicted in Fig. 9.

Fig. 8
figure 8

Limit state functions of numerical example 2. a Shifting scalar λ in the last cycle. b Shifting scalar λ∗ in the last cycle (a and b are created with Origin9.0)

Full size image
Fig. 9
figure 9

Convergence history of the object of numerical example 2

Full size image

4.3 Speed reducer design

The speed reducer shown in Fig. 10 is used to rotate an engine and propeller with an efficient velocity in a lightweight plane (Lee and Lee 2005). This problem has 7 statistically independent random variables with normal distribution: gear width (X1), gear module (X2), number of pinion teeth (X3), distance between the bearings (X4, X5), and diameter of each shaft (X6, X7). There are 11 probabilistic constraints related to physical quantities, such as the bending stress, contact stress, longitudinal displacement, stress of the shaft, and geometry constraints. The objective function minimizes the total weight. The initial design point is selected as the result of deterministic optimization. The description of the RBDO model of the speed reducer is as follows:

Fig. 10
figure 10

A speed reducer

Full size image

For problems with multiple random design variables and multiple constraint optimizations, regardless of whether the methods of PDF estimation are based on MEM or Edgeworth, the convergence of the SOMRA is stable and accurate. As shown in Tables 5 and 6, all methods give similar results. As the number of random design variables increases, the advantage of the efficiency of the proposed SOMRA becomes more obvious. Moreover, the proposed SOMRA is more efficient than SORA. The proposed SOMRA has the same number of iterations but fewer reliability assessments, meaning that the active constraint checking is effective. With almost the same result, the PDF estimation method of Edgeworth series expansion is more likely to be chosen because the modeling process does not require equations to be solved. The convergence history of the objective function is depicted in Fig. 11. As the number of design variables increases, the efficiency improvement of the decoupled loop strategy becomes more obvious.

Table 5 Summary of the optimization results for the speed reducer problem
Full size table
Table 6 Evaluation of the probabilistic constraints of the speed reducer problem at an optimum by MCS
Full size table
Fig. 11
figure 11

Convergence history of the object of the speed reducer design

Full size image

4.4 Automobile crashworthiness lightweight design

The lightweight design of automobiles provides a promising way to reduce energy consumption, and RBDO can effectively solve the passive safety problem in lightweight vehicle design. A vehicle front impact model is considered (Jiang and Deng 2014. The five components of the vehicle front-end structure, namely, the crash box inner and outer plates, the front longitudinal beam inner and outer plates, and the front bumper, are closely related to the crashworthiness of vehicles. The thicknesses of these five components are treated as random design variables. The design objective is the total mass M of the five components. The constraints involve three crashworthiness indexes obtained in high-speed frontal collision analysis, in which the damage to the passenger must be controlled and a safe space should be ensured. Therefore, the mean integration acceleration of the left backseat a and the intrusion quantities of the upper and lower mark points of the engine, IU and IL, are required to be less than the given allowable values a0, \( {I}_0^U \), and \( {I}_0^L \), respectively. The RBDO problem is then formulated as follows:

$$ {\displaystyle \begin{array}{l}\boldsymbol{find}\kern2em \mathbf{d}={\left[{d}_1,{d}_2,{d}_3,{d}_4,{d}_5\right]}^T\\ {}\min \kern1.25em f\left(\mathbf{d}\right)=2.088{d}_1+\mathrm{0.4.4}{d}_2+0.22{d}_3+1.2{d}_4+0.887{d}_5\\ {}\begin{array}{l}\mathrm{s}.\mathrm{t}.\kern2em P\left({g}_i\left(\mathbf{X}\right)\le 0\right)\ge \varPhi \left({\beta}_i\right),i=1,\dots, 3\\ {}\boldsymbol{where}\kern0.75em \begin{array}{l}{g}_1\left(\mathbf{X}\right)={I}^U\left(\mathbf{X}\right)-{I}_0^U\\ {}{g}_2\left(\mathbf{X}\right)={I}^L\left(\mathbf{X}\right)-{I}_0^L\\ {}\begin{array}{l}{g}_3\left(\mathbf{X}\right)=a\left(\mathbf{X}\right)-{a}_0,\\ {}{a}_0=40g,{I}_0^U=270\ mm,{I}_0^L=180\ mm\\ {}\begin{array}{l}2.0\mathrm{mm}\le {d}_1\le 3.0\mathrm{mm},1.0\mathrm{mm}\le {d}_2\le 3.0\mathrm{mm},1.0\mathrm{mm}\le {d}_3\le 2.5\mathrm{mm},\\ {}1.5\mathrm{mm}\le {d}_4\le 3.0\mathrm{mm},1.5\mathrm{mm}\le {d}_5\le 3.0\mathrm{mm},\\ {}\begin{array}{l}{\beta}_1,{\beta}_2,{\beta}_3=2.0,{X}_i\sim N\left({d}_i,{0.005}^2\right),i=1,\dots, 5,\\ {}{d}^{(0)}=\left[\mathrm{2.2,2.2,2.2,2.2,2.2}\right]\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}} $$

A frontal impact finite element model (FEM) is established to obtain the results, as shown in Fig. 12. The surrogate models of the second-order polynomial response surface are created based on 65 FEM results to improve the efficiency, as shown in Table 7.

Fig. 12
figure 12

High-speed frontal collision. at = 0 s. bt = 0.1 s

Full size image
Table 7 Surrogate models for the performance functions in engineering applications
Full size table

After RBDO analysis, the results are shown in Table 8. RBDO based on the SOMRA gives reliable results, and the SOMRA significantly improves the efficiency in terms of the number of reliability assessments and constraint evaluations. In the SOMRA, Edgeworth and MEM converge to similar points; however, the Edgeworth converges in three cycles, while the MEM converges in four cycles. In this example, the PMA is replaced with the reliability index approach (RIA) because of non-convergence, and the RIA uses the iHL-RF algorithm to search the MPP. It is obvious that the method based on the MPP obtains the minimal value of the objective function, while the reliability index of the constraint g1 is 1.85, which violates the required reliability index. The convergence history of the objective function is depicted in Fig. 13.

Table 8 Summary of the optimization results for the lightweight design of automobile crashworthiness
Full size table
Fig. 13
figure 13

Convergence history of the object of automobile crashworthiness lightweight design

Full size image

5 Conclusion

In this paper, a SOMRA-based decoupled loop method is proposed to improve the accuracy and efficiency of RBDO. The innovations of the proposed SOMRA involve a new mathematical model for optimization iteration, a corresponding calculation method of the probabilistic constraint shifting scalar based on moment reliability analysis, and a local shifting modified factor utilized to correct the shifting scalar. Additionally, an inactive constraint checking criterion in terms of the statistical moments is proposed to further improve the efficiency of optimization. The applicability of SOMRA depends on that of the moment-based reliability assessment method, which distinguishes the SOMRA from the existing SORA class methods.

By optimizing three numerical examples and a practical application, the following conclusions can be drawn: (1) The SOMRA gives almost the same result as the DLM based on the same moment method, but with much higher efficiency. (2) The RBDO solution of the SOMRA in this paper is slightly more accurate than the SORA in terms of objective function and reliability index. (3) Without the modified factor for the shifting vector, the SORA behaves well except that the optimal design point is near the saddle point of the limit state surface of the performance function. The modified factor is necessary for the SOMRA, and it enables the SOMRA to perform well even though the optimal design point is around the saddle point. (4) MEM is more accurate than Edgeworth series expansion in the calculation of reliability based on the same statistical moments. The proposed method is an alternative to SORA when (i) the MPP is hard to identify, (ii) there are multiple MPPs, (iii) the probability is close to the median where FORM cannot provide accurate solutions, and (iv) the PDF or CDF is required. Thus, the proposed SOMRA has potential in the RBDO of complex products. However, the SOMRA has the potential to further improve the convergence consistency of design variables compared with SORA. The application of the SOMRA in reliability design involving multidisciplinary analysis will be explored in our future work.