Large-scale level set topology optimization for elasticity and heat conduction

Abstract

We present a numerical study of a new large-scale level set topology optimization (LSTO) method for engineering design. Large-scale LSTO suffers from challenges in both slow convergence and high memory consumption. We address these shortcomings by adopting the spatially adaptive and temporally dynamic Volumetric Dynamic B+ (VDB) tree data structure, open sourced as OpenVDB, which is tailored to minimize the computational cost and memory footprint by not carrying high fidelity data outside the narrow band. This enables an efficient level set topology optimization method and it is demonstrated on common types of heat conduction and structural design problems. A domain decomposition–based finite element method is used to compute the sensitivities. We implemented a typical state-of-the-art LSTO algorithm based on a dense grid data structure and used it as the reference for comparison. Our studies demonstrate the level set operations in the VDB algorithm to be up to an order of magnitude faster.

1 Introduction

Level set topology optimization (LSTO) (Allaire et al. 2004; Wang et al. 2003) is a popular method for topology optimization. It incorporates an implicit representation of the boundary, commonly as a signed distance function. The level set function is updated by solving the level set equation (LSE), Osher and Fedkiw (2006) dϕ/dt + V ⋅∇ϕ = 0, which is a type of a Hamilton-Jacobi equation (HJE) (Osher and Sethian 1988) where ϕ is the level set function, t is the pseudo time step, and V is the velocity of the boundary. The LSE, which is a hyperbolic partial differential equation that can be solved using upwind schemes (Osher and Fedkiw 2001), is essential to track the boundary accurately. Wang et al. (2003) applied the level set method (LSM) to structural topology optimization by means of mathematical programming. Allaire et al. (2004) used classical shape derivatives to demonstrate LSM for structural topology optimization. Xia et al. (2006) introduced a semi-Lagrangian method to solve the LSE for structural topology optimization problems. Wang and Wang (2006) used a multi-quadratic radial basis function to approximate the level set function, which is updated by transforming the LSE into a system of ordinary differential equations. Sivapuram et al. (2016) used the level set method to simultaneously optimize microstructure and macrostructure topologies.

Other topology optimization methods where the level set is updated using strategies that differ from the LSE can also be found in the literature. Such methods typically have the advantage of nucleating holes inside the structure during the optimization. Norato et al. (2007) proposed a topological derivative method for topology optimization of structural compliance minimization problems. Suresh and Takalloozadeh (2013) introduced a topological derivative method using level sets for stress constrained topology optimization problems. Xia et al. (2019) integrated the material removal scheme of the bi-directional evolutionary structural optimization method into a level set method to nucleate holes. Yamada et al. (2010) developed a level set–based topology optimization method where the level set is updated using the reaction-diffusion equation. Pingen et al. (2010) studied a parametric level set approach for flow topology optimization, where the level set function is parameterized using reduced order radial basis functions. However, in the above methods, the level set function needs to be defined everywhere in the domain, thus necessitating a dense grid for representing the level set function.

On the other hand, when the level set function ϕ is a signed distance function and ϕ is updated using the LSE, the LSM becomes strictly a boundary-based method where ϕ can be limited to a narrow band around the boundary. Therefore, sparse data structures can be used to allocate computational memory only in the narrow band of the boundary to represent the level set function. An example of a sparse data structure is a tree data structure such as an octree (Laine and Karras 2011). The octree data structures have been successfully applied to level set methods (Min 2004; Min and Gibou 2007; Mirzadeh et al. 2016). However, a fundamental problem with octrees is that they tend to introduce deep tree structures with slow access time, typically $\mathcal {O}(n)$, where n is the number of levels in the tree. Additionally, level set implementations on octrees typically require the tree to be graded, i.e., the difference in levels between any two neighboring tree nodes cannot exceed one. This reduces the sparseness of the tree and incurs significant memory overheads. An innovative sparse data structure which offers fast (on average constant) access time is the Volumetric Dynamic B+ (VDB) tree (Museth 2013). Additionally, VDB enables highly efficient multi-threaded algorithms and dynamically updates the tree structure as the level set interface evolves, leading to faster advection and reinitialization processes for large-scale simulations.

There is an increased interest in large-scale topology optimization as it can discover new designs that cannot be obtained with low mesh density (Aage et al. 2017). Several efforts have already been made using the level set method. Deng and Suresh (2017) presented stress constrained topology optimization of an exhaust system using over 314,000 elements. Zong et al. (2018) designed microstructures with desired mechanical properties for 3D printing using over 160,000 elements. Villanueva and Maute (2017) used 720,000 elements to optimize the topology of 3D laminar incompressible flow problems. In Pizzolato et al. (2017), Pizzolato et al. used 507,000 elements to optimize the topology of latent heat thermal energy storage devices. Yaji et al. (2014), used 512,000 elements to optimize the topology of flow channels to minimize flow friction. In Martínez-Frutos et al. (2019), Martínez-Frutos et al. used 2,500,000 elements to optimize the topology of an L-bracket under stress and porosity constraints. Notably, in the above level set methods, the finite element analysis (FEA) mesh and the level set grid coincide, thus making the level set grid a dense grid. Defining the level set function on a dense volumetric data structure can be a significant shortcoming in terms of convergence time for large-scale LSTO. This is due to the complex operations involved in updating the level set, e.g. re-building the narrow-band, re-computing distances, and performing the velocity extension. Therefore, state-of-the-art sparse data structures, such as VDB, can be used to significantly improve the convergence time in such large-scale LSTO problems.

However, using VDB for large-scale LSTO involving FEA meshes is not straight forward. There are still a few challenges that need to be addressed for the efficient use of VDB in LSTO. Specifically, the challenges involve developing efficient algorithms that help in (a) communicating boundary information between VDB to the FEA mesh, (b) extracting the sensitivity information from the FEA mesh elements to the boundary, and (c) optimizing and assigning optimum velocities of the boundary on the VDB level set grid.

In this paper, we address the various challenges that impede an efficient and fast large-scale LSTO method. Specifically, we demonstrate how efficient algorithms and data structures can significantly reduce the computational times of large-scale elasticity and heat conduction LSTO problems. To the best of our knowledge, the use of fast and sparse data structures such as VDB in LSTO has not been investigated. The use of VDB in large-scale LSTO is not straight forward; and we address this by developing efficient algorithms. OpenVDB, an open-source implementation of the VDB data structure, is used in this study. A parallel FEA solver (Aage et al. 2015) is used to compute the sensitivities. For the sake of comparison, we implemented a typical state-of-the-art in-house LSTO algorithm based on a dense grid data structure popularly used in LSTO. This in-house algorithm is used as reference. The LSTO methods are used to minimize structural compliance and thermal compliance of the domain subject to a volume constraint. The benefits of using VDB-LSTO, in terms of computational time taken by the level set operations are presented. Our investigation reveals that the level set operations in VDB-LSTO are up to an order of magnitude faster than the reference algorithm. Using the VDB-LSTO method, we are able to explore large-scale design spaces using meshes with over 100 million degrees of freedom.

2 Level set topology optimization

In this section, we describe the implementation details of the reference LSTO and VDB-LSTO. The reference level set method is developed using current state-of-the-art algorithms popularly used in LSTO. In typical LSTO, the boundary of a structure or material is represented by an implicit function ϕ(x) (referred to as the level set function) and defined as

$$ \begin{array}{@{}rcl@{}} \phi(x)&>& 0, \ x \notin \varOmega\\ \phi(x) &=& 0, \ x \in \varGamma\\ \phi(x) &<& 0, \ x \in \varOmega \end{array} $$

(1)

where Ω is the domain, i.e., material, and Γ is the domain boundary, i.e., material surface. The level set function is updated by solving the following scalar level set equation:

$$ \frac{d\phi}{dt} + V_{n} | \nabla \phi | = 0 $$

(2)

where V_n is the scalar velocity in the normal direction of the boundary. In the computational algorithm, the values of ϕ are defined in a narrow band around the boundary surface.

The flowchart of our algorithm developed for both reference and VDB-LSTO is shown in Fig. 1. Our algorithm employs two separate grids: one to represent the level set function with a narrow bandwidth of six voxels and the other to conduct the FEA. The boundary is extracted from the level set function as a vector of polygons using mesh extraction algorithms (Section 2.3). The boundary points and classifications of each element that indicate whether it is inside, outside, or on the boundary are passed to the FEA mesh. The fractions of each element that are cut by the level set are computed as a vector of volume fractions (Section 2.4). The FEA and sensitivity analysis (Section 3) compute the boundary point sensitivities. The optimum velocities of the boundary points are calculated using the boundary point sensitivities and mathematical programming and are passed to the level set grid (Section 2.5). The level set is updated based on the boundary point velocities by extending the velocities into the narrow band followed by a numerical solution of the LSE (Section 2.6).

Fig. 1

A flowchart of the level set topology optimization method developed for both reference and VDB

2.1 Problem definition

In this section, we present the general problem statement of LSTO. The objective is to solve the following optimization problem

$$ \begin{array}{@{}rcl@{}} {\min} \ f &=& {\int}_{\varOmega} F(\varOmega) d\varOmega \\ \text{s.t.} \ \ \ g_{j} &=& {\int}_{\varOmega} G_{j}(\varOmega) d\varOmega \leq {g_{j}^{0}} \ \ \ j = 1,2,...,N_{g}, \end{array} $$

(3)

where f is the objective function, g_j is the j th constraint function, ${g_{j}^{0}}$ is the j th constraint value, and N_g is the number of constraints. f is also the integral of the integrand F(Ω), and g_j is the integral of the integrand G_j(Ω). In this study, the compliance (structural or thermal) is used as the objective function, and the sensitivities are computed using the finite element method (described in the following sections).

2.2 Data structure

We first describe a dense data structure, which is typical of the existing level set topology optimization methods. This dense grid algorithm is used as the reference LSTO method for comparison with the sparse VDB-LSTO algorithm. For a given grid which is discretized into n_x × n_y × n_z cells, computational memory is allocated for a total of (n_x + 1) × (n_y + 1) × (n_z + 1) nodes in an array, with each node containing information about its level set function ϕ value.

In contrast, VDB-LSTO uses a sparse data structure to represent the boundary interface. An illustration of the VDB data structure (Museth 2013) used for representing the narrow-band signed distance of a circle shown on the left-hand side of Fig. 2. The signed distance function of the circle (radius = r, center at the origin) is defined as $\phi (x,y) = \text {sign}(x^{2} + y^{2} - r^{2}) \sqrt { | x^{2} + y^{2} - r^{2} |}$. On the right-hand side, the hierarchical data structure shows the domain with two levels of internal nodes (green and orange squares), leaf nodes (blue), and active voxels (red). The level set function values are only stored for voxels in a narrow band around the boundary (the voxels in red), thus demonstrating the sparsity of the data structure.

Fig. 2

Description of data structure used in OpenVDB (Museth 2013). On the left-hand side, the level set function of the circle is shown. On the right-hand, the hierarchy of the data structure for representing the circle—with two levels of internal nodes (green and orange squares), leaf nodes (blue), and active voxels (red)— is shown. The level set function values are only stored for the voxels in red, thus demonstrating the sparsity of the data structure

2.3 Mesh extraction

In our LSTO algorithm, the sensitivities are computed on the boundary. For this purpose, the zero level set is discretized into a polygon surface mesh. For the reference LSTO method, the Marching Cubes algorithm is used to compute the surface mesh (Lorensen and Cline 1987). This algorithm visits each voxel, and identifies the edges of the element that are intersected by the level set using an edge table. Based on these edges, the algorithm produces a set of triangular faces from a static case table, which lies on the surface using a triangle table. The resulting representation of the level set surface is a triangular mesh, made up of a list of faces and corresponding vertices. The Marching Cubes algorithm is a simple-to-implement algorithm that is a popular state-of-the-art method in topology optimization for mesh extraction (Nobel-Jørgensen et al. 2015; Martínez-Frutos and Herrero-Pérez 2017; Dai et al. 2017; Nguyen and Kim 2019).

VDB-LSTO, on the other hand, employs Dual Marching Cubes (Nielson 2004), which is a faster and more robust meshing algorithm that produces fewer polygons of higher quality. The result is a compact quad mesh of much higher quality than the triangle mesh produced by the Marching Cubes algorithm. Specifically, for a given level set function represented on a VDB data structure, we use OpenVDB’s volumeToMesh function for the mesh extraction. The resulting boundary mesh is a vector of quadrilaterals and a vector of the boundary vertices of each quadrilateral.

2.4 Volume fraction calculation

The volume fractions v, which are the fractions of each element that are cut by the level set, are computed as the boundary is dynamically evolving. These volume fractions communicate whether or not a particular element is inside, outside, or on the boundary to the FEA mesh. The volume fraction of an element n is computed by the following equation:

$$ v(n) = {\int}_{\varOmega_{n}} H(\phi) d \varOmega $$

(4)

where Ω_n is the domain of the element n, and H is the Heaviside function. The above integral is computed numerically as follows:

$$ v(n) = \sum\limits_{i} \sum\limits_{j} \sum\limits_{k} \frac{H(\phi(x_{i} , y_{j}, z_{k}))}{n_{int}^{3}} $$

(5)

where n_int is the number of quadrature points used along each coordinate axis, and (x_i,y_j,z_k) are the quadrature points given by

$$ (x_{i}, y_{j}, z_{k}) = \left( \frac{i}{n_{\text{int}}+1}, \frac{j}{n_{\text{int}}+1} , \frac{k}{n_{\text{int}}+1}\right)\ ; i,j,k = 1,..,n_{\text{int}} $$

(6)

In the reference LSTO algorithm, threading is done over boundary points, and the volume fractions are modified for elements in the narrow band. The pseudo code for the volume fraction computation for the reference LSTO method is shown in Algorithm 1.

In VDB-LSTO, in order to efficiently compute the volume fractions of each element for a given VDB level set grid, we parallelize the algorithm over the leaf nodes of the VDB tree structure. Specifically, we use OpenVDB’s LeafManager to access the array of pointers to the data structure’s leaf nodes, which by construction are intersecting the narrow band. The fast access to the VDB’s leaf nodes can be exploited efficiently and the challenge of fast volume fraction calculation can be addressed. The array of pointers of the leaf nodes is broken down into smaller chunks and a computational thread is assigned to each chunk. Each computational thread visits the active voxels of the leaf nodes in its chunk and computes the volume fraction of the element. The pseudo code shown in Algorithm 2 illustrates the computation of a vector of volume fractions for a given VDB level set grid.

2.5 Optimization

In this section, we show the details of a fast algorithm that computes the optimal scalar velocity field V_n of the boundary using the method of Lagrangian multipliers (Arora 2007). Specifically, for a given polygon mesh of a level set function (which is computed using mesh extraction algorithms in Section 2.3) and boundary point sensitivities this algorithm computes the optimum velocities at the boundary points, for both reference and VDB-LSTO. The objective and constraint functions in (3) are linearized with the help of the sensitivities, and the optimum velocity field V_n,i for the reference LSTO and VDB-LSTO—which is required to advect the level set function ϕ—is computed by solving the following optimization problem (Dunning and Kim 2015):

$$ \begin{array}{@{}rcl@{}} \text{Minimize } \varDelta f = \sum ({f^{\prime}(P_{i})} A_{i} V_{n,i}) \varDelta t\\ \text{subject to } \varDelta g_{j}= \sum ({g_{j}^{\prime}(P_{i})} A_{i} V_{n,i}) \varDelta t \leq {g_{j}^{t}} \end{array} $$

(7)

where $f^{\prime }(P_{i})$ and $g_{j}^{\prime }(P_{i})$ are the sensitivities of the objective and constraint functions of the point P_i, V_n,i is the velocity of the point i in the normal direction, and A_i is the average area of all the polygons that have this current boundary point as a vertex, Δt = 1 is the pseudo time step, and ${g_{j}^{t}}$ is the target constraint for constraint j.

Equation (7) is solved using the method of Lagrangian multipliers. The steepest descent normal vector is given in terms of the Lagrangian multipliers as

$$ \bar{z}_{i} = V_{n,i} \varDelta t = \frac{{f^{\prime}(P)}_{i} + {\sum}_{j} \bar{\lambda}_{g,j}{g^{\prime}(P)}_{i} } {\Vert {f^{\prime}(P)} + {\sum}_{j} \bar{\lambda}_{g,j}{g^{\prime}(P)} \Vert} $$

(8)

where $\bar {\lambda }_{g,j}$ are the Lagrange multipliers, and $\bar {z}_{i}$ is the steepest descent direction of the boundary point P_i. The above equation is multiplied by a constant yielding the following descent vector without loss of generality:

$$ \hat{z}_{i} = \lambda_{f}{f^{\prime}(P)}_{i} + \sum\limits_{j} \lambda_{g,j}{g^{\prime}(P)}_{i} $$

(9)

where λ_f and λ_g,j are the unknown parameters describing the descent direction. The descent vector given by the above equation is capped between upper and lower bounds l_i and u_i as

$$ z_{i} = \min(\max(\hat{z}_{i},l_{i}) , u_{i}) $$

(10)

where z_i represents the capped descent. The upper and lower bounds are determined by the maximum allowable displacement of a boundary point, usually dictated by the Courant–Friedrichs–Lewy (CFL) condition (Courant et al. 1967). The optimization problem is now restated by substituting (9) and (10) into the constraint functions in (7) as follows:

$$ \begin{array}{@{}rcl@{}} &\text{Find} \ \lambda_{f} \ \text{and} \ \lambda_{g,j} \ \text{which} \\ &\text{minimize } \varDelta f = \sum ({f^{\prime}(P)}_{i} A_{i} V_{n,i}) \varDelta t,\\ \text{s.t.} \ \varDelta g_{j} &= \sum {g_{j}^{\prime}(P)}_{i} A_{i} (\min(\max(\lambda_{f} {f^{\prime}(P)}_{i}+ {\sum}_{j}\lambda_{g,j} {g_{j}^{\prime}(P)}_{i},l_{i}) , u_{i})) \leq{g_{j}^{t}}\\ \end{array} $$

(11)

Equation (11) is solved for λ_f and λ_g,j using the Newton-Raphson method. Finally, the optimum velocities are given by

$$ V_{i} = \min\left( \max(\lambda_{f} {f^{\prime}(P)}_{i} + \sum\limits_{j}\lambda_{g,j} {g_{j}^{\prime}(P)}_{i},l_{i}) , u_{i} \right) $$

(12)

2.6 Advection

The level set function is updated by solving the scalar level set (2). For the reference LSTO algorithm, the boundary point velocities are extended into the grid points within the narrow band using the Fast Marching Method (FMM). In the FMM, the grid point velocities are computed in ascending order of the level set function, which means that the level set function needs to be sorted by its value for every iteration. The FMM is a popular state-of-the-art algorithm used in topology optimization for velocity extension and advection (Xia et al. 2012; Xia and Shi 2015; Liu et al. 2016; Dunning and Kim 2015). The level set function is discretized in time using the first-order forward Euler method. The gradient of the level set function is calculated using the optimally fifth-order Hamilton-Jacobian Weighted Essentially Non-Oscillatory scheme (HJ-WENO (Osher and Fedkiw 2001)).

For the VDB-LSTO, the boundary velocities computed at the boundary vertices of the quadrilaterals (which are computed using mesh extraction algorithms in Section 2.3), are extended to the narrow-band grid points using the fast sweeping method (FSM) for sparse grids. The implementation details of the fast sweeping method can be found in Museth (2017). The FSM does not maintain a minimum heap data structure (as FMM) but instead performs multiple sweeps of all the grid points which can be performed concurrently resulting in much better computational performance than the FMM. The first-order forward Euler method is used to discretize the level set function in time, and spatial gradients are also computed using optimally fifth-order HJ-WENO.

3 Finite element analysis

This section presents the numerical scheme for the finite element method and sensitivity computation employed for the large-scale LSTO investigation for both VDB-LSTO and the reference LSTO. We employed an open-source FEA library (Aage et al. 2015), which was developed for large-scale SIMP based topology optimization methods (https://github.com/topopt/TopOpt_in_PETSc). This library uses the Message Passing Interface (MPI) (Gropp et al. 1999) and PETSc (Balay et al. 2017) for distributing the computational memory and workload over several processors. The FEA library decomposes the mesh into any given number of partitions specified by the user, and assigns each partition to a specific processor by default, while the topological details of the structure (e.g. the level set function) are stored in a separate processor. Eight-node hexahedral elements are used for the FEA. The details of the way LSTO computes sensitivities using the FEA is discussed here.

3.1 Finite element method using domain decomposition

As an illustrative example, a schematic of a simple 2D topology of a structure and the corresponding FEA mesh, simulated on a total of 9 processors (MPI ranks) is shown in Fig. 3. The topology of the structure represented by the level set is stored on Processor 0 (Fig. 3a). The FEA mesh used is split into 8 partitions, and each partition is assigned to Processor 1 to 8 (Fig. 3b). The volume fraction v_f (Section 2.4) of an element, computed by Processor 0, is passed on to the appropriate processor corresponding to the FEA mesh of the particular element (shown using the green arrow in Fig. 3). This is accomplished by the MPI_Scatter subroutine (Gropp et al. 1999).

Fig. 3

An illustration of mesh decomposition for distributed FEA. The level set function is stored on processor 0. The elemental volume fractions computed on processor 0 are passed on to the appropriate processor (shown using the green arrow). The sensitivity information computed by each element is passed on to the level set function cell (shown using the orange arrow)

Based on the volume fraction information, the elemental stiffness matrix K_e is constructed for each element by the appropriate processor using the following equation:

$$ K_{e} = (\alpha_{\min} + v_{f}(\alpha_{\max} - \alpha_{\min}) ){K_{e}^{0}} , $$

(13)

where α is the elasticity modulus (conductivity coefficient). $\alpha _{\max \limits }$ and $\alpha _{\min \limits }$ are the values of α for the solid material (v_f = 1) and void material (v_f = 0). ${K_{e}^{0}}$, which is a constant elemental stiffness matrix independent of the topology), is computed for α = 1 for a linear 8-noded brick element using piecewise linear shape functions. The global stiffness matrix K is then assembled from the elemental stiffness matrices.

The generalized minimum residual (GMRES) method is used with a multigrid preconditioner (Amir et al. 2014) to solve the linear system of equations

$$ K U = F $$

(14)

where U and F are the displacement (temperature) and force (heat) vectors. The state variable U at a mesh node is stored in the processor that owns the node. Therefore, U is distributed across all processors. This is followed by computing the centroid sensitivities of each element by its corresponding processor.

3.2 Boundary sensitivity interpolation

In this section, we describe a fast algorithm that computes the sensitivity at the boundary point from the element centroid sensitivities. The boundary points are stored on Processor 0, but the centroid sensitivities are distributed across all processors. Therefore, to speed up the computation of boundary sensitivities, the centroid sensitivities of all the elements are gathered on to processor 0. This is accomplished by the MPI_gather subroutine (Gropp et al. 1999), where the centroid sensitivities of all the elements from all the processors are copied on processor 0. For instance, the sensitivity of the element owned by processor 8 in Fig. 3b is passed on to the appropriate location of the level set cell on processor 0.

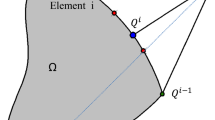
The sensitivity $f^{\prime }(P)$ of a boundary point P is interpolated based on the neighboring element centroid sensitivities, centroid coordinates, and volume fraction of the elements inside a support radius (Dunning et al. 2011). The computation is done on processor 0, since it has access to the gathered centroid sensitivities. Figure 4 shows a schematic of a boundary point of interest and its surrounding elements. For this boundary point, all the elements which lie inside a support radius (shown in red) are collected. Based on the sensitivity and the volume fraction of the collected elements, a polynomial function is fitted to compute the boundary sensitivity of the point.

Fig. 4

Interpolation of boundary sensitivities based on elemental centroid sensitivities

The pseudo code shown in Algorithm 3 illustrates the algorithm for collecting the neighboring centroid locations and sensitivities of a boundary point P_n = (p_x, p_y,p_z) inside a support radius SupRad.

The function ComputeBoundarySensitivities() shown in Algorithm 4 computes the boundary sensitivities $f^{\prime }(P_{n})$ of a point P_n from the neighboring element centroid sensitivity information. For each boundary point P_n, the following curve is fitted:

$$ f^{\prime}(P_{n}) = a_{0} + a_{x}(x - p_{x}) + a_{y}(y - p_{y}) + a_{z}(z - p_{z}) $$

(15)

where $f^{\prime }(P_{n})$ is the sensitivity of the boundary point, and a_x, a_y, and a_z are the coefficients, and a₀ is the intercept. The weighted least squares interpolation is used to fit the curve by visiting all the sample points for each boundary point and forming the following matrices:

$$ \begin{array}{@{}rcl@{}} A[n,1] &=& 1 ; A[n,2] = (p_{x} - x_{n}) ; \\ A[n,3] &=& (p_{y} - y_{n}) ; A[n,4] = (p_{z} - z_{n}) \\ B[n] &=& f^{\prime}(P_{n}) ; W[n,n] = w_{n} ; n = 1,...,n_{s} \end{array} $$

(16)

where n_s is the number of sample points in the collection, B is the sensitivity matrix, A is the coefficient matrix, and W a diagonal matrix containing the weights, given by

$$ w_{n} = v(n)/d(n)^{2} $$

(17)

where v(n) is the volume fraction of sample element n, and d(n) is the distance between the boundary point and the centroid of the sample element n. The interpolation can be now stated in the following matrix equations:

$$ W A X = W B $$

(18)

where X = [a₀,a_x,a_y,a_z]^T is the matrix containing the coefficients and the intercept. The least squares solution to (18) is given by

$$ X = inv[(WA)^{T}(WA)] (WA)^{T} W B $$

(19)

4 Numerical investigations

We investigate the numerical performance of VDB-LSTO by comparing it with the reference LSTO method for compliance minimization problems under a volume constraint. The computations are performed on the Texas Advanced Supercomputer Center (TACC) cluster (www.tacc.utexas.edu) where each node is equipped with 64 GB RAM and a Xeon E5-2690 v3 processor with 24 cores.

4.1 Michell sphere

The first example is a linear elastic topology optimization problem under torsion, known as the Michell sphere (Aage et al. 2015). Figure 5 shows the design domain, discretized into (n_x,n_y,n_z) elements in x,y,z directions, respectively. The structure is fixed on four nodes (0 , n_y/2 ± 1, n_z/2 ± 1) on the left-hand side, while unit forces corresponding to a torque are applied on the right-hand side at nodes (n_x, n_y/2 ± 1, n_z/2 ± 1). The FEA mesh is discretized into 160 × 192 × 192 = 5.9 million elements, using 160 processors (MPI ranks). The volume constraint used is 3% and the elasticity modulus is set to unity.

Fig. 5

Design domain (1.0 × 1.2 × 1.2) and boundary conditions for the Michell sphere

The initial topology is a hollow sphere of volume 10% of the domain (Fig. 6a). The optimized topology obtained using the reference LSTO is shown in Fig. 6b, while the optimized topology obtained using VDB-LSTO is shown in Fig. 6c. Figure 6b and c show that the optimum topologies represent truss-like structures on the surface of a sphere, similar to the results presented in Aage et al. (2015) and Lewiński (2004). The optimized compliance for the reference LSTO and VDB-LSTO are 2043.67 and 2041.36, respectively. From Fig. 6b and c, we can see that the optimum topologies of the reference LSTO and VDB-LSTO are similar, with a difference in their optimum compliance equal to 0.1%.

Fig. 6

a Initial topology for the Michell sphere. b Optimized topology using reference LSTO and 5.9 million elements for a volume constraint = 3%. c Optimized topology using VDB-LSTO and 5.9 million elements for a volume constraint = 3%. d Optimized topology using VDB-LSTO and 19.9 million elements for a volume constraint = 1%

Figure 7 shows the average time breakdown of the VDB-LSTO algorithm in comparison with the reference LSTO algorithm. From Fig. 7 we can see that VDB-LSTO is consistently faster than the reference LSTO. The mesh extraction time for VDB-LSTO (which uses dual marching cubes) is less than the reference algorithm (which uses marching cubes). This clearly shows the efficiency of the multi-threaded dual marching cubes method, which produces quadrilaterals of a higher quality than the marching cubes method. The volume fraction computation time for VDB-LSTO (0.52 s) is less than the time taken for the reference LSTO (0.66 s). In other words, the threading done over the leaf nodes in VDB-LSTO to compute volume fractions outperforms the threading done over the boundary points in the reference LSTO. The FEA solver time (the time history shown in Fig. 8) is the bottleneck for both of the algorithms—with an average of 11.42 s for VDB-LSTO and an average of 12.35 s for the reference LSTO. The solver time is high at the beginning (greater than 30 s) and then it drops significantly as the solution U for a given iteration is used as a starting point for computing the solution of the next iteration. The solution time is also strongly dependent on the condition number of the stiffness matrix. The time taken by the boundary sensitivity interpolation is significantly small for both the algorithms (under 0.1 s), while the time taken for optimization is 0.95 s for VDB-LSTO and 1.15 s for the reference LSTO. More importantly, we show the advection time savings achieved by VDB-LSTO. The advection procedure comprises velocity extension and level set update. The level set update is an embarrassingly parallel algorithm; and it only constituted approximately 2–4 % of the total advection time, while the rest of the time cost is due to velocity extension. The average time taken for advection for the reference LSTO is slow (approximately 9.5 seconds) relative to the time taken by advection using VDB-LSTO, which is less than 1 second. As such, we conclude that for this case VDB-LSTO advection is an order of magnitude faster than the reference advection.

Fig. 7

Average time (in seconds) breakdown of the VDB-LSTO and reference LSTO methods for the Michell sphere (mesh size of 160 × 192 × 192 = 5.9 million elements, using 160 processors (MPI ranks).) a Mesh extraction, where the level set is discretized into a surface mesh. b Volume fraction calculations, where the fraction of the element cut by the level set is computed. c FEA to solve the linear system of equations. d Boundary sensitivity interpolation, where the boundary point sensitivities are interpolated from element centroid sensitivities. e Optimization where the optimum velocity of the boundary is computed. f Advection, where the level set is updated using the LSE

Fig. 8

Time taken by FEA solver for reference LSTO and VDB-LSTO

Furthermore, the time taken for volume fraction calculation, boundary sensitivity interpolation, and optimization for VDB-LSTO is significantly smaller than the FEA solver time, thus addressing the challenges and demonstrating the efficiency of the developed algorithms for applying VDB in such large-scale LSTO problems.

In Table 1, we show the average time breakdown, as a percentage of the average iteration time for the VDB-LSTO and reference LSTO algorithms. From Table 1, we can see that the advection time for the reference LSTO is approximately 39% of the total iteration time, while the VDB-LSTO advection time is approximately 3.9% of the total iteration time. Additionally, for the reference LSTO, the FEA takes up 51.2 % of the time, while the level set operations (mesh extraction and advection) take up 40.9% of the iteration time. On the other hand, for VDB-LSTO, the FEA takes up 84.3% of the iteration time, while the level set operations (mesh extraction and advection) take up only 4.3% of the iteration time.

Table 1 Average time breakdown as a percentage of average iteration time for the Michell sphere for VDB-LSTO and reference LSTO, for a mesh size of 160 × 192 × 192 = 5.9 million elements, using 160 processors

Figure 6d shows the optimum topology obtained with VDB-LSTO, using a finer mesh of 240 × 288 × 288 = 19.9 million elements on 360 processors (MPI ranks), with a volume constraint of 1%. The topology converged in 200 iterations and in 2 hours, with the FEA solver taking approximately 89% of the total iteration time and the level set operations (mesh extraction and advection) taking 3.5% of the time. For this high resolution of the FEA mesh, we can obtain topologies with a volume constraint as low as 1%, which is not possible using the previous mesh of 5.9 million elements. Therefore, we can conclude that we can explore large design spaces with VDB-LSTO, and it significantly reduces the time taken by the level set related operations for high-resolution meshes.

4.1.1 Usage of the active stiffness matrix

For cases where the volume fraction is relatively small, such as 0.1, the FEA simulation can be performed in a memory-efficient way by ignoring the void elements, i.e, the elements which are completely outside the structure when assembling the stiffness matrix. We achieve this by treating the nodes which are surrounded by void elements as homogeneous Dirichlet boundary condition nodes with their DOFs set to 0. The resulting stiffness matrix, the active stiffness matrix (ASM) which only takes into account the active DOFs of all the elements inside the domain, has a reduced size compared to the regular stiffness matrix, therefore consuming less memory.

For example, consider the topology of a 2d torus discretized using a 20 × 20 FEA mesh as shown in Fig. 9. The red circles represent all the nodes that are active, i.e, the nodes that have at least one element that lies inside the torus. These nodes are included while assembling the ASM. All the other nodes are surrounded by void elements, and they are not included while assembling the ASM as they have negligible contribution towards the FEA.

The ASM method is used in VDB-LSTO for computing sensitivities so as to illustrate the reduction in the memory consumed by the stiffness matrix. Figure 10 shows the average FEA time taken and the number of assembled elements of the ASM method for the Michell sphere problem for a mesh size of 160 × 192 × 192 = 5.8 million elements. For the sake of comparison, we also show the average FEA time and number of elements assembled for the regular stiffness matrix method. For this mesh size, the regular stiffness matrix has all the elements in the FEA mesh assembled, while the ASM has only assembled the active 2.2 million elements (88% reduction in size and computational memory). However, the multigrid preconditioner used previously for the regular stiffness matrix, cannot be used for the ASM, as its size and structure change for as the design changes. Consequently, the average FEA solver time for the ASM method is 104.35 seconds, compared to 11.42 seconds for the multigrid preconditioner method using the regular stiffness matrix. In conclusion, the ASM method can be used to compute FEA sensitivities for topologies with low volume fractions when computational resources required for the multigrid-GMRES method are unavailable, albeit at an increased computational time.

Fig. 9

A schematic of a topology of a torus with a background FEA mesh. The elements that are outside the torus do not contribute to the stiffness matrix and hence their nodes are passive and can be ignored while assembling the stiffness matrix. The active stiffness matrix (ASM) can then be constructed using the active nodes

Fig. 10

The average FEA time taken and number of assembled elements of the ASM method and the regular stiffness matrix method for the Michell sphere problem for a mesh size of 160 × 192 × 192 = 5.8 million elements

4.2 Bridge

The design domain used for the bridge topology optimization is shown in Fig. 11. The structure is pinned at the bottom sides, and a uniform pressure load is applied on the top. Due to symmetry, only half of the domain is modeled. The volume constraint used is 12% and the elastic modulus is set to unity. The FEA mesh is discretized into 320 × 160 × 160 = 8.2 million elements, using 160 processors (MPI ranks). The geometry of the initial structure is a cuboid covering the entire domain. The optimized topology obtained using VDB-LSTO of the pinned-pinned bridge problem is shown in Fig. 12. Fine structures that transfer the load from the top of the domain to an arch-like structure can be seen in Fig. 12.

Fig. 11

Design domain (4.0 × 1.0 × 1.0 ) for the pinned-pinned bridge topology optimization problem with a distributed load on top

Fig. 12

Optimized topology of the obtained using VDB-LSTO using 8.2 million elements

Figure 13 shows the average time breakdown of the VDB-LSTO and reference LSTO algorithms. From Fig. 13, we can see that the FEA solver time is high (over 80 s) for both algorithms. As a result, the time taken for mesh extraction time, volume fraction computation, and boundary sensitivity interpolation and optimization is almost negligible compared to FEA for both LSTO algorithms. The time taken by advection is significant for the reference method (over 12 seconds), while the advection time is under 2 seconds for VDB-LSTO.

Fig. 13

Average time breakdown of the VDB-LSTO and reference LSTO methods for the bridge example (mesh size of 320 × 160 × 160 = 8.2 million elements, using 160 processors (MPI ranks)

The FEA solver time is shown in Fig. 14, where we can see that for the first few iterations, the FEA solver time is approximately 25 s, and the FEA solver time ranges from 50 to 100 s for most of the iterations.

Fig. 14

Time taken by FEA solver for reference LSTO and VDB-LSTO for the bridge problem

In Table 2, we show the average time breakdown of different parts of the algorithm. The average time is shown as a percentage of average iteration time for both of the algorithms. We can see that the time taken by the FEA solver is the bottleneck for both of the algorithms—96.6% for VDB-LSTO and 84.6% for the reference LSTO. However, the time taken by the level set operations (mesh extraction and advection) is 13.2%, while it is only 1.6% of the time for VDB-LSTO. Therefore, we can conclude that VDB-LSTO improves the level set operations by approximately an order of magnitude.

Table 2 Average time breakdown for the VDB-LSTO and reference LSTO, as a percentage of average iteration time for the bridge problem discretized using 8.2 million elements

In Fig. 15a, the optimum topology obtained using a dense mesh (512 × 256 × 256 = 34 million elements and 100 million degrees of freedom) is shown. Figure 15b visualizes the VDB tree data structure for the bridge. The green and orange boxes on the left represent the internal nodes, while the blue boxes represent the leaf nodes—showing the hierarchy of the VDB data structure. The active voxels that store the level set function values are the voxels that are in close proximity to the boundary. Comparing Figs. 12 and 15, we can see that the optimum structure has finer features for the higher resolution mesh.

Fig. 15

a Optimized topology of the obtained using VDB-LSTO using 34 million elements. b Visualization of the VDB data structure as a wireframe for representing the bridge. The green and orange boxes on the left represent the internal nodes, while the blue boxes represent the leaf nodes. The picture on the right shows the active voxels that store the level set function values

Table 3 shows the computational memory consumption for the FEA mesh and the VDB level set grid for different mesh sizes. For a mesh resolution of 512 × 256 × 256 elements, the memory required by the FEA mesh is over 208 GB, while the memory used by the level set grid function on the VDB grid is only 0.72 GB. Furthermore, we can see from Table 3 that the ratio between the FEA mesh memory and VDB level set function memory increases with the mesh resolution. This investigation shows that the memory consumed by the VDB level set function is insignificant compared to the memory consumed by the FEA mesh.

Table 3 Memory consumed by the FEA mesh and VDB level set grid for different mesh sizes, and the ratio of FEA mesh memory to VDB level set grid memory

The memory consumed by the level set function approximately scales with the surface area. This means that, on a log-log scale, the slope of a graph plotting the memory footprint as a function of the number of elements should be approximately 2/3. Such a relationship between memory footprint of VDB and the number of elements was shown for a geometry-based optimization in Kambampati et al. (2018), where detailed studies on the scaling of VDB memory with problem size are presented. In Fig. 16, we show the memory used by VDB and the number of elements on a log-log scale. The slope of the curve is approximately 0.61, which supports the dependency of VDB on the surface area, thus validating the sparseness of VDB.

Fig. 16

Memory (in GB) consumed by VDB level set function versus number of elements N_e (in millions)

4.3 Heat conduction

A cubic domain of dimension D, with unit heat being produced everywhere in the domain with adiabatic walls and a heat sink (0.1D × 0.1D) located on one of the walls of the cube, is shown in Fig. 17. The geometry of the initial structure for optimization is a cube covering the entire domain, and the volume constraint V₀ is 30 %.

Fig. 17

The design domain of a cube (1 × 1 × 1) with adiabatic walls and unit heat being produced everywhere in the domain

Figure 18 shows the optimized topology obtained using VDB-LSTO for the conductivity coefficient $k_{\min \limits } = 0.01$ and $k_{\max \limits } = 1.0$ for an FEA mesh size of 200 × 200 × 200 = 8 million elements on 48 processors (MPI ranks). The topology features a number of fine structures that emanate from the heat sink that spread out through the domain – conducting heat from different parts of the domain into the heat sink.

Fig. 18

Final topologies obtained using VDB-LSTO with an FEA mesh size of 200 × 200 × 200 = 8 million elements for $k_{\min \limits } = 0.01$ and $k_{\max \limits } = 1.0$

Figure 19 shows the average time breakdown for different parts of the VDB-LSTO and reference LSTO algorithms. From Fig. 19, we see that the time taken for the FEA solver is the computational bottleneck. The mean FEA solve time for the reference LSTO is 25.1 s, while the mean solve time for VDB-LSTO is 26.2 s. The time taken by mesh extraction, volume fraction computation, boundary sensitivity interpolation, and optimization is substantially lower than the time taken for FEA solver—for both the reference LSTO and VDB-LSTO algorithms. In addition, similar to the Michell sphere and bridge examples, the times taken by the VDB-LSTO for mesh extraction, volume fraction computation, and optimization are less than those taken by the reference LSTO. Furthermore, the time taken for advection is significant for the reference LSTO (about 10 seconds per iteration), whereas the advection time for the VDB-LSTO is an order of magnitude smaller (1 second per iteration).

Fig. 19

Average time breakdown of the VDB-LSTO and reference LSTO methods for the heat conduction problem (mesh size of 200 × 200 × 200 = 8 million elements, using 48 processors)

Table 4, shows the average time taken by different parts of the VDB-LSTO and reference LSTO algorithms as a percentage of the total iteration time. From Table 4, we can see that the percentage of time taken by the FEA solver is over 90% for VDB-LSTO, while percentage time taken by the FEA solver is 58.7% for the reference LSTO. More importantly, the time taken by the level set operations (mesh extraction and advection) for the reference LSTO is approximately 35.5%, while the time taken by the level set operations for VDB-LSTO is reduced to 4%.

Table 4 Average time breakdown as a percentage of average iteration time for the heat conduction example (8 million elements, $k_{\min \limits } = 1.0$, $k_{\max \limits }= 0.01$)

Figure 20 shows the optimum topologies obtained for the same mesh resolution (200 × 200 × 200 = 8 million elements) but for different ratios of conductivity coefficients. Specifically, the optimum topologies obtained for conductivity coefficients of $(k_{\min \limits }, k_{\max \limits }) = (1 , 0.001)$ and $(k_{\min \limits }, k_{\max \limits }) = (1 , 0.05)$ are shown in Fig. 20a and b, respectively. Interestingly, from Fig. 20, we can see that the optimum topology is clearly dependent on the ratio of $k_{\min \limits }$ to $k_{\max \limits }$. Also, for values of the ratio ($k_{\min \limits }$ / $k_{\max \limits }$ = 0.001), we can see that the optimum solution has smaller and slender features, while for higher values of this ratio ($k_{\min \limits }$ / $k_{\max \limits }$ = 0.05), the optimum solution produces bulkier features.

Fig. 20

Final topologies obtained using VDB-LSTO with an FEA mesh size of 200 × 200 × 200 = 8 million voxels. (a) $k_{\min \limits } = 0.001$ and $k_{\max \limits } = 1.0$. (b) $k_{\min \limits } = 0.05$ and $k_{\max \limits } = 1.0$

The optimum topology obtained by VDB-LSTO using a higher resolution mesh—320 × 320 × 320 = 32.768 million elements (33.076 million DOFs)—and 160 processors (ranks), for $k_{\min \limits } = 0.01$ and $k_{\max \limits } = 1.0$ is shown in Fig. 21. For this resolution, the FEA solver takes 86% of the time while the time taken by level set operations is approximately 5%. Comparing Figs. 18 and 21, we can see that the the higher resolution topology in Fig. 21 offers a more optimum solution compared to the lower resolution solution in Fig. 18. Thus, it is demonstrated that VDB-LSTO increases the possible design space that can be searched and can find a better solution.

Fig. 21

Final topology obtained using VDB-LSTO with an FEA mesh size of 360 × 360 × 360 = 32.768 million elements

5 Conclusions

A new level set topology optimization algorithm using a sparse hierarchical data structure (VDB) is introduced and demonstrated by solving large-scale structural and heat conduction problems using meshes with over 100 million degrees of freedom. OpenVDB, which is an open-source implementation of the VDB data structure, is used in this study. A reference LSTO method, based on a dense grid, is also developed using multi-threaded algorithms for a fair comparison with VDB-LSTO. An open-source FEA library, which uses domain decomposition methods to distribute the FEA mesh and workload to a given number of processors (MPI ranks) is used to compute the sensitivities. The challenges of efficiently applying VDB for large-scale LSTO are addressed by constructing new fast algorithms for communicating between the level set grid and FEA mesh for optimization.

The efficiency of the VDB-LSTO algorithm is shown for three large-scale FEA based examples. The level set operations in the VDB-LSTO algorithm are significantly faster (an order of magnitude reduction in most cases) than the reference LSTO. Specifically, the level set advection time for the reference LSTO is substantial—it takes approximately 9 to 12 seconds for the problems considered while the advection time for VDB-LSTO is under 2 seconds. Additionally, for the VDB-LSTO algorithm, the overall computational bottleneck is the FEA solver, which takes 90–95% of the total time while the level set related operations take less than 5% of the total time. We believe that the observed performance gain of the VDB-LSTO algorithm over the reference LSTO algorithm, is due to better cache reuse (due to VDBs blocking) more efficient multi-threading, improved choices of the algorithms (e.g. fast sweeping over fast marching and dual marching cubes over marching cubes), and the fact that VDB incurs a much lower memory footprint thus utilizing hardware resources better.

6 Replication of Results

Throughout this paper, we have included pseudo codes of all the key algorithms developed as a part of VDB-LSTO. These pseudo codes are useful in the replication of our results.