Integrated statistical modeling method: part I—statistical simulations for symmetric distributions

Abstract

The use of parametric and nonparametric statistical modeling methods differs depending on data sufficiency. For sufficient data, the parametric statistical modeling method is preferred owing to its high convergence to the population distribution. Conversely, for insufficient data, the nonparametric method is preferred owing to its high flexibility and conservative modeling of the given data. However, it is difficult for users to select either a parametric or nonparametric modeling method because the adequacy of using one of these methods depends on how well the given data represent the population model, which is unknown to users. For insufficient data or limited prior information on random variables, the interval approach, which uses interval information of data or random variables, can be used. However, it is still difficult to be used in uncertainty analysis and design, owing to imprecise probabilities. In this study, to overcome this problem, an integrated statistical modeling (ISM) method, which combines the parametric, nonparametric, and interval approaches, is proposed. The ISM method uses the two-sample Kolmogorov–Smirnov (K–S) test to determine whether to use either the parametric or nonparametric method according to data sufficiency. The sequential statistical modeling (SSM) and kernel density estimation with estimated bounded data (KDE-ebd) are used as the parametric and nonparametric methods combined with the interval approach, respectively. To verify the modeling accuracy, conservativeness, and convergence of the proposed method, it is compared with the original SSM and KDE-ebd according to various sample sizes and distribution types in simulation tests. Through an engineering and reliability analysis example, it is shown that the proposed ISM method has the highest accuracy and reliability in the statistical modeling, regardless of data sufficiency. The ISM method is applicable to real engineering data and is conservative in the reliability analysis for insufficient data, unlike the SSM, and converges to an exact probability of failure more rapidly than KDE-ebd as data increase.

1 Introduction

The analysis and design methods of engineering systems have extended from deterministic methods to probabilistic and statistical methods owing to high demand for high product quality. Even though a nonprobabilistic reliability-based design optimization using a convex model has been developed, the probabilistic approaches are still dominantly used (Hao et al. 2017, 2019a, b; Keshtegar and Chakraborty 2018). Statistical modeling, which estimates a distribution function of input or output random variables, is necessary in stochastic methods such as reliability analysis, reliability-based design optimization (RBDO), reliability-based topology optimization, and statistical model validation and calibration (Noh et al. 2010; Youn et al. 2011; Keshtegar and Chakraborty 2018; Wang et al. 2018; Hao et al. 2019a, b). Although statistical modeling is very important to obtain high accuracy in the statistical analysis or design, the statistical methods have been applied by assuming the distribution function as a normal distribution, without the statistical modeling of random variables owing to insufficient data or limitations of the existing statistical modeling techniques (Frangopol et al. 1997). However, studies have revealed that the distribution function of variables is not a normal distribution in engineering systems (Choi et al. 2011; Hess et al. 2002; Lukić and Cremona 2001; Socie 2014), and they subsequently showed the limitation in the assumption of a normal distribution of random variables for more accurate designs. Accordingly, the necessity for accurate statistical modeling methods has been reported.

Various statistical approaches have been developed to identify the probabilistic distribution of uncertain data. Statistical modeling approaches are classified as parametric, nonparametric, probabilistic, or interval approaches and have contrasting limitations. In particular, the limitations of parametric and nonparametric methods are different from each other. The parametric methods are convenient and easy to utilize in statistical modeling as they use specific types of distributions, and their parameters include information of statistical moments; thus, they can be easily applied to statistical analysis and design methods such as reliability and robustness analyses. For instance, a reliability or variance of output can be analytically calculated by using parametric models (Ayyub and McCuen 2012). However, their estimation accuracy is poor for limited data as errors occur in identifying the distributions and estimating the parameters simultaneously. In contrast, the nonparametric methods are more accurate than the parametric ones for insufficient data as they estimate a model only using data, without identifying distribution functions, and their distributions have high flexibility in describing nonlinearly distributed data. However, the estimated nonparametric distributions converge to the population model slowly as the sample size increases, and their mathematical formulations are not user friendly in statistical modeling and uncertainty propagation analysis. The interval approach uses interval information of data or random variables for statistical modeling instead of using specific parametric or nonparametric models. However, the interval information on the probability is difficult to use in uncertainty analysis or design owing to the imprecise probabilities (Tucker and Ferson 2003; Karanki et al. 2009; Betrie et al. 2014, 2016; Kang et al. 2018). Each approach includes a variety of statistical modeling methods, and they will be reviewed in detail in Sect. 2.

To overcome the limitations of the parametric, nonparametric, and interval approaches, an integrated statistical modeling (ISM) method, which combines these approaches, is proposed. Here, the kernel density estimation with bounded data (KDE-bd) with sequential statistical modeling (SSM), the KbSSM, which integrates the kernel density estimation with estimated bounded data (KDE-ebd) and SSM methods, is proposed. The ISM process is separated into two processes: a combined process of the KDE-ebd with SSM (KbSSM) and a parametric process that only conducts the SSM. If the quality of the given data is sufficient to model a parametric distribution, which is determined by the two-sample Kolmogorov–Smirnov (K–S) test, the parametric process is performed; otherwise, the KbSSM process is performed. In the KbSSM process, the KDE-ebd estimates the density function using the given and bounded data together, and then, the KDE-ebd function is converted to a parametric distribution using the SSM method when the given data are insufficient to directly model a parametric model. As the amount of given data increases, the parametric process will be repeatedly performed. Therefore, once the users provide data, the ISM method automatically selects the accurate and conservative distribution according to the quality and sufficiency of the given data. Due to this, ISM has the following advantages: (1) The output model is always a parametric distribution (usability); (2) it has no loss of accuracy and convergence compared to single parametric or nonparametric methods (accuracy and convergence); (3) it provides heavy tailed distributions for insufficient data (conservativeness).

To verify the performance of the proposed method, samples of various sizes are randomly generated from various types of distribution functions assumed by the true models to conduct the statistical simulation test, and a distribution function is estimated for the samples using the SSM, KDE-ebd, and ISM methods. Subsequently, the results of the statistical simulation using the ISM are compared to those using the SSM and KDE-ebd. Further, a simple numerical example for real experimental data is applied to show how the statistical modeling using the proposed method is conducted by comparing the modeling accuracy and conservativeness of the SSM, KDE-ebd, and ISM. In addition, through a reliability analysis problem, it is confirmed that the proposed method has more conservative and reliable analysis results than other methods.

In Sect. 2, the existing statistical modeling methods are briefly discussed. The proposed ISM method, SSM, and KDE-ebd will be explained in Sect. 3 in more detail. Section 4 describes the results of the statistical simulation tests using the parametric (SSM) and nonparametric (KDE-ebd) methods, along with the ISM to compare the accuracy and conservativeness of the statistical modeling with various distributions and sample sizes. In Sect. 5, the ISM is compared with the SSM and KDE-ebd and verified for its modeling accuracy, conservativeness, and reliable analysis result through statistical modeling and reliability analysis examples. For this, data from the compressive strength and reliability analysis of a two-member truss are used respectively. Finally, the conclusions are summarized in Sect. 6.

2 Overview of statistical modeling methods

Various statistical modeling methods have been developed to estimate the distribution of random variables. The statistical modeling methods are classified into the parametric and nonparametric approaches according to the type of the estimated distribution. The parametric approach provides a parametric distribution function that fits the given data using specific distribution types and their parameters, whereas the nonparametric approach provides a nonparametric distribution that describes the distribution of data without assuming any parametric distribution. The statistical modeling methods can also be categorized into the probabilistic or interval approach. The probabilistic approach can calculate a precise probability, which has one value for a specific random variable, while the interval approach estimates an imprecise probability, which has more than two values, such as the lower and upper bounds of the interval of a specific variable.

2.1 Interval approach

The interval approach represents the statistical model using intervals on the input or output variables when the number of samples is limited. Probability bounds approaches, such as the probability box (p-box) theory and evidence theory, also known as the Dempster–Shafer theory, are the most often used in the parametric and nonparametric methods, respectively (Verma et al. 2010). The p-box and Dempster–Shafer theories provide convenient and comprehensive methods to quantify uncertainties including imprecise specified distributions, small sample sizes, inconsistency in the quality of input data, or poorly known or unknown dependencies.

When the distribution is known to have a particular shape, but its parameters are imprecisely specified as intervals, the cumulative distribution functions (CDFs) have a parametric p-box, which shows the lower and upper bounds on the probabilistic distribution for a random variable. The lower and upper bounds of the CDFs are estimated using the confidence intervals of the distribution parameters. Similarly, when the parameters of the distributions are known precisely, but the distribution type is unknown, the envelopes of all distributions matching the given moments are generated, and then, they can be used to define the upper and lower bounds of the CDFs.

The statistical model using the Dempster–Shafer theory is similar to the discrete distribution; however, it allocates a basic probability assignment (BPA), which assigns a degree of belief to the intervals of each data element, called the focal element, whereas the discrete distribution has mass probabilities for specific data. The interval for the empirical CDF is determined through the combination of the overlapped focal elements of the data.

However, these methods still estimate an imprecise probability (Tucker and Ferson 2003; Karanki et al. 2009; Betrie et al. 2014, 2016). Further, they require a large number of computations in the uncertainty propagation. Moreover, the evidence theory requires a surrogate model for the estimated empirical distributions to be applied to numerical reliability analysis methods, such as the first-order reliability method (FORM), because of the discretization form of the estimated distribution functions (Agarwal et al. 2004; Zhang et al. 2014; Yao et al. 2013; Shah et al. 2015). Therefore, the interval approach is limited in the computation of uncertainty propagation in engineering applications.

2.2 Parametric approach

The parametric probabilistic approach quantifies the data distribution by selecting one of the probabilistic distributions among the parametric distribution functions. Subsequently, it estimates the parameters of the selected distribution function. Goodness of fit (GOF) tests such as the Anderson–Darling (A–D), chi-squared (χ²), and K–S tests (Anderson and Darling 1952; Ayyub and McCuen 2012), along with model selection methods such as the Akaike information criterion (AIC), Bayesian information criterion (BIC), and Bayesian method (Akaike 1974; Schwarz 1978; Burnham and Anderson 2004; Noh et al. 2010), are widely used to estimate the distribution function of data with uncertainty.

The GOF tests can evaluate the absolute adequacy of a candidate model to represent the given data through the hypothesis test for the candidate model with a certain significance level; however, the relative assessment between the candidate models is difficult. Conversely, the model selection methods can select the best-fit distribution among the candidate distributions based on likelihood function values evaluated at given data, but they cannot give users any warning message if the identified distribution is inadequate to represent the data. It is because the identified distribution is the best fitted one among all candidates, but it does not necessarily mean that it is a correct model for the given data. To use these contrastable advantages of both the GOF tests and the model selection methods, a sequential statistical modeling (SSM) combining the GOF tests and the model selection methods was developed. The SSM eliminates inappropriate distributions among the candidates by the absolute assessment of the GOF tests. Subsequently, the model selection methods choose the best-fit distribution among the candidate models reduced by the GOF tests. Kang et al. verified that SSM is more accurate and reliable than using the GOF tests or model selection methods for various types of distributions and sample sizes. In that case, the K–S test and BIC were used as the GOF test and model selection method, respectively, based on the accuracy test results (Kang et al. 2016).

The SSM was applied to quantify the statistical, spare, and interval variables (Peng et al. 2017a) and was applied to a hybrid reliability analysis (Peng et al. 2017b). An improved SSM method that adds a kernel function to candidate models in the previous SSM was developed and applied to real experimental data regarding the friction coefficient of bolt fastening (Joo et al. 2017) and fatigue life (Doh and Lee 2018).

The parametric method is user friendly and can be easily applied to various statistical methods because its distribution type and parameters are easily obtained from the given data; further, the estimated distribution quickly converges to a true distribution function as the sample size increases. However, unfortunately, it has errors in estimating both the type of distribution function and the statistical parameters. Therefore, in particular, the accuracy of statistical modeling could be jeopardized when the number of samples is limited because both errors affect the modeling accuracy.

2.3 Nonparametric approach

The nonparametric probabilistic approach estimates a distribution function using only the given data without estimating the type of distribution function and the statistical parameters. The KDE is the most often used nonparametric approach to quantify a probabilistic distribution. The KDE is recommended to model the given data using kernel functions if the random variables follow nonparametric distributions or the number of given data is insufficient, even though the true distribution of the data is a parametric distribution (Kang et al. 2017). It has higher estimation accuracy than the SSM (parametric) method for a small number of data because the KDE estimates a distribution using only the data, while the SSM has errors in estimating both the type of distribution and the parameters (Kang et al. 2017). However, if the number of data is small, e.g., n ≤ 10, the KDE is very sensitive to the quality of the given data and estimates a highly nonlinear KDE density function; therefore, the estimation accuracy is low, although the KDE is generally more accurate than the SSM. Therefore, to overcome the limitations of the KDE and use both the data information and intervals, the KDE-bd and KDE-ebd, which combine a nonparametric approach (KDE) and an interval approach (bounded data), have been developed.

The KDE-bd/KDE-ebd combine the nonparametric probabilistic method (KDE) with the interval representation. Thus, these methods use both the given and bounded data sampled from given intervals or estimated intervals from data to estimate the kernel density function, where the bounded data supplements the lack of given data and the missing data. In the KDE-ebd, the estimated bounded data are generated randomly from a uniform distribution with interval estimators using the interval estimation. Thus, the KDE-ebd can estimate a more accurate and conservative density function than the original KDE in statistical modeling and reliability analysis (Kang et al. 2018). However, the KDE, KDE-bd, and KDE-ebd slowly converge to a true distribution as the number of data increases when the true model has a parametric distribution, which is typical in engineering fields (Kang et al. 2018). In addition, the KDE, KDE-bd, and KDE-ebd are not user friendly with their highly nonlinear function shapes and complex formulations; thus, they are difficult to be applied in statistical analysis and design under uncertainties.

Although the existing statistical methods have some advantages, they also have limitations in terms of data quality, number of data, or given information. Therefore, an integrated statistical modeling method needs to be developed such that it can be widely applied to handle various types of statistical models in the engineering fields.

3 Integrated statistical modeling method

Although the SSM method is more accurate than the GOF tests or the model selection methods, it still has a low estimation accuracy and is sensitive to the amount of data; this is because of the limitations of the parametric statistical modeling approach, which has errors in estimating both the distribution type and the parameters of the distribution function for a small number of data. In addition, the SSM frequently estimates a narrower probability density function (PDF) than a true PDF; thus, it may underestimate the probability of failure in a reliability analysis (Kang 2018). The KDE-ebd overcomes the problems of the KDE and SSM by combining the nonparametric and interval approaches, but it slowly converges to a true distribution compared to SSM, and it estimates a nonparametric distribution function, thereby rendering it difficult for engineers to apply the probabilistic–statistical methods in the engineering fields.

To achieve a balance between the merits of the parametric and nonparametric approaches, a usable, accurate, quickly convergent, and conservative statistical modeling method for insufficient data needs to be developed. The KbSSM method achieves the merits of both the SSM and KDE-ebd by combining them. KDE-ebd is used as the nonparametric approach combined with the interval approach and SSM is used as the parametric approach, respectively; therefore, the combined statistical modeling approach is called here the KbSSM method. The ISM method uses either the KbSSM or the SSM according to the data quality and sufficiency, based on the two-sample K–S test; thus, it yields convergent, conservative, accurate, and user-friendly modeling results.

3.1 Integrated statistical modeling process

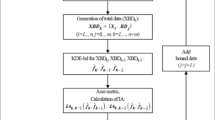
The integrated procedure is separated into two processes: a parametric modeling process that only performs SSM and a combined process (KbSSM) that performs KDE-ebd and SSM sequentially according to the quality of the given data. If the number of given data is sufficient to converge to any parametric distribution, i.e., the additional data do not change the shape of the distribution obtained from the previous data, the parametric modeling process is performed to estimate the distribution function for the given data; otherwise, the KbSSM process is performed. Figure 1 shows the ISM procedure. In step (1), the quality of the given data is verified by the two-sample K–S test. The two-sample K–S test is one of the hypothesis tests to check whether two data sets are sampled from the same continuous distribution. This is performed by comparing the empirical cumulative distribution functions (eCDF) of two data sets with n and n′ sample sizes using the two-sample K–S statistic, ${D}_{n,{n}^{\prime }}$. This statistic means the maximum distance between the eCDFs calculated from two data sets. If this statistic is smaller than the threshold statistic, ${D}_{n,{n}^{\prime}}^c\left(\alpha \right)$, the hypothesis is accepted at a significance level (α); otherwise, it is rejected.

Fig. 1

ISM process

The two-sample K–S statistic is expressed as

$$ {D}_{n,n\hbox{'}}=\underset{x}{\sup}\left(\left|{F}_{1,n}(x)-{F}_{2,n\hbox{'}}(x)\right|\right) $$

(1)

where F_{1, n}(x) and ${F}_{2,{n}^{\prime }}(x)$ are the eCDF of the two different data sets with n and n′ sample sizes, respectively.

To evaluate the data quality in step (1), two-sample K–S statistics are calculated for the n, n − 1, and n − 2 data and the two statistics are defined by

$$ {D}_{n,n-1}=\underset{x}{\sup}\left(\left|{F}_{1,n}(x)-{F}_{2,n-1}(x)\right|\right) $$

(2)

$$ {D}_{n,n-2}=\underset{x}{\sup}\left(\left|{F}_{1,n}(x)-{F}_{2,n-2}(x)\right|\right) $$

(3)

where F_{1, n}(x), F_{2, n − 1}(x), and F_{2, n − 2}(x) are the eCDF estimated from n, n − 1, and n − 2 sample sizes. Figure 2 shows the two-sample K–S statistics for n and n − 1 data.

Fig. 2

Two-sample K–S statistic

If the two-sample K–S statistics, D_{n, n − 1} and D_{n, n − 2}, are less than or equal to a critical value ${D}_{n,n\prime}^c$, it means that the distributions obtained from the n − 1 and n − 2 data are close to a certain parametric distribution for the n given data, i.e., the amount of data is sufficient to model the parametric distribution. Thus, the parametric modeling process (SSM) is performed; otherwise, the KbSSM modeling process, which results in a conservative distribution function to supplement the lack of data, needs to be performed. If the critical two-sample K–S statistic (${D}_{n,n\prime}^c$) increases, the probability of determining that the n − 1, n − 2 and n samples are from the same distribution increases, so the probability of performing SSM increases. In the opposite case, the probability of performing KbSSM increases. Therefore, if users want a parametric model well fit to their data, they can use a high critical statistic value. If users want a conservative parametric model, they can use a low critical statistic value. In this paper, the critical two-sample K–S statistics were selected as 0.05 for selecting the KbSSM and SSM processes reasonably.

3.1.1 Parametric process in ISM

If the amount of data is sufficient to represent a parametric distribution (“Yes” in the decision process of step (1)), then SSM will be performed. The SSM first performs the GOF tests to check the absolute appropriateness of the candidate models for the given data, and only some of the candidate models accepted by the GOF tests will be used as the candidate models for the model selection method. Accordingly, if all candidate models are rejected by the GOF test, and the number of initial candidate models (N_m) is less than the number of the total parametric distributions (${N}_m^{tot}$), new candidate models are assigned, and the GOF test is repeated. In this paper, parametric unimodal distributions were only selected as candidate models, but users also can add parametric multimodal distributions such as Gaussian mixture models as candidate models if they want to estimate them. If ${N}_m={N}_m^{\mathrm{tot}}$, it means that the parametric process in ISM cannot fit the given data to any parametric distribution and this process is terminated by the printout “FAIL.” In this case, a nonparametric modeling method such as the KDE is generally recommended because the data is likely to follow a nonparametric or multimodal distribution. If some of the candidate models are accepted by the GOF test, the model selection method is performed based on the remaining candidate models. From the previous study, the K–S test was verified as the most accurate GOF test (Kang et al. 2016); hence, it is used in our study. The K–S test is a hypothesis test to accept or reject the null hypothesis of the given data sampled from a candidate distribution using a K–S statistic. The K–S statistic indicates the maximum distance between the empirical CDF (eCDF) of the given data and the CDF of a specified candidate model. If the K–S statistic, D_n, is smaller than the critical statistic, ${D}_n^{\alpha }$, the candidate is accepted, where α is the significance level and n is the number of samples. The critical statistic values are given in the references about statistics (Ayyub and McCuen 2012). The K–S statistic is defined as

$$ {D}_n=\sup \left|{F}_n(x)-F(x)\right| $$

(4)

$$ {F}_n(x)=\left(\frac{1}{n}\right)\sum \limits_{i=1}^n{I}_{X_i\le x} $$

(5)

where F_n(x) is the eCDF of the data and F(x) is the CDF of a specified candidate model. X_i is the ith value of a random variable X, and ${I}_{X_i\le x}$ is the indicator function, which is 1 when X_i ≤ x; otherwise, it is 0.

Second, the model selection method is performed to select the best-fit distribution for the given data among the reduced candidate models. Based on the previous study, the BIC is selected as the model selection method (Kang et al. 2016). The BIC is calculated using the maximum likelihood function values, sample size, and number of parameters for each candidate model, as shown in (6) (Schwarz 1978). The candidate model with the smallest BIC values is selected as the best-fitted model to represent the given data.

$$ BIC=-2\ln L+k\ln (n) $$

(6)

$$ \ln L\left(\boldsymbol{\uptheta}; {X}_1,\dots, {X}_n\right)=\sum \limits_{i=1}^n\ln f\left({X}_i|\boldsymbol{\uptheta} \right) $$

(7)

where L is the maximum value of the likelihood function, k is the number of parameters of a candidate distribution, and n is the number of data. f(∙) is the PDF of a candidate model, and θ is the vector of the parameters.

Finally, the distribution parameters of the selected model by the BIC are estimated using the maximum likelihood estimation (MLE). The MLE is also used in the K–S test to calculate the parameters of candidate models, and the vector of the estimated parameters using the MLE is defined as

$$ \left\{{\hat{\boldsymbol{\uptheta}}}_{mle}\right\}\subseteq \left\{\underset{\theta \in \Theta}{\arg \max \mathrm{\ell}\left(\boldsymbol{\uptheta}; {X}_i\right)}\right\} $$

(8)

where ${\hat{\boldsymbol{\uptheta}}}_{\mathbf{mle}}$ is the estimated parameter and ℓ is the log-likelihood function.

Using a reasonable significance level in the K–S test can improve the accuracy of parametric modeling by filtering out models that are not absolutely suitable for data through K–S test and selecting the best fitted model through the model selection method. However, if users use high significance levels, a true model may not be chosen as a candidate model for SSM because the probability of rejecting a null hypothesis for the true model increases. Conversely, if a low-level significance is used, most models are used as candidate models and modeling errors could increase even though it is not absolutely suitable for data. Therefore, if users want to strictly filter out wrong models, they need to use higher significance levels, and if users want to reduce modeling errors due to GOF tests, they need to use lower significance levels (Kang et al. 2016).

3.1.2 KbSSM process in ISM

If data are lacking or missing (“No” in the decision process of step (1)), KDE-ebd and SSM will be sequentially performed. First, KDE-ebd is performed to model the given data by estimating a kernel density function using both the given and estimated bounded data. The KDE-ebd generates the bounded data, which are randomly generated from the intervals calculated from the given data; subsequently, it estimates the kernel density function using both the given and bounded data. The intervals are calculated from the given data using the interval estimation of a uniform distribution. For the interval estimation, the point estimators are calculated using the MLE and are defined by

$$ \left\{\hat{a},\hat{b}\right\}\subseteq \left\{\underset{\hat{a},\hat{b}\in \Theta}{\mathrm{argmax}}{\left(\frac{1}{x_u-{x}_l}\right)}^n\prod \limits_{i=1}^n{I}_{\left\{{x}_l\le x\le {x}_u\right\}}\left({x}_i\right)\right\} $$

(9)

where $\hat{a}$ and $\hat{b}$ are the point estimators of a uniform distribution, and x_l and x_u are the minimum and maximum values of the given data, respectively. ${I}_{\left\{{x}_l\le x\le {x}_u\right\}}$ is the indicator function, which is 1 when x_l ≤ x ≤ x_u; otherwise, it is 0. The interval estimators, ACI and BCI, are expressed as

$$ ACI=\left\{{\hat{a}}_L,{\hat{a}}_U\right\}=\left[\hat{b}-\frac{\hat{b}-\hat{a}}{{\alpha_{ebd}}^{1/n}},\hat{a}\right] $$

(10)

$$ BCI=\left\{{\hat{b}}_L,{\hat{b}}_U\right\}=\left[\hat{b},\hat{a}+\frac{\hat{b}-\hat{a}}{{\alpha_{ebd}}^{1/n}}\right] $$

(11)

where ${\hat{a}}_L$ and ${\hat{b}}_U$ are used as the lower (l) and upper (u) parameters of the uniform distribution to generate the bounded data, respectively; α_ebd is the significance level for the interval estimation. The interval range in the uniform distribution is varied with the significance level (α_ebd) value. If α_ebd is low, the KDE-ebd density function has a long tail, which yields a more conservative density estimation than the one with a high α_ebd. If α_ebd is high, the KDE-ebd density function has a short tail, which yields a less conservative density estimation than the one with a low α_ebd but fits better to the data distribution. In this study, α_ebd was chosen as 0.1, and thus, the accuracy and conservativeness are ensured for the estimated density functions (Kang et al. 2018).

The estimated bounded data are randomly sampled from a uniform distribution with the estimated lower and upper bounds of the parameters, l and u, respectively. The number of bounded data is determined by comparing the intersection areas of the kernel density functions obtained before and after the bounded data are updated. The intersection area is an area metric evaluating the coincidence rate between two PDFs. If two PDFs are completely coincident, the intersection area is 1; if two PDFs do not share an overlapped area, the intersection area is 0. Whenever the bounded data are added, the KDE-ebd density functions, f_k, f_k − 1, and f_k − 2 are generated, where k is the total number of given and bounded data, and f_k, f_k − 1, and f_k − 2 are the estimated KDE-ebd density functions using the k, k − 1, and k − 2 data (Kang et al. 2018; Kang 2018). The intersection areas, IA_{k, k − 1} and IA_{k, k − 2}, between f_k, f_k − 1, and f_k − 2 are calculated using the Riemann integral of the overlapped function (Kang et al. 2016), and the intersection areas are given by the following (Jung et al. 2017; Kang et al. 2018; Kang 2018)

$$ {IA}_{k,k-1}=\sum \limits_{l=1}^p{f}_{k,k-1}\left({x}_l\right)\cdotp \left({x}_l-{x}_{l-1}\right) $$

(12)

$$ {f}_{k,k-1}\left({x}_l\right)=\min \left\{{f}_k\left({x}_l\right),{f}_{k-1}\left({x}_l\right)\right\} $$

(13)

where p is the number of subintervals that encompasses the domain of the overlapped area.

If both f_k − 1 and f_k − 2 converge to f_k, both IA_{k, k − 1} and IA_{k, k − 2} become greater than the critical intersection area, IA_c, i.e., f_k, f_k − 1, and f_k − 2 are almost coincident, meaning that the KDE-ebd density function has converged. Thus, the additional bounded data is unnecessary, and the updated estimated bounded data are used to obtain the output density function using KDE-ebd (Kang et al. 2018; Kang 2018).

If the critical intersection area increases, the large number of bounded data is generated and the estimated density function using KDE-bd tends to oversmooth the data. Otherwise, a small number of bounded data are generated and the density function using KDE-bd tends to overfit the data. Accordingly, if users want conservative modeling, they can use a high critical intersection area. If the users want a model that fits their data well, they can use a low critical intersection area. In this paper, the critical intersection area was chosen as 0.95, which is known as the appropriate convergence criterion (Jung et al. 2017), and detailed description is included in the KDE-bd/bd paper (Kang et al. 2018).

The estimated kernel density function of the KDE-ebd is calculated using the real given data and the estimated bounded data, defined as (Kang et al. 2018)

$$ {\hat{f}}_{\mathrm{ebd}}=\frac{1}{\left(n+m\right)\cdotp h}\sum \limits_{k=1}^{n+m}K\left(\frac{x-\left(X{eBD}_k\right)}{h}\right) $$

(14)

where XeBD_k is the total data for k = 1, …, n + m; XeBD_k = {X_i, eBD_k}; X_i is the ith given data for i = 1, …, n; and eBD_k is the jth estimated bounded data for j = 1, …, m. ${\hat{F}}_{\mathrm{ebd}}$ is an estimated kernel density function of the KDE-ebd, K(∙) is a kernel function, and h is the bandwidth of the kernel function. In this study, a Gaussian kernel function is used as it has a simple mathematical formula and is the most commonly used in the KDE (Chen 2015; Guidoum 2015; Hansen 2009; Sheather 2004). As the bandwidth is important to determine the accuracy of the estimated kernel density function, in this study, the optimal bandwidth (h^*) is calculated using Silverman’s rule of thumb (Silverman 1986).

The estimated PDF using the KDE-ebd has a nonparametric formulation, and thus, it needs to be converted to a parametric distribution. Hence, new samples are resampled with the KDE-ebd to conduct the parametric method (SSM). A CDF obtained from the KDE-ebd is given by

$$ {\hat{F}}_{\mathrm{ebd}}\left({x}_k\right)=\underset{-\infty }{\overset{x}{\int }}{\hat{f}}_{\mathrm{ebd}}\left({x}_k\right) dx $$

(15)

where x_k is the total data and ${\hat{F}}_{\mathrm{ebd}}\left({x}_k\right)$ and ${\hat{f}}_{\mathrm{ebd}}\left({x}_k\right)$ are the CDF and PDF obtained from the KDE-ebd, respectively. The resampled data (RX_l) is randomly generated using a quantile function (also called an inverse CDF) defined as

$$ Q(p)=\operatorname{inf}\left\{{x}_k\in \mathrm{\mathbb{R}}:p\le {\hat{F}}_{\mathrm{ebd}}\left({x}_k\right)\right\},\kern0.5em \operatorname{}p\in \left[0,\kern0.5em 1\right] $$

(16)

where Q(p) is the quantile function that returns the resampled data RX_l shown in (17).

$$ {RX}_l=Q\left({p}_l\right) $$

(17)

where the p values are randomly selected between 0 and 1 and the estimated CDF using the KDE-ebd is used to find RX_l through the quantile function. The total number of the resampled data is l.

Next, the GOF test is performed to verify the absolute compatibility of the candidate models for the resampled data. The K–S test is also used as the GOF test in the parametric process. As the estimated bounded data of the KDE-ebd are randomly selected, the quality of the bounded data could still be poor. Therefore, the randomness of the bounded data in the KDE-ebd needs to be reduced through the GOF test for the resampled data and candidate models. If all of the candidate models are rejected by the GOF test, the KDE-ebd is performed again to estimate a new CDF using KDE-ebd; subsequently, new resampled data are generated from the new CDF using KDE-ebd. However, if the distribution of the given data does not match with any initial candidate models, the repetitive KDE-ebd process cannot satisfy the absolute appropriateness for the given data; thus, the number of iterations (r) is limited to 100 to avoid the infinite loop in the KDE-ebd process. If r is larger than 100, other types of parametric distributions will be added to the candidate models, and then the GOF test will be performed for the updated candidate models. If the estimated density function using KDE-ebd does not satisfy the GOF test, this program is terminated by the printout “FAIL.” This means that the ISM cannot fit any parametric distribution among all the candidate models to the given data. In this case, a nonparametric modeling is recommended.

Finally, the model selection method is performed for the resampled data based on the candidate models with absolute appropriateness. The BIC is also used as the model selection method in the parametric modeling process. Through this process, the nonparametric distribution using KDE-ebd is converted to the most suitable parametric distribution for the given data.

Figure 3 shows the estimated PDFs using various modeling methods for seven data generated from an assumed true distribution, NORM (50, 10). As the KDE uses only seven data and the data are irregularly distributed, the estimated density function is bimodal with high nonlinearity; thus, the intersection area between the estimated PDF and true PDF is only 0.6627. The SSM better describes the true PDF by identifying the Birnbaum–Saunders distribution and the intersection area is 0.8579. However, the PDF using the SSM tends to underestimate the density function values at the left tail, which might be unreliable in statistical analysis. The KDE-ebd and ISM using KbSSM estimate the mildly distributed PDFs over the wide domain by adding four bounded data to the given data. The estimated PDFs using KDE-ebd and ISM have heavier tails than those using SSM, and these heavy tailed PDFs lead to conservative results in the reliability analysis (Picheny et al. 2010; Wheeler 2012; Malekpour and Barmish 2017). In particular, the intersection area using the ISM (0.8690) is higher than the one using the KDE-ebd (0.8378), i.e., the PDF using the ISM is closer to the true PDF than the KDE-ebd. Consequently, the accuracy and conservativeness are ensured for the estimated density functions (Kang et al. 2018). To verify the modeling accuracy, convergence, and conservativeness of the ISM method, various symmetric distributions with various sample sizes were tested in Sect. 4. To verify the conservativeness of the ISM method, a reliability analysis example was tested in Sect. 5.

Fig. 3

Estimated PDFs using various modeling methods

4 Statistical simulation test

To verify the performance of the integrated approach, statistical simulation tests using the parametric modeling method (SSM), nonparametric modeling method (KDE-ebd), and integrated modeling method (ISM) are conducted for the sample data, and their results are compared. To conduct the simulation tests, true models are assumed by separately considering two cases, i.e., case I: normal distributions with several variations and case II: nonnormal symmetric distributions, and the characteristics of the true models are explained in detail in Sects. 4.1 and 4.2, respectively. Samples are randomly generated from the true models for various sample sizes, n = 3, 5, 7, 10, 20, 30, and 50 with 1000 repetitions to consider the randomness of the samples. Subsequently, the statistical modeling using the three methods is performed for each data set, and the intersection areas between the true PDFs and the estimated PDFs are calculated to compare the accuracy and convergence of the three methods in Sect. 4.3.1. The intersection area has a normalized value from 0 to 1 and symmetric feature regardless of the selection of reference distribution, so that it is possible to obtain consistent values. The Kullback–Leibler (K–L) divergence, which is also widely used as a modeling accuracy measure, can be used, but it has nonnormalized value and asymmetric feature (Kullback and Leibler 1951; Kang 2018); thus, it is not used in this study. If the intersection area is used to assess the modeling accuracy, quantile function value ratio (QFVR), which is a quantile function value evaluated at tail ends of distributions, is used to assess the modeling conservativeness. The performance of modeling methods is verified using the same true models and sample sizes as the accuracy in Sect. 4.3.2.

To perform a GOF test in the SSM and KbSSM, the Birnbaum–Saunders, exponential, logistic, extreme value, gamma, logistic, log-logistic, log-normal, Nakagami, normal, Rayleigh, t location scale, and Weibull distributions were selected as the candidate models. The K–S test was chosen as the GOF test with 5% significance level (α_GOF), and the BIC was selected as the model selection method (Kang et al. 2016). The KDE-ebd used a significance level α_ebd = 10% for estimating the bounds and a critical intersection area IA_c = 0.95 for generating the bounded data (Kang et al. 2018). In the KbSSM, a critical two-sample K–S statistic ${D}_{n,n\prime}^c$ = 0.05 was chosen to reasonably determine either the KbSSM or SSM process, and the number of resampled data (RX_l) used was 300 to ensure the efficiency and accuracy of conducting the SSM in the KbSSM process. This is because the SSM estimates a highly accurate distribution for 300 samples with various distributions (Kang et al. 2016; Kang et al. 2017).

4.1 Case I: normal distributions with various variations

The normal distribution is the most commonly used distribution in the engineering fields, e.g., in reliability analysis and reliability-based design optimization (Frangopol et al. 1997; Li et al. 2012; Yoo and Lee 2014; Park et al. 2015). In this section, three normal (NORM) distributions, i.e., NORM (50, 2.5), NORM (50, 5), and NORM (50, 10), are assumed as the true models with the same mean, 50, and different standard deviations, i.e., 2.5, 5, and 10. Figure 4 shows the PDFs of these three true distributions.

Fig. 4

PDFs of normal distributions

Tables 1, 2, and 3 present the average intersection areas between the estimated PDFs using the SSM, KDE-ebd, and ISM, respectively, for normal distributions with multiple variations and sample sizes. The numbers in the combined process (KbSSM) or parametric process (only the SSM) indicate the number of times each process is performed for the statistical modeling when the true models are NORM (50, 2.5), NORM (50, 5), and NORM (50, 10) distributions. In Tables 1, 2, and 3, the bold font indicates the highest intersection area.

Table 1 Average intersection areas in SSM, KDE-ebd, and ISM: X~NORM (50, 2.5)

Table 2 Average intersection areas in SSM, KDE-ebd, and ISM: X~NORM (50, 5)

Table 3 Average intersection areas in SSM, KDE-ebd, and ISM: X~NORM (50, 10)

First, when the NORM (50, 2.5) distribution is a true model, the intersection areas using the three methods increase and become close to one as the sample size increases. The number of performing SSM in the ISM process also increases while the number of performing KbSSM in the ISM process decrease, as presented in Table 1, because the SSM process more easily and accurately estimates the true distribution than the combined process for sufficient data. The intersection areas of the ISM are always greater than or equal to those resulting of conducting the SSM or KDE-ebd alone. When n ≤ 10, the ISM yields the largest intersection area, followed by the KDE-ebd and SSM; further, KbSSM is always performed in the ISM process. During the KbSSM process, the estimated distribution is almost the same as the one using KDE-ebd although the KbSSM estimates a parametric distribution while the KDE-ebd estimates a nonparametric distribution. However, the accuracy of the ISM is higher than that of the KDE-ebd because the conservative effect of the KDE-ebd is reduced by remodeling the density function using SSM in the KbSSM. The intersection areas using the KDE-ebd are larger than those using the SSM because the KDE-ebd has a high estimation accuracy even if the data quality is poor, contrary to the SSM (Kang et al. 2017, 2018). When n ≥ 20, the ISM still has the highest accuracy, followed by the SSM and KDE-ebd. The ISM is more accurate than the SSM for n = 20 because the KbSSM can reduce the errors caused by wrong identifications and inaccurate estimations of the distribution parameters that often occur in the SSM. However, the accuracy of the ISM is equal to that of the SSM for n = 30 and 50 because the identification and estimation errors are reduced for sufficient data. Finally, the SSM process will only be performed in the ISM for n = 50. The intersection areas using SSM are greater than those using KDE-ebd for n ≥ 20 because the SSM quickly converges to a true model as n increases, but the KDE-ebd does not (Kang et al. 2017, 2018).

Next, assume that the NORM (50, 5) distribution is a true model. As presented in Table 2, as the number of samples increases, the intersection areas using the three methods increase while the number of performing KbSSM decreases. The ISM always has the highest accuracy among the three methods, as in the NORM (50, 2.5) distribution. In the ISM, the KbSSM is always performed for a small number of data, n ≤ 10, whereas the SSM is used for n ≥ 20. When sufficient data are available (e.g., n = 50), the SSM is always performed in the ISM, as in the NORM (50, 2.5) distribution.

Subsequently, the true model is assumed to be a NORM (50, 10) distribution with a large variation. Table 3 lists the average intersection areas and the number of integrated processes. The tendency of the intersection areas is similar to that of NORM (50, 2.5) and NORM (50, 5) distributions. In this distribution, the ISM still shows the largest intersection area regardless of the sample size, and the KbSSM process is dominantly performed in the ISM method when n is very small, while SSM is primarily used for the sufficient number of data.

4.2 Case II: nonnormal symmetrical distributions

In this section, the normal (NORM (50, 5)), logistic (LOG (50, 2)), and t location scale (TLOC (50, 10, 5)) distributions are assumed as the true models. The 1st and 2nd numbers at the right of the distribution names indicate the location (mean) and scale parameter of the LOG distribution. The 1st, 2nd, and 3rd numbers denote the location (mean), scale, and shape parameter of the TLOC distribution. A LOG distribution has longer tails and a higher kurtosis than a NORM distribution. The TLOC distribution is a type of Student’s t distribution, also called the nonstandardized Student’s t distribution (Jackman 2009) and has heavier and longer tails than a NORM distribution. Therefore, the LOG distribution is more leptokurtic and has a narrower shape than a NORM distribution. The TLOC distribution is more leptokurtic and has a wider shape than the NORM distribution even though the mean and standard deviation of the three distributions are the same. To distinguish the difference between the distributions, the variances of three distributions were chosen differently in this study. The lengths and thicknesses of the distribution tails are very important characteristics in reliability analysis; thus, three models with different tail characteristics are selected as the true models to verify the performance of the proposed method. Figure 5 shows the PDFs of the three distributions, and the formulas of the PDF of these distributions are described in detail in Appendix 1.

Fig. 5

PDFs of symmetric distributions

Tables 4 and 5 list the intersection areas using the three methods, and the number of times either the KbSSM process or the SSM process is performed in the ISM process when the LOG and TLOC distributions are the true models. In Table 4, the italic font indicates that the intersection areas of the SSM or KDE-ebd are larger than those of the ISM.

Table 4 Average intersection areas in SSM, KDE-ebd, and ISM: LOG (50, 2)

Table 5 Average intersection areas in SSM, KDE-ebd, and ISM: TLOC (50, 10, 5)

First, when the LOG distribution is a true model, the intersection area using the three methods and the number of performing KbSSM or SSM processes in the ISM is as listed in Table 4. The estimation accuracy using the three methods and the number of performing SSM processes increase as n increases, and the ISM yields always more accurate results than the SSM and KDE-ebd do except for n = 20 and 30. The ISM has the highest accuracy, followed by KDE-ebd and SSM, and also, the intersection areas using the ISM are slightly larger than those using KDE-ebd for n ≤ 10. However, the SSM is slightly more accurate than the ISM, and KDE-ebd has the lowest accuracy for n ≥ 20.

The LOG distribution has the smallest COV with the highest kurtosis; thus, the SSM converges more rapidly to the true model than the other models by identifying distributions with estimated parameters, whereas the KbSSM process tends to model a heavy tailed distribution using bounded data for conservative modeling. Therefore, the intersection areas using ISM, which is a mixture of the KbSSM and SSM processes, are slightly smaller than those using SSM especially for insufficient data such as n = 20 and 30. However, it is noteworthy that the maximum difference between the ISM and SSM is only 0.33%, which means that the two methods show similar performance. Therefore, we confirmed that the ISM is the most accurate among the three methods, regardless of the sample size.

Comparing the obtained results for LOG (50, 2) with those for NORM (50, 5), the overall intersection areas using the ISM for the LOG (50, 2) distribution are smaller than those of the ISM for the NORM (50, 5) distributions for n ≤ 20 because the LOG distribution has longer tails and larger kurtosis than the NORM distribution.

Next, when the true model is the TLOC distribution, the intersection areas and the number of performing KbSSM processes or SSM processes are as presented in Table 5. A similar tendency to that for the NORM and LOG distributions is still observed for the TLOC distribution. The TLOC distribution has the lowest estimation accuracies among the three distributions because the TLOC distribution has heavier and longer tails than the other distributions. However, the ISM is still the most accurate among the three methods, regardless of the number of samples.

4.3 Comparison of all the true distributions

Statistical modeling method should provide accurate models, but if there is not enough data, conservative models need to be obtained to compensate for modeling errors. In this section, the intersection areas between the estimated models and the true models and the QFVR were used as the measures of accuracy and conservativeness, respectively. In the simulation tests, the performances of ISM, KDE-ebd, and SSM were compared by calculating the intersection areas and QFVR values from estimated models using each method for different true models and sample sizes.

4.3.1 Modeling accuracy

In this section, the variations in the intersection areas using the SSM, KDE-ebd, and ISM are compared to verify the modeling accuracy of the proposed method for NORM, LOG, and TLOC distributions with various sample sizes. Figure 6 depicts the boxplot of the intersection areas using the three methods with 1000 repetitions when the number of samples changes from 3 to 50. The boxplot is useful and widely used to present the distribution of statistical results. In the boxplot, the degree of biased distribution is inferred through the position of the boxes; the top and bottom bounds of the boxes mean the 1st quartile (Q₁) and 3rd quartile (Q₃) respectively, and the line across the boxes indicates the 2nd quartile (Q₂, median value). The two end lines of the boxes are the outermost values of the data inside the two fences that are bounded by [Q₁ − 1.5 × IQR,  Q₁ + 1.5 × IQR], with IQR = Q₃ − Q₁; the point symbols (outside the observations) are the outliers outside both fences (Tukey 1977; Frigge et al. 1989). In Fig. 6, most of the data (over 98–99%) are between both fences.

Fig. 6

Boxplots of intersection areas according to the number of data. a NORM (50, 2.5) distribution. b NORM (50, 5) distribution. c NORM (50, 10) distribution. d LOG (50, 2) distribution. e TLOC (50, 10, 5) distribution

In Fig. 6, for all true models, when n increases, the median values of the intersection areas using the SSM, KDE-ebd, and ISM increase and become close to 1; in addition, the height of the boxes become narrower. For n ≤ 10, the ISM has the highest median value and the smallest variation of the intersection areas, whereas the SSM has the lowest median value and the largest variation owing to the identification and parameter estimation errors. Thus, the ISM has the highest accuracy and the SSM has the lowest accuracy especially for n ≤ 10. When n ≥ 20, the ISM and SSM have similar median values and variations for the intersection areas, but the ISM still has the most accurate results. As observed in Tables 1, 2, 3, 4, and 5, the intersection areas for the long-tailed distributions, such as LOG and TLOC, are slightly smaller than those for NORM distributions in the ISM for all sample sizes because of the difficulty in modeling tailed parts of the distributions with insufficient data.

In summary, for all of the true models, the ISM is slightly more accurate than the KDE-ebd; SSM has the lowest accuracy for n ≤ 10, and the estimation accuracies of the ISM are greater than or equal to those of the SSM; KDE-ebd is the most inaccurate for n ≥ 20. As the ISM shows the best accuracy among the three methods regardless of the number of samples, it is highly recommended for statistical modeling.

4.3.2 Modeling conservativeness

For the same true models and same sample sizes as Sect. 4.3.1, the means and variations of QFVR values using the SSM, KDE-ebd, and ISM are compared to verify the conservativeness of estimated distribution function. The QFVR is the ratio between quantile function values (iCDF values) of the estimated functions and true distributions corresponding to a reliability index (β). The QFVR is defined by

$$ \mathrm{QFVR}=\frac{\hat{Q}\left(P\left[X\le {X}^{\ast}\left(\beta \right)\right]\right)}{Q\left(P\left[X\le {X}^{\ast}\left(\beta \right)\right]\right)} $$

(18)

where $\hat{Q}$ and Q are the quantile function values of the estimated CDF and true CDF, respectively. P[X ≤ X^∗(β)] is a probability corresponding to the reliability index β with X^∗(β) = F⁻¹(Φ(β)). If the QFVR value is 1, the estimated distribution exactly describes the tail end of the true distribution. If the QFVR exceeds 1, it means that the estimated distribution is more conservative than the true distribution because it has heavier tails than the true distribution; thus, it yields conservative results in the reliability analysis or RBDO. If the QFVR is less than 1, the estimated distribution has a shorter tail than the true distribution, which leads to unreliable reliability analysis or RBDO results.

Figure 7 depicts the boxplots of the QFVR values using the three methods with 1000 repetitions for NORM (50, 5), NORM (50, 10), and TLOC (50, 10, 5) models (other results are included in Fig. 15 of Appendix 4) when the number of data varies from 3 to 50. For n ≤ 10, because the SSM yields shorter tailed distributions than other methods and large modeling errors, the average QFVR values are lower than other methods but with extremely large variations. Thus, the estimated model using the SSM results in unreliable analysis and design for insufficient data. The KDE-ebd and ISM have larger QFVR values than the SSM because they estimate heavier tailed distributions than the SSM. Thus, two methods can yield conservative design for insufficient data.

Fig. 7

Boxplots of QFVR according to the number of data. a NORM (50, 5) with β = 1. b NORM (50, 5) with β = 2. c NORM (50, 5) with β = 3. d NORM (50, 10) with β = 1. e NORM (50, 10) with β = 2. f NORM (50, 10) with β = 3. g TLOC (50, 10, 5) with β = 1. h TLOC (50, 10, 5) with β = 2. i TLOC (50, 10, 5) with β = 3

For n ≥ 20, the SSM quickly converges to one because the data can better represent tails of distributions, and thus, the modeling accuracy rapidly increases while the KDE-ebd is still conservative due to its boundary effect. The QFVR values using the ISM also converge to one, but they tend to do in a more conservative way than SSM. As β increases, i.e., the tail of the distribution being modeled becomes longer, modeling error of the SSM becomes large and the QFVR values become much less than 1. On the other hand, the KDE-ebd and ISM have higher QFVR values, but the ISM yields modeling results that are relatively more conservative than the KDE-ebd, especially when the data is insufficient. This is because the ISM can represent long tails of distributions through the conversion of estimated models to parametric models, while the effect of bounded data in KDE-ebd decreases at the tail end. In addition, the larger the variance, the longer tail the estimated model has, so that TLOC with the highest variation has the highest average and variance of the QFVR values.

The ISM shows desirable modeling results in most cases, but not in the TLOC distribution with β = 3. Since the TLOC has extremely long and thick tails and small data cannot represent its tail end corresponding to β = 3, so that all three methods cannot show good performances in terms of conservativeness. Nevertheless, the modeling of the tail end does not much affect the accuracy of the overall model estimation, and the ISM still shows the higher conservativeness than other methods.

In summary, for all of the assumed true models, the ISM estimates more conservative distribution function than SSM for insufficient data while it quickly converges to true value rather than KDE-ebd as n increases. In addition, the conservativeness of ISM consistently increases as the reliability index increases unlike others. For the reliability analysis and design of systems requiring high reliability and accuracy, the ISM method is the most recommendable modeling method.

5 Numerical examples

5.1 Statistical modeling example

Numerical examplesStatistical modeling exampleTo demonstrate the performance of the ISM method, it is demonstrated how statistical modeling is conducted for real engineering data by comparing the intersection areas and QFVR values using the SSM, KDE-ebd, and ISM. In this study, the modeling was performed using 80 experimental data of the compressive strength of aluminum–lithium (Al–Li) alloy specimens (Montgomery and Runger 2003). A true distribution was assumed to be an estimated distribution from 80 data using SSM to compare the intersection areas and QFVR values between the estimated distributions and the true PDF using the three methods. This is because 80 data are considered sufficient to estimate the distribution function using the parametric method, which is commonly used for statistical modeling of compressive strength. Figure 8 shows the histogram and the estimated PDF by SSM of the Al–Li alloy with 80 data. The LOG distribution is estimated as the best-fit distribution, and the location and scale parameters of this distribution are 162.73 and 18.38, respectively, where the mean, standard deviation, skewness, and kurtosis are 162.73, 33.33 (COV = 20.48%), 0, and 4.2, respectively.

Fig. 8

Histogram and fitted distribution of the Al–Li alloy

To confirm the estimation accuracy and conservativeness using the ISM method, statistical modeling using SSM, KDE-ebd, and ISM is performed for n = 3, 5, 7, 10, 20, 30, 50, and 80 with 1000 repetitions, which are randomly generated from the given 80 data. The statistical modeling is repeated once only for n = 80, and the intersection areas and QFVR values using the three methods are compared for various sample sizes. Table 6 lists the average intersection areas using the three methods and the number of either SSM or KbSSM performed in the ISM process.

Table 6 Average intersection areas in SSM, KDE-ebd, and ISM: compressive strength

As presented in Table 6, the intersection areas using the three methods increase while the number of KbSSM processes decreases when n increases. The intersection areas of the ISM and SSM finally converge to one for n = 80, i.e., the estimated and true distributions are coincident. When n ≤ 7, the intersection areas using the ISM are always the largest and those using SSM are the smallest among the three methods. When n ≥ 10, the estimation accuracies of the ISM and SSM are almost the same and the accuracy of the KDE-ebd is the lowest. However, for n = 20, it is clearly shown that SSM is more accurate than ISM. It is because the samples are only randomly selected from 80 data in this example, which makes the SSM converge more rapidly to the true model obtained from 80 data rather than the ISM, whereas the ISM tends to perform a conservative modeling, rather than the SSM, using bounded data. However, for sufficient data such as n ≥ 30, ISM often uses SSM rather than KbSSM; thus, its performance becomes close to SSM.

Figure 9 presents the boxplots of the intersection area using the three methods for various sample sizes. As shown in Fig. 9, the median values of the ISM are always the highest among the three methods except n = 10, 20. Although the median value of the SSM is higher than that of the ISM for n = 10 and 20, the SSM range is wider than that of the ISM for n = 10, and the intersection areas using the SSM and ISM have similar variations for n = 20. The ranges of the intersection areas using the ISM and KDE-ebd are narrower than those using SSM for n ≤ 10; the ranges of the three methods become similar for n ≥ 20.

Fig. 9

Boxplots of intersection areas for Al–Li alloy according to the number of data

Figure 10 depicts the boxplots of the QFVR values using three methods. For n ≤ 10, the averages of QFVR values using SSM are quite lower than other methods with extremely high variation and ISM is slightly more conservative than KDE-ebd. For n ≥ 20, ISM and SSM tend to rapidly converge to one and KDE-ebd is still conservative. Finally, for n = 80, ISM and SSM equals to one since the estimated distribution using ISM becomes the assumed true distribution.

Fig. 10

Boxplots for QFVR for Al–Li alloy with β = 2 according to the number of data

In this example, the intersection areas using the ISM and KDE-ebd are smaller than those of the LOG distribution in the statistical simulations for n ≤ 10 because the experimental data of Al–Li may include bias or outliers, which could significantly affect the data quality for a small number of data; thus, the variations of QFVR values using three methods are larger than those of the LOG distribution in the simulation tests in Fig. 15 of Appendix 4. Accordingly, the ISM estimates a more conservative distribution than the LOG distribution estimated from 80 data owing to the characteristics of the KDE-ebd with thick tails. The accuracies of the three methods are higher than those of the LOG distribution in the statistical tests for n ≥ 20 because the effects of the bias or outliers become reduced and the population model is assumed as the estimated LOG distribution from 80 data. Because the ISM yields consistently more accurate, conservative, and robust statistical models than the SSM and KDE-ebd for both small and large number of data, we confirmed that the ISM is applicable to both real experimental and simulated data.

5.2 Reliability analysis example

In this section, a reliability analysis of a simple truss example was performed to show how statistical modeling results using the SSM, KDE-ebd, and ISM affect the estimation of probability of failure of the truss and how conservative their reliability analysis results are. This truss example has two members, and both horizontal and vertical loads act together on the joint between the two members, as shown in Fig. 11.

Fig. 11

Two-member truss

The two-member truss has both deterministic and random variables, and Table 7 indicates the properties of input variables with SI units (Park et al. 2015; Hong et al. 2018). Although the references have considered a correlation between random variables, in this study, all random variables are assumed to be independent because of the focus on modeling marginal distributions.

Table 7 Properties of input variables in the two-member truss

As this example has two elements, the probabilities of failure of the two elements are calculated, and then a system probability of failure is calculated. The two-member truss is a series system with members 1 and 2, and thus, this system fails when either member fails. The probability of failure of the series system is calculated as

$$ {P}_F^{SYS}=P\left[{g}_1>0\right]+P\left[{g}_2>0\right]-P\left[\left\{{g}_1>0\right\}\cap \left\{{g}_2>0\right\}\right] $$

(19)

where the 1st and 2nd terms are failure probabilities of elements 1 and 2, respectively, and the final term is the probability of failure when both members, 1 and 2, fail together. Given that members 1 and 2 are independent, the probability of failure of the system is represented as

$$ {P}_F^{SYS}=P\left[{g}_1>0\right]+P\left[{g}_2>0\right]-P\left[{g}_1>0\right]\cdotp P\left[{g}_2>0\right] $$

(20)

Therefore, the probability of failure of the two-member truss system can be obtained by calculating arithmetically the failure probabilities of both members. The performance functions of members 1 and 2 are defined as

$$ {g}_1=\frac{1}{2}\left(\frac{P_y}{\cos \alpha }+\frac{P_x}{\sin \alpha}\right)-{A}_1{\sigma}_{u1} $$

(21)

$$ {g}_2=\frac{1}{2}\left(\frac{P_y}{\cos \alpha }-\frac{P_x}{\sin \alpha}\right)-{A}_2{\sigma}_{u2} $$

(22)

As described in Table 7, all input random variables are independent and normally distributed, and also the performance functions, g₁ and g₂, are the linear combination of independent normal random variables; thus, g₁ and g₂ follow normal distributions. Accordingly, an exact probability of failure can be analytically calculated with the means and variances of g₁ and g₂. The means of g₁ and g₂ are obtained as

$$ {\mu}_{g_1}=\frac{1}{2}\left(\frac{\mu_{P_y}}{\cos \alpha }+\frac{\mu_{P_x}}{\sin \alpha}\right)-{A}_1{\mu}_{\sigma_{u1}} $$

(23)

$$ {\mu}_{g_2}=\frac{1}{2}\left(\frac{\mu_{P_y}}{\cos \alpha }-\frac{\mu_{P_x}}{\sin \alpha}\right)-{A}_2{\mu}_{\sigma_{u2}} $$

(24)

where ${\mu}_{g_1}$ and ${\mu}_{g_2}$ are the mean values of responses. ${\mu}_{P_x}$ and ${\mu}_{P_y}$ are the mean values of P_x and P_y, and ${\mu}_{\sigma_{u1}}$ and ${\mu}_{\sigma_{u2}}$ are the mean values of σ_u1 and σ_u2.

The variances of g₁ and g₂ are obtained as

$$ {\sigma}_{g_1}^2={\left(\frac{1}{2\cos \alpha}\right)}^2{\sigma}_{P_y}^2+{\left(\frac{1}{2\sin \alpha}\right)}^2{\sigma}_{P_x}^2+{A}_1^2{\sigma}_{\sigma_{u1}}^2 $$

(25)

$$ {\sigma}_{g_2}^2={\left(\frac{1}{2\cos \alpha}\right)}^2{\sigma}_{P_y}^2+{\left(\frac{1}{2\sin \alpha}\right)}^2{\sigma}_{P_x}^2+{A}_2^2{\sigma}_{\sigma_{u2}}^2 $$

(26)

where ${\sigma}_{g_1}$ and ${\sigma}_{g_2}$ are the variances of responses; ${\sigma}_{P_x}$ and ${\sigma}_{P_y}$ are the standard deviations of P_x and P_y; and ${\sigma}_{\sigma_{u1}}$ and ${\sigma}_{\sigma_{u2}}$ are the standard deviations of σ_u1 and σ_u2.

As g₁ and g₂ follow normal distributions, a probability of failure for each member is calculated by a linear transformation from normal distributions to standard normal distributions. The exact failure probabilities of the two members are obtained as

$$ {P}_F^1=1-\Phi \left(\frac{0-{\mu}_{g_1}}{\sigma_{g_1}}\right) $$

(27)

$$ {P}_F^2=1-\Phi \left(\frac{0-{\mu}_{g_2}}{\sigma_{g_2}}\right) $$

(28)

where Φ is the CDF of the standard normal distribution.

To carry out the reliability analysis using statistical models (PDFs), first, samples are randomly generated from the true models for n = 3, 5, 7, 10, 20, 30, and 50 with 200 repetitions, and then, the PDFs are estimated using ISM, SSM, and KDE-ebd for the randomly generated samples. Finally, the probabilities of failure are calculated using the reliability analysis methods. The probability of failure can be analytically calculated using (27) and (28) when all inputs have normal distributions, but they cannot be used for the estimated PDFs, such as nonparametric or nonnormal parametric distributions. Thus, the exact probability of failure is only calculated using (27) and (28), but the reliability analysis for the estimated PDFs is conducted using the Monte Carlo simulation (MCS) with 10⁶ samples.

To verify the accuracy of the estimated probabilities of failure of the system using the three methods, an exact probability of failure and lower and upper failure probabilities is employed as reference values. When increasing the number of data, the probabilities of failure calculated using each method tend to converge to the exact value, ${P}_{\mathrm{Sys}}^{\mathrm{Exact}}$ = 0.0838, but a large amount of data is required to show the convergence of each method to the true value. If probability bounds using p-box theory are used from sufficient data (e.g., 1000), it is possible to easily compare the convergence rate of each method even for reasonably sufficient data, such as 50. Thus, the estimated lower and upper bounds of the p-box from 1000 data, 0.0597 and 0.1123, were used as the lower and upper limits by assuming that input distribution types were known. Figure 12 shows the variations of the estimated probabilities of failure using SSM, KDE-ebd, and ISM.

Fig. 12

Boxplots of failure probabilities using ISM, KDE-ebd, and SSM

As n increases, the boxes of the SSM, KDE-ebd, and ISM become close to ${P}_{\mathrm{Sys}}^{\mathrm{Exact}}$ and are within the lower and upper limits while KDE-ebd does not. SSM is the closest to ${P}_{\mathrm{Sys}}^{\mathrm{Exact}}$ and has the fastest convergence regardless of the number of data, but it mostly underestimates the probabilities of failure for n ≤ 20 because the SSM often estimates a PDF with short tails for input variables. KDE-ebd is the farthest from ${P}_{\mathrm{Sys}}^{\mathrm{Exact}}$ and shows the slowest convergence rate despite of the sufficient number of data. This is because KDE-ebd yields conservative probabilities of failure owing to their heavy tails of distributions (Kang et al. 2018). The ISM estimates a conservative probability of failure of the system, similar to that of the KDE-ebd, but it is slightly more accurate than the KDE-ebd for n ≤ 10 and its boxes rapidly converge to be within the limits. This is similar to SSM, but ISM does not underestimate the probabilities of failure for n ≥ 20.

Table 8 presents the ratios of the number of values within the bounds of the p-box to the total number of repetitions. For example, results using SSM for n = 5 indicate that 33% of estimated system failure probabilities are larger than the upper limit, 25% of them are between the limits, and 42% of them are smaller than the lower limit.

Table 8 Ratios of failure probabilities to the lower and upper criteria

As shown in Table 8, KDE-ebd does not underestimate the system probabilities of failure regardless of the number of data, but it has the smallest ratios for the cases within the limits, even for sufficient data. The SSM has larger ratios for the cases within the limits than KDE-ebd, but it often underestimates the system failure probability. The ISM does not underestimate the system failure probability for n ≤ 10 and its ratios for the cases within the limits are the highest for n ≥ 20. Accordingly, it is shown that the ISM can yield conservative results for insufficient data and it can quickly converge to the exact probability of failure as n increases.

The ISM method obtains a conservative reliability results using conservative statistical modeling of distributions of input variables with limited data, but there are other conservative reliability analysis methods using distributions of performance functions. Bayesian approach was recently applied to estimate a distribution of a performance function using limited data of input random variables (Gunawan and Papalambros 2006; Youn and Wang 2008; Wang et al. 2009). However, it estimates a distribution of the performance function only for reliability analysis; thus, we cannot know a distribution of input random variables. On the other hand, conservative statistical modeling method like ISM directly estimates distributions of input or output random variables, so that the result of statistical modeling can be used in any probabilistic and statistical methods or uncertainty propagation methods such as reliability or robust analysis as well as the statistical model validation and calibration.

6 Conclusions

Various uncertainties of random variables can be quantified using either the parametric or nonparametric statistical modeling methods. The parametric modeling method is convenient, user friendly, and easy to be handled in the statistical modeling and uncertainty propagation. Further, it shows fast convergence to the population model for sufficient data; however, it is not accurate and conservative for insufficient data owing to the wrong identification of the distribution types and parameters. Conversely, the nonparametric modeling method is more accurate and conservative than the parametric one for insufficient data; however, it has a slower convergence to the population model than the parametric modeling method for sufficient data and is not user friendly. In this study, an ISM method, which achieves the merits of the parametric (SSM) and nonparametric modeling methods (KDE-ebd) and overcomes their demerits, was proposed. In the ISM method, SSM is used to model sufficient data using parametric distributions or KDE-ebd is used to model insufficient data using kernel density functions with the estimated bounded data according to the quality of the given data through a two-sample K–S test. Further, the estimated KDE-ebd density function is converted to a parametric distribution through a GOF test and model selection method in the KbSSM process, which can be easily used in various statistical analysis and yield conservative analysis results.

The intersection areas between the estimated PDF and the true PDF using the SSM, KDE-ebd, and ISM were calculated and compared to verify the accuracy of the proposed method by conducting statistical simulation tests for various symmetrical distribution types and sample sizes. The simulations verify that the ISM including the KbSSM is more accurate and reliable than the SSM and KDE-ebd for insufficient data, and it quickly converges to the true model for sufficient data when the true model follows various symmetrical distributions. Further, QFVR values evaluated at tails of estimated distributions were used to compare the conservativeness of the ISM with SSM and KDE-ebd. As a result, the ISM evaluates the tail of the distribution more conservatively and robustly than other methods, and as the number of data increases, the convergence to the true model is also superior. For the real experimental data of compressive strength of an Al–Li alloy, the ISM is still more accurate and reliable than the SSM and KDE-ebd, regardless of the number of data. Additionally, the ISM is confirmed to yield more conservative and reliable failure probabilities than the SSM and KDE-ebd through the reliability analysis of a two-member truss example. Consequently, the ISM can consistently estimate the true distribution more conservatively and accurately than either the SSM or KDE-ebd, regardless of the number of data. Moreover, the ISM fits data to a parametric distribution function using the KDE-ebd method. Therefore, it is convenient, familiar to engineers, and can be easily applied to the uncertainty propagation by analytically calculating statistical moments or performance functions.

In this study, only the theoretical explanations of the ISM and the simulation test results for the symmetrical distribution, which are commonly used in engineering applications, were presented. However, it is also necessary to test the ISM for nonsymmetrical and multimodal distributions and show how the estimated statistical model using the ISM affects the statistical analysis. If all these problems were to be handled in this study, the contents would be very extensive; therefore, only the ISM and the simulations tests for the symmetrical distribution were covered here. In part II of the paper, the simulation results for various shapes of distributions and how the ISM is applied to statistical analysis in practical engineering applications will be presented.

7 Replication of results

The procedure of the proposed method is described in detail in the flowchart of Fig. 1, and all the methods are implemented using MATLAB 2018a. The authors do not supply the MATLAB codes directly as the supplementary materials to void its use for commercialization purpose. However, we briefly describe how to implement the MATLAB codes to make them easier to reproduce all the results of this study.

If the input data are given by users, only the critical value for two-sample K–S test can be defined before step (1). For simulation, the input data need to be randomly generated using a MATLAB built-in function “random” according to the number of sample size (n). Since the samples are differently generated for every data set with n sample size, 1000 data sets were tested to reduce the randomness effect of the generated samples in simulation tests. Using the given or generated data, a two-sample K–S test is implemented to check whether two data sets are sampled from a same distribution using a built-in function “kstest2,” which are given as (1), (2), and (3). If the SSM process is selected, i.e., “Yes” in the decision box of step (1), the GOF test (K–S test) is implemented to input data for all candidate models using a function “kstest” ((4) and (5)), then the BIC values are calculated for remained models by the K–S test. To calculate BIC values, a probability distribution object (PD) is generated using a built-in function “fitdist,” and next, the negative log maximum likelihood value (NLL) is calculated ((7)) using a built-in function “PD = fitdist(x, “normal”)” and “NLL = PD.NLogL,” and then, the BIC values are calculated with (6). Finally, a model with the minimum BIC value is selected as the best-fitted model to input data. The probability distribution object of the obtained model includes information of statistical parameters where “PD” file of the best-fitted model can be opened for more detail information such as parameter name and values, “PD.ParameterNames” and “PD.ParameterValues,” which return the name of the parameters and their values for the obtained model ((8)). The flowchart of SSM is included in Fig. 13 of Appendix 2, and the detailed description is included in the original SSM paper by Kang et al. 2016. If the KbSSM process is selected, i.e., “No” in the decision box of step (1), the KDE-ebd and SSM processes are sequentially implemented. Firstly, in order to generate bounded data in KDE-ebd process, bounds are calculated by the interval estimation on a uniform distribution to input data using a built-in function “unifit” denoted as (9), (10), and (11). Next, kernel estimators, f_k, f_k−1, and f_k−2 (PDFs), are estimated on grid points, “xx” using a built-in function “ksdensity” with “[fk, xx]=ksdentiy (xk)”, “[fk_1] = ksdensity (xk_1, xx)”, and “[fk_2] =ksdensity (xk_2, xx).” Then, the intersection areas, IA_k,k−1 and IA_k,k−2, are calculated by using the Riemann integral on the grid points “xx” ((12) and (13)). If IA_k,k−1 and IA_k,k−2 do not satisfy the criterion of the decision box in Fig. 14 of Appendix 3, additional bounded data is added and iterations are repeated. Otherwise, the KDE-ebd process is terminated and the probability distribution object for the last f_k is estimated based on the given and estimated bounded data together using “fitdist” like “PD_k = fitdist(x_ebdk, “kernel”)” where x_ebdk is the given and bounded data at the last iteration ((14) and (15)). Subsequently, in order to convert the estimated nonparametric model using KDE-ebd to a parametric model, resampled data are generated using a quantile function (inverse CDF) of the kernel estimator by KDE-ebd using a built-in function “random” ((16) and (17)) where the number of resampled data is 300 in this study. Finally, the SSM method is implemented to the resampled data like the above SSM process, then the KbSSM process is terminated. The flowchart of KDE-ebd is included in Appendix 3 in this paper, and more detailed description is given in the original KDE-bd/KDE-ebd paper by Kang et al. (2018).

Fig. 13

SSM process

Fig. 14

KDE-ebd process

Fig. 15

Boxplots of QFVR according to the number of data. a NORM (50,2.5) with β=1. b LOG (50,2) with β=1. ~

Appendices

Appendix 1. Probability density functions

Types	PDF	Parameters
Normal	$f\left(x|\mu, \sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left\{\frac{-{\left(x-\mu \right)}^2}{2{\sigma}^2}\right\}$	μ: Location (mean) σ: Scale (standard deviation)
Logistic	$f\left(x|\mu, \sigma \right)=\frac{\exp \left(\frac{x-a}{b}\right)}{b{\left\{1+\exp \left(\frac{x-a}{b}\right)\right\}}^2}$	a: Location (mean) b: Scale
t Location scale	$f\left(x|\mu, \sigma, \nu \right)=\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\sigma \sqrt{\nu \pi}\Gamma \left(\frac{\nu }{2}\right)}{\left[\frac{\nu +{\left(\frac{x-\mu }{\sigma}\right)}^2}{\nu}\right]}^{-\left(\frac{\nu +1}{2}\right)}$	μ: Location (mean) σ: Scale ν: Shape

Appendix 2. Flow chart of SSM

Appendix 3. Flow chart of KDE-ebd

Appendix 4. Quantile function value ratio