Topology optimization method with elimination of enclosed voids

Abstract

In this paper, a side constraint scheme is presented for topology optimization considering structural connectivity. Void features are used as basic design primitives with their movements and shape changes to drive topology optimization. To ensure the structural connectivity, design variables related to the centers of all the void features are bounded outside the design domain by means of side constraints without introducing additional nonlinear constraints. It is shown that the side constraint scheme is effective to eliminate enclosed voids and well adapted to the additive manufacturing (AM) without concern of unmelted powders inside the structure. Several representative examples are tested to demonstrate the effectiveness of the proposed method.

1 Introduction

Topology optimization (Bendsøe and Sigmund 1999; Zhou and Rozvany 1991) has been regarded as a powerful design approach in determining the best material distribution to obtain desired functional performances within a given design domain. However, the complexity of the obtained solutions might be a major problem for conventional subtractive manufacturing techniques and the original design has to be modified accordingly. In recent years, additive manufacturing (AM) receives significant attention (Frazier 2014; Gao et al. 2015; Horn and Harrysson 2012; Wong and Hernandez 2012). This manufacturing technique has the characteristics of depositing materials layer by layer and thus provides a great flexibility for manufacturing of structures with complex geometries. Therefore, AM is considered as a better choice of achieving a seamless integration with the advanced topology optimization method to attain the lightweightness and high performance of a structure both in design and manufacturing.

Although AM significantly opens up the design space, it is not completely a free-form manufacturing technique. Two basic issues exist at the design stage: overhang angle and structural connectivity. The first one requires that the inclined angles along the overhang boundaries of a designed structure should be less than the critical overhang angle (COA). Otherwise, auxiliary supports would be added to prevent the overhang portions from collapsing during the AM process. As these supports are finally removed, their presence will lead to the waste of materials, high processing cost, and production time. For this reason, much effort has been devoted to this problem (Gaynor and Guest 2014, 2016; Guo et al. 2017; Langelaar 2016; Langelaar 2017; Qian 2017; Wang et al. 2018; Zhang and Zhou 2018). The second issue concerns the avoidance of enclosed voids inside the designed structure for structural connectivity. The existence of enclosed voids implies that there is no way to get the unmelted powders and inner supports out of these voids after the part is completed (Albakri et al. 2015; Chua and Leong 2014; Diegel et al. 2010; Hu et al. 2016; Liu and Ma 2016; Meisel and Williams 2015; Zhou and Saitou 2017) by the AM techniques, e.g., selective laser melting (SLM) and stereo lithography appearance (SLA). Besides, building accuracy, minimum feature size, interlayer mechanical properties, and surface finish are also important factors influencing the AM quality (Diegel et al. 2010; Qattawi and Ablat 2017).

Liu et al. (2015) and Li et al. (2016) proposed a virtual temperature method to force the connections of isolated voids for structural connectivity. In detail, a virtual heating source is introduced to each void field, while solid areas are filled with thermal insulation materials. In this way, isolated voids will be controlled by constraining the maximum temperature over the structure to release the accumulation of heat energy. Clearly, this method requires an additional temperature field analysis so that the final design depends upon the choices of temperature limit and conductivity parameters significantly.

Moreover, the elimination of enclosed voids in a structure is also required in casting, cutting, and some other manufacturing processes. Take casting process as an example. In order to facilitate the removal of casting mold, enclosed voids are not allowed in casting parts. As pointed out by Xia et al. (2010), a new void cannot be nucleated in the interior of a structure if the conventional level-set-based method without the topological derivative is adopted. Gersborg and Andreasen (2011) implicitly involved a connectivity constraint by using a Heaviside design parameterization. These methods are always tightly coupled to other casting constraints, which will generate too conservative results. Hence, there is still a lot of spaces exploiting a better approach for structural connectivity.

In this work, feature-driven topology optimization method (Zhang et al. 2017a, b, c; Zhang and Zhou 2018; Zhou et al. 2016) is extended to take into account the structural connectivity for the AM. The design procedure is as follows. Void features are modeled by level-set functions (LSFs) in terms of closed B-splines (CBS) or super-ellipses that act as basic primitives in topology optimization. A side constraint scheme is proposed to bound design variables related to center points of these features outside the contour of the design domain. This scheme implies that the avoidance of enclosed voids is realized without introducing additional nonlinear constraints and additional computing burden. Besides, fixed mesh technique is adopted for structural analysis and sensitivity analysis.

The paper is organized as follows. Section 2 gives an introduction about the topology modeling with closed B-spline and super-ellipse in form of level-set function (LSF). Moreover, the side constraint scheme is presented for the purpose of structural connectivity. Section 3 gives a brief presentation about structural analysis based on the fixed mesh technique and followed by sensitivity analysis. In Section 4, the effectiveness and merits of the proposed method are demonstrated with three numerical examples. Finally, conclusions are drawn out in Section 5.

2 Topology modeling with closed B-spline and super-ellipse

Level-set function Φ(x) is an implicit function defined in a higher dimensional space (Fedkiw and Osher 2002). The zero-value contour of a LSF can be used to represent the geometrical boundary of a feature or a structure. Figure 1 depicts a bounded domain Ω for which an arbitrary point x can obviously be classified according to the sign of Φ(x).

$$ \Big\{{\displaystyle \begin{array}{c}\varPhi \left(\boldsymbol{x}\right)>0\\ {}\varPhi \left(\boldsymbol{x}\right)<0\\ {}\varPhi \left(\boldsymbol{x}\right)=0\end{array}}{\displaystyle \begin{array}{c}\\ {}\\ {}\end{array}}{\displaystyle \begin{array}{c}\forall \\ {}\forall \\ {}\forall \end{array}}{\displaystyle \begin{array}{c}\boldsymbol{x}\in \\ {}\boldsymbol{x}\notin \\ {}\boldsymbol{x}\in \end{array}}{\displaystyle \begin{array}{c}\varOmega \\ {}\varOmega \\ {}\partial \varOmega \end{array}} $$

(1)

where ∂Ω is the solid-void interface.

Fig. 1

The LSF of a solid domain Ω. a A solid domain Ω. b The corresponding LSF Φ(x)

In this paper, topology optimization is achieved by the movements, intersections, and deformations of void features defined by closed B-splines (CBS) and super-ellipse. Based on our previous 2D works (Zhang et al. 2017b; Zhou et al. 2016), the LSFs of 3D void features are derived correspondingly.

2.1 Mathematical formulation of closed B-spline

B-spline has been extensively used in the CAD community due to its local modifiability and flexible controlling property. A 2D CBS is defined as a generalized circle whose radius r is parameterized as a linear combination of a set of control radii {R_i}. The LSF of the CBS is written as

$$ \Big\{{\displaystyle \begin{array}{l}{\phi}_v\left(x,y,r\right)=r-\sqrt{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}\\ {}r\left(\theta \right)=\sum \limits_{i=1}^m{R}_i{B}_{i,p}\left(\frac{\theta +\pi /2}{2\pi}\right)\end{array}} $$

(2)

where B_{i, p} is the ith B-spline basis function defined by uniform and open knot vectors with order p. θ is relevant to the coordinate system and calculated as

$$ \theta =\Big\{{\displaystyle \begin{array}{ll}\arctan \frac{y-{y}_0}{x-{x}_0}& x\ge {x}_0\\ {}\arctan \frac{y-{y}_0}{x-{x}_0}+\pi & x<{x}_0\end{array}}\kern0.5em \theta \in \left[-\frac{\pi }{2},\frac{3\pi }{2}\right] $$

(3)

Considering the closure of B-spline curves, R₁ and R_m are set to the same value. Figure 2 shows a quadratic CBS with a set of control radii R = {R_i} = {1.5, 2.5, 0.8, 3, 1.2, 3.2, 1.5} and the mapping relation from Cartesian coordinate θOR to xOy.

Fig. 2

Control points P_i and parameters R_i of a quadratic CBS. a In Cartesian coordinate system θOR. b In Cartesian coordinate system xOy

In 3D case, the LSF of the CBS is written as

$$ \Big\{{\displaystyle \begin{array}{l}{\phi}_v\left(x,y,z,r\right)=r-\sqrt{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2+\left(z-{z}_0\right)}\\ {}r\left(\theta, \beta \right)=\sum \limits_{i=1}^{m1}\sum \limits_{j=1}^{m2}{R}_{i,j}{B}_{i,p}\left(\frac{\theta +\pi /2}{2\pi}\right){B}_{j,q}\left(\frac{\beta +\pi /2}{\pi}\right)\end{array}} $$

(4)

with

$$ \beta =\arctan \frac{z-{z}_0}{\sqrt{{\left(x-{x}_0\right)}^2+{\left(y-{y}_0\right)}^2}}\kern0.5em \beta \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right] $$

(5)

where B_{i, p} and B_{j, q} are two independent B-spline basis functions. As shown in Fig. 3, θ and β represent inclined angles of radius r. The value of θ ranges within the interval [−π/2, 3π/2] and the range of β is [−π/2, π/2]. In addition, the closure of the CBS requires that

$$ \Big\{{\displaystyle \begin{array}{ll}{R}_{1,j}={R}_{m1,j}& j=1,2,...,m2\\ {}{R}_{1,1}={R}_{2,1}=...={R}_{m1,1}& \\ {}{R}_{1,m2}={R}_{2,m2}=...={R}_{m1,m2}& \end{array}} $$

(6)

Fig. 3

The definition of θ and β

Let us consider a set of control parameters R = {R_{i, j}} = {4, 4, ..., 4}. Suppose two knot vectors Ξ₁={0,0,0,1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,1,1,1} and Ξ₂={0, 0, 0, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1, 1, 1} are used to define two quadratic B-spline basis functions (p = 2, m1 = 11, q = 2, m2 = 9). Figure 4a represents the distribution of control points in the Cartesian coordinate system θβR and the resulting B-spline surface is shown in Fig. 4b. Clearly, a plane is obtained due to the same length of all control radii. Its conversion into Cartesian coordinate xyz produces a polyhedron of control points, as illustrated in Fig. 4c. Especially, m1 control points overlap at two poles. Figure 4d shows the constructed feature of the sphere with a radius of 4.

Fig. 4

Control points and biquadratic CBS. a The distribution of control points in Cartesian coordinate system θβR. b The corresponding surface in Cartesian coordinate system θβR. c The polyhedron of control points in Cartesian coordinate system xyz. d The corresponding surface in Cartesian coordinate system xyz

2.2 Mathematical formulation of super-ellipse

A super-ellipse can be seen as a generalized representation of circle, ellipse, square, and rectangle. The LSF of a 2D super-ellipse centered at point (x₀, y₀) with semi-length a, semi-width b, and inclined angle α (measured from the horizontal axis counterclockwise) is expressed as

$$ {\phi}_v\left(x,y\right)=1-\sqrt[s]{{\left|\frac{x^{\ast }}{a}\right|}^s+{\left|\frac{y^{\ast }}{b}\right|}^s} $$

(7)

with

$$ \left\{\begin{array}{c}{x}^{\ast}\\ {}{y}^{\ast}\end{array}\right\}=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ {}-\sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{c}x-{x}_0\\ {}y-{y}_0\end{array}\right] $$

(8)

s is a relatively large even integer number (s = 6 is taken in the present study). Figure 5a, b depicts the geometry and the corresponding LSF of a super-ellipse. Here, five design variables {x₀, y₀, a, b, α} are adopted to control a super-ellipse.

Fig. 5

The illustration of a super-ellipse. a Geometric description. b The corresponding LSF

According to (7), the LSF of a 3D super-ellipse corresponds to

$$ {\phi}_v\left(x,y,z\right)=1-\sqrt[s]{{\left|\frac{x^{\ast }}{a}\right|}^s+{\left|\frac{y^{\ast }}{b}\right|}^s+{\left|\frac{z^{\ast }}{c}\right|}^s} $$

(9)

where

$$ \left[\begin{array}{c}{x}^{\ast}\\ {}{y}^{\ast}\\ {}{z}^{\ast}\end{array}\right]=A\cdot B\cdot C\left[\begin{array}{c}x-{x}_0\\ {}y-{y}_0\\ {}z-{z}_0\end{array}\right] $$

(10)

with

$$ A=\left[\begin{array}{ccc}1& 0& 0\\ {}0& \cos {\alpha}_1& -\sin {\alpha}_1\\ {}0& \sin {\alpha}_1& \cos {\alpha}_1\end{array}\right] $$

(11)

$$ B=\left[\begin{array}{ccc}\cos {\alpha}_2& 0& \sin {\alpha}_2\\ {}0& 1& 0\\ {}-\sin {\alpha}_2& 0& \cos {\alpha}_2\end{array}\right] $$

(12)

$$ C=\left[\begin{array}{ccc}\cos {\alpha}_3& -\sin {\alpha}_3& 0\\ {}\sin {\alpha}_3& \cos {\alpha}_3& 0\\ {}0& 0& 1\end{array}\right] $$

(13)

The design variables involved in a 3D super-ellipse are {x₀, y₀, z₀, a, b, c, α₁, α₂, α₃}. Among them, (x₀, y₀, z₀) represent the coordinates of the center point. Semi-length a, semi-width b, and semi-height c describe the dimension of a super-ellipse. α₁, α₂, and α₃ denote the rotation angles around the x-axis, y-axis, and z-axis, respectively. It is noteworthy that the rotation angle is always considered to be enlarged for counterclockwise direction from the positive end of rotation axis. The order of rotation axis is strictly in accordance with the first x-axis, then y-axis, and the last z-axis. Figure 6 shows a super-ellipse with α₁ = 45^∘, α₂ = 45^∘, and α₃ = 45^∘.

Fig. 6

A 3D super-ellipse

2.3 Side constraint scheme for structural connectivity

Figure 7a shows an example in terms of structural connectivity without enclosed void. In contrast, the existence of two inner voids shown in Fig. 7b will make it difficult to remove unmelted powders or auxiliary supports produced in the AM process. The proposed side constraint scheme is to take locations of center points of void features as design variables and then constrain their variations outside the design domain.

Fig. 7

Connectivity of 2D structures. a Structure without enclosed void. b Structure with two enclosed voids

To make things clear, consider a rectangular domain with dimensions L₁ × L₂ in Fig. 8. All 10 void features are constrained to impose their center locations along the borders of the design domain at least. Each feature will only have a part inside the design domain so that enclosed voids are avoided to ensure the structural connectivity.

Fig. 8

Initial structure with 10 void features

A summary is made about the side constraints to the feature centers in Table 1. It is noteworthy that there are two options for the void features with centers located at the corners. The same method can be extended to 3D problems. Void features are initially distributed on the boundary surfaces of the design domain and the variation bounds of design variables are determined correspondingly.

Table 1 Specific requirements for void features

From the above presentation, we can see that structural connectivity can be effectively achieved without introducing any additional constraint in topology optimization. In this way, only proper bound values are imposed for design variables related to the void centers within the framework of feature-driven method.

3 Topology optimization and sensitivity analysis

3.1 Structural analysis with fixed computing mesh

According to Section 2, suppose n void features defined by the LSFs ϕ_v1(x),ϕ_v2(x),..., ϕ_vn(x) are involved in a design domain defined by the LSF ϕ_d(x). The LSF of the whole structure, Φ, can then be constructed through Boolean operations of void features and the design domain, i.e., union ∪ and intersection ∩. Figure 9 shows the construction process of a structure. Boolean operations are mathematically equivalent to the following min and max computing.

$$ \varPhi =\mathit{\min}\left({\phi}_d,-\mathit{\max}\left({\phi}_{v1},{\phi}_{v2},...,{\phi}_{vn}\right)\right) $$

(14)

Fig. 9

Topology modeling of a structure with Boolean operations. a Construction process. b Corresponding LSFs

Here, the negative sign means that each feature represents a void rather than a solid inclusion. Within this scope, KS function given below is utilized to formulate the expression approximately.

$$ KS=\frac{1}{2}\ln \left({e}^{w{\phi}_1}+{e}^{w{\phi}_2}+\dots +{e}^{w{\phi}_g}\right) $$

(15)

In this expression, ϕ₁,ϕ₂, …, ϕ_g denote the LSFs of g primitives. The sign of parameter w determines the type of Boolean operation. w > 0 and w < 0 correspond to max and min, respectively. Other functions, e.g., R-function and P-norm, can also be used for the max and min computing (Ricci 1973; Rvachev 1982; Shapiro 1991). Based on (14), Φ is expressed as

$$ \varPhi =\frac{1}{w}\ln \left({e}^{w{\phi}_d}+{e}^{-w{\varPhi}_v}\right)\kern0.5em w<0 $$

(16)

with

$$ {\varPhi}_v=\frac{1}{w}\ln \left({e}^{w{\phi}_{v1}}+{e}^{w{\phi}_{v2}}+...+{e}^{w{\phi}_{vn}}\right)\kern0.5em w>0 $$

(17)

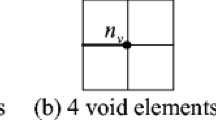
In our study, fixed mesh technique is adopted for structural analysis. Without loss of generality, Fig. 10 illustrates a 2D structure. The structural domain Ω is embedded into a rectangular domain $\overline{\varOmega}$ which is further discretized into regular quadrilateral elements. Thus, three kinds of elements exist: (i) void elements with all nodes located outside the physical domain Ω; (ii) solid elements with all nodes located inside the physical domain Ω; (iii) boundary elements cut by the structural boundary ∂Ω. Consider the general integral related to the solid domain defined by Φ.

$$ \varPsi \left(\varPhi \right)={\int}_{\overline{\varOmega}}\psi \left(\boldsymbol{x}\right)H\left(\varPhi \right) d\varOmega $$

(18)

when ψ(x) = B^TDB (B is the strain-displacement matrix and D is the elasticity matrix), Ψ(Φ) is equal to the structural stiffness matrix. When ψ(x) = 1, Ψ(Φ) is equal to the structural volume. H(·) denotes the Heaviside function.

$$ H\left(\varPhi \right)=\Big\{{\displaystyle \begin{array}{c}1\kern0.5em \varPhi \ge 0\\ {}0\begin{array}{cc}& \varPhi <0\end{array}\end{array}} $$

(19)

Fig. 10

The process of structural analysis for 2D problems

In numerical implementation, H(Φ) is often smoothed by its regularized version $\overline{H}\left(\varPhi \right)$. Here, the regularized Heaviside function $\overline{H}\left(\varPhi \right)$ in the form of piecewise polynomial (Wang et al. 2003) is adopted.

$$ \overline{H}\left(\varPhi \right)=\Big\{{\displaystyle \begin{array}{cc}1& \varPhi \ge \varDelta \\ {}\frac{3\left(1-\lambda \right)}{4}\left(\frac{\varPhi }{\varDelta }-\frac{\varPhi^3}{3{\varDelta}^3}\right)+\frac{1+\lambda }{2}& -\varDelta \le \varPhi <\varDelta \\ {}\lambda & \varPhi <-\varDelta \end{array}} $$

(20)

In this expression, a very small positive number λ (commonly, λ = 1 × 10⁻⁶ ∼ 1 × 10⁻³) is introduced as the “ersatz material” (Allaire et al. 2004) to prevent the singularity of stiffness matrix in structural analysis. Compared with Heaviside function in Fig. 11a, b has a significant transition near zero level-set. Δ determines the width of transition interval.

Fig. 11

Heaviside function and the regularized version. a Heaviside function. b The regularized Heaviside function

In our work, the value of LSF at the center point of each element is utilized for the assignment of material property.

$$ {E}_i=\overline{H}\left(\varPhi \left({\boldsymbol{x}}_{ci}\right)\right){E}_0 $$

(21)

where x_ci represents the coordinates of the center point of the ith element. E₀ and E_i are Young’s modulus of solid material and that of the ith element, respectively.

Take the plate with a hole in Fig. 12 as an example. The left side of the plate is fixed and a vertical force is applied at the lower right corner. The structure has a dimension of 20 × 20 and the radius of the circular hole centered at (10,10) is 5. Thus, the LSF of the whole structure responds to

$$ \varPhi =\sqrt{{\left(x-10\right)}^2+{\left(y-10\right)}^2}-5 $$

(22)

Fig. 12

A plate with a circular hole

The first step is to embed the structure into a regular domain with a dimension of 20 × 20. The domain is further discretized into rectangular elements of size 0.5 × 0.5. Figure 13 gives the material distributions with three different values of Δ. Obviously, the number of elements full of intermediate materials increases when Δ is set to a larger value. At the same time, the sensitivity accuracy cannot be guaranteed when Δ is too small, which will be tested in Section 4.3.

Fig. 13

Material distributions. aΔ = 0.05. bΔ = 0.25. cΔ = 2

The effects of Δ upon compliance and volume are further investigated and illustrated in Fig. 14a and b, respectively. When Δ is equal to 0.24, the compliance has the same value as the solution of finite element analysis (FEA). With the increase of Δ, the compliance keeps coming down and considerable errors produce. Notice that in FEA, element type and element size are consistent with the fixed mesh adopted in this paper. The volume also has a downward trend except for a small segment at the beginning and reaches the analytic solution at Δ = 0.27. In view of this, nearly half of the element size seems to be a good choice for Δ.

Fig. 14

The effects of Δ upon compliance and volume. a Compliance. b Volume

In addition, the LSF is normalized into a quasi-equidistant iso-contour needed in sensitivity analysis with narrow band scheme by means of the first-order approximation of signed distance function (Zhou et al. 2016). This treatment is important for the attainment of a clear material distribution in topology optimization.

3.2 Sensitivity analysis

Here, topology optimization related to the minimization of structural compliance with the volume constraint is considered. Since structural connectivity can be directly realized by the side constraints limiting the coordinates of the center points of all void features, no additional constraints are required in the optimization problem. The general mathematical formulation remains unchanged and is stated as

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Min}}\begin{array}{l}J={\boldsymbol{F}}^T\boldsymbol{U}\end{array}\\ {}s.t.\begin{array}{l}\end{array}\Big\{\begin{array}{ll}\boldsymbol{KU}=\boldsymbol{F}& \\ {}V={\int}_{\overline{\varOmega}}H\left(\varPhi \left(\boldsymbol{x}\right)\right) d\varOmega \le \overline{V}& \\ {}{\underset{\_}{\boldsymbol{d}}}_i\le {\boldsymbol{d}}_i\le \overline{{\boldsymbol{d}}_i}& i=1,2,...,n\end{array}\end{array}} $$

(23)

where J is the structural compliance. V is total volume of the structure with its upper bound $\overline{V}$. d_i refers to the vector of design variables involved in the ith feature with the lower bound ${\underset{\_}{\boldsymbol{d}}}_i$ and upper bound $\overline{{\boldsymbol{d}}_i}$. The composition of design variables is determined by specific void features adopted in the structure.

The derivative of the equilibrium equation KU = F at the both ends is

$$ \frac{\partial \boldsymbol{K}}{\partial {\boldsymbol{d}}_i}\boldsymbol{U}+\boldsymbol{K}\frac{\partial \boldsymbol{U}}{\partial {\boldsymbol{d}}_i}=\frac{\partial \boldsymbol{F}}{\partial {\boldsymbol{d}}_i} $$

(24)

Since load vector F is design-independent with ∂F/∂d_i = 0, the sensitivity of the compliance with respect to featured design variables can be expressed as

$$ \frac{\partial J}{\partial {\boldsymbol{d}}_i}=\frac{1}{2}{\boldsymbol{U}}^T\frac{\partial \boldsymbol{K}}{\partial {\boldsymbol{d}}_i}\boldsymbol{U}+{\boldsymbol{U}}^TK\frac{\partial \boldsymbol{U}}{\partial {\boldsymbol{d}}_i}=\frac{1}{2}{\boldsymbol{U}}^T\frac{\partial \boldsymbol{K}}{\partial {\boldsymbol{d}}_i}\boldsymbol{U}-{\boldsymbol{U}}^T\frac{\partial \boldsymbol{K}}{\partial {\boldsymbol{d}}_i}\boldsymbol{U}=-\frac{1}{2}{\boldsymbol{U}}^T\frac{\partial \boldsymbol{K}}{\partial {\boldsymbol{d}}_i}\boldsymbol{U} $$

(25)

Then, the general mathematical formulation for both stiffness matrix and volume in the form of (18) is considered. The sensitivity of Ψ(Φ) with respect to d_i is expressed as

$$ \frac{\partial \varPsi \left(\varPhi \right)}{\partial {\boldsymbol{d}}_i}={\int}_{\overline{\varOmega}}\psi \left(\boldsymbol{x}\right)\frac{\partial H\left(\varPhi \right)}{\partial \varPhi}\frac{\partial \varPhi }{\partial {\boldsymbol{d}}_i} d\varOmega ={\int}_{\overline{\varOmega}}\psi \left(\boldsymbol{x}\right)\delta \left(\varPhi \right)\frac{\partial \varPhi }{\partial {\boldsymbol{d}}_i} d\varOmega $$

(26)

with

$$ \delta \left(\varPhi \right)=\Big\{{\displaystyle \begin{array}{ll}+\infty & \varPhi =0\\ {}0& \varPhi \ne 0\end{array}} $$

(27)

δ(Φ) is discontinuous and is further replaced with the derivative of the regularized Heaviside function, $\overline{\delta}\left(\varPhi \right)$. As shown in Fig. 15, $\overline{\delta}\left(\varPhi \right)$ is nonzero only when values of the corresponding LSF fall into the transition interval [−Δ, Δ].

$$ \overline{\delta}\left(\varPhi \right)=\Big\{{\displaystyle \begin{array}{ll}\frac{3\left(1-\alpha \right)}{4}\left(\frac{1}{\varDelta }-\frac{\varPhi^2}{\varDelta^3}\right)& -\varDelta \le \varPhi <\varDelta \\ {}0& else\end{array}} $$

(28)

Fig. 15

The derivative of the regularized Heaviside function

Therefore, the sensitivities of element stiffness matrix and element volume are computed as

$$ \frac{\partial {\boldsymbol{k}}_e}{\partial {\boldsymbol{d}}_i}={\int}_{\varOmega_e}\boldsymbol{BDB}\overline{\delta}\left(\varPhi \left(\boldsymbol{x}\right)\right)\frac{\partial \varPhi \left(\boldsymbol{x}\right)}{\partial {\boldsymbol{d}}_i} d\varOmega $$

(29)

$$ \frac{\partial {V}_e}{\partial {\boldsymbol{d}}_i}={\int}_{\varOmega_e}\overline{\delta}\left(\varPhi \left(\boldsymbol{x}\right)\right)\frac{\partial \varPhi \left(\boldsymbol{x}\right)}{\partial {\boldsymbol{d}}_i} d\varOmega $$

(30)

In details, for solid or weak elements, the sensitivities are zero due to the zero-value of $\overline{\delta}\left(\varPhi \right)$. That is to say, only the elements full of intermediate materials are actually involved in the calculation.

4 Numerical examples

In this section, several numerical examples are provided to validate the effectiveness of the proposed method. The globally convergent method of moving asymptotes (GCMMA) (Svanberg 1995) within the Boss-Quattro™ optimization platform (Radovcic and Remouchamps 2002) is used as the optimizer. Young’s modulus of solid material and Poisson’s ratio are E₀ = 1 and ν = 0.3, respectively. The geometric data and loads are all dimensionless in the following examples.

4.1 A short beam

Figure 16 depicts a short beam. It is completely fixed along the left side and a vertical force is applied at the middle point of the right side. The model is discretized into a 80 × 40 quadrilateral mesh. The volume fraction of 50% is used as the upper bound of the volume constraint. Parameters Δ = 0.05 and λ = 1 × 10⁻⁶ are used in (20).

Fig. 16

A short beam. a Design domain. b The freely optimized result (Luo et al. 2009)

First, CBS curves are considered as void features to realize topological changes. In order to study the influence of connectivity constraint upon the optimized topologies, both free-form topology optimization and topology optimization considering structural connectivity are carried out. Figures 17a and 18a show the corresponding initial design models composed of 17 voids, each of which has 24 control radii. In total, 442 design variables exist. Figure 17b gives the freely optimized result, which shares the same topology as in Fig. 16b. Six inner holes violate the connectivity constraint. It is also observed that some void features move outside the design domain and become useless. Figure 17c depicts the convergence curves of compliance and volume.

Fig. 17

Free-form topology optimization with CBS void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

Fig. 18

Topology optimization considering structural connectivity with CBS void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

When void features in Fig. 18a are constrained to limit their locations of center points, each feature will have a portion that cannot enter the interior of the design domain. Hence, all voids are guaranteed to communicate with the outside of the design domain. The optimized result with connectivity is illustrated in Fig. 18b. The solution is a simply connected structure to favor the evacuation of the unmelted powders or liquids and removing support materials during the AM process. To have a clear idea about the topological changes, some intermediate iterations are given in Table 2. It is observed that structural optimization considering connectivity is actually a process of changing the boundary of the design domain. The convergence histories of compliance and volume are shown in Fig. 18c. In comparison, the free-form optimization achieves a compliance of 6011.72, while the compliance of the structure with connectivity has an increasing value of 19.78%.

Table 2 Evolutions of structural topology with connectivity

Now, the same number of super-ellipses is used to drive topology optimization. Each super-ellipse has five design variables related to the position, orientation, semi-length, and semi-width. There are a total number of 85 design variables, which is only one fifth of CBS features. Figure 19a represents the initial configuration without considering structural connectivity. Compared with CBS feature, super-ellipse tends to achieve topological change through intersection because of its insufficient deformation ability. This leads to a relatively simple topology with three inner holes in Fig. 19b. Figure 19c represents the convergence curves of compliance and volume. Usually, this deficiency is compensated by increasing the number of super-ellipses. When the initial structure consists of 34 super-ellipses distributed in a crossing way over the design domain, the corresponding optimized structure shares the topology similar to the result in Fig. 17b, as illustrated in Fig. 20.

Fig. 19

Free-form topology optimization with 17 super-elliptical void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

Fig. 20

Free-form topology optimization with 34 super-elliptical void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

Fig. 21

Topology optimization considering structural connectivity with 17 super-elliptical void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

For topology optimization considering structural connectivity, super-ellipses are initially distributed along the boundary of the design domain to facilitate the constraints on center points. Figures 21a and 22a give two initial structures with different numbers of super-ellipses. However, Figs. 21b and 22b illustrate that both two optimized structures are similar to the CBS-based result without enclosed void shown in Fig. 18b. The values of structural compliance correspond to 7880.14 and 7446.87. The convergence histories are shown in Figs. 21c and 22c, respectively.

Fig. 22

Topology optimization considering structural connectivity with 34 super-elliptical void features. a The initial layout. b The optimized result. c The convergence curves of compliance and volume

4.2 A simply supported hexahedron

A 3D hexahedron studied in (Li et al. 2016) is considered in Fig. 23. It has a dimension of 40 × 40 × 20 with four corners fixed at the bottom face in all three directions. A vertical force is applied at the center of the bottom face. Suppose that a bottom layer of 40 × 40 × 2 is a non-designable solid domain. Here, the structure is discretized with 50 × 50 × 25 8-node hexahedra elements. The volume fraction is limited to 30%, equally a volume of 9600. The smoothing parameter Δ is chosen to be 0.4 and λ is 1 × 10⁻⁶.

Fig. 23

A simply supported beam (Li et al. 2016)

Three cases are considered in Table 3 and initial layouts of CBS voids are shown in Fig. 24 to study the influences upon the optimized topology. Each void feature is represented by the CBS defined by 120 control radii. The initial structures will be used to perform both topology optimization without and with the consideration of structural connectivity, respectively. For the former, features are allowed to move freely rather than being restricted outside the design domain. Figure 25a–c gives the results of free-form optimization in three cases. Correspondingly, Fig. 25d–f provides the half models for the better observation of interior topologies. It can clearly be seen that even with different numbers of void features, the similar topology with one enclosed void is produced. Besides, compliance decreases as the number of features increase, but the amount of reduction is small.

Table 3 Three design cases of initial structure

Fig. 24

The initial structure with CBS void features. a 9 void features. b 13 void features. c 21 void features

Fig. 25

Free-form topology optimization. a The optimized result in case 1. b The optimized result in case 2. c The optimized result in case 3. d Half of the optimized structure in case 1. e Half of the optimized structure in case 2. f Half of the optimized structure in case 3

Now, side constraints are imposed for design variables related to the center coordinates of featured CBS. In detail, the z-coordinates of center points are all bounded by z₀ ≥ 20 for the features centered on the top surface. Similarly, other features are constrained for the x- or y-coordinates of center points. The optimized results and the corresponding half models are shown in Fig. 26. In three cases, the enclosed holes disappear. The compliance values are 239.71, 238.76, and 237.06 with the increasing values of 2.56%, 2.69%, and 2.60%.

Fig. 26

Topology optimization considering structural connectivity. a The optimized result in case 1. b The optimized result in case 2. c The optimized result in case 3. d Half of the optimized structure in case 1. e Half of the optimized structure in case 2. f Half of the optimized structure in case 3

In the results of free-form topology optimization, distributions of the center points of CBS features are depicted in Fig. 27. Black squares representing the center points inside the domain have a large number, while red solid circles representing the center points located outside the design domain are few. By contrast, all center points are successfully restricted outside the design domain owing to the imposed side constraints for the connectivity, as illustrated in Fig. 28. For two kinds of topology optimization, the convergence curves of compliance and volume are shown in Figs. 29 and 30, respectively. At the beginning of iterations, compliance changes sharply because the volume constraint is violated.

Fig. 27

The distribution of the center points of void features in the freely optimized results. a Case 1. b Case 2. c Case 3

Fig. 28

The distribution of the center points of void features in the optimized results considering structural connectivity. a Case 1. b Case 2. c Case 3

Fig. 29

The convergence curves of compliance and volume for free-form topology optimization. a Case 1. b Case 2. c Case 3

Fig. 30

The convergence curves of compliance and volume for topology optimization considering structural connectivity. a Case 1. b Case 2. c Case 3

Consider now the super-ellipse as an alternative feature. The initial structure is shown in Fig. 31 and the dimension of each void feature is 3 × 2 × 2. There are 65 super-ellipses perpendicular to the surfaces of the design domain. The total number of design variables is thus 65 × 9 = 585. Figure 32a, b shows the optimized result and the corresponding half model, respectively. In comparison with the CBS-based results, Fig. 32a produces the similar topology with one enclosed void.

Fig. 31

The initial structure with void features of super-ellipse (J = 226.69,V = 29185.60)

Fig. 32

Free-form topology optimization. a The optimized result. b Half of the optimized structure

Figure 33a represents the optimized result with the imposition of side constraints. From the half model shown in Fig. 33b, it can clearly be seen that no inner void exits. The compliance is 239.40, which is 2.96% higher than the freely optimized result (J = 232.51). Figure 34a, b depicts the distributions of the center points of super-ellipses in both optimized results. The convergence histories of compliance and volume are compared in Fig. 35a, b.

Fig. 33

Topology optimization considering structural connectivity. a The optimized result. b Half of the optimized structure

Fig. 34

The distribution of the center points of void features in the optimized results. a Freely optimized result. b Optimized result of connectivity

Fig. 35

The convergence curves of compliance and volume. a Free-form topology optimization. b Topology optimization considering structural connectivity

4.3 A torsion beam

Another 3D example of a torsion beam shown in Fig. 36 is studied. The structure is completely fixed along the left side and four loads are imposed on the four vertices of the right plane with an inclined angle of 45^∘. Suppose two cuboid zones with a dimension of 20 × 20 × 2 at both ends of the structure are chosen as non-design solid domains. The beam is discretized into hexahedral elements of size 0.8 × 0.8 × 0.8. Parameters λ = 1 × 10⁻⁶ are used in (20). The upper bound of volume is set to be 7200 with a volume fraction of 30%.

Fig. 36

A torsion beam (Liu et al. 2015)

As shown in Fig. 37, there are 44 CBS void features with 60 controlling radii in the initial structure and all features are centered on the surfaces. The total number of design variables is 44 × (60 + 3) = 2772. To highlight the effect of Δ, Fig. 38a, b gives the material distributions of the initial structure when Δ is set to 0.1 and 0.4, respectively. The latter has about one layer of intermediate elements around each hole, but only a few scattered intermediate elements exist in the former. The corresponding freely optimized results are illustrated in Fig. 39a, b. The half models in Fig. 39c, d indicate that a large enclosed void exists. Besides, compared with Fig. 39b, there are many pits on the surfaces of the structure in Fig. 39a.

Fig. 37

The initial structure with CBS void features

Fig. 38

Material distributions. aΔ = 0.1. bΔ = 0.4

Fig. 39

Free-form topology optimization. a The optimized result with Δ = 0.1. b The optimized result with Δ = 0.4. c Half of the optimized structure with Δ = 0.1. d Half of the optimized structure with Δ = 0.4

In Fig. 37, center points of all void features are restricted outside the design domain. The optimized results and the half models are shown in Fig. 40. Although structure configurations are no longer the same with different values of Δ, holes are always generated on the outer surface to realize structural connectivity. Similarly, the optimized result tends to have rough surfaces with Δ = 0.1. Compared with their respective freely optimized results, the compliance of the structure with connectivity goes up by 72.56% and 13.07%. Figures 41 and 42 give the convergence histories of two kinds of topology optimization. The curves with Δ = 0.1 always fluctuate greatly due to the sensitivity inaccuracy caused by too few intermediate elements. Therefore, a too small value of Δ causes a deterioration of structure smoothness and large fluctuations of the convergence curves.

Fig. 40

Topology optimization considering structural connectivity. a The optimized result with Δ = 0.1. b The optimized result with Δ = 0.4. c Half of the optimized structure with Δ = 0.1. d Half of the optimized structure with Δ = 0.4

Fig. 41

The convergence curves of compliance and volume for free-form topology optimization. aΔ = 0.1. bΔ = 0.4

Fig. 42

The convergence curves of compliance and volume for topology optimization considering structural connectivity. aΔ = 0.1. bΔ = 0.4

With a better choice (Δ = 0.4), topology optimization with void features of super-ellipse is also performed. The initial distribution of super-ellipses is demonstrated in Fig. 43. There are 120 super-ellipses centered on the surfaces of the design domain. The total number of design variable is 120 × 9 = 1080, which is about one third of the CBS-based topology optimization. Optimized topology is obtained after the movements, rotations, and deformations of super-ellipses and shown in Fig. 44a. The corresponding half model is illustrated in Fig. 44b. The big cavity is enclosed, which inevitably leads to the accumulation of a large amount of powders or liquids.

Fig. 43

The initial structure with void features of super-ellipses (J = 13021.15,V = 15400.96)

Fig. 44

Free-form topology optimization. a The optimized result. b Half of the optimized structure

Figure 45a represents the optimized structure considering connectivity and its half model is provided in Fig. 45b for a better observation. Clearly, it is the desired topology which has many accesses for the support structures or unmelted powers to be moved out. The final compliance corresponds to J = 12284.76 and it is 12.67% higher than that of unconstrained optimal solution (J = 10902.80). This is the price that should be paid for the structural connectivity. The convergence histories of compliance and volume are shown in Fig. 46 with the satisfaction of the prescribed volume constraint.

Fig. 45

Topology optimization considering structural connectivity. a The optimized result. b Half of the optimized structure

Fig. 46

The convergence curves of compliance and volume. a Free-form topology optimization. b Topology optimization considering structural connectivity

5 Conclusions

The present work presents a simple side constraint scheme in combination with void features for the design of structural connectivity in topology optimization. Both 2D and 3D examples show that the proposed method does have the capability of ensuring the structural connectivity in the optimized result. Compared with freely optimized results, the elimination of enclosed cavity always comes at the cost of increasing structure compliance. Moreover, the increase of void features contributes to a reduction of compliance. The choice of parameter Δ is also important to ensure the computing accuracy in structural analysis and sensitivity analysis. Half of the element size is a reasonable choice for Δ. In the future, the proposed method will be integrated with the minimum length scale and overhang constraint.