Structural topology optimization under limit analysis

Abstract

The objective of this paper is to look for structural designs arising from topological optimization procedures that aim at maximizing the loading capacity regarding incipient plastic collapse. The mechanical problem is described by limit analysis (LA) formulation that allows a direct determination of the load that produces the plastic collapse phenomenon without information about the load history. In case of proportional loading processes, LA consists of computing a critical load factor such that the structure undergoes plastic collapse when the reference load is amplified by this factor. In this case, LA can be cast mathematically as a convex constrained optimization problem. The design optimization is formally stated as the maximization of the collapse load factor subject to a fixed quantity of available material. The design is controlled by solid isotropic microstructure with penalization (SIMP) technique. In the particular case of the chosen objective function, the solution of the adjoint problem in sensitivity analysis coincides with the Newton–Raphson update vector obtained at the convergence of the procedure developed to solve the LA optimization problem, fact that reduces the numerical cost of gradient calculations. In order to keep the implementation straightforward, the optimality conditions are solved by a classical heuristic element-by-element density updating algorithm, well known in the literature. The set of tested examples brings encouraging results with structures being stressed to ultimate bearing states. Implementation was kept as simple as possible, leaving the field open to further investigations. Numerical tests show that, despite having similar geometries, plastic collapse factor obtained with compliance optimal designs are lower than those obtained with present formulation.

1 Introduction

Structural topology optimization is a continuous developing area due to the valuable benefits it brings at the early stages of design. Most approaches in the literature, however, are restricted to linear elastic models, leaving aside more complex material behaviors due to the relatively high costs to solve the state equation and corresponding sensitivity. Concerning plastic behavior, several authors (Zhang et al. 2017; Alberdi and Khandelwal 2017; Li et al. 2017a; Wallin et al. 2016) adopt classical incremental elastoplasticity to search for the topology of a structure that maximizes the dissipated energy. Amir (2017), using the same incremental basis, proposes alternative ways to treat stress-constrained problem, replacing them with a global measure of the accumulated plastic deformation. All these approaches have in common incremental formulations demanding relatively high computational costs to be used within optimization procedures.

According to the concept of limit state, a loaded structure made of a material that shows an upper bound on its strain–stress curve presents limited strength. Consequently, the load supported is also limited to a maximum value, such that any additional load increment produces plastic collapse. The plastic collapse is a phenomenon characterized by the development of kinematically admissible plastic strain rates under constant stress distribution (Cohn and Maier 1977; Feijóo and Zouain 1987; Lubliner 1990; Kamenjarzh 1996). Limit analysis (LA) deals with the direct determination of the maximum load amplitude, stress distribution, and corresponding plastic velocity fields at the incipient plastic collapse condition. Under processes of proportional loading, the main target of LA is to compute the critical loading factor such that plastic collapse takes place when the reference load is amplified by this load factor (Christiansen 1981, 1996; Borges et al. 1996; Zouain et al. 2014; Fusch et al. 2015). Since LA formulation does not involve information of the load history, it is the most suitable alternative for incipient plastic collapse analysis, mainly when only the limit stress field is required (Fusch et al. 2015; Kammoun and Smaoui 2015).

The variational characterization of plastic collapse allows to formulate LA under proportional loads as convex constrained optimization principles, namely the kinematical, statical, and mixed principles of limit analysis (Rockafellar 1970; Frémond and FRIAA 1982; Zouain et al. 1993; Christiansen 1996; Borges et al. 1996). The finite element method (FEM) can be chosen for the spatial discretization of these principles, leading to finite dimensional optimization problems solvable by mathematical programming algorithms. Among them, one can mention the procedures presented in Christiansen (1980, 1981); Andersen et al. (1998), the interior point algorithms proposed by Zouain et al. (1993, 2002); Borges et al. (1996); Pastor and Loute (2005); Krabbenhoft and Damkilde (2002) and the second-order cone programming, recently adopted by Makrodimopoulos and Martin (2007), to cite a few.

The literature associated with topology optimization of continuum media and limit analysis concepts is scarce. The work of Kammoun and Smaoui (2014) is the single journal paper devised by the authors on this subject. In that research work, the density field is not set as a design variable but as a new one in a modified limit analysis problem. Solving, therefore, a new optimization problem where it is sought simultaneously to find the stress and density fields that minimizes the structural mass while maintaining static equilibrium. This is done using LA static formulation modified to a conic format.

With this motivation in mind, this work proposes a topology optimization problem that uses the LA concept and the solid isotropic microstructure with penalization (SIMP) approach for the design control. The problem is formulated as the maximization of the plastic collapse load for a fixed available material.

The strategy chosen to solve the LA problem combines the mixed FEM framework, discussed in Borges et al. (1996) and Zouain et al. (2014), and the numerical procedure proposed by Zouain et al. (1993, 2002) and Borges et al. (1996). Analytical sensitivity expressions are derived and, due to the specific mathematical structure of the posed problem, gradient calculations reduce to simple vector products of already-available data. Moreover, classic element-by-element update heuristics based on the density optimality conditions are chosen to achieve the solution.

The manuscript follows a straightforward sequential presentation: limit analysis concept, formulation, and discretization procedure are shown in Section 2. The optimum design problem is presented in Section 3 and sensitivity analysis in Section 4. The chosen numerical algorithm is discussed in Section 5 while a set of examples are tested in Section 6. Final remarks are found in Section 7.

2 Limit analysis

Let ${\Omega }\subset \text {I\!R}^{n} (n = 2,3)$ an open domain with boundary $\partial {\Omega }$ occupied by a body $\mathcal {B}$. Traction forces $\boldsymbol {t}$ are applied over Γ_t ⊂ ∂Ω, while homogeneous (null) velocity boundary conditions are imposed on Γ_u ⊂ ∂Ω,Γ_u ∪Γ_t = ∂Ω,Γ_u ∩Γ_t = ⊘. The bilinear form 〈F,w〉 denotes the external power produced by the body forces $\boldsymbol {b}$ and traction forces $\boldsymbol {t}$ over a virtual velocity field $\boldsymbol {w}\in V:$

$$ \langle\boldsymbol{F},\boldsymbol{w}\rangle:={\int}_{\Omega}\boldsymbol{b}\cdot\boldsymbol{w} d{\Omega}+{\int}_{{\Gamma}_{t}}\boldsymbol{t}\cdot\boldsymbol{w} d{\Gamma}. $$

(1)

Every stress field $\boldsymbol {\sigma }\in W^{\prime }$ in equilibrium with the external generalized force $\boldsymbol {F}$ must satisfy the Principle of Virtual Power. Thus, S(F) denotes the subset of all the stress fields in equilibrium with the external forces:

$$ S(\boldsymbol{F}):=\left\{ \boldsymbol{\sigma}\in W^{\prime}|{\int}_{\Omega}\boldsymbol{\sigma}\cdot\mathfrak{D}\boldsymbol{w} d{\Omega}=\langle\boldsymbol{F},\boldsymbol{w}\rangle \forall\boldsymbol{w}\in V\right\}, $$

(2)

being $\mathfrak {D}=\nabla ^{s}$ the infinitesimal strain operator and $\mathfrak {D}\boldsymbol {w}\in W$ the virtual strain rate field.

The body $\mathcal {B}$ is composed by an ideally elastic–plastic material such that stresses satisfy the plastic admissibility condition $\mathcal {F}(\boldsymbol {\sigma }(x))\leqslant 0$ everywhere in ${\Omega }$. Those points whose stress is situated on the yield surface $\mathcal {F}(\boldsymbol {\sigma }(x)) = 0$ may undergo plastic deformations. The corresponding plastic strain rate $\mathbf {d}^{p}$ follow the flow rule :

$$ \mathbf{d}^{p}=\dot{\lambda}\mathbf{N\mathit{,}}\qquad\mathbf{N}=\frac{\partial\mathcal{F}}{\partial\boldsymbol{\sigma}} $$

(3)

with the complementarity conditions

$$ \mathcal{F}(\boldsymbol{\sigma}(x))\leqq0\qquad\qquad\dot{\lambda}\geqq0\qquad\qquad\dot{\lambda} \mathcal{F}(\boldsymbol{\sigma}(x))= 0 $$

(4)

It is said that the body $\mathcal {B}$ develops state of incipient plastic collapse, or is in plastic limit state, if there is a stress field $\boldsymbol {\sigma }\in W^{\prime }$ related to a purely plastic strain rate field $\mathbf {d}^{p}\in W$ and a velocity field $\boldsymbol {v}\in V$, such that the following conditions are satisfied:

• i The velocity and plastic strain rate are compatible; in other words, $\mathbf {d}^{p}=\mathfrak {D}\boldsymbol {v}\quad \boldsymbol {v}\in V$;

• ii Then stress field is in equilibrium with the external forces amplified by the load factor $\alpha \in \mathrm {I\!R^{+}}$, that is, $\boldsymbol {\sigma }\in S(\alpha \boldsymbol {F})$;

• iii The stress field is plastically admissible, which means, $\mathcal {F}(\boldsymbol {\sigma }(x))\leqq 0 \forall x\in {\Omega }$;

• iv The stress and plastic strain rates are related by the constitutive equation, defined by the plastic flow law (3)–(4);

Tools of convex analysis (subdifferentiability and duality principles Rockafellar 1970; de Saxcé and Bousshine 1998) allow to show that the solution of the system (i to iv) is also the solution of the so-called static, kinematical, and mixed formulations of limit analysis (Christiansen 1981, 1996; Zouain et al. 1993, 2014; de Saxcé and Bousshine 1998), the latter expressed by the following saddle point problem:

$$ \alpha=\sup\limits_{\boldsymbol{\sigma}\in W^{\prime}}\inf\limits_{\boldsymbol{v}\in V}\left\{ {\int}_{\Omega}\boldsymbol{\sigma}\cdot\mathfrak{D}\boldsymbol{v}d{\Omega}\quad\left|\begin{array}{c} \langle\boldsymbol{F},\boldsymbol{v}\rangle= 1\\ \mathcal{F}(\boldsymbol{\sigma}(x))\leqq0 \forall x\in{\Omega} \end{array}\right.\right. $$

(5)

It is worth emphasizing that domain ${\Omega }$ represents the deformed (spatial) configuration at the onset of plastic collapse.

Important differences distinguish LA from classical incremental elastoplastic formulations. Firstly, neither a reference configuration ${\Omega }_{0}$ nor a displacement field mapping Ω₀ to ${\Omega }$ exists in LA. Due to the same reason, no elasticity model relates stresses with elastic strains. Moreover, stress and plastic velocity fields are, in the limit state, independent from any loading path (Cohn and Maier 1977; Feijóo and Zouain 1987; Kamenjarzh 1996; Lubliner 1990) and their calculus do not demand any time integration procedure.

2.1 Discretization

A detailed discussion on possible FEM discretization procedures for LA formulations is found in Borges et al. (1996) and Zouain et al. (2014). Nevertheless, the mathematical structure of the discrete LA problem has important consequences on the effectiveness of the topological optimization procedure. Accordingly, a brief description of the discretization chosen is necessary.

For the sake of simplicity, the present study is restricted to 2D problems. The mixed triangle proposed in Borges et al. (1996) and Zouain et al. (2014) is used which comprises quadratic (six nodes) Lagrangian shape functions for the velocity and linear (three nodes) shape function for the stress.

The discrete LA version is obtained substituting the approximated velocity and stress fields in principle (5). These discrete fields are defined at each element e by:

$$ \boldsymbol{v^{e}}\approx\boldsymbol{N}_{\boldsymbol{v}}^{e}\tilde{\boldsymbol{v}}^{e}\qquad\sigma^{\boldsymbol{e}}\approx\boldsymbol{N}_{\boldsymbol{\sigma}}^{e}\tilde{\boldsymbol{\sigma}}^{e} $$

(6)

Vectors $\tilde {\boldsymbol {v}}^{e}$ and $\tilde {\boldsymbol {\sigma }}^{e}$ contain the elementary parameters while matrices $\boldsymbol {N}_{\boldsymbol {v}}^{e}$ and $\boldsymbol {N}_{\boldsymbol {\sigma }}^{e}$ are the shape functions for velocity and stress, respectively. The discrete velocity field is assumed to be continuous on ${\Omega }$ and, therefore, an appropriate assembly of the element-level vectors $\tilde {\boldsymbol {v}}^{e}$ into a global n-dimensional vector $\tilde {\boldsymbol {v}}$ is performed (n = 2n_N,n_N is the number of nodes of the mesh). In addition, stresses are assumed to be discontinuous among elements and all element-level vectors $\tilde {\boldsymbol {\sigma }}^{e}$ are directly collected into a q-dimensional vector $\tilde {\boldsymbol {\sigma }}$ (q = 18n_E,n_E is the number of elements of the mesh). Classical procedures are used to impose required homogenous kinematic constraints.

The mixed formulation (5) requires the plastic admissibility of the approximated stress field $\tilde {\boldsymbol {\sigma }}^{e}(x^{k})$. This condition can be exactly assured with present discretization since stress is given by piecewise linear function at each element and the plastic function $\mathcal {F}(\boldsymbol {\sigma }(x))$ is convex. Function $\mathcal {F}(\boldsymbol {\sigma }(x^{k}))$ is then evaluated at all three vertices (stress nodes) of each element and its values collected in an m-dimensional vector $\tilde {\mathcal {F}}(\tilde {\boldsymbol {\sigma }})$ with $m = 3n_{E}$. Plastic admissibility is then enforced by requiring $\tilde {\mathcal {F}}_{j}(\tilde {\boldsymbol {\sigma }}(x^{k})) \leqq 0, j = 1...m$. From now on, for the sake of brevity, the plastic admissibility condition will be symbolized simply by $\tilde {\mathcal {F}} \leqq 0$.

Substituting these approximations, the continuous principle (5) takes the following discrete form:

$$ \tilde{\alpha}=\max\limits_{\tilde{\boldsymbol{\sigma}}\in\mathrm{I\!R}^{q}} \min\limits_{\tilde{\boldsymbol{v}}\in\mathrm{I\!R^{n}}} \tilde{\boldsymbol{\sigma}}\cdot\boldsymbol{B}\tilde{\boldsymbol{v}}\quad\left|\begin{array}{c} \tilde{\mathcal{F}} \leqq 0\\ \boldsymbol{F}\cdot\tilde{\boldsymbol{v}}= 1 \end{array}\right. $$

(7)

where $\boldsymbol {B}$ is the discrete strain operator, that is, the matrix transforming velocities into strain rate, obtained from the assemblage of elementary contributions of the form

$$ \boldsymbol{B}^{e}={\int}_{{\Omega}^{e}}\boldsymbol{N}_{\boldsymbol{\sigma}}^{e}(x)^{T}\mathfrak{D}\boldsymbol{N}_{\boldsymbol{v}}^{e}(x)\quad d{\Omega}^{e} $$

(8)

and $\boldsymbol {F}$ is the global force vector obtained by assembling

$$ \boldsymbol{F}^{e}={\int}_{{\Omega}^{e}}\boldsymbol{N}_{\boldsymbol{v}}^{e}(x)^{T} b(x) d{\Omega}^{e}+{\int}_{{{\Gamma}_{t}^{e}}}\boldsymbol{N}_{\boldsymbol{v}}^{e}(x)^{T} t(x) d{{\Gamma}_{t}^{e}} $$

(9)

2.2 Solution of the discrete limit analysis problem

The non-linear system that represents the first-order optimality conditions of the discrete limit analysis problem (7) can be written as Zouain et al. (1993), Borges et al. (1996), Pastor and Loute (2005), de Saxcé and Bousshine (1998), and Fusch et al. (2015)

$$ \boldsymbol{R}(\tilde{\boldsymbol{\mathcal{X}}})= 0\quad\quad\quad\tilde{\mathcal{F}}\leqq 0\quad\quad\quad\tilde{\lambda}\geqq 0 $$

(10)

where the vector $\tilde {\lambda }\in \mathrm {I\!R}^{m}$ collets the plastic multipliers corresponding to each plastic mode $\tilde {\mathcal {F}}_{j}$. The inequalities should be understood as holding componentwise. Additionally, $\boldsymbol {R}(\tilde {\boldsymbol {\mathcal {X}}})$ and the argument of the problem, the vector $\tilde {\boldsymbol {\mathcal {X}}}$, are defined as:

$$ \boldsymbol{R}(\tilde{\boldsymbol{\mathcal{X}}})=\left[\begin{array}{c} \boldsymbol{B}\tilde{\boldsymbol{v}}-\nabla_{\tilde{\boldsymbol{\sigma}}}\mathcal{\tilde{F}}(\tilde{\boldsymbol{\sigma}})\tilde{\boldsymbol{\lambda}}\\ \boldsymbol{B}^{T}\tilde{\boldsymbol{\sigma}}-\tilde{\alpha}\tilde{\boldsymbol{F}}\\ -\tilde{\boldsymbol{F}}^{T}\tilde{\boldsymbol{v}}+ 1\\ -\boldsymbol{G}(\tilde{\boldsymbol{\sigma}})\tilde{\boldsymbol{\lambda}} \end{array}\right]\qquad\qquad\tilde{\boldsymbol{\mathcal{X}}}=\left[\begin{array}{c} \tilde{\boldsymbol{\sigma}}\\ \tilde{\boldsymbol{v}}\\ \tilde{\alpha}\\ \tilde{\boldsymbol{\lambda}} \end{array}\right] $$

(11)

The symbol $\boldsymbol {G}(\tilde {\boldsymbol {\sigma }})$ represents a diagonal matrix such that $\boldsymbol {G}_{jj}(\tilde {\boldsymbol {\sigma }})=\tilde {\mathcal {F}}_{j}(\tilde {\boldsymbol {\sigma }}),$$j = 1...m$. To solve the system defined by the optimality conditions (10), a Newton-like algorithm is employed, as proposed by Borges et al. (1996). The algorithm consists of two stages: the first one is a sequence of Newton iterations on the set of equalities, and the second one, a step relaxation and stress scaling in order to preserve plastic admissibility. Herein, only Newton’s iteration stage is detailed due to its relevance for the topological optimization strategy. A step-by-step description of the whole algorithm can be found in Borges et al. (1996).

The Newton–Raphson scheme provides the following linearized equation:

$$ \frac{\partial\boldsymbol{R}(\tilde{\boldsymbol{\mathcal{X}}})}{\partial\tilde{\boldsymbol{\mathcal{X}}}}|_{\tilde{\boldsymbol{\mathcal{X}}}_{0}}{\Delta}\tilde{\boldsymbol{\mathcal{ X}}}=-\boldsymbol{R}(\tilde{\boldsymbol{\mathcal{X}}})|_{\tilde{\boldsymbol{\mathcal{X}}}{}_{0}}, $$

(12)

where the tangent matrix $\boldsymbol {K}=\frac {\partial \boldsymbol {R}(\tilde {\boldsymbol {\mathcal {X}}})}{\partial \tilde {\boldsymbol {\mathcal {X}}}}$ takes the expression

$$ \boldsymbol{K}(\tilde{\boldsymbol{\mathcal{X}}})=\left[\begin{array}{cccc} -\boldsymbol{H} & \boldsymbol{B} & \boldsymbol{0} & -\nabla_{\tilde{\boldsymbol{\sigma}}}\tilde{\mathcal{F}}(\tilde{\boldsymbol{\sigma}}_{0})\\ \boldsymbol{B}^{T} & \boldsymbol{0} & -\boldsymbol{F} & \boldsymbol{0}\\ \boldsymbol{0} & -\boldsymbol{F}^{T} & 0 & \boldsymbol{0}\\ -\boldsymbol{{\Lambda} }\nabla_{\tilde{\boldsymbol{\sigma}}}^{T}\mathcal{\tilde{F}}(\tilde{\boldsymbol{\sigma}}_{0}) & \boldsymbol{0} & \boldsymbol{0} & -\boldsymbol{G}(\tilde{\boldsymbol{\sigma}}_{0}) \end{array}\right]. $$

(13)

The term $\boldsymbol {{\Lambda } }$ is a diagonal matrix, such that $\boldsymbol {{\Lambda } }_{jj}=\tilde {\boldsymbol {\lambda }_{j}}$. The new iterate $\tilde {\boldsymbol {\mathcal {X}}}$ is computed from the present one $\tilde {\boldsymbol {\mathcal {X}}}_{0}$, by defining a search direction ${\Delta }\tilde {\boldsymbol {\mathcal {X}}}$, in such a way that

$$ \tilde{\boldsymbol{\mathcal{X}}}=\tilde{\boldsymbol{\mathcal{X}}}_{0}+{\Delta}\tilde{\boldsymbol{\mathcal{X}}} $$

(14)

being ${\Delta }\tilde {\boldsymbol {\mathcal {X}}}$ obtained from the solution of the system (12) as follows. The matrix $\boldsymbol {K}$ is symmetrized by multiplying the last set of equations by $\boldsymbol {{\Lambda } }^{-1}$. This is possible because the updating performed at the end of each iteration enforces that each $\tilde {\lambda }_{j}$ is strictly positive for the new iteration (Borges et al. 1996). Denoting $\mathcal {O}(\bullet )$ the corresponding symmetrization operator, (12) is rewritten as

$$ \boldsymbol{K}^{s}{\Delta}\boldsymbol{\tilde{\mathcal{X}}}=-\boldsymbol{R}^{s} $$

(15)

where

$$ \boldsymbol{R}^{s}=\mathcal{O}\left( \boldsymbol{{\Lambda} }^{-1}\right)\boldsymbol{R}\left|\right._{\tilde{\boldsymbol{\mathcal{X}}}{}_{0}}=\left[\begin{array}{c} \boldsymbol{B}\tilde{\boldsymbol{v}}_{0}-\nabla_{\tilde{\boldsymbol{\sigma}}}\tilde{\mathcal{F}}(\tilde{\boldsymbol{\sigma}}_{0})\tilde{\boldsymbol{\lambda}}\\ \boldsymbol{B}^{T}\tilde{\boldsymbol{\sigma}}_{0}-\tilde{\alpha}_{0}\tilde{\boldsymbol{F}}\\ -\tilde{\boldsymbol{F}}^{T}\tilde{\boldsymbol{v}}_{0}+ 1\\ -{\Lambda}^{-1}\boldsymbol{G}(\tilde{\boldsymbol{\sigma}}_{0})\tilde{\boldsymbol{\lambda}}_{0} \end{array}\right], $$

(16)

$$\begin{array}{@{}rcl@{}} \boldsymbol{K}^{s}&=&\mathcal{O}(\boldsymbol{{\Lambda} }^{-1})\boldsymbol{K}\left|\right._{\tilde{\boldsymbol{\mathcal{X}}}{}_{0}}\\ &=&\left[\begin{array}{cccc} -\boldsymbol{H} & \boldsymbol{B} & \boldsymbol{0} & -\nabla_{\tilde{\boldsymbol{\sigma}}}\mathcal{\tilde{F}}(\tilde{\boldsymbol{\sigma}}_{0})\\ \boldsymbol{B}^{T} & \boldsymbol{0} & -\boldsymbol{F} & \boldsymbol{0}\\ \boldsymbol{0} & -\boldsymbol{F}^{T} & 0 & \boldsymbol{0}\\ -\nabla_{\tilde{\boldsymbol{\sigma}}}^{T}\mathcal{\tilde{F}}(\tilde{\boldsymbol{\sigma}}_{0}) & \boldsymbol{0} & \boldsymbol{0} & -\boldsymbol{{\Lambda} }^{-1}\boldsymbol{G}(\tilde{\boldsymbol{\sigma}}_{0}) \end{array}\right], \end{array} $$

(17)

The equilibrium constraint (second equation of the residuum $\boldsymbol {R}(\tilde {\boldsymbol {\mathcal {X}}})$) is exactly satisfied for the current values $\tilde {\boldsymbol {\sigma }}_{0}$ and $\tilde {\alpha }_{0}$. Then, expanding (15) and substituting ${\Delta }\tilde {\boldsymbol {v}}=\tilde {\boldsymbol {v}}-\tilde {\boldsymbol {v}}_{0}$ and ${\Delta }\tilde {\boldsymbol {\lambda }}=\tilde {\boldsymbol {\lambda }}-\tilde {\boldsymbol {\lambda }}_{0}$, the following linear system is obtained:

$$ \left[\begin{array}{cccc} -\boldsymbol{H} & \boldsymbol{B} & \boldsymbol{0} & -\nabla_{\tilde{\boldsymbol{\sigma}}}\tilde{\mathcal{F}}(\tilde{\boldsymbol{\sigma}}_{0})\\ \boldsymbol{B}^{T} & \boldsymbol{0} & -\boldsymbol{F} & \boldsymbol{0}\\ \boldsymbol{0} & -\boldsymbol{F}^{T} & 0 & \boldsymbol{0}\\ \!\!-\nabla_{\tilde{\boldsymbol{\sigma}}}^{T}\tilde{\mathcal{F}}(\tilde{\boldsymbol{\sigma}}_{0}) & \boldsymbol{0} & \boldsymbol{0} & -\boldsymbol{{\Lambda} }^{-1}\boldsymbol{G}(\tilde{\boldsymbol{\sigma}}_{0}) \end{array}\!\right]\!\left[\begin{array}{c} {\Delta}\tilde{\boldsymbol{\sigma}}\\ \tilde{\boldsymbol{v}}\\ {\Delta}\tilde{\alpha}\\ \tilde{\boldsymbol{\lambda}} \end{array}\right] = -\!\left[\begin{array}{c} \boldsymbol{0}\\ \boldsymbol{0}\\ 1\\ \boldsymbol{0} \end{array}\right] $$

(18)

where $\tilde {\boldsymbol {v}},\tilde {\boldsymbol {\lambda }}$ represent the updated values and ${\Delta }\tilde {\boldsymbol {\sigma }},{\Delta }\tilde {\alpha }$, are the corrections of the corresponding arguments within a Newton–Raphson iteration (Borges et al. 1996). It is worth mentioning that at convergence, ${\Delta }\tilde {\boldsymbol {\sigma }}\rightarrow \mathbf {0}$ and ${\Delta }\tilde {\alpha }\rightarrow 0$.

3 Optimum design problem

Consider a domain ${\Omega }\subset \mathrm {I\!R}^{n} (n = 2,3)$ with boundary $\partial {\Omega }$ separated in sub-domains ${\Omega }_{m}\subset {\Omega }$ and Ω_v = Ω ∖Ω_m representing respectively the regions occupied by a body B and the void associated with its complement in ${\Omega }$ (see Fig. 1). Assume that the boundary ${\Gamma }$ of ${\Omega }_{m}$ is sufficiently smooth and contains the part ${\Gamma }_{t}\in \partial {\Omega }$ where traction forces t are applied and the boundary ${\Gamma }_{u}$ where homogeneous velocity conditions are considered. The topology optimization problem is classically characterized as the search of a domain ${\Omega }_{m}$ contained in ${\Omega }$ that maximizes a performance function while satisfying design constraints, among them, the state equation defining the physical problem in study. Different ways to control ${\Omega }_{m}$ relate to different topology optimization techniques. One of the most used techniques is that called SIMP (Bendsoe and Kikuchi 1988), in which topology is controlled by a fictional density $\rho :{\Omega }\rightarrow \left [0,1\right ]$ ranging continuously between the extreme conditions of solid, ρ(x) = 1, and void material, $\rho (x)= 0$. Different approaches for the discretization of $\rho$ are seen in the literature. In the present case, the classical element-wise constant distribution is considered for simplicity reasons. Therefore, function $\rho$ is substituted by an $n_{E}$-dimensional vector $\tilde {\boldsymbol {\rho }}$ of elemental densities, being $n_{E}$ the number of elements of the mesh.

Fig. 1

Design domain comprised of solid and void regions

The present work aims to find the density distribution $\tilde {\rho }$ that maximizes the scaling factor $\alpha$ (or, equivalently, maximizing the limit load) for a given quantity of available material. This problem is formally described as

$$ \begin{array}{cc} \min & f\left( \tilde{\boldsymbol{\mathcal{X}}}\right)=-\tilde{\alpha}\\ \text{s.t.}\\ & \boldsymbol{R}\left( \tilde{\boldsymbol{\mathcal{X}}},\tilde{\boldsymbol{\rho}}\right)=\boldsymbol{0}\left|\begin{array}{c} \tilde{\boldsymbol{\lambda}}\geqq0\\ \tilde{\mathcal{F}}\leqq0 \end{array}\right.,\\ & M(\tilde{\boldsymbol{\rho}})=M_{0},\\ & \boldsymbol{\rho}_{min}\leqq\tilde{\boldsymbol{\rho}}\leqq\boldsymbol{1} \end{array} $$

(19)

where $M(\tilde{\rho})=\tilde{\boldsymbol{\rho}}\cdot \tilde{V}={\int}_{\Omega}\rho \mathrm{d}{\Omega}$ is a fictional mass measurement, being $\tilde {V}$ an $n_{E}$-dimensional vector of elemental volumes. The dependency of the state equation $\boldsymbol {R}\left (\tilde {\boldsymbol {\mathcal {X}}},\tilde {\boldsymbol {\rho }}\right )$ on $\rho$ is given by the yield function $\mathcal {F}$ now dependent on the fictitious density $\rho$ through the value of the yield stress:

$$ \mathcal{F}(\boldsymbol{\sigma},\rho)=\sigma_{vM}^{2}(\boldsymbol{\sigma})-\left[\rho^{p}\sigma_{y}\right]^{2}\leqq0, $$

(20)

$$ \sigma_{vM}^{2}(\boldsymbol{\sigma})=\frac{1}{2}\mathcal{C}\boldsymbol{\sigma}\cdot\boldsymbol{\sigma} $$

(21)

where $\sigma _{vM}(\boldsymbol {\sigma })$ represents the equivalent von Mises stress, $\mathcal {C}$ a projection matrix associated with the von Mises yield criterion, and p a penalization factor for intermediate densities. It is possible to see that (20) constrains the stress field in order to satisfy the following extreme conditions:

$$ \left\{\begin{array}{ll} \begin{array}{cc} \mathcal{F}(\boldsymbol{\sigma},1)=\sigma_{vM}^{2}(\boldsymbol{\sigma})-{\sigma_{y}^{2}}\leqq0 & \rightarrow\sigma_{vM}\leqq\sigma_{y},\\ \mathcal{F}(\boldsymbol{\sigma},0)=\sigma_{vM}^{2}(\boldsymbol{\sigma})\leqq0\quad & \rightarrow\sigma_{vM}= 0. \end{array} \end{array}\right. $$

(22)

4 Sensitivity analysis

Consider the optimization problem (19) where, for a given density field $\tilde {\boldsymbol {\rho }}$, the vector $\tilde {\boldsymbol {\mathcal {X}}}$ is obtained as the solution of the non-linear state equation, i.e.,:

$$ \begin{array}{c} \begin{array}{cc} \min & f\left( \tilde{\boldsymbol{\mathcal{X}}}(\tilde{\boldsymbol{\rho}})\right)=-\tilde{\alpha}\\ \text{s.t.}\\ & M(\tilde{\boldsymbol{\rho}})=M_{0},\\ & \boldsymbol{\rho}_{min}\leq\tilde{\boldsymbol{\rho}}\leqq\boldsymbol{1},\\ \end{array}\\ \tilde{\boldsymbol{\mathcal{X}}}(\tilde{\boldsymbol{\rho}})=arg\left\{ \boldsymbol{R}\left( \tilde{\boldsymbol{\mathcal{ X}}},\tilde{\boldsymbol{\rho}}\right)=\boldsymbol{0}\left|\begin{array}{c} \tilde{\boldsymbol{\lambda}}\geqq0\\ \tilde{\mathcal{F}}\leqq0 \end{array}\right.\right\} . \end{array} $$

(23)

In order to solve this constrained minimization problem, the following Lagrangian functional is defined,

$$\begin{array}{@{}rcl@{}} \mathcal{L}(\tilde{\boldsymbol{\rho}},\mu,\gamma^{+},\gamma^{-})&=&f\left( \tilde{\boldsymbol{\mathcal{X}}}(\tilde{\boldsymbol{\rho}})\right)+\mu\left( M(\tilde{\boldsymbol{\rho}})-M_{0}\right) \\&&+\gamma^{+}(\tilde{\boldsymbol{\rho}}-\boldsymbol{1})+\gamma^{-}(\boldsymbol{\rho}_{min}-\tilde{\boldsymbol{\rho}}) \end{array} $$

(24)

whose corresponding stationary conditions are given by

$$\begin{array}{@{}rcl@{}} \nabla_{\tilde{\boldsymbol{\rho}}}\mathcal{L}=\nabla_{\tilde{\boldsymbol{\rho}}}f\left( \tilde{\boldsymbol{{\mathcal X}}}(\tilde{\boldsymbol{\rho}})\right)+\mu\nabla_{\tilde{\boldsymbol{\rho}}}\left( M(\tilde{\boldsymbol{\rho}})-M_{0}\right) \end{array} $$

$$\begin{array}{@{}rcl@{}} +\gamma^{+}\nabla_{\tilde{\boldsymbol{\rho}}}(\tilde{\boldsymbol{\rho}}-\boldsymbol{1})+\gamma^{-}\nabla_{\tilde{\boldsymbol{\rho}}}(\boldsymbol{\rho}_{min}-\tilde{\boldsymbol{\rho}}) & =&0 \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} \nabla_{\mu}\mathcal{L}=M(\tilde{\boldsymbol{\rho}})-M & =&0 \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} \gamma^{+}(\tilde{\boldsymbol{\rho}}-\boldsymbol{1}) & =&0 \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} \gamma^{-}(\boldsymbol{\rho}_{min}-\tilde{\boldsymbol{\rho}}) & =&0 \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} \tilde{\boldsymbol{\rho}}-\boldsymbol{1} & \leqq&0 \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\rho}_{min}-\tilde{\boldsymbol{\rho}} & \leqq&0 \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} \gamma^{+} & \geqq&0 \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} \gamma^{-} & \geqq&0 \end{array} $$

(32)

being $\mu ,\gamma ^{+},\gamma ^{-}$ the Lagrangian multipliers related to volume and lateral constraints, respectively.

Due to the implicit dependency of $f\left (\tilde {\boldsymbol {\mathcal {X}}}(\tilde {\boldsymbol {\rho }})\right )$ on the density field, the conventional adjoint method is used to calculate its gradient (Komkov et al. 1986). Each component of $\nabla _{\rho }f$ is then computed by the expression

$$ \left[\nabla_{\rho}f\left( \tilde{\boldsymbol{\mathcal{X}}}(\rho)\right)\right]_{e}=\frac{\partial f}{\partial\tilde{\boldsymbol{\mathcal{ X}}}}\cdotp\frac{\partial\boldsymbol{\tilde{\boldsymbol{\mathcal{X}}}}}{\partial\rho_{e}}=-\frac{\partial\boldsymbol{R}^{s}}{\partial\rho_{e}}\cdot\boldsymbol{\omega}, $$

(33)

where $\boldsymbol {\omega }$ is the so-called adjoint vector, obtained from the solution of the following (adjoint) linear problem:

$$ \boldsymbol{K}^{s}\left|\right._{_{_{\tilde{\boldsymbol{\mathcal{X}}}_{sol}}}}\boldsymbol{\omega}=\frac{\partial f}{\partial\tilde{\boldsymbol{\mathcal{X}}}}\left|\right._{_{\tilde{\boldsymbol{\mathcal{X}}}_{sol}}}=-\left[\begin{array}{c} \boldsymbol{0}\\ \boldsymbol{0}\\ 1\\ \boldsymbol{0} \end{array}\right]. $$

(34)

being $\tilde {\boldsymbol {\mathcal {X}}}_{sol}$ the converged solution of the LA problem. Some algebraic manipulation show an interesting feature of the present formulation: linear system (34) is identical to that of the Newton iteration (18) evaluated at the converged argument. Consequently, identical solutions are obtained and the adjoint vector takes the form

$$ \boldsymbol{\omega}=\left[\begin{array}{c} {\Delta}\tilde{\boldsymbol{\sigma}}\\ \tilde{\boldsymbol{v}}\\ {\Delta}\tilde{\alpha}\\ \dot{\boldsymbol{\lambda}} \end{array}\right] $$

(35)

Substituting this result in (33), the gradient of the objective function writes

$$\begin{array}{@{}rcl@{}} \left[\nabla_{\rho}f\left( \tilde{\boldsymbol{\mathcal{X}}}(\tilde{\boldsymbol{\rho}})\right)\right]_{e}&=&\left[\begin{array}{c} \boldsymbol{0}\\ \boldsymbol{0}\\ 0\\ \frac{\partial}{\partial\rho_{e}}\boldsymbol{g}(\tilde{\boldsymbol{\sigma}},\tilde{\boldsymbol{\rho}}) \end{array}\right]\cdot\left[\begin{array}{c} {\Delta}\tilde{\boldsymbol{\sigma}}\\ \tilde{\boldsymbol{v}}\\ {\Delta}\tilde{\alpha}\\ \dot{\boldsymbol{\lambda}} \end{array}\right]\\&=&-2p\rho_{e}^{2p-1}{\sigma_{y}^{2}}\sum\limits_{j = 1}^{3}\dot{\lambda}_{j}^{e}, \end{array} $$

(36)

where $\boldsymbol {g}_{j}(\tilde {\boldsymbol {\sigma }},\tilde {\boldsymbol {\rho }})=\boldsymbol {G}_{jj}(\tilde {\boldsymbol {\sigma }},\tilde {\boldsymbol {\rho }})$ and ${\displaystyle \sum \limits _{j = 1}^{3}}\dot {\lambda }_{j}^{e}$ is the sum of all three j th plastic multipliers related to the plastic admissibility evaluated at each stress node of the e th element. Substituting this result in (25) and considering that

$$\begin{array}{@{}rcl@{}} \mu\frac{\partial}{\partial\rho_{e}}M(\tilde{\boldsymbol{\rho}})+\gamma^{+}\frac{\partial}{\partial\rho_{e}}(\tilde{\boldsymbol{\rho}}-\boldsymbol{1})+\gamma^{-}\frac{\partial}{\partial\rho_{e}}(\boldsymbol{\rho}_{min}-\tilde{\boldsymbol{\rho}})=\\\mu V_{e}+\gamma^{+}-\gamma^{-} \end{array} $$

the e th component of gradient (25) reduces to:

$$ \left[\nabla_{\rho}\mathcal{L}\right]_{e}=-2p\rho_{e}^{2p-1}{\sigma_{y}^{2}}\sum\limits_{j = 1}^{3}\dot{\lambda}_{j}^{e}+\mu V_{e}+\gamma^{+}-\gamma^{-}= 0 $$

(37)

Disregarding the last three terms of (37) related to volume and lateral constraints, the core of the sensitivity is given by the first term, whose simplicity deserves a comment. Since its arguments are non-negative, the larger (negative) amplitudes of the gradient are associated with elements with large plastic multipliers $\dot {\lambda }_{j}^{e}$. In other words, only those elements with high participation in power dissipation are relevant in the gradient vector. Therefore, in order to minimize the function $f\left (\tilde {\boldsymbol {\mathcal {X}}}(\tilde {\boldsymbol {\rho }})\right )=-\tilde {\alpha }$, mass should be added to such elements and removed from those with low or null values of $\dot {\lambda }_{j}^{e}$.

5 Algorithm

Sensitivity calculations usually provide gradient vectors with high differences among contiguous elements (gradient components), fact that leads to the well-known undesirable checkerboard-like solutions. Simple filtering techniques help to circumvent this inconvenience (Sigmund and Petersson 1998). To this aim, a smoothed gradient on the element e is calculated by a weighted mean of the gradient of neighbor elements, i.e.,

$$ \widehat{\left[\nabla_{\rho}f\left( \rho\right)\right]}_{e}=\frac{{\displaystyle \sum\limits_{i = 1}^{n_{E}}}\mathcal{ H}_{i}\rho_{i}\left[\nabla_{\rho}f\left( \rho\right)\right]_{i}}{\rho_{e}{\displaystyle \sum\limits_{i = 1}^{n_{E}}}\mathcal{H}_{i}} $$

(38)

being $\mathcal {H}_{i}$ the distance weighing factor, defined as

$$\left\{\begin{array}{ll} \begin{array}{c} \mathcal{H}_{i}:= R-\text{dist}(i,e)\\ \mathcal{H}_{i}:= 0\hfill \end{array} & \begin{array}{c} if\quad\text{dist}(i,e)<R\\ if\quad\text{dist}(i,e)\geqslant R \end{array} \end{array}\right., $$

and R an influence radius and $\text {dist}(i,e)$ the distance between the centers $\boldsymbol {c}^{i}$ and $\boldsymbol {c}^{e}$ of elements i and e respectively. The modified gradient vector is then given by

$$ \widehat{\left[\nabla_{\rho}\mathcal{L}\right]_{e}}=\widehat{\left[\nabla_{\rho}f\left( \rho\right)\right]}_{e}+\mu V_{e}+\gamma^{+}-\gamma^{-}= 0, $$

(39)

that reduces to second and third terms if an element with intermediate density is considered:

$$ \widehat{\left[\nabla_{\rho}\mathcal{L}\right]}_{e}=\widehat{\left[\nabla_{\rho}f\left( \rho\right)\right]}_{e}+\mu V_{e}= 0, $$

(40)

Based on this last equation, the parameter $\beta _{e}$ usually called sensitivity of e is defined:

$$ \beta_{e}=-\frac{\widehat{\left[\nabla_{\rho}f\left( \rho\right)\right]}_{e}}{\mu V_{e}} $$

(41)

such that $\beta _{e}\rightarrow 1$ as $\rho _{e}\rightarrow \rho _{e}^{opt}$ unless a lateral constraint is firstly reached. With these values at hand, the same heuristic updating scheme for the density of element e found in Bendsøe and Sigmund (2003) is used:

$$\begin{array}{@{}rcl@{}} \beta_{\max} & =&\max\left\{ (1-\xi){\rho_{e}^{k}},\rho_{min}\right\} \\ \beta_{\min} & =&\min\left\{ (1+\xi){\rho_{e}^{k}},1\right\}\\ \rho_{e}^{k + 1} & =&\left\{\begin{array}{ll} \begin{array}{ccc} \beta_{\max} & if & {\rho_{e}^{k}}\beta_{e}^{\eta}\leqslant\beta_{\max}\\ \beta_{\min} & if & {\rho_{e}^{k}}\beta_{e}^{\eta}\geqslant\beta_{\min}\\ {\rho_{e}^{k}}\beta_{e}^{\eta} & & \mathrm{other cases} \end{array} \end{array}\right., \end{array} $$

(42)

where $\eta <1$ is a regularization exponent in order to avoid algorithmic oscillations. It is important to note that $\beta _{e}$ is dependent on the Lagrangian multiplier $\mu$, whose value is iteratively modified in order to satisfy the volume constraint; this is done similarly to Sigmund (2001). Figure 2 presents the iterative procedure, starting from a density field $\rho ^{k}$ until the optimum design $\rho ^{opt}$ is reached.

Fig. 2

Fluxogram. Iterative procedure for optimum design

6 Results

A set of numerical tests were performed in order to assess the effectiveness of present formulation. The first two cases have simple and closed solutions allowing them to be used as initial tests. Further examples are classical bi-dimensional topology optimization problems. Their aim is to evaluate the capability of the method to deal with complex topology solutions. All the examples consider a traction force distribution $\boldsymbol {t}$ with unitary integral. Therefore, the value of the loading factor $\alpha$ represents the total load magnitude. The parameters used for all examples are $p = 2$, $\eta = 0.5$, and $\xi = 0.175$ unless explicitly indicated. Moreover, the available fictitious mass is fixed on $M_{0}= 0.5$.

6.1 Bar under traction

Figure 3 shows a domain ${\Omega }$ submitted to a constant load $\boldsymbol {t}$ distributed over half of the superior boundary. Symmetry conditions are applied on the inferior and left boundary, representing in this way the first quadrant of the whole problem.

Fig. 3

Boundary conditions for the bar problem

The element size chosen is $L_{e}= 0.02 L$ being $L = 1$. Based on this, the radius of influence $R = 0.021 L$ in order to guarantee the existence of at least two neighbor elements for filtering calculus. The yield stress is $\sigma _{y}= 2$. The optimum expected topology is of a bar of ${L}/{2}$ width, submitted to an homogeneous uniaxial stress field equal to the yield stress (fully stressed design) and plastic collapse factor $\alpha = 2$.

The final topology achieved is displayed in Fig. 4 and corresponds to the expectations, having reached the plastic collapse factor of $\alpha = 1.94$. The difference between this value and the theoretical one can be explained considering that the mass comprised by the solid column (ρ = 1) is slightly lower than that available. The remaining mass is distributed on a narrow band of intermediate density and a wide region with minimum density (ρ_min = 0.01), all of them with low contribution upon the overall resistance. The solid column recovered at the final topology occupies a volume of approximately $V_{\rho = 1}= 0.47$. Considering a height $L = 1$, the plastic collapse factor reached then an appropriate value. The stress field of the final topology is presented in Fig. 5, having the expected fully stressed characteristic. It is worth highlighting that present fully stressed bar design can be equally achieved by stress constrained or compliance formulations (see for example Fancello 2006).

Fig. 4

Bar under traction. Optimum topology–density field

Fig. 5

Bar under traction. von Mises stress field

6.2 Thick pressure vessel

Different from the first example, the next case shows new features. A squared domain with inner circular boundary of radius $R_{i}={L}/{2}$ submitted to a constant pressure is proposed. Due to the symmetry boundary conditions imposed, a thick pressure vessel–like geometry submitted to a fully stressed design condition is expected. This is the limit case reached for a cylinder when submitted to the pressure of plastic collapse. Considering plane-stress condition, the expected analytical value of the collapse pressure is $p=\frac {6}{5}\sigma _{y}\ln \left (\frac {R_{e}}{R_{i}}\right )$(Yu et al. 2009). Considering an available mass $M_{0}= 0.5$, the analytical external radius is $R_{e}= 0.8727$ which has p = 1.337 as limit pressure.

In order to represent this problem, symmetry conditions were used simulating the first quadrant of the design domain, having in the interior (curved) region a pressure load (see Fig. 6).The element size for this example was adopted $L_{e}= 0.025 L$ and influence radius $R = 0.026 L$ for $L = 1$.

Fig. 6

Boundary conditions for the thick pressure vessel problem

The final topology achieved is shown in Fig. 7 with a plastic fully stressed region ranging throughout the entire thickness of the vessel. The numerically obtained value of $\alpha = 1.18$, slightly different from the analytical one. However, if intermediate regions are disregarded, the radius associated with the plastic band is $R_{e}= 0.836$, which in return gives as limit pressure $p = 1.233$, quite close to what was obtained. Stress distribution is shown in Fig. 8.

Fig. 7

Pressure vessel. Optimum topology–density field

Fig. 8

Pressure vessel. von Mises stress field

The reader may wonder what would be the corresponding optimal designs if compliance or stress-constrained formulations would have been used. In the case of compliance formulation, the annular shape provides the maximum stiffness and therefore the same optimal design is achieved if same volume fraction is used.

The optimal design for the (elastic) problem of mass minimization with local stress constraints is, once again, an annulus whose inner radius is submitted to the maximum hoop stress. Its comparison with the present case, however, is not straightforward. A possible procedure for this comparison consists of using the optimal annular design achieved in the present case and calculating the maximum pressure it would support for a maximum hoop stress of $\sigma _{y}$. This is easily done with the aid of the analytical elastic solution of a thick (plane stress) disk, given by $p_{e} = \frac {(\frac {R_{e}}{R_{i}})^{2}-1}{\sqrt {3(\frac {R_{e}}{R_{i}})^{4}+ 1}}$ (Yu et al. 2009). This expression provides a pressure $p_{e} = 0.726$, approximately $40\%$ lower than that achievable with limit analysis.

6.3 L-shape support

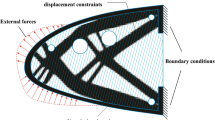
This case is a classical benchmark in topology optimization with stress constraints (Pereira et al. 2004; Fancello 2006) whose optimal design usually drives to a rounded corner in order to eliminate stress concentrations. In present formulation, however, the region close to the sharp corner achieves a plastic flow condition and, as it is shown in the sensitivity analysis section, the algorithm adds mass to those elements. Consequently, the sharp corner is expected to exist in the final topology. The boundary conditions used in this example are shown in Fig. 9, corresponding to a limit of plastic collapse of $\alpha = 1.640$.

Fig. 9

Boundary conditions for the L-shape problem

The element size is $L_{e}= 0.02 L$ and $L = 2.5$. The radius for filtering calculations is $R = 0.021 L$. The final solution is shown in Fig. 10, and its stress field in Fig. 11

Fig. 10

L-shape. Optimum topology–density field

Fig. 11

L-shape. von Mises stress field

The final design of Fig. 10 is clearly quite similar to that expected for a compliance minimization problem and it is reasonable to inquire which are the eventual differences between the optimal designs of both formulations. To this aim, this example was run with classical compliance formulation using the same element-by-element algorithm of Section 5. The optimal design is shown in Fig. 12. When a limit analysis calculus is performed with this last design, the plastic collapse factor achieved is $\alpha = 1.272$, approximately $77\%$ of that achieved by the LA formulation. The stress field achieved in this analysis is shown in Fig. 13.

Fig. 12

L-shape. Optimum topology–compliance formulation–density field

Fig. 13

L-shape: von Mises stress field–compliance formulation

A qualitative comparison between these present results and those of a stress-constrained problem is illustrative. Figure 14 shows a stress-constrained solution for the same geometry. In that case, yield stresses are usually found at the boundaries, as a consequence of bending. Moreover, a clear round corner is formed in order to keep the stress lower or equal than the yield value. Present results, on the other side, show a wider regions achieving yield stress on the limit of plastic failure.

Fig. 14

L-shape. von Mises stress constraint for the stress-constrained problem. Adapted from Emmendoerfer and Fancello (2015)

6.4 Cantilever beam

This example presents a cantilever beam problem. Two cases are investigated; the first one has a load applied on the middle right-side boundary as a shear force. The second one has the load applied on the upper right corner. The remaining boundary conditions are the same for both cases and are displayed in Figs. 15 and 18. A mesh sensitivity analysis is performed for the second case.

Fig. 15

Boundary conditions for the Cantilever beam problem, first case

The mesh element size used in the first example is $L_{e}= 0.03 L$ with $L = 1$. Analogous to previous, a radius $R = 0.031 L$ was chosen in order to keep minimal the number of elements used in the sensitivity filtering. The final configuration is presented in Fig. 16.

Fig. 16

Cantilever beam, first case. Optimum topology–density field

As consequence of the shear-like load applied, a local plastic hinge is created near the load application area (see Fig. 17); the load is not efficiently transmitted over the entire structure and limits the maximum achievable value of $\alpha = 1.45$.

Fig. 17

Cantilever beam, first case. von Mises stress field

The second cantilever beam has the applied force turned to a normal stress over the boundary (Fig. 18). Three meshes were tested, having element size of $L_{e}= 0.075 L$, $0.045 L$, and 0.025L, for the large, intermediate, and small element sizes, respectively, and $R = 0.076 L$, $0.046 L$, and $0.026 L$. The corresponding optimum plastic collapse factors are α_Large = 1.97, $\alpha _{Inter.}= 1.85$, and $\alpha _{Small}= 1.88$.

Fig. 18

Boundary conditions for the Cantilever beam problem, second case

The final topologies and stress fields for all of the mesh sizes are shown in Figs. 19, 20, 21, 22, 23, and 24.

Fig. 19

Cantilever beam, second case, large element size. Optimum topology–density field

Fig. 20

Cantilever beam, second case, intermediate element size. Optimum topology–density field

Fig. 21

Cantilever beam, second case, small element size. Optimum topology–density field

Fig. 22

Cantilever beam, second case, large element size. von Mises stress field

Fig. 23

Cantilever beam, second case, intermediate element size. von Mises stress field

Fig. 24

Cantilever beam, second case, small element size. von Mises stress field

It can be seen that the mesh size modifies the minimization sequence and the local minimum achieved with it. As in other problems, the topology complexity increases with the mesh refinement and perimeter penalization techniques can be used to recover some control on this issue (Cardoso and Fonseca 2003).

6.5 Clamped beam

This last example is usually presented in topology optimization problems concerning energy absorption and energy dissipation formulations. It refers to a hyperstatic beam, having both ends clamped and a distributed force applied to its center top as shown in Fig. 25.

Fig. 25

Boundary conditions for the clamped beam problem

Mesh element size used is $L_{e}= 0.0125 L$ with $L = 20$. Analogous to previous, a radius $R = 0.0126 L$ was chosen. Here, the available fictitious mass is set to $M_{0}= 0.4$ so it can be compared with the solution presented in Li et al. (2017b) Fig. 29, related to the maximum energy absorption problem, considering plasticity.

The final topology achieved is shown in Fig. 26, having as limit load $\alpha = 1.124$ and its von Mises stress field presented in Fig. 27. A sequence of density updates is shown in Fig. 28. One can see that the topology is already defined at the first updates and consolidated in update number 35. The final design of Fig. 26, however, has been collected at update number 300 in order to obtain a stable stress distribution shown in Fig. 27.

Fig. 26

Clamped beam. Optimum topology–density field

Fig. 27

Clamped beam. von Mises stress field

Fig. 28

Minimizing design sequence. Density-update iteration number. (A) 5, (B) 10, (C) 15, (D) 20, (E) 25, and (F) 35

Even though the two cases shown have different formulations, the similarities between topologies do not seem to be a simple coincidence. As seen in the sensitivity analysis, elements that contribute to the maximum structural load are also responsible for the maximum energy dissipation within the body (Fig. 29).

Fig. 29

Clamped beam. Density field for the maximum energy absorption problem—adapted from Li et al. (2017b)

Once again, a valuable comparison relates present optimal design with that obtained with compliance formulation, shown in Fig. 30. This design run with LA provides the von Mises stress field displayed in Fig. 31. Despite that the same essential topology is achieved, shape differences exist: the collapse factor for the compliance formulation is 0.752, 67% of that achieved by the present approach.

Fig. 30

Clamped beam. Density field–compliance formulation

Fig. 31

Clamped beam. von Mises stress field–compliance formulation

7 Discussion

The set of tested examples brings encouraging results. Although the numerical implementation is based on very simple and old-fashioned procedure for design updating and filtering technique, gradient information is powerful enough to drive the problem to local minima with sound appealing designs.

The first two examples are in fact test cases aiming to evaluate the ability of the procedure to recover the expected global minimum of the problem.

Special attention is deserved to the thick pressure vessel example. The best design and corresponding plastic collapse factor were indeed correctly identified. It is also verified that the admissible pressure for an elastic analysis with a maximum hoop stress $\sigma _{y}$ is approximately $40\%$ inferior to that achievable with the collapse failure condition.

The third numerical case addresses a benchmark for stress-constrained problems. As expected, no rounded corner designs are obtained with the present approach since the stress concentrations disappear in the plastic collapse response. A comparison between optimal designs for LA and compliance case was performed. As expected, the optimal design for the compliance case provides a lower plastic collapse factor (77%) of that achieved with present formulation.

Another interesting case is captured when shear loads are applied in the Cantilever beam problem revealing some tricky behaviors associated with plastic collapse. Even though plastic collapse is a condition associated with the whole structure, the lack of bearing capabilities is frequently due to plastic flow in small local regions. In this particular example, the load is applied in a manner that a plastic hinge is formed locally and then the bearing capability of the structure is globally lowered.

The fourth test explores the same cantilever solved with different meshes and a new load condition, revealing the expected change in design with increasing complexity for finer meshes. Again, the local nature of plastic collapse turns the problem plenty of local minima and therefore quite dependent on the chosen minimization sequence.

The last test (clamped beam) resulted in a topology much similar to that obtained by optimization procedures that sought to maximize the energy absorption of structures when loaded. From sensitivity analysis, it is verified that regions with high-energy dissipation are also the main responsible for maximizing the structural load, indicating a possible similarity between the two formulations and opens the subject to further investigations. A comparison between LA and compliance optimal designs showed, once again, that the former presents a higher plastic collapse factor than the latter, as expected.

8 Conclusions

A procedure that looks for the design that maximizes the load supported by an structure at its limit state of plastic collapse was proposed. The mechanical problem is described by a limit analysis formulation that, different from classical incremental plasticity, allows a direct (and consequently efficient) calculation of the collapse load factor. Design optimization is formally stated as the maximization of the collapse load factor subject to a fixed quantity of available material. To this aim, a fictitious material density distribution, widely known as SIMP approach, is used.

Limit analysis, besides being an appealing approach for the proposed task, provides appropriate mathematical structure for sensitivity calculations. In the particular case of the chosen objective function, it was shown that the solution of the adjoint problem is identical to the update vector of the Newton–Raphson procedure at the convergence of the limit state. Consequently, gradient calculations reduce to multiplicative array operations of already-available data.

In order to keep the implementation simple, a heuristic element-by-element density updating algorithm aiming to solve the optimality conditions is used. This procedure was inspired by those applied in compliance linear problems and makes use of conventional filtering techniques to preclude checkerboard patterns.

A global evaluation of the obtained results suggests the present formulation involving limit analysis as the physical problem within topology optimal design is promising and open for further investigations. Present work had a clear choice for the most simple operational solutions for design optimization and new, more efficient numerical techniques may be tested, providing a design method for a wide range of technological applications.

As a final conclusion, the results of the tested examples support the argument that, despite having similar geometries, optimal designs for the compliance problem provide plastic collapse factors that are lower than those obtained with the present formulation.