An efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization

Abstract

In the present work, a highly efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization is proposed. In this approach, high-resolution optimization results can be obtained with a smaller number of design variables and a relatively low degree of freedoms (DOFs). This is achieved by taking the advantage that the topology optimization model and the finite element analysis model are totally decoupled in the MMC-based problem formulation. A coarse mesh is used for structural response analysis and a design domain partitioning strategy is introduced to preserve the topological complexity of the optimized structures. Numerical examples are then provided so as to demonstrate that with the use of the proposed approach, computational efforts can be saved substantially for large-scale topology optimization problems.

1 Introduction

Structural topology optimization, which aims at distributing a certain amount of available materials within a prescribed design domain appropriately in order to achieve optimized structural performances, has been applied in a wide range of physical disciplines, such as acoustics, electromagnetics, and optics, since the pioneering work of Bendsøe and Kikuchi (1988). So far, classical topology optimization methods have already been integrated into commercial softwares (e.g., Altair-OptiStruct (HyperWorks 2013) and Abaqus (Simulia 2011)) for practical use. However, since systems of (sometimes nonlinear) partial differential equations must be solved iteratively to determine the structural response and sensitivity of information, solving topology optimization problems often involves large computational efforts. Therefore, for large-scale problems, topology optimization methods are generally not easy to implement, especially when high-resolution configurations containing members of small length scales are sought for.

In traditional implicit topology optimization methods (e.g., the classical solid isotropic material with penalization (SIMP) method and the classical level set method (LSM)), the finite element analysis (FEA) model and the topology description model are strongly coupled. This means that the density of the FE mesh determines not only the accuracy of FEA, but also the resolution of the obtained optimized solutions. As a result, very fine FE meshes must be employed if high-resolution optimized structures are needed! This, however, will inevitably lead to large-scale and time-consuming computational tasks especially for three-dimensional (3D) topology optimization problems. For example, if a cubic design domain is discretized into 100 × 100 × 100 elements, one needs to solve a FE model with 3 million degrees of freedoms (DOFs) as along with a nonlinear optimization problem with 1 million design variables for each iteration step. Furthermore, if one intends to double the resolution for more tiny structural features in the optimized design, the corresponding numbers of the DOFs and design variables would increase to 24 million and 8 million, respectively! Recently, with the use of a supercomputer with 8000 processors, Aage et al. (2017) found the optimal reinforcement of a full aircraft wing with 1.1 billion voxels for FE discretization via SIMP method in several days. This, however, is an almost impossible task for ordinary computers.

To improve the practical applicability of topology optimization method, attempts have been made to enhance the solution efficiency of large-scale problems. One direct approach is to use high performance computers and parallelize the solution process. To be specific, early research works mainly focused on how to obtain structural responses rapidly with the use of parallelization techniques (Borrvall and Petersson 2011; Kim et al. 2004; Vemaganti and Lawrence 2005; Evgrafov et al. 2007; Mahdavi et al. 2006; Aage et al. 2007). In addition, in order to reduce the computational time associated with the solution of large-scale nonlinear optimization problems bearing a huge number of design variables, Aage and Lazarov (2013) also parallelized the well-known MMA optimizer successfully. Although these achievements greatly enhanced the solvability of large-scale topology optimization problems, the corresponding computational complexity is not reduced essentially. Apart from resorting to high performance computing (HPC) techniques, some researchers have also made attempts to enhance the efficiency of FEA by employing some special solution schemes or reducing the total number of DOFs in FEA models directly. For example, Wang et al. (2007) proposed to recycle parts of the search space in a Krylov subspace solver to reduce the number of iterations for solving the equilibrium equations, and a significant reduction in computational effort is observed especially when the changes of design variables between two consecutive optimization steps are small enough. Amir et al. (2009a) developed a solution procedure in which exact FEA is performed only at certain stages of iterations while approximate reanalysis is used elsewhere. In Amir et al. (2009b), an alternative stopping criterion for a preconditioned conjugate gradient (PCG) iterative solver was adopted so that fewer iterations are required for obtaining a converged solution. Amir and Sigmund (2010) also suggested an approximate approach to solve the nested analysis equations in topology optimization problems, and it was reported that the computational cost can be reduced by one order of magnitude. It should be pointed out, however, that the above techniques are in general only suitable for dealing with some specific classes of problems and careful elaborations are needed for more general applications.

Considering the reduction of computational intensing of FE analysis, adaptive mesh refinement techniques (Kim et al. 2003; Stainko 2005; Guest and Smith Genut 2010) and model reduction method (Yoon 2010) have also been introduced in the implicit SIMP-based solution framework for optimal topology design. More recently, Nguyen et al. (2009) proposed a multi-resolution formulation for minimum compliance design where a coarse FE mesh is adopted for structural response analysis while a denser mesh is used for density field discretization. A filter scheme was also employed to eliminate numerical instabilities. Numerical examples provided in this work showed that the treatment by Nguyen et al. (2009) can greatly improve the computational efficiency of SIMP-based topology optimization method by reducing the FEA cost. Later on, the approach was further extended to incorporate an adaptive mesh refinement scheme (Nguyen et al. 2012). It should be noted that, in the original SIMP-based multi-resolution topology optimization approach (Nguyen et al. 2009), quadrilateral finite elements are adopted for structural analysis. Under this circumstance, in order to obtain meaningful designs with well-connected material distribution, the filter radius has to be comparable to the characteristic size of the adopted coarse FE mesh (not the characteristic size of the density mesh!). As a result, the optimized designs often suffered from blurred boundaries and may not contain structural details with small feature sizes, even though high-resolution density meshes are employed. Nevertheless, recent works (Nguyen et al. 2017; Groen et al. 2017) have shown that, such drawback can be overcome by introducing higher-order finite elements for structural analysis and advanced filter techniques (Guest et al. 2004; Sigmund 2007; Xu et al. 2010 and Wang et al. 2011). In those contributions, optimized designs with fine structural features and crisp boundaries are obtained successfully. However, using higher-order elements will inevitably result in higher computational cost for FEA, and as pointed out by Groen et al. (2017), when higher-order elements are used, the order of finite element interpolation also needs to be compatible with the resolution ratio between the mesh for density interpolation and the mesh for displacement interpolation, in order to circumvent the issue of artificially stiff patterns. Although the number of DOFs in FEA models can be greatly reduced in SIMP-based multi-resolution topology optimization framework, the number of design variables is still very large in the aforementioned approaches. This, as will be shown later, may also result in long computational time (corresponding to the solution of large-scale nonlinear/non-convex optimization problems) when large-scale multi-resolution topology optimization problems are considered. In addition, due to the implicit nature of geometry description, post-processing is always required to transfer the optimized designs obtained by implicit topology optimization approaches to computer aided design/engineering (CAD/CAE) systems. This issue to some extent restricts the application of the aforementioned multi-resolution topology optimization approach to large-scale problems because of the very complicated post-processing works involved.

In order to resolve the aforementioned challenging issues for solving large-scale multi-resolution optimization problems, the moving morphable components (MMC)-based topology optimization approach is extended to the multi-resolution framework in the present paper. The MMC-based topology optimization approach was first initialized by Guo et al. (2014b), where a number of structural components with explicit geometry descriptions are adopted as basic building blocks of optimization (see in Fig. 1 for reference). Therefore, optimized designs can be determined by optimizing the explicit geometry parameters characterizing the sizes, shapes, and layouts of the introduced components. Compared with traditional topology optimization approaches, in the MMC method, topology optimization actually can be achieved in an explicit and geometrical way. It has been shown that, this new solution framework, can not only reduce the number of design variables substantially, but also possesses the merit of controlling the structural geometry features such as minimum length scale (Zhang et al. 2016a), overhang angle (Guo et al. 2017), and the connectivity of a structure (Deng and Chen 2016) in a straightforward and explicit way. Actually, recent years witnessed a growing interest on developing topology optimization methods based on explicit geometry/topology descriptions (Guo et al. 2016, 2017; Zhang et al. 2017a, 2018; Lei et al. 2018; Norato et al. 2015; Hoang and Jang 2017; Hou et al. 2017; Takalloozadeh and Yoon 2017; Sun et al. 2018).

Fig. 1

a–c A schematic illustration of the MMC-based topology optimization method

As pointed in Guo et al. (2014b) and Liu et al. (2017), one of the distinctive features of the MMC-based topology optimization framework is that the corresponding FEA model and the topology description model are fully decoupled. In previous implementation of the MMC-based approaches (Guo et al. 2014b, 2016; Zhang et al. 2016a), since the same mesh is used for both the interpolation of displacement field and the description of explicit structural geometry, this distinguished description analysis-decoupling feature pertaining to the MMC method has not been fully utilized. In the present work, we aim for establishing a highly efficient multi-resolution MMC-based solution framework for structural topology optimization by adopting two sets of meshes with different resolutions for FEA and topology description, respectively. Actually, as will be shown in Section 5, compared with traditional methods, under the proposed MMC-based multi-resolution framework, for some tested problems, the average computational time of each optimization step can be reduced by one order of magnitude. More importantly, high-resolution designs can be obtained with a quite small number of design variables.

The rest of the paper is organized as follows. In Section 2, the formulation of topology optimization problems under the MMC-based solution framework is presented. Then the strategy for obtaining high-resolution designs efficiently using MMCs as basic building blocks is described in Section 3. Afterwards, some techniques, that are capable of improving the efficiency of numerical implementation of the proposed MMC-based approach and preserving the complexity of structural topology, are introduced in Section 4. In Section 5, several representative examples are presented to illustrate the effectiveness of the proposed approach. Finally, some concluding remarks are provided in Section 6.

2 Problem formulation

In the MMC-based topology optimization approach, the material distribution of a structure can be described by a so-called topology description function (TDF) in the following form:

$$ \left\{\begin{array}{c}{\phi}^{\mathrm{s}}\left(\boldsymbol{x}\right)>0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in }{\Omega}^{\mathrm{s}},\kern0.5em \\ {}\ {\phi}^{\mathrm{s}}\left(\boldsymbol{x}\right)=0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in }{\mathrm{\partial \Omega}}^{\mathrm{s}},\\ {}{\phi}^{\mathrm{s}}\left(\boldsymbol{x}\right)<0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in}\mathrm{D}\backslash \left({\Omega}^{\mathrm{s}}\bigcup {\mathrm{\partial \Omega}}^{\mathrm{s}}\right),\end{array}\right. $$

(2.1)

where D represents a prescribed design domain and Ω^s ⊂ D denotes the region constituted by n components made of the solid material. As shown in (Guo et al. 2014b), the TDF of the whole structure can be constructed as ϕ^s(x) = max(ϕ₁(x), ⋯, ϕ_n(x)) with ϕ_i(x) denoting the TDF of the i-th component (see Fig. 1 for a schematic illustration). In the present work, for the two-dimensional (2D) case, as shown in Fig. 2, ϕ_i(x) is constructed as:

$$ {\phi}_i\left(x,y\right)=1-{\left(\frac{x^{\prime }}{a_i}\right)}^p-{\left(\frac{y^{\prime }}{b_i\left({x}^{\prime}\right)}\right)}^p, $$

(2.2)

with

$$ \left\{\begin{array}{c}{x}^{\hbox{'}}\\ {}{y}^{\hbox{'}}\end{array}\right\}=\left[\begin{array}{cc}\cos {\theta}_i& \sin {\theta}_i\\ {}-\sin {\theta}_i& \cos {\theta}_i\end{array}\right]\left\{\begin{array}{c}x-{x}_{0i}\\ {}y-{y}_{0i}\end{array}\right\}, $$

(2.3)

and p is a relatively large even integer (p = 6 in this work). In (2.2) and (2.3), the symbols a_i, b_i(x^′), (x_0i, y_0i)^⊤ and θ_i denote the half-length, the variable half width, the vector of center coordinates and the inclined angle (measured from the horizontal axis anti-clockwisely) of the i-th component (see in Fig. 2 for reference), respectively. It should be noted that the variation of the width of the component b_i(x^′) can take different forms (Zhang et al. 2016b), and in this work it is chosen as

$$ {b}_i\left({x}^{\prime}\right)=\frac{t_i^1+{t}_i^2}{2}+\frac{t_i^2-{t}_i^1}{2{a}_i}{x}^{\prime }, $$

(2.4)

where ${t}_i^1$ and ${t}_i^2$ are parameters used to describe the thicknesses of the component.

Fig. 2

The geometry description of a two-dimensional structural component

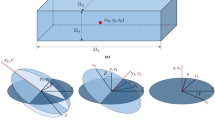
For the 3D case, we used the following TDF to characterize the region occupied by the i-th component:

$$ {\phi}_i\left(x,y,z\right)=1-{\left(\frac{x^{\prime }}{L_i^1}\right)}^p-{\left(\frac{y^{\prime }}{h_i\left({x}^{\prime}\right)}\right)}^p-{\left(\frac{z^{\prime }}{f_i\left({x}^{\prime },{y}^{\prime}\right)}\right)}^p, $$

(2.5)

with

$$ \left\{\begin{array}{c}{x}^{\hbox{'}}\\ {}{y}^{\hbox{'}}\\ {}{z}^{\hbox{'}}\end{array}\right\}=\left[\begin{array}{ccc}{R}_{11}& {R}_{12}& {R}_{13}\\ {}{R}_{21}& {R}_{22}& {R}_{23}\\ {}{R}_{31}& {R}_{32}& {R}_{33}\end{array}\right]\left\{\begin{array}{c}\begin{array}{c}x-{x}_{0i}\\ {}y-{y}_{0i}\end{array}\\ {}z-{z}_{0i}\end{array}\right\}, $$

(2.6)

and

$$ \left[\begin{array}{ccc}{R}_{11}& {R}_{12}& {R}_{13}\\ {}{R}_{21}& {R}_{22}& {R}_{23}\\ {}{R}_{31}& {R}_{32}& {R}_{33}\end{array}\right]=\left[\begin{array}{ccc}{c}_b\cdotp {c}_t& -{c}_b\cdotp {s}_t& {s}_b\\ {}{s}_a\cdotp {s}_b\cdotp {c}_t+{c}_a\cdotp {s}_t& -{s}_a\cdotp {s}_b\cdotp {s}_t+{c}_a\cdotp {c}_t& -{s}_a\cdotp {c}_b\\ {}-{c}_a\cdotp {s}_b\cdotp {c}_t+{s}_a\cdotp {s}_t& {c}_a\cdotp {s}_b\cdotp {s}_t+{s}_a\cdotp {c}_t& {c}_a\cdotp {\mathrm{c}}_b\end{array}\right], $$

(2.7)

respectively. In (2.7), ${s}_a=\sin \alpha, {s}_b=\sin \beta, {s}_t=\sin \theta, {c}_a=\sqrt{1-{s}_a^2},{c}_b=\sqrt{1-{s}_b^2}$, and ${c}_t=\sqrt{1-{s}_t^2}$ with α, β, and θ denoting the rotation angles of the component from a global coordinate system Oxyz to the local coordinate system O^′x^′y^′z^′, respectively (see Fig. 3 for reference). The vector of the coordinates of the central point and the half-length of the component are represented by the coordinate (x_0i, y_0i, z_0i)^⊤ and ${L}_i^1$, respectively. Furthermore, the functions h_i(x^′) and f_i(x^′, y^′) in (2.5) are used to describe the thickness profiles of the component in y and z directions, respectively. In this work, h_i(x^′) and f_i(x^′, y^′) are simply chosen as (see Fig. 4 for reference)

$$ {h}_i\left({x}^{\prime}\right)={L}_i^2,\kern0.75em {f}_i\left({x}^{\prime },{y}^{\prime}\right)={L}_i^3 $$

(2.8)

Fig. 3

a–c Coordinate transformation associated with a three-dimensional component

Fig. 4

The geometry description of a three-dimensional structural component

Other forms of h_i(x^′) and f_i(x^′, y^′) can be found in (Zhang et al., 2017b).

With the use of the above expressions, the region ${\Omega}_i^{\mathrm{s}}$ occupied by the i-th component can be described as:

$$ \left\{\begin{array}{c}{\phi}_i\left(\boldsymbol{x}\right)>0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in }{\Omega}_i^{\mathrm{s}},\kern0.5em \\ {}\ {\phi}_i\left(\boldsymbol{x}\right)=0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in }{\mathrm{\partial \Omega}}_i^{\mathrm{s}},\\ {}{\phi}_i\left(\boldsymbol{x}\right)<0,\mathrm{if}\ \boldsymbol{x}\mathbf{\in}\mathrm{D}\backslash \left({\Omega}_i^{\mathrm{s}}\bigcup {\mathrm{\partial \Omega}}_i^{\mathrm{s}}\right).\end{array}\right. $$

(2.9)

It is also obvious that ${\Omega}^{\mathrm{s}}={\cup}_{i=1}^n{\Omega}_i^{\mathrm{s}}$. At this position, it is also worth noting that topology optimization can also be carried out in the MMC-based solution framework without introducing TDF. Actually, the TDF is only employed for the convenience of performing FEA with fixed mesh. We refer the readers to (Zhang et al. 2017a, 2018) for the implementation of the MMC-based topology optimization approach without using TDFs.

Based on the above description, it is obvious that the layout of a structure can be solely determined by a vector of design variables, e.g., D = ((D¹)^⊤, …, (Dⁱ)^⊤, …(Dⁿ)^⊤)^⊤. To be specific, for the 2D case, we have ${\boldsymbol{D}}^i={\left({x}_{0i},{y}_{0i},{a}_i,{\boldsymbol{d}}_i^{\top },{\theta}_i\right)}^{\top },$ which contains the design variables associated with the i-th component with d_i denoting the vector of geometry parameters related to b_i(x^′). In the 3D case, Dⁱ can also be constructed in a similar way.

Based on the above descriptions, a typical topology optimization problem under the MMC-based solution framework can be formulated as follows:

$$ {\displaystyle \begin{array}{c}\mathrm{Find}\ \boldsymbol{D}={\left({\left({\boldsymbol{D}}^1\right)}^{\top },\dots, {\left({\boldsymbol{D}}^i\right)}^{\top },\dots, {\left({\boldsymbol{D}}^n\right)}^{\top}\right)}^{\top}\\ {}\operatorname{Minimize}\ I=I\left(\boldsymbol{D}\right)\\ {}\mathrm{S}.\mathrm{t}.\\ {}{g}_k\left(\boldsymbol{D}\right)\le 0,\kern0.8em k=1,\dots, m,\\ {}\boldsymbol{D}\subset {\mathcal{U}}_{\boldsymbol{D}},\end{array}} $$

(2.10)

where I(D) and g_k,  k = 1, …, m are the objective and constraint functions/functionals, respectively. In (2.10), ${\mathcal{U}}_{\boldsymbol{D}}$ is the admissible set that design variable vector D belongs to.

In the present study, structures are designed to minimize the structural compliance under the volume constraint of available solid material. Under this circumstance, the corresponding problem formulation can be specified as:

$$ {\displaystyle \begin{array}{c}\mathrm{Find}\kern1em \boldsymbol{D}={\left({\left({\boldsymbol{D}}^1\right)}^{\top },\dots, {\left({\boldsymbol{D}}^i\right)}^{\top },\dots, {\left({\boldsymbol{D}}^n\right)}^{\top}\right)}^{\top },\boldsymbol{u}\left(\boldsymbol{x}\right)\in {\boldsymbol{H}}^1\left({\Omega}^{\mathrm{s}}\right)\\ {}\operatorname{Minimize}\kern1em C=\underset{\mathrm{D}}{\int }H\left({\phi}^{\mathrm{s}}\left(\boldsymbol{x};\boldsymbol{D}\right)\right)\boldsymbol{f}\cdotp \boldsymbol{u}\mathrm{dV}+\underset{\Gamma_{\mathrm{t}}}{\int}\boldsymbol{t}\cdotp \boldsymbol{u}\mathrm{dS}\\ {}\mathrm{S}.\mathrm{t}.\kern0.75em \\ {}\underset{\mathrm{D}}{\int }{H}^q\left({\phi}^{\mathrm{s}}\left(\boldsymbol{x};\boldsymbol{D}\right)\right)\mathbb{E}:\boldsymbol{\upvarepsilon} \left(\boldsymbol{u}\right):\boldsymbol{\upvarepsilon} \left(\boldsymbol{v}\right)\mathrm{dV}=\underset{\mathrm{D}}{\int }H\left({\phi}^{\mathrm{s}}\left(\boldsymbol{x};\boldsymbol{D}\right)\right)\boldsymbol{f}\cdotp \boldsymbol{v}\mathrm{dV}\\ {}+\underset{\Gamma_{\mathrm{t}}}{\int}\boldsymbol{t}\cdotp \boldsymbol{v}\mathrm{dS},\forall \boldsymbol{v}\in {\mathcal{U}}_{\mathrm{ad}},\\ {}\underset{\mathrm{D}}{\int }H\left({\phi}^{\mathrm{s}}\left(\boldsymbol{x};\boldsymbol{D}\right)\right)\mathrm{dV}\le \overline{V},\\ {}\boldsymbol{D}\subset {\mathcal{U}}_{\boldsymbol{D}},\\ {}\boldsymbol{u}=\overline{\boldsymbol{u}},\mathrm{on}\ {\Gamma}_{\mathrm{u}},\end{array}} $$

(2.11)

where D, f, t, u, ε = sym(∇u), and $\overline{\boldsymbol{u}}$ represents the design domain, the body force density, the prescribed surface traction on Neumann boundary Γ_t, the displacement field, the linear strain tensor, and the prescribed displacement on Dirichlet boundary Γ_u, respectively. The symbol H = H(x) denotes the Heaviside function with H = 1 if x > 0 and H = 0 otherwise. For numerical implementation purpose, H(x) is often replaced by its regularized version H_ϵ(x). In the present work, H_ϵ(x) is taken as

$$ {H}_{\epsilon }(x)=\left\{\begin{array}{c}1,\kern17.25em \mathrm{if}\kern0.5em x>\epsilon, \\ {}\frac{3\left(1-\alpha \right)}{4}\left(\frac{x}{\epsilon }-\frac{x^3}{3{\epsilon}^3}\right)+\frac{1+\alpha }{2},\kern3.75em \mathrm{if}-\epsilon \le x\le \epsilon, \kern1.75em \\ {}\ \alpha, \kern16.25em \mathrm{otherwise},\end{array}\right. $$

(2.12)

where ϵ and α are two small positive numbers used for controlling the length of the transition zone and avoiding the singularity of the global stiffness matrix, respectively. In (2.11), ϕ^s(x; D) is the TDF of the whole structure while q > 1 is a penalization factor (in the present work, q = 2 is used). In (2.11), $\mathbb{E}={E}^{\mathrm{s}}/\left(1+{\nu}^{\mathrm{s}}\right)\left[\mathbb{I}+{\nu}^{\mathrm{s}}/\left(1-2{\nu}^{\mathrm{s}}\right)\boldsymbol{\updelta} \otimes \boldsymbol{\updelta} \right]$ is the fourth order elasticity tensor of the isotropic solid material with E^s, ν^s, $\mathbb{I}$, and δ denoting Young’s modulus as well as Poisson’s ratio of the solid material, the symmetric part of the fourth order identity tensor and the second order identity tensor, respectively. The symbol ${\mathcal{U}}_{\mathrm{ad}}=\left\{\boldsymbol{v}\right|\ \boldsymbol{v}\boldsymbol{\in }{\boldsymbol{H}}^1\left({\Omega}^{\mathrm{s}}\right),\boldsymbol{v}=\mathbf{0}\ \mathrm{on}\ {\mathrm{S}}_{\mathrm{u}}\Big\}$ represents the admissible set of virtual displacement vector v and $\overline{V}$ is the upper bound of the volume of the available solid material.

3 Solution strategies for multi-resolution topology optimization under the MMC-based framework

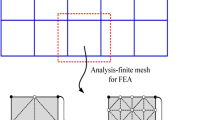
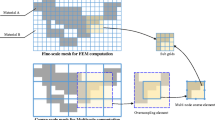
In this work, the decoupling approach proposed by Nguyen et al. (2009) is adopted in the MMC-based solution framework to construct a highly efficient multi-resolution topology optimization approach. As described in (Nguyen et al. 2009), the basic idea of the decoupling approach for multi-resolution topology optimization is introducing two sets of meshes with different resolutions to solve a topology optimization problem (see Fig. 5 for reference). A coarse mesh is used for interpolating the displacement field while a fine background mesh is used for describing the structural geometry. This approach has been proved to be very effective to reduce the computational cost associated with FEA in the SIMP method. It should be noted that, however, that when quadrilateral finite elements are adopted for structural analysis (Nguyen et al. 2009), the filter radius has to be comparable with the size of FE mesh to avoid the checkboard pattern/artificially stiff pattern in optimization results. As a result, the optimized structures always do not contain structural details with small feature sizes although high-resolution density meshes are employed.

Fig. 5

a–c A schematic illustration of the basic idea of the proposed MMC-based multi-resolution topology optimization approach.

However, if such analysis-element is applied under the MMC-based solution framework, the situation would be totally different. This is because in the MMC approach, the structural geometry is described by a set of explicit geometrical parameters. This means that, theoretically speaking, the structural topology has an infinitely high resolution in the MMC approach. In addition, the MMC method can intrinsically aggregate the material in components. This, to some extent, can alleviate the artificially stiff patterns. Based on this consideration, in the present work, we propose to investigate the multi-resolution topology optimization problems using MMC approach and coarse analysis-elements.

In the present work, following the idea adopted in traditional approaches, we also intend to use a fixed FE mesh and an ersatz material model for FEA, although adaptive FE mesh can also be applied to calculate structural responses since we have the explicit boundary representation in the MMC approach. Under this circumstance, refined background mesh are also needed to identify the small structural features. It is, however, worth noting that, unlike the traditional implicit topology optimization method, the refinement of the background mesh does not increase the number of design variables, and it only increases the computational effort associated with numerical integrations when the element stiffness matrix is calculated as shown below.

As the same in Nguyen et al. (2009), the stiffness matrix of the i-th analysis-element can be calculated as (see Fig. 6 for a schematic illustration):

$$ {\boldsymbol{K}}_i={\int}_{\Omega_i}\boldsymbol{B}{\left(\boldsymbol{x}\right)}^{\mathbf{\top}}{\boldsymbol{D}}_i\left(\boldsymbol{x}\right)\boldsymbol{B}\left(\boldsymbol{x}\right)\mathrm{d}\Omega \approx \sum \limits_{j=1}^{ng}{E}_{i,j}\boldsymbol{B}{\left({\boldsymbol{x}}_{i,j}^0\right)}^{\mathbf{\top}}{\boldsymbol{D}}_0\boldsymbol{B}\left({\boldsymbol{x}}_{i,j}^0\right){A}_g, $$

(3.1)

where Ω_i represents the region occupied by the i-th analysis-element, x = (x, y) is the vector of spatial coordinates, B and D_i are the strain-displacement matrix and the constitutive matrix, respectively. In (3.1), ng represents the number of background elements in the considered analysis-element, D₀ corresponds to the constitutive matrix of the solid material with unit Young’s modulus, and A_g is the area of a background element, respectively. The symbol ${\boldsymbol{x}}_{i,j}^0$ denotes the coordinate vector of the integration point (simply chosen as the central point of the corresponding background element in the present work) associated with the j-th background element in the i-th analysis-element (denoted as element (i, j) in the following text). In addition, E_i, j is the smeared Young’s modulus of element (i, j). Under the spirit of the ersatz material model, E_i, j can be calculated through the corresponding nodal values of the TDF as

$$ {E}_{i,j}\left({\phi}^{\mathrm{s}}\right)=\frac{E^{\mathrm{s}}\left({\sum}_{e=1}^4{\left(H\left({\phi}_{i,j}^{\mathrm{s}e}\right)\right)}^q\right)}{4}, $$

(3.2)

where ${\phi}_{i,j}^{\mathrm{s}e}$ is the value of TDF of the whole structure at the e-th node of element (i, j), E^s is Young’s modulus of the solid material.

Fig. 6

a–c A schematic illustration of an analysis-element, the corresponding background elements, and integration points.

Once the element stiffness matrix of each analysis-element is obtained, we can then assemble the global stiffness matrix K, solve the displacement vector U, and obtain the structural compliance as $C={\boldsymbol{U}}^{\boldsymbol{\top}}\boldsymbol{KU}={\sum}_{i=1}^{NS}{\boldsymbol{U}}_i^{\top }{\boldsymbol{K}}_i{\boldsymbol{U}}_i$ with U_i denoting the nodal displacement vector of the i-th analysis-element and NS representing the total number of analysis-elements, respectively. Furthermore, then the sensitivity of the structural mean compliance with respect to a design variable d (in the context of FEA) can be expressed as:

$$ {\displaystyle \begin{array}{c}\frac{\partial C}{\partial d}=-\sum \limits_{i=1}^{NS}{\boldsymbol{U}}_i^{\top}\frac{\partial {\boldsymbol{K}}_i}{\partial d}{\boldsymbol{U}}_i\\ {}=-\sum \limits_{i=1}^{NS}{\boldsymbol{U}}_i^{\top}\left(\frac{E^{\mathrm{s}}}{4}\sum \limits_{j=1}^{ng}\left(\sum \limits_{e=1}^4q{\left(H\left({\phi}_{i,j}^{\mathrm{s}e}\right)\right)}^{q-1}\frac{\partial H\left({\phi}_{i,j}^{\mathrm{s}e}\right)}{\partial d}\ \right)\boldsymbol{B}{\left({\boldsymbol{x}}_{i,j}^0\right)}^{\top }{\boldsymbol{D}}_0\boldsymbol{B}\left({\boldsymbol{x}}_{i,j}^0\right){A}_g\right){\boldsymbol{U}}_i\end{array}} $$

(3.3)

For the volume constraint, we also have

$$ \frac{\partial V}{\partial d}=\frac{1}{4}\sum \limits_{j=1}^{NG}\sum \limits_{e=1}^4\frac{\partial H\left({\phi}_j^{\mathrm{s}e}\right)}{\partial d} $$

(3.4)

The derivation of $\partial H\left({\phi}_j^{\mathrm{s}e}\right)/\partial d$ in (3.3) and (3.4) is trivial and will not be repeated here.

4 Numerical implementation aspects

In this section, we will discuss some numerical techniques that will be used to implement the proposed MMC-based multi-resolution topology optimization approach in a computationally efficient way. Actually, these techniques are not only applicable to the multi-resolution design case, but also capable of enhancing the computational efficiency of the original single-resolution-oriented MMC approach (Guo et al. 2014b; Zhang et al. 2016b). Moreover, a so-called design domain partitioning strategy is developed to preserve the topological complexity of the optimized designs obtained by the proposed multi-resolution topology optimization approach.

4.1 Generating the TDF of the structure and calculating sensitivities locally

As shown in Section 2, in the present work, the geometry of a component is described by a p-th order hyperelliptic function. In our previous numerical implementations (e.g., Zhang et al. 2016b), the TDF values associated with each component are calculated at every node of background FE mesh with the use of (2.2)–(2.4) (for the 2D case) or (2.5)–(2.8) (for the 3D case). If, for example, a problem with 500 components and 1000 × 500 background elements is considered, the TDF nodal values must be calculated (1000 + 1) × (500 + 1) × 500 times to generate the TDF of the whole structure. This treatment will definitely consume a large amount of computational time and computer memory. Therefore, it is not suitable for solving large scale problems.

Actually, the nodal TDF values of the background FE mesh are used for the following three purposes: 1) describing the geometry of the components through (2.9), 2) calculating the Heaviside function used in the ersatz material model using (2.12), and 3) carrying out the sensitivity analysis as shown in (3.3)–(3.4). Actually, a component only occupies a small portion of the design domain, so it is not necessary to calculate the nodal values of TDF on the whole region. Furthermore, from (2.12), it can also be observed that both the regularized Heaviside function and its derivative with respect to the TDF only vary in a narrow band Ω^BDY = {x| x ∈ D,   − ϵ ≤ ϕ^s(x) ≤ ϵ} around the structural boundary and keep constant in rest of the design domain. These observations inspire us that we can only generate and store the nodal values of the TDF of each component around its boundary locally (see Appendix for more details). Since the characteristic size of an individual component is usually relatively small, compared with that of the entire design domain, this strategy can save the computational effort and computer memory used to generate the corresponding TDF significantly.

In previous numerical implementation (e.g., Zhang et al. 2016b), the formula ϕ^s = max(ϕ₁, ϕ₂, ⋯, ϕ_n) is used to generate the TDF of whole structure. In the present work, the following well-known K-S function is used to approximate the max operation (Kreisselmeier and Steinhauser 1979):

$$ {\phi}^{\mathrm{s}}\approx \ln \left(\sum \limits_{i=1}^n\exp \left(l{\phi}_{\mathrm{i}}\right)\right)/l, $$

(4.1)

where l is a large positive number (e.g., l = 100). Actually, (4.1) can also be carried out only around the boundary region of each component (see more details in Appendix). Numerical experiments indicate that this treatment can also enhance the computational efficiency of generating the TDF of whole structure significantly.

In addition, since the derivative of the regularized Heaviside function with respect to the nodal values of TDF only has nonzero value near the structural boundary, the sensitivities of the objective and constraint functions also can be calculated locally. It is worth noting that, although the sensitivity analysis in the MMC approach is not as straightforward as that in the SIMP approach, the time cost for sensitivity analysis associated with the proposed new implementation of the MMC method is, however, much less than (or at least comparable to) that of the SIMP approach. This is due to the fact that, in the present MMC-based approach, the number of design variables is significantly reduced, and there is no chain rule operation resulting from the non-local filter operator. This point will be verified by the numerical examples provided in Section 5.

4.2 Design domain partitioning strategy for preserving structural complexity

In this subsection, we shall discuss how to control the topological complexity in the optimized designs. In the MMC approach, as shown in Fig. 7a, the components can move, morph, disappear, overlap, and intersect with each other to generate an optimized structure. Since the sensitivities are only nonzero in a narrow band near the structural boundary, the sensitivities of the objective/constraint functions with respect to the design variables associated with a hidden component are zero. In other words, once a component is fully covered by other components, the design variables of this component will remain unchanged until the components covering it move away. This mechanism might be responsible for the relatively simple topologies of the optimized designs obtained by MMC approach in some cases, since many components may be covered by other components in the final optimized results (see Fig. 7a for reference).

Fig. 7

a, b The basic idea of the design domain partitioning strategy

Although a design with simple topology may be more favorable from manufacturing point of view (Guo et al. 2014a); however, theoretical analysis indicated that optimal solutions of topology optimization problems may possess very complex structural topologies (e.g., the Michell truss (Sigmund et al. 2016; Dewhurst 2001)). As a result, it is very necessary to equip the MMC approach with the capability of producing optimized designs with complex structural topologies.

Actually, the aforementioned goal can be achieved by resorting to the so-called design domain partitioning strategy. The key point is to restrain the range of the motions of the components. As shown in Fig. 7b, in the proposed design domain partitioning strategy, the design domain D is divided into several non-overlapped sub-regions ${\Omega}_i^{\mathrm{sub}},\kern0.5em i=1,\dots, ns$, where a specific number of components are distributed in these sub-regions initially. During the entire process of optimization, it is required that the central point of a component initially located in a specific sub-region is always confined in that sub-region. This can be achieved easily by imposing some upper/lower bounds on the coordinates of central points of involved components in the MMC-based problem formulation. This strategy actually can provide a flexible way to control the structural complexity locally and adaptively. For instance, if it is intended to produce an optimized structure with high structural complexity in a specific region D_α ⊂ D, we can divide D_α into a relatively large number of sub-regions ${\Omega}_{j\alpha}^{\mathrm{sub}},\kern0.5em j=1,\dots, {n}_{\alpha}^s$ (i.e., ${\mathrm{D}}_{\alpha }={\bigcup}_{j=1}^{n_{\alpha}^s}{\Omega}_{j\alpha}^{\mathrm{sub}}$) and put a relatively large number of components in each ${\Omega}_{j\alpha}^{\mathrm{sub}}$. The effectiveness of this design domain partitioning strategy will be verified numerically in the forthcoming section.

At this position, it is also interesting to note that the proposed solution framework has some underlying relationship with the classical SIMP approach. Specifically, in the proposed method, the sub-regions can be selected as the finite elements used for interpolating the displacement field, and only one component is distributed in each sub-region (element) in a form shown in Fig. 8. Furthermore, we can only take the heights of the components as design variables and interpolate Young’s modulus of each element in terms of h_i as E_i = E^s(h_i/H_i)^p with h_i and H_i denoting the heights of the i-th component and the corresponding finite element (sub-region) (h_i ≤ H_i), respectively. Under the above treatment, it can be observed clearly that the proposed MMC-based multi-resolution topology optimization approach will degenerate to the classical SIMP approach, by defining the value of h_i/H_i as the corresponding element density.

Fig. 8

The degeneration of the MMC-based approach to the SIMP approach

5 Numerical examples

In this section, three plane stress examples with unit thickness and one 3D example are investigated to illustrate the effectiveness of the proposed MMC-based method for multi-resolution topology optimization. The computational time and the optimized objective function values are compared with their counterparts obtained by efficient implementations of the SIMP method (i.e., 88-lines 2D code in (Andreassen et al. 2010); 169-lines 3D code in (Liu and Tovar 2014)). In the 2D examples, the MMA algorithm (Svanberg 1987) is chosen as the optimizer for both the MMC and the SIMP methods. In the 3D example, the optimality criteria (Bendsøe 1995) and MMA algorithms are used in the SIMP and the proposed MMC method, respectively. The termination criteria is set as $\frac{\left|\left|{c}_i-{\overline{c^5}}_i\right|\right|}{{\overline{c^5}}_i}\le 5\times {10}^{-4}$, ${V}_i\le \overline{V}$ and $\frac{\left|\left|{V}_i-{\overline{V^5}}_i\right|\right|}{{\overline{V^5}}_i}\le 5\times {10}^{-4}$, i = 5, 6, 7, …, where c_i and V_i are the objective function value and the volume of solid material in the i-th step, ${\overline{c^5}}_i$ and ${\overline{V^5}}_i$ are the average value of the objective function and the average volume of solid material in the last five iterations, $\overline{V}$ is the upper bound of the available volume of the solid material. Without loss of generality, all involved quantities are assumed to be dimensionless. Young’s modulus and Poisson’s ratio of the isotropic solid material are chosen as E^s = 1 and ν^s = 0.3, respectively. In addition, all computations are carried out on a Dell-T5810 workstation with an Intel(R) Xeon(R) E5-1630 3.70 GHz CPU, 128 GB RAM of memory, Windows10 OS, and the program code is developed in MATLAB 2016b. The values of parameters in (3.2) and (2.12) are taken as q = 2, ϵ = 2 × min(Δx, Δy, Δz) and α = 10⁻³, respectively, unless otherwise stated. Here, Δx, Δy, and Δz are the sizes of the background elements along three coordinate directions.

5.1 A cantilever beam example

In this example, the well-known short cantilever beam problem is examined. The design domain, external load, and boundary conditions are all shown in Fig. 9. A 12 × 6 rectangular design domain is discretized by 1280 × 640 uniform quadrilateral background elements for geometry representation. A unit vertical load is imposed on the middle point of right boundary of the design domain. The available volume of the solid material is $\overline{V}=0.4{V}_{\mathrm{D}}$ with V_D denoting the volume of the design domain. Figure 10 shows the initial design composed of 576 components.

Fig. 9

The cantilever beam example

Fig. 10

The initial design of the cantilever beam example

Firstly, the effectiveness of the design domain partitioning strategy described in the previous section is examined. To this end, the design domain is divided into 1 × 1, 6 × 3, and 12 × 6 sub-regions, respectively. For all cases, 1280 × 640 uniform quadrilateral plane stress elements are used for FEA. The corresponding optimized designs are shown in Fig. 11. It is obvious that as the number of sub-regions is increased, the optimized structural topology becomes more complicated, meanwhile the objective function value is slightly decreased. This reflects that the design domain partitioning strategy is very effective to control the topological complexity of the optimized designs.

Fig. 11

a–c The optimized structures obtained with the design domain partitioning strategy

Next, the number of sub-regions is fixed as 12 × 6 and the efficiency of the proposed multi-resolution algorithm is further investigated. For different resolutions of analysis-element meshes for FEA while keeping the same number of background elements, the optimized designs, iteration numbers, and the average time costs for some key parts of the corresponding optimization process are shown in Table 1. In this table, the parameters ${\overline{t}}_{\mathrm{TDF}}$, ${\overline{t}}_{\mathrm{FEA}}$, ${\overline{t}}_{\mathrm{sen}}$, and ${\overline{t}}_{\mathrm{MMA}}$ represent the average time costs in one optimization step for constructing the TDFs of the components, assembling and solving the FEA equations, sensitivity analysis, and MMA optimizer respectively, and ${\overline{t}}_{\mathrm{total}}$ represents the average time costs of an entire optimization step. The symbol n_iter represents the iteration number at convergence. The quantities c_obj and c_post represent the values of the object function obtained with the analysis-element mesh and the background element mesh, respectively. It is found that, as the number of the analysis-elements is gradually reduced, the time cost of FEA decreases rapidly, which shares the same advantage of the SIMP-based multi-resolution topology optimization approaches (Nguyen et al. 2009, 2017; Groen et al. 2017). To be specific, for this example, the total number of degree of freedom is 1,642,242 when the background elements mesh (with a number of 1280 × 640 elements) is used for structural analysis, while this number decreases to 26,082 when 160 × 80 analysis-element mesh is used. Accordingly, as shown in Table 1, the average time cost of FEA is decreased sharply from 15.18 s to 0.47 s per optimization step.

Table 1 Optimization results of the cantilever beam example obtained by the proposed approach with different FE meshes

In Table 1, the converged values of the objective function as well as the relative errors of FEA results are provided. For this example, when the resolution ratio n_be between the background element mesh and analysis-element mesh is less than or equal to 8, the relative errors are less than 4%. It should be noted that, for n_be ≤ 8, with the same analysis-elements, optimized designs with more structural details can be obtained in the proposed MMC-based multi-resolution approach, as compared with the corresponding results in the SIMP approach with filter treatment to eliminate artificially stiff pattern (Nguyen et al. 2009). This verifies the intrinsic advantage of material aggregation in the MMC-based method. However, as seen in the last two cases in Table 1, when the resolution ratio is very large (e.g., n_be ≥ 10), unacceptable FEA error may be introduced, and optimized designs with small voids or even isolated islands are obtained. This is due to the fact that, in the adopted numerical integration scheme, even isolated islands can contribute to the overall stiffness of the element, and this would inevitably lead to the aforementioned artificially stiff pattern when extremely coarse mesh is introduced for FEA. As shown in Fig. 12, the integration scheme may identify that the upper-left element (with six black pixels) has a larger stiffness than the lower-right one (with five black pixels). Only when the FE analysis mesh is refined, it can be realized that the material distribution in the aforementioned upper-left analysis element is disconnected. This is the intrinsic mechanism leading to the existence of artificial stiff pattern. Although the MMC approach inherently has the capability of aggregating the material in the components, this artificially stiff pattern cannot be eliminated completely when too coarse FE analysis mesh and too many components are used to solve the optimization problems. One possible way to resolve this issue is to use more number of analysis elements or introduce higher order interpolation schemes as in (Burman et al. 2018; Nguyen et al. 2017; Groen et al. 2017). Another possible way is to take the connectivity constraint into consideration explicitly, for example, by using the connected morphable component approach proposed in Deng and Chen (2016).

Fig. 12

A schematic illustration of the intrinsic mechanism leading to the existence of artificial stiff pattern.

Furthermore, it is also worth noting that although the corresponding geometry description model of the MMC method is essentially independent of the background mesh resolution, the “visible” feature sizes of the components will inevitably be determined by the background integration mesh resolution as long as pre-defined fixed integration mesh is adopted for FE analysis. This is because the components with features sizes smaller than the characteristic size of the integration element may not be detected by numerical integration schemes. Actually, this is one of the intrinsic deficiencies associated with topology optimization approaches where fixed meshes are adopted for FEA. Of course, the fundamental way to resolve this problem is to introduce adaptive mesh for FEA. This research direction will be pursued in future works.

Finally, the optimization results obtained by the proposed method are also compared with the optimized designs obtained by the 88-line implementation of the SIMP method (Andreassen et al. 2010, with E_min = 10⁻⁹, penalty factor p = 3 and the radius of density filter r = 1.2, respectively, see the first row of Table 2 for more details) to illustrate the distinctive features of the proposed method. It can be observed that: 1) The proposed MMC method only needs a little time cost for updating the TDFs. 2) Most computational time in the SIMP approach is paid for FEA and updating design variables. For the same FE mesh, the computational time for FEA corresponding to the proposed method and the SIMP method are almost the same. If, however, the analysis-element technique is adopted, structural responses with reasonable accuracy (a relative error less than 5%) can be obtained with much less computational time (about 1/30). Moreover, since the number of design variables in the MMC method is only 3456 (as compared to 819,200 in the SIMP approach), the computational efficiency for updating design variables by MMA optimizer in the proposed approach can be improved by more than 200 times compared to that of the SIMP approach (actually 0.05 s vs 14.70 s!). As a result, when the same FE mesh is used, the average computational time for one optimization step is about 28.91 s in the SIMP approach while the value is about 18.62 s in the proposed approach, which can be further decreased to 3.13 s in the proposed multi-resolution approach. This comparison clearly verifies the effectiveness of our method for solving large scale topology optimization problems. 3) Since no filter operation is applied to eliminate numerical instabilities, the optimized designs obtained by the proposed approach are pure black-and-white and share some features of the classical Michell truss structures. It is also worth noting that by adopting the advanced filter technique (Wang et al. 2011) in companion with a continuation process (filter radius is 2; threshold parameter is η = 0.5; the projection parameter is initialized as β = 1 and doubled every 50 iterations until a maximum of β = 64), as shown in the second row of Table 2, an almost black-and-white design can be obtained (of course, extra computational efforts must be paid) although it does not share the features of Michell truss structures. The advantage of the proposed approach can be further illustrated by comparing the values of the objective functional. Actually, by adopting the same interpolation strategy for Young’s modulus of non-solid elements in the SIMP approach, the value of the objective functional for the optimized design obtained by 1280 × 640 FE mesh is 74.72, which is smaller than those (i.e., 80.29 and 80.98, respectively) of the designs obtained by the SIMP approach.

Table 2 Optimization results of the cantilever beam example obtained with the SIMP approach

5.2 The MBB example

The setting of this example is described schematically in Fig. 13. A vertical load f = 2 is imposed on the middle point of the top side of the beam. For simplicity, only half of the design domain is discretized by a 1280 × 640 uniform background element mesh for geometry description. In this example, the upper bound of the volume of available solid material is set to be $\overline{V}=0.4{\mathrm{V}}_{\mathrm{D}}$.

Fig. 13

a, b The MBB example

The design domain is divided into 12 × 6 equal square sub-regions to preserve structural complexity. The initial layout of the components is the same as that in the previous cantilever beam example (see Fig. 10 for reference). By interpolating the displacement field with 640 × 320, 320 × 160, 258 × 128, and 160 × 80 analysis-elements, respectively, as shown in Table 3, the computational time for FEA can be reduced by almost 25 times as compared with that in the case where the background element mesh (i.e., 1280 × 640) is adopted for FEA. It is found that when n_be = 8, the relative error of the value of objective functional may reach to 10.21%. The corresponding value of the objective functional recalculated by the background element mesh (i.e., 97.86), however, is still very close to those obtained under smaller resolution ratios (i.e., 96.98 for n_be = 5). From this point of view, the proposed multi-resolution approach is still supposed to be effective for such case. The first row of Table 4 provides the optimization result obtained by the SIMP approach under a 1280 × 640 FE mesh with E_min = 10⁻⁹, penalty factor p = 3, and the radius of density filter r = 1.2, respectively. The second row of Table 4 shows the result obtained by SIMP method by adopting the advanced filter scheme (Wang et al., 2011) in companion with a similar continuation process as example 5.1. By comparing the corresponding results in Table 3 and Table 4, similar conclusions can be made as in the previous example.

Table 3 Optimization results of the MBB example obtained with the proposed approach under different FE meshes

Table 4 Optimization results of the MBB example obtained with the SIMP approach

5.3 A cantilever beam subject to a distributed load

In this example, a cantilever beam under a uniformly distributed load introduced in (Groen et al., 2017) is revisited. The setting of the problem is described schematically in Fig. 14. A vertical distributed load is imposed on the top surface of the design domain uniformly with density f = 1/l. The design domain is discretized by a 1200 × 600 uniform background element for geometry representation and divided into 6 × 3 sub-regions to preserve structural complexity. The initial design is the same as that in the first cantilever beam example (see Fig. 10 for reference). A detailed discussion about this example can be found in (Groen et al., 2017) by adopting the SIMP-based higher-order multi-resolution topology optimization method.

Fig. 14

A cantilever beam example under uniformly distributed load

Firstly, the maximum available solid material volume is set as $\overline{V}=0.4{\mathrm{V}}_{\mathrm{D}}$ (the same as that in (Groen et al., 2017)), and 1200 × 600 uniform quadrilateral plane stress elements are used for FEA. The corresponding iteration histories are plotted in Fig. 15a. It is found that the value of the objective functional oscillates during the optimization process. This is because although the structural topology has been already obtained after about 150 iterations, some small voids emerge and disappear alternately in the region around the top surface of the structure (see Fig. 15b, c, d for reference). To circumvent this undesired behavior, the top layer of the background element mesh of the design domain is fixed as solid elements in numerical implementation. The optimized structure obtained under this treatment and corresponding iteration histories can be seen in Fig. 16. It is found that more stable convergence history is achieved and the value of the objective functional of the optimized structure is very close to that of the structure shown in Fig. 8a of (Groen et al. 2017).

Fig. 15

a–d The results of the cantilever beam example under uniformly distributed load obtained by the proposed approach ($\overline{V}=0.4{V}_{\mathrm{D}}$ and 1200 × 600 FE mesh)

Fig. 16

a, bThe results of the cantilever beam example under uniformly distributed load obtained by the proposed approach ($\overline{V}=0.4{V}_{\mathrm{D}}$, 1200 × 600 FE mesh, and one layer of fixed solid region)

Next, with the numbers of the background elements (1200 × 600) and the non-design domain (solid top layer) fixed, the effectiveness of the proposed multi-resolution approach is tested by adopting a smaller available volume of solid material $\overline{V}=0.3{\mathrm{V}}_{\mathrm{D}}$. The displacement field is discretized by 600 × 300, 400 × 200, 300 × 150, 200 × 100, and 120 × 60 analysis-elements, respectively, and the obtained results are summarized in Table 5. It is found that, for this example, if the optimized design obtained under a 1200 × 600 is analyzed by a 300 × 150 coarse mesh, the relative error of the value of the objective functional is 47.34%. This is not surprising since in the context of FE modeling, a distributed load will be modeled as a set of concentrated point loads imposing at every FE node equivalently (in the sense of virtual work principle). The higher the mesh resolution, the more number of concentrated point loads. In compliance minimization topology optimization problems, the material is prone to be distributed in the region adjacent to the concentrated point loads. Therefore, it can be expected that more and more “thin bars” will appear as the FE mesh is refined especially when pure black-and-white design is sought for. Under this circumstance, when a distributed load is considered, if one performs FE analysis of an optimized structure obtained under a coarse mesh using a refined mesh, the obtained value of structural compliance will be relatively large since some concentrated point loads are actually applied on weak material (see Fig. 17 for a schematic illustration)!

Table 5 Optimization results of the example under distributed load obtained by the proposed approach and different FE meshes

Fig. 17

a, b The original of the discrepancy between FEA results obtained under FE mesh with different resolutions (distributed load case)

A straightforward way to resolve this problem arising from mesh-dependent FE modeling is to introduce a non-designable solid layer with a small thickness under the top surface. This treatment can not only alleviate the problem of mesh-dependent FE discretization of the distributed load, but also make the FE analysis result insensitive to the mesh-resolution according to Saint-Venant principle. As shown in Fig. 18, when the thickness of this solid layer is six times larger than the side length of the background elements (only 1/100 of the thickness of the design domain), the acceptable resolution ratio n_be can reach the number of six. The corresponding optimized structures for the cases where 300 × 150, 200 × 100, and 120 × 60 analysis-elements are used, respectively, can also be found in Fig. 18.

Fig. 18

a–c The results of the cantilever beam example under uniformly distributed load obtained by the proposed approach ($\overline{V}=0.3{V}_{\mathrm{D}}$, 1200 × 600 background elements and six layers of fixed solid region)

Another way to resolve this issue is to use a non-uniform mesh. The idea is to refine the FE mesh in region close to the distributed load, as shown in Fig. 19, with the help of quadtree technique. To verify the effectiveness of this treatment, we analyzed the optimized design with respect to resolution ratio n_be = 4 in Table 5. The background mesh is used to discretize a number of top layers, and it is transited to the coarse mesh (n_be = 4) with the use of the quadtree mesh (see Fig. 19 for reference, and Zhang et al. (2018) for more technical details). The discretization of the distributed load under this non-uniform mesh treatment is the same as in the case where pure background mesh is used for FE analysis. The results listed in Table 6 show that, the relative FEA errors can be decreased sharply from 47.34 to 1.97%, when only three layers of background meshes are used to discretize the region adjacent to the distributed load. In addition, this treatment only introduces additional DOFs locally, and the computational efficiency still can be guaranteed. For example, when six layers of background meshes are introduced, the total number of DOFs is only increased from 90,902 to 107,112, which is still one order of magnitude smaller than that of the background mesh (14,43,602).

Fig. 19

Dealing with distributed load with quadtree technique

Table 6 Numerical results for different numbers of top layers discretized by background mesh

5.4 A 3D box example

This example is a variation of the one presented in (Sigmund et al. 2016). As illustrated in Fig. 20a, the design domain is a 12 × 10 × 12 box, which is subjected to a pair of torque. The torque load is simulated by four concentrated point-forces as described in Fig. 20 and the magnitudes of these point forces are chosen as f = 2. The radii of the two red disks are 1.5 and their thicknesses are 0.15, respectively. Two void parts (the gray cylinder regions in Fig. 20a) are fixed as non-design domains. For simplicity, only 1/8 of the design domain is optimized. The maximum volume fraction of the available solid material is 2%.

Fig. 20

a, b The 3D box example

This problem is solved with the use of the proposed approach for three sets of background elements (i.e., 42 × 35 × 42, 84 × 70 × 84, and 126 × 105 × 126, respectively). The same initial design containing 720 components, as shown in Fig. 20b, is adopted for all three tested cases. For the purpose of comparison, this example is also solved by the SIMP method with the use of its efficient numerical implementation described in Liu and Tovar (2014), where E_min = 10⁻⁹, penalty factor p = 3 and the radius of density filter r = 1.5, respectively. An optimality criterion (OC) method is used for updating the design variables in the SIMP method. Note that OC method is adopted here for updating the design variables since it is more efficient than the MMA method when large number of design variables is involved. It should be pointed out that, for the current hardware setting, the computer memory (128 G) would be run out when 84 × 70 × 84 eight-node brick elements are used for FEA, which is implemented in a MATLAB computing environment. Therefore, we only used a 42 × 35 × 42 FE meshes in the SIMP approach and 42 × 35 × 42 analysis-elements for the proposed approach, respectively.

The entire structure obtained by the SIMP method is shown in Fig. 21. The compliance of the 1/8 optimized structure is 120.49. Since the optimized solution obtained by the SIMP contains a lot of gray elements whose densities are neither zero nor one, we can only display the profile of the structure by using different values of the density threshold ρ_th. Actually, in our treatment, only the elements whose density values are greater than ρ_th are plotted (i.e., ρ > ρ_th). Fig. 21a, b, c show the profiles of the optimized structure for ρ_th = 0, ρ_th = 0.5, and ρ_th = 0.85, respectively. It can be observed from these figures that the plotted structural profiles are highly dependent on the value of ρ_th when low-value admissible volume fraction (i.e., 2%) is adopted. Besides, it is also not an easy task to transfer the optimization result to CAD/CAE systems for subsequent treatment (note that the structure may be disconnected when a large ρ_th is adopted while a small ρ_th may lead to infeasible design). Some post-processing techniques are necessary to extract the structural profile from the gray image. However, it is also worth noting that the percentage of gray elements can be greatly reduced by enlarging the admissible volume of solid material or using advanced filter technique (Sigmund et al. 2016). For example, when the maximum admissible volume is chosen as 0.1V_D, for different values of ρ_th, the corresponding optimized structures (obtained by the code of (Liu and Tovar 2014)) are indeed very similar, as shown in Fig. 22. In addition, by adopting the filter technique (Wang et al. 2011) in companion with a continuation process (filter radius is 2, threshold parameter is η = 0.5, and the projection steepness parameter β is gradually increased from 0.5 to 64), as shown in Fig. 23, an almost black-and-white solution can be obtained for $\overline{V}=0.02{V}_{\mathrm{D}}$ with some extra computational effort.

Fig. 21

a–c The optimized structure of the 3D box example obtained with the SIMP method (displayed with different values of ρ_th) at n_iter=108

Fig. 22

a–c The optimized structures of the 3D box example by SIMP method ($\overline{V}=0.1{V}_{\mathrm{D}}$ and 42 × 35 × 42 FE mesh) at n_iter=35

Fig. 23

a–c The optimized structures of the 3D box example by SIMP method via adopting both density filter and threshold projection techniques ($\overline{V}=0.02{V}_{\mathrm{D}}$ and 42 × 35 × 42 FE mesh) at n_iter=128

The entire structures obtained by the proposed method under three sets of background element meshes are shown in Fig. 24a, b, c, respectively. It can be observed that the optimized design obtained with a 42 × 35 × 42 background mesh is almost a lattice-like structure, which is quite different from the ball-like structure shown in Fig. 21a. This is due to the fact that the minimum length scale in the optimized structures of MMC-based approach is limited by the characteristic size of the background mesh. For components with characteristic sizes less than the background mesh size, their contributions to structural stiffness may not be detected by numerical integration procedure in FEA. Therefore, when the available material volume fraction is relatively small and the background mesh is not fine enough, it is extremely difficult to form a ball-like structure with very small thickness since the material distribution in MMC-based solution framework is purely black-and-white! Under this circumstance, only a lattice-like structure shown in Fig. 24a is selected to transmit the applied torque in a mechanically efficient way. Interestingly, by using the same FEA strategy in SIMP method to reanalyze the 1/8 structure of Fig. 24a, the compliance value is 126.62, which is very close to the result of SIMP approach. Of course, this problem can be well-addressed by adopting the adaptive mesh for FEA since we have explicit geometry description in the MMC-based approach. For the limitation of space, however, this issue will not be addressed in the present work. Furthermore, as shown in Fig. 24b, c, as the background element mesh is refined, the corresponding optimized structure gradually changes to a ball-like structure with more material distributing around the area where the external forces are applied. In addition, for the case where $\overline{V}=0.1{V}_{\mathrm{D}}$, by using a 126 × 105 × 126 background element mesh for geometry description and 42 × 35 × 42 analysis-elements for FEA, a closed sphere-like structure can be obtained successfully (see Fig. 25). Furthermore, by taking the advantage of the explicit geometric description of the components, the optimized results can be directly transferred to CAD/CAE systems without any post-processing. The final optimized design displayed in CAD system is shown in Fig. 26.

Fig. 24

a–c The optimized structures of the 3D box example obtained with 42 × 35 × 42 analysis-elements and different background elements by the proposed method

Fig. 25

The optimized structures of the 3D box example by the proposed method ($\overline{V}=0.1{V}_{\mathrm{D}}$, 126 × 105 × 126 background elements and 42 × 35 × 42 analysis-elements) at n_iter=116

Fig. 26

The CAD model of the optimized structure obtained by the proposed method ($\overline{V}=0.02{V}_{\mathrm{D}}$, 126 × 105 × 126 background elements and 42 × 35 × 42 analysis-elements)

In order to more accurately investigate the performances of the optimized designs with fine structural features obtained by the proposed approach, we transferred the 1/8 structures of Fig. 24a, b, c to Abaqus directly (thanks again to the explicit nature of geometry description in the MMC-based approach) and perform the FEA with a set of 126 × 105 × 126 meshes. It is found that the corresponding values of structural compliance are 297.97, 196.40 and 197.58 respectively, which reveals that better designs do can be obtained by increasing the resolution of background element mesh. It is also worth noting that a direct comparison of the computational time between the proposed approach and the SIMP approach is not made for this example, since different optimizers are adopted for numerical optimization (i.e., OC method for the SIMP approach and MMA method for the proposed approach). However, since the numbers of design variables are only 720 × 9 = 6480 in the proposed approach and about 62,000 in the SIMP-based approach, it can be expected that, the computational time for updating design variables with the MMC approach will be much less than that of the SIMP approach if the same MMA optimizer is adopted. A representative iteration curve is plotted in Fig. 27.

Fig. 27

The iteration curves of one considered cases using the proposed method ($\overline{V}=0.1{V}_{\mathrm{D}}$, 126 × 105 × 126 background elements and 42 × 35 × 42 analysis-elements)

6 Concluding remarks

In the present work, a highly efficient MMC-based approach for multi-resolution topology optimization is proposed. With the use of this approach, both the numbers of the DOFs for finite element analysis and design variables for design optimization can be reduced substantially. For some tested problems, the corresponding computational time for solving large-scale topology optimization problems can be substantially reduced by about one order of magnitude. Compared to other multi-resolution-based topology optimization methods, the proposed MMC-based multi-resolution method can generate optimized results with clearer boundaries and higher-resolution structural features with the use of linear finite elements more efficiently, and the optimized designs can be directly transferred to CAD/CAE systems without any post-processing. All these advantages can be attributed to the explicit nature of geometry description in the MMC-based solution framework. However, when low order analysis elements are adopted, for very large resolution ratios, artificially stiff pattern may still exist in the optimized results. As shown in (Groen et al. 2017), higher order elements or advanced integration method can be applied to alleviate this issue to some extent. Another possible way to circumvent this difficulty is to take the connectivity constraint into the problem formulation explicitly, for example, by using the connected morphable component approach proposed in (Deng and Chen 2016). Moreover, cautions should also be made when the proposed method is applied to deal with problems involving distributed loads. Either non-design solid layer or non-uniform mesh can be adopted to eliminate the mesh dependency phenomenon resulting from the FE modeling of the distributed load.

As a preliminary attempt, only minimum compliance design problems are considered in the present study to demonstrate the effectiveness of the proposed approach. It can be expected that the proposed approach can also find applications in other computationally intensive optimization problems (e.g., structural optimization considering geometry/material nonlinearity). Another interesting research direction is to integrate the advantages of the present explicit MMC-based approach and the implicit SIMP-based approaches to develop some hybrid approaches for solving topology optimization problems where more complicated objective/constraint functions/functionals are involved. This is highly possible since as discussed at the end of Section 4, the proposed solution framework is general enough to achieve this goal. Moreover, by combing with the DOF elimination technique proposed in (Zhang et al. 2017), it can be expected that the computational effort can be further reduced especially for 3D problems. Corresponding results will be reported elsewhere.

Appendix

The process of generating TDF locally can be elaborated as follows:

• 1) Generating a rectangle ${\Omega}_i^{\mathrm{ext}}$ (pink region), with the use of the parameters (o_i, θ_i, l_i, t_i), as shown in Fig. A1b. Here the symbol o_i = (x_i0, y_i0)^⊤ denotes the vector of the coordinates of the central point of the i-th component, θ_i is the corresponding inclined angle, while ${l}_i=2{a}_i\sqrt[6]{\left(1+\epsilon \right)}$ and ${t}_i=\max \left(2{t}_i^1,2{t}_i^2\right)\sqrt[6]{\left(1+\epsilon \right)}$ are the length and width of ${\Omega}_i^{\mathrm{ext}}$, respectively. Note that ${\Omega}_i^{\mathrm{ext}}\supset {\Omega}_i^{\prime }=\left\{\boldsymbol{x}|\boldsymbol{x}\in \mathrm{D},{\phi}_i\left(\boldsymbol{x}\right)\ge -\epsilon \right\}$ (yellow region in Fig. A1b);

• 2) From the vertexes (which can be found analytically) of ${\Omega}_i^{\mathrm{ext}}$, generating another rectangle ${\Omega}_i^{\mathrm{rec}}$ (light blue region in Fig. A1b);

• 3) Generating the TDF associated with ${\Omega}_i^{\mathrm{rec}}$;

• 4) Finding the TDF values in ${\Omega}_i^{\mathrm{rec}}$ such that −ϵ ≤ ϕ_i(x) ≤ ϵ, and only storing these values by sparse matrix for subsequent treatment.

The above treatment guarantees that only local values of ϕ_i(x) are evaluated in the corresponding manipulations, which reduce the computational effort substantially.

Fig. 28

A schematical illustration of generating the TDF locally