Multi-start Space Reduction (MSSR) surrogate-based global optimization method

Abstract

In this work, a new Multi-start Space Reduction (MSSR) and surrogate-based search algorithm is introduced for solving global optimization problems with computationally expensive black-box objective and/or expensive black-box constraint functions. In this new algorithm, the design space is classified into: the original design space or global space (GS), the reduced medium space (MS) that contains the promising region, and the local space (LS) that is a local area surrounding the present best solution in the search. During the search, a kriging-based multi-start optimization process is used for local optimization, sample selection and exploration. In this process, Latin hypercube sampling is used to acquire the starting points and sequential quadratic programming (SQP) is used for the local optimization. Based upon a newly introduced selection strategy, better sample points are obtained to supplement the kriging model, and the estimated mean square error of kriging is used to guide the search of the unknown areas. The multi-start search process is carried out alternately in GS, MS and LS until the global optimum is identified. The newly introduced MSSR algorithm was tested using various optimization benchmark problems, including fifteen bound constrained examples, two nonlinear constrained optimization problems, and four nonlinear constrained engineering applications. The test results revealed noticeable advantages of the new algorithm in dealing with computationally expensive black-box problems. In comparison with two nature-inspired algorithms, three space exploration methods, and two recently introduced surrogate-based global optimization algorithms, MSSR showed improved search efficiency and robustness.

1 Introduction

With rapid advances of computer modeling techniques, numerical simulations and analyses became common engineering design tools. However, most of these simulations and analyses are computationally intensive with black-box characteristics (Edke and Chang 2011; Xiang et al. 2012; Shan and Wang 2010). For instance, the design of airfoil and aircraft wings requires expensive black-box computational fluid dynamics (CFD) simulation to calculate the lift and finite element analysis (FEA) to ensure structure strength and light weight (Eves et al. 2012). Crash simulation of vehicle bodies using FEA is another example (Harmati et al. 2010; Zhang et al. 2008). In both cases, the identification of the optimized design parameters of the wing shape/structure and vehicle body requires global optimization using the computationally expensive black-box simulations and analyses as objective and constraint functions. Design optimization traditionally uses a large number of objective/constraint function evaluations in the iterative searches to identify the solution, and the number of search iterations increases dramatically for a non-unimodal optimization problem that requires global optimization algorithms. More efficient and robust global search methods thus become essential.

The classical genetic algorithm (GA) global optimization method usually needs thousands of evaluations of the objective and constraint functions, and each of these evaluations, if conducted using complex simulation and analysis, will take minutes or hours to complete, making these classical global optimization method unsuitable as a design tool. One effective way to reduce the number of the expensive function evaluations in global optimization is to employ the more efficient surrogate-based optimization (SBO) technology (Queipo et al. 2005; Forrester and Keane 2009). SBO takes advantage of the prediction capacity of surrogate models (SM), or metamodels, to avoid redundant evaluations of the expensive functions and to focus on the most promising region of the global optimum (Ong et al. 2003; Zhou et al. 2007; Jouhaud et al. 2007). Generally, the SBO search process consists of three main steps: a) select sample points using design of experiments (DOE); b) construct a SM; and c) resample promising points to refine the SM. To get a better initial SM with fewer sample points, a variety of DOE methods have been introduced, including grid sampling, Latin Hypercube Sampling (LHS) (Iman 2008), Optimized Latin Hypercube Sampling (OLHS) (Jin et al. 2005), etc. Among them, grid sampling produces uniformly distributed points in the design space; and LHS/OLHS usually yields sample locations with some randomness. SMs involve interpolation and regression to envisage the black-box function. Common SM methods include kriging, radial basis functions (RBF), polynomial response surface (PRS), etc. Kriging is a stochastic model that utilizes the best linear unbiased estimator to predict the function values at untested locations (Cressie 1990). Composed of many simple functions, RBF establishes an expression to emulate the complicated design space (Mullur and Messac 2005). PRS constructs a polynomial model using least square fitting to make predictions (Myers et al. 2009). Among the three, kriging and RBF have been found to be more appropriate in dealing with non-linear problems (Forrester and Keane 2009). At the start of the search, the initial SMs of the objective/constraint functions with fewer initial sample points would not likely be able to locate the black-box problem’s regions of optimum, especially for multimodal or high-dimensional problems. How to refine the SM with an adequate number of sample points is the key of the search technique, while to acquire the promising location or local optimum from the SM with a continuous mathematical expression subsequently using a regular optimization solver is a relatively straightforward task. In addition, it is normally difficult to solve multimodal and high-dimensional optimization problems only by supplementing the optimal solutions of the SM, and development of a generic infill strategy for a variety of optimization problems with fewer expensive function evaluations thus becomes critical.

2 Related work

Many researchers have contributed to the continuous developments of surrogate-based global optimization methods. Alexandrov et al. (1998) introduced a trust region approach to manage the use of SMs in engineering optimization. Jones et al. (1998) presented a widely cited global optimization algorithm for expensive black-box problems, which is known as EGO. EGO constructs the SM by kriging and updates the SM by maximizing an expected improvement function. Wang et al. (2001) provided an adaptive response surface method (ARSM), which creates a quadratic approximation model for the expensive objective function in a reduced space. Gutmann (2001) introduced a global optimization method based on RBF to solve problems with expensive function evaluations. Jin et al. (2001) explored the accuracy of SMs and how it affects the sampling strategies. Wang et al. (2004) developed the mode-pursuing sampling strategy (MPS) to refine the quadratic response surface. In the same year, Wang and Simpson (2004) utilized a fuzzy clustering method to get a reduced search space, which can efficiently find the global optimum on non-linear constrained optimization problems. A stochastic RBF method for the global optimization of expensive functions was proposed by Regis and Shoemaker (2007a), who also improved the Gutmann-RBF method by varying the size of the subdomain in different iterations (Regis and Shoemaker 2007b). Younis and Dong (2010) developed a kind of space reduction method called space exploration and unimodal region elimination (SEUMRE), which establishes a unimodal region to speed up the search. SEUMRE has been successfully used on several black-box automotive design optimization applications (Younis et al. 2011). Gu et al. (2012) introduced the hybrid and adaptive meta-model-based (HAM) method to divide the design space into several subdomains with different weights. In each iteration of the search, sample points are obtained from these sub-regions based on performance determined weights. HAM performed well in a FEA crash simulation based vehicle body design optimization problem. Villanueva et al. (2012) defined different sub-regions for the original design space and explored them using multiple SMs. Long et al. (2015) combined a type of intelligent space exploration strategy with ARSM to provide reduced regions for global optimization. These researches showed that the space reduction approach presents to be an efficiency global optimization search scheme for computationally expensive problems. In this work, a new multi-start approach is combined with a special space reduction strategy to form a new surrogate-based global optimization method. This multi-start approach provides multiple starting locations and utilizes local optimization solver to perform parallel searches in different sub-regions. The global optimal solution is identified from all obtained local optima. The general idea has been used in several global optimization algorithms, such as the GLOBAL algorithm (Csendes 1988), the Tabu cutting method (Lasdon et al. 2010), and the quasi-multistart framework (Regis and Shoemaker 2013). In this work, the multi-start approach is found to be ideal for the kriging-based optimization method. In the global optimization, the initial kriging-based prediction model will normally not be very precise, leading to solutions with some local optima. When the SM becomes more accurate after the updates, one of the estimated optima may approach the true global optimum while most of the others will either disappear or go closer to the nearby local optima. If all predicted local optima in the entire design space are added to refine the SM, the number of sample points will become considerably large and the search efficiency will be lower.

In this new kriging-based multi-start optimization process, the three spaces, GS, MS and LS, with different ranges are explored alternately. The sizes of MS and LS change adaptively based on the current best obtained value in optimizing the kriging-based SM; selecting the promising results; and exploring the unknown area. Exploration of the design space at three different space levels facilitates the handling of the multimodal objective function. Bound and nonlinear constrained benchmark global optimization problems are used to test the search efficiency and robustness of this new algorithm.

3 Multi-start space reduction approach

The proposed MSSR approach uses a kriging-based SM, a multi-start scheme, and alternating sampling over the GS, MS and LS spaces to carry out the global optimization search. The local optima obtained from the SM are stored in a database as “potential sample points”. In each iteration, several better sample points are selected from these “potential sample points” to refine the SM to allow it to have a better approximation in the close neighborhood of the global optimum. The detailed search algorithm is introduced in this section.

3.1 Kriging-based model

Kriging is an interpolation method widely used for prediction. The kriging predictor and its estimated mean square error (MSE) function have the following forms:

$$ \widehat{f}\left(\boldsymbol{x}\right)=\widehat{\mu}+{\boldsymbol{r}}^T\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\left(\boldsymbol{y}-\mathbf{1}\widehat{\mu}\right) $$

(1)

$$ {\widehat{s}}^2\left(\boldsymbol{x}\right)={\widehat{\sigma}}^2\left[1-{\boldsymbol{r}}^{\mathrm{T}}\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)+\frac{{\left(1-{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)\right)}^2}{{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\mathbf{1}}\right] $$

(2)

Given M sample points, R is a correlation matrix with M × M elements and the element in the j-th column of the i-th row is C(Θ, x ⁽ⁱ⁾, x ^(j)) that is a correlation function value. r(x) is an M-dimensional vector and C(Θ, x, x ⁽ⁱ⁾) is the i-th element of r(x), where x is the untested location. The values of $\widehat{\mu},\;{\widehat{\sigma}}^2,\;\boldsymbol{\Theta}$ are estimated using the maximum likelihood estimation (MLE) method and its detailed derivation can be found from (Jones et al. 1998; Forrester and Keane 2009).

Since $\widehat{f}\left(\boldsymbol{x}\right)$ is the approximation of the true function f(x), $\widehat{f}\left(\boldsymbol{x}\right)$ can be exploited to estimate the true optimum. ŝ ²(x) reflects the uncertainty of the predictor $\widehat{f}\left(\boldsymbol{x}\right)$. When the tested location x is far away from the known points, ŝ ²(x) will have a large value, indicating a large prediction error. The magnitude of ŝ ²(x) can thus be used to guide the exploration of the unknown region. The global optimization search process for the benchmark Banana function (Fig. 1) is used to show the kriging prediction scheme graphically. Fifteen sample points are used to construct the initial kriging model shown in Fig. 2 to capture the rough shape of the original function illustrated in Fig. 1. As the number of sample points increases, the predicted shape of the model will better approximate the true shape of the banana function in Fig. 1. The estimated MSE function of the kriging model is given in Fig. 3, and the local maxima of the MSE always appear in the unexplored area. As Forrester has suggested that the kriging predictor can be exploited to acquire promising solutions and the unknown design space can be explored by the estimated MSE of kriging. An optimization search process that can effectively utilize these two properties of the kriging model will be able to take the full advantage of the kriging method (Forrester and Keane 2009)

Fig. 1

Original Banana function

Fig. 2

Kriging prediction with 15 samples

Fig. 3

Estimated MSE of kriging

3.2 The proposed multi-start optimization process

The proposed multi-start optimization process for kriging-based model consists of three parts: local optimization using SM, selection of better potential sample points, and exploration of the unknown area.

To obtain the randomly selected starting points that also well cover the search space, the LHS is used. These different starting points will be used in each iteration during the iterative search process. The local optima from the kriging SM are identified using Sequential Quadratic Programming (SQP). All of the local optima obtained from the SM are stored in a database of “Potential Sample Points”. The SQP optimizers may sometimes converge to the same local optimum from different starting points, leading to repeated points in the database, and the local optimum may also be found at the existing sample points. To address these issues, new sample points need to have a defined distance from all obtained sample points. In other cases, there may not be any suitable local optimum in the defined space. For these occasions, the estimated MSE of kriging is maximized by the multi-start optimization process to explore the unknown area. As shown in details in the following pseudo codes a special sample point selection scheme has been introduced to identify more promising sample points from the acquired “potential sample points” list. These codes including optimization, selection and exploration on unknown area are summarized as follows.

Figure 4 shows the multi-start optimization process on the kriging model. Thirty starting points and two local optima were selected. The two selected solutions were in the valley of the Banana function, in which the best solution is located as shown in Fig. 1. Addition of these two sample points in this local area will make the kriging model more accurate locally.

Fig. 4

Multi-start process on kriging

3.3 Space reduction approach

A sample set, acquired using the DOE method is used to store the expensive data samples. According to the magnitude of the function values of these expensive sample points, three spaces, GS, MS and LS are created for the multi-start optimization. Global Space or GS is the entire region of the original design space; Medium-sized Space or MS is based on the portion of design space of the current better samples; and Local Space or LS is the neighborhood area of the best current sample point. In the iterative search process, the sample set is supplemented with new samples, and updated using better samples. MS and LS will constantly change until the iteration stops. The definitions of the two spaces are as follows:

$$ \begin{array}{c}\hfill di{s}_i=\left| max\left(\boldsymbol{S}{\left(1:k\right)}_i\right)- min\left(\boldsymbol{S}{\left(1:k\right)}_i\right)\right|,\kern1em i=1,2,\cdots \cdots n\hfill \\ {}\hfill Lo{b}_i=\left\{\begin{array}{l}{S}_i^{best}-di{s}_i,\kern0.5em {S}_i^{best}-di{s}_i\ge min\left( rang{e}_i\right)\hfill \\ {} min\left( rang{e}_i\right),\kern0.5em {S}_i^{best}-di{s}_i\le min\left( rang{e}_i\right)\hfill \end{array}\right.\hfill \\ {}\hfill U{b}_i=\left\{\begin{array}{l}{S}_i^{best}+di{s}_i,\kern0.5em {S}_i^{best}+di{s}_i\le max\left( rang{e}_i\right)\hfill \\ {} max\left( rang{e}_i\right),\kern0.5em {S}_i^{best}+di{s}_i\ge max\left( rang{e}_i\right)\hfill \end{array}\right.\hfill \\ {}\hfill range\_ loca{l}_i=\left[Lo{b}_i,\kern0.5em U{b}_i\right]\hfill \end{array} $$

(3)

$$ \begin{array}{c}\hfill Lo{b}_i= min\left(\boldsymbol{S}{\left(1:p\right)}_i\right)\hfill \\ {}\hfill U{b}_i= max\left(\boldsymbol{S}{\left(1:p\right)}_i\right)\hfill \\ {}\hfill range\_ mediu{m}_i=\left[Lo{b}_i,\kern0.5em U{b}_i\right],\kern0.5em i=1,2,\cdots \cdots n\hfill \end{array} $$

(4)

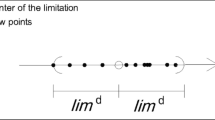
where, n is the dimension of a problem, S(1:k) _i is the i-th dimension of the first k best samples selected from the ranked sample set, range _i is the i-th dimension of the original design range, and S ^best _i is the i-th dimension of the current best sample. Formulas (3) and (4) define the Local and Medium-sized space, respectively. If the distance of Lob _i and Ub _i in Formulas (3) or (4) is smaller than 1e-5, it is suggested that Lob _i  = Lob _i  − 0.025 · (max(range _i ) − min(range _i )) and Ub _i  = Ub _i  + 0.025 · (max(range _i ) − min(range _i )). Meanwhile, the new range should also be the subset of the original design range. Both of the two spaces change their scopes based on the better samples acquired from the design space. Here, k and p are two user-defined parameters, which represent the number of the better samples. We define k and p as follows:

$$ k=\left\{\begin{array}{l}3\kern1.5em ,n\le 2\kern0.5em and\kern0.5em CS\le 150\hfill \\ {} round\left(CS/30\right)\kern1.5em ,n\le 2\kern0.5em and\kern0.5em CS>150\hfill \\ {}5\kern1.5em ,n>2\kern0.5em and\kern0.5em CS\le 150\hfill \\ {} round\left(CS/30\right)\kern1.5em ,n>2\kern0.5em and\kern0.5em CS>150\hfill \end{array}\right. $$

(5)

$$ p=\left\{\begin{array}{l} round\left(CS/3\right)\kern1.5em ,n\le 2\hfill \\ {}3n\kern1.5em ,n>2\kern0.5em and\kern0.5em CS\le 60\hfill \\ {} round\left(CS/3\right)\kern1.5em ,n>2\kern0.5em and\kern0.5em CS>60\hfill \end{array}\right. $$

(6)

where, CS is the number of current sample points. k will be smaller than p with continuous iterations. According to (3) to (6), MS will lead to a reduced region that may include several promising solutions and LS will make the search focus on one of them quickly. In some cases, when LS turns into a tiny space or the search in LS, MS or GS repeats around a local optimum, there will be no appropriate locations to be selected as new samples. As discussed previously in Section 3.2, if new samples cannot be found after the optimization and selection, the estimated MSE of kriging is used to explore the unknown area. The ranges for getting the local maxima of MSE in local, medium and global search are defined as follows:

$$ \begin{array}{c}\hfill di{s}_i=\left| max\left( rang{e}_i\right)- min\left( rang{e}_i\right)\right|,\kern0.5em i=1,2,\cdots \cdots n\hfill \\ {}\hfill Lo{b}_i=\left\{\begin{array}{l}{S}_i^{best}-0.5\cdotp di{s}_i,\kern0.5em {S}_i^{best}-0.5\cdotp di{s}_i\ge min\left( rang{e}_i\right)\hfill \\ {} min\left( rang{e}_i\right),\kern0.5em {S}_i^{best}-0.5\cdotp di{s}_i\le min\left( rang{e}_i\right)\hfill \end{array}\right.\hfill \\ {}\hfill U{b}_i=\left\{\begin{array}{l}{S}_i^{best}+0.5\cdotp di{s}_i,\kern0.5em {S}_i^{best}+0.5\cdotp di{s}_i\le max\left( rang{e}_i\right)\hfill \\ {} max\left( rang{e}_i\right),\kern0.5em {S}_i^{best}+0.5\cdotp di{s}_i\ge max\left( rang{e}_i\right)\hfill \end{array}\right.\hfill \\ {}\hfill range\_mse\_ loca{l}_i=\left[Lo{b}_i,\kern0.5em U{b}_i\right]\hfill \\ {}\hfill range\_mse\_ mediu{m}_i= rang e\_ mediu{m}_i\hfill \\ {}\hfill range\_mse\_ globa{l}_i= rang{e}_i\hfill \end{array} $$

(7)

Intuitively, these defined ranges enclose the current best solution and they may move with the continuous iterative search. On the one hand, the algorithm combines GS, MS and LS to sufficiently exploit the kriging predictor and accelerate the convergence to the global optimum. On the other hand, the algorithm explores the unknown area to allow the current best solution to jump out of the local area.

3.4 The entire optimization process

The complete multi-start space reduction (MSSR) global optimization process is summarized into the following steps, and illustrated by the flowchart in Fig. 5.

Fig. 5

Flowchart of the MSSR optimization process

The initial process

• (1) Design of experiment: apply OLHS (Jin et al. 2005) to generate DOE sample points over the entire design space.

• (2) Evaluate the expensive function using the DOE sample points and store the results in the sample set. (For nonlinear constrained problems, expensive functions include objective and constraint functions.)

• (3) Rank all expensive samples based on their function values. (Here, if a sample point does not satisfy the constraints, the sample values should add a large penalty factor of 1E6.)

The search loop

• (4) Construct the kriging-based SM. (For nonlinear constrained problems, SMs of objective and constraint functions are built, respectively. Here, sample values use the true objective values without the additional penalty factor.)

• (5) Determine which space should be explored based on the present number of iterations. The global search, medium-sized search and local search will be implemented alternately in the process.

• (6) Define the size of the search space, according to the expensive sample set.

• (7) Use the chosen multi-start local optimization approach, SQP, to optimize the kriging-based SM in the defined space.

• (8) Store the obtained local optimal solutions in the database “potential sample points” and select better samples. If there is no better samples, select two new samples from the unknown area.

• (9) Evaluate the expensive function at the selected sample points and update the order of the expensive samples as in step (3).

• (10) If the current best sample value satisfies the stopping criteria, terminate the loop. Otherwise, update the SM and repeat the steps (4) to (9) until the global stopping criteria are satisfied.

The commonly used global stopping criteria are:

$$ \left\{\begin{array}{l}\frac{\left|{y}_{best}-{y}_{optimal}\right|}{\left|{y}_{optimal}\right|}<1\%\kern1.5em if\kern0.5em {y}_{optimal}\ne 0\hfill \\ {}{y}_{best}<0.001\kern3.5em if\kern0.5em {y}_{optimal}=0\hfill \end{array}\right. $$

(8)

To better demonstrate the MSSR search process, generations and updates of sample points during global optimization on the Banana function are illustrated in Figs. 6a to e. The multi-start optimization process presented in Section 3.2 is used to explore the three defined spaces. Each figure shows three iterations of the searches in GS, MS and LS. At the start, the region of LS is larger than that of MS. As the iteration goes on and the number of expensive sample points increases, LS quickly shrinks to the local region around the global optimum. MS always provides a medium-sized region which includes the current best solution. Both MS and LS become smaller and smaller when more and more sample points are added. Intuitively, shrinking LS makes the search concentrate on more promising region and accelerate the convergence; MS provides a promising region which may include several local optima; and GS ensures that the multi-start optimization process explores the entire design space. As shown in Figs. 6a and c, LS may not include the true global optimum at some time, but it will follow the moving best sample point and eventually move close to the global optimum. In this example, 15 iterations and 37 expensive sample points are needed to find the global optimum. During the search process, the general shape of the SM at different stages, as shown in Figs. 6a to e, gradually approached the shape of the true objective function as shown in Fig. 1, and the SM became sufficiently precise to the objective function in the local region around the global optimum.

Fig. 6

MSSR optimization process on Benchmark Banana function

4 Test cases and results

To verify the capability and to demonstrate the advantage of the new MSSR algorithm, a number of commonly-used, constrained global optimization benchmark problems with 2 to 16 design variables were used as test examples. These included eight two-dimensional problems (Banana, Peaks, GP, SC, Shub, GF, HM, Leon), two four-dimensional problems (Shekel and Levy), two six-dimensional problems (HN6 and Trid6), two ten-dimensional problems (Sphere and Trid10), and one sixteen-dimensional problem F16 (Wang et al. 2004; Younis and Dong 2010; Gu et al. 2012) with variable bound constraints. These test problems have their own unique characteristics, and in combination they can better represent many different situations in design optimization. The detailed forms of these functions are given in Table 1. For optimization problems with nonlinear constraints, two mathematical functions and four benchmark design optimization cases were used in the testing. All of these test cases are given in Appendix. Ten runs on each of these benchmark problems have been made using the new MSSR search program. The obtained statistical results were compared with the results from the other recently introduced space reduction search methods for global optimization to compare their search efficiency and robustness.

Table 1 Bound constrained benchmark problems for global optimization

4.1 Bound constrained optimization problems

Firstly Harmony Search (HS, Yang 2010) and Differential Evolution (DE, Storn and Price 1997) algorithms, as examples of nature-inspired global optimization methods, were selected as references of high computation cost for the solution of optimization problem with expensive black-box functions. Secondly an effective space reduction algorithm DIRECT (Björkman and Holmström 1999) and a widely cited surrogate-based space exploration method MPS (Wang et al. 2004) were used as comparison. In addition, the EGO algorithm that uses the kriging model for expensive functions was compared to show the advantage of the algorithm, and the Mueller’s surrogate model toolbox (Mueller 2012) was used to carry out the “expected improvement” strategy in the EGO algorithm. Furthermore, the presented Multi-start (MS) optimization algorithm without using the “space reduction” strategy was also tested as another comparison. At last, the MSSR algorithm has been tested using the same benchmark problems and 3n + 2 DOE sample points have been generated to construct the initial SM during the tests.

Seven representative functions from Table 1 were used as test cases, and the seven different algorithms for comparison have run these tests for 10 times to get the statistical results. The collected median values of the number of function evaluations (NFE) and the obtained minimum values from the optimization are given in Table 2. The seven algorithms tried to get the values that satisfy the condition of Formula (8). Since the EGO method requires much higher CPU time than the other algorithms when the dimension of the problem increases, a maximum allowable NFE (250 for low-dimensional problem and 200 for high-dimensional problem) was used during its tests. The test results in Table 2 have indicated:

Table 2 Preliminary comparison results on seven representative benchmark functions

• HS and DE consistently required higher NFE than the other algorithms;

• DIRECT performed well on most cases except the Banana, Shub and F16 functions;

• EGO and MPS could easily approach the global optimum for simpler cases like GP and SC, but they generally needed higher NFE for complex cases like Shub, Shekel and F16; and

• The proposed MS and MSSR algorithms showed better performance on all test cases, and MSSR used fewer NFE than the MS. This showed that the “space reduction” strategy did improve the multi-start optimization algorithm.

In summary, non-surrogate based search methods generally require considerably more NFE since these algorithms directly call the original objective function during the search, and the surrogate-based search methods use predictive models to guide the exploration of the design space, effectively decreasing the NFE. These preliminary comparisons with the nature-inspired global optimization methods and existing SBO methods showed the advantages of the new MSSR method on optimization problems with intensive computation due to the lower NFE required.

To further compare the search efficiency and robustness of the algorithms, MSSR and other two recently introduced surrogate-based global optimization algorithms (HAM and SEUMRE) were tested using the 15 functions listed in Table 1. SEUMRE utilizes grid sampling to divide the design space into several unimodal regions. Once the key unimodal region is obtained, a kriging model is built using sampled data. The optimization and reconstruction of the kriging model are mainly carried out in this key region. However, the initial interpretation of the experiment data may miss the location of the true global optimum. The SEUMRE algorithm may thus be trapped around a local optimum for multimodal functions and/or high-dimensional problems. Although SEUMRE is highly efficient in search convergence, it is not stable for complex global optimization problems. HAM divides the original design space into several sub-spaces, applies three types of SMs, Kriging, RBF and PRS, to start the search, and acquires supplementary sample points using the better performing SM to adapt to the objective function on hand. The unique strategy effectively combines the predictive capacities of multiple SMs. However, once these SMs focus on the same region, the algorithm will likely converge to the local optimum and can hardly explore other promising areas. In this comparing test, the same termination criteria of Formula (8) and user-defined parameters in (Gu et al. 2012; Younis and Dong 2010) were used.

Since the grid sampling method may find the global optimum of the GP and Banana functions by chance before the iteration process of SEUMRE begins, the DOE range of the algorithm was changed to 95 % of the original range on the two problems. To deal with the randomness of these methods, ten experiment tests were made for each case. The mean number of NFEs and the range of the obtained best values from the searches are shown in Table 3. The statistical results of NFE with minimum NFE, maximum NFE and the median value are given in Table 4. The NFE values with the > sign indicate that at least one of the tests could not satisfy the stopping criteria within 500 function evaluations, and the numbers in the brackets represent how many failed searches it had. These results showed that the new MSSR method has successfully identified the global optimum in all test cases within 500 function evaluations and required the least number of NFE. The SEUMRE algorithm performed well on the Banana, Peaks, GP and SC functions, but it had difficulties in solving the multimodal and high-dimensional problems. Specifically, SEUMRE succeeded one time on Shekel, four times on Levy and six times on HN6 functions, but it failed all the ten runs on the Trid6, Sphere, Trid10 and F16 functions. The best value that the SEUMRE has obtained on F16 function is 27.524, which is much larger than the results from the MSSR and HAM methods.

Table 3 Mean values of NFE and ranges of optimal values obtained by the three algorithms

Table 4 Specific statistical results of NFE obtained by MSSR, SEUMRE and HAM

HAM is an effective search method that performed well on Banana, GP, SC, Shub, GF, HM, Leon, HN6 and Trid6 functions, but it showed poor performance on Shekel and Trid10. For high-dimensional problems Sphere and F16, HAM could get satisfactory solutions most of time.

A comparison on calculated objective function values and required NFEs of the three methods for high-dimensional problems is shown in Figs. 7a–f. In order to improve the readability, two adjacent dots keep a small interval that is roughly greater than 2 units of NFE. Results from the entire search process within 200 function evaluations are shown in Figs. 7a, c and e, while closer views on the results of HAM and MSSR from 100 to 200 NFE are given in Figs. 7b, d and f. The new MSSR algorithm has been found to be able to converge to the optimum much quicker than HAM and SEUMRE, and meet the given stopping criteria within 200 objective function evaluations. The computation time needed for the three methods to find the optimum using a PC with Core i7-4720HQ CPU (2.60 GHZ) and 16GB memory is given in Fig. 8. The MSSR and HAM methods used more time on two-dimensional problems since MSSR needed to call the SQP solver many times and HAM needed to construct three SMs in each iteration. All three methods require more computation time for higher-dimensional and multimodal problems.

Fig. 7

Iterative results on high-dimensional problems

Fig. 8

Execution time of MSSR, SEUMRE and HAM on benchmark functions

As the most important indicator for an algorithm’s search efficiency and computation time need for computationally expensive black-box problems, the results of required NFEs for different test problems put the computation performance of the three methods into perspective. The HAM method showed good performance most of the time, but it may sometimes be trapped into local optima. The SEUMRE method performed better on low-dimensional problems, but it could not function well on multimodal and high-dimensional optimization problems. The new MSSR method needed the least number of function evaluations and appeared to be most robust, presenting to be the most promising black-box global optimization technique.

4.2 Nonlinear constrained engineering applications

The new MSSR search methods have also been tested using six other nonlinear constrained optimization benchmark problems. These comprised the G6 function that came from the constrained optimization problems used by Hedar (2004), Egea (2008), Younis and Dong (2010); the widely used Himmelblau’s nonlinear problems (Him, Himmelblau 1972) (Gen and Cheng 1997); and four other structural design applications, including the Tension/Compression Spring Design (TSD), Welded Beam Design (WBD), Pressure Vessel Design (PVD), and Speed Reducer Design (SRD) (Coello 2002; Ao and Chi 2010; Garg 2014). All of these six test problems have their objectives and constraints in computation expensive black-box form. These test cases (G6, TSD, WBD, PVD, Him, SRD) have dimensions range from 2 to 7 with 2, 4, 7, 4, 6 and 11 constraints, respectively. The test results are given in Table 5 and the iterative processes are illustrated in Fig. 9. The new MSSR method could find the global optimum within 200 evaluations of the original objective and constraint functions on all the six cases. According to the results from previously published performance tests, the obtained optima are sufficiently accurate and the recorded NFEs are much lower (Coello 2002; Mezura-Montes et al. 2007; Mezura-Montes and Coello 2008; Ao and Chi 2010; Regis 2011, Akay and Karaboga 2012; Garg 2014). Furthermore, the MSSR program has been repeatedly applied on these cases ten times to assess its robustness with the results shown in Tables 6 and 7. In most cases, the MSSR method could obtain an accurate solution with a small number of function evaluations, showing good computation efficiency as well as robustness on nonlinear constrained optimization problems.

Table 5 Global optimal results obtained by MSSR on nonlinear constrained problems

Fig. 9

Iterative results obtained by MSSR on constrained optimization problems

Table 6 Summary of results obtained by MSSR on G6, TSD and Him

Table 7 Summary of results obtained by MSSR on WBD, PVD and SRD

5 Conclusions

A new multi-start space reduction (MSSR) algorithm for solving computationally expensive black-box global optimization problems has been introduced. In this new search method, sampling spaces at three different levels have been introduced. The entire design space is regarded as the Global Space (GS) and remains unchanged during the search. The other two varying spaces are Medium Space (MS) and Local Space (LS). As two reduced regions which contain the promising solutions, the locations and boundaries of MS and LS change automatically during the search due to the SM update mechanism of the algorithm. Each of the three spaces has its own role in the search for global optimum. The GS supports consideration of the entire design space and ensures that the true global optimum will not be easily missed; the MS directs the search to a promising region that contains several possible best solutions at the specific stage of the search; and the LS accelerates the search around a local optimum. A multi-start optimization strategy is introduced to carry out search in these three introduced spaces, using LHS to provide multiple starting points and SQP solver on the SM with starting points in the defined space. The new MSSR method utilizes the kriging model in the search of the global optimal solution to increase search efficiency and reduce the number of expensive function evaluation. In each of the iterative search loops, a new selection scheme is used to obtain several promising sample points. This selection scheme ensures that the kriging-based SM is sufficiently exploited, and the unknown area of the SM can be gradually explored. The estimated MSE of the kriging-based SM is used as an important tool to explore the unknown area of the design space. The new algorithm has been tested using a large number of optimization benchmark problems, including 15 bound constrained problems, 2 nonlinear constrained problems, and 4 structural engineering applications. All benchmark tests and comparisons with results from other optimization methods have showed superior performance and robustness of the new MSSR method in dealing with computationally expensive black-box optimization problems.

In our continuous research, the new MSSR method will be applied to large structural optimization and complex multidisciplinary optimization problems for further testing and improvements. Its applications to higher-dimensional black-box global optimization problems in various engineering fields will also be studied.

Appendix. List of benchmark test problems

• (1) Banana function, n = 2:

$$ f\left(\boldsymbol{x}\right)=100{\left({x}_2-{x}_1^2\right)}^2+{\left(1-{x}_1\right)}^2\kern1.5em -2\le {x}_i\le 2,\kern1em i=1,2 $$

• (2) Peaks function, n = 2:

$$ f\left(\boldsymbol{x}\right)=3{\left(1-{x}_1\right)}^2{e}^{-{x}_1^2-{\left({x}_2+1\right)}^2}-10\left(\frac{x_1}{5}-{x}_1^3-{x}_2^5\right){e}^{-{x}_1^2-{x}_2^2}-\frac{1}{3}{e}^{-{\left({x}_1+1\right)}^2-{x}_2^2}\kern0.5em -3\le {x}_1\le 3,\kern0.5em -4\le {x}_2\le 4 $$

• (3) Goldstein and Price function (GP), n = 2:

$$ \begin{array}{l}f\left(\boldsymbol{x}\right)=\left[1+{\left({x}_1+{x}_2+1\right)}^2\left(19-14{x}_1+3{x}_1^2-14{x}_2+6{x}_1{x}_2+3{x}_2^2\right)\right]\hfill \\ {}\times \left[30+{\left(2{x}_1-3{x}_2\right)}^2\left(18-32{x}_1+12{x}_1^2+48{x}_2-36{x}_1{x}_2+27{x}_2^2\right)\right]-2\le {x}_i\le 2,\kern0.5em i=1,2\hfill \end{array} $$

• (4) Six-hump Camel-back function (SC), n = 2:

$$ f\left(\boldsymbol{x}\right)=4{x}_1^2-2.1{x}_1^4+\frac{1}{3}{x}_1^6+{x}_1{x}_2-4{x}_2^2+4{x}_2^4\kern2em -2\le {x}_i\le 2,\kern0.5em i=1,2 $$

• (5) Shubert function (Shub), n = 2:

$$ f\left(\boldsymbol{x}\right)=\left({\displaystyle \sum_{i=1}^5i \cos \left(\left(i+1\right){x}_1+i\right)}\right)\left({\displaystyle \sum_{i=1}^5i \cos \left(\left(i+1\right){x}_2+i\right)}\right)\kern2em -10\le {x}_i\le 10,\kern0.5em i=1,2 $$

• (6) Generalized Polynomial function (GF), n = 2:

$$ f\left(\boldsymbol{x}\right)={\left(1.5-{x}_1\left(1-{x}_2\right)\right)}^2+{\left(2.25-{x}_1\left(1-{x}_2^2\right)\right)}^2+{\left(2.625-{x}_1\left(1-{x}_2^3\right)\right)}^2\kern2em -2\le {x}_i\le 2,\kern0.5em i=1,2 $$

• (7) Himmelblau function (HM), n = 2:

$$ f\left(\boldsymbol{x}\right)={\left({x}_1^2+{x}_2-11\right)}^2+{\left({x}_1+{x}_2^2-7\right)}^2\kern2.5em -6\le {x}_i\le 6,\kern0.5em i=1,2 $$

• (8) Leon function, n = 2:

$$ f\left(\boldsymbol{x}\right)=100{\left({x}_2-{x}_1^3\right)}^2+{\left({x}_1-1\right)}^2\kern2.5em -10\le {x}_i\le 10,\kern0.5em i=1,2 $$

• (9) Shekel function, n = 4:

$$ \begin{array}{l}f\left(\boldsymbol{x}\right)=-{{\displaystyle \sum_{i=1}^5\left({c}_i+{\displaystyle \sum_{j=1}^4{\left({x}_j-{a}_{ji}\right)}^2}\right)}}^{-1}\hfill \\ {}a=\left[\begin{array}{cccccccccc}\hfill 4\hfill & \hfill 1\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 3\hfill & \hfill 2\hfill & \hfill 5\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 7\hfill \\ {}\hfill 4\hfill & \hfill 1\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 7\hfill & \hfill 9\hfill & \hfill 5\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 3.6\hfill \\ {}\hfill 4\hfill & \hfill 1\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 3\hfill & \hfill 2\hfill & \hfill 3\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 7\hfill \\ {}\hfill 4\hfill & \hfill 1\hfill & \hfill 8\hfill & \hfill 6\hfill & \hfill 7\hfill & \hfill 9\hfill & \hfill 3\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 3.6\hfill \end{array}\right]\hfill \\ {}c=\left[\begin{array}{cccccccccc}\hfill 0.1\hfill & \hfill 0.2\hfill & \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill 0.4\hfill & \hfill 0.6\hfill & \hfill 0.3\hfill & \hfill 0.7\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill \end{array}\right]\hfill \\ {}\kern1.5em 0\le {x}_i\le 10,\kern0.5em i=1,2,3,4\hfill \end{array} $$

• (10) Levy function, n = 4:

$$ \begin{array}{l}f\left(\boldsymbol{x}\right)={ \sin}^2\left(\pi {y}_1\right)+{\displaystyle \sum_{i=1}^{n-1}\left[{\left({y}_i-1\right)}^2\left(1+10{ \sin}^2\left(\pi {y}_i+1\right)\right)\right]}+{\left({y}_n-1\right)}^2\left(1+10{ \sin}^2\left(2\pi {y}_n\right)\right)\hfill \\ {}{y}_i=1+\frac{x_i-1}{4},\kern3.5em i=1,\cdots, n.\kern1.5em -10\le {x}_i\le 10,\kern1.5em i=1,\cdots, n.\hfill \end{array} $$

• (11) Hartman6 function (HN6), n = 6:

$$ \begin{array}{l}f\left(\boldsymbol{x}\right)=-{\displaystyle \sum_{i=1}^4{\alpha}_i \exp \left[-{\displaystyle \sum_{j=1}^6{B}_{ij}{\left({x}_j-{Q}_{ij}\right)}^2}\right]}\hfill \\ {}\alpha ={\left[1,\;1.2,\;3,\;3.2\right]}^T,\kern2em B=\left[\begin{array}{cccccc}\hfill 10\hfill & \hfill 3\hfill & \hfill 17\hfill & \hfill 3.5\hfill & \hfill 1.7\hfill & \hfill 8\hfill \\ {}\hfill 0.05\hfill & \hfill 10\hfill & \hfill 17\hfill & \hfill 0.1\hfill & \hfill 8\hfill & \hfill 14\hfill \\ {}\hfill 3\hfill & \hfill 3.5\hfill & \hfill 1.7\hfill & \hfill 10\hfill & \hfill 17\hfill & \hfill 8\hfill \\ {}\hfill 17\hfill & \hfill 8\hfill & \hfill 0.05\hfill & \hfill 10\hfill & \hfill 0.1\hfill & \hfill 14\hfill \end{array}\right]\hfill \\ {}Q={10}^{-4}\left[\begin{array}{llllll}1312\hfill & 1696\hfill & 5569\hfill & 124\hfill & 8283\hfill & 5886\hfill \\ {}2329\hfill & 4135\hfill & 8307\hfill & 3736\hfill & 1004\hfill & 9991\hfill \\ {}2348\hfill & 1451\hfill & 3522\hfill & 2883\hfill & 3047\hfill & 6650\hfill \\ {}4047\hfill & 8828\hfill & 8732\hfill & 5743\hfill & 1091\hfill & 381\hfill \end{array}\right]\hfill \\ {}\kern1em 0\le {x}_i\le 1,\kern0.5em i=1,2,\cdots 6\hfill \end{array} $$

• (12) Trid function, n = 6, 10:

$$ f\left(\boldsymbol{x}\right)={\displaystyle \sum_{i=1}^n{\left({x}_i-1\right)}^2}-{\displaystyle \sum_{i=2}^n{x}_i{x}_{i-1}}\kern2em -{n}^2\le {x}_i\le {n}^2,\kern0.5em i=1,\cdots, n. $$

• (13) Sphere function, n = 10:

$$ f\left(\boldsymbol{x}\right)={\displaystyle \sum_{i=1}^{10}{x}_i^2}\kern2.5em -5.12\le {x}_i\le 5.12,\kern1.5em i=1,2,\cdots, 10. $$

• (14) 16 Variable function (F16), n = 16:

$$ \begin{array}{l}f\left(\boldsymbol{x}\right)={\displaystyle \sum_{i=1}^{16}{\displaystyle \sum_{j=1}^{16}{a}_{ij}\left({x}_i^2+{x}_i+1\right)\left({x}_j^2+{x}_j+1\right)}}\hfill \\ {}{a}_{ij\left( row\kern0.5em 1-8\right)}=\left[\begin{array}{llllllllllllllll}1\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ {}0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \end{array}\right]\kern1.5em {a}_{ij\left( row\kern0.5em 9-16\right)}=\left[\begin{array}{llllllllllllllll}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ {}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right]\hfill \\ {}-1\le {x}_i\le 1,\kern0.5em i=1,2,\cdots, 16.\hfill \end{array} $$

• (15) G6 function (G6), n = 2:

$$ \begin{array}{l} \min \kern1em f\left(\boldsymbol{x}\right)={\left({x}_1-10\right)}^3+{\left({x}_2-20\right)}^3\hfill \\ {}s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=-{\left({x}_1-5\right)}^2-{\left({x}_2-5\right)}^2+100\le 0,\hfill \\ {}\kern3.5em {g}_2\left(\boldsymbol{x}\right)={\left({x}_1-6\right)}^2+{\left({x}_2-5\right)}^2-82.81\le 0.\hfill \\ {}\kern4.5em 13\le {x}_1\le 100;\kern1em 0\le {x}_2\le 100.\hfill \end{array} $$

• (16) Tension/Compression Spring Design (TSD), n = 3:

This problem minimizes the weight of a spring and meanwhile is subject to constraints on minimum deflection, shear stress, surge frequency, limits on outside diameter and side constraints.

$$ \begin{array}{l} \min \kern1em f\left(\boldsymbol{x}\right)={x}_1^2{x}_2\left({x}_3+2\right)\hfill \\ {}s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=1-\frac{x_2^3{x}_3}{71785{x}_1^4}\le 0,\hfill \\ {}\kern3.5em {g}_2\left(\boldsymbol{x}\right)=\frac{4{x}_2^2-{x}_1{x}_2}{12566{x}_1^3\left({x}_2-{x}_1\right)}+\frac{1}{5108{x}_1^2}-1\le 0,\hfill \end{array} $$

$$ \begin{array}{l}\kern1.5em {g}_3\left(\boldsymbol{x}\right)=1-\frac{140.45{x}_1}{x_3{x}_2^2}\le 0,\hfill \\ {}\kern1.5em {g}_4\left(\boldsymbol{x}\right)=\frac{x_1+{x}_2}{1.5}-1\le 0.\hfill \\ {}\kern0.5em 0.05\le {x}_1\le 2;\kern1em 0.25\le {x}_2\le 1.3;\kern1em 2\le {x}_3\le 15\hfill \end{array} $$

• (17) Welded Beam Design (TSD), n = 4:

This problem is designed for minimum cost and meanwhile is subject to constraints on shear stress, bending stress in the beam, buckling load on the bar, end deflection of the beam and side constraints.

$$ \begin{array}{c}\hfill \min \kern1em f\left(\boldsymbol{x}\right)=1.10471{x}_1^2{x}_2+0.04811{x}_3{x}_4\left(14+{x}_2\right)\hfill \\ {}\hfill s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=\tau \left(\boldsymbol{x}\right)-{\tau}_{\max}\le 0,\hfill \\ {}\hfill {g}_2\left(\boldsymbol{x}\right)=\sigma \left(\boldsymbol{x}\right)-{\sigma}_{\max}\le 0,\hfill \\ {}\hfill {g}_3\left(\boldsymbol{x}\right)={x}_1-{x}_4\le 0,\hfill \\ {}\hfill {g}_4\left(\boldsymbol{x}\right)=0.10471{x}_1^2+0.04811{x}_3{x}_4\left(14+{x}_2\right)-5\le 0,\hfill \\ {}\hfill {g}_5\left(\boldsymbol{x}\right)=0.125-{x}_1\le 0,\hfill \\ {}\hfill {g}_6\left(\boldsymbol{x}\right)=\delta \left(\boldsymbol{x}\right)-{\delta}_{\max}\le 0,\hfill \\ {}\hfill {g}_7\left(\boldsymbol{x}\right)=P-{P}_c\left(\boldsymbol{x}\right)\le 0,\hfill \end{array} $$

where

$$ \begin{array}{l}\tau \left(\boldsymbol{x}\right)=\sqrt{{\left(\tau \prime \right)}^2+2\tau^{\prime}\tau^{\prime\prime}\frac{x_2}{2R}+{\left(\tau \prime \prime \right)}^2},\kern1em \tau^{\prime }=\frac{P}{\sqrt{2}{x}_1{x}_2},\kern1em \tau^{\prime\prime }=\frac{MR}{J},\hfill \\ {}M=P\left(L+\frac{x_2}{2}\right),\kern1em R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+{x}_3}{2}\right)}^2},\kern1em \sigma \left(\boldsymbol{x}\right)=\frac{6 PL}{x_4{x}_3^2},\hfill \\ {}\delta \left(\boldsymbol{x}\right)=\frac{4P{L}^3}{E{x}_3^3{x}_4},\kern1em J=2\left\{\sqrt{2}{x}_1{x}_2\left[\frac{x_2^2}{12}+{\left(\frac{x_1+{x}_3}{2}\right)}^2\right]\right\},\hfill \end{array} $$

$$ \begin{array}{l}{P}_c\left(\boldsymbol{x}\right)=\frac{4.013E\sqrt{x_3^2{x}_4^6/36}}{L^2}\left(1-\frac{x_3}{2L}\sqrt{\frac{E}{4G}}\right),\kern1em G=12\times {10}^6\kern0.5em psi,\\ {}P=6000\kern0.5em lb,\kern1em L=14\kern0.5em in,\kern1em {\delta}_{\max }=0.25\kern0.5em in,\kern0.5em E=30\times {10}^6\kern0.5em psi,\kern0.5em \\ {}{\tau}_{\max }=13600 psi,\kern1.5em {\sigma}_{\max }=30000\kern0.5em psi.\\ {}0.1\le {x}_1,{x}_4\le 2;\kern1em 0.1\le {x}_2,{x}_3\le 10\kern1.5em \end{array} $$

• (18) Pressure Vessel Design (PVD), n = 4:

This problem is to minimize the total cost of a cylindrical vessel, including the cost of material, forming and welding. Four design variables are thickness of the pressure vessel, thickness of the head, inner radius of the vessel and length of the vessel, respectively.

$$ \begin{array}{c}\hfill \min \kern1em f\left(\boldsymbol{x}\right)=0.6224{x}_1{x}_3{x}_4+1.7781{x}_2{x}_3^2+3.1661{x}_1^2{x}_4+19.84{x}_1^2{x}_3\hfill \\ {}\hfill s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=-{x}_1+0.0193{x}_3\le 0,\hfill \\ {}\hfill {g}_2\left(\boldsymbol{x}\right)=-{x}_2+0.00954{x}_3\le 0,\hfill \\ {}\hfill {g}_3\left(\boldsymbol{x}\right)=-\pi {x}_3^2{x}_4-\frac{4}{3}\pi {x}_3^3+1296000\le 0,\hfill \\ {}\hfill {g}_4\left(\boldsymbol{x}\right)={x}_4-240\le 0.\hfill \\ {}\hfill 1\times 0.0625\le {x}_1,{x}_2\le 99\times 0.0625;\kern1em 10\le {x}_3,{x}_4\le 200\hfill \end{array} $$

• (19) Himmelblau’s nonlinear optimization problem (Him), n = 5:

This problem has five design variables, six nonlinear inequality constraints and ten boundary conditions.

$$ \begin{array}{l} \min \kern1em f\left(\boldsymbol{x}\right)=5.3578547{x}_3^2+0.8356891{x}_1{x}_5+37.293239{x}_1-40792.141\hfill \\ {}s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=85.334407+0.0056858{x}_2{x}_5+0.00026{x}_1{x}_4-0.0022053{x}_3{x}_5,\hfill \\ {}\kern3.5em {g}_2\left(\boldsymbol{x}\right)=80.51249+0.0071317{x}_2{x}_5+0.0029955{x}_1{x}_2+0.0021813{x}_3^2,\hfill \\ {}\kern3.5em {g}_3\left(\boldsymbol{x}\right)=9.300961+0.0047026{x}_3{x}_5+0.0012547{x}_1{x}_3+0.0019085{x}_3{x}_4,\hfill \\ {}\kern3.5em 0\le {g}_1\left(\boldsymbol{x}\right)\le 92,\kern1em 90\le {g}_2\left(\boldsymbol{x}\right)\le 110,\kern1.5em 20\le {g}_3\left(\boldsymbol{x}\right)\le 25,\hfill \\ {}\kern3.5em 78\le {x}_1\le 102;\kern1em 33\le {x}_2\le 45;\kern1em 27\le {x}_3,{x}_4,{x}_5\le 45.\hfill \end{array} $$

• (20) Speed Reducer Design (SRD), n = 7:

This problem is to minimize the total weight of the speed reducer. It has eleven constraints which include the limits on the bending stress of the gear teeth, surface stress and transverse deflections of shafts.

$$ \begin{array}{c}\hfill \min \kern1em f\left(\boldsymbol{x}\right)=0.7854{x}_1{x}_2^2\left(3.3333{x}_3^2+14.9334{x}_3-43.0934\right)-1.508{x}_1\left({x}_6^2+{x}_7^2\right)\hfill \\ {}\hfill +7.4777\left({x}_6^3+{x}_7^3\right)+0.7854\left({x}_4{x}_6^2+{x}_5{x}_7^2\right)\hfill \\ {}\hfill s.t.\kern1.5em {g}_1\left(\boldsymbol{x}\right)=\frac{27}{x_1{x}_2^2{x}_3}-1\le 0,\kern1.5em {g}_6\left(\boldsymbol{x}\right)=\frac{{\left[{\left(745{x}_5/\left({x}_2{x}_3\right)\right)}^2+157.5\times {10}^6\right]}^{1/2}}{85{x}_7^3}-1\le 0,\hfill \\ {}\hfill {g}_2\left(\boldsymbol{x}\right)=\frac{397.5}{x_1{x}_2^2{x}_3^2}-1\le 0,\kern1.5em {g}_7\left(\boldsymbol{x}\right)=\frac{x_2{x}_3}{40}-1\le 0,\kern1.5em {g}_8\left(\boldsymbol{x}\right)=\frac{5{x}_2}{x_1}-1\le 0,\hfill \\ {}\hfill {g}_3\left(\boldsymbol{x}\right)=\frac{1.93{x}_4^3}{x_2{x}_3{x}_6^4}-1\le 0,\kern1.5em {g}_9\left(\boldsymbol{x}\right)=\frac{x_1}{12{x}_2}-1\le 0,\kern1em {g}_{10}\left(\boldsymbol{x}\right)=\frac{1.5{x}_6+1.9}{x_4}-1\le 0,\hfill \\ {}\hfill {g}_4\left(\boldsymbol{x}\right)=\frac{1.93{x}_5^3}{x_2{x}_3{x}_7^4}-1\le 0,\kern1.5em {g}_{11}\left(\boldsymbol{x}\right)=\frac{1.1{x}_7+1.9}{x_5}-1\le 0,\hfill \\ {}\hfill {g}_5\left(\boldsymbol{x}\right)=\frac{{\left[{\left(745{x}_4/\left({x}_2{x}_3\right)\right)}^2+16.9\times {10}^6\right]}^{1/2}}{110{x}_6^3}-1\le 0,\hfill \\ {}\hfill 2.6\le {x}_1\le 3.6;\kern1em 0.7\le {x}_2\le 0.8;\kern1em 17\le {x}_3\le 28;\kern0.5em 7.3\le {x}_4,{x}_5\le 8.3;\hfill \\ {}\hfill 2.9\le {x}_6\le 3.9;\kern1em 5.0\le {x}_7\le 5.5.\hfill \end{array} $$