Abstract
Secure computation enables n mutually distrustful parties to compute a function over their private inputs jointly. In 1988, Ben-Or, Goldwasser, and Wigderson (BGW) proved that any function can be computed with perfect security in the presence of a malicious adversary corrupting at most \(t< n/3\) parties. After more than 30 years, protocols with perfect malicious security, and round complexity proportional to the circuit’s depth, still require (verifiably) sharing a total of \(O(n^2)\) values per multiplication. In contrast, only O(n) values need to be shared per multiplication to achieve semi-honest security. Sharing \(\Omega (n)\) values for a single multiplication seems to be the natural barrier for polynomial secret-sharing-based multiplication. In this paper, we construct a new secure computation protocol with perfect, optimal resilience and malicious security that incurs (verifiably) sharing O(n) values per multiplication. Our protocol requires a constant number of rounds per multiplication. Like BGW, it has an overall round complexity that is proportional only to the multiplicative depth of the circuit. Our improvement is obtained by a novel construction for weak VSS for polynomials of degree 2t, which incurs the same communication and round complexities as the state-of-the-art constructions for VSS for polynomials of degree t. Our second contribution is a method for reducing the communication complexity for any depth 1 sub-circuit to be proportional only to the size of the input and output (rather than the size of the circuit). This implies protocols with sub-linear communication complexity (in the size of the circuit) for perfectly secure computation for important functions like matrix multiplication.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Secure multiparty computation is a major pillar of modern cryptography. Breakthrough results on secure multiparty computation in the late ’80s prove feasibility with optimal resilience: perfect, statistical, and computational security can be achieved as long as \(t<n/3\) [9], \(t<n/2\) (assuming broadcast) [41], and \(t<n\) [31, 45], respectively, where n is the number of computing parties such that at most t of them are controlled by a malicious adversary.
In this paper, we focus on secure computation with perfect security, which is the strongest possible guarantee: it provides unconditional, everlasting security. Such protocols come with desirable properties. They often guarantee adaptive security [14, 36] and remain secure under universal composition [13]. A central foundational result in this context is the Completeness Theorem of Ben-or, Goldwasser, and Wigderson [9] from 1988:
Theorem 1.1
(BGW with improvements [4, 9, 21, 29]-informal) Let f be an n-ary functionality and C its arithmetic circuit representation. Given a synchronous network with pairwise private channels and a broadcast channel, there exists a protocol for computing f with perfect security in the presence of a static malicious adversary controlling up to \(t < n/3\) parties, with round complexity \(O(\mathsf{depth}(C))\) and communication complexity of \(O(n^4 \cdot |C|)\) words over point-to-point channels and no broadcast in the optimistic case, and additional \(\Omega (n^4 \cdot |C|)\) words of broadcast in the pessimistic case.Footnote 1
The communication complexity in the above statement (and throughout the paper) is measured in words (i.e., field elements), and we assume a word of size \(O(\log n)\) bits. In the past three decades, there have been great efforts to improve the communication complexity of the BGW protocol [4, 29]. Theorem 1.1 states the round and communication complexity of the protocols after these improvements. Most recently, Goyal, Liu, and Song [32], building upon Beaver [6], and Beerliová and Hirt [8], achieved \(O(n|C|+n^3)\) communication words (including all broadcast costs) at the expense of increasing the round complexity to \(O(n + \mathsf{depth}(C))\).
In some natural settings, e.g., secure computation of shallow circuits in high-latency networks, this additive O(n) term in the round complexity might render the protocol inapplicable. This state of affairs leads to the fundamental question of whether the communication complexity of perfectly secure computation can be improved without sacrificing the round complexity. Moreover, from a theoretical perspective, the tradeoff between round complexity and communication complexity is interesting.
1.1 Our Results
We show an improvement in the communication complexity of perfectly secure protocols without incurring any cost in round complexity. Notably, our improvement applies both to the optimistic case and to the pessimistic case:
Theorem 1.2
(Main technical result—informal) Let f be an n-ary functionality and C its arithmetic circuit representation. Given a synchronous network with pairwise private channels and a broadcast channel, there exists a protocol for computing f with perfect security in the presence of a static malicious adversary controlling up to \(t < n/3\) parties, with round complexity \(O(\mathsf{depth}(C))\) and communication complexity of \(O(n^3 \cdot |C|)\) words on point-to-point channels and no broadcast in the optimistic case, and additional \(O(n^3 \cdot |C|)\) words of broadcast in the pessimistic case.
Our result strictly improves the state of the art and is formally incomparable to the result of Goyal et al. [32]. Our protocol will perform better in high-latency networks (e.g., the internet) on shallow circuits when \(\mathsf{depth}(C) \ll n\). Whereas the protocol of [32] performs better in low-latency networks (e.g., LAN), or when \(\mathsf{depth}(C) \approx \Omega (n)\).
Sub-linear perfect MPC for sub-circuits of depth 1 As our second main result, we show for the first time that for a non-trivial class of functions, there is in fact a sub-linear communication perfectly secure MPC (in the circuit size). Specifically, we design a perfectly secure MPC that supports all functionalities that can be computed by depth 1 circuits. The communication complexity of our protocol depends only on the input and output sizes of the function, but not on the circuit size, i.e., the number of multiplications. We prove the following:
Theorem 1.3
Let \(n > 3t\), and let \(\mathbb {F}\) be a finite field with \(|\mathbb {F}| > n\). For every arithmetic circuit \(G:\mathbb {F}^{L} \rightarrow \mathbb {F}^{M}\) of multiplication depth 1 (i.e., degree-2 polynomial), there exists a perfect t-secure protocol that computes \((y_1,\ldots ,y_M)=G(x_1,\ldots ,x_L)\) in O(1) rounds and \(O((M+L)\cdot n^3)\) words over the point-to-point channels in the optimistic case, and additional \(O((M+L)\cdot n^3)\) broadcast messages in the pessimistic case. Specifically, the communication complexity is independent of |G|.
The above theorem can also be applied to compute circuits with higher depth while paying only communication complexity that is proportional to the number of wires between the layers, and independent of the number of multiplications in each layer. Similar techniques were shown in the statistical case [16], but no protocol is known for perfect security.
Application: secure matrix multiplication As a leading example of the usefulness of our depth 1 circuit protocol, consider matrix multiplication of two \(T \times T\) matrices. This operation has inputs and outputs of size \(O(T^2)\), but implementing it requires \(O(T^3)\) multiplications (at least when implemented naïvely). The starting point (Theorem 1.1) is communicating \(\Omega (T^3\cdot n^4)\) words over point-to-point channels in the optimistic case (and additional \(\Omega (T^3 \cdot n^4)\) words of broadcast in the pessimistic case). Theorem 1.3 improves the communication complexity to \(O(T^2 \cdot n^3)\) in the point-to-point channels with no additional broadcast in the optimistic case (and additional \(O(T^2 \cdot n^3)\) words on broadcast in the pessimistic case). Our protocol also achieves O(1) rounds in both the optimistic and pessimistic cases.
Secure matrix multiplication is a key building block for various appealing applications. For example, anonymous communication [1] and secure collaborative learning. The latter involves the multiplication of many large matrices (see [5, 15, 37,38,39, 44], to name a few). For instance, the deep convolutional neural network (CNN) ResNet50 [43] requires roughly 2000 matrix multiplications, which, when computed securely, results in more than 4 billion multiplication gates. Using our protocol of matrix multiplication, computing this task reduces by orders of magnitudes, the communication being proportional to computing only millions of multiplications.
1.2 Secure Multiplication: A Natural Barrier of \(\Omega (n)\) Secret Sharings
We give a high-level overview of our technical contribution, pointing to the core of our improvements. When viewed from afar, all secret-sharing-based MPC protocols have a very similar flow. The starting point property is that polynomial secret sharing is additively homomorphic. This allows computing any linear combination (additional and multiplication by public constants) of secrets locally and with no interaction. The challenge is with multiplication gates: while multiplication can also be applied homomorphically (and non-interactively), it increases the degree of the underlying polynomial that hides the secret. Secure multiplication uses the fact that polynomial interpolation is just a linear combination of points on the polynomial, and hence a central part of the computation can be applied locally.
Given shares of the two inputs, every party shares a new secret which is the locally computed multiplication of its two shares. Then, all these new shares are locally combined using the linear combination of the publicly known Lagrange coefficients. This results in the desired new sharing of the multiplication of the two inputs.
This elegant framework for secure multiplication embeds a natural communication complexity barrier: each multiplication requires \(\Omega (n)\) secret sharing (each party needs to secret share its local multiplication). In the malicious case, the secret sharing protocol is called Verifiable Secret Sharing (VSS). Hence, the total communication complexity in this framework is at least \(\Omega (n \cdot \mathsf{comm}(VSS))\).
State-of-the-art MPC for almost all settings matches this natural barrier, obtaining constant-round protocols with optimal resilience using \(O(n \cdot \mathsf{comm}(VSS))\) communication per multiplication, where VSS is the best secret sharing for that setting.
The only exception we are aware of is the family of BGW protocols for a malicious adversary, where all known improvements until now [4, 9, 29] require \(\Omega (n^2 \cdot \mathsf{comm}(VSS))\) communication. This is because each party needs to share n invocations of VSSs of degree-t polynomials to prove that the secret it shared for the product is indeed equal to the multiplication of the already shared multiplicands.
Weak VSS and the complexity of perfect MPC The main technical contribution of this work is a multiplication protocol that meets the natural barrier and achieves communication complexity of \(O(n \cdot \mathsf{comm}(VSS))\). Since \(\mathsf{comm}(VSS)\) is \(O(n^2)\) words in the optimistic case (and no broadcast) and \(O(n^2)\) over the point-to-point channels and additional \(O(n^2)\) words of broadcast in the pessimistic case, Theorem 1.2 is obtained. Our improvement can thus be described as follows:
-
Semi-honest BGW requires \(O(n \cdot \mathsf{comm}(SS))\) communication per multiplication.
-
Malicious BGW requires \(O(n^2 \cdot \mathsf{comm}(VSS))\) communication per multiplication.
-
Our malicious protocol requires \(O(n \cdot \mathsf{comm}(VSS))\) communication per multiplication.
Our improved efficiency is obtained by replacing n invocations of degree-t VSSs with just one invocation of a weak VSS for degree 2t, which we denote by WSS. By weak VSS, we refer to the setting in which the parties’ shares define a single secret at the end of the sharing phase, and during the reconstruction phase, the parties can either recover that secret or \(\bot \). We show that a single weak VSS for a degree-2t polynomial (along with a constant number of strong VSS) is sufficient to prove that the secret-shared for the product is to equal the multiplication of its two already shared multiplicands.
Lemma 1.4
(informal) Given \(n>3t\), there is a protocol for implementing Weak Verifiable Secret Sharing with optimal resilience, for a polynomial of degree 2t with communication complexity of \(O(n^2)\) words on point-to-point channels in the optimistic case, and additional \(O(n^2)\) words of broadcast in the pessimistic case, and O(1) rounds.
Our new weak verifiable secret sharing of degree 2t has the same asymptotic complexity as the verifiable secret sharing of degree t. In addition to improving the efficiency of the core building block in secure computation (i.e., multiplication), we believe it also makes it simpler, which is a pedagogical benefit.
Adaptive security and UC We prove security in the classic setting of a static adversary and stand-alone computation. Protocols that achieve perfect security have substantial advantages over protocols that are only computationally secure: It was shown [36] that perfectly secure protocols in the stand-alone setting with a black-box straight-line simulator are also secure under universal composition [13]. Moreover, it was shown [2, 14, 23] that perfectly secure protocols in presence of a static malicious adversary for secure function evaluation that follows some standard MPC technique (as secret-sharing-based protocols, like BGW) enjoy also perfect security in the presence of an adaptive malicious adversary (albeit with inefficient simulation).
The broadcast channel model We analyze our protocol in the broadcast model and count messages sent over private channels and over the broadcast channel separately. In our setting (\(t<n/3\)) the broadcast channel can also be simulated over the point-to-point channels. However, this comes with some additional costs. There are two alternatives: replace each broadcast usage in the protocol requires \(O(n^2)\) communication but O(n) rounds [10, 19], or \(O(n^3)\) overhead in communication and expected constant rounds (even with bounded parallel composition [20, 28, 35]).Footnote 2
1.3 Related Work
Constant-round per multiplication In this paper, we focus on perfect security in the presence of a malicious adversary, optimal resilience, and constant-round per multiplication. Our protocol improves state of the art in this line of work. As mentioned in Asharov, Lindell, and Rabin [4], an additional verification protocol is needed for completing the specification of the multiplication step of BGW. In Theorem 1.1, we ignore the cost associated with those verification steps and just count the number of verifiable secret sharing needed, which is \(\Omega (n^2)\) VSSs per multiplication gate. The protocol presented by Asharov, Lindell, and Rabin [4] also requires \(O(n^2)\) VSSs per multiplication gate. It results in total communication of \(O(n^4)\) field elements over the point-to-point channels and \(O(n^4)\) field elements over a broadcast channel. Cramer, Damgård, and Maurer [21] presented a protocol that works differently from the BGW protocol, which also achieves a constant-round per multiplication. It has worst-case communication complexity of \(O(n^5)\) field elements over point-to-point channels and \(O(n^5)\) field elements over a broadcast channel. The optimistic cost is \(O(n^4)\) field elements over point-to-point channels and \(O(n^3)\) field elements over the broadcast channel. The work of Choudhury and Patra [18] also works in constant-round per multiplication, separates the protocol into offline phase and online phase, and requires per multiplication gate a total of \(O(n^4)\) field elements over the point-to-point channels and broadcast of \(O(n^4)\) field elements over the broadcast channel.
Protocols that are based on the player elimination technique There is a large body of work [8, 22, 32,33,34] that improves the communication complexity of information-theoretic protocols using the player elimination technique. All of these protocols have a (worst case) round complexity that is linear in the number of parties. This is inherent in the player elimination technique since every time cheating is detected, two players are eliminated, and some computations are repeated. In many cases, player elimination would give a more efficient protocol than our approach. However, there are some cases, specifically for a low-depth circuit where n is large and over high-latency networks, in which our protocol is more efficient. Moreover, our protocol can achieve communication complexity which is sub-linear in the number of multiplication gates, depending on the circuits to be evaluated. We do not know how to achieve similar results on protocols that are based on Beaver multiplication triplets [6], such as the protocol of Goyal et al. [32]. These lines of work are therefore incomparable.
Lower bounds Recently, Damgård and Schwartzbach [25] showed that for any n and all large enough g, there exists a circuit C with g gates such that any perfectly secure protocol implementing C must communicate \(\Omega (ng)\) bits. Note that Theorem 1.3 is sub-linear (in the circuit size) only for particular kind of circuits in which the circuit is much larger than the size of the inputs or its outputs. It is easy to find a circuit C with g gates in which our protocol must communicate \(O(n^4 g)\) in the pessimistic case. A lower bound by Damgård et al. [24] shows that any perfectly secure protocol that works in the “gate-by-gate” framework must communicate \(\Omega (n)\) bits for every multiplication gate. Our protocol deviates from this framework when computing an entire multiplication layer as an atomic unit.
Secret sharing Our solution is based on sharing a bivariate polynomial with degree 2t in x and degree t in y. We remark that sharing a bivariate polynomial with degree d in x and t in y for \(d > t\) was previously studied in the asynchronous setting [7, 40].
1.4 Open Problems
Our protocol improves the communication complexity of constant-round multiplication with optimal malicious resilience from \(O(n^2 \cdot \mathsf{comm}(VSS))\) to \(O(n \cdot \mathsf{comm}(VSS))\), matching the number of secret shares in the semi-honest protocol. The immediate open problem is exploring the optimal communication complexity of verifiable secret sharing protocol. To the best of our knowledge, we are unaware of any non-trivial lower bound for perfect VSS (also see the survey by C, Choudhury, and Patra [11]). The VSS protocol requires \(O(n^2)\) words in the optimistic case over the point-to-point channel and an additional \(O(n^2)\) words over the broadcast channel in the pessimistic case.
Another possible direction to generalize our work is to mitigate between the two approaches for perfect security: Design a “hybrid” protocol that computes some sub-circuits using the linear communication complexity approach and some sub-circuits using the constant-round per multiplication approach and achieve the best of both worlds. Another interesting direction is to make sub-linear communication complexity improvement compatible with the protocols that are based on multiplication triplets.
2 Technical Overview
In this section, we provide a technical overview of our results. We start with an overview of the BGW protocol in Sect. 2.1, and then we overview our protocol in Sect. 2.2.
2.1 Overview of the BGW Protocol
In the following, we give a high-level overview of the BGW protocol while incorporating several optimizations that were given throughout the years [4, 29].
Let f be the function that the parties wish to compute, mapping n inputs to n outputs. The input of party \(P_i\) is \(x_i\) and its output is \(y_i\), where \((y_1,\ldots ,y_n) = f(x_1,\ldots ,x_n)\). On a high level, the BGW protocol works by emulating the computation of an arithmetic circuit C that computes f and has three phases. In the first phase, the input sharing phase, each party secret shares its input with all other parties. At the end of this stage, the value of each input wire of the circuit C is secret-shared among the parties, such that no subset of t parties can reconstruct the actual values on the wires. In the second phase, the circuit emulation phase, the parties emulate a computation of the circuit gate-by-gate, computing shares on the output wire of each gate using the shares on the input wires. At the end of this stage, the output wires’ values are secret-shared among all parties. Finally, in the output reconstruction phase, \(P_i\) receives all the shares associated with its output wire and reconstructs its output, \(y_i\).
The invariant maintained in the original BGW protocol is that each wire in the circuit, carrying some value a, is secret-shared among the parties using some random polynomial A(x) of degree t with a as its constant term. We follow the invariant of [4], and in our protocol, the parties hold bivariate sharing and not univariate sharing. That is, the secret is hidden using a bivariate polynomial A(x, y) of degree t in both variables in which the share of each party \(P_i\) is defined as \(A(x,\alpha _i),A(\alpha _i,y)\), where \(\alpha _i\) is the evaluation point associated with \(P_i\). Maintaining bivariate sharing instead of univariate sharing removes one of the building blocks in the original BGW protocol, where parties sub-share their shares to verify that all the shares lie on a polynomial of degree t. Obtaining bivariate sharing essentially comes for free. In particular, when parties share a value, they use a verifiable secret sharing protocol (VSS, see Sect. 2.2) [17, 26, 28], which uses bivariate sharing to verify that all the shares are consistent. However, in BGW, the parties then disregard this bivariate sharing and project it to univariate sharing. We just keep the shares in the bivariate form.
The multiplication protocol In the input sharing phase, each party simply shares its input using the BGW’s VSS protocol. Emulating the computation of addition gates is easy using the linearity of the secret sharing scheme. The goal of the multiplication protocol is to obtain bivariate sharing of the value of the output wire of the multiplication gate using the shares on the input wires. Let a, b be the two values on the input wires, hidden with polynomials A(x, y), B(x, y), respectively. The protocol proceeds as follows:
-
1.
Each party \(P_i\) holds shares \(f_i^a(x)=A(x,\alpha _i)\) and \(f_i^b(x) = B(x,\alpha _i)\), each are univariate polynomials of degree t. Each party \(P_i\) shares a bivariate polynomial \(C_i(x,y)\) of degree t such that \(C_i(0,0) = f_i^a(0) \cdot f_i^b(0)\).
-
2.
Using a verification protocol, each party \(P_i\) proves in perfect zero-knowledge that \(C_i(0,0) = f_i^a(0)\cdot f_i^b(0)\). We elaborate on this step below.
-
3.
Given the shares on all (degree t) polynomials \(C_1(x,y),\ldots ,C_n(x,y)\), the parties compute shares of the polynomial \(C(x,y) {\mathop {=}\limits ^\mathrm{def}}\sum _{i=1}^{n} \lambda _i\cdot C_i(x,y)\), where \(\lambda _1,\ldots ,\lambda _n\) are the Lagrange coefficients, by simply locally computing a linear combination of the shares they obtained in the previous step.
To see why this protocol is correct, observe that since each one of the polynomials \(C_1(x,y),\ldots ,C_n(x,y)\) is a polynomial of degree t, then the resulting polynomial C(x, y) is also a polynomial of degree t. Moreover, define \(h(y) {\mathop {=}\limits ^\mathrm{def}}A(0,y)\cdot B(0,y)\) and observe that h(y) is a polynomial of degree 2t satisfying \(h(0) = A(0,0)\cdot B(0,0) =ab\). It holds that \(ab = \lambda _1\cdot h(\alpha _1)+\ldots +\lambda _n\cdot h(\alpha _n)\). Thus,
as required. Crucially, each \(C_i(x,y)\) must hide \(h(\alpha _i) = f_i^a(0)\cdot f_i^b(0)\) as otherwise, the above linear combination would not result in the correct constant term. This explains the importance of the verification protocol.
BGW’s verification protocol In the verification protocol, the dealer holds the univariate polynomials \(f_i^a(x),f_i^b(x)\) and a polynomial \(C_i(x,y)\), and each party \(P_j\) holds a share on those polynomials, that is, points \(f_i^a(\alpha _j), f_i^b(\alpha _j)\) and degree-t univariate polynomials \(C_i(x,\alpha _j)\), \(C_i(\alpha _j,y)\). The parties wish to verify that \(C_i(0,0) = f_i^a(0)\cdot f_i^b(0)\).
Toward that end, the dealer defines random degree-t polynomials \(D_1,\ldots ,D_t\) under the constraint that
As shown in [4, 9], the dealer can choose the polynomials \(D_1,\ldots ,D_t\) in a special way so as to cancel all the coefficients of degree higher than t of \(f_i^a(x)\cdot f_i^b(x)\) and to ensure that \(C_i(x,y)\) is of degree t. The dealer verifiably shares the polynomials \(D_1,\ldots ,D_t\) with all parties, and then each party \(P_k\) verifies that the shares it received satisfy Eq. (1). If not, it complaints against the dealer. Note that at this point, since all polynomials \(C_i, D_1,\ldots ,D_t\) are bivariate polynomial of degree t, and \(f_i^a(x),f_i^b(x)\) are univariate polynomials of degree t, it is possible to reconstruct the shares of any party \(P_k\) without the help of the dealer. The parties can then unequivocally verify the complaint. If a complaint was resolved to be a true complaint, the dealer is dishonest, we can reconstruct its points and exclude it from the protocol. If the complaint is false, we can also eliminate the complaining party.
An honest dealer always distributes polynomials that satisfy Eq. (1). For the case of a corrupted dealer, the term \(f_i^a(x)\cdot f_i^b(x) - \sum _{\ell =1}^{t} x^\ell \cdot D_\ell (x,0)\) defines a univariate polynomial of degree at most 2t for every choice of degree-t bivariate polynomials \(D_1,\ldots ,D_t\). If this polynomial agrees with the polynomial \(C_i(x,0)\) for all honest parties, i.e., on \(2t+1\) points, then those two polynomials are identical, and thus it must hold that \(C_i(0,0)=f_i^a(0)\cdot f_i^b(0)\), as required.
2.2 Our Protocol
Simplifying the verification protocol In the above verification protocol, the dealer distributes t polynomials \(D_1,\ldots ,D_t\) using VSS. We show how to use a more efficient technique for accomplishing the verification task. Namely, we introduce a weak secret sharing protocol, for sharing a polynomial D(x, y) of degree 2t in x and degree t in y. The dealer then chooses a single random polynomial D(x, y) under the constraint that:
The dealer distributes D(x, y) and the parties jointly verify that (a) Eq. (2) holds and (b) that \(D(0,0) = 0\).
Our weak secret sharing protocol for distributing such D(x, y) has the same complexity as verifiable secret sharing of a degree-t polynomial, and therefore we improve the verification protocol’s complexity by a factor of \(t=O(n)\). The secret sharing is weak in the sense that the parties cannot necessarily reconstruct the secret from the shares without the help of the dealer during the reconstruction. However, the verifiability part guarantees that there is a well-defined polynomial that can be reconstructed (or, if the dealer does not cooperate, then no polynomial would be reconstructed). Since the role of the polynomial D(x, y) is just in the verification phase and requires the involvement of the dealer, to begin with, this weak verifiability suffices. If the dealer does not cooperate during the verification phase, then the parties can reconstruct its inputs and resume the computation on its behalf.
Our weak secret sharing Our weak verifiable secret sharing protocol is similar to the BGW verifiable secret sharing protocol. Introducing modifications to the protocol enables sharing of a polynomial of a higher degree, but in that case—satisfies only weak verifiability. We start with an overview of the verifiable secret sharing protocol and then describe our weak secret sharing protocol.
The verifiable secret sharing protocol In a nutshell, the verifiable secret sharing protocol of BGW (with the simplifications of [26]) works as follows:
-
1.
Sharing The dealer wishes to distribute shares of a polynomial D(x, y) of degree t in both variables. The dealer sends to each party \(P_i\) the degree-t univariate polynomials \(f_i(x) = D(x,\alpha _i)\) and \(g_i(y) = D(\alpha _i,y)\).
-
2.
Exchange sub-shares Each party \(P_i\) sends to party \(P_j\) the pair \((f_i(\alpha _j),g_i(\alpha _j))\). Note that if indeed the dealer sent correct shares, then \(f_i(\alpha _j) = D(\alpha _j,\alpha _i) = g_j(\alpha _i)\) and \(g_i(\alpha _j) = D(\alpha _i,\alpha _j) = f_j(\alpha _i)\). If a party does not receive from \(P_j\) the shares it expects to receive, then it broadcasts a complaint. The complaint has the form of \(\mathsf{complaint}(i,j,f_i(\alpha _j),g_i(\alpha _j))\), i.e., \(P_i\) complaints that it receives from \(P_j\) wrong points, and publishes the two points that it expected to receive, corresponding to the information it had received from the dealer.
-
3.
Complaint resolution—the dealer The dealer publicly reveals all the shares of all parties that broadcast false complaints—i.e., if party \(P_i\) complaints with points different than those given in the first round, then the dealer makes the share \((f_i(x),g_i(y))\) public.
-
4.
Vote The parties vote that whatever they see is consistent. A party is happy with its share and broadcasts \(\mathsf{good}\) if: (a) Its share was not publicly revealed. (b) The dealer resolved all conflicts the party saw in the exchange sub-shares phase, i.e., all its complaints were resolved by the dealer by publicly opening the other parties’ shares. (c) All shares that the dealer broadcasts are consistent with its shares. (d) No parties (j, k) complain about each other, and the dealer did not resolve at least one of those complaints.
If \(2t+1\) parties broadcast \(\mathsf{good}\) then the parties accept the shares. A party whose share was publicly revealed updates its share to be the publicly revealed one.
Note that if at least \(2t+1\) parties broadcast \(\mathsf{good}\) then at least \(t+1\) honest parties are happy with their shares. Those shares determine a unique bivariate polynomial of degree t. Moreover, any polynomial that is publicly revealed must be consistent with this bivariate polynomial, as agreeing with the points of \(t+1\) honest parties uniquely determine a polynomial of degree t.
Weak secret sharing Consider this protocol when the dealer shares a polynomial D(x, y) that is of degree 2t in x and degree t in y, i.e., \(D(x,y) = \sum _{i=0}^{2t}\sum _{j=0}^{t} d_{i,j}x^iy^j\) for some set of coefficients \(\{d_{i,j}\}_{i,j}\). Here, if \(t+1\) honest parties are happy with their shares and broadcast \(\mathsf{good}\), their polynomials also define a unique polynomial D(x, y) of degree 2t in x and degree t in y. However, if there is a complaint and the dealer opens some party’s share, since \(f_i(x)\) is of degree 2t it is not sufficient that these \(t+1\) honest parties agree with that polynomial \(f_i(x)\), and \(f_i(x)\) might still be “wrong.” This implies that the honest parties cannot identify whether their shares are compatible with the shares of the other honest parties (that their shares were publicly revealed), and further verification is needed, which seems to trigger more rounds of complaints. Guaranteeing all honest parties obtain consistent shares is a more challenging task.
We, therefore, take a different route and do not require the dealer to publicly open any of the \(f_i(x)\) polynomials. Still, it has to publicly open only the \(g_i(y)\) polynomials, as those are of degree t. Each honest party broadcasts \(\mathsf{good}\) only if the same conditions as in VSS are met (in particular, they must hold both \(f_i(x),g_i(y)\) shares). At the end of this protocol, some honest parties might not hold \(f_i(x)\) shares on the polynomial D(x, y). Those parties will not participate in the reconstruction protocol.
Note that if \(2t+1\) parties broadcast \(\mathsf{good}\), then there are at least \(t+1\) honest parties that hold \(f_i(x)\) shares (which are of degree 2t). The shares of those parties agree with all the \(g_i(y)\) of all honest parties. The \(2t+1\) univariate polynomials \(g_i(y)\) of the honest parties define a unique bivariate polynomial of degree 2t in x and degree t in y.
In the reconstruction phase, since the corrupted parties might provide incorrect shares and since some honest parties do not have shares, we cannot guarantee reconstruction of the polynomial D(x, y) without the help of the dealer. However, we can guarantee that only the polynomial D(x, y) can be reconstructed, or no polynomial at all.
Concluding the multiplication protocol Recall that in our protocol, the parties also have to jointly verify that (a) Eq. 2 holds, and that (b) that \(D(0,0)=0\). We now elaborate on those two steps.
To verify that the polynomial D(x, y) satisfies \(D(x,0)= f_i^a(x)\cdot f_i^b(x)-C_i(x,0)\), each party \(P_j\) simply checks that its own shares satisfy this condition, i.e., whether \(D(\alpha _j,0)= f_i^a(\alpha _j)\cdot f_i^b(\alpha _j)-C_i(\alpha _j,0)\). Note that if this holds for \(2t+1\) parties, then the two polynomials are identical. Each party \(P_j\) checks its own shares, and if the condition does not hold then it broadcasts \(\mathsf{complaint}(j)\). With each complaint, the dealer has to publicly reveal the shares of \(P_j\). Since all those polynomials were shared using (weak or strong) verifiable secret sharing, the parties can easily verify whether the shares that the dealer opens are correct or not. Note, however, that the verification process involves the participation of the dealer since D(x, y) is shared using only weak secret sharing. However, if something goes wrong, then the dealer is disqualified.
To check that \(D(0,0)=0\), the parties simply reconstruct the polynomial D(0, y). This is a polynomial of degree t, and it can be reconstructed (with the dealer’s help, as D is shared using a weak secret sharing scheme). Moreover, it does not reveal any information on the polynomials \(f_i^a(x),f_i^b(x), C_i(x,0)\): In the case of an honest dealer, the adversary already holds t shares on the polynomial D(0, y) and it always holds that \(D(0,0)=0\), since the dealer is honest.
2.3 Extensions
Our zero-knowledge verification protocol allows the dealer to prove that its shares of a, b, c satisfy the relation \(c=ab\). The cost of the protocol is proportional to a constant number of VSSs. We show an extension of the protocol allowing a dealer to prove that its shares of \((x_1,\ldots ,x_L), (y_1,\ldots ,y_M)\) satisfy \((y_1,\ldots ,y_M)=G(x_1,\ldots ,x_L)\), where G is any circuit of multiplication depth 1 (i.e., a degree-2 polynomial). The communication complexity of the protocol is \(O(L+M)\) VSSs and not O(|G|) VSSs (where |G| is the number of multiplication gates in the circuit G). This allows computing the circuit in a layer-by-layer fashion and not gate-by-gate and leads to sub-linear communication complexity for circuits where \(|G| \in \omega (L+M)\).
2.4 Organization
The rest of the paper is organized as follows. In Sect. 3, we provide preliminaries and definitions. In Sect. 4, we cover our weak verifiable secret sharing, strong verifiable secret sharing, and some extensions. Our multiplication protocol (with a dealer) is provided in Sect. 5 and its generalization to arbitrary gates with multiplicative depth 1 is given in Sect. 6. In “Appendix A,” we overview how the dealer is removed and how to compute a general function, following the BGW approach.
3 Preliminaries
Notations We denote \(\{1,\ldots ,n\}\) by [n]. We denote the number of parties by n and a bound on the number of corrupted parties by t. Two random variables X and Y are identically distributed, denoted by \(X \equiv Y\), if for every z it holds that \(\Pr [X=z]=\Pr [Y=z]\). Two parametrized distributions \({{\mathcal {D}}}_1=\{{{\mathcal {D}}}_1(a)\}_{a}\) and \({{\mathcal {D}}}_2 = \{{{\mathcal {D}}}_2(a)\}_a\) are said to be identically distributed, if for every a the two random variables \((a,\mathcal{D}_1(a)), (a, {{\mathcal {D}}}_2(a))\) are identically distributed.
3.1 Definitions of Perfect Security in the Presence of Malicious Adversaries
We follow the standard, stand-alone simulation-based security of multiparty computation in the perfect settings [3, 12, 30]. Let \(f:({\{0,1\}}^*)^n \rightarrow ({\{0,1\}}^*)^n\) be an n-party functionality and let \(\pi \) be an n-party protocol over ideal (i.e., authenticated and private) point-to-point channels and an authenticated broadcast channel. Let the adversary, \({{\mathcal {A}}}\), be an arbitrary machine with auxiliary input z, and let \(I \subset [n]\) be the set of corrupted parties controlled by \({{\mathcal {A}}}\). We define the real and ideal executions:
-
The real execution In the real model, the parties run the protocol \(\pi \) where the adversary \({{\mathcal {A}}}\) controls the parties in I. The adversary is assumed to be rushing, meaning that in every round it can see the messages sent by the honest parties to the corrupted parties before it determines the message sent by the corrupted parties. The adversary cannot see the messages sent between honest parties on the point-to-point channels. We denote by
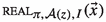 the random variable consisting of the view of the adversary \({{\mathcal {A}}}\) in the execution (consisting of all the initial inputs of the corrupted parties, their randomness, and all messages they received), together with the output of all honest parties.
the random variable consisting of the view of the adversary \({{\mathcal {A}}}\) in the execution (consisting of all the initial inputs of the corrupted parties, their randomness, and all messages they received), together with the output of all honest parties. -
The ideal execution The ideal model consists of all honest parties, a trusted party, and an ideal adversary \(\mathcal{SIM}\), controlling the same set of corrupted parties I. The honest parties send their inputs to the trusted party. The ideal adversary \(\mathcal{SIM}\) receives the auxiliary input z and sees the inputs of the corrupted parties. \(\mathcal{SIM}\) can substitute any \(x_i\) with any \(x_i'\) of its choice (for the corrupted parties) under the condition that \(|x_i'|=|x_i|\). Once the trusted party receives (possibly modified) inputs \((x_1',\ldots ,x_n')\) from all parties, it computes \((y_1,\ldots ,y_n) = {f(x'_1,\ldots ,x'_n)}\) and sends \(y_i\) to \(P_i\). The output of the ideal execution, denoted as
 is the output of all honest parties and the output of the ideal adversary \(\mathcal{SIM}\).
is the output of all honest parties and the output of the ideal adversary \(\mathcal{SIM}\).
Definition 3.1
Let f and \(\pi \) be as above. We say that \(\pi \) is t-secure for f if for every adversary \({{\mathcal {A}}}\) in the real world, there exists an adversary \(\mathcal{SIM}\) with comparable complexity to \({{\mathcal {A}}}\) in the ideal model, such that for every \(I \subset [n]\) of cardinality at most t it holds that

where \(\vec {x}\) is chosen from \(({\{0,1\}}^*)^n\) such that \(|x_1|=\ldots =|x_n|\).
Corruption-aware functionalities The functionalities that we consider are corruption-aware, namely, the functionality receives the set I of corrupted parties. We refer the reader to [3, Section 6.2] for further discussion and the necessity of this modeling when proving security.
Reactive functionalities, composition, and hybrid-world We also consider more general functionalities where the computation takes place in stages, where the trusted party can communicate with the ideal adversary (and sometimes also with the honest parties) in several stages, to obtain new inputs and send outputs in phases. See [30, Section 7.7.1.3].
The sequential modular composition theorem is an important tool for analyzing the security of a protocol in a modular way. Assume that \(\pi _f\) is a protocol that securely computes a function f that uses a subprotocol \(\pi _g\), which in return securely computes some functionality g. Instead of showing directly that \(\pi _f\) securely computes f, one can consider a protocol \(\pi _f^g\) that does not use the subprotocol \(\pi _g\) but instead uses a trusted party that ideally computes g (this is called a protocol for f in the g-hybrid model). Then, by showing that (1) \(\pi _g\) securely implements g, and; (2) \(\pi _f^g\) securely implements f, we obtain that the protocol \(\pi _f\) securely implements f in the plain model. See [12] for further discussion.
Remark 3.2
(Input assumption) Definition 3.1 requires that the ideal and real distributions are identical for any input of some specific size. We sometimes present functionalities and protocols that are defined only on some subset of inputs, or when the inputs are correlated. For instance, that the inputs of the honest parties are all points that lie on the same degree-t polynomial. To model it, i.e., defining the functionality and the protocol on all inputs while targeting only some promise on the inputs, we define that the functionality checks the input assumption (the promise), and in case it does not hold, then it sends the inputs of the honest parties to the adversary, and let the adversary singlehandedly determine all of the outputs of the honest parties. Any protocol can then be simulated relative to such functionality when the promise does not hold. This extends all our protocols and functionalities for general inputs.
3.2 Robust Secret Sharing
Let \(\mathbb {F}\) be a finite field of order greater than n, let \(\alpha _1,\ldots ,\alpha _n\) be any distinct nonzero elements from \(\mathbb {F}\) and denote \(\vec \alpha =(\alpha _1,\ldots ,\alpha _n)\). For a polynomial q, denote \(\mathsf{Eval}_{\vec \alpha }(q)=(q(\alpha _1),\ldots ,q(\alpha _n))\). The Shamir’s \(t+1\) out of n sharing scheme [42] consists of two procedures \(\mathsf{Share}\) and \(\mathsf{Reconstruct}\) as follows:
-
\(\mathsf{Share}(s)\). The algorithm is given \(s\in \mathbb {F}\), then it chooses t independent uniformly random elements from \(\mathbb {F}\), denoted \(q_1,\ldots ,q_t\), and defines the polynomial \(q(x)=s+\sum _{i=1}^t q_i x^i\). Finally, it outputs \(\mathsf{Eval}_{\vec \alpha }(q)=(q(\alpha _1),\ldots ,q(\alpha _n))\). Define \(s_i=q(\alpha _i)\) as the share of party \(P_i\).
-
\(\mathsf{Reconstruct}(\vec {s})\). For a set \(J \subseteq [n]\) of cardinality at least \(t+1\), let \(\vec {s} = \{s_i\}_{i \in J}\). Then, the algorithm reconstructs the secret s.
Correctness requires that every secret can be reconstructed from the shares for every subset of shares of cardinality \(t+1\), and secrecy requires that every set of less than t shares is distributed uniformly in \(\mathbb {F}\). We refer to [3] for a formal definition.
Reed Solomon code Recall that a linear [n, k, d]-code over a field \(\mathbb {F}\) is a code of length n, dimension k, and distance d. That is, each codeword is a sequence of n field elements, there are in total \(|\mathbb {F}|^k\) different codewords, and the Hamming distance of any two codewords is at least d. Any possible corrupted codeword \({\hat{c}}\) can be corrected to the closest codeword c as long as \(d(c,{\hat{c}})< (d-1)/2\), where d(x, y) denotes the Hamming distance between the words \(x,y \in \mathbb {F}^n\).
In Reed Solomon code, let \(m = (m_0,\ldots ,m_t)\) be the message to be encoded, where each \(m_i \in \mathbb {F}\). The encoding of the message is essentially the evaluation of the degree-t polynomial \(p_m(x) = m_0+m_1x +\ldots +m_tx^t\) on some distinct nonzero field elements \(\alpha _1,\ldots ,\alpha _n\). That is, \(\mathsf{Encode}(m)=(p(\alpha _1),\ldots ,p(\alpha _n))\). The distance of this code is \(n-t\). This is because any two distinct polynomials of degree t can agree on at most t points. We have the following fact:
Fact 3.3
The Reed Solomon code is a linear \([n, t+1, n-t]\) code over \(\mathbb {F}\). In addition, there exists an efficient decoding algorithm that corrects up to \((n-t-1)/2\) errors. That is, for every \(m \in \mathbb {F}^{t+1}\) and every \(x \in \mathbb {F}^n\) such that \(d(x,C(m)) \le (n-t-1)/2\), the decoding algorithm returns m.
For the case of \(t < n/3\) we get that is possible to efficiently correct up to \((3t+1-t-1)/2 = t\) errors. Putting it differently, when sharing of a polynomial of degree t, if during the reconstruction t errors were introduced by corrupted parties, it is still possible to (efficiently) recover the correct value.
3.3 Bivariate Polynomial
We call a bivariate polynomial of degree q in x and degree t in y as (q, t)-bivariate polynomial. If \(q = t\) then we simply call the polynomial as degree-t bivariate polynomial. Such a polynomial can be written as follows:
Looking ahead, in our protocol, we will consider degree-t bivariate polynomials and degree (2t, t)-bivariate polynomials.
Claim 3.4
(Interpolation) Let t be a nonnegative integer, and let \(\alpha _1,\ldots ,\alpha _{t+1}\) be distinct elements in \(\mathbb {F}\), and let \(f_1(x),\ldots ,f_{t+1}(x)\) be \(t+1\) univariate polynomials of degree at most q. Then, there exists a unique (q, t)-bivariate polynomial S(x, y) such that for every \(k=1,\ldots ,t+1\):
Proof
Define the bivariate polynomial S(x, y) via the Lagrange interpolation:
(where the values of the j in the product are \(1 \le j \le t+1\) with \(j \ne i\)). It is easy to see that S(x, y) has a degree (q, t). Moreover, for every \(k=1,\ldots ,t+1\) it holds that \(S(x,\alpha _k)=f_k(x)\). It remains to show that S(x, y) is unique. Assume that there exist two different degree (q, t)-bivariate polynomials \(S_1(x,y)=S_2(x,y)\) that satisfy the conditions in the claim. Consider the polynomial \(R(x,y)=S_1(x,y)-S_2(x,y)\). Since \(S_1,S_2\) are two (q, t)-bivariate polynomial, R is also (q, t)-bivariate polynomial. Moreover, for every \(1 \le k \le t+1\) it holds that \(R(x,\alpha _k)=S_1(x,\alpha _k)-S_2(x,\alpha _k)=0\). As a result, for every \(\beta \in \mathbb {F}\), the degree-t univariate polynomial \(R(\beta ,y)\) is 0 on \(t+1\) points \(R(\beta ,\alpha _1),\ldots ,R(\beta ,\alpha _{t+1})\), and therefore \(R(\beta ,y)\) is the all-zero polynomial. This implies that for every \(\beta ,\gamma \in \mathbb {F}\) it holds that \(R(\beta ,\gamma )=0\), i.e., R(x, y) is the all-zero polynomial, and thus \(S_1(x,y)=S_2(x,y)\). \(\square \)
Symmetrically, one can interpolate the polynomial S(x, y) from a set of \(q+1\) polynomials \(g_i(y)\). The proof is similar to Claim 3.4.
Claim 3.5
(Interpolation) Let t be a nonnegative integer, and let \(\alpha _1,\ldots ,\alpha _{q+1}\) be distinct elements in \(\mathbb {F}\), and let \(g_1(y),\ldots ,g_{q+1}(y)\) be \(q+1\) univariate polynomials of degree at most t each. Then, there exists a unique (q, t)-bivariate polynomial S(x, y) such that for every \(k=1,\ldots ,q+1\):
Hiding The following is the “hiding” claim, showing that if a dealer wishes to share some polynomial h(x) of degree q, it can choose a random (q, t)-polynomial S(x, y) that satisfies \(S(x,0)=h(x)\) and give each party \(P_i\) the shares \(S(x,\alpha _i), S(\alpha _i,y)\). The adversary cannot learn any information about h besides \(\{h(\alpha _i)\}_{i \in I}\), when it corrupts the set \(I \subset [n]\). We prove the following two claims in “Appendix B.”
Claim 3.6
(Hiding I) Let h(x) be an arbitrary univariate polynomial of degree q, and let \(\alpha _1,\ldots ,\alpha _k\) with \(k\le t\) be arbitrary distinct nonzero points in \(\mathbb {F}\). Consider the following distribution \(\mathsf{Dist}(h)\):
-
Choose a random (q, t)-bivariate polynomial S(x, y) under the constraint that \(S(x,0) = h(x)\).
-
Output \(\{(i,S(x,\alpha _i),S(\alpha _i,y))\}_{i \in [k]}\).
Then, for every two arbitrary degree-q polynomials \(h_1(x),h_2(x)\) for which \(h_1(\alpha _i) = h_2(\alpha _i)\) for every \(i \in [k]\) it holds that \(\mathsf{Dist}(h_1) \equiv \mathsf{Dist}(h_2)\).
Claim 3.7
(Hiding II) Same as Claim 3.6, except that it holds that \(h_1(0)=h_2(0)=\beta \) for some publicly known \(\beta \in \mathbb {F}\). The output of the distribution is \(\{(i,S(x,\alpha _i),S(\alpha _i,y))\}_{i \in [k]} \cup \{S(0,y)\}\).
4 Weak Verifiable Secret Sharing and Extensions
In this section, we show how to adapt the verifiable secret sharing protocol of [9, 27] to allow weak secret sharing of a polynomial with a degree greater than t (but at most 2t). We start with a description of the verifiable secret sharing protocol and highlight the main differences for getting a weak verifiable secret sharing protocol (sometimes we may omit the “verifiable” and write only “weak secret sharing”). We formally define the functionality of weak verifiable secret sharing (WSS) in Sect. 4.2 and then strong verifiable secret sharing in Sect. 4.4. We write “strong” just to emphasize the difference from weak secret sharing; Our strong verifiable secret sharing is just a standard verifiable secret sharing.
As part of the protocol, parties vote and publicly announce (over the broadcast channel) whether they are happy with their shares. Thus, the set of parties that are happy with their shares is known to all parties. In our formalization of weak secret sharing, this is part of the output of all parties. Moreover, the shares of the parties that are happy with their shares uniquely define the polynomial. Thus, only parties that are happy with their shares will participate in the reconstruction. The output of WSS is a set K of all parties that are happy with their shares, where parties in \(k\in K\) also output the pair \(f_k(x),g_k(y)\), whereas parties \(i \not \in K\) just output \(g_i(y)\).
Recall that in the BGW protocol, after the parties verify the shares and obtain \(f_i(x),g_i(y)\), they project the bivariate shares to univariate shares by outputting \(f_i(0)\). As mentioned previously, we maintain bivariate sharing and output \((f_i(x),g_i(y))\).
4.1 Verifying Shares of a (q, t)-Bivariate Polynomial

In the optimistic case, when there are no cheats, the protocol ends at Step 3c and incurs a communication overhead of \(O(n^2)\) point-to-point messages and no broadcast. In the pessimistic (worst) case, however, there may be O(n) and \(O(n^2) \) complaints (broadcasts) in Steps 2a and 3b, respectively. Then, in step 4, there are O(n) messages of total size \(O(n^2)\) that are broadcasted by the dealer (i.e., in order to reveal the polynomials of at most t parties who placed their complaint). Finally, there are O(n) broadcasts of the message \(\mathsf{good}\) if the secret sharing is successfully verified. Overall, the pessimistic case incurs a communication overhead of \(O(n^2)\) point-to-point messages and \(O(n^2)\) broadcast messages.
4.2 Weak Verifiable Secret Sharing
In weak verifiable secret sharing, the dealer wishes to distribute shares to all parties and then allow reconstruction only if it takes part in the reconstruction. The result of the reconstruction can be either a unique, well-defined polynomial which was determined in the sharing phase or \(\bot \). The functionality is defined as follows.

Theorem 4.3
Let \(t < n/3\). Then, Protocol 4.1 when using the WSS branch is t-secure for the \(f_\mathsf{WSS}\) functionality (Functionality 4.10) in the presence of a static malicious adversary. The protocol incurs \(O(n^2)\) point-to-point messages in the optimistic case and additional \(O(n^2)\) broadcast messages in the pessimistic case.
Proof
Let \({{\mathcal {A}}}\) be an adversary in the real world. We have two cases, depending on whether the dealer is corrupted or not. We note that the protocol is deterministic, as well as the functionality.
Case 1: The Dealer is Honest In this case in the ideal execution, the honest dealer always holds a polynomial S(x, y) that is of degree (q, t). We describe the simulator \(\mathcal{SIM}\).
The simulator \(\mathcal{SIM}\)
-
1.
\(\mathcal{SIM}\) invokes the adversary \({{\mathcal {A}}}\) on the auxiliary input z.
-
2.
\(\mathcal{SIM}\) receives from the trusted party the polynomials of the corrupted parties, that is, \(f_i(x),g_i(y)\), and simulates the protocol execution for \({{\mathcal {A}}}\):
-
(a)
Sharing Simulate sending the shares \(f_i(x),g_i(y)\) to each \(P_i\), \(i \in I\), as coming from the dealer \(P_1\).
-
(b)
Initial checks Initialize \(R = \emptyset \). An honest party never broadcasts \(\mathsf{complaint}(i)\). If the adversary broadcast \(\mathsf{complaint}(i)\), then add i to R.
-
(c)
Exchange sub-shares send to the adversary \({{\mathcal {A}}}\) the shares \((g_i(\alpha _j),f_i(\alpha _j))\) from each honest party \(P_j\), for each corrupted party \(i \in I {\setminus } R\).
Receive from the adversary \({{\mathcal {A}}}\) the points \((u_{i,j},v_{i,j})\) that are supposed to be sent from \(P_i\) to \(P_j\), for \(i \in I {\setminus } R\) and \(j \not \in I\).
-
(d)
Broadcast complaints The simulator checks the points \((u_{i,j},v_{i,j})\) that the adversary sent in the previous step. If \(u_{i,j} \ne f_i(\alpha _j)\) or \(v_{i,j} \ne g_i(\alpha _j)\) then \(\mathcal{SIM}\) simulates a broadcast of \(\mathsf{complaint}(j,i,g_i(\alpha _j),f_i(\alpha _j))\) as coming from party \(P_j\).
Moreover, receive \(\mathsf{complaint}(\cdot ,\cdot ,\cdot ,\cdot )\) broadcast messages from the adversary.
If no \(\mathsf{complaint}\) message was broadcasted by any party, then send I to the trusted party (which results in sending \(K=[n]\) to all parties by the functionality), and halt.
-
(e)
Resolve complaints—the dealer The dealer never reveals the shares of honest parties. For every \(\mathsf{complaint}(i,j,u,v)\) message received from the adversary, check that \(u = f_i(\alpha _j)\) and \(v = g_i(\alpha _j)\). If not, then broadcast \(\mathsf{reveal}(i,g_i(y))\) as coming from the dealer, and add \(i \in R\). Moreover, if there was a \(\mathsf{complaint}(i)\) in the initial checks step (Step 2a), then broadcast \(\mathsf{reveal}(i,g_i(y))\).
-
(f)
Evaluate complaint resolutions Simulate all honest parties broadcast \(\mathsf{good}\). Let \(I'\) be the set of corrupted parties that broadcast \(\mathsf{good}\).
-
(a)
-
3.
The simulator sends \(I' {\setminus } R\) to the trusted party. \(\square \)
It is easy to see by inspection of the protocol, and by inspection of the simulation, and since the two are deterministic, that the view of the adversary in the real and ideal executions is equal. Our next goal is to show that the output of the honest parties is the same in the real and ideal executions.
Consider the optimistic case, where no \(\mathsf{reveal}(i)\) messages are broadcasted by the dealer, and there are no \(\mathsf{complaint}\) messages by any party. Then, in the real execution, the output of all honest parties is [n] and likewise, in the simulation, the simulator sends I to the trusted party, which then sends [n] to all parties. The outputs in the ideal and real executions are therefore the same.
We now consider cases where there are complaints and a vote. An honest party \(P_j\) broadcasts \(\mathsf{good}\) if all the following conditions are met:
-
1.
The polynomial \(f_j(x)\) has degree at most q, \(g_j(y)\) has degree at most t and \(f_j(\alpha _j) = g_j(\alpha _j)\). An honest party \(P_j\) therefore never broadcasts \(\mathsf{complaint}(j)\).
-
2.
While resolving complaints, the dealer never broadcasts \(\mathsf{reveal}(j)\).
-
3.
Each \(\mathsf{complaint}(k)\) message is replied by the dealer with \(\mathsf{reveal}(k,\cdot )\) message.
-
4.
All \(\mathsf{reveal}(i,g_i(y))\) messages broadcasted by the dealer satisfy \(f_j(\alpha _i) = g_i(\alpha _j)\).
-
5.
The dealer resolves all joint complaints (see Step 5c).
It is easy to see that all those conditions are met in the case of an honest dealer. In particular: (1) holds by the assumption on the inputs; (2) an honest party \(P_j\) broadcasts \(\mathsf{complaint}(j,i,f_j(\alpha _i),g_j(\alpha _i))\) in Step 3b according to the polynomials \(f_j(\cdot ),g_j(\cdot )\) it received from the dealer; As a result, according to the specification of the protocol, the dealer never broadcasts \(\mathsf{reveal}(j)\); (3) is true by inspection of the code of the dealer; (4) When the dealer broadcasts a polynomial it always agrees with \(f_j(x)\) that was initially given to \(P_j\); (5) By the dealer’s code specifications, it resolves all joint complaints.
Therefore, in the real execution all honest parties broadcast \(\mathsf{good}\), and some additional parties \(I' \subseteq I\) that the adversary controls might also broadcast \(\mathsf{good}\). Then, all honest parties exclude from this set the parties in R, and output it. Since the view of the adversary is equal in the ideal execution, the same parties in the simulated ideal execution broadcast \(\mathsf{good}\). Let \(I' \subseteq I\) be the set of corrupted parties that broadcast \(\mathsf{good}\). The simulator sends \(I'{\setminus } R\) to the trusted party, which then defines K to be \(([n]{\setminus } I) \cup (I'{\setminus } R)\), i.e., all honest parties and all corrupted parties that broadcast \(\mathsf{good}\), excluding those that are in R. Thus, the outputs of the honest parties in the real and ideal are identical.
Case 2: The dealer is corrupted In this case, the honest parties have no input to the protocol, and the protocol is deterministic. The simulator can therefore perfectly simulate the protocol execution, and the view of the adversary in the real and ideal executions is equal. Nevertheless, we have to extract what input the dealer provides to the trusted party, and show that the output of the honest parties in the real and ideal executions is equal. The simulator is as follows.
The simulator \(\mathcal{SIM}\)
-
1.
\(\mathcal{SIM}\) invokes the adversary \({{\mathcal {A}}}\) on the auxiliary input z.
-
2.
\(\mathcal{SIM}\) simulates the execution of Protocol 4.1 while simulating the honest parties (which have no inputs).
-
3.
Let \(j \not \in I\) be the index of an arbitrary honest party. From its output in the simulated execution, let \(K \subseteq [n]\) be the set of parties that broadcast \(\mathsf{good}\) in the simulated execution. Then,
-
(a)
Accept If \(|K| \ge 2t+1\) then let \(G \subset K {\setminus } I\) be the set of all honest parties that broadcast \(\mathsf{good}\), and let \(G_0 \subseteq G\) be the set of the lexicographically first \(t+1\) elements in G. Let S(x, y) be the uniqueFootnote 3 bivariate polynomial in degree q in x and degree t in y that satisfies \(f_j(x) = S(x,\alpha _j)\) and \(g_j(y) = S(\alpha _j,y)\) for all \(j \in G_0\). The simulator sends (S, K) to the trusted party.
-
(b)
Reject If the output in the simulated execution results in reject (i.e., \(|K| < 2t+1\)), then send \(S(x,y) = x^{2t+1}\) to the trusted party (causing to all parties to output \(\bot \) in the ideal execution).
-
(a)
As the simulator just runs the honest parties as in the real execution, the view of the adversary in the real and ideal executions is the same. We now show that the output of the honest parties in the ideal execution, as received by the trusted party, is the same as in the real execution. We consider two cases:
Case I—there exists an honest party that outputs \(\bot \) in the real execution In this case, we claim that all honest parties output \(\bot \) in the real execution. An honest party outputs \(\bot \) only if less than \(2t+1\) parties broadcast \(\mathsf{good}\). Since the vote messages are broadcasted, then all honest parties output \(\bot \). Since the real execution and the simulated executions are identical, also in the ideal execution all simulated honest parties will output \(\bot \). In this case, the simulator sends \(S(x,y)= x^{2t+1}\) to the trusted party, and the functionality \(F_\mathsf{WSS}\) in return rejects S and gives \(\bot \) to all honest parties.
Case II—no honest party outputs \( \bot \) in the real execution As a result, we have that at least \(2t+1\) parties broadcast \(\mathsf{good}\), and therefore there are at least \(t+1\) honest parties that broadcast \(\mathsf{good}\). Similarly to the case of an honest dealer, an honest party \(P_j\) broadcasts \(\mathsf{good}\) if and only if all of the following conditions are met:
-
1.
Its share \(f_j(x)\) has degree at most q, \(g_j(y)\) has degree at most t and \(f_j(\alpha _j) = g_j(\alpha _j)\).
-
2.
All \(\mathsf{complaint}(i)\) messages were resolved by the dealer, which broadcasts \(\mathsf{reveal}(i,g_i(y))\),
-
3.
The dealer resolved all joint complaints (see Step 5c),
-
4.
All messages \(\mathsf{reveal}(i,g_i(y))\) that the dealer broadcasts, it holds that \(j \ne i\), and that \(g_i(\alpha _j)=f_j(\alpha _i)\).
Now, consider the set \(G_0\) of the first \(t+1\) honest parties that broadcast \(\mathsf{good}\), and let G be the set of all honest parties broadcast \(\mathsf{good}\). For the set of polynomials \(f_k(x),g_k(y)\) with \(k \in G_0\), we can reconstruct the polynomial S(x, y) of degree q in x and degree t in y that satisfies \(f_k(x)= S(x,\alpha _k)\), see Claim 3.4. From the pairwise verification step, \(g_j(\alpha _k) = f_k(\alpha _j)=S(\alpha _j,\alpha _k)\) for every \(j,k \in G_0\), and thus the two degree-t univariate polynomials \(g_j(y)\) and \(S(\alpha _j,y)\) agree on \(t+1\) points. Thus, \(g_j(y)=S(\alpha _j,y)\) for every \(j \in G_0\).
We claim that for all other honest parties \(H {\mathop {=}\limits ^\mathrm{def}}[n] {\setminus } (I \cup G_0)\), the polynomial \(g_j(y)\), either the one that was used by \(P_j\) as an input to the interaction (Steps 2 and 3), or was revealed by the dealer (Step 4), satisfies \(g_j(y) = S(\alpha _j,y)\). We separate the cases where \(g_j(y)\) was publicly revealed or not:
-
1.
If \(g_j(y)\) was publicly revealed, then it must be of degree at most t, and for all \(k \in G_0\) it holds that \(f_k(\alpha _j) = g_j(\alpha _k)\), as follows from Step 5d. In particular, if this does not hold, then the honest party \(P_k\) would have not broadcast \(\mathsf{good}\).
-
2.
If \(g_j(y)\) was not publicly revealed, then it must be that \(g_j(\alpha _k) = f_k(\alpha _j)\) for all \(k \in G_0\) as well. Otherwise, since both \(P_j\) and \(P_k\) are honest, during the exchange sub-shares phase both parties would have broadcast \(\mathsf{complaint}(j,k,\ldots ),\mathsf{complaint}(k,j,\ldots )\), and the dealer then must broadcast either \(\mathsf{reveal}(j)\) or \(\mathsf{reveal}(k)\). In the former case, the polynomial \(g_j(y)\) is publicly revealed. In the latter case, \(P_k\) would have not broadcast \(\mathsf{good}\). In both cases, we get a contradiction and conclude that \(g_j(\alpha _k) = f_k(\alpha _j)\) for all \(k \in G_0\).
Since \(|G_0| = t+1\), it holds that the two polynomials \(g_j(y)\) and \(S(\alpha _j,y)\) agree on \(t+1\) points. Since both \(g_j(y)\) and \(S(\alpha _j,y)\) are both of degree t, it holds that \(g_j(y)=S(\alpha _j,y)\). Moreover, we now claim that for all other honest parties \(j \in G {\setminus } G_1\) that broadcast \(\mathsf{good}\), it holds that \(f_j(x) = S(x, \alpha _j)\). Since \(P_j\) broadcast \(\mathsf{good}\) it must hold that \(f_j(\alpha _k) = g_k(\alpha _j)\) for all honest parties \(k \in [n]{\setminus } I\), where \(g_k(y)\) might be the original input of \(P_k\) or was revealed by the dealer later in the protocol. This follows from similar reasoning as above, and from the fact that all those parties broadcast \(\mathsf{good}\). As those define \(2t+1\) points, it holds that \(f_j(\alpha _k) = g_k(\alpha _j) = S(\alpha _k, \alpha _j)\) for every \(k \in [n]{\setminus } I\), and thus \(f_j(x) = S(x, \alpha _j)\).
In the ideal execution, the simulator first reconstructs S(x, y) using the parties in \(G_0\), and then sends S to the trusted party together with K. The trusted party then checks that S is of the degree at most (q, t). Note that when the simulator sends a polynomial S(x, y) and a set K to the trusted party, then:
-
1.
S(x, y) is of degree at most (q, t) from the way the simulator reconstructed S;
-
2.
We already saw that for every \(j \in K {\setminus } I\) it holds that \(S(x,\alpha _i) = f_i(x)\) and \(S(\alpha _i,y) = g_i(y)\).
The trusted party then gives K to all honest parties, and each honest party \(k \in K\) receives \(S(x,\alpha _k), S(\alpha _k,y)\), and all honest parties \(j \not \in K\) outputs \(S(\alpha _k,y)\). This is exactly the same output as the simulated honest parties in the simulated execution, which is identical to the output of the honest parties in the real execution. \(\square \)
4.3 Evaluation with the Help of the Dealer
We show how the parties can recover the secret polynomial using the help of the dealer. Toward this end, we show how the parties can evaluate polynomial \(g_\beta (y)\) for every \(\beta \in E\), where E is a set of elements in \(\mathbb {F}\). By taking E to be of cardinality \(q+1\), it is possible to completely recover S (see Claim 3.5). When we are only interested in the constant term of S, we take \(E = \{0\}\) to obtain \(g(y) = S(0,y)\) and then output g(0). Looking ahead, in Protocol 5.2, in the optimistic case, we will use just \(E = \{0\}\). In the pessimistic case, E will contain some other indices of parties that raised a complaint against the dealer.
The polynomials can be reconstructed with the help of the dealer.Footnote 4 This is what makes this sharing weak. When \(q \le t\), we can achieve (strong) verifiable secret sharing, in which reconstruction is guaranteed, and the adversary cannot lead to the reconstruction of \(\bot \) once the sharing phase is successful.


We will consider an alternative protocol in the optimistic case in which \(K=[n]\), which does not use broadcast. See Remark 4.7.
Theorem 4.6
Let \(t < n/3\). Protocol 4.5 is t-secure for the \({F_\mathsf{WEval}}\) functionality (Functionality 4.4) in the presence of a static malicious adversary. The protocol incurs \(O(n\cdot |E|)\) broadcast field elements.
Proof
The dealer broadcasts |E| polynomials, each of degree \(t \in O(n)\). Each party broadcasts (or not) \(\mathsf{good}\), and therefore there are \(O(n |E| + n)\) broadcasts.
We again discuss the case of honest and corrupted dealers separately.
The case of an honest dealer In the case of an honest dealer, by the input guarantees, we have that K includes all indices of all honest parties. We describe the simulator \(\mathcal{SIM}\):
-
1.
\(\mathcal{SIM}\) invokes \({{\mathcal {A}}}\) on the auxiliary input z.
-
2.
\(\mathcal{SIM}\) receives from the trusted party the polynomials \(S(x,\alpha _i),S(\alpha _i,y)\) for every \(i \in I\), the set E and all polynomials \(S(\beta ,y)\) for every \(\beta \in E\).
-
3.
\(\mathcal{SIM}\) simulates the dealer broadcasting the set \(\{S(\beta ,y)\}_{\beta \in E}\) and all honest parties broadcasting \(\mathsf{good}\).
The view of the adversary is deterministic, and it is easy to see that the adversary’s view is identical in the real and ideal executions. Moreover, as the adversary has no input to the functionality in the ideal world, the output of the honest parties in the ideal execution is always \(\{S(\beta ,y)\}_{\beta \in E}\). In the real world, from the input assumption, all the shares of the honest parties lie on the polynomial S(x, y), and all honest parties are part of the set K. Therefore, all honest parties always broadcast \(\mathsf{good}\), and the output of all honest parties is \(\{S(\beta ,y)\}_{\beta \in E}\).
The case of a corrupted dealer
-
1.
\(\mathcal{SIM}\) invokes \({{\mathcal {A}}}\) on the auxiliary input z.
-
2.
\(\mathcal{SIM}\) receives from the trusted party the polynomial S(x, y), and the sets K, E, and simulates an execution of the protocol where the input of each honest party for \(j \in K\) is \(S(x,\alpha _j),K,E\) and for every \(j \not \in K\) the input is K, E.
-
3.
If the output of the simulated honest parties is \(\bot \), then send \(\bot \) to the trusted party. Otherwise, send \(\mathsf{ok}\) to the trusted party.
From our assumption over the inputs, all honest parties hold the same sets K, E and all honest parties in K hold shares of a (q, t)-bivariate polynomial S(x, y). The ideal functionality first reconstructs this polynomial and then sends it to the ideal adversary. Thus, the inputs of the simulated honest parties in the ideal execution are identical to the inputs of the honest parties in the real execution, and thus the view of the adversary is identical in both executions. We now show that the outputs of the honest parties in the real and ideal executions are identical as well.
Clearly, since all messages in the protocol are broadcasted, the view of all honest parties is the same and therefore the output of all honest parties is the same. There are two cases to consider:
Case I If the output of the honest parties in the real execution is \(\bot \), then the output of the simulated honest parties in the ideal execution is \(\bot \) as well. The simulator sends \(\bot \) to the trusted party, and the output of the honest parties in the ideal execution is \(\bot \).
Case II Otherwise, there must be at least \(2t+1\) parties in K that broadcast \(\mathsf{good}\) in Step 2. Let \(K'\) be the set of honest parties in K that broadcast \(\mathsf{good}\). It must hold that \(|K'| \ge t+1\). Moreover, from our assumption on the input, there is a unique (q, t)-bivariate polynomial S(x, y) that is defined by the shares of the honest parties in K (and also by the parties in \(K'\)). Each polynomial \(g_\beta (y)\) for \(\beta \in E\) broadcasted by the dealer is of degree t and satisfies \(g_\beta (\alpha _j)=f_j(\beta )\) for every \(j \in K'\). This completely determines the polynomial \(g_\beta (y)\), and thus it must hold that \(S(\beta ,y) = g_\beta (y)\). \(\square \)
Remark 4.7
(On the optimistic case of Protocol 4.5) In the optimistic case, we can implement Protocol 4.5 without any broadcast messages and with \(O(n^2)\) field elements over the point-to-point channels. Specifically, in the optimistic case of the entire protocol (Protocol 5.2) we have that \(K=[n]\) and \(E=\{0\}\). Each party \(P_k\) can send on the point-to-point channel to every other party \(P_j\) the message \(f_k(0)\). Then, each party \(P_j\) uses the Reed Solomon decoding procedure to obtain the unique degree-t polynomial \(g_0(y)\) satisfying \(g_0(\alpha _k)=\gamma _k\) for at least \(2t+1\) indices \(k \in K\), where \(\gamma _k\) is the point received from party \(P_k\). Since there are \(2t+1\) honest parties in K, and since S(0, y) is guaranteed to be a polynomial of degree t, reconstruction works.
4.4 Strong Verifiable Secret Sharing
We provide the functionality for strong verifiable secret sharing, and prove its security. The protocol is Protocol 4.1 when using the VSS branch and with \(q=t\). The main difference from [3] is that the output is the two univariate polynomials and not the projection to univariate sharing, and we, therefore, provide proof for completeness.

Theorem 4.9
Let \(t < n/3\). Then, Protocol 4.1 when using the VSS branch and with \(q=t\) is t-secure for the \(f_\mathsf{VSS}\) functionality (Functionality 4.8) in the presence of a static malicious adversary. The protocol incurs \(O(n^2)\) field elements in the point-to-point channels in the optimistic case and additional \(O(n^2)\) field elements over the broadcast channel in the pessimistic case.
Proof
We again consider the case of a corrupted dealer and an honest dealer.
The dealer is honest In this case, we follow the case of an honest dealer in Theorem 4.3, while just making the necessary changes in the simulator as the difference between WSS and VSS in the protocol. Moreover, the simulator does not send \(I' \subseteq R\) to the trusted party at Step 3 in the simulation, and instead sends nothing. Clearly, the views in the real and ideal executions are equal, and the outputs of the honest parties in the real execution are the polynomials received by the honest dealer, exactly as in the ideal execution.
The dealer is corrupted We follow the same simulation strategy as in Theorem 4.3, but with the following Step 3:
Step 3: Let \((f_j(x),g_j(y))\) be the output of some arbitrary honest party \(P_j\)
- 1.
Accept: If at least \(2t+1\) parties broadcast \(\mathsf{good}\) in the simulated execution, the let \(G_0\) be the set of the first \(t+1\) honest parties. Let S(x, y) be the unique bivariate polynomial in degree t that satisfies \(f_j(x) = S(x,\alpha _j)\) for all \(j \in G_0\). The simulator sends S to the trusted party.
- 2.
Reject: Same as in Theorem 4.3.
Showing the outputs of ideal and real executions are identical also follows from Theorem 4.3.
In the simulation, we defined a polynomial S(x, y) according to the \(f_j(x)\) shares in the output of the simulated honest parties for some set \(G_0\). That is, for every \(j \in G_0\) it holds that \(f_j(x) = S(x,\alpha _j)\), by the definition of the polynomial S(x, y). We claim that also for every \(j \in G_0\) it holds that \(S(\alpha _j,y) = g_j(y)\). Clearly, since all parties in \(G_0\) broadcast \(\mathsf{good}\), we have for every pair \(j,k \in G\) that \(g_j(\alpha _k) = f_k(\alpha _j) = S(\alpha _k,\alpha _j)\), as otherwise those parties would have complain on each other and the dealer must have opened one of them. This implies that \(g_j(y)\) equals to \(S(\alpha _j,y)\) on \(t+1\) points, and since those are two polynomials of degree t, it must hold that \(g_j(y) = S(\alpha _j,y)\).
Now, we claim that for all other honest parties \(H {\mathop {=}\limits ^\mathrm{def}}[n]{\setminus } (I \cup G_0)\), the polynomials \(f_j(x),g_j(y)\) outputted by the simulated honest parties satisfy \(f_j(x) = S(x,\alpha _j)\) and \(g_j(y) = S(\alpha _j,y)\). Clearly, \(g_j(y)\) holds from similar reasoning as in Theorem 4.3, where for \(f_j(x)\) we can apply the same argument in a symmetric way: If \(f_j(x)\) was publicly revealed then it must agree with the \(g_k(y)\) for \(k \in G_0\), which determines the polynomial, that is, \(f_j(x) = S(x,\alpha _j)\) since the two polynomials agree on \(t+1\) points. If \(f_j(x)\) was not publicly revealed, then it also agrees with \(t+1\) points as part of the pairwise checks, again guaranteeing that \(f_j(x) = S(x,\alpha _j)\).
In the real execution, the honest parties just output \(f_i(x),g_i(y)\) and we just saw that all lie on the same polynomial S(x, y). In the ideal execution, the simulator reconstructs S(x, y), sends it to the trusted party, and each party \(P_j\) receives \(S(x,\alpha _j),S(\alpha _j,y)\). We just showed that for every \(j \not \in I\) it holds that \(S(x,\alpha _j) = f_j(x)\) and \(S(\alpha _j,y) = g_j(y)\).
\(\square \)
4.4.1 Evaluation
Once a polynomial was shared using strong VSS, reconstruction is always guaranteed. Moreover, the parties can also evaluate the polynomial on any value \(\beta \in \mathbb {F}\) to obtain \(S(x,\beta ),S(\beta ,y)\) without the help of the dealer (each party can provide \(f_j(\beta ), g_j(\beta )\) and the parties can use Reed Solomon decoding to obtain \(S(x,\beta ), S(\beta ,y)\)).
Nevertheless, for our purposes, whenever we need to evaluate a polynomial that was shared using VSS, we can use the weaker functionality in which the evaluation uses the help of the dealer. Therefore, we use Functionality 4.4 to evaluate points on the polynomial with the help of the dealer. Note that in this case we have that \(q=t\), and the parties use \(K = [n]\). Note that K might be different from the set of parties that broadcast \(\mathsf{good}\) when the polynomial was shared. However, since all honest parties hold shares \((f_j(x),g_j(y))\) it is safe to use \(K=[n]\). Thus, evaluating the points of E on a polynomial that was shared with VSS can be implemented using O(n|E|) field elements broadcasted, as in Theorem 4.6.
4.5 Extending Univariate Sharing to Bivariate Sharing with a Dealer
Sometimes each party \(P_i\) holds a share \(h(\alpha _i)\) of some univariate degree-t polynomial h(x). The following functionality allows a dealer, who holds h, to distribute shares of a bivariate polynomial S(x, y) satisfying \(S(x,0) = h(x)\). The protocol is very simple, demonstrating the advantage for working with bivariate sharing. This is the functionality \({\tilde{F}}_{extend}\) from [4]:


The communication cost of the protocol is the same as Protocol 4.1 for VSS. In the optimistic case, there are no complaints, and thus there are no additional broadcast messages.
Theorem 4.12
Let \(t < n/3\). Then, Protocol 4.11 is t-secure for the \({F_\mathsf{Extend}}\) functionality (Functionality 4.10) in the presence of a static malicious adversary, in the \({F_{VSS}}\)-hybrid model. The protocol incurs \(O(n^2)\) point-to-point messages in the optimistic case and additional \(O(n^2)\) broadcast messages in the pessimistic case.
Proof
We separate the cases of an honest dealer and a corrupted dealer.
The case of an honest dealer In this case, it always holds that \(S(x,0) = h(x)\). Therefore, in the ideal execution each honest party outputs \(S(x,\alpha _j),S(\alpha _j,y)\) for every \(j \not \in I\). The simulator receives all points \((S(x,\alpha _i),S(\alpha _i,y))\) from the trusted party and sends them to the adversary as being received from the \({F_{VSS}}\) functionality. Moreover, no honest party broadcast \(\mathsf{complaint}(\cdot )\). Clearly, the adversary’s view is identical in the real and ideal executions. Moreover, in the ideal execution, each honest party \(P_j\) for \(j \not \in I\) always outputs \((f_j(x),g_j(y))\), as received from the trusted party. In the real execution, no honest party complains, and the adversary can broadcast at most t complaints. In that case, the honest parties accept the dealer’s shares, and the outputs are identical to the ideal execution.
The case of a corrupted dealer The simulator receives h(x) from the trusted party. It then receives the polynomial S(x, y) that the adversary sends to the \({F_{VSS}}\) functionality. If S(x, y) is not of degree t, then it just replies with \(\bot \) and sends \(\bot \) to the trusted party. If S(x, y) is of degree t, then for every \(j \not \in I\) it checks that \(S(\alpha _j,0) = h(\alpha _j)\) (which is defined to be also \(g_j(0)\)), and if not, it simulates \(P_j\) broadcasting \(\mathsf{complaint}(j)\). It also listens to the complaints coming from the corrupted parties. If there were more than t broadcasts, then it sends \(\bot \) to the trusted party, and otherwise, it sends S(x, y).
Clearly, the view of the adversary is identical between the real and ideal. To show that the outputs of the honest parties are the same between the two executions, we only have to show why if there are less than t complaints in the simulated execution (i.e., when the simulated honest parties output \(f_j(x),g_j(y)\)) then it holds that \(S(x,0) = h(x)\) and thus the trusted party will deliver to each honest party the polynomials \(S(x,\alpha _j),S(\alpha _j,y)\). Clearly, if less than t parties broadcast \(\mathsf{complaint}\), then for \(t+1\) honest parties it holds that \(u_j=g_j(0)\). Since \(g_j(y)\) was obtained from \({F_{VSS}}\), and from our input assumption that all \(u_j\)’s lie on a polynomial of degree t, the two degree-t univariate polynomials S(x, 0) and h(x) agree on \(t+1\) points and therefore must be identical. \(\square \)
5 Multiplication with a Constant Number of VSSs and WSSs
We now turn to the multiplication protocol. The multiplication protocol reduces multiplication with no dealer to multiplication with a dealer, i.e., when one dealer holds two univariate polynomials \(f^a(x),f^b(x)\), each party holds a share on those polynomials, and the dealer wishes to distribute a polynomial C(x, y) of degree t in both variables in which \(C(0,0) = f^a(0)\cdot f^b(0)\). We refer the reader to “Appendix A” to see how this functionality suffices to compute any multiplication gate (i.e., when there is no dealer). In Sect. 5.1, we show the functionality of this building block, in Sect. 5.2 we show the protocol that realizes it.
5.1 Functionality—Multiplication with a Dealer

5.2 The Protocol
As mentioned in the technical overview, in our protocol the dealer distributes C(x, y) using verifiable secret sharing. Moreover, the dealer also distributes a random (2t, t)-polynomial D(x, y) under the constraint that \(D(x,0)= f^a(x)\cdot f^b(x)-C(x,0)\). The parties then verify that: (1) It holds that \(D(x,0)= f^a(x)\cdot f^b(x)-C(x,0)\); and (2) \(D(0,0) = 0\).
To verify that D(x, y) indeed satisfies that \(D(x,0)= f^a(x)\cdot f^b(x)-C(x,0)\), each party \(P_i\) verifies that \(D(\alpha _i,0)= f^a(\alpha _i)\cdot f^b(\alpha _i)-C(\alpha _i,0)\) using the shares it received from \(P_1\). If the verification fails, it broadcasts a complaint and all parties reconstruct the shares of \(P_i\). Since all polynomials are verifiably shared, it is possible to verify whether the complaint is justified. If the complaint is justified, then the dealer is disqualified. Moreover, if for all honest parties the verification holds, then it must be that the two degree-2t polynomials, D(x, 0) and \(f^a(x)\cdot f^b(x)-C(x,0)\) are equal, as they agree on \(2t+1\) points.
To verify that \(D(0,0)=0\), the parties publicly reconstruct the polynomial D(0, y) and check its constant term. Note that D(0, y) does not reveal any information on C(x, y), nor on \(f^a(x),f^b(x)\), besides the fact that \(C(0,0)=f^a(0)\cdot f^b(0)\) if indeed \(D(0,0)=0\).

The communication cost of the entire sharing phase (Step 1) is a constant number of invocations of VSS/WSS, since it calls to \({F_{VSS}}\) for C and \({F_{WSS}}\) for D. In Step 2 in the optimistic case we have no complaints, no complaint resolution is required, and therefore, there is no communication cost.
In the pessimistic case, the size of E may be O(n) in the worst case. This leads to two more invocations of VSS (of A and B, as part of \({F_\mathsf{Extend}})\) in Step 3. Moreover, the parties reconstruct \(O(n \cdot |E|)=O(n^2)\) field elements over the broadcast channel. In total, Step 3 results in communication overhead of \(O(n^2)\) over the point-to-point channels and \(O(n^2)\) over the broadcast channel in the pessimistic case.
Finally, in Step 4 there is a reconstruction of D(0, y). In the optimistic case, this can be done using \(O(n^2)\) words over the point-to-point channels and no broadcast (see Remark 4.5). In the pessimistic case, this requires a broadcast of O(n) field elements. Step 5b results in \(O(n^2)\) field elements over the point-to-point channels and no broadcast.
Overall, the optimistic case incurs a communication overhead of \(O(n^2)\) over the point-to-point channels, and the pessimistic case incurs an additional communication overhead of \(O(n^2)\) over the broadcast channel.
Theorem 5.3
Let \(t < n/3\). Then, Protocol 5.2 is t-secure for the \(F_{VSS}^{mult}\) functionality in the presence of a static malicious adversary, in the \(({F_{VSS}},{F_{WSS}},{F_\mathsf{Extend}},{F_\mathsf{WEval}})\)-hybrid model. The optimistic case incurs \(O(n^2)\) point-to-point field elements, and the pessimistic case incurs additional \(O(n^2)\) broadcast messages of field elements.
Proof
We again consider separately the case when the dealer is honest and when the dealer is corrupted.
Case 1—the dealer is honest We now describe the simulator \(\mathcal{SIM}\):
-
1.
\(\mathcal{SIM}\) invokes \({{\mathcal {A}}}\) on an auxiliary input z.
-
2.
\(\mathcal{SIM}\) receives from the trusted party all points \(f^a(\alpha _i),f^b(\alpha _i)\) and the polynomials \(C(x,\alpha _i),C(\alpha _i,y)\), for every \(i \in I\).
-
3.
\(\mathcal{SIM}\) simulates the view of the adversary \({{\mathcal {A}}}\) in the protocol:
-
(a)
It simulates the parties invoking \({F_{VSS}}\) with \(P_1\) as a dealer where the output of each corrupted \(P_i\) is \(C(x,\alpha _i), C(\alpha _i,y)\).
-
(b)
The simulator fixes a univariate polynomial d(x) of degree 2t arbitrarily, such that for every \(i \in I\) it holds that \(d(\alpha _i) = f^a(\alpha _i)\cdot f^b(\alpha _i)-C(\alpha _i,0)\) and \(d(0)=0\).
-
(c)
The simulator chooses a random (2t, t)-bivariate polynomial D(x, y) under the constraint that \(D(x,0)=d(x)\). Then, it gives to each party \(P_i\) the shares \(D(x,\alpha _i),D(\alpha _i,y)\) as coming from the \({F_{WSS}}\) functionality. It receives back a set \(I' \subseteq I\), defines \(K = ([n]{\setminus } I) \cup I'\) and sends K to the adversary.
-
(d)
An honest party never complains. If the adversary complains in the name of some corrupted party \(P_i\), then let R be the set of all complaining parties and define E accordingly.
-
i.
\(\mathcal{SIM}\) chooses a random polynomial A(x, y) satisfying \(A(\alpha _i,0) = f^a(\alpha _i)\) for every \(i \in I\), and a random polynomial B(x, y) satisfying \(B(\alpha _i,0) = f^b(\alpha _i)\) for every \(i \in I\).
-
ii.
It simulates the parties invoking the \({F_\mathsf{Extend}}\) functionality twice, where the output of each corrupted party \(P_i\) is \(A(x,\alpha _i),A(\alpha _i,y)\) in the first execution, and \(B(x,\alpha _i),B(\alpha _i,y)\) in the second execution.
-
iii.
It simulates the reconstruction of \(A(\alpha _i,y)\), \(B(\alpha _i,y)\) and \(C(\alpha _i,y)\) for every \(i \in R\) as coming from \({F_\mathsf{WEval}}\).
-
iv.
Simulate the reconstruction of \(D(\alpha _i,y)\) for every \(i \in R\) as coming from \({F_\mathsf{WEval}}\).
-
i.
-
(e)
Simulate the reconstruction of D(0, y) as an output of \({F_\mathsf{WEval}}\) and send it to the adversary.
-
(a)
We now show that the view of the adversary in the ideal execution and the output of the honest parties is identically distributed to the view of the adversary in the real execution and the output of the honest parties in the real execution. First, we show that the outputs are distributed identically. Then, we show that views are identically distributed conditioned on the outputs.
The output of the honest parties in the ideal execution is shares on a degree-t bivariate polynomial C. The polynomial is random under the constraint that \(C(0,0) = f^a(0)\cdot f^b(0)\). In the real execution, in Step 1a of the protocol, the dealer chooses a polynomial C exactly as the trusted party in the ideal execution. All parties receive shares on this polynomial as guaranteed by \({F_{VSS}}\). As follows from the description of \({F_\mathsf{WEval}}\), the honest parties always successfully reconstruct in the case of an honest dealer. Moreover, since the dealer chooses the polynomials C(x, y) and D(x, y) as described (and the polynomials A(x, y), B(x, y) if needed), all the verifications are guaranteed to hold and the corrupted parties cannot cause the honest parties to reject the dealer. In particular, an honest party never broadcast \(\mathsf{complaint}\). Moreover, every \(\mathsf{complaint}\) of a corrupted party results in opening shares that are already known to the adversary, and all satisfy the condition and do not result in reject. Thus, the outputs are identically distributed in the real and ideal executions.
We now fix the output of the honest parties, and show that the view of the adversary is identically distributed conditioned on the output. Fixing \(f^a(x),f^b(x),C(x,y)\), in the real execution the dealer chooses a polynomial D(x, y) of degree (2t, t) satisfying \(D(x,0) = f^a(x)\cdot f^b(x)-C(x,0)\). The view of the adversary is shares on the polynomial D(x, y). If the adversary falsely complains, then the dealer chooses also A(x, y) and B(x, y) at random such that \(A(x,0)= f^a(x)\) and \(B(x,0)=f^b(x)\).
In the ideal, we first choose an arbitrary polynomial d(x) that satisfies \(d(\alpha _i) = f^a(\alpha _i)\cdot f^b(\alpha _i)-C(\alpha _i,0)\) for every \(i \in I\), and then choose a random bivariate (2t, t)-polynomial \(D(x,0)=d(x)\). Following Claim 3.6, the distribution of the shares on such polynomial is identical. Moreover, if needed, we choose A(x, y) at random such that \(A(\alpha _i,0) = f^a(\alpha _i)\) and B(x, y) such that \(B(\alpha _i,0)=f^b(\alpha _i)\) for every \(i \in I\), which again has the same distribution from Claim 3.6.
We then claim that the \({F_\mathsf{WEval}}\) calls do not give any new information to the adversary. An honest party never complains, and thus the polynomials revealed as part of \({F_\mathsf{WEval}}\) reveal only shares that the adversary already knows and appear in its view. The revealing of the polynomial S(0, y) also does not give any new information, as shown in Claim 3.7. We therefore conclude that the views of both executions are distributed identically, conditioned on the outputs.
Case 2—corrupted dealer We describe the simulator \(\mathcal{SIM}\):
-
1.
The simulator invokes the adversary \({{\mathcal {A}}}\) on the auxiliary input z.
-
2.
The simulator receives the polynomials \(f^a(x),f^b(x)\) from the trusted party, and it simulates an execution of the protocol where the input of each honest party \(P_j\) is \(f^a(\alpha _j)\), \(f^b(\alpha _j)\) for every \(j \not \in I\), and simulates the ideal functionalities of \({F_\mathsf{WEval}}, {F_\mathsf{Extend}}, {F_{VSS}}, {F_{WSS}}\).
-
3.
If the output of the simulated honest parties in the execution is just \(f^a(0)\cdot f^b(0)\) then send \(C(x,y) = x^{2t+1}\) (causing the trusted party to reject the polynomial and send \(f^a(0)\cdot f^b(0)\) to all parties).
-
4.
Otherwise, let \(f^c_j(x),g^c_j(y)\) be the output of \(P_j\), for every \(j \not \in I\). Let \(G_0\) be the set of first \(t+1\) honest parties. Reconstruct the polynomial C(x, y) satisfying \(C(x,\alpha _j) = f_j^c(x)\) for every \(j \in G_0\), and send C(x, y) to the trusted party.
Clearly, the view of the adversary in the real and ideal executions is identical. Note that each party that is not the dealer is deterministic by the protocol specifications, that the simulator receives the inputs of the honest parties and therefore can perfectly simulate an execution of the protocol with the honest parties. We have to show that the output of the honest parties in both executions is the same, conditioned on the view of the adversary.
We have two cases to consider:
Reject Given a view of the adversary that results in reject, the simulator sends \(x^{2t+1}\) to the trusted party which, in return, sends \(f^a(0)\cdot f^b(0)\) to all parties. In the real execution, from the guarantee of \({F_{VSS}}, {F_{WSS}}, {F_\mathsf{Extend}}, {F_\mathsf{WEval}}\), if any honest party ever receive \(\bot \) in one of those executions then all honest parties receive \(\bot \), and all parties will proceed to Step 5b and reconstruct \(f^a(0)\cdot f^b(0)\). Moreover, if an honest party broadcast \(\mathsf{complaint}(i)\), then from the correctness of \({F_\mathsf{WEval}}\) it is guaranteed that its share will become public, and so all parties see that its complaint is justified, and all proceed to Step 5b and reconstruct \(f^a(0)\cdot f^b(0)\).
Accept Given a view of the adversary that results in accept, the simulator reconstructs a polynomial C(x, y) from the outputs of the first \(t+1\) honest parties and sends it to the trusted party. From the security of \({F_{VSS}}\), the shares that the honest parties output all lie on a degree-t bivariate polynomial. Therefore, clearly, all honest parties output shares on the same polynomial. The trusted party then checks that C(x, y) is of degree t (which is already guaranteed), and that \(C(0,0)=f^a(0)\cdot f^b(0)\) and if so send the shares on the polynomial C(x, y) to all honest parties in the ideal world. We now show that if the simulated honest parties accepted the shares then this must be the case.
Since the view does not result in reject, we claim that no honest party broadcast \(\mathsf{complaint}\). As we have seen, each complaint of an honest party must result in a rejection of the dealer. Since no honest party broadcasts a complaint, it must be that the dealer used D(x, y) satisfying \(D(x,0) = f^a(x)\cdot f^b(x)-C(x,0)\). This is because for \(2t+1\) points of honest parties \(\alpha _j\) it holds that \(D(\alpha _j,0) = f^a(\alpha _j)\cdot f^b(\alpha _j)-C(\alpha _j,0)\). The polynomial D(x, 0) is a univariate polynomial of degree 2t, and \(f^a(x)\cdot f^b(x)-C(x,0)\) is a univariate polynomial of degree 2t as well. They agree on \(2t+1\) points which implies that those two polynomials are identical.
From a similar reasoning, it holds that \(D(0,0)=0\). Specifically, parties reconstruct D(0, y) using \({F_\mathsf{WEval}}\). If \(D(0,0)\ne 0\), then the result is a view where all parties reject the dealer. We conclude that if all parties accepted the dealer then \(D(x,0)=f^a(x)\cdot f^b(x)-C(x,0)\) and \(D(0,0)=0\), which implies that \(f^a(0)\cdot f^b(0) = C(0,0)\). The simulator sends C(x, y) to the trusted party which performs this exact check, and then sends to each honest party its output \(C(x,\alpha _i),C(\alpha _i,y)\). We conclude that the outputs in the ideal and real execution are identical. \(\square \)
By combining Theorems 4.9, 4.3, 4.12, and 4.6 with Theorem 5.3, we obtain the following Corollary:
Corollary 5.4
Let \(t < n/3\). Then, there exists a protocol that is t-secure for the \(F_{VSS}^{mult}\) functionality in the presence of a static malicious adversary in the plain model.
6 Extension: Arbitrary Gates with Multiplicative Depth 1
We show how to extend the protocol in Sect. 5 to allow the dealer distributing any shares \(b_1,\ldots ,b_L\) given input shares \(a_1,\ldots ,a_M\) such that \((b_1,\ldots ,b_L) = G(a_1,\ldots ,a_M)\) where G is some circuit of multiplicative depth 1. Section 5 is a special case where \(a_1\cdot a_2 = G(a_1,a_2)\).

The protocol is similar to Protocol 5.2. Given such a circuit G with L outputs, we let \(G_1,\ldots ,G_L\) be the circuits that define each output. That is, for \((b_1,\ldots ,b_L) = G(a_1,\ldots ,a_m)\) we let \(b_\ell = G_\ell (a_1,\ldots ,a_m)\) for every \(\ell \in [L]\). In the protocol, the dealer distributes polynomials \(C_1(x,y),\ldots ,C_L(x,y)\) using VSS that are supposed to hide \(b_1,\ldots ,b_L\). Then, it defines L bivariate polynomials of degree(2t, t), \(D_1,\ldots ,D_L\) such that for every \(\ell \in [L]\) it holds that \(D_\ell (x,0) = G(f^{a_1}(x),\ldots ,f^{a_m}(x))-C_\ell (x,0)\). The dealer distributes them using \({F_{WSS}}\). The parties then check from the shares they received that each one of the polynomials \(C_1,\ldots ,C_L\) is correct, and that \(D_\ell (0,0)\) for every \(\ell \in [L]\). When a party \(P_i\) complains the parties open the shares of \(P_i\) and publicly verify the complaint.

Theorem 6.3
Let \(t< n/3\). Then, Protocol 5.2 is t-secure for the \(F_{VSS}^{G}\) functionality in the presence of a static malicious adversary, in the \(({F_{VSS}},{F_{WSS}},{F_\mathsf{Extend}},{F_\mathsf{WEval}})\)-hybrid model. The communication complexity of the protocol is just O(L) VSSs in the optimistic case. In the pessimistic case, it corresponds to \(O(L+M)\) VSSs.
Proof
The proof is similar to that of Theorem 5.3.
Honest dealer In case where the dealer is honest, observe that an honest dealer always chooses correct polynomials. The adversary receives from the trusted party the inputs and outputs of the corrupted parties and simulates the view of the adversary in a similar manner to the simulator in the proof of Theorem 5.3. In the real execution, the honest parties always accept the shares of the dealer. Clearly, the outputs of all honest parties have the same distribution in the ideal and real executions, as the honest dealer chooses \(C_1,\ldots ,C_L\) in a similar manner as the trusted party. The view of the adversary in the real and ideal executions is also identical, based on Claim 3.6. Moreover, if the adversary complains then it does not learn any new information as we just reveal its shares, i.e., information it already knows.
Corrupted dealer In the case where the dealer is corrupted, the simulator just receives from the trusted party all the inputs of the honest parties and can perfectly simulate the protocol execution. It then sees what the output of the honest parties is in the simulated execution, and it sends to the trusted party the inputs of the adversary accordingly. It is easy to see that the parties accept only if all honest parties did not complain, and any complaint of an honest party results in a rejection of the dealer. \(\square \)
Notes
In the optimistic case, the adversary does not deviate from the prescribed protocol. Thus, in the pessimistic case (when it does deviate from the protocol), the adversary might only make the execution more expensive.
A broadcast of one bit in constant expected rounds requires expected \(O(n^6 \log n)\) communication complexity in [35]. However, n parallel broadcasts of \(O(n^2\log n)\) size messages remains expected \(O(n^6 \log n)\). This is the case in our protocol, i.e., in each multiplication gate, each party invokes a VSS, which might lead to broadcasting messages of size \(O(n^2\log n)\) as a dealer, i.e., over the n parallel execution, each party receives \(O(n^3\log n)\) bits. \(O(n^6 \log n)\) bits is, therefore, an overhead of \(O(n^3)\).
The analysis will shortly show that this polynomial is unique.
It is easy to construct a more “balanced” protocol where the dealer does not play a special role in the reconstruction. However, when the reconstruction fails, we anyway disqualify the dealer. Therefore, for simplicity, we present the protocol where the responsibility is held accountable whenever the reconstructed value is \(\bot \).
References
I. Abraham, B. Pinkas, A. Yanai, Blinder: MPC based scalable and robust anonymous committed broadcast, in ACM CCS (2020)
G. Asharov, R. Cohen, O. Shochat, Static vs. adaptive security in perfect MPC: A separation and the adaptive security of BGW, in 3rd Conference on Information-Theoretic Cryptography, ITC 2022, July 5–7, 2022, Cambridge, MA, USA, volume 230 of LIPIcs, pp. 15:1–15:16. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022)
G. Asharov, Y. Lindell, A full proof of the BGW protocol for perfectly secure multiparty computation. J. Cryptol., 30(1), 58–151 (2017)
G. Asharov, Y. Lindell, T. Rabin, Perfectly-secure multiplication for any \({t < n}/3\), in P. Rogaway, editor, Advances in Cryptology - CRYPTO 2011 - 31st Annual Cryptology Conference, Santa Barbara, CA, USA, August 14–18, 2011. Proceedings, volume 6841 of Lecture Notes in Computer Science (Springer, 2011), pp. 240–258
A. Barak, D. Escudero, A.P.K. Dalskov, M. Keller, Secure evaluation of quantized neural networks. IACR Cryptol. ePrint Arch., 2019, 131 (2019)
D. Beaver, Efficient multiparty protocols using circuit randomization, in CRYPTO (1991), pp. 420–432
Z. Beerliová-Trubíniová, M. Hirt, Simple and efficient perfectly-secure asynchronous MPC, in K. Kurosawa, editor, Advances in Cryptology - ASIACRYPT 2007, 13th International Conference on the Theory and Application of Cryptology and Information Security, Kuching, Malaysia, December 2–6, 2007, Proceedings, volume 4833 of Lecture Notes in Computer Science (Springer, 2007), pp. 376–392
Z. Beerliová-Trubíniová, M. Hirt, Perfectly-secure MPC with linear communication complexity, in R. Canetti, editor, Theory of Cryptography, Fifth Theory of Cryptography Conference, TCC 2008, New York, USA, March 19–21, 2008, volume 4948 of Lecture Notes in Computer Science (Springer, 2008), pp. 213–230
M. Ben-Or, S. Goldwasser, A. Wigderson, Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract), in J. Simon, editor, STOC (ACM, 1988), pp. 1–10
P. Berman, J.A. Garay, K.J. Perry, Bit optimal distributed consensus, in Springer US, Boston, MA, 1992, Lecture Notes in Computer Science (1992), pp. 313–321
A. Chandramouli, A. Choudhury, A. Patra, A survey on perfectly-secure verifiable secret-sharing. IACR Cryptol. ePrint Arch., 2021, 445 (2021)
R. Canetti, Security and composition of multiparty cryptographic protocols, J. Cryptol., 13(1), 143–202 (2000)
R. Canetti, Universally composable security: A new paradigm for cryptographic protocols, in FOCS (IEEE Computer Society, 2001), pp. 136–145
R. Canetti, I. Damgård, S. Dziembowski, Y. Ishai, T. Malkin, Adaptive versus non-adaptive security of multi-party protocols, J. Cryptol., 17(3), 153–207 (2004)
H. Chen, M. Kim, I.P. Razenshteyn, D. Rotaru, Y. Song, S. Wagh. Maliciously secure matrix multiplication with applications to private deep learning, IACR Cryptol. ePrint Arch., 2020, 451 (2020)
K. Chida, D. Genkin, K. Hamada, D. Ikarashi, R. Kikuchi, Y. Lindell, A. Nof, Fast large-scale honest-majority MPC for malicious adversaries, in CRYPTO (2018), pp. 34–64
B. Chor, S. Goldwasser, S. Micali, B. Awerbuch, Verifiable secret sharing and achieving simultaneity in the presence of faults (extended abstract), in FOCS (IEEE Computer Society, 1985), pp. 383–395
A. Choudhury, A. Patra. An efficient framework for unconditionally secure multiparty computation, IEEE Trans. Inf. Theory, 63(1), 428–468 (2017)
B.A. Coan, J.L. Welch. Modular construction of a byzantine agreement protocol with optimal message bit complexity. Inf. Comput., 97(1), 61–85 (1992)
R. Cohen, S. Coretti, J.A. Garay, V. Zikas. Probabilistic termination and composability of cryptographic protocols, J. Cryptol. 32(3), 690–741 (2019)
R. Cramer, I. Damgård, U.M. Maurer, General secure multi-party computation from any linear secret-sharing scheme, in EUROCRYPT (2000), pp. 316–334
I. Damgård, J.B. Nielsen, Scalable and unconditionally secure multiparty computation, in A. Menezes, editor, CRYPTO, volume 4622 of Lecture Notes in Computer Science (Springer, 2007), pp. 572–590
I. Damgård, J.B. Nielsen, Adaptive versus static security in the UC model, in S. S. M. Chow, J. K. Liu, L.C.K. Hui, S.-M. Yiu, editors, Provable Security - 8th International Conference, ProvSec 2014, Hong Kong, China, October 9–10, 2014. Proceedings, volume 8782 of Lecture Notes in Computer Science (Springer, 2014), pp. 10–28
I. Damgård, J.B. Nielsen, A. Polychroniadou, M.A. Raskin, On the communication required for unconditionally secure multiplication, in M. Robshaw and J. Katz, editors, Advances in Cryptology - CRYPTO 2016 - 36th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 14–18, 2016, Proceedings, Part II, volume 9815 of Lecture Notes in Computer Science (Springer, 2016), pp. 459–488
I. Damgård, N.I. Schwartzbach, Communication lower bounds for perfect maliciously secure MPC, IACR Cryptol. ePrint Arch., 2020, 251 (2020)
P. Feldman, Optimal algorithms for byzantine agreement (1988)
P.N. Feldman, Optimal Algorithms for Byzantine Agreement. Ph.D. thesis, Massachusetts Institute of Technology (1988)
P. Feldman, S. Micali, An optimal probabilistic protocol for synchronous byzantine agreement, SIAM J. Comput., 26(4), 873–933 (1997)
R. Gennaro, M.O. Rabin, T. Rabin, Simplified VSS and fast-track multiparty computations with applications to threshold cryptography, in B. A. Coan and Y. Afek, editors, PODC (ACM, 1998), pp. 101–111
O. Goldreich, The Foundations of Cryptography - Volume 2: Basic Applications (Cambridge University Press, 2004).
O. Goldreich, S. Micali, A. Wigderson, How to play any mental game or A completeness theorem for protocols with honest majority, in A. V. Aho, editor, STOC (ACM, 1987), pp. 218–229
V. Goyal, Y. Liu, Y. Song, Communication-efficient unconditional MPC with guaranteed output delivery, in A. Boldyreva, D. Micciancio, editors, CRYPTO, volume 11693 of Lecture Notes in Computer Science (Springer, 2019), pp. 85–114
M. Hirt, U.M. Maurer, B. Przydatek, Efficient secure multi-party computation, in T. Okamoto, editor, Advances in Cryptology - ASIACRYPT 2000, 6th International Conference on the Theory and Application of Cryptology and Information Security, Kyoto, Japan, December 3–7, 2000, Proceedings, volume 1976 of Lecture Notes in Computer Science (Springer, 2000), pp. 143–161
M. Hirt, J.B. Nielsen, Robust multiparty computation with linear communication complexity, in C. Dwork, editor, Advances in Cryptology - CRYPTO 2006, 26th Annual International Cryptology Conference, Santa Barbara, California, USA, August 20–24, 2006, Proceedings, volume 4117 of Lecture Notes in Computer Science (Springer, 2006), pp. 463–482
J. Katz, C.-Y. Koo, On expected constant-round protocols for byzantine agreement, J. Comput. Syst. Sci., 75(2), 91–112 (2009)
E. Kushilevitz, Y. Lindell, T. Rabin, Information-theoretically secure protocols and security under composition, SIAM J. Comput., 39(5), 2090–2112 (2010)
J. Liu, M. Juuti, Y. Lu, N. Asokan, Oblivious neural network predictions via minionn transformations, in ACM CCS (2017), pp. 619–631
P. Mohassel, P. Rindal, Aby\({}^{\text{3}}\): A mixed protocol framework for machine learning, in CCS (2018), pp. 35–52
P. Mohassel, Y. Zhang, Secureml: A system for scalable privacy-preserving machine learning, in SP (2017), pp. 19–38
A. Patra, A. Choudhury, C.P. Rangan, Efficient asynchronous verifiable secret sharing and multiparty computation, J. Cryptol., 28(1), 49–109 (2015)
T. Rabin, M. Ben-Or, Verifiable secret sharing and multiparty protocols with honest majority (extended abstract), in D. S. Johnson, editor, Proceedings of the 21st Annual ACM Symposium on Theory of Computing, May 14–17, 1989, Seattle, Washington, USA (ACM, 1989), pp. 73–85
A. Shamir, How to share a secret, Commun. ACM, 22(11), 612–613 (1979)
A. Verma, H. Qassim, D. Feinzimer, Residual squeeze CNDS deep learning CNN model for very large scale places image recognition, in UEMCON (2017), pp. 463–469
S. Wagh, D. Gupta, N. Chandran, Securenn: 3-party secure computation for neural network training, Proc. Priv. Enhancing Technol., 2019(3), 26–49 (2019)
A.C.-C. Yao, How to generate and exchange secrets (extended abstract), in FOCS (IEEE Computer Society, 1986), pp. 162–167
Acknowledgements
Gilad Asharov would like to thank Ilan Komargodski and Ariel Nof for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Manoj Prabhakaran.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version of this paper appeared in IACR-TCC 2021. Gilad Asharov: Sponsored by the Israel Science Foundation (Grant No. 2439/20), by the BIU Center for Research in Applied Cryptography and Cyber Security in conjunction with the Israel National Cyber Bureau in the Prime Minister’s Office, and by the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement No. 891234.
Appendices
A General Secure Computation from Multiplication
1.1 A.1 Emulate a Multiplication Gate from O(n) Multiplications with a Dealer
We first show how the parties compute a multiplication gate in the \(({F_{VSS}},F_{VSS}^{mult})\)-hybrid model. Let a and b be the values on the two input wires, hidden using polynomials A(x, y) and B(x, y), respectively. The goal is that the parties would compute shares on a random degree-t polynomial C(x, y) for which \(C(0,0) = ab\). The subprotocol for computing a multiplication gate is as follows:
-
Input Each party \(P_i\) holds \(f_i^a(x) = A(x,\alpha _i)\), \(g_i^a(y) = A(\alpha _i,y)\), \(f_i^b(x) = B(x,\alpha _i)\) and \(g_i^b(y) = B(\alpha _i,y)\).
-
The protocol
-
1.
Each party \(P_i\) invokes \(F_{VSS}^{mult}\) as a dealer while using \(f_i^a(x),f_i^b(x)\) as its input. Each party \(P_j\) uses in that invocation the shares \(g_j^a(\alpha _i),g_j^b(\alpha _i)\) as its input.
As an output of this invocation, \(P_i\) holds a degree-t bivariate polynomial \(C_i(x,y)\) such that \(C_i(0,0)= f_i^a(0)\cdot f_i^b(0)\), and each party \(P_j\) holds \(f_j^{c_i}(x) = C_i(x,\alpha _j)\) and \(g_j^{c_i}(y) = C_i(\alpha _j,y)\).
-
2.
Let \((f_j^{c_1}(x),\ldots ,f_j^{c_n}(x))\) and \((g_j^{c_1}(y),\ldots ,g_j^{c_n}(y))\) be the obtained shares from the previous step after each party served as a dealer. Each party \(P_j\) locally computes its final share \(f_j^c(x) = \sum _{i=1}^{n}\lambda _i\cdot f_j^{c_i}(x)\) and \(g_j^c(y) = \sum _{i=1}^{n} \lambda _i \cdot g_j^{c_i}(y)\), where \(\lambda _1,\ldots ,\lambda _n\) are the publicly known Lagrange coefficients.
-
1.
-
Output Each party outputs \(f_j^c(x),g_j^c(y)\).
The output shares correspond to the polynomial \(C(x,y)= \sum _{i=1}^{n}\lambda _i\cdot C_i(x,y)\). Its constant term is \(\sum _{i=1}^{n}\lambda _i \cdot C_i(0,0) = \sum _{i=1}^{n}\lambda _i\cdot f_i^a(0)\cdot f_i^b(0) = ab\), as required.
1.2 A.2 Emulate Arbitrary Gates with Multiplicative Depth 1
Let G be a multiplicative depth 1 sub-circuit of C, with M inputs and L outputs. Let \(a_1,\ldots ,a_M\) be the values on the M input wires, hidden using degree-t bivariate polynomials \(A_1(x,y),\ldots ,A_M(x,y)\), respectively. The goal is for the parties to compute shares on random degree-t bivariate polynomials \(C_1(x,y),\ldots ,C_L(x,y)\) such that \(\big ( C_1(0,0), \ldots , C_L(0,0) \big ) = G\big ( A_1(0,0), \ldots , A_M(0,0) \big )\). The subprotocol for achieving those shares is as follows:
-
Input Each party \(P_i\) holds \(f_i^{a_m}(x) = A_m(x,\alpha _i)\) and \(g_i^{a_m}(y) = A_m(\alpha _i,y)\) for every \(m \in [M]\).
-
The protocol
-
1.
Each party \(P_i\) invokes \(F_{VSS}^{G}\) (Functionality 6.1) as a dealer while using \(f_i^{a_1}(x),\ldots ,f_i^{a_M}(x)\) as input. Each party \(P_j\) uses the shares \(g_j^{a_1}(\alpha _i),\ldots ,g_j^{a_M}(\alpha _i)\) as input.
As an output of this invocation, \(P_i\) holds degree-t bivariate polynomials \(C_{i,1}(x,y),\ldots ,C_{i,L}(x,y)\) such that \(\big ( C_{i,1}(0,0),\ldots , C_{i,L}(0,0) \big ) = G\big ( f_i^{a_1}(0), \ldots , f_i^{a_M}(0) \big )\). In addition, each party \(P_j\) holds \(f_j^{C_{i,\ell }}(x) = C_{i,\ell }(x,\alpha _j)\) and \(g_j^{C_{i,\ell }}(y) = C_{i,\ell }(\alpha _j,y)\) for all \(\ell \in [L]\).
-
2.
Let \((f_j^{C_{1,\ell }}(x),\ldots , f_j^{C_{n,\ell }}(x))\) and \((g_j^{C_{1,\ell }}(y),\ldots ,g_j^{C_{n,\ell }}(y))\) be the shares of \(C_{1,\ell }(x,y), \ldots , C_{n,\ell }(x,y)\) for \(\ell \in [L]\), obtained from the previous step, after each party served as a dealer.
Each party \(P_j\) locally computes its final share \(f_j^{C_\ell }(x) = \sum _{i=1}^{n}\lambda _i\cdot f_j^{C_{i,\ell }}(x)\) and \(g_j^{C_\ell }(y) = \sum _{i=1}^{n} \lambda _i \cdot g_j^{C_{i,\ell }}(y)\), for \(\ell \in [L]\), , where \(\lambda _1,\ldots ,\lambda _n\) are the publicly known Lagrange coefficients.
-
1.
-
Output Each party outputs \(f_j^{C_\ell }(x)\) and \(g_j^{C_\ell }(y)\) for \(\ell \in [L]\).
For every \(\ell \in [L]\), the output shares correspond to the polynomial \(C_\ell (x,y)= \sum _{i=1}^{n}\lambda _i\cdot C_{i,\ell }(x,y)\), which is a polynomial of degree t. Let \((b_1,\ldots ,b_L) = G(a_1,\ldots ,a_M)\). The constant term of \(C_\ell \) is:
where \(h_\ell (x) {\mathop {=}\limits ^\mathrm{def}}G_\ell (f^{a_1}(x),\ldots ,f^{a_M}(x))\) is a polynomial of degree 2, and from Functionality 6.1 it holds that \(C_{i,\ell }(0,0)=G_\ell (f^{a_1}(\alpha _i),\ldots ,f^{a_M}(\alpha _i))\).
Computing any function F
Let \(F:\mathbb {F}^n \rightarrow \mathbb {F}^n\) be any function that maps n inputs into n outputs, i.e., we assume for simplicity that the input and output of each party is a single field element. Let C be an arithmetic circuit over \(\mathbb {F}\) that computes F. To compute the circuit C:
-
Input sharing phase Each party \(P_i\) with input \(x_i\) chooses a random bivariate polynomial \(S_i\) of degree t such that \(S_i(0,0) = x_i\). It invokes \({F_{VSS}}\) on \(S_i\).
-
The circuit emulation stage The parties maintain the invariant in which each wire in the circuit is hidden by a bivariate sharing. Let \(G_1,\ldots ,G_\ell \) be the predetermined topological ordering of the gates of the circuit. For \(k=1,\ldots ,\ell \) the parties work as follows.
-
1.
Case 1—\(G_k\) is an addition gate Each \(P_i\) locally computes the shares on the output wires by adding the two input shares of the inputs wires of the gate.
-
2.
Case 2—\(G_k\) is a general gate The circuit has M input wires and L outputs wires. We invoke the subprotocol defined above to obtain shares on the output wires.
-
1.
-
Output reconstruction phase The parties hold bivariate sharing of the output wires. Each party \(P_i\) is supposed to learn some output \(y_i\). The parties send to \(P_i\) all the shares on that wire and \(P_i\) can reconstruct it.
In [3] it is shown that this protocol securely computes the functionality F (when using univariate sharing and not bivariate sharing, but the difference in the proof is straightforward). By combining Corollary 5.4 and Theorem 4.9, this leads to a protocol in the plain model.
B Proof of Claims 3.6 and 3.7
Claim B.1
(Hiding I, Claim 3.6, restated) Let h(x) be an arbitrary univariate polynomial of degree q, and let \(\alpha _1,\ldots ,\alpha _k\) with \(k\le t\) be arbitrary distinct nonzero points in \(\mathbb {F}\). Consider the following distribution \(\mathsf{Dist}(h)\):
-
Choose a random (q, t)-bivariate polynomial S(x, y) under the constraint that \(S(x,0) = h(x)\).
-
Output \(\{(i,S(x,\alpha _i),S(\alpha _i,y))\}_{i \in [k]}\).
Then, for every two arbitrary degree-q polynomials \(h_1(x),h_2(x)\) for which \(h_1(\alpha _i) = h_2(\alpha _i)\) for every \(i \in [k]\) it holds that \(\mathsf{Dist}(h_1) \equiv \mathsf{Dist}(h_2)\).
Proof
We start with the case where \(k=t\). Fix some \(h_1(x),h_2(x)\) as above, and fix degree-q polynomials \(\{f_i(x)\}_{i \in [k]}\) and degree-t polynomials \(\{g_i(y)\}_{i \in [k]}\) for which:
-
1.
\(f_i(\alpha _j)=g_j(\alpha _i)\) for every \(i,j \in [k]\),
-
2.
\(g_i(0) = h_1(\alpha _i) = h_2(\alpha _i)\).
We have to show that:
Note that if the set of polynomials \(f_i(x),g_i(y)\) does not satisfy the above two conditions, then the probability to get this set of polynomials is 0 in both distributions. Observe also that the support of the two distributions is the same. Now, by fixing the set \(\{f_i(x),g_i(y)\}_{i=1}^{k}\), we show that there exists exactly one bivariate polynomial in the support of \(\mathsf{Dist}(h_1)\). This follows from Claim 3.4 while taking \(\{f_i(x)\}_{i=1}^{k} \cup h_1(x)\). Let S(x, y) be the unique polynomial that is guaranteed to exist by the claim. For every \(j=[t], i\in [k]\), it holds that \(g_i(\alpha _j)=f_j(\alpha _i) = S(\alpha _i,\alpha _j)\). Moreover, we know that \(S(x,0)=h_1(x)\) and since \(g_i(0) = h_1(\alpha _i)\) it holds that \(g_i(0) = S(\alpha _i,0)\). We therefore conclude that \(g_i(y)\) agrees with the degree-t polynomial \(S(\alpha _i,y)\). Since \(\mathsf{Dist}(h_1)\) chooses each bivariate polynomial in the support with exactly the same probability, we get that the probability that those \(\{f_i(x),g_i(y)\}\) were chosen is exactly 1 over the support of \(\mathsf{Dist}(h_1)\). Exactly the same analysis can be applied for \(\mathsf{Dist}(h_2)\), and using the fact that the support of the two distributions is the same, we conclude that the two distributions are identical.
For the case of \(k < t\), one can just add arbitrary polynomials to \(f_i(x),g_i(y)\) (that satisfy the pairwise checks), and use the law of total probability (see [3, Claim 3.2] for a similar claim). \(\square \)
Claim B.2
(Hiding II, Claim 3.7, restated) Same as Claim 3.6, except that it holds that \(h_1(0)=h_2(0)=\beta \) for some publicly known \(\beta \in \mathbb {F}\). The output of the distribution is \(\{(i,S(x,\alpha _i),S(\alpha _i,y))\}_{i \in [k]} \cup S(0,y) \).
Proof
Let \(h_1(x),h_2(x)\) be arbitrary polynomials of degree q such that \(h_1(0)=h_2(0)=\beta \), and fix degree-q polynomials \(\{f_i(x)\}_{i \in [k]}\) and degree-t polynomials \(\{g_i(y)\}_{i \in [k]}\) for which \(g_i(0)=h_1(\alpha _i)=h_2(\alpha _i)\), and \(f_i(\alpha _j)=g_j(\alpha _i)\) for every \(i,j \in [k]\). Moreover, fix an arbitrary degree-t polynomial \(g_0(y)\) for which for every \(i\in [k]\) it holds that \(g_0(\alpha _i) = f_i(0)\). Note that in case of \(k=t\), the polynomial \(g_0(y)\) is already determined: conditioning that \(g_0(\alpha _i)=f_i(0)\) for every \(i \in [k]\) define t points on the polynomial, we know that \(g_0(0) = \beta \). So we have \(t+1\) points which uniquely define a polynomial of degree t.
We show that the probability to obtain \(\{f_i(x),g_i(y)\}_{i \in [k]} \cup \{g_0(y)\}\) is the same under both distributions. First, observe that the support of the two distributions is the same. Moreover, just like in the previous claim, for the case of \(k=t\) we can apply Claim 3.4, i.e., there exists a unique bivariate polynomial S(x, y) that is determined by the view \(\{f_i(x),g_i(y)\}_{i \in [k]} \cup \{g_0(y)\}\) in each one of the distributions. The probability of obtaining those polynomials is exactly 1 over the support size, which is the same in both cases. For the case of \(k<t\), one can just add arbitrary polynomials to the set of fixed polynomials (that satisfy the conditions), and use the law of total probability as in [3, Claim 3.2].
\(\square \)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Abraham, I., Asharov, G. & Yanai, A. Efficient Perfectly Secure Computation with Optimal Resilience. J Cryptol 35, 27 (2022). https://doi.org/10.1007/s00145-022-09434-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00145-022-09434-2





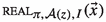 the random variable consisting of the view of the adversary
the random variable consisting of the view of the adversary  is the output of all honest parties and the output of the ideal adversary
is the output of all honest parties and the output of the ideal adversary