Abstract
We present a new multiparty protocol for the distributed generation of biprime RSA moduli, with security against any subset of maliciously colluding parties assuming oblivious transfer and the hardness of factoring. Our protocol is highly modular, and its uppermost layer can be viewed as a template that generalizes the structure of prior works and leads to a simpler security proof. We introduce a combined sampling-and-sieving technique that eliminates both the inherent leakage in the approach of Frederiksen et al. (Crypto’18) and the dependence upon additively homomorphic encryption in the approach of Hazay et al. (JCrypt’19). We combine this technique with an efficient, privacy-free check to detect malicious behavior retroactively when a sampled candidate is not a biprime and thereby overcome covert rejection-sampling attacks and achieve both asymptotic and concrete efficiency improvements over the previous state of the art.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A biprime is a number \(N\) of the form \(N=p\cdot q\) where \(p\) and \(q\) are primes. Such numbers are used as a component of the public key (i.e., the modulus) in the RSA cryptosystem [46], with the factorization being a component of the secret key. A long line of research has studied methods for sampling biprimes efficiently; in the early days, the task required specialized hardware and was not considered generally practical [44, 45]. In subsequent years, advances in computational power brought RSA into the realm of practicality and then ubiquity. Given a security parameter \({\kappa } \), the de facto standard method for sampling RSA biprimes involves choosing random \({\kappa } \)-bit numbers and subjecting them to the Miller–Rabin primality test [38, 43] until two primes are found; these primes are then multiplied to form a \(2{\kappa } \)-bit modulus. This method suffices when a single party wishes to generate a modulus, and is permitted to know the associated factorization.
Boneh and Franklin [4, 5] initiated the study of distributed RSA modulus generation.Footnote 1 This problem involves a set of parties who wish to jointly sample a biprime in such a way that no corrupt and colluding subset (below some defined threshold size) can learn the biprime’s factorization.
It is clear that applying generic multiparty computation (MPC) techniques to the standard sampling algorithm yields an impractical solution: implementing the Miller–Rabin primality test requires repeatedly computing \(a^{p-1}\bmod {p}\), where \(p\) is (in this case) secret, and so such an approach would require the generic protocol to evaluate a circuit containing many modular exponentiations over \({\kappa } \) bits each. Instead, Boneh and Franklin [4, 5] constructed a new biprimality test that generalizes Miller–Rabin and avoids computing modular exponentiations with secret moduli. Their test carries out all exponentiations modulo the public biprime \(N\), and this allows the exponentiations to be performed locally by the parties. Furthermore, they introduced a three-phase structure for the overall sampling protocol, which subsequent works have embraced:
-
1.
Prime Candidate Sieving: candidate values for \(p\) and \(q\) are sampled jointly in secret-shared form, and a weak-but-cheap form of trial division sieves them, culling candidates with small factors.
-
2.
Modulus Reconstruction: \(N:=p\cdot q\) is securely computed and revealed.
-
3.
Biprimality Testing: using a distributed protocol, \(N\) is tested for biprimality. If \(N\) is not a biprime, then the process is repeated.
The seminal work of Boneh and Franklin considered the semi-honest n-party setting with an honest majority of participants. Many extensions and improvements followed (as detailed in Sect. 1.3), the most notable of which (for our purposes) are two recent works that achieve malicious security against a dishonest majority. In the first, Hazay et al. [28, 29] proposed an n-party protocol in which both sieving and modulus reconstruction are achieved via additively homomorphic encryption. Specifically, they rely upon both ElGamal and Paillier encryption, and in order to achieve malicious security, they use zero-knowledge proofs for a variety of relations over the ciphertexts. Thus, their protocol represents a substantial advancement in terms of its security guarantee, but this comes at the cost of additional assumptions and an intricate proof, and also at substantial concrete cost, due to the use of many custom zero-knowledge proofs.
The subsequent protocol of Frederiksen et al. [23] (the second recent work of note) relies mainly on oblivious transfer (OT), which they use to perform both sieving and, via Gilboa’s classic multiplication protocol [24], modulus reconstruction. They achieved malicious security using the folklore technique in which a “Proof of Honesty” is evaluated as the last step and demonstrated practicality by implementing their protocol; however, it is not clear how to extend their approach to more than two parties in a straightforward way. Moreover, their approach to sieving admits selective-failure attacks, for which they account by including some leakage in the functionality. It also permits a malicious adversary to selectively and covertly induce false negatives (i.e., force the rejection of true biprimes after the sieving stage), a property that is again modeled in their functionality. In conjunction, these attributes degrade security, because the adversary can rejection-sample biprimes based on the additional leaked information, and efficiency, because ruling out malicious false-negatives involves running sufficiently many instances to make the probability of statistical failure in all instances negligible.
Thus, given the current state of the art, it remains unclear whether one can sample an RSA modulus among two parties (one being malicious) without leaking additional information or permitting covert rejection sampling, or whether one can sample an RSA modulus among many parties (all but one being malicious) without involving heavy cryptographic primitives such as additively homomorphic encryption, and their associated performance penalties. In this work, we present a protocol which efficiently achieves both tasks.
1.1 Results and Contributions
A Clean Functionality. We define  , a simple, natural functionality for sampling biprimes from the same well-known distribution used by prior works [5, 23, 29], with no leakage or conflation of sampling failures with adversarial behavior.
, a simple, natural functionality for sampling biprimes from the same well-known distribution used by prior works [5, 23, 29], with no leakage or conflation of sampling failures with adversarial behavior.
A Modular Protocol, with Natural Assumptions. We present a protocol  in the
in the  -hybrid model, where
-hybrid model, where  is an augmented multiplier functionality and
is an augmented multiplier functionality and  is a biprimality-testing functionality, and prove that it UC-realizes
is a biprimality-testing functionality, and prove that it UC-realizes  in the malicious setting, assuming the hardness of factoring. More specifically, we prove:
in the malicious setting, assuming the hardness of factoring. More specifically, we prove:
Theorem 1.1
(Main security theorem, informal) In the presence of a PPT malicious adversary corrupting any subset of parties,  can be securely computed with abort in the
can be securely computed with abort in the  -hybrid model, assuming the hardness of factoring.
-hybrid model, assuming the hardness of factoring.
Additionally, because our security proof relies upon the hardness of factoring only when the adversary cheats, we find to our surprise that our protocol achieves perfect security against semi-honest adversaries.
Theorem 1.2
(Semi-honest security theorem, informal) In the presence of a computationally unbounded semi-honest adversary corrupting any subset of parties,  can be computed with perfect security in the
can be computed with perfect security in the  -hybrid model.
-hybrid model.
Supporting Functionalities and Protocols. We define  , a simple, natural functionality for biprimality testing and show that it is UC-realized in the semi-honest setting by a well-known protocol of Boneh and Franklin [5], and in the malicious setting by a derivative of the protocol of Frederiksen et al. [23]. We believe this dramatically simplifies the composition of these two protocols and, as a consequence, leads to a simpler analysis. Either protocol can be based exclusively upon oblivious transfer.
, a simple, natural functionality for biprimality testing and show that it is UC-realized in the semi-honest setting by a well-known protocol of Boneh and Franklin [5], and in the malicious setting by a derivative of the protocol of Frederiksen et al. [23]. We believe this dramatically simplifies the composition of these two protocols and, as a consequence, leads to a simpler analysis. Either protocol can be based exclusively upon oblivious transfer.
We also define  , a functionality for sampling and multiplying secret-shared values in a special form derived from the Chinese remainder theorem. In the context of
, a functionality for sampling and multiplying secret-shared values in a special form derived from the Chinese remainder theorem. In the context of  , this functionality allows us to efficiently sample numbers in a specific range, with no small factors, and then compute their product. We prove that it can be UC-realized exclusively from oblivious transfer, using derivatives of well-known multiplication protocols [19, 20].
, this functionality allows us to efficiently sample numbers in a specific range, with no small factors, and then compute their product. We prove that it can be UC-realized exclusively from oblivious transfer, using derivatives of well-known multiplication protocols [19, 20].
Asymptotic Efficiency. We perform an asymptotic analysis of our composed protocols and find that our semi-honest protocol is a factor of \({\kappa }/\log {\kappa } \) more bandwidth-efficient than that of Frederiksen et al. [23], where \({\kappa } \) is the bit-length of the primes p and q. Our malicious protocol is a factor of \({\kappa }/{s} \) more efficient than theirs in the optimistic case (when parties follow the protocol), where \({s} \) is a statistical security parameter, and it is a factor of \({\kappa } \) more efficient when parties deviate from the protocol. Frederiksen et al. claim in turn that their protocol is strictly superior to the protocol of Hazay et al. [29] with respect to asymptotic bandwidth performance.
Concrete Efficiency. We perform a closed-form concrete communication cost analysis of our protocol (with some optimizations, including the use of random oracles), and compare our results to the protocol of Frederiksen et al. (the most efficient prior work). For \({\kappa } =1024\) (i.e., when sampling a 2048-bit biprime), our protocol outperforms theirs by a factor of roughly five in the presence of worst-case malicious adversaries, and by a factor of roughly eighty in the semi-honest setting. As the bitlength of the sampled prime grows, so too does the concrete performance advantage of our protocol.
1.2 Overview of Techniques
Constructive Sampling and Efficient Modulus Reconstruction. Most prior works use rejection sampling to generate a pair of candidate primes and then multiply those primes together in a separate step. Specifically, they sample a shared value \(p\leftarrow [0,2^{\kappa })\) uniformly, and then run a trial-division protocol repeatedly, discarding both the value and the work that has gone into testing it if trial division fails. This represents a substantial amount of wasted work in expectation. Furthermore, Frederiksen et al. [23] report that multiplication of candidates after sieving accounts for two thirds of their concrete cost.
We propose a different approach that leverages the Chinese remainder theorem (CRT) to constructively sample a pair of candidate primes and multiply them together efficiently. A similar sieving approach (in spirit) was initially formulated as an optimization in a different setting by Malkin et al. [37]. The CRT implies an isomorphism between a set of values, each in a field modulo a distinct prime, and a single value in a ring modulo the product of those primes (i.e., \({\mathbb {Z}}_{m_1}\times \cdots \times {\mathbb {Z}}_{m_\ell }\simeq {\mathbb {Z}}_{m_1\cdot \ldots \cdot m_\ell }\)). We refer to the set of values as the CRT form or CRT representation of the single value to which they are isomorphic. We formulate a sampling mechanism based on this isomorphism as follows: for each of the first \(O({\kappa }/\log {\kappa })\) odd primes, the parties jointly (and efficiently) sample shares of a value that is nonzero modulo that prime. These values are the shared CRT form of a single \({\kappa } \)-bit value that is guaranteed to be indivisible by any prime in the set sampled against. For technical reasons, we sample two such candidates simultaneously.
Rather than converting pairs of candidate primes from CRT form to standard form, and then multiplying them, we instead multiply them component-wise in CRT form and then convert the product to standard form to complete the protocol. This effectively replaces a single “full-width” multiplication of size \({\kappa } \) with \(O({\kappa }/\log {\kappa })\) individual multiplications, each of size \(O(\log {\kappa })\). We intend to perform multiplication via an OT-based protocol, and the computation and communication complexity of such protocols grows at least with the square of their input length, even in the semi-honest case [24]. Thus, in the semi-honest case, our approach yields an overall complexity of \(O({\kappa } \log {\kappa })\), as compared to \(O({\kappa } ^2)\) for a single full-width multiplication. In the malicious case, combining the best known multiplier construction [19, 20] with the most efficient known OT extension scheme [6] yields a complexity that also grows with the product of the input length and a statistical parameter \({s} \), and so our approach achieves an overall complexity of \(O({\kappa } \log {\kappa } + {\kappa } \cdot {s})\), as compared to \(O({\kappa } ^2+{\kappa } \cdot {s})\) for a single full-width malicious multiplication. Via closed-form analysis, we show that this asymptotic improvement is also reflected concretely.
Achieving Security with Abort Efficiently. The fact that we sample primes in CRT form also plays a crucial role in our security analysis. Unlike the work of Frederiksen et al. [23], our protocol achieves the standard, intuitive notion of security with abort: the adversary can instruct the functionality to abort regardless of whether a biprime is successfully sampled, and the honest parties are always made aware of such adversarial aborts. There is, in other words, absolutely no conflation of sampling failures with adversarial behavior. For the sake of efficiency, our protocol permits the adversary to cheat prior to biprimality testing and then rules out such cheats retroactively using one of two strategies. In the case that a biprime is successfully sampled, adversarial behavior is ruled out, retroactively, in a privacy-preserving fashion using well-known but moderately expensive techniques, which is tolerable only because it need not be done more than once. In the case that a sampled value is not a biprime, however, the inputs to the sampling protocol are revealed to all parties, and the retroactive check is carried out in the clear. Proving the latter approach secure turns out to be surprisingly subtle.
The challenge arises from the fact that the simulator must simulate the protocol transcript for the OT-multipliers on behalf of the honest parties without knowing their inputs. Later, if the sampling-protocol inputs are revealed, the simulator must “explain” how the simulated transcript is consistent with the true inputs of the honest parties. Specifically, in maliciously secure OT-multipliers of the sort we use [19, 20], the OT receiver (Bob) uses a high-entropy encoding of his input, and the sender (Alice) can, by cheating, learn a one-bit predicate of this encoding. Before Bob’s true input is known to the simulator, it must pick an encoding at random. When Bob’s input is revealed, the simulator must find an encoding of his input which is consistent with the predicate on the random encoding that Alice has learned. This task closely resembles solving a random instance of subset sum.
We are able to overcome this difficulty because our multiplications are performed component-wise over CRT-form representations of their operands. Because each component is of size \(O(\log {\kappa })\) bits, the simulator can simply guess random encodings until it finds one that matches the required constraints. We show that this strategy succeeds in strict polynomial time and that it induces a distribution statistically close to that of the real execution.
This form of “privacy-free” malicious security (wherein honest behavior is verified at the cost of sacrificing privacy) leads to considerable efficiency gains in our case: it is up to a multiplicative factor of \({s} \) (the statistical parameter) cheaper than the privacy-preserving check used in the case that a candidate passes the biprimality test (and the one used in prior OT-multipliers [19, 20]). Since most candidates fail the biprimality test, using the privacy-free check to verify that they were generated honestly results in substantial savings.
Biprimality Testing as a Black Box. We specify a functionality for biprimality testing and prove that it can be realized by a maliciously secure version of the Boneh–Franklin biprimality test. Our functionality has a clean interface and does not, for example, require its inputs to be authenticated to ensure that they were actually generated by the sampling phase of the protocol. The key insight that allows us to achieve this level of modularity is a reduction to factoring: if an adversary is able to cheat by supplying incorrect inputs to the biprimality test, relative to a candidate biprime \(N\), and the biprimality test succeeds, then we show that the adversary can be used to factor biprimes. We are careful to rely on this reduction only in the case that \(N\) is actually a biprime, and to prevent the adversary from influencing the distribution of candidates.
The Benefits of Modularity. We claim as a contribution the fact that modularity has yielded both a simpler protocol description and a reasonably simple proof of security. We believe that this approach will lead to derivatives of our work with stronger security properties or with security against stronger adversaries. As a first example, we prove that a semi-honest version of our protocol (differing only in that it omits the retroactive consistency check in the protocol’s final step) achieves perfect security. We furthermore observe that in the malicious setting, instantiating  and
and  with security against adaptive adversaries yields an RSA modulus sampling protocol that is adaptively secure.
with security against adaptive adversaries yields an RSA modulus sampling protocol that is adaptively secure.
Similarly, only minor adjustments to the main protocol are required to achieve security with identifiable abort [16, 32]. If we assume that the underlying functionalities  and
and  are instantiated with identifiable abort, then it remains only to ensure the use of consistent inputs across these functionalities, and to detect which party has provided inconsistent inputs if an abort occurs. This can be accomplished by augmenting
are instantiated with identifiable abort, then it remains only to ensure the use of consistent inputs across these functionalities, and to detect which party has provided inconsistent inputs if an abort occurs. This can be accomplished by augmenting  with an additional interface for revealing the input values provided by all the parties upon global request (e.g., when the candidate \(N\) is not a biprime). Given identifiable abort, it is possible to guarantee output delivery in the presence of up to \(n-1\) corruptions via standard techniques, although the functionality must be weakened to allow the adversary to reject one biprime per corrupt party.Footnote 2 A proof of this extension is beyond the scope of this work; we focus instead on the advancements our framework yields in the setting of security with abort.
with an additional interface for revealing the input values provided by all the parties upon global request (e.g., when the candidate \(N\) is not a biprime). Given identifiable abort, it is possible to guarantee output delivery in the presence of up to \(n-1\) corruptions via standard techniques, although the functionality must be weakened to allow the adversary to reject one biprime per corrupt party.Footnote 2 A proof of this extension is beyond the scope of this work; we focus instead on the advancements our framework yields in the setting of security with abort.
1.3 Additional Related Work
Frankel, MacKenzie, and Yung [22] adjusted the protocol of Boneh and Franklin [4] to achieve security against malicious adversaries in the honest-majority setting. Their main contribution was the introduction of a method for robust distributed multiplication over the integers. Cocks [11] proposed a method for multiparty RSA key generation under heuristic assumptions, and later attacks by Coppersmith (see [12]) and Joye and Pinch [33] suggested this method may be insecure. Poupard and Stern [42] presented a maliciously secure two-party protocol based on oblivious transfer. Gilboa [24] improved efficiency in the semi-honest two-party model, and introduced a novel method for multiplication from oblivious transfer, from which our own multipliers derive.
Malkin, Wu, and Boneh [37] implemented the protocol of Boneh and Franklin and introduced an optimized sieving method similar in spirit to ours. In particular, their protocol generates sharings of random values in \({\mathbb {Z}}_M^*\) (where M is a primorial modulus) during the sieving phase, instead of naïve random candidates for primes p and q. However, their method produces multiplicative sharings of p and q, which are converted into additive sharings for biprimality testing via an honest-majority, semi-honest protocol. This conversion requires rounds linear in the party count, and it is unclear how to adapt it to tolerate a malicious majority of parties without a significant performance penalty.
Algesheimer, Camenish, and Shoup [1] described a method to compute a distributed version of the Miller–Rabin test: they used secret-sharing conversion techniques reliant on approximations of \(1/p\) to compute exponentiations modulo a shared \(p\). However, each invocation of their Miller–Rabin test still has complexity in \(O({\kappa } ^3)\) per party, and their overall protocol has communication complexity in \(O({\kappa } ^5/\log ^2{{\kappa }})\), with \(\Theta ({\kappa })\) rounds of interaction. Concretely, Damgård and Mikkelsen [18] estimate that 10,000 rounds are required to sample a 2000-bit biprime using this method. Damgård and Mikkelsen also extended their work to improve both its communication and round complexity by several orders of magnitude, and to achieve malicious security in the honest-majority setting. Their protocol is at least a factor of \(O({\kappa })\) better than that of Algesheimer, Camenish, and Shoup, but it still requires hundreds of rounds. We were not able to compute an explicit complexity analysis of their approach. We give a summary of prior works in Table 1, for ease of comparison.
In a follow-up work, Chen et al. [10] make use of our CRT-based biprime sampling technique, but abandon our modular protocol and proof in favor of a monolithic construction that leverages recent advancements in additively-homomorphic encryption and zero-knowledge arguments. They focus on the setting wherein there is a powerful, semi-honest aggregator, and many weak, malicious clients. This mixed security model yields opportunities for optimization, and they show that their approach is sufficiently efficient for real-world use, even with thousands of participants spread around the world.
Finally, we note that the manipulation of values in what we have referred to as CRT form has long been studied under the guise of residue number systems [48]. Though we take few pains to formalize the connection or to generalize beyond what is required for this work, some of our techniques could be viewed as multiparty adaptations of techniques from the RNS literature.
1.4 Organization
Basic notation and background information are given in Sect. 2. Our ideal biprime-sampling functionality is defined in Sect. 3, and we give a protocol that realizes it in Sect. 4. In Sect. 5, we present our biprimality-testing protocol. In Sect. 6, we give an efficiency analysis. We defer full proofs of security and the details of our multiplication protocol to the appendices.
2 Preliminaries
Notation. We use \(=\) for equality, \(:=\) for assignment, \(\leftarrow \) for sampling from a distribution, \(\equiv \) for congruence, \(\smash {\approx _{\mathrm{c}}}\) for computational indistinguishability, and \(\smash {\approx _{\mathrm{s}}}\) for statistical indistinguishability. In general, single-letter variables are set in italic font, multiletter variables and function names are set in sans-serif font, and string literals are set in \(\texttt {slab-serif}\) font. We use \(\bmod {}\) to indicate the modulus operator, while \(\pmod {m}\) at the end of a line indicates that all equivalence relations on that line are to be taken over the integers modulo m. By convention, we parameterize computational security by the bit-length of each prime in an RSA biprime; we denote this length by \({\kappa } \) throughout. We use \({s} \) to represent the statistical parameter. Where concrete efficiency is concerned, we introduce a second computational security parameter, \({\lambda } \), which represents the length of a symmetric key of equivalent strength to a biprime of length \(2{\kappa } \).Footnote 3\({\kappa } \) and \({\lambda } \) must vary together, and a recommendation for the relationship between them has been laid down by NIST [2].
Vectors and arrays are given in bold and indexed by subscripts; thus, \({\varvec{\mathrm {x}}}_i\) is the \(i\)th element of the vector \({\varvec{\mathrm {x}}}\), which is distinct from the scalar variable x. When we wish to select a row or column from a two-dimensional array, we place a \(*\) in the dimension along which we are not selecting. Thus, \(\smash {{\varvec{\mathrm {y}}}_{*,j}}\) is the \(j\)th column of matrix \({\varvec{\mathrm {y}}}\), and \(\smash {{\varvec{\mathrm {y}}}_{j,*}}\) is the \(j\)th row. We use \(\mathcal{P} _i\) to denote the party with index i, and when only two parties are present, we refer to them as Alice and Bob. Variables may often be subscripted with an index to indicate that they belong to a particular party. When arrays are owned by a party, the party index always comes first. We use |x| to denote the bit-length of x and \(|{\varvec{\mathrm {y}}}|\) to denote the number of elements in the vector \({\varvec{\mathrm {y}}}\).
Universal Composability. We prove our protocols secure in the universal composability (UC) framework and use standard UC notation. In Appendix A, we give a high-level overview and refer the reader to Canetti [7] for further details. In functionality descriptions, we leave some standard bookkeeping elements implicit. For example, we assume that the functionality aborts if a party tries to reuse a session identifier inappropriately, send messages out of order, etc. For convenience, we provide a function \(\mathsf {GenSID} \), which takes any number of arguments and deterministically derives a unique Session ID from those arguments. For example, \(\mathsf {GenSID} (\mathsf {sid},x,\texttt {x})\) derives a new Session ID from the variables \(\mathsf {sid}\) and x, and the string literal “x”.
Chinese Remainder Theorem. The Chinese remainder theorem (CRT) defines an isomorphism between a set of residues modulo a set of respective pairwise-coprime values and a single value modulo the product of the same set of pairwise-coprime values. This forms the basis of our sampling procedure.
Theorem 2.1
(CRT) Let \({\varvec{\mathrm {m}}} \) be a vector of pairwise-coprime positive integers and let \({\varvec{\mathrm {x}}}\) be a vector of numbers such that \(|{\varvec{\mathrm {m}}} |=|{\varvec{\mathrm {x}}}|=\ell \) and \(0\le {\varvec{\mathrm {x}}}_j<{\varvec{\mathrm {m}}} _j\) for all \(j\in [\ell ]\), and finally let \(M:=\prod _{j\in [\ell ]} {\varvec{\mathrm {m}}} _j\). Under these conditions, there exists a unique value y such that \(0\le y<M\) and \(y\equiv {\varvec{\mathrm {x}}}_j\pmod {{\varvec{\mathrm {m}}} _j}\) for every \(j\in [\ell ]\).
We refer to \({\varvec{\mathrm {x}}}\) as the CRT form of y with respect to \({\varvec{\mathrm {m}}} \). For completeness, we give the  algorithm, which finds the unique y given \({\varvec{\mathrm {m}}} \) and \({\varvec{\mathrm {x}}}\).
algorithm, which finds the unique y given \({\varvec{\mathrm {m}}} \) and \({\varvec{\mathrm {x}}}\).

3 Assumptions and Ideal Functionality
We begin this section by discussing the distribution of biprimes from which we sample and thus the precise factoring assumption that we make, and then we give an efficient sampling algorithm and an ideal functionality that computes it.
3.1 Factoring Assumptions
The standard factoring experiment (Experiment 3.1) as formalized by Katz and Lindell [34] is parametrized by an adversary \(\mathcal{A} \) and a biprime-sampling algorithm \(\mathsf {GenModulus} \). On input \(1^{\kappa } \), this algorithm returns \((N,p,q)\), where \(N=p\cdot q\), and \(p\) and \(q\) are \({\kappa } \)-bit primes.Footnote 4

In many cryptographic applications, \(\mathsf {GenModulus} (1^{\kappa })\) is defined to sample \(p\) and \(q\) uniformly from the set of primes in the range \([2^{{\kappa }-1},2^{\kappa })\) [25], and the factoring assumption with respect to this common \(\mathsf {GenModulus}\) function states that for every PPT adversary \(\mathcal{A} \) there exists a negligible function \(\mathsf {negl}\) such that

Because efficiently sampling according to this uniform biprime distribution is difficult in a multiparty context, most prior works sample according to a different distribution, and thus using the moduli they produce requires a slightly different factoring assumption than the traditional one. In particular, several recent works use a distribution originally proposed by Boneh and Franklin [5], which is well adapted to multiparty sampling. Our work follows this pattern.
Boneh and Franklin’s distribution is defined by the sampling algorithm  , which takes as an additional parameter the number of parties n. The algorithm samples n integer shares, each in the range \([0,2^{{\kappa }-\log {n}})\),Footnote 5 and sums these shares to arrive at a candidate prime. This does not induce a uniform distribution on the set of \({\kappa } \)-bit primes. Furthermore,
, which takes as an additional parameter the number of parties n. The algorithm samples n integer shares, each in the range \([0,2^{{\kappa }-\log {n}})\),Footnote 5 and sums these shares to arrive at a candidate prime. This does not induce a uniform distribution on the set of \({\kappa } \)-bit primes. Furthermore,  only samples individual primes \(p\) or \(q\) that have \(p\equiv q\equiv 3\pmod {4}\), in order to facilitate efficient distributed primality testing, and it filters out the subset of otherwise-valid moduli \(N=p\cdot q\) that have \(p\equiv 1\pmod {q}\) or \(q\equiv 1\pmod {p}\).Footnote 6
only samples individual primes \(p\) or \(q\) that have \(p\equiv q\equiv 3\pmod {4}\), in order to facilitate efficient distributed primality testing, and it filters out the subset of otherwise-valid moduli \(N=p\cdot q\) that have \(p\equiv 1\pmod {q}\) or \(q\equiv 1\pmod {p}\).Footnote 6

Any protocol whose security depends upon the hardness of factoring moduli output by our protocol (including our protocol itself) must rely upon the assumption that for every PPT adversary \(\mathcal{A} \),

3.2 The Distributed Biprime-Sampling Functionality
Unfortunately, our ideal modulus-sampling functionality cannot merely call  ; we wish our functionality to run in strict polynomial time, whereas the running time of
; we wish our functionality to run in strict polynomial time, whereas the running time of  is only expected polynomial. Thus, we define a new sampling algorithm,
is only expected polynomial. Thus, we define a new sampling algorithm,  , which might fail, but conditioned on success outputs a distribution statistically indistinguishable from that of
, which might fail, but conditioned on success outputs a distribution statistically indistinguishable from that of  . Specifically, a coprimality constraint implies that there exists some concrete lower bound in \(O({\kappa })\) on the factors of the biprimes produced by
. Specifically, a coprimality constraint implies that there exists some concrete lower bound in \(O({\kappa })\) on the factors of the biprimes produced by  , whereas with probability negligible in \(\kappa \),
, whereas with probability negligible in \(\kappa \),  outputs biprimes with factors below this bound. Otherwise, for the appropriate (possibly non-integer) value of \({\kappa } \), the two output identical distributions, conditioned on success. However, we give
outputs biprimes with factors below this bound. Otherwise, for the appropriate (possibly non-integer) value of \({\kappa } \), the two output identical distributions, conditioned on success. However, we give  a specific distribution of failures that is tied to the design of our protocol. As a second concession to our protocol design (and following Hazay et al. [29]),
a specific distribution of failures that is tied to the design of our protocol. As a second concession to our protocol design (and following Hazay et al. [29]),  takes as input up to \(n-1\) integer shares of \(p\) and \(q\), arbitrarily determined by the adversary, while the remaining shares are sampled randomly. We begin with a few useful notions.
takes as input up to \(n-1\) integer shares of \(p\) and \(q\), arbitrarily determined by the adversary, while the remaining shares are sampled randomly. We begin with a few useful notions.
Definition 3.3
(Primorial Number) The \(i\)th primorial number is defined to be the product of the first i prime numbers.
Definition 3.4
(\(({\kappa },n)\)-Near-Primorial Vector) Let \(\ell \) be the largest number such that the \(\ell \)th primorial number is less than \(2^{{\kappa }-\log {n}-1}\), and let \({\varvec{\mathrm {m}}} \) be a vector of length \(\ell \) such that \({\varvec{\mathrm {m}}} _1=4\) and \({\varvec{\mathrm {m}}} _2,\ldots ,{\varvec{\mathrm {m}}} _\ell \) are the odd factors of the \(\ell ^\text {th}\) primorial number, in ascending order. \({\varvec{\mathrm {m}}} \) is the unique \(({\kappa },n)\)-near-primorial vector.
Definition 3.5
(\({\varvec{\mathrm {m}}} \)-Coprimality) Let \({\varvec{\mathrm {m}}} \) be a vector of integers. An integer x is \({\varvec{\mathrm {m}}} \)-coprime if and only if it is not divisible by any \({\varvec{\mathrm {m}}} _i\) for \(i\in [|{\varvec{\mathrm {m}}} |]\).

Boneh and Franklin [5, Lemma 2.1] showed that knowledge of \(n-1\) integer shares of the factors \(p\) and \(q\) does not give the adversary any meaningful advantage in factoring biprimes from the distribution produced by  . Hazay et al. [29, Lemma 4.1] extended this argument to the malicious setting, wherein the adversary is allowed to choose its own shares. A similar lemma must hold for
. Hazay et al. [29, Lemma 4.1] extended this argument to the malicious setting, wherein the adversary is allowed to choose its own shares. A similar lemma must hold for  , as a corollary of the fact that its output distribution differs only negligibly from that of
, as a corollary of the fact that its output distribution differs only negligibly from that of  .
.
Lemma 3.7
([5, 29]) Let \(n<{\kappa } \) and let \((\mathcal{A} _1,\mathcal{A} _2)\) be a pair of PPT algorithms. For \((\mathsf {state},\{(p_i,q_i)\}_{i\in [n-1]})\leftarrow \mathcal{A} _1(1^{\kappa },1^n)\), let \(N\) be a biprime sampled by running  . If \(\mathcal{A} _2(\mathsf {state},N)\) outputs the factors of \(N\) with probability at least \(\smash {1/{\kappa } ^d}\), then there exists an expected-polynomial-time algorithm \(\mathcal{B} \) that succeeds with probability at least \(1/2^4n^3{\kappa } ^d-\mathsf {negl}({\kappa })\) in the experiment
. If \(\mathcal{A} _2(\mathsf {state},N)\) outputs the factors of \(N\) with probability at least \(\smash {1/{\kappa } ^d}\), then there exists an expected-polynomial-time algorithm \(\mathcal{B} \) that succeeds with probability at least \(1/2^4n^3{\kappa } ^d-\mathsf {negl}({\kappa })\) in the experiment  .
.
Multiparty functionality. Our ideal functionality  is a natural embedding of
is a natural embedding of  in a multiparty functionality: it receives inputs \(\{(p_i,q_i)\}_{i\in {{\varvec{\mathrm {P}}}^*}}\) from the adversary and runs a single iteration of
in a multiparty functionality: it receives inputs \(\{(p_i,q_i)\}_{i\in {{\varvec{\mathrm {P}}}^*}}\) from the adversary and runs a single iteration of  with these inputs when invoked. It either outputs the corresponding modulus \(N:=p\cdot q\) if it is valid, or indicates that a sampling failure has occurred. Running a single iteration of
with these inputs when invoked. It either outputs the corresponding modulus \(N:=p\cdot q\) if it is valid, or indicates that a sampling failure has occurred. Running a single iteration of  per invocation of
per invocation of  enables significant freedom in the use of
enables significant freedom in the use of  , because it can be composed in different ways to tune the trade-off between resource usage and execution time. It also simplifies the analysis of the protocol
, because it can be composed in different ways to tune the trade-off between resource usage and execution time. It also simplifies the analysis of the protocol  that realizes
that realizes  , because the analysis is made independent of the success rate of the sampling procedure.
, because the analysis is made independent of the success rate of the sampling procedure.
The functionality may not deliver \(N\) to the honest parties for one of two reasons: either  failed to sample a biprime, or the adversary caused the computation to abort. In either case, the honest parties are informed of the cause of the failure, and consequently the adversary is unable to conflate the two cases. This is essentially the standard notion of security with abort, applied to the multiparty computation of the
failed to sample a biprime, or the adversary caused the computation to abort. In either case, the honest parties are informed of the cause of the failure, and consequently the adversary is unable to conflate the two cases. This is essentially the standard notion of security with abort, applied to the multiparty computation of the  algorithm. In both cases, the \(p\) and \(q\) output by
algorithm. In both cases, the \(p\) and \(q\) output by  are given to the adversary. This leakage simplifies our proof considerably, and we consider it benign, since the honest parties never receive (and therefore cannot possibly use) \(N\).
are given to the adversary. This leakage simplifies our proof considerably, and we consider it benign, since the honest parties never receive (and therefore cannot possibly use) \(N\).

4 The Distributed Biprime-Sampling Protocol
In this section, we present the distributed biprime-sampling protocol  , with which we realize
, with which we realize  . We begin with a high-level overview, and then in Sect. 4.2, we formally define the two ideal functionalities on which our protocol relies, after which in Sect. 4.3 we give the protocol itself. In Sect. 4.4, we present proof sketches of semi-honest and malicious security.
. We begin with a high-level overview, and then in Sect. 4.2, we formally define the two ideal functionalities on which our protocol relies, after which in Sect. 4.3 we give the protocol itself. In Sect. 4.4, we present proof sketches of semi-honest and malicious security.
4.1 High-Level Overview
As described in the Introduction, our protocol derives from that of Boneh and Franklin [5], the main technical differences relative to other recent Boneh–Franklin derivatives [23, 29] being the modularity with which it is described and proven, and the use of CRT-based sampling. Our protocol has three main phases, which we now describe in sequence.
Candidate Sieving. In the first phase of our protocol, the parties jointly sample two \({\kappa } \)-bit candidate primes \(p\) and \(q\) without any small factors, and multiply them to learn their product \(N\). Our protocol achieves these two tasks in an integrated way, thanks to the  .
.
Consider a prime \(m\) and a set of shares \(x_i\) for \(i\in [n]\) over the field \({\mathbb {Z}}_m\). As in the description of  , let a and b be defined such that \(a\cdot b\equiv 1\pmod {m}\), and let M be an integer. Observe that if m divides M, then
, let a and b be defined such that \(a\cdot b\equiv 1\pmod {m}\), and let M be an integer. Observe that if m divides M, then
Now consider a vector of coprime integers \({\varvec{\mathrm {m}}} \) of length \(\ell \), and let \(M\) be their product. Let \({\varvec{\mathrm {x}}}\) be a vector, each element secret shared over the fields defined by the corresponding element of \({\varvec{\mathrm {m}}} \), and let \({\varvec{\mathrm {a}}}\) and \({\varvec{\mathrm {b}}}\) be defined as in  (i.e., \({\varvec{\mathrm {a}}}_j :=M/{\varvec{\mathrm {m}}} _j\) and \({\varvec{\mathrm {a}}}_j\cdot {\varvec{\mathrm {b}}}_j \equiv 1 \pmod {{\varvec{\mathrm {m}}} _j}\)). We can see that for any \(k,j\in [\ell ]\) such that \(k\ne j\),
(i.e., \({\varvec{\mathrm {a}}}_j :=M/{\varvec{\mathrm {m}}} _j\) and \({\varvec{\mathrm {a}}}_j\cdot {\varvec{\mathrm {b}}}_j \equiv 1 \pmod {{\varvec{\mathrm {m}}} _j}\)). We can see that for any \(k,j\in [\ell ]\) such that \(k\ne j\),
and the conjunction of Eqs. 1 and 2 gives us
for all \(k\in [\ell ]\). Observe that this holds regardless of which order we perform the sums in, and regardless of whether the \(\bmod {\,M}\) operation is done at the end, or between the two sums, or not at all.
It follows then that we can sample n shares for an additive secret sharing over the integers of a \({\kappa } \)-bit value x (distributed between 0 and \(n\cdot M\)) by choosing \({\varvec{\mathrm {m}}} \) to be the \(({\kappa },n)\)-near-primorial vector (per Definition 3.4), instructing each party \(\mathcal{P} _i\) for \(i\in [n]\) to pick \({\varvec{\mathrm {x}}}_{i,j}\) locally for \(j\in [\ell ]\) such that \(0\le {\varvec{\mathrm {x}}}_{i,j}<{\varvec{\mathrm {m}}} _j\), and then instructing each party to locally reconstruct  , its share of x. It furthermore follows that if the parties can contrive to ensure that
, its share of x. It furthermore follows that if the parties can contrive to ensure that
for \(j\in [\ell ]\), then x will not be divisible by any prime in \({\varvec{\mathrm {m}}} \).
Observe next that if the parties sample two shared vectors \({\varvec{\mathrm {p}}}\) and \({\varvec{\mathrm {q}}}\) as above (corresponding to the candidate primes \(p\) and \(q\)) and compute a shared vector \({\varvec{\mathrm {N}}}\) of identical dimension such that
for all \(j\in [\ell ]\), then it follows that

and from this it follows that the parties can calculate integer shares of \(N=p\cdot q\) by multiplying \({\varvec{\mathrm {p}}}\) and \({\varvec{\mathrm {q}}}\) together element-wise using a modular-multiplication protocol for linear secret shares, and then locally running  on the output to reconstruct \(N\). In fact, our sampling protocol makes use of a special functionality
on the output to reconstruct \(N\). In fact, our sampling protocol makes use of a special functionality  , which samples \({\varvec{\mathrm {p}}}\), \({\varvec{\mathrm {q}}}\), and \({\varvec{\mathrm {N}}}\) simultaneously such that the conditions in Eqs. 3 and 4 hold.
, which samples \({\varvec{\mathrm {p}}}\), \({\varvec{\mathrm {q}}}\), and \({\varvec{\mathrm {N}}}\) simultaneously such that the conditions in Eqs. 3 and 4 hold.
There remains one problem: our vector \({\varvec{\mathrm {m}}} \) was chosen for sampling integer-shared values between 0 and \(n\cdot M\) (with each share no larger than \(M\)), but \(N\) might be as large as \(n^2\cdot M^2\). In order to avoid wrapping during reconstruction of \(N\), we must reconstruct with respect to a larger vector of primes (while continuing to sample with respect to a smaller one). Let \({\varvec{\mathrm {m}}} \) now be of length \({\ell '}\), and let \(\ell \) continue to denote the length of the prefix of \({\varvec{\mathrm {m}}} \) with respect to which sampling is performed. After sampling the initial vectors \({\varvec{\mathrm {p}}}\), \({\varvec{\mathrm {q}}}\), and \({\varvec{\mathrm {N}}}\), each party \(\mathcal{P} _i\) for \(i\in [n]\) must extend \({\varvec{\mathrm {p}}}_{i,*}\) locally to \({\ell '}\) elements, by computing

for \(j\in [\ell +1,{\ell '}]\), and then likewise for \({\varvec{\mathrm {q}}}_{i,*}\).Footnote 7 Finally, the parties must use a modular-multiplication protocol to compute the appropriate extension of \({\varvec{\mathrm {N}}}\); from this extended \({\varvec{\mathrm {N}}}\), they can reconstruct shares of \(N=p\cdot q\). They swap these shares, and thus, each party ends the sieving phase of our protocol with a candidate biprime \(N\) and an integer share of each of its factors, \(p_i\) and \(q_i\).
Each party completes the first phase by performing a local trial division to check if \(N\) is divisible by any prime smaller than some bound B (which is a parameter of the protocol). The purpose of this step is to reduce the number of calls to  and thus improve efficiency.
and thus improve efficiency.
Biprimality Test. The parties jointly execute a biprimality test, where every party inputs the candidate \(N\) and its shares \(p_i\) and \(q_i\), and receives back a biprimality indicator. This phase essentially comprises a single call to a functionality  , which allows an adversary to force spurious negative results, but never returns false positive results. Though this phase is simple, much of the subtlety of our proof concentrates here: we show via a reduction to factoring that cheating parties have a negligible chance to pass the biprimality test if they provide wrong inputs. This eliminates the need to authenticate the inputs in any way.
, which allows an adversary to force spurious negative results, but never returns false positive results. Though this phase is simple, much of the subtlety of our proof concentrates here: we show via a reduction to factoring that cheating parties have a negligible chance to pass the biprimality test if they provide wrong inputs. This eliminates the need to authenticate the inputs in any way.
Consistency Check. To achieve malicious security, the parties must ensure that none among them cheated during the previous stages in a way that might influence the result of the computation. This is what we have previously termed the retroactive consistency check. If the biprimality test indicated that \(N\) is not a biprime, then the parties use a special interface of  to reveal the shares they used during the protocol, and then they verify locally and independently that \(p\) and \(q\) are not both primes. If the biprimality test indicated that \(N\) is a biprime, then the parties run a secure test (again via a special interface of
to reveal the shares they used during the protocol, and then they verify locally and independently that \(p\) and \(q\) are not both primes. If the biprimality test indicated that \(N\) is a biprime, then the parties run a secure test (again via a special interface of  ) to ensure that length extensions of \({\varvec{\mathrm {p}}}\) and \({\varvec{\mathrm {q}}}\) were performed honestly. To achieve semi-honest security, this phase is unnecessary, and the protocol can end with the biprimality test.
) to ensure that length extensions of \({\varvec{\mathrm {p}}}\) and \({\varvec{\mathrm {q}}}\) were performed honestly. To achieve semi-honest security, this phase is unnecessary, and the protocol can end with the biprimality test.
4.2 Ideal Functionalities Used in the Protocol
Augmented Multiparty Multiplier. The augmented multiplier functionality  (Functionality 4.1) is a reactive functionality that operates in multiple phases and stores internal state across calls. It is meant to help in manipulating CRT-form secret shares, and to enforce correct reuse of a set of shares across multiple operations. It contains five basic interfaces.
(Functionality 4.1) is a reactive functionality that operates in multiple phases and stores internal state across calls. It is meant to help in manipulating CRT-form secret shares, and to enforce correct reuse of a set of shares across multiple operations. It contains five basic interfaces.
-
The \(\texttt {sample}\) interface allows the parties to sample shares of nonzero multiplication triplets over small primes. That is, given a prime \(m\), the functionality receives a triplet \((x_i,y_i,z_i)\) from every corrupted party \(\mathcal{P} _i\), and then samples a triplet \((x_j,y_j,z_j)\leftarrow {\mathbb {Z}}^3_m\) for every honest \(\mathcal{P} _j\) conditioned on
$$\begin{aligned} \sum \limits _{i\in [n]}z_i\equiv \sum \limits _{i\in [n]}x_i\cdot \sum \limits _{i\in [n]}y_i \not \equiv 0\pmod {m} \end{aligned}$$In the context of
 , this is used to sample CRT-shares of \(p\) and \(q\).
, this is used to sample CRT-shares of \(p\) and \(q\). -
The \(\texttt {input}\) and \(\texttt {multiply}\) interfaces, taken together, allow the parties to load shares (with respect to some small prime modulus \(m\)) into the functionality’s memory, and later perform modular multiplication on two sets of shares that are associated with the same modulus. That is, given a prime \(m\), each party \(\mathcal{P} _i\) inputs \(x_i\) and, independently, \(y_i\), and when the parties request a product, the functionality samples a share of z from \({\mathbb {Z}}_m\) for each party subject to
$$\begin{aligned} \sum \limits _{i\in [n]}z_i\equiv \sum \limits _{i\in [n]}x_i\cdot \sum \limits _{i\in [n]}y_i\pmod {m} \end{aligned}$$In the context of
 , this interface is used to perform length-extension on CRT-shares of \(p\) and \(q\).
, this interface is used to perform length-extension on CRT-shares of \(p\) and \(q\). -
The \(\texttt {check}\) interface allows the parties to securely compute a predicate over the set of stored values. In the context of
 , this is used to check that the CRT-share extension of \(p\) and \(q\) has been performed correctly, when \(N\) is a biprime.
, this is used to check that the CRT-share extension of \(p\) and \(q\) has been performed correctly, when \(N\) is a biprime. -
The \(\texttt {open}\) interface allows the parties to retroactively reveal their inputs to one another. In the context of
 , this is used to verify the sampling procedure and biprimality test when \(N\) is not a biprime.
, this is used to verify the sampling procedure and biprimality test when \(N\) is not a biprime.
These five interfaces suffice for the malicious version of the protocol, and the first three alone suffice for the semi-honest version. We make a final adjustment, which leads to a substantial efficiency improvement in the protocol with which we realize  (which we describe in Appendix B). Specifically, we give the adversary an interface by which it can request that any stored value be leaked to itself, and by which it can (arbitrarily) determine the output of any call to the \(\texttt {sample}\) or \(\texttt {multiply}\) interfaces. However, if the adversary uses this interface, the functionality remembers, and informs the honest parties by aborting when the \(\texttt {check}\) or \(\texttt {open}\) interfaces is used.
(which we describe in Appendix B). Specifically, we give the adversary an interface by which it can request that any stored value be leaked to itself, and by which it can (arbitrarily) determine the output of any call to the \(\texttt {sample}\) or \(\texttt {multiply}\) interfaces. However, if the adversary uses this interface, the functionality remembers, and informs the honest parties by aborting when the \(\texttt {check}\) or \(\texttt {open}\) interfaces is used.

Biprimality Test. The biprimality-test functionality  (Functionality 4.2) abstracts the behavior of the biprimality test of Boneh and Franklin [5]. The functionality receives from each party a candidate biprime \(N\), along with shares of its factors \(p\) and \(q\). It checks whether \(p\) and \(q\) are primes and whether \(N=p\cdot q\). The adversary is given an additional interface, by which it can ask the functionality to leak the honest parties’ inputs, but when this interface is used then the functionality reports to the honest parties that \(N\) is not a biprime, even if it is one.
(Functionality 4.2) abstracts the behavior of the biprimality test of Boneh and Franklin [5]. The functionality receives from each party a candidate biprime \(N\), along with shares of its factors \(p\) and \(q\). It checks whether \(p\) and \(q\) are primes and whether \(N=p\cdot q\). The adversary is given an additional interface, by which it can ask the functionality to leak the honest parties’ inputs, but when this interface is used then the functionality reports to the honest parties that \(N\) is not a biprime, even if it is one.

Realizations. In Appendix B, we discuss a protocol to realize  , and in Sect. 5, we propose a protocol to realize
, and in Sect. 5, we propose a protocol to realize  . Both make use of generic MPC, but in such a way that no generic MPC is required unless \(N\) is a biprime.
. Both make use of generic MPC, but in such a way that no generic MPC is required unless \(N\) is a biprime.
4.3 The Protocol Itself
We refer the reader back to Sect. 4.1 for an overview of our protocol. We have mentioned that it requires a vector of coprime values, which is prefixed by the \(({\kappa },n)\)-near-primorial vector. We now give this vector a precise definition. Note that the efficiency of our protocol relies upon this vector, because we use its contents to sieve candidate primes. Since smaller numbers are more likely to be factors for the candidate primes, we choose the largest allowable set of the smallest sequential primes.
Definition 4.3
(\(({\kappa },n)\)-Compatible Parameter Set) Let \({\ell '}\) be the smallest number such that the \({\ell '}^\text {th}\) primorial number is greater than \(2^{2{\kappa }-1}\), and let \({\varvec{\mathrm {m}}} \) be a vector of length \({\ell '}\) such that \({\varvec{\mathrm {m}}} _1=4\) and \({\varvec{\mathrm {m}}} _2,\ldots ,{\varvec{\mathrm {m}}} _{\ell '}\) are the odd factors of the \({\ell '}^\text {th}\) primorial number, in ascending order. \(({\varvec{\mathrm {m}}},{\ell '},\ell ,M)\) is the \(({\kappa },n)\)-compatible parameter set if \(\ell < {\ell '}\) and the prefix of \({\varvec{\mathrm {m}}} \) of length \(\ell \) is the \(({\kappa }, n)\)-near-primorial vector per Definition 3.4, and if \(M\) is the product of this prefix.



4.4 Security Sketches
We now informally argue that  realizes
realizes  in the semi-honest and malicious settings. We give a full proof for the malicious setting in Appendix C.
in the semi-honest and malicious settings. We give a full proof for the malicious setting in Appendix C.
Theorem 4.5
The protocol  perfectly UC-realizes
perfectly UC-realizes  in the
in the  ,
, -hybrid model against a semi-honest adversary that statically corrupts up to \(n-1\) parties.
-hybrid model against a semi-honest adversary that statically corrupts up to \(n-1\) parties.
Proof Sketch
In lieu of arguing for the correctness of our protocol, we refer the reader to the explanation in Sect. 4.1 and focus here on the strategy of a simulator \(\mathcal{S} \) against a semi-honest adversary \(\mathcal{A} \) who corrupts the parties indexed by \({{\varvec{\mathrm {P}}}^*} \). \(\mathcal S\) forwards all messages between \(\mathcal{A} \) and the environment faithfully.
In Step 1 of  , for each \(j\in [2,\ell ]\), \(\mathcal S\) receives the \(\texttt {sample}\) instruction with modulus \({\varvec{\mathrm {m}}} _j\) on behalf of
, for each \(j\in [2,\ell ]\), \(\mathcal S\) receives the \(\texttt {sample}\) instruction with modulus \({\varvec{\mathrm {m}}} _j\) on behalf of  from all parties indexed by \({{\varvec{\mathrm {P}}}^*} \). For each j, it then samples \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for \(i\in {{\varvec{\mathrm {P}}}^*} \), and returns each triple to the appropriate party.
from all parties indexed by \({{\varvec{\mathrm {P}}}^*} \). For each j, it then samples \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for \(i\in {{\varvec{\mathrm {P}}}^*} \), and returns each triple to the appropriate party.
Step 2 involves no interaction on the part of the parties, but it is at this point that \(\mathcal S\) computes \(p_i\) and \(q_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \), in the same way that the parties themselves do. Note that since \({\varvec{\mathrm {p}}}_{*,1}\) and \({\varvec{\mathrm {q}}}_{*,1}\) are deterministically chosen, they are known to \(\mathcal S\). The simulator then sends these shares to  via the functionality’s \(\texttt {adv-input}\) interface and receives in return either a biprime \(N\), or two factors \(p\) and \(q\) such that \(N:=p\cdot q\) is not a biprime. Regardless, it instructs
via the functionality’s \(\texttt {adv-input}\) interface and receives in return either a biprime \(N\), or two factors \(p\) and \(q\) such that \(N:=p\cdot q\) is not a biprime. Regardless, it instructs  to \(\texttt {proceed}\).
to \(\texttt {proceed}\).
In Step 3 of  , \(\mathcal S\) receives two \(\texttt {input}\) instructions from each corrupted party for each \(j\in [\ell +1,{\ell '}]\) on behalf of
, \(\mathcal S\) receives two \(\texttt {input}\) instructions from each corrupted party for each \(j\in [\ell +1,{\ell '}]\) on behalf of  , and confirms receipt as
, and confirms receipt as  would. Subsequently, for each \(j\in [\ell +1,{\ell '}]\), the corrupt parties all send a \(\texttt {multiply}\) instruction, and then \(\mathcal S\) samples \({\varvec{\mathrm {N}}}_{i,j}\leftarrow {\mathbb {Z}}_{{\varvec{\mathrm {m}}} _j}\) for \(i\in [n]\) subject to
would. Subsequently, for each \(j\in [\ell +1,{\ell '}]\), the corrupt parties all send a \(\texttt {multiply}\) instruction, and then \(\mathcal S\) samples \({\varvec{\mathrm {N}}}_{i,j}\leftarrow {\mathbb {Z}}_{{\varvec{\mathrm {m}}} _j}\) for \(i\in [n]\) subject to
and returns each share to the matching corrupt party.
In Step 4 of  , for every \(j\in [{\ell '}]\), every corrupt party \(\mathcal{P} _{i'}\) for \(i'\in {{\varvec{\mathrm {P}}}^*} \), and every honest party \(\mathcal{P} _i\) for \(i\in [n]{\setminus }{{\varvec{\mathrm {P}}}^*} \), \(\mathcal S\) sends \({\varvec{\mathrm {N}}}_{i,j}\) to \(\mathcal{P} _{i'}\) on behalf of \(\mathcal{P} _i\), and receives \({\varvec{\mathrm {N}}}_{i',j}\) (which it already knows) in reply.
, for every \(j\in [{\ell '}]\), every corrupt party \(\mathcal{P} _{i'}\) for \(i'\in {{\varvec{\mathrm {P}}}^*} \), and every honest party \(\mathcal{P} _i\) for \(i\in [n]{\setminus }{{\varvec{\mathrm {P}}}^*} \), \(\mathcal S\) sends \({\varvec{\mathrm {N}}}_{i,j}\) to \(\mathcal{P} _{i'}\) on behalf of \(\mathcal{P} _i\), and receives \({\varvec{\mathrm {N}}}_{i',j}\) (which it already knows) in reply.
To simulate the final steps of  , \(\mathcal S\) tries to divide \(N\) by all primes smaller than B. If it succeeds, then the protocol is complete. Otherwise, it receives \(\texttt {check-}\texttt {biprimality}\) from all of the corrupt parties on behalf of
, \(\mathcal S\) tries to divide \(N\) by all primes smaller than B. If it succeeds, then the protocol is complete. Otherwise, it receives \(\texttt {check-}\texttt {biprimality}\) from all of the corrupt parties on behalf of  , and replies with \(\texttt {biprime}\) or \(\texttt {not-biprime}\) as appropriate. It can be verified by inspection that the view of the environment is identically distributed in the ideal-world experiment containing \(\mathcal S\) and honest parties that interact with
, and replies with \(\texttt {biprime}\) or \(\texttt {not-biprime}\) as appropriate. It can be verified by inspection that the view of the environment is identically distributed in the ideal-world experiment containing \(\mathcal S\) and honest parties that interact with  , and the real-world experiment containing \(\mathcal A\) and parties running
, and the real-world experiment containing \(\mathcal A\) and parties running  .
.
Theorem 4.6
If factoring biprimes sampled by  is hard, then
is hard, then  UC-realizes
UC-realizes  in the
in the  -hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
-hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
Proof Sketch
We observe that if the adversary simply follows the specification of the protocol and does not cheat in its inputs to  or
or  , then the simulator can follow the same strategy as in the semi-honest case. At any point, if the adversary deviates from the protocol, the simulator requests
, then the simulator can follow the same strategy as in the semi-honest case. At any point, if the adversary deviates from the protocol, the simulator requests  to reveal all honest parties’ shares, and thereafter the simulator uses them by effectively running the code of the honest parties. This matches the adversary’s view in the real protocol as far as the distribution of the honest parties’ shares is concerned.
to reveal all honest parties’ shares, and thereafter the simulator uses them by effectively running the code of the honest parties. This matches the adversary’s view in the real protocol as far as the distribution of the honest parties’ shares is concerned.
It remains to be argued that any deviation from the protocol specification will also result in an abort in the real world with honest parties and will additionally be recognized by the honest parties as an adversarially induced cheat (as opposed to a statistical sampling failure). Note that the honest parties must only detect cheating when \(N\) is truly a biprime and the adversary has sabotaged a successful candidate; if \(N\) is not a biprime and would have been rejected anyway, then cheat detection is unimportant. We analyze all possible cases where the adversary deviates from the protocol below. Let \(N\) be defined as the value implied by parties’ sampled shares in Step 1 of  .
.
Case 1: \(N\) is a non-biprime and reconstructed correctly. In this case,  will always reject \(N\) as there exist no satisfying inputs (i.e., there are no two prime factors \(p,q\) such that \(p\cdot q=N\)).
will always reject \(N\) as there exist no satisfying inputs (i.e., there are no two prime factors \(p,q\) such that \(p\cdot q=N\)).
Case 2: \(N\) is a non-biprime and reconstructed incorrectly as \(N'\). If by fluke \(N'\) happens to be a biprime, then the incorrect reconstruction will be caught by the explicit secure predicate check during the consistency-check phase. If \(N'\) is a non-biprime, then the argument from the previous case applies.
Case 3: \(N\) is a biprime and reconstructed correctly. If consistent inputs are used for the biprimality test and nobody cheats, the candidate \(N\) is successfully accepted (this case essentially corresponds to the semi-honest case). Otherwise, if inconsistent inputs are used for the biprimality test, one of the following events will occur:
-
 rejects this candidate. In this case, all parties reveal their shares of \(p\) and \(q\) to one another (with guaranteed correctness via
rejects this candidate. In this case, all parties reveal their shares of \(p\) and \(q\) to one another (with guaranteed correctness via  ) and locally test their primality. This will reveal that \(N\) was a biprime and that
) and locally test their primality. This will reveal that \(N\) was a biprime and that  must have been supplied with inconsistent inputs, implying that some party has cheated.
must have been supplied with inconsistent inputs, implying that some party has cheated. -
 accepts this candidate. This case occurs with negligible probability (assuming factoring is hard). Because \(N\) only has two factors, there is exactly one pair of inputs that the adversary can supply to
accepts this candidate. This case occurs with negligible probability (assuming factoring is hard). Because \(N\) only has two factors, there is exactly one pair of inputs that the adversary can supply to  to induce this scenario, apart from the pair specified by the protocol. In our full proof (see Appendix C) we show that finding this alternative pair of satisfying inputs implies factoring \(N\). We are careful to rely on the hardness of factoring only in this case, where by premise \(N\) is a biprime with \({\kappa } \)-bit factors (i.e., an instance of the factoring problem).
to induce this scenario, apart from the pair specified by the protocol. In our full proof (see Appendix C) we show that finding this alternative pair of satisfying inputs implies factoring \(N\). We are careful to rely on the hardness of factoring only in this case, where by premise \(N\) is a biprime with \({\kappa } \)-bit factors (i.e., an instance of the factoring problem).
Case 4: \(N\) is a biprime and reconstructed incorrectly as \(N'\). If \(N'\) is a biprime then the incorrect reconstruction will be caught during the consistency-check phase, just as when \(N\) is a biprime. If \(N'\) is a non-biprime, then it will be rejected by  , inducing all parties to reveal their shares and find that their shares do not in fact reconstruct to \(N'\), with the implication that some party has cheated.
, inducing all parties to reveal their shares and find that their shares do not in fact reconstruct to \(N'\), with the implication that some party has cheated.
Thus, the adversary is always caught when trying to sabotage a true biprime, and it can never sneak a non-biprime past the consistency check. Because the real-world protocol always aborts in the case of cheating, it is indistinguishable from the simulation described above, assuming that factoring is hard. \(\square \)
5 Distributed Biprimality Testing
In this section, we present protocols realizing  . In Sect. 5.1, we discuss the semi-honest setting, and in Sect. 5.2, the malicious setting.
. In Sect. 5.1, we discuss the semi-honest setting, and in Sect. 5.2, the malicious setting.
5.1 The Semi-Honest Setting
In the semi-honest setting,  can be realized by the biprimality-testing protocol of Boneh and Franklin [5]. Loosely speaking, the Boneh–Franklin protocol is a variant of the Miller–Rabin test: for a randomly chosen \(\gamma \in {\mathbb {Z}}^*_N\) with Jacobi symbol 1, it checks whether \(\gamma ^{(N- p- q+1)/4} \equiv \pm 1 \pmod {N}\) (recall that \(\varphi (N)=N- p- q+1\)). A biprime will always pass this test, but non-biprimes may yield a false positive with probability 1/2. The test is repeated \({s} \) times (either sequentially or concurrently) in order to bound the probability of proceeding with a false positive to \(2^{-{s}}\) (where \({s} \) is the statistical security parameter).
can be realized by the biprimality-testing protocol of Boneh and Franklin [5]. Loosely speaking, the Boneh–Franklin protocol is a variant of the Miller–Rabin test: for a randomly chosen \(\gamma \in {\mathbb {Z}}^*_N\) with Jacobi symbol 1, it checks whether \(\gamma ^{(N- p- q+1)/4} \equiv \pm 1 \pmod {N}\) (recall that \(\varphi (N)=N- p- q+1\)). A biprime will always pass this test, but non-biprimes may yield a false positive with probability 1/2. The test is repeated \({s} \) times (either sequentially or concurrently) in order to bound the probability of proceeding with a false positive to \(2^{-{s}}\) (where \({s} \) is the statistical security parameter).
The above test filters out all non-biprimes except those with factors of the form \(p=a_1^{b_1}\) and \(q=a_2^{b_2}\), with \(q\equiv 1 \pmod {a_1^{b_1-1}}\). This final class of non-biprimes is filtered by securely sampling \(r\leftarrow {\mathbb {Z}}_N\), computing \(z:=r\cdot (p+q-1)\), and then testing whether \(\gcd (z,N)=1\).Footnote 8 Boneh and Franklin suggest that the secure sampling of r and the computation of z can be done via generic MPC; we provide a functionality  (see Appendix A.2) that is adequate for the task, but note that other strategies exist: for example, Frederiksen et al. use a bespoke protocol, which could be further optimized by performing its multiparty multiplication operations in CRT form, as we have outlined in this work. As we report in Sect. 6, this final GCD test does not represent a substantial fraction of the overall cost in the semi-honest setting, even if it is instantiated generically, and so the impact of such optimizations would be minimal. Regardless, we note that the GCD test does induce some false negatives (modeled by
(see Appendix A.2) that is adequate for the task, but note that other strategies exist: for example, Frederiksen et al. use a bespoke protocol, which could be further optimized by performing its multiparty multiplication operations in CRT form, as we have outlined in this work. As we report in Sect. 6, this final GCD test does not represent a substantial fraction of the overall cost in the semi-honest setting, even if it is instantiated generically, and so the impact of such optimizations would be minimal. Regardless, we note that the GCD test does induce some false negatives (modeled by  ) and refer the reader to Boneh and Franklin [5, Section 4.1] for a more comprehensive discussion. The following lemma is immediately implied by their work.
) and refer the reader to Boneh and Franklin [5, Section 4.1] for a more comprehensive discussion. The following lemma is immediately implied by their work.
Lemma 5.1
The biprimality-testing protocol described by Boneh and Franklin [5] UC-realizes  with statistical security in the
with statistical security in the  -hybrid model against a static, semi-honest adversary who corrupts up to \(n-1\) parties.
-hybrid model against a static, semi-honest adversary who corrupts up to \(n-1\) parties.
5.2 The Malicious Setting
Unlike a semi-honest adversary, we permit a malicious adversary to force a true biprime to fail our biprimality test and detect such behavior using independent mechanisms in the  protocol. However, we must ensure that a non-biprime can never pass the test with more than negligible probability. To achieve this, we use a derivative of the biprimality-testing protocol of Frederiksen et al. [23]. Our protocol takes essentially the same high-level approach as theirs, but the complexity of our protocol is reduced because we consider multiple soundness errors jointly instead of independently. Furthermore, by careful reordering and the right choice of functionalities, we eliminate the non-black-box use of commitments, as well as an expensive, redundant multiparty multiplication over \(2{\kappa } \)-bit inputs.
protocol. However, we must ensure that a non-biprime can never pass the test with more than negligible probability. To achieve this, we use a derivative of the biprimality-testing protocol of Frederiksen et al. [23]. Our protocol takes essentially the same high-level approach as theirs, but the complexity of our protocol is reduced because we consider multiple soundness errors jointly instead of independently. Furthermore, by careful reordering and the right choice of functionalities, we eliminate the non-black-box use of commitments, as well as an expensive, redundant multiparty multiplication over \(2{\kappa } \)-bit inputs.
Our protocol essentially comprises a randomized version of the semi-honest Boneh–Franklin test described previously, followed by a Schnorr-like protocol to verify that the test was performed correctly. The soundness error of the underlying biprimality test is compounded by the Schnorr-like protocol’s soundness error to yield a combined error of 3/4, which implies that the test must repeated \({s} \cdot \log _{4/3}(2)<2.5{s} \) times in order to achieve a soundness error no greater than \(2^{-{s}}\) overall. While this is sufficient to ensure the test itself is carried out honestly, it does not ensure the correct inputs are used. Consequently, generic MPC is used to verify the relationship between the messages involved in the Schnorr-like protocol and the true candidate given by \(N\) and shares of its factors. As a side effect, this generic computation samples \(r\leftarrow {\mathbb {Z}}_N\) and outputs \(z=r\cdot (p+q-1)\bmod {N}\) so that the GCD test can afterward be run locally by each party.
Our protocol makes use of a number of subfunctionalities, all of which are standard and described in Appendix A.2. Namely, we use a coin-tossing functionality  to uniformly sample an element from some set, the one-to-many commitment functionality
to uniformly sample an element from some set, the one-to-many commitment functionality  , the generic MPC functionality over committed inputs
, the generic MPC functionality over committed inputs  , and the integer-sharing-of-zero functionality
, and the integer-sharing-of-zero functionality  . In addition, the protocol uses the algorithm
. In addition, the protocol uses the algorithm  (Algorithm 5.3).
(Algorithm 5.3).



Below we present the algorithm  that is used for the GCD test. The inputs are the candidate biprime \(N\), an integer \(M\) (the bound on the shares’ size), a bit-vector \({\varvec{\mathrm {c}}}\) of length \(2.5{s} \), and for each \(i\in [n]\) a tuple consisting of the shares \(p_i\) and \(q_i\) with the Schnorr-like messages \({\varvec{\mathrm {\tau }}}_{i,*}\) and \({\varvec{\mathrm {\zeta }}}_{i,*}\) generated by \(\mathcal{P} _i\). The algorithm verifies that all input values are compatible and returns \(z=r\cdot (p+q-1) \bmod N\) for a random r.
that is used for the GCD test. The inputs are the candidate biprime \(N\), an integer \(M\) (the bound on the shares’ size), a bit-vector \({\varvec{\mathrm {c}}}\) of length \(2.5{s} \), and for each \(i\in [n]\) a tuple consisting of the shares \(p_i\) and \(q_i\) with the Schnorr-like messages \({\varvec{\mathrm {\tau }}}_{i,*}\) and \({\varvec{\mathrm {\zeta }}}_{i,*}\) generated by \(\mathcal{P} _i\). The algorithm verifies that all input values are compatible and returns \(z=r\cdot (p+q-1) \bmod N\) for a random r.

Theorem 5.4
The protocol  statistically UC-realizes
statistically UC-realizes  in the
in the  -hybrid model against a malicious adversary that statically corrupts up to \(n-1\) parties.
-hybrid model against a malicious adversary that statically corrupts up to \(n-1\) parties.
Proof Sketch
Our simulator \(\mathcal{S} \) for  receives \(N\) as common input. Let \({{\varvec{\mathrm {P}}}^*} \) and
receives \(N\) as common input. Let \({{\varvec{\mathrm {P}}}^*} \) and  be vectors indexing the corrupt and honest parties, respectively. To simulate Steps 1 through 3 of
be vectors indexing the corrupt and honest parties, respectively. To simulate Steps 1 through 3 of  , \(\mathcal S\) simply behaves as
, \(\mathcal S\) simply behaves as  ,
,  , and
, and  would in its interactions with the corrupt parties on their behalf, remembering the values received and transmitted. Before continuing, \(\mathcal S\) submits the corrupted parties’ shares of \(p\) and \(q\) to
would in its interactions with the corrupt parties on their behalf, remembering the values received and transmitted. Before continuing, \(\mathcal S\) submits the corrupted parties’ shares of \(p\) and \(q\) to  on their behalf. In response,
on their behalf. In response,  either informs \(\mathcal S\) that \(N\) is a biprime or leaks the honest parties’ shares. In Step 4, \(\mathcal S\) again behaves exactly as
either informs \(\mathcal S\) that \(N\) is a biprime or leaks the honest parties’ shares. In Step 4, \(\mathcal S\) again behaves exactly as  would. During the remainder of the protocol, the simulator must follow one of two different strategies, conditioned on whether or not \(N\) is a biprime. We will show that both strategies lead to a simulation that is statistically indistinguishable from the real-world experiment.
would. During the remainder of the protocol, the simulator must follow one of two different strategies, conditioned on whether or not \(N\) is a biprime. We will show that both strategies lead to a simulation that is statistically indistinguishable from the real-world experiment.
-
If
 reported that \(N\) is a biprime, then we know by the specification of
reported that \(N\) is a biprime, then we know by the specification of  that the corrupt parties committed to correct shares of \(p\) and \(q\) in Step 1 of
that the corrupt parties committed to correct shares of \(p\) and \(q\) in Step 1 of  . Boneh and Franklin [5, Proof of Lemma 4.2] showed that the value (i.e., sign) of the right-hand side of the equality in Step 7 is predictable and related to the value of \({\varvec{\mathrm {\gamma }}}_j\). We refer to them for a precise description and proof. If without loss of generality we take that value to be 1, then \(\mathcal S\) can simulate iteration j of Steps 6 and 7 as follows. First, \(\mathcal S\) computes \(\hat{{\varvec{\mathrm {\chi }}}}_{i,j}\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) to be the corrupt parties’ ideal values of \({\varvec{\mathrm {\chi }}}_{i,j}\) as defined in Step 4 of
. Boneh and Franklin [5, Proof of Lemma 4.2] showed that the value (i.e., sign) of the right-hand side of the equality in Step 7 is predictable and related to the value of \({\varvec{\mathrm {\gamma }}}_j\). We refer to them for a precise description and proof. If without loss of generality we take that value to be 1, then \(\mathcal S\) can simulate iteration j of Steps 6 and 7 as follows. First, \(\mathcal S\) computes \(\hat{{\varvec{\mathrm {\chi }}}}_{i,j}\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) to be the corrupt parties’ ideal values of \({\varvec{\mathrm {\chi }}}_{i,j}\) as defined in Step 4 of  . Then, \(\mathcal S\) samples \({\varvec{\mathrm {\chi }}}_{i,j}\leftarrow {\mathbb {Z}}^*_N\) uniformly for
. Then, \(\mathcal S\) samples \({\varvec{\mathrm {\chi }}}_{i,j}\leftarrow {\mathbb {Z}}^*_N\) uniformly for  subject to
subject to 
and simulates Step 6 by releasing \({\varvec{\mathrm {\chi }}}_{i,j}\) for
 to the corrupt parties on behalf of
to the corrupt parties on behalf of  . These values are statistically close to their counterparts in the real protocol. Finally, \(\mathcal S\) simulates Step 7 by running the test for itself and sending the \(\texttt {cheat}\) command to
. These values are statistically close to their counterparts in the real protocol. Finally, \(\mathcal S\) simulates Step 7 by running the test for itself and sending the \(\texttt {cheat}\) command to  on failure. Given the information now known to \(\mathcal S\), Steps 8 through 11 of
on failure. Given the information now known to \(\mathcal S\), Steps 8 through 11 of  can be simulated in a manner similar to the simulation of a common Schnorr protocol: \(\mathcal S\) simply chooses \({\varvec{\mathrm {\zeta }}}_{i,*} \leftarrow {\mathbb {Z}}^{2.5{s}}_{M\cdot 2^{{s} + 1}}\) uniformly for
can be simulated in a manner similar to the simulation of a common Schnorr protocol: \(\mathcal S\) simply chooses \({\varvec{\mathrm {\zeta }}}_{i,*} \leftarrow {\mathbb {Z}}^{2.5{s}}_{M\cdot 2^{{s} + 1}}\) uniformly for  , fixes \({\varvec{\mathrm {c}}}\leftarrow \{0,1\}^{2.5{s}}\) ahead of time, and then works backward via the equation in Step 11 to compute the values of \({\varvec{\mathrm {\alpha }}}_{i,*}\) for
, fixes \({\varvec{\mathrm {c}}}\leftarrow \{0,1\}^{2.5{s}}\) ahead of time, and then works backward via the equation in Step 11 to compute the values of \({\varvec{\mathrm {\alpha }}}_{i,*}\) for  that it must send on behalf of the honest parties in Step 8. These values are statistically close to their counterparts in the real protocol. \(\mathcal S\) finally simulates the remaining steps of
that it must send on behalf of the honest parties in Step 8. These values are statistically close to their counterparts in the real protocol. \(\mathcal S\) finally simulates the remaining steps of  by checking the
by checking the  predicate itself (since the final GCD test is purely local, no action need be taken by \(\mathcal S\)). If at any point after Step 4 the corrupt parties have cheated (i.e., sent an unexpected value or violated the
predicate itself (since the final GCD test is purely local, no action need be taken by \(\mathcal S\)). If at any point after Step 4 the corrupt parties have cheated (i.e., sent an unexpected value or violated the  predicate), then \(\mathcal S\) sends the \(\texttt {cheat}\) command to
predicate), then \(\mathcal S\) sends the \(\texttt {cheat}\) command to  . Otherwise, it sends the \(\texttt {proceed}\) command to
. Otherwise, it sends the \(\texttt {proceed}\) command to  , completing the simulation.
, completing the simulation.
-
If
 reported that \(N\) is not a biprime (which may indicate that the corrupt parties supplied incorrect shares of \(p\) or \(q\)), then it also leaked the honest parties’ shares of \(p\) and \(q\) to \(\mathcal S\). Thus, \(\mathcal S\) can simulate Steps 4 through 13 of
reported that \(N\) is not a biprime (which may indicate that the corrupt parties supplied incorrect shares of \(p\) or \(q\)), then it also leaked the honest parties’ shares of \(p\) and \(q\) to \(\mathcal S\). Thus, \(\mathcal S\) can simulate Steps 4 through 13 of  by running the honest parties’ code on their behalf. In all instances of the ideal-world experiment, the honest parties report to the environment that \(N\) is a non-biprime. Thus, we need only prove that there is no strategy by which the corrupt parties can successfully convince the honest parties that \(N\) is a biprime in the real world.
by running the honest parties’ code on their behalf. In all instances of the ideal-world experiment, the honest parties report to the environment that \(N\) is a non-biprime. Thus, we need only prove that there is no strategy by which the corrupt parties can successfully convince the honest parties that \(N\) is a biprime in the real world.In order to get away with such a real-world cheat, the adversary must cheat in every iteration j of Steps 4 through 6 for which
$$\begin{aligned} {\varvec{\mathrm {\gamma }}}_j^{(N-p-q)/4}\not \equiv \pm 1\pmod {N} \end{aligned}$$Specifically, in every such iteration j, the corrupt parties must contrive to send values \({\varvec{\mathrm {\chi }}}_{i,j}\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) such that
$$\begin{aligned} {\varvec{\mathrm {\gamma }}}_j^{(N - 5)/4} \cdot \prod \limits _{i\in [n]} {\varvec{\mathrm {\chi }}}_{i,j} \equiv {\varvec{\mathrm {\gamma }}}_j^{(N-p-q)/4 + {\varvec{\mathrm {\Delta }}}_{1,j}} \equiv \pm 1\pmod {N} \end{aligned}$$for some nonzero offset value \({\varvec{\mathrm {\Delta }}}_{1,j}\). We can define a similar offset \({\varvec{\mathrm {\Delta }}}_{2,j}\) for the corrupt parties’ transmitted values of \({\varvec{\mathrm {\alpha }}}_{i,j}\), relative to the values of \({\varvec{\mathrm {\tau }}}_{i,j}\) committed in Step 1:
$$\begin{aligned} {\varvec{\mathrm {\gamma }}}_j^{{\varvec{\mathrm {\Delta }}}_{2,j}}\cdot \prod \limits _{i\in [n]} {\varvec{\mathrm {\alpha }}}_{i,j} \equiv \prod \limits _{i\in [n]}{\varvec{\mathrm {\gamma }}}_j^{{\varvec{\mathrm {\tau }}}_{i,j}} \pmod {N} \end{aligned}$$Since we have presupposed that the protocol outputs \(\texttt {biprime}\), we know that the corrupt parties must transmit correctly calculated values of \({\varvec{\mathrm {\zeta }}}_{i,*}\) in Step 10 of
 , or else Step 12 would output \(\texttt {non-biprime}\) when these values are checked by the
, or else Step 12 would output \(\texttt {non-biprime}\) when these values are checked by the  predicate. It follows from this fact and from the equation in Step 11 that \({\varvec{\mathrm {\Delta }}}_{2,j} \equiv {\varvec{\mathrm {c}}}_j\cdot {\varvec{\mathrm {\Delta }}}_{1,j} \pmod {\varphi (N)}\), where \(\varphi (\cdot )\) is Euler’s totient function. However, both \({\varvec{\mathrm {\Delta }}}_{1,*}\) and \({\varvec{\mathrm {\Delta }}}_{2,*}\) are fixed before \({\varvec{\mathrm {c}}}\) is revealed to the corrupt parties, and so the adversary can succeed in this cheat with probability at most 1/2 for any individual iteration j. Per Boneh and Franklin [5, Lemma 4.1], a particular iteration j of Steps 4 through 6 of
predicate. It follows from this fact and from the equation in Step 11 that \({\varvec{\mathrm {\Delta }}}_{2,j} \equiv {\varvec{\mathrm {c}}}_j\cdot {\varvec{\mathrm {\Delta }}}_{1,j} \pmod {\varphi (N)}\), where \(\varphi (\cdot )\) is Euler’s totient function. However, both \({\varvec{\mathrm {\Delta }}}_{1,*}\) and \({\varvec{\mathrm {\Delta }}}_{2,*}\) are fixed before \({\varvec{\mathrm {c}}}\) is revealed to the corrupt parties, and so the adversary can succeed in this cheat with probability at most 1/2 for any individual iteration j. Per Boneh and Franklin [5, Lemma 4.1], a particular iteration j of Steps 4 through 6 of  produces a false positive result with probability at most 1/2 if the adversary behaves honestly. If we assume that the adversary cheats always and only when a false positive would not have been produced by honest behavior, then the total probability of an adversary producing a positive outcome in the \(j\)th iteration of Steps 4 through 6 is upper-bounded by 3/4. The probability that an adversary succeeds over all \(2.5{s} \) iterations is therefore at most \((3/4)^{2.5{s}}<2^{-{s}}\). Thus, the adversary has a negligible chance to force the acceptance of a non-biprime in the real world, and the distribution of outcomes produced by \(\mathcal S\) is statistically indistinguishable from the real-world distribution. \(\square \)
produces a false positive result with probability at most 1/2 if the adversary behaves honestly. If we assume that the adversary cheats always and only when a false positive would not have been produced by honest behavior, then the total probability of an adversary producing a positive outcome in the \(j\)th iteration of Steps 4 through 6 is upper-bounded by 3/4. The probability that an adversary succeeds over all \(2.5{s} \) iterations is therefore at most \((3/4)^{2.5{s}}<2^{-{s}}\). Thus, the adversary has a negligible chance to force the acceptance of a non-biprime in the real world, and the distribution of outcomes produced by \(\mathcal S\) is statistically indistinguishable from the real-world distribution. \(\square \)
6 Efficiency Analysis
In this section, we give both an asymptotic and a closed-form concrete cost analysis of our protocol, with both semi-honest and malicious security. We begin by addressing the success probability of our ideal functionality  , as determined by analysis of the sampling function
, as determined by analysis of the sampling function  that it uses. We also discuss various strategies for composing invocations of
that it uses. We also discuss various strategies for composing invocations of  to amplify the probability that a biprime is successfully produced. After this, we analyze the costs of the protocols realizing
to amplify the probability that a biprime is successfully produced. After this, we analyze the costs of the protocols realizing  and
and  in Sect. 6.2, and in Sect. 6.3, we compose those costs to give an overall cost for each invocation of
in Sect. 6.2, and in Sect. 6.3, we compose those costs to give an overall cost for each invocation of  . In Sect. 6.4, we discuss a compositional strategy that leads to constant or expected-constant rounds overall, and calculate the precise number of rounds required. Finally, in Sect. 6.5, we provide a performance comparison to the protocol of Frederiksen et al. [23].
. In Sect. 6.4, we discuss a compositional strategy that leads to constant or expected-constant rounds overall, and calculate the precise number of rounds required. Finally, in Sect. 6.5, we provide a performance comparison to the protocol of Frederiksen et al. [23].
6.1 Per-Instance Success Probability
By construction, the success probability of  is identical to that of
is identical to that of  . To bound the success probability of
. To bound the success probability of  , it suffices to determine the probability that a randomly chosen value is prime, conditioned on that value having \({\varvec{\mathrm {m}}} \)-coprimality (per Definition 3.5) relative to the \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}} \) of length \(\ell \). We begin by bounding the probability of finding a prime from below, relative to \(\max ({\varvec{\mathrm {m}}})\), the largest value in \({\varvec{\mathrm {m}}} \).
, it suffices to determine the probability that a randomly chosen value is prime, conditioned on that value having \({\varvec{\mathrm {m}}} \)-coprimality (per Definition 3.5) relative to the \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}} \) of length \(\ell \). We begin by bounding the probability of finding a prime from below, relative to \(\max ({\varvec{\mathrm {m}}})\), the largest value in \({\varvec{\mathrm {m}}} \).
Lemma 6.1
([5]) Given a \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}} \),
Observe that this is a concrete lower bound. Next, in the interest of asymptotic analysis, we bound the value of the maximum element in \({\varvec{\mathrm {m}}} \). We first adapt a lemma from Rosser and Schoenfeld [47] to bound \(\max ({\varvec{\mathrm {m}}})\) with respect to the product of the elements of \({\varvec{\mathrm {m}}} \), and we then use this to construct a bound with respect to \({\kappa } \).
Lemma 6.2
([47], Theorem 4) Given a \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}} \) and its product \(M\), it holds that \(\max ({\varvec{\mathrm {m}}})\in \Theta (\log M)\).
Lemma 6.3
Given a \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}}\), it holds that \(\max ({\varvec{\mathrm {m}}}) \in \Omega ({\kappa })\).
Proof
Let \(M\) be the product of \({\varvec{\mathrm {m}}} \). By Definition 3.4, M is the largest integer such that M/2 is a primorial and \(M < 2^{{\kappa }- \log n}\). From these facts, the prime number theorem gives us \(M\in \Omega (2^{{\kappa }- \log n - \log {\kappa }})\). Combining this with Lemma 6.2 yields \(\max ({\varvec{\mathrm {m}}})\in \Omega ({\kappa }- \log n - \log {\kappa })\) and finally, Lemma 3.7 constrains \(2\le n<{\kappa } \), which yields \(\max ({\varvec{\mathrm {m}}})\in \Omega ({\kappa })\). \(\square \)
Combining Lemmas 6.1 and 6.3 and considering that  must sample two primes simultaneously (but independently) yields an asymptotic figure for the success probability of
must sample two primes simultaneously (but independently) yields an asymptotic figure for the success probability of  . Since this governs the number of times
. Since this governs the number of times  must be invoked in order to generate a biprime, we refer to it as our sampling-efficiency theorem.
must be invoked in order to generate a biprime, we refer to it as our sampling-efficiency theorem.
Theorem 6.4
(Sampling-efficiency theorem) For any strict subset \({{\varvec{\mathrm {P}}}^*} \subset [n]\) and any \((p_i,q_i)\in {\mathbb {Z}}^2_{2^{\kappa }}\) for \(i\in {{\varvec{\mathrm {P}}}^*} \),  samples a biprime with probability \(\Omega (\log ^2 {\kappa }/{\kappa } ^2)\).
samples a biprime with probability \(\Omega (\log ^2 {\kappa }/{\kappa } ^2)\).
In order to understand the concrete efficiency of our approach, we determined the unique \(({\kappa },n)\)-near-primorial vectors corresponding to several common RSA security parameter values and then used Lemma 6.1 to derive concrete success probabilities. These are reported in Table 2. For completeness, we also report the asymptotic size of the \(({\kappa },n)\)-near-primorial vector; this can be derived by combining Lemma 6.2 with the following lemma:
Lemma 6.5
([47], Theorem 2) Given a \(({\kappa },n)\)-near-primorial vector \({\varvec{\mathrm {m}}} \) of length \(\ell \), it holds that \(\ell \in \Theta \left( \max ({\varvec{\mathrm {m}}})/\log \max ({\varvec{\mathrm {m}}})\right) \).
Compositional Strategies. As an immediate corollary to Theorem 6.4, the expected number of invocations of  required to produce a biprime is in \(O({\kappa } ^2/\log ^2 {\kappa })\). Concretely, this corresponds to 3607 invocations when \({\kappa } =1024\), or 11,832 invocations when \({\kappa } =2048\). As an alternative to sequential invocation,
required to produce a biprime is in \(O({\kappa } ^2/\log ^2 {\kappa })\). Concretely, this corresponds to 3607 invocations when \({\kappa } =1024\), or 11,832 invocations when \({\kappa } =2048\). As an alternative to sequential invocation,  can be invoked concurrently in batches tuned for a desired probability of success. \(O({\rho }/(\log {\kappa }-\log ({\kappa } ^2-\log ^2{\kappa })))\) concurrent invocations are required to sample a biprime with probability at least \(1-2^{-{\rho }}\). Concretely, with \({\rho } =40\), this corresponds to roughly 100,000 invocations for \({\kappa } =1024\), or 330,000 invocations for \({\kappa } =2048\). Two sequential batches of concurrent invocations are required in expectation if \({\rho } =1\), with roughly 2500 invocations of
can be invoked concurrently in batches tuned for a desired probability of success. \(O({\rho }/(\log {\kappa }-\log ({\kappa } ^2-\log ^2{\kappa })))\) concurrent invocations are required to sample a biprime with probability at least \(1-2^{-{\rho }}\). Concretely, with \({\rho } =40\), this corresponds to roughly 100,000 invocations for \({\kappa } =1024\), or 330,000 invocations for \({\kappa } =2048\). Two sequential batches of concurrent invocations are required in expectation if \({\rho } =1\), with roughly 2500 invocations of  per batch for \({\kappa } =1024\), or 8200 invocations per batch for \({\kappa } =2048\).
per batch for \({\kappa } =1024\), or 8200 invocations per batch for \({\kappa } =2048\).
6.2 The Cost of Instantiating  and
and 
Before we can discuss the concrete costs of our main sampling protocol, we must determine the costs of instantiating the functionalities it uses. Since  was specifically formulated to model the biprimality-testing protocol of Boneh and Franklin [5], it is natural to assume we use that protocol (or our malicious-secure extension) to instantiate it. On the other hand, in both the semi-honest and malicious settings, many sensible approaches exist for instantiating
was specifically formulated to model the biprimality-testing protocol of Boneh and Franklin [5], it is natural to assume we use that protocol (or our malicious-secure extension) to instantiate it. On the other hand, in both the semi-honest and malicious settings, many sensible approaches exist for instantiating  . We choose to base our instantiation on oblivious transfer in both settings. Although OT-based multiplication is not the most bandwidth-efficient option, it compares favorably to alternatives in the real world [19, 20], and OT can be built assuming only the hardness of factoring, if desired [21]. We also assume certain reasonable practical concessions are made. For example, we assume that
. We choose to base our instantiation on oblivious transfer in both settings. Although OT-based multiplication is not the most bandwidth-efficient option, it compares favorably to alternatives in the real world [19, 20], and OT can be built assuming only the hardness of factoring, if desired [21]. We also assume certain reasonable practical concessions are made. For example, we assume that  and
and  are both implemented via a Random Oracle. We note that under these instantiations, committing a value requires \(2{\lambda } \) bits to be broadcast,Footnote 9 and
are both implemented via a Random Oracle. We note that under these instantiations, committing a value requires \(2{\lambda } \) bits to be broadcast,Footnote 9 and  requires no communication at all. We also assume
requires no communication at all. We also assume  requires no communication: a trivial modification of the Pseudorandom Zero-Sharing protocol of Cramer et al. [17] yields a protocol that realizes
requires no communication: a trivial modification of the Pseudorandom Zero-Sharing protocol of Cramer et al. [17] yields a protocol that realizes  against active adversaries with no interaction in the
against active adversaries with no interaction in the  -hybrid model.
-hybrid model.
Broadcast. It is standard practice in the implementation of MPC protocols (e.g., [30, 49, 51]) to use the simple echo broadcast of Goldwasser and Lindell [27] for instantiating broadcast channels. This approach preserves all correctness and privacy guarantees, but only guarantees non-unanimous abort (i.e., each honest party either obtains the correct output or locally aborts, but there is no global agreement on abort). Echo broadcast doubles the round count and adds \((n-1)\cdot {\lambda } \) bits per party per original round to the communication cost, because each party is required to send a hash of the broadcast messages received in one round to all other parties before the next round.
In our setting, we can take the even simpler approach of running the protocol optimistically over point-to-point channels. At the end, every party hashes the entire transcript of broadcast-messages and sends the digest to all other parties. If the digests do not agree, the parties abort; otherwise, they terminate with the output value of the protocol. Therefore, for the sake of calculating concrete costs, we consider the cost of broadcasting a bit to be the same as the cost of transmitting it to all parties (apart from the sender) individually.
Oblivious Transfer. We give concrete efficiency figures assuming that Correlated OT (i.e., OT in which the sender chooses a correlation between two messages, instead of two independent messages) is used in place of standard OT, and assuming that it is instantiated via one of two specific OT-extension protocols. The more efficient of the two is the recently introduced Silent OT-extension protocol of Boyle et al. [6]. When used as a Correlated OT-extension on a correlation from the field \({\mathbb {Z}}_m\), it incurs a cost of \((|m|+1)/2\) bits transmitted per party (averaged over the sender and receiver), over two rounds. However, it requires a variant of the Learning Parity with Noise (LPN) assumption, and it has a large one-time setup cost.
As an alternative, the OT-extension protocol of Keller et al. [35] (hereafter referred to as “KOS OT”) assumes only a base OT functionality, and has a much cheaper one-time setup. When used as a Correlated OT-extension on a correlation from the field \({\mathbb {Z}}_m\), this protocol incurs a cost of \((|m|+{\lambda })/2\) bits transmitted per party (averaged over the sender and receiver) over two rounds. In addition to this cost, the sender must pay an overhead cost for each batch of OTs performed, where a batch may comprise polynomially many individual OTs with an arbitrary mixture of correlation lengths. Since this overhead does not depend on the total number of OTs or the correlation lengths, it can be amortized into irrelevance if the OTs in our protocol can be arranged into a small number of batches. Since this is indeed the case, we ignore the overhead cost for the remainder of our cost analysis. For the sake of analyzing concrete efficiency, we also ignore the one-time setup costs of both OT-extension protocols.
Both OT-extension protocols attain malicious security, but KOS OT has little overhead relative to the best semi-honest protocols, and Silent OT is the most efficient currently known OT protocol of any kind. Consequently, we use them in the semi-honest setting as well.
 in the Semi-Honest Setting. In the semi-honest setting, parties can be trusted to reuse inputs when instructed to do so, and the predicate check and input-revelation interfaces of
in the Semi-Honest Setting. In the semi-honest setting, parties can be trusted to reuse inputs when instructed to do so, and the predicate check and input-revelation interfaces of  need not be implemented, since
need not be implemented, since  will never call them in the semi-honest setting. Consequently, an extremely simple protocol suffices to realize
will never call them in the semi-honest setting. Consequently, an extremely simple protocol suffices to realize  against semi-honest adversaries. When the parties wish to use the \(\texttt {multiply}\) interface with a modulus \(m\), they simply engage in instances of Gilboa’s classic OT-multiplication protocol [24], arranged as per the GMW multiplication paradigm [26] to form a multiparty multiplier. This implies \(2|m|\) oblivious transfers per pair of parties, all with \(|m|\)-bit messages. If Silent OT is used, the total cost is \((n-1)\cdot |m| \cdot (|m| + 1)\) bits transmitted per party (averaged over all parties), over two rounds. If KOS OT is used, the total cost is instead \((n-1)\cdot |m| \cdot (|m| + {\lambda })\) bits. Note that this is substantially worse if \(|m|\) is small.
against semi-honest adversaries. When the parties wish to use the \(\texttt {multiply}\) interface with a modulus \(m\), they simply engage in instances of Gilboa’s classic OT-multiplication protocol [24], arranged as per the GMW multiplication paradigm [26] to form a multiparty multiplier. This implies \(2|m|\) oblivious transfers per pair of parties, all with \(|m|\)-bit messages. If Silent OT is used, the total cost is \((n-1)\cdot |m| \cdot (|m| + 1)\) bits transmitted per party (averaged over all parties), over two rounds. If KOS OT is used, the total cost is instead \((n-1)\cdot |m| \cdot (|m| + {\lambda })\) bits. Note that this is substantially worse if \(|m|\) is small.
The \(\texttt {sample}\) interface of  can be realized using the same multiplication protocol in a natural way: the parties simply choose random shares of two values and multiply those values together. They multiply their output shares together with another randomly sampled set of shares and then broadcast their shares of this second product. They repeat the whole process if the second product is found to be zero, or otherwise take their shares of the first product as their outputs. Each iteration of this sampling procedure succeeds with probability \((m-1)^3/m^3\). If iterations are run concurrently in batches of size c, then the expected number of batches is \(b=m^3/(m^3-3c\cdot m^2+3c\cdot m-c)\). Given this value b, the expected total cost is \((n-1)\cdot b\cdot c\cdot |m| \cdot (2|m| + 3)\) bits transmitted per party (on average) if Silent OT is used, or \((n-1)\cdot b\cdot c\cdot |m| \cdot (2|m| + 2{\lambda } + 1)\) bits if KOS OT is used. The number of rounds is 5b in expectation.
can be realized using the same multiplication protocol in a natural way: the parties simply choose random shares of two values and multiply those values together. They multiply their output shares together with another randomly sampled set of shares and then broadcast their shares of this second product. They repeat the whole process if the second product is found to be zero, or otherwise take their shares of the first product as their outputs. Each iteration of this sampling procedure succeeds with probability \((m-1)^3/m^3\). If iterations are run concurrently in batches of size c, then the expected number of batches is \(b=m^3/(m^3-3c\cdot m^2+3c\cdot m-c)\). Given this value b, the expected total cost is \((n-1)\cdot b\cdot c\cdot |m| \cdot (2|m| + 3)\) bits transmitted per party (on average) if Silent OT is used, or \((n-1)\cdot b\cdot c\cdot |m| \cdot (2|m| + 2{\lambda } + 1)\) bits if KOS OT is used. The number of rounds is 5b in expectation.
 in the Semi-Honest Setting. To realize
in the Semi-Honest Setting. To realize  in the semi-honest setting, we use the Boneh–Franklin biprimality test [5]. In this protocol, the parties begin by participating in up to \({s} \) iterations of a test in which they each broadcast a value of size \(2{\kappa } \) to all other parties. In the bandwidth-optimal protocol variant, these iterations are sequential. Each has a soundness error of 1/2, and so the expected number of iterations is two if \(N\) is not a biprime, yielding a concrete bandwidth cost for this first step of \(2(n-1)\cdot {s} \cdot {\kappa } \) bits per party if \(N\) is a biprime, or \(4(n-1)\cdot {\kappa } \) bits per party in expectation otherwise. In the round-optimal protocol variant, these iterations are concurrent, and the cost is always \(2(n-1)\cdot {s} \cdot {\kappa } \) bits per party, over one round.
in the semi-honest setting, we use the Boneh–Franklin biprimality test [5]. In this protocol, the parties begin by participating in up to \({s} \) iterations of a test in which they each broadcast a value of size \(2{\kappa } \) to all other parties. In the bandwidth-optimal protocol variant, these iterations are sequential. Each has a soundness error of 1/2, and so the expected number of iterations is two if \(N\) is not a biprime, yielding a concrete bandwidth cost for this first step of \(2(n-1)\cdot {s} \cdot {\kappa } \) bits per party if \(N\) is a biprime, or \(4(n-1)\cdot {\kappa } \) bits per party in expectation otherwise. In the round-optimal protocol variant, these iterations are concurrent, and the cost is always \(2(n-1)\cdot {s} \cdot {\kappa } \) bits per party, over one round.
If all iterations of the previous test succeed, then the parties perform the GCD test: they securely multiply two shared values modulo \(N\), and reveal the output. Whereas Boneh and Franklin recommend the BGW generic MPC protocol for this task, we will instead assume that Gilboa’s OT-multiplication protocol is used, in a GMW-like arrangement as previously described, followed by an exchanging of output shares. All shares in one of the two input sets are guaranteed to be smaller than \(2^{k+1}\); if we ensure that parties always play the OT-receiver when using shares from this set as input, then the concrete bandwidth cost for this second step is \((n-1)\cdot ({\kappa } +1) \cdot (2{\kappa } + 1) + 2(n-1)\cdot {\kappa } \) bits transmitted per party, assuming Silent OT is used, or \((n-1)\cdot ({\kappa } +1) \cdot (2{\kappa } + {\lambda }) + 2(n-1)\cdot {\kappa } \) bits if KOS OT is used. In either case, three additional rounds are required.
Instantiating
 . In the malicious settings, the
. In the malicious settings, the  and
and  protocols both require access to a generic MPC functionality with reusable inputs, which we give as
protocols both require access to a generic MPC functionality with reusable inputs, which we give as  . For the sake of concrete-efficiency figures, we will assume
. For the sake of concrete-efficiency figures, we will assume  is realized via the Authenticated Garbling protocol of Yang et al. [51]. We make no optimizations, and in particular, do not replace the OT that they use, even though Silent OT might yield a substantial improvement. This protocol has a total cost including preprocessing of
is realized via the Authenticated Garbling protocol of Yang et al. [51]. We make no optimizations, and in particular, do not replace the OT that they use, even though Silent OT might yield a substantial improvement. This protocol has a total cost including preprocessing of
bits transmitted per party, on average, where C is the number of AND gates, I is the number of input wires, and O is the number of output wires. Since this equation is quite complicated and gives little insight, we report costs associated with  simply in terms of gates and input/output wires, and convert them into bit costs only when calculating the overall total bandwidth cost for
simply in terms of gates and input/output wires, and convert them into bit costs only when calculating the overall total bandwidth cost for  . We note that supplying an input (i.e., calling the \(\texttt {commit}\) command of
. We note that supplying an input (i.e., calling the \(\texttt {commit}\) command of  ) to the protocol of Yang et al. requires two rounds, and reconstructing an output (i.e., calling the \(\texttt {compute}\) command) also requires two. We assume that all preprocessing can be run concurrently with other tasks, and thus, it does not contribute any additional rounds.
) to the protocol of Yang et al. requires two rounds, and reconstructing an output (i.e., calling the \(\texttt {compute}\) command) also requires two. We assume that all preprocessing can be run concurrently with other tasks, and thus, it does not contribute any additional rounds.
Using  involves converting functions into circuits. The functions we use are easily reduced to a handful of arithmetic operations. We list all non-trivial operations, with costs, in Table 3.
involves converting functions into circuits. The functions we use are easily reduced to a handful of arithmetic operations. We list all non-trivial operations, with costs, in Table 3.
 in the Malicious Setting. The protocol
in the Malicious Setting. The protocol  that realizes
that realizes  is complex and involves a number of sub-functionalities that we have not yet introduced. Consequently, we defer our full cost analysis to Appendix B, in which we also describe
is complex and involves a number of sub-functionalities that we have not yet introduced. Consequently, we defer our full cost analysis to Appendix B, in which we also describe  itself. We note here that the cost of the
itself. We note here that the cost of the  \(\texttt {multiply}\) command with modulus \(m\) is in \(O(n\cdot (|m|^2+|m|\cdot {s} +2{\lambda }))\) transmitted bits per party if Silent OT is used, or \(O(n\cdot (|m|^2+|m|\cdot {s} +(|m| + 2)\cdot {\lambda }))\) if KOS OT is used, and that the \(\texttt {input}\) command is free if it is not called until immediately before the first associated multiplication. The cost of the \(\texttt {open}\) command is in \(O(n\cdot (|m|^2+|m|\cdot {s}))\) transmitted bits per party. The \(\texttt {sample}\) command has the same expected bandwidth complexity as multiplication. Finally, the complexity of the \(\texttt {check}\) command depends upon the inputs it is given, but broadly, for each input with an associated modulus \(m\), one must pay \({s}/|m|\) times the cost of multiplication, plus a bandwidth cost in \(O(n\cdot {s} ^2/|m|+n\cdot {s} \cdot c)\), where c is the number of times the input was used in a multiplication, plus the cost of using
\(\texttt {multiply}\) command with modulus \(m\) is in \(O(n\cdot (|m|^2+|m|\cdot {s} +2{\lambda }))\) transmitted bits per party if Silent OT is used, or \(O(n\cdot (|m|^2+|m|\cdot {s} +(|m| + 2)\cdot {\lambda }))\) if KOS OT is used, and that the \(\texttt {input}\) command is free if it is not called until immediately before the first associated multiplication. The cost of the \(\texttt {open}\) command is in \(O(n\cdot (|m|^2+|m|\cdot {s}))\) transmitted bits per party. The \(\texttt {sample}\) command has the same expected bandwidth complexity as multiplication. Finally, the complexity of the \(\texttt {check}\) command depends upon the inputs it is given, but broadly, for each input with an associated modulus \(m\), one must pay \({s}/|m|\) times the cost of multiplication, plus a bandwidth cost in \(O(n\cdot {s} ^2/|m|+n\cdot {s} \cdot c)\), where c is the number of times the input was used in a multiplication, plus the cost of using  to evaluate a circuit of size
to evaluate a circuit of size  with \(O({s} +|m|)\) input wires. In addition to these per input costs, \(\texttt {check}\) uses
with \(O({s} +|m|)\) input wires. In addition to these per input costs, \(\texttt {check}\) uses  to evaluate an arbitrary circuit (with no additional inputs), and so costs must be paid proportionate to that circuit’s size.
to evaluate an arbitrary circuit (with no additional inputs), and so costs must be paid proportionate to that circuit’s size.
 in the Malicious Setting. In Sect. 5.2, we described a protocol
in the Malicious Setting. In Sect. 5.2, we described a protocol  realizing
realizing  . We now analyze its costs. The Boneh–Franklin Test phase is similar to the first phase of the semi-honest biprimality test, except that messages are committed before they are revealed, they are always decommitted concurrently, and \(2.5{s} \) iterations are required, as opposed to \({s} \). Consequently, this step incurs a cost of \(5(n-1)\cdot {s} \cdot {\kappa } +2(n-1)\cdot {\lambda } \) bits transmitted per party, over two rounds.
. We now analyze its costs. The Boneh–Franklin Test phase is similar to the first phase of the semi-honest biprimality test, except that messages are committed before they are revealed, they are always decommitted concurrently, and \(2.5{s} \) iterations are required, as opposed to \({s} \). Consequently, this step incurs a cost of \(5(n-1)\cdot {s} \cdot {\kappa } +2(n-1)\cdot {\lambda } \) bits transmitted per party, over two rounds.
This leaves input commitment and consistency check/GCD test phases. The former phase involves only a single commitment by each party. The latter phase is only evaluated if the above test passes, and therefore does not contribute to the cost when \(N\) is not a biprime. To perform the GCD test, the parties each transmit \(2.5{s} \cdot (n-1)\cdot (3{\kappa }-\log _2n+{s} +1)\) bits over two rounds, and in addition, they use  to compute a circuit, which is specified by Algorithm 5.3. If for clarity and simplicity we represent the cost of multiplication using the functions from Table 3, then the size of this circuit in AND gates is
to compute a circuit, which is specified by Algorithm 5.3. If for clarity and simplicity we represent the cost of multiplication using the functions from Table 3, then the size of this circuit in AND gates is

and furthermore, it has \(n\cdot (2.5{s} +2)\cdot ({\kappa }-\log _2n)+n\cdot 2.5{s} \cdot ({s} +1)+2n\cdot {\kappa } \) input wiresFootnote 10 and \(2n\cdot {\kappa } \) output wires.
6.3 Putting It All Together
In this section, we will break down the cost of our main protocol  in terms of calls to
in terms of calls to  and
and  , and also give the costs associated with the few protocol components that are not interactions with these functionalities. This breakdown (excepting the functionality calls in the consistency check phase) is identical in the malicious and semi-honest settings. We subsequently plug in the individual component costs that we derived in Sect. 6.2 and arrive at predicted concrete cost figures for one instance of our complete protocol. We then use the analysis in Sect. 6.1 to determine the concrete cost of sampling a biprime when our sampling protocol is called sequentially. We discuss alternative composition strategies for achieving constant or expected-constant round counts (and provide an exact round count) in the next section. We begin with a cost breakdown.
, and also give the costs associated with the few protocol components that are not interactions with these functionalities. This breakdown (excepting the functionality calls in the consistency check phase) is identical in the malicious and semi-honest settings. We subsequently plug in the individual component costs that we derived in Sect. 6.2 and arrive at predicted concrete cost figures for one instance of our complete protocol. We then use the analysis in Sect. 6.1 to determine the concrete cost of sampling a biprime when our sampling protocol is called sequentially. We discuss alternative composition strategies for achieving constant or expected-constant round counts (and provide an exact round count) in the next section. We begin with a cost breakdown.
-
1.
Candidate Sieving. For each \(j\in [2,\ell ]\), the parties invoke the \(\texttt {sample}\) instruction of
 using modulus \({\varvec{\mathrm {m}}} _j\). These invocations are concurrent. Following this, for \(j\in [\ell +1,{\ell '}]\), the parties invoke the \(\texttt {input}\) instruction of
using modulus \({\varvec{\mathrm {m}}} _j\). These invocations are concurrent. Following this, for \(j\in [\ell +1,{\ell '}]\), the parties invoke the \(\texttt {input}\) instruction of  with modulus \({\varvec{\mathrm {m}}} _j\) twice, and then the \(\texttt {multiply}\) instruction with modulus \({\varvec{\mathrm {m}}} _j\). As discussed in Appendix B.3, the \(\texttt {input}\) instructions are free under this pattern of invocations if we use
with modulus \({\varvec{\mathrm {m}}} _j\) twice, and then the \(\texttt {multiply}\) instruction with modulus \({\varvec{\mathrm {m}}} _j\). As discussed in Appendix B.3, the \(\texttt {input}\) instructions are free under this pattern of invocations if we use  (Protocol B.7) to realize
(Protocol B.7) to realize  . We assume the multiplications are done concurrently as well. In addition, every party broadcasts a value in \({\mathbb {Z}}_{{\varvec{\mathrm {m}}} _j}\) for \(j\in [2,{\ell '}]\). This incurs a cost of $$(n-1)\cdot \sum \limits _{j\in [2,{\ell '}]}|{\varvec{\mathrm {m}}} _j|$$
. We assume the multiplications are done concurrently as well. In addition, every party broadcasts a value in \({\mathbb {Z}}_{{\varvec{\mathrm {m}}} _j}\) for \(j\in [2,{\ell '}]\). This incurs a cost of $$(n-1)\cdot \sum \limits _{j\in [2,{\ell '}]}|{\varvec{\mathrm {m}}} _j|$$transmitted bits per party, and one additional round.
-
2.
Biprimality Test. The parties send \(\texttt {check-biprimality}\) to
 at most once. Since our protocol includes local trial division (see Step 5 of
at most once. Since our protocol includes local trial division (see Step 5 of  ), some protocol instances will skip the biprimality test entirely. However, for the sake of calculating concrete costs, we will assume that this local trial division is not executed. In other words, we assume that the biprimality test is run exactly once per protocol instance, and if local trial division would have rejected a candidate, then the biprimality test certainly fails.
), some protocol instances will skip the biprimality test entirely. However, for the sake of calculating concrete costs, we will assume that this local trial division is not executed. In other words, we assume that the biprimality test is run exactly once per protocol instance, and if local trial division would have rejected a candidate, then the biprimality test certainly fails. -
3.
Consistency Check. This phase has no cost in the semi-honest setting. In the malicious setting, its cost differs depending on whether the candidate biprime has passed the biprimality test (and local trial division), or failed. In the failure case, the parties send \(\texttt {open}\) to
 twice with modulus \({\varvec{\mathrm {m}}} _j\) for each \(j\in [2,{\ell '}]\). In the passing case, they instead send \((\texttt {check}, {\textsf {sids}},f)\), where \({\textsf {sids}}\) is the vector of session IDs associated with values sampled by or loaded into
twice with modulus \({\varvec{\mathrm {m}}} _j\) for each \(j\in [2,{\ell '}]\). In the passing case, they instead send \((\texttt {check}, {\textsf {sids}},f)\), where \({\textsf {sids}}\) is the vector of session IDs associated with values sampled by or loaded into  in the sieving phase, and f is a predicate specified in our protocol. This circuit representation of f comprises 2n invocations of
in the sieving phase, and f is a predicate specified in our protocol. This circuit representation of f comprises 2n invocations of  over the extended vector \({\varvec{\mathrm {m}}} \) of small moduli, 2n comparisons on inputs of size \(2{\kappa } \), two integer sums, each over n elements of \({\kappa }-\log _2n\) bits, one integer multiplication with inputs of length \({\kappa } \), and one equality check over values of length \(2{\kappa } \). We observe that the
over the extended vector \({\varvec{\mathrm {m}}} \) of small moduli, 2n comparisons on inputs of size \(2{\kappa } \), two integer sums, each over n elements of \({\kappa }-\log _2n\) bits, one integer multiplication with inputs of length \({\kappa } \), and one equality check over values of length \(2{\kappa } \). We observe that the  algorithm can be implemented in the following way: all intermediate operations can be performed over the integers, with a single modular reduction at the end. Because each intermediate product has one multiplicand that is much shorter than the other, we can use the asymmetric modular multiplication method previously described in Sect. 6.2. This circuit requires no additional inputs, relative to the ones supplied by
algorithm can be implemented in the following way: all intermediate operations can be performed over the integers, with a single modular reduction at the end. Because each intermediate product has one multiplicand that is much shorter than the other, we can use the asymmetric modular multiplication method previously described in Sect. 6.2. This circuit requires no additional inputs, relative to the ones supplied by  , and its overall gate countFootnote 11 is
, and its overall gate countFootnote 11 is 
Communication Complexity. In order to explore the asymptotic network costs of our protocol in terms of \({\kappa } \), \({s} \), and n, we consider \({\lambda } \) to be in \(O({s})\) for the purposes of this analysis. We also assume \({s} \in O({\kappa })\cap \omega (\log {\kappa })\). We give all our asymptotic figures in terms of data transmitted per party.
Combining the cost breakdown in this section with the asymptotic analysis of CRT sampling parameters in Sect. 6.1, we find that \(O({\kappa }/\log {\kappa })\) invocations of the \(\texttt {sample}\) and \(\texttt {multiply}\) interfaces of  are performed during the Candidate Sieving phase of
are performed during the Candidate Sieving phase of  . Let \(({\varvec{\mathrm {m}}},{\ell '},\ell ,M)\) be the \(({\kappa },n)\)-compatible parameter set of
. Let \(({\varvec{\mathrm {m}}},{\ell '},\ell ,M)\) be the \(({\kappa },n)\)-compatible parameter set of  , as specified by Definition 4.3. Each \(\texttt {sample}\) and \(\texttt {multiply}\) operation involves a modulus from \({\varvec{\mathrm {m}}} \). Per Lemma 6.2, \(\max ({\varvec{\mathrm {m}}})\in O(\log M)\), and we have from Definition 3.4 that \(M\in O(2^{\kappa })\); thus \(\max ({\varvec{\mathrm {m}}})\in O({\kappa })\). Via Sect. 6.2, this implies that all \(\texttt {multiply}\) and \(\texttt {sample}\) operations have a complexity of \(O(n\cdot \log ^2{\kappa })\) bits transmitted per party in the semi-honest setting, or \(O(n\cdot \log ^2{\kappa } +n\cdot {s} \cdot \log {\kappa })\) in the malicious setting (assuming Silent OT in both cases). The total per-party communication cost of the Sieving phase is therefore \(O(n\cdot {\kappa } \cdot \log {\kappa })\) in the semi-honest setting, or \(O(n\cdot {\kappa } \cdot {s})\) in the malicious setting.
, as specified by Definition 4.3. Each \(\texttt {sample}\) and \(\texttt {multiply}\) operation involves a modulus from \({\varvec{\mathrm {m}}} \). Per Lemma 6.2, \(\max ({\varvec{\mathrm {m}}})\in O(\log M)\), and we have from Definition 3.4 that \(M\in O(2^{\kappa })\); thus \(\max ({\varvec{\mathrm {m}}})\in O({\kappa })\). Via Sect. 6.2, this implies that all \(\texttt {multiply}\) and \(\texttt {sample}\) operations have a complexity of \(O(n\cdot \log ^2{\kappa })\) bits transmitted per party in the semi-honest setting, or \(O(n\cdot \log ^2{\kappa } +n\cdot {s} \cdot \log {\kappa })\) in the malicious setting (assuming Silent OT in both cases). The total per-party communication cost of the Sieving phase is therefore \(O(n\cdot {\kappa } \cdot \log {\kappa })\) in the semi-honest setting, or \(O(n\cdot {\kappa } \cdot {s})\) in the malicious setting.
In both the semi-honest and the malicious settings, the communication complexity of a successful biprimality test is dominated by the GCD Test. In the semi-honest case, this check comprises a secure multiplication over \({\kappa } \) bits, so the cost is in \(O(n\cdot {\kappa } ^2)\) bit transmitted per party. In the malicious case, per Sect. 6.2, this check is performed via a circuit with \(O(n\cdot {s} \cdot {\kappa } + {\kappa } ^{\log _23})\) gates,Footnote 12 and per Yang et al. [51], the dominant per-party asymptotic cost of their protocol is in \(O(n\cdot {s} \cdot C/\log C)\), where C is the gate count. Thus, the per-party complexity of a successful biprimality test is
in the malicious case. In both the semi-honest and the malicious settings, failed biprimality tests are unlikely to perform the GCD check,Footnote 13 leaving only the initial testing phase. If we choose the bandwidth-optimal protocol variant in the semi-honest setting, then we can take the communication complexity of a failed biprimality test to be in \(O(n\cdot {\kappa })\). In the malicious setting, it is in \(O(n\cdot {s} \cdot {\kappa })\).
Finally, in the malicious setting only, the consistency check phase is performed. For presumptive biprimes, the cost of this phase is dominated by its generic MPC component, which has \(O(n\cdot {\kappa } ^2)\) gates and, if we assume that Yang et al.’s protocol is used, a total complexity of
per party. For presumptive non-biprimes, the parties invoke the \(\texttt {open}\) interface of  a constant number of times for each element of \({\varvec{\mathrm {m}}} \). Reusing our analysis of the sieving phase, we find that the per-party network complexity of this case is \(O(n\cdot {s} \cdot {\kappa })\).
a constant number of times for each element of \({\varvec{\mathrm {m}}} \). Reusing our analysis of the sieving phase, we find that the per-party network complexity of this case is \(O(n\cdot {s} \cdot {\kappa })\).
In the case that a biprime is sampled by iterating  sequentially until a successful sampling occurs, we know (via Sect. 6.1) that \(O({\kappa } ^2/\log ^2{\kappa })\) iterations are required in expectation. All but one of these iterations are failures, and in the one successful case in the malicious setting, the size of the consistency check circuit dominates that of the biprimality test circuit. Thus, the overall per-party communication complexity to sample a biprime using this composition strategy is in
sequentially until a successful sampling occurs, we know (via Sect. 6.1) that \(O({\kappa } ^2/\log ^2{\kappa })\) iterations are required in expectation. All but one of these iterations are failures, and in the one successful case in the malicious setting, the size of the consistency check circuit dominates that of the biprimality test circuit. Thus, the overall per-party communication complexity to sample a biprime using this composition strategy is in
in the semi-honest or malicious settings, respectively.
Concrete Network Cost. We now perform all the substitutions necessary to collapse the cost figures we have reported into concrete values. We plug the costs of individual sub-protocols from Sect. 6.2 into the main protocol breakdown presented in this section, using bandwidth-optimal variants where appropriate, and convert gate counts into bit counts assuming the protocol of Yang et al. [51]. We also derive the expected cost of sampling a single biprime via sequential iteration of  until a success occurs: this strategy allows us to determine the number of iterations required by inverting the success probabilities calculated in Sect. 6.1. Finally, we set \({\lambda } =128\) and \({s} =80\). We report the results of this calculation for our semi-honest protocol variant in Table 4, and for our malicious protocol variant in Table 5.
until a success occurs: this strategy allows us to determine the number of iterations required by inverting the success probabilities calculated in Sect. 6.1. Finally, we set \({\lambda } =128\) and \({s} =80\). We report the results of this calculation for our semi-honest protocol variant in Table 4, and for our malicious protocol variant in Table 5.
6.4 Strictly Constant and Expected-Constant Rounds
In the foregoing sections, we have given costs for sampling a biprime under the assumption that  is iterated sequentially. While this ensures that no work or communication is wasted, since no additional instances of
is iterated sequentially. While this ensures that no work or communication is wasted, since no additional instances of  are run after the first success, it also yields an expected round complexity that grows with \(\Omega ({\kappa } ^2/\log ^2{\kappa })\) at the least (the inverse of the success probability of a single instance, per Sect. 6.1), and concretely yields tens or hundreds of thousands of rounds in expectation for the values of \({\kappa } \) used in practice. This is not satisfying.
are run after the first success, it also yields an expected round complexity that grows with \(\Omega ({\kappa } ^2/\log ^2{\kappa })\) at the least (the inverse of the success probability of a single instance, per Sect. 6.1), and concretely yields tens or hundreds of thousands of rounds in expectation for the values of \({\kappa } \) used in practice. This is not satisfying.
Unfortunately, we cannot achieve constant (or even expected constant) rounds by running instances of  concurrently, because the \(\texttt {sample}\) operation of
concurrently, because the \(\texttt {sample}\) operation of  (which samples pairs of secret-shared nonzero values) is also probabilistic, with termination in expected-constant rounds. When multiple expected-constant-round protocols are composed in parallel, the resulting protocol does not have constant rounds in expectation [3, 13, 14]. The naïve solution is to modify the \(\texttt {sample}\) operation of
(which samples pairs of secret-shared nonzero values) is also probabilistic, with termination in expected-constant rounds. When multiple expected-constant-round protocols are composed in parallel, the resulting protocol does not have constant rounds in expectation [3, 13, 14]. The naïve solution is to modify the \(\texttt {sample}\) operation of  to generate candidates concurrently instead of sequentially and set the parameters such that it succeeds with overwhelming probability. However, this leads to a factor of \(\Theta ({s})\) overhead with respect to communication complexity, relative to sequential composition, which is also not satisfying.
to generate candidates concurrently instead of sequentially and set the parameters such that it succeeds with overwhelming probability. However, this leads to a factor of \(\Theta ({s})\) overhead with respect to communication complexity, relative to sequential composition, which is also not satisfying.
Instead, we propose a non-black-box composition strategy. In order to invoke  x times concurrently, we must sample x pairs of nonzero values with respect to each modulus in \({\varvec{\mathrm {m}}} \). To do this, we run a pooled sampling procedure for each modulus, which concurrently samples enough candidates to ensure that there are at least x successes among them with overwhelming probability. For modulus \({\varvec{\mathrm {m}}} _j\), and candidate count \(y\ge x\), the probability of success is governed by the binomial distribution on y and \(({\varvec{\mathrm {m}}} _j-1)^3/{\varvec{\mathrm {m}}} _j^3\). Specifically, to ensure success with overwhelming probability, we must calculate y such that
x times concurrently, we must sample x pairs of nonzero values with respect to each modulus in \({\varvec{\mathrm {m}}} \). To do this, we run a pooled sampling procedure for each modulus, which concurrently samples enough candidates to ensure that there are at least x successes among them with overwhelming probability. For modulus \({\varvec{\mathrm {m}}} _j\), and candidate count \(y\ge x\), the probability of success is governed by the binomial distribution on y and \(({\varvec{\mathrm {m}}} _j-1)^3/{\varvec{\mathrm {m}}} _j^3\). Specifically, to ensure success with overwhelming probability, we must calculate y such that
holds. Although reasonable bounds and approximations exist, it is not easy to solve this equation for y in closed form. Given concrete values for the other parameters, we can compute a value for y.
As an example, consider the following concrete scenario: let x be the size of a batch of concurrent invocations of  , where x is tuned such that the batch samples at least one biprime with probability 1/2. Let \({\kappa } =1024\) and let \({s} =80\), and via Sect. 6.1, we have \(x=2500\). Now consider \({\varvec{\mathrm {m}}} _2=3\), the smallest modulus with respect to which sampling will occur. Solving Eq. 5, we find that if we sample 9989 candidate values modulo \({\varvec{\mathrm {m}}} _2\), then at least 2500 of them will be nonzero with probability \(1-2^{-{s}}\). Now, if we sample a biprime by running batches of size x, one batch after the next, until a biprime is sampled, then two batches are required in expectation, which implies that 19,978 total candidate pairs must be sampled with respect to \({\varvec{\mathrm {m}}} _2\), in expectation.
, where x is tuned such that the batch samples at least one biprime with probability 1/2. Let \({\kappa } =1024\) and let \({s} =80\), and via Sect. 6.1, we have \(x=2500\). Now consider \({\varvec{\mathrm {m}}} _2=3\), the smallest modulus with respect to which sampling will occur. Solving Eq. 5, we find that if we sample 9989 candidate values modulo \({\varvec{\mathrm {m}}} _2\), then at least 2500 of them will be nonzero with probability \(1-2^{-{s}}\). Now, if we sample a biprime by running batches of size x, one batch after the next, until a biprime is sampled, then two batches are required in expectation, which implies that 19,978 total candidate pairs must be sampled with respect to \({\varvec{\mathrm {m}}} _2\), in expectation.
For comparison, consider the sequentially composed case with sequential sampling, in which single instances of  are invoked one-at-a-time until a success occurs, and similarly
are invoked one-at-a-time until a success occurs, and similarly  samples candidate pairs of nonzero values until a success occurs. In this case, 3607 invocations of
samples candidate pairs of nonzero values until a success occurs. In this case, 3607 invocations of  are required in expectation, and during each invocation, \((3/2)^3\) candidate pairs are sampled in expectation by
are required in expectation, and during each invocation, \((3/2)^3\) candidate pairs are sampled in expectation by  with respect to the modulus \({\varvec{\mathrm {m}}} _2=3\). The total number of candidate pairs with respect to \({\varvec{\mathrm {m}}} _2\) is thus 12,174 in expectation over all invocations of
with respect to the modulus \({\varvec{\mathrm {m}}} _2=3\). The total number of candidate pairs with respect to \({\varvec{\mathrm {m}}} _2\) is thus 12,174 in expectation over all invocations of  . Thus, in terms of candidates-with-respect-to-\({\varvec{\mathrm {m}}} _2\), the overhead to achieve expected constant rounds using the above strategy is a factor of roughly 1.65, and it is easy to confirm that for all other elements in \({\varvec{\mathrm {m}}} \), this factor is smaller. We conclude from this example that the bandwidth overhead for sampling a biprime in expected-constant rounds is reasonable, relative to the bandwidth-optimal (i.e., sequential) composition strategy. By adjusting the batch-size parameter, it can be shown that there exists a biprime-sampling strategy that takes strict-constant rounds and succeeds in sampling a biprime with probability \(1-2^{-40}\) and that the bandwidth overhead of this strategy is a factor of less than 30 with respect to the bandwidth-optimal strategy (assuming, as before, that \({\kappa } =1024\) and \({s} =80\)).
. Thus, in terms of candidates-with-respect-to-\({\varvec{\mathrm {m}}} _2\), the overhead to achieve expected constant rounds using the above strategy is a factor of roughly 1.65, and it is easy to confirm that for all other elements in \({\varvec{\mathrm {m}}} \), this factor is smaller. We conclude from this example that the bandwidth overhead for sampling a biprime in expected-constant rounds is reasonable, relative to the bandwidth-optimal (i.e., sequential) composition strategy. By adjusting the batch-size parameter, it can be shown that there exists a biprime-sampling strategy that takes strict-constant rounds and succeeds in sampling a biprime with probability \(1-2^{-40}\) and that the bandwidth overhead of this strategy is a factor of less than 30 with respect to the bandwidth-optimal strategy (assuming, as before, that \({\kappa } =1024\) and \({s} =80\)).
An Exact Round Count. It remains only to determine the exact round count of a batch, which is the same as the round count of a single instance of  , assuming the sampling performed by
, assuming the sampling performed by  in that instance is performed concurrently, and that the round-optimal variants of the biprimality test are used. In the semi-honest setting, if we modify the simple semi-honest realization of
in that instance is performed concurrently, and that the round-optimal variants of the biprimality test are used. In the semi-honest setting, if we modify the simple semi-honest realization of  given in Sect. 6.2 to sample concurrently instead of sequentially then it requires exactly 5 rounds to sample. A similar modification yields 10 rounds for sampling using
given in Sect. 6.2 to sample concurrently instead of sequentially then it requires exactly 5 rounds to sample. A similar modification yields 10 rounds for sampling using  in the malicious setting. All other components of our combined protocol have constant round counts, and combining the round counts already given in Sects. 6.2, 6.3, and Appendix B yields a total of 12 rounds in the semi honest setting, or 35 rounds in the malicious setting. It is likely that both values can be reduced noticeably by interleaving and combining rounds, but we have made no attempt to do so. If the parties are interacting for the first time, they will need a small number of additional rounds to initialize OT-extensions, but this need only be done once.
in the malicious setting. All other components of our combined protocol have constant round counts, and combining the round counts already given in Sects. 6.2, 6.3, and Appendix B yields a total of 12 rounds in the semi honest setting, or 35 rounds in the malicious setting. It is likely that both values can be reduced noticeably by interleaving and combining rounds, but we have made no attempt to do so. If the parties are interacting for the first time, they will need a small number of additional rounds to initialize OT-extensions, but this need only be done once.
6.5 Comparison to Prior Work
The most relevant prior work is that of Frederiksen et al. [23], and in this section we provide an in-depth comparison of the two. Unfortunately, Frederiksen et al. do not report concrete communication costs, and so we must re-derive them as best as we can. Before we discuss concrete costs, however, we describe the high-level differences between the two approaches, and our methodology for comparison. As their protocol supports only two parties, we will assume for the duration of this section that \(n=2\).
Both their protocol and ours are based upon oblivious transfer, but the sampling mechanisms of the two protocols have substantial structural differences. Our CRT-form sampling mechanism has a complexity in \(O({\kappa } \cdot \log {\kappa })\) or \(O({\kappa } \cdot {s})\) in the semi-honest or malicious settings, respectively. This complexity includes the cost of computing the modulus \(N\) from shares of its factors. Their protocol instead samples integer shares of \(p\) and \(q\) uniformly in standard form and uses 1-of-many OT [40] to perform trial division efficiently. Subsequently, they use an OT-multiplier of their own design to compute \(N:=p\cdot q\). Because this multiplication is not performed in CRT form, it has a communication complexity of \(O({\kappa } ^2)\) in both the semi-honest and the malicious settings. In addition, their method induces some leakage, whereas ours leaks no more than Boneh and Franklin [5]. When a biprime is sampled successfully, their biprimality test uses another, similar multiplier, with inputs that are larger by a constant factor. Since their protocol makes black-box use of the KOS OT-extension protocol [35], our comparison will assume their protocol is upgraded to use the more-recent Silent OT-extension protocol [6]. Furthermore, we will assume their scheme amortizes the costs of both 1-of-2 and 1-of-many OT-extension in the best possible way (i.e., we will only count costs that can never be amortized).
In the malicious setting, Frederiksen et al.’s protocol makes use of a proof of honesty which consists mainly of a circuit evaluated by a generic MPC functionality. It is quite similar to a combination of the circuits used by our  protocol and the consistency check phase of our
protocol and the consistency check phase of our  protocol.Footnote 14 However, they must run their circuit twice, and on the other hand, because their protocol is two-party only and already admits leakage, they are able to use the very efficient leaky dual-execution method of Mohassel and Franklin [39] to evaluate their circuit, whereas we must use an n-party method with full malicious security. Our goal is to illustrate performance differences between our approach and theirs, not performance differences among underlying black-box components. Because we do not think there is a fair way to reconcile the discrepancy in the generic MPC techniques that the two works employ, we will report the number of AND gates required by both protocols,Footnote 15 and also the number of bits transmitted per party excluding those due to evaluation of these circuits.
protocol.Footnote 14 However, they must run their circuit twice, and on the other hand, because their protocol is two-party only and already admits leakage, they are able to use the very efficient leaky dual-execution method of Mohassel and Franklin [39] to evaluate their circuit, whereas we must use an n-party method with full malicious security. Our goal is to illustrate performance differences between our approach and theirs, not performance differences among underlying black-box components. Because we do not think there is a fair way to reconcile the discrepancy in the generic MPC techniques that the two works employ, we will report the number of AND gates required by both protocols,Footnote 15 and also the number of bits transmitted per party excluding those due to evaluation of these circuits.
Finally, as Frederiksen et al. observed and as we have previously discussed, their functionality allows a malicious adversary to covertly prevent successful sampling in a selective fashion. This is true regardless of the composition strategy employed. As a consequence, in the malicious setting, we will report both the best-case behavior, in which the adversary politely avoids covert cheating, and the worst-case behavior, in which they must run sufficiently many iterations to ensure a modulus should have been sampled with overwhelming probability (and thus there must be a corrupt party present if no moduli are produced).
The protocol of Frederiksen et al. takes as a free parameter a trial-division bound, which determines the amount of trial division to be done before the candidate biprime \(N\) is reconstructed and biprimality testing occurs. Since they do not report the trial-division bound used for their concrete experiments, nor do they make a recommendation about the value other than that it be tweaked to optimize the protocol cost concretely, we choose their trial-division bound to be the same as the largest element in a \(({\kappa },2)\)-near-primorial vector, per Definition 3.4. This is a reasonable choice in terms of concrete efficiency, but it also allows us to easily make a fair comparison, since with this parametrization sampling a biprime will require the same number of invocations of  (each with one biprimality test and one consistency check) in our case as there are executions of the biprimality test phase and proof-of-honesty in their case.Footnote 16
(each with one biprimality test and one consistency check) in our case as there are executions of the biprimality test phase and proof-of-honesty in their case.Footnote 16
The protocol of Frederiksen et al. also takes a second trial division bound, which is used for local trial division on the reconstructed modulus. For the sake of analysis, we assume this feature is not used (we have done likewise with the analogous feature in our own protocol). We calculate concrete costs for their protocol using \({s} =80\) and \({\lambda } =128\) and report the results alongside our own for the semi-honest setting in Table 6, and for the malicious setting in Table 7.
In the semi-honest setting, the asymptotic and concrete advantages of our approach are very clear: the overall expected cost advantage of our protocol is a factor of at least 75 and increases with the size of the biprime to be sampled. This advantage is a direct consequence of our CRT-form sampling strategy, since the two semi-honest protocols are otherwise very similar.
In the malicious setting, the relationship between the two protocols is more complex. It is still apparent that for non-successful instances, our protocol is both asymptotically and concretely better. This comes at the price of a larger circuit to be evaluated when an instance succeeds in sampling a biprime. We believe this to be a beneficial trade: only one successful instance is required to sample a biprime, whereas thousands of unsuccessful instances are to be expected in the best case. However, the most noticeable difference between the two arises due to the ability of a malicious adversary to covertly force instances of the Frederiksen et al. protocol to fail. This can cause the number of instances they require to be inflated by a factor of around fifty, assuming sequential iteration, giving our approach a clear advantage.
Notes
Prior works generally consider RSA key generation and include steps for generating shares of e and d such that \(e\cdot d \equiv 1 \pmod {\varphi (N)}\). This work focuses only on the task of sampling the RSA modulus \(N\). Prior techniques can be applied to sample (e, d) after sampling \(N\), and the distributed generation of an RSA modulus has standalone applications, such as for generating the trusted setup required by verifiable delay functions [41, 50]; consequently, we omit further discussion of e and d.
The folklore technique involves invoking the protocol iteratively, each iteration eliminating one corrupt party until a success occurs. For a constant fraction of corruptions, the implied linear round complexity overhead can be reduced to super-constant (e.g., \(\log ^*{n}\)) [15].
In other words, a biprime of length \(2{\kappa } \) provides \({\lambda } \) bits of security.
Technically, Katz and Lindell specify that sampling failures are permitted with negligible probability, and require \(\mathsf {GenModulus} \) to run in strict polynomial time. We elide this detail.
Boneh and Franklin actually propose two variations, one of which has no false negatives; we choose the other variation, as it leads to a more efficient sampling protocol.
This technique is known in the literature of residue number systems as the Szabo–Tanaka method for RNS base extension [48].
This is accomplished by testing \(\gcd (z \bmod {N},N)=1\), which is equivalent as any factor of z and N also divides \(z\bmod {N}\).
Where \({\lambda } \) is a computational security parameter as described in Sect. 2.
Including the wires required to input the randomness for the GCD test.
Assuming the intermediate products inside each invocation of
 are taken to be of length \(2{\kappa } +|\max ({\varvec{\mathrm {m}}})|\), and that each party’s shares of \(p\) and \(q\) are taken to be \({\kappa }-\log _2n\) bits after their lengths are checked.
are taken to be of length \(2{\kappa } +|\max ({\varvec{\mathrm {m}}})|\), and that each party’s shares of \(p\) and \(q\) are taken to be \({\kappa }-\log _2n\) bits after their lengths are checked.\(O({\kappa } ^{\log _23})\) is the cost of Karatsuba multiplication on \({\kappa } \)-bit inputs.
We do not know the precise probability, nor does any prior work, including that of Boneh and Franklin [5] themselves, make a statement about it. It seems empirically that the probability is very low indeed. For analysis purposes we take it to be zero.
As described in their work, their circuit contains additional gates for calculating parts of the RSA key-pair other than the modulus. We omit these parts from our analysis, for the sake of fairness.
We calculate their circuit size using the building blocks we previously described in Table 3 and use their estimate of 6000 gates for the cost of a single AES call.
Assuming that in their case, the adversary never forces the rejection of valid candidates.
We define a function in order to express other costs in terms of this cost; note that the variables n, \({s} \) and \({\lambda } \) are assumed to be global, and thus for simplicity we do not include them among the function’s parameters.
Note that the constituent multipliers in this case admit cheats, which are caught later by the Cheater Check command, if it is invoked
See the first branch of Step 5 of
 for a detailed algorithm to sample such views.
for a detailed algorithm to sample such views.The emulated honest parties abort upon discovering that the candidate really was a biprime during the privacy-free consistency check.
Note that because the protocol does not permit the adversary to input shares of \(p\) or \(q\) with the wrong residues modulo 4, the abort in the Sampling phase of
 can never be triggered.
can never be triggered.
References
Joy Algesheimer, Jan Camenisch, and Victor Shoup. Efficient computation modulo a shared secret with application to the generation of shared safe-prime products. In Advances in Cryptology – CRYPTO 2002, pages 417–432, 2002.
Elaine Barker. Nist special publication 800-57, part 1, revision 4. https://doi.org/10.6028/NIST.SP.800-57pt1r4, 2016.
Michael Ben-Or and Ran El-Yaniv. Resilient-optimal interactive consistency in constant time. Distributed Computing, 16(4):249–262, 2003.
Dan Boneh and Matthew K. Franklin. Efficient generation of shared RSA keys. In Advances in Cryptology – CRYPTO 1997, pages 425–439, 1997.
Dan Boneh and Matthew K. Franklin. Efficient generation of shared RSA keys. Journal of the ACM, 48(4):702–722, 2001.
Elette Boyle, Geoffroy Couteau, Niv Gilboa, Yuval Ishai, Lisa Kohl, Peter Rindal, and Peter Scholl. Efficient two-round OT extension and silent non-interactive secure computation. In Proceedings of the 26th ACM Conference on Computer and Communications Security, (CCS), pages 291–308, 2019.
Ran Canetti. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd Annual Symposium on Foundations of Computer Science (FOCS), pages 136–145, 2001.
Ran Canetti, Yehuda Lindell, Rafail Ostrovsky, and Amit Sahai. Universally composable two-party and multi-party secure computation. In Proceedings of the 34th Annual ACM Symposium on Theory of Computing (STOC), pages 494–503, 2002.
Megan Chen, Ran Cohen, Jack Doerner, Yashvanth Kondi, Eysa Lee, Schuyler Rosefield, and abhi shelat. Muliparty generation of an RSA modulus. In Advances in Cryptology – CRYPTO 2020, part III, pages 64–93, 2020.
Megan Chen, Carmit Hazay, Yuval Ishai, Yuriy Kashnikov, Daniele Micciancio, Tarik Riviere, abhi shelat, Muthuramakrishnan Venkitasubramaniam, and Ruihan Wang. Diogenes: Lightweight scalable RSA modulus generation with a dishonest majority. http://eprint.iacr.org/2020/374, 2020.
Clifford Cocks. Split knowledge generation of RSA parameters. In Proceedings of the 6th International Conference on Cryptography and Coding, pages 89–95, 1997.
Clifford Cocks. Split generation of RSA parameters with multiple participants. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.177.2600, 1998.
Ran Cohen, Sandro Coretti, Juan Garay, and Vassilis Zikas. Round-preserving parallel composition of probabilistic-termination cryptographic protocols. In Proceedings of the 44th International Colloquium on Automata, Languages, and Programming (ICALP), pages 37:1–37:15, 2017.
Ran Cohen, Sandro Coretti, Juan A. Garay, and Vassilis Zikas. Probabilistic termination and composability of cryptographic protocols. Journal of Cryptology, 32(3):690–741, 2019.
Ran Cohen, Iftach Haitner, Eran Omri, and Lior Rotem. From fairness to full security in multiparty computation. In Proceedings of the 11th Conference on Security and Cryptography for Networks (SCN), pages 216–234, 2018.
Ran Cohen and Yehuda Lindell. Fairness versus guaranteed output delivery in secure multiparty computation. Journal of Cryptology, 30(4):1157–1186, 2017.
Ronald Cramer, Ivan Damgård, and Yuval Ishai. Share conversion, pseudorandom secret-sharing and applications to secure computation. In Proceedings of the Second Theory of Cryptography Conference, TCC 2005, pages 342–362, 2005.
Ivan Damgård and Gert Læssøe Mikkelsen. Efficient, robust and constant-round distributed RSA key generation. In Proceedings of the 7th Theory of Cryptography Conference, TCC 2010, pages 183–200, 2010.
Jack Doerner, Yashvanth Kondi, Eysa Lee, and Abhi Shelat. Secure two-party threshold ECDSA from ECDSA assumptions. In Proceedings of the 39th IEEE Symposium on Security and Privacy, (S&P), pages 980–997, 2018.
Jack Doerner, Yashvanth Kondi, Eysa Lee, and Abhi Shelat. Threshold ECDSA from ECDSA assumptions: The multiparty case. In Proceedings of the 40th IEEE Symposium on Security and Privacy, (S&P), 2019.
Shimon Even, Oded Goldreich, and Abraham Lempel. A randomized protocol for signing contracts. Communications of the ACM, 28(6):637–647, 1985.
Yair Frankel, Philip D. MacKenzie, and Moti Yung. Robust efficient distributed RSA-key generation. In Proceedings of the 17th Annual ACM Symposium on Principles of Distributed Computing (PODC), page 320, 1998.
Tore Kasper Frederiksen, Yehuda Lindell, Valery Osheter, and Benny Pinkas. Fast distributed RSA key generation for semi-honest and malicious adversaries. In Advances in Cryptology – CRYPTO 2018, part II, pages 331–361, 2018.
Niv Gilboa. Two party RSA key generation. In Advances in Cryptology – CRYPTO 1999, pages 116–129, 1999.
Oded Goldreich. The Foundations of Cryptography - Volume 1: Basic Techniques. Cambridge University Press, 2001.
Oded Goldreich, Silvio Micali, and Avi Wigderson. How to play any mental game or A completeness theorem for protocols with honest majority. In Proceedings of the 19th Annual ACM Symposium on Theory of Computing (STOC), pages 218–229, 1987.
Shafi Goldwasser and Yehuda Lindell. Secure multi-party computation without agreement. Journal of Cryptology, 18(3):247–287, 2005.
Carmit Hazay, Gert Læssøe Mikkelsen, Tal Rabin, and Tomas Toft. Efficient RSA key generation and threshold Paillier in the two-party setting. In Topics in Cryptology - CT-RSA 2012 - The Cryptographers’ Track at the RSA Conference, pages 313–331, 2012.
Carmit Hazay, Gert Læssøe Mikkelsen, Tal Rabin, Tomas Toft, and Angelo Agatino Nicolosi. Efficient RSA key generation and threshold paillier in the two-party setting. Journal of Cryptology, 32(2):265–323, 2019.
Carmit Hazay, Peter Scholl, and Eduardo Soria-Vazquez. Low cost constant round MPC combining BMR and oblivious transfer. In Advances in Cryptology – ASIACRYPT 2017, part I, pages 598–628, 2017.
Russell Impagliazzo and Moni Naor. Efficient cryptographic schemes provably as secure as subset sum. Journal of Cryptology, 9(4):199–216, 1996.
Yuval Ishai, Rafail Ostrovsky, and Vassilis Zikas. Secure multi-party computation with identifiable abort. In Advances in Cryptology – CRYPTO 2014, part II, pages 369–386, 2014.
Marc Joye and Richard Pinch. Cheating in split-knowledge RSA parameter generation. In Workshop on Coding and Cryptography, pages 157–163, 1999.
Jonathan Katz and Yehuda Lindell. Introduction to Modern Cryptography, Second Edition, chapter Digital Signature Schemes, pages 443–486. Chapman & Hall/CRC, 2015.
Marcel Keller, Emmanuela Orsini, and Peter Scholl. Actively secure OT extension with optimal overhead. In Advances in Cryptology – CRYPTO 2015, part I, pages 724–741, 2015.
Donald E. Knuth. The Art of Computer Programming, Volume II: Seminumerical Algorithms. Addison-Wesley, 1969.
Michael Malkin, Thomas Wu, and Dan Boneh. Experimenting with shared RSA key generation. In Proceedings of the Internet Society’s 1999 Symposium on Network and Distributed System Security, pages 43–56, 1999.
Gary L. Miller. Riemann’s hypothesis and tests for primality. J. Comput. Syst. Sci., 13(3):300–317, 1976.
Payman Mohassel and Matthew K. Franklin. Efficiency tradeoffs for malicious two-party computation. In Proceedings of the 9th International Conference on the Theory and Practice of Public-Key Cryptography (PKC), pages 458–473, 2006.
Michele Orrù, Emmanuela Orsini, and Peter Scholl. Actively secure 1-out-of-n OT extension with application to private set intersection. In Topics in Cryptology - CT-RSA 2017 - The Cryptographers’ Track at the RSA Conference, pages 381–396, 2017.
Krzysztof Pietrzak. Simple verifiable delay functions. In Proceedings of the 10th Annual Innovations in Theoretical Computer Science (ITCS) conference, pages 60:1–60:15, 2019.
Guillaume Poupard and Jacques Stern. Generation of shared RSA keys by two parties. In Advances in Cryptology – ASIACRYPT 1998, pages 11–24, 1998.
Michael O. Rabin. Probabilistic algorithm for testing primality. Journal of Number Theory, 12(1):128–138, 1980.
Ronald L. Rivest. A description of a single-chip implementation of the RSA cipher, 1980.
Ronald L. Rivest. RSA chips (past/present/future). In Workshop on the Theory and Application of Cryptographic Techniques, pages 159–165. Springer, 1984.
Ronald L. Rivest, Adi Shamir, and Leonard M. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2):120–126, 1978.
J. Barkley Rosser and Lowell Schoenfeld. Approximate formulas for some functions of prime numbers. Illinois J. Math., 6:64–94, 1962.
Richard I. Szabo and Nicholas S. Tanaka. Residue Arithmetic and Its Application to Computer Technology. McGraw-Hill, 1967.
Xiao Wang, Samuel Ranellucci, and John Katz. Global-scale secure multiparty computation. In Proceedings of the 24th ACM Conference on Computer and Communications Security, (CCS), pages 39–56, 2017.
Benjamin Wesolowski. Efficient verifiable delay functions. In Advances in Cryptology – EUROCRYPT 2019, part III, pages 379–407, 2019.
Kang Yang, Xiao Wang, and Jiang Zhang. More efficient MPC from improved triple generation and authenticated garbling. In Proceedings of the 27th ACM Conference on Computer and Communications Security, (CCS), 2020.
Acknowledgements
The authors thank Muthuramakrishnan Venkitasubramaniam for the useful conversations and insights he provided, Tore Frederiksen for reviewing and confirming our cost analysis of his protocol [23], Peter Scholl and Xiao Wang for providing detailed cost analyses of their respective protocols [30, 49], and Nigel Smart for pointing out the connection to Residue Number Systems. This research was supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Project Activity (IARPA) under contract number 2019-19-020700009 (ACHILLES). The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of ODNI, IARPA, DoI/NBC, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nigel Smart.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version [9] of this work appeared in CRYPTO 2020.
Appendices
Appendix A. The UC Model and Useful Functionalities
1.1 Appendix A.1. Universal Composability
We give a high-level overview of the UC model and refer the reader to [7] for a further details.
The real-world experiment involves n parties \(\mathcal{P} _1,\ldots ,\mathcal{P} _n\) that execute a protocol \(\pi _{\mathsf {}} {}\), an adversary \(\mathcal{A} \) that can corrupt a subset of the parties, and an environment \(\mathcal{Z} \) that is initialized with an advice-string z. All entities are initialized with the security parameter \({\kappa } \) and with a random tape. The environment activates the parties involved in \(\pi _{\mathsf {}} {}\), chooses their inputs and receives their outputs, and communicates with the adversary \(\mathcal{A} \). A semi-honest adversary simply observes the memory of the corrupted parties, while a malicious adversary may instruct them to arbitrarily deviate from \(\pi _{\mathsf {}} {}\). In this work, we consider only static adversaries, who corrupt up to \(n-1\) parties at the beginning of the experiment. The real-world experiment completes when \(\mathcal{Z} \) stops activating parties and outputs a decision bit. Let \({{\textsc {real}}}_{\pi _{\mathsf {}} {}, \mathcal{A}, \mathcal{Z}}(z,{\kappa })\) denote the random variable representing the output of the experiment.
The ideal-world experiment involves n dummy parties \(\mathcal{P} _1,\ldots ,\mathcal{P} _n\), an ideal functionality \({\mathcal {F}}_{\mathsf {}} {}\), an ideal-world adversary \(\mathcal{S} \) (the simulator), and an environment \(\mathcal{Z} \). The dummy parties act as routers that forward any message received from \(\mathcal{Z} \) to \({\mathcal {F}}_{\mathsf {}} {}\) and vice versa. The simulator can corrupt a subset of the dummy parties and interact with \({\mathcal {F}}_{\mathsf {}} {}\) on their behalf; in addition, \(\mathcal S\) can communicate directly with \({\mathcal {F}}_{\mathsf {}} {}\) according to its specification. The environment and the simulator can interact throughout the experiment, and the goal of the simulator is to trick the environment into believing it is running in the real experiment. The ideal-world experiment completes when \(\mathcal{Z} \) stops activating parties and outputs a decision bit. Let \({{\textsc {ideal}}}_{{\mathcal {F}}_{\mathsf {}} {},\mathcal{S}, \mathcal{Z}}(z,{\kappa })\) denote the random variable representing the output of the experiment.
A protocol \(\pi _{\mathsf {}} {}\) UC-realizes a functionality \({\mathcal {F}}_{\mathsf {}} {}\) if for every probabilistic polynomial-time (PPT) adversary \(\mathcal{A} \) there exists a PPT simulator \(\mathcal{S} \) such that for every PPT environment \(\mathcal{Z} \)
If the above distributions are perfectly or statistically indistinguishable, then we say that \(\pi _{\mathsf {}} {}\) perfectly or statistically UC-realizes \({\mathcal {F}}_{\mathsf {}} {}\), respectively.
Communication model. We follow standard practice of MPC protocols: Every pair of parties can communicate via an authenticated channel, and in the malicious setting we additionally assume the existence of a broadcast channel. Formally, the protocols are defined in the \(({\mathcal {F}}_{\mathsf {auth}},{\mathcal {F}}_{\mathsf {bc}})\)-hybrid model (see [7, 8]). We leave this implicit in their descriptions.
1.2 Appendix A.2. Useful Functionalities
To realize  and
and  , we use a number of standard functionalities that have well-known realizations in the cryptography literature. For completeness, we give those functionalities in this section. First among them is a simple distributed coin-tossing functionality, which samples an element uniformly at random from an arbitrary domain.
, we use a number of standard functionalities that have well-known realizations in the cryptography literature. For completeness, we give those functionalities in this section. First among them is a simple distributed coin-tossing functionality, which samples an element uniformly at random from an arbitrary domain.

We also make use of a one-to-many commitment functionality, which we have taken directly from Canetti et al. [8].

In  (Protocol 5.2), we make use of a functionality for randomly sampling integer shares of zero. This functionality can be realized assuming two-party coin tossing via a slight modification of a protocol of Cramer et al. [17].
(Protocol 5.2), we make use of a functionality for randomly sampling integer shares of zero. This functionality can be realized assuming two-party coin tossing via a slight modification of a protocol of Cramer et al. [17].

In both  and
and  , we use a functionality for generic commit-and-compute multiparty computation. This functionality allows each party to commit to private inputs, after which the parties agree on one or more arbitrary circuits to apply to those inputs. It can be realized using many generic multiparty computation protocols.
, we use a functionality for generic commit-and-compute multiparty computation. This functionality allows each party to commit to private inputs, after which the parties agree on one or more arbitrary circuits to apply to those inputs. It can be realized using many generic multiparty computation protocols.

Finally, we use a delayed-transmission correlated oblivious transfer functionality as the basis of our multiplication protocols. This functionality can be realized by combining a standard OT protocol with a commitment scheme, as we discuss in Appendix B.1. Unlike an ordinary COT functionality, which allows the sender to associate a single correlation to each choice bit, this functionality allows the sender to associate an arbitrary number of correlations to each bit. The transfer action then commits the sender to the correlations, and the sender can later decommit them individually, at which point the receiver learns either a random pad, or the same pad plus the decommitted correlation, according to their choice. We suggest that this functionality be instantiated via either Silent OT-extension [6] or the KOS OT-extension protocol [35].

Appendix B. Instantiating Multiplication
In this section, we describe how to instantiate the  functionality and discuss the efficiency of our protocols. In Appendix B.1, we begin by using oblivious transfer and commitments to build delayed correlated oblivious transfer (
functionality and discuss the efficiency of our protocols. In Appendix B.1, we begin by using oblivious transfer and commitments to build delayed correlated oblivious transfer ( ). In Appendix B.2, we use
). In Appendix B.2, we use  to realize a two-party multiplier
to realize a two-party multiplier  that allows inputs to be reused and postpones the detection of malicious behavior. In Appendix B.3, we plug this into the classic GMW multiplication technique [26] in order to realize an n-party multiplier
that allows inputs to be reused and postpones the detection of malicious behavior. In Appendix B.3, we plug this into the classic GMW multiplication technique [26] in order to realize an n-party multiplier  , with the same properties of input-reuse and delayed cheat detection. Finally, in Appendix B.4, we combine this component with generic multiparty computation (
, with the same properties of input-reuse and delayed cheat detection. Finally, in Appendix B.4, we combine this component with generic multiparty computation ( ) via a simple MAC to realize
) via a simple MAC to realize  . We discuss security and give concrete efficiency analysis in parallel. In our efficiency analysis, we make the same assumptions and concessions as in Sect. 6.
. We discuss security and give concrete efficiency analysis in parallel. In our efficiency analysis, we make the same assumptions and concessions as in Sect. 6.
1.1 Appendix B.1. Delayed-Transmission Correlated Oblivious Transfer
Given groups \({\mathbb {G}}_1,\ldots ,{\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\), the functionality  with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) can be realized in the
with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) can be realized in the  -hybrid model, where
-hybrid model, where  is the standard oblivious-transfer functionality [8]. Our construction uses a collection of \({\ell _\mathsf {\scriptscriptstyle OT}}\) hash functions \(H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\) such that for \(r\leftarrow \{0,1\}^{\lambda } \), the vector \((H_1(r),\ldots ,H_{\ell _\mathsf {\scriptscriptstyle OT}}(r))\) is indistinguishable from \((g_1,\ldots ,g_{\ell _\mathsf {\scriptscriptstyle OT}})\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). This is trivial when each \(H_i\) is modeled as a random oracle.
is the standard oblivious-transfer functionality [8]. Our construction uses a collection of \({\ell _\mathsf {\scriptscriptstyle OT}}\) hash functions \(H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\) such that for \(r\leftarrow \{0,1\}^{\lambda } \), the vector \((H_1(r),\ldots ,H_{\ell _\mathsf {\scriptscriptstyle OT}}(r))\) is indistinguishable from \((g_1,\ldots ,g_{\ell _\mathsf {\scriptscriptstyle OT}})\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). This is trivial when each \(H_i\) is modeled as a random oracle.
-
1.
The sender samples two uniformly random messages \((r_0,r_1)\leftarrow \{0,1\}^{{\lambda }}\times \{0,1\}^{{\lambda }}\), and the receiver (who has an input bit \(\beta \in \{0,1\}\)) uses
 to receive \(r_\beta \).
to receive \(r_\beta \). -
2.
In order to commit to its input-correlation vector \({\varvec{\mathrm {\alpha }}}\), the sender sends \({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\) for \(i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]\) to
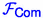 .
. -
3.
The sender and receiver use
 to sample an agreed-upon uniform vector \(\tilde{{\varvec{\mathrm {\rho }}}}\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). The sender outputs \({\varvec{\mathrm {\rho }}}:=\{H_i(r_0)+H_i({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1))-\tilde{{\varvec{\mathrm {\rho }}}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as its pads.
to sample an agreed-upon uniform vector \(\tilde{{\varvec{\mathrm {\rho }}}}\leftarrow {\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\). The sender outputs \({\varvec{\mathrm {\rho }}}:=\{H_i(r_0)+H_i({\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1))-\tilde{{\varvec{\mathrm {\rho }}}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as its pads. -
4.
To implement the transfer instruction for index i, the sender instructs
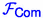 to decommit \(x\equiv {\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\), and then the receiver retrieves its output follows:
to decommit \(x\equiv {\varvec{\mathrm {\alpha }}}_i-H_i(r_0)-H_i(r_1)\), and then the receiver retrieves its output follows:-
If \(\beta =0\), then the receiver calculates its output as \(\tilde{{\varvec{\mathrm {\rho }}}}_i-H_i(r_0)-H_i(x)\). Note that this is equivalent to \(-{\varvec{\mathrm {\rho }}}_i\)
-
If \(\beta =1\), then the receiver calculates its output as \(x + \tilde{{\varvec{\mathrm {\rho }}}}_i+H_i(r_1)-H_i(x)\). Note that this is equivalent to \({\varvec{\mathrm {\alpha }}}_i-{\varvec{\mathrm {\rho }}}_i\).
-
It is clear to see that at the end of this protocol, the sender and receiver hold additive shares of \(\beta \cdot {\varvec{\mathrm {\alpha }}}_i\) for every index i that has been decommitted, and that the sender is committed to \({\varvec{\mathrm {\alpha }}}\).
Theorem B.1
Let \({\mathbb {G}}_1,\ldots ,{\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) be groups and assume there exists a collection \(\{H_i:\{0,1\}^{\lambda } \rightarrow {\mathbb {G}}_i\}_{i\in [{\ell _\mathsf {\scriptscriptstyle OT}}]}\) as described above. Then, there exists a protocol in the  ,
, -hybrid model that UC-realizes
-hybrid model that UC-realizes  with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) against a malicious PPT adversary that statically corrupts one party, and this protocol requires a single invocation of
with respect to \({\mathbb {G}}_1\times \cdots \times {\mathbb {G}}_{\ell _\mathsf {\scriptscriptstyle OT}}\) against a malicious PPT adversary that statically corrupts one party, and this protocol requires a single invocation of  .
.
We note that with a particular usage pattern, there is a more efficient instantiation available, based upon a non-black-box usage of either Silent OT [6] or KOS OT [35], which we introduced in Sect. 6.2. In particular, assume there is some specific point in time, and that all correlations are decommitted either immediately after they are committed, or at that point. Both Silent OT and KOS OT involve sending a message from the receiver to the sender first, followed by a message from the sender to the receiver, where each bit in this latter message corresponds to one bit of the correlation(s) transferred (and any correlation bit can be recovered from only the one associated message bit). Thus,  can be realized in the following context-optimized way: the receiver sends its message, and then the sender sends the bits of its message associated with the correlations to be immediately released, and commits (using a single commitment) to the other bits of its message. These bits are decommitted later. This eliminates the potential overhead associated with transferring the \(r_0\) and \(r_1\) values in our above construction. Furthermore, if many
can be realized in the following context-optimized way: the receiver sends its message, and then the sender sends the bits of its message associated with the correlations to be immediately released, and commits (using a single commitment) to the other bits of its message. These bits are decommitted later. This eliminates the potential overhead associated with transferring the \(r_0\) and \(r_1\) values in our above construction. Furthermore, if many  instances are invoked at once, and the delayed-release correlations are released simultaneously across all instances, then the instances can share a single commitment. Our usage of
instances are invoked at once, and the delayed-release correlations are released simultaneously across all instances, then the instances can share a single commitment. Our usage of  matches this pattern, and so its cost is equal (up to a few bits) to that of either Silent OT or KOS OT. When calculating concrete efficiency figures, we assume the overhead is exactly zero.
matches this pattern, and so its cost is equal (up to a few bits) to that of either Silent OT or KOS OT. When calculating concrete efficiency figures, we assume the overhead is exactly zero.
1.2 B.2. Two-Party Reusable-Input Multiplier
Our basic two-party multiplication functionality  allows parties to input arbitrarily many values, whereafter, on request, it returns additive shares of the product of any pair of them. Unlike the standard two-party multiplication functionality, however, we allow the adversary to both request the honest party’s inputs and determine the output products. We then add two explicit check commands which the parties can agree to invoke. One notifies the honest party if the adversary has used its power to cheat, and the other opens the private inputs to the multiplication, while also, as a side effect, notifying the honest party if the adversary has used its power to cheat.
allows parties to input arbitrarily many values, whereafter, on request, it returns additive shares of the product of any pair of them. Unlike the standard two-party multiplication functionality, however, we allow the adversary to both request the honest party’s inputs and determine the output products. We then add two explicit check commands which the parties can agree to invoke. One notifies the honest party if the adversary has used its power to cheat, and the other opens the private inputs to the multiplication, while also, as a side effect, notifying the honest party if the adversary has used its power to cheat.

Theorem B.3
There exists a protocol in the  -hybrid model that statistically UC-realizes
-hybrid model that statistically UC-realizes  against a malicious adversary that statically corrupts one party.
against a malicious adversary that statically corrupts one party.
The proof of this theorem is via construction of a protocol  , which we sketch here, along with a security argument. We adapt the multiplication protocols of Doerner et al., and refer the reader to their work [20, Section 3] for a more in-depth technical explanation. Our main changes involve making the security parameter independent of the working field, separating the input, multiplication, and cheater check components into separate phases such that inputs can be reused and checks performed retroactively, and adding an input-opening phase not originally present. For any input the parties can choose to use either the cheater check or the input-opening mechanism, but not both. Along with the sketch of each phase of the protocol, we provide a cost analysis of that phase, and sketch a simulation strategy and security argument. We omit a formal proof of security via hybrid experiments, as it would closely resemble proofs already provided by Doerner et al. [19, 20].
, which we sketch here, along with a security argument. We adapt the multiplication protocols of Doerner et al., and refer the reader to their work [20, Section 3] for a more in-depth technical explanation. Our main changes involve making the security parameter independent of the working field, separating the input, multiplication, and cheater check components into separate phases such that inputs can be reused and checks performed retroactively, and adding an input-opening phase not originally present. For any input the parties can choose to use either the cheater check or the input-opening mechanism, but not both. Along with the sketch of each phase of the protocol, we provide a cost analysis of that phase, and sketch a simulation strategy and security argument. We omit a formal proof of security via hybrid experiments, as it would closely resemble proofs already provided by Doerner et al. [19, 20].
Common parameters and hybrid functionalities. The protocol  is parametrized by the statistical security parameter \({s} \) and a prime \(m\) such that \(|m|\in O(\log {s})\). For convenience, we define a batch-size \({\xi } :=2{s} + |m|\) and a repetition count \(r=\left\lceil {s}/|m| \right\rceil \). Looking ahead, Bob will encode his input via the inner product of \({\xi } \) random bits and a uniformly sampled vector \({\varvec{\mathrm {g}}}\). Intuitively, the parameter \({\xi } \) is set so that even if \({s} \) bits of his codeword are revealed to Alice, she has negligible advantage in guessing his input. Note that unlike in prior works, \({\varvec{\mathrm {g}}}\) is not fixed ahead of time, but chosen uniformly after Alice is committed to her inputs. The participating parties have access to the coin-tossing functionality
is parametrized by the statistical security parameter \({s} \) and a prime \(m\) such that \(|m|\in O(\log {s})\). For convenience, we define a batch-size \({\xi } :=2{s} + |m|\) and a repetition count \(r=\left\lceil {s}/|m| \right\rceil \). Looking ahead, Bob will encode his input via the inner product of \({\xi } \) random bits and a uniformly sampled vector \({\varvec{\mathrm {g}}}\). Intuitively, the parameter \({\xi } \) is set so that even if \({s} \) bits of his codeword are revealed to Alice, she has negligible advantage in guessing his input. Note that unlike in prior works, \({\varvec{\mathrm {g}}}\) is not fixed ahead of time, but chosen uniformly after Alice is committed to her inputs. The participating parties have access to the coin-tossing functionality  , the commitment functionality
, the commitment functionality  , and the delayed-transfer COT functionality
, and the delayed-transfer COT functionality  .
.
The Input and Multiplication phases of
 . For the sake of succinctness, we will describe the input and multiplication processes jointly: each party will supply exactly one input, and they will receive shares of the product, in a single step. Later, we will discuss how the protocol can be generalized to allow the parties to input values independently, and to reuse those input values. Alice begins the protocol with an input \(a\in [0,m)\), and Bob with an input \(b\in [0,m)\), and they both know a fresh, agreed-upon session ID \(\mathsf {sid}\). They take the following steps:
. For the sake of succinctness, we will describe the input and multiplication processes jointly: each party will supply exactly one input, and they will receive shares of the product, in a single step. Later, we will discuss how the protocol can be generalized to allow the parties to input values independently, and to reuse those input values. Alice begins the protocol with an input \(a\in [0,m)\), and Bob with an input \(b\in [0,m)\), and they both know a fresh, agreed-upon session ID \(\mathsf {sid}\). They take the following steps:

While the correctness of the above procedure is easy to verify when both parties follow the protocol, we note that it omits some of the consistency-check components of the protocols of Doerner et al. [19, 20], which will appear in the next protocol phase. In particular, the consistency-check vector \({{\tilde{\mathbf{a}}}}\) is committed by the end of the protocol, but it has not yet been transferred to Bob. This omission admits cheating behavior, such as a corrupt Alice using different values for \(a\) in each iteration of Step 4b. We model these attacks in  by allowing the ideal adversary to fully control the results of a multiplication, once it has explicitly notified
by allowing the ideal adversary to fully control the results of a multiplication, once it has explicitly notified  that it wishes to cheat.
that it wishes to cheat.
If the parties agree that Alice should be compelled to reuse an input in multiple different multiplications, then she must also reuse the same consistency-check vector \({{\tilde{\mathbf{a}}}}\) in all of those multiplications. The consistency-check mechanism (in the next protocol phase) that ensures the internal consistency of a single multiplication will also ensure the consistency of many multiplications.
If the parties agree that Bob should be compelled to reuse an input in multiple different multiplications, then the above protocol is run exactly once, and Alice combines her inputs for all of those multiplications (and their associated, independent consistency-check vectors) into a single array, which she commits to in Step 4b. She then repeats Step 4c, changing the index as appropriate to cause the transfer of each of her inputs (but not, for now, the consistency-check vectors). The remaining steps in the protocol are repeated once for each multiplication, except for Step 8, which is performed exactly once, for Bob’s one input.
In the case that Bob wishes to input a value to be used in one or more later (potentially dynamically chosen) multiplications, the parties can run the above protocol until Step 4a is complete and then pause the protocol until a multiplication using Bob’s input must be performed. In the case that Alice wishes to input a value to be used later, Bob must input a dummy value, and compulsory input reuse is employed (as previously described) to ensure she uses her input again in the appropriate multiplications, when they occur.
We observe that the dominant cost of the above protocol is incurred by the \({\xi } =2s+|m|\) invocations of  per multiplication, each invocation with a correlation of size \(|m|\). If we realize
per multiplication, each invocation with a correlation of size \(|m|\). If we realize  via Silent OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \(2|m|+2{s} \) bits it total. If we realize
via Silent OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \(2|m|+2{s} \) bits it total. If we realize  via KOS OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \({\lambda } \cdot (|m|+2{s})+|m|\) bits in total. Regardless, they require three rounds if
via KOS OT, then Alice must transmit \(|m|\cdot (|m|+2{s})+4{\lambda } \) bits in total and Bob must transmit \({\lambda } \cdot (|m|+2{s})+|m|\) bits in total. Regardless, they require three rounds if  is realized non-interactively.
is realized non-interactively.
Simulator overview. Since our multiplication protocol has two asymmetric roles, we specify two separate simulation strategies: one against a corrupted Alice, and the other against a corrupted Bob. As in prior malicious-secure OT-based multipliers, Bob has few avenues via which he can cheat, and so his simulator is relatively straightforward. On the other hand, the division of the protocol into multiple independent phases and addition of a second cheater-checking mechanism has noticeably complicated simulation against Alice. Alice is committed to her inputs and to many components of the cheater-check mechanisms by the end of the input/multiplication phase. The simulation can thus analyze her cheats before returning an output to her. Based on certain attributes of her cheats, the simulator may decide to call the \(\texttt {cheat}\) interface of  , in which case the functionality will certainly abort when either the cheater check or input revelation phases is called, or the simulator may decide to avoid calling the \(\texttt {cheat}\) interface (thereby depriving the adversary of leakage and control over the output), and instead manually instruct
, in which case the functionality will certainly abort when either the cheater check or input revelation phases is called, or the simulator may decide to avoid calling the \(\texttt {cheat}\) interface (thereby depriving the adversary of leakage and control over the output), and instead manually instruct  to abort when one or both of the aforementioned phases is actually entered, or the simulator may not abort at all.
to abort when one or both of the aforementioned phases is actually entered, or the simulator may not abort at all.
Simulating Inputs and Multiplication. Simulation of this phase against a corrupt Bob is simple: he has no avenue for cheating, and his ideal input in any single instance of the above protocol is defined by \(b\equiv \delta +\langle {\varvec{\mathrm {g}}}, {\varvec{\mathrm {\beta }}} \rangle \pmod {m}\), which is available to the simulator. The only values that he receives during the course of the protocol are \({\varvec{\mathrm {g}}}\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\), which can be simulated by sampling them uniformly.
Simulating against a corrupt Alice is more involved: if she uses inconsistent values of \(a\) across the OT instances in Step 4b, then the simulator takes her most common value to be her ideal input (breaking ties arbitrarily). Let this ideal input be denoted by \(a\), and let the vector of (possibly inconsistent) she supplied in the OT instances be \({\varvec{\mathrm {\alpha }}}\). The length \({\varvec{\mathrm {\alpha }}}\) depends upon the number of multiplications in which Alice and Bob agreed that her input should be reused; for example \(|{\varvec{\mathrm {\alpha }}}|={\xi } \) if \(a\) was used in only one multiplication. Without loss of generality, we will assume one multiplication only for the rest of our simulator description, but note where generalizations must occur. Let c be the number of inconsistencies in \({\varvec{\mathrm {\alpha }}}\) with respect to \(a\), and let \({\varvec{\mathrm {I}}}\) be a vector of the indices of these inconsistencies; that is, a vector such that \(|{\varvec{\mathrm {I}}}|=c\) and \(\forall i\in [|{\varvec{\mathrm {\alpha }}}|], {\varvec{\mathrm {\alpha }}}_i \ne a\iff i\in {\varvec{\mathrm {I}}}\). We have two cases.
If \(c \ge {s} \), then the simulator activates the \(\texttt {cheat}\) interface of  and receives Bob’s inputs. Hereafter, the simulator can run Bob’s code in order to behave exactly as he would in the real world. Since neither the real Bob nor the
and receives Bob’s inputs. Hereafter, the simulator can run Bob’s code in order to behave exactly as he would in the real world. Since neither the real Bob nor the  aborts during the input and multiplication phases, regardless of Alice’s behavior, it is easy to see that the real and ideal world experiments are identically distributed insofar as those two phases are concerned. However, activating the \(\texttt {cheat}\) interface dooms
aborts during the input and multiplication phases, regardless of Alice’s behavior, it is easy to see that the real and ideal world experiments are identically distributed insofar as those two phases are concerned. However, activating the \(\texttt {cheat}\) interface dooms  to abort when the input-opening or cheater-check interfaces are used, and so it remains to prove that Bob aborts with overwhelming probability in the real word when the corresponding protocol phases are run. We will discuss this further in the relevant sections.
to abort when the input-opening or cheater-check interfaces are used, and so it remains to prove that Bob aborts with overwhelming probability in the real word when the corresponding protocol phases are run. We will discuss this further in the relevant sections.
If \(c < {s} \), then the simulator will not call the \(\texttt {cheat}\) interface of  , but will instead use the same interface as an honest Alice, compute and apply the effects of Alice’s inconsistencies locally, and potentially instruct
, but will instead use the same interface as an honest Alice, compute and apply the effects of Alice’s inconsistencies locally, and potentially instruct  to abort at a later time. The simulator begins by sampling \({\varvec{\mathrm {g}}}\leftarrow \smash {{\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\) uniformly. It then computes a vector \({\varvec{\mathrm {\Delta }}}\) of the offsets by which Alice has cheated, one for each OT instance,
to abort at a later time. The simulator begins by sampling \({\varvec{\mathrm {g}}}\leftarrow \smash {{\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\) uniformly. It then computes a vector \({\varvec{\mathrm {\Delta }}}\) of the offsets by which Alice has cheated, one for each OT instance,
after which it flips a coin for each location where Alice has cheated. That is, if we let \(\hat{{\varvec{\mathrm {\beta }}}}\) represent the simulator’s coins, then it samples \(\hat{{\varvec{\mathrm {\beta }}}}_i\leftarrow \{0,1\}\) for \(i\in {\varvec{\mathrm {I}}}\) and sets \(\hat{{\varvec{\mathrm {\beta }}}}_i:=\bot \) (where \(\bot \) is a special symbol indicating that no value has been chosen) otherwise.
Next, the simulator calls the input phase of  using \(a\) as its input value, and then, for each time that the input \(\varvec{\alpha }\) is supposed to be reused, it performs the following sequence of steps. First, it calls the multiply phase of
using \(a\) as its input value, and then, for each time that the input \(\varvec{\alpha }\) is supposed to be reused, it performs the following sequence of steps. First, it calls the multiply phase of  , and receives \({\hat{z}}_{{\mathsf {A}}} \) as output. In order to deliver a reply to Alice on behalf of
, and receives \({\hat{z}}_{{\mathsf {A}}} \) as output. In order to deliver a reply to Alice on behalf of  in Step 4b of the protocol, the simulator must apply Alice’s cheats. It samples a uniform \(\delta \leftarrow {\mathbb {Z}}_m\) and a set of ideal outputs for the OT instances; specifically, it finds a vector \(\smash {\hat{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{{\xi }}}\) such that
in Step 4b of the protocol, the simulator must apply Alice’s cheats. It samples a uniform \(\delta \leftarrow {\mathbb {Z}}_m\) and a set of ideal outputs for the OT instances; specifically, it finds a vector \(\smash {\hat{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{{\xi }}}\) such that
and using these values, the simulator computes the values that it must output to Alice on behalf of  :
:
Here again we have assumed that \(a\) is being used in only one multiplication, and so \(|{\varvec{\mathrm {\alpha }}}|=|\hat{{\varvec{\mathrm {\beta }}}}|=|{\varvec{\mathrm {\Delta }}}|={\xi } \); in generality, the simulator uses the appropriate slice of \({\varvec{\mathrm {\Delta }}}\) and \(\hat{{\varvec{\mathrm {\beta }}}}\) for each multiplication, and then concatenates the resulting vectors to form one unified vector \(\smash {{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|}}\). To simulate Step 4b of the protocol, the simulator sends each \(\smash {{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}}\) to Alice on behalf of the \(i^\text {th}\) instance of  .
.
In Step 6 of the protocol, the simulator receives \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\) and \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\) from Alice on behalf of  . Note that if Alice is honest, then \(a=a'\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}\), but in general Alice might cheat, and so these values are stored by the simulator for later. To simulate Step 7, the simulator sends \({\varvec{\mathrm {g}}}\) on behalf of
. Note that if Alice is honest, then \(a=a'\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}\), but in general Alice might cheat, and so these values are stored by the simulator for later. To simulate Step 7, the simulator sends \({\varvec{\mathrm {g}}}\) on behalf of  , which it previously sampled uniformly just as
, which it previously sampled uniformly just as  would. To simulate Step 8 of the protocol, the simulator sends the value \(\delta \) that it sampled previously to Alice on behalf of Bob. This completes the simulation for the input and multiplication phases of
would. To simulate Step 8 of the protocol, the simulator sends the value \(\delta \) that it sampled previously to Alice on behalf of Bob. This completes the simulation for the input and multiplication phases of  against a corrupt Alice, when \(c < {s} \).
against a corrupt Alice, when \(c < {s} \).
We will briefly argue for the indistinguishability of the real and ideal-world experiments with respect to adversaries corrupting Alice, when \(c<{s} \). The adversary’s view includes \({\varvec{\mathrm {\alpha }}}\), \(\delta \), \({\varvec{\mathrm {g}}}\), and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\), and additionally, the environment determines the input \(b\) and receives the output \(z_{{\mathsf {B}}} \). We must analyze the joint distribution of these six variables. In both the real and ideal worlds, \({\varvec{\mathrm {g}}}\) is chosen uniformly and independently. In the ideal world, \(\delta \) is chosen uniformly and independently, but in the real world, it is chosen as the difference between \(b\) and the inner product of \({\varvec{\mathrm {g}}}\) and Bob’s choice bits \({\varvec{\mathrm {\beta }}}\). These two distributions are statistically indistinguishable as previously shown by Impagliazzo and Naor [31, Proposition 1.1] (see also [20, Lemma B.5]). Finally, in the ideal world, \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) are chosen uniformly by  and the simulator, subject to the following constraints
and the simulator, subject to the following constraints
assuming that \(|{\varvec{\mathrm {\alpha }}}|=|\smash {\hat{{\varvec{\mathrm {\beta }}}}}|=|{\varvec{\mathrm {\Delta }}}|={\xi } \), as before. Substituting Eq. 8 into 7, and the result into 6 yields
and rearranging, we have
In the real world, on the other hand, \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) are chosen uniformly by  subject to
subject to
which implies that
Now, recall that \({\tilde{b}}\equiv b-\delta \pmod {m}\) and \(\left\langle {\varvec{\mathrm {g}}},{\varvec{\mathrm {\beta }}}\right\rangle \equiv {\tilde{b}}\pmod {m}\), which allows us to rewrite Eq. 10 by adding a zero-sum term to the right hand side:
where we take \(a\) to be the most common element of \({\varvec{\mathrm {\alpha }}}\), as in the ideal world. Rearranging, we have
Observe that Eqs. 9 and 11 are identical except for the difference between Bob’s choice bits \({\varvec{\mathrm {\beta }}}\) and the simulator’s simulated choice bits \(\smash {\hat{{\varvec{\mathrm {\beta }}}}}\). In the real world, Bob samples \({\varvec{\mathrm {\beta }}}\) uniformly. In the ideal world, the simulator samples \(\smash {\hat{{\varvec{\mathrm {\beta }}}}}\) uniformly at every index i where \({\varvec{\mathrm {\alpha }}}_i\ne a\). Thus, the constraints under which \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) are sampled are equivalent in the real and ideal worlds, and the two worlds are statistically indistinguishable when \(c<{s} \).
The Cheater Check phase of
 . In this phase of the protocol, the parties perform a process analogous to the consistency check in the multiplication protocols of Doerner et al. [20]. This reveals to the honest parties any cheats in the protocol phases described above. As we have previously noted, Bob does not have an opportunity to cheat; thus this check verifies only Alice’s behavior, via the consistency-check vectors \({{\tilde{\mathbf{a}}}}\), \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), to which she is committed. In addition to the consistency-check vector, Alice begins the protocol with an input \(a\), and both parties know a vector \({\textsf {sids}}\) of all the multiplications in which Alice was expected to use this input, along with a vector \(\textsf {bit-sids}\) of the individual
. In this phase of the protocol, the parties perform a process analogous to the consistency check in the multiplication protocols of Doerner et al. [20]. This reveals to the honest parties any cheats in the protocol phases described above. As we have previously noted, Bob does not have an opportunity to cheat; thus this check verifies only Alice’s behavior, via the consistency-check vectors \({{\tilde{\mathbf{a}}}}\), \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), to which she is committed. In addition to the consistency-check vector, Alice begins the protocol with an input \(a\), and both parties know a vector \({\textsf {sids}}\) of all the multiplications in which Alice was expected to use this input, along with a vector \(\textsf {bit-sids}\) of the individual  instances (over all of the multiplications associated with \({\textsf {sids}}\)) in which she was expected to commit \(\{a\}\Vert {{\tilde{\mathbf{a}}}}\). Bob begins with a vector of choice bits, \({\varvec{\mathrm {\beta }}}\), one bit for each entry in \(\textsf {bit-sids}\). We assume for the sake of simplicity that Bob was not expected to reuse his inputs. The parties take the following steps:
instances (over all of the multiplications associated with \({\textsf {sids}}\)) in which she was expected to commit \(\{a\}\Vert {{\tilde{\mathbf{a}}}}\). Bob begins with a vector of choice bits, \({\varvec{\mathrm {\beta }}}\), one bit for each entry in \(\textsf {bit-sids}\). We assume for the sake of simplicity that Bob was not expected to reuse his inputs. The parties take the following steps:
-
1.
For each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), Alice sends \((\texttt {transfer},\textsf {bit-sids}_i,j+1)\) to
 , and as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). Note that if Alice has behaved honestly, then per the specification of
, and as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). Note that if Alice has behaved honestly, then per the specification of  , it holds for all \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\) that $$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\equiv {\varvec{\mathrm {\beta }}}_i \cdot {{\tilde{\mathbf{a}}}}_{j}\pmod {m} \end{aligned}$$
, it holds for all \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\) that $$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\equiv {\varvec{\mathrm {\beta }}}_i \cdot {{\tilde{\mathbf{a}}}}_{j}\pmod {m} \end{aligned}$$ -
2.
Alice instructs
 to decommit \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\).
to decommit \(({\varvec{\mathrm {\zeta }}},{\varvec{\mathrm {\psi }}})\). -
3.
Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\),
$$\begin{aligned} {\varvec{\mathrm {\zeta }}}_{i,j} + {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i}\equiv {\varvec{\mathrm {\beta }}}_i\cdot {\varvec{\mathrm {\psi }}}_{j}\pmod {m} \end{aligned}$$and if this relationship does not hold, then he aborts.
The cheater check costs only one round and \(2{s} \cdot (|m|+2{s})\cdot |{\textsf {sids}}|\) bits of transmitted data for Alice, where \(|{\textsf {sids}}|\) is the number of multiplications in which the input to be checked was used.
Simulating the Cheater Check.Notice that in the foregoing procedure, Bob learns nothing about \(\alpha \) or \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\); all values derived from these are masked by Alice using uniformly sampled one-time pads before being transmitted to him. Notice furthermore that every value in Bob’s check in Step 3 is known to or determined by the simulator. Thus, simulation against Bob is trivial: the simulator can send Bob exactly the message that causes his check to pass, and then send the appropriate \(\texttt {check}\) message to  .
.
As before, simulation against Alice is more involved. Although Alice was instructed to reuse the same r-length vector \({{\tilde{\mathbf{a}}}}\) for all OT instances involving \(a\) in Step 4b of the input phase, she could have cheated and used different vectors in some OT instances. Thus, let \(\tilde{{\varvec{\mathrm {\alpha }}}}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|\times r}\) represent her actual inputs to the OTs, where \(\tilde{{\varvec{\mathrm {\alpha }}}}_{i,*} = \tilde{{\varvec{\mathrm {\alpha }}}}_{i',*} = {{\tilde{\mathbf{a}}}}\) for all \(i,i'\in [|{\varvec{\mathrm {\alpha }}}|]\) if Alice is honest. Note that \(|{\varvec{\mathrm {\alpha }}}|=|\textsf {bit-sids}|\). Upon the decommitment instruction from Alice on behalf of  , the simulator performs the following check for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\):
, the simulator performs the following check for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\):
-
1.
Let \({\varvec{\mathrm {J}}}\subseteq [r]\) be a vector containing every index j where the following equalities do not both hold:
$$\begin{aligned} {\varvec{\mathrm {\psi }}}_j&\equiv (\tilde{{\varvec{\mathrm {\alpha }}}}_{i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {\alpha }}}_{i}) \pmod {m}\\ {\varvec{\mathrm {\zeta }}}_{i,j}&\equiv ({\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}) \pmod {m} \end{aligned}$$Note that if Alice has acted honestly then these equalities will always hold.
-
2.
Compute \({\varvec{\mathrm {\beta }}}^*\in {\mathbb {Z}}_m^r\) such that
$$\begin{aligned} {\varvec{\mathrm {\beta }}}^*_j\equiv \left\{ \begin{aligned}&\frac{{\varvec{\mathrm {\zeta }}}_{i,j} - ({\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i})}{{\varvec{\mathrm {\psi }}}_j - (\tilde{{\varvec{\mathrm {\alpha }}}}_{i,j}+{\varvec{\mathrm {e}}}_j\cdot {\varvec{\mathrm {\alpha }}}_{i})}\pmod {m}&\hbox { if}\ j\in {\varvec{\mathrm {J}}}\\&\bot&\hbox { if}\ j\not \in {\varvec{\mathrm {J}}} \end{aligned}\right. \end{aligned}$$where \(\bot \) is a special symbol used to indicate no value, and an additional special symbol \(\infty \) is used to indicate an undefined value due to division by zero.
-
3.
If there exists any index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_{j}\not \in \{0,1,\bot \}\), or any pair \((j,j')\) such that \({\varvec{\mathrm {\beta }}}^*_{j},{\varvec{\mathrm {\beta }}}^*_{j'}\in \{0,1\}\wedge {\varvec{\mathrm {\beta }}}^*_{j} \ne {\varvec{\mathrm {\beta }}}^*_{j'}\), then immediately instruct
 to abort. If the simulator continues past this point, it must be the case that either \({\varvec{\mathrm {\beta }}}^*\in \{0,\bot \}^r\) or \({\varvec{\mathrm {\beta }}}^*\in \{1,\bot \}^r\). This means that there exists a set of choice bits that would cause Bob’s check to pass in the real world.
to abort. If the simulator continues past this point, it must be the case that either \({\varvec{\mathrm {\beta }}}^*\in \{0,\bot \}^r\) or \({\varvec{\mathrm {\beta }}}^*\in \{1,\bot \}^r\). This means that there exists a set of choice bits that would cause Bob’s check to pass in the real world. -
4.
If \(i\in {\varvec{\mathrm {I}}}\) and there exists an index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_j\not \in \{\hat{{\varvec{\mathrm {\beta }}}}_i,\bot \}\), then immediately instruct
 to abort.
to abort. -
5.
If \(i\not \in {\varvec{\mathrm {I}}}\) and there exists an index \(j\in [r]\) such that \({\varvec{\mathrm {\beta }}}^*_j \ne \bot \), then flip a uniform coin and immediately instruct
 abort if it lands on heads.
abort if it lands on heads.
If the check passes (i.e., no abort instruction is issued) for all \(i\in [|{\varvec{\mathrm {\alpha }}}|]\), then the simulator sends the appropriate \(\texttt {check}\) message to  (which will abort at this point if the \(\texttt {cheat}\) instruction was previously issued), completing the simulation.
(which will abort at this point if the \(\texttt {cheat}\) instruction was previously issued), completing the simulation.
We will briefly argue for indistinguishability of the real and ideal-world experiments, with respect to adversaries corrupting Alice. During this phase, no values are transmitted to Alice, and thus the two worlds are distinguishable only by the distribution of aborts. In the real world, Bob aborts unless
for every \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), per Step 3 of the protocol, and if we take \(a\) to be the most common input among Alice’s OT instances (breaking ties arbitrarily) and \({\varvec{\mathrm {\Delta }}}\) to be a vector of deviations from \(a\), then, rewriting, we have
On the other hand, in the ideal world, there are a number of abort conditions. We will argue that for every condition that triggers an abort in the ideal world, an abort is also observed by Alice in the real world with negligibly different probability.
-
1.
The abort condition in Step 3 of the simulator checks whether there exists any hypothetical set of choice bits that could allow Eq. 12 to hold, given Alice’s messages. If no such set of choice bits exists, then the simulator aborts, and clearly Bob must abort in the real world as well.
-
2.
The abort condition in Steps 4 and 5 of the simulator checks whether Eq. 12 holds, given a simulated set of Bob’s choice bits. The condition is split into two cases to ensure these choice bits are consistent with any simulated choice bits previously sampled when simulating the multiplication phase of the protocol, which the environment may have been able to infer from the outputs \(z_{{\mathsf {B}}} \) and \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it receives at the end of the multiplication phase. Regardless, the simulated choice bits are chosen uniformly in the ideal world after Alice is already committed to \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), and the real choice bits are chosen uniformly by Bob and information-theoretically hidden from Alice until after her commitments are made, and thus the probability of abort is the same in both worlds. Notice that this case technically subsumes the first.
-
3.
The abort condition in the cheater check phase of
 is triggered at the end of the simulation if and only if \(c\ge {s} \), which implies the vector \({\varvec{\mathrm {\Delta }}}\) is nonzero (i.e., Alice cheated when supplying inputs to
is triggered at the end of the simulation if and only if \(c\ge {s} \), which implies the vector \({\varvec{\mathrm {\Delta }}}\) is nonzero (i.e., Alice cheated when supplying inputs to  ) at at least \(s\) locations. We argue that under this condition, Bob aborts with overwhelming probability in the real world as well.
) at at least \(s\) locations. We argue that under this condition, Bob aborts with overwhelming probability in the real world as well.
Notice first that Alice commits to \({\varvec{\mathrm {\alpha }}}\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}\) before \({\varvec{\mathrm {e}}}\) is defined. After receiving \({\varvec{\mathrm {e}}}\), she commits to \({\varvec{\mathrm {\zeta }}}\) and \({\varvec{\mathrm {\psi }}}\), and only then does she receive \(\delta \) (and the environment receives \(z_{{\mathsf {B}}} \)), which might potentially allow \({\varvec{\mathrm {\beta }}}\) to be distinguished from uniform.
Consider Bob’s real-world check, Eq. 12. Since Alice knows every value on the left-hand side, and is permitted to freely choose \({\varvec{\mathrm {\zeta }}}_{i,j}\) after learning the others, the left-hand side is completely within her control. Now consider some index j and two indices i, \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\). Due to the order in which values are committed and sampled, we have
regardless of how Alice samples her variables (again, assuming \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\)). Over r independent repetitions, the probability that the above equality holds is \(1/m^r \le 2^{-{s}}\), and it follows that if there exists any pair of indices i and \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\), then with probability overwhelming in \({s} \) there exists some index j such that
Without loss of generality, then, let us say that the left-hand predicate holds. Since \({\varvec{\mathrm {\beta }}}_i\in \{0,1\}\) is uniformly sampled and information-theoretically hidden from Alice at the time she commits to \({\varvec{\mathrm {\zeta }}}_{i,j}\) and \({\varvec{\mathrm {\psi }}}_{j}\), she can pass Bob’s check (Eq. 12) for index i and all \(j\in [r]\) with probability at most \(1/2+\mathsf {negl}({s})\).
Consider that either Alice’s most-common OT input \(a\) is also her majority input, in which case we can pair each of the c OT instances where she has cheated with one where she is honest, or she has no majority input, in which case \(c\ge {s} + \lceil |m|/2\rceil \) and no more than \({s} + \lfloor |m|/2\rfloor \) of her cheats are identical. In the latter case, her identical cheats can be paired with honest OT instances an non-identically cheated OT instances. Thus, we can always find at least c pairs of indices i and \(i'\) such that \({\varvec{\mathrm {\Delta }}}_i\ne {\varvec{\mathrm {\Delta }}}_{i'}\), and such that all pairs are disjoint. Since we have supposed that \(c\ge {s} \), Alice’s probability of satisfying Eq. 12 over all combinations of indices is at most \((1/2+\mathsf {negl}({s}))^{s} \in \mathsf {negl}({s})\). Thus, in the ideal world,  always aborts, and in the real world, Bob aborts with probability overwhelming in \({s} \), and it follows that the real and ideal worlds are statistically indistinguishable in this case.
always aborts, and in the real world, Bob aborts with probability overwhelming in \({s} \), and it follows that the real and ideal worlds are statistically indistinguishable in this case.
Finally, we note that the above three cases partition the real-world conditions under which Eq. 12 does not hold. In other words, for every abort observed in the real world, an abort is also observed in the ideal world with negligibly different probability, and so the real and ideal worlds are statistically indistinguishable.
The Input Revelation phase of
 . In this phase of the protocol, the parties can open their inputs to one another. This phase may be run in place of the cheater check phase, but they may not both be run. It has no analogue in the protocols of Doerner et al. [19, 20]. For the sake of simplicity, we assume that both parties wish to reveal their inputs simultaneously, though the protocol may be extended to allow independent release. Alice begins the protocol with her input \(a\) and a check vector \(\tilde{{\varvec{\mathrm {a}}}}\), and output vectors \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\). Furthermore, she has an outstanding commitment to \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) from Step 6 of the multiplication phase. Bob begins with an input \(b\), a vector of choice bits \({\varvec{\mathrm {\beta }}}\) and an output vector \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}}}\). In addition, they both know the vector \(\textsf {bit-sids}\) of session IDs of all relevant
. In this phase of the protocol, the parties can open their inputs to one another. This phase may be run in place of the cheater check phase, but they may not both be run. It has no analogue in the protocols of Doerner et al. [19, 20]. For the sake of simplicity, we assume that both parties wish to reveal their inputs simultaneously, though the protocol may be extended to allow independent release. Alice begins the protocol with her input \(a\) and a check vector \(\tilde{{\varvec{\mathrm {a}}}}\), and output vectors \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) and \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {A}}},*}\). Furthermore, she has an outstanding commitment to \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) from Step 6 of the multiplication phase. Bob begins with an input \(b\), a vector of choice bits \({\varvec{\mathrm {\beta }}}\) and an output vector \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}}}\). In addition, they both know the vector \(\textsf {bit-sids}\) of session IDs of all relevant  instances (i.e., one instance for each of Bob’s bits, where Alice was expected to use the same input in all instances), and they both know the uniformly sampled vector \({\varvec{\mathrm {g}}}\). The parties take the following steps:
instances (i.e., one instance for each of Bob’s bits, where Alice was expected to use the same input in all instances), and they both know the uniformly sampled vector \({\varvec{\mathrm {g}}}\). The parties take the following steps:
-
1.
For each \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\), Alice sends \((\texttt {transfer},\textsf {bit-sids}_i,j+1)\) to
 as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\).
as a consequence, Bob receives \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}\) such that \(0\le {\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j}<m\). -
2.
In order to prove that he used b as his input, Bob sends b and \(({\varvec{\mathrm {\beta }}}_i,{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,*})\) for every \(i\in [|\textsf {bit-sids}|]\) to Alice, who verifies that
$$\begin{aligned} \delta \equiv \langle {\varvec{\mathrm {g}}},{\varvec{\mathrm {\beta }}}\rangle -b\pmod {m} \end{aligned}$$and that
$$\begin{aligned} {\tilde{\mathbf{z}}}_{{{\mathsf {A}}},i,j}+{\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,j} \equiv {\varvec{\mathrm {\beta }}}_i\cdot \tilde{{\varvec{\mathrm {a}}}}_{j}\pmod {m} \end{aligned}$$for every \(i\in [|\textsf {bit-sids}|]\) and \(j\in [r]\).
The security of this step lies in the inherent committing nature of OT; Bob is able to pass the test while also lying about his choice bit (without loss of generality, \({\varvec{\mathrm {\beta }}}_i\)) only by outright guessing the value for \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},i,*}\) that will cause the test to pass. This is as hard as guessing \(\tilde{{\varvec{\mathrm {a}}}}\), and Bob succeeds with probability less than \(2^{-{s}}\).
-
3.
In order to prove that she used an input a for all
 instances associated with the session IDs in \(\textsf {bit-sids}\), Alice decommits \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) via
instances associated with the session IDs in \(\textsf {bit-sids}\), Alice decommits \((a,{\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*})\) via 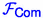 . Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\), it holds that $$\begin{aligned} {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i} + {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv a\cdot {\varvec{\mathrm {\beta }}}_i \pmod {m} \end{aligned}$$
. Bob verifies that for each \(i\in [|\textsf {bit-sids}|]\), it holds that $$\begin{aligned} {\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i} + {\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv a\cdot {\varvec{\mathrm {\beta }}}_i \pmod {m} \end{aligned}$$Alice is able to subvert this check for some index i if and only if she correctly guesses Bob’s corresponding choice bit \({\varvec{\mathrm {\beta }}}_i\) during the input phase, and appropriately offsets \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}\). Thus, her probability of success is negligible in the number of her cheats.
In the random oracle model, this protocol can be optimized by instructing Bob to send a \(2{s} \)-bit digest of his \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) values, instead of sending the values themselves, since Alice is able to recompute the same values herself using only \({\varvec{\mathrm {\beta }}}\) and the information already in her view. Under this optimization, the cost of this protocol is \(|m|+2{s} \) bits for Bob, \(|m|\cdot (|m|+2{s})\) bits for Alice, and 3 messages in total.
Simulating Input Revelation. Consider first a simulator against Bob. Recall that Bob has not thus far had an opportunity to cheat; each group of  instances commits him to an unambiguous input, which the simulator has previously extracted. The simulator sends a uniformly sampled vector \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) to Bob on behalf of
instances commits him to an unambiguous input, which the simulator has previously extracted. The simulator sends a uniformly sampled vector \({\tilde{\mathbf{z}}}_{{{\mathsf {B}}},*,*}\) to Bob on behalf of  , and aborts on behalf of Alice if any of the values it receives in Step 2 of the above protocol do not match the ones it has sent or extracted. On receiving Alice’s true input from
, and aborts on behalf of Alice if any of the values it receives in Step 2 of the above protocol do not match the ones it has sent or extracted. On receiving Alice’s true input from  , the simulator uses her input along with Bob’s extracted input and the values of \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) that it previously sent him to compute the correct value of \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it must send to Bob on behalf of
, the simulator uses her input along with Bob’s extracted input and the values of \({\varvec{\mathrm {z}}}_{{{\mathsf {B}}},*}\) that it previously sent him to compute the correct value of \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) that it must send to Bob on behalf of  . Under this simulation strategy, the ideal world is distinguishable from the real protocol to an adversary corrupting Bob only when Bob sends a combination of values in Step 2 that is incorrect (thus causing the simulator to abort) but nevertheless satisfies Alice’s check (avoiding an abort in the real world). The probability that he achieves this is negligible in the statistical parameter.
. Under this simulation strategy, the ideal world is distinguishable from the real protocol to an adversary corrupting Bob only when Bob sends a combination of values in Step 2 that is incorrect (thus causing the simulator to abort) but nevertheless satisfies Alice’s check (avoiding an abort in the real world). The probability that he achieves this is negligible in the statistical parameter.
Now consider simulation against Alice. Recall that if \(c\ge {s} \) (i.e., there were at least \({s} \) inconsistencies among Alice’s inputs to  in the input phase), then the simulator activated the \(\texttt {cheat}\) interface of
in the input phase), then the simulator activated the \(\texttt {cheat}\) interface of  and learned Bob’s input. If this happened, then we must prove that the real-world Bob always aborts during Input Revelation. If \(c<{s} \), then the simulator sampled a set of c simulated choice bits \(\hat{{\varvec{\mathrm {\beta }}}}\) (one bit for each location where Alice cheated) and used them to calculate Alice’s output in the multiplication phase. It is possible that the environment was able to learn those bits, and thus, we must prove that they are compatible with whatever input the simulator is required to reveal.
and learned Bob’s input. If this happened, then we must prove that the real-world Bob always aborts during Input Revelation. If \(c<{s} \), then the simulator sampled a set of c simulated choice bits \(\hat{{\varvec{\mathrm {\beta }}}}\) (one bit for each location where Alice cheated) and used them to calculate Alice’s output in the multiplication phase. It is possible that the environment was able to learn those bits, and thus, we must prove that they are compatible with whatever input the simulator is required to reveal.
As before, let \({\varvec{\mathrm {\alpha }}}\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {\alpha }}}|\times r}\) represent Alice’s her actual inputs to the OTs, where \(|{\varvec{\mathrm {\alpha }}}|=|\textsf {bit-sids}|\) and where \({{\varvec{\mathrm {\alpha }}}}_{i} = {{\varvec{\mathrm {\alpha }}}}_{i'} = a\) and \(\tilde{{\varvec{\mathrm {\alpha }}}}_{i,*} = \tilde{{\varvec{\mathrm {\alpha }}}}_{i',*} = {{\tilde{\mathbf{a}}}}\) for all \(i,i'\in [|{\varvec{\mathrm {\alpha }}}|]\) if Alice was honest. Additionally, let \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\) be the values to which Alice actually committed in Step 6 of the multiplication phase, where \(a'=a\) and \({\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*}={\varvec{\mathrm {z}}}_{{{\mathsf {A}}},*}\) if Alice was honest.
Let us first consider the case that \(c<{s} \). In this case, the simulator begins by sending an \(\texttt {open}\) message with the correct session ID to  , and in return it receives Bob’s input \(b\). In order to simulate Step 2 of the protocol, the simulator must sample a set of choice bits \({\varvec{\mathrm {\beta }}}\) such that
, and in return it receives Bob’s input \(b\). In order to simulate Step 2 of the protocol, the simulator must sample a set of choice bits \({\varvec{\mathrm {\beta }}}\) such that
for \(\delta \) and \(b\) and \({\varvec{\mathrm {g}}}\) that have previously been fixed. We can simplify the problem by rewriting it as follows: let \(b':=b+\delta -\langle {\varvec{\mathrm {g}}}, \hat{{\varvec{\mathrm {\beta }}}}\rangle \bmod {m}\) (recall that \(\hat{{\varvec{\mathrm {\beta }}}}_i=0\iff i\not \in {\varvec{\mathrm {I}}}\)), and let \(\smash {{\varvec{\mathrm {g}}}'\in {\mathbb {Z}}_m^{|{\varvec{\mathrm {g}}}|-c}}\) be the result of deleting from \({\varvec{\mathrm {g}}}\) each \({\varvec{\mathrm {g}}}_i\) with index \(i\in {\varvec{\mathrm {I}}}\). The simulator can clearly find \({\varvec{\mathrm {\beta }}}\) satisfying Eq. 13 if it can find \({\varvec{\mathrm {\beta }}}'\in \{0,1\}^{|{\varvec{\mathrm {g}}}|-c}\) such that \(\langle {\varvec{\mathrm {g}}}',{\varvec{\mathrm {\beta }}}'\rangle \equiv b'\pmod {m}\). We encapsulate the proof that the simulator can find such a \({\varvec{\mathrm {\beta }}}'\) efficiently into the following lemma:
Lemma B.4
There exists an algorithm \(\mathsf {Brute}\) such that for \(c\le {s} \) and any arbitrary \(b'\in [0, m)\),
where the probability is taken over the distribution of \({\varvec{\mathrm {g}}}'\) and the internal coins of \(\mathsf {Brute}\). If \(m\in O({s})\), then the running time of \(\mathsf {Brute}\) is in \(O({s} ^2)\).
Proof
The algorithm \(\mathsf {Brute}\) works by repeatedly guessing uniform values of \({\varvec{\mathrm {\beta }}}'\) until the predicate \(\smash {\langle {\varvec{\mathrm {g}}}',{\varvec{\mathrm {\beta }}}' \rangle \equiv b'\pmod {m}}\) is satisfied. Given a particular value of c, it follows from Impagliazzo and Naor [31, Proposition 1.1.2] that a single uniformly random assignment of \({\varvec{\mathrm {\beta }}}'\) satisfies the predicate with probability no less than
and since we have assumed that \(c\le {s} \), we have:
Thus, in order to find a satisfying assignment of \({\varvec{\mathrm {\beta }}}'\) with probability overwhelming in \({s} \), \(\mathsf {Brute}\) must make g guesses such that
Taking the natural log of both sides of this equation and using the fact that \(\ln (1+x)\ge x/(1+x)\) if \(x > -1\), we have
and it follows that if \(m\in O({s})\), then there is a sufficiently large value of g in \(O({s} ^2)\), and this determines the runtime of \(\mathsf {Brute}\). \(\square \)
Having found an appropriate set of choice bits \({\varvec{\mathrm {\beta }}}\) by brute force, the simulator sends it to Alice, along with the exact value of \(\tilde{{\varvec{\mathrm {z}}}}_{{{\mathsf {B}}},*,*}\) that will cause her check to pass (which the simulator can calculate, since it knows all other values used in her check), and thereby Step 2 of the protocol is simulated. To simulate Step 3 of the protocol, the simulator can simply evaluate Bob’s check exactly as he would, and then instruct  to abort if Bob’s check would fail. In the case that \(c<{s} \), the real and ideal world experiments are statistically indistinguishable.
to abort if Bob’s check would fail. In the case that \(c<{s} \), the real and ideal world experiments are statistically indistinguishable.
Now let us consider the case that \(c\ge {s} \). In this case, the simulator already knows Bob’s inputs, and thus, it can simulate his behavior exactly. Since  is doomed to abort in this case, we must prove that Bob aborts with overwhelming probability in the real world as well. Recall that \(|{\varvec{\mathrm {I}}}| = c\) and that \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}+{\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv {\varvec{\mathrm {\beta }}}_i\cdot (a+{\varvec{\mathrm {\Delta }}}_i)\pmod {m}\) and that \({\varvec{\mathrm {\Delta }}}_i\ne 0\iff i\in {\varvec{\mathrm {I}}}\) and that \({\varvec{\mathrm {\beta }}}\) was uniformly sampled and information-theoretically hidden from Alice when she committed to \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\). Given the value \(a'\) that she chooses, Alice must commit
is doomed to abort in this case, we must prove that Bob aborts with overwhelming probability in the real world as well. Recall that \(|{\varvec{\mathrm {I}}}| = c\) and that \({\varvec{\mathrm {z}}}_{{{\mathsf {A}}},i}+{\varvec{\mathrm {z}}}_{{{\mathsf {B}}},i} \equiv {\varvec{\mathrm {\beta }}}_i\cdot (a+{\varvec{\mathrm {\Delta }}}_i)\pmod {m}\) and that \({\varvec{\mathrm {\Delta }}}_i\ne 0\iff i\in {\varvec{\mathrm {I}}}\) and that \({\varvec{\mathrm {\beta }}}\) was uniformly sampled and information-theoretically hidden from Alice when she committed to \((a',{\varvec{\mathrm {z}}}'_{{{\mathsf {A}}},*})\). Given the value \(a'\) that she chooses, Alice must commit
in order to pass Bob’s check at some index i. If \(a'-a-{\varvec{\mathrm {\Delta }}}_i\not \equiv 0\pmod {m}\), then she will have committed the correct value with probability at most 1/2. When \(c\ge {s} \), it must hold that \(a'-a-{\varvec{\mathrm {\Delta }}}_i\not \equiv 0\pmod {m}\) for at least c indices i (notice that setting \(a' \ne a\) can only hurt Alice), and she avoids an abort in the real world with probability no more than \(2^{-c}\le 2^{-{s}}\). Thus, the real world is statistically indistinguishable from the ideal world, when \(c\ge {s} \).
1.3 B.3. Multiparty Reusable-Input Multiplier
Plugging  into a GMW-style multiplication protocol [26] yields an n-party equivalent of the same functionality, i.e.,
into a GMW-style multiplication protocol [26] yields an n-party equivalent of the same functionality, i.e.,  . This flavor of composition is standard (it is used, for example, by Doerner et al. [20]), and the security argument follows along similar lines to prior work. Note that we give the ideal adversary slightly more power than strictly necessary, in order to simplify our description: when it cheats, it always learns the secret inputs of all honest parties; in the real protocol, on the other hand, the adversary may cheat on honest parties individually.
. This flavor of composition is standard (it is used, for example, by Doerner et al. [20]), and the security argument follows along similar lines to prior work. Note that we give the ideal adversary slightly more power than strictly necessary, in order to simplify our description: when it cheats, it always learns the secret inputs of all honest parties; in the real protocol, on the other hand, the adversary may cheat on honest parties individually.

We defer an efficiency analysis of the protocol that realizes this functionality to the next subsection.
1.4 B.4. Augmented Multiplication
Finally, we describe a protocol  that realizes
that realizes  in the
in the  ,
, -hybrid model. It comprises five phases. Its input, multiplication, and input revelation phases essentially fall through to
-hybrid model. It comprises five phases. Its input, multiplication, and input revelation phases essentially fall through to  . Its cheater check phase falls through to the cheater check phase of
. Its cheater check phase falls through to the cheater check phase of  , but also takes additional steps to securely evaluate an arbitrary predicate over the checked values, using generic MPC. Finally, it adds a sampling phase, which samples pairs of nonzero values by running a sequence of
, but also takes additional steps to securely evaluate an arbitrary predicate over the checked values, using generic MPC. Finally, it adds a sampling phase, which samples pairs of nonzero values by running a sequence of  instructions.
instructions.
Theorem B.6
The protocol  statistically UC-realizes
statistically UC-realizes  in the
in the  ,
,  -hybrid model against a malicious adversary that statically corrupts \(n-1\) parties.
-hybrid model against a malicious adversary that statically corrupts \(n-1\) parties.




We now discuss security and efficiency of  , phase-by-phase.
, phase-by-phase.
Input. The input phase of  defers directly to
defers directly to  , and therefore inherits its security. When realized as we have discussed in Sect. B.3, a single call to
, and therefore inherits its security. When realized as we have discussed in Sect. B.3, a single call to  among all parties corresponds to all pairs of parties making two calls each to
among all parties corresponds to all pairs of parties making two calls each to  . Recall that in
. Recall that in  , loading inputs from the party playing Bob is effectively free, and as a consequence, we need only count costs due to inputs loaded from Alice. The first party, \(\mathcal{P} _1\), plays Alice in all of its interactions with
, loading inputs from the party playing Bob is effectively free, and as a consequence, we need only count costs due to inputs loaded from Alice. The first party, \(\mathcal{P} _1\), plays Alice in all of its interactions with  , and pays a cost of \((n-1)\cdot (|m|\cdot (|m|+2{s})+4{\lambda })\) bits if
, and pays a cost of \((n-1)\cdot (|m|\cdot (|m|+2{s})+4{\lambda })\) bits if  is realized via Silent OT [6] or KOS OT [35]. The last party, \(\mathcal{P} _n\), always plays Bob, and pays a cost of \((n-1)\cdot (2|m|+2{s})\) bits if
is realized via Silent OT [6] or KOS OT [35]. The last party, \(\mathcal{P} _n\), always plays Bob, and pays a cost of \((n-1)\cdot (2|m|+2{s})\) bits if  is realized via Silent OT, or \((n-1)\cdot ({\lambda } \cdot (|m|+2{s})+|m|)\) bits if
is realized via Silent OT, or \((n-1)\cdot ({\lambda } \cdot (|m|+2{s})+|m|)\) bits if  is realized via KOS OT. The other parties play a mixture of the roles, and thus in general they each pay an average costFootnote 17 of
is realized via KOS OT. The other parties play a mixture of the roles, and thus in general they each pay an average costFootnote 17 of

transmitted bits with Silent OT or

transmitted bits with KOS OT. Regardless, three rounds are required.
Multiplication. The input phase of  defers directly to
defers directly to  . As we have noted in Sect. B.2, the multiplication and input phases of
. As we have noted in Sect. B.2, the multiplication and input phases of  cost the same; however, whereas the input phase of
cost the same; however, whereas the input phase of  corresponds costwise to one invocation of the input phase of
corresponds costwise to one invocation of the input phase of  for each pair of parties (due to Bob’s inputs being free), the multiplication phase of
for each pair of parties (due to Bob’s inputs being free), the multiplication phase of  corresponds to two invocations of the multiplication phase of
corresponds to two invocations of the multiplication phase of  for each pair of parties. Thus, the parties pay three rounds and an average cost of
for each pair of parties. Thus, the parties pay three rounds and an average cost of  transmitted bits per party. Note that as an optimization two input phases can be fused with one multiplication (in which they are used), and the inputs will consequently add no additional cost.
transmitted bits per party. Note that as an optimization two input phases can be fused with one multiplication (in which they are used), and the inputs will consequently add no additional cost.
Input revelation. The input revelation phase of  defers directly to
defers directly to  , and corresponds to two invocations of the
, and corresponds to two invocations of the  open command for each pair of parties (where each invocation opens both parties’ inputs). Thus, the cost of this phase is
open command for each pair of parties (where each invocation opens both parties’ inputs). Thus, the cost of this phase is

transmitted bits per party on average, and three rounds.
Sampling. This procedure is probabilistic. Specifically, each iteration succeeds with probability \(((m-1)/m)^3\). We will analyze the costs associated with iterating sequentially until a value is successfully sampled (as described in  ). So long as only a single instance of the sampling procedure is considered, the expected number of sequential iterations depends only on \(m\), but we note that when multiple instances of the sampling procedure are run concurrently, the expected maximum number of iterations among the concurrent instances grows with the number of instances [14]. Such concurrency is required in order to achieve biprime sampling in expected-constant or constant rounds, as discussed in Sect. 6.4. In order to avoid huge overhead costs, an elaborate analysis is required. We perform this analysis in Sect. 6.4 and, as we have said, focus here on the sequential case.
). So long as only a single instance of the sampling procedure is considered, the expected number of sequential iterations depends only on \(m\), but we note that when multiple instances of the sampling procedure are run concurrently, the expected maximum number of iterations among the concurrent instances grows with the number of instances [14]. Such concurrency is required in order to achieve biprime sampling in expected-constant or constant rounds, as discussed in Sect. 6.4. In order to avoid huge overhead costs, an elaborate analysis is required. We perform this analysis in Sect. 6.4 and, as we have said, focus here on the sequential case.
In the sequential case, \((m/(m-1))^3\) iterations are required in expectation. Each iteration requires two calls to the  multiplication command (we will assume that the
multiplication command (we will assume that the  input command is coalesced and therefore free, as described previously), and all iterations after the first require two invocations of the
input command is coalesced and therefore free, as described previously), and all iterations after the first require two invocations of the  open command. In addition, every party broadcasts a value in \({\mathbb {Z}}_m\) to the other parties in each iteration. Thus, the average cost per party is
open command. In addition, every party broadcasts a value in \({\mathbb {Z}}_m\) to the other parties in each iteration. Thus, the average cost per party is

transmitted bits, in expectation, and the expected round count is \(10(m/(m-1))^3 -3\). For values of \(m\) of any significant size, these costs converge to the cost of two sequential multiplications, plus one additional round.
With respect to security, we observe that the values \({\tilde{z}}_i\) for \(i\in [n]\) jointly reveal nothing about the secret values \(x_i\) and \(y_i\), because the latter pair of values have been masked by \(r_i\). Thus, the security of a successful iteration reduces directly to the security of the constituent multipliers.Footnote 18 In failed iterations, all values are opened and the computations are checked locally by each party. This ensures that the adversary cannot force sampling failures by cheating, and thereby prevent the protocol from terminating.
Predicate cheater check. Unlike the other protocol phases, this phase takes an input of flexible dimension and therefore its cost does not have a convenient closed-form cost. Consequently, we will describe the cost piecemeal. For each input to be checked, let \(m\) be the modulus with which the input is associated and let c be the number of multiplications in which it has been used. The parties engage in \(\lceil {s}/|m|\rceil \) additional invocations of the  Multiplication command, with inputs that have previously been loaded, and then run the Cheater Check command of
Multiplication command, with inputs that have previously been loaded, and then run the Cheater Check command of  , which implies running the Cheater Check command of
, which implies running the Cheater Check command of  in a pairwise fashion. Together, these operations incur a cost of
in a pairwise fashion. Together, these operations incur a cost of

transmitted bits per party, on average. Finally, for every input to be checked, the parties each input \(\lceil {s}/|m| + 1\rceil \cdot |m|\) bits into a generic MPC, and then run a circuit that performs \(3\cdot (n-1)\cdot \lceil {s}/|m|\rceil \) modular additions and \(\lceil {s}/|m|\rceil \) modular multiplications and equality tests over \({\mathbb {Z}}_m\). Using the circuit component sizes reported in Sect. 6.2, the size of this circuit comprises \((3\cdot (n-1)\cdot \mathsf {modadd}(|m|)+\mathsf {modmul}(|m|) + |m| )\cdot \lceil {s}/|m|\rceil \) AND gates, with \(|m|\) additional gates in the case that the input to be checked was sampled. In addition to these costs for each input to be checked, the generic MPC also evaluates the predicate f, comprising |f| AND gates, over the inputs already loaded. A handful of additional AND gates are required to combine the results from the predicate and the per-input checks, and the circuit has exactly one output wire.
With respect to security, we note that the protocol effectively uses a straightforward composition of secure parts to implement an information-theoretic MAC over the shared values corresponding to the inputs to be checked, in order to ensure that they are transferred into the circuit of the generic MPC faithfully. Forced reuse ensures that the MACs are applied to the correct values, and because each MAC has soundness error \(1/m=2^{-|m|}\), it is necessary to repeat the process \({s}/|m|\) times in order to achieve a soundness error of \(2^{-{s}}\). The multiplications (including those used to apply the MACs) are then checked for cheats, and the MACs are verified inside the circuit before the predicate f is evaluated.
Appendix C. Proof of Security for Our Biprime-Sampling Protocol
In this section, we provide the full proof of Theorem 4.6, showing that  realizes
realizes  in the malicious setting.
in the malicious setting.
Theorem 4.6
If factoring biprimes sampled by  is hard, then
is hard, then  UC-realizes
UC-realizes  in the
in the  -hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
-hybrid model against a malicious PPT adversary that statically corrupts up to \(n-1\) parties.
Proof
We begin by describing a simulator  for the adversary \(\mathcal A\). Next, we prove by a sequence of hybrid experiments that no PPT environment can distinguish with more than negligible probability between running with the dummy adversary and real parties executing
for the adversary \(\mathcal A\). Next, we prove by a sequence of hybrid experiments that no PPT environment can distinguish with more than negligible probability between running with the dummy adversary and real parties executing  , and running with
, and running with  and dummy parties that interact with
and dummy parties that interact with  . Formally speaking, we show that
. Formally speaking, we show that

for all environments \(\mathcal{Z} \), assuming the hardness of factoring primes generated by  . Since the following simulator is quite long and involves complex state tracking, we invite the reader to revisit Sect. 4.4 for an overview of the simulation strategy.
. Since the following simulator is quite long and involves complex state tracking, we invite the reader to revisit Sect. 4.4 for an overview of the simulation strategy.







We now define our sequence of hybrid experiments. The output of each experiment is the output of the environment, \(\mathcal{Z} \). We begin with the real-world experiment, constructed per the standard formulation for UC-security.

Hybrid \(\mathcal {H}_{1}\). In this experiment, we replace the real honest parties with dummy parties. We then construct a simulator that plays the role of  in its interactions with the dummy parties, and also plays the roles of the honest parties in their interactions with the corrupt parties. Furthermore, the simulator plays the roles of
in its interactions with the dummy parties, and also plays the roles of the honest parties in their interactions with the corrupt parties. Furthermore, the simulator plays the roles of  and
and  in their interactions with the corrupt parties and with the adversary \(\mathcal A\). Internally, the simulator emulates each honest party by running its code, and it emulates
in their interactions with the corrupt parties and with the adversary \(\mathcal A\). Internally, the simulator emulates each honest party by running its code, and it emulates  and
and  similarly. By observing the output of each emulated honest party, the simulator can send the appropriate message to each dummy party on behalf of
similarly. By observing the output of each emulated honest party, the simulator can send the appropriate message to each dummy party on behalf of  , such that the outcome of the experiment for each dummy party matches the output for the corresponding honest party. The distribution of \(\mathcal {H}_{1}\) is thus clearly identical to that of \(\mathcal {H}_{0}\).
, such that the outcome of the experiment for each dummy party matches the output for the corresponding honest party. The distribution of \(\mathcal {H}_{1}\) is thus clearly identical to that of \(\mathcal {H}_{0}\).
Hybrid \(\mathcal {H}_{2}\). This hybrid experiment is identical to \(\mathcal {H}_{1}\), except that in \(\mathcal {H}_{2}\), the simulator does not internally emulate the honest parties for Steps 1 through 3 of  . Instead, the simulator takes one of the following two branches:
. Instead, the simulator takes one of the following two branches:
-
If \(\mathcal A\) sends a \(\texttt {cheat}\) message to
 before Step 4 of
before Step 4 of  , or if there is any \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) such that
, or if there is any \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) such that 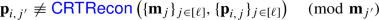
then at the time the cheat occurs, the simulator must retroactively construct views for the honest parties that are consistent with the outputs already delivered to the corrupt parties.Footnote 19 After this, the simulation is completed using the same strategy as in \(\mathcal {H}_{1}\) (i.e., the honest parties are internally emulated by the simulator). It follows immediately from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed in this branch.
-
If \(\mathcal A\) does not send a \(\texttt {cheat}\) message to
 before Step 4 of
before Step 4 of  , and if for all \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) it holds that
, and if for all \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j'\in [\ell +1,{\ell '}]\) it holds that 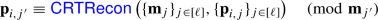
then before simulating Step 4, the simulator uses the corrupt parties’ inputs (which it received in its role as
 ) to compute
) to compute 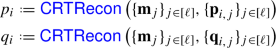
for \(i\in {{\varvec{\mathrm {P}}}^*} \). Next, the simulator runs
 internally, receives as output either \((\texttt {success}, p, q)\) or \((\texttt {failure}, p, q)\), and computes \(N:=p\cdot q\). With these values, the simulator retroactively constructs views for the honest parties by sampling \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for
internally, receives as output either \((\texttt {success}, p, q)\) or \((\texttt {failure}, p, q)\), and computes \(N:=p\cdot q\). With these values, the simulator retroactively constructs views for the honest parties by sampling \(({\varvec{\mathrm {p}}}_{i,j},{\varvec{\mathrm {q}}}_{i,j},{\varvec{\mathrm {N}}}_{i,j})\leftarrow {\mathbb {Z}}^3_{{\varvec{\mathrm {m}}} _j}\) uniformly for  and \(j\in [{\ell '}]\) subject to $$\begin{aligned} \sum _{i\in [n]} {\varvec{\mathrm {p}}}_{i,j}\equiv p\pmod {{\varvec{\mathrm {m}}} _j}&\qquad \text { and}\qquad \sum _{i\in [n]} {\varvec{\mathrm {q}}}_{i,j}\equiv q\pmod {{\varvec{\mathrm {m}}} _j} \\ \text {and}\qquad&\sum _{i\in [n]} {\varvec{\mathrm {N}}}_{i,j}\equiv N\pmod {{\varvec{\mathrm {m}}} _j} \end{aligned}$$
and \(j\in [{\ell '}]\) subject to $$\begin{aligned} \sum _{i\in [n]} {\varvec{\mathrm {p}}}_{i,j}\equiv p\pmod {{\varvec{\mathrm {m}}} _j}&\qquad \text { and}\qquad \sum _{i\in [n]} {\varvec{\mathrm {q}}}_{i,j}\equiv q\pmod {{\varvec{\mathrm {m}}} _j} \\ \text {and}\qquad&\sum _{i\in [n]} {\varvec{\mathrm {N}}}_{i,j}\equiv N\pmod {{\varvec{\mathrm {m}}} _j} \end{aligned}$$and then the simulator completes the simulation using the same strategy as in \(\mathcal {H}_{1}\) (i.e., it emulates the honest parties internally).
Recall that by construction
 samples from a distribution identical to that of
samples from a distribution identical to that of  , conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed if this branch is taken. Note furthermore that in \(\mathcal {H}_{2}\) the output of
, conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that \(\mathcal {H}_{2}\) and \(\mathcal {H}_{1}\) are identically distributed if this branch is taken. Note furthermore that in \(\mathcal {H}_{2}\) the output of  will be \(\texttt {biprime}\) only if
will be \(\texttt {biprime}\) only if
 returns \(\texttt {success}\) or if there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(p_i\ne p'_i\) or \(q_i\ne q'_i\), where \(p'_i\) and \(q'_i\) are corrupt inputs to
returns \(\texttt {success}\) or if there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(p_i\ne p'_i\) or \(q_i\ne q'_i\), where \(p'_i\) and \(q'_i\) are corrupt inputs to  .
.
Hybrid \(\mathcal {H}_{3}\). This hybrid experiment is identical to \(\mathcal {H}_{2}\), except in the way that  is simulated in Step 6 of
is simulated in Step 6 of  . Recall that in \(\mathcal {H}_{2}\), the simulator runs the code of
. Recall that in \(\mathcal {H}_{2}\), the simulator runs the code of  internally, and in order to do this, it must know the factorization of the candidate biprime \(N\) in all cases. In \(\mathcal {H}_{3}\), if no cheating occurs until after the biprimality test, and the candidate is in fact a biprime, then the simulator does not use the factorization of the candidate biprime to simulate
internally, and in order to do this, it must know the factorization of the candidate biprime \(N\) in all cases. In \(\mathcal {H}_{3}\), if no cheating occurs until after the biprimality test, and the candidate is in fact a biprime, then the simulator does not use the factorization of the candidate biprime to simulate  .
.
If cheating occurs before Step 4 of  is simulated, then \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identical: the simulator simply emulates the honest parties internally (retroactively sampling their views as previously described). The experiments differ, however, if no cheating occurs before Step 4 of
is simulated, then \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identical: the simulator simply emulates the honest parties internally (retroactively sampling their views as previously described). The experiments differ, however, if no cheating occurs before Step 4 of  . Recall that in \(\mathcal {H}_{2}\), under this condition, the simulator runs
. Recall that in \(\mathcal {H}_{2}\), under this condition, the simulator runs  internally and receives \(p\) and \(q\) (plus an indication as to whether they are both primes), from which values it constructs honest-party views that are subsequently used to simulate
internally and receives \(p\) and \(q\) (plus an indication as to whether they are both primes), from which values it constructs honest-party views that are subsequently used to simulate  . In \(\mathcal {H}_{3}\), if no cheating occurs before Step 4 of
. In \(\mathcal {H}_{3}\), if no cheating occurs before Step 4 of  , then there are four cases. Let \(N'\) be the candidate biprime reconstructed in Step 4 of
, then there are four cases. Let \(N'\) be the candidate biprime reconstructed in Step 4 of  , which may not equal \(N\) if cheating occurs, and let \((\texttt {check-biprimality},\mathsf {sid},N^{\prime \prime }_i,p'_i,q'_i)\) be the message received on behalf of
, which may not equal \(N\) if cheating occurs, and let \((\texttt {check-biprimality},\mathsf {sid},N^{\prime \prime }_i,p'_i,q'_i)\) be the message received on behalf of  from \(\mathcal{P} _i\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in Step 6 of
from \(\mathcal{P} _i\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in Step 6 of  . The four cases are as follows.
. The four cases are as follows.
-
1.
If
 reports that \(N\) is a biprime, and the adversary continues to behave honestly (i.e., in Steps 4 and 6 of
reports that \(N\) is a biprime, and the adversary continues to behave honestly (i.e., in Steps 4 and 6 of  , the corrupt parties transmit values that add up to the expected sums), then the simulator outputs \(\texttt {biprime}\) to \(\mathcal A\) on behalf of
, the corrupt parties transmit values that add up to the expected sums), then the simulator outputs \(\texttt {biprime}\) to \(\mathcal A\) on behalf of  , and reports the same outcome to the corrupt parties if it receives \(\texttt {proceed}\) from \(\mathcal A\) in reply. Note that knowledge of \(p\) and \(q\) is not used in this eventuality. If \(\mathcal A\) instead replies to
, and reports the same outcome to the corrupt parties if it receives \(\texttt {proceed}\) from \(\mathcal A\) in reply. Note that knowledge of \(p\) and \(q\) is not used in this eventuality. If \(\mathcal A\) instead replies to  with \(\texttt {cheat}\), then \(p\) and \(q\) are used to formulate the correct response.
with \(\texttt {cheat}\), then \(p\) and \(q\) are used to formulate the correct response. -
2.
If the previous case does not occur, and
 reports that \(N\) is a biprime, but there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(N^{\prime \prime }_i\ne N'\), then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of
reports that \(N\) is a biprime, but there exists some \(i\in {{\varvec{\mathrm {P}}}^*} \) such that \(N^{\prime \prime }_i\ne N'\), then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of  .
. -
3.
If neither of previous cases occurs, and
 reports that \(N\) is a biprime, and \(N^{\prime \prime }_i=N\) for all \(i\in {{\varvec{\mathrm {P}}}^*} \), but $$\begin{aligned} \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p_i \qquad \text { or}\qquad \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\end{aligned}$$
reports that \(N\) is a biprime, and \(N^{\prime \prime }_i=N\) for all \(i\in {{\varvec{\mathrm {P}}}^*} \), but $$\begin{aligned} \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}p_i \qquad \text { or}\qquad \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\ne \sum \limits _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\end{aligned}$$then the simulator sends \(\texttt {non-biprime}\) to the corrupt parties on behalf of
 .
. -
4.
If none of the previous cases occur, and
 reports that \(N\) is not a biprime, or for all \(i\in {{\varvec{\mathrm {P}}}^*} \) it holds that \(N^{\prime \prime }_i=N'\ne N\), then the simulator constructs honest-party views from \(p\) and \(q\) and runs the code of
reports that \(N\) is not a biprime, or for all \(i\in {{\varvec{\mathrm {P}}}^*} \) it holds that \(N^{\prime \prime }_i=N'\ne N\), then the simulator constructs honest-party views from \(p\) and \(q\) and runs the code of  , as in \(\mathcal {H}_{2}\).
, as in \(\mathcal {H}_{2}\).
It is easy to see that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are identically distributed in first, second, and fourth cases above, and also in the case that cheating occurs before Step 4 of  . It remains only to analyze the third case. In \(\mathcal {H}_{3}\), it leads to an unconditional abort,Footnote 20 whereas in \(\mathcal {H}_{2}\), the adversary can avoid an abort by sending \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) such that
. It remains only to analyze the third case. In \(\mathcal {H}_{3}\), it leads to an unconditional abort,Footnote 20 whereas in \(\mathcal {H}_{2}\), the adversary can avoid an abort by sending \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) such that
which can be achieved without falling into the first case by finding values of \(p'_i\) and \(q'_i\) such that the factors supplied to  are effectively switched relative to their honest order. This is the only condition under which \(\mathcal {H}_{3}\) differs observably from \(\mathcal {H}_{2}\), and thus the environment’s advantage in distinguishing the two hybrids is determined exclusively by the probability that the adversary triggers this condition. We wish to show that the two hybrids are computationally indistinguishable under the assumption that biprimes drawn from the distribution of
are effectively switched relative to their honest order. This is the only condition under which \(\mathcal {H}_{3}\) differs observably from \(\mathcal {H}_{2}\), and thus the environment’s advantage in distinguishing the two hybrids is determined exclusively by the probability that the adversary triggers this condition. We wish to show that the two hybrids are computationally indistinguishable under the assumption that biprimes drawn from the distribution of  are hard to factor. We begin by giving a simpler description of the adversary’s task in the form of a game that is won by the adversary if the following experiment outputs 1.
are hard to factor. We begin by giving a simpler description of the adversary’s task in the form of a game that is won by the adversary if the following experiment outputs 1.

Note that a reduction from winning the  game to distinguishing between \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) exists by construction and there is no loss of advantage. Now consider a variation on the classic factoring game (see Experiment 3.1) in which
game to distinguishing between \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) exists by construction and there is no loss of advantage. Now consider a variation on the classic factoring game (see Experiment 3.1) in which  is used in place of \(\mathsf {GenModulus}\), and the adversary supplies a set of corrupt shares to
is used in place of \(\mathsf {GenModulus}\), and the adversary supplies a set of corrupt shares to  .
.

We will show a lossless reduction from winning the  game to winning the
game to winning the  game, which implies as a corollary that any adversary enabling the environment to distinguish \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) can be used to factor biprimes produced by
game, which implies as a corollary that any adversary enabling the environment to distinguish \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) can be used to factor biprimes produced by  with adversarial shares.
with adversarial shares.
Lemma C.4
For every PPT adversary \(\mathcal{A} \), there exists a PPT adversary \(\mathcal{B} \) such that for all \({\kappa },n\in {\mathbb {N}}\) and \({{\varvec{\mathrm {P}}}^*} \subset [n]\), it holds that

Proof
Our reduction plays the role of \(\mathcal{B} \) in Experiment C.3, and the role of the challenger in Experiment C.2. It works as follows.
-
1.
When invoked as \(\mathcal{B} \) with inputs \({\kappa } \) and \({{\varvec{\mathrm {P}}}^*} \) in Experiment C.3, invoke \(\mathcal{A} (1^{\kappa },{{\varvec{\mathrm {P}}}^*})\) in Experiment C.2. On receiving \(p_i\) and \(q_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) from \(\mathcal{A} \), forward them to the challenger in Experiment C.3.
-
2.
On receiving \(N\) as \(\mathcal{B} \) in Experiment C.3, forward it to \(\mathcal{A} \) in Experiment C.2. Receive \(p'_i\) and \(q'_i\) for \(i\in {{\varvec{\mathrm {P}}}^*} \)
-
3.
Try to solve the following system of equations for unknowns \(p_\mathcal{H} \) and \(q_\mathcal{H} \)
$$\begin{aligned} \left( p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p_i\right) \cdot \left( q_\mathcal{H} + \sum _{i\in {{\varvec{\mathrm {P}}}^*}}q_i\right) = \left( p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\right) \cdot \left( q_\mathcal{H} + \sum _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i\right) = N\end{aligned}$$and if exactly one valid pair \((p_\mathcal{H},q_\mathcal{H})\) exists, then send
$$\begin{aligned} p':=p_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}p'_i\qquad \text { and}\qquad q':=q_\mathcal{H} +\sum _{i\in {{\varvec{\mathrm {P}}}^*}}q'_i \end{aligned}$$to the challenger in Experiment C.3. Otherwise, send \(\bot \) to the challenger.
This reduction is correct and lossless by construction. \(\mathcal{A} \) succeeds in Experiment C.2 only if it holds that
which implies exactly one solution to the system of equations in Step 3 of our reduction when \(\mathcal{A} \) succeeds. It follows easily by inspection that Experiment C.3 outputs 1 if and only if Experiment C.2 outputs 1, and so the reduction is perfect. \(\square \)
It remains only to apply Lemma 3.7 (see Sect. 3.1), which asserts that any PPT algorithm that factors biprimes produced by  with adversarial shares can be used (with polynomial loss in the probability of success) to factor biprimes produced by
with adversarial shares can be used (with polynomial loss in the probability of success) to factor biprimes produced by  without adversarial shares. Thus, if we assume factoring biprimes from the distribution of
without adversarial shares. Thus, if we assume factoring biprimes from the distribution of  to be hard, then we must conclude that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are computationally indistinguishable.
to be hard, then we must conclude that \(\mathcal {H}_{3}\) and \(\mathcal {H}_{2}\) are computationally indistinguishable.
Hybrid \(\mathcal {H}_{4}\). This experiment is identical to \(\mathcal {H}_{3}\), except in the way that the privacy-preserving check is simulated in Step 7 of  (the privacy-free check is simulated as in \(\mathcal {H}_{3}\)). In \(\mathcal {H}_{3}\), the simulator emulates both
(the privacy-free check is simulated as in \(\mathcal {H}_{3}\)). In \(\mathcal {H}_{3}\), the simulator emulates both  and the honest parties internally, using its knowledge of \(p\) and \(q\). Specifically, in \(\mathcal {H}_{3}\), the emulated honest parties abort during the check if
and the honest parties internally, using its knowledge of \(p\) and \(q\). Specifically, in \(\mathcal {H}_{3}\), the emulated honest parties abort during the check if  or
or  for any \(i\in {{\varvec{\mathrm {P}}}^*} \), or if a \(\texttt {cheat}\) instruction was sent to
for any \(i\in {{\varvec{\mathrm {P}}}^*} \), or if a \(\texttt {cheat}\) instruction was sent to  at any point, or if
at any point, or if

In \(\mathcal {H}_{4}\), the simulator avoids using knowledge of \(p\) or \(q\) when the privacy-preserving check is run. It does not emulate the honest parties or  . The simulation instead aborts on behalf of the honest parties if \(N'\ne N\) or if there exists any \(j\in [\ell +1,{\ell '}]\) such that
. The simulation instead aborts on behalf of the honest parties if \(N'\ne N\) or if there exists any \(j\in [\ell +1,{\ell '}]\) such that
We will argue that this new predicate is equivalent to the former one.
First, consider a protocol state such that the check in Eq. 15 fails. Without loss of generality, assume that the first half (dealing with \(p\)) fails, but an analogous argument exists for \(q\). If we define a vector of offset values \({\varvec{\mathrm {p}}}^\Delta \) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}=({p_{i}} - {{\varvec{\mathrm {p}}}_{i,j}})\bmod {{\varvec{\mathrm {m}}} _{j}}\) for every \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j\in [\ell +1,{\ell '}]\), then it is clear that when the parties behave honestly, \({\varvec{\mathrm {p}}}^{\Delta }_{i,j} = 0\) for every pair (i, j). On the other hand, a violation of Eq. 15 implies that there must exist some pair (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\). If we let
and we define \({\varvec{\mathrm {p}}}^{\Delta }_{i,j} = 0\) for \(i\in {{\varvec{\mathrm {P}}}^*} \) and \(j\in [\ell ]\) then we find that

where it is certain that \(p_i<M\). Notice by inspection of the  algorithm that it must hold that
algorithm that it must hold that  . Since it also clearly holds that \(M'\equiv 0 \pmod {M}\), we can conclude that
. Since it also clearly holds that \(M'\equiv 0 \pmod {M}\), we can conclude that

where the equality is taken over the integers. Thus, if the check in Eq. 15 fails in \(\mathcal {H}_{4}\), causing \(\mathcal {H}_{4}\) to abort, then the range check in \(\mathcal {H}_{3}\) must also fail, causing \(\mathcal {H}_{3}\) to abort. The converse also holds: Since honest behavior cannot yield  , it must be the case that if the range check in \(\mathcal {H}_{3}\) fails, then there exists some (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\), and thus the check in Eq. 15 fails in \(\mathcal {H}_{4}\).
, it must be the case that if the range check in \(\mathcal {H}_{3}\) fails, then there exists some (i, j) such that \({\varvec{\mathrm {p}}}^{\Delta }_{i,j}\ne 0\), and thus the check in Eq. 15 fails in \(\mathcal {H}_{4}\).
Now, consider a protocol state such that the check in Eq. 15passes. It is easy to see that in this case

which trivially yields

and thus, we can conclude that the two predicates are equivalent, and \(\mathcal {H}_{4}\) is distributed identically to \(\mathcal {H}_{3}\).
Hybrid \(\mathcal {H}_{5}\). During the entire sequence of hybrids thus far, our simulator has played the role of  . In this hybrid, the simulator instead interacts with the real
. In this hybrid, the simulator instead interacts with the real  as a black box. In particular, whenever the simulator would have called
as a black box. In particular, whenever the simulator would have called  in \(\mathcal {H}_{4}\), it instead sends \((\texttt {adv-sample}, \mathsf {sid}, i, {p_{i}}, {q_{i}})\) to
in \(\mathcal {H}_{4}\), it instead sends \((\texttt {adv-sample}, \mathsf {sid}, i, {p_{i}}, {q_{i}})\) to  for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in \(\mathcal {H}_{5}\). Whereas
for every \(i\in {{\varvec{\mathrm {P}}}^*} \) in \(\mathcal {H}_{5}\). Whereas  outputs factors of the candidate it sampled, regardless of whether that candidate is a biprime,
outputs factors of the candidate it sampled, regardless of whether that candidate is a biprime,  returns factors only if the candidate is not a biprime, and if the candidate is a biprime, then
returns factors only if the candidate is not a biprime, and if the candidate is a biprime, then  outputs the biprime itself.Footnote 21 Recall that in \(\mathcal {H}_{4}\), if the candidate is a biprime, and no cheating occurs, then the simulator does not use knowledge of the factors in its simulation. Thus, in \(\mathcal {H}_{5}\), it has enough information to simulate when
outputs the biprime itself.Footnote 21 Recall that in \(\mathcal {H}_{4}\), if the candidate is a biprime, and no cheating occurs, then the simulator does not use knowledge of the factors in its simulation. Thus, in \(\mathcal {H}_{5}\), it has enough information to simulate when  returns a biprime, until a cheat occurs. If a cheat occurs, and the simulator requires knowledge of the factors to continue, then the simulator sends \((\texttt {cheat},\mathsf {sid})\) to
returns a biprime, until a cheat occurs. If a cheat occurs, and the simulator requires knowledge of the factors to continue, then the simulator sends \((\texttt {cheat},\mathsf {sid})\) to  , which returns the factors and aborts. If no cheat occurs, then the simulator sends \((\texttt {proceed},\mathsf {sid})\) to
, which returns the factors and aborts. If no cheat occurs, then the simulator sends \((\texttt {proceed},\mathsf {sid})\) to  at the end of the simulation, so that it releases its output to the honest parties.
at the end of the simulation, so that it releases its output to the honest parties.
Since  simply calls
simply calls  internally, it is easy to see that \(\mathcal {H}_{5}\) is distributed identically to \(\mathcal {H}_{4}\). It is somewhat more difficult but nevertheless possible to see that our simulator is now identical to
internally, it is easy to see that \(\mathcal {H}_{5}\) is distributed identically to \(\mathcal {H}_{4}\). It is somewhat more difficult but nevertheless possible to see that our simulator is now identical to  as previously described; all remaining differences between the two are purely syntactic. Thus,
as previously described; all remaining differences between the two are purely syntactic. Thus,

and by the sequence of hybrids we have just shown, it holds that

for the adversary \(\mathcal{A} \) and all environments \(\mathcal{Z} \), assuming the hardness of factoring primes generated by  . \(\square \)
. \(\square \)
Rights and permissions
About this article
Cite this article
Chen, M., Doerner, J., Kondi, Y. et al. Multiparty Generation of an RSA Modulus. J Cryptol 35, 12 (2022). https://doi.org/10.1007/s00145-021-09395-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00145-021-09395-y





 , this is used to sample CRT-shares of
, this is used to sample CRT-shares of  , this interface is used to perform length-extension on CRT-shares of
, this interface is used to perform length-extension on CRT-shares of  , this is used to check that the CRT-share extension of
, this is used to check that the CRT-share extension of  , this is used to verify the sampling procedure and biprimality test when
, this is used to verify the sampling procedure and biprimality test when  rejects this candidate. In this case, all parties reveal their shares of
rejects this candidate. In this case, all parties reveal their shares of  ) and locally test their primality. This will reveal that
) and locally test their primality. This will reveal that  must have been supplied with inconsistent inputs, implying that some party has cheated.
must have been supplied with inconsistent inputs, implying that some party has cheated. accepts this candidate. This case occurs with negligible probability (assuming factoring is hard). Because
accepts this candidate. This case occurs with negligible probability (assuming factoring is hard). Because  to induce this scenario, apart from the pair specified by the protocol. In our full proof (see Appendix
to induce this scenario, apart from the pair specified by the protocol. In our full proof (see Appendix  reported that
reported that  that the corrupt parties committed to correct shares of
that the corrupt parties committed to correct shares of  . Boneh and Franklin [
. Boneh and Franklin [ . Then,
. Then,  subject to
subject to 
 to the corrupt parties on behalf of
to the corrupt parties on behalf of  . These values are statistically close to their counterparts in the real protocol. Finally,
. These values are statistically close to their counterparts in the real protocol. Finally,  on failure. Given the information now known to
on failure. Given the information now known to  can be simulated in a manner similar to the simulation of a common Schnorr protocol:
can be simulated in a manner similar to the simulation of a common Schnorr protocol:  , fixes
, fixes  that it must send on behalf of the honest parties in Step
that it must send on behalf of the honest parties in Step  by checking the
by checking the  predicate itself (since the final GCD test is purely local, no action need be taken by
predicate itself (since the final GCD test is purely local, no action need be taken by  predicate), then
predicate), then  . Otherwise, it sends the
. Otherwise, it sends the  , completing the simulation.
, completing the simulation. reported that
reported that  by running the honest parties’ code on their behalf. In all instances of the ideal-world experiment, the honest parties report to the environment that
by running the honest parties’ code on their behalf. In all instances of the ideal-world experiment, the honest parties report to the environment that  , or else Step
, or else Step  predicate. It follows from this fact and from the equation in Step
predicate. It follows from this fact and from the equation in Step  produces a false positive result with probability at most 1/2 if the adversary behaves honestly. If we assume that the adversary cheats always and only when a false positive would not have been produced by honest behavior, then the total probability of an adversary producing a positive outcome in the
produces a false positive result with probability at most 1/2 if the adversary behaves honestly. If we assume that the adversary cheats always and only when a false positive would not have been produced by honest behavior, then the total probability of an adversary producing a positive outcome in the  and
and 
 using modulus
using modulus  with modulus
with modulus  (Protocol B.7) to realize
(Protocol B.7) to realize  . We assume the multiplications are done concurrently as well. In addition, every party broadcasts a value in
. We assume the multiplications are done concurrently as well. In addition, every party broadcasts a value in  at most once. Since our protocol includes local trial division (see Step
at most once. Since our protocol includes local trial division (see Step  ), some protocol instances will skip the biprimality test entirely. However, for the sake of calculating concrete costs, we will assume that this local trial division is not executed. In other words, we assume that the biprimality test is run exactly once per protocol instance, and if local trial division would have rejected a candidate, then the biprimality test certainly fails.
), some protocol instances will skip the biprimality test entirely. However, for the sake of calculating concrete costs, we will assume that this local trial division is not executed. In other words, we assume that the biprimality test is run exactly once per protocol instance, and if local trial division would have rejected a candidate, then the biprimality test certainly fails. twice with modulus
twice with modulus  in the sieving phase, and f is a predicate specified in our protocol. This circuit representation of f comprises 2n invocations of
in the sieving phase, and f is a predicate specified in our protocol. This circuit representation of f comprises 2n invocations of  over the extended vector
over the extended vector  algorithm can be implemented in the following way: all intermediate operations can be performed over the integers, with a single modular reduction at the end. Because each intermediate product has one multiplicand that is much shorter than the other, we can use the asymmetric modular multiplication method previously described in Sect.
algorithm can be implemented in the following way: all intermediate operations can be performed over the integers, with a single modular reduction at the end. Because each intermediate product has one multiplicand that is much shorter than the other, we can use the asymmetric modular multiplication method previously described in Sect.  , and its overall gate count
, and its overall gate count
 are taken to be of length
are taken to be of length  for a detailed algorithm to sample such views.
for a detailed algorithm to sample such views. can never be triggered.
can never be triggered. to receive
to receive  .
. to sample an agreed-upon uniform vector
to sample an agreed-upon uniform vector  to decommit
to decommit  , and as a consequence, Bob receives
, and as a consequence, Bob receives  , it holds for all
, it holds for all  to decommit
to decommit  to abort. If the simulator continues past this point, it must be the case that either
to abort. If the simulator continues past this point, it must be the case that either  to abort.
to abort. abort if it lands on heads.
abort if it lands on heads. is triggered at the end of the simulation if and only if
is triggered at the end of the simulation if and only if  ) at at least
) at at least  as a consequence, Bob receives
as a consequence, Bob receives  instances associated with the session IDs in
instances associated with the session IDs in  . Bob verifies that for each
. Bob verifies that for each  before Step
before Step  , or if there is any
, or if there is any 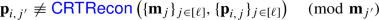
 before Step
before Step  , and if for all
, and if for all 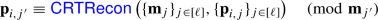
 ) to compute
) to compute 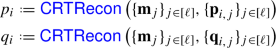
 internally, receives as output either
internally, receives as output either  and
and  samples from a distribution identical to that of
samples from a distribution identical to that of  , conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that
, conditioned on honest behavior during the Candidate Sieving phase of the protocol. Consequently, it follows from the perfect security of additive secret sharing that  will be
will be  returns
returns  .
. reports that
reports that  , the corrupt parties transmit values that add up to the expected sums), then the simulator outputs
, the corrupt parties transmit values that add up to the expected sums), then the simulator outputs  , and reports the same outcome to the corrupt parties if it receives
, and reports the same outcome to the corrupt parties if it receives  with
with  reports that
reports that  .
. reports that
reports that  .
. reports that
reports that  , as in
, as in