A semi-supervised learning method for surface defect classification of magnetic tiles

Abstract

Surface defect inspection is a crucial step to ensure the quality of magnetic tiles. Recently, deep learning methods have shown excellent performance on many vision tasks. Some deep learning-based methods have been applied to the surface defect inspection of magnetic tiles as well. However, related methods are based on supervised learning, which requires plenty of labeled samples to train deep neural networks. In industrial application scenarios, the annotation of large labeled datasets is extremely expensive, time-consuming, and error-prone. A semi-supervised learning method based on pseudo-labeling is proposed in this paper to address the problem of surface defect classification of magnetic tiles with limited labeled samples. The proposed method consists of two models: the teacher model and the student model. The training procedure is divided into two stages: pseudo-label generation and student model training. In the pseudo-label generation stage, the teacher model parameters and the pseudo-labels of unlabeled samples are alternatively optimized based on the idea of transductive learning. Curriculum learning is employed to reduce the impact of label noise so that high-quality pseudo-labels can be obtained. In the student model training stage, labeled samples and unlabeled samples with pseudo-labels are jointly used to train the classifier, with mixup to achieve information fusion and regularization. The experimental results show that the proposed method outperforms the supervised-only and semi-supervised baselines. With only 4.4% of labeled samples in the training set, the proposed method can still achieve the defect classification accuracy of 90.13%.

1 Introduction

Magnetic tile is a kind of tile-shaped magnet mainly used in permanent magnet motors. Its quality directly affects the performance and life of the motor. Therefore, it is necessary to assess the quality of magnetic tiles before they leave the factory. Currently, most factories still employ workers to inspect the surface defects on magnetic tiles. Manual inspection is characterized by inefficiency and expense, and it is difficult to ensure the consistency and accuracy of the results due to visual fatigue.

Many machine vision methods have been proposed to improve the accuracy and automation of the surface defect inspection of magnetic tiles. Most of these methods are based on image processing [1], wavelet [2], curvelet [3], and shearlet [4]. Due to the complexity of the surface texture, the diversity of defect shapes, and the uneven illumination caused by the curved shape, these conventional methods usually require carefully designed feature engineering and usually work well under specific conditions.

Deep learning methods have achieved outstanding success in a variety of computer vision tasks. For example, Convolutional Neural Networks (CNN) have achieved the best performance on visual tasks such as image classification, object detection, semantic segmentation, etc. Compared with manually designed feature representations, CNNs can learn richer and higher-level representations directly from the data, avoiding the laborious manual design. Therefore, some deep learning-based methods [5,6,7,8] were proposed for the surface defect inspection on magnetic tiles, achieving better results than conventional methods.

Although deep learning methods can achieve better defect inspection performance, current methods for magnetic tiles are all based on supervised learning. Supervised deep learning methods require large amounts of labeled data to obtain reliable performances. There is a risk of overfitting without sufficient training data, and thus the trained deep networks may have poor generalization performance. In real-world cases, unlabeled data are usually readily available, whereas the annotation of large labeled datasets is extremely expensive, time-consuming, and error-prone, especially in the industrial and medical fields. It certainly hinders the application of some deep learning techniques in real-world cases. Semi-supervised learning (SSL) provides a solution for this problem. Semi-supervised learning is a kind of learning algorithm that can train models using both labeled and unlabeled data, which aims to reduce the annotation cost. Therefore, only a few labeled data are needed for model training, while large amounts of unlabeled data are used to help improve the performance.

A semi-supervised learning method based on pseudo-labeling is proposed in this paper for the surface defect classification of magnetic tiles with limited labeled samples. The proposed method consists of two models: a teacher model and a student model. The training procedure is divided into two stages: pseudo-label generation and student model training. In the pseudo-label generation stage, the teacher model and the pseudo-labels of unlabeled samples are alternatively optimized based on the idea of transductive learning so that high-quality pseudo-labels can be obtained. During the alternating optimization process, curriculum learning is adopted to help the updating of the teacher model parameters. In the student model training stage, both labeled samples and unlabeled samples with pseudo-labels are used to train the student model, and mixup [26] is adopted to perform data augmentation and regularization.

The rest of the paper is organized as follows: Sect. 2 introduces some related works; Sect. 3 presents the problem definition and introduces pseudo-labeling; Sect. 4 illustrates the proposed semi-supervised method for the surface defect classification of magnetic tiles in detail; Sect. 5 shows the experimental results of our method on public and our collected datasets; Sect. 6 summarizes the work of this paper and draws conclusions.

2 Related work

2.1 Surface defect inspection of magnetic tiles

2.1.1 Conventional machine vision methods

Machine vision methods have been proposed to improve the accuracy and automation of the surface defect inspection of magnetic tiles. Tao et al. [1] used a comparison of the fitting and actual edge curves to detect defects on the end surface of magnetic tiles. Yang et al. [2] used the smooth wavelet transform (SWT) to perform surface defect detection on magnetic tile images with low contrast under various lighting conditions. Li et al. [3] used fast discrete curvelet transform (FDCT) and texture analysis to automatically detect crack defects in magnetic tile images with dark color and low contrast. The shearlet transform has higher orientation sensitivity, which helps extract geometric features from the data accurately. Based on this, Xie et al. [4] proposed a surface defect extraction method for magnetic tiles based on the shearlet transform.

2.1.2 Deep learning methods

A key step in traditional machine vision methods is to extract features from the image that can effectively distinguish defect regions from the background, known as feature engineering in machine learning. The design of feature engineering in industrial applications usually requires expertise and needs to be oriented to specific working environments. In contrast, deep learning methods can automatically learn useful features from training data and can tackle tasks that are difficult for conventional methods. On the other hand, the features extracted by the deep learning method provide an excellent generalization performance.

Huang et al. [5] proposed a real-time model called MCuePush U-Net for the saliency detection of surface defects on magnetic tiles. They fused saliency cues into the U-Net [6] through image arithmetic and embedded a Push network to highlight the predicted defects with bounding boxes. Xie et al. [7] proposed an end-to-end CNN architecture called FFCNN to address the problem of defect detection using multiple images from different perspectives of one magnetic tile sample. Cui et al. [8] proposed a fast and accurate network SDDNet for surface defect detection to address the challenge of large texture variation and small size of defects.

2.2 Semi-supervised surface defect inspection

To the best of our knowledge, there are no works related to the surface defect inspection of magnetic tiles based on semi-supervised methods so far. However, there are related works in the fields of rails [9], roads [10], steel [11,12,13], bearings [14, 15], and so on [16,17,18]. For example, Hajizadeh et al. [10] attempted to select potentially defect samples from a large number of unlabeled samples using semi-supervised learning methods, thus helping to mitigate the imbalance between the defect and defect-free classes. Di et al. [13] proposed a semi-supervised learning method based on Convolutional Autoencoder (CAE) and semi-supervised Generative Adversarial Networks (SGAN) for the surface defect classification of steel. He et al. [12] used GAN to generate unlabeled samples and utilized both labeled and unlabeled samples by multi-training of two models.

3 Preliminaries

3.1 Problem Definition

In semi-supervised learning, the training dataset $\mathcal{D}$ consists of two parts: the labeled dataset ${\mathcal{D}}_{l}=\{{x}_{i}^{l},{y}_{i}^{l}{\}}_{i=1}^{L}$ containing $L$ labeled samples and the unlabeled dataset ${\mathcal{D}}_{u}=\{{x}_{i}^{u}{\}}_{i=1}^{U}$ containing $U$ unlabeled samples. For each labeled sample ${x}_{i}^{l}\in {\mathcal{D}}_{l}$, ${y}_{i}^{l}\in \{0,1{\}}^{C}$ denotes its corresponding one-hot label vector, where $C$ denotes the number of classes. The general form of the objective function for semi-supervised learning can be described as:

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{\theta } L = \mathop \sum \limits_{i = 1}^{L} {\mathcal{L}}_{s} \left( {f_{\theta } \left( {x_{i}^{l} } \right),y_{i}^{l} } \right) + w{\mathcal{L}}_{u} \left( {\theta ,{\mathcal{D}}_{l} ,{\mathcal{D}}_{u} } \right)} \\ \end{array} $$

(1)

where ${\mathcal{L}}_{s}$ is the supervised loss term, ${\mathcal{L}}_{u}$ is the unsupervised loss term, ${f}_{\theta }$ is the model to be optimized parameterized by $\theta$, and $w$ is the weight of ${\mathcal{L}}_{u}$.

In this paper, the surface defect classification problem of magnetic tiles is considered as a binary classification task, i.e., to determine whether there are defects in the magnetic tile images. Therefore, $C=2$ by default. It is noted that our proposed method is not limited to the binary classification problem, so the number of defect classes is always denoted by $C$ in order not to lose generality.

3.2 Pseudo-labeling

Pseudo-labeling is a class of SSL algorithms that generate pseudo-labels on unlabeled data. These pseudo-labels are then used as targets along with the labeled data to train the model [19]. As a first attempt to use pseudo-labeling for deep neural networks, Pseudo-Label[20] utilized pseudo-labels at the fine-tuning stage of Denoising Auto-Encoder (DAE). The pseudo-label ${\widehat{y}}_{i}^{u}$ for an unlabeled sample ${x}_{i}^{u}\in {\mathcal{D}}_{u}$ was generated as follows:

$$ \begin{array}{*{20}c} {\hat{y}_{{{\text{ij}}}}^{{\text{u}}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;j = \mathop {\arg \max }\limits_{c} f_{\theta } \left( {c|x_{i}^{u} } \right)} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.} \\ \end{array} $$

(2)

where ${f}_{\theta }(c|{x}_{i}^{u})$ is the probability that the model ${f}_{\theta }$ predicts ${x}_{i}^{u}$ as class $c$, ${\widehat{y}}_{i}^{u}=[{\widehat{y}}_{i1}^{u},{\widehat{y}}_{i2}^{u},...,{\widehat{y}}_{iC}^{u}]\in \{0,1{\}}^{C}$ is the pseudo-label of ${x}_{i}^{u}$, which is a one-hot vector. The pseudo-labels were involved in model training in a supervised manner along with the ground-truth labels. The overall loss function is

$$ \begin{aligned} {\mathcal{L}} = & - \sum\limits_{{i = 1}}^{L} {\sum\limits_{{c = 1}}^{C} {y_{{ic}}^{l} } } \log f_{\theta } \left( {c|x_{i}^{l} } \right)\\ & - w\left( t \right)\sum\limits_{{i = 1}}^{U} {\sum\limits_{{c = 1}}^{C} {\hat{y}_{{ic}}^{u} } } \log f_{\theta } \left( {c|x_{i}^{u} } \right) \\ = & {\mathcal{L}}_{s} + w\left( t \right){\mathcal{L}}_{u} \\ \end{aligned} $$

(3)

where $w(t)$ is the weight of ${\mathcal{L}}_{u}$. $w(t)$ was adjusted according to the following strategy to avoid poor local minima [20]:

$$ \begin{array}{*{20}c} {w\left( t \right) = \left\{ {\begin{array}{*{20}c} 0 & {t < T_{1} } \\ {\frac{{t - T_{1} }}{{T_{2} - T_{1} }}w_{f} } & {T_{1} \le t < T_{2} } \\ {w_{f} } & {T_{2} \le t} \\ \end{array} } \right.} \\ \end{array} $$

(4)

where $t$ is the current training epoch, ${w}_{f}$ is the final value of $w(t)$. This strategy allows the value of $w(t)$ to be 0 at the beginning of training and then is slowly increased to ${w}_{f}$.

The clustering assumption states that the decision boundary should lie in low-density regions for better generalization performance [21]. Entropy Regularization [22] achieved this by minimizing the conditional entropy of the class probabilities of unlabeled data. Thus, Pseudo-Label [20] is equivalent to Entropy Regularization, which encourages the prediction of class probabilities close to the 1-of-$C$ code.

4 Proposed method

4.1 Overview

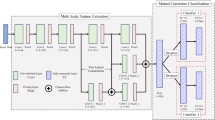
The proposed semi-supervised surface defect classification method consists of two models: a teacher model ${g}_{\varphi }$ and a student model ${f}_{\theta }$. As shown in Fig. 1, the training procedure comprises two stages: (1) pseudo-label generation and (2) student model training.

Fig. 1

Illustration of proposed SSL defect classification method

In the pseudo-label generation stage, the labeled samples ${\mathcal{D}}_{l}=\{{x}_{i}^{l},{y}_{i}^{l}{\}}_{i=1}^{L}$ are used jointly with the unlabeled samples ${\mathcal{D}}_{u}=\{{x}_{i}^{u}{\}}_{i=1}^{U}$ to train the teacher model to generate pseudo-labels $\widehat{Y}=\{{\widehat{y}}_{i}^{u}{\}}_{i=1}^{U}$ for unlabeled samples. After that, each sample in the unlabeled dataset ${x}_{i}^{u}$ is assigned a corresponding pseudo-label ${\widehat{y}}_{i}^{u}$, i.e., ${\mathcal{D}}_{u}=\{{x}_{i}^{u},{\widehat{y}}_{i}^{u}{\}}_{i=1}^{U}$. In the subsequent student model training stage, pseudo-labels, which are treated as if they are the true labels of unlabeled samples, are used together with the true labels of labeled samples to supervise the student model.

In our method, the teacher model and the student model are independent. The teacher model is responsible for generating pseudo-labels for unlabeled samples, and the student model is the resulting model for defect classification. In the following sections, we will introduce the two training stages mentioned above in detail.

4.2 Pseudo-label generation stage

The goal of this stage is to use the teacher model to generate pseudo-labels for unlabeled samples. A simple way to achieve this is to train the teacher model using only labeled samples in a supervised manner and then use the trained teacher model to predict pseudo-labels for the unlabeled samples. It is effective when there are sufficient labeled samples. If the number of labeled samples is limited, only using labeled samples is likely to prevent the teacher model from being well trained, and there is a risk of overfitting. Therefore, we use both labeled and unlabeled samples to train the teacher model in this stage.

4.2.1 Loss function

Inductive learning learns the rules with generalities from the training samples and applying them to the test samples that the model has not seen before. In contrast, transductive learning attempts to apply the learned rules to the training samples that the model has already seen. Typically, transductive learning works better since it simply expects to achieve the best performance on given samples, whereas inductive learning expects to learn a decision function with a low error rate over the entire sample distribution.

In the case of inductive learning, the optimization problem can be expressed as:

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{\varphi } L\left( {\varphi |X,Y} \right)} \\ \end{array} $$

(5)

where $\varphi$ are the parameters of teacher model ${g}_{\varphi }$, $X=\{{x}_{i}{\}}_{i=1}^{N}$ is the set of training samples, $Y=\{{y}_{i}{\}}_{i=1}^{N}$ is the set of corresponding labels, and $N$ is the number of samples.

As mentioned before, the teacher model in our method is responsible for predicting pseudo-labels on the unlabeled dataset, which means the teacher model does not need to consider the generalization on unseen samples. Therefore, we treat the pseudo-labels of unlabeled samples as optimization variables based on the principle of transductive semi-supervised learning and update them together with the teacher model parameters during the training. Thus the optimization problem in this stage can actually be expressed as:

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{\varphi ,Y} L\left( {\varphi ,Y|X} \right)} \\ \end{array} $$

(6)

Compared with (5), the difference is that the labels are also optimization variables. It should be noted that only the pseudo-labels of unlabeled samples are updated during training, and the true labels of labeled samples remain fixed.

In this paper, the KL-divergence is adopted for (6):

$$ \begin{aligned} {\mathcal{L}}\left( {\varphi ,Y|X} \right) = & \sum\limits_{{i = 1}}^{N} {D_{{KL}} } \left( {y_{i} \parallel g_{\varphi } \left( {x_{i} } \right)} \right) \\ = & \sum\limits_{{i = 1}}^{N} {\sum\limits_{{c = 1}}^{C} {y_{{ic}} } } \log y_{{ic}} - \sum\limits_{{i = 1}}^{N} {\sum\limits_{{c = 1}}^{C} {y_{{ic}} } } \log g_{\varphi } \left( {c|x_{i} } \right) \\ \end{aligned} $$

(7)

4.2.2 Alternating optimization

For the optimization variables $\varphi$ and $\widehat{Y}=\{{\widehat{y}}_{i}^{u}{\}}_{i=1}^{U}$, we apply the alternating optimization method as shown in Fig. 2. The corresponding pseudocode is shown in Algorithm 1. The optimization process is divided into the following two alternating steps:

Fig. 2

Alternating optimization method for the pseudo-label generation stage

• (a) Updating $\widehat{Y}$ with fixed $\varphi$. Since the training samples in the dataset are independent of each other, the optimization problem on $\widehat{Y}$ can be decomposed for each ${\widehat{y}}_{i}^{u}$. In semi-supervised learning, there are two types of pseudo-labels: hard labels and soft labels. In the case of hard labels, the pseudo-label ${\widehat{y}}_{i}^{u}\in \{0,1{\}}^{C}$ is a one-hot vector that can be updated in the following way:

  $$ \begin{array}{*{20}c} {\hat{y}_{ij}^{u} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;j = \arg \mathop {\max }\limits_{c} g_{\varphi } \left( {c|x_{i}^{u} } \right)} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.} \\ \end{array} $$

  (8)

  In the case of soft labels, the pseudo-label ${\widehat{y}}_{i}^{u}\in [0,1{]}^{C}$ is a probability distribution. When ${y}_{i}={g}_{\varphi }({x}_{i})$, the loss in (7) will obtain the minimum value, so the pseudo-label ${\widehat{y}}_{i}^{u}$ can be updated in the following way:

  $$ \begin{array}{*{20}c} {\hat{y}_{i}^{u} = g_{\varphi } \left( {x_{i}^{u} } \right)} \\ \end{array} $$

  (9)

  Compared with hard labels, soft labels usually contain less noise and more information. Unless otherwise indicated, soft labels are adopted in this paper.

• (b) Updating $\varphi$ with fixed $\widehat{Y}$. With pseudo-labels fixed, the KL divergence in (7) degenerates to cross-entropy, so the optimization of $\varphi$ in this step can be solved by the commonly used stochastic gradient descent algorithm (SGD). As shown in the bottom part of Fig. 2, the loss is calculated separately for the labeled and unlabeled samples when optimizing $\varphi$:

  $$ \begin{aligned} {\mathcal{L}} = & - \sum\limits_{{i = 1}}^{L} {\sum\limits_{{c = 1}}^{C} {y_{{{\text{ic}}}}^{l} } } \log g_{\varphi } \left( {c|x_{i}^{l} } \right) - w\sum\limits_{{i = 1}}^{U} {\sum\limits_{{c = 1}}^{C} {y_{{{\text{ic}}}}^{u} } } \log g_{\varphi } \left( {c|x_{i}^{u} } \right) \\ = & {\mathcal{L}}_{s} + w{\mathcal{L}}_{u} \\ \end{aligned} $$

  (10)

  where $w$ is the weight of ${\mathcal{L}}_{u}$, which is set to 1 by default.

A primary problem with semi-supervised learning methods based on pseudo-labeling is that the noise in pseudo-labels can be amplified during the training process, resulting in high-confidence but incorrect predictions from the model. Zhang et al. [23] showed that deep neural networks could learn any training dataset even if the labels in the training set are completely random. Therefore, directly training the model using noisy pseudo-labels will lead to complete overfitting of the model on noisy data. Although commonly used regularization techniques (e.g., dropout [24], early stop, L1 and L2 regularization) can alleviate the overfitting to some extent, all these methods prevent the reduction of training loss and therefore do not guarantee the optimization of the training process. In contrast, we update pseudo-labels together with the teacher model parameters, which is essential to mitigate the impact of noise in pseudo-labels on the training process from the perspective of optimization.

4.2.3 Curriculum learning

Curriculum learning [25] is a training strategy in machine learning that allows the model to learn easy samples at first and then gradually learn hard ones. The human learning process generally follows an easy-to-hard progression, and curriculum learning is exactly based on this idea. Bengio et al. [25] showed that curriculum learning could accelerate the training process and allow the model to obtain better generalization performance.

Compared with only optimizing the teacher model parameters, it is naturally more difficult to optimize pseudo-labels at the same time. Therefore, to better carry out the alternating optimization, we train the teacher model based on the idea of curriculum learning.

Specifically, for each unlabeled sample ${x}_{i}^{u}$, the maxima of the softmax probability vector output by the model are regarded as the confidence of its pseudo-label ${\widehat{y}}_{i}^{u}$, and the samples with high-confidence pseudo-labels are considered as easy samples. After updating the pseudo-labels in step (a), we first sort the unlabeled samples according to the confidence of pseudo-labels in descending order. After that, the unlabeled samples corresponding to the top $p\times 100$% most confident pseudo-labels are selected in each class. Finally, the selected unlabeled samples are used along with labeled samples to update the teacher model parameters $\varphi$.

The parameter $p$ is adjusted according to the following strategy:

$$ \begin{array}{*{20}c} {p = \left\{ {\begin{array}{*{20}l} 0 \hfill & {t < T_{0} } \hfill \\ {p_{0} + \left( {p_{1} - p_{0} } \right)e^{{ - 5(1 - \frac{{t - T_{0} }}{{T - T_{0} }})^{2} }} } \hfill & {T_{0} \le t} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(11)

where ${p}_{0}$ and ${p}_{1}$ are the minimum and maximum values of $p$, respectively, $t$ is the current training epoch, and $T$ is the total number of training epochs. This strategy keeps $p=0$ when $t<{T}_{0}$, meaning that no unlabeled samples are selected to train the teacher model. After $t\ge {T}_{0}$, $p$ gradually increases from ${p}_{0}$ to ${p}_{1}$ according to a sigmoid-shaped function $f(x)={e}^{-5(1-x{)}^{2}}$, where $x\in [0,1]$. When ${p}_{0}=0.2$, ${p}_{1}=0.5$, ${T}_{0}=40$, and $T=100$, the value of $p$ is adjusted as shown in Fig. 3.

Fig. 3

Value of $p$ adjusted according to (11), where ${p}_{0}=0.2$, ${p}_{1}=0.5$,${T}_{0}=40$, $T=100$

4.3 Student model training

This stage aims to train the student model using both labeled and unlabeled samples. The key in this stage is to make better use of the unlabeled samples and corresponding pseudo-labels. Instead of using all unlabeled samples, we select unlabeled samples corresponding to the top ${p}^{\mathrm{^{\prime}}}$×100% most confident pseudo-labels in each class to train the student model. Unless otherwise specified, ${p}^{\mathrm{^{\prime}}}=0.7$ by default. The training procedure in this stage is shown in Fig. 4, and the corresponding pseudocode containing implementation details is shown in Algorithm 2.

Fig. 4

Training procedure of the student model

4.3.1 Oversampling of labeled samples

There are usually more unlabeled samples in semi-supervised learning than labeled ones, which could easily result in overfitting to the loss of unlabeled samples. While training the student model, we address the problem of sample imbalance by oversampling the labeled samples. Specifically, we ensure that each mini-batch contains the same number of labeled and unlabeled samples during the training process. Since there are usually more unlabeled samples than labeled ones, the labeled samples have been looped through several times after the model has gone through the unlabeled samples once.

4.3.2 Loss function

As mentioned above, the labeled samples are oversampled to ensure that each mini-batch contains the same number of labeled and unlabeled samples. Let ${\mathcal{B}}_{l}=\{{x}_{i}^{l},{y}_{i}^{l}{\}}_{i=1}^{M/2}$ and ${\mathcal{B}}_{u}=\{{x}_{i}^{u},{\widehat{y}}_{i}^{u}{\}}_{i=1}^{M/2}$ denote labeled and unlabeled samples in a mini-batch, respectively, where M is the mini-batch size. When training the student model, the loss in a mini-batch can be expressed as:

$$ \begin{aligned} {\mathcal{L}} = & - \frac{1}{{\left| {{\mathcal{B}}_{l} } \right|}}\sum\limits_{{i = 1}}^{{M/2}} {\sum\limits_{{c = 1}}^{C} {y_{{{{ic}}}}^{l} } } \log f_{\theta } \left( {c|x_{i}^{l} } \right) \\ & - w\frac{1}{{\left| {{\mathcal{B}}_{u} } \right|}}\sum\limits_{{i = 1}}^{{M/2}} {\sum\limits_{{c = 1}}^{C} {\hat{y}_{{{{ic}}}}^{u} } } \log f_{\theta } \left( {c|x_{i}^{u} } \right) \\ = & {\mathcal{L}}_{s} + w{\mathcal{L}}_{u} \\ \end{aligned} $$

(12)

where $w$ is the weight of ${\mathcal{L}}_{u}$.

4.3.3 Augmentation with Mixup

Mixup [26] is a data augmentation method via interpolation of training samples and their labels as follows:

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{x} = \lambda x_{i} + \left( {1 - \lambda } \right)x_{j} } \\ {\tilde{y} = \lambda y_{i} + \left( {1 - \lambda } \right)y_{j} } \\ \end{array} } \\ \end{array} $$

(13)

where ${x}_{i}$ and ${x}_{j}$ are the two training samples, ${y}_{i}$ and ${y}_{j}$ are their labels, $\tilde{x }$ and $\tilde{y }$ are the augmented training samples and labels, respectively, $\lambda \in [0,1]$ and subject to the following Beta distribution:

$$ \begin{array}{*{20}c} {\lambda \sim {\text{Beta}}\;\left( {\alpha ,\;\alpha } \right)} \\ \end{array} $$

(14)

where $\alpha$ is the hyperparameter that controls the Beta distribution, $\alpha =0.75$ by default.

We use mixup augmentation to achieve information fusion between labeled and unlabeled samples. Specifically, for each unlabeled sample with pseudo-label $({x}^{u},{\widehat{y}}^{u})\in {\mathcal{B}}_{u}$ in a mini-batch, a labeled sample $({x}^{l},{y}^{l})\in {\mathcal{B}}_{l}$ is randomly selected, and the interpolated sample and its label can be obtained following (13):

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {x^{{{\text{um}}}} = \lambda x^{l} + \left( {1 - \lambda } \right)x^{u} } \\ {y^{{{\text{um}}}} = \lambda y^{l} + \left( {1 - \lambda } \right)\hat{y}^{u} } \\ \end{array} } \\ \end{array} $$

(15)

As a result, a batch of samples ${\mathcal{B}}_{um}=\{{x}_{i}^{um},{y}_{i}^{um}{\}}_{i=1}^{M/2}$ after mixup augmentation between labeled and unlabeled samples are obtained.

The pseudo-labels of unlabeled samples inevitably contain noise. Compared with the original pseudo-label ${y}^{u}$, we believe that the interpolated label ${y}^{um}$ contains less noise. For example, when $\lambda =0.5$, ${y}^{um}$ is considered to contain information from half of each of ${y}^{l}$ and ${\widehat{y}}^{u}$ according to (15). In this case, the information from ${y}^{l}$ can be assumed not containing any noise, and only the information from ${\widehat{y}}^{u}$ may contain some noise.

Mixup [26] is an effective regularization method in supervised learning, which has the effect of label smoothing and data augmentation. Therefore, we also apply mixup augmentation between labeled samples hoping to make full use of the labeled samples and regularize the model. Specifically, for each labeled sample $({x}_{i}^{l},{y}_{i}^{l})\in {\mathcal{B}}_{l}$ in a mini-batch, another labeled sample $({x}_{j}^{l},{y}_{j}^{l})\in {\mathcal{B}}_{l}$ is randomly selected, and the interpolated sample is then obtained following (13):

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {x^{{{\text{lm}}}} = \lambda x_{i}^{l} + \left( {1 - \lambda } \right)x_{j}^{l} } \\ {y^{{{\text{lm}}}} = \lambda y_{i}^{l} + \left( {1 - \lambda } \right)y_{j}^{l} } \\ \end{array} } \\ \end{array} $$

(16)

Similarly, a batch of samples ${\mathcal{B}}_{lm}=\{{x}_{i}^{lm},{y}_{i}^{lm}{\}}_{i=1}^{M/2}$ after mixup augmentation between labeled samples are obtained.

In summary, the final loss used for student model training is:

$$ \begin{array}{*{20}c} {{\mathcal{L}}_{s} = - \frac{1}{{\left| {{\mathcal{B}}_{l} } \right|}}\mathop \sum \limits_{i = 1}^{M/2} \mathop \sum \limits_{c = 1}^{C} y_{ic}^{l} \log \left( {f_{\theta } \left( {c|x_{i}^{l} } \right)} \right)} \\ \end{array} $$

(17)

$$ \begin{array}{*{20}c} {{\mathcal{L}}_{u} = - \frac{1}{{\left| {{\mathcal{B}}_{u} } \right|}}\mathop \sum \limits_{i = 1}^{M/2} \mathop \sum \limits_{c = 1}^{C} \hat{y}_{{{\text{ic}}}}^{u} \log \left( {f_{\theta } \left( {c|x_{i}^{u} } \right)} \right)} \\ \end{array} $$

(18)

$$ \begin{array}{*{20}c} {{\mathcal{L}}_{{{\text{lm}}}} = - \frac{1}{{\left| {{\mathcal{B}}_{{{\text{lm}}}} } \right|}}\mathop \sum \limits_{i = 1}^{M/2} \mathop \sum \limits_{c = 1}^{C} y_{{{\text{ic}}}}^{{{\text{lm}}}} \log \left( {f_{\theta } \left( {c|x_{i}^{{{\text{lm}}}} } \right)} \right)} \\ \end{array} $$

(19)

$$ \begin{array}{*{20}c} {{\mathcal{L}}_{{{\text{um}}}} = - \frac{1}{{\left| {{\mathcal{B}}_{{{\text{um}}}} } \right|}}\mathop \sum \limits_{i = 1}^{M/2} \mathop \sum \limits_{c = 1}^{C} y_{ic}^{{{\text{um}}}} \log \left( {f_{\theta } \left( {c|x_{i}^{{{\text{um}}}} } \right)} \right)} \\ \end{array} $$

(20)

$$ \begin{array}{*{20}c} {L = {\mathcal{L}}_{s} + w_{1} {\mathcal{L}}_{u} + w_{2} {\mathcal{L}}_{{{\text{lm}}}} + w_{3} {\mathcal{L}}_{{{\text{um}}}} } \\ \end{array} $$

(21)

where ${\mathcal{L}}_{s}$, ${\mathcal{L}}_{u}$, ${\mathcal{L}}_{{{\text{lm}}}}$ and ${\mathcal{L}}_{{{\text{um}}}}$ are the loss on ${\mathcal{B}}_{l}$, ${\mathcal{B}}_{u}$, ${\mathcal{B}}_{{{\text{lm}}}}$ and ${\mathcal{B}}_{{{\text{um}}}}$, respectively, and $w_{1}$, $w_{2}$ and $w_{3}$ are the weights for balancing ${\mathcal{L}}_{u}$, ${\mathcal{L}}_{{{\text{lm}}}}$ and ${\mathcal{L}}_{{{\text{um}}}}$.

5 Experiments

5.1 Image acquisition device

As shown in Figs. 5 and 6, an image acquisition device is designed in this paper to collect magnetic tile images from the production line. The device is mainly composed of cameras, light sources, conveyors, and controllers. Six cameras are used to capture images from different directions to achieve real-time performance. The light source is LED. The proximity switches and motors are controlled by a microcontroller. ARM processors are used for image reading and processing. All ARM controllers communicate with each other through a network switch.

Fig. 5

System diagram of the image acquisition device

Fig. 6

Image acquisition device

5.2 Datasets

We conducted experiments on the magnetic tile defect dataset collected by the Institute of Automation, Chinese Academy of Sciences (MT-CAS) [5], and the dataset collected by us (MT-Ours). MT-CAS contains five kinds of surface defects: blowhole, crack, fray, break, and uneven, as shown in Fig. 7. There are a total of 1344 grayscale images of variable size in MT-CAS, including 392 defect images and 952 defect-free images. In the subsequent experiments, 70% of the images are randomly selected to form the training set and the remaining to form the validation set. As a result, the training set contains 939 images, of which 275 are defective, and 664 are defect-free. The validation set contains 405 images, of which 117 are defective, and 288 are defect-free.

Fig. 7

Examples of the defect samples in MT-CAS

The images in MT-Ours were collected in a real industrial scenario, containing three kinds of surface defects: break, crack, and fray, as shown in Fig. 8. There are 3060 color images of size 400 $\times$ 400 in MT-Ours, including 751 defect images and 2309 defect-free images. In the subsequent experiments, 75% of the images are randomly selected to form the training set and the remaining to form the validation set. As a result, the training set contains 2296 images, of which 560 are defective, and 1736 are defect-free. The validation set contains 764 images, of which 191 are defective, and 573 are defect-free.

Fig. 8

Examples of the defect samples in MT-Ours

5.3 Implementation details

In this paper, ResNet-18 [27] and DenseNet-121 [28] are used as classifiers for defect classification. SGD is used as the optimizer to train the classifier with a momentum of 0.9 and a batch size of 32. The initial learning rate is 0.002 and is adjusted using a cosine decay policy:

$$ \begin{array}{*{20}c} {{\text{lr}} = \frac{1}{2}{\text{lr}}_{0} \cdot \left( {1 + \cos \left( {\frac{t}{T}\pi } \right)} \right)} \\ \end{array} $$

(22)

where $l{r}_{0}$ is the initial learning rate, $t$ is the current training epoch, and $T$ is the total number of training epochs. ${p}_{0}$, ${p}_{1}$ and ${T}_{0}$ in (11) are set to 0.2, 0.5, and 40, respectively. ${w}_{1}$, ${w}_{2}$ and ${w}_{3}$ in (21) are set to 1.0, 1.0, and 0.5, respectively.

In addition to the proposed SSL defect classification method, two semi-supervised learning methods, Pseudo-Label [20] and Mean Teacher [29] are used as the baselines for experiments. The teacher model in our method is trained for 100 epochs. Since the labeled samples are oversampled when training the student model, there are more iterations in each epoch. As mentioned before, the student model is used for defect classification. For a fair comparison, the number of training iterations for the student model is kept the same as baselines, which will be detailed later.

The classifier is trained with the following data augmentations: (1) random horizontal and vertical flipping, (2) resize the short edge to 256 while keeping the aspect ratio, (3) random cropping with a size of 224 $\times$ 224, and (4) color jittering (adjusting brightness, contrast, hue, and saturation).

5.4 Results on MT-CAS

To carry out the semi-supervised surface defect classification.

experiments, we randomly divided the training set into the labeled dataset and unlabeled dataset. Specifically, a portion of the samples in the training set are randomly selected to form the labeled dataset ${\mathcal{D}}_{l}=\{{x}_{i}^{l},{y}_{i}^{l}{\}}_{i=1}^{L}$ with true labels. The remaining are used to form the unlabeled dataset ${\mathcal{D}}_{u}=\{{x}_{i}^{u}{\}}_{i=1}^{U}$ and their true labels are ignored. To investigate the effect of the number of labeled samples $L$ on the defect classification performance, we divided the training set with $L$= 939, 500, 250, and 100, respectively. Note that there are no unlabeled samples when $L$= 939. We conducted experiments with different values of $L$ and evaluated the classification accuracy on the validation set. All the experiments were repeated five times with the same settings. Then the averages were taken as the final results.

In the experiments, the supervised-only method, Pseudo-Label [20], Mean Teacher [29], and the proposed method were used to train the classifier, respectively. For the supervised-only method, the classifier was trained for 3000 iterations when $L$= 939, for 1600 iterations when $L$= 500, for 800 iterations when $L$= 250, for 400 iterations when $L$= 100. For the semi-supervised method, including Pseudo-Label [20], Mean Teacher [29], and the proposed method, the classifier (the student model in our method) was trained for 6200 iterations when $L$= 500, for 3100 iterations when $L$= 250, for 1200 iterations when $L$= 100.

With ResNet-18 as the classifier, the experimental results are shown in Table 1. Note that we use the same network for the teacher and student model in our method. It can be seen that the accuracy of all methods drops as the number of labeled samples decreases, indicating that the number of labeled samples directly affects the performance of deep neural networks. The accuracy of all semi-supervised methods is higher than that of supervised-only methods, which proves that semi-supervised methods can indeed improve the performance by using additional unlabeled samples. The accuracy of our method is higher than that of Pseudo-Label [20] and Mean Teacher [29], which shows the superiority of our method. When $L$= 500, our method can achieve 98.91% accuracy, which is very close to the accuracy of the supervised-only method when $L$=939 (99.11%). This means that only 0.2% of the accuracy is lost while saving about half of the labeling cost.

Table 1 Defect Classification Accuracy on MT-CAS with ResNet-18

For a more intuitive comparison, the experimental results in Table 1 are plotted as a line graph shown in Fig. 9. The black horizontal dashed line represents the accuracy of the supervised-only method when $L$= 939. The effectiveness of our method and its superiority compared with baselines can be intuitively illustrated in Fig. 9.

Fig. 9

Defect classification accuracy on MT-CAS with ResNet-18

5.5 Results on MT-Ours

As in the previous section, the training set was randomly divided into labeled and unlabeled datasets with $L$=2296, 1000, 500, 250, and 100. For the supervised-only method, the classifier was trained for 7200 iterations when $L$=2296, for 3200 iterations when $L$=1000, for 1600 iterations when $L$=500, for 800 iterations when $L$=250, for 400 iterations when $L$=100. For semi-supervised method, including Pseudo-Label [20], Mean Teacher [29], and the proposed method, the classifier (the student model in our method) was trained for 6200 iterations when $L$=1000, for 6200 iterations when $L$=500, for 3100 iterations when $L$=250, for 1200 iterations when $L$=100.

With ResNet-18 as the classifier, the experimental results are shown in Table 2. We also use the same network for the teacher and student model in our method. Similar results as in the previous section can be observed from Table 2. Moreover, we can observe the following results:

Table 2 Defect Classification Accuracy on MT-Ours with ResNet-18

• (1) Compared with MT-CAS, the accuracy of all methods is lower on MT-Ours. This is because the region of defects in MT-CAS is relatively large, whereas there are many images with small defect regions in MT-Ours, so it is more difficult to classify.

• (2) The smaller the number of labeled samples, the more obvious the superiority of our method. For example, when $L$=1000, 500, 250, and 100, the accuracy of our method is 1.28%, 1.64%, 2.23%, and 5.11% higher than that of the supervised-only method, 0.84%, 1.12%, 1.52%, and 1.96% higher than that of Pseudo-Label [20], 0.73%, 1.39%, 1.63%, and 2.57% higher than that of Mean Teacher [29].

For a more intuitive comparison, the results in Table 2 are plotted as a line graph shown in Fig. 10. The black horizontal dashed line represents the accuracy of the supervised-only method when $L$=2296.

Fig. 10

Defect classification accuracy on MT-Ours with ResNet-18

Besides ResNet-18, we also adopted DenseNet-121 as the classifier and conducted experiments under the same settings. As shown in Table 3 and Fig. 11, our method still outperforms the baseline methods. Benefiting from the densely connected mechanism, DenseNet-121 can achieve a deeper network structure and more efficient feature reuse and extraction abilities with even fewer parameters than ResNet-18.

Table 3 Defect Classification Accuracy on MT-Ours with DenseNet-121

Fig. 11

Defect classification accuracy on MT-Ours with DenseNet-121

As mentioned before, the teacher model and the student model in our method are independent. The teacher model is responsible for generating pseudo-labels for unlabeled samples, and the student model is the resulting model for defect classification. With such design, we can choose a big network with powerful learning ability as the teacher model to get high-quality pseudo-labels, while selecting a small network as the student model for efficient deployment on embedded devices.

The architecture of MobileNet is specifically designed for mobile and embedded devices with fewer parameters and lower computational costs, making it ideal for applications requiring real-time performance. As shown in Table 4, the number of parameters and computational cost of MobileNetV2 [30] are 1/3 and 1/6 of those of ResNet-18, respectively. The size of the network can be further reduced by decreasing the width multiplier in MobileNetV2.

Table 4 Number of Parameters and Computational Cost of Networks

We then used MobileNetV2(0.25) as the defect classifier for experiments. For our method, only the student model needs to be replaced with MobileNetV2 (0.25), while the teacher model can still use DenseNet-121. In contrast, the teacher model and the student model in Mean Teacher [29] must have the same network structure. Therefore, both the teacher model and the student model in Mean Teacher [29] must be replaced with MobileNetV2(0.25).

The results are shown in Table 5 and Fig. 12. Ours(ResNet-18) and Ours(DenseNet-121) denote the teacher model in our method using ResNet-18 and DenseNet-121, respectively, while the student model using MobileNetV2(0.25). Compared with the results in Table 3, the accuracy of all methods decreases after using the lightweight network, but the decrease in accuracy of our method is slighter. For example, compared with Table 3, the accuracy of Pseudo-Label [20] decreases by 3.06%, 4.01%, 5.81%, and 5.70% when $L$=1000, 500, 250, and 100, respectively, while the accuracy of our method decreases by 2.09%, 1.68%, 2.17%, and 2.96%. This shows that our method can be efficiently deployed while maintaining promising performance.

Table 5 Defect Classification Accuracy on MT-Ours with MobileNetV2(0.25)

Fig. 12

Defect classification accuracy on MT-Ours with MobileNetV2(0.25)

It can be seen that the accuracy of Ours(ResNet-18) and Ours(DenseNet-121) when $L$=1000 is higher than that of the supervised-only method when $L$=2296. Compared with ResNet-18 and DenseNet-121, MobileNetV2(0.25) has a very limited number of parameters, so its learning ability is correspondingly much weaker. Therefore, it is hard for the supervised-only method to achieve very high accuracy even when all the samples in the training set are labeled ($L$=2296). In our method, the student model can learn transferable knowledge from the teacher model. Thus, our method can achieve higher accuracy with fewer labeled samples.

5.6 Ablation studies

We study the effects of some settings and parameters in the proposed method in this section. All ablation experiments were carried out on the MT-Ours dataset, changing one or a few hyperparameters at a time while the others remain fixed. In the following experiments, ResNet-18 is adopted as the classifier by default.

5.6.1 Generation of pseudo-labels

In the pseudo-label generation stage, the pseudo-labels of the unlabeled samples and the teacher model parameters are alternatively optimized. Another simple way is to train the teacher model using only labeled samples, then use the trained teacher model to predict pseudo-labels for unlabeled samples. Therefore, we generated the pseudo-labels of unlabeled samples using these two methods separately and evaluated the accuracy of pseudo-labels. The results are shown in Table 6. Naïve denotes training the teacher model using only labeled samples. Alt-optim denotes our alternating optimization method. We can see that the accuracy of pseudo-labels generated by Naïve is lower than that of Alt-optim, which illustrates the effectiveness of alternating optimization.

Table 6 Accuracy of Pseudo-Labels Generated by Different Methods

The pseudo-labels generated by these two methods were then used to train the student model separately. The corresponding defect classification accuracy is shown in Table 7. It can be seen that a higher accuracy of the pseudo-labels is associated with a higher defect classification performance. Note that the true labels of unlabeled samples are only used to assess the quality of the pseudo-labels.

Table 7 Defect Classification Accuracy of the Student Model Using Different Pseudo-Labels

5.6.2 Curriculum learning for teacher model

In the pseudo-label generation stage, curriculum learning is used to train the teacher model. The ${p}_{0}$, ${p}_{1,}$ and ${T}_{0}$ in (11) control the value of $p$ during the training. When $L$= 100 and ${T}_{0}$= 40, the accuracy of the generated pseudo-labels under different values of $({p}_{0},{p}_{1})$ is shown in Fig. 13. The pseudo-labels generated at $({p}_{0},{p}_{1})$= (0.2, 0.5) have relatively high accuracy. A too-small ${p}_{0}$ results in too few unlabeled samples participating in the training at the beginning, and thus the teacher model cannot make full use of unlabeled samples. On the contrary, a too large ${p}_{1}$ results in too many unlabeled samples with low confidence pseudo-labels participating in the training, thus introducing more label noise.

Fig. 13

Accuracy of generated pseudo-labels under different values of $({p}_{0},{p}_{1})$

When $({p}_{0},{p}_{1})$=(0.2, 0.5), the similar experiments were conducted under different values of ${T}_{0}$, and the results are shown in Fig. 14. The pseudo-labels generated at ${T}_{0}$=40 have relatively high accuracy. A too-small ${T}_{0}$ result in the unlabeled samples participating in the training of the teacher model too early, thus introducing label noise at the beginning. On the contrary, a too large ${T}_{0}$ result in unlabeled samples participating in the training of the teacher model until the training process is about to finish, making it hard to achieve the alternating optimization.

Fig. 14

Accuracy of the generated pseudo-labels under different values of ${T}_{0}$

5.6.3 Threshold of pseudo-label for student model

In the student model training stage, the unlabeled samples with high-confidence pseudo-labels are selected for training based on a threshold ${p}^{\mathrm{^{\prime}}}$. To investigate the effect of ${p}^{\mathrm{^{\prime}}}$ on the performance of the student model, we conducted experiments for different values of ${p}^{\mathrm{^{\prime}}}$. As shown in Fig. 15, the points with the highest accuracy under different values of ${p}^{\mathrm{^{\prime}}}$ are marked with hollow symbols. It can be seen that the optimal value of ${p}^{\mathrm{^{\prime}}}$ differs for different $L$. The optimal values of ${p}^{\mathrm{^{\prime}}}$ are 0.9, 0.7, 0.5 and 0.5 when $L$= 1000, 500, 250 and 100, respectively.

Fig. 15

Defect classification accuracy of the student model under different values of ${p}^{\mathrm{^{\prime}}}$

Since the total number of labeled and unlabeled samples in the training set is constant, there are fewer unlabeled samples with large $L$. In this case, a large value of ${p}^{\mathrm{^{\prime}}}$ ensures there are adequate unlabeled samples to help with the student model training, whereas a small value of ${p}^{\mathrm{^{\prime}}}$ leads to insufficient use of unlabeled samples. On the contrary, there are more unlabeled samples with small $L$. In this case, a small value of ${p}^{\mathrm{^{\prime}}}$ is enough, and a large value of ${p}^{\mathrm{^{\prime}}}$ introduces more label noise instead. Therefore, ${p}^{\mathrm{^{\prime}}}$ should have a large value when there are few unlabeled samples. Otherwise, the value of ${p}^{\mathrm{^{\prime}}}$ should be small. In previous experiments, the value of ${p}^{\mathrm{^{\prime}}}$ was not adjusted for a fair comparison with other methods but was set to 0.7 by default.

5.6.4 Mixup augmentation

In the student model training stage, mixup is applied to achieve information fusion between labeled and unlabeled samples as well as regularization. To investigate the effect of mixup on the performance of the student model, we trained the student model with or without mixup, respectively. Without mixup, only ${\mathcal{L}}_{s}$ and ${\mathcal{L}}_{u}$ in (21) are available. The results are shown in Table 8. It can be seen that mixup can improve the defect classification accuracy of the student model.

Table 8 Defect Classification Accuracy of the Student Model with or without Mixup

6 Conclusion

This paper proposes a semi-supervised learning method based on pseudo-labeling to inspect surface defects on magnetic tiles. The proposed method can effectively utilize unlabeled samples to reduce the annotation cost. Experiments on the public and our collected datasets show the effectiveness and superiority of our method. In addition, our method offers great flexibility for deployment on mobile and embedded devices. The limitations of the proposed method are as follows. Firstly, the proposed method requires tuning several hyperparameters, although we have observed that good performance can be achieved with rough tuning. Secondly, we directly adopted off-the-shelf CNN models as classifiers without exploring the network structure. Therefore, the future of this paper will focus on these two aspects. Firstly, it is necessary to reduce the number of hyperparameters or improve the robustness of the proposed method to the choice of hyperparameters. Secondly, the network structure needs to be optimized to further improve the defect classification performance.