Obtaining a high-precision spatial distribution map of regional soil heavy metals is considered an important basis for further pollution and risk assessments and decision and policy making in environmental management and conservation. To date, the main methods for the spatial interpolation of soil heavy metals include geostatistical kriging methods (Ren et al. 2018), non-geostatistical methods (e.g., inverse distance weighting, global polynomials, multiple linear regression, geographically weighted regression, neural networks) (Guan et al. 2019; Zhang et al. 2020), and their combination [e.g., regression kriging (RK), Bayesian maximum entropy (BME)] (Fei et al. 2019). In generally, the combined methods can obtain the highest interpolation accuracy because they can incorporate the spatial autocorrelation of soil heavy metals and their relationship with environmental factors (Yang et al. 2016). Among these combination methods, RK is the most commonly used combined method, which combines global multiple linear regression (MLR) and ordinary kriging (Zhu and Lin 2010). However, both soil heavy metal and environmental factors are related to spatial location and are heterogeneous over space (Li et al. 2017). The MLR model assumes that the relationships between dependent variables and independent variables are homogenous (Su et al. 2012), leading to biased parameter estimates and low fitting accuracy (Guo et al. 2008). Thus, some studies have explored the spatially varying relationships between soil heavy metals and environmental factors. That is, the underlying influence process of environmental factors on the content of heavy metals in soil varied across spatial area. For example, due to the prevailing wind, the relationship between soil heavy metals and the distance from pollution source to soil receptor varied in different directions around the pollution source. The geographically weighted regression (GWR) model (Wang et al. 2020), which was developed from the MLR model and further improved to take into account spatially varying relationships between the dependent variable and independent variables (Brunsdon et al. 1996). In general, GWR can provide better results than conventional models in terms of improving the understanding of the spatially varying relationships between soil heavy metals and environmental factors. Then, a geographically weighted regression kriging (GWRK) approach, replacing the RK method, was used to predict the spatial distributions of soil properties, such as organic carbon, total nitrogen, salinity, and available phosphorus (Kumar et al. 2012). The results of the above studies showed that GWRK can improve the precision for estimating soil properties compared to ordinary kriging (OK), GWR and RK because GWRK takes into account the spatially varying relationships between soil properties and environmental factors and the spatial autocorrelation of the residuals. Thus, compared with the common methods, GWRK method may improve the spatial interpolation accuracy of soil heavy metal.

In this context, the objectives of this study are (1) to predict the spatial distribution of soil heavy metals using the GWRK method and (2) to compare the accuracy of the GWRK method with those obtained from the OK and RK methods.

Materials and Methods

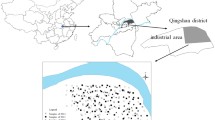
The study was conducted in Daye city (29°40′–30°15′ N, 114°31′–115°20′ E), Hubei Province, China, which is a famous mining city with a long mining and smelting history in China. In September 2019, we collected 202 topsoil samples (0–20 cm). After the standard analytical procedure (Hua et al. 2018), the concentrations of Pb in those soil samples were obtained. A total of 40 samples (see the red points in Fig. 1) were randomly selected to serve as the validation set, and the remaining 162 samples served as training points (see the black points in Fig. 1a).

Fig. 1
figure 1

Spatial distribution of sampling points, elevation (a), and land cover (b) in Daye city

Full size image

The heavy metals in soils might be affected by various environmental factors, such as terrain, land cover, location factors, and soil attributes (Schwarz et al. 2012; Shen et al. 2017; Chen et al. 2020). Thus, in this study, considering data availability, a total of 11 environmental factors in three categories were involved in the GWR model to obtain the trend value of each spatial position in the study area (see Table 1).

To compare the coefficients of the different independent variables, before performing MLR and GWR modeling, all independent variables were normalized using the following formula:

$${x}_{j}\left({\varvec{p}}_{0}\right)=\left({x}_{j}\left({\varvec{p}}_{0}\right)-{x}_{j,min}\right)/\left({x}_{j,max}-{x}_{j,min}\right)$$
(1)

where \({x}_{j,min}\) and \({x}_{j,max}\) are the minimum value and maximum value of the j-th independent variable, respectively. Thus, a positive and large coefficient will indicate a positive and strong impact on the dependent variable, and vice versa (Yang et al. 2020).

Table 1 The environmental factors involved in the RK and GWRK model
Full size table

In the GWRK model, the concentration value at position p0 can be expressed as the sum of the trend and residual, as shown in the following equation:

$$\left\{\begin{array}{c}{\widehat{z}}_{GWRK}\left({\varvec{p}}_{0}\right)={\widehat{z}}_{GWR}\left({\varvec{p}}_{0}\right)+{\widehat{\epsilon }}_{OK}\left({\varvec{p}}_{0}\right) \\ {\widehat{z}}_{GWR}\left({\varvec{p}}_{0}\right)={\beta }_{0}\left({\varvec{p}}_{0}\right)+\sum _{j=1}^{n}{\beta }_{j}\left({\varvec{p}}_{0}\right){x}_{j}\left({\varvec{p}}_{0}\right)\end{array}\right.$$
(2)

where \({\widehat{z}}_{GWRK}\left({\varvec{p}}_{0}\right)\) is the estimated value at position p0 obtained by the GWRK model, \({\widehat{z}}_{GWR}\left({\varvec{p}}_{0}\right)\) is the trend value at position p0 fitted using the GWR model, and \({\widehat{\epsilon }}_{OK}\left({\varvec{p}}_{0}\right)\) is the residual value at position p0 interpolated with the OK method. Specifically, the trend value \({\widehat{z}}_{GWR}\left({\varvec{p}}_{0}\right)\) was obtained with the GWR model.

In the RK method, the concentration value at position p0 is obtained by the following equation:

$${\widehat{z}}_{RK}\left({\varvec{p}}_{0}\right)={\widehat{z}}_{MLR}\left({\varvec{p}}_{0}\right)+{\widehat{\epsilon }}_{OK}\left({\varvec{p}}_{0}\right)$$
(3)

where \({\widehat{z}}_{RK}\left({\varvec{p}}_{0}\right)\) is the estimated concentration of soil heavy metals at location p0, \({\widehat{z}}_{MLR}\left({\varvec{p}}_{0}\right)\) is the fitted trend value of soil heavy metals at location p0 using a multiple linear regression model, and \({\widehat{\epsilon }}_{OK}\left({\varvec{p}}_{0}\right)\) is the residual value interpolated with the OK method.

With the validation sampling points, using the three quantitative measures computed from the pairs of estimated-observed soil heavy metals: the Pearson correlation coefficient (r), the mean error [ME, see Eq. (4)], and the mean absolute error [MAE, see Eq. (5)], the performance of GWRK was compared with the OK and RK methods.

$${ME}_{T}=\frac{1}{n}\sum _{i=1}^{n}\left[z\left({p}_{i}\right)-{\widehat{z}}_{T}\left({p}_{i}\right)\right]$$
(4)
$${MAE}_{T}=\frac{1}{n}\sum _{i=1}^{n}|z\left({p}_{i}\right)-{\widehat{z}}_{T}\left({p}_{i}\right)|$$
(5)

In Eqs. (4) and (5), \(z\left({p}_{i}\right)\) is the measured value of soil heavy metals at location \({p}_{i}\), and \({\widehat{z}}_{T}\left({p}_{i}\right)\) is the predicted value using the T (OK, RK, or GWRK) method. In addition, the quantitative indicator of relative improvement in MAE (Sumfleth and Duttmann, 2008) was employed to quantify the improvement in the prediction precision of one method relative to the other using the following equation:

$${RI}_{b/a}=\frac{{MAE}_{a}-{MAE}_{b}}{{MAE}_{a}}\times 100\%$$
(6)

where \({MAE}_{a}\) and \({MAE}_{b}\) are the MAE values of methods a and b, respectively. When the \({RI}_{b/a}\) value is positive, it indicates that the b-method is more accurate than the a-method; when the \({RI}_{b/a}\) value is negative, it indicates that the b-method’s prediction accuracy is lower than that of the a-method.

figure a

In addition, to quantitatively measure the smoothness effect of the spatial distribution, a smoothing index (SI) on the m-scale is defined as the mean value of the difference between the value of one grid and the values of its surrounding grids (see equation (7) and the diagram next to the equation).

$${SI}_{m}=\stackrel{-}{\sum _{i,j}\frac{\left|{z}_{i,j}-{z}_{i+1,j}\right|+\left|{z}_{i,j}-{z}_{i-1,j}\right|+\dots +\left|{z}_{i,j}-{z}_{i-1,j-1}\right|}{8\times {z}_{i,j}}}$$
(7)

where m is the grid size and \({z}_{i,j}\) is the predicted value of grid (i, j). The smaller the SIm is, the smoother it is on the m-scale. Similarly, after rasterizing the training points, the SI values at multiple scales based on the sample points can be calculated.

Results and Discussion

The histogram and summary statistical results of the training sampling points for Pb are shown in Fig. S2. According to the comparisons of the mean value of Pb and its background values (26.7 mg/kg, CNEMC 1990), the soils in the study area were seriously polluted by Pb. Meanwhile, the Coefficient of variation (CV) value of Pb is 0.95, indicating intense spatial variability and serious effects of human activities.

The Pearson correlation coefficients between the soil Pb and the standardized 11 environmental factors are listed in Table S1. Pb is significantly negatively correlated with the DtoMine (X8); that is, in general, the closer to the mines or smelters are, the higher the concentrations of Pb are in the soils, indicating that mines and mineral smelters are the main sources of Pb pollution in the soils of the study area. In addition, the soil CEC (X6) also exhibited a significant negative correlation with Pb. CEC, reflecting the amount of soil negative charge, can regulate Pb bioavailability by cation exchange for H+ on the micelle surface. High CEC will increase the activity of heavy metal ions and then reduce the concentration of heavy metal in soil (Zheng et al. 2020). Meanwhile, there are also significant or extremely significant correlations among the environmental factors themselves, such as elevation with pH, SOC, soil thickness, CEC, DtoResident, DtoRoad and DtoFactory; pH with soil thickness, CEC, DtoFarmland, DtoMine, and DtoResident; and SOC with soil thickness, DtoResident, and DtoFactory.

According to the Kolmogorov–Smirnov (K–S) values (see Fig. 2) obtained from the original data, the original Pb data in soils were not statistically normal. However, the logarithmically transformed data for Pb obtained a normal distribution. Thus, the logarithmically transformed training data were used in the following OK spatial interpolation. The experimental variogram and its fitted theoretical model for soil Pb are shown in Figure S3 (a) and Table S2. Based on the fitted theoretical model and the training soil samples, the spatial distribution generated by the OK method is shown in Fig. 2a.

Fig. 2
figure 2

Spatial distributions of soil Pb obtained by OK (a), RK (b) and GWRK (c)

Full size image

The 11 environmental factors mentioned in section  environmental factors were used as independent variables to fit the MLR in the RK method using stepwise regression, which can eliminate the independent variables that cause multicollinearity. As shown in Table S3, for Pb, only DtoMine (X8) was included in the global regression model and had a negative regression coefficient, once again indicating that mines and mineral smelters might be the main sources of soil Pb in the study area. The experimental variogram and its fitted theoretical models for the soil Pb residuals from the global multiple linear regression model are shown in Fig. S3 (b) and Table S2. The spatial distribution map generated by the RK method is shown in Fig. 2b.

All environmental factors were used as independent variables to fit the GWR model for the soil Pb with the help of GWR4.0 software. The optimal kernel size was determined through an interactive statistical optimization process to minimize the AIC. Summary statistics of the coefficients of the environmental variables in the GWR model are shown in Table S4. According to the absolute values of the mean regression coefficients, the spatial distribution of Pb was mainly affected by elevation (X1), soil thickness (X5), CEC (X6), and DtoMine (X8). The Moran’s I values ranged from 0.63 to 0.98, indicating significant spatial autocorrelation in those regression coefficients. In addition to providing estimates of spatially varying regression coefficients, the GWR4.0 software also provides several statistical tests to determine whether the GWR model is more useful than the global MLR model. As shown in Table S5, the results of the statistical tests show that the RSS and AIC values for the GWR are far lower than those for MLR, indicating that the local model provides a better fit than the global model. Meanwhile, the R2 generated by the GWR is much higher than that generated by the stepwise regression model (see the last column in Table S3) and by the global MLR model (see Table S5), meaning that GWR exhibits a large improvement in the explained variance of the dependent variable. The experimental variogram and its fitted theoretical model for the residuals from the GWR model are shown in Fig. S3c and Table S1. The spatial distribution map generated by the GWRK method is shown in Fig. 2c.

As shown in Fig. 2, the results obtained by OK, RK and GWRK have similar spatial distribution trends. The high Pb concentrations were mainly distributed in the eastern and northern parts of the study area, where mines and mineral smelters are concentrated. Thus, as mentioned in the above sections, mining activities could be determined as the main source of Pb in the soil of the study area. Then, the results obtained by OK, RK and GWRK are compared in terms of spatial smoothness, variability and interpolation accuracy.

As shown in Fig. 2, intuitively, the GWRK polygons were more fragmented than those of OK and RK. To quantitatively measure the smoothness effect of the spatial distribution for different methods, the SIs on multi-scales were calculated based on results generated by different methods. As shown in Fig. 3a, the overall trend of the SI values increases with increasing grid size, indicating that with increasing spatial scale, the difference in Pb in nearby soils increases. In addition, the SI values of the OK method at all scales were much lower than those of the RK and GWRK methods, indicating that the OK method has a strong smoothing effect. However, the average SI values of the spatial distributions generated by RK and GWRK were close to those of the original soil samples (see the data recorded in the brackets in Fig. 3a), showing that the RK and GWRK methods can maintain the variability of heavy metals in neighboring soils. Specifically, when the scale was less than 1600 m, the SI values of the spatial distributions generated by GWRK were greater than those of the spatial distributions generated by RK, resulting in the GWRK polygons being more fragmented than those of RK. That is, on small scales, the spatial distribution obtained by RK was smoother than that obtained by GWRK. This difference might be because in the RK method, only one environmental factor was selected into the linear regression model due to global collinearity, while in the GWR method, all environmental factors were involved in the regression model. Meanwhile, the mean SI values of RK, GWRK and the original sampling points are 0.68, 0.64, and 0.57, respectively, showing that the spatial smoothness of the GWRK method is closer to that of the original sampling points than the RK method.

Fig. 3
figure 3

a The smoothness index at multiple scales for the soil Pb (the number in brackets is the mean value of the smoothness index obtained by the corresponding method), and b Experimental variogram of log-transformed original soil samples and spatial distributions obtained by OK, RK, and GWRK for soil Pb

Full size image

The spatial points were obtained based on the spatial distribution grid data generated by the OK, RK and GWRK methods. Then, based on the logarithmically transformed data, the experimental variograms of different lag distances were calculated. As shown in Fig. 3b, the spatial distribution generated by the OK method had the smallest variogram values, indicating that the OK method reduced the spatial variability. Furthermore, the variogram values of the spatial distributions generated by the GWRK method were larger than those generated by the RK method and closer to those obtained based on the original sampling points. Thus, GWRK could better maintain the spatial variability of soil heavy metals than OK and RK.

To assess the performances of OK, RK and GWRK, 40 validation soil samples were used to test the spatial interpolation accuracies of the three methods. The comparison results are shown in Table 2. The results of OK prediction show the poorest spatial interpolation because it has the largest bias (ME value), the largest error (RMSE), and the smallest correlation relationship with the observed validation soil samples. Conversely, GWRK has the smallest ME and RMSE values and the largest r values, indicating that the spatial interpolation accuracy of GWRK is higher than those of OK and RK. Specifically, according to the RI values, compared to the OK method, RK and GWRK improved the accuracies by 39% and 55%, respectively.

Table 2 Comparison of the spatial interpolation accuracies of OK, RK and GWRK
Full size table

Conclusions

The relationships between soil heavy metals and environmental factors are related to their spatial variations, and the limitation of the global regression model is that it assumes that the relationships are uniform or stationary throughout the whole study region. Thus, in this study, the GWRK approach, composed of the GWR and kriging model, was used to estimate the soil heavy metal Pb in Daye city. The 11 environmental factors in three categories that might affect the spatial distribution of soil Pb were selected for the study case. Two common geostatistical methods (OK and RK) were also used to generate the spatial distributions of soil Pb and compared with the GWRK results in this study.

First, according to the SI values at multiple scales, the GWRK result was more consistent with the original data in terms of spatial smoothness. Second, according to the results of the experimental variogram of different lag distances, GWRK could maintain the spatial variability of the original sampling points better than OK and RK. Third, the GWRK approach yielded the minimum spatial interpolation error compared to those estimated from the OK and RK methods. Thus, in this case, GWRK generated the most reasonable spatial distribution pattern and higher accuracy results than OK and RK. The reasons may be as follows: (1) The study area in this case is a mining and metallurgy city, and heavy metals in soils are seriously affected by human activities (mining activities in this case). Thus, the spatial variability of soil heavy metals was too complex to characterize using one variogram model, which led to low interpolation accuracy in the OK method. (2) Compared with global MLR, the advantage of the GWR model is to describe the spatially varying relationships between the dependent variable and independent variables. In this case, GWR provided a better fit between soil Pb and environmental factors than the global MLR model (lower RSS and AIC, along with higher R2), resulting in a higher spatial interpolation accuracy and more reasonable spatial distribution pattern of GWRK than those of RK.