Super-Resolution of Positive Sources on an Arbitrarily Fine Grid

Abstract

In super-resolution it is necessary to locate with high precision point sources from noisy observations of the spectrum of the signal at low frequencies capped by $f_{\mathrm {lo}}$. In the case when the point sources are positive and are located on a grid, it has been recently established that the super-resolution problem can be solved via linear programming in a stable manner and that the method is nearly optimal in the minimax sense. The quality of the reconstruction critically depends on the Rayleigh regularity of the support of the signal; that is, on the maximum number of sources that can occur within an interval of side length about $1/f_{\mathrm {lo}}$. This work extends the earlier result and shows that the conclusion continues to hold when the locations of the point sources are arbitrary, i.e., the grid is arbitrarily fine. The proof relies on new interpolation constructions in Fourier analysis.

1 Introduction

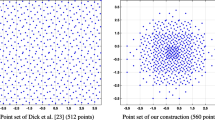
The super-resolution problem of positive sources (see Fig. 1) consists of recovering a high-frequency signal

$$\begin{aligned} x(w) = \sum _i x_i \delta (w - w_i) \end{aligned}$$

(1)

consisting of positive point sources (spikes, for short) located at unknown positions $w_i\in [0, 1)$ and of unknown intensity $x_i>0$; $\delta (\cdot )$ is the Dirac delta function. The signal is observed through a convolution measurement of the form

$$\begin{aligned} s(v) = \int k_{\mathrm {lo}}(v - w) x(w)d w + z(v), \end{aligned}$$

(2)

where $k_{\mathrm {lo}}(\cdot )$ is a low-frequency kernel that erases the high-frequency components of the signal and $z(\cdot )$ is noise.

Fig. 1

Microscope as a low-pass filter: signal in a and convolution measurement in b (Color figure online)

This problem arises in single-molecule super-resolution microscopy [7, 22, 33]. In this application, $w_i$’s encode the unknown locations of fluorescent molecules, $x_i$ is proportional to the number of photons emitted by the ith molecule during the observation time. Crucially, the number of photons is a nonnegative number, leading to the assumption $x_i>0$, which makes the problem much simpler. Assume that light of wavelength $\lambda _{\mathrm {lo}}$ is emitted by the molecules. Due to diffraction of light, the high-frequency spatial details of the signal are destroyed, no matter how perfect or large the microscope is. At the detector we record a blurred version of the signal, no details smaller than about $\lambda _{\mathrm {lo}}$ are visible. To restate this mathematically: the function $k_{\mathrm {lo}}(\cdot )$ models the (PSF) of the microscope; due to diffraction of light the PSF is band-limited to $f_{\mathrm {lo}}\triangleq 1 /\lambda _{\mathrm {lo}}$. The noise z(v) represents all sources of noise in the system. For example, the thermal noise at the detector, the Poisson quantum mechanical noise due to photon quantization in low-intensity imaging, and the noise originating from the imperfect knowledge of the PSF in the optical system. We refer the interested reader to [43], where the connection to super-resolution microscopy is worked out in details.

1.1 Discrete Model

In the earlier work [43] a discrete analog of the model in (1) and (2) has been considered. The signal is modeled by a discrete vector ${\mathbf {x}}= [x_0\ldots x_{N-1}]^{{\mathsf {T}}}\in {\mathbb {R}}^N$, where $N$ is the number of elements in the grid, corresponding to partitioning the interval $w_i\in [0, 1)$ into $N$ equispaced segments. Each nonzero element in ${\mathbf {x}}$ corresponds to one spike in (1). The PSF is modeled by matrix ${\mathbf {Q}}$ that implements an ideal low-pass filter in the sense that it has a flat spectrum with a sharp cut-off at $f_{\mathrm {lo}}$. Formally,

$$\begin{aligned} {\mathbf {Q}}= {\mathbf {F}}^{{\mathsf {H}}}{\hat{{\mathbf {Q}}}} {\mathbf {F}}, \end{aligned}$$

(3)

where ${\mathbf {F}}$ is the $N\times N$ discrete Fourier transform matrix

$$\begin{aligned}{}[{\mathbf {F}}]_{k,l} = \frac{1}{\sqrt{N}}e^{-\mathrm {i} 2\pi kl/N} \end{aligned}$$

and ${\hat{{\mathbf {Q}}}}={{\,\mathrm{diag}\,}}([{\hat{Q}}_{-N/2+1}\ldots {\hat{Q}}_{N/2}]^{{\mathsf {T}}})$ with

$$\begin{aligned} {\hat{Q}}_k = {\left\{ \begin{array}{ll} 1,&{}k=-f_{\mathrm {lo}},\ldots , f_{\mathrm {lo}},\\ 0,&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(4)

The wavelength $\lambda _{\mathrm {lo}}=1/f_{\mathrm {lo}}$ gives the width of the convolution kernel represented by ${\mathbf {Q}}$. This kernel is called the Dirichlet kernel. We assume throughout the paper that $N$ is even for simplicity.

Translated to discrete setting the model in (2) becomes

$$\begin{aligned} {\mathbf {s}}= {\mathbf {Q}}{\mathbf {x}}+ {\mathbf {z}}. \end{aligned}$$

(5)

1.2 Recovery Algorithm

Our recovery method from the observations ${\mathbf {s}}$ in (5) is extremely simple: solve

In other words, we are looking for a set of positive spikes such that the mismatch in received intensities is minimum. Note that this method does not make use of any knowledge other than the observations ${\mathbf {s}}$ and the PSF ${\mathbf {Q}}$. Furthermore, (CVX) is a simple convex optimization program, which can be recast as a linear program since both ${\mathbf {x}}$ and ${\mathbf {Q}}$ are real valued.

1.3 Rayleigh Regularity

Consider the discrete signal ${\mathbf {x}}\in {\mathbb {R}}^{N}$ as samples on the grid $\{0,1/N,\ldots ,1-1/N\}\subset {\mathbb {T}}$, where ${\mathbb {T}}$ is the circle in 1D, i.e., the interval [0, 1) with 0 and 1 identified. For $a, b\in {\mathbb {T}}$, the wrap-around distance between a and b is $\mathchoice{{\left|b-a\right|}}{{\bigl |b-a\bigr |}}{{\left|b-a\right|}}{{\left|b-a\right|}}\triangleq \min (b-a \mod 1,\ a-b \mod 1)$; for an interval $[a, b]\subset {\mathbb {T}}$, its wrap-around length is $\mathchoice{{\left|b-a\right|}}{{\bigl |b-a\bigr |}}{{\left|b-a\right|}}{{\left|b-a\right|}}$.

We introduce a definition of Rayleigh regularity inspired by [23, Def. 1]. Let $\mathrm {supp}({\mathbf {x}}) \triangleq \{l/N: x_l>0\}$ denote the support of the discrete signal. As we shall see, our ability to super-resolve the signal ${\mathbf {x}}$, will be fundamentally determined by how regular $\mathrm {supp}({\mathbf {x}})$ is in the following sense.

Definition 1

(Rayleigh regularity) We say that the set of points ${\mathcal {V}}\subset {\mathbb {T}}$ is Rayleigh-regular with parameters $(d,r)$ and write ${\mathcal {V}}\in {\mathcal {R}}(d,r)$ if it may be partitioned as ${\mathcal {V}}={\mathcal {V}}_1\cup \cdots \cup {\mathcal {V}}_r$, where the ${\mathcal {V}}_i$’s are disjoint, and each obeys a separation constraint:

• 1. for all $1\le i<j\le r$, ${\mathcal {V}}_i\cap {\mathcal {V}}_j=\varnothing$;

• 2. for all intervals ${\mathcal {D}}\subset {\mathbb {T}}$ of wrap-around length $\mathchoice{{\left|{\mathcal {D}}\right|}}{{\bigl |{\mathcal {D}}\bigr |}}{{\left|{\mathcal {D}}\right|}}{{\left|{\mathcal {D}}\right|}} = d$ and all i,

  $$\begin{aligned} \mathchoice{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}{{\bigl |{\mathcal {V}}_i\cap {\mathcal {D}}\bigr |}}{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}\le 1, \end{aligned}$$

  where $\mathchoice{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}{{\bigl |{\mathcal {V}}_i\cap {\mathcal {D}}\bigr |}}{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}{{\left|{\mathcal {V}}_i\cap {\mathcal {D}}\right|}}$ denotes the cardinality of the set ${\mathcal {V}}_i\cap {\mathcal {D}}$.

In this paper we are interested in super-resolving signals with Rayleigh-regular support: $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(d,r)$. Such signals are illustrated in Fig. 2.

As we will discuss, in the special case when $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}({{\tilde{c}}}\lambda _{\mathrm {lo}},1)$ [i.e., when $r=1$] with ${{\tilde{c}}}$ a bit larger than one (as in Fig. 2a), the super-resolution problem is particularly easy. In this case we will say that the spikes in ${\mathbf {x}}$ are well-separated.

Fig. 2

Examples of discrete $N$ dimensional signals whose support belongs to the Rayleigh classes ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ in a, ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$ in b and in c, ${\mathcal {R}}(6\lambda _{\mathrm {lo}},3)$ in d depicted on the grid $\{0,1/N,\ldots ,1-1/N\}\subset {\mathbb {T}}$. Note that the signals in b and in c both have support in ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$. In general, Rayleigh regularity does not require that all spikes in the signal are arranged into separated clusters as is the case in b and in d. The sine wave $\sin (2\pi f_{\mathrm {lo}}t)$ at the highest visible frequency is shown by the dotted line for reference. Here, $N=120$ and $f_{\mathrm {lo}}=14$, so that $\lambda _{\mathrm {lo}}=1/14$. By periodicity, the endpoints are identified (Color figure online)

1.4 Discrete Stability Estimates

The main result of the earlier work [43] is the following proposition.

Proposition 1

Assume ${\mathbf {x}}\ge {\mathbf {0}}$ and $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,r)$ with $\kappa \triangleq 1.87$ and $f_{\mathrm {lo}}\ge 128r$. Assume that the observations ${\mathbf {s}}$ are given by (5). Then the solution ${\hat{{\mathbf {x}}}}$ to ($\mathrm {CVX}$) obeys

$$\begin{aligned} \underbrace{\Vert {\hat{{\mathbf {x}}}}-{\mathbf {x}}\Vert _1}_\mathrm {Error} \le C_d(r) \cdot \left( \frac{N}{f_{\mathrm {lo}}}\right) ^{2r} \cdot \Vert {\mathbf {z}}\Vert _1 = C_d(r) \cdot \mathrm {DSRF}^{2 r} \cdot \Vert {\mathbf {z}}\Vert _1, \end{aligned}$$

(6)

where $C_d(r)$ only depends on $r$ (if $\mathrm {DSRF}\ge 3.03/r$, it can be taken to be $C_d(r)= r^{2r}\cdot 4 \cdot 17^r$).

The ratio $\mathrm {DSRF}\triangleq N/f_{\mathrm {lo}}$ is called the discrete super-resolution factor; this is the ratio between the scale at which we observe the data, $1/f_{\mathrm {lo}}$, and the scale of the finest details in the data, $1/N$.

1.5 Breakdown of Discrete Stability Estimates

In practice, signals do not belong to a discrete grid. In order to accurately approximate the continuous model in (1) we might need to make the grid very fine, i.e., take $N$ large.

The problem is that the theoretical result in (6) becomes meaningless when $f_{\mathrm {lo}}$ and $\Vert {\mathbf {z}}\Vert _1$ remain fixed, and $N\rightarrow \infty$. Indeed, observe that (6) guarantees accurate signal recovery when the right-hand side of (6) is much smaller than $\Vert {\mathbf {x}}\Vert _1$. When $N\rightarrow \infty$ with $f_{\mathrm {lo}}$ fixed, then $\mathrm {DSRF}^{2 r}\rightarrow \infty$ very quickly, so that the right-hand side of (6) becomes larger than $\Vert {\mathbf {x}}\Vert _1$, even for very small noise.

Fig. 3

Measuring the estimation error when the grid is very fine ($N$ is large) (Color figure online)

This is expected. Consider the hypothetical situation illustrated in Fig. 3. The true signal ${\mathbf {x}}$ consists of three spikes as depicted in Fig. 3a in solid purple. The grid is very fine ($N$ is large); the PSF is wide as shown in Fig. 3b (the solid purple curve, with characteristic width $\lambda _{\mathrm {lo}}$, represents ${\mathbf {s}}={\mathbf {Q}}{\mathbf {x}}+{\mathbf {z}}$ with ${\mathbf {x}}$ from Fig. 3a); and the data is noisy. Imagine an algorithm produced an estimate ${\hat{{\mathbf {x}}}}_{\mathrm {good}}$ as depicted in Fig. 3c by the dashed blue spikes. The estimate ${\hat{{\mathbf {x}}}}_{\mathrm {good}}$ is excellent: the dashed blue spikes are located in the neighboring discrete bins to the corresponding solid purple ground truth spikes, the magnitudes are estimated perfectly. In the presence of noise we cannot hope for infinite resolution, so for large $N$, we should be happy if we were able to obtain ${\hat{{\mathbf {x}}}}_{\mathrm {good}}$ as in Fig. 3c. Yet,

$$\begin{aligned} \Vert {\hat{{\mathbf {x}}}}_{\mathrm {good}}-{\mathbf {x}}\Vert _1 = 2 \Vert {\mathbf {x}}\Vert _1, \end{aligned}$$

i.e., the estimation error is about as large as it can possibly be. We conclude that the reason why the result in (6) becomes meaningless when $f_{\mathrm {lo}}$ and $\Vert {\mathbf {z}}\Vert _1$ remain fixed and $N\rightarrow \infty$ is that the error metric $\Vert {\hat{{\mathbf {x}}}}-{\mathbf {x}}\Vert _1$ becomes inadequate. We need a more forgiving error metric that should penalize small localization errors on the fine grid mildly.

We will explain in Sect. 2 how to construct the more forgiving error metric and how to change the definition of super-resolution factor accordingly. With these modifications we can generalize Proposition 1 and formulate the stability estimates in Theorem 1 that remain meaningful even when $N\rightarrow \infty$ and $f_{\mathrm {lo}}$ and $\Vert {\mathbf {z}}\Vert _1$ are fixed. With the appropriate new definitions, the result in Theorem 1 is nearly identical to that in Proposition 1. Surprisingly, the proof technique necessary to obtain Theorem 1 is much harder than the trick that was sufficient to prove Proposition 1. The proof relies on new trigonometric interpolation constructions that constitute the main mathematical contribution of this paper.

2 Main Results

2.1 Measuring the Reconstruction Error

To avoid penalizing the estimators that produce spikes very close to the original spikes on the fine grid, a natural approach is to convolve the difference ${\hat{{\mathbf {x}}}}-{\mathbf {x}}$ with a nonnegative kernel $k_{\mathrm {hi}}(\cdot )$ of width $\lambda _{\mathrm {hi}}$ (represented by the dotted green line in Fig. 3b) before computing the $\ell _1$ norm:

$$\begin{aligned} \text {error}=\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}- {\mathbf {x}})\Vert _1, \end{aligned}$$

where

$$\begin{aligned} \left[ k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\right] _n \triangleq \sum _{m=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m \end{aligned}$$

and ${\mathbf {h}}= [h_0, h_1, \ldots , h_{N-1}]^{{\mathsf {T}}} \triangleq {\hat{{\mathbf {x}}}}-{\mathbf {x}}$ is the difference vector. The new error metric is illustrated in Fig. 3c–f. When the estimated spikes are closer than $\lambda _{\mathrm {hi}}$ to the original spikes, as is the case for ${\hat{{\mathbf {x}}}}={\hat{{\mathbf {x}}}}_{\mathrm {good}}$ in Fig. 3c, the error, represented by the area of the shaded region in Fig. 3e, is very small. Conversely, when the estimated spikes are further than $\lambda _{\mathrm {hi}}$ from the original spikes, as is the case for ${\hat{{\mathbf {x}}}}={\hat{{\mathbf {x}}}}_{\mathrm {bad}}$ in Fig. 3d, we have, $\text {error}=\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1\approx 2\Vert {\mathbf {x}}\Vert _1$, so that the error is large, as illustrated in Fig. 3f.

The width, $\lambda _{\mathrm {hi}}$, of the kernel $k_{\mathrm {hi}}(\cdot )$ is a parameter of the theory. This parameter will be chosen to be (i) larger (or equal to) the finest scale of the data, $\lambda _{\mathrm {hi}}\ge 1/N$, and, simultaneously, (ii) smaller than the native resolution of the observations, $\lambda _{\mathrm {hi}}< \lambda _{\mathrm {lo}}$. Having chosen $\lambda _{\mathrm {hi}}$, we define the super-resolution factor as:

$$\begin{aligned} \mathrm {SRF}\triangleq \frac{\lambda _{\mathrm {lo}}}{\lambda _{\mathrm {hi}}}. \end{aligned}$$

The $\mathrm {SRF}$ will play the same role in our theory as the $\mathrm {DSRF}$ played in Proposition 1. In Fig. 3b, the $\mathrm {SRF}$ is the ratio between $\lambda _{\mathrm {lo}}$, the width of the kernel ${\mathbf {Q}}$, and $\lambda _{\mathrm {hi}}$, the width of the kernel $k_{\mathrm {hi}}(\cdot )$.

To be concrete, a reasonable situation might be: $\lambda _{\mathrm {lo}}= 1/10$, $1/N= 1/1000$ so that $\mathrm {DSRF}= 100$. This makes the right-hand side of (6) huge so that the stability estimate is useless. Now, choose $\lambda _{\mathrm {hi}}=1/100$ so that $\mathrm {SRF}=10$, which is much smaller than $\mathrm {DSRF}$. The main result of this paper, Theorem 1 below, shows that we can upper-bound the error $\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1$ in terms of $\mathrm {SRF}^{2r}$, which is much smaller than $\mathrm {DSRF}^{2r}$, keeping the bound tight for realistic values of the noise.

For $k_{\mathrm {hi}}(\cdot )$, in this paper we use the Fejér kernel:

$$\begin{aligned} k_{\mathrm {hi}}(t) \triangleq \frac{1}{N}\frac{1}{f_{\mathrm {hi}}+1} \left( \frac{\sin (\pi (f_{\mathrm {hi}}+1) t)}{\sin (\pi t)}\right) ^2,\quad f_{\mathrm {hi}}= 1/\lambda _{\mathrm {hi}}. \end{aligned}$$

(7)

The normalization is such that

$$\begin{aligned} \sum _{n=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n}{N}\right) = 1, \end{aligned}$$

(8)

which ensures that the “energy” in the error is preserved in the sense that $\text {error}=\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1\approx 2\Vert {\mathbf {x}}\Vert _1$ whenever the estimated spikes in ${\hat{{\mathbf {x}}}}$ are far away from the true spikes in ${\mathbf {x}}$. The concrete form of the kernel $k_{\mathrm {hi}}(\cdot )$ is not important. Our results hold for any other periodic nonnegative high-resolution kernel as long as it satisfies conditions (106) and (107) below.

When $N\rightarrow \infty$, the error metric defined here becomes the one used in [12] in the analysis of the continuous super-resolution problem. Compared to [12], the key novelty of this paper is that the results in [12] apply only when the spikes in the signal are well-separated [$\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(1.87\lambda _{\mathrm {lo}},1)$] as in Fig. 2a, a stringent assumption. In this paper we don’t assume that the spikes are well-separated and our results also hold for signals with $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(1.87\lambda _{\mathrm {lo}}r,r)$ and $r>1$ as in Fig. 2b–d. The price we pay is that our results are only valid for nonnegative signals, whereas the results in [12] are valid for complex-valued signals.

2.2 Stability Estimate on an Arbitrarily Fine Grid

In this paper we prove the following theorem.

Theorem 1

Assume ${\mathbf {x}}\ge {\mathbf {0}}$ and $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,r)$ with $\kappa \triangleq 1.87$ and $f_{\mathrm {lo}}\ge 128r$. Assume $\lambda _{\mathrm {hi}}<\lambda _{\mathrm {lo}}$, $\lambda _{\mathrm {hi}}\ge 1/N$, and $\mathrm {SRF}>12$. Assume, in addition, that the elements of $\mathrm {supp}({\mathbf {x}})$ are separated by at least $2\lambda _{\mathrm {hi}}$: if $t,t'\in \mathrm {supp}({\mathbf {x}})$ with $t\ne t'$, then $\mathchoice{{\left|t-t'\right|}}{{\bigl |t-t'\bigr |}}{{\left|t-t'\right|}}{{\left|t-t'\right|}}\ge 2\lambda _{\mathrm {hi}}$, where $\mathchoice{{\left|\cdot \right|}}{{\bigl |\cdot \bigr |}}{{\left|\cdot \right|}}{{\left|\cdot \right|}}$ is the wrap-around distance on ${\mathbb {T}}$. Assume that the observations ${\mathbf {s}}$ are given by (5). Then the solution ${\hat{{\mathbf {x}}}}$ to ($\mathrm {CVX}$) obeys

$$\begin{aligned} \Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1 \le C(r) \mathrm {SRF}^{2r} \Vert {\mathbf {z}}\Vert _1, \end{aligned}$$

(9)

where $C(r)\triangleq r^{2r+4} c^{r+1}$ and the positive numerical constant $c$ is defined in (128) below.

The theorem is proven in Sects. 5, 6, 7 and in the appendices. Before we embark on the proof, we discuss the significance and the accuracy of the result.

2.2.1 Significance of the Result

Theorem 1 gives essentially the same stability estimate for an arbitrarily fine grid as Proposition 1 does for a discrete grid. With the new definition for error metric, $\lambda _{\mathrm {hi}}$ in Theorem 1 plays the same role as the grid segment size, $1/N$, played in Proposition 1. In turn, the grid segment size, $1/N$, in Theorem 1 may be arbitrarily small without affecting the stability estimate at all. The only thing that changes when $N$ grows is that it becomes numerically harder to solve ($\mathrm {CVX}$).

2.2.2 Tightness

The result is information-theoretically tight in the following sense. It is possible to prove a converse theorem (see [43, Sec. 2.3]) that says that the best possible algorithm in the worst case (the minimax setting) cannot achieve stability estimate in (9) with super-resolution factor dependence better than $\mathrm {SRF}^{2r-1}$. In other words, the exponent of $\mathrm {SRF}$ in (9) is near-optimal.

We have made no attempt to optimize $C(r)$. Finding the tightest possible $C(r)$ is an important open problem, which seems to be hard to address with the mathematical techniques developed in this paper.

2.2.3 Mathematical Novelty

The reader might expect that since Theorem 1 is so similar to Proposition 1, the proof of Theorem 1 is a minor modification of the work done in [43]. Perhaps surprisingly, this is not the case.

The proof technique in [43] relied on a simple and elegant trigonometric interpolation construction reviewed in Sect. 6.2. In this paper, in addition, we had to develop a flexible set of techniques that allowed us to build trigonometric polynomials with specific interpolation properties. These techniques—that constitute the main mathematical contribution of this paper—are presented in Sects. 6.3, 6.4, and in Appendix 2 “Proof of Lemma 5”. We believe that the new techniques are interesting in their own right and may be useful in other projects.

2.2.4 Separation by $2\lambda _{\mathrm {hi}}$

Theorem 1 requires the assumption that no two spikes in ${\mathbf {x}}$ are closer than $2\lambda _{\mathrm {hi}}$. It is important to contrast this assumption with the separation assumption in [12, 13]. The results in [13] hold only when no two spikes in ${\mathbf {x}}$ are closer than $1.87\lambda _{\mathrm {lo}}$ (the spikes are well-separated). Our separation requirement is much weaker than the one needed in [12, 13]: we require the separation at the scale of $\lambda _{\mathrm {hi}}$ whereas the results in [12, 13] need separation on the scale of $\lambda _{\mathrm {lo}}$. Since the whole point of super-resolution is to reconstruct the original signal with accuracy about $\lambda _{\mathrm {hi}}\ll \lambda _{\mathrm {lo}}$, our assumption is mild, whereas the assumption in [12, 13] is restrictive.

Further, it follows from the proof of Theorem 1 that the $2\lambda _{\mathrm {hi}}$ separation requirement may be relaxed to, for example, $\lambda _{\mathrm {hi}}/2$, or, more generally, to $\lambda _{\mathrm {hi}}/\beta$ for any $\beta >1$. The result in Theorem 1 will not change, except that the constant $C(r)$ will now depend on $\beta$. Specifically, the result will read:

$$\begin{aligned} \Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1 \le r^{2r+4} c^{r+1} \beta ^{2r} \mathrm {SRF}^{2r} \Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

To keep the proof of Theorem 1 as clean as possible, we decided to stick with the $2\lambda _{\mathrm {hi}}$ separation assumption in the theorem.

Finally, it is not clear if the separation assumption of the form $\lambda _{\mathrm {hi}}/\beta$ is fundamentally necessary. Certainly, it is necessary for the proof technique developed in this paper. It is an open problem to either find a proof of Theorem 1 that does not rely on this assumption, or to prove a converse result showing that this assumption is unavoidable. Note that there is no explicit separation assumption in Proposition 1; however, since the spikes are on the grid, the separation assumption at the scale of $1/N$ is made implicitly.

2.2.5 Density Constant

We next discuss the following question: can the constant $\kappa =1.87$ in Theorem 1 be made smaller without changing the result? The answer is “probably yes”. Specifically, our proof builds upon Lemmas 1 and 2 below. The lemmas generalize [12, Lm. 2.4, Lm. 2.5, Sec. 2.5] and their proof exploits a construction developed in [13]. The specific value for $\kappa =1.87$ comes from the construction borrowed from [13]. An improved construction has recently been reported in [28] leading to a smaller value $\kappa =1.26$. To keep this paper as simple as possible, we decided not to accommodate this improvement. To do so, one would need to change Lemmas 1 and 2 below and the proof of Lemma 2 in Appendix 1 all other derivations in this paper will remain unchanged. The constant $C(r)$ in Theorem 1 would need to be updated accordingly.

We expect that there is a trade-off: the larger $\kappa$ is, the smaller the constant $C(r)$ can be made. However, our estimates do not provide the smallest possible constant. Hence, we cannot analyze the trade-off.

Finally, as explained in [43, Sec. 2.3.1], $\kappa >1$ is a fundamental limit, so our result is within the factor 1.87 from the optimum.

2.2.6 Gridless Super-Resolution

It has been shown in [8, 12, 13] that under the assumption that spikes are separated by at least $1.87\lambda _{\mathrm {lo}}$ (well-separated spikes), one can solve the gridless super-resolution problem in which the spikes have completely arbitrary locations on ${\mathbb {T}}$ (no need for the $1/N$ discretization). It turns out that in the gridless setup one needs to solve an infinite-dimensional, but convex, total-variation-minimization problem (see [13, eq. (1.4)]). Surprisingly, if one works in the dual domain and uses the idea of lifting, the equivalent problem becomes finite-dimensional and, therefore, may be solved on the computer. The solution to the original problem may then be reconstructed by duality. This approach is explained in [13, Sec. 4].

The approach, by now standard, may be carried over to the problem considered in this paper, where we work with a nonnegative signal ${\mathbf {x}}$ and the spikes need not be well-separated. The same trigonometric polynomials that certify optimality of ($\mathrm {CVX}$) and lead to Theorem 1 may also be used to prove stability of the corresponding gridless algorithm.

The reason why we chose to focus on the arbitrarily fine grid and not to discuss the gridless problem in details is the following practical consideration. In applications, for example in super-resolution microscopy, there is no real difference between the gridless problem and the problem with a very fine grid. The real sources have some finite nonzero size, perhaps small. Therefore, in practice, one has a choice between solving ($\mathrm {CVX}$) on a sufficiently fine grid or solving the infinite-dimensional total-variation-minimization problem via lifting. To solve ($\mathrm {CVX}$) with $N$ variables efficiently, one would use a first-order solver whose complexity is dominated by repeated multiplications by ${\mathbf {Q}}$, ${\mathbf {Q}}^{{\mathsf {T}}}$. Using (3) one would implement ${\mathbf {Q}}$ via the fast Fourier transform so that each matrix multiplication takes ${\mathcal {O}}(N\log N+ f_{\mathrm {lo}})$ multiplications. The gridless approach via lifting, in its standard implementation, requires one to solve a semidefinite convex optimization problem (see [13, eq. (4.3)]) with ${\mathcal {O}}(f_{\mathrm {lo}}^2)$ variables. The complexity of the gridless approach does not depend on $N$ at all, a very nice property. However, the necessity to deal with a semidefinite problem with ${\mathcal {O}}(f_{\mathrm {lo}}^2)$ variables make it more costly than solving ($\mathrm {CVX}$) on a sufficiently fine grid, for example, in the important applications in super-resolution microscopy. Having said this, recently very interesting new approaches to solve the gridless problem much faster have been developed. One idea is to construct a solver for the semidefinite problem that directly leverages the structure of the problem [15], another idea is to construct primal Frank-Wolfe based solvers with heuristics [10, 20, 29]. It would be interesting to see a rigorous study comparing the fine grid methods with the gridless methods in applied super-resolution microscopy problems. We refer to [20, Sec. 5] for fascinating work in this direction.

2.2.7 General PSFs

The sharp rectangular frequency cut-off of ${\mathbf {Q}}$ in (4) corresponds to the Dirichlet PSF $k_{\mathrm {lo}}(\cdot )$ in (2). The Dirichlet kernel takes negative values (as shown in Fig. 3b in solid purple), whereas all PSFs in microscopy take nonnegative values (as shown in Fig. 1). The simplest PSF that takes nonnegative values is the Fejèr kernel. The spectrum of ${\mathbf {Q}}$ that corresponds to the Fejèr kernel has a triangular decay of ${\hat{q}}_k$ in (4) as in [43, eq. 13] and in (196). The results for the rectangular spectrum can be translated into the results for the triangular spectrum (in fact for the spectrum of any reasonable shape) using the idea of spectrum equalization. We refer the reader to [43] for a detailed explanation on how this can be done. In this paper we focus on the basic case in (4) only.

2.2.8 The Use of $\ell _1$-norm in Stability Estimates

A careful reader may ask why do we use the $\ell _1$-norm in (9) and not the more usual $\ell _2$-norm. Interestingly, as explained in [43, Sect. 1.1], in super-resolution microscopy $\Vert {\mathbf {x}}\Vert _1$, and not $\Vert {\mathbf {x}}\Vert _2$, has the meaning of cumulative emitted intensity or the total energy of light emitted per second. Therefore, $\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1$ is a natural choice as it corresponds to the error (at high resolution) in cumulative emitted intensity, exactly the quantity one would like to minimize in microscopy.

The other reason for the choice of the $\ell _1$-norm is mathematical feasibility. It would be interesting to obtain similar bounds for the $\ell _2$-norm as this might be relevant for some applications. However, the dual certificates (see below) required to obtain such bounds need to have completely different properties, and, hence, new mathematical constructions seem to be necessary for such an extension.

3 Literature Review and Innovations

3.1 Prior Art

Prony’s method Prony’s method [46] is an algebraic approach for solving the gridless super-resolution problem from noiseless data when the number of spikes is known a priori. The observations ${\mathbf {s}}$ are used to form a trigonometric polynomial, whose roots coincide with the spike locations. The trigonometric polynomial is then factored, thus revealing those locations, and the amplitudes estimated by solving a system of linear equations. In the noiseless case, Prony’s method recovers ${\mathbf {x}}$ perfectly provided that $\Vert {\mathbf {x}}\Vert _0\le f_{\mathrm {lo}}$. Here and below, $\Vert \cdot \Vert _0$ is the pseudo-norm that denotes the number of nonzero elements in a vector. No further Rayleigh regularity assumption on the signal support is needed. With noise, however, the performance of Prony’s method degrades sharply. The difficulty comes from the fact that the roots of a trigonometric polynomial constructed by an algebraic method can shift dramatically even with small changes in the data. See [6] for quantitative analysis showing that Prony’s method is very sensitive to noise. Therefore, a crucial problem is to find a method for solving the super-resolution problem in the presence of noise whose performance decays gracefully with the amount of noise.

Fundamental limits In the pioneering work [23], Donoho studied limits of performance for the super-resolution problem and recognized the importance of Rayleigh regularity as the fundamental property that determines how easy it is to super-resolve the signal. He analyzed an intractable exhaustive search algorithm and demonstrated that assuming $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(2\lambda _{\mathrm {lo}}r,r)$, the estimator, ${\hat{{\mathbf {x}}}}$, produced by this algorithm satisfies:

$$\begin{aligned} \Vert {\hat{{\mathbf {x}}}}-{\mathbf {x}}\Vert _2\le {{\tilde{C}}}(r) \mathrm {SRF}^{2r+1}\Vert {\mathbf {z}}\Vert _2. \end{aligned}$$

(10)

The algorithm proposed by Donoho may only be applied to vectors ${\mathbf {x}}$ with very few dimensions. Therefore, the fundamental problem posed by Donoho is to find an efficient algorithm that is stable in the sense of (10). Donoho has also proven a converse to (10): the $\mathrm {SRF}$ dependence in (10) cannot be better than $\mathrm {SRF}^{2r-1}$ even for the best possible algorithm in the worst-case scenario (the minimax setting). The results of Donoho have been recently (partially) improved in [4, 17] where for the same intractable algorithm the following stability estimate was derived:

$$\begin{aligned} \Vert {\hat{{\mathbf {x}}}}-{\mathbf {x}}\Vert _2\le {{\tilde{C}}}(r, \Vert {\mathbf {x}}\Vert _0) \mathrm {SRF}^{2r-1}\Vert {\mathbf {z}}\Vert _2. \end{aligned}$$

(11)

The result is sharp in the sense that the $\mathrm {SRF}$ dependence matches Donoho’s converse. The weakness is that ${{\tilde{C}}}(r, \Vert {\mathbf {x}}\Vert _0)$ depends on the total number of spikes in the signal, which may be very large. This weakness has recently been (partially) removed in [5], where a model with clustered spikes is considered that is somewhat similar, but distinct from Rayleigh regularity; stability estimates for the spike locations and (complex-valued) spike magnitudes are derived and the estimate for the magnitudes scales as $\mathrm {SRF}^{2r-1}\Vert {\mathbf {z}}\Vert _2$. Note further that the stability estimates in (10), (11) are expressed in terms of $\ell _2$ norms, whereas our stability estimates in (9) are expressed in terms of $\ell _1$ norms.

Other works [6, 53, 54] study the stability of the super-resolution problem in the presence of noise, but likewise do not provide a tractable algorithm to perform recovery. Work in [31, 50, 51] analyzes the detection and separation of two closely-spaced spikes, but does not generalize to the case when there are more than two spikes in the signal. Recent papers [39, 40] analyze the problem of accurately recovering the number of spikes from the low-pass measurements.

Super-resolution of well-separated spikes Progress towards resolving the question posed in [23] in the general situation where ${\mathbf {x}}\in {\mathbb {C}}^N$—in this paper we consider the case ${\mathbf {x}}\ge {\mathbf {0}}$ only—has been made in [12, 13, 28]. The sharpest from this series of results [28] implies the following. Assume $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(1.26\lambda _{\mathrm {lo}},1)$, then the solution to $\ell _1$-minimization problem

$$\begin{aligned} {\hat{{\mathbf {x}}}} = {{\,\mathrm{\text {arg min}}\,}}_{{\tilde{{\mathbf {x}}}}} \Vert {\tilde{{\mathbf {x}}}}\Vert _1 \quad \text {subject to} \quad \Vert {\mathbf {s}}-{\mathbf {Q}}{\tilde{{\mathbf {x}}}}\Vert _1\le \delta \end{aligned}$$

(L1)

with $\delta$ chosen so that $\Vert {\mathbf {z}}\Vert _1\le \delta$ satisfies

$$\begin{aligned} \Vert {\mathbf {x}}-{\hat{{\mathbf {x}}}}\Vert _1\le {{\tilde{c}}}\cdot \mathrm {SRF}^{2}, \end{aligned}$$

where ${{\tilde{c}}}$ is a numerical constant. The requirement $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(1.26\lambda _{\mathrm {lo}},1)$ (well-separated spikes in our terminology) is restrictive because it means that the signal ${\mathbf {x}}$ cannot contain spikes that are at a distance less than $1.26\lambda _{\mathrm {lo}}$. This is a limitation for many applications including single-molecule microscopy, as it is usually understood that the goal of super-resolution is to distinguish spikes that are (significantly) closer than the Rayleigh diffraction limit, i.e., at a fraction of $\lambda _{\mathrm {lo}}$ apart. Unfortunately, if there are spikes at a distance smaller than $\lambda _{\mathrm {lo}}$, $\ell _1$ minimization does not, in general, return the correct solution even if there is no noise. The central question therefore is: which algorithms and under which assumptions are able to super-resolve signals robustly when the distance between some of the spikes may be substantially smaller than $\lambda _{\mathrm {lo}}$?

On a similar line of research, see [56] and [57] for related results on the denoising of line spectra and on the recovery of sparse signals from a random subset of their low-pass Fourier coefficients. The accuracy of support detection for well-separated spikes is analyzed in [2, 27].

Noise-aware algebraic methods Many noise-aware versions of Prony’s method are used frequently in engineering applications, for example in radar (see [52, Ch. 6]). The most popular methods are MUSIC and its numerous variations [3, 9, 11, 45, 49, 58], matrix-pencil [32], and ESPRIT [44, 47]. For more details on algebraic methods we refer the reader to the excellent book [52, Ch. 4]. It is important to point out that unlike convex optimization based methods like (L1), algebraic methods do not need the spikes to be well-separated (${\mathbf {x}}$ may contain spikes closer than $\lambda _{\mathrm {lo}}$) even when the signal is complex-valued, at least in the noiseless case.

The stability of noise-aware algebraic methods is an active area of research. Asymptotic results (at high signal-to-noise ratio) on the stability of MUSIC in the presence of Gaussian noise are derived in [16, 55]. More recently, some steps towards analyzing MUSIC and matrix-pencil in a non-asymptotic regime have been taken in [38] and in [42], respectively.

Especially important is the question of stability of algebraic methods when the spikes are not well-separated. Substantial progress in understanding this for MUSIC and ESPRIT algorithms has been made by Li and Liao in the last two years [35,36,37]. See also [34] for a simplified exposition of ideas in [36] and some extensions. The authors considered a separated cluster model for spike locations; the model is similar to Rayleigh regularity in spirit, but is more restrictive. For example, the signals depicted in Fig. 2b and c are both Rayleigh-regular with $r=2$ and $d=4\lambda _{\mathrm {lo}}$. At the same time, the signal in Fig. 2b has spike clusters that are separated by about $3\lambda _{\mathrm {lo}}$, but the signal in Fig. 2c has spike clusters that are separated by only about $2\lambda _{\mathrm {lo}}$. The separation between clusters determines the stability guarantee of the reconstruction in the presence of noise. Hence, the theory based on the separated cluster model predicts that the signal in Fig. 2b is easier to super-resolve than the signal in Fig. 2c. Intuitively, it is not clear why this should be the case. The theory based on Rayleigh regularity provides identical stability guarantees for the signals in Fig. 2b and c. Continuing this argument, it is possible to construct examples when the guarantees based on separated cluster model will be weak, yet the guarantees based on Rayleigh-regularity will be strong; the examples where the reverse is true do not exist. For MUSIC in [35, 36] and for ESPRIT in [37], assuming Gaussian noise and making a further (restrictive) assumption $f_{\mathrm {lo}}\gtrsim \Vert {\mathbf {x}}\Vert _0^2$, the authors derived bounds on signal-to-noise ratio in terms of $\mathrm {SRF}^{2r-2}$ and a factor that depend on $f_{\mathrm {lo}}$ so that the correct signal support recovery is guaranteed. There is still a large gap between these stability estimates and the minimax converse results. For example, for ESPRIT, the gap is a factor proportional to $f_{\mathrm {lo}}$, which may be very large for high-dimensional signals [37]. Hence, the problem of finding a super-resolution method for complex-valued signals that performs well empirically and has sharp theoretical stability estimates in the case when the spikes are not well-separated is still open.

Super-resolution of nonnegative signals The case of nonnegative signal, ${\mathbf {x}}\ge {\mathbf {0}}$, was analyzed in [24], see also [30] for a shorter exposition of the same idea. It is proven in [24] that as long as $\Vert {\mathbf {x}}\Vert _0\le f_{\mathrm {lo}}$, one can recover ${\mathbf {x}}$ by solving a simple convex feasibility problem in the noiseless setting. In the presence of noise, [24] does not provide sharp estimates: it does not reveal the correct $\mathrm {SRF}$ dependence in the stability estimate.

More recently, the authors of [48] generalized [24] to the case of more general point spread functions and sampling patterns in the noiseless case; further refinements have been obtained in [25]. The corresponding noisy case has been studied in [26]. Being very general, the results of [26] do not appear to be sharp enough to reveal the fundamental dependence between the stability of the algorithm, the regularity of the signal, and the super-resolution factor.

Most relevant to this work is the earlier paper [43] where Proposition 1 has been proven. The key question remained: what happens if the grid becomes arbitrarily fine or when there is no grid at all (the gridless setting). Some progress towards answering this question has since been made in [19] where stability estimates for the detection of signal support have been expressed in terms of $\mathrm {SRF}^{2\Vert {\mathbf {x}}\Vert _0-1}$. Note that $\Vert {\mathbf {x}}\Vert _0$ may be arbitrarily large for high-dimensional signals, and so the bounds in [19] become highly suboptimal for the practically relevant case in which the spikes are distributed in a regular way in the signal. It was shown in [18, Sect. 2.4] that the results of [19] may be generalized to a separated cluster model, in which case the $\Vert {\mathbf {x}}\Vert _0$ in the estimate above is substituted with $r$, the number of spikes in one cluster. However, the result in [18, Sect. 2.4, Theorem 4] requires the clusters to be far enough, and there is no quantification of how far the clusters need to be. In other words, the clusters need to be arbitrarily far away from one another. In contrast, the Rayleigh regularity concept in this paper specifies exactly how far the clusters need to be for stability estimates to hold and, further, this distance is tight to within a factor of 1.87 [43, Sect. 2.3.1]. Also see the discussion above explaining that Rayleigh regularity is generally a more forgiving requirement than the separated cluster model.

3.2 Innovations

The innovations in this paper may be summarized as follows:

• Generalization of the results of [43] to the case when the grid is arbitrarily fine.

• Seamless connection between the super-resolution results for the discrete grid and the results for the gridless (continuous) setting. This has theoretical as well as practical implications.

• Mathematically the paper builds on the ideas from [12] and [43] and develops these methods further. The interpolation constructions in Lemmas 4 and 5 are new. These constructions may be of independent interest and may be useful for other problems.

4 Notation

Sets are denoted by calligraphic letters ${\mathcal {A}}, {\mathcal {B}}$, and so on. Boldface letters ${\mathbf {A}},{\mathbf {B}},\ldots$ and ${\mathbf {a}},{\mathbf {b}},\ldots$ denote matrices and vectors, respectively. The element in the ith row and jth column of a matrix ${\mathbf {A}}$ is $a _{i j}$ or $[{\mathbf {A}}]_{i,j}$, and the ith element of a vector ${\mathbf {a}}$ is $a _i$ or $[{\mathbf {a}} ]_i$. For a vector ${\mathbf {a}}$, ${{\,\mathrm{diag}\,}}({\mathbf {a}})$ stands for the diagonal matrix that has the entries of ${\mathbf {a}}$ on its main diagonal. The vector of all zeros is denoted ${\mathbf {0}}$. The superscript $^{{\mathsf {T}}}$ stands for transposition. For $a, b\in {\mathbb {T}}$, the wrap-around distance between a and b is $\mathchoice{{\left|b-a\right|}}{{\bigl |b-a\bigr |}}{{\left|b-a\right|}}{{\left|b-a\right|}}\triangleq \min (b-a \mod 1,\ a-b \mod 1)$; for an interval $[a, b]\subset {\mathbb {T}}$, its wrap-around length is $\mathchoice{{\left|b-a\right|}}{{\bigl |b-a\bigr |}}{{\left|b-a\right|}}{{\left|b-a\right|}}$. For a finite set ${\mathcal {I}}$, we write $\mathchoice{{\left|{\mathcal {I}}\right|}}{{\bigl |{\mathcal {I}}\bigr |}}{{\left|{\mathcal {I}}\right|}}{{\left|{\mathcal {I}}\right|}}$ for the cardinality. Note that the notation $\mathchoice{{\left|\cdot \right|}}{{\bigl |\cdot \bigr |}}{{\left|\cdot \right|}}{{\left|\cdot \right|}}$ is overloaded. For $x\in {\mathbb {R}}$, $\lceil x\rceil \triangleq \min \{m\in {\mathbb {Z}}\mid m\ge x\}$. We use $[l \text {: }k]$ to designate the set of natural numbers $\left\{ l, l+1,\ldots ,k\right\}$. For a vector ${\mathbf {a}} \in {\mathbb {C}}^n$, $\Vert {\mathbf {a}} \Vert _1=\sum _{j=0}^{n-1} \mathchoice{{\left|a _j\right|}}{{\bigl |a _j\bigr |}}{{\left|a _j\right|}}{{\left|a _j\right|}}$ denotes the $\ell _1$ norm; $\Vert {\mathbf {a}} \Vert _2=\bigl (\sum _{j=0}^{n-1} a _j^2\bigr )^{1/2}$ denotes the $\ell _2$ norm; $\Vert {\mathbf {a}} \Vert _{\infty }=\max _{j}\mathchoice{{\left|a _j\right|}}{{\bigl |a _j\bigr |}}{{\left|a _j\right|}}{{\left|a _j\right|}}$ denotes the $\ell _\infty$ norm; and $\Vert {\mathbf {a}} \Vert _0$ denotes the number of nonzero elements in ${\mathbf {a}}$. For a function $f (\cdot ):{\mathbb {R}}\rightarrow {\mathbb {R}}$, $\Vert f (\cdot )\Vert _{\infty }=\max _{t\in {\mathbb {R}}}\mathchoice{{\left|f (t)\right|}}{{\bigl |f (t)\bigr |}}{{\left|f (t)\right|}}{{\left|f (t)\right|}}$. The indicator function is denoted as ${I[\cdot ]}$, it is equal to one if the condition in the brackets is satisfied and zero otherwise. We use c with various subindexes and superindexes to denote positive numerical constants; to track things simpler, we use the convention that the numerical constants with the subscript u, like $c_{u1}$, satisfy $c_{u1}>1$, and the numerical constants with subscript l, like $c_{l1}$, satisfy $0<c_{l1}<1$. Throughout the paper we use the convention: $f_{\mathrm {lo}}$ denotes the frequency cut-off of the measured data [see (4)], $\lambda _{\mathrm {lo}}=1/f_{\mathrm {lo}}$ is the corresponding wavelength; $f_c$ denotes an abstract frequency cut-off (this value changes in different places in the paper) and $\lambda _c=1/f_c$ is the corresponding wavelength. To simplify writing, we follow the conventions: $\prod _{i=1}^r a_i=1$ and $\{a_1,\ldots , a_r\}=\varnothing$ when $r=0$.

5 Structure of the Proof

Previous results in the field [12, 13, 43] suggest that Theorem 1 may be proven by constructing an appropriate dual certificate. Specifically, consider a compressed sensing type problem in which an unknown signal is being recovered from an incomplete set of noiseless linear measurements using a convex optimization procedure with prior constraints on the signal (such as nonnegativity) and regularization (such as $\ell _1$ norm minimization); see, for example, [14] for a short exposition of the classical ideas. Then the dual certificate is a vector from the range of the adjoint of the measurement matrix that satisfies specific interpolation conditions determined by the properties of the true unknown signal (such as sparsity) and by the type of prior constraints and regularization used. Geometrically, the existence of the dual certificate guarantees that the null space of the measurement matrix is oriented in a favorable way: starting from the true unknown signal it is not possible to move along the null space of the measurement matrix while satisfying the prior constraints and making the solution more regularized. Therefore, the true unknown signal is the optimal solution of the convex optimization problem. In other words, the existence of the dual certificate guarantees that the convex optimization problem recovers the correct solution. In the presence of noise a similar approach allows one to prove stability of the reconstruction, but the dual certificate often must satisfy additional properties [43].

In our problem, since the measurement operator is a low-pass kernel, the dual certificate is a real-valued trigonometric polynomial frequency-limited to $f_{\mathrm {lo}}$ with additional properties. In fact, since we work on an arbitrarily fine grid, similar to [12], we will need three trigonometric polynomials instead of one, each with its own properties; they will be called $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$. These dual trigonometric polynomials are constructed in Lemmas 3, 4, and 5 in Sect. 6; $q_0(\cdot )$ is borrowed from [43], $q_1(\cdot )$ and $q_2(\cdot )$ are new—they are the main mathematical contribution of this paper. In Sect. 7 we use $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$ to derive the stability estimates and prove Theorem 1.

We invite the reader unfamiliar with the concept of dual certificates in convex optimization or the use of dual certificates in super-resolution problems to study the short proof of [43, Lm. 1, pp. 426–427] before reading this paper further. The derivations in Sect. 7 generalize [43, Lm. 1] to the arbitrarily fine grid setting, but they are much more involved.

Some calculations in this paper are complicated, but we tried to present the key new ideas in a simple way. At the first pass through the paper we suggest that the reader studies Sects. 6.1–6.2; then focuses on the formulations of Lemmas 4 and 5 and the new constructions in Sects. 6.3.1 and in Appendix “Proof of Lemma 5-construction” skips the details in Sects. 6.3.2–6.3.6 and in the remainder of Appendix “Proof of Lemma 5” and finally studies the stability estimates in Sect. 7. After this, return to the technical details in Sects. 6.3.2–6.3.6 and in Appendix “Proof of Lemma 5”.

6 Dual Certificates

Throughout the paper we will use the following definitions. Define the error vector

$$\begin{aligned} {\mathbf {h}}= [h_0, \ldots , h_{N-1}]^{{\mathsf {T}}}\triangleq {\hat{{\mathbf {x}}}} - {\mathbf {x}}\end{aligned}$$

and the set of points where the error vector takes on negative values

$$\begin{aligned} {\mathcal {T}}= \{t_1, \ldots , t_S\}\triangleq \{m/N: h_m<0\}. \end{aligned}$$

(12)

The points are ordered according to $t_1<\cdots <t_S$. Recall, ${\hat{{\mathbf {x}}}}\ge {\mathbf {0}}$ and ${\mathbf {x}}\ge {\mathbf {0}}$. Therefore, $h_m$ can only take on negative values on $\mathrm {supp}({\mathbf {x}})$, which implies ${\mathcal {T}}\subset \mathrm {supp}({\mathbf {x}})$. Since $\mathrm {supp}({\mathbf {x}})\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,r)$ and since the elements of $\mathrm {supp}({\mathbf {x}})$ are separated by at least $2\lambda _{\mathrm {hi}}$, it follows ${\mathcal {T}}\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,r)$ and the elements of ${\mathcal {T}}$ are also separated by at least $2\lambda _{\mathrm {hi}}$. As we will see below, the dual trigonometric polynomials $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$ need to satisfy specific interpolation constraints on ${\mathcal {T}}$.

Throughout the paper we will use the following neighborhood notations.

Definition 2

For $\tau \in {\mathbb {T}}$, $\delta >0$,

$$\begin{aligned} {\mathcal {N}}(\delta ,\tau )\triangleq \{t\in {\mathbb {T}}: \mathchoice{{\left|t-\tau \right|}}{{\bigl |t-\tau \bigr |}}{{\left|t-\tau \right|}}{{\left|t-\tau \right|}}\le \delta \}, \end{aligned}$$

where $\mathchoice{{\left|\cdot \right|}}{{\bigl |\cdot \bigr |}}{{\left|\cdot \right|}}{{\left|\cdot \right|}}$ denotes the wrap-around distance on ${\mathbb {T}}$. Above, ${\mathcal {N}}(\cdot ,\cdot )$ stands for “near” (i.e., the points near $\tau$).

For a set ${\mathcal {V}}\subset {\mathbb {T}}$ and $\delta >0$,

$$\begin{aligned} {\mathcal {N}}(\delta ,{\mathcal {V}})&\triangleq \cup _{\tau \in {\mathcal {V}}} {\mathcal {N}}(\delta ,\tau ),\\ {\mathcal {F}}(\delta ,{\mathcal {V}})&\triangleq {\mathbb {T}}\setminus {\mathcal {N}}(\delta ,{\mathcal {V}}). \end{aligned}$$

Above, ${\mathcal {F}}(\cdot ,\cdot )$ stands for “far” (i.e., the points far from ${\mathcal {V}}$).

6.1 Building Blocks

The following two lemmas serve as common building blocks for the construction of trigonometric polynomials $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$.

Lemma 1 allows us to construct a trigonometric polynomial frequency-limited to $f_c$ that interpolates zeros at well-separated points as illustrated in Fig. 4a.

Fig. 4

a Illustration of Lemma 1. Trigonometric polynomial frequency-limited to $f_c=6$ interpolates zeros at well-separated points $\{v_1, v_2\}\in {\mathcal {R}}(2.5\lambda _c,1)$. Specifically, $q_{\lambda _c, {\mathcal {V}}}(v_j)=q_{\lambda _c, {\mathcal {V}}}'(v_j)=0$ and the curvature in the neighborhoods of $v_1$ and $v_2$ is controlled (indicated in red) according to (13). b Illustration of Lemma 2. Trigonometric polynomial frequency-limited to $f_c=6$ interpolates values $f_1$ and $f_2$ at well-separated points $\{v_1, v_2\}\in {\mathcal {R}}(2.5\lambda _c,1)$. Specifically, $q_{\lambda _c, {\mathcal {V}}, \{f_j\}, \{d_j\}}(v_j)=f_j$ and the derivatives at $v_1$ and $v_2$ are constrained (indicated in red) according to $q'_{\lambda _c, {\mathcal {V}},\{f_j\}, \{d_j\}}(v_j)=d_j$ (Color figure online)

Lemma 1

Let $\lambda _c\in (0,1/128)$, set $f_c\triangleq 1/\lambda _c$. Consider a collection of points $v_1< v_2< \cdots < v_{V}$, define ${\mathcal {V}}\triangleq \{v_1, v_2, \ldots , v_{V}\}$ and assume ${\mathcal {V}}\in {\mathcal {R}}(\kappa \lambda _c,1)$. Then, there exists a real-valued trigonometric polynomial $q(\cdot ) = q_{\lambda _c,{\mathcal {V}}}(\cdot )$ that satisfied the following properties.

• 1. Frequency limitation to $f_c$: $q(t)=\sum _{k=-f_c}^{f_c} {\hat{q}}_k e^{-\mathrm {i} 2\pi kt}$ for some ${\hat{q}}_k\in {\mathbb {C}}$.

• 2. Zero values and zero derivatives on ${\mathcal {V}}$: for all $v\in {\mathcal {V}}$, $q(v)=q'(v)=0$.

• 3. Uniform confinement between zero and one: for all $\tau \in {\mathbb {R}}$, $0\le q(\tau )\le 1$.

• 4. Quadratic behavior near ${\mathcal {V}}$: for all $v\in {\mathcal {V}}$ and for all $\tau \in {\mathcal {N}}(\Delta \lambda _c,v)$

  $$\begin{aligned} \frac{c_l(v-\tau )^2}{\lambda _c^2}\le q(\tau ) \le \frac{c_u(v-\tau )^2}{\lambda _c^2}. \end{aligned}$$

  (13)

• 5. Boundedness away from zero far from ${\mathcal {V}}$: for all $\tau \in {\mathcal {F}}(\Delta \lambda _c,{\mathcal {V}})$, $q(\tau ) \ge c_{l1}>0$.

• 6. Uniform confinement of the derivative: $\Vert q'(\cdot )\Vert _{\infty }\le 2\pi /\lambda _c$.

• 7. Uniform confinement of the second derivative: $\Vert q''(\cdot )\Vert _{\infty }\le 4\pi ^2/\lambda _c^2$.

Above, all the constants are positive numerical constants. Specifically,

$$\begin{aligned} \begin{array}{ll} \Delta \triangleq 0.17, &{}c_l\triangleq 0.029\\ c_u\triangleq 2\pi ^2, &{}c_{l1}\triangleq \Delta ^2 c_l= 8.3 \times 10^{-4}. \end{array} \end{aligned}$$

(14)

Proof

This lemma is a direct consequence of the technique developed in [13]. Let $q_{CFG}(\cdot )$ be the trigonometric polynomial constructed as in [13, eq. (2.4)] to interpolate $-1$ on ${\mathcal {V}}$. Then, according to [13, Lm. 2.4, Lm. 2.5, Sec. 2.5], $q(\cdot ) = 0.5(q_{CFG}(\cdot )+1)$ satisfies Properties 1, 2, 3, 5 of the lemma, and the lower bound in (13). Since, by Property 3, $\Vert q(\cdot )\Vert _{\infty }\le 1$, Properties 6 and 7 follow by applying (129) [Bernstein theorem]. Finally, the upper bound in (13) follows from Property 2 and Property 7 by (195) [Mean Value theorem].$\square$

Lemma 2 allows us to construct a trigonometric polynomial frequency-limited to $f_c$ that interpolates arbitrary values and has constrained derivatives at well-separated points as illustrated in Fig. 4b.

Lemma 2

Let $\lambda _c\in (0,1/128)$, set $f_c\triangleq 1/\lambda _c$. Consider a collection of points $v_1< v_2< \cdots < v_{V}$, define ${\mathcal {V}}\triangleq \{v_1, v_2, \ldots , v_{V}\}$ and assume ${\mathcal {V}}\in {\mathcal {R}}(\kappa \lambda _c,1)$. Consider two sets of real numbers $\{f_1, f_2,\ldots , f_V\}$ and $\{d_1, d_2, \ldots , d_V\}$ that satisfy

$$\begin{aligned} \mathchoice{{\left|f_j\right|}}{{\bigl |f_j\bigr |}}{{\left|f_j\right|}}{{\left|f_j\right|}}\le 1\quad \text {and}\quad \mathchoice{{\left|d_j\right|}}{{\bigl |d_j\bigr |}}{{\left|d_j\right|}}{{\left|d_j\right|}}\le \frac{1}{\lambda _c} \end{aligned}$$

(15)

for all $j=1,\ldots , V$. Then, there exists a real-valued trigonometric polynomial $q(\cdot )=q_{\lambda _c,{\mathcal {V}}, \{f_j\}, \{d_j\}}(\cdot )$ that satisfies the following properties.

• 1. Frequency limitation to $f_c$: $q(t)=\sum _{k=-f_c}^{f_c} {\hat{q}}_k e^{-\mathrm {i} 2\pi kt}$ for some ${\hat{q}}_k\in {\mathbb {C}}$.

• 2. Constrained values and derivatives on ${\mathcal {V}}$: for all $j=1,\ldots , V$,

  $$\begin{aligned} q(v_j)=f_j\quad \text {and}\quad q'(v_j)=d_j. \end{aligned}$$

• 3. Uniform confinement: $\Vert q(\cdot )\Vert _{\infty }\le c_{u0}$.

• 4. Uniform confinement of the derivative: $\Vert q'(\cdot )\Vert _{\infty }\le c_{u1}/\lambda _c$.

• 5. Uniform confinement of the second derivative: $\Vert q''(\cdot )\Vert _{\infty }\le c_{u2}/\lambda _c^2$.

Above, $c_{u0}$, $c_{u1}$, and $c_{u2}$ are positive numerical constants that are defined in the proof of the lemma in Appendix 1 “Proof of Lemma 2”.

The proof of the lemma generalizes the results in [13, Lm. 2.4, Lm. 2.5, Sec. 2.5] slightly in several technical aspects; it is given in Appendix 1 “Proof of Lemma 2”.

6.2 Dual Certificate $q_0(\cdot )$

We are now ready to construct the trigonometric polynomial $q_0(\cdot )$. This trigonometric polynomial, illustrated in Fig. 5, is frequency-limited to $f_{\mathrm {lo}}$, interpolates zeros on a Rayleigh-regular set, is confined between zero and one, and quickly grows around its zeros.

Fig. 5

Illustration of Lemma 3. Trigonometric polynomial frequency-limited to $f_{\mathrm {lo}}=12$ interpolates zeros on Rayleigh-regular set ${\mathcal {T}}=\{t_1, t_2, t_3, t_4\}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},2)$ and bounces away from zeros “quickly”: the curvature in the neighborhoods of each point $t_i$ is “high” in the sense of (17). In the figure, $\mathchoice{{\left|t_3-t_1\right|}}{{\bigl |t_3-t_1\bigr |}}{{\left|t_3-t_1\right|}}{{\left|t_3-t_1\right|}}\ge 5\lambda _{\mathrm {lo}}=5/12$, $\mathchoice{{\left|t_4-t_2\right|}}{{\bigl |t_4-t_2\bigr |}}{{\left|t_4-t_2\right|}}{{\left|t_4-t_2\right|}}\ge 5\lambda _{\mathrm {lo}}=5/12$, $\mathchoice{{\left|t_2-t_1\right|}}{{\bigl |t_2-t_1\bigr |}}{{\left|t_2-t_1\right|}}{{\left|t_2-t_1\right|}}\sim 2\lambda _{\mathrm {hi}}$, $\mathchoice{{\left|t_3-t_4\right|}}{{\bigl |t_3-t_4\bigr |}}{{\left|t_3-t_4\right|}}{{\left|t_3-t_4\right|}}\sim 2\lambda _{\mathrm {hi}}$ (Color figure online)

The key difference between the trigonometric polynomial $q_0(\cdot )$ and the building block $q_{\lambda _c,{\mathcal {V}}}(\cdot )$ constructed in Lemma 1 is that the points where $q_0(\cdot )$ must take zero values may belong to a Rayleigh-regular set from a class ${\mathcal {R}}(d,r)$ with $r>1$. Zeros of $q_0(\cdot )$ may be close, whereas zeros of $q_{\lambda _c,{\mathcal {V}}}(\cdot )$ are well-separated (compare Figs. 4a to 5). This is the reason why the technique of [13] and [12] that was used to prove Lemma 1 cannot be applied directly to construct $q_0(\cdot )$.

Lemma 3

There exists a real-valued trigonometric polynomial $q_0(\cdot )$ that satisfies the following properties.

• 1. Frequency limitation to $f_{\mathrm {lo}}$: $q_0(t)=\sum _{k=-f_{\mathrm {lo}}}^{f_{\mathrm {lo}}} {\hat{q}}_{0,k} e^{-\mathrm {i} 2\pi kt}$ for some ${\hat{q}}_{0,k}\in {\mathbb {C}}$.

• 2. Zero values and zero derivatives on ${\mathcal {T}}$: for all $t\in {\mathcal {T}}$, $q_0(t)=q_0'(t)=0$.

• 3. Uniform confinement between zero and one: for all $\tau \in {\mathbb {R}}$, $0\le q_0(\tau )\le 1$.

• 4. Controlled behavior near ${\mathcal {T}}$: Take $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}})$, where $\Delta =0.17$ as before. Let $\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}$. [Note: since ${\mathcal {T}}\in {\mathcal {R}}(r\kappa \lambda _{\mathrm {lo}},r)$ and $\Delta <\kappa$, it follows that $1\le {{\hat{r}}}\le r$.] Set $v^\tau \triangleq {{\,\mathrm{\text {arg min}}\,}}_{v\in \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}} \mathchoice{{\left|v-\tau \right|}}{{\bigl |v-\tau \bigr |}}{{\left|v-\tau \right|}}{{\left|v-\tau \right|}}$. Then, the following estimates hold.

  • 1. Lower bound:

    $$\begin{aligned} q_0(\tau )&\ge c_{l2}^r\frac{ \prod _{l=1}^{{{\hat{r}}}}(v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \end{aligned}$$

    (16)
    $$\begin{aligned}&\ge c_{l2}^r\frac{ (v^\tau -\tau )^2 \lambda _{\mathrm {hi}}^{2(r-1)}}{(r\lambda _{\mathrm {lo}})^{2r}}. \end{aligned}$$

    (17)

  • 2. Upper bound:

    $$\begin{aligned} q_0(\tau )&\le c_u^{{{\hat{r}}}} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

    (18)

• 3. Boundedness away from zero far from ${\mathcal {T}}$: for all $\tau \in {\mathcal {F}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}})$,

  $$\begin{aligned} q_0(\tau ) \ge c_{l1}^{r}>0. \end{aligned}$$

  (19)

• 4. Fast growth immediately away from ${\mathcal {T}}$: for all $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}})$,

  $$\begin{aligned} q_0(\tau )\ge c_l^r\frac{\lambda _{\mathrm {hi}}^{2r}}{(r\lambda _{\mathrm {lo}})^{2r}}. \end{aligned}$$

Above, $c_{l2}$ is a positive numerical constant, defined in the proof below.

The trick to prove this lemma is the main contribution of the earlier paper [43]. The key observation is the following. It is possible to construct the nonnegative trigonometric polynomial $q_0(\cdot )$ frequency-limited to $f_{\mathrm {lo}}$ that is zero on all the points of the set ${\mathcal {T}}\in {\mathcal {R}}(r\kappa \lambda _{\mathrm {lo}},r)$ as a product of $r$ trigonometric polynomials. Each of these trigonometric polynomials is zero on a set that belongs to ${\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$ and is constructed via Lemma 1. We reproduce the proof below because it motivates the new construction in Sect. 6.3.

Proof

Set

$$\begin{aligned} {\mathcal {T}}_k\triangleq \Bigl \{t_{jr+k}: j\in [0 \text {: }\lfloor (S-1)/r \rfloor ]\Bigr \},\quad k=1,\ldots ,r. \end{aligned}$$

(20)

Observe that ${\mathcal {T}}= {\mathcal {T}}_1\cup \cdots \cup {\mathcal {T}}_r$ and ${\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. Set

$$\begin{aligned} q_0(t)\triangleq q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_1}(t)\times \cdots \times q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_r}(t), \end{aligned}$$

(21)

where $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\cdot ),\ k=1,\ldots ,r,$ are the trigonometric polynomials constructed¹ via Lemma 1 with $\lambda _c=r\lambda _{\mathrm {lo}}$ and ${\mathcal {V}}={\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. The idea of this construction for $r=2$ is illustrated in Fig. 6.

Fig. 6

Illustration of the proof of Lemma 3. The set ${\mathcal {T}}=\{t_1, t_2, t_3, t_4\}$ is Rayleigh-regular: ${\mathcal {T}}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},2)$, with $r=2$ and $\lambda _{\mathrm {lo}}=1/12$. The idea is to split this set as ${\mathcal {T}}={\mathcal {T}}_1\cup {\mathcal {T}}_2$ with ${\mathcal {T}}_1=\{t_1,t_3\}$ and ${\mathcal {T}}_2=\{t_2,t_4\}$ and observe ${\mathcal {T}}_i\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},1)$. The trigonometric polynomials are frequency-limited to $f_{\mathrm {lo}}/2=6$ and satisfy the interpolation constraints $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_1}(t)=q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_1}'(t)=0$ for all $t\in {\mathcal {T}}_1$ and $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_2}(t)=q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_2}'(t)=0$ for all $t\in {\mathcal {T}}_2$. Then, $q_0(\cdot )=(q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_1}\times q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_2})(\cdot )$ satisfies $q_0(t)=q_0'(t)=0$ for all $t\in {\mathcal {T}}$ and is frequency-limited to $2\times f_{\mathrm {lo}}/2=12$. The trigonometric polynomial $q_0(\cdot )$ is displayed in Fig. 5. In the figure, $\mathchoice{{\left|t_2-t_1\right|}}{{\bigl |t_2-t_1\bigr |}}{{\left|t_2-t_1\right|}}{{\left|t_2-t_1\right|}}\sim 2\lambda _{\mathrm {hi}}$, $\mathchoice{{\left|t_3-t_4\right|}}{{\bigl |t_3-t_4\bigr |}}{{\left|t_3-t_4\right|}}{{\left|t_3-t_4\right|}}\sim 2\lambda _{\mathrm {hi}}$ (Color figure online)

It remains to verify that Properties 1–6 are satisfied. Broadly, this follows from (21) and Lemma 1; the details are given below.

Property 1 is satisfied because each of trigonometric polynomials $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\cdot ),$ $k=1,\ldots ,r$ is frequency-limited to $f_{\mathrm {lo}}/r$. Hence, the product in (21) is frequency-limited to $r(f_{\mathrm {lo}}/r)=f_{\mathrm {lo}}$.

Properties 2 and 3 follow from (21) and from Lemma 1, Properties 2 and 3, respectively.

To prove (16) we lower-bound the terms in (21) separately as follows. Assume that $k\in \{1,\ldots ,r\}$ is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k\ne \varnothing$, i.e., there exist $l\in \{1,\ldots ,{\hat{r}}\}$ that satisfies $v^\tau _l\in {\mathcal {T}}_k$. In this case, we use the left-hand side of (13) to write

$$\begin{aligned} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\tau )\ge c_l\frac{(v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(22)

Note that there are exactly ${{\hat{r}}}$ such terms in (21). Assume that $k\in \{1,\ldots ,r\}$ is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k=\varnothing$. In this case, use Lemma 1, Property 5, to write

$$\begin{aligned} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\tau )\ge c_{l1}. \end{aligned}$$

(23)

Note that there are exactly $r-{{\hat{r}}}$ such terms in (21). The desired bound (16) is obtained by plugging (22) and (23) into (21) and setting $c_{l2}\triangleq \min (c_l, c_{l1})$.

Bound (17) follows because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$ and because $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$.

To prove (18) we upper-bound the terms in (21) separately as follows. Assume that $k\in \{1,\ldots ,r\}$ is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k\ne \varnothing$, i.e., there exist $l\in \{1,\ldots ,{\hat{r\}}}$ that satisfies $v^\tau _l\in {\mathcal {T}}_k$. In this case, we use the right-hand side of (13) to write

$$\begin{aligned} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\tau )\le c_u\frac{(v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(24)

Assume that $k\in \{1,\ldots ,r\}$ is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k=\varnothing$. In this case, we use Lemma 1, Property 3, to write

$$\begin{aligned} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(\tau )\le 1. \end{aligned}$$

(25)

The desired bound (18) is obtained by plugging (24) and (25) into (21).

Property 5 follows by (21) and Lemma 1, Property 5.

Finally, Property 6 follows from (21), (13), Lemma 1, Property 5, and (14).$\square$

6.3 Dual Certificate $q_1(\cdot )$

We are now ready to construct the trigonometric polynomial $q_1(\cdot )$. This construction and its analysis is the main mathematical contribution of this paper. Trigonometric polynomial $q_1(\cdot )$, illustrated in Fig. 7, is frequency-limited to $f_{\mathrm {lo}}$ and, on the points $t_j\in {\mathcal {T}}$, $q_1(\cdot )$ interpolates the set of signs

$$\begin{aligned} s_{j}\triangleq {{\,\mathrm{sign}\,}}\left( \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right) ,\ j=1,\ldots ,S, \end{aligned}$$

(26)

at a (low) level $\rho /2$, $\rho =(\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}})^{2r}\ll 1$. The behavior of $q_1(\cdot )$ is controlled by $q_0(\cdot )$ as explained in Lemma 4 below.

Fig. 7

Illustration of Lemma 4. Trigonometric polynomial frequency-limited to $f_{\mathrm {lo}}=12$ interpolates the sign pattern $\{s_1, s_2, s_3, s_4\} = \{+1, +1, +1, -1\}$ at a (low) level $\rho /2$. Specifically, $q_1(t_i)=s_i \rho /2$ and $q'_1(t_i)=0$. The set ${\mathcal {T}}=\{t_1, t_2, t_3, t_4\}$ is Rayleigh-regular: ${\mathcal {T}}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},2)$ with $\lambda _{\mathrm {lo}}=1/f_{\mathrm {lo}}$ and $\mathchoice{{\left|t_2-t_1\right|}}{{\bigl |t_2-t_1\bigr |}}{{\left|t_2-t_1\right|}}{{\left|t_2-t_1\right|}}\sim 2\lambda _{\mathrm {hi}}$, $\mathchoice{{\left|t_3-t_4\right|}}{{\bigl |t_3-t_4\bigr |}}{{\left|t_3-t_4\right|}}{{\left|t_3-t_4\right|}}\sim 2\lambda _{\mathrm {hi}}$ (Color figure online)

Lemma 4

Set $\rho \triangleq \lambda _{\mathrm {hi}}^{2r}/\lambda _{\mathrm {lo}}^{2r}$. Then, there exists a real-valued trigonometric polynomial $q_1(\cdot )$ that satisfies the following properties.

• 1. Frequency limitation to $f_{\mathrm {lo}}$: $q_1(t)=\sum _{k=-f_{\mathrm {lo}}}^{f_{\mathrm {lo}}} {\hat{q}}_{1,k} e^{-\mathrm {i} 2\pi kt}$ for some ${\hat{q}}_{1,k}\in {\mathbb {C}}$.

• 2. Constrained sign pattern (at level $\rho$) on ${\mathcal {T}}$ and controlled behavior near ${\mathcal {T}}$: for all $j=1,\ldots ,S$ and all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$,

  $$\begin{aligned} \mathchoice{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}}{{\bigl |q_1(\tau )-\frac{\rho s_j}{2}\bigr |}}{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}}{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}} \le r^{2r+4} c_{u27}^{r+1} q_0(\tau ), \end{aligned}$$

  (27)

  where $s_j$ are defined² in (26). Since $q_0(\tau )=0$ for $\tau \in {\mathcal {T}}$, (27) implies, in particular, that $q_1(\cdot )$ interpolates the sign pattern in (26) at level $\rho /2$ on ${\mathcal {T}}$.

• 3. Uniform confinement: $\Vert q_1(\cdot )\Vert _{\infty }\le r^{2r+1}c_{u55}^{r}$.

• 4. Boundedness far from ${\mathcal {T}}$: for all $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}})$,

  $$\begin{aligned} \mathchoice{{\left|q_1(\tau )\right|}}{{\bigl |q_1(\tau )\bigr |}}{{\left|q_1(\tau )\right|}}{{\left|q_1(\tau )\right|}}\le r^{2r+2} c_{u29}^rq_0(\tau ), \end{aligned}$$

  (28)

The positive numerical constants $c_{u27}$, $c_{u55}$, and $c_{u29}$ are defined in the proof below.

Discussion Let’s compare $q_1(\cdot )$ illustrated in Fig. 7 to $q_{\lambda _c,{\mathcal {V}}, \{f_j\}, \{d_j\}}(\cdot )$ constructed in Lemma 2 and illustrated in Fig. 4b. In $q_{\lambda _c,{\mathcal {V}}, \{f_j\}, \{d_j\}}(\cdot )$, the behavior at a well-separated set of points is independently controlled: the trigonometric polynomial can take arbitrary values (between $-1$ and 1). Reminder: we say that the points are well-separated if the distances between the points are no smaller than $\sim {{\tilde{c}}}/f_c$, where $f_c$ is the frequency limitation of the trigonometric polynomial under consideration and ${{\tilde{c}}}$ is a bit larger than 1. In the case of $q_1(\cdot )$, the points where the behavior is controlled are not well-separated as illustrated on Fig. 7: $\mathchoice{{\left|t_2-t_1\right|}}{{\bigl |t_2-t_1\bigr |}}{{\left|t_2-t_1\right|}}{{\left|t_2-t_1\right|}}\sim 2\lambda _{\mathrm {hi}}\ll 1/f_{\mathrm {lo}}$, $\mathchoice{{\left|t_3-t_4\right|}}{{\bigl |t_3-t_4\bigr |}}{{\left|t_3-t_4\right|}}{{\left|t_3-t_4\right|}}\sim 2\lambda _{\mathrm {hi}}\ll 1/f_{\mathrm {lo}}$. Therefore, by Bernstein theorem (see Theorem 2), the behavior of $q_1(\cdot )$ at nearby points cannot be controlled independently. To be concrete: suppose we require that $q_1(t_1)=-1$ and $q_1(t_2)=+1$. Since the points $t_1$ and $t_2$ are separated by about $2\lambda _{\mathrm {hi}}\ll \lambda _{\mathrm {lo}}$ (not well-separated), Bernstein theorem says that these two requirements cannot be satisfied simultaneously. Indeed, since $\Vert q_1(\cdot )\Vert _{\infty }\le {{\tilde{C}}}(r)=r^{2r+1}c_{u55}$, by (129), $\Vert q_1'(\cdot )\Vert _{\infty }\le 2\pi {{\tilde{C}}}(r)f_{\mathrm {lo}}$. If the two requirement had been satisfied simultaneously, the derivative of $q_1(\cdot )$ between the points $t_1$ and $t_2$ would have been about $(q_1(t_2)-q_1(t_1))/(2\lambda _{\mathrm {hi}})=2/(2\lambda _{\mathrm {hi}})=f_{\mathrm {hi}}\gg 2\pi {{\tilde{C}}}(r)f_{\mathrm {lo}}$ (we are assuming that $\mathrm {SRF}$ is large). However, if we require that $q_1(t_1)=-\rho$ and $q_1(t_2)=+\rho$ and $\rho$ is small enough, the two requirements may be satisfied simultaneously. This is the reason why $\rho$ is set to $\lambda _{\mathrm {hi}}^{2r}/\lambda _{\mathrm {lo}}^{2r}\ll 1$ in the formulation of Lemma 4.

Let’s compare $q_1(\cdot )$ to the trigonometric polynomial $q_0(\cdot )$ constructed in Lemma 3 and illustrated in Fig. 5. In both trigonometric polynomials the behavior is controlled on a Rayleigh-regular set, whose points are not well-separated in general. The difference is that $q_0(\cdot )$ takes the same value (zero) on all the points of the Rayleigh-regular set. This allows us to use the multiplication trick illustrated in Fig. 6 to prove Lemma 3. In the case of $q_1(\cdot )$ this does not work because we need to interpolate an arbitrary sign pattern on the Rayleigh-regular set. A method to resolve this problem, presented next, is the main mathematical contribution of this paper.

Proof

Lemma 4 is proven in Sects. 6.3.1–6.3.6 below. $\square$

6.3.1 Construction

We first describe how the trigonometric polynomial $q_1(\cdot )$ is constructed. In Sects. 6.3.2–6.3.6 we prove that the construction is valid and that it satisfies the required Properties 1–4.

Recall, ${\mathcal {T}}=\{t_1,\ldots , t_S\}$ is defined in (12) and, as before, define ${\mathcal {T}}_k$, $k=1,\ldots ,r$, as in (20); remember that ${\mathcal {T}}= {\mathcal {T}}_1\cup \cdots \cup {\mathcal {T}}_r$ and ${\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. Set $\eta _j=\rho (s_j+1)/2$ for $j=1,\ldots ,S$.

We will construct the trigonometric polynomial $q_1(\cdot )$ as a (shifted) sum of $r$ trigonometric polynomials $\{\phi _k(\cdot )\}_{k=1}^r$ (see Fig. 8):

$$\begin{aligned} q_1(t)=\sum _{k=1}^r\phi _k(t)-\rho /2. \end{aligned}$$

(29)

Each of the trigonometric polynomials $\{\phi _k(\cdot )\}_{k=1}^r$ is frequency-limited to $f_{\mathrm {lo}}$,

$$\begin{aligned} \phi _k(t) =\sum _{l=-f_{\mathrm {lo}}}^{f_{\mathrm {lo}}} \hat{\phi }_{k,l} e^{-\mathrm {i} 2\pi l t} \quad \text {for some}\quad \hat{\phi }_{k, l}\in {\mathbb {C}}\end{aligned}$$

(30)

and is constructed separately to satisfy the following interpolation constraints on ${\mathcal {T}}$:

$$\begin{aligned} \phi _k(t_l)&= {\left\{ \begin{array}{ll} \eta _l, &{}\text { if } t_l\in {\mathcal {T}}_k,\\ 0, &{}\text { if } t_l\in {\mathcal {T}}_k^c\triangleq {\mathcal {T}}\setminus {\mathcal {T}}_k, \end{array}\right. } \end{aligned}$$

(31)

$$\begin{aligned} \phi '_k(t)&=0 \text { for all } t\in {\mathcal {T}}. \end{aligned}$$

(32)

Constraints (31), (32), and definition (29) guarantee that for all $l=1,\ldots ,S$

$$\begin{aligned} q_1(t_l)&=\rho s_l/2, \end{aligned}$$

(33)

$$\begin{aligned} q'_1(t_l)&=0. \end{aligned}$$

(34)

To develop intuition, observe that (30) and (29) guarantee that Property 1 is satisfied. Further, observe that the interpolation constraints (33) and (34) are needed for (27) to hold because $q_0(t)=q'_0(t)=0$ for all $t\in {\mathcal {T}}$.

For $r=2$ the construction is illustrated in Fig. 8. The trigonometric polynomials $\phi _1(\cdot )$ and $\phi _2(\cdot )$ are displayed in Fig. 8a; they satisfy the interpolation constraints (31) and (32) as indicated by the points highlighted in bold. When we compute $(\phi _1+\phi _2)(\cdot )$ we obtain the trigonometric polynomial displayed in Fig. 8b, which, when shifted down by $\rho /2$, is equal to the desired $q_1(\cdot )$ displayed in Fig. 7.

Fig. 8

Construction of the trigonometric polynomial $q_1(\cdot )$ (displayed in Fig. 7) with target sign pattern $\{s_1, s_2, s_3, s_4\} = \{+1, +1, +1, -1\}$. a trigonometric polynomials $\phi _1(\cdot )$ and $\phi _2(\cdot )$ satisfy interpolation constraints (31) and (32) as indicated by the points highlighted in bold. Specifically, $\phi _1(t_1)=\phi _1(t_3)=\rho$, $\phi _1(t_2)=\phi _1(t_4)=0$, $\phi _2(t_1)=\phi _2(t_3)=\phi _2(t_4)=0$ and $\phi _2(t_3)=\rho$; and further $\phi _i'(t_j)=0$. b the sum of $\phi _1(\cdot )$ and $\phi _2(\cdot )$ that, after shifting down by $\rho /2$, is equal to $q_1(\cdot )$. In this figure, $\phi _1(\cdot )$ and $\phi _2(\cdot )$ are frequency-limited to $f_{\mathrm {lo}}=12$; ${\mathcal {T}}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},2)$ with $\lambda _{\mathrm {lo}}=1/f_{\mathrm {lo}}$ is represented as ${\mathcal {T}}={\mathcal {T}}_1\cup {\mathcal {T}}_2$ with ${\mathcal {T}}_1=\{t_1, t_3\}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},1)$, ${\mathcal {T}}_2=\{t_2, t_4\}\in {\mathcal {R}}(5\lambda _{\mathrm {lo}},1)$; $\mathchoice{{\left|t_2-t_1\right|}}{{\bigl |t_2-t_1\bigr |}}{{\left|t_2-t_1\right|}}{{\left|t_2-t_1\right|}}\sim 2\lambda _{\mathrm {hi}}$, $\mathchoice{{\left|t_3-t_4\right|}}{{\bigl |t_3-t_4\bigr |}}{{\left|t_3-t_4\right|}}{{\left|t_3-t_4\right|}}\sim 2\lambda _{\mathrm {hi}}$ (Color figure online)

The difficulty remains: how to construct trigonometric polynomials $\phi _k(\cdot )$? Set

$$\begin{aligned} {\mathcal {T}}_k^0\triangleq \Bigl \{t_{jr+k}: j\in [0 \text {: }\lfloor (S-1)/r \rfloor ] \text { and } \eta _{jr+k}=0\Bigr \} \end{aligned}$$

and ${\mathcal {T}}_k^+\triangleq {\mathcal {T}}_k\setminus {\mathcal {T}}_k^0$ for $k=1,\ldots ,r$. The idea now is to construct $\phi _k(\cdot )$ as a product of two trigonometric polynomials (see Fig. 9):

$$\begin{aligned} \phi _k(t)\triangleq \phi _{0,k}(t)\times \phi _{+,k}(t). \end{aligned}$$

(35)

The first term in the product is defined as

$$\begin{aligned} \phi _{0,k}(t)\triangleq \prod _{\begin{array}{c} 1\le l\le r,\ l\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_l}(t), \end{aligned}$$

(36)

where $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_l}(\cdot ),\ l=1,\ldots ,r$, are the trigonometric polynomials constructed via Lemma 1 with $\lambda _c=r\lambda _{\mathrm {lo}}$ and ${\mathcal {V}}={\mathcal {T}}_l\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. Observe similarity to the trigonometric polynomial in (21); the difference is that the kth term is missing from the product.

Fig. 9

Left column: constructing $\phi _1(\cdot )$ as a product of $\phi _{0,1}(\cdot )$ and $\phi _{+,1}(\cdot )$. The trigonometric polynomial $\phi _{0,1}(\cdot )$ is constrained to take zero values (bold blue points) on ${\mathcal {T}}_2=\{t_2, t_4\}$ and it is strictly positive everywhere else. The function values of $\phi _{0,1}(\cdot )$ on ${\mathcal {T}}_1=\{t_1, t_3\}$ are unconstrained. The trigonometric polynomial $\phi _{+,1}(\cdot )$, in turn, is only constrained on ${\mathcal {T}}_1$ (bold green points). In this case ${\mathcal {T}}_1={\mathcal {T}}_1^0\cup {\mathcal {T}}_1^+$ with ${\mathcal {T}}_1^+=\{t_1, t_3\}$ and ${\mathcal {T}}_1^0=\varnothing$. The function values and derivatives of $\phi _{+,1}(\cdot )$ are constrained on ${\mathcal {T}}_1$ to “compensate” for the function values and derivatives of $\phi _{0,1}(\cdot )$ on ${\mathcal {T}}_1$ in the sense of (38) and (39). The compensation is such that once the two polynomials are multiplied we obtain $\phi _1(\cdot )$ with the local maxima at level $\rho$ on ${\mathcal {T}}_1$ as shown in (c) (bold green points). The local minima of $\phi _1(\cdot )$ on ${\mathcal {T}}_2$ are produced “automatically”, because $\phi _{0,1}(\cdot )$ has zeros on ${\mathcal {T}}_2$. Note that the function values and the derivatives of $\phi _{+,1}(\cdot )$ can be controlled at $t_1$ and $t_3$ independently, because these two points are well-separated and this would have been impossible if these points where not well-separated. Right column: constructing $\phi _2(\cdot )$ as a product of $\phi _{0,2}(\cdot )$ and $\phi _{+,2}(\cdot )$. The construction is similar, with the roles of ${\mathcal {T}}_1$ and ${\mathcal {T}}_2$ reversed. The difference is that in this case ${\mathcal {T}}_2 = {\mathcal {T}}_2^0\cup {\mathcal {T}}_2^+$ with ${\mathcal {T}}_2^+=\{t_2\}$ and ${\mathcal {T}}_2^0=\{t_4\}$. Since ${\mathcal {T}}_2^0$ is nonempty, we set $\phi _{+,2}(t_4)=\phi '_{+,2}(t_4)=0$. Finally: observe that the scale in a and b is different from the scale in c and d; the level $\rho$ is marked for reference in a and b by a dotted line just above the zero line. The fact that $\rho =1/\mathrm {SRF}^{2r} \ll 1$ is responsible for the noise amplification. The setup is the same as in Figs. 7 and 8 (Color figure online)

The second term in the product,

$$\begin{aligned} \phi _{+,k}(t)\triangleq r^{2r}c_{u8}^{r}q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(t) \end{aligned}$$

(37)

is a (rescaled) trigonometric polynomial $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ constructed via Lemma 2 with $\lambda _c=r\lambda _{\mathrm {lo}}$, and ${\mathcal {V}}={\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$ and $c_{u8}$ is a positive numerical constant defined in (62) below. Further, the function-values and derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ are constrained on ${\mathcal {T}}_k={\mathcal {T}}_k^0\cup {\mathcal {T}}_k^+$ so that $\phi _{+,k}(\cdot )$ satisfies the following:

$$\begin{aligned} \phi _{+,k}(t)&={\left\{ \begin{array}{ll} 0, &{}t\in {\mathcal {T}}_k^0,\\ \rho \frac{1}{\phi _{0,k}(t)}, &{}t\in {\mathcal {T}}_k^+, \end{array}\right. } \end{aligned}$$

(38)

$$\begin{aligned} \phi '_{+,k}(t)&={\left\{ \begin{array}{ll} 0, &{}t\in {\mathcal {T}}_k^0,\\ -\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}, &{}t\in {\mathcal {T}}_k^+. \end{array}\right. } \end{aligned}$$

(39)

We will prove in Sect. 6.3.3 below, that this specification is valid, in the sense that the corresponding function values and derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ on ${\mathcal {T}}_k$ satisfy requirements (15) of Lemma 2.

It follows from (35), (36), (38), Lemma 1, Properties 2, 4, and 5 that the interpolation constraint (31) is satisfied:

$$\begin{aligned} \phi _k(t)= & {} \underbrace{\phi _{0,k}(t)}_0 \phi _{+,k}(t)=0 \text { for all } t\in {\mathcal {T}}_k^c,\\ \phi _k(t)= & {} \phi _{0,k}(t) \underbrace{\phi _{+,k}(t)}_0=0 \text { for all } t\in {\mathcal {T}}_k^0,\\ \phi _k(t)= & {} \phi _{0,k}(t) \phi _{+,k}(t)=\rho \text { for all } t\in {\mathcal {T}}_k^+. \end{aligned}$$

Next, by (35),

$$\begin{aligned} \phi '_k(t)=\phi '_{0,k}(t)\phi _{+,k}(t)+\phi _{0,k}(t)\phi '_{+,k}(t). \end{aligned}$$

Therefore, by (38), (39), Lemma 1, Properties 2, 4, and 5, the interpolation constraint (32) is satisfied:

$$\begin{aligned} \phi '_k(t)= & {} \underbrace{\phi '_{0,k}(t)}_0 \phi _{+,k}(t) +\underbrace{\phi _{0,k}(t)}_0\phi '_{+,k}(t)=0,\ \text {for all } t\in {\mathcal {T}}_k^c,\\ \phi '_k(t)= & {} \phi '_{0,k}(t)\underbrace{\phi _{+,k}(t)}_0 +\, \phi _{0,k}(t) \underbrace{\phi '_{+,k}(t)}_0=0,\ \text {for all } t\in {\mathcal {T}}_k^0,\\ \phi '_k(t)= & {} \phi '_{0,k}(t)\phi _{+,k}(t)+\phi _{0,k}(t)\phi '_{+,k}(t)\\= & {} \phi '_{0,k}(t)\rho \frac{1}{\phi _{0,k}(t)}-\phi _{0,k}(t)\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}=0,\ \text {for all }t\in {\mathcal {T}}_k^+. \end{aligned}$$

Finally, (30) follows from (35) because $\phi _{0,k}(\cdot )$ in (36) is frequency-limited to $(r-1)/(\lambda _{\mathrm {lo}}r)$ [Lemma 1, Property 1] and $\phi _{+,k}(\cdot )$ in (37) is frequency-limited to $1/(\lambda _{\mathrm {lo}}r)$ [Lemma 2, Property 1] so that $\phi _k(\cdot )$ is frequency-limited to $(r-1)/(\lambda _{\mathrm {lo}}r)+1/(\lambda _{\mathrm {lo}}r)=1/\lambda _{\mathrm {lo}}=f_{\mathrm {lo}}.$ Therefore, by (29), $q_1(\cdot )$ is also frequency-limited to $f_{\mathrm {lo}}$, which proves Property 1.

For $r=2$ the construction is illustrated in Fig. 9. In Fig. 9a trigonometric polynomials $\phi _{0,1}(\cdot )$ and $\phi _{+,1}(\cdot )$ are displayed; $\phi _{0,1}(t)=0$ for $t\in {\mathcal {T}}_2$ as indicated by the bold blue points; $\phi _{+,1}(\cdot )$ satisfies the interpolation constraints (38) and (39) on ${\mathcal {T}}_1$ as indicated by the bold green points. When we compute $\phi _1(\cdot )=(\phi _{0,1}\times \phi _{+,1})(\cdot )$ we obtain the trigonometric polynomial in Fig. 9c. The same process is displayed in Fig. 9b and d for $\phi _{0,2}(\cdot )$ and $\phi _{+,2}(\cdot )$. The trigonometric polynomials $\phi _1(\cdot )$ and $\phi _2(\cdot )$ in Fig. 9c and d are the same ones as in Fig. 8a.

6.3.2 Properties of $\phi _{0,k}(\cdot )$

We will now record useful properties of $\phi _{0,k}(\cdot )$ that are needed in the proof below. For $r=1$, according to (36), $\phi _{0,k}(t)=1$ for all t. For $r>1$, the following properties hold.

• 1. Controlled behavior near ${\mathcal {T}}_k^c$: Take $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$. Let

  $$\begin{aligned} \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k^c. \end{aligned}$$

  Note that since ${\mathcal {T}}_k^c\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,r-1)$ and $\Delta <\kappa$, it follows that $1\le {{\hat{r}}}\le r-1$. Then, the following estimates hold.

  • 1. Lower bound:

    $$\begin{aligned} \phi _{0,k}(\tau )&\ge c_{l2}^{r-1} \frac{ \prod _{l=1}^{{{\hat{r}}}}(v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

    (40)

  • 2. Upper bound:

    $$\begin{aligned} \phi _{0,k}(\tau )&\le c_u^{{{\hat{r}}}} \frac{ \prod _{l=1}^{{{\hat{r}}}}(v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

    (41)

  • 3. Upper bound on modulus of the first derivative:

    $$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(\tau )\right|}}{{\bigl |\phi _{0,k}'(\tau )\bigr |}}{{\left|\phi _{0,k}'(\tau )\right|}}{{\left|\phi _{0,k}'(\tau )\right|}}&\le \sum _{m=1}^{{{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _{l}-\tau )^{2}\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}\nonumber \\&+(r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}+1}}, \end{aligned}$$

    (42)

    where $c_{u3}$ is a positive numerical constant defined in the proof below.

  • 4. Upper bound on modulus of the second derivative:

    $$\begin{aligned}&\mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}}\nonumber \\&\ \le \sum _{1\le m\le {{\hat{r}}}} \sum _{\begin{array}{c} 1\le m'\le {{\hat{r}}}\\ m\ne m' \end{array}} {I[{{\hat{r}}}\ge 2]} c_{u3}^{{{\hat{r}}}} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m,\ l\ne m' \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-2)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2} \frac{\mathchoice{{\left|v^\tau _{m'}-\tau \right|}}{{\bigl |v^\tau _{m'}-\tau \bigr |}}{{\left|v^\tau _{m'}-\tau \right|}}{{\left|v^\tau _{m'}-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&\ +2(r-1-{{\hat{r}}})\sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}+1} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\frac{1}{r\lambda _{\mathrm {lo}}}\nonumber \\&\ +(r-1-{{\hat{r}}})^2 c_{u3}^{{{\hat{r}}}+2} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&\ + \sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{(r\lambda _{\mathrm {lo}})^2} \nonumber \\&\ + (r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}\frac{1}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

    (43)

• 5. Boundedness away from zero far from ${\mathcal {T}}_k^c$: for all $\tau \in {\mathcal {F}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$,

  $$\begin{aligned} \phi _{0,k}(\tau ) \ge c_{l1}^{r-1}>0. \end{aligned}$$

  (44)

• 6. Uniform confinement of the derivative:

  $$\begin{aligned} \Vert \phi _{0,k}'(\cdot )\Vert _{\infty }\le 2\pi /\lambda _{\mathrm {lo}}. \end{aligned}$$

  (45)

• 7. Uniform confinement of the second derivative:

  $$\begin{aligned} \Vert \phi _{0,k}''(\cdot )\Vert _{\infty }\le c_{u5}/\lambda _{\mathrm {lo}}^2. \end{aligned}$$

  (46)

• 8. Fast growth immediately away from ${\mathcal {T}}_k^c$: for all $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}}_k^c)$,

  $$\begin{aligned} \phi _{0,k}(\tau )\ge c_l^{r-1} \frac{\lambda _{\mathrm {hi}}^{2(r-1)}}{(r\lambda _{\mathrm {lo}})^{2(r-1)}}. \end{aligned}$$

  (47)

Next, we give the proofs of the properties.

Proof of properties 1a–1b These properties are derived in the same way as Properties 4a and 4b in Lemma 3.

Proof of property 1c To prove (42), observe

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(\tau )\right|}}{{\bigl |\phi _{0,k}'(\tau )\bigr |}}{{\left|\phi _{0,k}'(\tau )\right|}}{{\left|\phi _{0,k}'(\tau )\right|}} = \mathchoice{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] '\right|}}{{\bigl |\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] '\bigr |}}{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] '\right|}}{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] '\right|}} \le \sum _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} \mathchoice{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}} \mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}'(\tau )\right|}}. \end{aligned}$$

(48)

Above, we applied the chain rule for derivative to (36) and used the triangle inequality.

To upper-bound the sum in (48), we upper-bound quantities $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}$ and $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}$ separately. To upper-bound $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}$ we use the same bounds as in (24) and (25). To upper-bound $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}$ we use a similar strategy as follows. Assume that m is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_m\ne \varnothing$, i.e., there exist $l\in \{1,\ldots ,{{\hat{r}}}\}$ that satisfies $v^\tau _l\in {\mathcal {T}}_m$. In this case, according to Lemma 1, Property 2, $q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(v^\tau _l)=0$ and according to Lemma 1, Property 7, $\mathchoice{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(t)\right|}}{{\bigl |q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(t)\bigr |}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(t)\right|}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(t)\right|}}\le 4\pi ^2/(r\lambda _{\mathrm {lo}})^2$ for all t. This, by (194) [Mean Value theorem], gives the following bound:

$$\begin{aligned} \mathchoice{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\bigl |q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\bigr |}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}\le c_{u2}\frac{\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(49)

Assume that m is such that ${\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_m=\varnothing$. In this case, we use Lemma 1, Property 6, to write

$$\begin{aligned} \mathchoice{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\bigl |q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\bigr |}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}\le 2\pi \frac{1}{r\lambda _{\mathrm {lo}}}. \end{aligned}$$

(50)

Plugging the estimates for $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}$ [(24) and (25)], (49), and (50) into (48), setting $c_{u3}\triangleq \max (2\pi , 4\pi ^2, c_u)$ we obtain (42).

Proof of property 1d To prove (43), observe

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}}&= \mathchoice{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] ''\right|}}{{\bigl |\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] ''\bigr |}}{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] ''\right|}}{{\left|\left[ \prod _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right] ''\right|}} \nonumber \\&\le \!\!\sum _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}}\!\! \sum _{\begin{array}{c} 1\le m'\le r\\ m'\ne k, m'\ne m \end{array}} \!\mathchoice{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m, j\ne m' \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m, j\ne m' \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m, j\ne m' \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m, j\ne m' \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}} \mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}} \mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m'}}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m'}}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m'}}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m'}}'(\tau )\right|}}\nonumber \\&+\sum _{\begin{array}{c} 1\le m\le r\\ m\ne k \end{array}} \mathchoice{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|\prod _{\begin{array}{c} 1\le j\le r\\ j\ne k, j\ne m \end{array}} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}} \mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}. \end{aligned}$$

(51)

To upper-bound the sum in (51), we upper-bound the quantities $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}$, $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}'(\tau )\right|}}$, and $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_{m}}''(\tau )\right|}}$ separately. To upper-bound $\mathchoice{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\bigl |q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\bigr |}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}{{\left|q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_j}(\tau )\right|}}$ and $\mathchoice{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\bigl |q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\bigr |}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\left|q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}$ we use estimates (24), (25) and (49), (50), respectively. To upper-bound $\mathchoice{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\bigl |q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\bigr |}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}$ we use Lemma 1, Property 7, to write

$$\begin{aligned} \mathchoice{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\bigl |q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\bigr |}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}{{\left|q''_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_m}(\tau )\right|}}\le 4\pi ^2\frac{1}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

Plugging these estimates into (51), we obtain (43).

Proof of properties 2–5 Property 2 follows by (36) and Lemma 1, Property 5. Property 3 follow from (48) and from Lemma 1, Property 6:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(\tau )\right|}}{{\bigl |\phi _{0,k}'(\tau )\bigr |}}{{\left|\phi _{0,k}'(\tau )\right|}}{{\left|\phi _{0,k}'(\tau )\right|}}\le (r-1)\frac{2\pi }{r\lambda _{\mathrm {lo}}}<\frac{2\pi }{\lambda _{\mathrm {lo}}}. \end{aligned}$$

Property 4 follow from (51) and from Lemma 1, Properties 6 and 7:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}} \le (r-1)(r-2)\frac{4\pi ^2}{(r\lambda _{\mathrm {lo}})^2} +(r-1)\frac{4\pi ^2}{(r\lambda _{\mathrm {lo}})^2}<\frac{8\pi ^2}{\lambda _{\mathrm {lo}}^2}, \end{aligned}$$

where we defined $c_{u5}\triangleq 8\pi ^2$. Finally, Property 5 follows from (36), (13), Lemma 1, Property 5, and (14).

6.3.3 Existence of $\phi _{+,k}(\cdot )$

In this subsection, we check that trigonometric polynomial $\phi _{+,k}(\cdot )$ that satisfies (38) and (39) can indeed be defined according to (37) with $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}$ constructed via Lemma 2 with $\lambda _c=r\lambda _{\mathrm {lo}}$ and ${\mathcal {V}}={\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. To this end, we need to show that the constraints on the function values $\{f_j\}$ and on the derivatives $\{d_j\}$ that are implied by the constraints (38) and (39) satisfy requirements (15) of Lemma 2.

First consider the case $r=1$. As already discussed, in this case $\phi _{0,k}(t)=1$ for all t, and, therefore, $\phi '_{0,k}(t)=0$ for all t. Plugging these values into (38) and (39) we see from (37) that the requirements (15) of Lemma 2 are satisfied.

Next, consider the case $r>1$.

For $t\in {\mathcal {T}}_k^0$, by (37), (38), (39), $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(t)=q'_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(t)=0$ so that requirements (15) of Lemma 2, are satisfied.

To check that requirements (15) are also satisfied for $t\in {\mathcal {T}}_k^+$, we need to find upper bounds on $\mathchoice{{\left|\phi _{+,k}(\cdot )\right|}}{{\bigl |\phi _{+,k}(\cdot )\bigr |}}{{\left|\phi _{+,k}(\cdot )\right|}}{{\left|\phi _{+,k}(\cdot )\right|}}$ and $\mathchoice{{\left|\phi _{+,k}'(\cdot )\right|}}{{\bigl |\phi _{+,k}'(\cdot )\bigr |}}{{\left|\phi _{+,k}'(\cdot )\right|}}{{\left|\phi _{+,k}'(\cdot )\right|}}$.

Take $t\in {\mathcal {T}}_k^+$ and observe:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(t)\right|}}{{\bigl |\phi _{+,k}(t)\bigr |}}{{\left|\phi _{+,k}(t)\right|}}{{\left|\phi _{+,k}(t)\right|}}&{\mathop {=}\limits ^{(a)}}\mathchoice{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}}{{\bigl |\rho \frac{1}{\phi _{0,k}(t)}\bigr |}}{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}}{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}} {\mathop {\le }\limits ^{(b)}} \frac{\lambda _{\mathrm {hi}}^{2r}}{\lambda _{\mathrm {lo}}^{2r}} \frac{1}{\frac{\lambda _{\mathrm {hi}}^{2(r-1)}}{(r\lambda _{\mathrm {lo}})^{2(r-1)}}} \frac{1}{c_l^{r-1}} {\mathop {\le }\limits ^{(c)}} r^{2(r-1)} \frac{1}{c_l^{r}} \frac{\lambda _{\mathrm {hi}}^{2}}{\lambda _{\mathrm {lo}}^{2}} \end{aligned}$$

(52)

$$\begin{aligned}&\le r^{2r}\frac{1}{c_l^{r}}. \end{aligned}$$

(53)

Above, (a) follows by (38); (b) follows by (47) which is valid because $t\in {\mathcal {T}}_k^+$ implies $t\in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}}_k^c)$; (c) follows because $c_l<1$.

Next, take $t\in {\mathcal {T}}_k^+$ and observe, according to (39),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}}=\mathchoice{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\bigl |\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\bigr |}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}. \end{aligned}$$

(54)

Consider two cases.

Case 1: $t\in {\mathcal {F}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$. Then, by (44), $\phi _{0,k}(t) \ge c_{l1}^{r-1}$, and, by (45), $\mathchoice{{\left|\phi _{0,k}'(t)\right|}}{{\bigl |\phi _{0,k}'(t)\bigr |}}{{\left|\phi _{0,k}'(t)\right|}}{{\left|\phi _{0,k}'(t)\right|}}\le 2\pi /\lambda _{\mathrm {lo}}$. Plugging these estimates into (54) we obtain

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}} \le \mathchoice{{\left|\rho \frac{2\pi }{c_{l1}^{r-1}}\frac{1}{\lambda _{\mathrm {lo}}}\right|}}{{\bigl |\rho \frac{2\pi }{c_{l1}^{r-1}}\frac{1}{\lambda _{\mathrm {lo}}}\bigr |}}{{\left|\rho \frac{2\pi }{c_{l1}^{r-1}}\frac{1}{\lambda _{\mathrm {lo}}}\right|}}{{\left|\rho \frac{2\pi }{c_{l1}^{r-1}}\frac{1}{\lambda _{\mathrm {lo}}}\right|}} {\mathop {\le }\limits ^{(a)}} \frac{2\pi }{c_{l1}^{2r-2}}\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2} {\mathop {<}\limits ^{(b)}} r^{2r-1} \left( \frac{2\pi }{c_{l1}^{2}}\right) ^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(55)

Above, in (a) we used $\rho =(\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}})^{2r}\le \lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}$; (b) is a crude inequality where we used $c_{l1}<1$.

Case 2: $t\in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$. In this case set $\{v_1,\ldots ,v_{{{\hat{r}}}}\}\triangleq {\mathcal {T}}_k^c\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},t)$ and note $1\le {{\hat{r}}}\le r-1$. Hence, by (40):

$$\begin{aligned} \phi _{0,k}(t)\ge c_{l2}^{r-1}\frac{ \prod _{j=1}^{{{\hat{r}}}}(v_j-t)^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

(56)

By (42):

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(t)\right|}}{{\bigl |\phi _{0,k}'(t)\bigr |}}{{\left|\phi _{0,k}'(t)\right|}}{{\left|\phi _{0,k}'(t)\right|}}\le \sum _{m=1}^{{{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v_{l}-t)^{2}\mathchoice{{\left|v_m-t\right|}}{{\bigl |v_m-t\bigr |}}{{\left|v_m-t\right|}}{{\left|v_m-t\right|}}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} +(r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v_{l}-t)^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}+1}}.\nonumber \\ \end{aligned}$$

(57)

Plugging (56) and (57) into (54):

$$\begin{aligned} \frac{\mathchoice{{\left|\phi '_{0,k}(t)\right|}}{{\bigl |\phi '_{0,k}(t)\bigr |}}{{\left|\phi '_{0,k}(t)\right|}}{{\left|\phi '_{0,k}(t)\right|}}}{\phi _{0,k}^2(t)}&\le \sum _{m=1}^{{{\hat{r}}}} \frac{c_{u3}^{{{\hat{r}}}}}{c_{l2}^{2(r-1)}} \frac{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}{\prod _{\begin{array}{c} 1\le j\le {{\hat{r}}}\\ j\ne r \end{array}} (v_{j}-t)^{2}\mathchoice{{\left|v_m-t\right|}}{{\bigl |v_m-t\bigr |}}{{\left|v_m-t\right|}}{{\left|v_m-t\right|}}^3} \nonumber \\&+(r-1-{{\hat{r}}}) \frac{c_{u3}^{{{\hat{r}}}+1}}{c_{l2}^{2(r-1)}} \frac{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}-1}}{\prod _{j=1}^{{{\hat{r}}}} (v_{j}-t)^{2}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2{{\hat{r}}}+1}\frac{c_{u3}^{{{\hat{r}}}+1}}{c_{l2}^{2(r-1)}} \left( \frac{\lambda _{\mathrm {lo}}^{2{{\hat{r}}}}}{\lambda _{\mathrm {hi}}^{2{{\hat{r}}}+1}}+\frac{\lambda _{\mathrm {lo}}^{2{{\hat{r}}}-1}}{\lambda _{\mathrm {hi}}^{2{{\hat{r}}}}}\right) \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r-1}\frac{c_{u3}^{r}}{c_{l2}^{2(r-1)}} \left( \frac{\lambda _{\mathrm {lo}}^{2r-2}}{\lambda _{\mathrm {hi}}^{2r-1}} +\frac{\lambda _{\mathrm {lo}}^{2r-3}}{\lambda _{\mathrm {hi}}^{2r-2}}\right) \nonumber \\&{\mathop {\le }\limits ^{(c)}} 2r^{2r-1}\left( \frac{c_{u3}}{c_{l2}^2}\right) ^r\frac{\lambda _{\mathrm {lo}}^{2r-2}}{\lambda _{\mathrm {hi}}^{2r-1}} {\mathop {\le }\limits ^{(d)}} r^{2r-1} c_{u6}^r\frac{\lambda _{\mathrm {lo}}^{2r-2}}{\lambda _{\mathrm {hi}}^{2r-1}}. \end{aligned}$$

(58)

Above, in (a) we used that $\mathchoice{{\left|v_{j}-t\right|}}{{\bigl |v_{j}-t\bigr |}}{{\left|v_{j}-t\right|}}{{\left|v_{j}-t\right|}}\ge 2\lambda _{\mathrm {hi}}$ for all $j=1,\ldots ,{{\hat{r}}}$, $r-1-{{\hat{r}}}\le r$, and $c_{u3}>1$; in (b) we used that ${{\hat{r}}}\le r-1$, $\lambda _{\mathrm {lo}}/\lambda _{\mathrm {hi}}>1$, and $c_{u3}>1$; in (c) we used $\lambda _{\mathrm {lo}}/\lambda _{\mathrm {hi}}>1$ and $c_{l2}<1$; in (d) we defined $c_{u6}\triangleq 2 c_{u3}/c_{l2}^2$. Plugging the estimate (58) into (54),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}}&\le r^{2r-1} c_{u6}^r\frac{\lambda _{\mathrm {hi}}^{2r}}{\lambda _{\mathrm {lo}}^{2r}} \frac{\lambda _{\mathrm {lo}}^{2r-2}}{\lambda _{\mathrm {hi}}^{2r-1}} =r^{2r-1} c_{u6}^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(59)

Combining (55) and (59) we find that for all $t\in {\mathcal {T}}_k^+$,

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}}&\le r^{2r-1}c_{u7}^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2} \end{aligned}$$

(60)

$$\begin{aligned}&\le r^{2r-1}c_{u7}^r\frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(61)

where we defined $c_{u7}\triangleq \max (c_{u6}, c_{u1}/c_{l1}^{2})$.

It follows from (53) and (61) that the function values and derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(t)=\phi _{+,k}(t)/(r^{2r}c_{u8}^{r})$ with

$$\begin{aligned} c_{u8}\triangleq \max (c_{u7}, 1/c_l) \end{aligned}$$

(62)

satisfy requirements (15) of Lemma 2 on ${\mathcal {T}}_k^+$. We conclude that $\phi _{+,k}(\cdot )$ can indeed be defined according to (37). According to Properties 3, 4, and 5 of Lemma 2, and (37), $\phi _{+,k}(\cdot )$ satisfies the following properties:

$$\begin{aligned}&\Vert \phi _{+,k}(\cdot )\Vert _{\infty }\le r^{2r}c_{u8}^{r}c_{u0}, \end{aligned}$$

(63)

$$\begin{aligned}&\Vert \phi _{+,k}'(\cdot )\Vert _{\infty }\le r^{2r-1}c_{u8}^{r} c_{u1}\frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(64)

$$\begin{aligned}&\Vert \phi _{+,k}''(\cdot )\Vert _{\infty }\le r^{2r-2}c_{u8}^{r} c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(65)

6.3.4 Proof of Property 2

Take $j\in \{1,\ldots , S\}$ and consider $t_j\in {\mathcal {T}}$. There exists a unique $l\in \{1,\ldots ,r\}$ such that $t_j\in {\mathcal {T}}_l$. We will show that for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$

$$\begin{aligned} \mathchoice{{\left|\phi _l(\tau )-\eta _j\right|}}{{\bigl |\phi _l(\tau )-\eta _j\bigr |}}{{\left|\phi _l(\tau )-\eta _j\right|}}{{\left|\phi _l(\tau )-\eta _j\right|}}\le r^{2r+3} c_{u24}^{r+1} q_0(\tau ) \end{aligned}$$

(66)

and

$$\begin{aligned} \mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}}\le r^{2r+3} c_{u26}^{r+1} q_0(\tau ),\ \text {for}\ k\in \{1,\ldots , r\},\ k\ne l, \end{aligned}$$

(67)

where the positive numerical constants $c_{u24}$ and $c_{u26}$ are defined below.

From this we will conclude that

$$\begin{aligned} \mathchoice{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}}{{\bigl |q_1(\tau )-\frac{\rho s_j}{2}\bigr |}}{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}}{{\left|q_1(\tau )-\frac{\rho s_j}{2}\right|}}&=\mathchoice{{\left|\sum _{k=1}^r\phi _k(\tau ) -\frac{\rho }{2}-\frac{\rho s_j}{2}\right|}}{{\bigl |\sum _{k=1}^r\phi _k(\tau ) -\frac{\rho }{2}-\frac{\rho s_j}{2}\bigr |}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\frac{\rho }{2}-\frac{\rho s_j}{2}\right|}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\frac{\rho }{2}-\frac{\rho s_j}{2}\right|}}\\&=\mathchoice{{\left|\sum _{k=1}^r\phi _k(\tau ) -\eta _j\right|}}{{\bigl |\sum _{k=1}^r\phi _k(\tau ) -\eta _j\bigr |}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\eta _j\right|}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\eta _j\right|}}\\&\le \sum _{k\ne l}^r\mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}}+ \mathchoice{{\left|\phi _l(\tau ) -\eta _j\right|}}{{\bigl |\phi _l(\tau ) -\eta _j\bigr |}}{{\left|\phi _l(\tau ) -\eta _j\right|}}{{\left|\phi _l(\tau ) -\eta _j\right|}} \le r^{2r+4} c_{u27}^{r+1} q_0(\tau ) \end{aligned}$$

with $c_{u27}\triangleq 2\max (c_{u24}, c_{u26})$, as desired.

To prove (66) and (67), recall, by (31) and (32):

$$\begin{aligned}&\mathchoice{{\left|\phi _l(t_j)-\eta _j\right|}}{{\bigl |\phi _l(t_j)-\eta _j\bigr |}}{{\left|\phi _l(t_j)-\eta _j\right|}}{{\left|\phi _l(t_j)-\eta _j\right|}} = 0 = q_0(t_j), \end{aligned}$$

(68)

$$\begin{aligned}&\phi _k(t_j) = 0 = q_0(t_j), \text {for}\ k\in \{1,\ldots , r\},\ k\ne l, \end{aligned}$$

(69)

$$\begin{aligned}&\phi '_k(t_j)=0=q'_0(t_j), \text {for}\ k\in \{1,\ldots , r\}. \end{aligned}$$

(70)

Hence, in order to prove the bounds in (67) and (66), we will derive upper bounds on the second derivatives $\mathchoice{{\left|\phi ''_k(\tau )\right|}}{{\bigl |\phi ''_k(\tau )\bigr |}}{{\left|\phi ''_k(\tau )\right|}}{{\left|\phi ''_k(\tau )\right|}}$, $k\in \{1,\ldots ,r\}$, valid for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ and use the Mean Value theorem (see Theorem 3).

Taking the second derivative of (35) and applying the triangle inequality we find:

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}} \le \underbrace{\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}}_{E_{1}(\tau )} +2\underbrace{\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}}_{E_{2}(\tau )} +\underbrace{\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}}_{E_3(\tau )}. \end{aligned}$$

(71)

In the derivation below we upper-bound the terms separately.

We will need the following notations. Set $\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k^c$ and set $\{v_1,\ldots ,v_{{\tilde{r}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\cap {\mathcal {T}}_k^c$. Note that the set $\{v_1,\ldots ,v_{{\tilde{r}}}\}$ does not depend on $\tau$ and also $\{v_1,\ldots ,v_{{\tilde{r}}}\}\subset \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$ so that ${\tilde{r}}\le {{\hat{r}}}$.

The remainder of the proof of Property 2 is organized as follows. First, consider the case $t_j\in {\mathcal {T}}_k$ and prove (66), next consider the case $t_j\in {\mathcal {T}}_k^c$ and prove (67).

Proof of (66): case $t_j\in {\mathcal {T}}_k$. Bounding $E_1(\tau )$: By (195) [Mean Value theorem] and the triangle inequality we can write

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi _{+,k}(t_j)\right|}}{{\bigl |\phi _{+,k}(t_j)\bigr |}}{{\left|\phi _{+,k}(t_j)\right|}}{{\left|\phi _{+,k}(t_j)\right|}}+\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}\mathchoice{{\left|\tau - t_j\right|}}{{\bigl |\tau - t_j\bigr |}}{{\left|\tau - t_j\right|}}{{\left|\tau - t_j\right|}} +\frac{1}{2}\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}(\tau - t_j)^2 \end{aligned}$$

with $\tau _m\in (t_j, \tau )$. Next, we use (38) and (52) to upper-bound $\mathchoice{{\left|\phi _{+,k}(t_j)\right|}}{{\bigl |\phi _{+,k}(t_j)\bigr |}}{{\left|\phi _{+,k}(t_j)\right|}}{{\left|\phi _{+,k}(t_j)\right|}}$ by the right-hand side of (52); use (39) and (60) to upper bound $\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}$ by the right-hand side of (60); use (65) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&\le r^{2r-1}c_{u9}^r\left( \frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2} +\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}} +\frac{1}{\lambda _{\mathrm {lo}}^2}(\tau -t_j)^2\right) \le r^{2r-1}c_{u10}^r\frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(72)

Above, we defined $c_{u9}\triangleq \max (1/c_l,c_{u7}, c_{u8}c_{u2})$, $c_{u10}\triangleq 3 c_{u9}$, and used

$\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\le \lambda _{\mathrm {hi}}$.

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that we can use (43) to upper-bound $\mathchoice{{\left|\phi ''_{0,k}(t)\right|}}{{\bigl |\phi ''_{0,k}(t)\bigr |}}{{\left|\phi ''_{0,k}(t)\right|}}{{\left|\phi ''_{0,k}(t)\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}}&\le \sum _{1\le m\le {{\hat{r}}}} \sum _{\begin{array}{c} 1\le m'\le {{\hat{r}}}\\ m\ne m' \end{array}} {I[{{\hat{r}}}\ge 2]}c_{u3}^{{{\hat{r}}}} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m,\ l\ne m' \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-2)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2} \frac{\mathchoice{{\left|v^\tau _{m'}-\tau \right|}}{{\bigl |v^\tau _{m'}-\tau \bigr |}}{{\left|v^\tau _{m'}-\tau \right|}}{{\left|v^\tau _{m'}-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&+2(r-1-{{\hat{r}}})\sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\frac{1}{r\lambda _{\mathrm {lo}}}\nonumber \\&+(r-1-{{\hat{r}}})^2 c_{u3}^{{{\hat{r}}}+2} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&+ \sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{(r\lambda _{\mathrm {lo}})^2} \nonumber \\&+(r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}\frac{1}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(73)

Multiplying (72) and (73) and simplifying we obtain the following upper bound on $E_1$:

$$\begin{aligned} E_1(\tau )=\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r+1} c_{u11}^{r+1} \frac{\prod _{1\le l\le {{\hat{r}}}} (v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}\frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r+1} c_{u11}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(74)

Above, in (a) we used (multiple times) the bound $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}$, which is true for all $l\in \{1,\ldots ,{{\hat{r}}}\}$ (follows because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$), used $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$, and defined $c_{u11}\triangleq \max (6 c_{u3}c_{u10}, c_{u8}c_{u0}c_{u5})$; in (b) we used the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper-bound (74) also holds by (46) and (63).

Bounding $E_2(\tau )$: By (194) [Mean Value theorem] we can write

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi '_{+,k}(t_j)\right|}}{{\bigl |\phi '_{+,k}(t_j)\bigr |}}{{\left|\phi '_{+,k}(t_j)\right|}}{{\left|\phi '_{+,k}(t_j)\right|}}+\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}\mathchoice{{\left|\tau - t_j\right|}}{{\bigl |\tau - t_j\bigr |}}{{\left|\tau - t_j\right|}}{{\left|\tau - t_j\right|}} \end{aligned}$$

with $\tau _m\in (t_j, \tau )$. Next, we use (39) and (60) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}$ by the right-hand side of (60); use (65) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}&\le r^{2r-1} c_{u12}^r\left( \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}+\frac{1}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\right) \le r^{2r-1} c_{u13}^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(75)

Above, we defined $c_{u12}\triangleq \max (c_{u7}, c_{u2}c_{u8})$, $c_{u13}\triangleq 2 c_{u12}$, and used $\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\le \lambda _{\mathrm {hi}}$.

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that we can use (42) to upper-bound $\mathchoice{{\left|\phi '_{0,k}(t)\right|}}{{\bigl |\phi '_{0,k}(t)\bigr |}}{{\left|\phi '_{0,k}(t)\right|}}{{\left|\phi '_{0,k}(t)\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(\tau )\right|}}{{\bigl |\phi _{0,k}'(\tau )\bigr |}}{{\left|\phi _{0,k}'(\tau )\right|}}{{\left|\phi _{0,k}'(\tau )\right|}} \le \sum _{m=1}^{{{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _{l}-\tau )^{2}\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} +(r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}+1}}. \nonumber \\ \end{aligned}$$

(76)

Multiplying (75) and (76) and simplifying we obtain the following upper bound on $E_2$:

$$\begin{aligned} E_2(\tau )=\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r} c_{u14}^{r} \frac{\prod _{1\le l\le {{\hat{r}}}} (v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r} c_{u14}^{r} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(77)

Above, in (a) we used the bound $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}$, which is true for all $l\in \{1,\ldots ,{{\hat{r}}}\}$ (follows because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$), used $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$, and defined $c_{u14}\triangleq \max (2 c_{u13}c_{u3}, 2\pi c_{u8}c_{u1})$; in (b) we used the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper bound (77) also holds by (45) and (64).

Bounding $E_3(\tau )$: By (65),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}''(\tau )\right|}}{{\bigl |\phi _{+,k}''(\tau )\bigr |}}{{\left|\phi _{+,k}''(\tau )\right|}}{{\left|\phi _{+,k}''(\tau )\right|}}\le r^{2r-2}c_{u8}^{r} c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(78)

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that we can use (41) to upper-bound $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}&\le c_u^{{{\hat{r}}}}\frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

(79)

Multiplying (78) and (79) and simplifying we obtain the following upper bound on $E_3$:

$$\begin{aligned} E_3(\tau ) =\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r-2}c_{u15}^{r} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r-2}c_{u15}^{r} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(80)

Above, (a) we defined $c_{u15}\triangleq c_{u8}c_{u2}c_u$; in (b) we use the fact that

$\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper-bound (80) also holds by (78) because by (36) and Lemma 1, Property 3, $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}<1$ and because $c_u>1$ and $c_{u2}>1$.

From (71), (74), (77), and (80) we conclude that

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}} \le r^{2r+1} c_{u16}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}, \end{aligned}$$

(81)

where we defined $c_{u16}\triangleq 4 \max (c_{u11}, c_{u14}, c_{u15})$.

Putting pieces together: On the one hand, by (195) [Mean Value theorem], using (68), (70), (81) and we can write for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$:

$$\begin{aligned} \mathchoice{{\left|\phi _l(\tau )-\eta _j\right|}}{{\bigl |\phi _l(\tau )-\eta _j\bigr |}}{{\left|\phi _l(\tau )-\eta _j\right|}}{{\left|\phi _l(\tau )-\eta _j\right|}}&{\mathop {\le }\limits ^{(a)}} \frac{1}{2} r^{2r+1} c_{u16}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} \frac{1}{2} r^{2r+1} c_{u16}^{r+1} 2^{{\tilde{r}}} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+3} c_{u23}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(82)

Above, in (a) $\tau _m\in (t_j, \tau )$; in (b) we used that $\mathchoice{{\left|v_l-\tau _m\right|}}{{\bigl |v_l-\tau _m\bigr |}}{{\left|v_l-\tau _m\right|}}{{\left|v_l-\tau _m\right|}}<\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}$, which is true because $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ and because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$; in (c) we defined $c_{u23}\triangleq 2c_{u16}$.

On the other hand, let $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}$. Then, by (16),

$$\begin{aligned} q_0(\tau )&\ge c_{l2}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}} \nonumber \\&{\mathop {\ge }\limits ^{(a)}} c_{l2}^r\frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{(r\lambda _{\mathrm {lo}})^2} \underbrace{ \left( \frac{(r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}})^2}{(r\lambda _{\mathrm {lo}})^2}\right) ^{\breve{r}-{\tilde{r}}-1} }_{P_1} \nonumber \\&{\mathop {\ge }\limits ^{(b)}} c_{l3}^r\frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(83)

Above, in (a) we use the fact that $\{v_1,\ldots ,v_{\tilde{r}}\}\cup \{t_j\}\subset \{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}$ and the fact that by construction of the set $\{v_1,\ldots ,v_{\tilde{r}}\}$ it follows that if, for some k, $u^\tau _k\notin \{v_1,\ldots ,v_{{{\tilde{r}}}}\}\cup \{t_j\}$, then $\mathchoice{{\left|u^\tau _k-\tau \right|}}{{\bigl |u^\tau _k-\tau \bigr |}}{{\left|u^\tau _k-\tau \right|}}{{\left|u^\tau _k-\tau \right|}}\ge r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}}$; in (b) we used the assumption $\mathrm {SRF}\ge 12$ so that $\lambda _{\mathrm {hi}}\le \lambda _{\mathrm {lo}}/12$ and therefore $r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}}\ge r(\Delta -1/6)\lambda _{\mathrm {lo}}$, used that $0<\Delta -1/6<1$, which implies that $P_1\ge (\Delta -1/6)^{2r}$, and defined $c_{l3}\triangleq c_{l2}(\Delta -1/6)^2$ that satisfies $0<c_{l3}<1$.

The bound (66) follows from (82) and (83) by defining $c_{u24}\triangleq c_{u23}/c_{l3}$.

Proof of (67): case $t_j\in {\mathcal {T}}^c_k$. We only need to consider this case when $r>1$. Indeed, when $r=1$, the sum in (29) only contains one element, $\phi _l(\cdot )$, and, necessarily, $t_j\in {\mathcal {T}}_l$ because ${\mathcal {T}}_l^c$ is empty.

In this case $t_j$ is one of the elements among $\{v_1,\ldots ,v_{{\tilde{r}}}\}\subset \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$; in other words, $t_j=v_{{{\tilde{m}}}}=v^\tau _{{\hat{m}}}$ for some $1\le {{\tilde{m}}}\le {\tilde{r}}, 1\le {\hat{m}}\le {{\hat{r}}}$. The set ${\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)$ is either empty or contains exactly one element. Let $b\triangleq \mathchoice{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}{{\bigl |{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\bigr |}}{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}$. In the case when $b=1$, let $\{{{\tilde{t}}}\}\triangleq {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)$.

Bounding $E_1(\tau )$: Consider the case $b=1$. By (195) [Mean Value theorem] we can write

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi _{+,k}(\tilde{t})\right|}}{{\bigl |\phi _{+,k}(\tilde{t})\bigr |}}{{\left|\phi _{+,k}(\tilde{t})\right|}}{{\left|\phi _{+,k}(\tilde{t})\right|}}+\mathchoice{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}}{{\bigl |\phi _{+,k}'({{\tilde{t}}})\bigr |}}{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}}{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}} \mathchoice{{\left|\tau - \tilde{t}\right|}}{{\bigl |\tau - \tilde{t}\bigr |}}{{\left|\tau - \tilde{t}\right|}}{{\left|\tau - \tilde{t}\right|}}+\frac{1}{2}\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}(\tau - {{\tilde{t}}})^2 \end{aligned}$$

with $\tau _m\in ({{\tilde{t}}}, \tau )$. Next, we use (38) and (52) to upper-bound $\mathchoice{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\bigl |\phi _{+,k}({{\tilde{t}}})\bigr |}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}$ by the right-hand side of (52); use (39) and (60) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\bigl |\phi _{+,k}'(\tilde{t})\bigr |}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}$ by the right-hand side of (60); use (65) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&\le r^{2r-1}c_{u9}^r\left( \frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2} +\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -{{\tilde{t}}}\right|}}{{\bigl |\tau -{{\tilde{t}}}\bigr |}}{{\left|\tau -{{\tilde{t}}}\right|}}{{\left|\tau -{{\tilde{t}}}\right|}} +\frac{1}{\lambda _{\mathrm {lo}}^2}(\tau -{{\tilde{t}}})^2\right) \nonumber \\&\le r^{2r+1} c_{u10}^r\frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2} = r^{2r+1} c_{u10}^r\left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]}, \end{aligned}$$

(84)

where we used that $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$ because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ with ${{\tilde{t}}}\ne t_j$. According to (63) the upper bound (84) also holds for $b=0$.

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that we can use (43) to upper-bound $\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}}&\le \sum _{1\le m\le {{\hat{r}}}} \sum _{\begin{array}{c} 1\le m'\le {{\hat{r}}}\\ m\ne m' \end{array}} {I[{{\hat{r}}}\ge 2]} c_{u3}^{{{\hat{r}}}} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m,\ l\ne m' \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-2)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2} \frac{\mathchoice{{\left|v^\tau _{m'}-\tau \right|}}{{\bigl |v^\tau _{m'}-\tau \bigr |}}{{\left|v^\tau _{m'}-\tau \right|}}{{\left|v^\tau _{m'}-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&+2(r-1-{{\hat{r}}})\sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^2}\frac{1}{r\lambda _{\mathrm {lo}}}\nonumber \\&+(r-1-{{\hat{r}}})^2 c_{u3}^{{{\hat{r}}}+2} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{(r\lambda _{\mathrm {lo}})^2}\nonumber \\&+ \sum _{1\le m\le {{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{ \prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{(r\lambda _{\mathrm {lo}})^2} \nonumber \\&+(r-1-{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{(r\lambda _{\mathrm {lo}})^2} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^2c_{u17}^{r+1} \frac{ \prod _{1\le l\le {{\hat{r}}}, l\ne {\hat{m}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}. \end{aligned}$$

(85)

Above, in (a) we used (multiple times) the fact that $\mathchoice{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\bigl |v^\tau _{{\hat{m}}}-\tau \bigr |}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}\le \mathchoice{{\left|v^\tau _{l}-\tau \right|}}{{\bigl |v^\tau _{l}-\tau \bigr |}}{{\left|v^\tau _{l}-\tau \right|}}{{\left|v^\tau _{l}-\tau \right|}}$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, the fact ${{\hat{r}}}\le r-1$, and defined $c_{u17}\triangleq 6 c_{u3}$.

Multiplying (84) and (85) and simplifying we obtain the following upper bound on $E_1$:

$$\begin{aligned} E_1(\tau )&=\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u18}^{r+1} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{ \prod _{1\le l\le {{\hat{r}}}, l\ne {\hat{m}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u18}^{r+1} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(86)

Above, in (a) we defined $c_{u18}\triangleq c_{u10}c_{u17}$; in (b) we used that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

Bounding $E_2(\tau )$: Consider the case $b=1$. By (194) [Mean Value theorem] we can write

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}\le \mathchoice{{\left|\phi '_{+,k}(\tilde{t})\right|}}{{\bigl |\phi '_{+,k}(\tilde{t})\bigr |}}{{\left|\phi '_{+,k}(\tilde{t})\right|}}{{\left|\phi '_{+,k}(\tilde{t})\right|}}+\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}\mathchoice{{\left|\tau - {{\tilde{t}}}\right|}}{{\bigl |\tau - {{\tilde{t}}}\bigr |}}{{\left|\tau - {{\tilde{t}}}\right|}}{{\left|\tau - {{\tilde{t}}}\right|}} \end{aligned}$$

with $\tau _m\in ({{\tilde{t}}}, \tau )$. Next, we use (39) and (60) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\bigl |\phi _{+,k}'(\tilde{t})\bigr |}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}$ by the right-hand side of (60); use (65) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \le r^{2r-1}c_{u12}^r\left( \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2} +\frac{1}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -\tilde{t}\right|}}{{\bigl |\tau -\tilde{t}\bigr |}}{{\left|\tau -\tilde{t}\right|}}{{\left|\tau -\tilde{t}\right|}}\right)&\le r^{2r}c_{u13}^r\frac{\mathchoice{{\left|\tau -{{\tilde{t}}}\right|}}{{\bigl |\tau -{{\tilde{t}}}\bigr |}}{{\left|\tau -{{\tilde{t}}}\right|}}{{\left|\tau -{{\tilde{t}}}\right|}}}{r\lambda _{\mathrm {lo}}}\frac{1}{\lambda _{\mathrm {lo}}} \nonumber \\&= r^{2r}c_{u13}^r\left[ \frac{\mathchoice{{\left|\tau -\tilde{t}\right|}}{{\bigl |\tau -\tilde{t}\bigr |}}{{\left|\tau -\tilde{t}\right|}}{{\left|\tau -\tilde{t}\right|}}}{r\lambda _{\mathrm {lo}}}\right] ^{{I[b=1]}} \frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(87)

where we used that $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$. According to (64) the upper bound (87) also holds for $b=0$.

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that we can use (42) to upper-bound $\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}'(\tau )\right|}}{{\bigl |\phi _{0,k}'(\tau )\bigr |}}{{\left|\phi _{0,k}'(\tau )\right|}}{{\left|\phi _{0,k}'(\tau )\right|}}&\le \sum _{m=1}^{{{\hat{r}}}} c_{u3}^{{{\hat{r}}}} \frac{\prod _{\begin{array}{c} 1\le l\le {{\hat{r}}}\\ l\ne m \end{array}} (v^\tau _{l}-\tau )^{2}\mathchoice{{\left|v^\tau _m-\tau \right|}}{{\bigl |v^\tau _m-\tau \bigr |}}{{\left|v^\tau _m-\tau \right|}}{{\left|v^\tau _m-\tau \right|}}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} +(r\!-\!1\!-\!{{\hat{r}}}) c_{u3}^{{{\hat{r}}}+1} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}+1}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} c_{u19}^r\frac{\prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \left[ \frac{\mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}}{r\lambda _{\mathrm {lo}}}\right] ^{{I[b=1]}} \frac{1}{\lambda _{\mathrm {lo}}}. \end{aligned}$$

(88)

Above, in (a) we used the fact that $\mathchoice{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\bigl |v^\tau _{{\hat{m}}}-\tau \bigr |}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}\le \mathchoice{{\left|v^\tau _{l}-\tau \right|}}{{\bigl |v^\tau _{l}-\tau \bigr |}}{{\left|v^\tau _{l}-\tau \right|}}{{\left|v^\tau _{l}-\tau \right|}}$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, and the fact that $\mathchoice{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\bigl |v^\tau _{{\hat{m}}}-\tau \bigr |}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$, and defined $c_{u19}\triangleq 2 c_{u3}$.

Multiplying (87) and (88) and simplifying we obtain the following upper bound on $E_2$:

$$\begin{aligned} E_2(\tau )&=\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r} c_{u20}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{ \prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r} c_{u20}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{\prod _{1\le l\le {\tilde{r}},l\ne {{\tilde{m}}}} (v_{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(89)

Above, in (a) we defined $c_{u20}\triangleq c_{u13}c_{u19}$; in (b) we used the fact that

$\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

Bounding $E_3(\tau )$: By (65),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}''(\tau )\right|}}{{\bigl |\phi _{+,k}''(\tau )\bigr |}}{{\left|\phi _{+,k}''(\tau )\right|}}{{\left|\phi _{+,k}''(\tau )\right|}}\le r^{2r-2}c_{u8}^{r}c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(90)

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that we can use (41) to upper-bound $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}} \le c_u^{{{\hat{r}}}}\frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}&{\mathop {\le }\limits ^{(a)}} c_u^{{{\hat{r}}}} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{ \prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}}. \end{aligned}$$

(91)

Above, in (a) we used the fact that $\mathchoice{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\bigl |v^\tau _{{\hat{m}}}-\tau \bigr |}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}\le \mathchoice{{\left|v^\tau _{l}-\tau \right|}}{{\bigl |v^\tau _{l}-\tau \bigr |}}{{\left|v^\tau _{l}-\tau \right|}}{{\left|v^\tau _{l}-\tau \right|}}$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$, and the fact that $\mathchoice{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\bigl |v^\tau _{{\hat{m}}}-\tau \bigr |}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}{{\left|v^\tau _{{\hat{m}}}-\tau \right|}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$. Multiplying (90) and (91) and simplifying we obtain the following upper bound on $E_3$:

$$\begin{aligned} E_3(\tau )&=\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}\nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r-2}c_{u21}^{r} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{\prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r-2}c_{u21}^{r} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(92)

Above, in (a) we defined $c_{u21}\triangleq c_{u8}c_{u2}c_u$; in (b) we used that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

From (71), (86), (89), and (92) we conclude that

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}} \le r^{2r+1}c_{u22}^{r+1} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}, \end{aligned}$$

(93)

where we defined $c_{u22}\triangleq 4\max (c_{u18}, c_{u20}, c_{u21})$.

Putting pieces together: On the one hand, by (195) [Mean Value theorem], using (69), (70), (93), and we can write for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$:

$$\begin{aligned} \mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} \frac{1}{2} r^{2r+1}c_{u22}^{r+1} \left[ \frac{(\tilde{t}-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} \frac{1}{2} r^{2r+1}c_{u22}^{r+1} 2^{{\tilde{r}}} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+3} c_{u25}^{r+1} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}}. \end{aligned}$$

(94)

Above, in (a) $\tau _m\in (t_j, \tau )$; in (b) we used the fact that, for $l\ne {{\tilde{m}}}$, $\mathchoice{{\left|v_l-\tau _m\right|}}{{\bigl |v_l-\tau _m\bigr |}}{{\left|v_l-\tau _m\right|}}{{\left|v_l-\tau _m\right|}}<\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}$ and $\mathchoice{{\left|{{\tilde{t}}}-\tau _m\right|}}{{\bigl |{{\tilde{t}}}-\tau _m\bigr |}}{{\left|{{\tilde{t}}}-\tau _m\right|}}{{\left|{{\tilde{t}}}-\tau _m\right|}}<\mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|\tilde{t}-\tau \right|}}{{\bigl |\tilde{t}-\tau \bigr |}}{{\left|\tilde{t}-\tau \right|}}{{\left|\tilde{t}-\tau \right|}}$, which is true because $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ and because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$; in (c) we defined $c_{u25}\triangleq 2c_{u22}$ and used the fact that $t_j=v_{{{\tilde{m}}}}$.

On the other hand, let $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}$. Then by (16),

$$\begin{aligned} q_0(\tau )&\ge c_{l2}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}}\nonumber \\&{\mathop {\ge }\limits ^{(a)}} c_{l2}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \underbrace{ \left( \frac{(r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}})^2}{(r\lambda _{\mathrm {lo}})^2}\right) ^{\breve{r}-{\tilde{r}}-{I[b=1]}} }_{P_2}\nonumber \\&{\mathop {\ge }\limits ^{(b)}} c_{l3}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}}. \end{aligned}$$

(95)

Above, in (a) we used the fact that $\{v_1,\ldots ,v_{\tilde{r}}\}\subset \{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}$, the fact that if $b=1$, then ${{\tilde{t}}}\in \{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}$, and the fact that by construction of the set $\{v_1,\ldots ,v_{{{\tilde{r}}}}\}$ it follows that if, for some k, $u^\tau _k\notin \{v_1,\ldots ,v_{{{\tilde{r}}}}\}$ and $u^\tau _k\ne \tilde{t}$, then $\mathchoice{{\left|u^\tau _k-\tau \right|}}{{\bigl |u^\tau _k-\tau \bigr |}}{{\left|u^\tau _k-\tau \right|}}{{\left|u^\tau _k-\tau \right|}}\ge r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}}$; in (b) we used the assumption $\mathrm {SRF}\ge 12$ so that $\lambda _{\mathrm {hi}}\le \lambda _{\mathrm {lo}}/12$ and therefore $r\Delta \lambda _{\mathrm {lo}}-2\lambda _{\mathrm {hi}}\ge r(\Delta -1/6)\lambda _{\mathrm {lo}}$, used that $0<\Delta -1/6<1$, which implies that $P_2\ge (\Delta -1/6)^{2r}$.

The bound (67) follows from (94) and (95) by defining $c_{u26}\triangleq c_{u25}/c_{l3}$.

6.3.5 Proof of Property 3

By (29) and the triangle inequality:

$$\begin{aligned} \Vert q_1(\cdot )\Vert _{\infty }&\le \rho /2+r\max _{1\le k\le r}\Vert \phi _k(\cdot )\Vert _{\infty }\\&{\mathop {\le }\limits ^{(a)}} \rho /2+r\max _{1\le k\le r}\Vert \phi _{+,k}(\cdot )\Vert _{\infty }\\&{\mathop {=}\limits ^{(b)}} \rho /2+r^{2r+1}c_{u8}^{r} \max _{1\le k\le r}\Vert q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )\Vert _{\infty }\\&{\mathop {\le }\limits ^{(c)}} \rho /2+r^{2r+1}c_{u0}c_{u8}^{r} {\mathop {\le }\limits ^{(d)}} r^{2r+1}c_{u55}^{r}. \end{aligned}$$

Above, in (a) we used (35) and the fact that by (36) and Lemma 1, Property 3, $\Vert \phi _{0,k}(\cdot )\Vert _{\infty }\le 1$; in (b) we used (37); in (c) we used Lemma 2, Property 3; in (d) we defined $c_{u55}\triangleq 2c_{u0}c_{u8}$ and used the fact that $\rho /2<1<c_{u0}c_{u8}$.

6.3.6 Proof of Property 4

Take $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}})$. As above, let $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}$. Then by (16),

$$\begin{aligned} q_0(\tau ) \ge c_{l2}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}}. \end{aligned}$$

(96)

By (19) this bound is also valid when $\breve{r}=0$.

Fix k. If $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, then we can use (41) to upper-bound $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}&\le c_u^{{{\hat{r}}}}\frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}, \end{aligned}$$

(97)

where, as before, $\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k^c$. If $\tau \notin {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, we will use that by (36) and by Lemma 1, Property 3,

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}} \le 1. \end{aligned}$$

(98)

The set ${\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )$ is either empty or contains exactly one element. Let $b\triangleq \mathchoice{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}{{\bigl | {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\bigr |}}{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}$ denote the size of this set; when $b=1$, let $\{{{\tilde{t}}}\}\triangleq {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}, \tau )$. Following the steps that lead to (84), we obtain

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \le r^{2r+1}c_{u10}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \end{aligned}$$

(99)

and the bound is valid for both cases $b=0$ and $b=1$.

Case ${{\hat{r}}}\ge 1$: Then, $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}=\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\cup \{{{\tilde{t}}}\}$ if $b=1$, and

$\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}=\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$ if $b=0$. Therefore,

$$\begin{aligned} \mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}}&=\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}\nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u10}^rc_u^{{{\hat{r}}}} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}\nonumber \\&= r^{2r+1} c_{u10}^rc_u^{{{\hat{r}}}} \frac{ \prod _{l=1}^{\breve{r}} (u^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}} {\mathop {\le }\limits ^{(b)}} r^{2r+1} c_{u28}^rq_0(\tau ). \end{aligned}$$

(100)

Above, (a) follows by (97) and (99); (b) follows by (96) with $c_{u28}\triangleq c_{u10}c_u/c_{l2}$.

Case ${{\hat{r}}}= 0$: Then, $\breve{r}=1$ and $\{u^\tau _{\breve{r}}\}= \{{{\tilde{t}}}\}$ if $b=1$ and $\breve{r}=0$ if $b=0$. Therefore,

$$\begin{aligned} \mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}}&=\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}\nonumber \\&{\mathop {\le }\limits ^{(a)}} c_{u10}^rr^{2r+1} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]}\nonumber \\&=r^{2r+1}c_{u10}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}} {\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u28}^rq_0(\tau ). \end{aligned}$$

(101)

Above, (a) follows by (98) and (99); (b) follows by (96) because $c_u>1$.

By Lemma 3, Property 6,

$$\begin{aligned} \frac{\rho }{2}=\frac{\lambda _{\mathrm {hi}}^{2r}}{2\lambda _{\mathrm {lo}}^{2r}} \le \frac{r^{2r}}{c_l^r} q_0(\tau ). \end{aligned}$$

(102)

Therefore, by (29), (100), (101), (102),

$$\begin{aligned} \mathchoice{{\left|q_1(\tau )\right|}}{{\bigl |q_1(\tau )\bigr |}}{{\left|q_1(\tau )\right|}}{{\left|q_1(\tau )\right|}} \le \sum _{k=1}^r\mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}} + \rho /2 \le r^{2r+2} c_{u29}^rq_0(\tau ), \end{aligned}$$

where we defined $c_{u29}\triangleq c_{u28}+1/c_l$. $\square$

6.4 Dual Certificate $q_2(\cdot )$

Finally, we construct the trigonometric polynomial $q_2(\cdot )$. This trigonometric polynomial is conceptually similar to $q_1(\cdot )$. The difference is that in $q_1(\cdot )$ we control the function values on ${\mathcal {T}}$ and the derivatives on ${\mathcal {T}}$ are zero; in $q_2(\cdot )$ we control the derivatives on ${\mathcal {T}}$ and the function values on ${\mathcal {T}}$ are zero.

Specifically, on the point $t_j\in {\mathcal {T}}$, $q_2(\cdot )$ is approximated by a linear function whose derivative is controlled by the sign

$$\begin{aligned} s'_{j}\triangleq {{\,\mathrm{sign}\,}}\left( \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)}\left( \frac{m}{N}-t_j\right) h_m\right) ,\quad j=1,\ldots ,S, \end{aligned}$$

(103)

as explained in Lemma 5 below.

Lemma 5

Set $\gamma \triangleq \rho /\lambda _{\mathrm {hi}}=\lambda _{\mathrm {hi}}^{2r-1}/\lambda _{\mathrm {lo}}^{2r}$. Then, there exists a real-valued trigonometric polynomial $q_2(\cdot )$ that satisfies the following properties.

• 1. Frequency limitation to $f_{\mathrm {lo}}$: $q_2(t)=\sum _{k=-f_{\mathrm {lo}}}^{f_{\mathrm {lo}}} {\hat{q}}_{2,k} e^{-\mathrm {i} 2\pi kt}$ for some ${\hat{q}}_{2,k}\in {\mathbb {C}}$.

• 2. Constrained derivative on ${\mathcal {T}}$ and controlled behavior near ${\mathcal {T}}$: for all $j=1,\ldots ,S$ and all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$,

  $$\begin{aligned} \mathchoice{{\left|q_2(\tau )-\gamma s'_{j}(\tau -t_j)\right|}}{{\bigl |q_2(\tau )-\gamma s'_{j}(\tau -t_j)\bigr |}}{{\left|q_2(\tau )-\gamma s'_{j}(\tau -t_j)\right|}}{{\left|q_2(\tau )-\gamma s'_{j}(\tau -t_j)\right|}} \le r^{2r+4}c_{u34}^{r+1} q_0(\tau ), \end{aligned}$$

  (104)

  where $s'_j$ are defined³ in (103). Since $q_0(\tau )=0$ for $\tau \in {\mathcal {T}}$, (104) implies, in particular, that the derivative of $q_2(\cdot )$ interpolates the sign pattern in (103) scaled by $\gamma$ on ${\mathcal {T}}$.

• 3. Uniform confinement: $\Vert q_2(\cdot )\Vert _{\infty }\le r^{2r+1}c_{u56}^{r}$.

• 4. Boundedness far from ${\mathcal {T}}$: for all $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}})$,

  $$\begin{aligned} \mathchoice{{\left|q_2(\tau )\right|}}{{\bigl |q_2(\tau )\bigr |}}{{\left|q_2(\tau )\right|}}{{\left|q_2(\tau )\right|}}\le r^{2r+2} c_{u52}^rq_0(\tau ). \end{aligned}$$

  (105)

The positive numerical constants $c_{u34}$, $c_{u56}$, and $c_{u52}$ are defined in the proof below.

The proof of the lemma parallels that of Lemma 4 but contains some important differences; it is given in Appendix 2 “Proof of Lemma 5”.

7 Stability Estimates

In this section we use the dual trigonometric polynomials $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$ to prove Theorem 1.

We will use the fact that the high-resolution kernel $k_{\mathrm {hi}}(\cdot )$ satisfies the following estimates:

$$\begin{aligned}&\sum _{n=0}^{N-1} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}\le \frac{c_k'}{\lambda _{\mathrm {hi}}}, \end{aligned}$$

(106)

$$\begin{aligned}&\frac{1}{2}\sum _{n=0}^{N-1} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, n/N)} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \le \frac{c_k''}{\lambda _{\mathrm {hi}}^2}, \end{aligned}$$

(107)

where $c_k'$ and $c_k''$ are positive numerical constants. The bounds are proven in Appendix 4 “Properties of Fejér Kernel”.

We will use the following shorthand notations:

$$\begin{aligned} {\mathcal {N}}_{\mathrm {hi}}&\triangleq \cup _{t\in {\mathcal {T}}} {\mathcal {N}}(\lambda _{\mathrm {hi}},t),\\ {\mathcal {F}}_{\mathrm {hi}}&\triangleq {\mathbb {T}}\setminus {\mathcal {N}}_{\mathrm {hi}}. \end{aligned}$$

7.1 Basic Estimates

We begin by decomposing the error $\Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1$ into a sum of simpler terms; each of the terms will then be upper-bounded separately:

$$\begin{aligned} \Vert k_{\mathrm {hi}}\star ({\hat{{\mathbf {x}}}}-{\mathbf {x}})\Vert _1&= \sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{m=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}\nonumber \\&\le \sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}} \nonumber \\&+\sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}. \end{aligned}$$

(108)

The first term in (108) can be written as follows:

$$\begin{aligned} \sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}&{\mathop {=}\limits ^{(a)}} \sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \left( \sum _{n=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) \right) h_m\nonumber \\&{\mathop {=}\limits ^{(b)}} \sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \left( \sum _{n=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n}{N}\right) \right) h_m\nonumber \\&{\mathop {=}\limits ^{(c)}} \underbrace{\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} h_m}_{A_0}. \end{aligned}$$

(109)

Above, (a) follows because $h_m\ge 0$ for $m/N\in {\mathcal {F}}_{\mathrm {hi}}$ and $k_{\mathrm {hi}}(\cdot )\ge 0$; (b) follows by periodicity of $k_{\mathrm {hi}}(\cdot )$; (c) follows by (8).

The second term in (108) can be upper-bounded as follows:

$$\begin{aligned} \sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}&{\mathop {=}\limits ^{(a)}} \sum _{n=0}^{N-1} \mathchoice{{\left|\sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(b)}} \underbrace{\sum _{n=0}^{N-1} \sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}}_{B}. \end{aligned}$$

(110)

Above, (a) follows because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect; (b) follows by the triangle inequality. To upper-bound B in (110) we will use that for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)\cap {\mathbb {T}}$ and all $t\in {\mathbb {T}}$,

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}(t-\tau )-k_{\mathrm {hi}}(t- t_j)-k_{\mathrm {hi}}'(t-t_j)(t_j-\tau )\right|}}{{\bigl |k_{\mathrm {hi}}(t-\tau )-k_{\mathrm {hi}}(t- t_j)-k_{\mathrm {hi}}'(t-t_j)(t_j-\tau )\bigr |}}{{\left|k_{\mathrm {hi}}(t-\tau )-k_{\mathrm {hi}}(t- t_j)-k_{\mathrm {hi}}'(t-t_j)(t_j-\tau )\right|}}{{\left|k_{\mathrm {hi}}(t-\tau )-k_{\mathrm {hi}}(t- t_j)-k_{\mathrm {hi}}'(t-t_j)(t_j-\tau )\right|}} \le \!\!\sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t- t_j)}\! \frac{1}{2} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} (t_j-\tau )^2. \end{aligned}$$

(111)

The inequality follows by expanding $k_{\mathrm {hi}}(t-\tau )$ in Taylor series in $\tau$ around $\tau =t_j$ up to first order and writing the remainder in Lagrange form. We have:

$$\begin{aligned}&\mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) h_m\right|}} \nonumber \\&\ {\mathop {\le }\limits ^{(a)}} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) h_m\right|}} \nonumber \\&\ + \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) h_m\right|}} \nonumber \\&\ +\!\!\!\!\! \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\!\! \mathchoice{{\left|k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) -k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) -k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) -k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) -k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) -k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) -k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}\left( \frac{n-m}{N}\right) -k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) -k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \left( t_j-\frac{m}{N}\right) \right|}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&\ {\mathop {\le }\limits ^{(b)}} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}} \nonumber \\&\ + \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}} \nonumber \\&\ + \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, n/N- t_j)} \frac{1}{2} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}\left( t_j-\frac{m}{N}\right) ^2 \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}. \end{aligned}$$

(112)

Above, (a) follows by adding and subtracting the corresponding terms and applying the triangle inequality; (b) follows by (111) with $t=n/N$ and $\tau = m/N$ and because $k_{\mathrm {hi}}(\cdot )\ge 0$.

Using (112) we can upper-bound B in (110) as follows:

$$\begin{aligned} B&\le \sum _{j=1}^{S} \left( \sum _{n=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n}{N}-t_j\right) \right) \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}} \nonumber \\&+\sum _{j=1}^{S} \left( \sum _{n=0}^{N-1} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}-t_j\right) \right|}}\right) \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}} \nonumber \\&+\sum _{j=1}^{S}\sum _{n=0}^{N-1} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, n/N-t_j)} \frac{1}{2} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) ^2 \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(a)}} \left( \sum _{n=0}^{N-1} k_{\mathrm {hi}}\left( \frac{n}{N}\right) \right) \sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}} \nonumber \\&+\left( \sum _{n=0}^{N-1} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}\right) \sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}} \nonumber \\&+\left( \sum _{n=0}^{N-1} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, n/N)} \frac{1}{2} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \right) \sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) ^2 \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(b)}} \underbrace{\sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}}_{A_1} +\,c_k'\underbrace{\frac{1}{\lambda _{\mathrm {hi}}}\sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) h_m\right|}}}_{A_2} \nonumber \\&\qquad +c_k''\underbrace{\frac{1}{\lambda _{\mathrm {hi}}^2}\sum _{j=1}^{S} \sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\left( t_j-\frac{m}{N}\right) ^2 \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}}_{A_3}. \end{aligned}$$

(113)

Above, (a) follows by periodicity of $k_{\mathrm {hi}}(\cdot )$; (b) follows by (8), (106), (107).

To complete the proof of Theorem 1, it remains to upper-bound each of the terms $A_0$, $A_1$, $A_2$, and $A_3$ by $\sim C(r) \mathrm {SRF}^{2r} \Vert {\mathbf {z}}\Vert _1$. To do this we will use extended duality arguments that will rely on the trigonometric polynomials $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$.

7.2 Upper Bound on $A_0$

In this section we use the trigonometric polynomial $q_0(\cdot )$ from Lemma 3 to upper-bound $A_0$. Let

$$\begin{aligned} {\mathbf {q}}^0 = [q^0_0, \ldots , q^0_{N-1}]^{{\mathsf {T}}} \triangleq [q_{0}(l/N): l\in [0:N-1]]^{{\mathsf {T}}} \end{aligned}$$

be the vector that consists of the samples of $q_{0}(\cdot )$.

On the one hand,

$$\begin{aligned} \left\langle {\mathbf {q}}^0,{\mathbf {h}}\right\rangle {\mathop {=}\limits ^{(a)}}\left\langle {\mathbf {Q}}{\mathbf {q}}^0,{\mathbf {h}}\right\rangle&{\mathop {=}\limits ^{(b)}}\left\langle {\mathbf {q}}^0,{\mathbf {Q}}{\mathbf {h}}\right\rangle \nonumber \\&{\mathop {\le }\limits ^{(c)}} \Vert {\mathbf {q}}^0\Vert _{\infty }\Vert {\mathbf {Q}}{\mathbf {h}}\Vert _1 \nonumber \\&{\mathop {\le }\limits ^{(d)}} \Vert {\mathbf {Q}}{\hat{{\mathbf {x}}}} -{\mathbf {s}}+{\mathbf {s}}-{\mathbf {Q}}{\mathbf {x}}\Vert _1 \nonumber \\&{\mathop {\le }\limits ^{(e)}} \Vert {\mathbf {Q}}{\hat{{\mathbf {x}}}} -{\mathbf {s}}\Vert _1+\Vert {\mathbf {s}}-{\mathbf {Q}}{\mathbf {x}}\Vert _1 {\mathop {\le }\limits ^{(f)}} 2\Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(114)

Above, (a) follows because by Lemma 3, Property 1, $q_0(\cdot )$ is frequency-limited to $f_{\mathrm {lo}}$, and, therefore, the vector of its samples is also frequency limited (in discrete sense) so that ${\mathbf {q}}^0={\mathbf {Q}}{\mathbf {q}}^0$; (b) follows because ${\mathbf {Q}}$ is self-adjoint; (c) follows by Cauchy-Schwartz inequality; (d) follows by Lemma 3, Property 3; (e) follows by the triangle inequality; (f) follows since ($\mathrm {CVX}$) implies $\Vert {\mathbf {Q}}{\hat{{\mathbf {x}}}} -{\mathbf {s}}\Vert _1\le \Vert {\mathbf {Q}}{\mathbf {x}}-{\mathbf {s}}\Vert _1$ and, by assumption, ${\mathbf {s}}={\mathbf {Q}}{\mathbf {x}}+{\mathbf {z}}$.

On the other hand,

$$\begin{aligned} \left\langle {\mathbf {q}}^0,{\mathbf {h}}\right\rangle {\mathop {=}\limits ^{(a)}} \sum _{m=0}^{N-1} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} {\mathop {\ge }\limits ^{(b)}} \sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} {\mathop {\ge }\limits ^{(c)}} c_l^r\frac{\lambda _{\mathrm {hi}}^{2r}}{(r\lambda _{\mathrm {lo}})^{2r}}\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}. \end{aligned}$$

(115)

Above, (a) follows because, by construction, $q_0(t)=0$ for all $t\in {\mathcal {T}}$, which means that $h_m<0$ implies $q_m^0=q_0(m/N)=0$, so that $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$; (b) follows because all terms in the sum are nonnegative; (c) follows from Lemma 3, Property 6. From (114) and (115), we conclude that

$$\begin{aligned} A_0 =\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \le \frac{r^{2r}}{c_l^r} \mathrm {SRF}^{2r}\Vert {\mathbf {z}}\Vert _1, \end{aligned}$$

(116)

where the equality follows because $h_m\ge 0$ for $m/N\in {\mathcal {F}}_{\mathrm {hi}}$ and we remind the reader that $c_l<1$.

7.3 Upper Bound on $A_3$

In this section we use ${\mathbf {q}}^0$ to upper-bound $A_3$. We have,

$$\begin{aligned} 2\Vert {\mathbf {z}}\Vert _1 {\mathop {\ge }\limits ^{(a)}} \sum _{m=0}^{N-1} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}&{\mathop {\ge }\limits ^{(b)}} \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}\\&{\mathop {\ge }\limits ^{(c)}} \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} c_{l2}^{r} \frac{ (t_j-m/N)^2 \lambda _{\mathrm {hi}}^{2(r-1)}}{(r\lambda _{\mathrm {lo}})^{2r}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}}. \end{aligned}$$

Above, (a) follows from (114) because $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$; (b) follows because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect since the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$; (c) follows from (17). Hence,

$$\begin{aligned} A_3 =\frac{1}{ \lambda _{\mathrm {hi}}^2 }\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( t_j-\frac{m}{N}\right) ^2 \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \le \frac{r^{2r}}{c_{l2}^r} \mathrm {SRF}^{2r}2\Vert {\mathbf {z}}\Vert _1 \end{aligned}$$

(117)

and we remind the reader that $c_{l2}<1$.

7.4 Upper Bound on $A_1$

In this section we use trigonometric polynomial $q_1(\cdot )$ constructed in Lemma 4 to upper-bound $A_1$. Set

$$\begin{aligned} {\mathbf {q}}^1&= [q^1_0, \ldots , q^1_{N-1}]^{{\mathsf {T}}} \triangleq [q_{1}(l/N): l\in [0:N-1]]^{{\mathsf {T}}}. \end{aligned}$$

We now proceed as follows:

$$\begin{aligned} A_1&= \sum _{j=1}^S\mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(a)}} \frac{2}{\rho }\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \frac{\rho s_j}{2} h_m \nonumber \\&{\mathop {=}\limits ^{(b)}} \frac{2}{\rho } \mathchoice{{\left|\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{\rho s_j}{2}-q^1_m\right) h_m+\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^1_m h_m\right|}}{{\bigl |\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{\rho s_j}{2}-q^1_m\right) h_m+\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^1_m h_m\bigr |}}{{\left|\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{\rho s_j}{2}-q^1_m\right) h_m+\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^1_m h_m\right|}}{{\left|\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{\rho s_j}{2}-q^1_m\right) h_m+\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^1_m h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(c)}} \frac{2}{\rho } \underbrace{\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \mathchoice{{\left|\frac{\rho s_j}{2}-q^1_m\right|}}{{\bigl |\frac{\rho s_j}{2}-q^1_m\bigr |}}{{\left|\frac{\rho s_j}{2}-q^1_m\right|}}{{\left|\frac{\rho s_j}{2}-q^1_m\right|}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} }_{A_{11}} +\frac{2}{\rho } \underbrace{\mathchoice{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^1_m h_m\right|}}{{\bigl | \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^1_m h_m\bigr |}}{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^1_m h_m\right|}}{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^1_m h_m\right|}}}_{A_{12}}. \end{aligned}$$

(118)

Above, (a) follows by (26); (b) follows by adding and subtracting the corresponding term and because the expression in (a) is nonnegative; (c) follows by the triangle inequality and because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect since the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$. Next, we upper-bound the terms $A_{11}$ and $A_{12}$ separately.

The first term in (118), $A_{11}$, can be upper-bounded as follows:

$$\begin{aligned} A_{11}&{\mathop {\le }\limits ^{(a)}} r^{2r+4} c_{u27}^{r+1} \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(b)}} r^{2r+4} c_{u27}^{r+1} \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^0_m h_m \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+4} c_{u27}^{r+1} \sum _{m=0}^{N-1} q^0_m h_m {\mathop {\le }\limits ^{(d)}} r^{2r+4} 2c_{u27}^{r+1} \Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(119)

Above, (a) follows by (27) and because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect; (b) follows because $h_m<0$ implies $q_m^0=0$; (c) follows because $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$; (d) follows by (114).

Following exactly the same steps as in (114), changing $q_m^0$ to $q_m^1$, and using in step (d) that by Lemma 4, Property 3, $\Vert {\mathbf {q}}^1\Vert _{\infty }\le r^{2r+1}c_{u55}^{r}$, we obtain:

$$\begin{aligned} \mathchoice{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}{{\bigl |\sum _{m=0}^{N-1} q^1_m h_m\bigr |}}{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}\le 2r^{2r+1} c_{u55}^{r}\Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(120)

Using this, the second term in (118), $A_{12}$, can be upper-bounded as follows

$$\begin{aligned} A_{12}&{\mathop {\le }\limits ^{(a)}} \mathchoice{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}{{\bigl |\sum _{m=0}^{N-1} q^1_m h_m\bigr |}}{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}{{\left|\sum _{m=0}^{N-1} q^1_m h_m\right|}}+\mathchoice{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^1_m h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^1_m h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^1_m h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^1_m h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(b)}} 2r^{2r+1}c_{u55}^{r}\Vert {\mathbf {z}}\Vert _1+\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \mathchoice{{\left|q^1_m\right|}}{{\bigl |q^1_m\bigr |}}{{\left|q^1_m\right|}}{{\left|q^1_m\right|}}\mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(c)}} 2r^{2r+1}c_{u55}^{r}\Vert {\mathbf {z}}\Vert _1+r^{2r+2} c_{u29}^r\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(d)}} 2r^{2r+1}c_{u55}^{r}\Vert {\mathbf {z}}\Vert _1+r^{2r+2} c_{u29}^r\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^0_m h_m \nonumber \\&{\mathop {\le }\limits ^{(e)}} 4 r^{2r+2} c_{u57}^r\Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(121)

Above, (a) follow by the triangle inequality and because ${\mathcal {F}}_{\mathrm {hi}}$ is complementary to ${\mathcal {N}}_{\mathrm {hi}}$; (b) follow by (120) and by the triangle inequality; (c) follow by (28); (d) follows because $h_m>0$ for $m/N\in {\mathcal {F}}_{\mathrm {hi}}$; (e) follows by (114) because $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$, because $c_{u29}>1$, and by defining $c_{u57}\triangleq \max (c_{u55}, c_{u29})$.

Substituting (119) and (121) into (118), using that $1/\rho =\mathrm {SRF}^{2r}$, we finally obtain

$$\begin{aligned} A_1=\sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}\le r^{2r+4}c_{u53}^{r+1} \mathrm {SRF}^{2r} \Vert {\mathbf {z}}\Vert _1, \end{aligned}$$

(122)

where we defined $c_{u53}\triangleq 12\max (c_{u27}, c_{u57})$.

7.5 Upper Bound on $A_2$

In this section we use trigonometric polynomial $q_2(\cdot )$ to upper-bound $A_2$. Set

$$\begin{aligned} {\mathbf {q}}^2&= [q^2_0, \ldots , q^2_{N-1}]^{{\mathsf {T}}} \triangleq [q_{2}(l/N): l\in [0:N-1]]^{{\mathsf {T}}}. \end{aligned}$$

We now proceed as follows:

$$\begin{aligned} A_2&= \frac{1}{\lambda _{\mathrm {hi}}}\sum _{j=1}^S\mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{m}{N} - t_j\right) h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{m}{N} - t_j\right) h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{m}{N} - t_j\right) h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \left( \frac{m}{N} - t_j\right) h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(a)}} \frac{1}{\rho }\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \gamma s'_j \left( \frac{m}{N} - t_j\right) h_m \nonumber \\&{\mathop {=}\limits ^{(b)}} \frac{1}{\rho } \mathchoice{{\left| \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\!\!\!\! \left( \gamma s'_j \left( \frac{m}{N} -t_j\right) -q^2_m\right) h_m +\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^2_m h_m\right|}}{{\bigl | \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\!\!\!\! \left( \gamma s'_j \left( \frac{m}{N} -t_j\right) -q^2_m\right) h_m +\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^2_m h_m\bigr |}}{{\left| \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\!\!\!\! \left( \gamma s'_j \left( \frac{m}{N} -t_j\right) -q^2_m\right) h_m +\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^2_m h_m\right|}}{{\left| \sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)}\!\!\!\! \left( \gamma s'_j \left( \frac{m}{N} -t_j\right) -q^2_m\right) h_m +\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} q^2_m h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(c)}} \frac{1}{\rho } \underbrace{\sum _{j=1}^S\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} \mathchoice{{\left|\gamma s'_j \left( \frac{m}{N} - t_j\right) -q^2_m\right|}}{{\bigl |\gamma s'_j \left( \frac{m}{N} - t_j\right) -q^2_m\bigr |}}{{\left|\gamma s'_j \left( \frac{m}{N} - t_j\right) -q^2_m\right|}}{{\left|\gamma s'_j \left( \frac{m}{N} - t_j\right) -q^2_m\right|}} \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} }_{A_{21}} +\frac{1}{\rho } \underbrace{\mathchoice{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^2_m h_m\right|}}{{\bigl | \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^2_m h_m\bigr |}}{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^2_m h_m\right|}}{{\left| \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^2_m h_m\right|}}}_{A_{22}}. \end{aligned}$$

(123)

Above, (a) follows by (103) and because $\gamma =\rho /\lambda _{\mathrm {hi}}$; (b) follows by adding and subtracting the corresponding term and because the expression in (a) is nonnegative; (c) follows by the triangle inequality and because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect. Next, we upper-bound the terms $A_{21}$ and $A_{22}$ separately.

The first term in (123), $A_{21}$, can be upper-bounded as follows

$$\begin{aligned} A_{21}&{\mathop {\le }\limits ^{(a)}} r^{2r+4}c_{u34}^{r+1} \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} {\mathop {=}\limits ^{(b)}} r^{2r+4}c_{u34}^{r+1} \sum _{m/N\in {\mathcal {N}}_{\mathrm {hi}}} q^0_m h_m \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+4}c_{u34}^{r+1} \sum _{m=0}^{N-1} q^0_m h_m {\mathop {\le }\limits ^{(d)}} 2r^{2r+4}c_{u34}^{r+1} \Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(124)

Above, (a) follows by (104) and because the sets ${\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)$ do not intersect; (b) follows because $h_m<0$ implies $q_m^0=0$; (c) follows because $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$; (d) follows by (114).

Following exactly the same steps as in (114), changing $q_m^0$ to $q_m^2$, and using that by Lemma 5, Property 3, $\Vert {\mathbf {q}}_2\Vert _{\infty }\le r^{2r+1}c_{u56}^{r}$, we obtain:

$$\begin{aligned} \mathchoice{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}{{\bigl |\sum _{m=0}^{N-1} q^2_m h_m\bigr |}}{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}\le 2r^{2r+1}c_{u56}^{r}\Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(125)

Using this, the second term in (123), $A_{22}$, can be upper-bounded as follows

$$\begin{aligned} A_{22}&{\mathop {\le }\limits ^{(a)}} \mathchoice{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}{{\bigl |\sum _{m=0}^{N-1} q^2_m h_m\bigr |}}{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}{{\left|\sum _{m=0}^{N-1} q^2_m h_m\right|}}+\mathchoice{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^2_m h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^2_m h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^2_m h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^2_m h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(b)}} 2r^{2r+1}c_{u56}^{r}\Vert {\mathbf {z}}\Vert _1+\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} \mathchoice{{\left|q^2_m\right|}}{{\bigl |q^2_m\bigr |}}{{\left|q^2_m\right|}}{{\left|q^2_m\right|}}\mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {\le }\limits ^{(c)}} 2r^{2r+1}c_{u56}^{r}\Vert {\mathbf {z}}\Vert _1+r^{2r+2} c_{u52}^r\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^0_m \mathchoice{{\left|h_m\right|}}{{\bigl |h_m\bigr |}}{{\left|h_m\right|}}{{\left|h_m\right|}} \nonumber \\&{\mathop {=}\limits ^{(d)}} 2r^{2r+1}c_{u56}^{r}\Vert {\mathbf {z}}\Vert _1+r^{2r+2} c_{u52}^r\sum _{m/N\in {\mathcal {F}}_{\mathrm {hi}}} q^0_m h_m {\mathop {\le }\limits ^{(e)}} 4r^{2r+2} c_{u58}^r\Vert {\mathbf {z}}\Vert _1. \end{aligned}$$

(126)

Above, (a) follow by the triangle inequality and because ${\mathcal {F}}_{\mathrm {hi}}$ is complementary to ${\mathcal {N}}_{\mathrm {hi}}$; (b) follow by (125) and by the triangle inequality; (c) follow by (105); (d) follows because $h_m>0$ for $m/N\in {\mathcal {F}}_{\mathrm {hi}}$; (e) follows by (114) because $q^0_m h_m\ge 0$ for $m=0,\ldots , N-1$, because $c_{u52}>1$, and by defining $c_{u58}\triangleq \max (c_{u56}, c_{u52})$.

Substituting (124) and (126) into (123), using that $1/\rho =\mathrm {SRF}^{2r}$, we finally obtain:

$$\begin{aligned} A_2=\frac{1}{\lambda _{\mathrm {hi}}}\sum _{j=1}^{S} \mathchoice{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\bigl |\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\bigr |}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}}{{\left|\sum _{m/N\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t_j)} h_m\right|}} \le r^{2r+4}c_{u54}^{r+1} \mathrm {SRF}^{2r} \Vert {\mathbf {z}}\Vert _1, \end{aligned}$$

(127)

where we defined $c_{u54}\triangleq 6\max (c_{u34}, c_{u58})$.

7.6 Putting Pieces Together

Substituting (116) into (109); substituting (117), (122), (127) into (113) and the result into (110); then, substituting (109) and (110) into (108), and defining

$$\begin{aligned} c\triangleq 4 \max (1/c_l, c_k''/c_{l2}, c_{u53}, c_k'c_{u54}) \end{aligned}$$

(128)

we obtain the desired bound (9) and complete the proof of Theorem 1. $\square$

8 Connection to Bernstein Theorem

The famous Bernstein theorem states the following [21, Ch. 4, eq. (1.1)].

Theorem 2

(Bernstein) Consider a trigonometric polynomial frequency-limited to $f_c$: $q(t)=\sum _{k=-f_c}^{f_c} {\hat{q}}_k e^{-\mathrm {i} 2\pi kt}$. Then,

$$\begin{aligned} \Vert q'(\cdot )\Vert _{\infty }\le 2\pi f_c\Vert q(\cdot )\Vert _{\infty }. \end{aligned}$$

(129)

In other words, if a trigonometric polynomial is uniformly bounded, its derivative cannot be too large anywhere.

Bernstein theorem helped us construct trigonometric polynomials $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$ with the required properties by telling us what may be achievable and what is forbidden. We now describe these connections to provide more intuition about our constructions.

Independent control Consider $q(\cdot ) = q_{\lambda _c, {\mathcal {V}}, \{f_j\}, \{d_j\}}(\cdot )$ in Fig. 4. Since we require $\Vert q(\cdot )\Vert _{\infty }\le c_{u0}$, then, by Bernstein theorem, $\Vert q'(\cdot )\Vert _{\infty }\le 2\pi c_{u0}f_c$. Suppose, $q(v_1)$ = 0. How large $q(v_2)$ may possibly be? Since $\Vert q'(\cdot )\Vert _{\infty }\le 2\pi c_{u0}f_c$, we must have $q(v_2)\le 2\pi c_{u0}(v_2-v_1)f_c$. Now, if the points $v_1$ and $v_2$ are well-separated, i.e., if $v_2-v_1$ is order $\lambda _c$, Bernstein theorem puts no restrictions on $q(v_2)$. However, if $v_2-v_1\ll \lambda _c$, then $\mathchoice{{\left|q(v_1)-q(v_2)\right|}}{{\bigl |q(v_1)-q(v_2)\bigr |}}{{\left|q(v_1)-q(v_2)\right|}}{{\left|q(v_1)-q(v_2)\right|}}\le 2\pi c_{u0}(v_2-v_1)f_c\ll 1$. Generalizing: it may be possible to independently control $q(v_1)$ and $q(v_2)$ only if the points $v_1$ and $v_2$ are well-separated. This is the reason why $q_0(\cdot )$, $q_1(\cdot )$, and $q_2(\cdot )$ are constructed in an interlaced way. We control the building blocks on sets of interlaced points that are well-separated, then we multiply the resulting trigonometric polynomials. See (21) and Fig. 6 for an easy example of interlacing; see (35), (36), Figs. 8, and 9 for a more sophisticated example of interlacing.

For readers familiar with using $\ell _1$-minimization for super-resolution of real-valued (spikes may be positive and negative) and complex-valued signals [13]: Bernstein theorem is responsible for the fact that $\ell _1$-minimization fails when the spikes are not well-separated (closer than $\lambda _{\mathrm {lo}}$ to one another). The dual certificate in the real-valued case is a trigonometric polynomial $q(\cdot )$ with $\Vert q(\cdot )\Vert _{\infty }\le 1$ that interpolates the sign of the spikes in the signal. If, say $q(v_1)=-1$, and $v_2-v_1\ll \lambda _c$, it is not possible that $q(v_2)=+1$ because $\Vert q'(\cdot )\Vert _{\infty }\le 2\pi f_c$. The required dual trigonometric polynomial does not exist and the algorithm fails.

In contrast to the real-valued case, consider our trigonometric polynomial $q_1(\cdot )$, displayed in Fig. 7. Here, we interpolate the sign of the sequence $s_1, s_2, s_3, s_4$ at a set of points $t_1, t_2, t_3, t_4$ that are not well-separated. How is that possible? The difference is that we interpolate the sign sequence at a low level $\rho =(\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}})^{2r}\ll 1$, i.e., we interpolate the points $s_i\rho /2$, and not the points $s_i$. The transitions $q_1(\cdot )$ needs to make between the points, are small; for example $\mathchoice{{\left|q_1(t_3)-q_1(t_4)\right|}}{{\bigl |q_1(t_3)-q_1(t_4)\bigr |}}{{\left|q_1(t_3)-q_1(t_4)\right|}}{{\left|q_1(t_3)-q_1(t_4)\right|}}=\rho \ll 1$ and this is not disallowed by Bernstein theorem.

High curvature As should be clear by now, the curvature of the building block $q_{\lambda _c, {\mathcal {V}}}(\cdot )$ in the vicinity of its zeros expressed by (13) (see also the sections marked in red in Fig. 4a) determines the noise amplification in our bounds. How curvy can $q_{\lambda _c, {\mathcal {V}}}(\cdot )$ possibly be? Since $\Vert q_{\lambda _c, {\mathcal {V}}}(\cdot )\Vert _{\infty }\le 1$, applying Bernstein theorem twice, we conclude that the second derivative must satisfy $\Vert q''_{\lambda _c, {\mathcal {V}}}(\cdot )\Vert _{\infty }\le 4\pi ^2f_c^2$. Therefore, for $v\in {\mathcal {V}}$, it must hold that $q_{\lambda _c, {\mathcal {V}}}(v-\tau )\le 2\pi ^2(v-\tau )^2/\lambda _c^2$. We conclude that the curvature of $q_{\lambda _c, {\mathcal {V}}}(\cdot )$ in (13) depends on $\lambda _c$ in an optimal way (up to a constant). This leads to the near-optimal stability estimate in Theorem 1.

9 Numerical Results

In this section we describe a simple numerical experiment that demonstrates how the bounds developed in this paper reflect the true error accurately in the setting where the error metric used in the previous work [43] leads to an unreasonably pessimistic conclusion.

Set $f_{\mathrm {lo}}=9$. For $\mathrm {DSRF}\in \{8, 16, 32, 64, 128\}$ set $N=f_{\mathrm {lo}}\cdot \mathrm {DSRF}$. For each $N$ we generate 50 signals from each of the classes ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ and ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$. To focus on the worst-case setup described by the theorems, the signals from ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ were generated so that pairs of spikes are forced to be close together. Specifically, for signals from ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$, each spike has a pair that is no further than $3/N$ away (assuming the signal is depicted on the (0, 1] interval as in Fig. 2). All spikes were chosen to have equal magnitude set to one. The observations are generated according to ${\mathbf {s}}={\mathbf {Q}}{\mathbf {x}}+{\mathbf {z}}$. The noise is taken to be low-pass filtered Guassian: ${\mathbf {z}}= c\cdot {\mathbf {Q}}{\mathbf {z}}_G$, where ${\mathbf {z}}_G$ has independent identically distributed entries that are standard Gaussian with mean zero and unit variance, the constant $c$ controls the signal-to-noise ratio (SNR) taken to be $\mathrm {SNR} = \Vert {\mathbf {x}}\Vert _1/\Vert {\mathbf {z}}\Vert _1=100000$ in all simulations.

In Fig. 10a we depict $\log \left( \frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1/\Vert {\mathbf {s}}_i-{\mathbf {Q}}{\mathbf {x}}_i\Vert _1\right)$, i.e., the log of the noise amplification factor (NAF), averaged over the 50 trials, as a function of $\log (\mathrm {DSRF})$. Observe that on the log-log scale the data are well approximated by straight lines (displayed). We found the slopes of these lines to be 1.02 for ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ data and 2.85 for ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$ data. This matches the conclusions of Proposition 1 and the corresponding converse [43, Sec. 2.3], which together predict $(2r-1)\log (\mathrm {SRF})\le \log (\Vert {\mathbf {x}}-{\hat{{\mathbf {x}}}}\Vert _1/\Vert {\mathbf {s}}-{\mathbf {Q}}{\mathbf {x}}\Vert _1)\le (2r) \log (\mathrm {SRF})$. Note that for $r=2$, the exponent in the NAF, 2.85, estimated in the simulation, happened to be a bit more optimistic than the range between $2r-1=3$ and $2r=4$ predicted by theory, presumably because the Gaussian noise is not the worst case. In Fig. 10b, for reference, we depict the average relative error, $\frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1 / \Vert {\mathbf {x}}_i\Vert _1$ and observe that for all $\mathrm {DSRF}$ values and for both ensembles, the average relative error is significantly below one, implying that the reconstructed signals are high quality.

Fig. 10

In a and c, $\log (\frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1/\Vert {\mathbf {s}}_i-{\mathbf {Q}}{\mathbf {x}}_i\Vert _1)$, as a function of $\log (\mathrm {DSRF})$ and $\log (\mathrm {DSRF}_f)$, respectively. In e, $\log (\frac{1}{50} \sum _{i=1}^{50} \Vert k_{\mathrm {hi}}\star ({\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i)\Vert _1/\Vert {\mathbf {s}}_i-{\mathbf {Q}}{\mathbf {x}}_i\Vert _1)$, as a function of $\log (\mathrm {SRF})$. In b and d, $\frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1 / \Vert {\mathbf {x}}_i\Vert _1$, as a function of $\log (\mathrm {DSRF})$ and $\log (\mathrm {DSRF}_f)$, respectively. In f, $\frac{1}{50} \sum _{i=1}^{50} \Vert k_{\mathrm {hi}}\star ({\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i)\Vert _1/\Vert {\mathbf {x}}_i\Vert _1$, as a function of $\log (\mathrm {DSRF})$. In all plots, blue diamonds represent signals from class ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ and green circles (and green stars) represent signals from class ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$ (Color figure online)

Next, consider a 20 times higher super-resolution factor $\mathrm {DSRF}_f\in \{160, 320, 640, 1280, 2560\}$ with $N_f=f_{\mathrm {lo}}\cdot \mathrm {DSRF}_f=20N$ (‘f’ stands for fine-scale) and repeat the above experiment with all other parameters kept the same. We use the same random signals from the experiment above, when depicted on the interval (0, 1]. Since the grid is now 20 times finer, in the vector representation the index of each nonzero element of ${\mathbf {x}}$ has been multiplied by 20. To be sure: if before the first and the second elements of ${\mathbf {x}}$ were equal to one, all others being zero, now the 20th and the 40th elements of ${\mathbf {x}}$ are equal to one, all others being zero. This construction guarantees that for signals from ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$, each spike has a pair that is no further than $3\cdot 20/N_f=3/N$ away (assuming the signal is depicted on the (0, 1] interval as in Fig. 2), precisely as before.

In Fig. 10c we depict $\log \left( \frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1/\Vert {\mathbf {s}}_i-{\mathbf {Q}}{\mathbf {x}}_i\Vert _1\right)$, i.e., the log of the NAF, averaged over the 50 trials as a function of $\log (\mathrm {DSRF}_f)$ for the fine-scale experiment. The curve for signals from ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ [blue diamonds] looks very similar to how it did for the coarse grid in Fig. 10a. In contrast, the curve for signals from ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$ [green circles and stars] now looks different: it saturates for large values of $\mathrm {DSRF}_f$ ($\mathrm {DSRF}_f\in \{1280, 2560\}$, as marked by the green stars). By looking at Fig. 10d, where we depict the average relative error $\frac{1}{50} \sum _{i=1}^{50} \Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1/\Vert {\mathbf {x}}_i\Vert _1$ as a function of $\log (\mathrm {DSRF}_f)$, we see that for the large values of $\mathrm {DSRF}_f$, the norm of the error, $\Vert {\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i\Vert _1$, is comparable to the norm of the signal $\Vert {\mathbf {x}}_i\Vert _1$, so that the error is nearly as large as it can possibly be (see the points marked by green stars). Does this mean that the algorithm produced bad reconstructions? The point of this paper is that the reconstructions are still good, even for the high values of $\mathrm {DSRF}_f\in \{1280, 2560\}$, if the error is measured at the appropriate scale. To see this, in Fig. 10f we depict $\frac{1}{50} \sum _{i=1}^{50} \Vert k_{\mathrm {hi}}\star ({\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i)\Vert _1/\Vert {\mathbf {x}}_i\Vert _1$ with $\lambda _{\mathrm {hi}}=1/(\mathrm {DSRF}\cdot f_{\mathrm {lo}})$ so that $\mathrm {SRF}= \lambda _{\mathrm {lo}}/\lambda _{\mathrm {hi}}= \mathrm {DSRF}$, matching the resolution of the first experiment, as a function of $\log (\mathrm {SRF})$. We observe that $\Vert k_{\mathrm {hi}}\star ({\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i)\Vert _1\ll \Vert {\mathbf {x}}_i\Vert _1$ for all values of $\mathrm {SRF}$. In other words, if the error is measured at the scale $\lambda _{\mathrm {hi}}$ the reconstruction is good for all values of $\mathrm {SRF}$. For example, for $\mathrm {DSRF}_f=1280$ in Fig. 10d the error on average is 1.5 times larger than the signal (in l1-norm), but for the corresponding $\mathrm {SRF}=64$ in Fig. 10f, the l1-norm of the error on average is only 0.02 of the l1-norm of the signal—small. By comparing Fig. 10d and f, we infer that in the fine-scale case and for high $\mathrm {DSRF}\in \{1280, 2560\}$ the reconstruction algorithm disperses the spikes, but the estimated dispersed spikes are still concentrated around the correct locations with dispersion smaller than $\lambda _{\mathrm {hi}}$ (recall illustration in Fig. 3). Next, in Fig. 10e we depict $\log \left( \frac{1}{50} \sum _{i=1}^{50} \Vert k_{\mathrm {hi}}\star ({\mathbf {x}}_i-{\hat{{\mathbf {x}}}}_i)\Vert _1/\Vert {\mathbf {s}}_i-{\mathbf {Q}}{\mathbf {x}}_i\Vert _1\right)$ as a function of $\log (\mathrm {SRF})$. We see that the saturation effect disappeared and, as in the first experiment, on the log-log scale the data are well approximated by straight lines (displayed). We found the slopes of these lines to be 1.25 for ${\mathcal {R}}(2\lambda _{\mathrm {lo}},1)$ data and 3.28 for ${\mathcal {R}}(4\lambda _{\mathrm {lo}},2)$ data. This demonstrates that the bounds in Theorem 1 together with the converse [43, Sec. 2.3] reflect the true error on the scale $\lambda _{\mathrm {hi}}$ accurately: $(2r-1)\log (\mathrm {SRF})\le \log (\Vert k_{\mathrm {hi}}\star ({\mathbf {x}}-{\hat{{\mathbf {x}}}})\Vert _1/\Vert {\mathbf {s}}-{\mathbf {Q}}{\mathbf {x}}\Vert _1)\le (2r) \log (\mathrm {SRF})$, i.e., the exponents in the NAF are predicted to be between 1 and 2 for $r=1$ and between 3 and 4 for $r=2$, as observed in the experiment.

10 Conclusion

When a signal is positive and Rayleigh-regular, then linear programming solves the super-resolution problem with near-optimal worst-case performance. This result holds independently on how fine the discretization grid is, approximating the continuum arbitrarily closely. The proof relies on new trigonometric interpolation constructions; the underlying ideas might be useful for other problems.

Finding an efficient algorithm that solves the same problem with a near-optimal worst-case performance for complex-valued signals is still an open problem. Despite recent work that derives stability estimates for MUSIC and ESPRIT algorithms in certain cases, the question of how far are these algorithms from the optimal performance is not yet answered completely.

In a different direction, all results in this paper are valid for the 1D model. The discrete results have been generalized to the 2D model in [43]. It would be interesting to see if the techniques developed in this paper may also be extended to the 2D model.

Appendices

Proof of Lemma 2

Let

$$\begin{aligned} g_{}(t)\triangleq \left[ \frac{\sin \left( \pi (f_c/2+1) t\right) }{\left( f_c/2+1\right) \sin (\pi t)}\right] ^4 \end{aligned}$$

and set

$$\begin{aligned} q(t)\triangleq \sum _{j=1}^{V} \alpha _j g_{}(t-v_j)+\beta _j g_{}'(t-v_j), \end{aligned}$$

where $\{\alpha _j\}_{j=1}^V$ and $\{\beta _j\}_{j=1}^V$ are free coefficients that will be determined in the following. Because $g_{}(\cdot )$ is frequency-limited to $[-f_c, f_c]$ [cf. (7), (196)], $q(\cdot )$ satisfies Property 1. Note,

$$\begin{aligned} q'(t)=\sum _{j=1}^{V} \alpha _j g_{}'(t-v_j)+\beta _j g_{}''(t-v_j). \end{aligned}$$

Define matrices ${\mathbf {D}}_0,{\mathbf {D}}_1,{\mathbf {D}}_2\in {\mathbb {R}}^{V\times V}$ with the elements

$$\begin{aligned}{}[{\mathbf {D}}_0]_{jk}=g_{}(v_j-v_k),\quad [{\mathbf {D}}_1]_{jk}=g_{}'(v_j-v_k),\quad [{\mathbf {D}}_2]_{jk}=g_{}''(v_j-v_k). \end{aligned}$$

To satisfy the interpolation constraints in Property 2 we define

$\upalpha =[\alpha _1,\ldots ,\alpha _V]^{{\mathsf {T}}}$, $\upbeta =[\beta _1,\ldots ,\beta _V]^{{\mathsf {T}}}$, ${\mathbf {f}}=[f_1,\ldots ,f_V]^{{\mathsf {T}}}$, ${\mathbf {d}}=[d_1,\ldots ,d_V]^{{\mathsf {T}}}$, demand

$$\begin{aligned} \underbrace{ \begin{bmatrix} {\mathbf {D}}_0 &{} {\mathbf {D}}_1\\ {\mathbf {D}}_1 &{} {\mathbf {D}}_2 \end{bmatrix}}_{\mathbf {D}}\begin{bmatrix} \upalpha \\ \upbeta \end{bmatrix} = \begin{bmatrix} {\mathbf {f}}\\ {\mathbf {d}}\end{bmatrix} \end{aligned}$$

and solve for $\upalpha$ and $\upbeta$. It can be verified that ${\mathbf {D}}_0$ and ${\mathbf {D}}_2$ are both invertible; the corresponding Schur complements

$$\begin{aligned} {\mathbf {E}}&={\mathbf {D}}_2-{\mathbf {D}}_1 {\mathbf {D}}_0^{-1} {\mathbf {D}}_1\\ {\mathbf {F}}&={\mathbf {D}}_0-{\mathbf {D}}_1 {\mathbf {D}}_2^{-1} {\mathbf {D}}_1 \end{aligned}$$

are well defined and are also both invertible (see [13, Sec. 2.3.1, pp. 925–926], [12, App. B, p. 1249] for the relevant results). Therefore, ${\mathbf {D}}$ is invertible and the inverse can be written as [41, Sec. 9.11.3.(2)]

$$\begin{aligned} {\mathbf {D}}^{-1}= \begin{bmatrix} {\mathbf {F}}^{-1} &{} -{\mathbf {D}}_0^{-1} {\mathbf {D}}_1 {\mathbf {E}}^{-1}\\ -{\mathbf {D}}_2^{-1} {\mathbf {D}}_1 {\mathbf {F}}^{-1} &{} {\mathbf {E}}^{-1} \end{bmatrix}. \end{aligned}$$

We know (see [13, Sec. 2.3.1, pp. 925–926], [12, App. B, p. 1249]):

$$\begin{aligned} \Vert {\mathbf {D}}_1\Vert _{\infty }&\le \frac{{{{\tilde{c}}}}_1}{\lambda _c}, \end{aligned}$$

(130)

$$\begin{aligned} \Vert {\mathbf {D}}_0^{-1}\Vert _{\infty }&\le \frac{1}{1-{{{\tilde{c}}}}_0}={{\bar{c}}}_0, \end{aligned}$$

(131)

$$\begin{aligned} \Vert {\mathbf {E}}^{-1}\Vert _{\infty }&\le \left( \frac{\pi ^2f_c(f_c+4)}{3}-\left( {{{\tilde{c}}}}_2+\frac{{{{\tilde{c}}}}_1^2}{1-{{{\tilde{c}}}}_0}\right) f_c^2\right) ^{-1} \le {{\bar{c}}}_E\lambda _c^2, \end{aligned}$$

(132)

$$\begin{aligned} \Vert {\mathbf {F}}^{-1}\Vert _{\infty }&\le {{\bar{c}}}_F, \nonumber \\ \Vert {\mathbf {D}}_2^{-1}\Vert _{\infty }&\le {{\bar{c}}}_2\lambda _c^2. \end{aligned}$$

(133)

Above, $\Vert {\mathbf {A}}\Vert _{\infty }$ is the infinity norm of a matrix defined as

$$\begin{aligned} \Vert {\mathbf {A}}\Vert _{\infty } = \max _{\Vert {\mathbf {y}}\Vert _{\infty }=1} \Vert {\mathbf {A}}{\mathbf {y}}\Vert _{\infty } = \max _i \sum _j \mathchoice{{\left|a_{ij}\right|}}{{\bigl |a_{ij}\bigr |}}{{\left|a_{ij}\right|}}{{\left|a_{ij}\right|}} \end{aligned}$$

and

$$\begin{aligned}&{{{\tilde{c}}}}_0\le 0.007,\quad {{{\tilde{c}}}}_1\le 0.08,\quad {{{\tilde{c}}}}_2\le 1.06,\\&{{\bar{c}}}_0\le 1.008,\quad {{\bar{c}}}_E\le 0.47,\quad {{\bar{c}}}_2\le 0.43, \quad {{\bar{c}}}_F\le 1.009. \end{aligned}$$

Now we have

$$\begin{aligned} \Vert \upalpha \Vert _{\infty }&=\Vert {\mathbf {F}}^{-1}{\mathbf {f}}-{\mathbf {D}}_0^{-1}{\mathbf {D}}_1 {\mathbf {E}}^{-1}{\mathbf {d}}\Vert _{\infty }\\&\le \Vert {\mathbf {F}}^{-1}{\mathbf {f}}\Vert _{\infty }+\Vert {\mathbf {D}}_0^{-1}{\mathbf {D}}_1 {\mathbf {E}}^{-1}{\mathbf {d}}\Vert _{\infty }\\&\le \Vert {\mathbf {F}}^{-1}\Vert _{\infty }\Vert {\mathbf {f}}\Vert _{\infty }+\Vert {\mathbf {D}}_0^{-1}{\mathbf {D}}_1 {\mathbf {E}}^{-1}\Vert _{\infty }\Vert {\mathbf {d}}\Vert _{\infty }\\&{\mathop {\le }\limits ^{(a)}} \Vert {\mathbf {F}}^{-1}\Vert _{\infty }+\frac{1}{\lambda _c}\Vert {\mathbf {D}}_0^{-1}\Vert _{\infty }\Vert {\mathbf {D}}_1\Vert _{\infty }\Vert {\mathbf {E}}^{-1}\Vert _{\infty }\\&{\mathop {\le }\limits ^{(b)}} {{\bar{c}}}_F+{{\bar{c}}}_0{{{\tilde{c}}}}_1{{\bar{c}}}_E\triangleq c_\alpha . \end{aligned}$$

Above, (a) follows because $\mathchoice{{\left|f_j\right|}}{{\bigl |f_j\bigr |}}{{\left|f_j\right|}}{{\left|f_j\right|}}\le 1$ and $\mathchoice{{\left|d_j\right|}}{{\bigl |d_j\bigr |}}{{\left|d_j\right|}}{{\left|d_j\right|}}\le 1/\lambda _c$ for all $j=1,\ldots V$; (b) follows by (130), (131), (132), and (133); and $c_\alpha$ can be upper-bounded as $c_\alpha \le 1.05$. Similarly,

$$\begin{aligned} \Vert \upbeta \Vert _{\infty }&=\Vert -{\mathbf {D}}_2^{-1}{\mathbf {D}}_1 {\mathbf {F}}^{-1} {\mathbf {f}}+{\mathbf {E}}^{-1}{\mathbf {d}}\Vert _{\infty }\\&\le \Vert -{\mathbf {D}}_2^{-1}{\mathbf {D}}_1 {\mathbf {F}}^{-1} {\mathbf {f}}\Vert _{\infty }+\Vert {\mathbf {E}}^{-1}{\mathbf {d}}\Vert _{\infty }\\&\le \Vert -{\mathbf {D}}_2^{-1}{\mathbf {D}}_1{\mathbf {F}}^{-1} \Vert _{\infty } \Vert {\mathbf {f}}\Vert _{\infty }+\Vert {\mathbf {E}}^{-1}\Vert _{\infty }\Vert {\mathbf {d}}\Vert _{\infty }\\&\le \Vert {\mathbf {D}}_2^{-1}\Vert _{\infty } \Vert {\mathbf {D}}_1\Vert _{\infty }\Vert {\mathbf {F}}^{-1} \Vert _{\infty } +\frac{1}{\lambda _c} \Vert {\mathbf {E}}^{-1}\Vert _{\infty }\\&\le c_\beta \lambda _c\end{aligned}$$

with $c_\beta \triangleq {{\bar{c}}}_2{{{\tilde{c}}}}_1{{\bar{c}}}_F+{{\bar{c}}}_E$ that can be upper-bounded as $c_\beta \le 0.51$.

The following lemma, proven in the end of this section, records bounds on $\sum _{j=1}^{V} \mathchoice{{\left| g_{}^{(l)}(t-v_j)\right|}}{{\bigl | g_{}^{(l)}(t-v_j)\bigr |}}{{\left| g_{}^{(l)}(t-v_j)\right|}}{{\left| g_{}^{(l)}(t-v_j)\right|}}$, $l=0,1$.

Lemma 6

The following estimates hold:

$$\begin{aligned}&\sum _{j=1}^{V} \mathchoice{{\left| g_{}(t-v_j)\right|}}{{\bigl | g_{}(t-v_j)\bigr |}}{{\left| g_{}(t-v_j)\right|}}{{\left| g_{}(t-v_j)\right|}}\le c_{s0},\\&\sum _{j=1}^{V} \mathchoice{{\left|g_{}'(t-v_j)\right|}}{{\bigl |g_{}'(t-v_j)\bigr |}}{{\left|g_{}'(t-v_j)\right|}}{{\left|g_{}'(t-v_j)\right|}}\le c_{s1}/\lambda _c, \end{aligned}$$

where $c_{s0}$, $c_{s1}$ are positive numerical constants defined in the proof of the lemma below.

Using the bounds we obtain the required estimates as follows. Observe,

$$\begin{aligned} \mathchoice{{\left|q(t)\right|}}{{\bigl |q(t)\bigr |}}{{\left|q(t)\right|}}{{\left|q(t)\right|}}&=\mathchoice{{\left|\sum _{j=1}^{V} \alpha _j g_{}(t-v_j)+\beta _j g_{}'(t-v_j)\right|}}{{\bigl |\sum _{j=1}^{V} \alpha _j g_{}(t-v_j)+\beta _j g_{}'(t-v_j)\bigr |}}{{\left|\sum _{j=1}^{V} \alpha _j g_{}(t-v_j)+\beta _j g_{}'(t-v_j)\right|}}{{\left|\sum _{j=1}^{V} \alpha _j g_{}(t-v_j)+\beta _j g_{}'(t-v_j)\right|}}\nonumber \\&\le \Vert \upalpha \Vert _{\infty }\underbrace{\sum _{j=1}^{V} \mathchoice{{\left| g_{}(t-v_j)\right|}}{{\bigl | g_{}(t-v_j)\bigr |}}{{\left| g_{}(t-v_j)\right|}}{{\left| g_{}(t-v_j)\right|}}}_{\le c_{s0}} +\Vert \upbeta \Vert _{\infty }\underbrace{\sum _{j=1}^{V} \mathchoice{{\left|g_{}'(t-v_j)\right|}}{{\bigl |g_{}'(t-v_j)\bigr |}}{{\left|g_{}'(t-v_j)\right|}}{{\left|g_{}'(t-v_j)\right|}}}_{\le c_{s1}/\lambda _c} \nonumber \\&\le c_\alpha c_{s0}+c_\beta c_{s1}\triangleq c_{u0}. \end{aligned}$$

(134)

This proves Property 3. Property 4 in the lemma follows from (134) by (129) [Bernstein theorem], using that $q'(t)$ is also a trigonometric polynomial frequency-limited to $f_c$:

$$\begin{aligned} \mathchoice{{\left|q'(t)\right|}}{{\bigl |q'(t)\bigr |}}{{\left|q'(t)\right|}}{{\left|q'(t)\right|}} \le c_{u1}f_c,\quad c_{u1}\triangleq 2\pi c_{u0}. \end{aligned}$$

(135)

In turn, Property 5 follows from (135) by (129) [Bernstein theorem], using that $q''(t)$ is also a trigonometric polynomial frequency-limited to $f_c$:

$$\begin{aligned} \mathchoice{{\left|q''(t)\right|}}{{\bigl |q''(t)\bigr |}}{{\left|q''(t)\right|}}{{\left|q''(t)\right|}} \le c_{u2}f_c^2,\quad c_{u2}\triangleq 4\pi ^2 c_{u0}. \end{aligned}$$

This completes the proof of Lemma 2. $\square$

Proof of Lemma 6

For all $t\in [-1/2,1/2]$, we have the following bounds [13, Sec. 2.3.2, p. 928]:

$$\begin{aligned}&\mathchoice{{\left|g_{}(t)\right|}}{{\bigl |g_{}(t)\bigr |}}{{\left|g_{}(t)\right|}}{{\left|g_{}(t)\right|}}\le 1, \end{aligned}$$

(136)

$$\begin{aligned}&\mathchoice{{\left|g_{}'(t)\right|}}{{\bigl |g_{}'(t)\bigr |}}{{\left|g_{}'(t)\right|}}{{\left|g_{}'(t)\right|}}\le \frac{\pi ^2}{3}f_c(f_c+4)\mathchoice{{\left|t\right|}}{{\bigl |t\bigr |}}{{\left|t\right|}}{{\left|t\right|}}. \end{aligned}$$

(137)

For all t with $\lambda _c/2\le \mathchoice{{\left|t\right|}}{{\bigl |t\bigr |}}{{\left|t\right|}}{{\left|t\right|}}\le 1/2$ and $l=0,1$, by inspection it follows from [13, Lm. 2.6] that the following bound holds:

$$\begin{aligned} \mathchoice{{\left|g_{}^{(l)}(t)\right|}}{{\bigl |g_{}^{(l)}(t)\bigr |}}{{\left|g_{}^{(l)}(t)\right|}}{{\left|g_{}^{(l)}(t)\right|}}\le \frac{\pi ^l c_g^l}{(f_c+2)^{4-l}t^4} \end{aligned}$$

(138)

with $c_g^0\triangleq 1, c_g^1\triangleq 6$. [To obtain this result from [13, Lm. 2.6], observe that, in the terminology of [13], for all t with $\lambda _c/2\le \mathchoice{{\left|t\right|}}{{\bigl |t\bigr |}}{{\left|t\right|}}{{\left|t\right|}}\le \sqrt{2}/\pi$, $b(t)<2 a(t)$ and $a(t)<1$.]

Define $u_{k_j} \triangleq t - v_j$, ordered in such a way that $\mathchoice{{\left|u_1\right|}}{{\bigl |u_1\bigr |}}{{\left|u_1\right|}}{{\left|u_1\right|}}<\ldots <\mathchoice{{\left|u_V\right|}}{{\bigl |u_V\bigr |}}{{\left|u_V\right|}}{{\left|u_V\right|}}$. Since $\{v_1, v_1, \ldots , v_V\}\in {\mathcal {R}}(\kappa \lambda _c,1)$, we have

$$\begin{aligned} \mathchoice{{\left|u_{2j}\right|}}{{\bigl |u_{2j}\bigr |}}{{\left|u_{2j}\right|}}{{\left|u_{2j}\right|}}> \lambda _c\kappa (j-1)\ \text {and}\ \mathchoice{{\left|u_{2j-1}\right|}}{{\bigl |u_{2j-1}\bigr |}}{{\left|u_{2j-1}\right|}}{{\left|u_{2j-1}\right|}} > \lambda _c\kappa (j-1), \ \text {for}\ j \ge 2, \end{aligned}$$

(139)

and also,

$$\begin{aligned} \mathchoice{{\left|u_{j}\right|}}{{\bigl |u_{j}\bigr |}}{{\left|u_{j}\right|}}{{\left|u_{j}\right|}}> \frac{\lambda _c}{2} \kappa j,\ \text {for}\ j > 1. \end{aligned}$$

(140)

First,

$$\begin{aligned} \sum _{j=1}^{V} \mathchoice{{\left|g_{}(t-v_j)\right|}}{{\bigl |g_{}(t-v_j)\bigr |}}{{\left|g_{}(t-v_j)\right|}}{{\left|g_{}(t-v_j)\right|}} =\sum _{j=1}^{V} \mathchoice{{\left|g_{}(u_j)\right|}}{{\bigl |g_{}(u_j)\bigr |}}{{\left|g_{}(u_j)\right|}}{{\left|g_{}(u_j)\right|}}&{\mathop {\le }\limits ^{(a)}} 2+\frac{1}{(f_c+2)^4} \sum _{j=3}^{V} \frac{1}{u_j^4}\\&{\mathop {\le }\limits ^{(b)}} 2+\frac{2}{(f_c+2)^4} \sum _{j=1}^{\lceil V/2\rceil } \frac{1}{(\lambda _c\kappa j)^4}\\&\le 2+\frac{1}{f_c^4} \frac{2}{(\lambda _c\kappa )^4}\sum _{j=1}^{\infty } \frac{1}{j^4} {\mathop {\le }\limits ^{(c)}} 2+\frac{2}{\kappa ^4} \frac{4}{3} {\mathop {\le }\limits ^{(d)}} c_{s0}. \end{aligned}$$

Above, in (a) we used (136) to bound the terms for $j=1,2$ and used (138) to bounds the terms for $j>2$ [(138) is applicable because $u_3>\lambda _c\kappa /2>\lambda _c/2$ since $\kappa {=}1.87$]; in (b) we used (139); in (c) we used

$$\begin{aligned} \sum _{j=1}^{\infty } \frac{1}{j^4}=\frac{\pi ^2}{90}\le \frac{4}{3}; \end{aligned}$$

and in (d) we defined $c_{s0}\triangleq 2.22$.

Second,

$$\begin{aligned} \sum _{j=1}^{V} \mathchoice{{\left|g_{}'(t-v_j)\right|}}{{\bigl |g_{}'(t-v_j)\bigr |}}{{\left|g_{}'(t-v_j)\right|}}{{\left|g_{}'(t-v_j)\right|}}&=\mathchoice{{\left|g_{}'(u_1)\right|}}{{\bigl |g_{}'(u_1)\bigr |}}{{\left|g_{}'(u_1)\right|}}{{\left|g_{}'(u_1)\right|}} + \sum _{j=2}^{V} \mathchoice{{\left|g_{}'(u_j)\right|}}{{\bigl |g_{}'(u_j)\bigr |}}{{\left|g_{}'(u_j)\right|}}{{\left|g_{}'(u_j)\right|}}\\&{\mathop {\le }\limits ^{(a)}} \frac{\pi ^2}{3}f_c(f_c+4) \frac{\lambda _c}{2}\kappa + \frac{1}{(f_c+2)^3} \frac{6\pi }{((\lambda _c/2) \kappa )^4} + \sum _{j=2}^{V} \mathchoice{{\left|g_{}'(u_j)\right|}}{{\bigl |g_{}'(u_j)\bigr |}}{{\left|g_{}'(u_j)\right|}}{{\left|g_{}'(u_j)\right|}} \\&{\mathop {\le }\limits ^{(b)}} \frac{\pi ^2}{3}f_c(f_c+4) \frac{\lambda _c}{2}\kappa + \frac{1}{(f_c+2)^3} \frac{6\pi }{((\lambda _c/2) \kappa )^4} + \frac{1}{(f_c+2)^3} \sum _{j=2}^{V} \frac{6\pi }{u_j^4}\\&{\mathop {\le }\limits ^{(c)}} \frac{\pi ^2}{3}f_c(f_c+4)\frac{\lambda _c}{2}\kappa + \frac{1}{(f_c+2)^3} \sum _{j=1}^{V} \frac{6\pi }{((\lambda _c/2) \kappa j)^4}\\&\le \frac{\pi ^2}{6}(f_c+4)\kappa +\frac{6\pi }{f_c^3} \frac{2^4}{(\lambda _c\kappa )^4} \sum _{j=1}^{\infty } \frac{1}{j^4}\\&{\mathop {\le }\limits ^{(d)}} \frac{\pi ^2}{6}(f_c+4)\kappa +35 f_c\le 12.4+38.1 f_c{\mathop {\le }\limits ^{(e)}} c_{s1}f_c. \end{aligned}$$

Above, in (a) we used that if $\mathchoice{{\left|u_1\right|}}{{\bigl |u_1\bigr |}}{{\left|u_1\right|}}{{\left|u_1\right|}} < \lambda _c\kappa /2$, then $\mathchoice{{\left|g_{}'(u_1)\right|}}{{\bigl |g_{}'(u_1)\bigr |}}{{\left|g_{}'(u_1)\right|}}{{\left|g_{}'(u_1)\right|}}<(\pi ^2/3)f_c(f_c+4)\lambda _c\kappa /2$ by (137) and otherwise $\mathchoice{{\left|g_{}'(u_1)\right|}}{{\bigl |g_{}'(u_1)\bigr |}}{{\left|g_{}'(u_1)\right|}}{{\left|g_{}'(u_1)\right|}}<6\pi /[(f_c+2)^3((\lambda _c/2) \kappa )^4]$ by (138); in (b) we used (138), which is applicable because $\mathchoice{{\left|u_j\right|}}{{\bigl |u_j\bigr |}}{{\left|u_j\right|}}{{\left|u_j\right|}}>\lambda _c\kappa >\lambda _c/2$ by (140); in (c) we used (140); in (d) we used $\sum _{j=1}^{\infty } 1/j^4<4/3$; in (e) we used that $f_c> 128$ and defined $c_{s1}\triangleq 38.2$.$\square$

Proof of Lemma 5

1.1 Construction

We first describe how the trigonometric polynomial $q_2(\cdot )$ is constructed. In the following four subsections, we prove that the construction is valid and that it satisfies the required Properties 1–4.

Recall, ${\mathcal {T}}=\{t_1,\ldots , t_S\}$ is defined in (12) and, as before, define ${\mathcal {T}}_k$, $k=1,\ldots ,r$, as in (20); remember that ${\mathcal {T}}= {\mathcal {T}}_1\cup \ldots \cup {\mathcal {T}}_r$ and ${\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$.

We will construct the trigonometric polynomial $q_2(\cdot )$ as a (shifted) sum of $r$ trigonometric polynomials $\{\phi _k(\cdot )\}_{k=1}^r$:

$$\begin{aligned} q_2(t)=\sum _{k=1}^r\phi _k(t)-\rho . \end{aligned}$$

(141)

Note that we are overloading the notations here and $\phi _k(\cdot )$ in this section are different from $\phi _k(\cdot )$ in Sect. 6.3.1. Each of the trigonometric polynomials $\{\phi _k(\cdot )\}_{k=1}^r$ is frequency-limited to $f_{\mathrm {lo}}$,

$$\begin{aligned} \phi _k(t) =\sum _{l=-f_{\mathrm {lo}}}^{f_{\mathrm {lo}}} \hat{\phi }_{k,l} e^{-\mathrm {i} 2\pi l t} \quad \text {for some}\quad \hat{\phi }_{k, l}\in {\mathbb {C}}\end{aligned}$$

(142)

and is constructed separately to satisfy the following interpolation constraints on ${\mathcal {T}}$:

$$\begin{aligned} \phi _k(t_l)&= {\left\{ \begin{array}{ll} \rho , &{}\text { if } t_l\in {\mathcal {T}}_k,\\ 0, &{}\text { if } t_l\in {\mathcal {T}}_k^c\triangleq {\mathcal {T}}\setminus {\mathcal {T}}_k, \end{array}\right. } \end{aligned}$$

(143)

$$\begin{aligned} \phi '_k(t_l)&={\left\{ \begin{array}{ll} \gamma s'_l, &{}\text { if } t_l\in {\mathcal {T}}_k,\\ 0, &{}\text { if } t_l\in {\mathcal {T}}_k^c. \end{array}\right. } \end{aligned}$$

(144)

Constraints (143), (144), and definition (141) guarantee, for all $l=1,\ldots ,S$,

$$\begin{aligned} q_2(t_l)&=0, \end{aligned}$$

(145)

$$\begin{aligned} q'_2(t_l)&=\gamma s'_l. \end{aligned}$$

(146)

To develop intuition about our construction, observe that (142) and (141) guarantee that Property 1 is satisfied. Further, observe that interpolation constraints (145) and (146) are needed for (104) to hold because $q_0(t)=q'_0(t)=0$ for all $t\in {\mathcal {T}}$.

Next, we explain how to construct the trigonometric polynomials $\phi _k(\cdot )$, $k=1,\ldots ,r$. The idea is to construct $\phi _k(\cdot )$ as a product of two trigonometric polynomials:

$$\begin{aligned} \phi _k(t)\triangleq \phi _{0,k}(t)\times \phi _{+,k}(t). \end{aligned}$$

(147)

The first term in the product is defined as

$$\begin{aligned} \phi _{0,k}(t)\triangleq \prod _{l\ne k} q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_l}(t), \end{aligned}$$

(148)

where $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_l}(\cdot ),\ l=1,\ldots ,r$ are the trigonometric polynomials constructed via Lemma 1 with $\lambda _c=r\lambda _{\mathrm {lo}}$ and ${\mathcal {V}}={\mathcal {T}}_l\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. The second term,

$$\begin{aligned} \phi _{+,k}(t)\triangleq r^{2r}c_{u31}^{r}q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(t) \end{aligned}$$

(149)

is a (rescaled) trigonometric polynomial $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ constructed via Lemma 2 with $\lambda _c=r\lambda _{\mathrm {lo}}$, and ${\mathcal {V}}={\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$ and $c_{u31}$ is a positive numerical constant defined in (160) below. Further, the function-values and derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ are constrained on ${\mathcal {T}}_k$ so that $\phi _{+,k}(\cdot )$ satisfies the following:

$$\begin{aligned} \phi _{+,k}(t)= & {} \rho \frac{1}{\phi _{0,k}(t)}, \text { for all } t\in {\mathcal {T}}_k, \end{aligned}$$

(150)

$$\begin{aligned} \phi '_{+,k}(t_l)= & {} -\rho \frac{\phi '_{0,k}(t_l)}{\phi ^2_{0,k}(t_l)} +\frac{\gamma s'_l}{\phi _{0,k}(t_l)}, \text { for all } t_l\in {\mathcal {T}}_k. \end{aligned}$$

(151)

Note that $\phi _{0,k}(\cdot )$ in this section is identical to $\phi _{0,k}(\cdot )$ defined in Sect. 6.3.1 and, therefore, satisfies all the properties derived in Sect. 6.3.2; $\phi _{+,k}(\cdot )$ in this section is different from $\phi _{+,k}(\cdot )$ in Sect. 6.3.1 and the notation is overloaded.

We will prove in the next subsection, that this specification is valid, in the sense that the corresponding function values and derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ on ${\mathcal {T}}_k$ satisfy requirements (15) of Lemma 2.

It follows from (147), (148), (150), Lemma 1, Properties 2, 4, and 5, that the interpolation constraint (143) is satisfied:

$$\begin{aligned} \phi _k(t)= & {} \phi _{0,k}(t) \phi _{+,k}(t)=\rho , \text { for all } t\in {\mathcal {T}}_k,\\ \phi _k(t)= & {} \underbrace{\phi _{0,k}(t)}_0 \phi _{+,k}(t)=0, \text { for all } t\in {\mathcal {T}}_k^c. \end{aligned}$$

Next, by (147),

$$\begin{aligned} \phi '_k(t)=\phi '_{0,k}(t)\phi _{+,k}(t)+\phi _{0,k}(t)\phi '_{+,k}(t). \end{aligned}$$

Therefore, by (150) and (151),

$$\begin{aligned} \phi '_k(t_l)&=\phi '_{0,k}(t_l)\phi _{+,k}(t_l)+\phi _{0,k}(t_l)\phi '_{+,k}(t_l)\\&=\phi '_{0,k}(t_l)\rho \frac{1}{\phi _{0,k}(t_l)} +\phi _{0,k}(t_l)\left( -\rho \frac{\phi '_{0,k}(t_l)}{\phi ^2_{0,k}(t_l)} +\frac{\gamma s'_l}{\phi _{0,k}(t_l)}\right) =\gamma s'_l, \end{aligned}$$

for all $t_l\in {\mathcal {T}}_k$. Further, by (148), Lemma 1, Property 2,

$$\begin{aligned} \phi '_k(t) =\underbrace{\phi '_{0,k}(t)}_0 \phi _{+,k}(t) +\underbrace{\phi _{0,k}(t)}_0\phi '_{+,k}(t)=0, \end{aligned}$$

for all $t\in {\mathcal {T}}_k^c$. We conclude that the interpolation constraint (144) is satisfied.

Finally, (142) follows from (147) because $\phi _{0,k}(\cdot )$ in (148) is frequency-limited to $(r-1)/(\lambda _{\mathrm {lo}}r)$ [Lemma 1, Property 1] and $\phi _{+,k}(\cdot )$ in (149) is frequency-limited to $1/(\lambda _{\mathrm {lo}}r)$ [Lemma 2, Property 1] so that $\phi _k(\cdot )$ is frequency-limited to $(r-1)/(\lambda _{\mathrm {lo}}r)+1/(\lambda _{\mathrm {lo}}r)=1/\lambda _{\mathrm {lo}}=f_{\mathrm {lo}}.$ Therefore, by (141), $q_2(\cdot )$ is also frequency-limited to $f_{\mathrm {lo}}$, which proves Property 1.

1.2 Existence of $\phi _{+,k}(\cdot )$

In this subsection, we check that the trigonometric polynomial $\phi _{+,k}(\cdot )$ that satisfies (150) and (151) can be defined according to (149) with $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )$ constructed via Lemma 2 with $\lambda _c=r\lambda _{\mathrm {lo}}$ and ${\mathcal {V}}={\mathcal {T}}_k\in {\mathcal {R}}(\kappa \lambda _{\mathrm {lo}}r,1)$. To this end, we need to show that the constraints on the function values $\{f_j\}$ and on the derivatives $\{d_j\}$ that are implied by the constraints (150) and (151) satisfy requirements (15) of Lemma 2.

First consider the case $r=1$. As already discussed, in this case $\phi _{0,k}(t)=1$ for all t, and, therefore, $\phi '_{0,k}(t)=0$ for all t. Plugging these values into (150) and (151) we see from (149) that the requirements (15) of Lemma 2 are satisfied.

Next, consider the case $r>1$.

To check that requirements (15) are satisfied for $t\in {\mathcal {T}}_k$, we need to find upper bounds on $\mathchoice{{\left|\phi _{+,k}(t)\right|}}{{\bigl |\phi _{+,k}(t)\bigr |}}{{\left|\phi _{+,k}(t)\right|}}{{\left|\phi _{+,k}(t)\right|}}$ and on $\mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}}$.

Take $t\in {\mathcal {T}}_k$ and observe:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(t)\right|}}{{\bigl |\phi _{+,k}(t)\bigr |}}{{\left|\phi _{+,k}(t)\right|}}{{\left|\phi _{+,k}(t)\right|}}&{\mathop {=}\limits ^{(a)}} \mathchoice{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}}{{\bigl |\rho \frac{1}{\phi _{0,k}(t)}\bigr |}}{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}}{{\left|\rho \frac{1}{\phi _{0,k}(t)}\right|}} {\mathop {\le }\limits ^{(b)}} \frac{\lambda _{\mathrm {hi}}^{2r}}{\lambda _{\mathrm {lo}}^{2r}} \frac{1}{\frac{\lambda _{\mathrm {hi}}^{2(r-1)}}{(r\lambda _{\mathrm {lo}})^{2(r-1)}}} \frac{1}{c_l^{r-1}} \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2(r-1)}\frac{1}{c_l^{r}}\frac{\lambda _{\mathrm {hi}}^{2}}{\lambda _{\mathrm {lo}}^{2}} \end{aligned}$$

(152)

$$\begin{aligned}&\le r^{2r}\frac{1}{c_l^{r}}. \end{aligned}$$

(153)

Above, (a) follows by (150); (b) follows by (47), which is valid because $t\in {\mathcal {T}}_k$ implies $t\in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}}_k^c)$; (c) follows because $c_l<1$.

Next, take $t\in {\mathcal {T}}_k$ and observe, according to (151),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}} \le \mathchoice{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\bigl |\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\bigr |}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}+\mathchoice{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\bigl |\frac{\gamma }{\phi _{0,k}(t)}\bigr |}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}. \end{aligned}$$

(154)

The first term above can be upper-bounded following exactly the same steps that lead from (54) to (60). This gives:

$$\begin{aligned} \mathchoice{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\bigl |\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\bigr |}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}}{{\left|\rho \frac{\phi '_{0,k}(t)}{\phi ^2_{0,k}(t)}\right|}} \le r^{2r-1}c_{u7}^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(155)

To upper-bound the second term in (154), consider two cases.

Case 1: $t\in {\mathcal {F}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$. Then, by (44), $\phi _{0,k}(t) \ge c_{l1}^{r-1}$ and, therefore,

$$\begin{aligned} \mathchoice{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\bigl |\frac{\gamma }{\phi _{0,k}(t)}\bigr |}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}} \le \frac{\gamma }{c_{l1}^{r-1}} = \frac{1}{c_{l1}^{r-1}} \frac{\lambda _{\mathrm {hi}}^{2r-1}}{\lambda _{\mathrm {lo}}^{2r}} \le r^{2r-1} \left( \frac{1}{c_{l1}^2}\right) ^{r} \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(156)

Above, in the last (crude) inequality we used that $c_{l1}<1$ and that $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$.

Case 2: $t\in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$. In this case set $\{v_1,\ldots ,v_{{{\hat{r}}}}\}\triangleq {\mathcal {T}}_k^c\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},t)$ and note that $1\le {{\hat{r}}}\le r-1$. Hence, by (40),

$$\begin{aligned} \phi _{0,k}(t) \ge c_{l2}^{r-1}\frac{ \prod _{j=1}^{{{\hat{r}}}}(v_j-t)^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \ge c_{l2}^{r-1}\frac{ \lambda _{\mathrm {hi}}^{2{{\hat{r}}}}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}, \end{aligned}$$

where we used that $\mathchoice{{\left|v_{j}-t\right|}}{{\bigl |v_{j}-t\bigr |}}{{\left|v_{j}-t\right|}}{{\left|v_{j}-t\right|}}\ge 2\lambda _{\mathrm {hi}}$ for all $j=1,\ldots ,{{\hat{r}}}$ because all elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$. Therefore,

$$\begin{aligned} \mathchoice{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\bigl |\frac{\gamma }{\phi _{0,k}(t)}\bigr |}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}}{{\left|\frac{\gamma }{\phi _{0,k}(t)}\right|}} \le \frac{\gamma }{c_{l2}^{r-1}}\frac{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}{\lambda _{\mathrm {hi}}^{2{{\hat{r}}}}} = \frac{1}{c_{l2}^{r-1}} \frac{\lambda _{\mathrm {hi}}^{2r-1}}{\lambda _{\mathrm {lo}}^{2r}} \frac{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}{\lambda _{\mathrm {hi}}^{2{{\hat{r}}}}} \le r^{2r-1} \left( \frac{1}{c_{l2}^2}\right) ^{r} \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(157)

Above, in the last (crude) inequality we used that $c_{l2}<1$, $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$, and ${{\hat{r}}}\le r-1$.

Plugging (155), (156), and (157) into (154) we obtain

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}'(t)\right|}}{{\bigl |\phi _{+,k}'(t)\bigr |}}{{\left|\phi _{+,k}'(t)\right|}}{{\left|\phi _{+,k}'(t)\right|}}&\le r^{2r-1} c_{u30}^{r} \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2} \end{aligned}$$

(158)

$$\begin{aligned}&\le r^{2r-1} c_{u30}^{r} \frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(159)

where we used that $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$ and defined $c_{u30}\triangleq 2\max (c_{u7}, 1/c_{l1}^2, 1/c_{l2}^2)$.

It follows from (153) and (159) that the function values and the derivatives of $q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k}(t)=\phi _{+,k}(t)/(r^{2r}c_{u31}^{r})$ with

$$\begin{aligned} c_{u31}\triangleq \max (c_{u30}, 1/c_l) \end{aligned}$$

(160)

satisfy requirements (15) of Lemma 2 on ${\mathcal {T}}_k$. We conclude that $\phi _{+,k}(\cdot )$ can indeed be defined according to (149). According to Properties 3, 4, and 5 of Lemma 2, and (149), $\phi _{+,k}(\cdot )$ satisfies the following properties:

$$\begin{aligned}&\Vert \phi _{+,k}(\cdot )\Vert _{\infty }\le r^{2r}c_{u31}^{r}c_{u0}, \end{aligned}$$

(161)

$$\begin{aligned}&\Vert \phi _{+,k}'(\cdot )\Vert _{\infty }\le r^{2r-1}c_{u31}^{r} c_{u1}\frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(162)

$$\begin{aligned}&\Vert \phi _{+,k}''(\cdot )\Vert _{\infty }\le r^{2r-2}c_{u31}^{r} c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(163)

1.3 Proof of Property 2

Take $j\in \{1,\ldots , S\}$ and consider $t_j\in {\mathcal {T}}$. There exists a unique $l\in \{1,\ldots ,r\}$ such that $t_j\in {\mathcal {T}}_l$. We will show that for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$

$$\begin{aligned} \mathchoice{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau -t_j)\right|}}{{\bigl |\phi _l(\tau )-\rho -\gamma s'_j(\tau -t_j)\bigr |}}{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau -t_j)\right|}}{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau -t_j)\right|}} \le r^{2r+3}c_{u44}^{r+1} q_0(\tau ) \end{aligned}$$

(164)

and

$$\begin{aligned} \mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}} \le r^{2r+3}c_{u50}^{r+1} q_0(\tau ),\ \text {for}\ k\in \{1,\ldots , r\},\ k\ne l, \end{aligned}$$

(165)

where the positive numerical constants $c_{u44}$ and $c_{u50}$ are defined below.

From this we will conclude:

$$\begin{aligned} \mathchoice{{\left|q_2(\tau )-\gamma s'_j(\tau -t_j)\right|}}{{\bigl |q_2(\tau )-\gamma s'_j(\tau -t_j)\bigr |}}{{\left|q_2(\tau )-\gamma s'_j(\tau -t_j)\right|}}{{\left|q_2(\tau )-\gamma s'_j(\tau -t_j)\right|}}&=\mathchoice{{\left|\sum _{k=1}^r\phi _k(\tau ) -\rho -\gamma s'_j(\tau -t_j)\right|}}{{\bigl |\sum _{k=1}^r\phi _k(\tau ) -\rho -\gamma s'_j(\tau -t_j)\bigr |}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\rho -\gamma s'_j(\tau -t_j)\right|}}{{\left|\sum _{k=1}^r\phi _k(\tau ) -\rho -\gamma s'_j(\tau -t_j)\right|}}\\&\le \sum _{k\ne l}\mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}}+ \mathchoice{{\left|\phi _l(\tau ) - \rho -\gamma s'_j(\tau -t_j)\right|}}{{\bigl |\phi _l(\tau ) - \rho -\gamma s'_j(\tau -t_j)\bigr |}}{{\left|\phi _l(\tau ) - \rho -\gamma s'_j(\tau -t_j)\right|}}{{\left|\phi _l(\tau ) - \rho -\gamma s'_j(\tau -t_j)\right|}}\\&\le r^{2r+4}c_{u34}^{r+1} q_0(\tau ), \end{aligned}$$

with $c_{u34}\triangleq 2\max (c_{u44}, c_{u50})$, as desired.

To prove (164) and (165) recall, by (143) and (144),

$$\begin{aligned}&\left. \phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j) \right| _{\tau = t_j} = 0 = q_0(t_j), \end{aligned}$$

(166)

$$\begin{aligned}&\left. \frac{d(\phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j))}{d \tau }\right| _{\tau = t_j} =\phi '_l(t_j)-\gamma s'_j=0=q'_0(t_j), \end{aligned}$$

(167)

$$\begin{aligned}&\phi _k(t_j) = 0 = q_0(t_j)\ \text {for}\ k\in \{1,\ldots , r\},\ k\ne l, \end{aligned}$$

(168)

$$\begin{aligned}&\phi '_k(t_j)=0=q'_0(t_j)\ \text {for}\ k\in \{1,\ldots , r\},\ k\ne l. \end{aligned}$$

(169)

Hence, in order to prove the bounds in (165) and (164), we will derive upper bounds on the second derivatives $\mathchoice{{\left|\phi ''_k(\tau )\right|}}{{\bigl |\phi ''_k(\tau )\bigr |}}{{\left|\phi ''_k(\tau )\right|}}{{\left|\phi ''_k(\tau )\right|}}$, $k\in \{1,\ldots ,r\}$, valid for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, and use the Mean Value theorem (see Theorem 3).

Taking the second derivative of (147) and applying the triangle inequality we find:

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}} \le \underbrace{\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}}_{E_{1}(\tau )} +2\underbrace{\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}}_{E_{2}(\tau )} +\underbrace{\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}}_{E_3(\tau )}. \end{aligned}$$

(170)

In the derivation below we upper-bound the terms separately.

We will need the following notations. Set $\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k^c$. Also, set $\{v_1,\ldots ,v_{{\tilde{r}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\cap {\mathcal {T}}_k^c$. Note that the set $\{v_1,\ldots ,v_{{\tilde{r}}}\}$ does not depend on $\tau$ and also $\{v_1,\ldots ,v_{{\tilde{r}}}\}\subset \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$ so that ${\tilde{r}}\le {{\hat{r}}}$.

The remainder of the proof of Property 2 is organized as follows. First, consider the case $t_j\in {\mathcal {T}}_k$ and prove (164), next consider the case $t_j\in {\mathcal {T}}_k^c$ and prove (165).

Proof of (164): case $t_j\in {\mathcal {T}}_k$.

Bounding $E_1(\tau )$: By (195) [Mean Value theorem] and the triangle inequality we can write

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi _{+,k}(t_j)\right|}}{{\bigl |\phi _{+,k}(t_j)\bigr |}}{{\left|\phi _{+,k}(t_j)\right|}}{{\left|\phi _{+,k}(t_j)\right|}} +\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}\mathchoice{{\left|\tau - t_j\right|}}{{\bigl |\tau - t_j\bigr |}}{{\left|\tau - t_j\right|}}{{\left|\tau - t_j\right|}} +\frac{1}{2}\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}(\tau - t_j)^2 \end{aligned}$$

with $\tau _m\in (t_j, \tau )$. Next, we use (152) to upper-bound $\mathchoice{{\left|\phi _{+,k}(t_j)\right|}}{{\bigl |\phi _{+,k}(t_j)\bigr |}}{{\left|\phi _{+,k}(t_j)\right|}}{{\left|\phi _{+,k}(t_j)\right|}}$; use (158) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}$; use (163) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&\le r^{2r-1}c_{u35}^r\left( \frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2} +\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}+\frac{1}{\lambda _{\mathrm {lo}}^2}(\tau -t_j)^2\right) \nonumber \\&\le r^{2r-1}c_{u36}^r\frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(171)

Above, we defined $c_{u35}\triangleq \max (1/c_l, c_{u30}, c_{u31}c_{u2})$, $c_{u36}\triangleq 3 c_{u35}$, and used $\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\le \lambda _{\mathrm {hi}}$.

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that $\mathchoice{{\left|\phi _{0,k}''(\tau )\right|}}{{\bigl |\phi _{0,k}''(\tau )\bigr |}}{{\left|\phi _{0,k}''(\tau )\right|}}{{\left|\phi _{0,k}''(\tau )\right|}}$ can be upper-bounded by (73).

Multiplying (171) and (73) and simplifying we obtain the following upper bound on $E_1$:

$$\begin{aligned} E_1(\tau ) =\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u37}^{r+1} \frac{\prod _{1\le l\le {{\hat{r}}}} (v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u37}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(172)

Above, in (a) we used (multiple times) the bound $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}$, which is true for all $l\in \{1,\ldots ,{{\hat{r}}}\}$ (follows because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$), used $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$, and defined $c_{u37}\triangleq \max (6 c_{u3}c_{u36}, c_{u31}c_{u0}c_{u5})$; in (b) we used the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper bound (74) also holds by (46) and (161).

Bounding $E_2(\tau )$: By (194) [Mean Value theorem] we can write

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi '_{+,k}(t_j)\right|}}{{\bigl |\phi '_{+,k}(t_j)\bigr |}}{{\left|\phi '_{+,k}(t_j)\right|}}{{\left|\phi '_{+,k}(t_j)\right|}}+\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}\mathchoice{{\left|\tau - t_j\right|}}{{\bigl |\tau - t_j\bigr |}}{{\left|\tau - t_j\right|}}{{\left|\tau - t_j\right|}} \end{aligned}$$

with $\tau _m\in (t_j, \tau )$. Next, we use (158) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(t_j)\right|}}{{\bigl |\phi _{+,k}'(t_j)\bigr |}}{{\left|\phi _{+,k}'(t_j)\right|}}{{\left|\phi _{+,k}'(t_j)\right|}}$; use (163) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \le r^{2r-1}c_{u38}^r\left( \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}+\frac{1}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\right) \le r^{2r-1}c_{u39}^r\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(173)

Above, we defined $c_{u38}\triangleq \max (c_{u30}, c_{u2}c_{u31})$, $c_{u39}\triangleq 2 c_{u38}$, and used $\mathchoice{{\left|\tau -t_j\right|}}{{\bigl |\tau -t_j\bigr |}}{{\left|\tau -t_j\right|}}{{\left|\tau -t_j\right|}}\le \lambda _{\mathrm {hi}}$.

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that $\mathchoice{{\left|\phi '_{0,k}(t)\right|}}{{\bigl |\phi '_{0,k}(t)\bigr |}}{{\left|\phi '_{0,k}(t)\right|}}{{\left|\phi '_{0,k}(t)\right|}}$ can be upper-bounded by (76). Multiplying (173) and (76) and simplifying, we obtain the following upper bound on $E_2$:

$$\begin{aligned} E_2(\tau ) =\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r}c_{u40}^{r} \frac{\prod _{1\le l\le {{\hat{r}}}} (v^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r}c_{u40}^{r} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(174)

Above, in (a) we used the bound $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}$, which is true for all $l\in \{1,\ldots ,{{\hat{r}}}\}$ (follows because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$), used $\lambda _{\mathrm {hi}}/\lambda _{\mathrm {lo}}<1$, and defined $c_{u40}\triangleq \max (2 c_{u39}c_{u3}, 2\pi c_{u31}c_{u1})$; in (b) we use the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper bound (174) also holds by (45) and (162).

Bounding $E_3(\tau )$: By (163),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}''(\tau )\right|}}{{\bigl |\phi _{+,k}''(\tau )\bigr |}}{{\left|\phi _{+,k}''(\tau )\right|}}{{\left|\phi _{+,k}''(\tau )\right|}}\le r^{2r-2}c_{u31}^{r} c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(175)

Assume ${\tilde{r}}\ge 1$ (the case ${\tilde{r}}=0$ will be treated separately below) so that ${{\hat{r}}}\ge 1$ and $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, which implies that $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$ can be upper-bounded by (79). Multiplying (175) and (79) and simplifying, we obtain the following upper bound on $E_3$:

$$\begin{aligned} E_3(\tau ) =\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r-2}c_{u41}^{r} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r-2}c_{u41}^{r} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(176)

Above, (a) we defined $c_{u41}\triangleq c_{u31}c_{u2}c_u$; in (b) we use the fact that

$\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

For the case ${{\tilde{r}}}=0$, the upper bound (176) also holds by (175) because by (148) and Lemma 1, Property 3, $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}<1$ and because $c_u>1$ and $c_{u2}>1$.

From (170), (172), (174), and (176) we conclude that

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}} \le r^{2r+1}c_{u42}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{1}{\lambda _{\mathrm {lo}}^2}, \end{aligned}$$

(177)

where we defined $c_{u42}\triangleq 4 \max (c_{u37}, c_{u40}, c_{u41})$.

Putting pieces together: Applying (195) [Mean Value theorem] to the function $f (\cdot ) = \phi _l(\cdot )-\rho -\gamma s'_j(\cdot - t_j)$ with $a=t_j$ and $b=\tau$ and using (166), (167), (177) and we can write for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$:

$$\begin{aligned} \mathchoice{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j)\right|}}{{\bigl |\phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j)\bigr |}}{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j)\right|}}{{\left|\phi _l(\tau )-\rho -\gamma s'_j(\tau - t_j)\right|}}&{\mathop {\le }\limits ^{(a)}} \frac{1}{2} r^{2r+1}c_{u42}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} \frac{1}{2} r^{2r+1}c_{u42}^{r+1} 2^{{\tilde{r}}} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+3}c_{u43}^{r+1} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}} \frac{(\tau -t_j)^2}{(r\lambda _{\mathrm {lo}})^2}. \end{aligned}$$

(178)

Above, in (a) $\tau _m\in (t_j, \tau )$; in (b) we used that $\mathchoice{{\left|v_l-\tau _m\right|}}{{\bigl |v_l-\tau _m\bigr |}}{{\left|v_l-\tau _m\right|}}{{\left|v_l-\tau _m\right|}}<\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}$, which is true because $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ and because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$; in (c) we defined $c_{u43}\triangleq 2c_{u42}$.

The bound (164) follows from (178) and (83) by defining $c_{u44}\triangleq c_{u43}/c_{l3}$.

Proof of (165): case $t_j\in {\mathcal {T}}^c_k$. We only need to consider this case when $r>1$. Indeed, when $r=1$, the sum in (141) only contains one element, $\phi _l(\cdot )$, and, necessarily, $t_j\in {\mathcal {T}}_l$ because ${\mathcal {T}}_l^c$ is empty.

In this case $t_j$ is one of the elements among $\{v_1,\ldots ,v_{{\tilde{r}}}\}\subset \{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$; in other words, $t_j=v_{{{\tilde{m}}}}=v^\tau _{{\hat{m}}}$ for some $1\le {{\tilde{m}}}\le {\tilde{r}}$, $1\le {\hat{m}}\le {{\hat{r}}}$. The set ${\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)$ is either empty or contains exactly one element. Let $b\triangleq \mathchoice{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}{{\bigl |{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\bigr |}}{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}{{\left|{\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)\right|}}$. In the case when $b=1$, let $\{{{\tilde{t}}}\}\triangleq {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}-\lambda _{\mathrm {hi}},t_j)$.

Bounding $E_1(\tau )$: Consider the case $b=1$. By (195) [Mean Value theorem] we can write:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \le \mathchoice{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\bigl |\phi _{+,k}({{\tilde{t}}})\bigr |}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}} +\mathchoice{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}}{{\bigl |\phi _{+,k}'({{\tilde{t}}})\bigr |}}{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}}{{\left|\phi _{+,k}'({{\tilde{t}}})\right|}}\mathchoice{{\left|\tau - {{\tilde{t}}}\right|}}{{\bigl |\tau - {{\tilde{t}}}\bigr |}}{{\left|\tau - {{\tilde{t}}}\right|}}{{\left|\tau - {{\tilde{t}}}\right|}} +\frac{1}{2}\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}(\tau - {{\tilde{t}}})^2 \end{aligned}$$

with $\tau _m\in ({{\tilde{t}}}, \tau )$. Next, we use (152) to upper-bound $\mathchoice{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\bigl |\phi _{+,k}({{\tilde{t}}})\bigr |}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}{{\left|\phi _{+,k}({{\tilde{t}}})\right|}}$; use (158) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\bigl |\phi _{+,k}'(\tilde{t})\bigr |}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}$; use (163) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&\le r^{2r-1}c_{u35}^r\left( \frac{\lambda _{\mathrm {hi}}^2}{\lambda _{\mathrm {lo}}^2} +\frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -{{\tilde{t}}}\right|}}{{\bigl |\tau -{{\tilde{t}}}\bigr |}}{{\left|\tau -{{\tilde{t}}}\right|}}{{\left|\tau -{{\tilde{t}}}\right|}} +\frac{1}{\lambda _{\mathrm {lo}}^2}(\tau -{{\tilde{t}}})^2\right) \nonumber \\&\le r^{2r+1}c_{u36}^r\frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2} = r^{2r+1}c_{u36}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]}, \end{aligned}$$

(179)

where we used that $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$ because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ with ${{\tilde{t}}}\ne t_j$. According to (161) the upper bound (179) also holds for $b=0$.

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that $\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}$ can be upper-bounded by (85).

Multiplying (179) and (85) and simplifying, we obtain the following upper bound on $E_1$:

$$\begin{aligned} E_1(\tau )&=\mathchoice{{\left|\phi ''_{0,k}(\tau )\right|}}{{\bigl |\phi ''_{0,k}(\tau )\bigr |}}{{\left|\phi ''_{0,k}(\tau )\right|}}{{\left|\phi ''_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u45}^{r+1} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{ \prod _{1\le l\le {{\hat{r}}}, l\ne {\hat{m}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u45}^{r+1} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{ \prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(180)

Above, in (a) we defined $c_{u45}\triangleq c_{u36}c_{u17}$; in (b) we used that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

Bounding $E_2(\tau )$: Consider the case $b=1$. By (194) [Mean Value theorem] we can write:

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}\le \mathchoice{{\left|\phi '_{+,k}(\tilde{t})\right|}}{{\bigl |\phi '_{+,k}(\tilde{t})\bigr |}}{{\left|\phi '_{+,k}(\tilde{t})\right|}}{{\left|\phi '_{+,k}(\tilde{t})\right|}}+\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}\mathchoice{{\left|\tau - {{\tilde{t}}}\right|}}{{\bigl |\tau - {{\tilde{t}}}\bigr |}}{{\left|\tau - {{\tilde{t}}}\right|}}{{\left|\tau - {{\tilde{t}}}\right|}} \end{aligned}$$

with $\tau _m\in ({{\tilde{t}}}, \tau )$. Next, we use (158) to upper-bound $\mathchoice{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\bigl |\phi _{+,k}'(\tilde{t})\bigr |}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}{{\left|\phi _{+,k}'(\tilde{t})\right|}}$; use (163) to upper-bound $\mathchoice{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\bigl |\phi _{+,k}''(\tau _m)\bigr |}}{{\left|\phi _{+,k}''(\tau _m)\right|}}{{\left|\phi _{+,k}''(\tau _m)\right|}}$. With these estimates we can further upper-bound $\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}$ as follows:

$$\begin{aligned} \mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}}&\le r^{2r-1}c_{u38}^r\left( \frac{\lambda _{\mathrm {hi}}}{\lambda _{\mathrm {lo}}^2}+\frac{1}{\lambda _{\mathrm {lo}}^2}\mathchoice{{\left|\tau -{{\tilde{t}}}\right|}}{{\bigl |\tau -{{\tilde{t}}}\bigr |}}{{\left|\tau -{{\tilde{t}}}\right|}}{{\left|\tau -{{\tilde{t}}}\right|}}\right) \nonumber \\&\le r^{2r}c_{u39}^r\frac{\mathchoice{{\left|\tau -\tilde{t}\right|}}{{\bigl |\tau -\tilde{t}\bigr |}}{{\left|\tau -\tilde{t}\right|}}{{\left|\tau -\tilde{t}\right|}}}{r\lambda _{\mathrm {lo}}}\frac{1}{\lambda _{\mathrm {lo}}} = r^{2r}c_{u39}^r\left[ \frac{\mathchoice{{\left|\tau -\tilde{t}\right|}}{{\bigl |\tau -\tilde{t}\bigr |}}{{\left|\tau -\tilde{t}\right|}}{{\left|\tau -\tilde{t}\right|}}}{r\lambda _{\mathrm {lo}}}\right] ^{{I[b=1]}}\frac{1}{\lambda _{\mathrm {lo}}}, \end{aligned}$$

(181)

where we used that $\lambda _{\mathrm {hi}}\le \mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}$. According to (162) the upper bound (181) also holds for $b=0$.

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that $\mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}$ can be upper-bounded by (88).

Multiplying (181) and (88) and simplifying we obtain the following upper bound on $E_2$:

$$\begin{aligned} E_2(\tau )= & {} \mathchoice{{\left|\phi '_{0,k}(\tau )\right|}}{{\bigl |\phi '_{0,k}(\tau )\bigr |}}{{\left|\phi '_{0,k}(\tau )\right|}}{{\left|\phi '_{0,k}(\tau )\right|}}\mathchoice{{\left|\phi '_{+,k}(\tau )\right|}}{{\bigl |\phi '_{+,k}(\tau )\bigr |}}{{\left|\phi '_{+,k}(\tau )\right|}}{{\left|\phi '_{+,k}(\tau )\right|}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r} c_{u46}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{\prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r} c_{u46}^r\left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{ \prod _{1\le l\le {\tilde{r}},l\ne {{\tilde{m}}}} (v_{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(182)

Above, in (a) we defined $c_{u46}\triangleq c_{u39}c_{u19}$; in (b) we used that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

Bounding $E_3(\tau )$: By (163),

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}''(\tau )\right|}}{{\bigl |\phi _{+,k}''(\tau )\bigr |}}{{\left|\phi _{+,k}''(\tau )\right|}}{{\left|\phi _{+,k}''(\tau )\right|}}\le r^{2r-2}c_{u31}^{r} c_{u2}\frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(183)

Since $t_j\in {\mathcal {T}}^c_k$ and $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$, it follows $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$ so that ${{\hat{r}}}\ge 1$, which implies that $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$ can be upper-bounded as in (91). Multiplying (183) and (91) and simplifying, we obtain the following upper bound on $E_3$:

$$\begin{aligned} E_3(\tau )&=\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi ''_{+,k}(\tau )\right|}}{{\bigl |\phi ''_{+,k}(\tau )\bigr |}}{{\left|\phi ''_{+,k}(\tau )\right|}}{{\left|\phi ''_{+,k}(\tau )\right|}}\nonumber \\&{\mathop {\le }\limits ^{(a)}} r^{2r-2}c_{u47}^{r} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{ \prod _{1\le l\le {{\hat{r}}},l\ne {\hat{m}}} (v^\tau _{l}-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2({{\hat{r}}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(b)}} r^{2r-2}c_{u47}^{r} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{{I[b=1]}} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}. \end{aligned}$$

(184)

Above, in (a) we defined $c_{u47}\triangleq c_{u31}c_{u2}c_u$; in (b) we used the fact that $\mathchoice{{\left|v^\tau _l-\tau \right|}}{{\bigl |v^\tau _l-\tau \bigr |}}{{\left|v^\tau _l-\tau \right|}}{{\left|v^\tau _l-\tau \right|}}/(\lambda _{\mathrm {lo}}r)\le \Delta <1$ for all $l\in \{1,\ldots ,{{\hat{r}}}\}$.

From (170), (180), (182), and (184) we conclude that

$$\begin{aligned} \mathchoice{{\left|\phi ''_{k}(\tau )\right|}}{{\bigl |\phi ''_{k}(\tau )\bigr |}}{{\left|\phi ''_{k}(\tau )\right|}}{{\left|\phi ''_{k}(\tau )\right|}}\le r^{2r+1}c_{u48}^{r+1} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{1}{\lambda _{\mathrm {lo}}^2}, \end{aligned}$$

(185)

where we defined $c_{u48}\triangleq 4\max (c_{u45}, c_{u46}, c_{u47})$.

Putting pieces together: Applying (195) [Mean Value theorem] to the function $f (\cdot ) = \phi _l(\cdot )$ with $a=t_j$ and $b=\tau$ and using (168), (169), (185), and we can write for all $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$:

$$\begin{aligned} \mathchoice{{\left|\phi _k(\tau )\right|}}{{\bigl |\phi _k(\tau )\bigr |}}{{\left|\phi _k(\tau )\right|}}{{\left|\phi _k(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} \frac{1}{2} r^{2r+1}c_{u48}^{r+1} \left[ \frac{(\tilde{t}-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau _m)^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2}\nonumber \\&{\mathop {\le }\limits ^{(b)}} \frac{1}{2} r^{2r+1}c_{u48}^{r+1} 2^{{\tilde{r}}} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}, l\ne {{\tilde{m}}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2({\tilde{r}}-1)}} \frac{(\tau -t_j)^2}{\lambda _{\mathrm {lo}}^2} \nonumber \\&{\mathop {\le }\limits ^{(c)}} r^{2r+3}c_{u49}^{r+1} \left[ \frac{(\tilde{t}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{\prod _{1\le l\le {\tilde{r}}} (v_l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2{\tilde{r}}}}. \end{aligned}$$

(186)

Above, in (a) $\tau _m\in (t_j, \tau )$; in (b) we used the fact that, for $l\ne {{\tilde{m}}}$, $\mathchoice{{\left|v_l-\tau _m\right|}}{{\bigl |v_l-\tau _m\bigr |}}{{\left|v_l-\tau _m\right|}}{{\left|v_l-\tau _m\right|}}<\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|v_l-\tau \right|}}{{\bigl |v_l-\tau \bigr |}}{{\left|v_l-\tau \right|}}{{\left|v_l-\tau \right|}}$ and $\mathchoice{{\left|{{\tilde{t}}}-\tau _m\right|}}{{\bigl |{{\tilde{t}}}-\tau _m\bigr |}}{{\left|{{\tilde{t}}}-\tau _m\right|}}{{\left|{{\tilde{t}}}-\tau _m\right|}}<\mathchoice{{\left|{{\tilde{t}}}-\tau \right|}}{{\bigl |{{\tilde{t}}}-\tau \bigr |}}{{\left|{{\tilde{t}}}-\tau \right|}}{{\left|{{\tilde{t}}}-\tau \right|}}+\lambda _{\mathrm {hi}}<2\mathchoice{{\left|\tilde{t}-\tau \right|}}{{\bigl |\tilde{t}-\tau \bigr |}}{{\left|\tilde{t}-\tau \right|}}{{\left|\tilde{t}-\tau \right|}}$, which is true because $\tau \in {\mathcal {N}}(\lambda _{\mathrm {hi}},t_j)$ and because the elements of ${\mathcal {T}}$ are separated by at least $2\lambda _{\mathrm {hi}}$; in (c) we defined $c_{u49}\triangleq 2c_{u48}$ and used the fact that $t_j=v_{{{\tilde{m}}}}$.

The bound (165) follows from (186) and (95) by defining $c_{u50}\triangleq c_{u49}/c_{l3}$.

1.4 Proof of Property 3

By (141) and the triangle inequality:

$$\begin{aligned} \Vert q_2(\cdot )\Vert _{\infty }&\le \rho +r\max _{1\le k\le r}\Vert \phi _k(\cdot )\Vert _{\infty }\\&{\mathop {\le }\limits ^{(a)}} \rho +r\max _{1\le k\le r}\Vert \phi _{+,k}(\cdot )\Vert _{\infty }\\&{\mathop {=}\limits ^{(b)}} \rho +r^{2r+1}c_{u31}^{r} \max _{1\le k\le r}\Vert q_{r\lambda _{\mathrm {lo}},{\mathcal {T}}_k,\{f_j\},\{d_j\}}(\cdot )\Vert _{\infty }\\&{\mathop {\le }\limits ^{(c)}} \rho +r^{2r+1}c_{u31}^{r}c_{u0}{\mathop {\le }\limits ^{(d)}} r^{2r+1}c_{u56}^{r}. \end{aligned}$$

Above, in (a) we used (147) and the fact that by (148) and Lemma 1, Property 3, $\Vert \phi _{0,k}(\cdot )\Vert _{\infty }\le 1$; in (b) we used (149); in (c) we used Lemma 2, Property 3; in (d) we defined $c_{u56}\triangleq 2c_{u0}c_{u31}$ and used the fact that $\rho<1<c_{u0}c_{u31}$.

1.5 Proof of Property 4

Take $\tau \in {\mathcal {F}}(\lambda _{\mathrm {hi}},{\mathcal {T}})$. As above, let $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}$. Then by (16),

$$\begin{aligned} q_0(\tau ) \ge c_{l2}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}}. \end{aligned}$$

(187)

By (19) this bound is also valid when $\breve{r}=0$.

Fix k. If $\tau \in {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, then we can use (41) to upper-bound $\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}$:

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}&\le c_u^{{{\hat{r}}}}\frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}}, \end{aligned}$$

(188)

where, as before, $\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\triangleq {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\cap {\mathcal {T}}_k^c$. If $\tau \notin {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},{\mathcal {T}}_k^c)$, we will use that by (36) and by Lemma 1, Property 3,

$$\begin{aligned} \mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}} \le 1. \end{aligned}$$

(189)

The set ${\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )$ is either empty or contains exactly one element. Let $b\triangleq \mathchoice{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}{{\bigl | {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\bigr |}}{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}{{\left| {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}},\tau )\right|}}$ denote the size of this set; when $b=1$, let $\{{{\tilde{t}}}\}\triangleq {\mathcal {T}}_k\cap {\mathcal {N}}(r\Delta \lambda _{\mathrm {lo}}, \tau )$. Following the steps that lead to (179), we obtain:

$$\begin{aligned} \mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}\le r^{2r+1}c_{u36}^r\left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \end{aligned}$$

(190)

and the bound is valid for both cases $b=0$ and $b=1$.

Case ${{\hat{r}}}\ge 1$: Then, $\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}=\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}\cup \{{{\tilde{t}}}\}$ if $b=1$, and

$\{u^\tau _1,\ldots ,u^\tau _{\breve{r}}\}=\{v^\tau _1,\ldots ,v^\tau _{{{\hat{r}}}}\}$ if $b=0$. Therefore,

$$\begin{aligned} \mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}} =\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u36}^rc_u^{{{\hat{r}}}} \left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]} \frac{ \prod _{l=1}^{{{\hat{r}}}} (v^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2{{\hat{r}}}}} \nonumber \\&= r^{2r+1}c_{u36}^rc_u^{{{\hat{r}}}} \frac{ \prod _{l=1}^{\breve{r}} (u^\tau _l-\tau )^{2}}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}} {\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u51}^rq_0(\tau ). \end{aligned}$$

(191)

Above, (a) follows by (188) and (190); (b) follows by (187) with $c_{u51}\triangleq c_{u36}c_u/c_{l2}$.

Case ${{\hat{r}}}= 0$: Then, $\breve{r}=1$ and $\{u^\tau _{\breve{r}}\}= \{{{\tilde{t}}}\}$ if $b=1$ and $\breve{r}=0$ if $b=0$. Therefore,

$$\begin{aligned} \mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}} =\mathchoice{{\left|\phi _{0,k}(\tau )\right|}}{{\bigl |\phi _{0,k}(\tau )\bigr |}}{{\left|\phi _{0,k}(\tau )\right|}}{{\left|\phi _{0,k}(\tau )\right|}}\mathchoice{{\left|\phi _{+,k}(\tau )\right|}}{{\bigl |\phi _{+,k}(\tau )\bigr |}}{{\left|\phi _{+,k}(\tau )\right|}}{{\left|\phi _{+,k}(\tau )\right|}}&{\mathop {\le }\limits ^{(a)}} r^{2r+1}c_{u36}^r\left[ \frac{({{\tilde{t}}}-\tau )^2}{(r\lambda _{\mathrm {lo}})^2}\right] ^{I[b=1]}\nonumber \\&= r^{2r+1}c_{u36}^r\frac{ \prod _{l=1}^{\breve{r}}(u^\tau _l-\tau )^2}{(r\lambda _{\mathrm {lo}})^{2\breve{r}}} {\mathop {\le }\limits ^{(b)}} r^{2r+1}c_{u51}^rq_0(\tau ). \end{aligned}$$

(192)

Above, (a) follows by (189) and (190); (b) follows by (187) because $c_u>1$.

By Lemma 3, Property 6,

$$\begin{aligned} \rho =\frac{\lambda _{\mathrm {hi}}^{2r}}{\lambda _{\mathrm {lo}}^{2r}} \le r^{2r} \frac{1}{c_l^r}q_0(\tau ). \end{aligned}$$

(193)

Therefore, by (141), (191), (192), (193),

$$\begin{aligned} \mathchoice{{\left|q_2(\tau )\right|}}{{\bigl |q_2(\tau )\bigr |}}{{\left|q_2(\tau )\right|}}{{\left|q_2(\tau )\right|}}\le \sum _{k=1}^r\mathchoice{{\left|\phi _{k}(\tau )\right|}}{{\bigl |\phi _{k}(\tau )\bigr |}}{{\left|\phi _{k}(\tau )\right|}}{{\left|\phi _{k}(\tau )\right|}} + \rho \le r^{2r+2} c_{u52}^rq_0(\tau ), \end{aligned}$$

where we defined $c_{u52}\triangleq c_{u51}+1/c_l$. $\square$

Mean Value Theorem

We repeatedly use the Taylor series approximation with the remained expressed via the Mean Value theorem [1, p. 880, 25.2.25] given below for the convenience of the reader.

Theorem 3

Assume that $f (t)$ is twice differentiable on the interval [a, b]. Then, there exists $t_1\in (a,b)$ such that

$$\begin{aligned} f (b) = f (a) + f '(t_1) (b-a). \end{aligned}$$

(194)

and there exists $t_2\in (a,b)$ such that

$$\begin{aligned} f (b) = f (a) + f '(a) (b-a) + \frac{f ''(t_2)}{2} (b-a)^2. \end{aligned}$$

(195)

Properties of Fejér Kernel

The results proven in subsections below are analogous to the results in [12, eq. (1.11) and eq. (2.6)] with the difference that here we need bounds on sums and in [12] bounds on the corresponding integrals are provided.

Below, we will need uniform upper bounds on $\mathchoice{{\left|k_{\mathrm {hi}}(\cdot )\right|}}{{\bigl |k_{\mathrm {hi}}(\cdot )\bigr |}}{{\left|k_{\mathrm {hi}}(\cdot )\right|}}{{\left|k_{\mathrm {hi}}(\cdot )\right|}}$, $\mathchoice{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}{{\bigl |k_{\mathrm {hi}}'(\cdot )\bigr |}}{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}$, and $\mathchoice{{\left|k_{\mathrm {hi}}''(\cdot )\right|}}{{\bigl |k_{\mathrm {hi}}''(\cdot )\bigr |}}{{\left|k_{\mathrm {hi}}''(\cdot )\right|}}{{\left|k_{\mathrm {hi}}''(\cdot )\right|}}$; these are derived next.

Fejér kernel (7) can be written as a Fourier sum as follows:

$$\begin{aligned} k_{\mathrm {hi}}(t) = \frac{1}{N}\sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) e^{\mathrm {i} 2\pi t k}. \end{aligned}$$

(196)

Taking the absolute value of both sides in (196) and applying the triangle inequality we find:

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}(t)\right|}}{{\bigl |k_{\mathrm {hi}}(t)\bigr |}}{{\left|k_{\mathrm {hi}}(t)\right|}}{{\left|k_{\mathrm {hi}}(t)\right|}}&\le \frac{1}{N}\sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) =\frac{1}{N}\left( 1+f_{\mathrm {hi}}\right) . \end{aligned}$$

Above, the equality follows by summing up the simple series.

Differentiating (196) we obtain:

$$\begin{aligned} k_{\mathrm {hi}}'(t) = \frac{\mathrm {i} 2\pi }{N} \sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) k e^{\mathrm {i} 2\pi t k}. \end{aligned}$$

(197)

Taking the absolute value of both sides in (197) and applying the triangle inequality we find:

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}'(t)\right|}}{{\bigl |k_{\mathrm {hi}}'(t)\bigr |}}{{\left|k_{\mathrm {hi}}'(t)\right|}}{{\left|k_{\mathrm {hi}}'(t)\right|}} \le \frac{2\pi }{N} \sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} \mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}} \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) {\mathop {=}\limits ^{(a)}}\frac{2\pi }{3 N}f_{\mathrm {hi}}(2 + f_{\mathrm {hi}}) {\mathop {\le }\limits ^{(b)}} \frac{2\pi }{N}f_{\mathrm {hi}}^2. \end{aligned}$$

(198)

Above, (a) follows by summing up the simple power series; (b) follows because $f_{\mathrm {hi}}>1$.

Differentiating (197) we obtain:

$$\begin{aligned} k_{\mathrm {hi}}''(t) = - \frac{(2\pi )^2}{N} \sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) k^2 e^{\mathrm {i} 2\pi t k}. \end{aligned}$$

(199)

Taking the absolute value of both sides in (199) and applying the triangle inequality we find:

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\bigl |k_{\mathrm {hi}}''(t)\bigr |}}{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\left|k_{\mathrm {hi}}''(t)\right|}} \le \frac{(2\pi )^2}{N} \sum _{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}\le f_{\mathrm {hi}}} k^2 \left( 1-\frac{\mathchoice{{\left|k\right|}}{{\bigl |k\bigr |}}{{\left|k\right|}}{{\left|k\right|}}}{f_{\mathrm {hi}}+1}\right) {\mathop {=}\limits ^{(a)}}\frac{2\pi ^2}{3 N} f_{\mathrm {hi}}(2 + 3f_{\mathrm {hi}}+ f_{\mathrm {hi}}^2) {\mathop {\le }\limits ^{(b)}} \frac{4\pi ^2}{N}f_{\mathrm {hi}}^3. \end{aligned}$$

(200)

Above, (a) follows by summing up the simple power series; (b) follows because $f_{\mathrm {hi}}>1$.

The bounds derived below in this section are crude in the sense that no attempt has been made to obtain the tightest possible constants; for this reason some of the steps below may appear unnecessarily wasteful.

1.1 Proof of (106)

Begin by splitting the summation interval and recombining the terms in the following way:

$$\begin{aligned} \sum _{n=0}^{N-1} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}&=\!\sum _{\frac{n}{N}\in [0, \lambda _{\mathrm {hi}})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}\,\, +\!\!\sum _{\frac{n}{N}\in [\lambda _{\mathrm {hi}}, \frac{1}{2})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}} \nonumber \\&+\!\!\sum _{\frac{n}{N}\in [\frac{1}{2}, 1-\lambda _{\mathrm {hi}})} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}\,\, +\!\!\sum _{\frac{n}{N}\in [1-\lambda _{\mathrm {hi}}, 1)} \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}} \nonumber \\&\le \,2\!\!\!\!\!\!\!\sum _{\frac{n}{N}\in [0, \lambda _{\mathrm {hi}}+\frac{1}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}\, +\, 2\!\!\!\!\!\!\!\!\!\sum _{\frac{n}{N}\in [\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}.\nonumber \\ \end{aligned}$$

(201)

Above, the inequality follows by symmetry of $k_{\mathrm {hi}}'(\cdot )$ around 1/2. Next, we upper-bound the two sums separately.

To upper-bound the first sum in (201) we proceed as follows:

$$\begin{aligned} \sum _{\frac{n}{N}\in [0, \lambda _{\mathrm {hi}}+\frac{1}{N})}\!\!\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}} \le (\lambda _{\mathrm {hi}}+1/N)N\max _t \mathchoice{{\left|k_{\mathrm {hi}}'\left( t\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( t\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( t\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( t\right) \right|}} {\mathop {\le }\limits ^{(a)}} 2\lambda _{\mathrm {hi}}2\pi f_{\mathrm {hi}}^2 {\mathop {=}\limits ^{(b)}} 4\pi /\lambda _{\mathrm {hi}}. \nonumber \\ \end{aligned}$$

(202)

Above, in (a) we used (198) and the assumption that $1/N\le \lambda _{\mathrm {hi}}$; in (b) we used that $f_{\mathrm {hi}}= 1/\lambda _{\mathrm {hi}}$.

To upper-bound the second term in (201) we observe that $\mathchoice{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}{{\bigl |k_{\mathrm {hi}}'(\cdot )\bigr |}}{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}{{\left|k_{\mathrm {hi}}'(\cdot )\right|}}$ can be upper-bounded as follows for $t\in [0,0.55]$:

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}'(t)\right|}}{{\bigl |k_{\mathrm {hi}}'(t)\bigr |}}{{\left|k_{\mathrm {hi}}'(t)\right|}}{{\left|k_{\mathrm {hi}}'(t)\right|}}&{\mathop {=}\limits ^{(a)}} \frac{2\pi \sin (\pi (f_{\mathrm {hi}}+1)t)}{N} \left| \frac{ \cos (\pi (f_{\mathrm {hi}}+1) t)}{\sin ^2(\pi t)}-\frac{\cos (\pi t)\sin (\pi (f_{\mathrm {hi}}+1)t)}{(f_{\mathrm {hi}}+1) \sin ^3(\pi t)} \right| \nonumber \\&{\mathop {\le }\limits ^{(b)}} \frac{1}{N}\left( \frac{2\pi }{\sin ^2(\pi t)}+\frac{2\pi }{(f_{\mathrm {hi}}+1)\sin ^3(\pi t)}\right) {\mathop {\le }\limits ^{(c)}} \frac{1}{N}\left( \frac{2}{(f_{\mathrm {hi}}+1) t^3}+\frac{2}{t^2}\right) . \end{aligned}$$

(203)

Above, (a) follows by differentiating $k_{\mathrm {hi}}(\cdot )$ in (7); in (b) we used the triangle inequality and the fact that $\mathchoice{{\left|\sin (\cdot )\right|}}{{\bigl |\sin (\cdot )\bigr |}}{{\left|\sin (\cdot )\right|}}{{\left|\sin (\cdot )\right|}}\le 1$, $\mathchoice{{\left|\cos (\cdot )\right|}}{{\bigl |\cos (\cdot )\bigr |}}{{\left|\cos (\cdot )\right|}}{{\left|\cos (\cdot )\right|}}\le 1$; in (c) we used the inequalities $\sin (\pi t)^2\ge \pi t^2$ and $\sin (\pi t)^3\ge \pi t^3$ for $t\in [0, 0.55]$. Therefore,

$$\begin{aligned}&\sum _{\frac{n}{N}\in [\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\!\! \mathchoice{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\bigl |k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \bigr |}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}}{{\left|k_{\mathrm {hi}}'\left( \frac{n}{N}\right) \right|}} \nonumber \\&\qquad \qquad {\mathop {\le }\limits ^{(a)}} \frac{2}{1+f_{\mathrm {hi}}} \frac{1}{N}\!\!\!\!\sum _{\frac{n}{N}\in [\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\!\! \frac{1}{(n/N)^3} + \frac{2}{N}\!\!\!\!\sum _{\frac{n}{N}\in [\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\!\! \frac{1}{(n/N)^2} \nonumber \\&\qquad \qquad {\mathop {\le }\limits ^{(b)}} \frac{2}{1+f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^3}+\int _{\lambda _{\mathrm {hi}}}^{1/2+1/N} \frac{1}{t^3}dt\right) + \frac{2}{N}\frac{1}{\lambda _{\mathrm {hi}}^2}+2\int _{\lambda _{\mathrm {hi}}}^{1/2+1/N} \frac{1}{t^2}dt \nonumber \\&\qquad \qquad \le \frac{2}{1+f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^3}+\int _{\lambda _{\mathrm {hi}}}^\infty \frac{1}{t^3}dt\right) +\frac{2}{N}\frac{1}{\lambda _{\mathrm {hi}}^2}+2\int _{\lambda _{\mathrm {hi}}}^\infty \frac{1}{t^2}dt \nonumber \\&\qquad \qquad =\frac{2}{1+f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^3}+\frac{1}{2\lambda _{\mathrm {hi}}^2}\right) + \frac{2}{N}\frac{1}{\lambda _{\mathrm {hi}}^2}+\frac{2}{\lambda _{\mathrm {hi}}} \nonumber \\&\qquad \qquad {\mathop {\le }\limits ^{(c)}} \frac{3}{1+f_{\mathrm {hi}}} \frac{1}{\lambda _{\mathrm {hi}}^2}+\frac{4}{\lambda _{\mathrm {hi}}} <\frac{7}{\lambda _{\mathrm {hi}}}. \end{aligned}$$

(204)

Above, (a) follows from (203) because $1/2+1/N<0.55$; in (b) the bound for the first term follows because the function $1/t^3$ is monotonically decreasing and the bound for the second term follows because the function $1/t^2$ is monotonically decreasing; (c) follows because $1/N\le \lambda _{\mathrm {hi}}$.

Finally, plugging (202) and (204) into (201) and defining $c_k'=8\pi +14$ we obtain (106).

1.2 Proof of (107)

Begin by splitting the summation interval and recombining the terms in the following way:

$$\begin{aligned} \frac{1}{2}\sum _{n=0}^{N-1} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}&= \frac{1}{2}\!\sum _{\frac{n}{N}\in [0, 2\lambda _{\mathrm {hi}})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}\nonumber \\&+\frac{1}{2}\!\sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, 1/2)}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}\nonumber \\&+\frac{1}{2}\!\sum _{\frac{n}{N}\in [1/2, 1-2\lambda _{\mathrm {hi}})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \nonumber \\&+ \frac{1}{2}\!\sum _{\frac{n}{N}\in [1-2\lambda _{\mathrm {hi}}, 1)}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \nonumber \\&\le \sum _{\frac{n}{N}\in [0, 2\lambda _{\mathrm {hi}}+\frac{1}{N})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \nonumber \\&+ \sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}. \end{aligned}$$

(205)

Above, the inequality follows by symmetry of $\sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \cdot )} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}$ around 1/2. Next, we upper-bound the two sums separately.

To upper-bound the first sum in (205) we proceed as follows:

$$\begin{aligned} \sum _{\frac{n}{N}\in [0, 2\lambda _{\mathrm {hi}}+\frac{1}{N})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\!\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}&\le \left( 2\lambda _{\mathrm {hi}}+\frac{1}{N}\right) N\max _t \mathchoice{{\left|k_{\mathrm {hi}}''\left( t\right) \right|}}{{\bigl |k_{\mathrm {hi}}''\left( t\right) \bigr |}}{{\left|k_{\mathrm {hi}}''\left( t\right) \right|}}{{\left|k_{\mathrm {hi}}''\left( t\right) \right|}} \nonumber \\&{\mathop {\le }\limits ^{(a)}} 3\lambda _{\mathrm {hi}}4\pi ^2f_{\mathrm {hi}}^3 {\mathop {=}\limits ^{(b)}} \frac{12\pi ^2}{\lambda _{\mathrm {hi}}^2}. \end{aligned}$$

(206)

Above, in (a) we used (200) and the assumption that $1/N\le \lambda _{\mathrm {hi}}$; in (b) we used that $f_{\mathrm {hi}}= 1/\lambda _{\mathrm {hi}}$.

To upper-bound the second term in (205) we differentiate $k_{\mathrm {hi}}(\cdot )$ in (7) twice to obtain:

$$\begin{aligned} k_{\mathrm {hi}}''(t)&= \frac{\pi ^2}{N} \frac{ (\sin (2\pi t) \sin (2\pi f_{\mathrm {hi}}t)-\cos (2\pi t) \cos (2\pi f_{\mathrm {hi}}t) - 2\cos (2\pi f_{\mathrm {hi}}t))}{(f_{\mathrm {hi}}+1) \sin ^4(\pi t)}\\&+\frac{\pi ^2}{N} \frac{ (\cos (2\pi t)+2)}{(f_{\mathrm {hi}}+1) \sin ^4(\pi t)}\\&-\frac{4 \pi ^2}{N}\frac{f_{\mathrm {hi}}\sin (\pi (2 f_{\mathrm {hi}}+1) t)}{(f_{\mathrm {hi}}+1) \sin ^3(\pi t)} +\frac{2 \pi ^2}{N}\frac{f_{\mathrm {hi}}^2 \cos (2 \pi (f_{\mathrm {hi}}+1) t)}{(f_{\mathrm {hi}}+1) \sin ^2(\pi t)}. \end{aligned}$$

This leads to the following upper bound on $\mathchoice{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\bigl |k_{\mathrm {hi}}''(t)\bigr |}}{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\left|k_{\mathrm {hi}}''(t)\right|}}$ for $t\in [0,0.55]$:

$$\begin{aligned} \mathchoice{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\bigl |k_{\mathrm {hi}}''(t)\bigr |}}{{\left|k_{\mathrm {hi}}''(t)\right|}}{{\left|k_{\mathrm {hi}}''(t)\right|}}&{\mathop {\le }\limits ^{(a)}}\frac{1}{N} \left( \frac{7 \pi ^2}{(f_{\mathrm {hi}}+1) \sin ^4(\pi t)} +\frac{4 \pi ^2 f_{\mathrm {hi}}}{(f_{\mathrm {hi}}+1) \sin ^3(\pi t)} +\frac{2 \pi ^2 f_{\mathrm {hi}}^2}{(f_{\mathrm {hi}}+1) \sin ^2(\pi t)} \right) \nonumber \\&{\mathop {\le }\limits ^{(b)}}\frac{1}{N} \left( \frac{7 \pi }{f_{\mathrm {hi}}t^4} +\frac{4 \pi }{t^3} +\frac{2 \pi f_{\mathrm {hi}}}{t^2} \right) . \end{aligned}$$

(207)

Above, in (a) we used the triangle inequality and the fact that $\mathchoice{{\left|\sin (\cdot )\right|}}{{\bigl |\sin (\cdot )\bigr |}}{{\left|\sin (\cdot )\right|}}{{\left|\sin (\cdot )\right|}}\le 1$, $\mathchoice{{\left|\cos (\cdot )\right|}}{{\bigl |\cos (\cdot )\bigr |}}{{\left|\cos (\cdot )\right|}}{{\left|\cos (\cdot )\right|}}\le 1$; in (b) we used the inequalities $\sin (\pi t)^2\ge \pi t^2$, $\sin (\pi t)^3\ge \pi t^3$, $\sin (\pi t)^4\ge \pi t^4$ for $t\in [0, 0.55]$. Next observe that since the right-hand side of (207) is monotonically decreasing for $t>0$ we have for $t\in (\lambda _{\mathrm {hi}}, 0.55]$:

$$\begin{aligned} \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, t)} \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}} \le \frac{1}{N} \left( \frac{7 \pi }{f_{\mathrm {hi}}(t-\lambda _{\mathrm {hi}})^4} +\frac{4 \pi }{(t-\lambda _{\mathrm {hi}})^3}+\frac{2 \pi f_{\mathrm {hi}}}{(t-\lambda _{\mathrm {hi}})^2} \right) . \end{aligned}$$

(208)

Therefore, the second term in (205) can be upper-bounded as follows:

$$\begin{aligned}&\sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\! \sup _{u\in {\mathcal {N}}(\lambda _{\mathrm {hi}}, \frac{n}{N})}\! \mathchoice{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\bigl |k_{\mathrm {hi}}''(u)\bigr |}}{{\left|k_{\mathrm {hi}}''(u)\right|}}{{\left|k_{\mathrm {hi}}''(u)\right|}}\nonumber \\&\quad \qquad \qquad \qquad \qquad {\mathop {\le }\limits ^{(a)}} \frac{7 \pi }{f_{\mathrm {hi}}}\frac{1}{N}\!\!\!\!\!\sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\!\frac{1}{ (n/N-\lambda _{\mathrm {hi}})^4} \nonumber \\&\quad \qquad \qquad \qquad \qquad +4 \pi \frac{1}{N}\!\!\!\!\!\sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\!\!\frac{1}{(n/N-\lambda _{\mathrm {hi}})^3}\nonumber \\&\quad \qquad \qquad \qquad \qquad +2 \pi f_{\mathrm {hi}}\frac{1}{N}\!\!\!\!\!\sum _{\frac{n}{N}\in [2\lambda _{\mathrm {hi}}, \frac{1}{2}+\frac{1}{N})}\frac{1}{(n/N-\lambda _{\mathrm {hi}})^2}\nonumber \\&\quad \qquad \qquad \qquad \qquad {\mathop {\le }\limits ^{(b)}} \frac{7 \pi }{f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{(2\lambda _{\mathrm {hi}}-\lambda _{\mathrm {hi}})^4} + \int _{2\lambda _{\mathrm {hi}}}^{1/2+1/N} \frac{1}{(t-\lambda _{\mathrm {hi}})^4}d t\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad +4 \pi \left( \frac{1}{N}\frac{1}{(2\lambda _{\mathrm {hi}}-\lambda _{\mathrm {hi}})^3} + \int _{2\lambda _{\mathrm {hi}}}^{1/2+1/N} \frac{1}{(t-\lambda _{\mathrm {hi}})^3}d t\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad +2 \pi f_{\mathrm {hi}}\left( \frac{1}{N}\frac{1}{(2\lambda _{\mathrm {hi}}-\lambda _{\mathrm {hi}})^2} + \int _{2\lambda _{\mathrm {hi}}}^{1/2+1/N} \frac{1}{(t-\lambda _{\mathrm {hi}})^2}d t\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad {\mathop {\le }\limits ^{(c)}} \frac{7 \pi }{f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^4} + \int _{\lambda _{\mathrm {hi}}}^{\infty } \frac{1}{t^4}d t\right) +4 \pi \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^3} + \int _{\lambda _{\mathrm {hi}}}^{\infty } \frac{1}{t^3}d t\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad +2 \pi f_{\mathrm {hi}}\left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^2} + \int _{\lambda _{\mathrm {hi}}}^{\infty } \frac{1}{t^2}d t\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad = \frac{7 \pi }{f_{\mathrm {hi}}} \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^4} + \frac{1}{3\lambda _{\mathrm {hi}}^3}\right) +4 \pi \left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^3} + \frac{1}{2\lambda _{\mathrm {hi}}^2}\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad +2 \pi f_{\mathrm {hi}}\left( \frac{1}{N}\frac{1}{\lambda _{\mathrm {hi}}^2} + \frac{1}{\lambda _{\mathrm {hi}}}\right) \nonumber \\&\quad \qquad \qquad \qquad \qquad {\mathop {\le }\limits ^{(d)}} \left( \frac{28}{3}\pi + 6\pi + 4\pi \right) \frac{1}{\lambda _{\mathrm {hi}}^2} = \frac{58\pi }{3} \frac{1}{\lambda _{\mathrm {hi}}^2}. \end{aligned}$$

(209)

Above, (a) follows from (208) because $1/2+1/N<0.55$; (b) follows because the functions $1/(t-\lambda _{\mathrm {hi}})^4$, $1/(t-\lambda _{\mathrm {hi}})^3$, and $1/(t-\lambda _{\mathrm {hi}})^2$ are monotonically decreasing; (c) follows by changing the integration variable; (d) follows because $1/N\le \lambda _{\mathrm {hi}}$ and because $f_{\mathrm {hi}}=1/\lambda _{\mathrm {hi}}$.

Finally, plugging (206) and (209) into (205) and defining $c_k''\triangleq 12\pi ^2+58\pi /3$ we obtain (107).