Abstract
We provide several new answers on the question: how do radial projections distort the dimension of planar sets? Let \(X,Y \subset \mathbb{R}^{2}\) be non-empty Borel sets. If X is not contained in any line, we prove that
If dimHY>1, we have the following improved lower bound:
Our results solve conjectures of Lund-Thang-Huong, Liu, and the first author. Another corollary is the following continuum version of Beck’s theorem in combinatorial geometry: if \(X \subset \mathbb{R}^{2}\) is a Borel set with the property that dimH(X ∖ ℓ)=dimHX for all lines \(\ell \subset \mathbb{R}^{2}\), then the line set spanned by X has Hausdorff dimension at least min{2dimHX,2}.
While the results above concern \(\mathbb{R}^{2}\), we also derive some counterparts in \(\mathbb{R}^{d}\) by means of integralgeometric considerations. The proofs are based on an ϵ-improvement in the Furstenberg set problem, due to the two first authors, a bootstrapping scheme introduced by the second and third author, and a new planar incidence estimate due to Fu and Ren.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Statement of main results in the plane
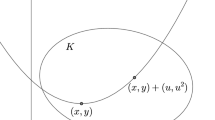
We study the distortion of Hausdorff dimension under radial projections \(\pi _{x} \colon \mathbb{R}^{d} \, \setminus \, \{x\} \to S^{d - 1}\) defined by
This is our first main result:
Theorem 1.1
Let \(X \subset \mathbb{R}^{2}\) be a (non-empty) Borel set which is not contained in any line. Then, for every Borel set \(Y \subset \mathbb{R}^{2}\),
Clearly, this statement fails if X and Y are contained in a common line. If Y is contained in a line ℓ, and X=X′∪{x0} where X′⊂ℓ and x0∉ℓ, then πx(Y ∖ {x}) is a singleton for all x∈X except x0. So, in general, it is not possible to hope that the supremum is (nearly) attained for a large set of x. Nevertheless, if the hypotheses of Theorem 1.1 are slightly strengthened, we have the following conclusion:
Corollary 1.2
Let \(X \subset \mathbb{R}^{2}\) be a Borel set satisfying dimH(X ∖ ℓ)=dimHX for all lines \(\ell \subset \mathbb{R}^{2}\). Then, for every ϵ>0, the exceptional set Eϵ:={x∈X:dimHπx(Y ∖ {x})≤min{dimHX,dimHY,1}−ϵ} satisfies dimH(X ∖ Eϵ)=dimHX.
Proof
Assume to the contrary that dimH(X ∖ Eϵ)<dimHX. This implies two things. First, Eϵ cannot be contained on any line \(\ell \subset \mathbb{R}^{2}\), since otherwise dimH(X ∖ ℓ)<dimHX contrary to our hypothesis. Second, dimHEϵ=dimHX. The first fact implies that Theorem 1.1 is applicable to the pair Eϵ, Y, and the second fact implies
Since ϵ>0, this contradicts the definition of Eϵ. □
We mention a few further corollaries of Theorem 1.1. First, it can be applied to the case Y=X, assuming that X is a Borel set which does not lie on a line. Then,
In particular, the direction set S(X):={(x−y)/|x−y|:x,y∈X, x≠y} has
This solves [Orp19, Conjecture 1.9]. These results were earlier proved under the additional assumption that X has equal Hausdorff and packing dimension by the second and third author in [SW21, Theorem 1.6]. Weaker bounds on the dimension of πx(X ∖ {x}) for sets X not contained in a line were previously obtained in [Orp19, Shm23, LS20].
As a second application of Theorem 1.1, we solve [Liu21, Conjecture 1.2] in \(\mathbb{R}^{2}\):
Corollary 1.4
Let \(Y \subset \mathbb{R}^{2}\) be a Borel set with dimHY≤1. Then,
Proof
Assume to the contrary that there exists ϵ>0 such that
has dimHX>1. Then X evidently does not lie on a line. Now, Theorem 1.1 tells us that there exists a point x∈X such that dimHπx(Y ∖ {x})>dimHY−ϵ, a contradiction. □
Finally, Theorem 1.1 yields continuum analogues of several results in geometric combinatorics. Ungar [Ung82] proved that a finite set P of non-collinear points in the plane determine at least |P|−1 directions; shortly after, Beck [Bec83] improved this (up to constants) by showing that there is a point x∈P such that |πx(P ∖ {x})|≳|P|. The bound (1.3) provides a natural Hausdorff dimension analogue of these results. Another result from [Bec83], which is nowadays often called Beck’s theorem, states that if \(P \subset \mathbb{R}^{2}\) is a finite set of points, then either ≳|P| points lie on a single line, or else P spans ≳|P|2 distinct lines. This is a simple consequence of the Szemerédi-Trotter incidence bound [ST83]. We have the following continuum version:
Corollary 1.5
Let \(X \subset \mathbb{R}^{2}\) be a Borel set such that dimH(X ∖ ℓ)=dimHX for all lines \(\ell \subset \mathbb{R}^{2}\). Then, the line set \(\mathcal{L}(X)\) spanned by pairs of (distinct) points in X satisfies
Proof
Let 0≤σ<min{dimHX,1} and B:={x∈X:dimHπx(X ∖ {x})≤σ}. We claim that
In fact, this will complete the proof: by definition, for each x∈X ∖ B there exists a line set \(\mathcal{L}_{x} \subset \mathcal{L}(X)\) which contains x and has \(\dim _{\mathrm {H}}\mathcal{L}_{x} \geq \sigma \). Therefore,
contains a (dual) (σ,σ)-Furstenberg set, and thus \(\dim _{\mathrm {H}}\mathcal{L}(X) \geq 2\sigma \) by [HSY22, Theorem A.1]. The corollary follows by letting σ↗min{dimHX,1}.
Let us prove (1.6). If (1.6) fails, then clearly dimHB=dimHX. Then B must lie on a line, say B⊂ℓ. Otherwise, Theorem 1.1 tells us that there exists a point x∈B such that dimHπx(X ∖ {x})>σ, contrary to the definition of B. But now dimH(X ∖ B)≥dimH(X ∖ ℓ)=dimHX by assumption, so actually (1.6) holds. □
In the case dimHY>1, we have the following lower bound which improves upon Theorem 1.1:
Theorem 1.7
Let \(X,Y \subset \mathbb{R}^{2}\) be Borel sets with X≠∅ and dimHY>1. Then,
This result solves the planar case of [LPT22, Conjecture 1.2]. In fact, the numerology may be more recognisable if we restate Theorem 1.7 as follows:
Corollary 1.8
Let \(Y \subset \mathbb{R}^{2}\) be a Borel set with dimHY>1. Then,
Proof
Consider first the case σ∈[0,1). Assume to the contrary that the exceptional set “X” on the left has dimension dimHX>max{1+σ−dimHY,0}. In particular X≠∅. Then, by Theorem 1.7,
which is a contradiction. The case σ=1 can finally be deduced by noticing that {x:dimHπx(Y ∖ {x})<1} is a countable union of the sets {x:dimHπx(Y ∖ {x})<1−1/j}. □
As is often the case, we deduce our main results from corresponding quantitative, discretised versions: they are Corollary 2.22 for Theorem 1.1 (see also Corollary 2.25), and Theorem 3.17 for Theorem 1.7. These statements involve a constant “C” (arising as the Frostman constant of various measures and, separately, the distance between their supports). We emphasize that C is allowed to depend on the scale δ, and Corollary 2.22 and Theorem 3.17 are meaningful even if C is as large as δ−ϵ for some small but fixed ϵ>0.
1.2 Connection with orthogonal projections
Theorems 1.1 and 1.7 can be viewed as stronger versions of classical results in fractal geometry regarding orthogonal projections. For e∈S1, let Pe(x):=(x⋅e)e be the orthogonal projection to the line spanned by e. If \(Y \subset \mathbb{R}^{2}\) is a Borel set, then Kaufman [Kau68] in 1968 proved that
If dimHY>1, then the following improved estimate holds:
Estimate (1.10) is due to Peres and Schlag [PS00], but the special case σ=1 was proven already in 1982 by Falconer [Fal82]. The proof of (1.10) is based on Fourier analysis. The proofs of (1.9)-(1.10) can be conveniently read from Mattila’s book [Mat15, Chap. 5].
Let us then explain the relationship between Theorems 1.1-1.7 and the bounds (1.9)-(1.10). If \(\ell \subset \mathbb{R}^{2}\) is a line, then there exists a projective transformation Fℓ with the property
where the map x↦e(x)∈S1 is locally bi-Lipschitz (and in particular preserves Hausdorff dimension). For more details, see Remark 4.14. In particular, the estimates (1.9)-(1.10) hold as stated for radial projections to points on “ℓ”. For example, (1.10) yields
assuming that dimHY>1. Since \(\mathbb{R}^{2}\) is foliated by parallel lines, one might guess by a heuristic “Fubini argument” that
This is not rigorous, but nevertheless the bound above follows from Peres and Schlag’s general theory of transversal projections [PS00, Theorem 7.3] applied to radial projections. Now, compare these estimates with Corollary 1.8, which was a restatement of Theorem 1.7. Corollary 1.8 allows one to replace “ℓ” by “\(\mathbb{R}^{2}\)” in (1.11) while keeping the right-hand side unchanged. So, the “Fubini argument” is extremely unsharp!
The Kaufman estimate (1.9) bears a similar relationship to Theorem 1.1. To see this, let us begin by mentioning that (1.9) is formally equivalent to the following: if ∅≠X⊂S1 and \(Y \subset \mathbb{R}^{2}\) are Borel sets, then supe∈XdimHPe(Y)≥min{dimHX,dimHY,1}. This version looks more like Theorem 1.1. Moreover, by applying the projective transformation Fℓ as above, one could deduce the following corollary for every fixed line \(\ell \subset \mathbb{R}^{2}\): if ∅≠X⊂ℓ and \(Y \subset \mathbb{R}^{2} \, \setminus \, \ell \) are Borel sets, then
Theorem 1.1 almost looks like (1.12) without the restrictions “X⊂ℓ” and “\(Y \subset \mathbb{R}^{2} \, \setminus \, \ell \)”. The only problem is that such a statement is completely false: if X, Y happen to lie on a common line, then dimHπx(Y ∖ {x})=0 for all x∈X. Theorem 1.1 takes this obstruction into account by assuming that X is not contained in any line.
1.3 Related work and higher dimensions
Proving Corollary 1.4 does not require the full strength of Theorem 1.1. In fact, it could also be deduced from (a quantitative version of) Theorem 1.7, combined with a “swapping trick” introduced by Liu in [Liu21]. The reason is partially visible from the proof of Corollary 1.4: one is allowed to make the counter assumption that the “exceptional set” X has dimHX>1, and this simplifies matters (the hardest case of Theorem 1.1 occurs when dimHX,dimHY≤1). This approach of deducing Corollary 1.4 from Theorem 1.7 is carried out in the unpublished preprint [OS221], which this paper supesedes, and where a proof of Theorem 1.7 first appeared. Thus, at the level of appropriate quantitative versions of the statements, both Theorems 1.7 and 1.1 imply Corollary 1.4, but neither of these theorems imply each other (as far as we know).
After [OS221] appeared on the arXiv, Dote and Gan [DG22] proved a higher dimensional version of Theorem 1.7, and then used the “swapping trick” to obtain a higher dimensional counterpart of Corollary 1.4. Their results are the following:
Theorem 1.13
Dote-Gan
Let \(Y \subset \mathbb{R}^{d}\) be a Borel set with dimHY∈(k,k+1] for some k∈{1,…,d−1}. Then,
Theorem 1.14
Dote-Gan
Let \(Y \subset \mathbb{R}^{d}\) be a Borel set with dimHY∈(k−1,k] for some k∈{1,…,d−1}. Then,
We give new proofs for Theorems 1.13-1.14 at the end of this paper, Sect. 4. In fact, both statements can be deduced from (quantitative versions of) their planar cases via an integralgeometric argument (due to the second and third author in [SW21, Theorem 6.7]). Moreover, we are able to prove a partial higher-dimensional analogue of Theorem 1.1 that implies Theorem 1.14 as a by-product:
Theorem 1.15
Let \(X,Y\subset \mathbb{R}^{d}\), d≥2, be Borel sets with dimHX>k−1 and dimHY∈(k−1,k] for some k∈{1,…,d−1}.
-
(i)
If dimHX>k, then supx∈XdimHπx(Y ∖ {x})=dimHY.
-
(ii)
If k−1<dimHX≤k, but X is not contained on any k-plane, the following holds. If dimHY>k−1/k−η for a sufficiently small constant η=η(d,k,dimHX)>0, then
$$ \sup _{x \in X} \dim _{\mathrm {H}}\pi _{x}(Y \, \setminus \, \{x\}) \geq \min \{ \dim _{\mathrm {H}}X,\dim _{\mathrm {H}}Y\}. $$
For k=1, we require no lower bound from dimHY in part (ii).
Part (i) is just a restatement of Theorem 1.14. The lower bound dimHY>k−1/k−η in part (ii) may appear odd, and is likely an artefact of the proof. We conjecture that it can be replaced by dimHY>k−1. Our argument would yield this if the following was true:
Conjecture 1.16
Let t∈(d−2,d]. Let μ be a Borel probability measure on \(\mathbb{R}^{d}\) that satisfies μ(B(x,r))≤C rt for all \(x \in \mathbb{R}^{d}\), r>0, and some C>0. Further, assume that μ(W)=0 for every affine (d−1)-plane \(W\subset \mathbb{R}^{d}\). Then, for almost every affine 2-plane \(W \subset \mathbb{R}^{d}\) (with respect to the natural measure on the affine Grassmanian), if the sliced measure μW on W is non-trivial, then it does not give full mass to any line.
We refer to [Mat99, Chap. 10] or [Mat19, Chap. 6.1] for the definition of the measures μW. In [SW21, Proposition 6.8], the last two authors proved a weaker statement under the assumption t>d−1−1/(d−1)−η(d). This explains the numerology in Theorem 1.15.
There are plenty of earlier relevant results on radial projections; sometimes this topic is also studied under the name visibility. The finite field counterparts of Theorems 1.13-1.14 were proven a little earlier by Lund, Thang, and Huong Thu in [LPT22]. This is also where the continuum version of Theorem 1.13 was conjectured. We are not aware of a finite field counterpart to Theorem 1.1. As we already mentioned, the continuum version of Theorem 1.14 was conjectured by Liu [Liu21], who also proved partial results. The special case k=d−1=σ of Theorem 1.13 was contained in [Orp18, Theorem 1.1]. Partial results also follow from Peres and Schlag’s general framework of transversal projections [PS00].
In 2021, Raz and Zahl [RZ23, Theorem 1.13] proved a radial projection theorem which gives non-trivial information if the set of “viewpoints” (the set “X” in the results described above) only has 4 elements, all 3 of which span a non-degenerate triangle. Earlier, in [BLZ16, Theorem 1.6], Bond, Łaba and Zahl and proved “single-scale” estimates for radial projections of planar sets which are unconcentrated on lines. This result is in the spirit of Theorem 1.1, and perhaps its earliest precedent in the literature.
A little further away from the topic of this paper, radial projections and visibility have also been investigated in the context of rectifiability. The heuristic is that purely 1-unrectifiable sets \(Y \subset \mathbb{R}^{2}\) with \(\mathcal{H}^{1}(Y) < \infty \) should have radial projections of zero length for “most” viewpoints \(x \in \mathbb{R}^{2}\). Marstrand [Mar54, Theorem VI] already proved that if Y is as above, then \(\mathcal{H}^{1}(\pi _{x}(Y \, \setminus \, \{x\})) = 0\) for all \(x \in \mathbb{R}^{2} \, \setminus \, X\), where dimHX≤1. Whether the same is true for \(\mathcal{H}^{1}\) almost all x∈Y is a well-known open problem. For more information on this question, and related ones, see [Cso00, SS0607] and [Mat04, Sect. 6].
1.4 Some words on the proofs
The starting point of this work was the observation that while Beck’s Theorem can be deduced from the Szemerédi-Trotter incidence bound, in fact it doesn’t require the full strength of Szemerédi-Trotter – any “ϵ-improvement” over the elementary double-counting bound is enough. Recently, the first two authors [OS222] obtained an ϵ-improvement in the Furstenberg set problem, which can be seen as a continuous analogue of the point-line incidence problem from discrete geometry. (The actual discretised result we use is stated below as Theorem 2.8.) As it is often the case in this area, while the discrete result (in this case, Beck’s Theorem and its proof) provided the inspiration for our work, the proof is substantially more involved than in the discrete case (and the way in which the incidence result is applied is qualitatively different).
Our general strategy is to embed the ϵ-improvement on the Furstenberg set problem into a “bootstrapping” argument where one gradually improves the lower bound in Theorem 1.1, up to the threshold min{dimHX,dimHY,1}. The main work is contained in Lemma 2.9 and Corollary 2.22. A similar bootstrapping scheme had appeared in previous work of the second and third author, see [SW21, Lemmas 5.11 and 5.17]. However, the proof of the bootstrapping step in [SW21] relied on a linearization argument that only yields optimal results for sets with additional regularity, such as equal Hausdorff and packing dimension. Hence, the main innovation of this article lies in the proof of the bootstrapping step (Lemma 2.9). Arguing by contradiction under the assumption that a lower bound σ<min{dimHX,dimHY,1} cannot be improved, we are able to pigeonhole a small scale 0<r≪1 and a family of “well-behaved” r-tubes \(\mathcal{T}\) through X and Y with \(|\mathcal{T}|\ge r^{-2\sigma -\eta}\), where η>0 ultimately comes from the ϵ-improvement in [OS222]. This allows us to view Y as a sort of discretised Furstenberg-type set at scale r. If the mass of Y∩T for a typical r-tube in \(\mathcal{T}\) is not too concentrated inside a ball of radius rκ (where κ is a carefully chosen parameter, depending on η), then we can use a variant of the classical “two-ends” argument for Furstenberg sets to derive a contradiction (arising from η>0). On the other hand, if Y∩T is often concentrated on an rκ-ball, we can use a double-counting argument to show that for many y∈Y there will be many tubes T through y with this property, and this leads to the absurd conclusion that the ball B(y,rξ) has too large mass to be compatible with σ<dimH(Y).
The proof of Theorem 1.7 is based on a reduction to a recent incidence estimate of Fu and Ren [FR22], combined with some elementary estimates on Furstenberg sets (these will be discussed later). The proof of Fu and Ren, further, involves a Fourier-analytic component, due to Guth, Solomon, and Wang [GSW19]. So, while this paper contains no Fourier transforms, they play a role in the proof of Theorem 1.7. As we already mentioned, the higher-dimensional counterpart, Theorem 1.13, can be deduced from (a quantitative version) of the planar case via integralgeometric considerations, see Sect. 4. This is not the approach of Dote and Gan: in [DG22], Theorem 1.13 is proved more directly in general dimensions, although the proof still involves Fourier analysis.
1.5 Connections and applications
Part of the impetus for the study of radial projections in recent years came from the realization that they are closely connected to the Falconer distance set problem. In particular, a radial projection theorem of the first author [Orp19, Theorem 1.11] plays a key rôle in the partial results on the planar version of Falconer’s problem achieved in [KS19, G+20, Stu22]. However, the radial projection result in question only applies to planar sets of dimension >1. Theorem 1.1 (or rather its quantitative version, Corollary 2.22) can be seen as a substitute of [Orp19, Theorem 1.11] for sets of dimension ≤1, and thus opens the door to improvements on the distance set problem in the critical case of dimension 1. Similar considerations are valid in higher dimensions.
Restricting to cartesian products, Theorem 1.1 enables progress on another classical problem in geometric measure theory, the discretised sum-product problem. For example, the following new estimate of sum-product type follows from Theorem 1.1:
Corollary 1.17
Let \(A, B\subset \mathbb{R}\) be Borel sets. Then
Proof
We may assume that both A, B contain at least two points. We apply Theorem 1.1 to the sets X=−A×B and Y=−B×A. Since X is a Borel set not contained on a line, for every ϵ>0 there exists a point x=(−a,b)∈X such that
Now, it remains to observe that dimHπx(Y ∖ {x}) agrees with the dimension of “slopes” spanned between the point x=(−a,b) and the set Y ∖ {x}, namely
Since the quotient set (A−B)/(A−B) contains all such slopes, the corollary follows. □
We hope to explore these connections further in future work.
1.6 Paper outline
Theorem 1.1 and its more quantitative counterpart, Corollary 2.22, is proved in Sect. 2. Theorem 1.7 is proved in Sect. 3. More precisely, we start with Theorem 3.1: this is a δ-discretised statement vaguely reminiscent of Theorem 1.7, which can be deduced from the incidence theorem of Fu and Ren [FR22] with some effort. This version is still some distance away from proving Theorem 1.7. To bridge the gap, we resort to another “bootstrapping” argument, see Theorem 3.17 and Lemma 3.18.
In Sect. 4, we apply the quantitative versions of Theorems 1.1 and 1.7 in \(\mathbb{R}^{2}\), combined with an integralgeometric tool [SW21, Theorem 6.7], to give new proofs of Dote and Gan’s results, Theorems 1.13-1.14, in general dimensions.
1.7 Notation and some preliminaries
The notation B(x,r) stands for a closed ball of radius r>0 and centre x∈X, in a metric space (X,d). In the case \(X=\mathbb{R}^{d}\), we denote Bd=B(0,1). If A⊂X is a bounded set, and r>0, we write |A|r for the r-covering number of A, that is, the smallest number of closed balls of radius r required to cover A. Cardinality is denoted |A|, and Lebesgue measure Leb(A). The closed r-neighbourhood of A is denoted A(r).
If X, Y are positive numbers, then X≲Y means that X≤CY for some constant C, while X≳Y, X∼Y stand for Y≲X, X≲Y≲X. If the implicit constant C depends on a parameter this will be mentioned explicitly or denoted by a subscript.
If μ is a positive finite measure on \(\mathbb{R}^{d}\) and t≥0, the t-energy is defined as
It is well known that if μ satisfies a Frostman condition μ(B(x,r))≤Crt for all balls B(x,r) and some C,t>0, then Is(μ)<∞ for all s<t. Conversely, if It(μ)<∞, then for every ϵ>0 there are a compact set K with \(\mu (\mathbb{R}^{d}\setminus K)<\epsilon \) and a constant C such that μ|K(B(x,r))≤Crt for all balls B(x,r). Frostman’s Lemma asserts that if \(X\subset \mathbb{R}^{d}\) is a Borel set with dimH(X)>t≥0, then there is a Borel probability measure μ with \(\operatorname {spt}(\mu )\subset X\) and It(μ)<∞. See e.g. [Mat99, Chap. 8]. In the sequel we will use these facts without further reference.
2 Proof of Theorem 1.1
2.1 Preliminaries
In order to prove Theorem 1.1, we need two black boxes. The first one is a weaker (although more quantitative) version of the statement itself, recorded in [Shm23, Theorem B.1]. The second one is a recent ϵ-improvement [OS222] in the Furstenberg set problem.
We begin by recalling [Shm23, Theorem B.1]. We write \(\mathcal{P}(B)\) for the family of Borel probability measures on the metric space B (usually \(\mathbb{R}^{d}\) or the unit ball Bd of \(\mathbb{R}^{d}\)). Throughout this section and the next, we use the following notation. If \(X,Y \subset \mathbb{R}^{d}\) and G⊂X×Y, we write
for all x∈X and y∈Y. We note that if \(G \subset \mathbb{R}^{d} \times \mathbb{R}^{d}\) is a Borel set, then G|x and G|y are also Borel for every \(x,y \in \mathbb{R}^{d}\) (this is because \(\mathrm{Bor}(\mathbb{R}^{d} \times \mathbb{R}^{d}) = \mathrm{Bor}(\mathbb{R}^{d}) \times \mathrm{Bor}(\mathbb{R}^{d})\)).
Definition 2.1
Thin tubes
Let K,t≥0 and c∈(0,1]. Let \(\mu , \nu \in \mathcal{P}(\mathbb{R}^{d})\) with \(\operatorname {spt}(\mu ) =: X\) and \(\operatorname {spt}(\nu ) =: Y\). We say that (μ,ν) has (t,K,c)-thin tubes if there exists a Borel set G⊂X×Y with (μ×ν)(G)≥c with the following property. If x∈X, then
We also say that (μ,ν) has t-thin tubes if (μ,ν) has (t,K,c)-thin tubes for some K,c>0.
Here, and below, an r-tube is the r-neighbourhood of some line. The terminology of thin tubes was introduced in [SW21], and there it was in fact called strong thin tubes. We have no use for the notion of (weak) thin tubes, so we prefer the simpler terminology. We note that the terminology “thin” refers to the mass of the tubes, rather than their size.
Remark 2.3
Assume that \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{d})\) are such that the pair (μ,ν) has t-thin tubes for some t>0. Then there exists \(x \in \operatorname {spt}(\mu )\) such that \(\mathcal{H}^{t}(\pi _{x}(Y \, \setminus \, \{x\})) > 0\). To see this, pick x∈X such that ν(G|x)>0. Then also ν(G|x ∖ {x})>0, since otherwise (2.2) is not possible with exponent t>0. Therefore, we may pick a compact set K⊂G|x ∖ {x}⊂Y ∖ {x} with ν(K)>0. Now (2.2) implies that the push-forward πx(ν|K) satisfies a t-dimensional Frostman condition, and therefore \(\mathcal{H}^{t}(\pi _{x}(K)) > 0\).
We are now prepared to state [Shm23, Theorem B.1], although we do so directly using the terminology of thin tubes (see [SW21, Proposition 5.10]).
Proposition 2.4
For every C,δ,ϵ,s>0, there exist
all depending continuously on the parameters, such that the following holds. Assume that \(\mu ,\nu \in \mathcal{P}(B^{2})\) satisfy \(\operatorname {dist}(\operatorname {spt}(\mu ),\operatorname {spt}(\nu )) \geq C^{-1}\), and the s-dimensional Frostman condition
Assume further that ν(T)≤τ for all δ-tubes \(T \subset \mathbb{R}^{2}\). Then (μ,ν) has (β,K,1−ϵ)-thin tubes.
Remark 2.5
The hypothesis that the supports are separated is not stated explicitly in [Shm23, Theorem B.1], but it used in the proof. It is likely it can be dropped with some additional work, but we prefer to keep it for simplicity.
Next, we discuss the discretised Furstenberg set estimate from [OS222]. It is essentially [OS222, Theorem 1.3], but again we already state it in a language suitable for our later application. We need to introduce the notion of (δ,s)-sets:
Definition 2.6
(δ,s,C)-sets
Let (X,d) be a metric space, let P⊂X be a set, and let δ,C>0, and s≥0. We say that P is a (δ,s,C)-set if
The definition of a (δ,s,C)-set, above, is slightly different from a more commonly used notion in the area, introduced by Katz and Tao [HT01]. However, Definition 2.6 is not new either: these variants of (δ,s,C)-sets were for example used in [OS222]. It is worth noting that a (δ,s,C)-set is not required to be δ-separated to begin with; however, it is easy to check that every (δ,s,C)-set contains a δ-separated (δ,s,C′)-set with C′∼C. Another remark, to be employed without further mention, is that if \(P \subset \mathbb{R}^{d}\) is a (δ,s,C)-set, and P′⊂P satisfies |P′|δ≥c|P|δ, then P′ is a (δ,s,C/c)-set.
Definition 2.7
(δ,s,C)-sets of lines and tubes
Let \(\mathcal{A}(2,1)\) be the metric space of all (affine) lines in \(\mathbb{R}^{2}\) equipped with the metric
Here \(\pi _{L_{j}} \colon \mathbb{R}^{2} \to L_{j}\) is the orthogonal projection to the subspace Lj parallel to ℓj, and \(\{a_{j}\} = L_{j}^{\perp} \cap \ell _{j}\). A set \(\mathcal{L} \subset \mathcal{A}(2,1)\) is called a (δ,s,C)-set if \(\mathcal{L}\) is a (δ,s,C)-set in the metric space \((\mathcal{A}(2,1),d_{\mathcal{A}(2,1)})\), in the sense of Definition 2.6.
As before, a δ-tube stands for the δ-neighbourhood of some line \(\ell \in \mathcal{A}(2,1)\). A family of δ-tubes \(\mathcal{T} = \{\ell (\delta ) : \ell \in \mathcal{L}\}\) is called a (δ,s,C)-set if the line family \(\mathcal{L}\) is a (δ,s,C)-set. Similarly, we define the δ-covering number \(|\mathcal{T}|_{\delta}\) to be \(|\mathcal{L}|_{\delta}\).
We can now state [OS222, Theorem 1.3] in our language:
Theorem 2.8
Given s∈(0,1) and t∈(s,2) there exists ϵ=ϵ(s,t)>0 such that the following holds for all 0<δ≤δ0(s,t): if X⊂B2 is a (δ,t,δ−ϵ)-set, and for each x∈X there is a (δ,s,δ−ϵ)-set \(\mathcal{T}'_{x} \subset \mathcal{T}^{\delta}\) of tubes passing through x, then
Moreover, ϵ can be taken uniform in any compact subset of {(s,t):s∈(0,1),t∈(s,2)}.
To be precise, [OS222, Theorem 1.3] is stated in terms of dyadic tubes and sets of dyadic squares, but it is straightforward to deduce Theorem 2.8 from it (see also [OS222, Theorem 3.1] for a similar deduction). The uniformity of ϵ over compact sets is [OS222, Remark 1.4].
2.2 The key lemma
The next lemma contains the main work needed for Theorem 1.1.
Lemma 2.9
Let 0<s≤1 and \(\epsilon \in (0,\tfrac{1}{10})\). Let \(\mu ,\nu \in \mathcal{P}(B^{2})\) such that
for some constant C>0. Let β=β(s)>0 be the parameter from Proposition 2.4. If both (μ,ν) and (ν,μ) have (σ,K,1−ϵ)-thin tubes for some β≤σ<s then there exist η=η(s,σ)>0 and K′=K′(s,σ,ϵ,K,C) such that (μ,ν) and (ν,μ) have (σ+η,K′,1−3ϵ)-thin tubes. We can take
Moreover, the value of η(s,σ) is bounded away from zero on any compact subset of {(σ,s)∈(0,1]2:β(s)≤σ<s}.
Proof
We argue by contradiction. Since the roles of μ, ν are symmetric, we can assume that (μ,ν) do not have (σ+η,K′,1−3ϵ)–thin tubes for
where R>0 is a constant that may depend on η, to be determined in the course of the proof. Let \(X=\operatorname {spt}(\mu )\) and \(Y=\operatorname {spt}(\nu )\).
Since both (μ,ν) and (ν,μ) have (σ,K,1−ϵ)–thin tubes, there is a Borel set G⊂X×Y with μ×ν(G)>1−2ϵ such that
For every x∈X and \(r \in 2^{-\mathbb{N}}\), let \(\mathcal{T}_{x,r}''\) consist of those r-tubes T which contain x and satisfy
The collection \(\mathcal{T}_{x,r}''\) may be infinite, and this will cause inconvenience later. We fix this as follows. Let \(\mathcal{T}^{r}\) be a family of 2r-tubes such that
-
(i)
\(|\mathcal{T}^{r}| \sim r^{-2}\),
-
(ii)
if \(T \subset \mathbb{R}^{2}\) is an r-tube, then T∩B2 is contained in at least one and at most O(1) tubes from \(\mathcal{T}^{r}\),
-
(iii)
\(\mathcal{T}^{r}\) is cr-separated for some universal c>0. This means that if ℓ1, ℓ2 are the core lines of two distinct \(T_{1},T_{2} \in \mathcal{T}^{r}\), then \(d_{\mathcal{A}(2,1)}(\ell _{1},\ell _{2}) \geq cr\), as in Definition 2.7.
The family \(\mathcal{T}^{r}\), is easy to find, picking ∼r−1 tubes in each direction from an r-net of directions. Note that a consequence of (iii) is that if x,y∈B2, then
Let \(\mathcal{T}_{x,r}' \subset \mathcal{T}^{r}\) be a minimal set with the property that each intersection T∩B2 with \(T \in \mathcal{T}_{x,r}''\) is contained in at least one element of \(\mathcal{T}_{x,r}'\). Evidently (2.12) remains valid for all \(T \in \mathcal{T}_{x,r}'\), and moreover
We also note that since all the tubes in \(\mathcal{T}_{x,r}' \subset \mathcal{T}^{r}\) contain \(x \in \operatorname {spt}(\mu )\), they have overlap bounded by O(C) on \(\operatorname {spt}(\nu )\) (this follows from \(\operatorname {dist}(\operatorname {spt}(\mu ),\operatorname {spt}(\nu )) \geq C^{-1}\) and property (2.13) of \(\mathcal{T}^{r}\)). Therefore, we get from (2.12) that
We define
We claim that
Indeed, assume to the contrary that (μ×ν)(H)<ϵ, thus
Since (μ,ν) do not have (σ+η,K′,1−3ϵ)-thin tubes by assumption, we infer that there exists a point x∈X, and an r-tube \(T \subset \mathbb{R}^{2}\) containing x which satisfies
While a priori this holds for some r∈(0,1], we may take r to be dyadic by enlarging T and replacing K′ by 4K′. However, this means by definition (and the inclusion in (2.14)) that T⊂H|x, so it is absurd that ν(T∩(Hc)|x)>0. This contradiction completes the proof of (μ×ν)(H)≥ϵ.
Let
where R is a large constant that may depend on η. Note that this matches the claimed form for K′. In the proof we will assume that \(r_{0}^{\eta}\) is smaller than various universal implicit constants without further mention; this can be achieved since \(r_{0}^{\eta}\le 1/R\). It follows from (2.12) and the definition of K′ in (2.16) that \(\mathcal{T}_{x,r}' =\emptyset \) for all r>r0. This in particular implies that \(H_{r}|_{x} \subset \cup \mathcal{T}_{x,r}'\) is empty for all x∈X and r>r0. In other words Hr=∅ for r>r0, which implies that H is contained in the union of the sets Hr with r≤r0. Note that \(\sum _{r_{0} \ge r\in 2^{-\mathbb{N}}} r^{\eta }< \epsilon /2\) by the choice of r0 in (2.16). Since (μ×ν)(H)≥ϵ,
We fix this value of “r” for the remainder of the proof. We define
and note that μ(Xheavy)≥rη. Recall from the definition of \(\bar{H}_{r} \supset H_{r}\) that the fibres Hr|x are covered by the tube families \(\mathcal{T}_{x,r}'\), and by (2.15) that \(|\mathcal{T}_{x,r}'| \lesssim r^{ -\sigma -\eta}\). For x∈Xheavy, define
Since ν(Hr|x)≥rη for x∈Xheavy and to form Yx we are removing ≲r−σ−η tubes of mass <rσ+3η, we have ν(Yx)≥r2η for all x∈Xheavy. For every x∈Xheavy, the set \(\mathcal{T}_{x}\) of r-tubes covers Yx and satisfies
where the upper bound follows from Yx⊂H|x⊂G|x, the choice of r0, and (2.10). In fact, more generally
Putting these facts together, we see that
and
for all \(T\in \mathcal{T}_{x}\). Since for the axial line ℓ of T we have
we deduce that \(\mathcal{T}_{x}\) is an (r,σ,r−8η)–set for each x∈Xheavy.
Let
(This choice will become clear at the end of the proof.) Call a tube \(T\in \mathcal{T}_{x}\) concentrated if there is a ball BT of radius rκ with
Suppose first that there is \(X_{\mathrm{heavy}}'\subset X_{\mathrm{heavy}}\) with \(\mu (X_{\mathrm{heavy}}')\ge \mu (X_{\mathrm{heavy}})/2\) such that at least half of the tubes \(\mathcal{T}_{x}\) are not concentrated for \(x\in X_{\mathrm{heavy}}'\). Since \(\mu (X_{\mathrm{heavy}}')\ge r^{\eta}/2\), we get from the mass distribution principle and the Frostman assumption on μ that \(\mathcal{H}^{s}_{\infty}(X_{\mathrm{heavy}}')\gtrsim C^{-1}r^{\eta}\). By the choice (2.16) and the discrete form of Frostman’s Lemma [FO14, Proposition A.1], there exists an (r,s,r−2η)-set \(P \subset X_{\mathrm{heavy}}'\). Let \(\mathcal{T}'_{x}\) be the subset of non-concentrated tubes for each x∈P; it is a (r,σ,2r−8η)–set of tubes. Let \(\mathcal{T}' = \bigcup _{x\in P} \mathcal{T}'_{x}\).
Take η≤ϵ(s,σ)2 for the function ϵ(s,σ) in Theorem 2.8; we may assume ϵ(s,σ)<1/9. Note that the uniformity of ϵ(s,σ) over compact subsets yields the corresponding uniformity of η claimed in the statement. Then
Counting cardinality makes sense, because each \(\mathcal{T}_{x}' \subset \mathcal{T}_{x,r}' \subset \mathcal{T}^{r}\) was defined as subset of the common finite family \(\mathcal{T}^{r}\), recall below (2.12). Moreover, by the separation property (iii) of \(\mathcal{T}^{r}\), cardinality is comparable to r-covering number in this case.
It follows from (2.17) and the non-concentrated property that for each \(T\in \mathcal{T}'\) there are two rκ-separated sets YT,1,YT,2⊂T with ν(YT,j)≥rσ+4η. Thus, recalling from property (2.13) of the family \(\mathcal{T}^{r}\) that \(|\{T \in \mathcal{T}^{r} : (y_{1},y_{2}) \in T\}| \lesssim |y_{1} - y_{2}|^{-1}\), we may infer that
Thus, \(|\mathcal{T}'| \lesssim r^{-2\sigma - 8\eta - \kappa}\), which contradicts (2.19) if first η is taken small enough in terms of s−σ and then R is taken large enough in terms of η.
Assume next that there is a subset \(X_{\mathrm{heavy}}' \subset X_{\mathrm{heavy}}\) with \(\mu (X_{\mathrm{heavy}}') \geq \mu (X_{\mathrm{heavy}})/2\) such that at least half of the tubes in \(\mathcal{T}_{x}\) are concentrated for all \(x \in X_{\mathrm{heavy}}'\). Let \(\mathcal{T}'_{x}\) denote the concentrated tubes, and let \(\{ B_{T}: T\in \mathcal{T}'_{x}\}\) be the corresponding “heavy” rκ-balls, as in the definition. Since the family \(\mathcal{T}_{x}\) has overlap bounded by O(C) on \(\operatorname {spt}(\nu )\), the set
satisfies
Note that if (x,y)∈H′, then there is a tube \(T(x,y) \in \mathcal{T}^{r}\) containing x, y such that
Further, this ν measure cannot be too concentrated near y, because
assuming that 4η<s−σ and using (2.16). Therefore, for each (x,y)∈H′ we can pigeonhole a dyadic number r≤ξ(x,y)≤rκ such that
where \(A(y,\xi ,2\xi ) = \{x \in \mathbb{R}^{2} : \xi \le |x-y| <2\xi \}\). Then, recalling that (μ×ν)(H′)≳r8η, we can further pigeonhole a value r≤ξ≤rκ such that
Fix y∈Y such that μ(H″|y)≥r9η for the rest of the proof. Observe that H″|y can be covered by a collection of tubes \(\mathcal{T}_{y} \subset \mathcal{T}^{r}\) which contain y, and satisfy
We claim that \(\mathcal{T}_{y}\) contains ≳r10η⋅(ξ/r)σ elements whose directions are separated by ≥(r/ξ). Indeed, if T is any (r/ξ)-tube containing y, then
Thus, it takes ≳μ(H″|y)⋅rη⋅(ξ/r)σ≳r10η⋅(ξ/r)σ tubes of width (r/ξ) to cover H″|y, and perhaps even more (r/ξ)-tubes to cover the union \(\cup \mathcal{T}_{y}\). Let \(\mathcal{T}_{y}' \subset \mathcal{T}_{y}\) be a maximal subset with (r/ξ)-separated directions. Thus \(|\mathcal{T}_{y}'| \gtrsim r^{10\eta} \cdot (\xi /r)^{\sigma}\). This proves the claim.
The usefulness of the previous claim stems from the simple geometric fact that the family \(\mathcal{T}'_{y}\) has bounded overlap in \(\mathbb{R}^{2} \, \setminus \, B(y,\xi )\), due to the (r/ξ)-separation between the directions. Therefore, we may infer from a combination of (2.20) and the Frostman condition on ν that
or in other words r15η≲sξs−σ≤rκ(s−σ). This is a contradiction to the choice κ=16η/(s−σ). □
Remark 2.21
The proof shows that the set G′ witnessing the (σ+η,K′,1−3ϵ)-thinness of tubes in the conclusion of Lemma 2.9 can be taken to be contained in the set G witnessing the (σ,K,1−ϵ)-thinness of tubes in the assumption of Lemma 2.9. Also, the ‘3ϵ’ in the statement arises as 1−(μ×ν)(G)+ϵ; this explains why K′ increases as ϵ decreases, even though the thin tubes assumption becomes stronger.
2.3 Conclusion of the proof
Lemma 2.9 will be used (multiple times) to infer the following corollary:
Corollary 2.22
For all 0<σ<s≤1 and C,ϵ,δ>0, there exist τ=τ(ϵ,σ,s)>0 and K=K(C,δ,ϵ,s,σ)>0 such that the following holds. Assume that \(\mu ,\nu \in \mathcal{P}(B^{2})\) satisfy μ(B(x,r))≤Crs, ν(B(x,r))≤Crs, \(\operatorname {dist}(\operatorname {spt}(\mu ),\operatorname {spt}(\nu )) \geq C^{-1}\), and
for all δ-tubes \(T \subset \mathbb{R}^{2}\).
Then, both (μ,ν) and (ν,μ) have (σ,K,1−ϵ)-thin tubes.
Proof
It is immediate from Proposition 2.4 that both (μ,ν) and (ν,μ) have (β,K,1−ϵ)-thin tubes for some β=β(s)∈(0,s) and K=K(C,δ,ϵ,s)>0. If β≥σ, the proof ends here. Otherwise 0<β<σ, and our task is to upgrade β to σ. This will be done by iterating Lemma 2.9.
We turn to the details. The first point is to be careful with “ϵ”. Indeed, let us fix \(\bar{\epsilon} = \bar{\epsilon}(\epsilon ,s,\sigma ) > 0\) to be determined later, see (2.24). Then, instead of applying Proposition 2.4 directly with the parameter “ϵ” given in Corollary 2.22, we apply Proposition 2.4 with the parameter “\(\bar{\epsilon}\)”. The conclusion is the same as before: (μ,ν) and (ν,μ) have \((\beta ,K_{1},1 - \bar{\epsilon})\)-thin tubes for some \(K_{1} = K_{1}(C,\delta ,\bar{\epsilon},\sigma ,s) > 0\), provided that
for all δ-tubes \(T \subset \mathbb{R}^{2}\).
Now, if \(\bar{\epsilon} > 0\) is sufficiently small, Lemma 2.9 shows that both (μ,ν) and (ν,μ) have \((\beta + \eta ,K_{2},1 - 3\bar{\epsilon})\)-thin tubes for some
If β+η≥σ, we are done. Otherwise, if \(3\bar{\epsilon}\) remains sufficiently small, Lemma 2.9 says that (μ,ν) and (ν,μ) have \((\beta + 2\eta ,K_{3},1 - 3^{2}\bar{\epsilon})\)-thin tubes.
Continuing in this manner for N∼η−1∼s,σ1 steps, Lemma 2.9 will bring us to a point where (μ,ν) and (ν,μ) have \((\sigma ,K_{N},1 - 3^{N}\bar{\epsilon})\)-thin tubes. Now, we choose \(\bar{\epsilon} = \bar{\epsilon}(s,\sigma ,\epsilon ) > 0\) to be initially so small that
With this choice, we have shown that (μ,ν) and (ν,μ) have (σ,K,1−ϵ)-thin tubes with constant K=KN>0. This completes the proof. □
As a corollary of the corollary, we record the following statement which is less quantitative, but more pleasant to use:
Corollary 2.25
Let s∈(0,1], and let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{2})\) be measures which satisfy the s-dimensional Frostman condition μ(B(x,r))≲rs and ν(B(x,r))≲rs for all \(x \in \mathbb{R}^{2}\) and r>0. Assume that μ(ℓ)ν(ℓ)<1 for every line \(\ell \subset \mathbb{R}^{2}\). Then (μ,ν) has σ-thin tubes for all 0≤σ<s.
Proof
Assume first that ν(ℓ)>0 for some line \(\ell \subset \mathbb{R}^{2}\). Then either μ(ℓ)=1 or μ(ℓ)<1. The second case is easy: then \(\mu (\mathbb{R}^{2} \, \setminus \, \ell ) > 0\), so there exists a compact set \(K \subset \mathbb{R}^{2} \, \setminus \, \ell \) with μ(K)>0. Now (μ|K,ν|ℓ) has s-thin tubes. This implies that (μ,ν) has s-thin tubes. Assume then that μ(ℓ)=1. Then ν(ℓ)<1 by assumption, so there exists a compact set \(K \subset \mathbb{R}^{2} \, \setminus \, \ell \) such that ν(K)>0. Now it follows from Lemma 2.26 below that (μ|ℓ,ν|K) (and hence (μ,ν)) has σ-thin tubes for all 0≤σ<s.
We may assume in the sequel that ν(ℓ)=0 for all lines \(\ell \subset \mathbb{R}^{2}\). Assume next that μ(ℓ)>0 for some line \(\ell \subset \mathbb{R}^{2}\). Since ν(ℓ)=0, there exists a compact set \(K \subset \mathbb{R}^{2} \, \setminus \, \ell \) such that ν(K)>0. Then (μ|ℓ,ν|K) has σ-thin tubes for all 0≤σ<s by Lemma 2.26 below, which formally implies that (μ,ν) has σ-thin tubes for all 0≤σ<s.
Assume finally that μ(ℓ)=0=ν(ℓ) for all lines \(\ell \subset \mathbb{R}^{2}\). Pick two disjoint closed balls Bμ, Bν such that μ(Bμ)>0 and ν(Bν)>0. Restrict and renormalise μ and ν to Bμ and Bν, respectively, and denote these measures by \(\bar{\mu},\bar{\nu} \in \mathcal{P}(B^{2})\). Then, there exists a constant C>0 such that
for all \(x \in \mathbb{R}^{2}\), r>0. Next, fix σ<s, and let \(\tau = \tau (\tfrac{1}{2},\sigma ,s) > 0\) be the parameter given by Corollary 2.22. By [Orp19, Lemma 2.1], there exists δ>0 such that \(\max \{\bar{\mu}(T),\bar{\nu}(T)\} \leq \tau \) for all δ-tubes \(T \subset \mathbb{R}^{2}\). Now, Corollary 2.22 says that \((\bar{\mu},\bar{\nu})\) has \((\sigma ,K,\tfrac{1}{2})\)-thin tubes for the constant \(K = K(C,\delta ,\tfrac{1}{2},s,\sigma ) > 0\). In particular, \((\bar{\mu},\bar{\nu})\) has σ-thin tubes, and as a formal consequence also (μ,ν) has σ-thin tubes. This concludes the proof. □
In the proof above, we needed the following lemma:
Lemma 2.26
Let s∈(0,1], and let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{2})\) be measures with separated supports satisfying the s-dimensional Frostman condition μ(B(x,r))≲rs and ν(B(x,r))≲rs for all \(x \in \mathbb{R}^{2}\) and r>0. Assume, moreover, that there exists a line \(\ell \subset \mathbb{R}^{2}\) such that \(\operatorname {spt}(\mu ) \subset \ell \) and \(\operatorname {spt}(\nu ) \subset \mathbb{R}^{2} \, \setminus \, \ell \). Then (μ,ν) have σ-thin tubes for all 0≤σ<s.
Proof
Fix 0≤σ<s. Then Iσ(ν)<∞, and the standard proof of Kaufman’s projection theorem, see [Mat15, p. 56], shows that
Indeed, the only estimate needed to prove this inequality is
for all δ>0 small enough, and this is easy to verify by hand under the assumptions of the lemma. Alternatively, (2.27) follows by applying a projective transformation that sends ℓ to the line at infinity, under which the radial projections πx, x∈ℓ become orthogonal projections, and then one can literally apply the calculation in [Mat15, p. 56] before undoing the projective transformation.
From (2.27) it follows that for μ almost every x∈ℓ, the measure πxν restricted to a subset of positive measure satisfies a σ-dimensional Frostman condition. This implies that (μ,ν) has σ-thin tubes, as claimed. □
We are then prepared to prove Theorem 1.1, whose statement we repeat here:
Theorem 2.28
Let \(X,Y \subset \mathbb{R}^{2}\) be non-empty Borel sets, where X is not contained on any line. Then, supx∈XdimHπx(Y ∖ {x})≥min{dimHX,dimHY,1}.
Proof
Abbreviate t:=min{dimHX,dimHY,1}. We may assume that t>0, since otherwise there is nothing to prove. We start by disposing of a special case where
If the above holds, then for every ϵ>0, there exists a line \(\ell _{\epsilon} \subset \mathbb{R}^{2}\) such that dimH(Y∩ℓϵ)≥t−ϵ. Since we assumed that X does not lie on a line, we may choose points xϵ∈X ∖ ℓϵ, and then
Next, we assume the opposite of (2.29): there exists ϵ0>0 such that
Fix t−ϵ0<s<t≤min{dimHX,dimHY}, and let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{2})\) with \(\operatorname {spt}(\mu ) \subset X\) and \(\operatorname {spt}(\nu ) \subset Y\) such that μ(B(x,r))≤Crs and ν(B(x,r))≤Crs for all \(x \in \mathbb{R}^{2}\) and r>0. Assume, first, that μ(ℓ)=1 for some line \(\ell \subset \mathbb{R}^{2}\). In this case, we infer from (2.30) that ν(ℓ)=0 for this particular line ℓ, and therefore ν(K)>0 for some compact set \(K \subset \mathbb{R}^{2} \, \setminus \, \ell \). Now it follows from Lemma 2.26 that (μ|ℓ,ν|K) has σ-thin tubes for all σ<s, and in particular supx∈XdimHπx(Y ∖ {x})≥s.
Finally, assume that μ(ℓ)<1 for all lines \(\ell \subset \mathbb{R}^{2}\). In this case it follows directly from Corollary 2.25 that (μ,ν) has σ-thin tubes for all σ<s, so supx∈XdimHπx(Y ∖ {x})≥s. Since s<t was arbitrary, this completes the proof. □
3 Proof of Theorem 1.7
3.1 A discretised version of Theorem 1.7
The purpose of this section is to prove Theorem 1.7. The main work consists of establishing a δ-discretised version, stated in Theorem 3.1. This theorem will discuss (δ,s,C)-sets of δ-tubes \(\mathcal{T}_{x}\), x∈B2, with the special property that x∈T for all \(T \in \mathcal{T}_{x}\). In this case, it is easy to check that the (δ,s,C)-set property of \(\mathcal{T}_{x}\) is equivalent to the statement that the directions of the tubes (as a subset of S1) form a (δ,s,C′)-set for some C′∼C.
Theorem 3.1
For every t∈(1,2], σ∈[0,1), and ζ>0, there exist ϵ=ϵ(σ,t,ζ)>0 and δ0=δ0(σ,t,ζ)>0 such that the following holds for all δ∈(0,δ0].
Let s∈[0,2]. Let PK⊂B2 be a δ-separated (δ,t,δ−ϵ)-set, and let PE⊂B2 be a δ-separated (δ,s,δ−ϵ)-set. Assume that for every x∈PE, there exists a (δ,σ,δ−ϵ)-set of tubes \(\mathcal{T}_{x}\) with the properties x∈T for all \(T \in \mathcal{T}_{x}\), and
Then σ≥s+t−1−ζ.
Remark 3.2
It is easy to decipher from the proof the value of ϵ(σ,t,ζ)>0 is bounded away from zero on compact subsets of [0,1)×(1,2]×(0,1].
Remark 3.3
The lower bound σ≥s+t−1−ζ may appear odd if s+t>2. In this case the lemma simply says that the hypotheses cannot hold for any σ∈[0,1) (and for δ,ϵ>0 sufficiently small). This is consistent with the fact that if μ, ν are disjointly supported Frostman probability measures with exponents s∈[0,2] and t∈(1,2], respectively, and s+t>2, then \(\pi _{x}(\nu ) \ll \mathcal{H}^{1}|_{S^{d - 1}}\) for μ almost every \(x \in \mathbb{R}^{2}\), see [Orp19, Theorem 1.11].
Theorem 3.1 will be derived from a recent incidence theorem of Fu and Ren [FR22, Theorem 1.5] concerning (δ,s)-sets of points and (δ,t)-sets of tubes. Given a set of points P and a set of tubes \(\mathcal{T}\), we let \(\mathcal{I}(P,\mathcal{T}) := \{(p,T) : p \in T\}\) be the set of incidences between P and \(\mathcal{T}\).
Theorem 3.4
Fu and Ren
Let 0≤s,t≤2 such that s+t>1. Then, for every ϵ>0, there exist δ0=δ0(ϵ)>0 such that the following holds for all δ∈(0,δ0]. If P⊂B2 is a δ-separated (δ,s,δ−ϵ)-set, and \(\mathcal{T}\) is a δ-separated (δ,t,δ−ϵ)-set, then
where κ=κ(s,t)=min{1/2,1/(s+t−1)}.
In [FR22], Theorem 3.4 is formulated in terms of a slightly different (and more classical) notion of (δ,s,C)-sets. The above statement follows, after some algebra, by noticing that if P is a δ-separated (δ,s,C)-set (in the sense of this article) then the union of δ balls with centres in P is a (δ,s,|P|δsC)-set (in the sense of [FR22]), and likewise for sets of tubes. We also note that the theorem is also true if s+t≤1, but it is trivial in that case.
The next lemma allows us to find (δ,s)-sets inside δ-discretised Furstenberg sets.
Lemma 3.5
For every ξ>0, there exists δ0=δ0(ξ)>0 and ϵ=ϵ(ξ)>0 such that the following holds for all δ∈(0,δ0]. Let s∈[0,1] and t∈[0,2]. Assume that \(\mathcal{T}\) is a non-empty (δ,t,δ−ϵ)-set of δ-tubes in \(\mathbb{R}^{2}\). Assume that for every \(T \in \mathcal{T}\) there exists a non-empty (δ,s,δ−ϵ)-set PT⊂T∩B2. Then, the union
contains a non-empty (δ,γ(s,t),δ−ξ)-set, where
Remark 3.8
The constants δ0,ϵ>0 can indeed be taken independent of s, t, the chief reason being that the lemma also holds with s∈{0,1} and t∈{0,2}.
Proof of Lemma 3.5
We only sketch the argument, since it nearly follows from existing statements, and the full details are very standard (if somewhat lengthy). The main point is the following: it is known that the Hausdorff dimension of every (s,t)-Furstenberg set \(F \subset \mathbb{R}^{2}\) satisfies dimHF≥γ(s,t), where γ(s,t) is the function defined in (3.7). The case t≤s is due to Lutz and Stull [LS20]; they used information theoretic methods, but a more classical proof is also available, see [HSY22, Theorem A.1]. The case t≥s essentially goes back to Wolff in [Wol99], but also literally follows from [HSY22, Theorem A.1].
While the statement in [HSY22, Theorem A.1] only concerns Hausdorff dimension, the proof goes via Hausdorff content, and the following statement can be extracted from the argument. Let P be the set defined in (3.6). Then, the γ(s,t)-dimensional Hausdorff content of the δ-neighbourhood P(δ) satisfies
assuming that ϵ=ϵ(ξ)>0 and the upper bound δ0=δ(ξ)>0 for the scale δ were chosen small enough. The claim in the lemma immediately follows from (3.9), and [FO14, Proposition A.1]. This proposition, in general, states that if \(B \subset \mathbb{R}^{d}\) is a set with \(\mathcal{H}^{s}_{\infty}(B) = \kappa > 0\), then B contains a non-empty (δ,s,Cκ−1)-set for some absolute constant C>0. In particular, from (3.9) we see that P(δ) contains a (δ,γ(s,t),Cδ−ξ)-set. This easily implies a similar conclusion about P itself. □
By standard point-line duality considerations (see a few details below the statement), Lemma 3.5 is equivalent to the following statement concerning tubes:
Lemma 3.10
For every ξ>0, there exists δ0=δ0(ξ)>0 and ϵ=ϵ(ξ)>0 such that the following holds for all δ∈(0,δ0]. Let s∈[0,1] and t∈[0,2]. Assume that P⊂B2 is a non-empty (δ,t,δ−ϵ)-set. Assume that for every x∈P there exists a non-empty (δ,s,δ−ϵ)-set of tubes \(\mathcal{T}_{x}\) with the property that x∈T for all \(T \in \mathcal{T}_{x}\). Then, the union
contains a non-empty (δ,γ(s,t),δ−ξ)-set, where γ(s,t)=s+min{s,t}.
If the reader is not familiar with point-line duality, then the full details in a very similar context are recorded in [DOV22, Sects. 6.1-6.2]. Here we just describe the key ideas. To every point \((a,b) \in \mathbb{R}^{2}\), we associate the line \(\mathbf{D}(a,b) := \{y = ax + b : x \in \mathbb{R}\} \in \mathcal{A}(2,1)\). Conversely, to every line \(\ell = \{y = cx + d : x \in \mathbb{R}\}\) we associate the point D∗(ℓ)=(−c,d). Then, it is easy to check that
For (a,b),(c,d)∈[0,1]2, say, the maps D and D∗ are bilipschitz between the Euclidean metric, and the metric on \(\mathcal{A}(2,1)\). Therefore the property of “being a (δ,s)-set” is preserved (up to inflating the constants). Now, roughly speaking, Lemma 3.10 follows from Lemma 3.5 by first applying the transformations D, D∗ to the points P and the tubes \(\mathcal{T}_{x}\), x∈P, respectively. The main technicalities arise from the fact that \(\mathcal{T}_{x}\) is a set of δ-tubes, and not a set of lines. Let us ignore this issue for now, and assume that \(\mathcal{T}_{x} = \mathcal{L}_{x}\) is actually a (δ,s)-set of lines such that x∈ℓ for all \(\ell \in \mathcal{L}_{x}\). In this case Lemma 3.10 is simple to infer from Lemma 3.5.
Write \(P = \mathbf{D}^{\ast}(\mathcal{L})\) for some (δ,t)-set of lines \(\mathcal{L} \subset \mathcal{A}(2,1)\), and write also \(\mathcal{L}_{x} = \mathbf{D}(P_{x})\) for some (δ,s)-set of points \(P_{x} \subset \mathbb{R}^{2}\). Now, if \(\ell \in \mathcal{L}\), then D∗(ℓ)=x∈D(y) for all y∈Px by assumption. By (3.12), this is equivalent to Px⊂ℓ. Thus, every line \(\ell = (\mathbf{D}^{\ast})^{-1}(x) \in \mathcal{L}\), x∈P, contains a (δ,s)-set Px=:Pℓ. This places us in a position to apply Lemma 3.5.
A similar argument still works if \(\mathcal{L}_{x}\) is replaced by the (δ,s)-set of tubes \(\mathcal{T}_{x}\). One only needs to make sure that if \(x \in T \in \mathcal{T}_{x}\), then the line ℓ=(D∗)−1(x) is O(δ)-close to a certain (δ,s)-set Pℓ; this set can be derived from \(\mathcal{T}_{x}\) by using the idea above. For the technical details, we refer to [DOV22, Sects. 6.1-6.2], in particular [DOV22, Lemma 6.7].
We are finally equipped to prove Theorem 3.1:
Proof of Theorem 3.1
Fix s∈[0,2], t∈(1,2], σ∈[0,1), and ζ>0. Let PK,PE⊂B2 be as in the statement of the theorem: thus PK is a (δ,t,δ−ϵ)-set, and PE is a (δ,s,δ−ϵ)-set. Recall also the (δ,σ,δ−ϵ)-sets of tubes \(\mathcal{T}_{x}\) passing through x, for every x∈PE, with the property
The claim is that
if δ,ϵ>0 are chosen small enough, depending only on ζ, σ, t.
By Lemma 3.10, the union \(\bigcup _{x \in P_{E}} \mathcal{T}_{x}\) contains a non-empty (δ,γ(σ,s),δ−ξ)-set \(\mathcal{T}\), where
and ξ>0 can be made as small as we like by choosing ϵ,δ>0 sufficiently small (independently of s, σ). We may assume that ξ≥ϵ (otherwise \(\mathcal{T}\) is a (δ,γ(σ,s),δ−ϵ)-set, which would work even better in the sequel). Now we are prepared to spell out all the requirements on ϵ:
By (3.13), we have
We next compare this lower bound for \(|\mathcal{I}(P_{K},\mathcal{T})|\) against the upper bounds from Theorem 3.4. Recall the exponent “κ” from the statement of Theorem 3.4. Since PK is a (δ,t)-set and \(\mathcal{T}\) is a (δ,γ(σ,s))-set, the useful quantity for us is
The remainder of the proof splits into four cases:
-
(i)
Assume first that s≤σ. Thus γ(σ,s)=s+σ, so \(\mathcal{T}\) is a (δ,s+σ,δ−ξ)-set.
-
(a)
Assume that \(\bar{\kappa}(s,\sigma ,t) = 1/2\). Then, by Theorem 3.4,
$$ |\mathcal{I}(P_{K},\mathcal{T})| \leq |P_{K}||\mathcal{T}| \cdot \delta ^{(t + (s + \sigma ) - 1)/2 - 5\xi}. $$Comparing this against (3.16) yields δ2σ+2ϵ≤δt+s+σ−1−10ξ, and therefore σ≥s+t−1−10ξ−2ϵ. This yields (3.14), since we assumed that 10ξ+2ϵ≤ζ.
-
(b)
Assume that \(\bar{\kappa}(s,\sigma ,t) = 1/(t + s + \sigma - 1)\). Then,
$$ |\mathcal{I}(P_{K},\mathcal{T})| \leq |P_{K}||\mathcal{T}| \cdot \delta ^{1 - 5\xi}. $$Comparing against (3.16) yields δσ≤δ1−5ξ−ϵ, contradicting (3.15).
-
(a)
-
(ii)
Assume second that s>σ. Thus γ(σ,s)=2σ, so \(\mathcal{T}\) is a (δ,2σ,δ−ξ)-set.
-
(a)
Assume that \(\bar{\kappa}(s,\sigma ,t) = \tfrac{1}{2}\). Then,
$$ |\mathcal{I}(P_{K},\mathcal{T})| \leq |P_{K}||\mathcal{T}| \cdot \delta ^{(t + 2\sigma - 1)/2 - 5\xi}. $$Comparing this against (3.16) yields 1≤δ(t−1)/2−5ξ−ϵ, contradicting (3.15).
-
(b)
Assume finally that \(\bar{\kappa}(s,\sigma ,t) = 1/(t + 2\sigma - 1)\). Then,
$$ |\mathcal{I}(\mathcal{P}_{K},\mathcal{T})| \leq |P_{K}||\mathcal{T}| \cdot \delta ^{1 - 5\xi}. $$As in case (i)(b) above, this leads to the impossible situation δσ≤δ1−5ξ−ϵ.
-
(a)
We have now seen that the cases (i)(b) and (ii)(a)-(b) are not possible for δ, ϵ small enough, depending only on ζ>0, σ<1 and t>1. Case (i)(a), on the other hand, yields the desired inequality (3.14) for 10ξ+2ϵ≤ζ. This completes the proof of Theorem 3.1. □
3.2 Proof of Theorem 1.7
Theorem 1.7 follows immediately from the following “thin tubes version”, whose proof is further based on Theorem 3.1 from the previous section.
Theorem 3.17
Let s∈[0,2], t∈(1,2], 0≤σ<min{s+t−1,1}, C>0 and ϵ∈(0,1]. Then, there exists K=K(C,ϵ,s,σ,t)>0 such that the following holds. Assume that \(\mu ,\nu \in \mathcal{P}(B^{2})\) satisfy μ(B(x,r))≤Crs and ν(B(x,r))≤Crt, or alternatively Is(μ)≤C and It(ν)≤C. Then (μ,ν) has (σ,K,1−ϵ)-thin tubes.
In particular, whenever s∈[0,2], t∈(1,2], Is(μ)<∞ and It(ν)<∞, then (μ,ν) has σ-thin tubes for every 0≤σ<min{s+t−1,1}.
The proof of Theorem 3.17 is similar to the proof of Corollary 2.22. We establish an “ϵ-improvement” version of the result, Lemma 3.18 below, which can then be iterated multiple times to derive Theorem 3.17.
Lemma 3.18
Let s∈[0,2], t∈(1,2], and 0≤σ<min{s+t−1,1}. Let \(\epsilon \in (0,\tfrac{1}{10})\) and C,K>0. Let \(\mu ,\nu \in \mathcal{P}(B^{2})\) such that μ(B(x,r))≤Crs and ν(B(y,r))≤Crt for all \(x,y \in \mathbb{R}^{2}\) and r>0. If (μ,ν) has (σ,K,1−ϵ)-thin tubes, then there exist η=η(s,σ,t)>0 and K′=K′(C,K,ϵ,σ,s,t)>0 such that (μ,ν) has (σ+η,K′,1−4ϵ)-thin tubes. Moreover, η(s,σ,t) is bounded away from zero on any compact subset of
Before proving Lemma 3.18, we complete the proof of Theorem 3.17:
Proof of Theorem 3.17 assuming Lemma 3.18
The starting point is that (μ,ν) has (t−1,K0,1)-thin tubes for some K0∼C by the Frostman condition on ν alone: ν(T)≲C⋅rt−1 for all r-tubes \(T \subset \mathbb{R}^{2}\). In particular, (μ,ν) has \((t - 1,K_{0},1 - \bar{\epsilon})\)-thin tubes for every \(\bar{\epsilon} \in (0,\tfrac{1}{10})\). If s=0 or t=2, we are done. Otherwise, min{s+t−1,1}>t−1, and we need to apply Lemma 3.18 a few times. Fix 0≤σ<min{s+t−1,1}, and let
where η(s,σ′,t) is the function in Lemma 3.18. We have η>0, since η(s,σ′,t) is bounded away from zero on compact subsets of Ω, as in (3.19). We also choose
where ϵ>0 is the constant given in the statement.
The first application of Lemma 3.18 implies that (μ,ν) has \((t - 1 + \eta ,K_{1},1 - 4\bar{\epsilon})\)-thin tubes for some K1=K1(C,ϵ,s,σ,t)>0.Footnote 1 If t−1+η>σ, we are done. Otherwise, a second application of Lemma 3.18 shows that (μ,ν) has \((t - 1 + 2\eta ,K_{2},1 - 4^{2}\bar{\epsilon})\)-thin tubes for some K2>0. We proceed in the same manner. After N≤1/η steps, we find that (μ,ν) has \((\sigma ,K_{N},1 - 4^{N}\bar{\epsilon})\)-thin tubes for some KN>0, and the iteration terminates. At this point, notice that \(4^{N}\bar{\epsilon} \leq 4^{1/\eta}\bar{\epsilon} \leq \epsilon \). Also, KN only depends on C, ϵ, s, σ, t and N=N(η)=N(s,σ,t), as desired. This completes the proof. □
Finally, we prove Lemma 3.18:
Proof of Lemma 3.18
The scheme of the proof is very similar to that of Lemma 2.9. The main difference lies in the geometric input, which is provided by Theorem 3.1.
We argue by contradiction. Assume that (μ,ν) does not have (σ+η,K′,1−4ϵ)-thin tubes for K′=K′(C,K,ϵ,σ,s,t)≥1 and η=η(s,σ,t)>0 to be determined in the course of the proof. In fact, we explain immediately the dependence of η on s, t, σ. Since σ<s+t−1, we may choose ζ=ζ(s,σ,t)>0 such that
The proof will be concluded by applying Theorem 3.1 with the parameters s, t, and this ζ(s,σ,t)>0. Theorem 3.1 gives us a parameter η′=η′(σ,t,ζ)=η′(s,σ,t)>0 associated with these constants. Our choice of η=η(s,t,σ) needs to be so small that Cη<η′ for a certain absolute constant C>0. Since the value of η′(σ,t,ζ) is bounded away from zero on compact subsets of [0,1)×(1,2]×[0,1), the value of η will be (or can be taken to be) bounded away from zero on compact subsets of the set Ω in (3.19).
We then begin the proof in earnest. Write \(X=\operatorname {spt}(\mu )\), \(Y=\operatorname {spt}(\nu )\). Since (μ,ν) has (σ,K,1−ϵ)–thin tubes, there is a Borel set G⊂X×Y with (μ×ν)(G)>1−ϵ such that
For every x∈X and \(r \in 2^{-\mathbb{N}}\), let \(\mathcal{T}_{x,r}''\) consist of those r-tubes which contain x and satisfy
We pick a maximal subset of \(\mathcal{T}_{x,r}''\) with r-separated angles, and inflate each element of this subset by a factor of 10. Let \(\mathcal{T}_{x,r}'\) be the family of 10r-tubes so obtained. Evidently,
We define \(\bar{H}_{r} := \{(x,y) \in X \times Y : y \in \cup \mathcal{T}_{x,r}' \}\) and \(\bar{H} := \bigcup _{r} \bar{H}_{r}\). We claim that
Indeed, assume to the contrary that \((\mu \times \nu )(\bar{H}) < 2\epsilon \), thus \((\mu \times \nu )(\bar{H}^{c}) > 1 - 2\epsilon \), and
Since (μ,ν) does not have (σ+η,K′,1−4ϵ)-thin tubes by assumption, we infer that there exists a point x∈X, and an r-tube \(T \subset \mathbb{R}^{2}\), \(r \in 2^{-\mathbb{N}}\), containing x which satisfies
However, this means by the definition of \(\mathcal{T}_{x,r}''\), and the inclusion in (3.23), that \(T \cap B^{2} \subset \bar{H}|_{x}\), so it is absurd that \(\nu (T\cap (\bar{H}^{c})|_{x}) > 0\). This contradiction completes the proof of \((\mu \times \nu )(\bar{H}) \geq 2\epsilon \).
We now set
and we infer from a combination of (μ×ν)(G)≥1−ϵ and \((\mu \times \nu )(\bar{H}) \geq 2\epsilon \) that
Fix \(r_{0}=r_{0}(C,K,\epsilon ,s,\sigma )\in 2^{-\mathbb{N}}\) such that \(\sum _{r\le r_{0}} r^{\eta }< \epsilon /2\) (recall that η was determined by s, σ, t). Later we will impose further upper bounds on r0, always depending on C, K, ϵ, s, σ, t only. If K′ is taken so large that \((K'/2) \cdot r_{0}^{\sigma +\eta}>1\) (hence in terms of C, K, ϵ, s, σ, t only), then we see from (3.22) that \(\mathcal{T}_{x,r}' =\emptyset \) for all r>r0. This in particular implies that \(H_{r}|_{x} \subset \cup \mathcal{T}_{x,r}'\) is empty for all x∈X and r>r0. In other words Hr=∅ for r>r0, which implies that H is contained in the union of the sets Hr with r≤r0. Since (μ×ν)(H)≥ϵ, it now follows from the choice of r0 that
We will fix this value of “r” for the remainder of the proof. We define
and note that μ(Xheavy)≥rη. Recall from the definition of \(\bar{H}_{r} \supset H_{r}\) that the fibres Hr|x are covered by the tube families \(\mathcal{T}_{x,r}'\), and by (3.23) that \(|\mathcal{T}_{x,r}'| \lesssim r^{ -\sigma -\eta}\). For x∈Xheavy, define
Since ν(Hr|x)≥rη for x∈Xheavy, we have ν(Yx)≥r2η for all x∈Xheavy. For every x∈Xheavy, the set \(\mathcal{T}_{x}\) of r-tubes covers Yx and satisfies
where the upper bound follows from Yx⊂H|x⊂G|x and (3.21). In fact, more generally
Putting these facts together, we see that
and \(\mathcal{T}_{x}\) is an (r,σ,r−8η)–set for x∈Xheavy (see below (2.18) for full details).
We now discretise everything at scale r. First, apply the discrete Frostman’s Lemma [FO14, Proposition A.1] to obtain an (r,s,r−O(η))-set PX⊂Xheavy. We would also like to select an (r,t,r−O(η))-set PY⊂Y, but we need to do this a little more carefully. For each index j≥0, let
Then Y is contained in the union of the sets Yj. In particular, each of the sets Yx, x∈PX, is contained in this union. Therefore, for each x∈PX, there exists j=j(x)≥0 such that ν(Yx∩Yj)≥r3η (since there are only ≤Clog(1/r)≤r−η choices of “j” which need to be considered here). By the pigeonhole principle, we may then find a subset \(P_{X}' \subset P_{X}\) such that \(|P_{X}'| \geq r^{\eta}|P_{X}|\), and j(x)=j is constant for \(x \in P_{X}'\). Since \(P_{X}'\) remains an (r,s,r−O(η))-set, we keep denoting \(P_{X}'\) by PX in the sequel.
For the index “j” found above, let PY⊂Yj be a maximal r-separated set. Obviously |PY|≲2j⋅Cr−t, but since, for any x∈PX,
we also have the nearly matching lower bound |PY|≳C−1⋅2jr−t+3η. After this observation, it follows from the calculation
that PY is an (r,t,r−O(η))-set (we suppress the dependence on “C” by choosing r smaller in a manner depending on C).
We next study the cardinality of PY inside the tubes 2T for \(T \in \mathcal{T}_{x}\), x∈PX. Fix x∈PX. Recall that
and \(|\mathcal{T}_{x}| \lesssim r^{-\sigma - \eta}\). Since ν(Yx∩Yj)≥r3η, there is a subset \(\mathcal{T}_{x}' \subset \mathcal{T}_{x}\) of cardinality \(|\mathcal{T}_{x}'| \geq r^{O(\eta )} \cdot |\mathcal{T}_{x}|\) such that ν(Yx∩Yj∩T)≥rσ+O(η) for all \(T \in \mathcal{T}_{x}'\). Evidently \(\mathcal{T}_{x}'\) remains a (r,σ,r−O(η))-set. Now, if \(T \in \mathcal{T}_{x}'\), we have
and therefore |PY∩2T|≳rσ+O(η)⋅(2jr−t)≳rσ+O(η)|PY|. Finally, define
Then \(\mathcal{T}_{x}''\) is an (r,σ,r−O(η))-set of 2r-tubes for all x∈PX, where PX is an (r,s,r−O(η))-set. Moreover, |T∩PY|≥rσ+O(η)|PY| for all \(T \in \mathcal{T}_{x}''\), where PY is an (r,t,r−O(η))-set. These are precisely the hypotheses of Theorem 3.1. Thus, if η,r>0 are small enough, depending on σ, t, ζ (therefore s, σ, t), it follows that σ≥s+t−1−ζ. This contradicts our choice of “ζ” at (3.20), and completes the proof. □
4 Higher dimensions
In this section, we give new proofs of Theorems 1.13-1.14, due to Dote and Gan, by reducing them to planar statements, more precisely Corollary 2.25 and Theorem 3.17. In fact, as discussed in the introduction, we prove a sharper version of Theorem 1.14 that can be seen as a partial extension of Theorem 1.1 to higher dimensions. We first recall the statements:
Theorem 4.1
Let \(Y \subset \mathbb{R}^{d}\) be a Borel set with dimHY∈(k,k+1] for some k∈{1,…,d−1}. Then,
Theorem 4.2
Let \(X,Y\subset \mathbb{R}^{d}\) be Borel sets with dimHX>k−1 and dimHY∈(k−1,k] for some k∈{1,…,d−1}.
-
(i)
If dimHX>k, then supx∈XdimHπx(Y ∖ {x})=dimHY.
-
(ii)
If k−1<dimHX≤k, but X is not contained in any k-plane, the following holds. If dimHY>k−1/k−η for a sufficiently small constant η=η(d,k,dimHX)>0, then
$$ \sup _{x \in X} \dim _{\mathrm {H}}\pi _{x}(Y \, \setminus \, \{x\}) \geq \min \{ \dim _{\mathrm {H}}X,\dim _{\mathrm {H}}Y\}. $$
For k=1, we require no lower bound from dimHY in part (ii).
We introduce some additional notation. The Grassmanian of linear m-planes in \(\mathbb{R}^{d}\) will be denoted by \(\mathcal{G}(d,m)\). We endow \(\mathcal{G}(d,m)\) with the natural Borel probability measure γd,m invariant under the action of the orthogonal group – see [Mat99, Chap. 3]. The orthogonal projection onto \(V\in \mathcal{G}(d,m)\) is denoted by PV. Similarly, the Grassmanian of affine m-planes in \(\mathbb{R}^{d}\) is denoted by \(\mathcal{A}(d,m)\) and the natural isometry-invariant measure on it by λd,m – see [Mat99, §3.16] for its definition. Given a finite Borel measure μ on \(\mathbb{R}^{d}\), the sliced measures of μ on the affine planes V+x (where \(V\in \mathcal{G}(d,m)\) and x∈V⊥) are denoted by μV,x. We extend the definition to \(x\in \mathbb{R}^{d}\) by setting \(\mu _{V,x}:=\mu _{V,P_{V^{\perp}}x}\). See [Mat99, Chap. 10] for the definition and key properties of sliced measures. Finally, to lighten up notation we denote πy(X)=πy(X ∖ {y}).
We start by reducing Theorems 4.1–4.2 to the special case k=d−1. Similar arguments, involving lifting radial projection estimates from a random projection to a suitable lower dimensional subspace, appeared earlier in [D+21, SW21].
Proposition 4.3
Theorems 4.1-4.2 follow from their special case k=d−1.
Proof
Let Σ(x):=x/|x| for \(x \in \mathbb{R}^{d} \, \setminus \, \{0\}\). We start by proving the following inclusion, valid for every m-plane \(V \in \mathcal{G}(d,m)\), and for every 0<m<d−1:
To see this, fix \(x \in \mathbb{R}^{d}\) and \(e \in \pi _{P_{V}(x)}(P_{V}(Y)) \in S^{d - 1}\). Thus, there exists PV(y)∈PV(Y), with y∈Y, such that PV(y)≠PV(x) (in particular y≠x), and
The right hand side is an element of Σ(PV(πx(Y))), as claimed.
We then prove the proposition. More precisely, we will establish the following: let 0<k<d, and assume that Theorems 4.1-4.2 hold in \(\mathbb{R}^{d}\) for this “k”. Then they also hold in \(\mathbb{R}^{d + 1}\) with the same value of “k”. In particular, if the theorems hold for the value k=d−1 in some \(\mathbb{R}^{d}\), then they also hold for k=d−1 in every \(\mathbb{R}^{D}\) for D≥d.
We start by establishing the statement above for Theorem 4.2. Parts (i) and (ii) are very similar, but (ii) is slightly harder, so we spell out the details for (ii). Assume to the contrary that there exist Borel sets \(X,Y \subset \mathbb{R}^{d + 1}\) with
such that X is not contained in any k-plane, and
In order to apply the “known” \(\mathbb{R}^{d}\)-version of Theorem 4.2 (and then reach a contradiction), we plan to find a suitable orthogonal projection to a d-plane \(V \in \mathcal{G}(d + 1,d)\). The Marstrand-Mattila projection theorem, [Mat99, Corollary 9.4], shows that for γd+1,d-almost every \(V \in \mathcal{G}(d + 1,d)\) we have
On the other hand, (4.4) shows that, for γd+1,d-almost all V,
This violates the \(\mathbb{R}^{d}\)-version of Theorem 4.2 in \(V \cong \mathbb{R}^{d}\), applied with PV(X) and PV(Y), except for one problem: PV(X) may be contained in a k-plane, even if X is not. However, we claim that the set of \(V \in \mathcal{G}(d + 1,d)\) such that this happens has zero γd+1,d measure. Indeed, pick x0,x1,…,xk+1∈X such that the subspace W spanned by \(\{x_{j}-x_{0}\}_{j=1}^{k+1}\) is (k+1)-dimensional. Since dimW≤d<d+1, we have θ∉W for σd-almost all \(\theta \in S^{d}\subset \mathbb{R}^{d+1}\) (here σd is the normalized spherical measure). But γd+1,d is the push-forward of σd under θ→θ⊥, so PV|W is invertible for γd+1,d-almost all V, and in particular the span of PV(X−x0) contains \(P_{V}(W)\in \mathcal{G}(d+1,k+1)\), giving the claim. The proof can now be concluded by choosing \(V \in \mathcal{G}(d + 1,d)\) which satisfies (4.5), and such that PV(X) is not contained in a k-plane.
We turn to the proof of Theorem 4.1. Assume to the contrary that there exist k∈{1,…,d−1}, 0≤σ<k, and Borel sets \(X,Y \subset \mathbb{R}^{d + 1}\) with dimHY∈(k,k+1],
such that dimHπx(Y)<σ for all x∈X. Note that
since k≥1 and σ<k<dimHY. In particular, by the Marstrand-Mattila projection theorem, there exists a plane \(V \in \mathcal{G}(d + 1,d)\) such that dimHPV(Y)=dimHY, and
On the other hand, (4.4) shows that
In other words PV(X)⊂{z∈V:dimHπz(PV(Y))<σ}, and therefore
This contradicts Theorem 4.1 in \(V \cong \mathbb{R}^{d}\), and the proof of the proposition is complete. □
It remains to prove the 1-codimensional cases. The constant “η>0” in Theorem 4.2(ii) will arise from an application of [SW21, Proposition 6.8], which we recall here:
Proposition 4.7
Let t∈(d−2,d−1] and s∈((d−1)−1/(d−1)−η,d−1], where η=η(d,t)>0 is a sufficiently small constant. Let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{d})\) be measures with disjoint supports such that It(μ)<∞ and Is(ν)<∞. Assume moreover that μ(W)=0=ν(W) for all (d−1)-planes \(W \subset \mathbb{R}^{d}\). Assume also that \(\dim _{\mathrm {H}}\operatorname {spt}(\nu ) < s + \eta \). Then, possibly after restricting μ and ν to subsets of positive measure, we have
We also recall [SW21, Theorem 6.7], which provides the mechanism to upgrade “thin tubes” information from lower to higher dimensions:
Theorem 4.8
Let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{d})\) be measures with Is(μ)<∞, Is(ν)<∞ with s∈(k,k+1] for some k∈{1,…,d−2}. Suppose that there is t>0 such that the sliced measures (μW,z,νW,z) have t-thin tubes for (γd,d−k×μ)-almost all (W,z).
Then (μ,ν) have (k+t)-thin tubes.
We begin with Theorem 4.2, since the numerology is slightly simpler.
Proof of Theorem 4.2 for k=d−1
We start by proving the following claim about thin tubes.
Claim 4.9
Let μ, ν be measures on \(\mathbb{R}^{d}\) with It(μ)<∞ and Is(ν)<∞, where either
with the constant η=η(d,t)>0 from Proposition 4.7, or
In the case (4.10), assume moreover that μ(W)=0=ν(W) for all (d−1)-planes \(W \subset \mathbb{R}^{d}\), and \(\dim _{\mathrm {H}}\operatorname {spt}(\nu ) < s + \eta \). Then (μ,ν) has σ-thin tubes for all 0≤σ<min{s,t}.
The case d=2 follows immediately from Corollary 2.25. Consider now the case d≥3. Since t>d−2, by the Marstrand-Mattila projection theorem (in this application the absolutely continuous case, [Mat15, Theorem 9.7]), the push-forward of μ×γd,2 under (x,V)→V+x is absolutely continuous with respect to λd,2 (for details, see [SW21, Lemma 6.3]). Since also s>d−2, we then deduce from the Marstrand-Mattila slicing theorem, [Mat99, Theorem 10.7], that
In the case (4.10), and under the assumptions μ(W)=0=ν(W) and \(\dim _{\mathrm {H}}\operatorname {spt}(\nu ) < s + \eta \), we may infer the following from Proposition 4.7: for (μ×γd,2) almost every pair (x,V) such that μV,x≠0≠νV,x, we have
for every line ℓ⊂V+x. The same is also true in the case (4.11), for the simpler reason that t−(d−2)>1: this implies that μV,x(ℓ)=0 for all lines ℓ⊂V+x whenever It−(d−2)(μV,x)<∞, and thus for (μ×γd,2) almost every (x,V).
In both cases (4.10)-(4.11), we have now checked that μV,x and νV,x satisfy the hypotheses of Corollary 2.25 for (μ×γd,2) almost every (x,V). Consequently, (μV,x,νV,x) has σ-thin tubes for all 0≤σ<min{s−(d−2),t−(d−2)}. Finally, it follows from Theorem 4.8, applied with k=d−2, that (μ,ν) has σ-thin tubes for all 0≤σ<min{s,t}, as claimed.
We are then equipped to prove the case k=d−1 of Theorem 4.2. We only spell out the details for Theorem 4.2(ii), which uses the case (4.10) of the thin tubes statement above. Theorem 4.2(i) uses the case (4.11) and is substantially simpler.
Let \(X,Y \subset \mathbb{R}^{d}\) be Borel sets with
Assume that X is not contained in any (d−1)-plane, and write u:=min{dimHX,dimHY}. We claim that supx∈XdimHπx(Y)≥u. We first dispose of a special case where
Since πx|W is locally bi-Lipschitz for any (d−1)-plane W and \(x\in \mathbb{R}^{d}\setminus W\), and since for any such plane W we may by assumption find x∈X∖W, we see that supx∈XdimHπx(Y)≥u in this case.
Assume next that there exists ϵ0>0 such that dimH(Y∩W)≤u−ϵ0 for all (d−1)-planes \(W \subset \mathbb{R}^{d}\). Then, pick d−2<t<dimHX and u−ϵ0<s<dimHY satisfying
Let \(\mu ,\nu \in \mathcal{P}(\mathbb{R}^{d})\) with It(μ)<∞, Is(ν)<∞ and \(\operatorname {spt}(\mu ) \subset X\) and \(\operatorname {spt}(\nu ) \subset Y\). Note that ν(W)=0 for all (d−1)-planes \(W \subset \mathbb{R}^{d}\), because otherwise
contrary to our assumption. Also, \(\dim _{\mathrm {H}}\operatorname {spt}(\nu ) \leq \dim _{\mathrm {H}}Y < s + \eta \).
These observations nearly place us in a position where we can apply the case (4.10) of the first part of the proof. We are only missing the information that μ(W)=0 for all (d−1)-planes \(W \subset \mathbb{R}^{d}\). So, let us now treat the special case where μ(W)>0 for some (d−1)-plane \(W \subset \mathbb{R}^{d}\).
Since ν(W)=0, there exists a compact set K⊂Y ∖ W such that ν(K)>0. Now, since W is a (d−1)-plane, the family of radial projections {πx}x∈W is “morally the same” as the family of orthogonal projections \(\{P_{V}\}_{V \in \mathcal{G}(d,d - 1)}\). More precisely, there exist (dimension preserving) projective maps \(F \colon \mathbb{R}^{d} \to \mathbb{R}^{d}\) and x↦V(x) from W to \(\mathcal{G}(d,d - 1)\) such that
We outsource the justification to Remark 4.14. By the Kaufman-Mattila exceptional set estimate for orthogonal projections [Mat15, Theorem 5.10], combined with (4.13), we have
for all 0≤σ<dimHK. Since \(\dim _{\mathrm {H}}(X \cap W) \geq \dim _{\mathrm {H}}(\operatorname {spt}(\mu ) \cap W) \geq s\), we therefore get
This proves our claim by letting s↗dimHY.
We have now reduced the proof to the case where μ(W)=0=ν(W) for all (d−1)-planes \(W \subset \mathbb{R}^{d}\). Since also It(μ)<∞ and Is(ν)<∞, where s satisfies (4.12), we may apply Claim 4.9 in the case (4.10). The conclusion is that (μ,ν) has σ-thin tubes for all 0≤σ<min{s,t}. Therefore supx∈XdimHπx(Y)≥min{s,t}, and the proof is completed by letting s↗dimHY and t↗dimHX. □
Remark 4.14
Let \(W := \mathbb{R}^{d - 1} \times \{0\} \subset \mathbb{R}^{d}\). The purpose of this remark is to justify the (well-known) fact that the family of radial projections {πx}x∈W is “morally the same” as the family of orthogonal projections \(\{P_{V}\}_{V \in \mathcal{G}(d,d - 1)}\), and in particular (4.13). To see this, let \(F \colon \mathbb{R}^{d} \, \setminus \, W \to \mathbb{R}^{d}\) be the projective transformation
For \(w \in \mathbb{R}^{d - 1}\) and e∈Sd−1 ∖ W, let \(\ell _{w}(e) := (w,0) + \operatorname {span}(e)\). The family
then contains all the lines passing through (w,0)∈W which are not contained in W. These lines are the fibres of the radial projections π(w,0), restricted to \(\mathbb{R}^{d} \, \setminus \, W\). Now, a straightforward calculation shows that
where \(L_{e}(w) = \operatorname {span}(w,1) + (\bar{e}/e_{d},0)\). Therefore, F transforms the lines in \(\mathcal{L}(w)\) passing through (w,0)∈W into lines parallel to the vector (w,1). Since \((\bar{e}/e_{d},0)\) can take any value in W, in fact \(\{F(\ell ) : \ell \in \mathcal{L}(w)\}\) consists of all lines parallel to (w,1). These lines are the fibres of the orthogonal projection πV(w) to \(V(w) := (w,1)^{\perp} \in \mathcal{G}(d,d - 1)\). It follows from these observations (with a little more effort) that
as we claimed in (4.13).
Finally, we prove the case k=d−1 of Theorem 4.1.
Proof of Theorem 4.1 for k=d−1
We first claim the following. Let d−1<t≤d and d−2<s≤d. Let μ, ν be finite Borel measures on \(\mathbb{R}^{d}\) with Is(μ)<∞ and It(ν)<∞. Then (μ,ν) has σ-thin tubes for
Since s,t>d−2, the same argument as in the previous proof (applying the Marstrand-Mattila projection and slicing theorems) yields that
We then apply the planar case, Theorem 3.17 to the measures μV,x and νV,x (the hypotheses are evidently valid). The conclusion is that (μV,x,νV,x) has σ-thin tubes for all
Now, observe that
Consequently, it follows from Theorem 4.8 that (μ,ν) has σ-thin tubes for all 0≤σ≤min{s+t−(d−1),d−1}, as we claimed.
The rest is standard, but let us spell out the details anyway. Assume, to reach a contradiction, that there exists a Borel set \(Y \subset \mathbb{R}^{d}\) with d−1<dimHY≤d such that
for some σ∈[0,d−1) and ϵ0>0. We may infer from this counter assumption that σ>dimHY−1 because \(\{x \in \mathbb{R}^{d} : \dim _{\mathrm {H}}\pi _{x}(Y \, \setminus \, \{x\}) < \dim _{\mathrm {H}}Y - 1 \} = \emptyset \). Indeed, Y ∖ {x}⊂πx(Y ∖ {x})×(0,∞) when viewed in polar coordinates centred at x, and so dimHY≤1+dimHπx(Y ∖ {x}). Therefore,
Let \(\mu \in \mathcal{P}(\mathbb{R}^{d})\) with \(\operatorname {spt}(\mu ) \subset \{x : \dim _{\mathrm {H}}\pi _{x}(Y) < \sigma - \epsilon _{0}\}\) with Is(μ)<∞. Let
and let \(\nu \in \mathcal{P}(\mathbb{R}^{d})\) with \(\operatorname {spt}(\nu ) \subset Y\) with It(ν)<∞. By the claim established in the first part of the proof, it follows that (μ,ν) has ξ-thin tubes for all 0≤ξ<min{s+t−(d−1),d−1}. We pick
so that (μ,ν) in particular has (σ−ϵ0)-thin tubes. This implies that there exists a point \(x \in \operatorname {spt}(\mu )\) with dimHπx(Y)≥σ−ϵ0. This contradicts \(\operatorname {spt}(\mu ) \subset \{x : \dim _{\mathrm {H}}\pi _{x}(Y) < \sigma - \epsilon _{0}\}\), and completes the proof. □
Notes
The upper bound for “K1” in Lemma 3.18 also depends on the lower bound for ϵ>0, so the argument here does not show that (μ,ν) has (t−1+η,K1,1)-thin tubes. This would indeed be false in general.
References
Beck, J.: On the lattice property of the plane and some problems of Dirac, Motzkin and Erdős in combinatorial geometry. Combinatorica 3(3–4), 281–297 (1983)
Bond, M., Łaba, I., Zahl, J.: Quantitative visibility estimates for unrectifiable sets in the plane. Trans. Am. Math. Soc. 368(8), 5475–5513 (2016)
Csörnyei, M.: On the visibility of invisible sets. Ann. Acad. Sci. Fenn., Math. 25(2), 417–421 (2000)
Dąbrowski, D., Orponen, T., Villa, M.: Integrability of orthogonal projections, and applications to Furstenberg sets. Adv. Math. 407, Paper No. 108567, 34 (2022)
Dote, P., Gan, S.: Exceptional set estimates for orthogonal and radial projections in \(\mathbb{R}^{n}\). arXiv e-prints, (2022). arXiv:2208.03597
Du, X., Iosevich, A., Ou, Y., Wang, H., Zhang, R.: An improved result for Falconer’s distance set problem in even dimensions. Math. Ann. 380(3–4), 1215–1231 (2021)
Falconer, K.J.: Hausdorff dimension and the exceptional set of projections. Mathematika 29(1), 109–115 (1982)
Fässler, K., Orponen, T.: On restricted families of projections in \(\mathbb{R}^{3}\). Proc. Lond. Math. Soc. (3) 109(2), 353–381 (2014)
Fu, Y., Ren, K.: Incidence estimates for α-dimensional tubes and β-dimensional balls in \(\mathbb{R}^{2}\). J. Fractal Geom. (2022, to appear). arXiv:2111.05093v2
Guth, L., Iosevich, A., Ou, Y., Wang, H.: On Falconer’s distance set problem in the plane. Invent. Math. 219(3), 779–830 (2020)
Guth, L., Solomon, N., Wang, H.: Incidence estimates for well spaced tubes. Geom. Funct. Anal. 29(6), 1844–1863 (2019)
Héra, K., Shmerkin, P., Yavicoli, A.: An improved bound for the dimension of (α,2α)-Furstenberg sets. Rev. Mat. Iberoam. 38(1), 295–322 (2022)
Hawk Katz, N., Tao, T.: Some connections between Falconer’s distance set conjecture and sets of Furstenburg type. N.Y. J. Math. 7, 149–187 (2001)
Kaufman, R.: On Hausdorff dimension of projections. Mathematika 15, 153–155 (1968)
Keleti, T., Shmerkin, P.: New bounds on the dimensions of planar distance sets. Geom. Funct. Anal. 29(6), 1886–1948 (2019)
Liu, B.: On Hausdorff dimension of radial projections. Rev. Mat. Iberoam. 37(4), 1307–1319 (2021)
Liu, B., Shen, C.-Y.: Intersection between pencils of tubes, discretized sum-product, and radial projections. Asian J. Math. (2020, to appear). arXiv:2001.02551
Lund, B., Pham, T., Huong Thu, V.T.: Radial projection theorems in finite spaces. arXiv e-prints (2022). arXiv:2205.07431
Lutz, N., Stull, D.M.: Bounding the dimension of points on a line. Inf. Comput. 275, 104601 (2020)
Marstrand, J.M.: Some fundamental geometrical properties of plane sets of fractional dimensions. Proc. Lond. Math. Soc. 3(4), 257–302 (1954)
Mattila, P.: Geometry of Sets and Measures in Euclidean Spaces. Fractals and Rectifiability, 1st paperback edn. Cambridge University Press, Cambridge (1999)
Mattila, P.: Hausdorff dimension, projections, and the Fourier transform. Publ. Mat. 48(1), 3–48 (2004)
Mattila, P.: Fourier Analysis and Hausdorff Dimension. Cambridge Studies in Advanced Mathematics, vol. 150. Cambridge University Press, Cambridge (2015)
Mattila, P.: Hausdorff dimension, projections, intersections, and Besicovitch sets. In: Akram Aldroubi, S.J., Cabrelli, C., Molter, U. (eds.) New Trends in Applied Harmonic Analysis, Volume 2, Applied and Numerical Harmonic Analysis, pp. 129–157. Brikhäuser, Cham (2019)
Orponen, T.: A sharp exceptional set estimate for visibility. Bull. Lond. Math. Soc. 50(1), 1–6 (2018)
Orponen, T.: On the dimension and smoothness of radial projections. Anal. PDE 12(5), 1273–1294 (2019)
Orponen, T., Shmerkin, P.: On exceptional sets of radial projections. arXiv e-prints. Unpublished preprint. (2022). arXiv:2205.13890
Orponen, T., Shmerkin, P.: On the Hausdorff dimension of Furstenberg sets and orthogonal projections in the plane. Duke Math. J. (2022, to appear). arXiv:2106.03338
Peres, Y., Schlag, W.: Smoothness of projections, Bernoulli convolutions, and the dimension of exceptions. Duke Math. J. 102(2), 193–251 (2000)
Raz, O.E., Zahl, J.: On the dimension of exceptional parameters for nonlinear projections, and the discretized Elekes-Rónyai theorem. Geom. Funct. Anal. (2023, to appear). arXiv:2108.07311
Shmerkin, P.: A non-linear version of Bourgain’s projection theorem. J. Eur. Math. Soc. 25(10), 4155–4204 (2023)
Shmerkin, P., Wang, H.: On the distance sets spanned by sets of dimension d/2 in \(\mathbb{R}^{d}\). arXiv e-prints (2021). arXiv:2112.09044
Simon, K., Solomyak, B.: Visibility for self-similar sets of dimension one in the plane. Real Anal. Exch. 32(1), 67–78 (2006/07)
Stull, D.M.: Pinned distance sets using effective dimension. arXiv e-prints (2022). arXiv:2207.12501
Szemerédi, E., Trotter, W.T. Jr.: Extremal problems in discrete geometry. Combinatorica 3(3–4), 381–392 (1983)
Ungar, P.: 2N noncollinear points determine at least 2N directions. J. Comb. Theory, Ser. A 33(3), 343–347 (1982)
Wolff, T.: Recent work connected with the Kakeya problem. In: Prospects in Mathematics (Princeton, NJ, 1996), pp. 129–162. Am. Math. Soc., Providence (1999)
Acknowledgements
Some ideas for this paper were conceived while the first two authors were visiting the Hausdorff Research Institute for Mathematics, Bonn, during the trimester Interactions between Geometric measure theory, Singular integrals, and PDE. We would like to thank the institute and its staff for their generous hospitality. We also thank Katrin Fässler, Jiayin Liu, and Josh Zahl for useful discussions. Part of this research was done while the third author was visiting Po Lam Yung at the Australian National University, she would like to thank him and the analysis group for the warm hospitality.
We are grateful to the reviewers for reading the manuscript with great care, and for making numerous helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
T.O. is supported by the Academy of Finland via the projects Quantitative rectifiability in Euclidean and non-Euclidean spaces and Incidences on Fractals, grant Nos. 309365, 314172, 321896.
P.S. is supported by an NSERC Discovery Grant.
H.W. is supported by NSF Grant DMS-2055544.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Orponen, T., Shmerkin, P. & Wang, H. Kaufman and Falconer Estimates for Radial Projections and a Continuum Version of Beck’s Theorem. Geom. Funct. Anal. 34, 164–201 (2024). https://doi.org/10.1007/s00039-024-00660-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-024-00660-3