1 Introduction

The observer design constitutes a pivotal concern in many engineering domains, as evidenced by the works in [1, 2, 19, 26, 28, 31]. The estimation of states or outputs holds particular significance for tasks such as system variable monitoring and control law formulation [16]. With the growing intricacy inherent to diverse control systems, the presence of disturbances within the system’s state equations has become increasingly commonplace. It is important to acknowledge that, in general, the error in state estimation will persist in the presence of disturbances, and its complete elimination is often unattainable. In such scenarios, the pursuit of interval state estimation methods may offer a viable alternative.

Interval observers, arising as a contemporary robust state estimation alternative [6, 9, 20], have significantly advanced in observer design research due to their practical efficacy, evident in studies such as [10, 25, 29, 32]. Differing from traditional observer design methodologies, interval observers consist of pairs of Luenberger-type observers. Their dynamic equations and initial states are specifically tailored to represent the interval boundaries of real state values at any time. The principal constraint in interval observer design lies in establishing the cooperative behavior of the interval estimation error dynamical system through a well-structured approach. Researchers have successfully addressed this challenge for a variety of system classes, encompassing linear time-invariant (LTI) systems [4, 17], linear time-varying systems [5], linear parameter-varying systems [3], and special classes of nonlinear systems [18, 33].

In practical engineering applications, the inputs to the system are constrained due to the physical structure of the execution unit, triggering the input saturation phenomenon [22,23,24, 27, 30]. This phenomenon is prevalent in real systems, e.g., the output of an aircraft drive system is bounded in both amplitude and rate of change, and the output of a motor is similarly finite in terms of speed and torque. On the one hand, the presence of saturation can significantly compromise the performance of the whole system, potentially culminating in instability; on the other hand, tackling the control of plants subject to input saturation poses formidable theoretical challenges. Therefore, the study of control systems featuring input saturation is of great importance both at the level of practical engineering applications and at the theoretical level. In general, approaches to address the saturation problem can be categorized into two primary methods: one is called the compensator design method [8], and another is known as the direct design method [11, 13, 14, 34]. The latter involves thoroughly considering saturation issues in the initial control system design process and purposefully designing constrained control signals to stabilize the entire system. In this study, we adopt the latter approach. For instance, Lin [13] and Zhou et al. [34] investigated the stability of a single linear system subject to input saturation and proposed a parametric low-gain feedback control method and a low-high-gain feedback control method to ensure that the input-constrained system is capable of achieving semi-global stabilization. The core idea of the low-gain feedback control method is to set the low-gain parameter \(\epsilon \) small enough to ensure that the control input does not saturate, thereby avoiding nonlinear saturation. The low-gain feedback control approach of [13] is established using the parametric algebraic Riccati equation (PARE). The matrix \(P(\epsilon )\) can only be solved by stepwise iteration and cannot be directly described by the equations of the \(\epsilon \). Unlike the other approaches mentioned above, a low-gain feedback control scheme based on the parametric Lyapunov equation (PLE) was first proposed in [34]. The low-gain matrix \(P(\epsilon )\) is also obtained by solving a PLE using the low-gain feedback control method used in this paper. In this case, it is possible to express \(P(\epsilon )\) directly in terms of the \(\epsilon \) without repeatedly solving the Lyapunov matrix equation for a distinct \(\epsilon \). As a result, we may write the gain matrix \(P(\epsilon )\) explicitly in advance for different pre-selected \(\epsilon \), skipping the iterative procedure and comparatively lowering the computing cost.

Inspired by the aforementioned discussion, this article addresses the problem of robust control based on interval observers for continuous-time LTI systems with input saturation and disturbances via a low-gain feedback method. Limited research has explored interval observer construction in saturated systems. Due to the inclusion of interval observers, the complexities considered in this paper surpass those in [14, 34]. The main contributions are listed as follows: Firstly, by resorting to the system’s output information and the upper and lower bounds on the disturbances, we devise an interval state estimation technique to estimate unmeasurable states at any time by means of positive system theory. Secondly, unlike the PARE-based approach, which demands an iterative solution to the PARE online, our proposed low-gain design algorithm determines all parameters offline in advance, reducing computational complexity. Thirdly, considering the characteristics of the interval observer, a new architecture of stability analysis is given by utilizing a quadratic and copositive type Lyapunov function, which is different from the stability analysis in [34].

The rest of this work follows a structured organization as outlined below: In Sect. 2, we provide a foundation of preliminary concepts and outline the problem statements. Section 3 is dedicated to the presentation of interval observer design and controller design. In Sect. 4, we present a series of numerical simulation results that serve to demonstrate the validity of the adopted methods. In the end, we offer a conclusive summary in Sect. 5.

2 Preliminaries

In this section, we provide some symbolic representations and fundamental background information related to positive systems for the subsequent analysis and then introduce the formation of our problem.

2.1 Notation

\({\mathbb {R}}_{+}\) and \({\mathbb {R}}^{m\times {n}}\) are, respectively, the set of nonnegative real numbers and the set of \(m\times n\) real matrices. Denote the sequence of integers \(1,\dots ,n\) as \(\widehat{1,n}\). The symbol I stands for the identity matrix with the appropriate dimension. \({\textbf {1}}_{n}\in {{\mathbb {R}}^{n}}\) represents the vector with all elements equaling 1. For a matrix \(A\in {{\mathbb {R}}^{m\times {n}}}\), \(a_{ij}\) is the (i, j)-th element. For two matrices A and B with the same size, we denote \(A\succ B\) \((A\succeq B)\) if \(a_{ij}> b_{ij}\) \((a_{ij}\ge b_{ij})\). For a matrix \(A=[a_{ij}]\in {{\mathbb {R}}^{m\times {n}}}\), denote \(A^{+}=[a^{+}_{ij}]\) with \(a^{+}_{ij}=\max \left\{ 0,a_{ij}\right\} \ge 0 \) and \(A^{-}=A^{+}-A\). The matrix \(A\in {{\mathbb {R}}^{n\times {n}}}\) is said to be Metzler provided that all its entries outside the main diagonal are nonnegative. For two sets X and Y, \(X\times Y\) represents the Cartesian product of these two sets. \(\lambda (A)\), \(\textrm{Re}(\lambda (A))\) denote, respectively, the eigenvalues and the set comprising the real parts of the eigenvalues of matrix A. The 2-norm for a matrix \(A\in {{\mathbb {R}}^{m\times {n}}}\) will be represented by \(\Vert A\Vert _2\). \(P>0\) implies that \(P\in {\mathbb {R}}^{n\times n}\) is positive definite. For a vector \(g\in {\mathbb {R}}^{n}\), the 1-norm, 2-norm, and \(\infty \)-norm are formally defined as \(\Vert g\Vert _{1} = \sum \nolimits _{i=1}^n|g_i|\), \(\Vert g\Vert _{2} =\sqrt{\sum \nolimits _{i=1}^n{g_i}^{2}}\) and \(\Vert g\Vert _{\infty }=\max _{1\le i\le n} |g_i|\), respectively. The \(L_{\infty }\)-norm of a vector-valued function g(t) is defined as \(\Vert g\Vert _{L_{\infty }}=ess \sup _{t\ge 0} \Vert g(t)\Vert _{\infty }\). The space \({\mathcal {L}}_{\infty }\) is defined as \({\mathcal {L}}_{\infty }=\left\{ g:\Vert g\Vert _{L_{\infty }}<\infty \right\} \).

2.2 Positive System Theory

In this subsection, we first present several important results with respect to positive linear systems that will be utilized in this work. Considering the subsequent positive linear system:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x}(t)=Ax(t)+Bu(t),\\&y(t)=Cx(t)+Du(t), \\&x(0)=x_0, \end{aligned} \right. \end{aligned}$$
(1)

in which \(x(t)\in {\mathbb {R}}^{n}\), \(u(t)\in {\mathbb {R}}^m\) and \(y(t)\in {\mathbb {R}}^p\) denote, respectively, the state vector, the input vector and the output vector of the dynamic system; \(x_0\in {\mathbb {R}}^{n}\) represents the initial condition.

Definition 1

[7] System (1) is said to be positive provided that for every \(u(t)\succeq 0\) and \(x_0\succeq 0\), we get that \(x(t)\succeq 0\) and \(y(t)\succeq 0\).

Lemma 1

[7] System (1) is a positive system provided that matrices \(A\in {{\mathbb {R}}^{n\times {n}}}\) is Metzler, \(B\in {{\mathbb {R}}^{n\times {m}}_{+}}\), \(C\in {{\mathbb {R}}^{p\times {n}}_{+}}\) and \(D\in {{\mathbb {R}}^{p\times {m}}_{+}}\).

2.3 Problem Statement

Consider the subsequent saturated system with disturbances:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x}(t)=Ax(t)+B\textrm{sat}(u(t))+d(t),\\&y(t)=Cx(t)+v(t), \\&x(0)=x_0, \end{aligned} \right. \end{aligned}$$
(2)

in which \(x(t)\in {\mathbb {R}}^{n}\), \(u(t)\in {\mathbb {R}}^m\), \(d(t)\in {\mathbb {R}}^n\), \(v(t)\in {\mathbb {R}}^p\) and \(y(t)\in {\mathbb {R}}^p\) are, respectively, the state vector, the input vector, the external disturbance, the measurement noise and the output vector of the dynamic system; \(x_0\in {\mathbb {R}}^{n}\) is the initial condition. The function \(\textrm{sat}\) \(:{\mathbb {R}}^{m}\rightarrow {\mathbb {R}}^{m}\) denotes a vector-valued standard saturation function, which is defined as follows:

$$\begin{aligned} \textrm{sat}(u) = [\textrm{sat}(u_1),\textrm{sat}(u_2),\dots ,\textrm{sat}(u_m) ]^T, \end{aligned}$$

and for every \(i=\widehat{1,m}\), the individual components of \(\textrm{sat}(u_i)\) are defined as:

$$\begin{aligned} \begin{aligned} \textrm{sat}(u_i)= \left\{ \begin{array}{ll} 1, &{} \quad u_i\ge 1,\\ u_i, &{} \quad -1<u_i<1,\\ -1, &{} \quad u_i\le -1. \end{array} \right. \end{aligned} \end{aligned}$$
(3)

Furthermore, we also need the subsequent assumptions.

Assumption 1

Let \(x_0\in \left[ \underline{x}_0,{\bar{x}}_0\right] \) for two given \({\bar{x}}_0, \underline{x}_0\in {\mathbb {R}}^{n}\), let also four known Lipschitz functions \(\bar{d}(t)\), \(\underline{d}(t)\), \(\bar{v}(t)\) and \(\underline{v}(t)\) be given as follows:

$$\begin{aligned} \underline{d}(t)\preceq d(t)\preceq \bar{d}(t), \quad \underline{v}(t)\preceq v(t)\preceq \bar{v}(t), \quad \forall t\ge 0. \end{aligned}$$
(4)

Moreover, \(\max \left\{ \Vert \bar{d}(t)\Vert _2,\Vert \underline{d}(t)\Vert _2 \right\} \le {d}^{*}\) with \({d}^{*}>0\) be a scalar and \(\max \left\{ \Vert \bar{v}(t)\Vert _2,\Vert \underline{v}(t)\Vert _2 \right\} \le {v}^{*}\) with \({v}^{*}>0\) be a constant for all \(t\ge 0\).

Assumption 2

(A, B) is asymptotically null controllable with bounded control, that is, (A, B) is stabilizable, and the eigenvalues of A are situated within the closed left-half of the complex s-plane.

Remark 1

The above assumption is a necessary condition for the low-gain feedback method. One can refer to [14] for details. If we insist on using a low-gain linear feedback control algorithm for a saturated system, then the best control objective it can reach is semi-global stabilization. In simpler terms, within any arbitrarily defined large bounded region, it is feasible to identify a low-gain linear feedback configuration that ensures the convergence of all states whose initial values lie within this designated region towards the system’s equilibrium point.

Assumption 3

(A, C) is detectable.

Next, several useful lemmas that will be adopted in interval observers design and controller design in Sect. 3 are established.

Lemma 2

[5] Given a matrix \(A\in {{\mathbb {R}}^{m\times {n}}}\), and a vector \(g\in {{\mathbb {R}}^{n}}\) that satisfies \(\underline{g} \preceq g \preceq {\bar{g}}\), where \(\underline{g},{\bar{g}} \in {{\mathbb {R}}^{n}}\) are two known vectors, then the following relation holds:

$$\begin{aligned} A^{+}\underline{g}-A^{-}\bar{g} \preceq Ag \preceq A^{+}\bar{g}-A^{-}\underline{g} . \ \end{aligned}$$
(5)

Lemma 3

[14, 34] Suppose that (A, B) is controllable, and there is a scalar \(\epsilon >0\) such that

$$\begin{aligned} \ \epsilon >-2\min \left\{ \textrm{Re}(\lambda (A))\right\} , \ \end{aligned}$$
(6)

then, we can solve the subsequent Lyapunov matrix equation:

$$\begin{aligned} W(\epsilon )(A+\tfrac{\epsilon }{2}I)^T + (A+\tfrac{\epsilon }{2}I)W(\epsilon ) = BR^{-1}B^T, \end{aligned}$$
(7)

where \(R\succ 0\), and \(W(\epsilon )\) is analytically given by

$$\begin{aligned} W(\epsilon ) = \int _{0}^{\infty } e^{-(A+\tfrac{\epsilon }{2}I)t}BR^{-1}B^Te^{-(A+\tfrac{\epsilon }{2}I)^Tt} \, dt. \end{aligned}$$
(8)

Next, calculating the \(P(\epsilon )\) defined as

$$\begin{aligned} P(\epsilon ) = W^{-1}(\epsilon ), \end{aligned}$$
(9)

in which \(P(\epsilon )>0\) denotes the solution to the subsequent PARE:

$$\begin{aligned} A^{T}P(\epsilon )+P(\epsilon )A-P(\epsilon )BR^{-1}B^TP(\epsilon )+\epsilon P(\epsilon )=0 .\ \end{aligned}$$
(10)

Lemma 4

[34] Let the pair (A, B) be controllable, and assume that the eigenvalues of matrix A lie on the imaginary axis. If there is an \(\epsilon >0\) such that \(P(\epsilon )>0\) satisfies the PARE given in (10), then we have

$$\begin{aligned} \lim _{\epsilon \rightarrow 0^+} P(\epsilon ) = 0. \end{aligned}$$
(11)

There are two problems addressed in this work. The first one involves constructing an interval observer for the system described in (2), which includes input saturation and disturbances. The second problem revolves around constructing a controller based on the adopted interval observer to ensure the semi-global boundedness of such a system. Therefore, the central focus of this work is on designing an interval observer for (2). The primary objective that follows is the design of \({\bar{x}}(t)\) and \(\underline{x}(t)\) such that the subsequent conditions are satisfied:

$$\begin{aligned}&\underline{x}(t) \preceq x(t) \preceq {\bar{x}}(t),\quad \forall t\ge 0, \end{aligned}$$
(12)
$$\begin{aligned}&{\bar{x}},\underline{x} \in {\mathcal {L}}^{n}_{\infty }. \end{aligned}$$
(13)

3 Main Result

Next, we will first construct an interval observer for system (2) and then leverage the previously established interval observer to construct the controller using a low-gain feedback technique.

3.1 Interval Observer Design

This section is dedicated to the development of interval observer design techniques for (2). The cooperative error method [6], based on positive systems theory, is the predominant approach for interval observer design. The fundamental idea of this method is to construct an interval observer to ensure the nonnegativity and stability of the error system.

Firstly, we need to transform the system coordinates with input saturation and disturbances as follows. In the new coordinates \(z=P^{-1}x\), where P is a non-singular transformation matrix, then system (2) has the subsequent form:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{z}=\tilde{A}z+\tilde{B}\textrm{sat}(u)+P^{-1}d,\\&y=\tilde{C}z+v, \\&z(0)=P^{-1}x_0, \\ \end{aligned} \right. \end{aligned}$$
(14)

in which \(\tilde{A}=P^{-1}AP\), \(\tilde{B}=P^{-1}B\), \(\tilde{C}=CP\).

By utilizing the output information of the system, equation (14) can be rewritten as follows:

$$\begin{aligned} \dot{z}&=(\tilde{A}-L\tilde{C})z+\tilde{B}\textrm{sat}(u)+Ly+w, \ \end{aligned}$$
(15)

where \(w=-Lv+P^{-1}d\), \(L\in {\mathbb {R}}^{n\times {p}}\) denotes the observer gain matrix. According to Assumption 1 and Lemma 2, we obtain

$$\begin{aligned}&L^{+}\underline{v}-L^{-}\bar{v} \preceq Lv \preceq L^{+}\bar{v}-L^{-}\underline{v},\nonumber \\&(P^{-1})^{+}\underline{d}-(P^{-1})^{-}\bar{d} \preceq P^{-1}d \preceq (P^{-1})^{+}\bar{d}-(P^{-1})^{-}\underline{d}. \end{aligned}$$
(16)

Then the interval observer can be defined as

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\bar{z}}=(\tilde{A}-L\tilde{C})\bar{z}+\tilde{B}\textrm{sat}(u)+Ly+\bar{w},\\&\dot{\underline{z}}=(\tilde{A}-L\tilde{C})\underline{z}+\tilde{B}\textrm{sat}(u)+Ly+\underline{w},\\&\bar{z}(0)=(P^{-1})^{+}\underline{x}_0-(P^{-1})^{-}\bar{x}_0,\\&\underline{z}(0)=(P^{-1})^{+}\bar{x}_0-(P^{-1})^{-}\underline{x}_0, \\ \end{aligned} \right. \end{aligned}$$
(17)

where \(\bar{w}=L^{-}\bar{v}-L^{+}\underline{v}+(P^{-1})^{+}\bar{d}-(P^{-1})^{-}\underline{d},\) and \(\underline{w}=L^{-}\underline{v}-L^{+}\bar{v}+(P^{-1})^{+}\underline{d}-(P^{-1})^{-}\bar{d}.\)

Based on the upper and lower bound information \(\bar{z}\) and \(\underline{z}\) given in (17), define

$$\begin{aligned} \left\{ \begin{aligned}&\bar{x}=P^{+}\bar{z}-P^{-}\underline{z},\\&\underline{x}=P^{+}\underline{z}-P^{-}\bar{z}. \end{aligned} \right. \end{aligned}$$
(18)

Definition 2

The observer constructed in (17) is said to be an interval observer for (15) if \(\underline{z}(t) \preceq z(t) \preceq {\bar{z}}(t)\) and \( {\bar{z}},\underline{z} \in {\mathcal {L}}^{n}_{\infty }\) hold.

Interval observation error dynamics of \({\bar{e}}={\bar{z}}-z\) and \(\underline{e}=z-\underline{z}\) are given by

$$\begin{aligned} \left\{ \begin{aligned} \dot{\bar{e}}=(\tilde{A}-L\tilde{C})\bar{e}+\bar{w}-w,\\ \dot{\underline{e}}=(\tilde{A}-L\tilde{C})\underline{e}+w-\underline{w}.\\ \end{aligned} \right. \end{aligned}$$
(19)

Denote \(e=\left[ \bar{e}^T, \underline{e}^T\right] ^T\), \(\Phi =\left[ \begin{array}{ccccc} \tilde{A}-L\tilde{C}&{} 0 \\ 0&{} \tilde{A}-L\tilde{C} \end{array} \right] \) and \(\delta =\left[ \bar{\delta }^T, \underline{\delta }^T\right] ^T=\left[ \begin{array}{ccccc} \bar{w}-w \\ w-\underline{w} \end{array} \right] \), then the error system (19) is represented by

$$\begin{aligned} \dot{e}=\Phi e+\delta , \end{aligned}$$
(20)

where e denotes the state variable of the error system (20), and the initial state \(e(0)\succeq 0\). By Lemmas 1 and 2, if \(\tilde{A}-L\tilde{C}\) is a Metzler matrix, then it is straightforward to verify that the inequality \(\underline{z}(t) \preceq z(t) \preceq {\bar{z}}(t)\) holds, which further implies that condition (12) is satisfied. The subsequent lemma presents a methodology for interval observer design.

Lemma 5

[9] Suppose that Assumptions 1, 3 are met, and the matrix \(\tilde{A}-L\tilde{C}\) is both Metzler and Hurwitz, then the observer constructed in equation (17) serves as an interval observer for (14).

3.2 Controller Design

This section mainly deals with the second problem, that is, how to construct a controller based on the interval observer, which can ensure the semi-global boundedness of system (2).

Firstly, let \(\tilde{d}=P^{-1}d\), then we use two sub-states \(z_1\) and \(z_2\) to represent the coordinate transformed system (14) in the subsequent form:

$$\begin{aligned} \left\{ \begin{aligned} \left[ \begin{array}{cc} \dot{z}_1 \\ \dot{z}_2 \\ \end{array}\right]&=\tilde{A}\left[ \begin{array}{cc} z_1 \\ z_2 \\ \end{array} \right] +\tilde{B} \textrm{sat}(u) +\left[ \begin{array}{cc} \tilde{d_1} \\ \tilde{d_2} \\ \end{array} \right] ,\\ y&=\tilde{C}\left[ \begin{array}{cc} z_1 \\ z_2 \\ \end{array} \right] +v, \\ \end{aligned} \right. \end{aligned}$$
(21)

where

$$\begin{aligned} \tilde{A}=\left[ \begin{array}{cc} A_0 &{} 0 \\ 0 &{} A_{-} \\ \end{array} \right] ,\quad \tilde{B}=\left[ \begin{array}{cc} B_{0} \\ B_{-} \\ \end{array} \right] ,\quad \tilde{C}=\left[ \begin{array}{cc} C_0 \quad C_- \\ \end{array} \right] . \end{aligned}$$

\(A_0\in {\mathbb {R}}^{n_{z_1}\times {n_{z_1}}}\) comprises the eigenvalues of \(\tilde{A}\) situated along the imaginary axis, \(A_{-}\in {\mathbb {R}}^{n_{z_2}\times {n_{z_2}}}\) encompasses the eigenvalues of \(\tilde{A}\) with negative real parts, \((A_0, B_0)\) is controllable, and \(n_{z_1}+n_{z_2}=n\).

Secondly, we can divide it into two sub-systems, which can be represented as follows:

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}_1&=A_0z_1+B_0\textrm{sat}(u)+\tilde{d_1},\\ \dot{z}_2&=A_{-}z_2+B_-\textrm{sat}(u)+\tilde{d_2},\\ y&=C_0z_1+C_-z_2+v .\\ \end{aligned} \right. \end{aligned}$$
(22)

The error system (20) is obtained from the interval observer design in Sect. 4. We represent L as

$$\begin{aligned} L=\left[ \begin{array}{cc} L_1 \\ L_2 \\ \end{array} \right] . \end{aligned}$$

Let \(\bar{e}_{z_1}=\bar{z}_1-z_1\), \(\bar{e}_{z_2}=\bar{z}_2-z_2\), \(\underline{e}_{z_1}=z_1-\underline{z}_1\) and \(\underline{e}_{z_2}=z_2-\underline{z}_2\), then, similarly, the error system (19) is divided as

$$\begin{aligned} \left\{ \begin{aligned} \dot{\bar{e}}_{z_1}&=(A_0-L_1C_0)\bar{e}_{z_1}-L_1C_-\bar{e}_{z_2}+\bar{\delta _1},\\ \dot{\bar{e}}_{z_2}&=(A_{-}-L_2C_-)\bar{e}_{z_2}-L_2C_0\bar{e}_{z_1}+\bar{\delta _2},\\ \dot{\underline{e}}_{z_1}&=(A_0-L_1C_0)\underline{e}_{z_1}-L_1C_-\underline{e}_{z_2}+\underline{\delta }_1,\\ \dot{\underline{e}}_{z_2}&=(A_{-}-L_2C_-)\underline{e}_{z_2}-L_2C_0\underline{e}_{z_1}+\underline{\delta }_2, \end{aligned} \right. \end{aligned}$$
(23)

where \(n_{\bar{\delta }_1}+n_{\bar{\delta }_2}=n\), and \(n_{\underline{\delta }_1}+n_{\underline{\delta }_2}=n\).

The algorithm for low-gain design based on the PARE for system (22) is executed through a three-step process.

  1. Step 1

    Construct the low-gain feedback control law:

    $$\begin{aligned} \ u=\bar{F}(\epsilon )\bar{z}_1+\underline{F}(\epsilon )\underline{z}_1,\ \end{aligned}$$
    (24)

    where \(\bar{F}(\epsilon )=-R^{-1}{B_0}^TP(\epsilon )\bar{K}\), \(\underline{F}(\epsilon )=-R^{-1}{B_0}^TP(\epsilon )\underline{K}\) are controller gains, and the matrices \(\bar{K},\underline{K}\in {\mathbb {R}}^{n_{z_1}\times {n_{z_1}}}\) are the tuning weight of the upper and lower bound estimation.

  2. Step 2

    Choose \(\bar{K}+\underline{K}=I\), and \(P(\epsilon )\) denotes the solution of the subsequent PARE:

    $$\begin{aligned} {A}_0^{T}P(\epsilon )+P(\epsilon ){A}_0-P(\epsilon )B_0R^{-1}{B_0}^TP(\epsilon )+\epsilon P(\epsilon )=0. \ \end{aligned}$$
    (25)

    According to Lemma 4, we have

    $$\begin{aligned} \lim _{\epsilon \rightarrow 0^{+}}P(\epsilon )=0. \end{aligned}$$
    (26)
  3. Step 3

    Substitute the control (24) into the sub-systems (22) which need to be controlled:

    $$\begin{aligned} \left\{ \begin{aligned} \dot{z}_1&=A_0z_1+B_0\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon )(\bar{K}\bar{z}_1+\underline{K} \underline{z}_1))+\tilde{d_1},\\ \dot{z}_2&=A_-z_2+B_-\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon )(\bar{K}\bar{z}_1+\underline{K} \underline{z}_1))+\tilde{d_2},\\ y&=C_0z_1+C_-z_2+v .\\ \end{aligned} \right. \end{aligned}$$
    (27)

    Then the closed-loop system constituted by \(z_1\), \(z_2\), \(\bar{e}_{z_1}\), \(\underline{e}_{z_1}\), \(\bar{e}_{z_2}\) and \(\underline{e}_{z_2}\) is

    $$\begin{aligned} \left\{ \begin{aligned} \dot{z}_1&=A_{0}z_1+B_0\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon )z_1-R^{-1}{B_0}^TP(\epsilon )\bar{K}\bar{e}_{z_1}\\&\quad +R^{-1}{B_0}^TP(\epsilon )\underline{K}\underline{e}_{z_1})+\tilde{d_1},\\ \dot{z}_2&=A_{-}z_2+B_-\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon )z_1-R^{-1}{B_0}^TP(\epsilon )\bar{K}\bar{e}_{z_1}\\&\quad +R^{-1}{B_0}^TP(\epsilon )\underline{K}\underline{e}_{z_1})+\tilde{d_2},\\ \dot{\bar{e}}_{z_1}&=(A_0-L_1C_0)\bar{e}_{z_1}-L_1C_-\bar{e}_{z_2}+\bar{\delta _1},\\ \dot{\bar{e}}_{z_2}&=(A_{-}-L_2C_-)\bar{e}_{z_2}-L_2C_0\bar{e}_{z_1}+\bar{\delta _2},\\ \dot{\underline{e}}_{z_1}&=(A_0-L_1C_0)\underline{e}_{z_1}-L_1C_-\underline{e}_{z_2}+\underline{\delta }_1,\\ \dot{\underline{e}}_{z_2}&=(A_{-}-L_2C_-)\underline{e}_{z_2}-L_2C_0\underline{e}_{z_1}+\underline{\delta }_2.\\ \end{aligned} \right. \end{aligned}$$
    (28)

    Let \(e=[{\bar{e}}^T_{z_1}, {\bar{e}}^T_{z_2}, {\underline{e}}^T_{z_1}, {\underline{e}}^T_{z_2}]^T\), then the above equation is converted as

    $$\begin{aligned} \left\{ \begin{aligned} \dot{{z}}_1&={A}_0{z}_1+B_0\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e)+\tilde{d_1} ,\\ \dot{z}_2&=A_{-}z_2+B_-\textrm{sat}(-R^{-1}{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e)+\tilde{d_2} ,\\ \dot{e}&=\Phi e+\delta .\\ \end{aligned} \right. \end{aligned}$$
    (29)

Remark 2

In existing works, there are three main approaches to designing low-gain feedback, namely the eigenstructure assignment method, the PARE-based low-gain feedback control method [11], and the PLE-based low-gain feedback control method [34]. It is noteworthy that the PARE-based low-gain feedback control method utilized in this paper is functionally equivalent to the PLE-based low-gain feedback control method. This method combines the merits of the first two methods. Furthermore, using the PLE-based low-gain feedback control method, the gain matrix \(P(\epsilon )\) can be expressed with the \(\epsilon \) without having to resolve the Lyapunov equation each time for a different low-gain parameter \(\epsilon \). This characteristic significantly reduces the computational complexity associated with the PLE-based low-gain feedback control method.

Remark 3

In this paper, a low-gain feedback control method based on the PLE is used, which can reduce the computational complexity but assumes conservative preconditions, i.e., the eigenvalues of the system matrix are required to lie on the imaginary axis. Future research can consider the use of nested saturation functions, convex packet analysis, and other methods to deal with saturated nonlinearities for a more comprehensive study of input-constrained systems, which is a problem of significant research value.

Lemma 6

For matrices \(S\in {\mathbb {R}}^{n_{z_1}\times n_{z_1}}\), \(H\in {\mathbb {R}}^{n_{z_1}\times 2n}\) and positive vectors \(p\in {\mathbb {R}}^{2n}_{+}\), \(q\in {\mathbb {R}}^{1\times 2n}_{+}\), \(e\in \left\{ e\in {\mathbb {R}}^{2n}_{+}:\lambda _{\max }^{\frac{1}{2}}(P(\epsilon )) {p}^Te\le 1\right\} \), where \(P(\epsilon )\) satisfies (26), then there is an \(\epsilon ^{*}>0\) such that, for any \(\epsilon \in \left( 0,\epsilon ^{*}\right] \), the subsequent inequality holds:

$$\begin{aligned} \left( He\right) ^TP(\epsilon )SP(\epsilon )He \le \dfrac{1}{8}\lambda _{\max }^{\frac{1}{2}}(P(\epsilon )) qe. \end{aligned}$$
(30)

Proof

Since \(\min _{i} p_i \Vert e\Vert _{1}= \min _{i} p_i{{\textbf {1}}}^T_{2n}e \le {p}^Te\le \frac{1}{\lambda _{\max }^{\frac{1}{2}}(P(\epsilon ))}\), we have that \(\Vert e\Vert _{1}\le \frac{1}{\min _{i} p_i} \frac{1}{\lambda _{\max }^{\frac{1}{2}}(P(\epsilon ))}\). Then there is a scalar \(c_1>0\) such that \(\Vert e\Vert _{2}\le \frac{c_1}{\lambda _{\max }^{\frac{1}{2}}(P(\epsilon ))}\). Moreover, it is obvious that \(\Vert e\Vert _{2}\le c_2qe\), where \(c_2\) is a positive constant. Therefore, we can derive that \(\Vert e\Vert _{2}^{2}\le \frac{c_1c_2}{\lambda _{\max }^{\frac{1}{2}}(P(\epsilon ))}qe\).

Since \(P(\epsilon )>0\), there exists an orthogonal matrix \(U(\epsilon )\) such that \(P(\epsilon )=U^T(\epsilon )\Lambda (\epsilon ) U(\epsilon )\), where \(\Vert U(\epsilon )\Vert _2=1\) and \(\Lambda (\epsilon )\) is a diagonal matrix whose diagonal elements denote the eigenvalues of \(P(\epsilon )\).

Let \(l(\epsilon )=U(\epsilon )He\), we have

$$\begin{aligned} \begin{aligned} \left( He\right) ^TP(\epsilon )SP(\epsilon )He&= e^TH^TU^T(\epsilon )\Lambda (\epsilon ) U(\epsilon )SU^T(\epsilon )\Lambda (\epsilon ) U(\epsilon )He \\&= l^T(\epsilon )\Lambda (\epsilon ) U(\epsilon )SU^T(\epsilon )\Lambda (\epsilon ) l(\epsilon ) \\&\le \Vert \Lambda (\epsilon )l(\epsilon )\Vert _{2} \Vert U(\epsilon )SU^T(\epsilon )\Lambda (\epsilon )l(\epsilon )\Vert _{2} \\&\le \Vert \Lambda (\epsilon )\Vert _{2}^2 \Vert U(\epsilon )SU^T(\epsilon )\Vert _{2} \Vert l(\epsilon )\Vert _{2}^2 \\&\le \lambda _{\max }^{2}(P(\epsilon ))\Vert S\Vert _{2} \Vert H\Vert _{2}^2\Vert e\Vert _{2}^2 \\&\le \lambda _{\max }^{\frac{3}{2}}(P(\epsilon ))\Vert S\Vert _{2} \Vert H\Vert _{2}^2c_1c_2qe .\\ \end{aligned} \end{aligned}$$
(31)

According to (26), there exists an \(\epsilon ^{*}>0\), when \(\epsilon \in \left( 0,\epsilon ^{*}\right] \), we get \(\Vert P(\epsilon )\Vert _{2}\le \frac{1}{8c_1c_2\Vert S\Vert _{2} \Vert H\Vert _{2}^2}\). Furthermore, since \(P(\epsilon )>0\), we get that \(\lambda _{\max }(P(\epsilon ))=\Vert P(\epsilon )\Vert _{2}\), then we get

$$\begin{aligned} \lambda _{\max }^{\frac{3}{2}}(P(\epsilon ))\Vert S\Vert _{2} \Vert H\Vert _{2}^2c_1c_2qe&\le \dfrac{1}{8}\lambda _{\max }^{\frac{1}{2}}(P(\epsilon )) qe . \end{aligned}$$
(32)

This completes the proof. \(\square \)

Next, the most important theorem obtained in this paper is introduced.

Theorem 1

Suppose that Assumptions 1–3 are met, and the eigenvalues of \(A_0\) and \(A_-\) are on the imaginary axis and have negative real parts, respectively. Then, under the low-gain feedback control law (24), the system (14) is semi-globally uniformly ultimately bounded. That is, for the initial conditions belonging to a given arbitrarily large bounded region \(X\subset {\mathbb {R}}^{n_{z_1}}\times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}\), there is an \(\epsilon ^{*}>0\) such that, for every \(\epsilon \in \left( 0,\epsilon ^{*}\right] \), the closed-loop system is uniformly ultimately bounded.

Proof

Construct the subsequent Lyapunov function:

$$\begin{aligned} V= & {} V_1+V_2+V_3, \\ V_1= & {} {{z}_1}^TP(\epsilon ){z}_1,\\ V_2= & {} \gamma {z_2}^TQz_2,\\ V_3= & {} \gamma {p}^Te, \end{aligned}$$

where \(\gamma =\lambda _{\max }^{\frac{1}{2}}(P(\epsilon ))\), \(Q>0\) is such that

$$\begin{aligned} {A_{-}}^TQ+QA_{-}=-4I , \end{aligned}$$
(33)

and \(p\in {\mathbb {R}}^{2n}_{+}\) satisfy

$$\begin{aligned} {p}^T\Phi =-q , \end{aligned}$$
(34)

where \(q\in {\mathbb {R}}^{1\times 2n}_{+}\) is a given positive row vector. By [21], since \(\Phi \) is Metzler and Hurwitz, we get that \(-\Phi ^{-1}\ge 0\). Moreover, from the equation (34), we get that \({p}^T=-q\Phi ^{-1}\). Thus, the presence of such a p can be ensured.

Consider the subsequent level set of Lyapunov function V:

$$\begin{aligned} L(V)=\left\{ ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}}\times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}:{{z}_1}^TP(\epsilon ){z}_1+\gamma {z_2}^TQz_2+\gamma {p}^Te\le 1\right\} . \end{aligned}$$

Then, there is an \(\epsilon ^{*}_{1}>0\) such that, for every \(\epsilon \in \left( 0,\epsilon ^{*}_{1}\right] \), we get

$$\begin{aligned} X\subset L(V)\subset {\mathcal {L}}( -2R^{-1}{B_0}^TP(\epsilon ) ) \times \left\{ (z^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}} \times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} , \end{aligned}$$

where \( {\mathcal {L}}( -2R^{-1}{B_0}^TP(\epsilon ) ) = \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^TP(\epsilon ) {z}_1\Vert _{\infty }\le 1\right\} ,\) and \({\mathcal {L}}( -2R^{-1}{B_0}^TP(\epsilon ) )\times \left\{ (z^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} \subset \)

$$\begin{aligned}{} & {} \left\{ ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}} \times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}:\right. \\{} & {} \quad \left. \Vert -R^{-1}{B_0}^TP(\epsilon ) {z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty }\le 1\right\} . \end{aligned}$$

\(\big \lbrace ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}}\times {\mathbb {R}}^{n_{z_2}} \times {\mathbb {R}}^{2n}_{+}:\Vert -R^{-1}{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon ) \left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty }\le 1\big \rbrace \) is a region within the state space in which the actuator does not saturate.

We next explain that such an \(\epsilon ^{*}_{1}= \min \left\{ \epsilon ^{*}_{2},\epsilon ^{*}_{3},\epsilon ^{*}_{4}\right\} \) exists, where \(\epsilon ^{*}_{2}\), \(\epsilon ^{*}_{3}\) and \(\epsilon ^{*}_{4}\) are positive scalars.

Firstly, since X is bounded, there is a scalar \(r>0\) such that

$$\begin{aligned} X \subset B_{r}=\big \lbrace ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}} \times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}:{{z}_1}^T{z}_1 +{{z}_2}^T{z}_2 +{e}^T{e} \le r \big \rbrace . \end{aligned}$$

Moreover, since the inequality \({{z}_1}^T{z}_1 +{{z}_2}^T{z}_2 +{e}^T{e} \le r \) holds for all \(({z}^T_1,{z}^T_2,e^T)^T\in B_{r}\), we have that \({{z}_1}^T{z}_1\le r\), \({{z}_2}^T{z}_2\le r\) and \({e}^T{e} \le r\). Then we have

$$\begin{aligned} \begin{aligned} {{z}_1}^TP(\epsilon ){z}_1+\gamma {z_2}^TQz_2+\gamma {p}^Te&\le \gamma ^{2}\Vert z_1\Vert _2^2+\gamma \lambda _{\max }(Q)\Vert z_2\Vert _2^2+\gamma \Vert p\Vert _2 \Vert e\Vert _2 \\&\le \gamma ^{2}r+\gamma \lambda _{\max }(Q)r+\gamma \Vert p\Vert _2 \sqrt{r} . \end{aligned} \end{aligned}$$

Since \(\gamma \rightarrow 0\) as \(\epsilon \rightarrow 0\), there is an \(\epsilon ^{*}_{2}>0\) such that, for every \(\epsilon \in \left( 0,\epsilon ^{*}_{2}\right] \), we get that \(\gamma ^{2}r+\gamma \lambda _{\max }(Q)r+\gamma \Vert p\Vert _2 \sqrt{r} \le 1\). That is, we have that \({{z}_1}^TP(\epsilon ){z}_1+\gamma {z_2}^TQz_2+\gamma {p}^Te \le 1\), which implies that \(({z}^T_1,{z}^T_2,e^T)^T\in L(V)\). Thus, we obtain

$$\begin{aligned} X \subset B_{r} \subset L(V). \end{aligned}$$

Secondly, since the inequality \( {{z}_1}^TP(\epsilon ){z}_1+\gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \) holds for all \(({z}^T_1,{z}^T_2,e^T)^T\in L(V)\), we have that \({{z}_1}^TP(\epsilon ){z}_1\le 1\) and \(\gamma {z_2}^TQz_2+\gamma {p}^Te\le 1\). Then we get

$$\begin{aligned}{} & {} ({z}^T_1,{z}^T_2,e^T)^T\in \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}: {{z}_1}^TP(\epsilon ){z}_1 \le 1 \right\} \\{} & {} \quad \times \left\{ ({z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} . \end{aligned}$$

Thus, we obtain

$$\begin{aligned}{} & {} L(V) \subset \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}: {{z}_1}^TP(\epsilon ) {z}_1 \le 1 \right\} \\{} & {} \quad \times \left\{ ({z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}} \times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} . \end{aligned}$$

Moreover, since the inequality \({{z}_1}^TP(\epsilon ){z}_1 \le 1 \) holds for all \({z}_1\in \big \lbrace {z}_1\in {\mathbb {R}}^{n_{z_1}}: {{z}_1}^T P(\epsilon ){z}_1 \le 1\big \rbrace \), we have

$$\begin{aligned} \begin{aligned} \Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }&\le \Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{2} \\&\le \Vert -2R^{-1}{B_0}^TP^{1/2}(\epsilon )\Vert _{2} \Vert P^{1/2}(\epsilon ){z}_1\Vert _{2} \\&\le \Vert -2R^{-1}{B_0}^T\Vert _{2} \Vert P^{1/2}(\epsilon )\Vert _{2} . \end{aligned} \end{aligned}$$

Since \(\Vert P^{1/2}(\epsilon )\Vert _{2}\rightarrow {0}\) as \(\epsilon \rightarrow 0\), there is an \(\epsilon ^{*}_{3}>0\) such that, for every \(\epsilon \in \left( 0,\epsilon ^{*}_{3}\right] \), we have that \( \Vert -2R^{-1}{B_0}^T\Vert _{2} \Vert P^{1/2}(\epsilon )\Vert _{2} \le 1\). That is, we have that \(\Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty } \le 1\), which implies that \({z}_1\in \big \lbrace {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^T P(\epsilon ){z}_1\Vert _{\infty }\le 1\big \rbrace \). Then we get

$$\begin{aligned} \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}: {{z}_1}^TP(\epsilon ){z}_1 \le 1\right\} \subset \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }\le 1\right\} . \end{aligned}$$

Therefore, we obtain

$$\begin{aligned}{} & {} L(V) \subset \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }\le 1\right\} \\{} & {} \quad \times \left\{ (z^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}} \times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} . \end{aligned}$$

Thirdly, the inequalities \(\Vert R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }\le \frac{1}{2} \) and \({p}^Te\le \frac{1}{\gamma }\) hold for all

$$\begin{aligned} \begin{aligned}&({z}^T_1,{z}^T_2,e^T)^T\in \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }\le 1\right\} \\&\quad \times \left\{ (z^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} . \end{aligned} \end{aligned}$$

Moreover, since \(\min _{i} p_i \Vert e\Vert _{1}= \min _{i} p_i{{\textbf {1}}}^T_{2n}e \le {p}^Te\), we have that \(\Vert e\Vert _{1}\le \frac{1}{\min _{i} p_i} \frac{1}{\gamma }\). Thus, we get that \(\Vert e\Vert _{2}\le \Vert e\Vert _{1}\le \frac{1}{\min _{i} p_i} \frac{1}{\gamma }\). On the other hand, since \(P(\epsilon )>0\), there is an orthogonal matrix \(U(\epsilon )\) such that \(P(\epsilon )=U^T(\epsilon ) \Lambda (\epsilon ) U(\epsilon )\), where \(\Vert U(\epsilon )\Vert _2=1\) and \(\Lambda (\epsilon )\) denotes a diagonal matrix whose diagonal entries are the eigenvalues of \(P(\epsilon )\). Then we get

$$\begin{aligned} \begin{aligned}&\Vert R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty }\\&\quad \le \Vert R^{-1}{B_0}^TU^T(\epsilon ) \Lambda (\epsilon ) U(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{2} \\&\quad \le \Vert R^{-1}{B_0}^T\Vert _{2} \Vert U^T(\epsilon )\Vert _{2} \Vert \Lambda (\epsilon )\Vert _{2} \Vert U(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] U^T(\epsilon )\Vert _{2} \Vert U(\epsilon )e\Vert _{2} \\&\quad = \Vert R^{-1}{B_0}^T\Vert _{2} \Vert \left[ \bar{K}, 0, -\underline{K}, 0 \right] \Vert _{2} \Vert \Lambda (\epsilon )\Vert _{2} \Vert e\Vert _{2} \\&\quad \le \dfrac{1}{\min _{i} p_i}\Vert R^{-1}{B_0}^T\Vert _{2} \Vert \left[ \bar{K}, 0, -\underline{K}, 0 \right] \Vert _{2} \gamma . \end{aligned} \end{aligned}$$

Since \(\gamma \rightarrow 0\) as \(\epsilon \rightarrow 0\), there is an \(\epsilon ^{*}_{4}>0\) such that, for every \(\epsilon \in \left( 0,\epsilon ^{*}_{4}\right] \), we get that

$$\begin{aligned} \dfrac{1}{\min _{i} p_i}\Vert R^{-1}{B_0}^T\Vert _{2} \Vert \left[ \bar{K}, 0, -\underline{K}, 0 \right] \Vert _{2} \gamma \le \dfrac{1}{2}. \end{aligned}$$

That is, we have that \(\Vert R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty } \le \frac{1}{2}\). Then we have

$$\begin{aligned} \begin{aligned} \Vert -R^{-1}&{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty } \\&\le \Vert R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }+ \Vert R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty } \\&\le \frac{1}{2}+\frac{1}{2}\\&=1, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned}&({z}^T_1,{z}^T_2,e^T)^T\in \left\{ ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}}\times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}: \right. \\&\quad \left. \Vert -R^{-1}{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty }\le 1\right\} . \end{aligned} \end{aligned}$$

Hence, we obtain

$$\begin{aligned}{} & {} \left\{ {z}_1\in {\mathbb {R}}^{n_{z_1}}:\Vert -2R^{-1}{B_0}^TP(\epsilon ){z}_1\Vert _{\infty }\le 1\right\} \\{} & {} \quad \times \left\{ (z^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}: \gamma {z_2}^TQz_2+\gamma {p}^Te\le 1 \right\} \subset \\{} & {} \left\{ ({z}^T_1,{z}^T_2,e^T)^T\in {\mathbb {R}}^{n_{z_1}} \times {\mathbb {R}}^{n_{z_2}}\times {\mathbb {R}}^{2n}_{+}:\right. \\{} & {} \quad \left. \Vert -R^{-1}{B_0}^TP(\epsilon ){z}_1-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e\Vert _{\infty }\le 1\right\} . \end{aligned}$$

Therefore, we now consider any \(\epsilon \in \left( 0,\epsilon ^{*}_{1}\right] \). For any \(({z}^T_1,{z}^T_2,e^T)^T\in L(V)\), the actuator does not saturate and equation (29) can be simplified by

$$\begin{aligned} \left\{ \begin{aligned} \dot{{z}}_1&=({A}_0-B_0R^{-1}{B_0}^TP(\epsilon )){z}_1-B_0R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e+\tilde{d_1},\\ \dot{z}_2&=A_{-}z_2-B_-R^{-1}{B_0}^TP(\epsilon ){z}_1-B_-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e+\tilde{d_2} ,\\ \dot{e}&=\Phi e+\delta .\\ \end{aligned} \right. \end{aligned}$$
(35)

Taking the derivative of \(V_1\) according to (35) and utilizing the PARE (25), we have

$$\begin{aligned} \begin{aligned} \ \dot{V}_1&=-\epsilon {{z}_1}^TP(\epsilon ){z}_1-{{z}_1}^TP(\epsilon )B_0R^{-1}{B_0}^TP(\epsilon ){z}_1\\&\quad +2{{z}_1}^TP(\epsilon )B_0R^{-1}{B_0}^TP(\epsilon )\left[ -\bar{K}, 0, \underline{K}, 0 \right] e +2{{z}_1}^TP(\epsilon )\tilde{d}_1, \end{aligned} \end{aligned}$$

and according to (35), the derivative of \(V_2\) is

$$\begin{aligned} \begin{aligned} \ \dot{V}_2&=-4\gamma {z_2}^Tz_2-2\gamma {z_2}^TQB_-R^{-1}{B_0}^TP(\epsilon ){z}_1\\&\quad -2\gamma {z_2}^TQB_-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e +2\gamma {{z}_2}^TQ\tilde{d}_2. \end{aligned} \end{aligned}$$

Similarly, the derivative of \(V_3\) with reference to equation (35) is given by

$$\begin{aligned} \ \dot{V}_3&=-\gamma qe+\gamma {{p}^T} \delta . \end{aligned}$$

Therefore, we can get

$$\begin{aligned} \begin{aligned} \ \dot{V}&=\dot{V}_1+\dot{V}_2+\dot{V}_3 \\&=-\epsilon {{z}_1}^TP(\epsilon ){z}_1-{{z}_1}^TP(\epsilon )B_0R^{-1}{B_0}^TP(\epsilon ){z}_1\\&\quad +2{{z}_1}^TP(\epsilon )B_0R^{-1}{B_0}^TP(\epsilon )\left[ -\bar{K}, 0, \underline{K}, 0 \right] e \\&\quad -4\gamma {z_2}^Tz_2-2\gamma {z_2}^TQB_-R^{-1}{B_0}^TP(\epsilon ){z}_1\\&\quad -2\gamma {z_2}^TQB_-R^{-1}{B_0}^TP(\epsilon )\left[ \bar{K}, 0, -\underline{K}, 0 \right] e \\&\quad -\gamma qe +2{{z}_1}^TP(\epsilon )\tilde{d}_1+2\gamma {{z}_2}^TQ\tilde{d}_2 +\gamma {p}^T \delta .\\ \end{aligned} \end{aligned}$$
(36)

By completing the square, we have

$$\begin{aligned} \begin{aligned} \ \dot{V}&\le -\epsilon {{z}_1}^T P(\epsilon ) {z}_1 -\gamma {z_2}^Tz_2+2\left( \left[ -\bar{K}, 0, \underline{K}, 0 \right] e\right) ^T \\&\quad \times P(\epsilon )B_0R^{-1}{B_0}^T(B_0R^{-1}{B_0}^T)^{-1}B_0R^{-1}{B_0}^TP(\epsilon ) \left[ -\bar{K}, 0, \underline{K}, 0 \right] e \\&\quad +\gamma \left( \left[ \bar{K}, 0, -\underline{K}, 0 \right] e\right) ^TP(\epsilon )B_0R^{-1}{B_-}^TQQB_-R^{-1}{B_0}^TP(\epsilon ) \left[ \bar{K}, 0, -\underline{K}, 0 \right] e \\&\quad -\gamma qe +\chi , \end{aligned} \end{aligned}$$
(37)

where \(\chi =4{\tilde{d}_1}^T(B_0R^{-1}{B_0}^T)^{-1}\tilde{d}_1 +\gamma {\tilde{d}_2}^TQQ\tilde{d}_2+\gamma {p}^T \delta \).

The term \(\chi \) given in (37) is bounded by

$$\begin{aligned} \chi \le 4\lambda _{\max }((B_0R^{-1}{B_0}^T)^{-1})\Vert \tilde{d}_1\Vert _{2}^{2} +\gamma \lambda _{\max }(QQ)\Vert \tilde{d}_2\Vert _{2}^{2}+\gamma \Vert p\Vert _{2} \Vert \delta \Vert _{2}. \end{aligned}$$

Under the premise that \(\max \left\{ \Vert \bar{d}(t)\Vert _2,\Vert \underline{d}(t)\Vert _2 \right\} \le {d}^{*}\) and \(\max \left\{ \Vert \bar{v}(t)\Vert _2,\Vert \underline{v}(t)\Vert _2 \right\} \le {v}^{*}\), then we can obtain that \(\Vert d(t)\Vert _2\le d^{*}\) and \(\Vert v(t)\Vert _2\le v^{*}\). Thus, we get that \(\Vert \tilde{d}_1(t)\Vert _{2} \le \tilde{d}_1^{*}\) and \(\Vert \tilde{d}_2(t)\Vert _{2} \le \tilde{d}_2^{*}\) with \(\tilde{d}_1^{*}>0\) and \(\tilde{d}_2^{*}>0\) be two constants. Moreover, it is clear that \(\Vert \delta (t)\Vert _{2} \le \delta ^{*}\) with \(\delta ^{*}>0\) be a constant.

Therefore, by Lemma 6, it is evident that there is an \(\epsilon ^{*}\in \left( 0,\epsilon ^{*}_{1}\right] \) such that, for any \(\epsilon \in \left( 0,\epsilon ^{*}\right] \),

$$\begin{aligned} \begin{aligned} \dot{V}&\le -\epsilon {{z}_1}^TP(\epsilon ){z}_1-\gamma {z_2}^Tz_2-\dfrac{3}{8}\gamma qe +\omega \\&\le -\varsigma V +\omega \\&=-\varsigma \left( V-\dfrac{\omega }{\varsigma } \right) , \end{aligned} \end{aligned}$$
(38)

where \(\varsigma =\min \left\{ \frac{3\max _{i} q_i}{8\min _{i} p_i}, \frac{1}{\lambda _{\max }(Q)}, \epsilon \right\} \), \(\omega =4\lambda _{\max }((B_0R^{-1}{B_0}^T)^{-1})\tilde{d}_1^{*2} +\gamma \lambda _{\max }(QQ) \tilde{d}_2^{*2}+\gamma \Vert p\Vert _{2} \delta ^{*}\).

Hence, by equation (38), we obtain that for all \(({z}^T_1,{z}^T_2,e^T)^T\in \bigg \lbrace ({z}^T_1,{z}^T_2,e^T)^T: \frac{\omega }{\varsigma }\le V\le 1\bigg \rbrace \), there holds \(\dot{V}\le 0\), in which the equality sign is satisfied if and only if \(V=\frac{\omega }{\varsigma }\). By the comparison lemma in [12], we get that \(V\le (V(0)-\frac{\omega }{\varsigma }) e^{-\varsigma t}+\frac{\omega }{\varsigma }\). Thus, for all \(({z}^T_1,{z}^T_2,e^T)^T\in \left\{ ({z}^T_1,{z}^T_2,e^T)^T:\frac{\omega }{\varsigma }\le V\le 1\right\} \), \(({z}^T_1,{z}^T_2,e^T)^T\) will approach \(V=\frac{\omega }{\varsigma }\) as the time approaches infinity. This implies that, for every \(\epsilon \in \left( 0,\epsilon ^{*}\right] \), the whole system is semi-globally uniformly ultimately bounded.

This completes the proof. \(\square \)

4 Numerical Simulation

In this section, numerical simulations are presented to demonstrate the ascendancy of the adopted approaches. The first example is that the eigenvalues of A are on the imaginary axis. The second is that the eigenvalues of A are not only on the imaginary axis but also have negative real parts.

4.1 Example 1

We consider a saturated system in the presence of disturbances (2) with system matrices

$$\begin{aligned} A=\left[ \begin{array}{c c} 0 &{} 1 \\ -1 &{} 0 \\ \end{array} \right] ,\quad B=\left[ \begin{array}{c} 0\\ 1\\ \end{array} \right] ,\quad C=\left[ \begin{array}{c c} -1 &{} 2 \\ \end{array} \right] .\quad \end{aligned}$$

The initial values for interval estimation are set with \(x_0\) having upper and lower bounds represented as \(\bar{x}_0=\left[ 2, 2 \right] ^T\) and \(\underline{x}_0=\left[ -2, -2 \right] ^T\). The external disturbances, denoted as d(t), and the measurement noises, denoted as v(t), are described by the following expressions:

$$\begin{aligned} \ d(t)=\left[ \begin{array}{cc} 0.05\cos (t)\\ 0.02\sin (t) \\ \end{array} \right] , \ v(t)=0.02\sin (t), \end{aligned}$$

and they are restricted as \(\underline{d}(t)\le d(t)\le \bar{d}(t)\) and \(\underline{v}(t)\le v(t)\le \bar{v}(t)\), in which

$$\begin{aligned} \ \bar{d}(t)=\left[ \begin{array}{cc} 0.05\\ 0.02\\ \end{array} \right] , \ \underline{d}(t)=\left[ \begin{array}{cc} -0.05\\ -0.02 \\ \end{array} \right] , \ \bar{v}(t)=0.02, \ \underline{v}(t)=-0.02. \end{aligned}$$

Note that \(\lambda (A)=\left\{ -j,j\right\} \). We select \(R=I\). By using the interval observer design in Sect. 4, one can easily obtain the gain L of an interval observer through YALMIP [15]:

$$\begin{aligned} \ L=\left[ \begin{array}{cc} -1.3078\\ 1.3275\\ \end{array} \right] . \end{aligned}$$

The matrices \(\bar{K}, \underline{K}\) can be selected as \(\bar{K}{=}\left[ \! \begin{array}{cc} 0.5635&{} 0 \\ 0&{} 0.3532 \\ \end{array}\! \right] \), \(\underline{K}{=}\left[ \! \begin{array}{cc} 0.4365&{} 0 \\ 0&{} 0.6468 \\ \end{array}\! \right] \). Next, \(P(\epsilon )\) can be obtained by PARE (25). By selecting \(\epsilon =0.5\) and \(\epsilon =0.1\), we obtain positive definite matrices

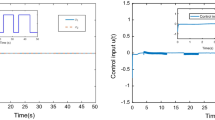
$$\begin{aligned} P(0.5)=\left[ \begin{array}{cc} 1.1250&{} 0.2500 \\ 0.2500&{} 1.0000\\ \end{array} \right] ,\quad P(0.1)=\left[ \begin{array}{cc} 0.2010 &{} 0.0100 \\ 0.0100&{} 0.2000\\ \end{array} \right] .\quad \end{aligned}$$

Figures 1 and 2 plot the trajectories of estimation and the control signal with \(\epsilon =0.5\), respectively. Figures 3 and 4 plot the trajectories of estimation and the control signal with \(\epsilon =0.1\), respectively. From Figs. 1 to 4, it is evident that the actual state vector x consistently resides within the boundaries of the defined interval, which demonstrates the accuracy of the constructed interval observer. Moreover, the whole system can finally reach semi-global boundedness as time goes on. The visual evidence from these plots also highlights that, under identical initial conditions, the maximum magnitude of the input signal diminishes with the reduction of the parameter \(\epsilon \), thereby illustrating the validity of the low-gain feedback control strategy.

Fig. 1
figure 1

System states and the interval estimates with \(\epsilon =0.5\)

Full size image
Fig. 2
figure 2

System control signal with \(\epsilon =0.5\)

Full size image
Fig. 3
figure 3

System states and the interval estimates with \(\epsilon =0.1\)

Full size image
Fig. 4
figure 4

System control signal with \(\epsilon =0.1\)

Full size image

4.2 Example 2

Then, we take into account a system in the presence of input saturation and disturbances (2) with system matrices

$$\begin{aligned} A=\left[ \begin{array}{ccc} 0 &{} 1 &{}0 \\ -2 &{} 0 &{}1 \\ 1 &{} 1 &{}-1 \\ \end{array} \right] ,\quad B=\left[ \begin{array}{ccc} 1 &{} 2\\ 3 &{} 1\\ 1 &{} 2\\ \end{array} \right] ,\quad C=\left[ \begin{array}{cccccc} 1 &{}2&{}0 \\ 2 &{} 0&{}3 \\ \end{array} \right] .\quad \end{aligned}$$

The interval bounds of \(x_0\) are selected as \(\bar{x}_0=\left[ 1.19, 1.341,1.492 \right] ^T\) and \(\underline{x}_0=\left[ -2.551, -2.46,-3.214 \right] ^T\), respectively. The extraneous disturbances d(t) and the measurement noises v(t) are selected as

$$\begin{aligned} \ d(t)=\left[ \begin{array}{cc} 0.012\cos (t)\\ 0\\ 0.013\sin (t) \\ \end{array} \right] , \ v(t)=\left[ \begin{array}{cc} 0.015\\ -0.013\sin (t) \\ \end{array} \right] , \end{aligned}$$

and they are restricted as \(\underline{d}(t)\le d(t)\le \bar{d}(t)\), \(\underline{v}(t)\le v(t)\le \bar{v}(t)\), in which

$$\begin{aligned} \ \bar{d}(t)=\left[ \begin{array}{cc} 0.012\\ 0\\ 0.013\\ \end{array} \right] , \ \underline{d}(t)=\left[ \begin{array}{cc} -0.012\\ 0\\ -0.013 \\ \end{array} \right] , \ \bar{v}(t)=\left[ \begin{array}{cc} 0.015\\ 0.013\\ \end{array} \right] , \ \underline{v}(t)=\left[ \begin{array}{cc} 0.015\\ -0.013\\ \end{array} \right] . \end{aligned}$$

One can easily check that \(\lambda (A)=\left\{ -1,-j,j\right\} \). Since there is an eigenvalue with a negative real part, we need to transform the coordinates. In the novel coordinates \(z=P^{-1}x\), where

$$\begin{aligned} P=\left[ \begin{array}{cccccc} 0.5774&{} 0.5774&{}-0.3015 \\ 0.5774&{}-0.5774&{}0.3015\\ 0.5774&{} 0.5774&{}-0.9045\\ \end{array} \right] , \end{aligned}$$

then we can obtain the transformed system (14) with system matrices

$$\begin{aligned} \tilde{A}=\left[ \begin{array}{ccc} 0 &{} -1 &{}0 \\ 1 &{} 0 &{}0 \\ 0 &{} 0 &{}-1 \\ \end{array} \right] ,\quad \tilde{B}=\left[ \begin{array}{ccc} 3.4638 &{} 2.5979 \\ -1.7319 &{} 0.8660 \\ 0&{} 0 \\ \end{array} \right] ,\quad \tilde{C}=\left[ \begin{array}{cccccc} 1.7322 &{}-0.5774&{}0.3015 \\ 2.8870 &{} 2.8870&{}-3.3165 \\ \end{array} \right] . \end{aligned}$$

We select \(R=I\). By using YALMIP, one can easily obtain the gain L of an interval observer:

$$\begin{aligned} \ L=\left[ \begin{array}{cccc} 21.8736 &{}3.3567 \\ -0.1190&{}-0.1190 \\ -0.0905&{}-0.1670 \\ \end{array} \right] . \end{aligned}$$

Next, in the new coordinates, we can also get the sub-systems (22) that need to be controlled with system matrices

$$\begin{aligned}&A_0=\left[ \begin{array}{cc} 0 &{} -1 \\ 1 &{} 0 \\ \end{array} \right] ,\quad B_0=\left[ \begin{array}{cc} 3.4638&{}2.5979\\ -1.7319&{}0.8660\\ \end{array} \right] ,\quad A_-= -1 ,\quad B_-=\left[ \begin{array}{cc} 0&{}0\\ \end{array} \right] .\quad \end{aligned}$$

Obviously, \((A_0,B_0)\) is controllable. The matrices \(\bar{K}, \underline{K}\) can be selected as \(\bar{K}=\left[ \begin{array}{cc} 0.6365&{} 0\\ 0&{} 0.5438\\ \end{array} \right] \), \(\underline{K}=\left[ \begin{array}{cc} 0.3635&{} 0 \\ 0&{} 0.4562\\ \end{array} \right] \). Then, \(P(\epsilon )\) can be obtained by PARE (25). By selecting \(\epsilon =0.5\) and \(\epsilon =0.1\), we obtain positive definite matrices

$$\begin{aligned} P(0.5)=\left[ \begin{array}{cc} 0.0478&{} 0.0081 \\ 0.0081&{}0.0442\\ \end{array} \right] ,\quad P(0.1)=\left[ \begin{array}{cc} 0.0090&{} 0.0003 \\ 0.0003&{} 0.0088\\ \end{array} \right] .\quad \end{aligned}$$

Figures 5 and 6 plot the simulation results for estimation and the control signal with \(\epsilon =0.5\), respectively. Figures 7 and 8 plot the simulation results for estimation and the control signal with \(\epsilon =0.1\), respectively. From Figs. 5 to 8, it is evident that x is always encapsulated in the interval bounds, which again confirms the accuracy of the designed interval observer. Moreover, with time passing, the whole system can finally reach semi-global boundedness, which also verifies the validity of the designed low-gain feedback algorithm.

Fig. 5
figure 5

System states and the interval estimates with \(\epsilon =0.5\)

Full size image
Fig. 6
figure 6

System control signal with \(\epsilon =0.5\)

Full size image
Fig. 7
figure 7

System states and the interval estimates with \(\epsilon =0.1\)

Full size image
Fig. 8
figure 8

System control signal with \(\epsilon =0.1\)

Full size image

5 Conclusion

This article has tackled the semi-global robust control problem for continuous-time LTI systems, considering the presence of input saturation and disturbances. To address this challenge, an interval observer has been developed, providing a pair of interval state estimates for system variables that lack direct real-time measurements. We have utilized a PLE-based low-gain feedback control strategy to guarantee semi-global boundedness. Compared with the PARE-based method, in which a PARE needs to be resolved online by iteration, the adopted method enables pre-determination of controller parameters offline.