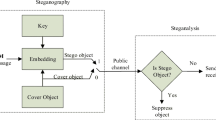
Abstract
In recent years, researchers have considered quantum steganography and its various methods with the development and progress of research in computation theory and quantum signals processing. The destructive use of quantum steganography methods to establish illegal covert communications is rising, so it is essential to introduce ways to detect hidden data in a quantum medium. Accordingly, this paper presents a frequency-based universal audio steganalysis approach to detecting quantum steganography. First, based on the quantum Fourier transform, the characteristic of the quantum spectrum centroid (QSC) was computed, and its circuit network was implemented to extract feature vectors. The proposed method classifies quantum audio signals using a quantum machine learning approach called a quantum ensemble of quantum classifiers. This approach was implemented within the framework of the Deutsch–Jozsa algorithm, which uses the superposition property to create an ensemble of classifiers evaluated in parallel, significantly increasing the computational speed. The accuracy weight of the classifiers is adjusted based on the classifiers' performance in training data classification; finally, the measurement of the first n qubits of the Deutsch–Jozsa algorithm predicts whether the quantum audio signals belong to the stego or clean class. The idea stems from the classic ensemble methods that try to build more robust models by combining different classifiers. The results show that the proposed frequency domain steganalysis method with 95% accuracy performs better than the previous methods in the time domain.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In recent years, steganalysis of audio signals as a cover media has been one of the most important research topics because audio data are becoming a good platform for hiding confidential data. The main goal of steganalysis is to distinguish the modified signals “stego” relative to the original signals “cover”. Hence, steganalysis techniques are based on learning algorithms and feature extraction methods. With the advent of quantum computing theory and quantum communication networks, communicating confidentially and securely has become challenging. The quantum audio signal represents digital audio as it stores the whole digital audio in a superposition state. The first attempt at digital audio quantum representation was made by Wang et al. (2015) under the title quantum representation digital audio (QRDA) [23]. The QRDA representation inspired novel enhanced quantum representation (NEQR) to store digital audio signals; it uses two entangled qubit sequences to store amplitude and time information. Yan et al. (2017) proposed a flexible representation of the quantum audio (FRQA) method, which displays the information of the sample amplitude values in 2's complement system, providing a more realistic representation of the time samples of a quantum audio signal, compared to the previous methods [4]. Li et al. (2018) suggested a quantum representation of digital signals (QRDS) that, similar to previous methods, uses two quantum sequences to store the amplitude and time information of a digital audio signal; the amplitude information can be a non-integer value in 2's complement system [10]. Therefore, the amplitude value of an audio signal sample is n + 1-qubit, including one sign qubit, m integer qubits, and n − m fractional qubits. Moreover, Sahin et al. (2019) have proposed a quantum representation of multichannel audio (QRMA) using three-qubit sequences [17].
A study divides the classical audio steganalysis approach into two general categories, compressed and non-compressed [7]. Non-compressed methods are of two types: calibrated and non-calibrated. In the non-calibrated method, the steganalysis features are extracted directly from the audio signal. While in calibrated methods, the steganalysis features are obtained by comparing the audio signal with an estimated cover signal or the hidden message. Non-calibrated methods are of two categories: time domain and frequency domain. Steganography in the frequency domain has several advantages. First, perceptual models can increase the permeability of data-hiding methods. Second, the distribution of energy from the transform allows data to be hidden throughout the audio signals. Third, changes in the frequency domain can be more easily embedded when working with compressed audio or video. Despite using the advantages of the frequency domain and their versatility, these methods cause inevitable changes in the statistical features of host signals that can be used as an efficient and effective tool in building comprehensive and accurate steganalysis. Steganography methods try to hide data in areas of frequency and time signals. The human auditory system does not understand embedded data in frequency ranges. Therefore, feature extraction in the signal frequency domain can significantly improve the differentiation power of audio steganalysis. Liu et al. (2009) have used the features based on the short-time Fourier transform (STFT), which include components of mean, standard deviation, skewness on the second-order derivation, and Mel frequency cepstral coefficients (MFCC) [11, 12]. Wei et al. (2011) introduced a combination of STFT-based features that consists of second-order derivation features, MFCC, audio quality metrics, and linear prediction residue features [24].
A study by Chen et al. in 2017 suggested two LSB-based quantum audio steganography protocols [4]. The FRQA representation is used in these protocols to store a quantum audio signal's amplitude and time information [4]. Furthermore, the qubit layer concept in the LSQb algorithm is used to demonstrate the position of the qubits in the cover quantum audio signal. So, the sequence's least significant qubit is called the 1st qubit layer, and the most significant qubit of the sequence is called Mst qubit layer. The first protocol used the least significant qubit of the amplitude information sequence. The second protocol to increase the robustness of the cLSQ method used the qubit layers with the more substantial number for the embedding operation. In 2020, two quantum audio steganography–steganalysis methods were presented for quantum audio signals. The steganalysis section uses the quantum power module and the quantum Mean module in the time domain to extract the features. It performs classification based on the quantum K-nearest neighbour (QKNN) algorithm and the Hamming distance criterion [2, 3].
Steganography causes inevitable changes in the frequency domain's statistical characteristic of the host signal. It can be used as an efficient and effective tool to build comprehensive and accurate steganalysis. This paper proposes a blind steganalysis method in the quantum frequency domain. First, the quantum Fourier transform is applied to the input quantum audio signals. Then, statistical feature vectors are extracted from the proposed feature extraction circuit network. Finally, a quantum ensemble classifier distinguishes "cover-audio" and "stego-audio" within the framework of the Deutsch–Jozsa quantum algorithm.
The remaining paper is organized as follows. Section 2 introduces QRDS representation, some quantum arithmetic modules required in the proposed feature extraction method, the Deutsch–Jozsa algorithm, and the quantum Fourier transform. Section 3 presents the proposed steganalysis method, which includes implementing the quantum circuits network to extract the statistical features and the proposed quantum ensemble classifier. Simulation results of the proposed steganalysis scheme and analysis are presented in Sect. 4. The paper ends with a conclusion and future work.
2 Preliminaries
The first subsection introduces the quantum audio representation approach used in this paper. The second subsection presents some of the fundamental quantum arithmetical modules, and at the end of the subsection, the quantum Fourier transformation and its quantum circuit network are described.
2.1 QRDS Representation
The QRDS is one of the methods of representing digital signals in a quantum manner. A fractional quantum sequence is used in this representation, which displays quantum signals more accurately than other methods. The QRDS is a fractional quantum sequence with length \(\left( {n + 1 + l} \right)\), in which \(n + 1\)-qubit is related to the storage of signal amplitude information, and \(l\)-qubit is associated with the storage of signal time information. Equations (1–4) express the QRDS representation for an audio signal.
where the signal amplitude information is stored using sequence \(\left| {A_{t} } \right\rangle\), which is a fractional sequence in 2's complement notation. In this sequence, \(A_{m}^{t}\) is the sign qubit, \(A_{t}^{m - 1} \ldots { }A_{t}^{0}\) are integer qubits, and \(A_{t}^{ - 1} \ldots { }A_{t}^{m - n}\) are fractionally qubits. The time information stored by the one-qubit sequence \(\left| t \right\rangle\). Figure 1 shows the audio signal \(A = \left\{ {3,0.5, - 1.5, - 1.125, - 1.25,2} \right\}\) using the QRDS method.
Example of a QRDS audio signal (figures and descriptions adapted from [10])
2.2 Quantum Basic Arithmetic Modules
This subsection presents two basic arithmetic modules: adder and sum. Furthermore, fundamental quantum modules are required to design circuits related to the proposed feature extraction module in Sect. 3.3, like comparator [10, 22], multiplier [10, 21], divider [10, 20], and absolute value [3]. The relevant references fully explain how to perform the computation of these modules and their quantum circuit network.
2.2.1 Quantum Adder
The quantum addition operation adds two quantum numbers together. Because sample values of an audio signal in the QRDS representation are signed numbers, the adder module has been used, as suggested in [5, 10, 13, 19, 21]. The quantum ADD module adds two quantum sequences \(\left| a \right\rangle\) and \(\left| b \right\rangle\), representing numbers \(a\) and \(b\), respectively. The quantum circuit network and the ADD module are shown in Fig. 2. The operation of the ADD module can be defined using Eq. (5).
where two sequences \(\left| b \right\rangle\) and \(\left| a \right\rangle\) are input' signed numbers with length \(\left( {n + 1} \right)\) qubits, also two outcomes \(\left| b \right\rangle\) and \(\left| {a + b} \right\rangle\). According to Fig. 2, a quantum adder includes \(2n - 1\) “carry” and \(2n\) “sum” sub-modules.
The quantum circuit and its corresponding module for sum (a), carry (b), and addition for two signed numbers (c) ((figures and descriptions adapted from [10])
2.2.2 Quantum Sum
The quantum sum is another essential quantum arithmetic operation that computes the algebraic sum of a series of quantum numbers, such as the sum of the amplitude values of some samples of quantum audio. The quantum sum module suggested in [10, 21] computes the algebraic sum of a series of QRDS audio samples. This module and its circuit network are shown in Fig. 3, where \(\left| {A_{t} } \right\rangle = \left| {a_{n} \ldots a_{1} { }a_{0} } \right\rangle { }\) is amplitude information of the audio signal samples with length \(n + 1\)-qubits and \(\left| t \right\rangle = \left| {t_{l - 1} \ldots t_{1} { }t_{0} } \right\rangle { }\) is time information with length \(l\)-qubits; Moreover, \( n + 1\) ancillary qubits \(\left| 0 \right\rangle\) are employed to store the final result of the sum module. In this implementation, \(2^{l}\) addition modules are used to calculate the sum of \(\left| {A_{t} } \right\rangle\) in \(2^{l}\) time position \(\left| t \right\rangle\). In addition, quantum subtraction could be performed using a quantum addition circuit network. A black bar is placed on the left side of the ADD module to indicate the subtraction module.
The quantum circuit and its corresponding module for the sum of all amplitude values (figures and descriptions adapted from [10])
2.3 The Deutsch–Jozsa Algorithm
The Deutsch–Jozsa algorithm uses quantum parallelism and entanglement properties to determine whether a function is constant or balanced [1, 8]. Consider a function \(f:\left\{ {0,1} \right\}^{n} \to \left\{ {0,1} \right\}\), where f is constant (all zeros or all ones) or balanced (half zero and half ones). This algorithm can determine if the function is constant or balanced with just one call. The circuit of this algorithm is shown in the figure. The steps of the algorithm, according to Fig. 4, are as follows[8]:
-
Step1 Prepare the initial state \(\left| {\psi_{0} } \right\rangle = \left| 0 \right\rangle^{ \otimes n} \left| 1 \right\rangle\).
Fig. 4 The Deutsch–Jozsa algorithm for functions with n-qubit input (figures and descriptions adapted from [8])
-
Step2 Apply Hadamard gate on all qubits and create the quantum states as follows :
$$ \left| {\psi_{1} } \right\rangle = \frac{1}{{\sqrt {2^{n} } }}\mathop \sum \limits_{{x\left\{ {0,1} \right\}^{n} }} \left| x \right\rangle \left[ {\frac{1}{\sqrt 2 }\left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right)} \right] $$(6) -
Step 3 The function \(f\) is applied using a unitary transform \(U_{f} :\left| {x,y} \right\rangle \to \left| {x ,y \oplus f\left( x \right)} \right\rangle\):
$$ \left| {\psi_{2} } \right\rangle = \mathop \sum \limits_{x} \frac{{\left( { - 1} \right)^{f\left( x \right)} \left| x \right\rangle }}{{\sqrt {2^{n} } }} \left[ {\frac{\left| 0 \right\rangle - \left| 1 \right\rangle }{{\sqrt 2 }}} \right] $$(7) -
Step 4 Applying the Hadamard gate to the first \(n\) qubits and the quantum state as follow:
$$ \left| {\psi_{3} } \right\rangle = \mathop \sum \limits_{z} \mathop \sum \limits_{x} \frac{{\left( { - 1} \right)^{x.z + f\left( x \right)} \left| z \right\rangle }}{{2^{n} }} \left[ {\frac{\left| 0 \right\rangle - \left| 1 \right\rangle }{{\sqrt 2 }}} \right] $$(8)where \(x.z\) is the bitwise inner product modulo 2. Finally, the probability of measuring the state \(\left| 0 \right\rangle^{{ \otimes {\varvec{n}}}}\) is as follows:
$$ p\left( {0 \ldots 0} \right) = \left| {\frac{1}{{2^{n} }}\mathop \sum \limits_{x} \left( { - 1} \right)^{f\left( x \right)} } \right|^{2} $$(9)If the result of the probability function is 0, then \(f\left( x \right)\) is balanced; else, the \(f\left( x \right)\) is constant.
2.4 Quantum Fourier Transform
The quantum Fourier transform (QFT) is a vital ingredient of many quantum algorithms [6, 14]. The QFT is defined to be a linear operator with the following action based on states \(\left| 0 \right\rangle ,\left| 1 \right\rangle , \ldots ,\left| {N - 1} \right\rangle\) as:
where \({\text{exp}}\left( {2\pi ijk/N} \right) = \omega_{N}^{jk}\) and \(N = 2^{n} .\)
Equivalently, the action on an arbitrary state may be written as:
where the amplitudes \(\{ X_{k} \}\) are the classical discrete Fourier transform of a amplitudes \(\{ x_{j} \}\). The QFT performs a unitary operation only on basis states and does not act on coefficients of basis states. Figure 5 shows an illustration of how QFT acts on basis states \(\left| 0 \right\rangle\) and \(\left| 1 \right\rangle\).
\({\text{QFT}}\frac{1}{\sqrt 2 }\left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right) = \frac{1}{\sqrt 2 }\left( {{\text{QFT}}\left| 0 \right\rangle + {\text{QFT}}\left| {1} \right\rangle } \right)\) (figures adapted from [15])
An efficient quantum circuit for computing QFT with the n qubit state is presented in [14]. The states \(\left| 0 \right\rangle , \ldots , \left| {2^{n} - 1} \right\rangle\) are the computational basis for an \(n\) qubit quantum computer. In this case, the state \(\left| j \right\rangle\) can be written using binary representation \(j = j_{1} j_{2} \ldots j_{n}\) or \(j = j_{1} 2^{n - 1} + j_{2} 2^{n - 2} + \cdots + j_{n} 2^{0}\). Furthermore, the notation \(0 \cdot j_{L} j_{L + 1} \ldots j_{m}\) represents the binary fraction \(j_{L} /2 + j_{L + 1} /4 + \cdots + j_{m} /2^{m - L + 1}\). Using algebra, the quantum Fourier transform is obtained as:
Equation (10) makes it possible to implement a QFT circuit and proves a unitary operator. This circuit has been implemented using elementary gates, Hadamard's, and Controlled-R, as shown in Fig. 6.
The QFT circuit using \(R_{k} ,\) Hadamard gates and \(N = 2^{n}\) input or \(n\)-qubit (figures adapted from [14])
According to the QFT circuit, each term requires one Hadamard gate; hence, an \(n\)-qubit Fourier transform will require \(n\) Hadamard gates. Also, the first term requires \(\left( {n - 1} \right)\) Controlled-R gates, the next one requires \(\left( {n - 2} \right)\) Controlled-R gates, and each following term requires one fewer Controlled-R gates. By summing up the number of gates, \(n + \left( {n - 1} \right) + \cdots + 1 = n\left( {n + 1} \right)/2 = {\text{\rm O}}\left( {n^{2} } \right)\) the gate is obtained. Therefore, the computational complexity of the QFT circuit is \({\text{\rm O}}\left( {n^{2} } \right)\).
3 Proposed Quantum Audio Steganalysis Schemes
The proposed steganalysis method is organized in the following four sections.
-
Sect. 1: Quantum audio dataset preparation
-
Sect. 2: Introduces the statistical feature extraction method based on the second-order derivative of the quantum audio spectrum.
-
Sect. 3: Implementation of the quantum feature circuit obtained from step 2.
-
Sect. 4: Implementation of the quantum ensemble classifier.
3.1 Quantum Audio Dataset Preparation
Since there is no dataset for quantum signals in general, the necessary quantum audio datasets must be created by converting classical signals into quantum form. For this purpose, our classical audio dataset consists of 200 WAV audio files. This database contains various audio files like music and male and female speech. These audio samples are with the specification of 44,100 Hz Sample Rates, mono, 16-bit quantization in uncompressed, PCM encoded WAV files. They have a duration ranging from 10 to 60 s. All audio samples from the classical dataset are first converted to quantum audio signals using the QRDS representation to produce quantum audio datasets. These quantum signals constitute clean (cover) quantum datasets. The next step is converting the classic secret image to a quantum one using FRQA representation. In the final step, using the three methods of cLSQ1 and pMSQ4 presented in [4], and LSFQ presented in [2, 3], the quantum image is embedded in the host's quantum audio signal to form the stego quantum dataset. Eventually, the necessary quantum audio dataset will consist of the clean and stego quantum audio signals. The details of producing the quantum audio dataset can be described as follows:
-
Step 1 Prepare a classic audio dataset and perform pre-processing operations on its samples.
-
Step 2 Prepare the classic secret image and perform pre-processing operations on it.
-
Step 3 Converting audio samples of the classical audio dataset to quantum audio samples using QRDS representation and obtaining quantum clean audio samples.
-
Step 4 Converting classical image to quantum image using FRQA representation.
-
Step 5 Embedding the secret quantum image into quantum audio samples using the cLSQ1, pMSQ4, and LSFQ methods to obtain quantum stego audio samples.
-
Step 6 Creating quantum audio datasets using clean and stego quantum audio samples.
3.2 The Proposed Feature Extraction Method for the Quantum Audio Spectrum
In audio signal processing, second-order derivatives are used to identify confidential data. Given that most of the power of an audio signal is concentrated at low and middle frequencies, hidden data are more embedded in the high-frequency domain. The second-order derivatives can reveal changes in high-frequency components relative to the original audio [24]. This paper uses the quantum spectrum centroid (QSC) feature to show introduced changes. Since the amplitude of the signal samples is sketched only at their corresponding time index, sequence \(\left| {A_{i} \left[ n \right]} \right\rangle { }n = 0,1, \ldots ,N - 1\) in Eq. (13) is the amplitude of the nth sample of the quantum audio signal, where \(n\) is the time index or sample number, and \(i\) is the current frame number. Also, sequence \(\left| {A_{i} \left[ k \right]} \right\rangle ,k = 0,1, \ldots ,N - 1\) is the amplitude of the kth sample of the quantum Fourier transform (QFT) coefficients, where \(k\) is the frequency index or sample number.
The spectrum centroid represents the spectral energy distribution center and is a measure for evaluating the “center of gravity” using the Fourier transforms frequency and magnitude information. The energy of the second-order derivation concentrates at the high-frequency domain; hence, the stego audio's spectral centroid is greater than the cover audio's. Given the formula of Spectral Centroid of the digital audio signal in [16], Quantum Spectral Centroid (QSC) can be defined as:
Here, \(\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\) is the high-frequency amplitude of “cover audio” and “stego audio” of the ith frame after the QFT operation, N is the length of the frame, and the center frequency is \(\left| {c\left( k \right)} \right\rangle\). Note that only half of the data are calculated due to the symmetry of the spectrum.
3.3 Quantum Basic Arithmetic Modules
This subsection presents some modules and corresponding quantum circuits, which are the basis for constructing the proposed feature extraction methods.
3.3.1 QFT Circuit
We need a quantum circuit that performs QFT operations on the audio signals in QRDS format to design the module and the circuits associated with the extracted feature. Inspired by [9], quantum Fourier transforms on QRDS audio signals are proposed as Eq. (15).
The QFT transforms the QRDS content from time to frequency domain. Amplitude information in the frequency domain in the form of fractional 2's complement is \(A_{k}\). \(\left| c \right\rangle\), which is the same range as \(\left| t \right\rangle\) that records the new sample position of the QRDS signal in the frequency domain. The proposed QFT circuit on the QRDS signal is shown in Fig. 7.
3.3.2 Proposed QFT-Based Quantum Squared-Magnitude Module
According to article [2], to compute the amplitude squared-magnitude of a sample of a QRDS signal \(\left| {A\left( k \right)} \right\rangle = \left| {a_{m} \ldots a_{0} a_{ - 1} \ldots { }a_{m - n} } \right\rangle\), first the absolute value of the signal \(\left| {\left| {A\left( k \right)} \right|} \right\rangle\) has been computed by QABS Module, next, applying the multiplier module, amplitude magnitude \(\left| {\left| {A\left( k \right)} \right|} \right\rangle\) is multiplied by a duplicate of itself to obtain the amplitude squared-magnitude \(\left| {\left| {A\left( k \right)} \right|^{2} } \right\rangle\). Here, a comparator module has been used to multiply the simultaneous samples of signal \(\left| {\left| {A\left( k \right)} \right|} \right\rangle\) and its copy signal. The quantum circuit of amplitude spectrum squared-magnitude of a sample of a QRDS signal and its quantum module is shown in Fig. 8.
3.3.3 Proposed Quantum Multiplication Circuit for Two Value Amplitude Squared-Magnitude and Frequency
A quantum multiplier is similar to classical multiplication, executing the multiplication operation between two quantum numbers. To compute the quantum multiplication of two values \(\left| {\left| {A\left( k \right)} \right|^{2} } \right\rangle\), \({\text{c}}\left( {\text{k}} \right)\), we used the quantum multiplication operations presented in [9, 25]. In addition, for ease of presentation, we suppose \(\left| {\text{y}} \right\rangle = \left| {y_{m} \ldots y_{1} y_{0} \ldots y_{m - n} = } \right\rangle \left| {\left| {A\left( k \right)} \right|^{2} } \right\rangle\) and \(\left| k \right\rangle = c\left( k \right)\). The amplitude square of signal QRDS is a fractional quantum sequence with length \(n + 1\). So that the most significant qubit is the sign of qubit, the integer and fractional parts of the amplitude have lengths m and m − n, respectively. Quantum multiplication operation (MUL module) can be defined according to relation (16):
The qubits \(\left| z \right\rangle\) and \(\left| 0 \right\rangle\) (including \(n + m\) and \(n + 1\) qubits, respectively) are ancillary qubits to temporarily store the result and the final results of the multiplication operation, respectively. The ancillary qubit \(\left| p \right\rangle\) stores intermediate results at each step of the multiplication operation. The qubits \(\left| z \right\rangle\) and \(\left| p \right\rangle\) are initialized with a sequence of \(\left| 0 \right\rangle\) s. The proposed multiplication operation circuit is shown in Fig. 9.
-
Step 1 After applying a quantum Fourier transform on the input quantum audio signal, \(n + 1\) Toffoli gates (controlled by the \(\left| y \right\rangle\) and \(\left| {x_{i} } \right\rangle\) for \(i = 0\)) are applied on the qubit \(\left| z \right\rangle\), and outcome \(\left| z \right\rangle = \left| {y_{m} \ldots y_{1} y_{0} \ldots y_{m - n} } \right\rangle { }\left| {x_{0} } \right\rangle\) will be obtained, which is one of the input values from the first adder module. The other input from the first adder module is initialized as \(\left| 0 \right\rangle^{ \otimes n + 1}\). The intermediate result of the addition is stored in qubit \(\left| p \right\rangle\), which in step2 has been considered the input of the second adder module. At each step, immediately after of adder module, \(n + 1\) Toffoli gates are employed to reset \(\left| z \right\rangle\) to its original state, i.e. \(\left| 0 \right\rangle^{ \otimes n + m}\).
From the second step onwards: \(n + 1\) Toffoli gates (controlled by the \(\left| y \right\rangle\) and \(\left| {x_{i} } \right\rangle\) for \(i = 1, \ldots ,m - 1\)) applied on qubit \(\left| z \right\rangle\) and the outcome \(\left| z \right\rangle = \left| {y_{m} \ldots y_{1} y_{0} \ldots y_{m - n} } \right\rangle \left| 0 \right\rangle^{ \otimes i} { }\left| {x_{1} } \right\rangle\) is obtained, which is one of the input values for the following adder modules. Another input of the adder modules is obtained from the sum of the previous steps. The final result of the multiplication operation is as follows:
3.3.4 Proposed Quantum Circuit for the Sum of the Products of Amplitude Squared-Magnitude and Frequency
To compute the sum of products, \(c\left( k \right)\) and \(\left| {\left| {A\left( k \right)} \right|^{2} } \right\rangle\) for all samples \(k \) of the i-th frame of a quantum audio signal, i.e. \(\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\), is shown in Fig. 10. Given that only half of the data are computed due to spectrum symmetry, we need \(\frac{N}{2}\) MULL modules and \(\frac{N}{2} - 1\) Adder module.
3.3.5 Proposed Quantum Circuit for the Sum of the Amplitudes Squared-Magnitude
Here,\({ }\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\) is the sum values of QFT amplitudes squared-magnitude of the i-th frame of a QRDS audio signal. The module presented in [10] regarding Fig. 11 is used to compute it.
3.3.6 Proposed Quantum Spectral Centroid (QSC) Circuit
This feature determines the centrality of the quantum spectrum or the amplitude-weighted average of the QFT frequency spectrum. The QSC is obtained from the quantum division of the results of the previous two subsections, i.e.\({ }\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle } \right.\) as the numerator and \(\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle } \right.\) as the denominator of division. Here, for ease of presentation, suppose \(\left| y \right. = \left| {y_{m} \ldots y_{0} } \right. = \mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle } \right.\) and \(\left| x \right. = \left| {x_{n} \ldots x_{0} } \right. = \mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\). The quantum division operation has been performed by the quantum division module presented in [25]. Like the classical state, the quantum division is extended to a series of subtraction operations. Additional information is stored at a qubit of \(\left| {\mathop x\limits^{{\prime }} } \right\rangle = \left| {\mathop {x_{m} }\limits^{{\prime }} \ldots { }\mathop x\limits^{{\prime }}_{1} } \right\rangle \mathop x\limits^{{\prime }}_{0}\) to record the step-by-step execution of the division operation. The circuit network and the quantum division module are shown in Fig. 12, implemented through the following steps.
-
Step 1 At the start of this step, according to Fig. 12, the state \(\left| {x_{n} \ldots x_{1} } \right\rangle x_{0}\) is mapped to state \( \left| {\mathop {x_{{m{ }}} }\limits^{{\prime }} \mathop x\limits^{{\prime }}_{m - 1} \ldots { }} \right\rangle \mathop x\limits_{m - n}\) by the \(n + 1\) CNOT gates. Following that, the states \(\left| {y_{m} \ldots y_{1} } \right\rangle y_{0}\) and \( \left| {\mathop {x_{m} }\limits \mathop {x_{m - 1} }\limits \ldots { }} \right.\mathop x\limits_{0}\) are compared using the COM module. When \(\left| y \right\rangle \ge \left| {\mathop x\limits^{{\prime }} } \right\rangle\), value \(\left| {e_{0} } \right\rangle\) of COM module outcome becomes \(\left| 0 \right\rangle\) so the SUB module is activated to compute the subtraction of \(\left| {v_{1} } \right\rangle = \left| {\mathop x\limits^{{\prime }} } \right\rangle - \left| {\mathop x\limits^{{\prime }} } \right\rangle\), which in step2 is an input of the COM module. After the SUB module, the first CNOT gate (e0-controlled) stores the quotient or first qubit of the division resulting in a qubit \(\left| {q_{m} } \right\rangle\). Before going to Step 2, the second CNOT gate on \(e_{0}\) guarantees that \(\left| {e_{0} } \right\rangle = \left| 0 \right\rangle\) and also another \(n + 1{ }\) CNOT gate is used to reset the state \(\left| {\mathop x\limits^{{\prime }} } \right\rangle\) to its initialized state (sequence of \(\left| 0 \right\rangle^{ \otimes m}\) entries), to prepare Step2.
-
Step 2 The value \(\left| 0 \right\rangle x\left| 0 \right\rangle^{ \otimes m - 1}\) is assigned to the qubit \(\left| {\mathop x\limits^{{\prime }} } \right\rangle\) using \(n + 1\) CNOT gates; to compare with the outcome of step 1. Like step 1, \(\left| {e_{0} } \right\rangle = \left| 0 \right\rangle\) determined \(\left| {v_{1} } \right\rangle \ge \left| {\mathop x\limits^{{\prime }} } \right\rangle\), so the subtraction operation \( \left| {v_{2} } \right. = \left| {v_{1} } \right. - \left| {\mathop x\limits } \right.\) is performed. After the subtraction operation, such as the previous step, the first CNOT gate (controlled by the \(\left| {e_{0} } \right\rangle\)) is applied on \(\left| {q_{m - 2} } \right\rangle\) to obtain the second division result and the second CNOT gate ensures \(\left| {e_{0} } \right\rangle = \left| 0 \right\rangle\) before proceeding to the next step. At the end of step 2, additional \(n + 1\) CNOT gates are similarly used to reset the state \(\left| {\mathop x\limits^{{\prime }} } \right\rangle\) from \(\left| 0 \right\rangle x\left| 0 \right\rangle^{ \otimes m - 1}\) to \(\left| 0 \right\rangle^{ \otimes m}\). Iterating the above steps, the outcome of the DIV module includes quotient, i.e. \(\left| q \right\rangle\), and the result of the subtraction in the final step, i.e. \(\left| r \right\rangle\), are stored.
The QSC attribute depicts the change in high-frequency components caused by data embedding. The circuit network of computing the quantum spectral centroid is illustrated in Fig. 13. This circuit calculates the QSC attribute for one frame of the QRDS audio signal in the following four steps.
-
Step 1 Amplitude squared-magnitude, i.e. \(\left| {\left| {A\left( k \right)} \right|^{2} } \right\rangle\), is computed by the QSM module presented in Sect. 3.3.2.
-
Step 2 Using the Mul module presented in Sect. 3.3.3 is computed \(c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\).
-
Step 3 Using the SUM module presented in Sects. 3.3.4 and 3.3.5 is computed \(\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\) and \(\mathop \sum \limits_{k = 0}^{{\frac{N}{2} - 1}} \left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle\).
-
Step 4 Using the Divider module presented in Sects. 3.3.6 is computed \({\text{QSC}}_{i} = \frac{{\mathop \sum \nolimits_{k = 0}^{{\frac{N}{2} - 1}} \left| {c\left( k \right)\left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle } \right.}}{{\mathop \sum \nolimits_{k = 0}^{{\frac{N}{2} - 1}} \left| {\left| {A_{i} \left( k \right)} \right|^{2} } \right\rangle }}\).
3.4 Proposed Quantum Ensemble Classifier within Deutsch–Jozsa Algorithm Framework
A quantum machine learning approach is termed a quantum ensemble of quantum classifiers. It uses the superposition property to create a set of classifiers. This approach combines a set of classifiers as composite predictions to achieve higher generalizability performance. The classifier can be described as a decision function \(f:X \to Y\) that maps the input space \(X\) to the label \(Y\). This function depends on a set of parameters \(\theta\) and training the classifier to determine the function model \(f\left( {x;\theta } \right) x \in X\) is done by fitting the parameters to the training data sample. In a binary classifier problem where the labels are \(y = \left\{ { - 1,1} \right\} ,y \in Y\), if a set of classifiers is denoted by \(E = \left\{ {\theta_{0} ,\theta_{1} , \ldots ,\theta_{n - 1} } \right\}\), to compute the test data label \(\hat{x}\) the output result of all the classifiers is combined as:
where the sign is the sign function. Weight proportional to the accuracy of each classifier in a training dataset is \(w_{\theta }\). For more details on why accuracy can be a good weighting scheme, refer to reference [18].
The quantum algorithm for the classification of the quantum ensemble can be computed in the framework of the Deutsch–Jozsa algorithms. The Deutsch–Jozsa algorithm provides a simple problem that a quantum computer can solve exponentially faster than classical [1]. Accordingly, in this paper, to determine the probability of an input audio signal belonging to the clean or steg dataset, we used the quantum ensemble classifier in the framework of the Deutsch–Jozsa algorithm, which is illustrated in Fig. 14. The steps of quantum ensemble classification operation in the framework of the Deutsch–Jozsa algorithm using five quantum registers are as follows:
-
Step 1 Dividing quantum dataset into two parts of training and test data (30% training data and 70% test data).
-
Step 2 The proposed feature-extracting method is applied to the training and test data sample using the QSC circuit network.
-
Step 3 The registers \(\left| \theta \right\rangle\) and \(\left| {\hat{y}_{\theta } } \right\rangle\) are initialized in state \(\left| 0 \right\rangle\), and hence, the initial state is \(\left| {\psi_{0} } \right\rangle = \left| 0 \right\rangle^{ \otimes n + 1} \left| 1 \right\rangle\). Here, \(n\) is the parameter register length \(\left( \theta \right),\) and the output result of the classifier is stored in the register of one-qubit \(\left| {\hat{y}_{\theta } } \right\rangle\). Also, in this step, the data register \(\left| x \right\rangle\) and label register \(\left| y \right\rangle\) are empty \(\left( {\left| x \right\rangle \;{\text{and}}\;\left| y \right\rangle = \emptyset } \right)\).
-
Step 4 The Hadamard gate is applied to all qubits in step 3 as follows:
$$ \left| {\psi_{1} } \right\rangle = \left| x \right\rangle \frac{1}{{\sqrt {2^{n} } }}\mathop \sum \limits_{\theta E} \left| \theta \right\rangle \left| 0 \right\rangle \left| y \right\rangle \left( {\frac{\left| 0 \right\rangle - \left| 1 \right\rangle }{{\sqrt 2 }}} \right) $$(20)where parameter register \(\left| \theta \right\rangle\) is placed into a uniform superposition.
-
Step 5 First, the training data and the actual label are loaded into their registers, and then, the unitary operator \(U_{f}\) is applied to implement non-uniform weights and compute the function \(f\left( {x;\theta } \right)\). This function returns the output result of the classifier \(\hat{y}_{\theta }\) as:
$$ \left| {\psi_{2} } \right\rangle = \left| x \right\rangle \frac{1}{{\sqrt {2^{n} } }}\mathop \sum \limits_{\theta \in E} \left| \theta \right\rangle \left| {\hat{y}_{\theta } } \right\rangle \left| y \right\rangle \left( {\frac{\left| 0 \right\rangle - \left| 1 \right\rangle }{{\sqrt 2 }}} \right) $$(21)Now, if the output result of the classifier was equal to the actual label of class Y, by using the rotating-Gate \(R_{z}\), The last qubit \(a_{\theta }\) is rotated towards \(\left| 0 \right\rangle\) and otherwise rotated towards \(\left| 1 \right\rangle\). This step is repeated for all training data one after the other. Finally, the accuracy qubit is entanglement with the parameter qubits as:
$$ \frac{1}{{\sqrt {2^{n} } }}\mathop \sum \limits_{\theta \in E} \left| {\left| \theta \right\rangle } \right\rangle \left( {\sqrt {a_{\theta } } \left| 0 \right\rangle + \sqrt {1 - a_{\theta } } \left| 1 \right\rangle } \right) $$(22)Before the test data sample can be loaded into the data register, the \(\left| 0 \right\rangle\)-branch of the accuracy qubit must be postselected; in other words, the measurement of the n-qubits first (step7) occurs only when the \(\left| 0 \right\rangle\)-branch of the accuracy qubit is postselected, and this is done by applying the Hadamard gate and then the \(X\)-gate on the accuracy qubit. In the last phase of this step, the test data are loaded into the data register and the unitary operator \(U_{f}\) is applied.
-
Step 6 Hadamard gates are applied to n-qubits first to achieve the desired state for the quantum ensemble as:
$$ \left| {\psi_{3} } \right\rangle = \frac{1}{{\sqrt {E\chi } }}\left| {\hat{x}} \right\rangle \mathop \sum \limits_{\theta \in E} \sqrt {a_{\theta } } \left| \theta \right\rangle \left| {\hat{y}_{\theta } } \right\rangle $$(23)where the normalization factor is \(\frac{1}{{\sqrt {E\chi } }}\).
-
Step 7 The probability of measuring \(\left| {\hat{y}_{\theta } } \right\rangle\) as:
$$ p\left( {\hat{y}_{\theta } } \right) = \mathop \sum \limits_{\theta \in E} \frac{{a_{\theta } }}{E\chi } = \left| 0 \right\rangle \;{\text{or}}\;\left| 1 \right\rangle $$(24)So that state \(\left| 0 \right\rangle\) is corresponded to class prediction \(\hat{y}_{\theta } = - 1\) and state \(\left| 1 \right\rangle\) is corresponded to class prediction \(\hat{y}_{\theta } = + 1\).
Note that for simplicity, data are processed sample by sample without probabilistic quantum memory. The superposition of the ensemble would be broken by measuring, so to predict the class of each test sample, the entire quantum ensemble construction process must be repeated.
4 Experimental Results of the Proposed Steganalysis Scheme
The proposed quantum steganalysis scheme simulation has been done on a computer with Intel(R) Core(TM) i7-6500U CPU 2.59 GHz 8 GB RAM and 64-bit operating system, using MATLAB 2019b. The details of this implementation and the proposed steganalyser results are as follows.
These experiments used 200 classical audio files to prepare quantum datasets, sampled at 44.1 kHz and 16-bit precision. These audio signals are down-sampled in the range [−1, 1], and each signal has 1024 samples. These files were selected as host audio signal datasets and converted to the quantum format using the QRDS method (n = 7, m = 4, t = 10). Then, to create the stego database, a quantum image in NEQR format with size 1 × 1024 as confidential data in the frequency domain was embedded in 200 audio files using the quantum audio steganography techniques presented so far, including cLSQ1, pMSFQ4 [4], and LSFQ [2, 3].
According to the above steps, 100 stego quantum audio files were created from 200 existing ones. In the next step, based on the quantum spectral centroid (QSC) circuit network (Fig. 13), the feature vector is extracted for each quantum signal frame. The mean of these feature vectors for all signal frames forms the final feature vector. Finally, the obtained vectors from the test and training dataset are given to the quantum ensemble's classifier within the Deutsch–Jozsa algorithm’s framework. For the evaluation and test of the proposed steganalysis scheme, 30% of the clean and stego datasets were used to construct the learning datasets, and another 70% were used as test samples.
Table 1 shows the classification result of a test data instance based on the quantum ensemble classifier proposed in Sect. 3.4. A quantum ensemble classifier is a classification method in which the outputs of different classifiers are combined to obtain the final answer of the ensemble classifier. For binary classification of quantum audio signals into stego and pure audio signals, the set of classes is \(y = \left\{ { - 1,1} \right\}\). If we consider the set of classifiers as \(E = \left\{ {\theta_{0} ,\theta_{1} , \ldots ,\theta_{n - 1} } \right\}\). The accuracy of the classifier is set each time according to the output results of the classifier \(\hat{y}_{\theta }\) in the previous training instance [18]. According to Eq. (19), five quantum registers were used to store samples of the training \(\left| x \right\rangle\) and test data \(\left| {\hat{x}} \right\rangle\), classifier (model) \(\left| \theta \right\rangle\), response of each classifier \(\left| {\hat{y}_{\theta } } \right\rangle\), actual label of the training data sample \(\left| y \right\rangle\) and ancillary (last qubit). The steps to achieve the results of the proposed quantum ensemble classifier prediction are as follows:
-
Step 1 Prepare training data set of QRDS audio signal (clean/stego).
-
Step 2 Prepare an unlabelled QRDS audio signal as a test instance.
-
Step 3 Compute an average value of QSC feature related to frames of an audio signal in steps 1and step 2 as the training instance \(\left| x \right\rangle\) and test instance \(\left| {\hat{x}} \right\rangle\).
-
Step 4 Given Eq. (20), the classifier \(\left| \theta \right\rangle\) and the ancillary register (last qubit) are put in a superposition state. The training instance \(\left| x \right\rangle\) and its label \(\left| y \right\rangle\) are empty in this step. Therefore, classifier response \(\left| {\hat{y}_{\theta } } \right\rangle\) would be initialized in the state \(\left| 0 \right\rangle\).
-
Step 5 Inputting the first training instance and its actual label. Compute class of the first instance (classifier response \(\hat{y}_{\theta }\)), using Eq. (21). In this step, the classifier response \(\hat{y}_{\theta }\) is compared with actual label y, if \(\hat{y}_{\theta } = y\), the last qubit, must be rotated towards \(\left| 0 \right\rangle\) otherwise towards \(\left| 1 \right\rangle\), by using the rotating-Gate \(R_{z} = \left( {\begin{array}{*{20}c} {e^{{\frac{ - i}{2}}} } & 0 \\ 0 & {e^{\frac{i}{2}} } \\ \end{array} } \right)\).
-
Step 6 Repeat step 5 for all training instances. Once all training instances have been processed, Hadamard gate and then X-gate is applied on the last qubit; the reason for this is the elimination of classifiers with low accuracy and random guessing and the selection of accurate classifiers (models with accuracy higher than 0.5) [1]. At the end of this step, the quantum ensemble classifier is ready to classify the test instance \(\left| {\hat{x}} \right\rangle\).
-
Step 7 The Hadamard gate is applied in four elementary registers according to Eq. (23). To combine the quantum ensemble classifier and predict the belonging of the test instance, predicting the test instance class \(p\left( {\hat{y}_{\theta } } \right) = \left| 0 \right\rangle\) indicates audio signal probability belonging to class − 1 and \(p\left( {\hat{y}_{\theta } } \right) = \left| 1 \right\rangle\) indicates class + 1. After the new test instance has been classified, all previous steps must be repeated to determine the class of the following test instance due to the collapse of the quantum ensemble superposition.
4.1 Performance Analysis
The set of quantum audio datasets presented in the previous section have been used to evaluate the accuracy of the proposed quantum audio steganalysis. In order to create the stego training datasets, we used a combination of three quantum steganography methods presented so far: cLSQ1,pMSQ4, and LSFQ. In contrast, all quantum stego audio was tested with one quantum steganography method. The performance evaluation of the proposed audio steganalysis method has been performed based on the criteria of sensitivity (SE), specificity (SP), and accuracy (ACC). These criteria are defined as follows [3]:
The probability of correctly detecting a stego audio signal is called sensitivity (SE), and its formula is as follows:
The probability of correctly detecting the clean audio signal is called specificity (SP) and is defined as:
Table 2 shows the mean values of the accuracy (ACC) detection. This criterion expresses the probability of correct classification and is defined as follows:
In the above equations, the parameters TN, TP, FN, and FP are defined as follows [3]:
-
True-negative (TN): The number of clean signals that are correctly classified as clean signals.
-
True-positive (TP): The number of stego signals that are correctly classified as stego signals.
-
False-negative (FN): The number of stego signals that are incorrectly classified as clean signals.
-
False-positive (FP): The number of clean signals that are incorrectly classified as stego signals.
In quantum audio steganalysis, there are only two references, [2, 3], and a comparison has been made with these references. The experimental results in Table 2 are based on 100 test samples that were processed sample by sample. For each test instance, the training set includes 100 samples of clean audio and 100 samples of the corresponding stego audio. Also, a 32 × 32 binary image was used for embedding into the quantum host audio signal with a length of 1024 samples. Table 2 results indicate that the proposed steganalysis based on statistical features of the quantum frequency domain is more accurate in detecting and classifying quantum audio signals than the previously presented time-domain method.
5 Conclusion and Future Work
Steganalysis of quantum signals in the context of quantum communication networks is an issue that has been less studied despite its high importance. In this respect, this paper presents a universal frequency domain-based steganalysis method for quantum audio signals. First, the QRDS quantum audio database is generated from the classical audio dataset. Then, existing quantum steganography techniques such as LSFQ, cLSQ1, and pMSQ4 methods have also been used for embedding secret quantum images into host quantum audio signals. Second, a feature based on quantum Fourier transforms called the quantum spectral centroid (QSC) is defined. Then, its quantum circuit network is implemented to extract a quantum feature vector. Finally, using the quantum ensemble classification algorithm, which is implemented within the framework of the Deutsch–Jozsa algorithm, clean and stego quantum audio signals are classified. The results obtained from the proposed method and its comparison with two methods previously in the time domain show more accuracy for the proposed method. In the future work, we will try to offer new approaches to quantum audio steganalysis based on other features based on quantum Fourier transform and quantum neural networks.
References
A. Abbas, M. Schuld, F. Petruccione, On quantum ensembles of quantum classifiers. Quant. Mach. Intell. 2(1), 1–8 (2020)
M.J. Chaharlang, S. Mosleh, H. Rasouli, A novel quantum audio steganography–steganalysis approach using LSFQ-based embedding and QKNN-based classifier. Circuits Syst. Signal Process. 39(8), 3925–3957 (2020). https://doi.org/10.1007/s00034-020-01345-6
J. Chaharlang, M. MoslehS, A. Rasouli-Heikalabad, A novel quantum steganography-Steganalysis system for audio signals. Multimedia Tools Appl. 79(25), 17551–17577 (2020). https://doi.org/10.1007/s11042-020-08694-z
K. Chen, F. Yan, A.M. Iliyasu, J. Zhao, Exploring the implementation of steganography protocols on quantum audio signals. Int. J. Theor. Phys. 57(2), 476–494 (2018). https://doi.org/10.1007/s10773-017-3580-7
S.A. Cuccaro, T.G. Draper, S.A. Kutin, D.P. Moulton, A new quantum ripple-carry addition circuit. arXiv preprint quant-ph/0410184. (2004). https://doi.org/10.48550/arXiv.quant-ph/0410184
A. GalindoM, A. Martin-Delgado, Information and computation: classical and quantum aspects. Rev. Mod. Phys. 74(2), 347 (2002). https://doi.org/10.1103/RevModPhys.74.347
H. GhasemzadehM, H. Kayvanrad, Comprehensive review of audio steganalysis methods. IET Signal Proc. 12(6), 673–687 (2018). https://doi.org/10.1049/iet-spr.2016.0651
S. Gulde, M. Riebe, G.P. Lancaster, C. Becher, J. Eschner, H. Häffner, F. Schmidt-Kaler, I.L. Chuang, R. Blatt, Implementation of the Deutsch-Jozsa algorithm on an ion-trap quantum computer. Nature 421(6918), 48–50 (2003). https://doi.org/10.1038/nature01336
P. Li, X. Liu, Bilinear interpolation method for quantum images based on quantum Fourier transform. Int. J. Quant. Inform. 16(04), 1850031 (2018). https://doi.org/10.1142/S0219749918500314
P. Li, B. Wang, H. Xiao, X. Liu, Quantum representation and basic operations of digital signals. Int. J. Theor. Phys. 57(10), 3242–3270 (2018). https://doi.org/10.1007/s10773-018-3841-0
Q. Liu, A.H. Sung, M. Qiao. Spectrum steganalysis of WAV audio streams, in International Workshop on Machine Learning and Data Mining in Pattern Recognition. (2009). Springer
Q. Liu, A.H. Sung, M. Qiao, Temporal derivative-based spectrum and mel-cepstrum audio steganalysis. IEEE Trans. Inf. Forensics Secur. 4(3), 359–368 (2009). https://doi.org/10.1109/TIFS.2009.2024718
X. Lu, N. Jiang, H. HuZ, Ji, Quantum adder for superposition states. Int. J. Theor. Phys. 57(9), 2575–2584 (2018). https://doi.org/10.1007/S10773-018-3779-2
M.A. NielsenI, L. Chuang, Quantum computation and quantum information. Am. J. Phys. 26(4), 37 (2010)
C.-Y. Pang, R.-G. Zhou, B.-Q. Hu, W. Hu, A. El-Rafei, Signal and image compression using quantum discrete cosine transform. Inf. Sci. 473, 121–141 (2019). https://doi.org/10.1016/j.ins.2018.08.067
P. Rao, Audio Signal Processing. (2007). p. 169–189.https://doi.org/10.1007/978-3-540-75398-8_8
E. Şahin, I. Yilmaz, QRMA: quantum representation of multichannel audio. Quant. Inf. Process. 18(7), 1–30 (2019). https://doi.org/10.1007/s11128-019-2317-3
M. Schuld, F. Petruccione, Quantum ensembles of quantum classifiers. Sci. Rep. 8(1), 1–12 (2018). https://doi.org/10.1038/s41598-018-20403-3
Y. Takahashi, N. Kunihiro, A linear-size quantum circuit for addition with no ancillary qubits. Quant. Inf. Comput. 5(6), 440–448 (2005)
S. Tang, The Principle of Computer Composition (Higher Education Process, Beijing, 2008), pp.258–269
V. Vedral, A. Barenco, A. Ekert, Quantum networks for elementary arithmetic operations. Phys. Rev. A 54(1), 147 (1996). https://doi.org/10.1103/PhysRevA.54.147
D. Wang, Z.-H. Liu, W.-N. Zhu, S.-Z. Li, Design of quantum comparator based on extended general Toffoli gates with multiple targets. Comput. Sci. 39(9), 302–306 (2012)
J. Wang, QRDA: quantum representation of digital audio. Int. J. Theor. Phys. 55(3), 1622–1641 (2016)
Y. Wei, L. Guo, Y. Wang, C. Wang, A blind audio steganalysis based on feature fusion. J. Electron. 28(3), 265–276 (2011)
F. Yan, K. Chen, A.M. Iliyasu, K. Hirota, Circuit-based modular implementation of quantum ghost imaging. IEEE Access. 8, 23054–23068 (2020). https://doi.org/10.1109/ACCESS.2020.2970016
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Norouzi Larki, S., Mosleh, M. & Kheyrandish, M. Quantum Audio Steganalysis Based on Quantum Fourier Transform and Deutsch–Jozsa Algorithm. Circuits Syst Signal Process 42, 2235–2258 (2023). https://doi.org/10.1007/s00034-022-02208-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00034-022-02208-y