1 Introduction

The electroencephalogram (EEG) signals show information of the synchronous components of the multiple electrical activity. The study of the EEG can reveal a variety of behavioural, pathological and drug patterns, due to which its usefulness in medical applications has increased. Nowadays, the EEG has been a very useful and important part in the analysis of brain functions, diagnosis and treatment of mental diseases. Therefore, it is important to research the properties of brain waves in mental diseases and to utilise the results in medical applications, including early diagnosis, prediction, rehabilitation and treatment. Visual EEG analysis for pathology detection varies according to human experience. Therefore, an automatic diagnosis of a bipolar disorders is important in medical settings [46].

On the other hand, early diagnosis of bipolar disorders (BD) may significantly reduce health care costs [31]. The prevalence of bipolar disorder is between 2.6 and 5% of the population [5]. According to diverse authors, misdiagnosed patients received inadequate and expensive therapeutic schemes entailing suboptimal medication treatment [8, 30]. When the patient does not receive treatment, there is a high risk of morbidity and mortality. Furthermore, the high rate of suicide in this type of patient compared to unipolar depression should be highlighted [40]. BD is a leading cause of global disability. Therefore, the correct diagnosis of BD must be a priority item in healthcare systems, for clinical, research and administrative purposes.

For 60 years, psychiatric case records have been considered important epidemiological research tools for estimating the incidence and prevalence of treatment and care patterns [51]. The classification is considered a tool for investigating medical problems that has a useful scope focused on medical diagnosis. There are different techniques used in classification such as expert systems, artificial neural networks, fuzzy system, machine learning (ML) and deep learning. [3, 7, 24, 32, 38].

As for classification algorithms, conventional classifiers such as neural network [24, 42], singular value decomposition (SVD) [19, 58] and Bayesian linear discriminant analysis (BLDA) [60, 62] are widely used. In addition, researchers have also attempted different ML methods such as support vector machines (SVM) [18, 22, 26, 32, 57], k-nearest neighbour (KNN) [18, 53, 59], Bayes Classification [6, 13], Gaussian Naïve Bayes (GNB) [12, 16], random forest (RF) [17, 50], decision tree (DT) [18, 41], adaptive boosting (Adaboost) [27, 52] and adaptive neuro-fuzzy systems [23, 43] to classify data. In this study, we propose an extreme gradient boosting (XGB) method for the classification of patients with bipolar disorder. XGB is one of the variants of gradient boosting, and it is a supervised learning algorithm. It is a decision-tree-based ensemble ML algorithm that uses a gradient boosting framework. XGB is designed to enhance the performance and speed of a ML model. The implementation of XGB provides several advanced features for model fitting, algorithm improvement and computer environments [9, 11, 49]. As a result, this algorithm was implemented for the creation of a new tool that allows physicians to make decisions based on real clinical data.

The article is structured in several sections. Section 2 presents the materials used in this study. Section 3 shows our proposed approach. The description of the results and the discussion are given in Sects. 4 and 5, respectively. Finally, the conclusions are shown in Sect. 6.

2 Material

In this study, real EEG recordings have been used to review the operation of the ML system. One hundred and five euthymic bipolar disorder and two hundred and five comparison subjects were tested for brain-disorder diagnosis measured by EEG recording. The Structured Clinical Interview for DSM-IV (SCID) was given to all subjects to obtain the DSM-IV diagnoses. Participants in the study lived in the Cuenca region (Spain) and the patients with BD belonged to the Severe Mental Disorders Program of the Psychiatric Service of the Virgen de la Luz Hospital, Cuenca (Spain). All participants provided written informed consent after being given an explanation of the study and the procedures involved. The study was approved by the Clinical Research Ethics Committee of the Cuenca Health Area. The EEG records were recorded at the Psychiatric Service of the Virgen de la Luz Hospital in Cuenca (Spain). The equipment available at the Hospital was used to perform the EEGs, specifically the 32-channel Brain Vision system with a sampling frequency of 500 Hz. The International System 10-20 was used to place the electrodes by the medical staff. The EEG records of the different patients presented various noise samples, such as muscle noise, artefacts, and baseline. To get a more accurate result of the proposed XGB method, these signals were filtered out [29, 46, 48]. It should be noted that the datasets generated and/or analysed during the present study are not publicly accessible. Nevertheless, they are available from the corresponding author upon reasonable request.

Fig. 1 shows an example the raw EEG recording and scalp maps, the colours representing the value of the signal at that point. Scalp maps display the distribution of voltage in the head in the time or frequency domain. Information about the position of the electrodes is used to create the maps. In our case, according to the 10/20 system for data acquisition. The algorithm used to create the scalp map is based on spherical spline interpolation [35]. To calculate the spherical splines, different parameters are used: the order of the splines and the maximum degree of the Legendre polynomial. The interpolation will be flatter or wavier, depending on which values are used for the order. The interpolation with an increasing order of splines becomes flatter. The Lambda approximation parameter defines the accuracy with which the spherical splines are approximated to the data to be interpolated [35].

Fig. 1
figure 1

In the figure, a signal from a patient can been observed. In this graph, the raw EEG recording and the scalp maps are shown

Full size image

The proposed methodology consists of three main steps, as shown in Fig. 2. First, the EEG recordings were pre-processed to eliminate the interference and noise present. Then, the different features were calculated for each EEG channel. Once the study database was built, the last phase was the classification of bipolar disorders using the ML methods.

Fig. 2
figure 2

Organisation of the proposed system for detecting patients with bipolar disorders

Full size image

3 Model Development

XGB is a supervised learning method designed to be highly efficient, flexible and portable. It implements automatic learning algorithms under the Gradient Boosting framework. XGB provides a parallel tree reinforcement (also known as GBDT, GBM) that solves many data science problems quickly and accurately. Some of the main benefits of XGB are that it is highly scalable/parallel, fast to run and that it normally outperforms other algorithms [9, 11, 37]. For these reasons, in this study, this method has been used. XGB is adopted to construct the model to identify patients with bipolar disorder. Given a data set \(S=\{x_{j},y_{j}\}\), an ensemble model was designed by

$$\begin{aligned} \widehat{y_{j}}=\sum _{p=1}^{P}t_{p}(x_{j}), \end{aligned}$$
(1)

where \(y_{j}\) is the output, \(x_{j}\) represents the input vector with m temporal variables, \(\widehat{y_{j}}\) symbolizes the predicted output, \(j=1;2;..;n\), P is the number of trees, \(t_{p}\) belongs to a tree with the weight of the leaf \(w_{p}\) and with the structure \(u_{p}\). Trees are predictive models formed by rules that distribute the observations according to their attributes and thus predict the value of the response variable. The proposed model is formed by a set of individual trees, trained sequentially, so that each new tree tries to improve the errors of the previous trees. The prediction of a new observation is obtained by aggregating the predictions of all the individual trees that make up the model.

A change from ensemble systems is the term regulation. The weight of the leaf nodes and the tree depth represent the term of regulation of the objective function of XGB, which can control the complexity of the model and avoid overfitting. In this study, Taylor’s second-order expansion is used to approximate the XGB objective function as it improves the accuracy of the prediction [9, 11, 37]. In the proposed method, the regularized objective function is described as follows

$$\begin{aligned} R=\sum _{j}r(\widehat{y_{j}},y_{j})+\sum _{p}\varPsi (t_{p}), \end{aligned}$$
(2)

where \(\sum _{j}r(\widehat{y_{j}},y_{j}\) is a differentiable convex loss function between true and predicted labels to measure how well the classification model fit the training data, and \(\sum _{p}\varPsi (t_{p})\) is a regularisation term which controls the complexity of the model

$$\begin{aligned} \varPsi (t_{p})=\lambda f_{p}+\frac{1}{2}\gamma \left\| w_{p}\right\| ^{2}, \end{aligned}$$
(3)

where \(f_{p}\) corresponds to the number of leaves in the tree. \(f_{p}\) shows the pruning of trees, used to monitor overfitting. Pruning is a method to improve generalization in trees. Once the trees are built, the proposed XGBoost performs a “pruning” step that, starting at the bottom (where the leaves are) and moving up to the root node, looks to see if the gain falls below \(\lambda \). If the first node encountered has a gain value below \(\lambda \), then the node is pruned and the pruner moves up the tree to the next node. If, on the other hand, the node has a gain greater than \(\lambda \), the node is left and the pruner does not check the parent nodes [9, 11, 37]. The function \(\varPsi ()\) punishes the complexity of the method. R() represents a function that measures the difference between the expected output \(\widehat{y_{j}}\) and the target output \(y_{j}\). The learning rate is symbolised by \(\lambda \), and w represents the vector of scores on leaves. To control the weight of the complexity of the system, a parameter \(\gamma \) is used [9, 11, 37]. The proposed method seeks to minimise Eq. (2) to improve the performance.

The tree set model incorporates the functions of the functions into Eq. (2). Because of this, Eq. (2) cannot be optimised by applying traditional systems of optimisation in Euclidean space. Therefore, in this work, \(\widehat{y_{j}}\) was the estimation of the sample j-th in the iteration s-th. Eq. (2) is left as follows

$$\begin{aligned} R^{(s)}=\sum _{j=1}r(\widehat{y_{j}}^{(s-1)},y_{j}+C_{s}(x_{j}))+\varPsi (C_{s}). \end{aligned}$$
(4)

To decrease the objective function, the generated tree \(C_{s}\) by the j-th sample in the s-th iteration is aggregated. In the proposed algorithm, a second-order approximation is used to improve the objective function [9, 11, 37]

$$\begin{aligned} R^{(s)}\thickapprox \sum _{j=1}\left[ r(\widehat{y_{j}} ^{(s-1)},y_{j})+h_{j}C_{s}(x_{j})+\frac{1}{2}b_{j}C_{s}^{2}(x_{j})\right] +\varPsi (C_{s}), \end{aligned}$$
(5)

where \(h_{j}=\partial _{\widehat{y_{j}}^{(s-1)}}r(\widehat{y_{j}}^{(s-1)},y_{j})\) is the first-order gradient statistic in the loss function R() and \(b_{j}=\partial _{\widehat{y_{j}}^{(s-1)}}^{2}r(\widehat{y_{j}}^{(s-1)},y_{j})\) is the second.

\(r(\widehat{y_{j}}^{(s-1)},y_{j})\) represents a constant value for the tree \(s-1\). At the current step s, the prediction of step \(s-1\) and everything before the regularization s are known values, so they are constant values in the object function of step s, so it can be eliminated to simplify Eq. (5) [9, 11, 37]. If we consider that \(K_{j}=\{j|u(x_{i})=v\}\) is the sample set of the leaf v, \(v=1,2,..,f_{p}\) and we extend \(\varPsi ()\), Eq. (5) would be shown as

$$\begin{aligned} {\widetilde{R}}^{(s)}\thickapprox \sum _{j=1}\left[ \sum _{j\in K_{v}}(h_{j})w\_r_{v}+\frac{1}{2}\sum _{j\in K_{v}}(b_{j}+\gamma )w\_r_{v}^{2} \right] +\lambda F, \end{aligned}$$
(6)

where \({\widetilde{R}}^{(s)}\) represents the simplification of \(R^{(s)}\) by eliminating the constant terms. A leave represents a node that can no more be divided. The optimal weight \(w\_r_{v}\) of the leave v for a fixed structure u(x) can be calculated as

$$\begin{aligned} w\_r_{v}=-\frac{\sum _{j\in K_{v}}(h_{j})}{\sum _{j\in K_{v}}(b_{j}+\gamma )}. \end{aligned}$$
(7)

And finally, for the proposed method the optimal value can be obtained by

$$\begin{aligned} {\widetilde{R}}^{(s)}(u)=-\frac{1}{2}\sum _{v=1}^{f_{p}}\frac{(\sum _{j\in K_{v}}(h_{j}))^{2}}{\sum _{j\in K_{v}}(b_{j}+\gamma )}+\lambda F. \end{aligned}$$
(8)

As the number of tree structures is infinite, not all viable tree structures can be listed. Because of this, the optimal splitting point is sought by constructing the tree from a single leaf and adding branches to the tree iteratively. \(K_{L}\) and \(K_{R}\) represent the samples of the left and right nodes after the splitting and \(k=K_{L} \cup K_{R}\), the reduction in the loss after the split is given by

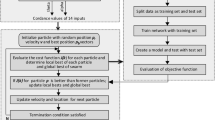
$$\begin{aligned} R_{split}=\frac{1}{2}\left[ \frac{(\sum _{j\in K_{L}}(h_{j}))^{2}}{\sum _{j\in K_{L}}(b_{j}+\gamma )}+\frac{(\sum _{j\in K_{R}}(h_{j}))^{2}}{\sum _{j\in K_{R}}(b_{j}+\gamma )}-\frac{(\sum _{j\in K}(h_{j}))^{2}}{\sum _{j\in K}(b_{j}+\gamma )} \right] -\lambda . \end{aligned}$$
(9)

Five broadly known ML methods were used to train the models for classifying the patients in two groups, patients with bipolar disorder and healthy patients. The methods included DT [18, 41], GNB [16], KNN [18, 53, 59], SVM [18, 22, 57] and the proposed method XGB [9, 11]. The ML methods were implemented using the statistics and machine learning MatLab toolbox (Matlab 2020a), The Mathworks Inc., Natick, MA, USA. For the evaluation cohort of patients, 10-fold cross-validation was used to validate algorithm performance [18]. For each fold of the validation, 70% of the patients were used to train and the remaining 30% were used for testing and validation. Patient data were not shared across training and testing subsets to avoid the algorithm being tested on data from the same patients used for training. Fig. 3 describes the process followed to carry out the complete study. As can be observed, first the subjects to be studied were selected. Once the database was created, the training and validation of the implemented ML methods was carried out.

Fig. 3
figure 3

Training and validation scheme for machine learning methods

Full size image

ML techniques usually have one or more hyperparameters that allow a different adjustment of the algorithm during the training process. The different values of these hyperparameters (number of splits, learners, neighbours, distance metric, distant weight, kernel, box constraint level, multiclass method, etc) for each method lead to algorithms with different prediction performances in order to obtain the best possible performance. In order to optimise these hyperparameters for each ML technique used in this study, each model was trained with a Bayesian optimisation approach. Bayesian optimisation aims to estimate which is the configuration of hyperparameters that would maximise the performance of the algorithm from the previous attempts, based on the assumption that there is a relationship between the various hyperparameters and the performance achieved by the algorithm. The area under the AUC and the balanced accuracy were used as performance measures to be maximised. 100 repetitions were used to calculate the mean and standard deviation values of the various performance result numbers computed, given the stochastic nature of machine starting and ML in all simulations. In order to decrease the effects of noise on the data, to calculate accurate area under the curve (AUC) values and to obtain statistically significant results, the experiments were repeated in a uniformly random way.

3.1 Methods Used for Comparison

3.1.1 Gaussian Naive Bayes (GNB) Method

GNB is one of the simplest classification algorithms. It consists in assigning the label of the class that maximizes the posterior probability of each sample, under the assumption that the voxel contributions are conditionally independent and obey a Gaussian distribution. The GNB decision rule is written in terms of the discriminant function for each class k at each searchlight s (the searchlight index is omitted in the next equation to avoid visual clutter). The discriminant function is defined as the sum of the squared distances to the centroid of each class, across all voxels in the searchlight, weighted by the variance, and the logarithm of the a priori probability \(p_{k}\) computed in the training set, according to the Bayes rule (see equation (2)). The predicted class for sample i in the test set is assigned by selecting the label of the class having the discriminant function with the largest value, which implies maximal posterior probability, within discriminant functions of all classes [12, 16].

3.1.2 Decision Tree (DT) Method

This classifier partitions the input space into small segments and labels these small segments with one of the various output categories. However, conventional decision tree only does the partitioning to the coordinate axes. With the growth of the tree, the input space can be partitioned into very small segments so as to recognize subtle patterns [18, 41]. The main drawback is that overgrown trees could lead to overfitting.

3.1.3 Support Vector Machines (SVM) Method

The support-vector machine or network is a supervised learning technique for two-group classification problems. The machine conceptually implements the following idea: input vectors are nonlinearly mapped to a very high-dimension feature space. In this feature space, a linear decision surface is constructed. Special properties of the decision surface ensure high generalization ability of the learning machine. Given a training set, whose elements are marked as belonging to one of two categories, the SVM builds a model that assigns the elements of the testing set to one category or the other, making it a non-probabilistic binary linear classifier. The SVM model represents the samples as points in space, mapped so that the samples of the separate categories are divided by a clear gap that is as wide as possible. New samples are then mapped into that same space and predicted as belonging to a category based on which side of the gap they fall in. The SVM algorithm can efficiently perform both a linear and a nonlinear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces. Using a cubic or a Gaussian function for the kernel, we obtain the so-called cubic SVM and Gaussian SVM, respectively [18, 22, 57].

3.1.4 K-Nearest Neighbour (KNN) Method

This classifier is one of the most popular neighbourhood classifiers in pattern recognition and machine learning because of its simplicity and efficiency. It categorizes each unlabelled test example using the label of the majority of examples among its k-nearest (most similar) neighbours in the training data set. The similarity depends on a specific distance metric; therefore, the performance of the classifier strictly depends on the distance metric used. However, it suffers of memory requirements and time complexity, because it is fully dependent on every example in the training set [18, 53, 59].

SVM and KNN exemplify several important trade-offs in machine learning. SVM is less computationally demanding than KNN and is easier to interpret but can identify only a limited set of patterns. On the other hand, KNN can find very complex patterns, but its output is more challenging to interpret. SVM take cares of outliers better than KNN. If training data are much larger than no. of features(m\(\gg \)n), KNN is better than SVM. SVM outperforms KNN when there are large features and lesser training data. On the other hand, in almost all cases, the SVM is better than the GNB. From a theoretical point of view, it is a little bit hard to compare the two methods. One is probabilistic in nature, while the second one is geometric. With respect to DT and KNN methods, it should be noted that both are nonparametric methods. Decision tree supports automatic feature interaction, whereas KNN cannot. Decision tree is faster due to KNN’s expensive real-time execution.

3.2 Feature Extraction

3.2.1 Approximate Entropy

Approximate entropy (ApEn) was developed by Pincus [36] as a measure of system complexity. ApEn presents a non-negative number to quantify the complexity of the time series data. The higher the value of ApEn, the more complex or irregular the time series data are [36, 39, 55].

Suppose the original time series with N data points \(\{x(l),l=1,...,N\}\). The calculation of the ApEn is shown in the following steps ([36, 39, 55].

  1. 1.

    Construct a series of vectors in the embedding space \(R^{m}\) defined by

    $$\begin{aligned} X(i)=[x(i),x(i+1),...,x(i+m-1)], \end{aligned}$$
    (10)

    where \(1\le i\le N-m+1\).

  2. 2.

    Compute the distance between X(i) and X(j), 

    $$\begin{aligned} d_{ij}=\max _{k=0\thicksim m-1}\left| x(i+k)-x(j+k)\right| , \end{aligned}$$
    (11)

    where \(0\le k\le m-1\) and \(1\le i,j\le N-m+1\).

  3. 3.

    Given the vector comparison distance \(r(r>0)\), for each X(i), count the number of \(d_{ij}\le r,\) denoted as \(N_{i}^{m}(r)\). And then define the ratio between the number \(N_{i}^{m}(r)\) and the total number of the vectors as \(C_{i}^{m}(r)\)

    $$\begin{aligned} C_{i}^{m}(r)=\frac{N_{i}^{m}(r)}{N-m+1}. \end{aligned}$$
    (12)
  4. 4.

    Compute the natural logarithm of the ratio \(C_{i}^{m}(r)\), then average it over i

    $$\begin{aligned} \varPhi ^{m}(r)=\frac{1}{N-m+1} {\displaystyle \sum \limits _{i=1}^{N-m+1}} \ln \text { }C_{i}^{m}(r). \end{aligned}$$
    (13)
  5. 5.

    Increase m by one and repeat steps (1)—(4). Thereby, \(C_{i}^{m}(r)\) and \(\varPhi ^{m+1}(r)\) are obtained.

  6. 6.

    ApEn is given by \(\varPhi ^{m}(r)\) and \(\varPhi ^{m+1}(r)\) as follows

    $$\begin{aligned} ApEn(mr)=\lim _{N\rightarrow \infty }\left[ \varPhi ^{m}(r)-\varPhi ^{m+1}(r)\right] . \end{aligned}$$
    (14)
  7. 7.

    If the number of data point N is limited, ApEn is estimated by the statistic values, i.e.

    $$\begin{aligned} ApEn(m,r,N)=\varPhi ^{m}(r)-\varPhi ^{m+1}(r). \end{aligned}$$
    (15)

Based on the works of Pincus [36, 39, 55], the embedding dimension m and vector comparison distance r were, respectively, set to 2 and 0.05 times the standard deviation of the EEG time series.

3.2.2 EEG Band Power

To extract the four frequency bands (delta (0.5-4 Hz), theta (4-8 Hz), alpha (8-13 Hz) and beta (13-30 Hz)), the EEG signals were filtered out by a Butterworth bandpass filter. Welch method was selected to obtain the power spectrum of each band. To calculate the power, the time series were divided into segments and then averaged with all the segments [4].

Denote the mth windowed, zero-padded frame from the signal x by

$$\begin{aligned} xm(n)=w(n)x(n+mR),{ \ \ \ }n=0,1,..M-1{, \ }m=0,1,..,k-1, \end{aligned}$$
(16)

where R is defined as the window hop size, and let K denote the number of available frames. Then, the periodogram of the mth block is given by

$$\begin{aligned} P_{x_{m}},_{M}(w_{k})=\frac{1}{M}\left| {\displaystyle \sum \limits _{n=0}^{N-1}} x_{m}(n)e^{-j2\pi nk/N}\right| ^{2}, \end{aligned}$$
(17)

as before, and the Welch estimate of the power spectral density is given by

$$\begin{aligned} {\widehat{S}}_{x}^{W}(w_{k})=\frac{1}{K} {\displaystyle \sum \limits _{m=0}^{K-1}} P_{x_{m},M}(wk). \end{aligned}$$
(18)

When w(n) is the rectangular window.

The relative power contained in these bands is defined as

$$\begin{aligned} \delta= & {} \frac{1}{P} {\displaystyle \sum \limits _{f=0.5Hz}^{4Hz}} p_{f}{ , \ }\theta =\frac{1}{P} {\displaystyle \sum \limits _{f=4Hz}^{8Hz}} p_{f}, \end{aligned}$$
(19)
$$\begin{aligned} \alpha= & {} \frac{1}{P} {\displaystyle \sum \limits _{f=8Hz}^{13Hz}} p_{f}{ , \ }\beta =\frac{1}{P} {\displaystyle \sum \limits _{f=13Hz}^{30Hz}} p_{f}, \end{aligned}$$
(20)

where P is the total power of the signal and p\(_{f}\) the power spectrum.

3.2.3 Higuchi

To calculate the fractal dimension (FD) of time series, Higuchi proposed an efficient algorithm [14]. This algorithm calculates the FD directly from the time series. This algorithm can be used to measure the complexity of the EEG records and self-similarity of a signal [1, 20].

Higuchi proposed in 1988 an efficient algorithm for measuring the FD of discrete time sequences. Higuchi’s algorithm calculates the FD directly from time series. As the reconstruction of the attractor phase space is not necessary, this algorithm is simpler and faster than D2 and other classical measures derived from chaos theory. FD can be used to quantify the complexity and self-similarity of a signal. Higuchi fractal dimension (HFD) has already been used to analyse the complexity of brain recordings and other biological signals [1, 14, 20].

Given a one-dimensional time series \(X=x[1],x[2],...,x[N]\), the algorithm to compute the HFD can be described as follows [1, 14, 20]

  1. 1.

    Form k new time series \(X_{k}^{m}\)defined by

    $$\begin{aligned} X_{k}^{m}=\left\{ x[m],x[m+k],x[m+2k],...,x\left[ m+int\left( \frac{N-m}{k}\right) \cdot k\right] \right\} , \end{aligned}$$
    (21)

    where k and m are integers, and \(int(\bullet )\) is the integer part of \(\bullet \). k indicates the discrete time interval between points, whereas \(m=1,2,...,k\) represents the initial time value.

  2. 2.

    The length of each new time series can be defined as follows

    $$\begin{aligned} L(m,k)=\frac{\left\{ \left( {\displaystyle \sum \limits _{i=1}^{int\left( \frac{N-m}{k}\right) }} \left| x[m+ik]-x[m+(i-1)\cdot k]\right| \right) \frac{N-1}{nt\left( \frac{N-m}{k}\right) \cdot k}\right\} }{k}, \end{aligned}$$
    (22)

    where N is length of the original time series X and \((N-1)/\{int[(N-m)k]\cdot k\}\) is a normalization factor.

  3. 3.

    Then, the length of the curve for the time interval k is defined as the average of the k values L(m, k), for \(m=1,2,\ldots ,k:\)

    $$\begin{aligned} L(k)=\frac{1}{k}\sum _{m=1}^{k}L(m,k). \end{aligned}$$
    (23)
  4. 4.

    Finally, when L(k) is plotted against 1/k on a double logarithmic scale, with \(k=1,2,...,k_{max}\), the data should fall on a straight line, with a slope equal to the FD of X. Thus, HFD is defined as the slope of the line that fits the pairs \(\{ln[L(k)],ln(1/k)\}\) in a least-squares sense [1, 14, 20].

3.2.4 Detrended Fluctuation Analysis

Another technique used to obtain information from the EEG is the detraction analysis fluctuation (DFA). This algorithm allows the quantification of long-range temporal correlations in the EEG time series. In addition, DFA can eliminate trends of different order caused by noise from EEG time series and is robust to non-seasonality. DFA is based on calculating the root mean square error of the fluctuation time series [21, 25].

DFA provides different values of alfa. With \(\alpha =0.5\), the EEG signal is a random walk. When \(0<\alpha <0.5\), there exist anti-correlation ship power laws in the EEG signal. When \(0.5<\alpha <1\), there exist long-range correlations of the power law [21, 25].

DFA is a method for quantifying fractal scaling and correlation properties in the signal. The advantages of this method are that it distinguishes between intrinsic fluctuation generated by the system and those caused by external system. In the DFA computation of a time series, x(t) of finite length N is integrated to generate a new time series y(k) shown in (1) [21, 25]

$$\begin{aligned} y(k)=\sum _{i=1}^{k}\left[ x(i)-\left\langle x\right\rangle \right] , \end{aligned}$$
(24)

where \(\left\langle x\right\rangle \) is the average of x, is given by

$$\begin{aligned} \left\langle x\right\rangle =\frac{1}{N} {\displaystyle \sum \limits _{i=1}^{k}} x(i). \end{aligned}$$
(25)

Next, the integrated time series, y(k), is divided into boxes of equal length and a least squares line is fit to the data of each box, represents by \(y_{n}(k)\). Then, the time series y(k) is detrended by subtracting the local linear fit \(y_{n}(k)\) for each segment. The detrended fluctuation is given after removing the trend in the root-mean-square fluctuation

$$\begin{aligned} F(n)=\sqrt{\frac{1}{N}\sum _{k=1}^{N}\left[ y(k)-y_{n}(k)\right] ^{2}}. \end{aligned}$$
(26)

This computation is repeated for different box sizes (time scale) to characterize the relation between F(n) and the box size n. A linear relation between logarithm of F(n) and size of the box indicates the presence of power-law scaling: \(F(n)\sim n^{\alpha }\) . The scaling exponent, \(\alpha \), can be calculated as the slope of log F(n) versus log n. This parameter represents the correlation properties of the time series [21, 25].

3.2.5 Hurst Exponent

Hurst exponent was utilised to describe the correlation properties and the self-similarity of the physiological timeline data. Hurst exponent measures the smoothness of a fractal time series supported by the asymptotic performance of the reprogrammed process range [2, 33].

Assuming a time series is \(x(i),i=1,...,N\) . The deviation from the mean \(\overline{x(n)}\) for the first k data points is defined as

$$\begin{aligned} W_{k}=(x_{1}+x_{2}+\cdots +x_{k})-k\overline{x(n)}, \end{aligned}$$
(27)

where \(1\le k\le n\) and \(1\le n\le N\).

Then, the difference between the maximum value and minimum value of the deviations corresponding to n is acquired by

$$\begin{aligned} R(n)=max(0,W_{1},\ldots ,W_{n})-min(0,W_{1},{\ldots \cdots \ldots },W_{n}),\quad n=1,\ldots ,N. \end{aligned}$$
(28)

If S(n) denotes the standard deviation of the time series \(\{x(i),i=1,\ldots ,n\}\) , R(n)/S(n) increases as a power law

$$\begin{aligned} \frac{R(n)}{S(n)}=C\times n^{H},\quad n=1,\ldots ,N, \end{aligned}$$
(29)

where C is a constant and H is the estimated value of the Hurst exponent, i.e.

$$\begin{aligned} H=\frac{\log \text { }\left[ R(n)/S(n)\right] }{\log \text { }n},\quad n=1,\ldots ,N. \end{aligned}$$
(30)

3.3 Performance Evaluation

Performance was measured using the most familiar metrics: sensitivity (SE) (also known as the recall), positive predictive value (PPV) (also known as the precision), negative predictive value (NPV), specificity (SP), degenerated Youden’s index (DYI) [63], receiver operating characteristic (ROC) and AUC. The F1-score is defined as

$$\begin{aligned} Precision= & {} \frac{TP}{TP+FP}, \end{aligned}$$
(31)
$$\begin{aligned} Recall= & {} \frac{TP}{TP+FN}, \end{aligned}$$
(32)
$$\begin{aligned} F_{1}score= & {} 2\frac{Precision\cdot Recall}{Precision+Recall}. \end{aligned}$$
(33)

Another measure of overall model classification performance is the Matthew’s correlation coefficient (MCC), and it is defined as

$$\begin{aligned} MCC=\frac{TP\cdot TN-FP\cdot FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}, \end{aligned}$$
(34)

where TP represents the number of true positives, FP the number of false positives, TN the number of true negatives, and FN the number of false negatives. And finally, Cohen’s Kappa (CK), CK is another metric estimating overall model performance, attempts to leverage the Accuracy by normalizing it to the probability that the classification would agree by chance [63].

4 Results

This section describes the results obtained with the EEG records used for training and validation in the classification of bipolar disorder. The performance of the proposed system has been compared with different classification ML methods accepted in the scientific community.

The data obtained through the different features were used for the training of the ML techniques. As can be seen in Fig. 4, these were applied to each of the features separately and finally, the systems were trained with the integration of all of them. According to the data obtained, the proposed XGB method achieves a better classification for the different features.

Fig. 4
figure 4

Results obtained using different features for the proposed system and other machine learning methods analysed

Full size image

Table 1 shows the values of balanced accuracy, recall, precision and \(F_{1}\) score of the classification methods for patients with bipolar disorder and healthy patients, such as SVM, DT, GNB, KNN and proposed system with the integration of the features. Systems based on SVM and GNB obtain lower classification values than other methods with accuracy values close to 86%, and this value is considerably improved with DT and KNN methods that reached values around 88%. On the other hand, the proposed system, based on a XGB, obtained a higher performance than the rest of the methods analysed. Achieving accuracy values close to 94% for real EEG records. As for the Precision and Recall values, the KNN and DT methods are the closest to the proposed XGB system. In the case of the \(F_{1}\) score value, the SVM and GNB methods obtain values close to 86%. The DT and KNN systems improve this data again. As for DT and KNN, they do not reach the result achieved by the proposed method that improves them in 4.9%.

Table 1 The table presents the mean values and standard deviation of balanced accuracy, recall, precision and \(F_{1}\) score of the machine learning models and the proposed method implemented in this article
Full size table

Other parameters used in the scientific community, such as AUC, MCC, DYI and Kappa index, have also been analysed to check the operation of the proposed XGB system. These parameters will help us to check the correct functioning of the methods when classifying the two classes investigated in the study. The Matthews correlation coefficient (MCC) is a more reliable statistical rate which produces a high score only if the prediction obtained good results in all of the four confusion matrix categories (true positives, false negatives, true negatives, and false positives), proportionally both to the size of positive elements and the size of negative elements in the dataset. As can be seen in Table 2, the XGB method achieves an MCC value closer to 1 than the other methods. DT and KNN are the systems that present a MCC value closer to the proposed method. The rest of the methods obtain a smaller value. Another parameter used is the kappa index; in this case, the proposed XGB system obtains again a higher value than KNN and DT. The other methods used in the comparison reach values further away from 1.

Table 2 The table shows the mean values and standard deviation of AUC, MCC, DYI and Kappa of all the tested machine learning models and the proposed method implemented in our study
Full size table

Figure 5 compares the proposed XGB with the existing classifiers, i.e. GNB, SVM, DT and KNN with respect to accuracy, recall and precision metrics. The values of obtained by the proposed XGB are 0.941, 0.941 and 0.944, respectively, while KNN are 0.896, 0.897 and 0.889. Fig. 6 shows the values obtained for MCC, Kappa and F1-score. As can be seen, the proposed method achieves values of 0.910, 0.915 and 0.947, respectively. The next system that comes closest to XGB is KNN with values of 0.790, 0.797 and 0.892. As can be observed in these two figures, for all the metrics compared, the proposed XGB presents a superior performance in predicting patients with bipolar disorder.

Fig. 5
figure 5

Graphical representation of the precision, recall and accuracy values in percentages

Full size image
Fig. 6
figure 6

Graphical representation of the MCC, Kappa and \(F_{1}\) score values in percentages

Full size image

The receiver operating characteristic (ROC) has been applied to compare the classification capability of the proposed system with other ML methods. The curve is the result of representing, for each threshold value, the sensitivity and specificity measurements [15]. Fig. 7 shows the result obtained by the different systems for the classification between patients with bipolar disorder and healthy patients. According to Table 1, the proposed XGB method has a larger area under the curve (0.94) and the KNN method (0.89) is the closest to the proposed method. With all this, the XGB method achieves an improvement of 4.5% over KNN for DYI (DYI parameter, values nearer to 1 indicate a better classification). KNN an improvement of 2.11% with respect to the SVM method and 3.33% with respect to GNB.

Fig. 7
figure 7

ROC curves for the five assessed machine learning predictors

Full size image

For clarity, all metrics have been grouped by each training and test data set and presented as radar plot. A perfect score on all metrics would be represented by a circle the size of the entire grid. In our study, the model training sets have high scores on all training set metrics and generally have lower scores for the test set. The shape of the plots may also be indicative of the quality of the models. The larger the circle of the test set, the better the model. The proposed XGB system (Fig. 8) is a good example of a well-balanced model. The training and test sets are both virtually represented by similar circular plots. As can be observed, the GNB method has the worst performance in most metrics.

Fig. 8
figure 8

The figure shows the radar plot of the training phase (left) and test (right) for the prediction of bipolar disorders

Full size image

With these results, the proposed system can achieve a high accuracy of classification of bipolar disorder patients automatically, resulting in a tool that could help the physician for clinical practice.

5 Discussion

The discrimination of bipolar disorders is a hard classification problem which requires the use of a strong optimizing algorithm and an effective feature set selection procedure. Automated detection can guide treatment decisions, help prognostication and study the pathophysiology of bipolar disorders [46].

In this work, the XGB method has been selected because it has excellent scalability and a high running speed, which have made it a successful ML method [10]. In addition, machine learning approaches allow for the parallel testing of multiple variables and their complex interactions and enable nonlinearity in the production of predictive models [10]. This method has been applied to various machine learning problems. In biomedical fields, XGB has been used to classify cancer patients [28], patients with epilepsy [47] and to diagnosis chronic kidney disease [34]. Especially, Sodmann et al. [45] trained a convolutional neural network for ECG annotation and employed XGB to classify atrial fibrillation (AF). Shi et al. [44] also used XGB for the classification of AF aimed at single heartbeat classification, and Ye et al. [54] implemented the state-wide electronic health record to predict the risk of hypertension with the XGB method. Yu et al. [56] and Zhong et al. [61] also took advantage of the XGB method for predicting the location of submitochondrial and essential proteins in their respective works.

In this study, a XGB was effectively applied to this pattern recognition task. The results show that discriminating between BD patients and healthy control with a high accuracy can be possible by using our proposed XGB classification framework. A maximum classification accuracy of 94.13% was obtained demonstrating the potential clinical use of our XGB framework to classify BD patients with an EEG data. The proposed system was analysed with different ML methods described in the literature, as can be seen in Tables 1 and 2. The comparison of the systems showed the considerable improvement that XGB produced over the other methods analysed. SVM and GNB methods performed less well than the other systems compared. The system that most closely approximates the recall accuracy values of the proposed method is KNN. In addition, a balanced radar plot was provided between the training and test phases. The proposed XGB system can handle the high dimensions of the data avoiding overtraining. The results show that the proposal can effectively improve the performance of other classification methods. Because of this, the proposed system can be a reliable tool that facilitates automatic analysis to assist in the diagnosis of bipolar disorder.

6 Conclusion

In this paper, the proposed XGB method is applied for classification between patients with bipolar disorder and healthy patients. Four supervised ML algorithms including a k-nearest neighbours (KNN), decision tree (DT), Gaussian Naïve Bayes (GNB) and support vector machine (SVM) were compared with the proposed XGB method. The proposed system in this work has achieved higher values of precision, recall and accuracy than those achieved by other methods. This guarantees its reliability for the automatic classification of the pathology treated in this study. Finally, it is important to see that high performance has been achieved with the XGB method, so this system would facilitate the physicians in the decision-making process.