1 Introduction

Estimating for the parameters of multi-frequency signal models and dynamical systems has many engineering applications, such as channel sounding, power quality analysis, wireless communication systems [16,17,18,19,20,21,22]. Moreover, a periodic signal can be transformed into the sum of multi-sine or multi-cosine signals in accordance with the Fourier transform. In addition, parameter estimation of sinusoidal signals plays a vital role for the quality monitoring and reliability assessment of power systems [55, 58, 99]. Sine waves are easily generated within a wide frequency range and can be simply analyzed in frequency domain and time domain which are widely used as excitation signals in devices, circuits and control systems [62, 68]. Many engineering applications need to accurately estimate the signal parameters of sine waves, and many parameter estimation algorithms for sine waves were proposed in time domain and frequency domain such as the three-parameter sine-fitting least squares method or four parameter least squares method [1, 5, 34]. All these methods are supposed that the frequencies of the noisy sine-waves are known. However, many practical applications need to accurately obtain the parameter estimates of signals in real-time in the condition that no priori knowledge on frequencies is known [4]. Practically, the unknown signal parameters describing circuits or devices can be estimated by discrete measurements based on the minimization of the squared residual error between a practical signal and the available output measurements of the signal [35]. In most cases, for the sine-wave signals, all of the characteristic parameters comprising the amplitude, frequency and phase of the basic wave and each harmonic wave component are unknown. Therefore, it is meaningful to estimate all of the signal parameters under the circumstances that frequency, phase and amplitude parameters are unknown in advance.

Various parameter estimation algorithms with regard to multi-sine signals have been addressed and used widely in engineering fields. Zhao et al. [96] proposed a least squares multi-frequency identification approach to estimate the amplitude and phase of signals having multiple frequencies, but this method is realized on the premise of known main frequency values. Chaudhary et al. proposed a fractional order LMS parameter estimation algorithm to estimate power signal with the form of a multi-frequency sine signal. However, all of the characteristic parameters cannot be estimated simultaneously [9]. Moreover, some estimation methods by means of discrete-time Fourier transform have been presented for identifying the parameters of sine-waves or multi-sine signals. Belega et al. [2, 6] developed a two-point interpolated discrete-time Fourier transform method to estimate the amplitude and phase of the noisy sine-waves. Moreover, they studied the performance of interpolated DFT algorithms based on few observed cycles [3]. Wang et al. proposed a four-point interpolated discrete-time Fourier transform estimation method simultaneously taking into consideration the fundamental component, frequency parts and direct-current component [75]. These methods based on the discrete-time Fourier transform need signal transformation, which can result in new errors. Therefore, the estimation processing is complicated and the parameter estimates are not accurate. In this study, we try to develop a parameter estimation method aiming to obtain all of the characteristic parameter estimates simultaneously and directly.

Separable techniques are used widely to solve nonlinear problems with a special structure in which the objective function to be minimized with respect to a number of parameters can separate two different characteristic parameter sets in accordance with different parameter characteristics. It is noted that one parameter set enters the objective function through a linear form and the other parameter set enters in a nonlinear form [10,11,12, 26,27,28,29,30]. By means of the separable techniques, the dimension of the parameter space is reduced for solving nonlinear optimization problems and the conditioned optimization problem can be improved. In system identification, the separable techniques are adopted to reduce the complexity of the identification algorithms, which are also called hierarchical identification methods [79]. The basic principle of the separable techniques is parameter decomposition or model decomposition. Generally, the identification model is separated into several identification models after decomposition. Then, many complicated nonlinear optimization problems can be solved by some linear optimal methods [85,86,87,88,89,90,91]. For example, Ngia proposed a separable nonlinear least-squares algorithm for offline and online identification through Kautz and Laguerre filters, in which a nonlinear least squares minimization problem became separable regarding the linear coefficients and got better condition than the original unseparated one [56]. Mahata et al. investigated a separable nonlinear least squares estimation algorithm in terms of the condition of complex valued data and established the convergence properties of the proposed parameter estimation algorithm [54]. In this study, the separable technique is expanded into the field of signal modeling to develop more effective parameter estimation methods.

It is well know that the observations contain the information of the systems or signals. If the observed data are collected in real time and used in identification methods, the obtained parameter estimates are more accurate than those obtained by offline measurements [33, 42, 67]. In general, the dynamical measurements can be single datum or batch data containing the dynamical information of the systems or signals to be identified. If more measurements are employed into identification algorithms, one can get more accurate estimation results [15, 69, 70]. Moreover, sliding window is widely employed in communication, control engineering and data processing, which are used to capture dynamical information [8, 66, 76]. In this study, we design the dynamical sliding window data to estimate the signal parameters by iterative strategies, which is called the multi-innovation iterative algorithm. In this method, the sliding window data dynamically change with time increasing. After new observed data are introduced to the sliding window, an iterative process happens until the satisfactory estimates are obtained. The multi-innovation has been used widely for the identification of linear systems and nonlinear systems [78]. Multi-innovation identification algorithms are proposed based on dynamical batch data and recursive estimation, which can be used in online identification. The multi-innovation is effective to improve the identification accuracy by expanding a scalar innovation into the innovation vector. Moreover, external disturbances, modeling errors and various uncertainties in real systems will influence the model accuracy. In order to overcome these problems, the filtering techniques are effective to cope with them [13, 23, 64, 65, 101]. In this paper, we study the parameter estimation methods for the multi-frequency signals by means of the multi-innovation and iterative estimation for presenting high-performance identification algorithms.

The main contributions of this paper are summarized as follows:

  • In accordance with different features of the parameters of the multi-frequency signals, the parameters are separated into a linear parameter set and a nonlinear parameter set to reduce parameter dimensions. Based on the separable parameter sets, two different objective functions are constructed, which shows linear form and nonlinear form.

  • In terms of different objective functions, two dynamical iterative sub-algorithms are derived by Newton optimization. Because the signal parameters are separated into a linear set and a nonlinear set, one of the sub-algorithms derived by the Newton optimization becomes the linear least squares method.

  • In order to capture the dynamical information of the signals to be modeled and obtain higher estimation accuracy, a sliding window and an iterative scheme are designed to employ the observations into the estimation computation. In the proposed signal modeling method, the iterative process and the real-time acquisition happen interactively, which can seize more dynamical information and obtain higher estimation accuracy.

The remainder of this paper is outlined as follows. In Sect. 2, the parameter estimation problems are described and the separable principle for the multi-frequency sine signal is introduced. In Sect. 3, we derive a multi-innovation Newton iterative parameter estimation sub-algorithm for the linear amplitude parameters. In Sect. 4, we present a multi-innovation Newton iterative estimation algorithm for the nonlinear angular frequency parameters. In Sect. 5, a separable multi-innovation Newton iterative parameter estimation algorithm is developed by combining two sub-algorithms. In Sect. 6, some numerical examples are provided to test the performance of the proposed method. Finally, we summarize the conclusions of this paper in Sect. 7.

2 Problem Description

Consider the following identification problem of the multi-frequency sine signal:

$$\begin{aligned} y(t)= & {} \sum _{i=1}^na_i\sin (\omega _i t)+v(t), \end{aligned}$$
(1)

where \(a_i\) is the amplitude parameters, \(\omega _i\) is the angular frequency parameter, \(i=1,2,\ldots ,n\), y(t) is the output of the signal model and v(t) is the noise with mean zero.

For measuring technique, oscilloscopes are convenient instruments for signal test and are used widely in many applications. However, the oscilloscopes only can obtain the single frequency of the periodic signal or the sine signal with a few frequencies. In statistical identification, the system models can be obtained by means of the measurement data from identification experiments. According to the statistical identification theory, we use the discrete measurement data \(y(t_k)\), \(k=1,2,\ldots \) to fit the multi-frequency sine signal. Using these discrete sampled data \(y(t_k)\) to fit the multi-frequency sine signal, we can obtain the fitting signal, see Fig. 1. The procedure for obtaining the parameter estimates of the signal models is called signal modeling.

Fig. 1
figure 1

Fitting multi-frequency sine signal using the discrete measurement

Full size image

From (1), we can see that the amplitude parameters \(a_i\), \(i=1,2,\ldots ,n\) are linear regarding y(t) while the angular frequencies \(\omega _i\) are nonlinear regarding y(t). This inspires us to decompose the characteristic parameters of the multi-frequency sine signal into separated parameter sets with different characteristics. Then, we separate the total parameter vector into two parameter sets, i.e., the amplitude parameter vector \(\varvec{a}\) and the angular frequency parameter vector \(\varvec{\omega }\):

$$\begin{aligned} \varvec{a}:=[a_1,a_2,\ldots ,a_n]^{\tiny \text{ T }}\in {\mathbb R}^n,\quad \varvec{\omega }:=[\omega _1,\omega _2,\ldots ,\omega _n]^{\tiny \text{ T }}\in {\mathbb R}^n. \end{aligned}$$

The current sampling moment is denoted by \(t=t_k\), \(k=0,1,2,\ldots \). Define the error between the observed output \(y(t_k)\) and the model output \(\sum \limits _{i=1}^na_i\sin (\omega _it_k)\) as

$$\begin{aligned} v(\varvec{a},\varvec{\omega },t_k):=y(t_k)-\sum _{i=1}^na_i\sin (\omega _it_k)\in {\mathbb R}. \end{aligned}$$

Using the latest window data with the length p up to the current time \(t=t_k\) to define the objective function of the sliding window data gives

$$\begin{aligned} J_1(\varvec{a},\varvec{\omega }):=\frac{1}{2}\sum _{m=k-p+1}^kv^2(\varvec{a},\varvec{\omega },t_m). \end{aligned}$$

Based on the separable parameter sets, the above objective function can be separated into two objective functions: One is with respect to the linear parameter set \(\varvec{a}\), and the other is with respect to the nonlinear parameter set \(\varvec{\omega }\). Therefore, the parameter decomposition leads to two identification sub-models and two identification sub-algorithms. In the next sections, we give the separable signal modeling method.

3 Multi-innovation Newton Iterative Parameter Estimation Sub-algorithm for Amplitude Parameters

In this section, the proposed algorithm is on the condition that the angular frequency parameters are known. In this case, the criterion function \(J_1(\varvec{a},\varvec{\omega })\) is a function with respect to the amplitude parameter vector \(\varvec{a}\), which can be rewritten as

$$\begin{aligned} J_2(\varvec{a}):=J_1(\varvec{a},\varvec{\omega })=\frac{1}{2} \sum _{m=k-p+1}^k\bigg [y(t_m)-\sum _{i=1}^na_i\sin (\omega _it_m)\bigg ]^2. \end{aligned}$$

Define the information vector \(\varvec{\varphi }_a(\varvec{\omega },t_k)\) and the piled information matrix as

$$\begin{aligned} \varvec{\varphi }_a(\varvec{\omega },t_k):= & {} [\sin (\omega _1t_k),\sin (\omega _2t_k),\ldots ,\sin (\omega _nt_k)]^{\tiny \text{ T }}\in {\mathbb R}^n,\nonumber \\ \varvec{\Phi }_a(p,\varvec{\omega },t_k):= & {} [\varvec{\varphi }_a(\varvec{\omega },t_k),\varvec{\varphi }_a(\varvec{\omega },t_{k-1}),\ldots ,\varvec{\varphi }_a(\varvec{\omega },t_{k-p+1})]^{\tiny \text{ T }}\in {\mathbb R}^{p\times n}.\nonumber \end{aligned}$$
(2)

Define the piled observation output as

$$\begin{aligned} \varvec{Y}(p,t_k):=[y(t_k),y(t_{k-1}),\ldots ,y(t_{k-p+1})]^{\tiny \text{ T }}\in {\mathbb R}^p. \end{aligned}$$

Then, the criterion function \(J_2(\varvec{a})\) can be further expressed as

$$\begin{aligned} J_2(\varvec{a}):=\frac{1}{2}\Vert \varvec{Y}(p,t_k)-\varvec{\Phi }_a(p,\varvec{\omega },t_k)\varvec{a}\Vert ^2. \end{aligned}$$

The gradient vector of the criterion function \(J_2(\varvec{a})\) with respect to the parameter vector \(\varvec{a}\) is obtained by taking the first-order derivative:

$$\begin{aligned} \mathrm{grad}[J_2(\varvec{a})]:=\frac{\partial J_2(\varvec{a})}{\partial \varvec{a}} =-\varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)[\varvec{Y}(p,t_k)-\varvec{\Phi }_a (p,\varvec{\omega },t_k)\varvec{a}]\in {\mathbb R}^n. \end{aligned}$$

Taking the second-order derivative of the criterion function \(J_2(\varvec{a})\) with respect to the amplitude parameter vector \(\varvec{a}\) obtains the Hessian matrix:

$$\begin{aligned} \varvec{H}_a(p,\varvec{\omega },t_k):= & {} \frac{\partial ^2J_2(\varvec{a})}{\partial \varvec{a}\partial \varvec{a}^{\tiny \text{ T }}} =\frac{\partial \mathrm{grad}[J_2(\varvec{a})]}{\partial \varvec{a}^{\tiny \text{ T }}}\\= & {} \varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)\varvec{\Phi }_a(p,\varvec{\omega },t_k)\in {\mathbb R}^{n\times n}. \end{aligned}$$

Let l be an iterative variable and let \(\hat{\varvec{a}}_l(t_k)\) \(:=[\hat{a}_{1,l}(t_k)\), \(\hat{a}_{2,l}(t_k)\), \(\cdots \), \(\hat{a}_{n,l}(t_k)]^{\tiny \text{ T }}\in {\mathbb R}^n\) denote the lth iterative estimate of the amplitude parameter vector \(\varvec{a}\) at time \(t=t_k\). By means of the Newton iterative principle, minimizing the criterion function \(J_2(\varvec{a})\) yields the multi-innovation Newton iterative algorithm (MINI) for estimating the amplitude parameter vector \(\varvec{a}\):

$$\begin{aligned} \hat{\varvec{a}}_l(t_k)= & {} \hat{\varvec{a}}_{l-1}(t_k)-\varvec{H}_a^{-1}(p,\varvec{\omega },t_k)\mathrm{grad}[J_2(\hat{\varvec{a}}_{l-1}(t_k))]\nonumber \\= & {} \hat{\varvec{a}}_{l-1}(t_k)-\varvec{H}_a^{-1}(p,\varvec{\omega },t_k)\mathrm{grad}[J_1(\hat{\varvec{a}}_{l-1}(t_k),\varvec{\omega })]\nonumber \\= & {} \hat{\varvec{a}}_{l-1}(t_k)+[\varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)\varvec{\Phi }_a(p,\varvec{\omega },t_k)]^{-1}\nonumber \\&\qquad \varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)[\varvec{Y}(p,t_k)-\varvec{\Phi }_a(p,\varvec{\omega },t_k)\hat{\varvec{a}}_{l-1}(t_k)]\nonumber \\= & {} [\varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)\varvec{\Phi }_a(p,\varvec{\omega },t_k)]^{-1}\varvec{\Phi }_a^{\tiny \text{ T }}(p,\varvec{\omega },t_k)\varvec{Y}(p,t_k), \end{aligned}$$
(3)
$$\begin{aligned} \varvec{Y}(p,t_k)= & {} [y(t_k),y(t_{k-1}),\ldots ,y(t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(4)
$$\begin{aligned} \varvec{\Phi }_a(p,\varvec{\omega },t_k)= & {} [\varvec{\varphi }_a(\varvec{\omega },t_k),\varvec{\varphi }_a(\varvec{\omega },t_{k-1}),\ldots ,\varvec{\varphi }_a(\varvec{\omega },t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(5)
$$\begin{aligned} \varvec{\varphi }_a(\varvec{\omega },t_k)= & {} [\sin (\omega _1t_k),\sin (\omega _2t_k),\ldots ,\sin (\omega _nt_k)]^{\tiny \text{ T }}, \end{aligned}$$
(6)
$$\begin{aligned} \hat{\varvec{a}}_l(t_k)= & {} [\hat{a}_{1,l}(t_k),\hat{a}_{2,l}(t_k),\ldots ,\hat{a}_{n,l}(t_k)]^{\tiny \text{ T }}. \end{aligned}$$
(7)

Remark 1

From (2), we can see that when the criterion function is the quadratic function of the parameter vector \(\varvec{a}\), the multi-innovation Newton iterative algorithm is reduced to the least squares algorithm, which is a sliding window least squares algorithm in (2)–(6).

Remark 2

The proposed MINI sub-algorithm in (2)–(6) is derived on the premise that the angular frequency parameter vector \(\varvec{\omega }\) is known. If the angular frequency parameter vector \(\varvec{\omega }\) is unknown, the algorithm cannot calculate the estimate of the amplitude parameter vector \(\varvec{a}\).

4 Multi-innovation Newton Iterative Estimation Sub-algorithm for Angular Frequency Parameters

When the amplitude parameters \(a_i\) \((i=1,2,\ldots ,n)\) are known, the parameter vector \(\varvec{a}\) does not need to be identified. Under this condition, the criterion function \(J_1(\varvec{a},\varvec{\omega })\) is the function with respect to the angular frequency parameter vector \(\varvec{\omega }\), which can be denoted by

$$\begin{aligned} J_3(\varvec{\omega }):=J_1(\varvec{a},\varvec{\omega })=\frac{1}{2} \sum _{m=k-p+1}^k\bigg [y(t_m)-\sum _{i=1}^na_i\sin (\omega _it_m)\bigg ]^2. \end{aligned}$$

Taking the first-order derivative of the criterion function \(J_3(\varvec{\omega })\) with respect to the parameter vector \(\varvec{\omega }\) obtains the gradient vector of the criterion function as follows:

$$\begin{aligned} \mathrm{grad}[J_3(\varvec{\omega })]:= & {} \frac{\partial J_3(\varvec{\omega })}{\partial \varvec{\omega }} =\left[ \frac{\partial J_3(\varvec{\omega })}{\partial \omega _1},\frac{\partial J_3(\varvec{\omega })}{\partial \omega _2},\ldots , \frac{\partial J_3(\varvec{\omega })}{\partial \omega _n}\right] ^{\tiny \text{ T }}\in {\mathbb R}^n,\\ \frac{\partial J_3(\varvec{\omega })}{\partial \omega _j}= & {} -\sum _{m=k-p+1}^k \bigg [y(t_m)-\sum _{i=1}^na_i\sin (\omega _it_m)\bigg ]a_jt_m \cos (\omega _jt_m). \end{aligned}$$

Define the information vector:

$$\begin{aligned} \varvec{\varphi }_{\omega }(\varvec{a},\varvec{\omega },t_k):=[a_1t_k \cos (\omega _1t_k),a_2t_k\cos (\omega _2t_k), \cdots ,a_nt_k\cos (\omega _nt_k)]^{\tiny \text{ T }}\in {\mathbb R}^n. \end{aligned}$$

Define the piled information matrix:

$$\begin{aligned} \varvec{\Phi }_{\omega }(p,\varvec{a},\varvec{\omega },t_k):=[\varvec{\varphi }_{\omega } (\varvec{a},\varvec{\omega },t_k),\varvec{\varphi }_{\omega }(\varvec{a},\varvec{\omega },t_{k-1}),\ldots ,\varvec{\varphi }_{\omega }(\varvec{a},\varvec{\omega },t_{k-p+1})]^{\tiny \text{ T }}\in {\mathbb R}^{p\times n}. \end{aligned}$$

Define the error vector:

$$\begin{aligned} \varvec{V}(p,\varvec{a},\varvec{\omega },t_k):=[v(\varvec{a},\varvec{\omega },t_k), v(\varvec{a},\varvec{\omega },t_{k-1}),\ldots ,v(\varvec{a},\varvec{\omega },t_{k-p+1})]^{\tiny \text{ T }}\in {\mathbb R}^p. \end{aligned}$$

Then, the gradient vector \(\mathrm{grad}[J_3(\varvec{\omega })]\) can be rewritten as

$$\begin{aligned} \mathrm{grad}[J_3(\varvec{\omega })]=-\varvec{\Phi }_{\omega }^{\tiny \text{ T }}(p,\varvec{a},\varvec{\omega },t_k) \varvec{V}(p,\varvec{a},\varvec{\omega },t_k). \end{aligned}$$

Taking the second-order derivative of the criterion function \(J_3(\varvec{\omega })\) with respect to the parameter vector \(\varvec{\omega }\) obtains the Hessian matrix as follows:

$$\begin{aligned} \varvec{H}_{\omega }(p,\varvec{a},\varvec{\omega },t_k):= & {} \frac{\partial ^2J_3(\varvec{\omega })}{\partial \varvec{\omega }\partial \varvec{\omega }^{\tiny \text{ T }}} =\left[ \frac{\partial ^2J_3(\varvec{\omega })}{\partial \omega _j\partial \omega _r}\right] \in {\mathbb R}^{n\times n},\quad j,r=1,2,\ldots ,n,\\ \frac{\partial ^2J_3(\varvec{\omega })}{\partial \omega _j\partial \omega _r}= & {} \sum _{m=k-p+1}^ka_ja_rt_m^2\cos (\omega _jt_m)\cos (\omega _rt_m), \quad j\ne r,\\ \frac{\partial ^2J_3(\varvec{\omega })}{\partial \omega _j\partial \omega _j}= & {} \sum _{m=k-p+1}^ka_j^2t_m^2\cos ^2(\omega _jt_m) +\bigg [y(t_m)-\sum _{i=1}^na_i\sin (\omega _it_m)\bigg ]a_j t_m^2\sin (\omega _jt_m)\\= & {} \sum _{m=k-p+1}^ka_j^2t_m^2+\bigg [y(t_m)- \sum _{i\not =j}^na_i\sin (\omega _it_m)\bigg ]a_jt_m^2\sin (\omega _jt_m). \end{aligned}$$

Let \(\hat{\varvec{\omega }}_l(t_k):=[\hat{\omega }_{1,l}(t_k), \hat{\omega }_{2,l}(t_k),\ldots ,\hat{\omega }_{n,l(t_k)}]^{\tiny \text{ T }}\) denote the lth iterative estimate of the amplitude parameter vector \(\varvec{\omega }\) at time \(t=t_k\). According to the Newton search, minimizing the criterion function \(J_3(\varvec{\omega })\) gives the multi-innovation Newton iterative algorithm for estimating the angular frequency parameter vector \(\varvec{\omega }\):

$$\begin{aligned} \hat{\varvec{\omega }}_l(t_k)= & {} \hat{\varvec{\omega }}_{l-1}(t_k)-\varvec{H}_{\omega }^{-1}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\mathrm{grad}[J_3(\hat{\varvec{\omega }}_{l-1}(t_k))]\nonumber \\= & {} \hat{\varvec{\omega }}_{l-1}(t_k)-\varvec{H}_{\omega }^{-1}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\mathrm{grad}[J_1(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k))]\nonumber \\= & {} \hat{\varvec{\omega }}_{l-1}(t_k)+\varvec{H}_{\omega }^{-1}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\&\times \varvec{\Phi }_{\omega }^{\tiny \text{ T }}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\varvec{V}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k), \end{aligned}$$
(8)
$$\begin{aligned} \hat{\varvec{\Phi }}_{\omega }(p,t_k):= & {} \varvec{\Phi }_{\omega }(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [\varvec{\varphi }_{\omega }(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k),\varvec{\varphi }_{\omega }(\varvec{a}, \hat{\varvec{\omega }}_{l-1}(t_k),t_{k-1}),\ldots ,\nonumber \\&\varvec{\varphi }_{\omega }(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(9)
$$\begin{aligned} \hat{\varvec{\varphi }}_{\varvec{a},\omega }(t_k)= & {} \varvec{\varphi }_{\omega }(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [a_1t_k\cos (\hat{\omega }_{1,l-1}(t_k)t_k),a_2t_k\cos (\hat{\omega }_{2,l-1}(t_k)t_k),\ldots ,\nonumber \\&a_nt_k\cos (\hat{\omega }_{n,l-1}(t_k)t_k)]^{\tiny \text{ T }},\\ \hat{\varvec{V}}(p,t_k)= & {} \varvec{V}(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [v(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k),v(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k), t_{k-1}),\ldots ,\nonumber \\&v(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(10)
$$\begin{aligned} \hat{v}(\varvec{a},t_k)= & {} v(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} y(t_k)-\sum _{i=1}^na_i\sin (\hat{\omega }_{i,l-1}(t_k)t_k), \end{aligned}$$
(11)
$$\begin{aligned} \hat{\varvec{H}}_{\omega }(p,t_k)= & {} \varvec{H}_{\omega }(p,\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [h_{jr}(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)],\quad j,r=1,2,\ldots ,n, \end{aligned}$$
(12)
$$\begin{aligned} \hat{h}_{jr}(t_k)= & {} h_{jr}(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} \sum _{m=k-p+1}^ka_ja_rt_m^2\cos (\hat{\omega }_{j,l-1}(t_k)t_m)\cos (\hat{\omega }_{r,l-1}(t_k)t_m),\quad j\ne r, \end{aligned}$$
(13)
$$\begin{aligned} \hat{h}_{jj}(t_k)= & {} h_{jj}(\varvec{a},\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} \sum _{m=k-p+1}^ka^2_jt_m^2 +\bigg [y(t_m)-\sum _{i\not =j}^na_i\sin (\hat{\omega }_{i,l-1}(t_k)t_m)\bigg ] a_jt_m^2\nonumber \\&\sin (\hat{\omega }_{j,l-1}(t_k)t_m), \end{aligned}$$
(14)
$$\begin{aligned} \hat{\varvec{\omega }}_l(t_k):= & {} [\hat{\omega }_{1,l}(t_k), \hat{\omega }_{2,l}(t_k),\ldots ,\hat{\omega }_{n,l}(t_k)]^{\tiny \text{ T }}. \end{aligned}$$
(15)

Remark 3

The multi-innovation Newton iterative sub-algorithm in (7)–(15) for estimating the angular frequency parameter vector \(\varvec{\omega }\) is proposed under the hypothesis that the amplitude vector \(\varvec{a}\) is known. If the amplitude vector \(\varvec{a}\) is unknown, the proposed multi-innovation Newton iterative algorithm in (7)–(15) cannot estimate the angular frequency parameter vector \(\varvec{\omega }\).

5 Separable Multi-innovation Newton Iterative Parameter Estimation Algorithm

In practice, for modeling the multi-frequency sine signal, all of the signal parameters are unknown. In order to develop the signal modeling method for estimating the whole signal parameters, the proposed two sub-algorithms for estimating parameter vector \(\varvec{a}\) in (2)–(6) and \(\varvec{\omega }\) in (7)–(15) are combined to construct an interactive estimation algorithm. It is noted that the combination of these two sub-algorithms contains unknown related parameters, i.e., the unknown parameters lie in the sub-algorithms. Therefore, we present a separable algorithm to remove the related parameter terms by interactive estimation. Jointing the MINI sub-algorithm in (2)–(6) for estimating parameter vector \(\varvec{a}\) and the MINI sub-algorithm in (7)–(15) for estimating parameter vector \(\varvec{\omega }\) and replacing the unknown parameter vectors \(\varvec{\omega }\) and \(\varvec{a}\) with their previous iterative estimates \(\hat{\varvec{\omega }}_{l-1}(t_k)\) and \(\hat{\varvec{a}}_{l-1}(t_k)\) yield the separable multi-innovation Newton iterative (SMINI) parameter estimating algorithm for estimating all parameters of the multi-frequency sine signal as follows:

$$\begin{aligned} \hat{\varvec{a}}_l(t_k)= & {} \hat{\varvec{a}}_{l-1}(t_k)-\varvec{H}_a^{-1}(p,\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\mathrm{grad}[J_1(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k))]\nonumber \\= & {} [\varvec{\Phi }_a^{\tiny \text{ T }}(p,\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\varvec{\Phi }_a(p,\hat{\varvec{\omega }}_{l-1}(t_k),t_k)]^{-1}\nonumber \\&\varvec{\Phi }_a^{\tiny \text{ T }}(p,\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\varvec{Y}(p,t_k)\nonumber \\= & {} [\hat{\varvec{\Phi }}_{a,l}^{\tiny \text{ T }}(p,t_k)\hat{\varvec{\Phi }}_{a,l}(p,t_k)]^{-1}\hat{\varvec{\Phi }}_{a,l}^{\tiny \text{ T }}(p,t_k)\varvec{Y}(p,t_k), \end{aligned}$$
(16)
$$\begin{aligned} \varvec{Y}(p,t_k)= & {} [y(t_k),y(t_{k-1}),\ldots ,y(t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(17)
$$\begin{aligned} \hat{\varvec{\Phi }}_{a,l}(p,t_k):= & {} \varvec{\Phi }_a(p,\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [\varvec{\varphi }_a(\hat{\varvec{\omega }}_{l-1}(t_k),t_k),\varvec{\varphi }_a(\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-1}),\ldots ,\varvec{\varphi }_a(\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-p+1})]^{\tiny \text{ T }}\nonumber \\= & {} [\hat{\varvec{\varphi }}_{a,l}(t_k),\hat{\varvec{\varphi }}_{a,l}(t_{k-1}),\ldots ,\hat{\varvec{\varphi }}_{a,l}(t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(18)
$$\begin{aligned} \hat{\varvec{\varphi }}_{a,l}(t_{k-j}):= & {} \varvec{\varphi }_a(\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-j})\nonumber \\= & {} [\sin (\hat{\omega }_{1,l-1}(t_k)t_{k-j}),\sin (\hat{\omega }_{2,l-1}(t_k)t_{k-j}),\ldots ,\sin (\hat{\omega }_{n,l-1}(t_k)t_{k-j})]^{\tiny \text{ T }},\nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} \hat{\varvec{\omega }}_l(t_k)= & {} \hat{\varvec{\omega }}_{l-1}(t_k)-\varvec{H}_{\omega }^{-1}(p,\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\&\qquad \mathrm{grad}[J_1(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k))]\nonumber \\= & {} \hat{\varvec{\omega }}_{l-1}(t_k)+\varvec{H}_{\omega }^{-1}(p,\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k) \varvec{\Phi }_{\omega }^{\tiny \text{ T }}(p,\hat{\varvec{a}}_{l-1}(t_k),\nonumber \\&\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\varvec{V}(p,\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} \hat{\varvec{\omega }}_{l-1}(t_k)+\hat{\varvec{H}}_{\omega ,l}^{-1}(p,t_k) \hat{\varvec{\Phi }}_{\omega ,l}^{\tiny \text{ T }}(p,t_k)\hat{\varvec{V}}_l(p,t_k), \end{aligned}$$
(20)
$$\begin{aligned} \hat{\varvec{\Phi }}_{\omega ,l}(p,t_k):= & {} \varvec{\Phi }_{\omega }(p,\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [\varvec{\varphi }_{\omega }(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k),\varvec{\varphi }_{\omega }(\hat{\varvec{a}}_{l-1}(t_k),\nonumber \\&\qquad \hat{\varvec{\omega }}_{l-1}(t_k),t_{k-1}),\ldots ,\varvec{\varphi }_{\omega }(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-p+1})]^{\tiny \text{ T }}\nonumber \\= & {} [\hat{\varvec{\varphi }}_{\omega ,l}(t_k),\hat{\varvec{\varphi }}_{\omega ,l}(t_{k-1}),\ldots ,\hat{\varvec{\varphi }}_{\omega ,l}(t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(21)
$$\begin{aligned} \hat{\varvec{\varphi }}_{\omega ,l}(t_{k-j}):= & {} \varvec{\varphi }_{\omega }(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-j})\nonumber \\= & {} [\hat{a}_{1,l-1}(t_k)t_{k-j}\cos (\hat{\omega }_{1,l-1}(t_k)t_{k-j}),\ldots ,\nonumber \\&\hat{a}_{n,l-1}(t_k)t_{k-j}\cos (\hat{\omega }_{n,l-1}(t_k)t_{k-j})]^{\tiny \text{ T }}, \end{aligned}$$
(22)
$$\begin{aligned} \hat{\varvec{V}}_l(p,t_k):= & {} \varvec{V}(p,\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [v(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k),v(\hat{\varvec{a}}_{l-1}(t_k),\nonumber \\&\qquad \hat{\varvec{\omega }}_{l-1}(t_k),t_{k-1}),\ldots ,v(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-p+1})]^{\tiny \text{ T }}\nonumber \\= & {} [\hat{v}_l(t_k),\hat{v}_l(t_{k-1}),\ldots ,\hat{v}_l(t_{k-p+1})]^{\tiny \text{ T }}, \end{aligned}$$
(23)
$$\begin{aligned} \hat{v}_l(t_{k-j}):= & {} v(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_{k-j})\nonumber \\= & {} y(t_{k-j})-\sum _{i=1}^n\hat{a}_{i,l-1}(t_k)\sin (\hat{\omega }_{i,l-1}(t_k)t_{k-j}), \end{aligned}$$
(24)
$$\begin{aligned} \hat{\varvec{H}}_{\omega ,l}(p,t_k):= & {} \varvec{H}_{\omega }(p,\hat{\varvec{a}}_{l-1}(t_k), \hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} [h_{jr}(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)]\nonumber \\= & {} [\hat{h}_{jr,l}(t_k)],\quad j,r=1,2,\ldots ,n, \end{aligned}$$
(25)
$$\begin{aligned} \hat{h}_{jr,l}(t_k):= & {} h_{jr}(\hat{\varvec{a}}_{l-1}(t_k),\hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} \sum _{m=k-p+1}^k\hat{a}_{j,l-1}(t_k)\hat{a}_{r,l-1}(t_k)t_m^2\cos (\hat{\omega }_{j,l-1} (t_k)t_m)\nonumber \\&\cos (\hat{\omega }_{r,l-1}(t_k)t_m),\quad j\ne r, \end{aligned}$$
(26)
$$\begin{aligned} \hat{h}_{jj,l}(t_k):= & {} h_{jj}(\hat{\varvec{a}}_{l-1}(t_k), \hat{\varvec{\omega }}_{l-1}(t_k),t_k)\nonumber \\= & {} \sum _{m=k-p+1}^k\hat{a}^2_{j,l-1}(t_k)t_m^2\nonumber \\&+\bigg [y(t_m)-\sum _{i=1}^n\hat{a}_{i,l-1}(t_k) \sin (\hat{\omega }_{i,l-1}(t_k)t_m)\bigg ]\nonumber \\&\hat{a}_{j,l-1}(t_k)t_m^2\sin (\hat{\omega }_{j,l-1}(t_k)t_m), \end{aligned}$$
(27)
$$\begin{aligned} \hat{\varvec{a}}_l(t_k)= & {} [\hat{a}_{1,l}(t_k),\hat{a}_{2,l}(t_k), \cdots ,\hat{a}_{n,l}(t_k)]^{\tiny \text{ T }}, \end{aligned}$$
(28)
$$\begin{aligned} \hat{\varvec{\omega }}_l(t_k)= & {} [\hat{\omega }_{1,l}(t_k), \hat{\omega }_{2,l}(t_k),\ldots ,\hat{\omega }_{n,l}(t_k)]^{\tiny \text{ T }}. \end{aligned}$$
(29)

The computing procedure of the proposed SMINI algorithm in (16)–(29) is shown in Fig. 2. The steps for computing the parameter estimation vectors \(\hat{\varvec{a}}_l(t_k)\) and \(\hat{\varvec{\omega }}_l(t_k)\) are as follows:

  1. (1)

    Initialize: Set the innovation length \(p\gg n\) and let \(k=p\). Give the maximal iterative length \(l_{\max }\) and the parameter estimation accuracy \(\varepsilon \). Set the initial values \(\hat{\varvec{a}}_0(t_k)=[\hat{a}_{1,0}(t_k)\), \(\hat{a}_{2,0}(t_k)\), \(\cdots \), \(\hat{a}_{n,0}(t_k)]^{\tiny \text{ T }}\) as a random real vector, \(\hat{\varvec{\omega }}_0(t_k)=[\hat{\omega }_{1,0}(t_k)\), \(\hat{\omega }_{2,0}(t_k)\), \(\cdots \), \(\hat{\omega }_{n,0}(t_k)]^{\tiny \text{ T }}\) as a random real vector. Collect the observations \(y(t_m)\), \(m=0,1,\ldots , p-1\).

  2. (2)

    Let \(l=1\). Collect the observed data \(y(t_k)\), construct the output vector \(\varvec{Y}(p,t_k)\) in accordance with (17).

  3. (3)

    Compute the information vector \(\hat{\varvec{\varphi }}_{a,l}(t_{k-j})\) by (19), compute the information vector \(\hat{\varvec{\varphi }}_{\omega ,l}(t_{k-j})\) by (22), and compute the residual \(\hat{v}_l(t_{k-j})\), \(j=0,1,\ldots ,p-1\) by (24).

  4. (4)

    Construct the stacked information matrix \(\hat{\varvec{\Phi }}_{a,l}(p,t_k)\) by (18), construct the stacked information matrix \(\hat{\varvec{\Phi }}_{\omega ,l}(p,t_k)\) by (21), and construct the residual vector \(\hat{\varvec{V}}_l(p,t_k)\) by (23).

  5. (5)

    Compute each element \(\hat{h}_{jr,l}(t_k)\) and \(\hat{h}_{jj,l}(t_k)\), \(j,r=1,2,\ldots ,n\) of the Hessian matrix in accordance with (26)–(27) and construct the Hessian matrix \(\hat{\varvec{H}}_{\omega ,l}(p,t_k)\) by (25).

  6. (6)

    Update the amplitude parameter estimation vector \(\hat{\varvec{a}}_l(t_k)\) by (16); update the angular frequency parameter estimation vector \(\hat{\varvec{\omega }}_l(t_k)\) by (20). Read the amplitude parameter estimate \(\hat{a}_{i,l}(t_k)\) from (28) and read the angular frequency parameter estimate \(\hat{\omega }_{i,l}(t_k)\) from (29), \(i=1,2,\ldots ,n\).

  7. (7)

    If \(l<l_{\max }\), then \(l:=l+1\) and go to Step 3); otherwise, jump to the next step.

  8. (8)

    If \(\Vert \hat{\varvec{a}}_l(t_k)-\hat{\varvec{a}}_{l-1}(t_k)\Vert +\Vert \hat{\varvec{\omega }}_l (t_k)-\hat{\varvec{\omega }}_{l-1}(t_k)\Vert >\varepsilon \), then \(\hat{\varvec{a}}_0(t_{k+1})=\hat{\varvec{a}}_l(t_k)\), \(\hat{\varvec{\omega }}_0(t_{k+1})=\hat{\varvec{\omega }}_l(t_k)\) and increase k by 1 and go to Step 2); otherwise, obtain the parameter estimates \(\hat{\varvec{a}}_l(t_k)\) and \(\hat{\varvec{\omega }}_l(t_k)\) and terminate the iterative procedure.

Fig. 2
figure 2

Flowchart of the SMINI estimation algorithm

Full size image

Remark 4

The proposed SMINI algorithm in (16)–(29) is composed of two MINI sub-algorithms. For the linear parameter identification, the MINI sub-algorithm reduces to the least squares algorithm for estimating the linear parameter set \(\varvec{a}\). Moreover, because the SMINI algorithm uses the sliding window data, the iterative procedure alternates with the real-time datum collection. However, the sub-algorithm for estimating the nonlinear parameters cannot be realized by the linear least squares optimization, i.e., the least squares method for estimating the whole parameters of the multi-frequency sine signal cannot exist.

Remark 5

The goal of the proposed separable multi-innovation Newton iterative parameter estimation method is to reduce the computational burden compared with the inseparable multi-innovation Newton iterative parameter estimation method. In this study, an obvious problem is the parameter vector \(\varvec{\theta }:=[a_1,\ldots ,a_n,\omega _1,\ldots ,\omega _n]^{\tiny \text{ T }}\) is separated into two parameter vectors \(\varvec{a}\) and \(\varvec{b}\). Because the Newton search needs to compute the Hessian matrix and its inverse matrix, the computation burden is reduced obviously after the parameter separation, in which the dimension of the Hessian matrix with respect to \(\varvec{\theta }\) is 2n and the dimension of the Hessian matrix with respect to \(\varvec{a}\) and \(\varvec{\omega }\) is n. Comparing the proposed algorithm with the gradient-based method, the computation burden of the SMINI algorithm is heavier than the gradient-based method because of the Hessian matrix and its inverse. Therefore, in order to obtain better estimation accuracy, the algorithm needs more computational burden in some cases. The methods proposed in this paper can combine other estimation approaches [14, 50, 57, 80,81,82,83] to study the parameter estimation problems of linear systems [52, 53, 59,60,61] and bilinear systems [43,44,45,46,47,48] and nonlinear systems [25, 36, 37, 39, 49] and can be applied to some engineering application systems.

6 Numerical Scenarios

This section presents two parameter estimation examples of a power signal and a periodic signal to illustrate the performance of the proposed method. In the simulation, a comparison is provided under different noise levels. The parameter estimation error is defined as

$$\begin{aligned} \delta (t_k):=\sqrt{\frac{\Vert \varvec{a}-\hat{\varvec{a}}_l (t_k)\Vert ^2+\Vert \varvec{\omega }-\hat{\varvec{\omega }}_l(t_k)\Vert ^2}{\Vert \varvec{a}\Vert ^2+\Vert \varvec{\omega }\Vert ^2}}\times 100\%. \end{aligned}$$

Example 1

The parameter vector of the power signal to be estimated involves the amplitudes and phases

$$\begin{aligned} \varvec{a}=[10,14,20]^{\tiny \text{ T }}, \quad \varvec{\omega }=[3,1.5,2.5]^{\tiny \text{ T }}. \end{aligned}$$

In the simulations, the noise v(t) corresponds to a normal distributed noise signal with zero mean and constant variance, i.e., \(N(0,\sigma ^2)\), where the noise variance \(\sigma ^2=0.50^2\) is evaluated. Moreover, the data length is 200 and the window lengths are \(p=10\) and \(p=30\); the sampling period is 2s. The maximum iteration is \(l_{max}=20\) at each data window. The collected observations with noise are shown in Fig. 3. The parameter estimates and their estimation errors obtained by the proposed SMINI method are illustrated in Table 1 and the estimation errors versun l is shown in Fig. 4.

Fig. 3
figure 3

Discrete observations

Full size image
Table 1 SMINI estimates and their estimation errors
Full size table
Fig. 4
figure 4

Parameter estimation errors versus l under different innovation length

Full size image

In accordance with the estimated parameters when \(p=30\) and \(k=3000\), we obtain the following estimated multi-frequency sine signal:

$$\begin{aligned} f(t)=9.93201\sin 3.01483t+13.86639\sin 1.44152t+20.04096\sin 2.48655t. \end{aligned}$$

In order to test the accuracy of the estimated signal, the power spectrum density of the true signal and the estimated signal is shown in Fig. 5, where the blue line is the estimated signal and the black line is the true signal.

Fig. 5
figure 5

Power spectrum density of the estimated and true signals with box window

Full size image

Example 2

In order to evaluate the performance of the proposed SMINI algorithm for estimating other periodic signals, a triangular wave is provided to test the proposed method which is shown in Fig. 6.

Fig. 6
figure 6

Triangular wave

Full size image

The mathematical description of the above triangular wave is illustrated as follows:

$$\begin{aligned} f(t)={\left\{ \begin{array}{ll} \frac{4A}{T}t, \quad -\frac{T}{4}\le t\le \frac{T}{4},\\ -\frac{4A}{T}t+2A, \quad \frac{T}{4}\le t\le \frac{3T}{4}. \end{array}\right. } \end{aligned}$$
(30)

As we all know, any periodic function f(t) can be expanded the combination of sine and cosine terms according to the Fourier series, i.e.,

$$\begin{aligned} f(t)=\frac{a_0}{2}+\sum _{n=1}^\infty [a_n\cos n\omega t+b_n\sin n\omega t], \end{aligned}$$

where \(a_0/2\) is the direct current component, \(\omega \) is the angular frequency of the basic wave, \(a_n\) and \(b_n\) are the coefficients of each fundamental and harmonic waves.

Because f(t) is an odd function, coefficients of the Fourier series are as zero, i.e., \(\frac{a_0}{2}=0, \quad a_n=0, \quad n=1,2,\ldots \). The coefficients \(b_n\) are determined in accordance with

$$\begin{aligned} b_n= & {} \frac{2}{T}\int _{t_0}^{t_0+T}f(t)\sin nwt \mathrm{d}t \\= & {} \frac{2}{T}\int _{-\frac{T}{4}}^{\frac{T}{4}}\frac{4A}{T}\sin (n\omega t)t\mathrm{d}t +\frac{2}{T}\int _{\frac{T}{4}}^{\frac{3T}{4}}(A-\frac{4A}{T})\sin (n\omega t)t\mathrm{d}t\\= & {} {\left\{ \begin{array}{ll} \frac{8A}{n^2\pi ^2}, \quad n=1,5,9,\ldots ,\\ -\frac{8A}{n^2\pi ^2}, \quad n=3,7,11,\ldots . \end{array}\right. } \end{aligned}$$

As a result, the triangular wave in (30) can be described by the following Fourier series:

$$\begin{aligned} f(t)=\frac{8A}{\pi ^2}\sin \omega t-\frac{8A}{9\pi ^2}\sin 3\omega t+\frac{8A}{25\pi ^2}\sin 5\omega t-\frac{8A}{47\pi ^2}\sin 7\omega t\cdots . \end{aligned}$$
(31)

The first three terms in (31) can be used to represent the original triangular wave in (30) because of the fast attenuation of the higher harmonic, i.e.,

$$\begin{aligned} f(t)=\frac{8A}{\pi ^2}\sin \omega t-\frac{8A}{9\pi ^2}\sin 3\omega t+\frac{8A}{25\pi ^2}\sin 5\omega t. \end{aligned}$$
(32)

Define \(a_1=\frac{8A}{\pi ^2}\), \(a_2=-\frac{8A}{9\pi ^2}\), \(a_3=\frac{8A}{25\pi ^2}\), \(\omega _1=\omega \), \(\omega _2=3\omega \) and \(\omega _3=5\omega \). Then, f(t) in (32) becomes

$$\begin{aligned} f(t)=a_1\sin \omega _1t+a_2\sin \omega _2t+a_3\sin \omega _3t. \end{aligned}$$

Therefore, the proposed signal modeling methods can be used to estimate the parameters of the triangular wave in (30). In the simulation, the parameters of the triangular wave are \(A=6\), \(T=0.4\omega \). The simulation conditions are set as follows: (1) The white noise is \(\sigma ^2=0.05^2\), \(\sigma ^2=0.30^2\), \(\sigma ^2=0.60^2\) and \(\sigma ^2=1.00^2\); (2) The data length is \(L=150\); (3) The frequency sampling period is \(h_\omega =0.15\); (4) The innovation length \(p=10\); (5) The maximum iteration at each data window is \(l_{max}=5\). The discrete measurements of the triangular wave contained different white noise in this example are shown in Fig. 7.

Fig. 7
figure 7

Measurements of the triangular wave of Example  2

Full size image

Employing the proposed SMINI algorithm to model the triangular wave, the parameter estimates and the estimation errors under different noise are listed in Table 2 and the estimation errors versus iteration l is shown in Fig. 8.

Table 2 SMINI estimates and their estimation errors
Full size table
Fig. 8
figure 8

Parameter estimation errors versus iteration l of Example 2

Full size image

Based on the estimated parameters in Table 2, we get four estimated signals obtained under different noise variance as follows:

$$\begin{aligned} f_1(t)= & {} 4.88676\sin 0.19128t-0.56693\sin 0.54267t+0.19162\sin 1.15690t,\\ f_2(t)= & {} 5.00346\sin 0.19769t-0.69971\sin 0.54497t+0.17703\sin 1.19952t,\\ f_3(t)= & {} 5.14350\sin 0.20546t-0.85904\sin 0.54298t+0.15953\sin 1.47889t,\\ f_4(t)= & {} 5.33022\sin 0.21595t-1.07147\sin 0.53344t+0.13620\sin 1.25569t. \end{aligned}$$

The Fourier series with three terms of the original triangular waves is

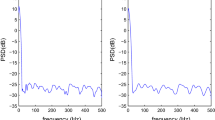
$$\begin{aligned} f(t)=4.86342\sin 0.2t-0.54038\sin 0.6t+0.19454\sin 1.0t. \end{aligned}$$

In order to test the accuracy of the estimated signals, we compare the signal waves and the power spectrum density between the estimated signals and the original signals. The signal waves are shown in Fig. 9, where the blue dot line denotes the estimated signal waves and the black dash line denotes the original signals. The power spectral density curves of the signals are shown in Fig. 10, where the blue solid line denotes the original signal and the green dot line denotes the estimated signals.

Fig. 9
figure 9

Parameter estimation errors versus iteration l of Example 2

Full size image
Fig. 10
figure 10

Power spectral density curves of the estimated and original signals

Full size image

From the simulation results of Examples 1 and 2, we can conclude the following remarks.

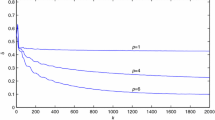
  • Example 1 shows a multi-sine signal with three different angular frequencies, in which the signal parameters are estimated by the proposed SMINI method. From the obtained parameter estimates, we can see that the parameter estimates are obtained when the innovation length \(p=30\) is more accurate than those when the innovation length \(p=10\). Because the multi-innovation method dynamically uses sliding window measurements, the larger innovation length p means more dynamical data can be absorbed to the iterative estimation computation. Therefore, the SMINI method using larger innovation length can adequately use the dynamical information of the signal to be modeled and obtain higher estimation accuracy.

  • Example 2 shows a triangular wave signal to test the performance of the proposed SMINI method for modeling periodic signals. Figure 8 shows parameter estimation errors versus iteration l under different noise. An obvious phenomenon is that the parameter estimation errors are lager when the noise variance is larger. Moreover, with the increasing of iteration l, the parameter estimation errors become smaller in general confirming the effectiveness of the SMINI algorithm. When the observation data contain large disturbance, the parameter estimation errors fluctuate greatly.

  • Figures 9 and 10 show the signal waves and power spectral density curves of the estimated signals and original signals. From them, we can see that the signal waves and power spectral density curves of the estimated signals and original signals are close, which means the estimated signals can seize the characteristic of the original signal. In other words, the proposed SMINI method is effective for signal modeling.

7 Conclusions

This paper studies the modeling problem for the sine multi-frequency signals or periodic signals. A parameter decomposition method is presented in terms of different characteristics between the signal output and the signal parameters. Based on a separated linear parameter set and a nonlinear parameter set, a full nonlinear optimization problem is converted into a combination of linear and nonlinear optimization problems. Then, a separable multi-innovation Newton iterative signal modeling method is derived and implemented to estimate the sine multi-frequency signals and periodic signals, in which the measurements are sampled and used dynamically. By testing the performance of the proposed SMINI algorithm to a multi-sine signal and a periodic signal via the simulation experiments, the results are found to be effective of modeling dynamic signals. For the reason that the proposed method is based on dynamic sliding measurement window, it can be used for online estimation applications. The proposed separable multi-innovation Newton iterative modeling algorithm for multi-frequency signals based on the sliding measurement window can combine other techniques and strategies [24, 31, 32, 51, 63, 84, 93, 94, 98] to explore new identification methods of some linear and nonlinear systems [7, 73, 74] and can be applied to other fields [38, 40, 41, 71, 72, 77, 92, 95, 97, 100] such as information processing and communication.