$H_{\infty }$ Filtering for Discrete-Time Singular Markovian Jump Systems with Generally Uncertain Transition Rates

Abstract

This paper is devoted to the problem of $H_{\infty }$ filtering for a class of discrete-time singular Markovian jump systems with generally uncertain transition rates. Each transition rate of the jumping process is completely unknown or only the estimated value is known. The objective is to design a $H_{\infty }$ filter such that the resulting filtering error system is stochastically admissible (regular, causal and stochastically stable) while satisfying a prescribed $H_{\infty }$ performance $\gamma$. Sufficient conditions are derived that can guarantee the filtering error system is $H_{\infty }$ stochastically admissible. Moreover, explicit expression of the filter gains is obtained by solving a set of strict linear matrix inequalities. Finally, a numerical example is included to illustrate the effectiveness of the proposed method.

1 Introduction

Singular systems, also known as generalized state space systems, descriptor systems, semi-state systems or differential–algebraic systems, have been widely applied in the field of electrical circuits, power systems, robotic systems and so on [2]. The analysis of singular systems is complicated than that of normal ones, since the regularity, impulse-free (in continuous case) or causality (in discrete case) and the stability of the close-loop systems should be considered simultaneously. During the past decades, considerable attention has been paid to the stability analysis, stochastically admissibility and filtering problems for singular systems [7, 11, 18, 22, 27, 29].

On the other hand, stochastic systems with structural variations such as machine faults and repairs in manufacturing systems can be better modelled by Markovian jump systems than normal systems [16]. For example, the large time-delay and packet loss in computer network systems are usually random and cannot be predicted in advance. In this case, the normal work state can be set to be one mode, and the state with packet loss or large time-delay can be set to be another mode, and then the computer network system can be modelled to be a Markovian jump system with two modes; meanwhile, the real computer network system switches randomly between these two modes. In recent years, more and more attention has been devoted to the filtering [12, 24] and control [9, 25] problems of Markovian jump systems. It should be mentioned that in the literature [12, 24, 25], the transition rates of jumping process are assumed to be completely known. However, in practice, due to the limitations of equipment and the influence of uncertain complex factors, the transition rates are usually uncertain. At present, there are three kinds of uncertain transition rates [32]. The first kind is bounded uncertain transition rates (BUTRs) [6, 14], where the precise value of each transition rate may not be known while the upper bound and lower bound of each transition rate are known. The second one is partly unknown transition rates (PUTRs) [21, 26, 36], where each transition rate is completely known or unknown. The third one is generally uncertain transition rates (GUTRs), where each transition rate is unknown or only known with its estimate. It is obvious that BUTRs and PUTRs are special case of the GUTRs. Recently, the problem of stability and state feedback control for normal Markovian jump systems with GUTRs were studied in [5, 20], respectively. In addition, for continuous-time singular Markovian jump systems (SMJSs) with GUTRs, the stabilization and $H_{\infty }$ filtering problems were considered in [8] and [33], respectively. To the best of our knowledge, there are few papers studied about discrete-time SMJSs with GUTRs, especially considering the $H_{\infty }$ filtering and GUTRs simultaneously for SMJSs.

Motivated by above discussion, $H_{\infty }$ filtering for a class of discrete-time SMJSs with GUTRs is considered in this paper. Compared with the traditional Kalman filtering [15, 17], $H_{\infty }$ filtering requires no assumptions about the statistical properties of noise [1, 3, 4, 13, 19, 23, 31, 34, 35]. $H_{\infty }$ filtering devotes to develop a proper filter to minimize the upper bound of the ${\mathcal{L}}_{2} \left( {l_{2} } \right)$ gain from the noise to the filtering error. The main contributions of this paper are as follow: (1) Sufficient conditions in terms of strict linear matrix inequalities (LMIs) are given, which can guarantee the discrete-time singular Markovian jump filtering error system with GUTRs is regular, causal and stochastically stable while satisfying a prescribed $H_{\infty }$ performance; (2) the desired normal full-order filter is designed while the explicit expression of the filter parameters is also given.

This paper is organized as follows. In Sect. 2, the problem statement and preliminaries are formulated including some definitions and lemmas for further usage. The desired filter is of full order and normal structure. In Sect. 3, based on the Lemma 4 proposed in Sect. 2, sufficient conditions are obtained in Theorem 1 such that the filtering error systems is stochastically admissible with a prescribed $H_{\infty }$ performance $\gamma$. Furthermore, by using LMI approach, the filter design method is obtained in Theorem 2. In Sect. 4, a numerical example is illustrated to demonstrate the effectiveness of the proposed method. Section 5 is the conclusion. The end is appendixes.

Notation Through this paper, ${{R}}^{m \times n}$ represents the set of all $m \times n$ real matrices, and $R^{n}$ denotes the n-dimensional Euclidean space. $\ell_{2} \left[ 0 \right.$, $\left. { + \infty } \right)$ denotes the space of square summable infinite sequence over $\left[ 0 \right.$, $\left. { + \infty } \right)$. $\varepsilon \left\{ \cdot \right\}$ denotes the expectation operator. I denotes the identity matrix of appropriate dimension. $N^{ + }$ represents the positive integers and ${\mathbb{C}}$ represents the set of complex numbers. The superscripts ‘T’ and ‘− 1’ represent the transpose and the inverse of a matrix, respectively, and ‘$*$’ denotes the symmetric term in a symmetric matrix.

2 Preliminaries and problem formulation

Consider the following discrete-time SMJSs with GUTRs:

$$ \left\{ {\begin{array}{*{20}l} {Ex\left( {k + 1} \right) = A\left( {r_{k} } \right)x\left( k \right) + B\left( {r_{k} } \right)\omega \left( k \right)} \hfill \\ {y\left( k \right) = C\left( {r_{k} } \right)x\left( k \right) + D\left( {r_{k} } \right)\omega \left( k \right)} \hfill \\ {z\left( k \right) = L\left( {r_{k} } \right)x\left( k \right)} \hfill \\ \end{array} } \right., $$

(1)

where $x\left( k \right) \in R^{n}$ is the state, $y\left( k \right) \in R^{q}$ is the measured output, $z\left( k \right) \in R^{p}$ is the signal to be estimated and $\omega \left( k \right)$ is the external disturbance which belongs to $\ell_{2} [$0, +$\infty )$. $E \in R^{n \times n}$ is singular with rank $E = r < n$. $A\left( {r_{k} } \right)$, $B\left( {r_{k} } \right)$, $C\left( {r_{k} } \right)$, $L\left( {r_{k} } \right)$ are known real constant matrices with appropriate dimensions for each $r_{k} \in S$. And $r_{k}$ is a discrete-time Markovian process taking value in a finite set S = {1, 2, …,$s\}$ with

$$ \Pr \left\{ {r_{k + 1} = j |r_{k} = i} \right\} = \pi_{ij} , $$

(2)

where $0 \le \pi_{ij} \le 1$ is the transition rate and $\sum\nolimits_{j = 1}^{s} {\pi_{ij} } = 1$. The transition rate matrix is considered to be generally uncertain and described as follows:

$$ \left[ {\begin{array}{*{20}l} {\hat{\pi }_{11} + \Delta_{11} } & ? & {\hat{\pi }_{13} + \Delta_{13} } & \cdots & ? \\ ? & ? & {\hat{\pi }_{23} + \Delta_{23} } & \cdots & {\hat{\pi }_{2s} + \Delta_{2s} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ ? & {\hat{\pi }_{s2} + \Delta_{s2} } & ? & \cdots & {\hat{\pi }_{ss} + \Delta_{ss} } \\ \end{array} } \right], $$

(3)

where $\hat{\pi }_{ij}$ and $\Delta_{ij} \in [ - \delta_{ij}$, $\delta_{ij} ](\delta_{ij} > 0$, $i$, $j \in S)$ denote the estimate value and estimate error of the transition rate, respectively, and “?” represents the complete unknown transition rate.

Let $U^{i} \left( {i \in S} \right)$ be $U^{i} = U_{k}^{i} \cup U_{uk}^{i}$, where $U_{k}^{i} \triangleq$ {j: The estimate value of $\pi_{ij}$ is known for $j \in S$}, and $U_{uk}^{i} \triangleq${j: The estimate value of $\pi_{ij}$ is unknown for $j \in S$}. Moreover, if $U_{k}^{i} \ne \emptyset$, it can be described as $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$, where $k_{m}^{i} \in N^{ + }$ denote the mth bound-known element with the index $k_{m}^{i}$ in the ith row of the transition rate matrix. And then, the following three assumptions can be defined reasonable, since they can be directly derived from the features of transition rates that $\pi_{ij} \ge 0$ and $\sum\nolimits_{j = 1}^{s} {\pi_{ij} = 1}$.

Assumption 1

If $U_{k}^{i} \ne S$, and $i \notin U_{k}^{i}$, then $\hat{\pi }_{ij} \ge 0$, (($\forall j \in U_{k}^{i}$) and $\sum\nolimits_{{j \in U_{uk}^{i} ,j \ne i}} {\pi_{ij} = 1 - \pi_{ii} } - \sum\nolimits_{{j \in U_{uk}^{i} }} {\pi_{ij} }$;

Assumption 2

If $U_{k}^{i} \ne S$, and $i \in U_{k}^{i}$, then $\hat{\pi }_{ij} \ge 0$, ($\forall j \in U_{k}^{i}$), and $\sum\nolimits_{{j \in U_{uk}^{i} }} {\pi_{ij} = 1} - \sum\nolimits_{{j \in U_{uk}^{i} }} {\pi_{ij} }$;

Assumption 3

If $U_{k}^{i} = S$, then $\hat{\pi }_{ij} \ge 0$, ($\forall j \in S$, $j \ne i$) and $\sum\nolimits_{j = 1,j \ne i}^{S} {\pi_{ij} } = 1 - \pi_{ii}$.

Consider the following full-order filter

$$ \left\{ {\begin{array}{*{20}l} {E_{f} x_{f} \left( {k + 1} \right) = A_{f} \left( {r_{k} } \right)x_{f} \left( k \right) + B_{f} \left( {r_{k} } \right)y\left( k \right)} \hfill \\ {z_{f} \left( k \right) = L_{f} \left( {r_{k} } \right)x_{f} \left( k \right) } \hfill \\ \end{array} } \right.. $$

(4)

Remark 1

For the filter’s physical implementation convenience in practical engineering, set $E_{f} = I$, which means that a normal filter rather than a singular filter is considered in this paper.

Define $\tilde{x}\left( k \right)^{\text{T}} = \left[ {x\left( k \right)^{\text{T}} x_{f} \left( k \right)^{\text{T}} } \right]^{\text{T}}$ and $\tilde{z}\left( k \right) = z\left( k \right) - z_{f} \left( k \right)$. It follows from (1) and (4) that the filtering error dynamics can be written as

$$ \left\{ {\begin{array}{*{20}l} {\tilde{E}\tilde{x}\left( {k + 1} \right) = \tilde{A}\tilde{x}\left( k \right) + \tilde{B}\omega \left( k \right)} \hfill \\ {\tilde{z}\left( k \right) = \tilde{L}\tilde{x}\left( k \right)} \hfill \\ \end{array} } \right., $$

(5)

where

$$ \begin{aligned} & \tilde{E} = \left[ {\begin{array}{*{20}l} E & 0 \\ 0 & I \\ \end{array} } \right],\quad \tilde{A} = \left[ {\begin{array}{*{20}l} {A\left( {r_{k} } \right)} \hfill & 0 \hfill \\ {B_{f} \left( {r_{k} } \right)C\left( {r_{k} } \right)} \hfill & {A_{f} \left( {r_{k} } \right)} \hfill \\ \end{array} } \right], \\ & \tilde{L} = \left[ {\begin{array}{*{20}l} {L\left( {r_{k} } \right)} & { - L_{f} \left( {r_{k} } \right)} \\ \end{array} } \right]. \\ \end{aligned} $$

(6)

Definition 1

Consider discrete-time singular Markovian jump system

$$ Ex\left( {k + 1} \right) = A\left( {r_{k} } \right)x\left( k \right), $$

(7)

System (7) is said to be regular if for any $r_{k} = i$($i \in S$), if there exists a scalar $s \in {\mathbb{C}}$ such that $\det \left( {sE - A\left( {r_{k} } \right)} \right) \ne 0$;

System (7) is said to be causal if for any $r_{k} = i$($i \in S$), if there exists a scalar $s \in {\mathbb{C}}$ such that $\deg \left( {\det \left( {sE - A\left( {r_{k} } \right)} \right)} \right) = {\text{rank}}\left( E \right)$;

System (7) is said to be stochastically stable if there exists Lyapunov functional $V\left( k \right) > 0$, such that $\varepsilon \left( {\Delta V\left( k \right)} \right) = \varepsilon \left( {V\left( {k + 1} \right) - V\left( k \right)} \right) < 0$;

System (7) is said to be stochastically admissible if it is regular, causal and stochastically stable, simultaneously.

Definition 2

The Markovian jump system (1) is said to be stochastically stable while satisfying a prescribed $H_{\infty }$ performance $\gamma$ if under zero initial condition, for any non-zero $\omega \left( k \right) \in \ell_{2} [$ 0, +$\infty )$, the following condition holds:

$$ \varepsilon \left( {\sum\nolimits_{k = 0}^{\infty } {\tilde{z}} \left( k \right)^{\text{T}} \tilde{z}\left( k \right)} \right) \le \gamma^{2} \sum\nolimits_{k = 0}^{\infty } {\omega^{\text{T}} } \left( k \right)\omega \left( k \right). $$

The objective of this paper is to design a normal full-order filter (4) for system (1) such that the filtering error system (5) is stochastically admissible with a prescribed $H_{\infty }$ performance index $\gamma$. For notational simplicity, in this paper, when $r_{k} = i\left( {i \in S} \right)$, $A\left( {r_{k} } \right)$, $B\left( {r_{k} } \right)$, $C\left( {r_{k} } \right)$, $D\left( {r_{k} } \right)$, $L\left( {r_{k} } \right)$, $A_{f} \left( {r_{k} } \right)$, $B_{f} \left( {r_{k} } \right)$, $L_{f} \left( {r_{k} } \right)$ are denoted by $A_{i}$, $B_{i}$, $C_{i}$, $D_{i}$, $L_{i}$, $A_{\mathrm{fi}}$, $B_{\mathrm{fi}}$, $L_{\mathrm{fi}}$ and so on. And for further explanation, some lemmas are introduced as follows.

Lemma 1

[10] Given $x_{k} \in R^{n}$, $\varTheta = \varTheta^{\text{T}} \in R^{n \times n}$ and $B \in R^{m \times n}$, if ${\text{rank}}\left( B \right) < n$, the following conditions are equivalent

• 1. $x_{k}^{\text{T}} \varTheta x_{k} < 0$, $\forall Bx_{k} = 0$, $x_{k} \ne 0$,

• 2. $\exists {\mathcal{X}}$, such that $\varTheta + {\mathcal{X}}B + B^{\text{T}} {\mathcal{X}}^{\text{T}} < 0$.

Lemma 2

[30] Given any real scalar $\alpha$ and any matrix ${\mathcal{Q}}$, the matrix inequality

$$ \alpha \left( {{\mathcal{Q}} + {\mathcal{Q}}^{\text{T}} } \right) \le \alpha^{2} T + {\mathcal{Q}}T^{ - 1} {\mathcal{Q}}^{\text{T}} $$

holds for any matrix $T > 0.$

Lemma 3

[28] Given matrices X, Y, Z with appropriate dimensions, and Y is symmetric positive definite, then the following inequality holds:

$$ - Z^{\text{T}} YZ \le X^{\text{T}} Z + Z^{\text{T}} X + X^{\text{T}} Y^{ - 1} X. $$

Lemma 4

The filtering error system (5) with GUTRs is stochastically admissible while satisfying a prescribed $H_{\infty }$ performance index $\gamma$, if there exist matrices $G$, $F$ and $P_{i} > 0 \left( {i \in S} \right)$, such that

$$ \theta = \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 \\ * & {\tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{s} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E}} & {\tilde{A}^{T} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right] < 0. $$

(8)

Proof

See “Appendix A”.□

3 Main results

In the sequel, the sufficient conditions for the existence of $H_{\infty }$ filter are derived such that the resulting filtering error system (5) is stochastically admissible with a prescribed $H_{\infty }$ performance $\gamma$. And the desired filter design method is also given. Firstly, based on Lemma 4, and corresponding to the aforementioned three assumptions, the following Theorem 1 is immediate.

Theorem 1

Given scalars $\delta_{ij} (i$, $j \in S)$, the filtering error system (5) with GUTRs is stochastically admissible while satisfying a prescribed $H_{\infty }$ performance index $\gamma$, if there exist matrices $G$, $F$ and symmetric matrix $P_{i} > 0 \left( {i \in S} \right)$, such that

Case I. If $i \notin U_{k}^{i}$, $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$ there exist a set of positive definite matrices $T_{ij} \in R^{n \times n} (i \notin U_{k}^{i}$, $j \in U_{k}^{i} )$ such that

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 & 0 & \cdots & 0 \\ * & {\theta_{1} } & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{i} } \right)^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 & 0 & \cdots & 0 \\ * & * & * & { - I} & 0 & \cdots & 0 \\ * & * & * & * & { - T_{{iK_{1}^{i} }} } & \cdots & 0 \\ * & * & * & * & * & \ddots & \vdots \\ * & * & * & * & * & \cdots & { - T_{{iK_{m}^{i} }} } \\ \end{array} } \right] < 0, $$

(9)

where $P_{j} - P_{i} \le 0( j \in U_{uk}^{i}$, $j \ne i)$.

Case II If $i \in U_{k}^{i}$, $U_{uk}^{i} \ne \emptyset$ and $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$, there exist a set of positive definite matrices $V_{ijl} \in R^{n \times n} (i$, $j \in U_{k}^{i}$, $l \in U_{uk}^{i} )$ such that

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 & 0 & \cdots & 0 \\ * & {\theta_{2} } & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{l} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{l} } \right)^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 & 0 & \cdots & 0 \\ * & * & * & { - I} & 0 & \cdots & 0 \\ * & * & * & * & { - V_{{iK_{1}^{i} l}} } & \cdots & 0 \\ * & * & * & * & * & \ddots & \vdots \\ * & * & * & * & * & \cdots & { - V_{{iK_{m}^{i} l}} } \\ \end{array} } \right] < 0, $$

(10)

Case III If $i \in U_{k}^{i}$, $U_{uk}^{i} = \emptyset$, there exist a set of positive definite matrices $R_{ij} \in R^{n \times n} (i$, $j \in U_{k}^{i} )$ such that

$$ \begin{aligned} & \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 & 0 & \cdots & 0 \\ * & {\theta_{3} } & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } & {\tilde{A}^{\text{T}} \left( {P_{1} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{i - 1} - P_{i} } \right)^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 & 0 & \cdots & 0 \\ * & * & * & { - I} & 0 & \cdots & 0 \\ * & * & * & * & { - R_{i1} } & \cdots & 0 \\ * & * & * & * & * & \ddots & 0 \\ * & * & * & * & * & \cdots & { - R_{{i\left( {i - 1} \right)}} } \\ * & * & * & * & * & \cdots & * \\ * & * & * & * & * & \cdots & * \\ * & * & * & * & * & \cdots & * \\ \end{array} } \right. \\ & \left. {\begin{array}{*{20}l} 0 & \cdots & 0 \\ {\tilde{A}^{\text{T}} \left( {P_{i + 1} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{s} - P_{i} } \right)^{\text{T}} } \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ { - R_{{i\left( {i + 1} \right)}} } & \cdots & 0 \\ * & \ddots & \vdots \\ * & \cdots & { - R_{is} } \\ \end{array} } \right] < 0, \\ \end{aligned} $$

(11)

where

$$ \begin{aligned} & \theta_{1} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \tilde{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}, \\ & \theta_{2} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{l} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl} \tilde{A} + \tilde{A}^{\text{T}} P_{l} \tilde{A}, \\ & \theta_{3} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{s} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{s} \frac{{\delta_{ij}^{2} }}{4}R_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}. \\ \end{aligned} $$

Proof

See “Appendix B”.□

Remark 2

In Theorem 1, there is a one-to-one corresponding relationship between the Assumptions 1, 2, 3 and the Cases I, II, III. In addition, in the system (1), $r_{k}$ is a discrete-time Markovian process taking value in a finite set S = $\{ 1$,2,…,$s\}$, then system (1) has s modes, and each mode must correspond to Assumption 1 or Assumption 2 or Assumption 3, that is to say, each mode of system (1) corresponds to Case I or Case II or Case III. So does Theorem 2.

Theorem 1 gives sufficient conditions for solving the $H_{\infty }$ stochastic admissibility of the filtering error system (5). It should be noted that the formulas (9), (10) and (11) in Theorem 1 are nonlinear matrix inequalities including the cross-term between determined matrices $G$, $F$ and filter parameters $A_{\text{fi}}$, $B_{\text{fi}}$, $L_{\text{fi}}$. By using some appropriate matrix transformations, the corresponding sufficient conditions based on LMIs are obtained in the following Theorem 2.

Theorem 2

Given scalars $\delta_{ij} (i$, $j \in S)$, $\alpha_{k} \left( {k \in U_{k}^{i} } \right)$, the filtering error system (5) with GUTRs is stochastically admissible while satisfying a prescribed performance $H_{\infty }$ index $\gamma$, if there exist approximate dimension matrices $G_{11}$, $G_{12}$, $G_{22}$, $F_{11}$, $F_{12}$, $a_{\text{fi}}$, $b_{\text{fi}}$, $l_{\text{fi}}$ and ${\text{symmetric matrix }}P_{i} > 0$ ($i \in U_{k}^{i}$), such that

Case I If $i \notin U_{k}^{i}$, $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$,$k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$, there exist a set of positive definite matrices $T_{ij} \in R^{n \times n} (i \notin U_{k}^{i}$, $j \in U_{k}^{i} )$ such that

$$ \left[ {\begin{array}{*{20}l} {\varOmega_{11} } & {\varOmega_{12} } & {\varOmega_{13} } & 0 & 0 & 0 & 0 & \cdots & 0 \\ * & {\varOmega_{22} } & {\varOmega_{23} } & {\varOmega_{24} } & {\varOmega_{25} } & {\varOmega_{26} } & {M_{21} } & \cdots & {M_{2m} } \\ * & * & {\varOmega_{33} } & 0 & 0 & 0 & 0 & \cdots & 0 \\ * & * & * & { - I} & 0 & 0 & 0 & \cdots & 0 \\ * & * & * & * & {\varOmega_{55} } & 0 & 0 & \cdots & 0 \\ * & * & * & * & * & {\varOmega_{66} } & 0 & \cdots & 0 \\ * & * & * & * & * & * & { - T_{{ik_{1}^{i} }} } & \cdots & 0 \\ * & * & * & * & * & * & * & \ddots & \vdots \\ * & * & * & * & * & * & * & * & { - T_{{ik_{m}^{i} }} } \\ \end{array} } \right] < 0, $$

(12)

where

$$ \begin{aligned} & \varOmega_{11} = \left[ {\begin{array}{*{20}l} { - G_{11} - G_{11}^{\text{T}} } \hfill & { - G_{22} - G_{21}^{\text{T}} } \hfill \\ * \hfill & { - G_{22} - G_{22}^{\text{T}} } \hfill \\ \end{array} } \right],\quad \varOmega_{12} = \left[ {\begin{array}{*{20}l} {G_{11} A_{i} + b_{\text{fi}} C_{i} } & {a_{\text{fi}} } \\ {G_{21} A_{i} + b_{\text{fi}} C_{i} } & {a_{\text{fi}} } \\ \end{array} } \right], \\ & \varOmega_{13} = \left[ {\begin{array}{*{20}l} { - F_{11}^{\text{T}} + G_{11} B_{i} + b_{\text{fi}} D_{i} } & { - F_{21}^{\text{T}} } \\ { - G_{22}^{\text{T}} + G_{21} B_{i} + b_{\text{fi}} D_{i} } & { - G_{22}^{\text{T}} } \\ \end{array} } \right], \\ & \varOmega_{22} = \left[ {\begin{array}{*{20}l} { - E^{\text{T}} P_{i1} E + A_{i}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j1} - P_{i1} } \right)A_{i} } \hfill & 0 \hfill \\ 0 \hfill & { - P_{i2} } \hfill \\ \end{array} } \right], \\ & \varOmega_{23} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} F_{11}^{\text{T}} + C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill & {A_{i}^{\text{T}} F_{21}^{\text{T}} + C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill \\ {a_{\mathrm{fi}}^{\text{T}} } \hfill & {a_{\mathrm{fi}}^{\text{T}} } \hfill \\ \end{array} } \right],\quad \varOmega_{24} = \left[ {\begin{array}{*{20}l} {L_{i}^{\text{T}} } \\ { - l_{\text{fi}}^{\text{T}} } \\ \end{array} } \right], \\ & \varOmega_{25} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} G_{11}^{\text{T}} + C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill & {A_{i}^{\text{T}} G_{21}^{\text{T}} + C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill \\ {a_{\text{fi}}^{\text{T}} } \hfill & {a_{\text{fi}}^{\text{T}} } \hfill \\ \end{array} } \right],\quad \varOmega_{26} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} P_{i1}^{\text{T}} } & {\alpha_{i} C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \\ 0 & {\alpha_{i} a_{\text{fi}}^{\text{T}} } \\ \end{array} } \right], \\ & M_{2k} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} \left( {P_{k1} - P_{i1} } \right)^{\text{T}} } \hfill & {\left( {\alpha_{k} - \alpha_{i} } \right)C_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill \\ 0 \hfill & {\left( {\alpha_{k} - \alpha_{i} } \right)a_{\text{fi}}^{\text{T}} } \hfill \\ \end{array} } \right]\left( {k \in U_{k}^{i} } \right), \\ & \varOmega_{33} = \left[ {\begin{array}{*{20}l} {B_{i}^{\text{T}} F_{11}^{\text{T}} + D_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} + F_{11} B_{i} + b_{\text{fi}} D_{i} - \gamma^{2} I} \hfill & {B_{i}^{\text{T}} F_{21}^{\text{T}} + D_{i}^{\text{T}} b_{\text{fi}}^{\text{T}} } \hfill \\ * \hfill & { - \gamma^{2} I} \hfill \\ \end{array} } \right], \\ & \varOmega_{55} = \left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij1} - G_{11} - G_{11}^{\text{T}} } & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij2} - G_{22} - G_{21}^{\text{T}} } \\ * & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij3} - G_{22} - G_{22}^{\text{T}} } \\ \end{array} } \right], \\ & \varOmega_{66} = \left[ {\begin{array}{*{20}l} { - P_{i1} } & 0 \\ 0 & { - P_{i2} } \\ \end{array} } \right],\quad T_{ij} = \left[ {\begin{array}{*{20}l} {T_{ij1} } & {T_{ij2} } \\ * & {T_{ij3} } \\ \end{array} } \right]. \\ \end{aligned} $$

Case II If $i \in U_{k}^{i}$, $U_{uk}^{i} \ne \emptyset$ and $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$, there exist a set of positive definite matrices $V_{ijl} \in R^{n \times n} (i$, $j \in U_{k}^{i}$, $l \in U_{uk}^{i} )$ such that

$$ \left[ {\begin{array}{*{20}l} {\varOmega_{11} } & {\varOmega_{12} } & {\varOmega_{13} } & 0 & 0 & 0 & 0 & \cdots & 0 \\ * & {\varOmega_{22}^{'} } & {\varOmega_{23} } & {\varOmega_{24} } & {\varOmega_{25} } & {\varOmega_{26}^{\prime } } & {M_{21} } & \cdots & {M_{2m} } \\ * & * & {\varOmega_{33} } & 0 & 0 & 0 & 0 & \cdots & 0 \\ * & * & * & { - I} & 0 & 0 & 0 & \cdots & 0 \\ * & * & * & * & {\varGamma_{55} } & 0 & 0 & \cdots & 0 \\ * & * & * & * & * & {\varGamma_{66} } & 0 & 0 & 0 \\ * & * & * & * & * & * & { - V_{{ik_{1}^{i} l}} } & \cdots & 0 \\ * & * & * & * & * & * & * & \ddots & \vdots \\ * & * & * & * & * & * & * & * & { - V_{{ik_{m}^{i} l}} } \\ \end{array} } \right] < 0, $$

(13)

where $\varOmega_{11}$, $\varOmega_{12}$, $\varOmega_{13}$, $\varOmega_{23}$, $\varOmega_{24}$, $\varOmega_{25}$, $\varOmega_{33}$ and $M_{2k} \left( {k \in U_{k}^{i} } \right)$ are the same as that in Case I and

$$ \begin{aligned} & \varOmega_{22}^{\prime } = \left[ {\begin{array}{*{20}l} { - E^{\text{T}} P_{l1} E + A_{i}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j1} - P_{l1} } \right)A_{i} } \hfill & 0 \hfill \\ 0 \hfill & { - P_{l2} } \hfill \\ \end{array} } \right],\quad V_{ijl} = \left[ {\begin{array}{*{20}l} {V_{ijl1} } & {V_{ijl2} } \\ * & {V_{ijl3} } \\ \end{array} } \right], \\ & \varGamma_{55} = \left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl1} - G_{11} - G_{11}^{\text{T}} } & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl2} - G_{22} - G_{21}^{\text{T}} } \\ * & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl3} - G_{22} - G_{22}^{\text{T}} } \\ \end{array} } \right],\quad \varGamma_{66} = \left[ {\begin{array}{*{20}l} { - P_{l1} } & 0 \\ 0 & { - P_{l2} } \\ \end{array} } \right], \\ & \varOmega_{26}^{\prime } = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} P_{l1}^{\text{T}} } & {\alpha_{l} C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \\ 0 & {\alpha_{l} a_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right]. \\ \end{aligned} $$

Case III If $i \in U_{k}^{i}$, $U_{uk}^{i} = \emptyset$, there exist a set of positive definite matrices $R_{ij} \in R^{n \times n} (i$, $j \in U_{k}^{i} )$ such that

$$ \left[ {\begin{array}{*{20}l} {\varOmega_{11} } \hfill & {\varOmega_{12} } \hfill & {\varOmega_{13} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & {\varOmega_{22}^{\prime \prime } } \hfill & {\varOmega_{23} } \hfill & {\varOmega_{24} } \hfill & {\varOmega_{25} } \hfill & {\varOmega_{26} } \hfill & {M_{21} } \hfill & \ldots \hfill & {M_{{2\left( {i - 1} \right)}} } \hfill & {M_{{2\left( {i + 1} \right)}} } \hfill & \ldots \hfill & {M_{2s} } \hfill \\ * \hfill & * \hfill & {\varOmega_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & { - I} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & {I_{55} } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & {\varOmega_{66} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - R_{i1} } \hfill & \ldots \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill & \ldots \hfill & \vdots \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - R_{{i\left( {i - 1} \right)}} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - R_{{i\left( {i + 1} \right)}} } \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & \ddots \hfill & \vdots \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & \ldots \hfill & { - R_{is} } \hfill \\ \end{array} } \right] < 0, $$

(14)

where $\varOmega_{11}$, $\varOmega_{12}$, $\varOmega_{13}$, $\varOmega_{23}$, $\varOmega_{24}$, $\varOmega_{25}$, $\varOmega_{26}$, $\varOmega_{33}$, $M_{2k} (k \in S$, $k \ne i)$ and $\varOmega_{66}$ are the same as that in Case I and

$$ \begin{aligned} & \varOmega_{22}^{\prime \prime } = \left[ {\begin{array}{*{20}l} { - E^{\text{T}} P_{i1} E + A_{i}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{s} \hat{\pi }_{ij} \left( {P_{j1} - P_{i1} } \right)A_{i} } \hfill & 0 \hfill \\ 0 \hfill & { - P_{i2} } \hfill \\ \end{array} } \right],\quad R_{ij} = \left[ {\begin{array}{*{20}l} {R_{ij1} } & {R_{ij2} } \\ * & {R_{ij3} } \\ \end{array} } \right], \\ & I_{55} = \left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1,j \ne i}^{s} \frac{{\delta_{ij}^{2} }}{4}R_{ij1} - G_{11} - G_{11}^{\text{T}} } \hfill & {\mathop \sum \limits_{j = 1,j \ne i}^{s} \frac{{\delta_{ij}^{2} }}{4}R_{ij2} - G_{22} - G_{21}^{\text{T}} } \hfill \\ * \hfill & {\mathop \sum \limits_{j = 1,j \ne i}^{s} \frac{{\delta_{ij}^{2} }}{4}R_{ij3} - G_{22} - G_{22}^{\text{T}} } \hfill \\ \end{array} } \right]. \\ \end{aligned} $$

Moreover, the parameters of the filter are given as

$$ A_{\text{fi}} = G_{22}^{ - 1} a_{\text{fi}} ,\quad B_{\text{fi}} = G_{22}^{ - 1} b_{\text{fi}} ,\quad L_{\text{fi}} = l_{\text{fi}} . $$

(15)

Proof

See “Appendix C”.□

Remark 3

In Theorem 2, $\varOmega_{22}$ in Case I, $\varOmega_{22}^{\prime }$ in Case II and $\varOmega_{22}^{\prime \prime }$ in Case III contain estimate values $\hat{\pi }_{ij}$, which are known for $\forall j \in U_{k}^{i}$, so the inequalities (12), (13) and (14) are LMIs since parameters in each inequality have no nonlinear cross-term.

4 Numerical example

In this section, a numerical example is demonstrated to illustrate the effectiveness of the proposed method. Consider the discrete-time singular Markovian jump system (1) with three modes and of the following transition probability matrix:

$$ \left[ {\begin{array}{*{20}l} ? & {0.4 + \Delta_{12} } & ? \\ ? & {0.4 + \Delta_{22} } & ? \\ {0.4 + \Delta_{31} } & {0.25 + \Delta_{32} } & {0.35 + \Delta_{33} } \\ \end{array} } \right], $$

where $\Delta_{12} \in \left[ { - 0.15,0.15} \right]$, $\Delta_{22} \in \left[ { - 0.05,0.05} \right]$, $\Delta_{31} \in \left[ { - 0.09,0.09} \right]$, $\Delta_{32} \in \left[ { - 0.11,0.11} \right]$, $\Delta_{33} \in \left[ { - 0.06,0.06} \right]$.

The system parameters are given as follows:

$$ E = \left[ {\begin{array}{*{20}l} I & 0 \\ 0 & 0 \\ \end{array} } \right], $$

for mode 1, $r_{k} = i = 1$, $U_{k}^{i} = \left\{ 2 \right\}$, and $i \in U_{uk}^{i} = \left\{ {1,3} \right\}$, then

$$ A_{1} = \left[ {\begin{array}{*{20}l} { - 0.5} & {0.1} \\ { - 0.1} & {0.5} \\ \end{array} } \right],\quad B_{1} = \left[ {\begin{array}{*{20}l} {0.5} \\ {0.5} \\ \end{array} } \right],\quad C_{1} = \left[ {\begin{array}{*{20}l} { - 0.9} & 1 \\ \end{array} } \right],\quad D_{1} = 0.2,\quad L_{1} = \left[ {\begin{array}{*{20}l} {0.3} & {0.5} \\ \end{array} } \right]. $$

for mode 2, $r_{k} = i = 2$, $i \in U_{k}^{i} = \left\{ 2 \right\}$, and $U_{uk}^{i} = \left\{ {1,3} \right\}$, then

$$ A_{2} = \left[ {\begin{array}{*{20}l} { - 0.5} & 0 \\ {0.5} & { - 0.7} \\ \end{array} } \right],\quad B_{2} = \left[ {\begin{array}{*{20}l} { - 0.5} \\ {0.5} \\ \end{array} } \right],\quad C_{2} = \left[ {\begin{array}{*{20}l} {0.3} & { - 0.2} \\ \end{array} } \right],\quad D_{2} = - 0.1,\quad L_{2} = \left[ {\begin{array}{*{20}l} {0.2} & { - 0.1} \\ \end{array} } \right]. $$

for mode 3, $r_{k} = i = 3$, $i \in U_{k}^{i} = \{ 1,2$, $3\}$, and $U_{uk}^{i}$ = $\emptyset$, then

$$ A_{3} = \left[ {\begin{array}{*{20}l} { - 0.4} & 1 \\ 0 & {0.6} \\ \end{array} } \right],\quad B_{3} = \left[ {\begin{array}{*{20}l} { - 1} \\ {0.4} \\ \end{array} } \right],\quad C_{3} = \left[ {\begin{array}{*{20}l} { - 0.4} & {0.5} \\ \end{array} } \right],\quad D_{3} = 0.3,\quad L_{3} = \left[ {\begin{array}{*{20}l} {0.3} & { - 0.2} \\ \end{array} } \right]. $$

Set $\alpha_{1} = 680$, $\alpha_{2} = 10$, $\alpha_{3} = 900$, and the prescribed $H_{\infty }$ performance $\gamma$ = 0.8, by solving LMIs (12), (13) and (14) simultaneously, the filter parameters can be obtained as follows:

$$ \begin{aligned} & A_{{{\text{f}}1}} = \left[ {\begin{array}{*{20}l} {0.5513} & {0.1058} \\ {0.1120} & {0.3017} \\ \end{array} } \right],\quad B_{{{\text{f}}1}} = \left[ {\begin{array}{*{20}l} {1.2555} & {2.1446} \\ { - 3.2567} & { - 5.5859} \\ \end{array} } \right],\quad C_{{{\text{f}}1}} = \left[ {\begin{array}{*{20}l} { - 0.2903} & { - 0.4646} \\ \end{array} } \right]. \\ & A_{{{\text{f}}2}} = \left[ {\begin{array}{*{20}l} {0.8196} & {0.1911} \\ {0.1934} & {0.3529} \\ \end{array} } \right],\quad B_{{{\text{f}}2}} = \left[ {\begin{array}{*{20}l} { - 0.7295} & { - 1.2464} \\ {7.5637} & {12.8708} \\ \end{array} } \right],\quad C_{{{\text{f}}2}} = \left[ {\begin{array}{*{20}l} {0.0101} & {0.0191} \\ \end{array} } \right]. \\ & A_{{{\text{f}}3}} = \left[ {\begin{array}{*{20}l} {0.4543} & {0.0900} \\ {0.0976} & {0.2464} \\ \end{array} } \right],\quad B_{{{\text{f}}3}} = \left[ {\begin{array}{*{20}l} {0.4544} & {0.7711} \\ { - 2.9314} & { - 5.0439} \\ \end{array} } \right],\quad C_{{{\text{f}}3}} = \left[ {\begin{array}{*{20}l} {0.0062} & {0.0071} \\ \end{array} } \right]. \\ \end{aligned} $$

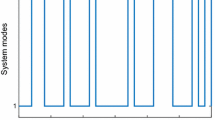
Suppose the external disturbance $\omega \left( k \right) = 10\sin \left( k \right){\text{e}}^{ - 0.2k}$ and a set of initial condition $x_{1} \left( 0 \right) = 1$, $x_{2} \left( 0 \right) = 0.0571$, $z\left( 0 \right) = 0.32855$. Figure 1 shows the Markovian jump system switches between jumping mode 1 and jumping mode 3 and it follows from Fig. 1 that the initial mode is $r_{0}$ = 1. Figure 2 shows the curve of resulting filtering error $\tilde{z}\left( k \right)$. It can be seen from Fig. 2 that filtering error $\tilde{z}\left( k \right)$ approaches to 0 when the number of jump times is about to 30, so filtering error system (5) is stochastic admissibility with a prescribed $H_{\infty }$ performance index $\gamma$ according to Theorem 2.

Fig. 1

System jumping modes

Fig. 2

The curve of the resulting filtering error $\tilde{z}\left( k \right)$

It can be calculated from Fig. 2 that the $H_{\infty }$ performance $\gamma$ = $\left( {\frac{{\varepsilon (\mathop \sum \nolimits_{k = 0}^{100} \tilde{z}\left( k \right)^{\text{T}} \tilde{z}\left( k \right))}}{{\mathop \sum \nolimits_{k = 0}^{100} \omega^{\text{T}} \left( k \right)\omega \left( k \right)}}} \right)^{1/2} =$ 0.2143, which is less than the given $H_{\infty }$ performance 0.8, that is to say, the proposed filter design method is effective.

5 Conclusion

In this paper, $H_{\infty }$ filtering problem for a class of linear discrete-time singular Markovian jump system with GUTRs has been studied. Sufficient conditions in terms of LMIs are obtained such that the filtering error system is stochastically admissible while satisfying a prescribed $H_{\infty }$ performance; meanwhile, the corresponding normal full-order filter design method is also given. Finally, a numerical example shows validity of the proposed approach.

Appendices

Appendix A: Proof of Lemma 4

Firstly, the regularity and causality of filtering error dynamics (5) are considered. Since the matrix $\tilde{E}$ is singular, there must exist two non-singular matrices M and N such that

$$ \tilde{E} = M\left[ {\begin{array}{*{20}l} {I_{n + r} } & 0 \\ 0 & 0 \\ \end{array} } \right]N, $$

and write

$$ M^{\text{T}} P_{i} M = \left[ {\begin{array}{*{20}l} {\hat{P}_{i1} } & {\hat{P}_{i2} } \\ {\hat{P}_{i1}^{\text{T}} } & {\hat{P}_{i3} } \\ \end{array} } \right],\quad M^{ - 1} \tilde{A}N^{ - 1} = \left[ {\begin{array}{*{20}l} {A_{1i} } & {A_{2i} } \\ {A_{3i} } & {A_{4i} } \\ \end{array} } \right]. $$

(16)

It can obtain from (8) that

$$ \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E} < 0. $$

(17)

Pre- and post-multiplying (17) by $N^{{ - {\text{T}}}}$ and $N^{ - 1}$, it can get that

$$ N^{{ - {\text{T}}}} \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A}N^{ - 1} - N^{{ - {\text{T}}}} \tilde{E}^{\text{T}} P_{i} \tilde{E}N^{ - 1} < 0. $$

(18)

Subscribe (16) to (18), then

$$ N^{{ - {\text{T}}}} N^{\text{T}} \left[ {\begin{array}{*{20}l} {A_{1i} } & {A_{2i} } \\ {A_{3i} } & {A_{4i} } \\ \end{array} } \right]^{\text{T}} M^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} M\left[ {\begin{array}{*{20}l} {A_{1i} } & {A_{2i} } \\ {A_{3i} } & {A_{4i} } \\ \end{array} } \right]NN^{ - 1} - N^{{ - {\text{T}}}} N^{\text{T}} \left[ {\begin{array}{*{20}l} {I_{n + r} } & 0 \\ 0 & 0 \\ \end{array} } \right]^{\text{T}} M^{\text{T}} P_{i} M\left[ {\begin{array}{*{20}l} {I_{n + r} } & 0 \\ 0 & 0 \\ \end{array} } \right]NN^{ - 1} < 0, $$

which implies

$$ \left[ {\begin{array}{*{20}l} {Q_{1i} } & {Q_{2i} } \\ {Q_{2i}^{T} } & {Q_{3i} } \\ \end{array} } \right] < 0, $$

(19)

where

$$ Q_{3i} = A_{2i}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} \hat{P}_{j1} A_{2i} + A_{2i}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} \hat{P}_{j2} A_{4i} + A_{4i}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} \hat{P}_{j2}^{\text{T}} A_{2i} + A_{4i}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} \hat{P}_{j3} A_{4i} . $$

It follows from (19) that $Q_{3i} < 0$, note that $\hat{P}_{j1} > 0\left( {j \in S} \right)$, which implies that $A_{4i} \left( {i \in S} \right)$ is non-singular. Thus, by Definition 1, the inequality (8) guarantees that the filtering error system (5) is regular and causal.

Now, if the inequality (8) holds, define the following Lyapunov functional

$$ V\left( k \right) = \tilde{x}^{\text{T}} \left( k \right)\tilde{E}^{\text{T}} P_{i} \tilde{E}\tilde{x}\left( k \right). $$

Then, when $\omega \left( k \right) = 0$, one can get that

$$ \begin{aligned} \varepsilon \left[ {\Delta V\left( k \right)} \right] &= \varepsilon \left\{ {V(} \right.\tilde{x}\left( {k + 1} \right), r_{k + 1} )|\tilde{x}\left( k \right)\left. {r_{k} = i} \right\} - \varepsilon \left\{ {V(\tilde{x}\left( k \right)} \right.,\left. {r_{k} = i)} \right\} \\ & = \tilde{x}^{\text{T}} \left( k \right)\left\{ {\tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{s} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E}} \right\} \tilde{x}\left( k \right). \\ \end{aligned} $$

It follows from (17) that

$$ \begin{aligned} \varepsilon \left[ {\Delta V\left( k \right)} \right] &= \tilde{x}^{\text{T}} \left( k \right)\left\{ {\tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{s} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E}} \right\}\tilde{x}\left( k \right) \\ & < 0. \\ \end{aligned} $$

Thus, from Definition 1, the filtering error system (5) is stochastically stable.

Next, consider the following performance

$$ {\mathcal{J}} \triangleq \mathop \sum \limits_{k = 0}^{\infty } [\varepsilon (\tilde{z}\left( k \right)^{\text{T}} \tilde{z}\left( k \right)) - \gamma^{2} \omega^{\text{T}} \left( k \right)\omega \left( k \right)]. $$

Under zero-initial condition, it is easy to see

$$ \begin{aligned} {\mathcal{J}} & \le \mathop \sum \limits_{k = 0}^{\infty } [\varepsilon (\tilde{z}\left( k \right)^{\text{T}} \tilde{z}\left( k \right)) - \gamma^{2} \omega^{\text{T}} \left( k \right)\omega \left( k \right) + \varepsilon \Delta V\left( k \right)] \\ & = \mathop \sum \limits_{k = 0}^{\infty } \sigma^{\text{T}} \left( k \right)\varTheta \sigma \left( k \right), \\ \end{aligned} $$

where $\sigma \left( k \right) = \left[ {\tilde{x}^{\text{T}} \left( {k + 1} \right)\tilde{E} ^{\text{T}} \tilde{x}^{\text{T}} \left( k \right) \omega^{\text{T}} \left( k \right)} \right]^{\text{T}} ,$

$$ \varTheta = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 \\ 0 & {\tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{L}^{\text{T}} \tilde{L}} & 0 \\ 0 & 0 & { - \gamma^{2} I} \\ \end{array} } \right]. $$

In addition, the system (5) implies

$$ \left[ {\begin{array}{*{20}l} { - I} & {\tilde{A}} & {\tilde{B}} \\ \end{array} } \right]\sigma \left( k \right) = 0. $$

Set

$$ B = \left[ {\begin{array}{*{20}l} { - I} & {\tilde{A}} & {\tilde{B}} \\ \end{array} } \right]\quad \quad {\mathcal{X}} = \left[ {\begin{array}{*{20}l} G \\ 0 \\ F \\ \end{array} } \right], $$

Then

$$ \varTheta + {\mathcal{X}}B + B^{\text{T}} {\mathcal{X}}^{\text{T}} \, = \,\left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} \\ * & {\tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{s} \pi_{ij} P_{j} \tilde{A} - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{L}^{\text{T}} \tilde{L}} & {\tilde{A}^{\text{T}} F^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} \\ \end{array} } \right]. $$

Since

$$ \left[ {\begin{array}{*{20}l} 0 & 0 & 0 \\ 0 & {\tilde{L}^{\text{T}} \tilde{L}} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}l} 0 \\ {\tilde{L}^{\text{T}} } \\ 0 \\ \end{array} } \right]\left( { - I} \right)\left[ {\begin{array}{*{20}l} 0 & {\tilde{L}} & 0 \\ \end{array} } \right], $$

From the Schur complement formula, the inequality (8) is equivalent to $\varTheta + {\mathcal{X}}B + B^{\text{T}} {\mathcal{X}}^{\text{T}} < 0$.

By Lemma 1, $\varTheta + {\mathcal{X}}B + B^{\text{T}} {\mathcal{X}}^{\text{T}} < 0$ is equivalent to

$$ \sigma^{\text{T}} \left( k \right)\varTheta \sigma \left( k \right) < 0. $$

Hence, ${\mathcal{J}}$ < 0, that is to say, $\varepsilon \left\{ {z^{\text{T}} \left( k \right)z\left( k \right)} \right\} \le \gamma^{2} \omega^{\text{T}} \left( k \right)\omega \left( k \right)$, the $H_{\infty }$ performance is satisfied. To sum up, the condition (8) can guarantee the filtering error system (5) is stochastically stable with a prescribed $H_{\infty }$ performance $\gamma$. This completes the proof of Lemma 4.

Appendix B: Proof of Theorem 1

Case I If $i \notin U_{k}^{i}$, $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$. In this case, $P_{j} - P_{i} \le 0$ ($j \in U_{uk}^{i}$, $j \ne i$) and $\sum\nolimits_{{j \in U_{uk}^{i} ,j \ne i}} {\pi_{ij} } + \sum\nolimits_{{j \in U_{k}^{i} }} {\pi_{ij} + \pi_{ii} } = 1$, then one has

$$ \begin{aligned} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} &= \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} + \pi_{ii} P_{i} + \mathop \sum \limits_{{j \in U_{uk}^{i} ,j \ne i}} \pi_{ij} P_{j} = \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} + \pi_{ii} P_{i} + \left( {1 - \pi_{ii} - \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} } \right)P_{j} \\ & \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} + \pi_{ii} P_{i} + \left( {1 - \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} - \pi_{ii} } \right)P_{i} = \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} \left( {P_{j} - P_{i} } \right) + P_{i} \\ & = \mathop \sum \limits_{{j \in U_{k}^{i} }} (\hat{\pi }_{ij} + \Delta_{ij} )\left( {P_{j} - P_{i} } \right) + P_{i} = \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right) + \mathop \sum \limits_{{j \in U_{k}^{i} }} \Delta_{ij} \left( {P_{j} - P_{i} } \right) + P_{i} . \\ \end{aligned} $$

It follows from Lemma 2 that

$$ \begin{aligned} & \mathop \sum \limits_{{j \in U_{k}^{i} }} \Delta_{ij} \left( {P_{j} - P_{i} } \right) = \mathop \sum \limits_{{j \in U_{k}^{i} }} \left[ {\frac{1}{2}\Delta_{ij} \left( {P_{j} - P_{i} } \right) + \frac{1}{2}\Delta_{ij} \left( {P_{j} - P_{i} } \right)} \right] \\ & \quad \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \left[ {\frac{{\delta_{ij}^{2} }}{4}T_{ij} + \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)} \right]. \\ \end{aligned} $$

Thus

$$ \begin{aligned} & \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right) + \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} + \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right) + P_{i} , \\ & \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A} \le \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}. \\ \end{aligned} $$

(20)

By Lemma 4, the following is immediate

$$ \begin{aligned} & \theta \le \beta_{1} = \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 \\ * & {\theta_{1} + \mathop \sum \limits_{{j \in U_{k}^{i} }} \tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A}} & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right], \\ & \theta_{1} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}, \\ & \beta_{1} = \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 \\ * & {\theta_{1} } & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right] \\ & \quad - \left[ {\begin{array}{*{20}l} 0 & \cdots & 0 \\ {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{i} } \right)^{\text{T}} } \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ \end{array} } \right] \,\, \left[ {\begin{array}{*{20}l} { - T_{{ik_{1}^{i} }}^{ - 1} } & 0 & \cdots & 0 \\ 0 & { - T_{{ik_{2}^{i} }}^{ - 1} } & \cdots & 0 \\ \vdots & \cdots & \ddots & \vdots \\ 0 & 0 & \cdots & { - T_{{ik_{m}^{i} }}^{ - 1} } \\ \end{array} } \right]\,\,\,\left[ {\begin{array}{*{20}l} 0 & \cdots & 0 \\ {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{i} } \right)^{\text{T}} } \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ \end{array} } \right]^{\text{T}} . \\ \end{aligned} $$

(21)

Using Schur complement formula, the condition (9) is equal to $\beta_{1} < 0$. Then, it follows from (21) that $\theta \le \beta_{1}$ < 0. Thus, according to Lemma 4, the filtering error system (5) with GUTRs is stochastically admissible with a prescribed $H_{\infty }$ performance index $\gamma$. Thus, the proof of Case I is completed.

Case II If $i \in U_{k}^{i}$, $U_{uk}^{i} \ne \emptyset$ and $U_{k}^{i} = \left\{ {k_{1}^{i} } \right.$, $k_{2}^{i}$,…,$\left. {k_{m}^{i} } \right\}$. There must be an $l \in U_{uk}^{i}$ for $\forall j \in U_{uk}^{i}$, $P_{l} \ge P_{j}$. Let

$$ \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} = \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} + \mathop \sum \limits_{{j \in U_{uk}^{i} }} \pi_{ij} P_{j} . $$

Since $\sum\nolimits_{j = 1}^{s} {\pi_{ij} } = 1$, then $\sum\nolimits_{{j \in U_{uk}^{i} }} {\pi_{ij} } = 1 - \sum\nolimits_{{j \in U_{k}^{i} }} {\pi_{ij} }$. Similar to Case I, one can derive that

$$ \begin{aligned} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} & \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} + \left( {1 - \mathop \sum \limits_{{j \in U_{uk}^{i} }} \pi_{ij} } \right)P_{l} = \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{j} - \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} P_{l} + P_{l} \\ & = \mathop \sum \limits_{{j \in U_{k}^{i} }} \pi_{ij} \left( {P_{j} - P_{l} } \right) + P_{l} = \mathop \sum \limits_{{j \in U_{k}^{i} }} (\hat{\pi }_{ij} + \Delta_{ij} )\left( {P_{j} - P_{l} } \right) + P_{l} \\ & = \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{l} } \right) + \mathop \sum \limits_{{j \in U_{k}^{i} }} \Delta_{ij} \left( {P_{j} - P_{l} } \right) + P_{l} \\ & \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{l} } \right) + \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl} + \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{l} } \right)^{\text{T}} V_{ijl}^{ - 1} \left( {P_{j} - P_{l} } \right) + P_{l} . \\ \end{aligned} $$

Thus

$$ \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A} \le \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{l} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl} \tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{l} } \right)^{\text{T}} V_{ijl}^{ - 1} \left( {P_{j} - P_{l} } \right)\tilde{A} + \tilde{A}^{\text{T}} P_{l} \tilde{A}. $$

(22)

It follows from Lemma 4 that

$$ \begin{aligned} & \theta \le \beta_{2} = \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 \\ * & {\theta_{2} + \mathop \sum \limits_{{j \in U_{k}^{i} }} \tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)^{\text{T}} V_{ijl}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A}} & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right], \\ & \theta_{2} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{l} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}V_{ijl} \tilde{A} + \tilde{A}^{\text{T}} P_{l} \tilde{A}. \\ \end{aligned} $$

(23)

Similar to Case I, the condition (10) is equal to $\beta_{2} < 0$, and $\theta \le \beta_{2}$ < 0 holds. Hence, the condition (8) in Lemma 4 is satisfied. Thus, the proof of Case II is completed.

Case III If $i \in U_{k}^{i}$, $U_{uk}^{i} = \emptyset$, similar to Case I and Case II, one can get that

$$ \begin{aligned} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} &= \mathop \sum \limits_{j = 1,j \ne i}^{S} \pi_{ij} P_{j} + \pi_{ii} P_{i} = \mathop \sum \limits_{j = 1,j \ne i}^{S} \pi_{ij} (P_{j} - P_{i} ) + P_{i} = \mathop \sum \limits_{j = 1,j \ne i}^{S} (\hat{\pi }_{ij} + \Delta_{ij} )(P_{j} - P_{i} ) + P_{i} \\ & \le \mathop \sum \limits_{j = 1,j \ne i}^{S} \hat{\pi }_{ij} (P_{j} - P_{i} ) + \mathop \sum \limits_{j = 1,j \ne i}^{S} \frac{{\delta_{ij}^{2} }}{4}R_{ij} + \mathop \sum \limits_{j = 1,j \ne i}^{S} \left( {P_{j} - P_{i} } \right)^{\text{T}} R_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right) + P_{i} , \\ & \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1}^{S} \pi_{ij} P_{j} \tilde{A} \le \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{S} \hat{\pi }_{ij} (P_{j} - P_{i} )\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{S} \frac{{\delta_{ij}^{2} }}{4}R_{ij} \tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{S} \left( {P_{j} - P_{i} } \right)^{\text{T}} R_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}. \\ \end{aligned} $$

(24)

From Lemma 4

$$ \begin{aligned} & \theta \le \beta_{3} = \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{T} + G\tilde{B}} & 0 \\ * & {\theta_{3} + \mathop \sum \limits_{j = 1,j \ne i}^{s} \tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)^{\text{T}} R_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A}} & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right], \\ & \theta_{3} = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{s} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} + \tilde{A}^{\text{T}} \mathop \sum \limits_{j = 1,j \ne i}^{s} \frac{{\delta_{ij}^{2} }}{4}R_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}. \\ \end{aligned} $$

(25)

Similar to Case I and Case II, the condition (11) is equal to $\beta_{3} < 0$, and then $\theta \le \beta_{3} < 0$ holds. Hence, the condition (8) in Lemma 4 is satisfied. Thus, the proof of Case III is completed.

In conclusion, it completes the proof of Theorem 1.

Appendix C: Proof of Theorem 2

Choose the structure of $G$, $F$ and $P_{i}$ in (8) as follows:

$$ G = \left[ {\begin{array}{*{20}l} {G_{11} } & {G_{22} } \\ {G_{21} } & {G_{22} } \\ \end{array} } \right],\quad F = \left[ {\begin{array}{*{20}l} {F_{11} } & {G_{22} } \\ {F_{21} } & {G_{22} } \\ \end{array} } \right],\quad P_{i} = \left[ {\begin{array}{*{20}l} {P_{i1} } & 0 \\ 0 & {P_{i2} } \\ \end{array} } \right], $$

(26)

where $P_{i2} = \alpha_{i} G_{22} \left( {i \in U_{k}^{i} } \right)$.

Case I From the formulas (6), (15) and (26), one has

$$ \begin{aligned} & - G - G^{\text{T}} = \left[ {\begin{array}{*{20}l} { - G_{11} - G_{11}^{\text{T}} } & { - G_{22} - G_{21}^{\text{T}} } \\ * & { - G_{22} - G_{22}^{\text{T}} } \\ \end{array} } \right],\quad - \tilde{F} + G\tilde{B} = \left[ {\begin{array}{*{20}l} { - F_{11}^{\text{T}} + G_{11} B_{i} + b_{\mathrm{fi}} D_{i} } & { - F_{21}^{\text{T}} } \\ { - G_{22}^{\text{T}} + G_{21} B_{i} + b_{\mathrm{fi}} D_{i} } & { - G_{22}^{\text{T}} } \\ \end{array} } \right], \\ & G\tilde{A} = \left[ {\begin{array}{*{20}l} {G_{11} A_{i} + b_{\mathrm{fi}} C_{i} } & {a_{\mathrm{fi}} } \\ {G_{21} A_{i} + b_{\mathrm{fi}} C_{i} } & {a_{\mathrm{fi}} } \\ \end{array} } \right],\quad \tilde{L}^{\text{T}} = \left[ {\begin{array}{*{20}l} {L_{i}^{\text{T}} } \\ { - l_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right],\quad \tilde{A}^{\text{T}} F^{\text{T}} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} F_{11}^{\text{T}} + C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } & {A_{i}^{\text{T}} F_{21}^{\text{T}} + C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \\ {a_{\mathrm{fi}}^{\text{T}} } & {a_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right], \\ & \tilde{A}^{\text{T}} G^{\text{T}} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} G_{11}^{\text{T}} + C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } & {A_{i}^{\text{T}} G_{21}^{\text{T}} + C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \\ {a_{\mathrm{fi}}^{\text{T}} } & {a_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right],\quad T_{ij} = \left[ {\begin{array}{*{20}l} {T_{ij1} } & {T_{ij2} } \\ * & {T_{ij3} } \\ \end{array} } \right], \\ & \tilde{A}^{\text{T}} \left( {P_{k} - P_{i} } \right)^{\text{T}} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} \left( {P_{k1} - P_{i1} } \right)^{\text{T}} } & {\left( {\alpha_{k} - \alpha_{i} } \right)C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \\ 0 & {\left( {\alpha_{k} - \alpha_{i} } \right)a_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right],(k \in U_{k}^{i} )\quad \tilde{A}^{\text{T}} P_{i}^{\text{T}} = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} P_{i1}^{\text{T}} } & {\alpha_{i} C_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \\ 0 & {\alpha_{i} a_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right], \\ & \tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I = \left[ {\begin{array}{*{20}l} {B_{i}^{\text{T}} F_{11}^{\text{T}} + D_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} + F_{11} B_{i} + b_{\mathrm{fi}} D_{i} - \gamma^{2} I} \hfill & {B_{i}^{\text{T}} F_{21}^{\text{T}} + D_{i}^{\text{T}} b_{\mathrm{fi}}^{\text{T}} } \hfill \\ * \hfill & { - \gamma^{2} I} \hfill \\ \end{array} } \right], \\ & \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} - G - G^{\text{T}} = \left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij1} - G_{11} - G_{11}^{\text{T}} } \hfill & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij2} - G_{22} - G_{21}^{\text{T}} } \hfill \\ * \hfill & {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij3} - G_{22} - G_{22}^{\text{T}} } \hfill \\ \end{array} } \right]. \\ \end{aligned} $$

So, the inequality (12) can be rewritten as

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } \hfill & {G\tilde{A}} \hfill & { - \tilde{F} + G\tilde{B}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & {\varOmega_{22} } \hfill & {\tilde{A}^{\text{T}} F^{\text{T}} } \hfill & {\tilde{L}^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} G^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} P^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } \hfill & \ldots \hfill & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{i} } \right)^{\text{T}} } \hfill \\ * \hfill & * \hfill & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & { - I} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & {\theta^{\prime } } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - P_{i} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - T_{{ik_{1}^{i} }} } \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & \ddots \hfill & \vdots \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - T_{{ik_{1}^{i} }} } \hfill \\ \end{array} } \right] < 0, $$

(27)

where $\theta^{\prime } = \sum\nolimits_{{j \in U_{k}^{i} }} {\frac{{\delta_{ij}^{2} }}{4}T_{ij} - G - G^{\text{T}} }$.

Substituting (6) and (26) into $\tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)\tilde{A}$ yields

$$ \begin{aligned} & \tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)\tilde{A} = \left[ {\begin{array}{*{20}l} {A_{i} } & 0 \\ {B_{\mathrm{fi}} C_{i} } & {A_{\mathrm{fi}} } \\ \end{array} } \right]^{\text{T}} \left[ {\begin{array}{*{20}l} {P_{j1} - P_{i1} } & 0 \\ 0 & {P_{j2} - P_{i2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {A_{i} } & 0 \\ {B_{\mathrm{fi}} C_{i} } & {A_{\mathrm{fi}} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} (P_{j1} - P_{i1} )A_{i} + C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )B_{\mathrm{fi}} C_{i} } \hfill & {C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )A_{\mathrm{fi}} } \hfill \\ {A_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )B_{\mathrm{fi}} C_{i} } \hfill & {A_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )A_{\mathrm{fi}} } \hfill \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} (P_{j1} - P_{i1} )A_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )B_{\mathrm{fi}} C_{i} } & {C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )A_{\mathrm{fi}} } \\ {A_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )B_{\mathrm{fi}} C_{i} } & {A_{\mathrm{fi}}^{\text{T}} (P_{j2} - P_{i2} )A_{\mathrm{fi}} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} (P_{j1} - P_{i1} )A_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} } \\ {A_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right](P_{j2} - P_{i2} )\left[ {\begin{array}{*{20}l} {B_{\mathrm{fi}} C_{i} } & {A_{\mathrm{fi}} } \\ \end{array} } \right]. \\ \end{aligned} $$

Since $P_{j} - P_{i} \le 0$, then $(P_{j2} - P_{i2} ) \le 0$, which implies $\left[ {\begin{array}{*{20}l} {C_{i}^{\text{T}} B_{\mathrm{fi}}^{\text{T}} } \\ {A_{\mathrm{fi}}^{\text{T}} } \\ \end{array} } \right](P_{j2} - P_{i2} )\left[ {\begin{array}{*{20}l} {B_{\mathrm{fi}} C_{i} } & {A_{\mathrm{fi}} } \\ \end{array} } \right] \le 0$, so

$$ \tilde{A}^{\text{T}} \left( {P_{j} - P_{i} } \right)\tilde{A} \le \left[ {\begin{array}{*{20}l} {A_{i}^{\text{T}} (P_{j1} - P_{i1} )A_{i} } & 0 \\ 0 & 0 \\ \end{array} } \right]. $$

(28)

In addition,

$$ - \tilde{E}^{\text{T}} P_{i} \tilde{E} = - \left[ {\begin{array}{*{20}l} {E^{\text{T}} } & 0 \\ 0 & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {P_{i1} } & 0 \\ 0 & {P_{i2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} E & 0 \\ 0 & I \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - E^{\text{T}} P_{i1} E} & 0 \\ 0 & { - P_{i2} } \\ \end{array} } \right]. $$

(29)

It can be obtained from (28) and (29) that

$$ - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A} \le \left[ {\begin{array}{*{20}l} { - E^{\text{T}} P_{i1} E + A_{i}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \hat{\pi }_{ij} \left( {P_{j1} - P_{i1} } \right)A_{i} } & 0 \\ 0 & { - P_{i2} } \\ \end{array} } \right] = \varOmega_{22} . $$

(30)

From Lemma 3, one can get that

$$ - G\left( {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} } \right)^{ - 1} G^{\text{T}} \le \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} - G - G^{\text{T}} . $$

(31)

It follows from (30), (31) that

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } \hfill & {G\tilde{A}} \hfill & { - \tilde{F} + G\tilde{B}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & {\theta^{\prime \prime } } \hfill & {\tilde{A}^{\text{T}} F^{\text{T}} } \hfill & {\tilde{L}^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} G^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} P^{\text{T}} } \hfill & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } \hfill & \ldots \hfill & {\tilde{A}^{\text{T}} \left( {P_{{k_{m}^{i} }} - P_{i} } \right)^{\text{T}} } \hfill \\ * \hfill & * \hfill & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & { - I} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & {\theta^{\prime \prime \prime } } \hfill & 0 \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - P_{i} } \hfill & 0 \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - T_{{ik_{1}^{i} }} } \hfill & \ldots \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & \ddots \hfill & \vdots \hfill \\ * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & * \hfill & { - T_{{ik_{1}^{i} }} } \hfill \\ \end{array} } \right] < 0, $$

(32)

where $\theta^{\prime \prime } = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \sum\nolimits_{{j \in U_{k}^{i} }} {\hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A}}$, $\theta^{\prime \prime \prime } = - G\left( {\sum\nolimits_{{j \in U_{k}^{i} }} {\frac{{\delta_{ij}^{2} }}{4}T_{ij} } } \right)^{ - 1} G^{\text{T}}$.

For each $j \in U_{k}^{i}$, it is obvious that

$$ \begin{aligned} & \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ & = - \left[ {\begin{array}{*{20}l} 0 & \cdots & 0 \\ {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} { - T_{{ik_{1}^{i} }}^{ - 1} } & \cdots & 0 \\ 0 & \ddots & 0 \\ 0 & \cdots & { - T_{{ik_{m}^{i} }}^{ - 1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} 0 & \cdots & 0 \\ {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } & \cdots & {\tilde{A}^{\text{T}} \left( {P_{{k_{1}^{i} }} - P_{i} } \right)^{\text{T}} } \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ 0 & \cdots & 0 \\ \end{array} } \right]^{\text{T}} . \\ \end{aligned} $$

(33)

Then, according to Schur complement formula, it follows from (32) and (33) that

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 & 0 & 0 \\ * & {\theta^{\prime \prime } + \tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)\tilde{A}} & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } & {\tilde{A}^{\text{T}} G^{\text{T}} } & {\tilde{A}^{\text{T}} P^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 & 0 & 0 \\ * & * & * & { - I} & 0 & 0 \\ * & * & * & * & {\theta^{\prime \prime \prime } } & 0 \\ * & * & * & * & * & { - P_{i} } \\ \end{array} } \right] < 0. $$

(34)

Since $\tilde{A}^{\text{T}} \left( {\sum\nolimits_{{j \in U_{k}^{i} }} {\frac{{\delta_{ij}^{2} }}{4}T_{ij} } } \right)\tilde{A} = \tilde{A}^{\text{T}} G^{\text{T}} G^{{ - {\text{T}}}} \left( {\sum\nolimits_{{j \in U_{k}^{i} }} {\frac{{\delta_{ij}^{2} }}{4}T_{ij} } } \right)G^{ - 1} G\tilde{A}$ and $\tilde{A}^{\text{T}} P_{i} \tilde{A} = \tilde{A}^{\text{T}} P_{i}^{\text{T}} P_{i}^{ - 1} P_{i} \tilde{A}$ one has

$$ \begin{aligned} & \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 \\ 0 & {\tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A}} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}l} 0 \\ {\tilde{A}^{\text{T}} G^{\text{T}} } \\ 0 \\ 0 \\ \end{array} } \right]G^{{ - {\text{T}}}} \left( {\mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} } \right)G^{ - 1} \left[ {\begin{array}{*{20}l} 0 & {G\tilde{A}} & 0 & 0 \\ \end{array} } \right], \\ & \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 & 0 \\ 0 & {\tilde{A}^{\text{T}} P_{i} \tilde{A}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}l} 0 \\ {\tilde{A}^{\text{T}} P_{i}^{\text{T}} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]P_{i}^{ - 1} \left[ {\begin{array}{*{20}l} 0 & {P_{i} \tilde{A}} & 0 & 0 & 0 \\ \end{array} } \right]. \\ \end{aligned} $$

(35)

Using Schur complement formula, it follows from (34) and (35) that

$$ \left[ {\begin{array}{*{20}l} { - G - G^{\text{T}} } & {G\tilde{A}} & { - F^{\text{T}} + G\tilde{B}} & 0 \\ * & {\theta^{\prime \prime \prime \prime } } & {\tilde{A}^{\text{T}} F^{\text{T}} } & {\tilde{L}^{\text{T}} } \\ * & * & {\tilde{B}^{\text{T}} F^{\text{T}} + F\tilde{B} - \gamma^{2} I} & 0 \\ * & * & * & { - I} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & 0 \\ 0 & {\tilde{A}^{\text{T}} \mathop \sum \limits_{{j \in U_{k}^{i} }} \frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] < 0, $$

(36)

where $\theta^{\prime \prime \prime \prime } = - \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \sum\nolimits_{{j \in U_{k}^{i} }} {\hat{\pi }_{ij} \left( {P_{j} - P_{i} } \right)\tilde{A}} + \tilde{A}^{\text{T}} \sum\nolimits_{{j \in U_{k}^{i} }} {\left( {P_{j} - P_{i} } \right)^{\text{T}} T_{ij}^{ - 1} \left( {P_{j} - P_{i} } \right)} \tilde{A}$.

Inequality (24) can be rewritten as $\tilde{A}^{\text{T}} \sum\nolimits_{j = 1}^{S} {\pi_{ij} P_{j} \tilde{A} \le \theta^{\prime \prime \prime \prime } } + \tilde{E}^{\text{T}} P_{i} \tilde{E} + \tilde{A}^{\text{T}} \sum\nolimits_{{j \in U_{k}^{i} }} {\frac{{\delta_{ij}^{2} }}{4}T_{ij} \tilde{A} + \tilde{A}^{\text{T}} P_{i} \tilde{A}}$, which implies that (36) can guarantee (8). Thus, the filtering error system (5) with GUTRs is stochastically admissible with a prescribed performance $H_{\infty }$ index $\gamma$ in Case I.

The proofs of Case II and Case III are similar to that of Case I, so they are omitted here.

Thus, it completes the proof of Theorem 2.