1 Introduction

Adaptive filters play a significant role in signal processing fields such as system identification, channel equalization, network and acoustic echo cancellation, and active noise control [8, 9, 21]. The least mean square (LMS) and normalized LMS (NLMS) algorithms are the most popular adaptive filter algorithms due to their simplicity and ease of realization. However, the LMS algorithm has slow convergence in highly correlated signals [14]. To overcome the slow convergence in highly correlated signals, the affine projection algorithm (APA) has been proposed. In the APA, the convergence rate and the computational complexity increase along with increasing the recent input vectors in adaptation [13, 14].

The variable step-size APA (VSS-APA) is derived by minimizing the MSD to improve the convergence rate in the APA [17]; however, the APA and the VSS-APA are unstable against the impulsive noise interference. When the \(\ell _2\)-norm minimization is used for adaptive algorithms in impulsive noise interference, their performances are deteriorated. To address this problem, the sign algorithm was introduced based on the \(\ell _1\)-norm minimization. In comparison with conventional adaptive algorithms, the sign algorithms utilize the error signal sign in filter coefficients adaptation. The sign algorithms not only reduce the computation cost, but also improve the stability in impulsive noise interference [7, 15, 20, 27]. In another class of sign adaptive algorithm, the sign operation is applied into the input signal regressors. The computational complexity can be significantly reduced by this approach [2, 3].

In the case of APA, various sign algorithms have been proposed. The affine projection sign algorithm (APSA) was proposed to utilize the benefits of the affine projection and the sign algorithm [16]. Additionally, the variable step-size APSA (VSS-APSA) was introduced to decrease the mean square deviation (MSD) in APSA [18]. To increase the tracking ability, the VSS-SA and VSS-APSA with reset methods were also introduced in [24, 25]. Furthermore, by minimizing the \(\ell _1\)-norm, the VSS-APA-SA was proposed in [10]. The results in [10] show that the performance of the presented algorithm is better than other APSA algorithms in [18, 25] and [24].

It should be noted that the transform domain filters such as the discrete Fourier transform (DFT), the discrete cosine transform (DCT) and the wavelet transform (WT) improve the convergence performance of the LMS-type algorithms by prewhitening the input signal. In the case of WT, different WT domain LMS (WTDLMS) algorithms were proposed [1, 4, 5, 22]. In recent studies, the WTDLMS with dynamic subband coefficients update (WTDLMS-DU) was introduced [1]. In comparison with WTDLMS, the WTDLMS-DU has a faster convergence speed and lower computational complexity.

In the current research, we extend the affine projection approach to WTDLMS algorithm to improve the performance of the WTDLMS. The improved WTDLMS (IWTDLMS) has a faster convergence speed than WTDLMS, especially for colored input signal. Since the performances of the WTDLMS and IWTDLMS are degraded in impulsive noise interference, the IWTDLMS sign adaptive algorithm (IWTDLMS-SA) is introduced based on \(\ell _1\)-norm minimization. In the following, the variable step-size IWTDLMS-SA (VSS-IWTDLMS-SA) is established to improve the performance of IWTDLMS-SA. In this algorithm, the variable step size is obtained by minimizing a posteriori error vector. Also, the modified VSS-IWTDLMS-SA is proposed which has a better tracking capability than VSS-IWTDLMS-SA. Table 1 compares the features of other studies and the proposed algorithms.

What we propose in this paper can be summarized as follows:

  1. 1.

    The establishment of the IWTDLMS: This algorithm utilizes the strategy of APA to speed up the convergence rate of WTDLMS.

  2. 2.

    The establishment of the IWTDLMS-SA: To improve the convergence speed of IWTDLMS against impulsive interference, the IWTDLMS-SA is proposed.

  3. 3.

    The establishment of the VSS-IWTDLMS-SA: The VSS approach is extended to IWTDLMS-SA in order to achieve a fast convergence speed and low steady-state error.

  4. 4.

    The establishment of the MVSS-IWTDLMS-SA: To increase the tracking ability of VSS-IWTDLMS-SA, the MVSS-IWTDLMS-SA is introduced.

This paper is organized as follows. Section 2 presents the data model and background on NLMS and APA. In Sect. 3, the IWTDLMS algorithm is introduced. Section 4 presents the IWTDLMS-SA, VSS-IWTDLMS-SA and the MVSS-IWTDLMS-SA. The computational complexity of the proposed algorithms is studied in Sect. 5. Section 6 introduces the convergence conditions for the proposed algorithms. Finally, before concluding the paper, the usefulness of the proposed algorithms is demonstrated by presenting several experimental results. Table 2 summarizes the notations and abbreviations which are used in the paper.

Table 1 The features of different algorithms
Full size table
Table 2 The notations and abbreviations
Full size table
Fig. 1
figure 1

Structure of the WTDLMS algorithm

Full size image

2 Data Model and Background on APA

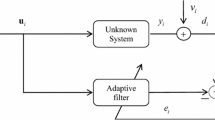
Consider a linear data model for d(n) as

$$\begin{aligned} d(n)={\mathbf {x}}^T(n){\mathbf {w}}_t+v(n), \end{aligned}$$
(1)

where \({\mathbf {w}}_t\) is an unknown M-dimensional vector that we expect to estimate, v(n) is the measurement noise with variance \(\sigma _{v}^2\), and \({\mathbf {x}}(n) =[x(n),x(n-1),\ldots ,x(n-M+1)]^T\) denotes an M-dimensional input (regressor) vector. It is assumed that v(n) is zero mean, white, Gaussian, and independent of \({{\mathbf {x}}}(n)\). The update equation for NLMS algorithm is given by

$$\begin{aligned} {\mathbf {w}}(n+1)={\mathbf {w}}(n) + \mu \frac{{\mathbf {x}}(n)}{\Vert {\mathbf {x}}(n)\Vert ^2}e(n), \end{aligned}$$
(2)

where \({\mathbf {w}}(n)\) is \(M \times 1\) weight coefficients of adaptive filter, \(\mu \) is the step size, and \(e(n)=d(n)-{\mathbf {w}}^T(n){\mathbf {x}}(n)\). To improve the performance of NLMS, the APA was proposed. By defining the input signal matrix and desired signal vector as

$$\begin{aligned} {\mathbf {X}}(n)&=[{\mathbf {x}}(n),{\mathbf {x}}(n-1), \ldots ,{\mathbf {x}}(n-K+1)] \end{aligned}$$
(3)
$$\begin{aligned} {\mathbf {d}}(n)&=[d(n),d(n-1), \ldots ,d(n-K+1)], \end{aligned}$$
(4)

where K is the number of recent regressors, the update equation for APA is obtained by

$$\begin{aligned} {\mathbf {w}}(n+1)={\mathbf {w}}(n) + \mu {\mathbf {X}}(n) [ {\mathbf {X}}^T(n) {\mathbf {X}}(n) ]^{-1} {\mathbf {e}}(n), \end{aligned}$$
(5)

where \({\mathbf {e}}(n)={\mathbf {d}}(n)-{\mathbf {X}}^T(n){\mathbf {w}}(n)\).

3 The IWTDLMS Adaptive Algorithm

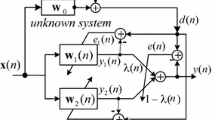
Figure 1 shows the structure of the WTDLMS algorithm [4]. In this figure, the \(M \times M\) matrix \(\mathbf {T}\) is an orthogonal matrix derived from a uniform N-band filter bank with filters denoted by \(h_0, h_1,\ldots , h_{N-1}\) following the procedure given in [4, 19, 23]. In matrix form, the orthogonal WT can be expressed as \({\mathbf {z}}(n)={\mathbf {T}}{\mathbf {x}}(n)\). This vector is represented as \({\mathbf {z}}(n)=[{\mathbf {z}}_{h_0}^T(n),{\mathbf {z}}_{h_1}^T(n),\ldots ,{\mathbf {z}}_{h_{N-1}}^T(n)]^T\) where \({\mathbf {z}}_{h_i}(n)\)’s are output vectors of an N-band filter bank. By splitting the wavelet transform domain adaptive filter coefficients at time n, \({\mathbf {g}}(n)\), into N subfilters, each having \(\frac{M}{N}\) coefficients, \({\mathbf {g}}(n)=[{\mathbf {g}}_{h_0}^T(n),{\mathbf {g}}_{h_1}^T(n),\ldots ,{\mathbf {g}}_{h_{N-1}}^T(n)]^T\), the output signal can be stated as

$$\begin{aligned} y(n)=\sum _{i=0}^{N-1} {\mathbf {g}}_{h_i}^T(n){\mathbf {z}}_{h_i}(n), \end{aligned}$$
(6)

and the error signal is obtained by \(e(n)=d(n)-y(n)\). The update equation for each subfilter in WTDLMS is given by

$$\begin{aligned} {\mathbf {g}}_{h_i}(n+1)={\mathbf {g}}_{h_i}(n)+\mu \frac{{\mathbf {z}}_{h_i}(n)}{\sigma ^2_{h_i}(n)}e(n), \end{aligned}$$
(7)

where \(\mu \) is the step size and \(\sigma ^2_{h_i}(n)\) can be computed iteratively by

$$\begin{aligned} \sigma ^2_{h_i}(n)=\alpha \sigma ^2_{h_i}(n-1)+(1-\alpha ) \Vert {\mathbf {z}}_{h_i}(n)\Vert ^2, \end{aligned}$$
(8)

with the smoothing factor \(\alpha \) (\(0\ll \alpha <1\)). The new improved WTDLMS (IWTDLMS) scheme is proposed based on the following cost function

$$\begin{aligned} \mathrm {min}\Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^2 \end{aligned}$$
(9)

subject to

$$\begin{aligned} {\mathbf {d}}(n)={\mathbf {Z}}^{T}(n){\mathbf {g}}(n+1), \end{aligned}$$
(10)

where

$$\begin{aligned} {\mathbf {Z}}(n)=[{\mathbf {z}}(n),{\mathbf {z}}(n-1),\ldots ,{\mathbf {z}}(n-K+1)], \end{aligned}$$
(11)

and

$$\begin{aligned} {\mathbf {d}}(n)=[d(n),d(n-1),\ldots ,d(n-K+1)]^{T}. \end{aligned}$$
(12)

In comparison with WTDLMS, the IWTDLMS applies K input vector and the desired signal for the establishment of the update equation. It means that K constraints are used based on (10) to achieve the IWTDLMS algorithm. This strategy improves the convergence speed of the proposed algorithm. The IWTDLMS algorithm is obtained from the solution of the following constraint minimization problem:

$$\begin{aligned} {\mathbf {J}}(n)=\Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^2+{{\varvec{\varLambda }}}[{\mathbf {d}}(n)-{\mathbf {Z}}^{T}(n){\mathbf {g}}(n+1)] \end{aligned}$$
(13)

which can be represented as

$$\begin{aligned} {\mathbf {J}}(n)&=\sum _{j=0}^{N-1}\Vert {\mathbf {g}}_{h_j}(n+1)-{\mathbf {g}}_{h_j}(n)\Vert ^2 \nonumber \\&\quad +{\varvec{\varLambda }}[{\mathbf {d}}(n)-\sum _{j=0}^{N-1}{\mathbf {Z}}_{h_j}^T(n){\mathbf {g}}_{h_j}(n+1)], \end{aligned}$$
(14)

where

$$\begin{aligned} {\mathbf {Z}}_{h_i}(n)=[{\mathbf {z}}_{h_i}(n),{\mathbf {z}}_{h_i}(n-1),\ldots ,{\mathbf {z}}_{h_i}(n-K+1)], \end{aligned}$$
(15)

and \({\varvec{\varLambda }}=[\lambda _{1},\lambda _{2},\ldots ,\lambda _{K}]\) is the Lagrange multipliers vector with length K. Using \(\frac{\partial {\mathbf {J}}(n)}{\partial {\mathbf {g}}_{h_i}(n+1)}=0\) and \(\frac{\partial {\mathbf {J}}(n)}{\partial {\varvec{\varLambda }}}=0\), we get

$$\begin{aligned} {\mathbf {g}}_{h_i}(n+1)={\mathbf {g}}_{h_i}(n)+\frac{1}{2}{\mathbf {Z}}_{h_i}(n){\varvec{\varLambda }}^{T}, \end{aligned}$$
(16)

where

$$\begin{aligned} {\varvec{\varLambda }}^{T}=2[{\mathbf {Z}}^{T}(n){\mathbf {Z}}(n)]^{-1}{\mathbf {e}}(n), \end{aligned}$$
(17)

and \({\mathbf {e}}(n)=[e(n),e(n-1),\ldots ,e(n-K+1)]^{T}\), which is expressed as

$$\begin{aligned} {\mathbf {e}}(n)={\mathbf {d}}(n)-{\mathbf {Z}}^{T}(n){\mathbf {g}}(n). \end{aligned}$$
(18)

Substituting (17) into (16), the update equation for IWTDLMS is given by

$$\begin{aligned} {\mathbf {g}}_{h_i}(n+1)={\mathbf {g}}_{h_i}(n)+{\mathbf {Z}}_{h_i}(n)[{\mathbf {Z}}^{T}(n){\mathbf {Z}}(n)]^{-1} {\mathbf {e}}(n), \end{aligned}$$
(19)

which can be reformulated as

$$\begin{aligned} {\mathbf {g}}(n+1)={\mathbf {g}}(n)+\mu {\mathbf {Z}}(n)[{\mathbf {Z}}^{T}(n){\mathbf {Z}}(n)]^{-1} {\mathbf {e}}(n). \end{aligned}$$
(20)

To take care of the possibility that \([{\mathbf {Z}}^{T}(n){\mathbf {Z}}(n)]\) may be close to singular, it is replaced by \([\epsilon {\mathbf {I}}+{\mathbf {Z}}^{T}(n){\mathbf {Z}}(n)]\), where \(\epsilon \) is the regularization parameter. Also, the parameter \(\mu \) controls the convergence rate in IWTDLMS. Note that for \(K=1\), the conventional WTDLMS is established. Tables 3 and 4 summarize all the notations and the IWTDLMS algorithm.

Table 3 The notations in IWTDLMS algorithm
Full size table
Table 4 Summary of IWTDLMS adaptive algorithm
Full size table

4 The IWTDLMS Sign Adaptive Algorithms

This section presents two IWTDLMS sign adaptive algorithms. In the first algorithm, the sign approach extended to IWTDLMS and IWTDLMS-SA is established. In the second algorithm, the variable step-size IWTDLMS-SA (VSS-IWTDLMS-SA) is proposed which has better performance than IWTDLMS-SA. Finally, to increase the tracking capability, the modified VSS-IWTDLMS-SA is introduced.

4.1 The IWTDLMS Sign Adaptive Algorithms

The IWTDLMS-SA minimizes the following cost function:

$$\begin{aligned} \mathrm {min}\Vert {\mathbf {e}}_{p}(n)\Vert _{1}, \end{aligned}$$
(21)

subject to

$$\begin{aligned} \Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^{2}\le \delta ^2, \end{aligned}$$
(22)

where \({\mathbf {e}}_{p}(n)\) is a posteriori error vector defined as

$$\begin{aligned} {\mathbf {e}}_{p}(n)={\mathbf {d}}(n)-{\mathbf {Z}}^{T}(n){\mathbf {g}}(n+1). \end{aligned}$$
(23)

Therefore, the cost function is obtained as

$$\begin{aligned} {\mathbf {J}}(n)=\Vert {\mathbf {e}}_{p}(n)\Vert _{1}+\beta (\Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^{2}-\delta ^2). \end{aligned}$$
(24)

This equation can be expressed as

$$\begin{aligned} {\mathbf {J}}(n)&=|d(n)-{\mathbf {z}}^{T}(n){\mathbf {g}}(n+1)| \nonumber \\&\quad +|d(n-1)-{\mathbf {z}}^{T}(n-1){\mathbf {g}}(n+1)|\nonumber \\&\quad + \cdots +|d(n-K+1)-{\mathbf {z}}^{T}(n-K+1){\mathbf {g}}(n+1)| \nonumber \\&\quad +\, \beta [\sum _{j=0}^{N-1}\Vert {\mathbf {g}}_{h_j}(n+1)-{\mathbf {g}}_{h_j}(n)\Vert ^2-\delta ^2]. \end{aligned}$$
(25)

Equation (25) can be rewritten as

$$\begin{aligned} {\mathbf {J}}(n)&=|d(n)-\sum _{j=1}^{N}{\mathbf {z}}_{h_j}^{T}(n){\mathbf {g}}_{h_j}(n+1)| \nonumber \\&\quad +|d(n-1)-\sum _{j=1}^{N}{\mathbf {z}}_{h_j}^{T}(n-1){\mathbf {g}}_{h_j}(n+1)| \nonumber \\&\quad +\cdots +|d(n-K+1)-\sum _{j=1}^{N}{\mathbf {z}}_{h_j}^{T}(n-K+1){\mathbf {g}}_{h_j}(n+1)| \nonumber \\&\quad +\, \beta [\sum _{j=0}^{N-1}\Vert {\mathbf {g}}_{h_j}(n+1)-{\mathbf {g}}_{h_j}(n)\Vert ^2-\delta ^2]. \end{aligned}$$
(26)

Taking the derivative of (26) with respect to the tap-weight vector \(\partial {\mathbf {g}}_{h_i}(n+1)\), we have

$$\begin{aligned} \frac{\partial {\mathbf {J}}(n)}{\partial {\mathbf {g}}_{h_i}(n+1)}&=-{\mathbf {z}}_{h_i}(n)\frac{e_{p}(n)}{|e_{p}(n)|} \nonumber \\&\quad -{\mathbf {z}}_{h_i}(n-1)\frac{e_{p}(n-1)}{|e_{p}(n-1)|}-\cdots \nonumber \\&\quad -{\mathbf {z}}_{h_i}(n-K+1)\frac{e_{p}(n-K+1)}{|e_{p}(n-K+1)|}\nonumber \\&\quad +2\beta [{\mathbf {g}}_{h_i}(n+1)-{\mathbf {g}}_{h_i}(n)], \end{aligned}$$
(27)

where \({\mathbf {e}}_{p}(n)=[e_{p}(n),e_{p}(n-1),\ldots ,e_{p}(n-K+1)]^{T}\) and the elements of \({\mathbf {e}}_{p}(n)\) for \(0 \le m \le K-1\) are given by

$$\begin{aligned} e_{p}(n-m)=d(n-m)-{\mathbf {z}}^{T}(n-m){\mathbf {g}}(n+1). \end{aligned}$$
(28)

By combining (28) and (27), we get

$$\begin{aligned} \frac{\partial {\mathbf {J}}(n)}{\partial {\mathbf {g}}_{h_i}(n+1)}&=-\sum _{m=0}^{K-1}{\mathbf {z}}_{h_i}(n-m)\mathrm {sgn}[e_p(n-m)] \nonumber \\&\quad +2\beta [{\mathbf {g}}_{h_i}(n+1)-{\mathbf {g}}_{h_i}(n)] \nonumber \\&=-{\mathbf {Z}}_{h_i}\mathrm {sgn}[{\mathbf {e}}_{p}(n)] \nonumber \\&\quad +2\beta [{\mathbf {g}}_{h_i}(n+1)-{\mathbf {g}}_{h_i}(n)], \end{aligned}$$
(29)

where \(\mathrm {sgn}[{\mathbf {e}}_{p}(n)]=[\mathrm {sgn}(e_{p}(n)),\mathrm {sgn}(e_{p}(n-1)),\ldots ,\mathrm {sgn}(e_{p}(n-K+1))]^{T}\). Setting \(\frac{\partial {\mathbf {J}}(n)}{\partial {\mathbf {g}}_{h_i}(n+1)}=0\), we obtain

$$\begin{aligned} {\mathbf {g}}_{h_i}(n+1)={\mathbf {g}}_{h_i}(n)+\frac{1}{2\beta }{\mathbf {Z}}_{h_i}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]. \end{aligned}$$
(30)

From (30), we can get

$$\begin{aligned} \Vert {\mathbf {g}}_{h_i}(n+1)-{\mathbf {g}}_{h_i}(n)\Vert ^2=\frac{\Vert {\mathbf {Z}}_{h_i}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2}{(2\beta )^2}. \end{aligned}$$
(31)

Therefore,

$$\begin{aligned} \Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^2= & {} \sum _{i=1}^{N}\Vert {\mathbf {g}}_{h_i}(n+1)-{\mathbf {g}}_{h_i}(n)\Vert ^2 \nonumber \\= & {} \frac{\sum _{i=1}^{N}\Vert {\mathbf {Z}}_{h_i}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2}{(2\beta )^2}\nonumber \\= & {} \frac{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2}{(2\beta )^2}. \end{aligned}$$
(32)

Finally, we have

$$\begin{aligned} \frac{1}{(2\beta )^2}=\frac{\Vert {\mathbf {g}}(n+1)-{\mathbf {g}}(n)\Vert ^2}{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2}, \end{aligned}$$
(33)

and then

$$\begin{aligned} \frac{1}{2\beta }=\frac{\delta }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2+\epsilon }}. \end{aligned}$$
(34)

From the above analyses, the update equation for IWTDLMS-SA is established as

$$\begin{aligned} {\mathbf {g}}_{h_i}(n+1)={\mathbf {g}}_{h_i}(n)+\mu \frac{{\mathbf {Z}}_{h_i}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2+\epsilon }}, \end{aligned}$$
(35)

which can be represented as

$$\begin{aligned} {\mathbf {g}}(n+1)={\mathbf {g}}(n)+\mu \frac{{\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}_{p}(n)]\Vert ^2+\epsilon }}. \end{aligned}$$
(36)

As the a posteriori error vector \({\mathbf {e}}_{p}(n)\) depends on \({\mathbf {g}}(n+1)\) which is not accessible, it is reasonable to approximate it with the a priori error vector \({\mathbf {e}}(n)\). Therefore, the update equation of IWTDLMS-SA becomes

$$\begin{aligned} {\mathbf {g}}(n+1)={\mathbf {g}}(n)+\mu \frac{{\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]\Vert ^2+\epsilon }}. \end{aligned}$$
(37)

Table 5 summarizes the relations of IWTDLMS-SA.

Table 5 Summary of the IWTDLMS-SA
Full size table
Table 6 Summary of the VSS-IWTDLMS-SA
Full size table
Table 7 Summary of the MVSS-IWTDLMS-SA
Full size table

4.2 IWTDLMS-SA with Variable Step Size

By substituting (37) into (23) and using the variable step size \(\mu (n)\), we have

$$\begin{aligned} {\mathbf {e}}_{p}(n)={\mathbf {e}}(n)-\mu (n)\frac{{\mathbf {Z}}^T(n) {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]\Vert ^2+\epsilon }} \end{aligned}$$
(38)

which can be written as

$$\begin{aligned} {\mathbf {e}}_{p}(n)={\mathbf {e}}(n)-\mu (n) {\mathbf {r}}(n), \end{aligned}$$
(39)

where

$$\begin{aligned} {\mathbf {r}}(n)=\frac{{\mathbf {Z}}^T(n) {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]\Vert ^2+\epsilon }}. \end{aligned}$$
(40)

The IWTDLMS-SA minimizes the following cost function:

Fig. 2
figure 2

The diagram of the MVSS-IWTDLMS-SA

Full size image
$$\begin{aligned} \mathrm {min}\Vert {\mathbf {e}}_{p}(n)\Vert _{1}=\Vert {\mathbf {e}}(n)-\mu (n) {\mathbf {r}}(n)\Vert _1=f[\mu (n)], \end{aligned}$$
(41)

subject to

$$\begin{aligned} \mu _L \le \mu (n) \le \mu _U. \end{aligned}$$
(42)

In (41), \(f[\mu (n)]\) is a function of \(\mu (n)\). In practice, the lower bound \(\mu _{L}\) in (42) should be selected to be a small positive constant to force the step size to be positive and the upper bound \(\mu _U\) in (42) should be selected to be smaller than one in order to guarantee the convergence of the introduced algorithm [10]. Since the objective function (41) is a piecewise linear convex one, the minimum of (41) is obtained by

$$\begin{aligned} \mu _{\mathrm{sol}}(n)=\mathrm {argmin}f[\mu _{j}(n)], \end{aligned}$$
(43)

where

$$\begin{aligned} \mu _{j}(n)=\frac{e(n-j+1)}{r_{j}(n)+\epsilon },\quad j=1,2,\ldots ,K \end{aligned}$$
(44)

and \({\mathbf {r}}(n)=[r_{1}(n),r_{2}(n),\ldots ,r_{K}(n)]^T\) and \(\epsilon \) is a small positive constant introduced to avoid dividing by zero. If \(\mu _{\mathrm{sol}}(n)>\mu _U\), then \(\mu _{\mathrm{sol}}(n)=\mu _U\), and if \(\mu _{\mathrm{sol}}(n)<\mu _L\) then \(\mu _{\mathrm{sol}}(n)=\mu _L\). If several consecutive impulsive noises occur, they add to the filter output. In this situation, \(\mu _{\mathrm{sol}}(n)\) may increase and the performance of VSS-IWTDLMS-SA is degraded. To avoid such possibility, the proposed step size is designed to decrease monotonically by adopting the following time-average scheme:

$$\begin{aligned} \mu (n)=\alpha \mu (n-1)+(1-\alpha )\mathrm {min} \{\mu _{\mathrm{sol}}(n),\mu (n-1)\}. \end{aligned}$$
(45)

Therefore, the update equation of VSS-IWTDLMS-SA is given by

$$\begin{aligned} {\mathbf {g}}(n+1)={\mathbf {g}}(n)+\mu (n) \frac{{\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]}{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]\Vert ^2+\epsilon }}. \end{aligned}$$
(46)

Table 6 describes the relations of VSS-IWTDLMS-SA. To improve the tracking capability of VSS-IWTDLMS-SA, the modified VSS-IWTDLMS-SA is proposed. If the filter coefficients of the unknown system are constant during the iterations, then \(\mu (n)\) begins from \(\mu _U\) and goes to \(\mu _L\). Thus, if the filter coefficients of the unknown system change at the middle of the iterations, then \(\mu (n)\) needs to be reset and start from \(\mu _U\) to have a good tracking of the filter coefficients of the unknown system. But the parameter \(\mu (n)\) in Eq. (45) cannot increase during the iterations due to the \(\mathrm {min} \{\mu _{\mathrm{sol}}(n),\mu (n-1)\}\). The parameter \(\mu _{\mathrm{sol}}(n)\) increases to high values in two situations (when the strong interference takes place at iteration n and when the weight vector of the unknown system changes). The effect of the changing of the unknown system on \(\mu _{\mathrm{sol}}(n)\) is very high during the iterations. Therefore, we propose the following relation for detecting this iteration as

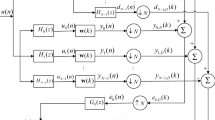
$$\begin{aligned} \bar{\mu }_{\mathrm{sol}}(n)=\beta \bar{\mu }_{\mathrm{sol}}(n-1)+(1-\beta )\mu _{\mathrm{sol}}(n). \end{aligned}$$
(47)

Table 7 presents the MVSS-IWTDLMS-SA. Also, Fig. 2 describes the diagram of MVSS-IWTDLMS-SA. The dotted line box in this diagram shows the process of updating the equation in the proposed algorithm.

5 Computational Complexity

Table 8 shows the number of multiplications for each term in MVSS-IWTDLMS-SA at every adaptation. We can calculate the computational complexity of other algorithms through this strategy. Table 9 describes the computational complexity of the IWTDLMS, IWTDLMS-SA, VSS-IWTDLMS-SA, and MVSS-IWTDLMS-SA. The number of multiplications has been calculated for each algorithm at every adaptation. In this table, M is the number of filter coefficients and K is the number of recent regressors. In comparison with IWTDLMS, the IWTDLMS-SA needs \(M^2+M(K+2)+1\) multiplications which is lower than IWTDLMS. The VSS-IWTDLMS-SA needs \(M^2+M(2K+1)+K^2+2K+3\) multiplications. This algorithm has also lower computational complexity than IWTDLMS. But the performance of VSS-IWTDLMS-SA is significantly better than that of IWTDLMS.

Table 8 The computational complexity of MVSS-IWTDLMS-SA
Full size table
Table 9 The computational complexity of IWTDLMS, IWTDLMS-SA, VSS-IWTDLMS-SA, and MVSS-IWTDLMS-SA
Full size table

6 Convergence Analysis

To study the convergence analysis of the proposed methods, the weight error vector is defined as \(\tilde{\mathbf {g}}(n)={\mathbf {g}}^\circ -{\mathbf {g}}(n)\), where \({\mathbf {w}}^\circ \) is an unknown system vector of the filter coefficients and \({\mathbf {g}}^\circ = {\mathbf {T}}{\mathbf {w}}^\circ \). By taking the squared Euclidean norm and then expectation from both sides of (37), we have

$$\begin{aligned} E[\Vert \tilde{\mathbf {g}}(n+1)\Vert ^2]= E[\Vert \tilde{\mathbf {g}}(n)\Vert ^2]+\varDelta , \end{aligned}$$
(48)

where

$$\begin{aligned} \varDelta =-2\mu E[\frac{\tilde{\mathbf {g}}^T(n) {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] \Vert ^2+\epsilon }}]+\mu ^2. \end{aligned}$$
(49)

By defining the noise-free vector, \({\mathbf {e}_a}(n)={\mathbf {e}}(n)-{\nu (n)}={\mathbf {Z}}^T(n)\tilde{\mathbf {g}}(n)\), the numerator of (49) becomes

$$\begin{aligned} \tilde{\mathbf {g}}^T(n){\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] ={\mathbf {e}_a^T}(n)\mathrm {sgn}[{\mathbf {e}}(n)]. \end{aligned}$$
(50)

In (49), \(\varDelta \) can be approximated as [24]:

$$\begin{aligned} \varDelta&=-2\mu E[\frac{{\mathbf {e}_a^T}(n)\mathrm {sgn}[{\mathbf {e}}(n)] }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] \Vert ^2+\epsilon }}]+\mu ^2 \nonumber \\&=-2\mu E[\frac{ \left( {\mathbf {e}}^T(n)-{\nu }^T(n)\right) \mathrm {sgn}[{\mathbf {e}}(n)] }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] \Vert ^2+\epsilon }}]+\mu ^2 \nonumber \\&=-2\mu E[\frac{ \left( \Vert {\mathbf {e}}(n) \Vert _1-{\nu }^T(n)\right) \mathrm {sgn}[{\mathbf {e}}(n)] }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] \Vert ^2+\epsilon }}]+\mu ^2 \nonumber \\&\approx -2\mu E[\frac{ \Vert {\mathbf {e}}(n) \Vert _1- K.\sqrt{\frac{2}{\pi }}\sigma _\nu }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)] \Vert ^2+\epsilon }}]+\mu ^2. \end{aligned}$$
(51)

If \(\varDelta <0\), (48) is stable. Therefore, from (51), the range of \(\mu \) is given by

$$\begin{aligned} 0<\mu < 2 E[\frac{\Vert {\mathbf {e}}(n) \Vert _1-K.\sqrt{\frac{2}{\pi }}\sigma _\nu }{\sqrt{\Vert {\mathbf {Z}}(n)\mathrm {sgn}[{\mathbf {e}}(n)]\Vert ^2+\epsilon }}]. \end{aligned}$$
(52)

This range guarantees the convergence of the IWTDLMS-SA, VSS-IWTDLMS-SA, and MVSS-IWTDLMS-SA.

7 Simulation Results

We demonstrate the performance of the proposed algorithms by several computer simulations in a system identification and acoustic echo cancellation (AEC) scenarios. For the system identification, two unknown systems (\({\mathbf {w}}_t\)) have been used. The first unknown impulse response is randomly selected with 16 taps (\(M=16\)), and the second one is the car echo path with \(M=256\) (Fig. 3). The input signal is an AR(1) signal generated by passing a zero-mean white Gaussian noise through a first-order system \(H(z)=\frac{1}{1-0.9z^{-1}}\). In AEC, the input signal is real speech (Fig. 3) and the unknown system is the car echo path. An additive white Gaussian noise with variance \(\sigma ^2_v=10^{-3}\) is added to the system output, setting the signal-to-noise ratio (\(\mathrm {SNR}\)) to 30 dB. The Haar wavelet transform (HWT) is used in all simulations which leads to the reduction in computational complexity due to the elements (+1 and -1) in HWT. In all simulations, we show the normalized mean square deviation (NMSD) which is evaluated by ensemble averaging over 30 independent trials.

Figure 4a compares the NMSD learning curves of WTDLMS and IWTDLMS algorithms with \(M = 16\). The value of the step size is set to 0.3, and different values for K are chosen. As we can see, by increasing the parameter K, the convergence speed and the steady-state NMSD values increase. Figure 4b presents the NMSD learning curves of WTDLMS and IWTDLMS algorithms with \(M = 256\). Again, the IWTDLMS has a higher convergence speed than WTDLMS algorithm. As we can see, for large values of M, the convergence speed of IWTDLMS is significantly higher than that of WTDLMS.

In the simulations, a strong interference signal is also added to the system output with a signal-to-interference (SIR) of -30 dB. The Bernoulli–Gaussian (BG) distribution is used for modeling the interference signal, which is generated as the product of a Bernoulli process and a Gaussian process, w(n)b(n), where b(n) is a white Gaussian random sequence with zero mean and variance \(\sigma ^2_b\) and w(n) is a Bernoulli process with the probability mass function given as \(P(w)=1-P_r\) for \(w=0\), and \(P(w)=P_r\) for \(w=1\). The average power of a BG process is \(P_r.\sigma ^2_b\). Keeping the average power constant, a BG process is spikier when it is smaller. It reduces to a Gaussian process when \(P_r=1\) [16].

Fig. 3
figure 3

The impulse response of the car echo path and real speech input signal

Full size image
Fig. 4
figure 4

a The NMSD learning curves of WTDLMS and IWTDLMS (\(M = 16\)), b the NMSD learning curves of WTDLMS and IWTDLMS (\(M = 256\)), input: colored Gaussian AR(1)

Full size image
Fig. 5
figure 5

a The NMSD learning curves of WTDLMS, IWTDLMS, IWTDLMS-SA, and VSS-IWTDLMS-SA (\(M=16\), \(\mu =0.01\)), input: colored Gaussian AR(1) with impulsive noise. b The NMSD learning curves of WTDLMS, IWTDLMS, IWTDLMS-SA, and VSS-IWTDLMS-SA (\(M=256\)), input: colored Gaussian AR(1) with impulsive noise

Full size image
Fig. 6
figure 6

a The tracking performance of WTDLMS, IWTDLMS, IWTDLMS-SA, VSS-IWTDLMS-SA, and MVSS-IWTDLMS-SA (\(M=16\)), input: colored Gaussian AR(1) with impulsive noise. b Variation of the step size in VSS-IWTDLMS-SA and MVSS-IWTDLMS-SA

Full size image
Fig. 7
figure 7

a The NMSD learning curves of DCT-LMS, VSS-TDlMS, VSS-APA-SA, WTDLMS, and IWTDLMS (\(M=256\)), input: real speech signal. b The tracking performance of DCT-LMS, VSS-TDlMS, VSS-APA-SA, WTDLMS, IWTDLMS, and MVSS-IWTDLMS-SA (\(M=256\)), input: real speech signal

Full size image
Table 10 The parameters in DCT-LMS, VSS-TDLMS, VSS-APA-SA, VSS-IWTDLMS-SA, and MVSS-IWTDLMS-SA
Full size table
Fig. 8
figure 8

a The ERLE of DCT-LMS, VSS-TDlMS, VSS-APA-SA, WTDLMS, and IWTDLMS (\(M=256\)), input: real speech signal. b The ERLE tracking performance of DCT-LMS, VSS-TDlMS, VSS-APA-SA, WTDLMS, IWTDLMS, and MVSS-IWTDLMS-SA (\(M=256\)), input: real speech signal

Full size image

Figure 5a shows the NMSD learning curves of WTDLMS, IWTDLMS, IWTDLMS-SA, and VSS-IWTDLMS-SA when the impulsive noise is added to the system output. The parameter M is set to 16, and the value of the step size is set to 0.01. The results show that the IWTDLMS-SA and VSS-IWTDLMS-SA have better performance than IWTDLMS and conventional WTDLMS. In Fig. 5b, we present the results for \(M=256\). The step size is set to 0.01. We observe that the IWTDLMS-SA and VSS-IWTDLMS-SA have better performance than other algorithms in impulsive noise interference environments.

In Fig. 6a, the impulsive noise is added to the system output. The results show that the proposed MVSS-IWTDLMS-SA and IWTDLMS-SA have better performance than other algorithms in this environment. It is important to note that the tracking ability of VSS-IWTDLMS-SA is weaker than other algorithms. Figure 6b describes the variation of the defined step sizes (\(\mu (n),\mu _{\mathrm{sol}}(n),\bar{\mu }_{\mathrm{sol}}(n)\)) in VSS-IWTDLMS-SA and MVSS-IWTDLMS-SA. In VSS-IWTDLMS-SA, the step size does not change when the impulse response of the unknown system changes. But in MVSS-IWTDLMS-SA, the step size changes when the impulse response of the unknown system changes.

Figure 7a and 7b shows the performance of the proposed algorithms for real speech input signal. Figure 7a compares the NMSD learning curves of WTDLMS and IWTDLMS with those of the proposed algorithms in [6, 11, 12, 26] and [10]. The parameters in these algorithms are set according to Table 10. The results show that the IWTDLMS has better performance than other algorithms. The tracking capability of the proposed algorithm for real speed input is justified in Fig. 7b. Due to the good tracking performance of MVSS-IWTDLMS-SA, we added the learning curve of this algorithm in Fig. 7b. We observe that the tracking performance of MVSS-IWTDLMS-SA is better than other algorithms.

Also, to measure the effectiveness of the proposed algorithms, we compute the echo return loss enhancement (ERLE). The ERLE is obtained by evaluating the difference between the powers of the echo and the error signal. The segmental ERLE curves for the measured speech and echo signals are shown in Fig. 8. Figure 8a illustrates the ERLE of the simulated algorithm in Fig. 7a. As can be seen, a good performance is observed for IWTDLMS. Figure 8b compares the ERLE of the simulated algorithms in Fig. 7b. This figure shows that the MVSS-IWTDLMS-SA performs well for tracking situation.

8 Conclusion

In this paper, the IWTDLMS adaptive algorithm was established. The IWTDLMS had better convergence speed than conventional WTDLMS in highly colored input signals. The IWTDLMS-SA was introduced which is useful for impulsive noise interference. To improve the performance of IWTDLMS-SA, the VSS-IWTDLMS-SA was proposed. Finally, the MVSS-IWTDLMS-SA was established which had better tracking capability in comparison with other algorithms. We demonstrated the good performance of the proposed algorithms through different simulation results.