1 Introduction

Accurate estimation of speech presence probability (SPP) is required in many speech-related applications [4, 5, 8, 14, 19, 22, 28, 30, 33]. In general, a significant improvement in noise reduction from speech is achieved by considering the speech presence uncertainty [4, 5, 8, 22, 28, 30]. In [8], in each time-frequency unit (TFU), using the SPP, a combination of single-channel Wiener and multi-frame minimum variance distortion-less response filter was proposed, leading to speech quality improvement. By incorporating the conditional SPP in the speech distortion weighted multi-channel Wiener filter in [30], an adaptive parameter was introduced, providing a good trade-off between signal distortion and noise reduction.

In addition, the accurate estimation of SPP is important in the update of the noise correlation matrix [4, 14, 19, 33]. In [4], a time-varying frequency-dependent parameter based on the SPP was considered, introducing a recursive smoothing technique for noise power spectral density (PSD) estimation. It was shown that the proposed method is able to obtain low estimation error in the case of nonstationary and low signal-to-noise ratio (SNR) environments. A soft SPP-dependent minimum mean square error (MMSE)-based technique was proposed in [14], which presents an appropriate estimation of the noise PSD in the case of nonstationary environments. In [19], it was shown that by applying a two-dimensional hidden Markov model and incorporating the spectro-temporal (ST) correlation in the estimation of SPP, an improved PSD estimation of noise could be achieved.

So far, several attempts have been made to improve the SPP estimation accuracy [9,10,11, 13, 15, 29, 32, 33]. In [13], the authors proposed to consider the ST correlation and fixed a priori SNR,Footnote 1 and a priori SPP,Footnote 2 to obtain a more accurate SPP estimation. Indeed, to reduce random fluctuations, they employed a smoothed observation over neighbor TFUs, achieving SPP close to one when speech is present, and close to zero when speech is absent. In [15], it was shown that by averaging over the a posteriori SNRFootnote 3 in the Cepstrum domain and incorporating the fixed priors, a significant reduction of noise leakage and speech distortion could be obtained in both cases of stationary and nonstationary noises.

Most of the previous works have been focused on computing the SPP based on the Gaussian statistical properties of speech signal; however, other distributions have also been investigated in this regard [9,10,11]. An MMSE estimation of the spectral amplitude was proposed in [9] using the generalized Gamma distribution. In [11], a super-Gaussian speech model and a smoothed observation in adjacent TFUs were considered. This work was extended in [10], where a closed-form solution was proposed considering the advantages of fixed a priori SNR.

Although most of the existing works in the context of SPP estimation have been focused on the single-microphone techniques, the concept of SPP has also been examined in multi-channel scenarios. Multi-channel algorithms are able to gather spatial information in addition to ST, providing higher degrees of freedom. In [32], a multi-channel SPP (MCSPP) estimator under the Gaussian statistical assumption was presented. The MCSPP can be expressed as the generalization of the single channel-SPP proposed in [7] to the multi-channel case. It was shown that the detection accuracy achieved by the MCSPP is superior than that by single-channel one [32]. Also, by incorporating the MCSPP with the generalization of the minima controlled recursive averaging algorithm [5], a practical method was proposed in [33] for multi-microphone noise tracking and reduction.

This paper introduces a distributed SPP (DSPP) estimation method that is employed in wireless acoustic sensor networks (WASNs). WASN consists of several spatially distributed nodes with arbitrary geometry and desired number of microphones. Benefiting from the wireless connection, nodes are able to cover a larger area and exploit more spatial information in comparison with the traditional microphone array with fixed geometry. In addition, some nodes may be located at a small distance from the desired speaker/noise source, providing signals with a high SNR/good estimation of the noise signal. Consequently, a considerable improvement can be obtained by the usage of WASN which utilizes the observations of different nodes. Recently, WASNs have attracted much attention and several contributions have been devoted to them [2, 3, 6, 17, 18, 20, 21, 23, 24, 31, 34, 35]. In WASN, it is important that all available information of recorded signals is optimally used in the estimation procedure. The main objective of this work is to introduce a distributed SPP estimation that provides a good balance between computational complexity and performance. The proposed DSPP estimator decreases the number of transmitted signals, while the cooperation between nodes still exists.

In the context of WASNs, speech signals can be processed into two different ways: first, when one physical fusion center (FC) is available and all microphones of all nodes transmit their recorded signals to the physical FC. In this case, since the FC has direct access to all recorded signals in the whole network, the WASN usually performs well in terms of noise reduction, SPP estimation, direction of arrival estimation and etc. However, the performance of the network is rather sensitive to physical FC; if the FC does not work well, the whole network fails to perform properly.

As an alternative, distributed algorithms have been employed in this framework; in these algorithms, there is no physical FC and nodes cooperate and transmit signals between themselves to obtain the final result. One solution to achieve the performance similar to the case of existence of physical FC is that all nodes transmit all recorded signals to each others, which is referred to as the centralized mode in the rest of his paper. However, this procedure imposes high computational complexity to the network. In the current work, to decrease the computational complexity, we propose a DSPP estimator using a cooperative distributed maximum a posteriori (MAP) noise reduction algorithm. In the proposed DSPP estimator, each node computes the SPP using its local signal along with the compressed signals from the other nodes, under the Gaussian statistical assumption of signals.

The Gaussian statistical assumption is not only justified by the central limit theorem (CLT),Footnote 4 but also simplifies the derivation of the estimators. In fact, other distributions might be able to model the speech and noise signals more precisely [25,26,27]; however, utilizing non-Gaussian distributions gives rise to the excessive complexity of estimator, and in some cases, leads to the lack of a closed-form solution. Hence, we have relied on Gaussian distribution in this research. Besides, the proposed DSPP estimator is a generalization of the MCSPP estimator [32], which has been developed for utilization in WASNs in a distributed way.Footnote 5

The remaining of this paper is organized as follows. We review the statistical properties of signals and the MCSPP algorithm in a fully connected WASN in Sect. 2. In Sect. 3, we introduce the DSPP estimator. Section 4 illustrates how noise reduction performance is affected by the use of DSPP estimator compared to the local and centralized SPP estimators. Finally, some concluding remarks will be presented in Sect. 5.

2 Problem formulation

Consider a fully connected WASN including K nodes, where each node is able to receive signals from other nodes. The k-th node contains \( M_k \) microphones and the total number of microphones is equal to \( M=\sum _{k=1}^K M_k \). Consider the noisy signal of the m-th microphone of the k-th node at time index t, i.e.,

$$\begin{aligned} y_{m,k}(t) = x_{m,k}(t) + v_{m,k}(t), \quad m=1,\ldots , M_k , \quad k=1,\ldots , K \end{aligned}$$
(1)

where \( x_{m,k}(t)\) and \( v_{m,k}(t) \) denote the speech signal and the additive noise in time domain, respectively. After segmentation and using the window function h(t) , the noisy signal in STFT domain can be expressed as

$$\begin{aligned} \begin{aligned} Y_{m,k}(l,n) =&\sum _{t=0}^{L}y_{m,k}(lQ+t)h(t)e^{-j\dfrac{2\pi tn}{L}}\\&= \sum _{t=0}^{L}x_{m,k}(lQ+t)h(t)e^{-j\dfrac{2\pi tn}{L}}+\sum _{t=0}^{L}v_{m,k}(lQ+t)h(t)e^{-j\dfrac{2\pi tn}{L}}, \end{aligned}\nonumber \\ \end{aligned}$$
(2)

where L denotes the discrete Fourier transform frame size and window is shifted by Q samples, respectively. Considering the central limit theorem, a common trend in short-time Fourier transform (STFT)-based algorithms is to model real and imaginary parts of discrete Fourier transform (DFT) coefficients by independent identical Gaussian distribution [7].

In the STFT domain, the noisy signal of the m-th microphone of the k-th node can be expressed as

$$\begin{aligned} Y_{m,k}(l,n) = X_{m,k}(l,n) + V_{m,k}(l,n), \quad m=1,\ldots , M_k , \end{aligned}$$
(3)

where \( X_{m,k}(l,n)\) and \( V_{m,k}(l,n) \) denote the speech signal and the additive noise, respectively, with l the frame index and n the discrete frequency index. For brevity, we omit the frame and frequency indices in the remainder of the paper and only mention them when referring to a specific TFU.

The \(M_k\)-dimensional noisy vector of the k-th node is given by

$$\begin{aligned} {\mathbf {y}}_{k}={\mathbf {x}}_{k}+{\mathbf {v}}_{k} \end{aligned}$$
(4)

with \({\mathbf {y}}_{k} =[ Y_{1,k},\ldots ,Y_{M_k,k} ] ^T\), \( {\mathbf {x}}_{k} = [ X_{1,k},\ldots , X_{M_k,k} ] ^T \) and \( {\mathbf {v}}_{k} = [ V_{1,k},\ldots ,V_{M_k,k} ] ^T \), where \( ^T \) denotes the transpose operation. In a fully connected WASN, where each node has access to all noisy signals of the whole network, the M-dimensional centralized noisy vector is given by

$$\begin{aligned} {\mathbf {y}}={\mathbf {x}}+{\mathbf {v}} \end{aligned}$$
(5)

with \({\mathbf {y}} =[ {\mathbf {y}}_{1}^T,\ldots ,{\mathbf {y}}_{K}^T ] ^T\), and \({\mathbf {x}}\) and \({\mathbf {v}}\) are defined similarly. Assuming that the speech and noise signals are uncorrelated, the \(M\times M\) dimensional centralized noisy correlation matrix can be expressed as \({\varvec{\Phi }}_{{\mathbf {y}}} = {\mathbb {E}}\left\{ {\mathbf {y}}{\mathbf {y}}^H \right\} = {\varvec{\Phi }}_{{\mathbf {x}}} + {\varvec{\Phi }}_{{\mathbf {v}}},\) where \({\varvec{\Phi }}_{{\mathbf {x}}}\) and \({\varvec{\Phi }}_{{\mathbf {v}}}\) denote the centralized speech and noise correlation matrices, respectively. In practice, the centralized noisy correlation matrix can be recursively estimated using the noisy signals and the forgetting factor, \( \lambda _y \), as follows:

$$\begin{aligned} \hat{{\varvec{\Phi }}}_{{\mathbf {y}}}(l,n) = \lambda _y \hat{{\varvec{\Phi }}}_{{\mathbf {y}}}(l-1,n) + (1-\lambda _y) {\mathbf {y}}(l,n){\mathbf {y}}^H(l,n). \end{aligned}$$
(6)

Similarly, in silent frames, the centralized correlation matrix of noise is given by

$$\begin{aligned} \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n) = \lambda _v \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l-1,n) + (1-\lambda _v) {\mathbf {v}}(l,n){\mathbf {v}}^H(l,n). \end{aligned}$$
(7)

where \( \lambda _v \) denotes forgetting factor of noise. As can be seen, an estimate of the centralized correlation matrix of the clean speech signal is given by

$$\begin{aligned} \hat{{\varvec{\Phi }}}_{{\mathbf {x}}}(l,n) = \hat{{\varvec{\Phi }}}_{{\mathbf {y}}}(l,n)- \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n). \end{aligned}$$
(8)

Due to the errors that occur in the estimation of correlation matrices, negative eigenvalues of \( \hat{{\varvec{\Phi }}}_{{\mathbf {x}}}(l,n) \) should be set to zero to ensure that the resulting matrix is positive semi-definite.

We assume that in a fully connected WASN, each node has the authority to receive and process all recorded signals of the whole network. We refer to this situation as the centralized mode in the remainder of this paper. In the following, we review the centralized SPP estimator.

In WASNs, nodes are randomly distributed. Therefore, it is more sensible to formulate the estimators without the knowledge of nodes geometry. In [32], an MCSPP estimator was proposed under the Gaussian statistical assumption for both speech and noise signals. This estimator computes the SPP without requiring the knowledge of geometry, and it is only based on the second-order statistical properties of the signal and noise. Considering two hypotheses (\( H_1 \) and \( H_0 \)) for speech presence and absence, respectively, the centralized SPP estimation can be proceed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} H_1: \quad {\mathbf {y}}={\mathbf {x}}+{\mathbf {v}},\qquad &{}\text {speech is present}\\ H_0: \quad {\mathbf {y}}={\mathbf {v}},\qquad &{}\text {speech is absent} \end{array}\right. } \end{aligned}$$
(9)

Using Bayes’ rule [32] indicating

$$\begin{aligned} p[H_1|{\mathbf {y}}]=\dfrac{p[{\mathbf {y}}|H_1]p[H_1]}{p[{\mathbf {y}}|H_1]p[H_1]+p[{\mathbf {y}}|H_0]p[H_0]} \end{aligned}$$
(10)

and also considering the fact \( p[H_1] +p[H_0] =1 \), the centralized SPP can be expressed as

$$\begin{aligned} \mathrm{CSPP} = p[H_1|{\mathbf {y}}]=\dfrac{\varLambda }{1+\varLambda } \end{aligned}$$
(11)

where \( \varLambda =\dfrac{1-q}{q}\dfrac{p[{\mathbf {y}}|H_1]}{p[{\mathbf {y}}|H_0]} \) denotes the generalized likelihood ratio, and \( q = p[H_0] \) is the a priori probability of speech absence [32]. Assuming the real and imaginary parts of the speech and noise signals to be independent zero-mean Gaussian random variables, the following likelihood functions are obtained:

$$\begin{aligned} {\left\{ \begin{array}{ll} p[{\mathbf {y}}|H_1] = \dfrac{1}{\pi ^M \det [{\varvec{\Phi }}_{{\mathbf {x}}}+{\varvec{\Phi }}_{{\mathbf {v}}}]}\exp \{-{\mathbf {y}}^H[{\varvec{\Phi }}_{{\mathbf {x}}}+{\varvec{\Phi }}_{{\mathbf {v}}}]^{-1}{\mathbf {y}}\},\\ p[{\mathbf {y}}|H_0] = \dfrac{1}{\pi ^M \det [{\varvec{\Phi }}_{{\mathbf {v}}}]}\exp \{-{\mathbf {y}}^H{\varvec{\Phi }}_{{\mathbf {v}}}^{-1}{\mathbf {y}}\}. \end{array}\right. } \end{aligned}$$
(12)

It is easily seen that

$$\begin{aligned} \varLambda =\dfrac{1-q}{q} \dfrac{\det [{\varvec{\Phi }}_{{\mathbf {v}}}]}{\det [{\varvec{\Phi }}_{{\mathbf {x}}}+{\varvec{\Phi }}_{{\mathbf {v}}}]} \exp \{{\mathbf {y}}^H[{\varvec{\Phi }}_{{\mathbf {v}}}^{-1}-[{\varvec{\Phi }}_{{\mathbf {x}}}+{\varvec{\Phi }}_{{\mathbf {v}}}]^{-1}]{\mathbf {y}}\} \end{aligned}$$
(13)

Finally, using the matrix inversion lemma and also trace of matrix proprieties, the centralized SPP can be expressed as [32]

$$\begin{aligned} \mathrm{CSPP} = \{1+\frac{q}{1-q} [1+\xi ] \exp [\frac{-\beta }{1+\xi }] \}^{-1}, \end{aligned}$$
(14)

where \( \xi = \mathrm {trace}[{\varvec{\Phi }}_{{\mathbf {v}}}^{-1}{\varvec{\Phi }}_{{\mathbf {x}}}] \) and \( \beta ={\mathbf {y}}^H {\varvec{\Phi }}_{{\mathbf {v}}}^{-1}{\varvec{\Phi }}_{{\mathbf {x}}}{{\varvec{\Phi }}_{{\mathbf {v}}}^{-1}}{\mathbf {y}} \).

3 Distributed SPP estimator

As mentioned before, using the centralized algorithm, a significant improvement is obtained in the performance of SPP estimation. However, this improvement comes at the price of more computational complexity. Let us assume a fully connected WASN in the centralized mode, where each node transmits all its noisy signals to others, resulting in \( M_1(K-1)+\cdots +M_K(K-1)=M(K-1) \) transmitted signals. The enlargement of matrix dimensions imposes high computational complexity. Also, nodes that are far from the speaker, receive a weak signal at low SNR. Hence, it is more sensible to improve the signals before transmitting. As an alternative, distributed algorithms can be employed to transmit only the compressed and denoised signals. So far, several distributed algorithms have been presented in WASNs, applying similar idea: sending a filtered version of the signals instead of transmitting all of them [2, 3, 6, 23, 24, 31]. In this research, we use the iterative DMAP estimator proposed in [31], where all nodes update their estimates simultaneously.

In order to compute the DSPP, each node utilizes its own local noisy signals, and only the compressed signals, instead of all of them, from other nodes. The compressed signals are computed as the enhanced speech signals, estimated by other nodes. Let us define the K-dimensional vector \( {\mathbf {z}}=[Z_{1},Z_{2},\ldots ,Z_{K}]^T \), containing filtered signals of all nodes. Also, the \((K-1)\)-dimensional vector \({{\mathbf {z}}}_{-k}\) is defined by excluding \( Z_{k} \) from vector \( {{\mathbf {z}}} \), i.e., \( {{\mathbf {z}}}_{-k}=[Z_{1},Z_{2},\ldots ,Z_{k-1},Z_{k+1},\ldots ,Z_{K}]^T \). The filtered signal of node k, \( Z_{k} \), is computed as the estimated speech signal of node k [31]. For each node, without loss of generality, we consider the first microphone as the reference microphone. Therefore, \( Z_{k} \) is computed as

$$\begin{aligned} Z_k= G_{1,k} Y_{1,k}=G_{1,k}X_{1,k}+G_{1,k}V_{1,k}, \end{aligned}$$
(15)

where \( G_{1,k} \) represents a deterministic gain applied to the first noisy signal of node k, \(Y_{1,k} \). It is beyond the scope of this paper to explain the calculation of \( G_{1,k} \), so we briefly introduce it in the next part and refer to [31] for more details.

It should be noted that under the Gaussian statistical assumption for both speech and noise signals, \( G_{1,k}X_{1,k}\) and \( G_{1,k}V_{1,k} \) still represent independent Gaussian variables; so, they satisfy the Gaussian likelihood function, which are crucial to develop the DSPP estimator. For node k, we define the new distributed noisy vector consisting of its own local noisy signals, \( {\mathbf {y}}^i_{k} \), and the received signals \( {{\mathbf {z}}}^i_{-k} \) from other nodes, as

$$\begin{aligned} \tilde{{\mathbf {y}}}^i_{k} =\begin{bmatrix} {\mathbf {y}}^i_{k} \\ {{\mathbf {z}}}^i_{-k} \end{bmatrix} \end{aligned}$$
(16)

The superscript i denotes the iteration index required by the DMAP algorithm (in a practical implementation, the iteration index is replaced by the frame index [31], means that all nodes in each frame, simultaneously update their estimates). Indeed, the \( M_k+K-1 \) dimensional distributed noisy vector of node k contains the \( M_k \) local noisy signals and \( K-1 \) compressed signals. The \((M_k+K-1)\times (M_k+K-1)\) dimensional correlation matrix of the distributed noisy signal is given by

$$\begin{aligned} {\varvec{\Phi }}^i_{\tilde{{\mathbf {y}}}_{k}} = \mathrm { E}\left\{ \tilde{{\mathbf {y}}}^i_{k}\tilde{{\mathbf {y}}}_{k}^{iH} \right\} = {\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} + {\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}, \end{aligned}$$
(17)

where \({\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}}\) and \({\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}\) denote the distributed speech and noise correlation matrices, respectively. In practice the distributed noisy correlation matrix is obtained as follows:

$$\begin{aligned} \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {y}}}_{k}}(l,n) = \lambda _y \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {y}}}_{k}}(l-1,n) + (1-\lambda _y)\tilde{{\mathbf {y}}}^i_{k} (l,n)\tilde{{\mathbf {y}}}^{iH}_{k} (l,n). \end{aligned}$$
(18)

Similarly, in silent frames, the distributed correlation matrix of noise is given by

$$\begin{aligned} \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {v}}}_{k}}(l,n) = \lambda _v \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {v}}}_{k}}(l-1,n) + (1-\lambda _v)\tilde{{\mathbf {v}}}^i_{k} (l,n)\tilde{{\mathbf {v}}}^{iH}_{k} (l,n). \end{aligned}$$
(19)

where \( \tilde{{\mathbf {v}}}^i_{k} (l,n)\) denotes the noise component in the signal \( \tilde{{\mathbf {y}}}^i_{k} (l,n) \). An estimate of the distributed correlation matrix of the clean speech signal is given by

$$\begin{aligned} \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {x}}}_{k}}(l,n) = \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {y}}}_{k}}(l,n)- \hat{{\varvec{\Phi }}}^i_{\tilde{{\mathbf {v}}}_{k}}(l,n). \end{aligned}$$
(20)

Considering two hypothesis

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{H}}^i_1: \quad \tilde{{\mathbf {y}}}^i_{k}=\tilde{{\mathbf {x}}}^i_{k}+\tilde{{\mathbf {v}}}^i_{k},\qquad &{}\text {speech is present},\\ {\tilde{H}}^i_0: \quad \tilde{{\mathbf {y}}}^i_{k}=\tilde{{\mathbf {v}}}^i_{k},\qquad &{}\text {speech is absent}, \end{array}\right. } \end{aligned}$$
(21)

the DSPP of node k at each iteration can be obtained as

$$\begin{aligned} \mathrm{DSPP}^i_k = p[{\tilde{H}}^i_1|\tilde{{\mathbf {y}}}^i_{k}]=\dfrac{{\tilde{\varLambda }}}{1+{\tilde{\varLambda }}} \end{aligned}$$
(22)

where \( {\tilde{\varLambda }}=\dfrac{1-q}{q}\dfrac{p[ \tilde{{\mathbf {y}}}^i_{k}|{\tilde{H}}^i_1]}{p[\tilde{{\mathbf {y}}}^i_{k}|{\tilde{H}}^i_0]} .\)

Fig. 1
figure 1

Comparison of the required transmitted signals in centralized and distributed configurations

Full size image

In theory, all elements of \( \tilde{{\mathbf {y}}}^i_{k} \) have the same statistical properties (i.e., summation of two independent Gaussian random variables), leading to the following likelihoods:

$$\begin{aligned} {\left\{ \begin{array}{ll} p[ \tilde{{\mathbf {y}}}^i_{k}|{\tilde{H}}^i_1] = \\ \qquad \dfrac{1}{\pi ^{{\tilde{M}}} \det [{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} + {\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]} \exp \{-\tilde{{\mathbf {y}}}^{iH}_{k}[{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} + {\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]^{-1}\tilde{{\mathbf {y}}}^i_{k}\},\\ \\ p[ \tilde{{\mathbf {y}}}^i_{k}|{\tilde{H}}^i_0] = \dfrac{1}{\pi ^{{\tilde{M}}} \det [{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]}\exp \{-\tilde{{\mathbf {y}}}^{iH}_{k}{{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}}^{-1}\tilde{{\mathbf {y}}}^i_{k}\}, \end{array}\right. } \end{aligned}$$
(23)

where \({\tilde{M}} = M_k+K-1 \). Again it is observed that

$$\begin{aligned} {\tilde{\varLambda }}=\dfrac{1-q}{q} \dfrac{\det [{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]}{\det [{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} + {\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]} \exp \{\tilde{{\mathbf {y}}}^{iH}_{k}[{{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}}^{-1}-[{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} + {\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}]^{-1}]\tilde{{\mathbf {y}}}^i_{k}\} \end{aligned}$$
(24)

Finally, the proposed DSPP estimator can be expressed as

$$\begin{aligned} \mathrm{DSPP}^i_k = \{1+\frac{q}{1-q} [1+{\tilde{\xi }}^i] \exp [\frac{-{\tilde{\beta }}^i}{1+{\tilde{\xi }}^i}] \}^{-1}, \end{aligned}$$
(25)

where

$$\begin{aligned} {\tilde{\xi }}^i = \mathrm{{trace}}[{{\varvec{\Phi }}^i_{{\tilde{{\mathbf {v}}}}_{k}}}^{-1}{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}}], \qquad {\tilde{\beta }}^i=\tilde{{\mathbf {y}}}^{iH}_{k} {{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}}^{-1}{\varvec{\Phi }}^i_{\tilde{{\mathbf {x}}}_{k}} {{\varvec{\Phi }}^i_{\tilde{{\mathbf {v}}}_{k}}}^{-1} \tilde{{\mathbf {y}}}^i_{k}. \end{aligned}$$
(26)

A comparison between the required number of transmitted signals in centralized and distributed configurations is illustrated in Fig.  1. In centralized case, each node has to transmit/receive all signals to/from other nodes; this results in \( M_1(K-1)+\cdots +M_K(K-1)=M(K-1) \) transmitted signals between nodes. Also, the dimension of correlation matrices in each node are equal \( M\times M \). In distributed algorithm, nodes transmit/receive a filtered signal to/from the other nodes. In this case, each node only transmits/receives one signal; this results in \((K-1)+\cdots +(K-1)=K(K-1) \) transmitted signals between nodes. In this case, the dimension of correlation matrices in each node are equal \( (M_k+K-1)\times (M_k+K-1) \). So, this proposed distributed procedure decreases the number of transmitted signals as well as the dimension of the correlation matrices, while the cooperation between nodes still exists.

3.1 Simultaneous distributed MAP estimator

In simultaneous distributed MAP estimator, all nodes update their estimates simultaneously. Without loss of generality, in each node the first microphone is considered as the reference microphone. Assuming MAP criteria, the estimator provides an estimation of clean speech signal at the reference microphone in each node. This estimator aims at maximizing the posterior distribution of the amplitude of the reference speech signal given the amplitude of the distributed noisy vector at each node [31].

In polar representation, (3) can be written as

$$\begin{aligned} Y_{m,k} = R_{m,k}{} \textit{e}^{j\vartheta _{m,k}} = A_{m,k}{} \textit{e}^{j\alpha _{m,k}}+V_{m,k}, \end{aligned}$$
(27)

where \( R_{m,k} \), \(\vartheta _{m,k}\), \(A_{m,k}\) and \(\alpha _{m,k}\) denote the spectral amplitude and phase of the noisy signal and the speech signal of the m-th microphone of the k-th node, respectively. Under the Gaussian statistical assumption of signals, the optimization problem of simultaneous distributed MAP estimator is written as follows

$$\begin{aligned} \begin{aligned} {\hat{A}}^i_{1,k} =\arg \max _{A^i_{1,k}} p(A^i_{1,k}|\tilde{{\mathbf {r}}}^i_k), \end{aligned} \end{aligned}$$
(28)

where \( \tilde{{\mathbf {r}}}^i_{k} \) corresponds to the amplitude of the distributed noisy vector, \(\tilde{{\mathbf {y}}}^i_{k}\). The procedure of solving this optimization problem has been explained in [31], indicating that the enhanced signal is obtained by applying a gain factor to the amplitude of noisy signal at reference microphone. In other word, the solution of the simultaneous distributed MAP estimator is \({\hat{A}}^i_{1,k} = R^i_{1,k}G^i_{1,k}\), where at each iteration, \( (i+1) \), the gain is equal to [31]:

$$\begin{aligned} \begin{aligned} G^{i+1}_{1,k}&= \frac{1}{i} G^{i}_{1,k}\\&\quad + \left( 1-\frac{1}{i}\right) \dfrac{\sqrt{\dfrac{{\tilde{\zeta }}^i_{1,k}}{{\tilde{\gamma }}^i_{1,k}}}}{2+2\sum _{m=1}^{{\tilde{M}}}{\tilde{\zeta }}^i_{m,k}}\mathrm {Re}\Bigg \{ \sum _{m=1}^{{\tilde{M}}}\sqrt{{\tilde{\zeta }}_{m,k}{\tilde{\gamma }}_{m,k}}\\&\quad + \sqrt{\left( \sum _{m=1}^{{\tilde{M}}}\sqrt{{\tilde{\zeta }}^i_{m,k}{\tilde{\gamma }}^i_{m,k}}\right) ^2+(2-{\tilde{M}})\left( 1+\sum _{m=1}^{{\tilde{M}}}{\tilde{\zeta }}^i_{m,k}\right) } \Bigg \}, \end{aligned} \end{aligned}$$
(29)

and \({\tilde{M}} = M_k+K-1 \). Also, the distributed a priori and a posteriori SNRs are given by

$$\begin{aligned} {\tilde{\zeta }}^i_{m,k}=\dfrac{({\tilde{\sigma }}^{i}_x(m,k))^2}{({\tilde{\sigma }}^{i}_v(m,k))^2}, \qquad {\tilde{\gamma }}^i_{m,k}=\dfrac{({\tilde{R}}_{m,k}^{i})^2}{({\tilde{\sigma }}^{i}_v(m,k))^2}, \end{aligned}$$
(30)

where \( {\tilde{R}}_{m,k}^{i} \) is directly computed as the amplitude of the distributed noisy signals. The distributed variances, \({\tilde{\sigma }}^{i}_x(m,k) \) and \({\tilde{\sigma }}^{i}_v(m,k) \), can be computed as the diagonal elements of the distributed speech and noise correlation matrices, respectively.

3.2 Implementation of DSPP

Totally, the proposed DSPP estimator runs as follows:

  1. 1.

    The algorithm is initialized with iteration index \( i=0 \). Also, \( G^i_{1,k} \) , \( k=1, 2,\ldots , K\), are set to with a random positive number between 0 and 1.

  2. 2.

    For each node \( k=1, 2,\ldots , K\), while \( l<= \mathrm{{number of frames}} \):

    • Broadcast \(Z^i_{k} = G^i_{1,k}Y^i_{1,k} \) to the other nodes.

    • Collect the vector \( {\mathbf {z}}^i_{-k} \).

    • Construct the vector \( \tilde{{\mathbf {y}}}^i_{k} \) using (16).

    • Update the distributed correlation matrices for \( \tilde{{\mathbf {y}}}^i_{k} \), \(\tilde{{\mathbf {v}}}^i_{k} \) and \( \tilde{{\mathbf {x}}}^i_{k} \).

    • Compute the distributed \( {\tilde{\xi }} \) and \({\tilde{\beta }}\) using (26).

    • Compute the DSPP using (25).

    • Compute the distributed a priori and a posteriori SNRs using (30).

    • Update the node-specific gain using (29)

  3. 3.

    \( i\leftarrow i+1 \)

  4. 4.

    return to step 2.

In practical implementation, the iteration index is replaced by the frame index [31]; so, all nodes in each frame update their estimates simultaneously; this procedure continuous until the last frame of signal. A general schematic of computation of the DSPP estimator in node 1 is illustrated in Fig. 2

Fig. 2
figure 2

General schematic of computation of DSPP in node 1

Full size image

4 Simulation results

In this section, we evaluate the effect of DSPP estimation on noise reduction performance, compared to two benchmark algorithms: (1) the local SPP estimation, and (2) the centralized SPP estimation. In the case of local SPP estimation, each node only uses its local noisy signals, \({\mathbf {y}}_{k}\), recorded by its microphones.Footnote 6 In the case of centralized SPP estimation, each node uses all recorded noisy signals of the whole network, \({\mathbf {y}}\), as mentioned in (14).

The performance of the considered SPP estimators, namely centralized, local, and DSPP estimators, is compared in terms of two objective measures, namely noise leakage (NL) and signal distortion (SD) as introduced in [13]. The NL value can be interpreted as the false alarm rate, which represents the percentage of the noise energy that the SPP estimator fails to attenuate. The SD value can be interpreted as the miss-hit rate, which denotes the percentage of speech energy that the SPP estimator fails to detect; the lower NL and SD values, the better SPP estimation.

During these experiments, the STFT is implemented using NFFT\( = \)512 with \(50\%\)-overlapping frames and Hamming analysis window. Also, signals are recorded at sampling frequency \( f_s = 16 \) kHz. The initial estimate of noise correlation matrices is computed from the first ten silence frames where the speech is absent.

Fig. 3
figure 3

Description of the simulated acoustic scenario

Full size image

4.1 Performance in simulated scenario

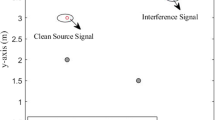
As the performance evaluation on simulated data, we perform Monte Carlo simulation using 85 randomized trials. It is assumed that the considered WASN contains 3 nodes in a rectangular room with dimensions 6 m \( \times \) 5.5 m \( \times \) 2.7 m (width\( \times \)length\( \times \)height) with reverberation time \( RT_{60} = 200 \) ms. In each trial, the position of the desired speaker, the interference noise, and the microphones of each node are randomly chosen inside the assumed room. Also, the number of microphones in each node is randomly chosen between \( M_k\in {1,\ldots ,5}\). An example of these configurations has been depicted in Fig. 3.

We use sample utterances of eight male and eight female speakers from the TIMIT database [12] as the clean speech samples. The presented evaluation results are the averages on these 16 samples and 85 trials. The microphone signals are corrupted by additive white Gaussian noise at full-band input SNRs ranging from \( -10 \) to 15 dB (full-band input SNRs \(=10\times \log \dfrac{\sum |x_{1,1}(t)|^2}{\sum |v_{1,1}(t)|^2} \)).Footnote 7

Actually, we have repeated the above-mentioned Monte Carlo simulation three times (each containing 85 trials) to cover three different cases regarding the existence of directional interference noise. These cases include: (1) no directional interference, (2) directional non-stationary babble interference, and (3) directional stationary pink interference.

The image method [1] is used to generate the room impulse responses between the sources of the signals (speech and interference) and the microphones. This method is a common way to model the acoustic scenario and to generate a good approximation of impulse responses between the speaker and the microphones. This method makes it possible to simulate an acoustic room, using the position of microphones, position of speaker, the reflection coefficients, room dimensions, and reverberation time.

As can be seen in (25), in order to estimate the proposed DSPP estimator, it is sufficient to have the values of q, \( {\tilde{\xi }} \) and \({\tilde{\beta }}\) in each iteration/frame (in a practical implementation, the iteration index is replaced by the frame index). The value of q was considered as a fixed value \( q= 0.5 \) as presented in [13]. Based on (26), it is seen that \( {\tilde{\xi }} \) and \({\tilde{\beta }}\) are dependent on the distributed correlation matrices of noise and clean signals. Also, the proposed DSPP algorithm uses the denoised signal at the reference microphone, which again only requires to compute the distributed correlation matrices, and consequently is dependent only on the second-order statistical properties. In fact, based on [16], when only noise reduction is of interest, there is no need to compute the impulse response and also model the dynamic situation. This is one of the advantages of the proposed DSPP estimator.

To avoid the effect of the errors in estimating noise correlation matrices, first we consider an oracle situation, where the noise correlation matrices are updated based on noise signals. Also, we experimentally found that the best performance is obtained by choosing \( \lambda _y=\lambda _v=0.92 \).

Fig. 4
figure 4

Performance of the centralized SPP estimator, local SPP estimator, and proposed DSPP estimator in terms of NL and SD for several full-band input SNR, in the presence of white Gaussian noise and no directional interference, and \(RT_{60} = 200\) ms

Full size image

Figure 4 depicts the performance of the considered SPP estimators in terms of NL and SD considering the additive white Gaussian noise at full-band input SNRs ranging from \( -10 \) to 15 dB. In this case, we have considered no directional interference. It is seen that the proposed DSPP estimator delivers less NL than the local SPP estimator, especially in high SNRs. In terms of SD, the DSPP obtains better performance in low SNRs; also in mid and high SNRs, the DSPP results in slightly lower speech distortion. It should be noted that the local SPP estimator needs to compute the inverse of the \(M_k\times M_k\) dimensional local noise correlation matrix, while the DSPP estimator requires the computation of \((M_k+K-1)\times (M_k+K-1)\) dimensional distributed noise correlation matrix. Indeed, the DSPP estimator provides better trade-off between NL and SD rather than the local SPP estimator. This can be justified by considering the fact that the DSPP estimator utilizes the information of the other nodes as well as its local observations. Considering the centralized SPP estimator, we observe that the centralized SPP makes a better trade-off between these two measures, attenuating more noise while speech signal is preserved more effectively. It should be noted that the centralized SPP estimator needs to compute the inverse of the \(M\times M\) dimensional centralized noise correlation matrix, leading considerable increase in computational complexity.

Fig. 5
figure 5

Performance of the centralized SPP estimator, local SPP estimator, and proposed DSPP estimator in terms of NL and SD in the case of non-stationary babble interference signal, when SIR \( =5 \) dB and the SNR for additive white Gaussian noise ranges from \( -10 \) to 15 dB, \(RT_{60} = 200\) ms

Full size image

In the next series of experiments, we also add two different directional interference signals, non-stationary babble and stationary pink at full-band input signal to interference ratio (SIR) \( =5 \) dB.

Figures 5 and 6, respectively, present the performance results for the cases that ” non-stationary babble” or ”stationary pink” noise is considered as the directional interference. These figures illustrate the performance of the considered SPP estimators in terms of NL and SD when the SNR for additive white Gaussian noise ranges from \( -10 \) to 15 dB, while maintaining the level of interference at SIR \( =5 \) dB. It is seen that in the presence of interference signals the same trend is observed for NL and SD. As expected, the best performance is obtained by the centralized SPP estimator. However, this comes at the price of more transmitted signals. On the other hand, the local SPP estimator results in the worst performance, while requiring the lowest complexity. These figures demonstrate that the performance and the required number of transmitted signals of the proposed DSPP estimator lies between the local and the centralized SPP estimators.

Fig. 6
figure 6

Performance of the centralized SPP estimator, local SPP estimator, and proposed DSPP estimator in terms of NL and SD in the case of stationary pink interference signal, when SIR \( =5 \) dB and the SNR for additive white Gaussian noise ranges from \( -10 \) to 15 dB, \(RT_{60} = 200\) ms

Full size image

4.2 Performance in realistic scenario

In the following we use the data recorded in a laboratory located at the University of Oldenburg [31] for the evaluations. The laboratory dimension is \( (x=7 \) m, \(y=6\) m, \(z= 2.7\) m) with reverberation time \(RT_{60} \simeq 350 \) ms. We considered a WASN containing 3 nodes. The first node, including 2 microphones corresponds to a hearing aid with the intra space \( \simeq 7.6 \) mm, placed in the middle of the room. The second node consists of two microphones located at \( (x=4.64\) m, \(y=4.13\) m, \(z=2\) m) and \((x=4.64\) m, \( y=2.63\) m, \( z=2 \) m), respectively, and the third node consists of one microphone located at \((x= 2.36\) m, \(y=4.13\) m, \(z=2\) m). The speech signal is a 24 s. utterance from a male speaker, played by a loudspeaker located at \((x= 4.64\) m, \(y=4.63\) m, \(z=2\) m). The microphones record the received signals at sampling frequency \(f_s = 16\) \( \mathrm {kHz} \). Also, in this case, we found that the best performance is achieved by choosing \( \lambda _y=\lambda _n=0.985 \).

Fig. 7
figure 7

a Spectrogram of clean signal, b the local SPP estimates, c the distributed SPP estimates, and d the central SPP estimates (full-band input SNR \(= 5 \) dB, stationary white Gaussian noise, \(RT_{60} = 350\) ms)

Full size image

Figure 7 illustrates the spectrogram of the clean speech signal, along with the resulting local SPP, proposed DSPP and centralized SPP estimations at the first node in the presence of stationary white Gaussian noise at full-band input SNR \(=5 \) dB. It can be seen that the DSPP estimator outperforms the local SPP estimator, which only considers its recorded signals, especially in high frequencies. Also, it is observed that the DSPP provides SPP which is similar to that from the centralized SPP estimator (i.e., SPP is close to one when speech is present and close to zero in speech absence). Compared to the distributed case, the centralized SPP estimator requires to transmit \(M(K-1)\) signals instead of \(K(K-1)\).

In the following, we have also considered a more practical situation, where four loudspeakers were used to generate the realistic noises. These loudspeakers were facing the corners of the laboratory and playing different realizations of babble and factory noises, respectively.

Also, to update the noise correlation matrices, we use the recursive approach as proposed in [33], where only noisy signals are available. In this case, the noise correlation matrices, e.g., the centralized one is given by:

$$\begin{aligned} \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n) = \lambda _v \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l-1,n) + (1-\lambda _v) {\mathbf {y}}(l,n){\mathbf {y}}^H(l,n). \end{aligned}$$
(31)

with \( \lambda _v = \lambda _n +(1-\lambda _n)\mathrm {CSPP}(l,n) \), where \( \lambda _n \) denotes the forgetting factor. It is observed that the value of \( \mathrm {CSPP} \) is required for the computation of \( {\varvec{\Phi }}_{{\mathbf {v}}} \); on the other hand, the \( \mathrm {CSPP} \) depends on the \( {\varvec{\Phi }}_{{\mathbf {v}}} \). Thus, in [33] the authors proposed an iterative algorithm for this issue. In the first step, the noise correlation matrix of the previous frame is used to estimate an initial CSPP; in the second step, the initial CSPP is used to update the forgetting factor, and consequently the noise correlation matrix. It is mentioned in [33] that two repetitions of this procedure are quite enough.

We assume that the first 10 frames consist of noise only, and accordingly use them to obtain an initial correlation matrix of noise and noisy signal. Considering [33], the noise correlation matrix is briefly computed as follows:

  • Compute the initial correlation matrix of noisy signal using (6) for the first \(l_{\mathrm {init}} = 10 \) frames.

  • Set \( \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n)\longleftarrow \hat{{\varvec{\Phi }}}_{{\mathbf {y}}}(l,n), \qquad l\le l_{\mathrm {init}}\)

  • Set \( \mathrm {CSPP}(l,n) =0, \qquad l\le l_{\mathrm {init}} \)

  • For \( l> l_{\mathrm {init}} \)

    1. 1.

      Use \( \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l-1,n) \) to compute the initial \( \mathrm {CSPP}_\mathrm{init}(l,n)\) according to (14)

    2. 2.

      Smooth the \( \mathrm {CSPP}_\mathrm{init}(l,n)\) as

      $$\begin{aligned} \hat{\mathrm {CSPP}}_\mathrm{smooth-init}(l,n) = \lambda _p \mathrm {CSPP}(l-1) + (1-\lambda _p) \mathrm {CSPP}_\mathrm{init}(l,n), \end{aligned}$$
      (32)
    3. 3.

      Compute the initial estimate of \( \lambda _{v} \) as :

      $$\begin{aligned} \lambda _{v} = \lambda _n +(1-\lambda _n)\hat{\mathrm {CSPP}}_\mathrm{smooth-init}(l,n) \end{aligned}$$
      (33)
    4. 4.

      Compute the first estimation of \(\hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n)\) as \( \lambda _v \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l-1,n) + (1-\lambda _v) {\mathbf {y}}(l,n){\mathbf {y}}^H(l,n), \)

    5. 5.

      Use \( \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l,n) \) instead of \( \hat{{\varvec{\Phi }}}_{{\mathbf {v}}}(l-1,n) \) to perform step (1) and compute the \( \mathrm {CSPP}(l,n)\)

    6. 6.

      Update the forgetting factor for noise

      $$\begin{aligned} \lambda _{v} = \lambda _n +(1-\lambda _n)\mathrm {CSPP}(l,n) \end{aligned}$$
      (34)
    7. 7.

      Compute the noise correlation matrix using (31)

Fig. 8
figure 8

Performance of the centralized SPP estimator, local SPP estimator, and proposed DSPP estimator in terms of NL and SD for several full-band input SNRs, in the presence of babble noise (first column), and factory noise (second column), when noisy signals are available, \(RT_{60} = 350\) ms

Full size image

Figure 8 depicts the performance of the considered SPP estimators in terms of NL and SD in the presence of different additive noises (including babble and factory noises), in realistic scenario. For babble noise, Fig. 8a shows that the noise leakage obtained by the DSPP estimator is superior than both the centralized and the local SPP estimators, in low and mid SNRs. This can be justified by the fact that the DSPP estimator needs to compute the inverse of smaller matrix (i.e., \((M_k+K-1)\times (M_k+K-1)\) dimensional) compared to the centralized matrix (i.e., \(M\times M\) dimensional). In general, matrices with smaller dimensions yield a smaller estimation errors compared to those with larger dimensions. It is also seen that the centralized SPP estimator outperforms the others at SNR \( =15\) dB. For factory noise case, Fig. 8b indicates that the proposed DSPP estimator delivers the best performance in low SNRs. In mid and high SNRs the centralized SPP estimator outperforms the others.

Concerning the SD, for both the babble and the factory noises, the usual trade-off between noise leakage and signal distortion is more evident in Fig. 8c, d. At SNR \( =-10 \) dB, the DSPP estimator results in the lowest NL and the highest SD. In mid and high SNRs, we observe that the local SPP estimator obtains the highest value of NL and the lowest SD. Also, it is seen that the performance of DSPP estimator lies between the local and centralized SPP estimators in mid and high SNRs.

5 Conclusion

In this work, we proposed a DSPP estimation technique that is employed in a distributed noise reduction algorithm. We utilized a simultaneous iterative DMAP estimator, in which the compressed signal is computed as the estimated speech signal. We compared the performance of the proposed estimator with the local and centralized counterparts in terms of noise leakage and signal distortion. The evaluations were done on both simulated and real recorded signals. The results show that when the noise signal is a mixture of both point source interference (including babble, pink and factory noises) and additive white noise, our proposed technique yields good performance, while it considerably decreases the number of transmitted signals compared to the centralized one. Indeed, the proposed DSPP estimator provides a good trade-off between the number of transmitted signals, as an indicator of computational complexity, and the detection accuracy, as a measure of system performance. Indeed, compared to the centralized mode, which each node has direct access to all recorded signals in the whole network, the DSPP estimator requires less transmitted signals and, consequently, less computational complexity. On the other hand, compared to the local case, which there is no connection and cooperation between different nodes, the DSPP estimator provides better performance.

In this work, the DSPP estimator was derived using the DMAP estimator, which considers MAP criteria to estimate the clean speech signal. Although the proposed estimator delivers good performance, other estimation method, especially Kalman filter which overcomes both dynamic and non-Gaussian noise scenarios, can be considered in the future works.

In current work, benefiting a fully connected structure in WASN, a DSPP estimator was derived. The proposed DSPP estimator can be considered as a starting point for computing speech presence probability in WASNs in a distributed way. Utilizing other structures like tree structure or graph-theory based ones would be suggested as topics for future work. As an example, utilizing the graph concept, it is possible to replace the reference microphone of each node by an enhanced signal from another node with higher SNR and achieve better performance improvement.

A combination of the current work with some other techniques (e.g., considering the spatial temporal correlation, or implementation in the Cepstrum domain, which were mostly considered for single microphone cases) can be worthwhile for the future works. In addition, other statistical distributions for both speech and noise have also been considered in the speech-related applications. Although the proposed DSPP estimator provides good performance in the presence of non-Gaussian interference noises, a theoretical derivation of distributed SPP estimation based on non-Gaussian distribution would be suggested.