Quasi-time-Dependent $l_2-l_\infty$ Filtering of Discrete-Time Switched Systems with Admissible Edge-Dependent Average Dwell Time

Abstract

The $l_2-l_{\infty }$ filtering problem is studied for a class of discrete-time switched systems under the admissible edge-dependent average dwell time (AED-ADT) switching. Firstly, a new multiple convex Lyapunov function (MCLF) is established as a convex combination form in the context of the $l_2-l_{\infty }$ filtering problem. Then, corresponding to the MCLF, the quasi-time-dependent switched filter is proposed for the considered switched system, and the sufficient conditions are derived to ensure that the filtering error system is globally uniformly exponentially stable with a prescribed $l_2-l_{\infty }$ performance index. Owing to the quasi-time-dependent and multi-degree-of-freedom properties of the designed switched filter, the wider feasibility regions of system parameters, more desirable $l_2-l_{\infty }$ disturbance attenuation levels and tighter bounds on the AED-ADT can be acquired. Finally, a numerical example is given to expound that our approach outperforms the extant results.

1 Introduction

A switched system [19] is a special hybrid system, which is composed of a few dynamical subsystems and a switching rule responsible for arranging which subsystem and when to be activated. Due to the modeling flexibility, switched systems have been used as modeling tools or controller design strategies to investigate various kinds of practical systems, such as networked control systems [20], DC/DC converters [6], flight control systems [15] and chaos generators [14]. Up to now, many stability analysis and control synthesis results have been obtained for switched systems such as [4, 5, 9, 12, 18, 21, 28] and the references therein.

During the past decades, several Lyapunov function approaches have been proposed to study the stability problem of switched systems. When all the subsystems of a switched system share a common Lyapunov function (CLF) [11], the underlying system is stable under arbitrary switching signals. Nevertheless, many times, the CLF can not be found for switched systems. Because of this, the multiple Lyapunov function (MLF) approach [1, 3, 29] is designed for studying switched systems with constrained switching signals. Recently, Zhao et al. in [24, 25, 31] propose a multiple discontinuous Lyapunov function for continuous-time switched systems and discrete-time switched systems, respectively, where the Lyapunov function for each subsystem is piecewise continuous. In the approach, a parameter $0<\rho _i<1$ contributes to the deduction of mode-dependent average dwell time (MDADT) bounds. However, a problem also arises that a series of added inequalities $P_{is}\le \rho _i P_{i(s-1)}$ may bring about the infeasibility of other relevant LMI conditions. It is of significance to develop new Lyapunov functions with more degrees of freedom for decreasing the conservativeness of the obtained results.

Among constrained switching signals, average dwell time (ADT) switching [10] has been extensively employed to study the stability and control problems of switched systems, where the average time between consecutive switchings is required to be not less than a constant. Then, the paper [33] introduces the MDADT, which is more flexible than the general ADT switching [4, 23]. Recently, a novel notion of AED-ADT is proposed in [27] and [7] for designing switching signals. It is defined by means of a directed graph, where an admissible transition edge (ATE) signifies a switching from one subsystem to another. Each ATE has its own transition weight, which is the key of making the AED-ADT switching superior to the MDADT switching. Up to date, there exist very few works that concern AED-ADT switching in the stability analysis and control synthesis fields of switching systems. Furthermore, regardless of which switching method above is adopted, inequalities $P_{j}\le \mu _jP_i$ or $P_{j}\le \mu _{ij}P_i$ are necessary at switching points. However, the feasible evaluation of parameters $\mu _j$ and $\mu _{ij}$ often induces the conservativeness of ADT bounds, which hinders us from choosing a broader range of switching signals in practical applications.

When unexpected disturbances and measurement missing phenomena happen in practice, the filtering is the popular method to estimate the state or output signals [2]. In recent years, a great deal of attention has been focused on studying the filtering problem of switched systems [13, 22, 30]. The authors in [26] investigate the event-triggered $H_{\infty }$ filtering problem for discrete-time switched linear systems, where the system output and switching signal are transmitted to the filter via a communication network. As for the asynchronous $H_{\infty }$ filtering, the paper [17] considers the switched T–S fuzzy systems with applications to the single-link robot arm system, and in [16], the state-dependent switching mechanism is utilized for switched linear systems with unstable subsystems to guarantee that the resulting filtering error system is exponentially mean square stable with a weighted $l_2$-gain performance. In [7], the $l_2-l_{\infty }$ filtering is studied for discrete-time switched systems under the AED-ADT switching, where the traditional MLF approach is used to derive the exponential stability results of the filtering error system. Although the filtering problem has been investigated extensively, the great majority of the extant works focus on the $H_\infty$ filtering. So far, very few studies have been devoted to the $l_2-l_{\infty }$ filtering of switched systems, which aims at energy-to-peak disturbance attenuation, completely different from the energy-to-energy performance of the $H_\infty$ filtering. Besides, another two important issues should be observed for the $l_2-l_{\infty }$ filtering research of switched systems. On the one hand, the extant $l_2-l_{\infty }$ filtering results suffer from the conservativeness of the feasibility regions of system parameters. Their slight variations cause frequently the infeasibility of the existing results. In addition, the $l_2-l_{\infty }$ performance indexes are not reduced to sufficiently low levels in the current literature, which results in the inapplicability of the existing results in many practical situations.

Based on the above discussions of the filtering research status for switched systems, we are motivated to consider the $l_2-l_{\infty }$ filtering of discrete-time switched systems. The main contributions are shown in the following aspects:

• (1) A MCLF for the filtering problem is proposed resorting to a set of quasi-time-dependent functions. It is pointed out below that the MLF typically used in the filtering research of switched systems is the special form of our MCLF and our obtained results generalize the existing ones.

• (2) The AED-ADT switching strategy is used to design switching signals, and tighter AED-ADT bounds can be obtained by virtue of our MCLF’s capability to slacken the restricted conditions at switching points.

• (3) The quasi-time-dependent $l_2-l_{\infty }$ switched filter is developed according to the structure of the MCLF, under which the wider feasible regions of system parameters and smaller $l_2-l_{\infty }$ performance indexes can be achieved.

The remainder of this paper is organized as follows. Section 2 presents the preliminaries and the problem formulation. In Sect. 3, the main results in the paper are put forth. We firstly introduce a MCLF for discrete-time switched systems, and then, an $l_2-l_{\infty }$ switched filter is derived in a quasi-time-dependent form, where the filtering error system is ensured to be exponentially stable with a prescribed $l_2-l_{\infty }$ performance. Section 4 gives the numerical example to illustrate the effectiveness of the obtained results. Eventually, the paper is concluded.

Notations The notations in this paper are fairly standard. We use $A>0$ ($A<0$) to stand for a positive definite (negative definite) matrix A. $A^T$ refers to the transpose of a matrix A. Let ${\mathbf {R}}^n$, ${\mathbf {S}}^n$ and ${\mathbf {Z}}_{\ge 0}$ denote the n-dimensional Euclidean space, the set of n-dimensional symmetric matrices and the set of nonnegative integers, respectively. $\Vert \cdot \Vert$ is used to denote the vector Euclidean norm. $l_2[0,\infty )$ is the space of square summable infinite vector sequences, and for $\omega =\{\omega (k)\}\in l_2[0,\infty )$, its norm is given by $\Vert \omega \Vert _2=\sqrt{\sum _{k=0}^{\infty }\omega ^T(k)\omega (k)}$; $l_\infty [0,\infty )$ is the space of all essentially bounded vector functions, and for $e=\{e(k)\}\in l_\infty [0,\infty )$, its norm is given by $\Vert e\Vert _\infty =\sqrt{\sup _ke^T(k)e(k)}$. As is commonly used in other literature, $*$ denotes the elements below the main diagonal of a symmetric matrix, and $\max$ and $\min$, respectively, stand for the maximum and minimum. In addition, matrices, if not explicitly stated, are assumed to have compatible dimensions for algebraic operations.

2 Preliminaries and Problem Formulation

Consider the following discrete-time switched system ($\varSigma _s$)

$$\begin{aligned} x(k+1)= & {} A_{\sigma (k)}x(k)+B_{\sigma (k)}\omega (k), \end{aligned}$$

(1)

$$\begin{aligned} y(k)= & {} C_{\sigma (k)}x(k)+D_{\sigma (k)}\omega (k), \end{aligned}$$

(2)

$$\begin{aligned} z(k)= & {} E_{\sigma (k)}x(k), \end{aligned}$$

(3)

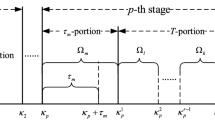
where $x(k)\in {{\mathbf {R}}^n}$ and $y(k)\in {{\mathbf {R}}^{n_y}}$ are the state and measured output, respectively; $z(k)\in {\mathbf {R}^{n_z}}$ is the signal to be estimated; $\omega (k)\in {\mathbf {R}^{n_\omega }}$ is the disturbance input belonging to $l_2[0,\infty )$; the matrices $A_i$, $B_i$, $C_i$, $D_i$, $E_i$ are assumed to be known and with appropriate dimensions; $\sigma (k)$ is a piecewise constant function of time, called a switching signal, which takes its values in a finite set ${\underline{N}}=\{1,2,\ldots ,n_s\}$, $n_s>1$ is the number of subsystems. For a switching signal $\sigma (k)$, let $k_1<k_2<\cdots<k_m<\cdots$ denote the switching instants of $\sigma (k)$. When $k_m\le k<k_{m+1}$, the $\sigma (k_m)$th subsystem is activated, where we use the notation $H_{\sigma (k_m)}$ to stand for the length of the time interval $[k_m,k_{m+1})$. Besides, we assume that the switching signal $\sigma (k)$ is available to the designed filter.

To proceed, some necessary definitions and lemma are reviewed for deriving the main results.

Definition 1

([33]) The equilibrium $x=0$ of system (1) with $\omega =0$ is globally uniformly exponentially stable (GUES) under a switching signal $\sigma (k)$, if there exist constants $\gamma >0$, $\lambda >1$ such that the solution x(k) of system (1) satisfies $\Vert x(k)\Vert \le \gamma \lambda ^{-(k-k_0)}\Vert x(k_0)\Vert$, $\forall k\ge k_0$ with arbitrary initial conditions.

Definition 2

([33]) For a switching signal $\sigma (k)$, $\forall k\ge k_0\ge 0$, let $N_{\sigma i}(k_0,k)$, $\forall \, i\in {\underline{N}}$ be the number of times that subsystem i is activated over the interval $[k_0,k)$, and $T_i(k_0,k)$ denote the total running time of subsystem i over the interval $[k_0,k)$. We say that $\sigma (k)$ has a mode-dependent average dwell time $\tau _{ai}$ if there exist positive numbers $N_{0i}$ and $\tau _{ai}$ such that

$$\begin{aligned} N_{\sigma i}(k_0,k)\le N_{0i}+\frac{T_i(k_0,k)}{\tau _{ai}},\ \ \forall k\ge k_0\ge 0. \end{aligned}$$

(4)

Definition 3

([27]) For a directed switching graph G and $i,j\in {\underline{N}}$$(i\ne j)$, if a directed edge from i to j is admissible, then we call S(i, j) as an admissible transition edge (ATE) of G, whose set is denoted by $S({\underline{N}})$. An ATE S(i, j) has an admissible transition edge-dependent weight (ATEDW) $\beta _{ij}$, which describes the switching property from i to j and the set of which is signified by W.

In Fig. 1, the periodic switching signal $\sigma (k):1\rightarrow 3\rightarrow 2\rightarrow \cdots$ has the ATE set $S({\underline{N}}) = \{ S(1,3), S(3,2), S(2,1)\}$ with the set of ATEDWs $W = \{\beta _{13}, \beta _{32}, \beta _{21}\}$. The dotted line represents that the corresponding transition edge is not admissible. Next, the definition of AED-ADT is given on the basis of Definition 3.

Fig. 1

$S({\underline{N}})$ and W of $\sigma (k)$

Definition 4

([27]) For a switching signal $\sigma (k)$, $\forall k\ge k_0\ge 0$, $\forall S(i,j)\in S({\underline{N}})$, let $N_{ij}^{\sigma }(k_0,k)$ be the switching count from i to j over the interval $[k_0,k)$, and $T_{ij}(k_0,k)$ denote the total running time of subsystem j over the interval $[k_0,k)$, where i is the previously active subsystem. We say that $\sigma (k)$ has an AED-ADT $\tau _{ij}^a$ if there exist positive numbers $N_{ij}^0$ and $\tau _{ij}^a$ such that

$$\begin{aligned} N_{ij}^{\sigma }(k_0,k)\le N_{ij}^0+\frac{T_{ij}(k_0,k)}{\tau _{ij}^a},\ \ \forall S(i,j)\in S({\underline{N}}), \ \forall k\ge k_0\ge 0, \end{aligned}$$

(5)

where $N_{ij}^0$ are called as the admissible edge-dependent chatter bounds.

Lemma 1

([8]) Let $P \in {\mathbf {S}}^n$, $\varLambda \in {\mathbf {S}}^p$, $\varPhi$ and $\varPsi$ be matrices of appropriate dimensions. Then, the following statements are equivalent:

• (i) Find $P>0$ such that $\varPhi ^TP\varPhi -\varLambda <0$;

• (ii) Find $P>0$ and $\varPsi$ such that $\left[ \begin{array}{cc} -\varLambda &{}*\\ \varPsi \varPhi &{}-\varPsi -\varPsi ^T+P \end{array}\right] <0$.

Next, a new switched filter ($\varSigma _f$) is proposed in the following:

$$\begin{aligned} x_f(k+1)= & {} A_{\sigma (k)}^f(k)x_f(k)+B_{\sigma (k)}^f(k)y(k), \end{aligned}$$

(6)

$$\begin{aligned} z_f(k)= & {} C_{\sigma (k)}^f(k)x_f(k), \end{aligned}$$

(7)

where $x_f(k)\in {{\mathbf {R}}^n}$ is the state of the filter, $z_f(k)\in {{\mathbf {R}}^{n_z}}$ is the estimation of z(k), and for any $k\in [k_m,k_{m+1}), \sigma (k_m)\!=\!i,$$A_i^f(k),\ B_i^f(k),\ C_i^f(k)$ are the filter gains to be determined afterward.

Combining system ($\varSigma _s$) with filter ($\varSigma _f$), the augmented filtering error system ($\varSigma _e$) is obtained as follows:

$$\begin{aligned} \xi (k+1)= & {} {\overline{A}}_{\sigma (k)}(k)\xi (k)+{\overline{B}}_{\sigma (k)}(k)\omega (k), \end{aligned}$$

(8)

$$\begin{aligned} e(k)= & {} {\overline{E}}_{\sigma (k)}(k)\xi (k), \end{aligned}$$

(9)

where $\xi (k)=\left[ \begin{array}{cc} x^T(k)&x_f^T(k) \end{array}\right] ^T,\ e(k)=z(k)-z_f(k)$ and

$$\begin{aligned} {\overline{A}}_{\sigma (k)}(k)= & {} \left[ \begin{array}{cc} A_{\sigma (k)}&{}0\\ B_{\sigma (k)}^f(k)C_{\sigma (k)}&{}A_{\sigma (k)}^f(k) \end{array}\right] ,\ \ {\overline{B}}_{\sigma (k)}(k)=\left[ \begin{array}{c} B_{\sigma (k)}\\ B_{\sigma (k)}^f(k)D_{\sigma (k)} \end{array}\right] ,\\ {\overline{E}}_{\sigma (k)}(k)= & {} \left[ \begin{array}{cc} E_{\sigma (k)}&-C_{\sigma (k)}^f(k) \end{array}\right] . \end{aligned}$$

Our goal within the paper is to design an $l_2-l_\infty$ switched filter of the form ($\varSigma _f$), and find a set of AED-ADT switching signals such that the resulting filtering error system is GUES with $\omega (k)=0$ and has a guaranteed $l_2-l_\infty$ disturbance attenuation performance under the zero initial condition, i.e., $\Vert e\Vert _\infty <\gamma \Vert \omega \Vert _2$ for a constant $\gamma >0$ and all nonzero $\omega (k)\in l_2[0,\infty )$.

3 Main Results

In this section, a MCLF is firstly constructed by a convex combination of positive definite matrices so that the restricted conditions of Lyapunov functions at switching points can be relaxed. And the concrete filter gains are set forth in the quasi-time-dependent form. Then, the filter is designed to ensure that the filtering error system is GUES with a prescribed $l_2-l_\infty$ performance index.

3.1 Lyapunov Function Design

First of all, a MCLF is given for the filtering error system as follows:

$$\begin{aligned} V_{i}(k)= & {} \xi ^T(k)P_{i}(k)\xi (k)=\xi ^T(k)\sum _{l=1}^Lf_{il}(k-k_m)P_{il}\xi (k)\nonumber \\ \!\!\!=\!\! & {} \!\left[ \!\! \begin{array}{c} x^T(k)\\ x^T_f(k) \end{array} \!\!\right] ^T\!\!\left[ \! \begin{array}{cc} \sum _{l=1}^Lf_{il}(k-k_m)P^1_{il}&{}\sum _{l=1}^Lf_{il}(k-k_m)P^2_{il}\\ \sum _{l=1}^Lf_{il}(k-k_m)(P^2_{il})^T&{}\sum _{l=1}^Lf_{il}(k-k_m)P^3_{il} \end{array}\! \right] \!\!\left[ \!\! \begin{array}{c} x(k)\\ x_f(k) \end{array}\!\! \right] \!\!, \end{aligned}$$

(10)

where $\forall k\in [k_m,k_{m+1})$, $\sigma (k_m)=i\in {{\underline{N}}}$; $P_{il}=\left[ \begin{array}{cc} P_{il}^1&{}P_{il}^2\\ (P_{il}^2)^T&{}P_{il}^3 \end{array} \right]$, $l\in {\mathcal {L}}=\{1,2,\ldots ,L\}$, are positive definite matrices; continuous functions $f_{il}(k-k_m)$, $l\in {\mathcal {L}}$, are defined on the interval $[k_m,k_{m+1})$ satisfying $f_{il}(k-k_m)\ge 0,\ \sum _{l=1}^Lf_{il}(k-k_m)=1.$

Now, it is necessary to develop an effective method to construct functions $f_{il}(k-k_m),i\in {{\underline{N}}},l\in {\mathcal {L}}$ for further executing the filter design. For any $i\in {{\underline{N}}},l\in {\mathcal {L}}$, we provide

$$\begin{aligned} f_{il}(k-k_m)=a(k-k_m)+b,\ \ \forall k\in [k_m,k_{m+1}), \end{aligned}$$

(11)

where parameters a and b will be determined in the following.

Set

$$\begin{aligned} f_{il}(0)=a_{il},\ f_{il}(H_i)=b_{il}, \end{aligned}$$

(12)

where $0\le a_{il}\le 1,0\le b_{il}\le 1,\sum _{l=1}^La_{il}=1,\sum _{l=1}^Lb_{il}=1$.

From (11) and (12), a simple calculation gives

$$\begin{aligned} a=\frac{b_{il}-a_{il}}{H_{i}},\ b=a_{il}. \end{aligned}$$

Thus, we have

$$\begin{aligned} f_{il}(k-k_m)=\frac{b_{il}-a_{il}}{H_{i}}(k-k_m)+a_{il},\ \ \forall i\in {\underline{N}}, \forall l\in {\mathcal {L}}, \forall k\in [k_m,k_{m+1}), \end{aligned}$$

(13)

and it can be easily verified that

$$\begin{aligned} f_{il}(k-k_m)\ge 0,\ \sum _{l=1}^Lf_{il}(k-k_m)=1,\nonumber \\ f_{il}(k+1-k_m)-f_{il}(k-k_m)=\frac{b_{il}-a_{il}}{H_{i}}. \end{aligned}$$

(14)

Remark 1

In many filtering-related studies of switched linear systems, although the used Lyapunov functions are of diversified forms, they are essentially the traditional MLFs [7, 16, 26]. By contrast, our MCLF has convex structure and quasi-time dependency due to the introduction of functions $f_{il}(k-k_m), l\in {\mathcal {L}}$, which can play a vital role in providing the possibility of further extending the feasibility regions of system parameters and slackening the restricted conditions of Lyapunov functions at switching points. These can be verified by the excellent performance of our designed filter in the simulation. And it should be also pointed out that our method is different from the quasi-time-dependent Lyapunov function proposed in [3, 4, 17]. Their quasi-time dependency signifies that Lyapunov function, controller or filter themselves are established as time-scheduled forms, i.e., each step corresponds to different Lyapunov functions or updates of controller matrices and filter matrices, which can effectively reduce the conservativeness of the obtained results. However, our quasi-time dependency is mainly manifested in the coefficients $f_{il}(k-k_m)$ of the MCLF (10), which, integrated with the convexity, helps to reduce the conservativeness of the obtained filter.

Via the MCLF (10), the filter gains of ($\varSigma _f$) are designed as follows:

$$\begin{aligned} A_i^f(k)= & {} \sum _{l=1}^Lf_{il}(k-k_m)A_{il}^f,\ \ B_i^f(k)=\sum _{l=1}^Lf_{il}(k-k_m)B_{il}^f,\nonumber \\ C_i^f(k)= & {} \sum _{l=1}^Lf_{il}(k-k_m)C_{il}^f, \end{aligned}$$

(15)

where $k\in [k_m,k_{m+1}),$$A_{il}^f$, $B_{il}^f$ and $C_{il}^f$, $i\in {\underline{N}}, l\in {\mathcal {L}}$, will be determined later.

Remark 2

Corresponding to the MCLF in (10), the switched filter ($\varSigma _f$) is also distinct from the ones in the extant literature. The filter gains $A_i^f(k),$$B_i^f(k),$$C_i^f(k)$ are quasi-time-dependent ones and of convex structure, which depend on $k-k_m$ and carry multiple vertex matrices. For example, $A_i^f(k)$ has L vertex matrices $A_{il}^f$. Such features are conducive to decreasing the conservativeness of the designed filter, which will be elaborated below.

3.2 $l_2-l_\infty$ Filter Design

Now, it is in a position to cope with the $l_2-l_\infty$ filter design problem for the switched system ($\varSigma _s$).

Theorem 1

Consider the filtering error system ($\varSigma _e$). For scalars $0<\alpha _j<1, \beta _{ij}>1, \forall S(i,j)\in S({\underline{N}})$, $\gamma >0$, suppose that there exist positive definite matrices $P_{jl}^1,P_{jl}^3$, invertible matrices $M^2_{j}$ and matrices $P_{jl}^2$, $A_{jl}^F$, $B_{jl}^F$, $C_{jl}^F$, $M^1_{jl}$, $M^3_{jl}$, such that the following inequalities hold

$$\begin{aligned}&\left[ \begin{array}{ccc} -(1-\alpha _j)P_{jl}&{}*&{}*\\ 0&{}-I&{}*\\ \varTheta _{31}&{}\varTheta _{32}&{}\varTheta _{33} \end{array} \right] <0,\! \ \ \, \ \forall j\in {\underline{N}}, \forall l\in {\mathcal {L}}, \end{aligned}$$

(16)

$$\begin{aligned}&\left[ \begin{array}{cc} -\gamma ^2\delta P_{jl}&{}*\\ \varPi _{21}&{}-I \end{array} \right] <0,\qquad \qquad \ \, \, \ \ \ \forall j\in {\underline{N}}, \forall l\in {\mathcal {L}}, \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{l=1}^La_{jl}P_{jl}\le \beta _{ij}\sum _{l=1}^Lb_{il}P_{il},\qquad \, \, \, \quad \! \forall S(i,j)\in S({\underline{N}}), \end{aligned}$$

(18)

where

$$\begin{aligned}&P_{jl}=\left[ \begin{array}{cc} P_{jl}^1&{}P_{jl}^2\\ (P_{jl}^2)^T&{}P_{jl}^3 \end{array} \right] ,\ \varTheta _{31}=\left[ \begin{array}{cc} M^1_{jl}A_j+B^F_{jl}C_i&{}A_{jl}^F\\ M^3_{jl}A_i+B^F_{jl}C_i&{}A_{jl}^F \end{array} \right] ,\\&\varTheta _{32}=\left[ \begin{array}{c} M_{jl}^1B_j+B_{jl}^FD_j\\ M_{jl}^3B_j+B_{jl}^FD_j \end{array} \right] ,\ \varTheta _{33}=P_{jl}+\sum _{l=1}^L\frac{b_{jl}-a_{jl}}{H_{j}}P_{jl}-M_{jl}-M_{jl}^T,\\&M_{jl}=\left[ \begin{array}{cc} M^1_{jl}&{}M^2_{j}\\ M^3_{jl}&{}M^2_{j} \end{array} \right] ,\ \varPi _{21}=\left[ \begin{array}{cc} E_j&-C_{jl}^F \end{array} \right] ,\ \ \delta =\exp \Bigg (\!\! -\!\!\sum _{S(i,j)\!\in \! S({\underline{N}})}\!\!N_{ij}^0\ln \beta _{ij} \Bigg ). \end{aligned}$$

Then, there exists an $l_2-l_\infty$ switched filter in the form of ($\varSigma _f$) such that the resulting filtering error system ($\varSigma _e$) is GUES and has the $l_2-l_\infty$ performance index $\gamma$ for any AED-ADT switching signal satisfying

$$\begin{aligned} \tau _{ij}^a>\tau _{ij}^{a*}=\frac{-\ln \beta _{ij}}{\ln (1-\alpha _j)},\ \ \forall S(i,j)\in S({\underline{N}}). \end{aligned}$$

(19)

Moreover, the filter gains are given as follows:

$$\begin{aligned} A_{j}^f(k)= & {} \sum _{l=1}^Lf_{jl}(k-k_m)A_{jl}^f,\ \ A_{jl}^f=(M_{j}^2)^{-1}A_{jl}^F, \end{aligned}$$

(20)

$$\begin{aligned} B_{j}^f(k)= & {} \sum _{l=1}^Lf_{jl}(k-k_m)B_{jl}^f,\ \ B_{jl}^f=(M_{j}^2)^{-1}B_{jl}^F, \end{aligned}$$

(21)

$$\begin{aligned} C_{j}^f(k)= & {} \sum _{l=1}^Lf_{jl}(k-k_m)C_{jl}^f,\ \ C_{jl}^f=C_{jl}^F, \ \ \sigma (k_m)=j,\ k\in [k_m,k_{m+1}). \end{aligned}$$

(22)

Proof

Construct matrices

$$\begin{aligned} M_j(k)=\left[ \begin{array}{cc} M^1_j(k)&{}M^2_j\\ M^3_j(k)&{}M^2_j \end{array} \right] =\left[ \begin{array}{cc} \sum _{l=1}^Lf_{jl}(k-k_m)M^1_{jl}&{}M^2_j\\ \sum _{l=1}^Lf_{jl}(k-k_m)M^3_{jl}&{}M^2_j \end{array} \right] . \end{aligned}$$

Noting (14) and (16), (20), (21), one can infer that

$$\begin{aligned} \left[ \begin{array}{ccc} -(1-\alpha _j)P_{j}(k)&{}*&{}*\\ 0&{}-I&{}*\\ \varTheta _{31}(k)&{}\varTheta _{32}(k)&{}\varTheta _{33}(k) \end{array} \right] <0, \end{aligned}$$

(23)

where

$$\begin{aligned}&\varTheta _{31}(k)=\left[ \begin{array}{cc} M^1_{j}(k)A_j+M_j^2B_{j}^f(k)C_j&{}M_j^2A_{j}^f(k)\\ M^3_{j}(k)A_j+M_j^2B_{j}^f(k)C_j&{}M_j^2A_{j}^f(k) \end{array} \right] ,\\&\varTheta _{32}(k)=\left[ \begin{array}{c} M_{j}^1(k)B_j+M_j^2B_{j}^f(k)D_j\\ M_{j}^3(k)B_j+M_j^2B_{j}^f(k)D_j \end{array} \right] ,\\&\varTheta _{33}(k)=P_{j}(k+1)-M_{j}(k)-(M_{j}(k))^T. \end{aligned}$$

On the basis of Lemma 1, it can be derived that inequality (23) for matrix $M_{j}(k)$ is equivalent to the following inequality

$$\begin{aligned} \left[ \begin{array}{c} {\overline{A}}_i^T(k)\\ {\overline{B}}_i^T(k) \end{array}\right] P_{i}(k+1) \left[ \begin{array}{cc} {\overline{A}}_i(k)&{\overline{B}}_i(k) \end{array} \right] -\left[ \begin{array}{cc} (1-\alpha _i)P_{i}(k)&{}0\\ 0&{}I \end{array} \right] <0. \end{aligned}$$

(24)

Along the trajectory of system (8), $\forall k\in [k_m,k_{m+1}), \sigma (k_m)=i$, we calculate

$$\begin{aligned}&V_{i}(k+1)-(1-\alpha _i)V_{i}(k)\nonumber \\&\quad =\xi ^T(k+1)P_{i}(k+1)\xi (k+1)-(1-\alpha _i)\xi ^T(k)P_{i}(k)\xi (k) \nonumber \\&\quad = \left[ \begin{array}{c} \xi (k)\\ \omega (k) \end{array} \right] ^T \left[ \begin{array}{c} {\overline{A}}_i^T(k)\\ {\overline{B}}_i^T(k) \end{array}\right] P_{i}(k+1) \left[ \begin{array}{cc} {\overline{A}}_i(k)&{\overline{B}}_i(k) \end{array} \right] \left[ \begin{array}{c} \xi (k)\\ \omega (k) \end{array} \right] \!\!-\!\!(1\!\!-\!\!\alpha _i)\xi ^T(k)P_{i}(k)\xi (k)\nonumber \\&\quad = \left[ \! \begin{array}{c} \xi (k)\\ \omega (k) \end{array} \!\right] ^T\left\{ \!\left[ \! \begin{array}{c} {\overline{A}}_i^T(k)\\ {\overline{B}}_i^T(k) \end{array}\!\right] P_{i}(k\!+\!1) \left[ \! \begin{array}{cc} {\overline{A}}_i(k)&{\overline{B}}_i(k) \end{array} \!\right] \!-\!\left[ \! \begin{array}{cc} (1\!-\!\alpha _i)P_{i}(k)&{}0\\ 0&{}0 \end{array} \!\right] \!\right\} \left[ \! \begin{array}{c} \xi (k)\\ \omega (k) \end{array} \!\right] .\nonumber \\ \end{aligned}$$

(25)

On the other hand, it is easy to obtain

$$\begin{aligned}&V_{i}(k)-(1-\alpha _i)^{k-k_m}V_{i}(k_m)-\sum _{s=k_m}^{k-1}(1-\alpha _i)^{k-1-s}\omega ^T(s)\omega (s)\nonumber \\&\quad =\sum _{s=k_m}^{k-1}(1-\alpha _i)^{k-1-s}\left[ V_{i}(s+1)-(1-\alpha _i)V_{i}(s)-\omega ^T(s)\omega (s) \right] . \end{aligned}$$

(26)

Integrating (24) with (25), (26) gives

$$\begin{aligned}&V_{i}(k)\le (1-\alpha _i)^{k-k_m}V_{i}(k_m)+\sum _{s=k_m}^{k-1}(1-\alpha _i)^{k-1-s}\omega ^T(s)\omega (s),\nonumber \\&\quad \forall k\in [k_m,k_{m+1}), \ \forall \omega (k)\in l_2[0,\infty ). \end{aligned}$$

(27)

Noting (18), $\forall k\in [k_m,k_{m+1})$, one gets

$$\begin{aligned} V_{\sigma (k)}(k)\le & {} (1-\alpha _{\sigma (k_m)})^{k-k_m}V_{\sigma (k_m)}(k_m)+\sum _{s=k_m}^{k-1}{(1-\alpha _{\sigma (k_m)})^{k-1-s}\omega ^T(s)\omega (s)}\\\le & {} (1-\alpha _{\sigma (k_m)})^{k-k_m}\beta _{\sigma (k_{m-1})\sigma (k_{m})}V_{\sigma (k_{m-1})}(k_m)\\&+\sum _{s=k_m}^{k-1}{(1-\alpha _{\sigma (k_m)})^{k-1-s}\omega ^T(s)\omega (s)}\\\le & {} (1-\alpha _{\sigma (k_m)})^{k-k_m}\beta _{\sigma (k_{m-1})\sigma (k_{m})}\Bigg ((1-\alpha _{\sigma (k_{m-1})})^{k_m-k_{m-1}}\\&\times V_{\sigma (k_{m-1})}(k_{m-1})+\sum _{s=k_{m-1}}^{k_m-1}{(1-\alpha _{\sigma (k_{m-1})})^{k_m-1-s}\omega ^T(s)\omega (s)}\Bigg )\\&+\sum _{s=k_m}^{k-1}{(1-\alpha _{\sigma (k_m)})^{k-1-s}\omega ^T(s)\omega (s)}. \end{aligned}$$

In a recurrent fashion, this, integrated with (18) and (27), yields

$$\begin{aligned} V_{\sigma (k)}(k)\le & {} (1-\alpha _{\sigma (k_m)})^{k-k_m}\prod _{s=0}^{m-1}\beta _{\sigma (k_s)\sigma (k_{s+1})}(1-\alpha _{\sigma (k_s)})^{k_{s+1}-k_s}V_{\sigma (k_0)}(k_0)\nonumber \\&+\,(1-\alpha _{\sigma (k_m)})^{k-k_m}\beta _{\sigma (k_{m-1})\sigma (k_m)}\sum _{q=1}^{m-1}\Bigg (\prod _{p=q}^{m-1} (1-\alpha _{\sigma (k_p)})^{k_{p+1}-k_p}\nonumber \\&\times \beta _{\sigma (k_{p-1})\sigma (k_p)}\sum _{s=k_{q-1}}^{k_q-1} (1-\alpha _{\sigma (k_{q-1})})^{k_q-1-s}\omega ^T(s)\omega (s)\Bigg )\nonumber \\&+\,(1-\alpha _{\sigma (k_m)})^{k-k_m}\beta _{\sigma (k_{m-1})\sigma (k_m)}\nonumber \\&\times \sum _{s=k_{m-1}}^{k_m-1}{(1-\alpha _{\sigma (k_{m-1})})^{k_m-1-s}\omega ^T(s)\omega (s)}\nonumber \\&+\sum _{s=k_m}^{k-1}{(1-\alpha _{\sigma (k_m)})^{k-1-s}\omega ^T(s)\omega (s)}\nonumber \\\le & {} e^{\sum _{S(i,j)\in S({\underline{N}})}N^0_{ij}\ln \beta _{ij}}e^{\sum _{S(i,j)\in S({\underline{N}})}(\frac{\ln \beta _{ij}}{\tau ^a_{ij}}+\ln (1-\alpha _j))T_{ij}(k_0,k)}V_{\sigma (k_0)}(k_0)\nonumber \\&+\sum _{q=1}^m\Bigg (e^{\sum _{S(i,j)\in S({\underline{N}})}N^0_{ij}\ln \beta _{ij}}e^{\sum _{S(i,j)\in S({\underline{N}})}(\frac{\ln \beta _{ij}}{\tau ^a_{ij}}+\ln (1-\alpha _j))T_{ij}(k_q,k)}\nonumber \\&\times \sum _{s=k_{q-1}}^{k_q-1}{(1-\alpha _{\sigma (k_{q-1})})^{k_q-1-s}\omega ^T(s)\omega (s)}\Bigg )\nonumber \\&+\sum _{s=k_m}^{k-1}{(1-\alpha _{\sigma (k_m)})^{k-1-s}\omega ^T(s)\omega (s)}. \end{aligned}$$

(28)

$\square$

Remark 3

The detailed steps for deriving (28) are omitted since the proof for (28) is regular and the similar proof can be seen in [7].

Then, the subsequent discussions fall into two parts in the light of $\omega (k)=0$ or not:

• (1) If $\omega (k)=0$, (28) becomes

  $$\begin{aligned} V_{\sigma (k)}\!(k)\!&\!\le \!&e^{\sum _{S(i,j)\in S({\underline{N}})}\!N^0_{ij}\ln \beta _{ij}}\!e^{\sum _{S(i,j)\in S({\underline{N}})}\!(\frac{\ln \beta _{ij}}{\tau ^a_{ij}}+\ln (1-\alpha _j))T_{ij}(k_0,k)}V_{\sigma (k_0)}\!(k_0). \end{aligned}$$

  From (19), it follows that $\frac{\ln \beta _{ij}}{\tau ^a_{ij}}+\ln (1-\alpha _j)<0$, and then, we can deduce that system $(\sum _e)$ is GUES according to Definition 1.

• (2) For $\forall S(i,j)\in S({\underline{N}})$, from $0<\alpha _j<1, \beta _{ij}>1$ and (19), we have

  $$\begin{aligned} 0<1-\alpha _j<1,\ \ e^{\sum _{S(i,j)\in S({\underline{N}})}{N_{ij}^0\ln \beta _{ij}}}\ge 1,\\ 0<e^{\sum _{S(i,j)\in S({\underline{N}})}{\Big (\ln (1-\alpha _j)+\frac{\ln \beta _{ij}}{\tau _{ij}^a}\Big )T_{ij}(k_q,k)}}\le 1. \end{aligned}$$

  Thus, under zero initial condition, inequality (28) implies

  $$\begin{aligned} V_{\sigma (k)}(k)\le & {} e^{\sum _{S(i,j)\in S({\underline{N}})}{N_{ij}^0\ln \beta _{ij}}}\sum _{q=1}^{m}\sum _{s=k_{q-1}}^{k_q-1}{\omega ^T(s)\omega (s)} +\sum _{s=k_m}^{k-1}{\omega ^T(s)\omega (s)}\nonumber \\= & {} e^{\sum _{S(i,j)\in S({\underline{N}})}{N_{ij}^0\ln \beta _{ij}}}\sum _{s=k_0}^{k_m-1}{\omega ^T(s)\omega (s)}+\sum _{s=k_m}^{k-1}{\omega ^T(s)\omega (s)}\nonumber \\\le & {} e^{\sum _{S(i,j)\in S({\underline{N}})}{N_{ij}^0\ln \beta _{ij}}}\sum _{s=k_0}^{k-1}{\omega ^T(s)\omega (s)}\nonumber \\= & {} \delta ^{-1}\sum _{s=k_0}^{k-1}{\omega ^T(s)\omega (s)}, \end{aligned}$$

  (29)

  where $\delta =e^{-\sum _{S(i,j)\in S({\underline{N}})}{N_{ij}^0\ln \beta _{ij}}}$.

  Integrated with (14), (17) and (22), Schur lemma yields

  $$\begin{aligned} {\overline{E}}^T_j(k){\overline{E}}_j(k)-\gamma ^2\delta P_{j}(k)<0, \end{aligned}$$

  (30)

  which together with (29) gives

  $$\begin{aligned}&e^T(k)e(k)-\gamma ^2\sum _{s=k_0}^{k-1}{\omega ^T(s)\omega (s)}\le e^T(k)e(k)-\gamma ^2\delta V_{\sigma (k)}(k)\nonumber \\&\quad =\xi ^T(k)({\overline{E}}^T_{\sigma (k)}(k){\overline{E}}_{\sigma (k)}(k)-\gamma ^2\delta P_{\sigma (k)}(k))\xi (k)<0. \end{aligned}$$

  (31)

  Therefore, under zero initial condition, $\Vert e\Vert _\infty <\gamma \Vert \omega \Vert _2$ is concluded for any $\omega (k)\in l_2[0,\infty )$.

The proof is completed.

Remark 4

It is easily observed that when $L=1$, our MCLF (10) will reduce to the used Lyapunov function in [7], and conditions (16), (17) and (18) in Theorem 1 become inequalities (30), (31) and (32) in Theorem 3 of [7]. This means that Theorem 3 of [7] can be viewed as the special case of our Theorem 1, i.e., our Theorem 1 generalizes Theorem 3 of [7].

Remark 5

Because the MCLF (10) and the switched filter ($\varSigma _f$) carry more degrees of freedom, condition (18) can be loosened largely and further smaller $\beta _{ij}$ can be selected. Consequently, AED-ADT bounds can be decreased, which enhances the application flexibility of our designed switching signals. On the other hand, it can be found that the evaluations of parameters $\beta _{ij}$ severely affect the magnitude of the $l_2-l_{\infty }$ performance index $\gamma$. From (17), the smaller parameters $\beta _{ij}$ are chosen, the smaller index $\gamma$ can be allowed. All the discussions will be verified in the simulation by comparing our result with the one in [7].

Remark 6

As stated above, our filter design method is based on the available switching signals. Once all the switching instants or some switching instants are unknown, our method cannot be utilized. In the future, we will further consider the prediction algorithms of switching signals, the asynchronous filtering problem [17] and the delay control method [32], or develop new filter design methods without switching information or only with partial switching information.

The following corollaries can be obtained by the similar proof, which ensure that the resulting filtering error system ($\varSigma _e$) is GUES with an $l_2-l_\infty$ performance under the MDADT and ADT switching strategies, respectively.

Corollary 1

Consider the filtering error system ($\varSigma _e$). For scalars $0<\alpha _j<1, \beta _{j}>1, \forall j\in {\underline{N}}, \gamma >0$, suppose that there exist positive definite matrices $P_{jl}^1,P_{jl}^3$, invertible matrices $M^2_{j}$ and matrices $P_{jl}^2,A_{jl}^F,B_{jl}^F,C_{jl}^F,M^1_{jl},M^3_{jl}$, such that inequalities (16), (17) hold and

$$\begin{aligned} \sum _{l=1}^La_{jl}P_{jl}\le \beta _{j}\sum _{l=1}^Lb_{il}P_{il},\ \, \ \quad \! \forall (i,j)\in {\underline{N}}\times {\underline{N}}, i \ne j, \forall l\in {\mathcal {L}}, \end{aligned}$$

(32)

where $\delta =\exp \Bigg ( -\sum _{j\in {\underline{N}}}N_{0j}\ln \beta _{j} \Bigg ).$ Then, there exists an $l_2-l_\infty$ switched filter in the form of ($\varSigma _f$) such that the filtering error system ($\varSigma _e$) is GUES and has the $l_2-l_\infty$ performance index $\gamma$ for any MDADT switching signal satisfying

$$\begin{aligned} \tau _{aj}>\tau _{aj}^{*}=\frac{-\ln \beta _{j}}{\ln (1-\alpha _j)},\ \ \forall j \in {\underline{N}}. \end{aligned}$$

(33)

Moreover, the filter gains are given as shown in (20), (21) and (22).

Remark 7

The ATEDW $\beta _{ij}$ is the key of making the AED-ADT switching superior to the MDADT switching. For the MDADT switching [33], the parameter $\beta _j$ in (32) represents the switching cost from all other subsystems to subsystem j, which relies on all ATEs $S(i,j)\in S({\underline{N}})$ ending in j for all $i\in {\underline{N}}$. In the case of AED-ADT switching, the ATEDW $\beta _{ij}$ in (18) denotes the switching cost from subsystem i to subsystem j, which only relies on ATE S(i, j) and has nothing to do with other subsystems or ATEs. The AED-ADTs $\tau _{i_1j}^{a}$ and $\tau _{i_2j}^{a},\, i_1\ne i_2$ may be separated due to the different ATEs $S(i_1,j)$ and $S(i_2,j)$, respectively. Therefore, it follows from (19) and (33) that $\tau _{ij}^{a*}\le \tau _{aj}^*, \forall S(i,j)\in S({\underline{N}})$. From this, the MDADT switching can be viewed as the special case of the AED-ADT switching, and the latter is of better flexibility and less conservativeness than the former.

Corollary 2

Consider the filtering error system ($\varSigma _e$). For scalars $0<\alpha <1, \beta>1, \gamma >0$, suppose that there exist positive definite matrices $P_{jl}^1,P_{jl}^3$, invertible matrices $M^2_{j}$ and matrices $P_{jl}^2,A_{jl}^F,B_{jl}^F,C_{jl}^F,M^1_{jl},M^3_{jl}$, such that inequalities (16), (17) hold and

$$\begin{aligned} \sum _{l=1}^La_{jl}P_{jl}\le \beta \sum _{l=1}^Lb_{il}P_{il},\ \ \ \ \quad \! \forall (i,j)\in {\underline{N}}\times {\underline{N}}, i \ne j, \forall l\in {\mathcal {L}}, \end{aligned}$$

where $\alpha _j$ is replaced as $\alpha$, and $\delta =\exp ( -N_{0}\ln \beta ).$ Then, there exists an $l_2-l_\infty$ switched filter in the form of ($\varSigma _f$) such that the filtering error system ($\varSigma _e$) is GUES and has the $l_2-l_\infty$ performance index $\gamma$ for any ADT switching signal satisfying

$$\begin{aligned} \tau _{a}>\tau _{a}^{*}=\frac{-\ln \beta }{\ln (1-\alpha )}. \end{aligned}$$

Moreover, the filter gains are given as shown in (20), (21) and (22).

Remark 8

For any $i\in {\underline{N}}$, it is reasonable that the length of each switching interval of subsystem i is assumed to be no larger than a positive integer $\tau _{\max }^i$. For any $k\in [k_m,k_{m+1}),$ there exists a constant $\eta \in {\mathbf {Z}}_{\ge 0}$ such that $k\!=\!k_m+\eta ,$$0\!\le \! \eta \!\le \! \tau _{\max }^i$. Since $A_i^f(k)\!=\!\sum _{l=1}^Lf_{il}(\eta )A_{il}^f,\, B_i^f(k)\!=\!\sum _{l=1}^Lf_{il}(\eta )B_{il}^f,\, C_i^f(k)\!=\!\sum _{l=1}^Lf_{il}(\eta )C_{il}^f$, the filter gains $A_i^f(k),\, B_i^f(k),\, C_i^f(k)$ can be calculated and stored in advance by $\sum _{l=1}^Lf_{il}(\eta )A_{il}^f,$$\sum _{l=1}^Lf_{il}(\eta )B_{il}^f,$$\sum _{l=1}^Lf_{il}(\eta )C_{il}^f,$$\eta =0, 1,\ldots , \tau _{\max }^i$, which can avoid recalculating the filter gains as the updates of time k happen. Furthermore, the computational complexity of both the filter gains and the LMI conditions in Theorem 1, Corollary 1 and Corollary 2 is closely related to the parameter L, the subsystem number $n_s$ and the dimensions $n, n_y, n_z, n_w$ of the system state, the measured output, the estimated signal and the disturbance input. Making a compromise of the disturbance attenuation level and the computational complexity, the above parameter L should be selected cautiously. For example, if the underlying switched system carries large subsystem number $n_s$ and state dimension n, large parameter L will generate enormous computational burden. Appropriate L, such as $L=2 and L=3$, should be chosen.

Fig. 2

The feasible regions of system parameters a, b, c by Theorem 1 ($\triangle , +$) and Theorem 3 in [7] ($+$)

4 Numerical Example

Now, we provide an example to demonstrate the validity of the main results in this paper. Consider the switched system ($\varSigma _s$) including three subsystems as follows:

$$\begin{aligned} A_1= & {} \left[ \begin{array}{cc} 0.6&{}0\\ a&{}0.32 \end{array} \right] , A_2=\left[ \begin{array}{cc} b&{}0.1\\ 0.3&{}0.7 \end{array} \right] , A_3=\left[ \begin{array}{cc} -1.5&{}1.75\\ -2.25&{}2.5 \end{array} \right] ,\\ B_1= & {} \left[ \begin{array}{c} 0.2\\ 0.4 \end{array} \right] , B_2=\left[ \begin{array}{c} 0.35\\ 0.15 \end{array} \right] , B_3=\left[ \begin{array}{c} 0.15\\ c \end{array} \right] ,\\ C_1= & {} \left[ \begin{array}{cc} 2&2 \end{array} \right] , C_2=\left[ \begin{array}{cc} 1&1.5 \end{array} \right] , C_3=\left[ \begin{array}{cc} 1&1 \end{array} \right] ,\\ D_1= & {} -0.2, D_2=0.2, D_3=0.3,\\ E_1= & {} \left[ \begin{array}{cc} 0.5&0.2 \end{array} \right] , E_2=\left[ \begin{array}{cc} 0.15&0.1 \end{array} \right] , E_3=\left[ \begin{array}{cc} 0.1&0.15 \end{array} \right] . \end{aligned}$$

For the usage of the MCLF, we choose parameters

$$\begin{aligned}&L=2,\ a_{11}=a_{12}=a_{21}=a_{22}=a_{31}=a_{32}=0.5,\\&b_{11}=b_{21}=b_{31}=0.4, \ \ b_{12}=b_{22}=b_{32}=0.6. \end{aligned}$$

Under parameters $\alpha _1=\alpha _2=\alpha _3=0.76, \beta _{21}=\beta _{31}=\beta _{12}=\beta _{32}=\beta _{13}=\beta _{23}=3.0$ and $\gamma ^2=0.25$, the feasibility regions for parameters $a=[-0.5,1], b=[0,1], c=[0,1]$ will be identified, respectively, via our Theorem 1 and Theorem 3 in [7], which are depicted in Fig. 2. Intuitively, red marks $\triangle$ surround blue marks $+$, by virtue of which an initial judgement can be given that our approach is preferable to the one in [7]. Through statistical analysis, the count ratio of marks $\triangle$ to marks $+$ can be obtained: $56.93\%$. In other words, our Theorem finds much more feasible points than Theorem 3 of [7]. This corroborates our judgement from a different perspective.

On the other hand, for system parameters $a=0.1, b=0.7, c=0.6$, Table 1 and Table 2 list the relevant parameters and the corresponding results obtained by our Theorem 1 and Theorem 3 of [7] under two periodic switching signals, respectively. Regardless of which switching signal is adopted, the MCLF achieves the tighter AED-ADT bounds $\tau _{ij}^{a*}$ and more desirable minimum $l_2-l_{\infty }$ performance indexes $\gamma _{min}$.

Table 1 Comparison results under the periodic switching path $1\rightarrow \! 3\rightarrow \! 2 \ldots$

Table 2 Comparison results under the periodic switching path $1\rightarrow 2\rightarrow 3 \ldots$

Choose the periodic switching path $1\rightarrow 3\rightarrow 2\cdots$, and parameters for Theorem 1 shown in Table 1. The corresponding filter parameters can be computed as follows:

$$\begin{aligned} A_{11}^f= & {} \left[ \begin{array}{cc} 0.4082&{}-0.1918\\ -0.1007&{}0.1192 \end{array} \right] , A_{12}^f=\left[ \begin{array}{cc} 0.4073 &{} -0.1923 \\ -0.1006&{}0.1195 \end{array} \right] ,\\ \ A_{21}^f= & {} \left[ \begin{array}{cc} 0.2695 &{} -0.1708\\ -0.1223&{}0.0664 \end{array} \right] , A_{22}^f=\left[ \begin{array}{cc} 0.2484 &{} -0.2024\\ -0.1364 &{} 0.0453 \end{array} \right] ,\\ A_{31}^f= & {} \left[ \begin{array}{cc} -2.0189 &{} 1.2291\\ -2.9926 &{} 1.7568 \end{array} \right] , \ \;\, A_{32}^f=\left[ \begin{array}{cc} -2.0189 &{} 1.2291\\ -2.9926 &{} 1.7568 \end{array} \right] ,\\ B_{11}^f= & {} \left[ \begin{array}{c} -0.0959\\ -0.1004 \end{array} \right] , B_{12}^f=\left[ \begin{array}{c} -0.0962\\ -0.1003 \end{array} \right] , B_{21}^f=\left[ \begin{array}{c} -0.1805\\ -0.4224 \end{array} \right] ,\\ B_{22}^f= & {} \left[ \begin{array}{c} -0.2016 \\ -0.4364 \end{array} \right] , B_{31}^f=\left[ \begin{array}{c} -0.5201\\ -0.7432 \end{array} \right] , B_{32}^f=\left[ \begin{array}{c} -0.5201 \\ -0.7432 \end{array} \right] ,\\ C_{11}^f= & {} \left[ \begin{array}{cc} -0.4999&-0.2000 \end{array} \right] , C_{12}^f=\left[ \begin{array}{cc} -0.4999&-0.2000 \end{array} \right] ,\\ C_{21}^f= & {} \left[ \begin{array}{cc} -0.1500&-0.0996 \end{array} \right] , C_{22}^f=\left[ \begin{array}{cc} -0.1500&-0.1000 \end{array} \right] ,\\ C_{31}^f= & {} \left[ \begin{array}{cc} -0.1001&-0.1499 \end{array} \right] , C_{32}^f=\left[ \begin{array}{cc} -0.1007&-0.1493 \end{array} \right] . \end{aligned}$$

Setting the initial value $\xi (0)=\left[ \begin{array}{cccc} 0.5&0.2&0.3&-0.4 \end{array} \right] ^T$, the trajectories of system state x(k) and filter state $x_f(k)$, and the switching signal with $\tau _{13}^a=4,\tau _{32}^a=3,\tau _{21}^a=1$ are shown in Fig. 3. We also present the filtering error e(k) in Fig. 4. They display that the designed switched filter ($\varSigma _f$) by the MCLF is effective.

Fig. 3

The system state x(k) and the filter state $x_f(k)$ under the switching signal $\sigma (k)$

Fig. 4

The filtering error e(k)

5 Conclusion

This paper concerns the problem of $l_2-l_\infty$ filtering for discrete-time switched systems with AED-ADT. By the aid of the MCLF approach, the quasi-time-dependent $l_2-l_\infty$ switched filter has been designed such that the filtering error system is GUES with a guaranteed $l_2-l_\infty$ performance. It has been pointed out that we obtain more general theoretic results than the existing results. In the end, an interesting example is offered to illustrate the effectiveness of the developed results.