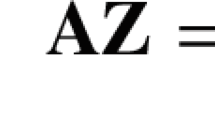Bayesian Robust Principal Component Analysis with Adaptive Singular Value Penalty

Abstract

Robust principal component analysis (RPCA) has recently seen ubiquitous activity for dimensionality reduction in image processing, visualization and pattern recognition. Conventional RPCA methods model the low-rank component as regularizing each singular value equally. However, in numerous modern applications, each singular value has different physical meaning and should be treated differently. This is one of the main reasons why RPCA techniques cannot work well in dealing with many realistic problems. To solve this problem, a novel hierarchical Bayesian RPCA model with adaptive singular value penalty is proposed. This model enforces the low-rank constraint by introducing an adaptive penalty function on the singular values of the low-rank component. In particular, we impose a hierarchical Exponent-Gamma prior on the singular values of the low-rank component and the Beta-Bernoulli prior on sparsity indicators. The variational Bayesian framework and the Markov chain Monte Carlo-based Bayesian inference are considered for inferring the posteriors of all latent variables involved in low-rank and sparse components. Numerical experiments demonstrate the competitive performance of the proposed model on synthetic and real data.

1 Introduction

Robust principal component analysis (RPCA) has been a common tool instead of principal component analysis (PCA) [12, 16, 23, 30, 34, 35, 40] for dimensionality reduction in numerous modern applications such as face modeling [21, 39], video surveillance [18], subspace clustering [25]. This is motivated by the theoretical advances for extracting low-dimensional information from the observed high-dimensional data matrix and addressing the fragility of PCA with respect to outlier sparse noise [1, 5, 11]. Essentially, RPCA incorporates low-rank and sparse constraints on the observed matrix and searches the best low-rank approximation of the observed data.

A typical RPCA assumes that the observed matrix $Y\in \mathbb {R}^{m\times n}$ can be decomposed into a low-rank component $L\in \mathbb {R}^{m\times n}$ (with the rank $r<<\min \{m,n\}$) and a sparse component $S\in \mathbb {R}^{m\times n}$ (corresponding to the sparse outliers). The objective is to recover the low-rank component L and the sparse component S. A standard approach is to find L and S from Y by solving

$$\begin{aligned} \min _{L,S} \text {rank}(L) + \nu \Vert S\Vert _0, ~~~~\mathrm{s.t.} ~~ Y = L + S, \end{aligned}$$

(1)

where $\nu$ is a tuning parameter and $\Vert S\Vert _0$ is the number of nonzero entries in S. Unfortunately, (1) is a non-deterministic polynomial (NP)-hard problem. To overcome this problem, several methods based on the nuclear norm and $\ell _1$-norm minimization have been proposed, which relaxed the rank function into the nuclear norm and replaced the $\ell _0$-norm with the $\ell _1$-norm. Subsequently, one has the following convex optimization problem

$$\begin{aligned} \min _{L,S} \Vert L\Vert _* +\ \nu \Vert S\Vert _1, \ \ \ \mathrm{s.t.}\ \ \ Y = L + S, \end{aligned}$$

(2)

where $\Vert L\Vert _*$ is the nuclear norm (the sum of singular values) of L, and $\Vert S\Vert _1$ is the $\ell _1$-norm (the sum of absolute values of the entries) of S. Cand$\grave{e}$s et al. [5] showed that L and S can be exactly recovered from Y with high probability under broad condition by solving the optimization problem (2).

Many effective methods [1, 4, 11, 13,14,15, 24, 29, 38] have been presented to solve the optimization problem (2). On the one hand, heuristic deterministic approaches including singular value thresholding (SVT) [4], accelerated proximal gradient algorithm (APG) [38] and augmented Lagrange multiplier (ALM) [24] have been developed. On the other hand, there has been a significant interest in Bayesian approaches. For example, Gao [13] and Luttinen et al. [29] proposed the probabilistic RPCA models by introducing the heavy-tail random noise component. Ding et al. [11] modeled the entries of sparse component S and the singular values of low-rank component L with Beta-Bernoulli prior and proposed using Markov chain Monte Carlo (MCMC) method to approximate inference. Babacan et al. [1] presented the sparse Bayesian learning (SBL) principles for solving probabilistic RPCA models, which started from a matrix factorization formulation and enforced the low-rank constraint in estimating the sparse component. In real scenarios, noises commonly appear in the measurements. The deterministic models cannot deal with the noises well since the convergence of the solution and its stability are influenced by the noises [36, 37]. In contrary, the probabilistic models can deal with noises well. For example, in [7, 43], complex noises were added in probabilistic RPCA models to improve their recovery performances in real scenarios. By exploiting structural dependencies between the values and locations of the sparse component, Han et al. [19] proposed Bayesian RPCA with the structured sparse component. Overall, these probabilistic RPCA models offer three main advantages over the deterministic methods. Firstly, it is not necessary to know the prior knowledge about the rank of the low-rank component and the way to estimate the unknown rank is similar to the automatic relevance determination strategy. Secondly, algorithmic parameters are insensitive to the initialization of parameters since they are treated as stochastic quantities in the Bayesian framework. Thirdly, the probabilistic RPCA models allow us to exploit and explain complex noise structure in observation matrix Y, which are robust to a broad of noises and provide high recovery performance.

However, the present probabilistic RPCA models obviously impose the low-rank constraint on each singular value of the low-rank component L equally and ignore the physical meaning, i.e., the prior knowledge, on these singular values [1, 9,10,11, 19, 26, 27, 42]. In numerous modern applications, the weight distributions of each singular value of the low-rank component L are not truly uniformly distributions, and should be treated differently so that the information contained in the small singular values covered by that of the big singular values can be recovered well. There have been nonconvex low-rank constraints used in some deterministic RPCA models. For example, Hu et al. [22] proposed the truncated nuclear norm regularization (TNNR) by minimizing the sum of the largest few singular values; Lu et al. [28] proposed to minimize the rank using a family of nonconvex surrogates of $\ell _0$-norm on the singular values. By now, however, these works do not extend to the probabilistic RPCA models.

Motivated by the trajectory of deterministic methods in addressing the aforementioned problem, in this paper, we present a novel hierarchical Bayesian RPCA model with adaptive singular value penalty for decomposing the observed matrix into low-rank and sparse components. To boost the performance of recovering low-rank component of RPCA model, we enforce the low-rank constraint by introducing an adaptive penalty function on the singular values of the low-rank component. In particular, we impose a hierarchical Exponent-Gamma prior on the singular values of the low-rank component and the Beta-Bernoulli prior on sparsity indicators. The exponential prior for low-rank matrix recovery has been widely used and researched, and the Gamma prior penalizes the singular values (see Sect. 2 for details); thus, an Exponent-Gamma framework is employed on the singular values of the low-rank component, which provides more flexibility-weighted structures for the learning of the low-rank component. The zero elements in singular values of low-rank component are further guaranteed to be exactly zero by introducing the binary latent factor indicators [19]. The variational Bayesian framework and the Markov chain Monte Carlo (MCMC)-based Bayesian inference are considered for inferring the posteriors of all latent variables involved in low-rank and sparse components. Besides, different initial values of the input parameters may affect the outcome. The optimal parameters should be selected carefully [32]. We discussed the possible initial conditions that provided satisfactory results.

The rest of this paper is organized as follows. Section 2 presents the motivations. The proposed Bayesian robust principal component analysis model with the adaptive penalty on the singular values (APSV-BRPCA) is proposed in Sect. 3. A variational Bayesian inference algorithm is employed to estimate the posterior distributions in Sect. 4. We present an analysis of the APSV-BRPCA approach in Sect. 5. Experiments including synthetic and real data are shown in Sect. 6. Finally, Sect. 7 gives the conclusion.

2 Motivations

The Bayesian model presented in this paper is closely related to some deterministic models. In this section, we provide insights into understanding the low-rank Bayesian model with the adaptive penalty on singular values.

In sparse Bayesian learning, the penalty function (i.e., the log-likelihood of the singular value vector $\lambda$) is assumed to be an exponential prior

$$\begin{aligned} f(\lambda )=-\ln p(\lambda )=\text {constant}+\gamma \Vert X\Vert _{*}, \end{aligned}$$

(3)

where $p(\lambda )=\prod _{i=1}^{r}\gamma \exp (-\gamma \lambda _{i})$, r is the rank of X and $f(\lambda )$ is penalty function. This penalty function is equal to the nuclear norm of matrix x

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}} \Vert x\Vert _{*}, \ \ \ \mathrm{s.t.}\ \ \ y=\varPsi x, \end{aligned}$$

(4)

where $\Vert x\Vert _{*}=|\lambda |_{1}=\sum _{i=1}^{r}\lambda _{i}$, $\lambda =[\lambda _{1},\ldots ,\lambda _{r}]$ is the singular value vector of x.

To improve the $\ell _{1}$-minimization problem for compressive sensing, the reweighted $\ell _{1}$ minimization [6] is given by

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}} \sum _{i}w_{i}|x_{i}|, \ \ \ \mathrm{s.t.}\ \ \ y=\varPsi x, \end{aligned}$$

(5)

where $w_{i}$ is positive weight.

Meanwhile, the prior model (3) corresponding to the traditional nuclear norm can be further elaborated by introducing the hierarchical Exponent-Gamma prior

$$\begin{aligned} \begin{aligned} p(\lambda |\gamma )&=\prod _{i=1}^{r}\gamma _{i}\exp (-\gamma _{i}\lambda _{i}),\\ p(\gamma _{i})&=\mathrm{Gamma}(\gamma _{i}|a,b), \end{aligned} \end{aligned}$$

(6)

where $\lambda _{i}$ represents the ith singular value and $\gamma =[\gamma _{1},\ldots ,\gamma _{r}]$ is a weighted parameter vector of the singular values. Here, the penalty function as calculated in model (3) is given by

$$\begin{aligned} f(\lambda )=-\ln p(\lambda |\gamma )=\text {constant}+\sum _{i=1}^{r}\gamma _{i}\lambda _{i}. \end{aligned}$$

(7)

Consequently, model (7) is actually related to the reweighted $\ell _{1}$-norm (5),

which means the new hierarchical prior (6) adaptively imposes weights on different singular values so that it potentially improves the flexibility of sparse Bayesian learning.

3 APSV-BRPCA Model

The Bayesian model treats its parameters as stochastic quantities and uses the hierarchical Bayesian framework for the factorized form of measurements to connect stochastic parameters. Generally, the observed data matrix $Y\in \mathbb {R}^{m\times n}$ is assumed to be the superposition of three parts: the low-rank component $L\in \mathbb {R}^{m\times n}$, the sparse component $S\in \mathbb {R}^{m\times n}$ and the noise term $N\in \mathbb {R}^{m\times n}$, i.e., $Y=L+S+N$. Utilizing singular value decomposition, any matrix L of rank r can be decomposed as $L=U\varLambda V^{T}$, where U and V are $m\times r$ and $n\times r$ matrices, respectively, and diagonal matrix $\varLambda =\mathrm{diag}(\lambda _1,\ldots ,\lambda _r)\in \mathbb {R}^{r\times r}$ is consisted of nonzero singular values of L. Then the proposed factorized form of measurements for the Bayesian frame is as follows:

$$\begin{aligned} Y = U(D\varLambda )V^{T}+B\circ E +N, \end{aligned}$$

(8)

where $\circ$ denotes the Hadamard product. The diagonal matrix D and the sparse indicator matrix B are binary matrices which are used for enforcing sparsity.

3.1 Hierarchical Low-Rank Model

The low-rank component proposed in (8) is given by $L = U(D\varLambda )V^{T}$. Our main goal is to add the adaptive penalty on the singular values in Bayesian RPCA model. To track this issue, as mentioned in Sect. 2, the hierarchical prior of $\varLambda$ is drawn from an Exponent-Gamma distribution

$$\begin{aligned} \begin{aligned} \lambda _{k}&\sim \mathrm{Exp}(\lambda _{k}|\gamma _{k}),\\ \gamma _{k}&\sim \mathrm{Gamma}(a_{0}, b_{0}), \end{aligned} \ \ \ \ k=1, \dots , r, \end{aligned}$$

where $\mathrm{Exp}(\lambda _{k}|\gamma _{k})=\gamma _k\mathrm{exp}(-\gamma _k\lambda _{k})$.

The diagonal matrix $D = \mathrm{diag}(d_1,\ldots ,d_r)$ has binary entries along the diagonal, i.e., $d_{k}\in \{0,1\}, k = 1, \dots , r$. Then $D\varLambda$ is still a diagonal matrix. In the Bayesian model, diagonal matrix D decouples the rank learning and the singular value learning [11]. We can infer the magnitudes of the singular values using $\varLambda$ and the rank of L by $r = ||D||_0$. An appropriate choice for modeling D is based on a product of Bernoulli-Beta prior distribution

$$\begin{aligned} \begin{aligned} d_{k}\sim \mathrm{Bernoulli}(d_{k}|\pi _{k}) ,\\ \pi _{k}\sim \mathrm{Beta}(\pi _{k}|\theta _{0},\eta _{0}), \end{aligned} \ \ \ \ k=1, \dots , r. \end{aligned}$$

(9)

Note that the sparse of diagonal elements of D is controlled by the hyperparameters $\theta _{0}>0$ and $\eta _{0}>0$. Specifically, the expectation of $\pi _{k}$ is $\frac{\theta _{0}}{\theta _{0}+\eta _{0}}$, thus one can set $\frac{\theta _{0}}{\theta _{0}+\eta _{0}}\ll 1$ (e.g., $\theta _{0}=\min \{\frac{1}{r},\frac{1}{150}\}$, $\eta _{0}=1-\theta _{0}$) to encourage the sparse of diagonal elements of D.

The columns of matrices $U=[\mathbf {u}_{\cdot i}]$ and rows of $V=[\mathbf {v}_{j\cdot }]$ are assumed to be drawn from Gaussian distributions

$$\begin{aligned} \begin{aligned} { u}_{\cdot i}&\sim \mathscr {N}({ u}_{\cdot i}|{ 0}, \frac{1}{m}{ I}_m), \ \ \ i=1,\dots , r,\\ { v}_{j \cdot }&\sim \mathscr {N}({ v}_{j \cdot }|{ 0}, { I}_r), \ \ \ j=1,\dots , n. \end{aligned} \end{aligned}$$

(10)

Fig. 1

APSV-BRPCA model

3.2 Sparse Model

The sparse component proposed in (8) is given by $S = B\circ E$, where B is a binary matrix. Again, the binary matrix is used for enhancing the recovery of the sparse component, such that the Bayesian model can keep the sparse nature of E. Each column of the binary matrix $B=[\mathbf {b}_{\cdot j}]$ is modeled as follows:

$$\begin{aligned} \begin{aligned}&\mathbf {b}_{\cdot j}\sim \prod _{i = 1}^{m} \mathrm{Bernoilli} (b_{ij}|\omega _i), \ \ \ j = 1,\ldots ,n,\\&\omega _i\sim \mathrm{Beta}(\omega _i|\alpha _0,\beta _0), \ \ \ i = 1,\ldots , m, \end{aligned} \end{aligned}$$

(11)

where $\alpha _{0}=\min \{\frac{1}{n},\frac{1}{150}\}$, $\beta _{0}=1-\alpha _{0}$.

The element $e_{ij}$ in E follows a Gaussian-Gamma distribution

$$\begin{aligned} \begin{aligned}&\mathbf {e}_{i\cdot }\sim \mathscr {N}(\mathbf {e}_{i\cdot }|\mathbf {0}, \mathbf {\tau }^{-1}I_n), \ \ \ i = 1,\ldots ,m, \\&\mathbf {\tau }\sim \mathrm{Gamma}(\tau |c_0,d_0). \end{aligned} \end{aligned}$$

(12)

If necessary, one can learn different noise precisions for different parts of E. But it will result in overfitting because of limited observations and too many parameters. To avoid the overfitting, we use one precision $\tau$ to model the element $e_{ij}$.

3.3 Noisy Observation Model

One advantage of probability RPCA is the robustness for the additive interference. The elements $n_{ij}$ in N are assumed drawn from a Gaussian distribution as follows:

$$\begin{aligned} \begin{aligned} n_{ij}&\sim \mathscr {N}(n_{ij}|0, \beta ^{-1}), \ \ \ i = 1,\ldots ,m, \ \ \ j = 1,\ldots ,n, \\ \beta&\sim \mathrm{Gamma}(\beta |e_0,f_0). \end{aligned} \end{aligned}$$

(13)

The noise precision is assumed unknown and learnt within the model inference. As discussed above, to avoid the overfitting and improve the adaptivity, the same precision parameter $\beta$ is imposed on the noise $n_{ij}$. The common choice in sparse Bayesian learning such as [8, 19, 41] has shown that it can reduce model complexity and increase robustness.

Given the prior defined as above mentioned, the conditional distribution for the observation model is as follows:

$$\begin{aligned} p(Y|U,D,\varLambda ,V,B,E)=\mathscr {N}(Y|U(D\varLambda )V^{T}+B\circ E,\beta ^{-1}I_{mn}). \end{aligned}$$

(14)

To facilitate the illustration of the proposed Bayesian model, Fig. 1 shows the complete graphical model.

4 Variational Bayesian Inference

Bayesian inference is evaluating the posterior distributions of unknowns given the observation. However, the posterior distribution is computationally intractable since the marginal distribution p(Y) is not calculated analytically. In this paper, to deal with the tractable joint posterior distribution problem, the approximate posterior distribution factorized with respect to the partition $q(\varTheta )=\prod \limits _{k}q_{k}(\varTheta _{k})=q_{k}$ is considered, and the variational Bayesian method [3] is used to obtain the Bayesian inference of $q(\varTheta )$. In particular, the variational Bayesian method estimates the posterior distribution of each unknown parameter by holding the other parameters fixed [3].

The objective of the variational Bayesian method is to select the parameters to minimize the Kullback–Leibler (KL) divergence between $q(\varTheta )$ and the true posterior distribution $p(\varTheta |Y)$, i.e.,

$$\begin{aligned} \min \limits _{q(\varTheta )} KL(q(\varTheta )\Vert p(\varTheta ))=\int q(\varTheta )\ln \frac{q(\varTheta )}{p(\varTheta |Y)}\mathrm{d}\varTheta , \end{aligned}$$

where $\varTheta$=$\{U,D,\varLambda ,V,\pi ,\lambda ,\gamma ,B,E,\omega ,\tau ,\beta \}$ denotes the set contained all parameter variables. It is equivalent to the following problem

$$\begin{aligned} \max \limits _{q(\varTheta )} -KL(q(\varTheta )\Vert p(\varTheta ))=\int q(\varTheta )\ln \frac{p(\varTheta ,Y)}{q(\varTheta )p(Y)}\mathrm{d}\varTheta . \end{aligned}$$

Since $KL(q(\varTheta )\Vert p(\varTheta ))\ge 0$ and $\int q(\varTheta )\mathrm{d}\varTheta =1$, the key procedure is to estimate the marginal likelihood p(Y) with a maximal lower bound, i.e.,

$$\begin{aligned} \ln p(Y)\ge \mathscr {L}(\theta )=\int q(\varTheta )\ln \frac{p(\varTheta ,Y)}{q(\varTheta )}\mathrm{d}\varTheta . \end{aligned}$$

The problem is developed to maximize the lower bound $\mathscr {L}(\theta )$.

$$\begin{aligned} \begin{aligned} \mathscr {L}(\theta )&=\int \prod \limits _{k}q_{k}[\ln p(\varTheta ,Y)-\sum _{k}\ln q_{k}]\mathrm{d}\varTheta \\&=\int \prod \limits _{k}q_{k}\ln p(\varTheta ,Y)\prod \limits _{k}\mathrm{d}\varTheta _{k}-\sum _{k}\int \prod \limits _{j}q_{j}\ln q_{k}\prod \limits _{j}\mathrm{d}\varTheta _{j}\\&=\int q_{k}[\ln p(\varTheta ,Y)\prod \limits _{j\ne k}(q_{j}\mathrm{d}\varTheta _{j})]\mathrm{d}\varTheta _{k}-\sum _{k}\int q_{k}\ln q_{k}\mathrm{d}\varTheta _{k}\\&=\int q_{k}[\ln p(\varTheta ,Y)\prod \limits _{j\ne k}(q_{j}\mathrm{d}\varTheta _{j})]\mathrm{d}\varTheta _{k}-\int q_{k}\ln q_{k}\mathrm{d}\varTheta _{k}-\sum _{j\ne k}\int q_{j}\ln q_{j}\mathrm{d}\varTheta _{j}\\&=\int q_{k}\ln {\overline{p}}(\varTheta _{k},Y)\mathrm{d}\varTheta _{k}-\int q_{k}\ln q_{k}\mathrm{d}\varTheta _{k}-\sum _{j\ne k}\int q_{j}\ln q_{j}\mathrm{d}\varTheta _{j}\\&=-KL(q_{k}\Vert {\overline{p}})-\sum _{j\ne k}\int q_{j}\ln q_{j}\mathrm{d}\varTheta _{j}, \end{aligned}\nonumber \\ \end{aligned}$$

(15)

where $\ln {\overline{p}}(\varTheta _{k},Y)=E_{\varTheta \setminus \varTheta _{k}}[\ln p(\varTheta ,Y)]=\int \ln p(\varTheta ,Y)\prod \limits _{j\ne k}(q_{j}\mathrm{d}\varTheta _{j})$ and $\int q_{j}\mathrm{d}\varTheta _{j}=1~(j=1,\cdots )$. The expectation $E_{\varTheta \setminus \varTheta _{k}}$ is taken about the set $\varTheta$ with $\varTheta _{k}$ removed. Clearly, the bound in (15) is maximized when $q_{k}(\varTheta _{k})={\overline{p}}(\varTheta _{k},y)$. In this case, the KL divergence is equal to zero. Consequently, the optimal posterior estimation $q_{k}(\varTheta _{k})$ with other variables fixed is as follows:

$$\begin{aligned} \ln q_{k}(\varTheta _{k})=E_{\varTheta \setminus \varTheta _{k}}[\ln p(Y,\varTheta )]+\text {C}, \end{aligned}$$

(16)

where C is a constant. In the next subsection, we calculate each parameter in its turn holding other parameters fixed with respect to their most recent distributions and separately show the update rules for each parameter. For notational simplicity, the expectation of the approximate posterior $q(\cdot )$ is denoted by $\langle \cdot \rangle$.

4.1 Estimation of Low-Rank Component

The parameters involved in the low-rank component are U, D, $\varLambda$, V, d, $\pi$, $\lambda$, $\gamma$. Invoking the prior model (10), the observed model (14), one can obtain the posterior distribution of the row $u_{i\cdot }$ of U,

$$\begin{aligned} q({ u}_{i \cdot })=\mathscr {N}({ u}_{i \cdot }\mid \mu _{{ u}_{i \cdot }},\varSigma ^U), \end{aligned}$$

(17)

with mean and covariance

$$\begin{aligned} \begin{aligned} \varSigma ^{U}&=(\langle \beta \rangle \langle D\varLambda V^{T}V\varLambda ^{T}D^{T}\rangle +m{ I}_r)^{-1}, \\ \mu _{{ u}_{i \cdot }}^{T}&=\langle \beta \rangle \varSigma ^{U}\langle V\varLambda ^{T} D^{T}\rangle ^{T}(y_{i\cdot }-\langle b_{i\cdot }\rangle \circ \langle e_{i\cdot }\rangle )^T. \end{aligned} \end{aligned}$$

Similarly, for each row of V (i.e., $v_{j\cdot }$), we get

$$\begin{aligned} q({ v}_{j \cdot })=\mathscr {N}({ v}_{j \cdot }\mid \mu _{{ v}_{i \cdot }},\varSigma ^{V}), \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{aligned} \varSigma ^{V}&=(\langle \beta \rangle \langle D^{T}\varLambda ^{T}U^{T}UD\varLambda \rangle +{I}_r)^{-1}\, ,\\ \mu _{{ v}_{j \cdot }}^{T}&=\langle \beta \rangle \varSigma ^V\langle U\varLambda D\rangle ^{T}(y_{\cdot j}-\langle b_{\cdot j}\rangle \circ \langle e_{\cdot j}\rangle ). \end{aligned} \end{aligned}$$

The required expectations in (17) and (18) can be calculated as follows:

$$\begin{aligned}&\langle D\varLambda V^{T}V\varLambda ^{T}D^{T}\rangle =\langle d^Td\rangle \circ \langle \lambda ^T\lambda \rangle \circ \langle V^TV\rangle ,\\&\langle D^{T}\varLambda ^{T}U^{T}UD\varLambda \rangle =\langle d^Td\rangle \circ \langle \lambda ^T\lambda \rangle \circ \langle U^TU\rangle ,\\&\langle U^TU\rangle =m\varSigma ^U+\langle U^T\rangle \langle U\rangle ,\\&\langle V^TV\rangle =n\varSigma ^V+\langle V^T\rangle \langle V\rangle ,\\&\langle d^Td\rangle =\varSigma _d+\langle d^T\rangle \langle d\rangle ,\\&\langle \lambda ^T\lambda \rangle =\varSigma _\lambda +\langle \lambda ^T\rangle \langle \lambda \rangle , \end{aligned}$$

where d =diag(D) and $\lambda$= diag$(\varLambda )$ are row vectors, $\varSigma _d$= diag(Var$(d_{k})$) and $\varSigma _\lambda =$diag(Var$(\lambda _{k}))$ are diagonal matrices.

The posterior approximation of D is a Bernoulli distribution

$$\begin{aligned} q(d_{k})=\mathrm{Bernoulli}\left( \frac{\xi ^{d_{k}}}{\xi ^{d_{k}}+\zeta ^{d_{k}}}\right) , \end{aligned}$$

(19)

where

$$\begin{aligned} \xi ^{d_{k}}&=\exp \{\langle \ln \pi _{k}\rangle -\frac{\langle \beta \rangle }{2}\sum _{ij}[\langle u_{ik}^{2}v_{jk}^{2}\lambda _{k}^{2}\rangle -2(y_{ij}-\langle b_{ij}\rangle \langle e_{ij}\rangle ) \langle \lambda _{k}u_{ik}v_{jk}\rangle \\&\ \ \ +2\langle { u}_{i \cdot }^{-k}D^{-k}\varLambda ^{-k}({ v}_{j \cdot }^{-k})^{T}\lambda _{k}u_{ik}v_{jk}\rangle ]\},\\ \zeta ^{d_{k}}&=\exp \{\langle \ln (1-\pi _{k})\rangle \}, \end{aligned}$$

$a^{-k}$ means that the kth coordinate of a is deleted,

$$\begin{aligned}&\langle d_{k}\rangle =\frac{\xi ^{d_{k}}}{\xi ^{d_{k}}+\zeta ^{d_{k}}},\\&\langle u_{ik}^{2} v_{jk}^{2}\lambda _{k}^{2}\rangle =\langle u_{ik}^{2}\rangle \langle v_{jk}^{2}\rangle \langle \lambda _{k}^{2}\rangle ,\\&\langle { u}_{i \cdot }^{-k}D^{-k}\varLambda ^{-k}({ v}_{j \cdot }^{-k})^{T}\lambda _{k}u_{ik}v_{jk}\rangle =\{\langle { u}_{i \cdot }^T{ u}_{i \cdot }\rangle \circ \langle \lambda ^T\lambda \rangle \circ \langle { v}_{j \cdot }^T{ v}_{j \cdot }\rangle \}_{\cdot k}^{T}\langle d^k\rangle ,\\&\langle d^k\rangle =(\langle d_{1}\rangle ,\dots ,0,\dots ,\langle d_{r}\rangle ),\\&\langle { u}_{i \cdot }^T{ u}_{i \cdot }\rangle =\varSigma ^U+\langle { u}_{i \cdot }^T\rangle \langle { u}_{i \cdot }\rangle ,\\&\langle { v}_{j \cdot }^T{ v}_{j \cdot }\rangle =\varSigma ^V+\langle { v}_{j \cdot }^T\rangle \langle { v}_{j \cdot }\rangle . \end{aligned}$$

According to the prior model (9), one can find $q(\pi _{k})$ follows a Beta distribution,

$$\begin{aligned} q(\pi _k)=\mathrm{Beta}(\pi _k\mid \langle d_{k}\rangle +\theta _{0},1-\langle d_{k}\rangle +\eta _0). \end{aligned}$$

(20)

Then we have

$$\begin{aligned} \langle \ln \pi _k\rangle&=\psi (\langle d_{k}\rangle +\theta _{0})-\psi (\theta _{0}+\eta _{0}+1),\\ \langle \ln (1-\pi _k)\rangle&=\psi (1-\langle d_{k}\rangle +\eta _0)-\psi (\theta _{0}+\eta _{0}+1), \end{aligned}$$

where $\psi (x)=\frac{\mathrm{d} \ln \Gamma (x)}{\mathrm{d}x}$ is a digamma function.

The variational posterior of $\lambda _{k}$ is a truncated Gaussian distribution

$$\begin{aligned} q(\lambda _{k})=\frac{\mathscr {N}(\lambda _{k}\mid \mu _{\lambda _{k}}, \sigma ^2_{\lambda _{k}})}{1-\varPhi (\epsilon )}I_{\{\lambda _{k}>0\}}, \epsilon =-\frac{\mu _{\lambda _{k}}}{\sigma _{\lambda _{k}}}, \end{aligned}$$

(21)

where

$U_i=\mathrm{diag}({ u}_{i \cdot })$ is a diagonal matrix, $\phi (x)=N(x\mid 0,1)$, $\varPhi (x)$ is a standard Gaussian distribution function. Then we can get

$$\begin{aligned} \langle \lambda _{k}\rangle&=\mu _{\lambda _{k}}+\sigma _{\lambda _{k}}\frac{\phi (\epsilon )}{1-\varPhi (\epsilon )},\\ \mathrm{Var}(\lambda _{k})&=\sigma ^2_{\lambda _{k}}[1+\epsilon \frac{\phi (\epsilon )}{1-\varPhi (\epsilon )}-(\frac{\phi (\epsilon )}{1-\varPhi (\epsilon )})^2],\\ \langle \lambda ^{-k}U_i^{-k}D^{-k}({ v}_{j \cdot }^{-k})^{T}d_{k}u_{ik}v_{jk}\rangle&=\{\langle { u}_{i \cdot }^T{ u}_{i \cdot }\rangle \circ \langle d^Td\rangle \circ \langle { v}_{j \cdot }^T{ v}_{j \cdot }\rangle \}_{\cdot k}^{T}\langle \lambda ^k\rangle ,\\ \langle \lambda ^k\rangle&=(\langle \lambda _{1}\rangle ,\dots ,0,\dots ,\langle \lambda _{r}\rangle ). \end{aligned}$$

Similarly, the posterior approximation of $\gamma$ can be derived as follows:

$$\begin{aligned} q(\gamma _k)=\mathrm{Gamma}(\gamma _k\mid a_{0}+1,b_0+\langle \lambda _{k}\rangle ). \end{aligned}$$

(22)

Then we have

$$\begin{aligned} \langle \gamma _k\rangle =\frac{a_0+1}{b_0+\langle \lambda _{k}\rangle }. \end{aligned}$$

4.2 Estimation of Sparse Component

The parameters involved in the sparse component are E, B, $\omega$, $\tau$. With the Bernoulli (11) and the Gaussian observation likelihood (14), $b_{ij}$ follows a Bernoulli distribution,

$$\begin{aligned} q(b_{ij})=\mathrm{Bernoulli}\left( \frac{\xi ^{b_{ij}}}{\xi ^{b_{ij}}+\zeta ^{b_{ij}}}\right) , \end{aligned}$$

(23)

where

$$\begin{aligned} \xi ^{b_{ij}}&=\exp \{\langle \ln \omega _{i}\rangle -\frac{\langle \beta \rangle }{2}(\langle e_{ij}^{2}\rangle -2\langle e_{ij}\rangle (y_{ij}-\langle u_{i\cdot }D\varLambda v_{j\cdot }^T\rangle ))\},\\ \zeta ^{b_{ij}}&=\exp \{\langle \ln (1-\omega _{i})\rangle \}. \end{aligned}$$

Similarly, the approximate posterior of each column $e_{\cdot j}$ is as follows:

$$\begin{aligned} q(e_{\cdot j}) = \mathscr {N}(e_{\cdot j}\mid \mu _{e_{\cdot j}}, \varSigma _{e_{\cdot j}}), \end{aligned}$$

(24)

where

$$\begin{aligned} \varSigma _{e_{\cdot j}}&=(\langle \tau \rangle I_m+\langle \beta \rangle \langle B_{j}\rangle )^{-1},\\ \mu _{e_{\cdot j}}&=\langle \beta \rangle \varSigma _{e_{\cdot j}}\langle B_{j}\rangle ^T(y_{\cdot j}-\langle UD\varLambda \mathbf {v}_{\cdot j}^T\rangle ), \end{aligned}$$

where $B_i=\mathrm{diag}(\langle { b}_{\cdot j}\rangle )$ is a diagonal matrix.

The posterior approximation of $\omega _i$ is a Beta distribution

$$\begin{aligned}&q(\omega _i)=\mathrm{Beta}(\omega _i\mid \alpha _{0}+\sum _{j = 1}^n\langle b_{ij}\rangle ,\beta _0+n-\sum _{j = 1}^n\langle b_{ij}\rangle ), i = 1,2,\ldots ,m, \nonumber \\&\quad \langle \ln \omega _i\rangle =\psi (\alpha _{0}+\sum _{j = 1}^n\langle b_{ij}\rangle )-\psi (\alpha _{0}+\beta _{0}+n),\nonumber \\&\quad \langle \ln (1-\omega _i)\rangle =\psi (\beta _0+n-\sum _{j = 1}^n\langle b_{ij}\rangle )-\psi (\alpha _{0}+\beta _{0}+n). \end{aligned}$$

(25)

The variational posterior of $\tau$ is as follows:

$$\begin{aligned}&q(\tau )=\mathrm{Gamma}(\tau \mid c_{0}+0.5mn, d_0+0.5\sum _{j = 1}^n\langle e_{\cdot j}^Te_{\cdot j}\rangle ), \nonumber \\&\langle \tau \rangle =\frac{c_{0}+0.5mn}{d_0+0.5\sum _{j = 1}^n\langle e_{\cdot j}^Te_{\cdot j}\rangle }, \langle e_{\cdot j}^Te_{\cdot j}\rangle =tr(\varSigma _{e_{\cdot j}})+\langle e_{\cdot j}\rangle ^T\langle e_{\cdot j}\rangle . \end{aligned}$$

(26)

4.3 Estimation of Noise Precision

Finally, the variational distribution of $\beta$ is a Gamma distribution,

$$\begin{aligned}&q(\beta )=\mathrm{Gamma}(\beta \mid e_{0}+0.5mn, f_0+0.5\langle \Vert Y-UD\varLambda V^T-B\circ E\Vert _F^2\rangle ),\nonumber \\&\quad \langle \beta \rangle =\frac{e_{0}+0.5mn}{f_0+0.5\langle \Vert Y-UD\varLambda V^T-B\circ E\Vert _F^2\rangle }, \end{aligned}$$

(27)

where

$$\begin{aligned} \langle \Vert Y-UD\varLambda V^T-B\circ E\Vert _F^2\rangle =&\Vert Y-\langle U\rangle \langle D\rangle \langle \varLambda \rangle \langle V^T\rangle -\langle B\rangle \circ \langle E\rangle \Vert _F^2\\&+tr(\langle U^{T}U\rangle \langle D\varLambda V^{T}V\varLambda ^TD^T\rangle )\\&-tr(\langle U^{T}\rangle \langle U\rangle \langle D\varLambda V^{T}\rangle \langle V\varLambda ^T D^T\rangle )\\&+|\langle B\circ B\rangle \circ \langle E\circ E\rangle |_1\\&\quad -tr((\langle B\rangle \circ \langle E\rangle )^T(\langle B\rangle \circ \langle E\rangle )), \end{aligned}$$

$\langle B\circ B\rangle =\varSigma ^B+\langle B\rangle \circ \langle B\rangle$, $\varSigma ^B = ($Var$(b_{ij}))$, $\langle E\circ E\rangle = \varSigma ^E+\langle E\rangle \circ \langle E\rangle$, and $\varSigma ^E = ($diag$(\varSigma _{e_{\cdot j}})).$

In summary, the VB procedure approximates the posterior distributions of the unknowns iteratively and the whole algorithm is outlined in Algorithm 1.

5 Discussion and MCMC-Based Bayesian Inference

5.1 The Connection Between APSV-BRPCA and Deterministic Approach

There exists a connection between the proposed APSV-BRPCA and WNNM-RPCA [6, 11, 17]. To see the connection clearly, we show the negative logarithm of the full posterior density function of the proposed APSV-BRPCA model as follows:

$$\begin{aligned}&-\log p(\varTheta |Y,\mathscr {H})\nonumber \\&\quad =\parallel \varLambda \parallel _{\omega ,*}-\log [g_{BB}(D;\mathscr {H})]+\frac{m}{2}\sum _{j=1}^R\Vert \mathbf {u}_{\cdot ,j}\Vert _2^2+\frac{1}{2}\sum _{i=1}^n \Vert \mathbf {v}_{i,\cdot }\Vert _2^2+\frac{\tau }{2}\Vert E\Vert _F^2\nonumber \\&\qquad -\log [g_{BB}(B;\mathscr {H})]+\frac{\beta }{2}\Vert Y-L-S\Vert _F^2\nonumber \\&\qquad -\log [\mathrm{Gamma}(\gamma |\mathscr {H})\mathrm{Gamma}(\tau |\mathscr {H})\mathrm{Gamma}(\beta |\mathscr {H})] + \text {C}, \end{aligned}$$

(28)

where C denotes a constant, $\varTheta$ is the set of all model parameters, $g_{BB}(\cdot |\mathscr {H})$ is the Beta-Bernoulli prior in (9) or (11), and $\mathscr {H}$ represents the set of all model hyperparameters.

For the low-rank component, rather than employing a constraint on Frobenius matrix norm to impose the sparseness of the singular values by using a Gaussian prior, we employ an Exponent-Gamma prior to obtain a constraint on weight nuclear norm, together with a Beta-Bernoulli distribution to encourage the sparseness of the singular values (like [11]). Note that for the low-rank component, an exponent prior is imposed on the singular values so that a big weight for a small nonzero singular value is desired. The main difference between the proposed APSV-BRPCA model and the WNNM-RPCA model is that we use numerical methods to estimate the distribution of unknown parameters, while one effectively seeks a single solution to minimize a function in WNNM-RPCA.

5.2 Convergence Analysis

The convergence of the proposed algorithm can be transformed into the convergence of the variational Bayesian method because the proposed algorithm is derived based on the variational Bayesian method. The expression (16) of the optimal solution $q(\varTheta _{k})$ depends on the expectation of other factors $q(\varTheta _{j})$ for $j\ne k$. To obtain the maximum value of the lower bound (15), all the factors need to be circulated. One needs to initialize all the factors $q(\varTheta _{j})$ for conducting the variational inference. Then, using the current solution of all other factors, we can estimate each factor in turn with the updated value obtained in (16). Since the bound is convex for each of the factors $q(\varTheta _{j})$, convergence is guaranteed [2, 20].

5.3 MCMC-Based Bayesian Inference

The posterior density function can also be approximated using Gibbs sampler. In the Gibbs sampler, the Markov chain Monte Carlo (MCMC) analysis is implemented and the posterior distributions of model parameters are approximated by samples drawing from the corresponding conditional posterior distributions, respectively. The MCMC-based Bayesian inference method is summarized in Algorithm 2, where $\mathbf {y}_s$ represents the sth column in Y and $(a|-)$ represents random variable a given all the other random variables in the model, $\mathscr {N}(\mu ,\varSigma )_+$ represents a truncation normal distribution from 0.

5.4 Computational Complexity

In each iteration of the VB inference, the matrix inversion is required and leads to much computational cost. More specifically, to obtain the approximate posterior of each column $e_{\cdot j}$, one needs to calculate the inverses of nm-order matrices. The computational complexity is $n\mathscr {O}(m^3)$ in each iteration. In addition to the above computational cost, the rest posterior parameters can be rapidly computed. For the MCMC-based Bayesian inference, the computational complexity of each sampling is approximately the same as the VB method.

6 Experiments

In this section, we illustrate the recovery accuracy and efficiency of the proposed APSV-BRPCA algorithm compared with four state-of-the-art methods: augmented Lagrange multiplier method (ALM) [24], weight nuclear norm minimization for RPCA (WNNM-RPCA) [17], Bayesian robust principal component analysis (BRPCA) [11], and sparse Bayesian methods for low-rank matrix estimation (VBRPCA) [1]. All experiments are implemented in Matlab R2014b on a PC with 4.0 GHz CPU and 31.4 GB RAM.

6.1 Parameter Setting

In our experiments, very small values (e.g., $10^{-6}$) are assigned to the parameters $c_0,d_0,e_0,f_0,\theta _0,\eta _0,\alpha _0,\beta _0$, respectively. Such strategies can lead to broad hyperpriors. Next, we illustrate the choice of tuning parameters $a_0$ and $b_0$. In [17], an effective reweighted strategy is proposed to assign weights on different singular values by the following formula

$$\begin{aligned} \omega _k^l=\frac{C}{\sigma _k(L_l)+\varepsilon }, \end{aligned}$$

(29)

where $\sigma _k(L_l)$ is the kth singular value in the lth iteration and $\omega _k^l$ is the corresponding regularization parameter in the lth iteration, C is chosen as the square root of matrix size, i.e., $C=\sqrt{mn}$ and $\varepsilon$ is a small positive number to make the inequality $\varepsilon < \min (\sqrt{C}, \frac{C}{\sigma _1(Y)})$ hold. Comparing (29) with the expectation of the posterior of weight $\gamma _k$ in (22), we can see that the tuning parameters $a_0$ and $b_0$ correspond to the parameters C and $\varepsilon$, respectively. Hence, we let $a_0\in (0,\sqrt{mn}]$ and let $b_0\in (0,\min (\sqrt{C}, \frac{C}{\sigma _1(Y)})]$. We randomly generate a synthetic matrix of size $300 \times 300$ with rank $\mathbf {rank}(L)$. The low-rank component of the synthetic matrix consists of a product of two matrices generated from a standard Gaussian distribution. The sparse component consists of nonzero entries drawn uniformly in the range $[-100, 100]$ and located uniformly at random. We use notations $\rho _r = \mathbf {rank}(L)/N$ and $\rho _s = \Vert S\Vert _0/N^2$, where $N=300 and \rho _r,\rho _s\in \{0.05, 0.15, 0.25, 0.3\}$ represent the rank and the sparsity, respectively. The noiseless case and the noisy case with $\sigma ^2 = 10^{-3}$ are considered.

Fig. 2

The noiseless case: reconstruction errors of low-rank $\Vert L-{\hat{L}}\Vert _F/\Vert L\Vert _F$ for varying ranks and sparsity computed by APSV-BRPCA

Fig. 3

The noise case: reconstruction errors of low-rank $\Vert L-{\hat{L}}\Vert _F/\Vert L\Vert _F$ for varying ranks and sparsity computed by APSV-BRPCA

The experimental results with $a_0\in (0,40]$ and $b_0\in (0,7]$ are shown in Figs. 2 and 3. It can be seen that the preferable parameter $b_0$ can be obtained in the range [4, 7], and the parameter $a_0$ can be chosen in the range [1, 40]. The experiments of synthetic matrices of sizes $100 \times 100$, $500 \times 500$ and $1000 \times 1000$ show the same results. Meanwhile, the experiment results demonstrate that the tuning parameters $a_0$ and $b_0$ are robust for different ranks, sparsity and noise levels. Without loss of generality, we set the tuning parameters $a_0=10$ and $b_0=4$ in all experiments.

6.2 Synthetic Experiments

In synthetic experiments, we randomly generate two low-rank square matrices with sizes $200 \times 200$, $500 \times 500$ and ranks 5, 20, respectively. Each of these matrices is generated by the product of two matrices which obey a standard Gaussian distribution. The magnitudes of nonzero entries in S are drawn uniformly in the range $[-100, 100]$. The sparsity levels $\rho$ of different sparse matrices with sizes $200 \times 200$, $500 \times 500$ are 0.05 and 0.08, respectively. We introduce the following metrics to evaluate the recovery performance: the reconstruction errors of low-rank and sparse components, $\mathbf {rank}({\hat{X}})$, $||{\hat{S}}||_0$ (the number of nonzero elements). For synthetic matrices with sizes $200 \times 200$, the noiseless case and the noisy case with $\sigma ^2 = 10^{-2}$ are considered. The noise with variance $\sigma ^2 = 10^{-3}$ is added to synthetic matrices with size $500 \times 500$.

Experimental results are shown in Table 1. To avoid the random disturbance of Gaussian noise, the experiment results are calculated by averaging the results of 100 independent trials. From Table 1, it can be seen that WNNM-RPCA achieves minimal error among all algorithms in the noiseless case. However, its performance is not robust for noise and corrupted as the noise level increases. The Bayesian algorithms achieve greater robustness than deterministic approaches. The reason may be that the Bayesian approaches regard the noise as a random variable. In addition, the proposed APSV-BRPCA algorithm has the best performance compared with other algorithms in the noisy case.

Table 1 Reconstruction errors, estimated rank and the number of nonzero elements

We demonstrate the ability of APSV-BRPCA by varying ranks, sparsity and noise levels. In this experiment, synthetic matrices with size $100 \times 100$ are generated. For each triple tuple $(\rho _r,\rho _s,\sigma ^2)$, $\sigma ^2\in \{0, 10^{-4},10^{-3},10^{-2}\}$, $\rho _r$, and $\rho _s\in \{0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4\}$ represent the noise variance, the rank and the sparsity, respectively. We conduct ten random experiments. The following criterion proposed in [11] is employed to measure the successful reconstruction of L, i.e., $(\Vert L-{\hat{L}}\Vert _F/\Vert L\Vert _F)\le Th$, where Th is a threshold depending on the noise level. The noise standard deviations of different thresholds Th with magnitudes $10^{-4}, 5\times 10^{-3}, 10^{-2}, 10^{-1}$ are $\sigma ^2=0, 10^{-4}, 10^{-3}$ and $10^{-2}$, respectively.

Fig. 4

Fraction of successful recovery for varying ranks, sparsity, and noise levels, computed by ALM, WNNM-RPCA, VBRPCA, BRPCA and APSV-BRPCA. Given a tuple $(\rho _r,\rho _s,\sigma ^2)$, white represents that all the 10 trials are successfully recovered, and black means no trials is successfully recovered

Figure 4 depicts the fraction of successful recovery of different algorithms for each triple tuple. The experimental results show that the proposed APSV-BRPCA algorithm has more comprehensive ability than other methods in terms of recovery accuracy and robustness. As shown in Fig. 5, the MMSE demonstrates the effectiveness of the proposed algorithm.

Fig. 5

MMSE for rank equals 0.05 where MMSE $=\mathrm{mean}(\frac{||{\hat{Y}}-Y||_F}{||Y||_F})$ and varying sparsity and noise levels, computed by ALM, WNNM-RPCA, VBRPCA, BRPCA and APSV-BRPCA. Given a tuple $(0.2,\rho _s,\sigma ^2)$, color point represents that mean of the 10 trials

6.3 Video Example

In this section, we investigate the application of background subtraction with different methods. The objective of background subtraction is to reconstruct the static background and the moving foreground from the video sequence [11]. Background subtraction can be considered as a binary segmentation of video sequences, in which the video sequences consist of the invariant background and the time-varying foreground. A video stream can be modeled as the combination of low-rank and sparse components, since static backgrounds of different frames are the same, while moving foregrounds are relatively sparse. If we stack the video frames as columns of a matrix, the low-rank component represents the static background and the sparse component corresponds to the moving foreground. Under this assumption, we can use RPCA to reconstruct low-rank and sparse components from the video stream. A video surveillance with slow-changing foreground is considered for examining the performance of different algorithms.

The video sequence is sampled from a shopping center [11], which consists of 158 frames with resolution $144\times 192$. We stack the video sequence as an observed matrix of size $27648\times 158$. The noiseless case is shown in Fig. 6. It can be observed that the proposed algorithm and BRPCA can effectively distinguish the slow foreground and the static background and achieve better results than ALM and WNNM-RPCA. Furthermore, the Gaussian noise with mean 0 and variance 25 is added to the observed data and the result is shown in Fig. 7. It suggests that our approach gets satisfied results in discovering the low-rank background and sparse foreground from the observed matrix and shows that ALM algorithm, WNNM-RPCA algorithm and VBRPCA algorithm are sensitive to noise.

Fig. 6

Reconstruction of the background and the foreground. First row: original image; second row: reconstruction of the low-rank component (background); bottom row: reconstruction of the sparse component (foreground)

Fig. 7

Reconstruction of the background and the foreground under noisy observation. The additive white Gaussian noise has variance $\sigma ^2=25$. First row: original image; second row: reconstruction of the low-rank component (background); bottom row: reconstruction of the sparse component (foreground)

Fig. 8

The noise-free case: background standard deviation (first row) and error bars (second row) of the proposed APSV-BRPCA algorithm and BRPCA algorithm

Fig. 9

The noise case where the additive white Gaussian noise has variance 25 and mean 0: background standard deviation (first row) and error bars (second row) of the proposed APSV-BRPCA algorithm and BRPCA algorithm

To evaluate the reconstruction performance of different algorithms, we plot the background standard deviation and error bars for the noiseless case and the noisy case with $\sigma ^2 = 25$ in Figs. 8 and 9, respectively. For each pixel, the background standard deviation is defined as the standard deviation of the extracted background of the video sequence, and the error bars are calculated as the standard deviation of the original noiseless video sequence minus the summation of extracted background and foreground. From Fig. 8, we observe that the error bars of the proposed algorithm and BRPCA are similar; however, the extracted background via the proposed algorithm is more robust. In Fig. 9, it can be seen that, for most inferred pixels, the proposed algorithm presents more accurate entries of background standard deviation than BRPCA. At the same time, we can also observe that the proposed algorithm achieves the lowest error bars. It demonstrates the ability of our method in dealing with the real data.

7 Conclusion

In this paper, we propose a novel Bayesian RPCA model by introducing new penalty strategies on the singular values of the low-rank component. The key ingredient of the proposed method is the adaptive penalty on the singular values, which uses a more realistic low-rank prior model that goes beyond the simple low-rank prior. Specifically, in the proposed Bayesian RPCA model, an Exponent-Gamma framework is employed, which adaptively imposes weights on different singular values so that it potentially improves the flexibility of the exiting Bayesian models. The parameters can be estimated by variational Bayesian inference and MCMC-based Bayesian inference. Meanwhile, the proposed model is closely related to the deterministic models, such as the reweighted $\ell _{1}$ minimization. We systematically compare the recovery performance of different Bayesian and deterministic models to demonstrate the advantages of the proposed model. In comparison with the numerical experiment results of these models, we observe that the proposed Bayesian model has more comprehensive ability than other methods in noise cases. Moreover, the real case shows that the proposed Bayesian model achieves the lowest error bars and is more robust. These experimental evaluations with simulated and real data demonstrate the superiority of the proposed Bayesian model.

One main limitation of the proposed model in practical applications is that the measurement noise is assumed to be Gaussian distribution. In the real cases, the noises in measurements are complex and may copy with non-Gaussian distributions. In the future research, we shall focus on the non-Gaussian noises. Besides, to achieve faster convergence and better reconstruction performance, some optimal algorithms, such as [31] and [33], are going to be used to select the optimal values of the parameters in the future research.