1 Introduction

Noise reduction is an indispensable part of image processing applications. It aims to preserve as much detailed information and important features of the image as possible while effectively attenuating the noise [33, 39, 48]. Specifically, in camera systems, different types of noise can emerge, including thermal noise, quantization noise, or photon noise. Thermal noise is produced in analog circuits and has a zero-mean Gaussian distribution and is the most common noise encountered in different applications. In the present paper, the additive white Gaussian noise is considered as the noise model.

Noise removal can be performed in both transform and pixel domains [5, 31]. Spatial denoising methods such as local and non-local algorithms use the similarity between pixels and patches in an image, and the transform domain-based methods exploit the similarities among the transform coefficients. In these methods, the smaller coefficients are the high-frequency part of the image, which is related to noise and image details. By adjusting these small coefficients of the noisy image, the reconstructed image will have less noise.

In recent decades, there has been a fair amount of research on image denoising in the wavelet domain, mainly because of its localized properties in time and frequency domains as well as its capability in retaining the detailed features of the images [7, 8, 41]. In particular, the discrete wavelet transform (DWT) has been utilized in various applications including image analysis and image denoising. Nevertheless, it suffers from shift variance [2, 13, 21, 28, 29, 40], that is small shifts in the input signal will cause substantial variations in the distribution of wavelet coefficients’ energy. In recent years, the dual-tree complex wavelet transform (DT-CWT) has been proposed, which offers a more compact representation and near shift invariance property and improved the directional selectivity by six directional sub-bands per scale [40]. This transform has been used in various techniques [3, 14, 25] wherein the real and imaginary components of the complex-valued sub-band coefficients are used separately. In fact, in these techniques, the relationship between the complex coefficients (real and imaginary parts) is altered without any regard to the original phase relationship; this will introduce undesirable phases into the denoised coefficients. However, the phase has been recognized as being vital in carrying important visual information [16]. Some researchers have proposed methods to overcome this disadvantage. The authors in [28, 29] have used DT-CWT together with de-rotated phase to improve the denoising results by exploiting correlations between coefficients near edges. Rakvongthai et al. [38] proposed complex Gaussian scale mixtures (CGSM) as an extension of the Gaussian scale mixtures denoising algorithm, to use complex coefficients. The authors in [24] have modeled the distribution of complex wavelet coefficient magnitudes using various forms of pdfs for characterization and retrieval applications.

Wavelet thresholding is an effective method for image denoising, in which a wavelet transform is implemented on the image that is corrupted by the additive white Gaussian noise (AWGN). Then, each coefficient is being compared with the selected threshold, and in case it is smaller than the threshold, the coefficient is set to zero, and otherwise, it is either kept (i.e., hard thresholding) or modified (i.e., soft thresholding). Visueshrink [20, 39], Sureshrink [10], and Bayesshrink [5] are algorithms which use the thresholding method for denoising [32]. Recently, some researchers have developed statistical wavelet-based image denoising as a fundamental tool in image processing, which is still an expanding area of research. In the statistical approach, the idea is to estimate the clean coefficients from noisy data with Bayesian estimation techniques such as MAP estimator [45]. When MAP estimator is used for denoising, the prior distributions for the original image and noise will have a considerable effect on the denoising process’s performance [45].

Since natural images contain smooth areas interspersed with occasional sharp transmissions (e.g., edges), the wavelet transform of the images is sparse. Therefore, the marginal distributions of clean coefficients are significantly non-Gaussian. They are heavy-tailed distributions and have a large peak around zero [30]. Various probability distribution functions (pdfs) were proposed on modeling the clean wavelet coefficients, e.g., Laplace, Cauchy, generalized Gaussian, α-stable, and Bessel k form distributions [4, 26, 27, 35, 37, 47].

Scale mixtures of Gaussian distribution are heavy-tailed distributions which have recently been used in different machine learning and signal processing problems. They can be expressed as scale mixtures of normal distribution and are sufficiently flexible to appropriately model the wavelet coefficients of the images [46]. In Sect. 3, the scale mixtures of Gaussian distribution are presented in detail.

Wavelet coefficients have a dependency on one another [6, 34]; therefore, many of recent works such as bivariate [2, 8, 42], trivariate [6, 48], and multivariate [34, 39] models take into account the coefficients dependency to achieve a proper estimate. All these studies imply that considering different information such as neighbors is helpful for preserving the details and removing the noise in image denoising. In [16], the authors propose the MAP estimator using a bivariate Rayleigh–Cauchy distribution for modeling the magnitude of the noise-free coefficients. The authors in [16] have used the undecimated dual-tree complex wavelet transform [15], that is, an undecimated form of DT-CWT, which offers exact translational invariance property through removing the down-sampling of filter outputs together with the up-sampling of the complex filter pairs of DT-CWT. We contribute our work specifically to model the magnitude of coefficients using bivariate Rayleigh–Student’s t distribution and bivariate Rayleigh–Laplace distribution, which are scale mixtures of bivariate Rayleigh distribution. To the best of our knowledge, these distributions were introduced in this paper for the first time. This paper is focused on emphasizing the advantages of using Rayleigh–Student’s t and Rayleigh–Laplace distributions over the Rayleigh–Cauchy distribution that is proposed in [16]. Also, we used the dual-tree complex wavelet transform because it is less time-consuming. We also contribute our work to estimating the necessary parameters of the bivariate distributions in a locally adaptive way to improve the denoising results by using the correlation between the amplitudes of neighbor coefficients. The simulation results conducted in this paper confirmed that our denoising algorithm using the bivariate Rayleigh–Student’s t distribution and bivariate Rayleigh–Laplace distribution as the prior density of the magnitude of coefficients outperformed the denoising algorithm proposed in [16] (which uses the bivariate Rayleigh–Cauchy distribution as the prior density), both in PSNR and in MSSIM metrics.

The remainder of the paper is structured as follows. In Sect. 2, the denoising algorithm is presented. The scale mixtures of Gaussian distribution and scale mixtures of Rayleigh distribution are presented in Sect. 3. The MAP estimator and the hyper-parameter estimations of the proposed distributions are described in Sect. 4. Comparison of different denoising algorithms and the simulation results is presented in Sect. 5, and finally, the paper is concluded in Sect. 6.

2 The Denoising Algorithm

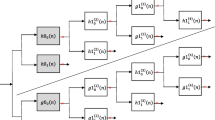
Similar to several reported works in the field of image denoising, our image denoising model uses three levels: (a) decomposing the noisy image into sub-bands at different orientations and scales through the multi-scale transform, (b) denoising each high-pass sub-band, and (c) applying the inverse implemented transform to get a noise-free image. The denoising algorithm is depicted in Fig. 1. The block that is depicted with dash-line includes our proposed algorithm and will be described in detail in the following sections. In fact, in our work, we propose to use two new distributions, bivariate Rayleigh–Student’s t distribution and bivariate Rayleigh–Laplace distribution, as the probability distribution function of the magnitude of noise-free coefficients.

Fig. 1
figure 1

Denoising block diagram

Full size image

3 Scale Mixtures of Rayleigh Distribution

It has been observed that the marginal distributions of the wavelet coefficient are heavy-tailed and have a large peak at zero [30]. Various pdfs were proposed on modeling clean wavelet coefficients, among which Student’s t, Laplace, and Cauchy distributions have modeled the coefficients’ distributions more accurately because of their heavy-tailed characteristics [1, 3, 12, 35, 37]. These techniques have used the real and imaginary components of the complex-valued sub-band coefficients separately, so the relationship between the complex coefficients (real and imaginary parts) is altered without any regard to the original phase relationship; this will introduce undesirable phases into the denoised coefficients. Since the phase information has been recognized as being vital in carrying important visual information [16], we modeled the magnitude of coefficients.

In addition to the heavy-tailed marginal behavior, many of the recent works show that, even when wavelet coefficients and their neighbors are second-order de-correlated, they exhibit striking dependencies [7, 34]. In the present paper, by using bivariate Rayleigh–Student’s t distribution (that is a generalization of the Rayleigh–Cauchy distribution) and bivariate Rayleigh–Laplace distribution, which are scale mixtures of bivariate Rayleigh distribution, we can exploit the dependency between the wavelet coefficients and their parents to improve the denoising results. In the following subsections, we will describe the scale mixtures of Gaussian distribution and scale mixtures of Rayleigh distribution, respectively.

3.1 Scale Mixtures of Multivariate Gaussian Distribution

A p-dimensional random vector \( x \) is said to have a multivariate Gaussian (or normal) distribution with mean vector \( \mu \in R^{p} \) and positive definite covariance matrix, \( \varSigma \in R^{p \times p} \), if its pdf is given by

$$ \varphi_{p} \left( {x;\mu ,\varSigma } \right) = \frac{\text{1}}{{\left( {2\pi } \right)^{p/2} \left| \varSigma \right|^{1/2} }}\exp \left( { - \frac{1}{2}\left( {x - \mu } \right)^{T} \varSigma^{ - 1} \left( {x - \mu } \right)} \right),\quad x \in R^{p} . $$
(1)

We denote as \( x \sim N_{p} \left( {\mu ,\varSigma } \right) \). The multivariate scale mixtures of Gaussian distribution are alternatives to the multivariate Gaussian in robustness studies for data with outliers and/or heavy tails. A p-dimensional random vector \( x \) is said to have a multivariate scale mixture of Gaussian distribution if it has the representation

$$ x\mathop = \limits^{d} \mu + {\text{u}}^{ - 1/2} z, $$
(2)

where \( \mathop = \limits^{d} \) denotes equality in distribution and \( z \sim N_{p} \left( {{\mathbf{0}}_{p} ,{\varvec{\Sigma}}} \right) \), where \( {\mathbf{0}}_{p} \) denotes the vector of zeros of dimension \( p \), independent from \( u \), and \( u \) is an arbitrary positive random variable with cumulative distribution function (CDF) \( H(.;\varvec{\upsilon}) \). The CDF \( H(.;\varvec{\upsilon}) \) is the scale mixing distribution indexed by (the possibly multivariate) vector \( \varvec{\upsilon} \).

In the cases that \( u \) has a pdf, we denote it by \( h(.;\varvec{\upsilon}) \). We denote \( x \) in (2) by \( x \sim SMN_{p} \left( {\mu ,{\mathbf{\varSigma ,}}\upsilon } \right). \) Because the conditional distribution of \( x \), in (2), given \( u \) is \( N_{p} \left( {\mu ,u^{ - 1} {\varvec{\Sigma}}} \right) \), the marginal pdf of \( x \) is given by

$$ \begin{aligned} f_{{{\text{SMN}}_{p} }} \left( {\varvec{x};\varvec{\mu},\varvec{\varSigma},\varvec{\upsilon}} \right) & = \int_{0}^{\infty } {\varphi_{p} \left( {\varvec{x};\varvec{\mu},\varvec{\varSigma}u^{ - 1} } \right)\,{\text{d}}H(u;\varvec{\upsilon})} \\ & = \int_{0}^{\infty } {\varphi_{p} \left( {\varvec{x};\varvec{\mu},\varvec{\varSigma}u^{ - 1} } \right)h(u;\varvec{\upsilon})} \,{\text{d}}u. \\ \end{aligned} $$
(3)

The multivariate Student’s t, multivariate Cauchy, and multivariate Laplace distributions are some special cases of multivariate scale mixtures of Gaussian distribution. In the following, we review these distributions in more detail.

3.1.1 Multivariate Student’s t Distribution

The multivariate Student’s t distribution with location vector \( \mu \in R^{p} \) and positive definite dispersion matrix \( \varSigma \in R^{p \times p} \), and \( \upsilon > 0 \) degrees of freedom can be generated by (2), where \( u \) follows a gamma distribution with scale parameter \( \upsilon /2 \) and shape parameter \( \upsilon /2 \) (denoted by \( u \sim G\left( {\frac{\upsilon }{2},\frac{\upsilon }{2}} \right) \)). In this case, we denote \( x \sim t_{p} \left( {\mu ,{\mathbf{\varSigma ,}}\upsilon } \right). \) From (3), the pdf of \( x \) can be obtained as [22]

$$ t_{p} (\varvec{x ;\mu },\varvec{\varSigma},\upsilon ) = \frac{{\varGamma \left( {\frac{\upsilon + p}{2}} \right)}}{{\varGamma \left( {\frac{\upsilon }{2}} \right)\left( {\pi \upsilon } \right)^{p/2} \left| {\varvec{\Sigma}} \right|^{1/2} }}\left( {1 + \frac{{\left( {\varvec{x} -\varvec{\mu}} \right)^{T} {\varvec{\Sigma}}^{ - 1} \left( {\varvec{x} -\varvec{\mu}} \right)}}{\upsilon }} \right)^{{ - \left( {\frac{\upsilon + p}{2}} \right)}} ,\,\,x \in R^{p} , $$
(4)

where \( \varGamma \left( . \right) \) denotes the gamma function. Furthermore, from (2) the mean vector and covariance matrix \( x \sim t_{p} \left( {\mu ,{\mathbf{\varSigma ,}}\upsilon } \right) \) are given by

$$ E(\varvec{x}) =\varvec{\mu}\,\,\upsilon > \text{1 }, $$
(5)
$$ cov\left( \varvec{x} \right) = {\varvec{\Sigma}}\frac{\upsilon }{\upsilon - 2},\upsilon > 2. $$
(6)

3.1.2 Multivariate Cauchy Distribution

The Cauchy distribution is derived from Eq. (1) by taking \( u \) to be distributed as gamma distribution with shape parameter \( 1/2 \) and scale parameter \( 1/2 \). In fact, the Student’s t distribution is a generalization of Cauchy distribution. Therefore, the multivariate form of Cauchy distributions can be derived from multivariate Student’s t distributions by setting the parameter \( \upsilon = 1 \). The multivariate Cauchy distribution with location vector \( \mu \in R^{p} \) and positive definite dispersion matrix \( {\varvec{\Sigma}} \) is denoted by \( x \sim C_{p} \left( {\mu ,{\varvec{\Sigma}}} \right) \), and can be obtained as

$$ C_{p} (\varvec{x};\varvec{\mu},\varvec{\varSigma}) = \frac{{\varGamma \left( {\frac{1 + p}{2}} \right)}}{{\varGamma \left( {\frac{1}{2}} \right)\left( \pi \right)^{p/2} \left| {\varvec{\Sigma}} \right|^{1/2} }}\left( {1 + \left( {\varvec{x} -\varvec{\mu}} \right)^{T} {\varvec{\Sigma}}^{ - 1} \left( {\varvec{x} -\varvec{\mu}} \right)} \right)^{{ - \left( {\frac{1 + p}{2}} \right)}} ,\,\,\,x \in R^{p} \text{.} $$
(7)

3.1.3 Multivariate Laplace Distribution

The Laplace distribution is derived from Eq. (2) by taking \( u \) to be distributed as inverse gamma distribution with shape parameter 1 and scale parameter 1/2 (denoted by \( u \sim IG\left( {1,\frac{1}{2}} \right) \)) [23]. The multivariate Laplace distribution with location vector \( \mu \in R^{p} \) and positive definite dispersion matrix \( {\varvec{\Sigma}} \) is denoted by \( x \sim L_{p} \left( {\mu ,{\varvec{\Sigma}}} \right) \) and can be obtained as [23]

$$ L_{p} (\varvec{x};\varvec{\mu},\varvec{\varSigma}) = \frac{1}{{\left( {2\pi } \right)^{{\frac{p}{2}}} \left| {\varvec{\Sigma}} \right|^{1/2} }}\left( {\text{(}\varvec{x} -\varvec{\mu}\text{)}^{T} {\varvec{\Sigma}}^{ - 1} \text{(}\varvec{x} -\varvec{\mu}\text{)}} \right)^{{\frac{\upsilon }{2}}} K_{\upsilon } \left( {\sqrt {\text{(}\varvec{x} -\varvec{\mu}\text{)}^{T} {\varvec{\Sigma}}^{ - 1} \text{(}\varvec{x} -\varvec{\mu}\text{)}} } \right),x \in R^{p} , $$
(8)

where \( \upsilon = \left( {2 - p} \right)/2 \), and \( K \) is the modified Bessel function of the second kind.

3.2 Scale Mixtures of Rayleigh Distribution

A univariate random variable \( r \) is said to have Rayleigh distribution with scale parameter \( \sigma > 0 \), denoted by \( r \sim R\left( \sigma \right) \), if its pdf is given by

$$ f_{r} \left( {r;\sigma } \right) = \frac{r}{{\sigma^{2} }}\exp \left( { - \frac{{r^{2} }}{{2\sigma^{2} }}} \right),r > 0. $$
(9)

It is clear that \( r \) has the representation

$$ r\mathop = \limits^{d} \sigma \sqrt {x_{1}^{2} + x_{2}^{2} } , $$
(10)

where \( \left( {x_{1} ,x_{2} } \right)^{T} \sim N_{2} \left( {{\mathbf{0}}_{2} ,{\mathbf{I}}_{2} } \right), \) and \( {\mathbf{I}}_{2} \) denotes the identity matrix of dimension 2. Equivalently, \( x_{1} \) and \( x_{2} \) are independent identically distributed (iid) from the univariate standard normal distribution, \( N\left( {0,1} \right). \)

Definition 1

A univariate random variable \( r_{\text{SMN}} \) is said to have a scale mixture of Rayleigh distribution if it follows the representation

$$ r_{\text{SMN}} \mathop = \limits^{d} u^{ - 1/2} r, $$
(11)

where \( r \sim R(\sigma ). \) We denote this as \( r_{\text{SMN}} \sim {\text{RSMN}}(\sigma ,\varvec{\upsilon}). \)

From (11), we can easily obtain the following integration form for pdf of \( r_{\text{SMN}} \)

$$ f_{\text{RSMN}} \left( {r;\sigma ,\varvec{\upsilon}} \right) = \int_{0}^{\infty } {\frac{r}{{\sigma^{2} }}u\exp \left( { - \frac{{r^{2} u}}{{2\sigma^{2} }}} \right)} h\left( {u;\varvec{\upsilon}} \right){\text{d}}u. $$
(12)

Lemma 1

If \( r_{\text{SMN}} \sim {\text{RSMN}}(\sigma ,\varvec{\upsilon}), \) then we have

$$ r_{\text{SMN}} \mathop = \limits^{d} \sigma \sqrt {x_{1}^{2} + x_{2}^{2} } , $$
(13)

where

$$ \left( {x_{1} ,x_{2} } \right)^{T} \sim {\text{SMN}}_{2} \left( {{\mathbf{0}}_{2} ,{\mathbf{I}}_{2} ,\varvec{\upsilon}} \right)\text{.} $$
(14)

3.2.1 Rayleigh–Student’s t Distribution

The univariate Rayleigh–Student’s t distribution with positive dispersion parameter \( \sigma > 0 \), and \( \upsilon > 0 \) degrees of freedom, can be generated by (11), where \( u \sim G\left( {\frac{\upsilon }{2},\frac{\upsilon }{2}} \right) \). In this case, we denote \( x \sim rt\left( {\sigma {\mathbf{,}}\upsilon } \right). \) From (12), the pdf of \( x \) can be obtained as:

$$ f_{{rt_{\text{SMN}} }} (r;\sigma ,\upsilon ) = \upsilon^{{\frac{\upsilon + 2}{2}}} \frac{{r\sigma^{\upsilon } }}{{(\upsilon \sigma^{2} + r^{2} )^{{\frac{\upsilon + 2}{2}}} }}. $$
(15)

For the derivation of Eq. (15), see “Appendix 1.”

From Eq. (15), it can be concluded that when degrees of freedom \( \upsilon = 1 \), we will have the univariate Cauchy–Rayleigh distribution as the authors have derived in [16]:

$$ f_{{rC_{\text{SMN}} }} (r;\sigma ) = \frac{r\sigma }{{(\sigma^{2} + r^{2} )^{{\frac{3}{2}}} }}. $$
(16)

3.2.2 Rayleigh–Laplace Distribution

The univariate Rayleigh–Laplace distribution with positive dispersion parameter \( \sigma > 0 \) can be generated by (11), where \( u \sim IG\left( {1,\frac{1}{2}} \right) \). In this case, we denote \( x \sim rL\left( \sigma \right). \) From (12), the pdf of \( x \) can be obtained as:

$$ f_{{rL_{\text{SMN}} }} (r;\sigma ) = \frac{r}{{\sigma^{2} }}K_{0} \left( {\frac{r}{\sigma }} \right). $$
(17)

For the derivation of Eq. (17), see “Appendix 1.”

3.3 Scale Mixtures of Bivariate Rayleigh Distribution

Let \( r_{1} \sim R(\sigma ) \) and \( r_{2} \sim R(\sigma ) \) are uncorrelated variables, for \( \sigma > 0 \). Then, we have the following definition.

Definition 2

A bivariate random variable \( \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \) is said to have a scale mixture of bivariate Rayleigh distribution if it follows the representation

$$ \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \mathop = \limits^{d} u^{ - 1/2} \left( {r_{1} ,r_{2} } \right)^{T} , $$
(18)

and we denote this as \( \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \sim {\text{BRSMN}}\left( {\sigma ,\varvec{\upsilon}} \right) \).From (9) and (18), we can obtain the following integration form for the pdf of \( \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \)

$$ f_{\text{BRSMN}} \left( {r_{1} ,r_{2} ;\sigma ,\varvec{\upsilon}} \right) = \frac{{r_{1} r_{2} }}{{\left( \sigma \right)^{4} }}\int_{0}^{\infty } {u^{2} \exp \left( { - \frac{1}{2}\left( {\frac{{r_{1}^{2} + r_{2}^{2} }}{{\sigma^{2} }}} \right)u} \right)} h\left( {u;\varvec{\upsilon}} \right){\text{d}}u. $$
(19)

Lemma 2

If \( \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \sim {\text{BRSMN}}\left( {\sigma ,\varvec{\upsilon}} \right) \), then we have

$$ \left( {r_{{ 1 {\text{SMN}}}} ,r_{{ 2 {\text{SMN}}}} } \right)^{T} \mathop = \limits^{d} \left( {\sigma \sqrt {x_{11}^{2} + x_{12}^{2} } ,\sigma \sqrt {x_{21}^{2} + x_{22}^{2} } } \right)^{T} , $$
(20)

where \( \left( {x_{11} ,x_{12} ,x_{21} ,x_{22} } \right)^{T} \sim {\text{SMN}}_{4} \left( {{\mathbf{0}}_{4} ,{\mathbf{I}}_{4} ,\varvec{\upsilon}} \right) \).

3.3.1 Bivariate Rayleigh–Student’s t Distribution

In the special case when in (18), \( u \sim G\left( {\frac{\upsilon }{2},\frac{\upsilon }{2}} \right),\text{ }\upsilon > 0 \), we obtain a bivariate Rayleigh–Student’s t distribution, denoted by \( \left( {r_{1t} ,r_{2t} } \right)^{T} \sim {\text{BRt}}\left( {\sigma ,\upsilon } \right) \). In this case, from (19), the pdf of \( \left( {r_{1t} ,r_{2t} } \right)^{T} \) can be obtained as:

$$ f_{\text{BRt}} \left( {r_{1} ,r_{2} ;\sigma ,\upsilon } \right) = \frac{{\left( {\upsilon + 2} \right)r_{1} r_{2} }}{{\upsilon \left( \sigma \right)^{4} }}\left( {1 + \frac{{r_{1}^{2} + r_{2}^{2} }}{{\sigma^{2} \upsilon }}} \right)^{{ - \left( {\frac{\upsilon + 4}{2}} \right)}} \text{,}\quad r_{1} > 0,r_{2} > 0. $$
(21)

For the derivation of Eq. (21), see “Appendix 2.”

Corollary 1

Let \( \left( {r_{1t} ,r_{2t} } \right)^{T} \sim {\text{BRt}}\left( {\sigma ,\upsilon } \right) \). Then,

  1. 1.

    For \( i = 1,2 \), \( r_{it} \sim Rt\left( {\sigma ,\upsilon } \right). \)

  2. 2.

    We have

$$ \left( {r_{1t} ,r_{2t} } \right)^{T} \mathop = \limits^{d} \left( {\sigma \sqrt {x_{11}^{2} + x_{12}^{2} } ,\sigma \sqrt {x_{21}^{2} + x_{22}^{2} } } \right)^{T} , $$
(22)

where \( \left( {x_{11} ,x_{12} ,x_{21} ,x_{22} } \right)^{T} \sim t_{4} \left( {{\mathbf{0}}_{4} ,{\mathbf{I}}_{4} ,\upsilon } \right) \).

From Eq. (22), it can be concluded that when degrees of freedom \( \upsilon = 1 \), we will have the bivariate Rayleigh–Cauchy distribution as the authors have derived in [16]:

$$ f_{\text{BRC}} (r_{1} ,r_{2} ,\sigma ) = \frac{{3\sigma r_{1} r_{2} }}{{\left( {\sigma^{2} + r_{1}^{2} + r_{2}^{2} } \right)^{{\frac{5}{2}}} }}\text{.} $$
(23)

3.3.2 Bivariate Rayleigh–Laplace Distribution

In the special case when in (18) \( u \sim IG\left( {1,\frac{1}{2}} \right) \), we obtain a bivariate Rayleigh–Laplace distribution, denoted by \( \left( {r_{1l} ,r_{2l} } \right)^{T} \sim {\text{BRL}}\left( \sigma \right) \). In this case, from (19), the pdf of \( \left( {r_{1l} ,r_{2l} } \right)^{T} \) can be obtained as:

$$ f_{\text{BRL}} \left( {r_{1} ,r_{2} ;\sigma } \right) = \frac{{r_{1} r_{2} }}{{\left( \sigma \right)^{4} }}\frac{{K_{1} \left( {\sqrt {\frac{{r_{1}^{2} + r_{2}^{2} }}{{\sigma^{2} }}} } \right)}}{{\left( {\frac{{r_{1}^{2} + r_{2}^{2} }}{{\sigma^{2} }}} \right)^{1/2} }}\text{,}\quad r_{1} > 0,\,\,r_{2} > 0. $$
(24)

For the derivation of Eq. (24), see “Appendix 2.”

Corollary 2

Let \( \left( {r_{1l} ,r_{2l} } \right)^{T} \sim {\text{BRL}}\left( \sigma \right) \). Then,

  1. 1.

    For \( i = 1,2 \), \( r_{il} \sim {\text{RL}}\left( \sigma \right). \)

  2. 2.

    We have

$$ \left( {r_{1l} ,r_{2l} } \right)^{T} \mathop = \limits^{d} \left( {\sigma \sqrt {x_{11}^{2} + x_{12}^{2} } ,\sigma \sqrt {x_{21}^{2} + x_{22}^{2} } } \right)^{T} , $$
(25)

where \( \left( {x_{11} ,x_{12} ,x_{21} ,x_{22} } \right)^{T} \sim l_{4} \left( {{\mathbf{0}}_{4} ,{\mathbf{I}}_{4} } \right) \).

4 Statistical Modeling of DT-CWT Wavelet Coefficient Magnitudes

We consider the case of image denoising corrupted by additive white Gaussian noise:

$$ G = D + E, $$
(26)

where \( G \), \( D \), and \( E \) are the noisy image, the original image, and independent white Gaussian noise, respectively. Let \( Y = {\mathcal{W}}G \), \( X = {\mathcal{W}}D \), \( N = {\mathcal{W}}E \), where \( {\mathcal{W}} \) represents the two-dimensional dual-tree complex wavelet transform. By applying the transform, the noisy image will be decomposed into \( j = 1,2, \ldots ,J \) scales and \( d = 1,2, \ldots ,D \) directional sub-bands, so we have:

$$ y_{m,l}^{d,j} = x_{m,l}^{d,j} + n_{m,l}^{d,j} , $$
(27)

where \( y_{m,l}^{d,j} \) is the coefficient of the noisy image at orientation \( d \), scale \( j \) and location \( \left( {m,l} \right) \), and in a similar way, for \( x_{m,l}^{d,j} \) and \( n_{m,l}^{d,j} \) for original image and noise, respectively.

The denoising algorithm would be applied to all sub-bands (except for the low-pass sub-band) independently. For the sake of simplicity, the subscript and indices have been dropped through the present paper.

In order to obtain a proper estimate via using the influence of the parent coefficient (i.e., the wavelet coefficient at the same spatial position, but at the next coarser scale), the bivariate model was applied; thus, for each coefficient and its parent we have:

$$ y = x + n $$
(28)

where \( \varvec{y} = (y_{1} ,y_{2} )^{T} \) is a vector of the noisy coefficients in which the elements \( y_{1} \) and \( y_{2} \) are the coefficient and parent coefficient, respectively. The corresponding vector \( \varvec{x} \) and \( n \) can be similarly defined for the noise-free image and noise term, respectively.

4.1 Probability Distribution Function for the Magnitude of Free-Noise Coefficients

In this paper, we model the magnitude of coefficients using bivariate Rayleigh–Student’s t distribution, bivariate Rayleigh–Cauchy distribution, and bivariate Rayleigh–Laplace- distribution using Eqs. (21), (23), and (24), respectively.

4.2 Hyper-parameter Estimation

4.2.1 Parameter Estimation of Student’s t Distribution

The standard deviation of noise \( \sigma_{n} \) could be estimated using a robust median estimator by taking the median absolute deviation (MAD) of the coefficients at the first level, \( y_{1} \), of the DT-CWT decomposition as follows [47]:

$$ \hat{\sigma }_{n} = \frac{{MAD\left( {y_{1} } \right)}}{0.6745}. $$
(29)

Variance and kurtosis of Student’s t distribution are:

$$ {\text{var}}\left( x \right) = \sigma^{2} \frac{\upsilon }{\upsilon - 2},\upsilon > 2, $$
(30)
$$ {\text{kurtosis}}\left( x \right) = \frac{6}{\upsilon - 4} + 3. $$
(31)

Kurtosis is a measure of the tailedness of the probability distribution of a random variable. Kurtosis is a descriptor of the shape of a probability distribution which is related to the tails of the distribution. It is common to compare the kurtosis of a distribution with the kurtosis of the normal distribution. Distributions with kurtosis greater than the kurtosis of the normal distribution are regarded as leptokurtic, which have tails that asymptotically approach zero more slowly than a Gaussian distribution.

The parameter \( \upsilon \) of Student’s t distribution can be estimated using the second- and fourth-order cumulants \( k_{2} \) and \( k_{4} \) of \( x \) as follows (see “Appendix 3”):

$$ \text{var}\left( x \right) = k_{2} , $$
(32)
$$ \text{kurtosis}\left( x \right) = \frac{{k_{4} }}{{k_{2}^{2} }} + 3. $$
(33)

To estimate \( k_{2} \) and \( k_{4} \), we used \( k \) statistic unbiased estimator, which has minimum variance among all other unbiased estimators [11, 44]:

$$ \hat{k}_{2} = \frac{n}{n - 1}\hat{M}_{2} , $$
(34)
$$ \hat{k}_{4} = \frac{{n^{2} \left( {\left( {n + 1} \right)\hat{M}_{4} - 3\left( {n - 1} \right)\hat{M}_{2}^{2} } \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}, $$
(35)

where \( n \) is the number of samples and \( M_{2} \) and \( M_{4} \) are the second and fourth sample central moments, respectively. When two or more random variables are statistically independent, the nth-order cumulant of their sum is equal to the sum of their nth-order cumulants. Also, the third- and higher-order cumulants of a normal distribution are zero, and it is the only distribution with this property. Therefore, we have:

$$ k_{2,y} = \sigma_{y}^{2} = \text{var}(x) + \sigma_{n}^{2} . $$
(36)

Finally, using Eqs. (31), (33), and (36), for Student’s t distribution, we can drive the following estimation of \( \upsilon \):

$$ \hat{\upsilon } = \frac{{6\left( {\hat{k}_{2} - \hat{\sigma }_{n}^{2} } \right)^{2} }}{{\hat{k}_{4} }} + 4. $$
(37)

For estimating the parameter \( \sigma \), by using Eqs. (30), (32), and (36), we have:

$$ \hat{\sigma }^{2} = \left\{ {\begin{array}{*{20}l} {(\hat{\sigma }_{y}^{2} - \hat{\sigma }_{n}^{2} )\frac{{\hat{\upsilon } - 2}}{{\hat{\upsilon }}}} \hfill & {\quad \text{if}\quad \hat{\sigma }_{y}^{2} \ge \hat{\sigma }_{n}^{2} } \hfill \\ 0 \hfill & {\quad \text{otherwise}} \hfill \\ \end{array} ,} \right. $$
(38)

where \( \hat{\sigma }_{y}^{2} \) is computed empirically by:

$$ \hat{\sigma }_{y}^{2} = \frac{1}{M}\sum\limits_{{y_{i} \in R}} {y_{i}^{2} } , $$
(39)

where \( M \) is the size of neighborhood \( R \).

Estimation of the parameter \( \sigma \) of wavelet coefficients based on a local window will lead to a more robust estimation. In fact, because of the locality property of wavelet transform, if a particular wavelet transform is small/large, then the spatial adjacent coefficients are also very likely small/large.

4.2.2 Parameter Estimation of Cauchy Distribution

From Eq. (28), the pdf of observed coefficients \( y \) can be considered as the convolution of the signal \( x \) and noise \( n \); therefore, the characteristic function of \( y \) is the product of characteristic functions of \( x \) and \( n \)

$$ \varPhi_{y} (\omega ) = \exp ( - \,\sigma \left| \omega \right|) \cdot \exp \left( { - \frac{{\sigma_{n}^{2} }}{2}\left| \omega \right|^{2} } \right). $$
(40)

This leads to

$$ \hat{\sigma } = \frac{{ - \log \varPhi_{y}^{2} \left( \omega \right) - \hat{\sigma }_{n}^{2} \left| \omega \right|^{2} }}{2\left| \omega \right|}. $$
(41)

By solving Eq. (41), we can obtain the dispersion parameter \( \sigma \); this can be done for any nonzero value of \( \omega \). However, we averaged the results from a small selection of \( \omega \) values, to reduce the overall variance of the estimate, as authors suggested in [16, 19].

It should be noted that the parameter estimation is done on a local basis, i.e., using a fixed window surrounding the coefficient’s location.

4.2.3 Parameter Estimation of Laplace Distribution

The variance of Laplace distribution is:

$$ \text{var}\left( x \right) = 2\sigma^{2} . $$
(42)

From Eq. (3)

$$ \sigma_{y}^{2} = \text{var}(x) + \sigma_{n}^{2} . $$
(43)

Therefore,

$$ \hat{\sigma }^{2} = \frac{{\hat{\sigma }_{y}^{2} - \hat{\sigma }_{n}^{2} }}{2}. $$
(44)

That \( \hat{\sigma }_{y}^{2} \) will be computed locally as mentioned before

$$ \hat{\sigma }_{y}^{2} = \frac{1}{M}\sum\limits_{{y_{i} \in R}} {y_{i}^{2} } , $$
(45)

where \( M \) is the size of the neighborhood \( R \).

It should be noted that we use the same method for estimating the parameters of Rayleigh–Student’s t, Rayleigh–Cauchy, and Rayleigh–Laplace distributions. This is done using just the real component of the sub-band. (Near-identical results were obtained from the imaginary component.)

4.3 MAP Estimator

As mentioned above, we considered the case of denoising of an image corrupted by white Gaussian noise. Based on Eq. (28), in the wavelet domain, we have \( y = x + n \) where \( y = \text{(}y_{1} ,y_{2} \text{)}^{T} \) is the vector of noisy coefficients in which \( y_{1} \) and \( y_{2} \) are the coefficient and its parent, respectively. \( x = \text{(}x_{\text{1}} ,x_{\text{2}} \text{)}^{T} \) and \( n = \text{(}n_{\text{1}} ,n_{\text{2}} \text{)}^{T} \) are similarly defined for the clean wavelet coefficients and noise values, respectively .

The standard MAP estimator for \( x \) given the corrupted observation \( y \) is [43]

$$ \hat{\varvec{x}} = \mathop {\arg \,\hbox{max} }\limits_{\varvec{x}} \,\,p\left( {\varvec{x}\left| \varvec{y} \right.} \right). $$
(46)

Using the Bayes’ rule, we have [36]

$$ \hat{\varvec{x}} = \mathop {\arg \,\hbox{max} }\limits_{\varvec{x}} \,\,p\left( {\varvec{x}\left| \varvec{y} \right.} \right) = \mathop {\arg \,\hbox{max} }\limits_{\varvec{x}} \,\,\frac{{p\left( {\varvec{y}|\varvec{x}} \right)p_{X} \left( \varvec{x} \right)}}{{p_{Y} (\varvec{y})}}, $$
(47)

Because \( p_{Y} (\varvec{y}) \) is independent of \( x \), the denominator of the right-hand side of Eq. (47) can be omitted; therefore, we have:

$$ \hat{\varvec{x}} = \mathop {\arg \,\hbox{max} }\limits_{\varvec{x}} \,\,p\left( {\varvec{y}|\varvec{x}} \right)p_{X} \left( \varvec{x} \right). $$
(48)

Because \( y = x + n \) and \( p\left( {\varvec{y}|\varvec{x}} \right) \) is the pdf of the normal distribution, we have:

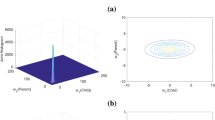
$$ \hat{\varvec{x}} = \mathop {\arg \,\hbox{max} }\limits_{\varvec{x}} \,\,p_{N} \left( {\varvec{y} - \varvec{x}} \right)p_{X} \left( \varvec{x} \right). $$
(49)

We use Eqs. (21), (23), and (24) as the prior probability density function \( p_{X} \left( \varvec{x} \right) \) for calculating the denoising MAP estimator; the simulation results are presented in Sect. 5. It is worthwhile to mention that the solution was found numerically using the MATLAB function fminsearch since there is no a closed form for Eq. (49). This function uses the Nelder–Mead simplex method. Plots depicted in Fig. 2 are the observed and the estimated densities (using the bivariate Rayleigh–Laplace distribution, bivariate Rayleigh–Student’s t distribution, and bivariate Rayleigh–Cauchy distribution) for one Direction of scale 2 of DT-CWT coefficients magnitude of the Lena image on the log scale. The image was corrupted by a zero-mean Gaussian noise (\( \sigma_{n} \) = 20). As we can see, the estimations using bivariate Rayleigh–Laplace distribution and bivariate Rayleigh–Student’s t distribution are in better agreement with those obtained from noise-free images rather than the estimator using bivariate Rayleigh–Cauchy distribution.

Fig. 2
figure 2

Estimated (red-dashed) and observed (blue-solid) densities (in log scale) of UDT-CWT coefficients for Lena image that was corrupted by Gaussian noise (\( {\varvec{\upsigma}}_{{\mathbf{n}}} \) = 20), a estimated using bivariate Rayleigh–Laplace distribution, b estimated using bivariate Rayleigh–Student’s t distribution, c estimated using bivariate Rayleigh–Cauchy distribution (Color figure online)

Full size image

5 Simulation Results

In order to validate the effectiveness of the proposed probability distributions, we have implemented image denoising experiments. The standard grayscale images “Lena,” “Barbara” and “Boat” were used as test images with different noise levels with standard deviations \( \sigma_{n} \) varying from 10 to 40. The original images are represented in Fig. 3. It should be noted that this work is focused on emphasizing the advantages of using two new distributions, bivariate Rayleigh–Student’s t distribution and bivariate Rayleigh–Laplace distribution over bivariate Rayleigh–Cauchy distribution; therefore, we have not compared results with the state-of-the-art denoising methods such as BM3D [9].

Fig. 3
figure 3

Test grayscale images used for denoising: a Lena, b Barbara, c Boat

Full size image

Performance analysis was done using the peak signal-to-noise ratio (PSNR) [18], using the following equations:

$$ \text{PSNR} = 10\text{log}\left( {\frac{{255^{2} }}{{\text{MSE}}}} \right), $$
(50)

where MSE is the minimum square error given by:

$$ \text{MSE} = \frac{1}{mn}\mathop \sum \limits_{i = 0}^{m - 1} \mathop \sum \limits_{j = 0}^{n - 1} \left[ {x\left( {i,j} \right) - \hat{x}\left( {i,j} \right)} \right]^{2} , $$
(51)

where \( x \) and \( \hat{x} \) denote the noise-free and the denoised images, respectively. \( m \) and \( n \) are the numbers of columns and rows of the image. We also compared the denoising results using the MSSIM measure, which represents the perceptual quality of the two images [49].Table 1 shows the denoising results of the proposed methods in terms of PSNR value. Each PSNR value was averaged over 10 independent runs of the algorithms. The highest PSNR value is shown with boldface style, as it can be observed that the denoising algorithm using bivariate Rayleigh–Laplace and bivariate Rayleigh–Student’s t was superior to the method using the bivariate Rayleigh–Cauchy distribution proposed in [16]; also, as the simulation results represent, as the noise level increases, the performance of the method using bivariate Rayleigh–Laplace as the prior distribution is better than the one using bivariate Rayleigh–Student’s t prior distribution.

Table 1 PSNR results for denoising
Full size table

The comparison methods using the perceptually quality metric MSSIM are depicted in Table 2. This shows that the proposed denoising method using bivariate Rayleigh–Laplace was superior to the other methods in terms of MSSIM in most cases. Figures 4 and 5 show the performance of the denoising methods visually. These denoised figures illustrate that the denoising methods using bivariate Rayleigh–Laplace and bivariate Rayleigh–Student’s t as the prior probability for noise-free coefficients have less denoising and ringing artifacts.

Table 2 MSSIM results for denoising
Full size table
Fig. 4
figure 4

Denoised results, a, original image, b image corrupted by additive white Gaussian noise with \( \sigma_{n} = 15 \), c denoised image using bivariate Rayleigh–Cauchy distribution, d denoised image using bivariate Rayleigh–Student’s t distribution, e denoised image using bivariate Rayleigh–Laplace distribution

Full size image
Fig. 5
figure 5

Cropped denoised results (Lena same as 3), a, original image, b denoised image using bivariate Rayleigh–Cauchy distribution, c denoised image using bivariate Rayleigh–Student’s t distribution, d denoised image using bivariate Rayleigh–Laplace distribution

Full size image

6 Conclusion

Wavelet thresholding is an effective method for image denoising; in the present study, we implemented our denoising algorithm using the dual-tree complex wavelet transform (DT-CWT), which offers more compact representation, near shift invariance property, and improved directional selectivity by six directional sub-bands per scale.

In this paper, an image denoising method based on the maximum a posteriori density function estimator was presented. The performance of MAP estimator depends on the proposed model for noise-free wavelet coefficients. Since natural images contain smooth areas interspersed with occasional sharp transmissions, such as edges, the wavelet transform of the images is sparse. Therefore, the marginal distributions of clean coefficients are significantly non-Gaussian and heavy-tailed distributions and have a large peak around zero. Scale mixtures of Gaussian distribution are heavy-tailed distributions that are sufficiently flexible to appropriately model the wavelet coefficients of the images.

Many previous MAP denoising algorithms have denoised the complex DT-CWT real and imaginary components separately, leading to an increase in the phase noise of the transform. To circumvent this issue, we chose to denoise the magnitude of wavelet coefficients. In this paper, we modeled the magnitude of noise-free coefficients using bivariate Rayleigh–Student’s t distribution (that is a generalization of bivariate Rayleigh–Cauchy distribution) and bivariate Rayleigh–Laplace distribution, which are scale mixtures of Rayleigh distribution. These distributions were introduced in this paper for the first time. The simulation results conducted in this paper confirmed that our denoising algorithm using these two proposed distributions outperformed the one proposed in [16], both in PSNR and MSSIM metrics. Better denoising results can be achieved by considering groups of wavelet coefficients together, using multivariate statistical models, which will be investigated in our future works.

Also, in our paper, we have implemented the denoising algorithm in DT-CWT domain; this method could be used for other transforms such as UDT-CWT that is the undecimated form of DT-CWT and is able to provide exact translational invariance and improve the correlation between each coefficient and its parent.