Finite-Time Stability and Stabilization of Fractional-Order Switched Singular Continuous-Time Systems

Abstract

The finite-time stability and stabilization of a class of fractional-order switched singular continuous-time systems with order $0<\alpha <1$ are investigated in this paper. First, by employing the average dwell time switching technique, together with the introduction of multiple Lyapunov functions, some sufficient conditions of the finite-time stability and finite-time boundedness are derived for the considered system. Second, based on the obtained conditions, suitable state feedback controllers can be designed if a set of linear matrix inequalities are feasible. Finally, an illustrative example is presented to show the effectiveness of the proposed results.

1 Introduction

Recently, fractional differential equations and fractional calculus have been studied due to their wide applications in different science and engineering fields, such as electrochemistry [10], electrode–electrolyte polarization [20], viscous damping [8], viscoelastic systems [2], electric fractal networks [4] and electromagnetic waves [7]. Moreover, it has been confirmed that compared with the frequently used integer-order calculus, the fractional-order differential state equations can be used to model certain physical systems and many mathematical problems in a more appropriate and precise fashion [21, 23].

As an important kind of hybrid dynamical systems, switched systems consist of a family of subsystems and a switching rule that regulates the switching among these subsystems, which have many applications in traffic control, switching power converters [7], networked control [33] and multi-agent consensus [9]. In [13], optimal switching time control was studied to realize the best switching between different modes. With the help of different event-triggered methods, the sufficient conditions for an event-triggered fault detection filter for complex networked jump systems were presented in [27]. On another research front, Markov jump systems (MJSs) are a class of jump systems that are also very suitable for modeling systems with random variations in parameters or structures. A number of results on MJSs have been obtained in the past several decades. For example, the problem of quantized feedback control of nonlinear MJSs was addressed in [31]. The issue of network-based fuzzy control for nonlinear MJSs with unreliable communication links was studied in [30].

It is well known that stability analysis is a primary and important problem for control systems [34, 35, 39]. In general, it is sufficient to study classical Lyapunov asymptotic stability; up to now, the study of asymptotic stability for fractional-order systems and fractional-order switched systems has achieved fruitful results [12, 14, 16, 17, 22]. However, in practical applications, large values of the system states are always unacceptable in some specific cases, for example, a system with saturation elements. In these special cases, the concept of finite-time stability (FTS) was proposed in the 1960s, mainly focusing on the transient behavior of the systems. A system is said to be finite-time stable if, given a bound on the initial condition, the system states remain within a certain threshold in a prescribed time interval [41], while FTS in the presence of exogenous inputs becomes finite-time boundedness (FTB).

As a result, stability analysis of fractional-order systems and switched systems in a finite-time interval has been given in recent literature. In [18], the FTS and FTB of fractional-order linear systems with $0<\alpha <1$ were studied. The FTS of switched positive linear systems was addressed in [3]. In [24], robust finite-time stabilization of the positive semi-Markovian switching systems was discussed. At the same time, an analysis of FTS for fractional-order positive switched systems was given in [29].

However, to the best of our knowledge, few results have been carried out for the FTS of a fractional-order switched singular system, which means that the fractional-order switched system contains at least one singular subsystem. In reality, these systems are suitable for modeling many natural and man-made systems, such as electrical networks, robotics and dynamic economic systems. On the one hand, stability analysis of fractional-order switched singular systems becomes more complicated and challenging than that for fractional-order switched regular systems, because regularity, impulse elimination and stability should be considered simultaneously for fractional-order switched singular systems. On the other hand, although remarkable contributions to stability analysis of fractional-order singular systems have been made in [15, 19, 26, 32], for switching-type fractional-order singular systems, another problem that cannot be ignored is that state inconsistency phenomena may occur at the switching instants; that is, switching will result in the last reached state and may not be a consistent initial condition for the next active subsystem. Physically, some problems, such as impulse voltage and currents, sparks and short circuits may occur.

Therefore, it is important and, in fact, necessary to study fractional-order switched singular systems, which motivates this study. The main contributions of this paper are as follows: (i) The concept of FTS is extended to a fractional-order switched singular system for the first time; (ii) based on the average dwell time switching technique, an improved Lyapunov function is constructed to derive the sufficient conditions of FTB; (iii) LMI-based state feedback controllers are designed to guarantee the FTS and FTB of the closed-loop systems.

The organization of this paper is as follows. Section 2 presents some preliminaries and problem statements. The main results are developed in Sect. 3. In Sect. 4, a numerical example is provided. Section 5 concludes this paper.

Notations: $R^{n}$ is the set of n-dimensional real vectors. For a given vector $x\in R^{n}$, $\parallel x\parallel$ denotes the Euclidean norm, which is defined by $\parallel x\parallel =(\sum _{i=1}^nx_i^2)^{\frac{1}{2}}$. $R^{n\times s}$ denotes the set of all $n\times s$ real matrices. For a given matrix X, the superscript T stands for the matrix transpose. $\parallel X\parallel$ denotes its spectral norm. $\lambda _{\min }(X)$ stands for the minimum eigenvalue of X, and $\lambda _{\max }(X)$ stands for the maximum eigenvalue of X. ${\hbox {rank}}(X)$ stands for the matrix rank of X. For given symmetric matrices X and Y, $X>0~(X<0)$ signifies that X is a positive-definite (negative-definite) matrix. $X>Y~(X<Y$) signifies that $X-Y$ is a positive-definite (negative-definite) matrix.

2 Preliminaries

2.1 Fractional-Order Calculus

The Caputo fractional-order operator is adopted in this paper. Given the noninteger order $\alpha >0$, the fractional integral of the integrable function f(t) is defined as

$$\begin{aligned} {_{t_{0}}D^{-\alpha }_{t}}f(t)=\frac{1}{\varGamma (\alpha )}\int _{t_{0}}^{t}\frac{f(\tau )}{{(t-\tau )}^{1-\alpha }}{\hbox {d}}\tau , \end{aligned}$$

(2.1)

where f(t) is an arbitrary integrable function, ${_{t_{0}}D^{-\alpha }_{t}}$ represents the fractional integral of order $\alpha$ on $[t_{0}, t]$ and $\varGamma (s)=\int _{0}^{\infty }t^{s-1}e^{-t}{\hbox {d}}t$ is the Gamma function.

The Caputo fractional derivative with order $\alpha$ of function f(t) is given by

$$\begin{aligned} {_{t_{0}}^{C}D^{\alpha }_{t}}f(t)=\frac{1}{\varGamma (n-\alpha )}\int _{t_{0}}^{t}\frac{f^{(n)}(\tau )}{{(t-\tau )}^{1+\alpha -n}}{\hbox {d}}\tau , \end{aligned}$$

(2.2)

where n is the first integer lager than $\alpha$, that is, $n-1<\alpha \le n, n\in Z^+$. In particular, when $0<\alpha <1$, the Caputo fractional derivative is defined as

$$\begin{aligned} {_{t_{0}}^{C}D^{\alpha }_{t}}f(t)=\frac{1}{\varGamma (1-\alpha )}\int _{t_{0}}^{t}\frac{f'(\tau )}{{(t-\tau )}^\alpha }{\hbox {d}}\tau , \end{aligned}$$

(2.3)

where ${_{t_{0}}^{C}D^{\alpha }_{t}}$ represents the Caputo fractional derivative of order $\alpha$ on $[t_0, t]$.

Next, some properties of the Caputo fractional derivative and integral are given, which will be used in the sequel.

Property 1

The Gamma function satisfies:

$$\begin{aligned} \varGamma (\alpha +1)=\alpha \varGamma (\alpha ). \end{aligned}$$

(2.4)

Property 2

For any real numbers a and b, it holds that

$$\begin{aligned} _{t_0}^CD^{\alpha }_t[ax(t)+by(t)]=a_{t_{0}}^CD^{\alpha }_tx(t)+b_{t_{0}}^{C}D^{\alpha }_ty(t). \end{aligned}$$

(2.5)

Property 3

For $0<\alpha <1$, if we take the fractional integral of order $\alpha$ to $_{t_0}^CD^{\alpha }_tx(t)$, then

$$\begin{aligned} ~_{t_0}D^{-\alpha }_t(_{t_0}^CD^{\alpha }_tx(t))=x(t)-x(t_0). \end{aligned}$$

(2.6)

2.2 Some Inequalities

To prove the main theorems in the following sections, some useful lemmas and inequalities should be given.

Lemma 1

[1] Suppose that $0<\alpha <1$, and let $x(t)\in R^n$ be a continuous and differentiable vector function defined over $[0, \infty )$. Then, the following inequality holds

$$\begin{aligned} \frac{1}{2}~^CD_t^\alpha [x^T(t)x(t)]\le x^T(t)^CD_t^\alpha x(t),~~\forall t\ge 0. \end{aligned}$$

Corollary 1

Suppose that $0<\alpha <1$, and let $x(t)\in R^n$ be a continuous and differentiable vector function, $P\in R^{n\times n}, P\ge 0$. Then, the following inequality holds

$$\begin{aligned} \frac{1}{2}~^CD_t^\alpha [x^T(t)Px(t)]\le x^T(t)P~^CD_t^\alpha x(t),~~\forall t\ge 0. \end{aligned}$$

Proof

Since $P\ge 0$, a matrix Q can be found such that $P=Q^TQ$, it can be obtained from Lemma 1 that

$$\begin{aligned} \frac{1}{2}~^CD_t^\alpha [x^T(t)Px(t)]= & {} \frac{1}{2}~^CD_t^\alpha [x^T(t)Q^TQx(t)]\\\le & {} x^T(t)Q^T~^CD_t^\alpha [Qx(t)]\\= & {} x^T(t)Q^TQ~^CD_t^\alpha x(t)\\= & {} x^T(t)P~^CD_t^\alpha x(t). \end{aligned}$$

The proof is completed. $\square$

Lemma 2

[5] Let a(t), b(t) and g(t) be real-valued piecewise-continuous functions. If a(t) is nonnegative and g(t) satisfies

$$\begin{aligned} g(t)\le {a(t)}+\int _{t_0}^{t}{b(s)g(s)}\mathrm{d}s, \end{aligned}$$

then

$$\begin{aligned} g(t)\le {a(t)}+\int _{t_0}^{t}{a(s)b(s)}exp{\left( \int _{s}^{t}b(r)dr\right) }\mathrm{d}s. \end{aligned}$$

In particular, if a(t) is a constant, then it holds that

$$\begin{aligned} g(t)\le {a(t)}\exp \left( \int _{t_0}^{t}{b(s)}\mathrm{d}s\right) . \end{aligned}$$

Lemma 3

($C_{p}$ inequality) Let $0<\alpha <1$, $x_{1}$, $x_{2}$ , $\cdot \cdot \cdot$,$x_{k}$ be positive real numbers, it holds that

$$\begin{aligned} \sum _{k=1}^{n}x_{k}^{\alpha }\le {n}^{1-\alpha }\left( \sum _{k=1}^{n}x_{k}\right) ^\alpha . \end{aligned}$$

Lemma 4

(Young’s inequality) Let a and b be positive real numbers and x and y be real numbers, then the following inequality holds

$$\begin{aligned} |x|^a|y|^b\le \frac{a}{a+b}|x|^{a+b}+\frac{b}{a+b}|y|^{a+b}. \end{aligned}$$

Lemma 5

[22] Let $A\in R^{n\times n}$, then A is nonsingular if and only if there exists a nonsingular matrix $X\in R^{n\times n}$ such that

$$\begin{aligned} AX+X^TA^T<0. \end{aligned}$$

2.3 Fractional-Order Switched Singular Continuous-Time System

Consider the fractional-order switched singular continuous-time system:

$$\begin{aligned} { E}_{\sigma (t)} ~ _{t_0}^CD_t^\alpha { x}(t)={ A}_{\sigma (t)}{ x}(t)+{ B}_{\sigma (t)}{ u}(t)+{ C}_{\sigma (t)}{ w}(t), \end{aligned}$$

(2.7)

where $0<\alpha <1$, ${ x}(t)\in {R^n}$ is the state vector, ${ u}(t)\in {R^m}$ is the control input, ${ w}(t)\in {R^q}$ is the exogenous disturbance signal and satisfies the constraint condition ${ w}(t)^T{ w}(t)\le d,~d\ge 0$, the switching signal is $\sigma (t): [0, \infty )\longrightarrow S=\{1, 2,\cdot \cdot \cdot , N\}$ (N denotes the total number of subsystems), and for a switching sequence $0\le t_0<t_1<\cdots$, when $t\in [t_m,t_{m+1})$, we say that the $\sigma (t_m)$th subsystem is active. For $\forall {i}\in S, { E}_i,{ A}_i\in R^{n\times n}, { B}_i\in R^{n\times m}, { C}_i\in R^{n\times q}$ are known constant matrices, and ${\hbox {rank}}({ E}_i)=r_i\le n$.

Consider the following unforced fractional-order singular subsystem

$$\begin{aligned} { E}_i ~ _{t_0}^CD_t^\alpha { x}(t)={ A}_i{ x}(t), \end{aligned}$$

(2.8)

where ${ E}_i, { A}_i\in R^{n\times n}, {\hbox {rank}}({ E}_i)=r<n$. For the sake of simplicity, $({ E}_i, { A}_i)$ is used to denote the singular system in (2.8).

The continuous singular system (2.8) may have an impulsive solution. However, only regularity and non-impulsiveness can guarantee the existence and uniqueness of an impulsive-free solution of system (2.8). Therefore, parallel to the integer-order singular system, the following definitions and useful lemmas for the fractional-order singular system (2.8) are presented.

Definition 1

[32] The singular system $({ E}_i, { A}_i)$ is said to be regular if there exists a scalar $\lambda \in {\mathcal {C}}$ such that $det(\lambda ^\alpha { E}_i-{ A}_i)\ne 0$ holds.

Definition 2

[32] The singular system $({ E}_i, { A}_i)$ is said to be impulse-free if $deg(det(\lambda { E}_i-{ A}_i))={\hbox {rank}}({ E}_i)$, where $\lambda \in {\mathcal {C}}$.

Definition 3

The fractional-order switched singular continuous-time system (2.7) is called regular and impulse-free if each subsystem $({ E}_i, { A}_i)$ is regular and impulse-free.

Lemma 6

[32] For the system $({ E}_i, { A}_i)$, it is always possible to find two nonsingular matrices ${ M}_i, { N}_i\in R^{n\times n}$ such that $({ E}_i, { A}_i)$ takes the following decomposition form

$$\begin{aligned} { M}_i{ E}_i{ N}_i=\left[ \begin{array}{c@{\quad }c} { I}_r &{} 0 \\ 0 &{} 0 \\ \end{array} \right] , ~~~{ M}_i{ A}_i{ N}_i=\left[ \begin{array}{c@{\quad }c} { A}_{i11} &{} { A}_{i12} \\ { A}_{i21} &{} { A}_{i22} \\ \end{array} \right] . \end{aligned}$$

In this form, the system $({ E}_i, { A}_i)$ is regular and impulse-free if and only if ${ A}_{i22}$ is nonsingular.

Definition 4

The switching of system (2.7) is called consistent switching if the state of system (2.7) at every switching instant is the consistent initial value of the next active subsystem.

To ensure the consistent switching of system (2.7), the following projector is given

$$\begin{aligned} { \varPi }_i={ N}_i\left[ \begin{array}{c@{\quad }c} I &{} 0 \\ -{ A}_{i22}^{-1}{ A}_{i21} &{} 0 \\ \end{array} \right] { N}_i^{-1}. \end{aligned}$$

Lemma 7

[38] If the state of system (2.7) satisfies

$$\begin{aligned} { x}(t_m)={ \varPi }_i{ x}(t_m^-), \end{aligned}$$

where $t_m$ is any switching instant, ${ x}(t_m^-)$ signifies the state before $t_m$, and then the state jump behaviors can be evaluated via the above consistency projector ${ \varPi }_i$.

Definition 5

For any time interval $[t_1,t_2]$ and a switching signal $\sigma (t)$, let $N_\sigma (t_1,t_2)$ denote the number of switchings of $\sigma (t)$ over $[t_1,t_2]$. If there exist constants $N_0\ge 0$ and $\tau _a>0$ such that

$$\begin{aligned} N_{\sigma }(t_{1}, t_{2})\le N_{0}+\frac{t_{2}-t_{1}}{\tau _a}, \end{aligned}$$

(2.9)

then the positive constant $\tau _a$ is called the average dwell time and $N_0$ is called the chatter bound.

Definition 6

The fractional-order switched singular continuous-time system

$$\begin{aligned} { E}_{\sigma (t)} ~ _{t_0}^CD_t^\alpha { x}(t)={ A}_{\sigma (t)}{ x}(t) \end{aligned}$$

(2.10)

is finite-time stable with respect to $(c_1, c_2, { R}, T_f, \sigma )$, if the following conditions hold

$$\begin{aligned} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)\le c_1\Longrightarrow { x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t)< c_2, \end{aligned}$$

for $\forall t\in [t_0, T_f]$, where ${ R}>0, c_2>c_1>0, T_f>0$.

Definition 7

The fractional-order switched singular continuous-time system

$$\begin{aligned} { E}_{\sigma (t)} ~ _{t_0}^CD_t^\alpha { x}(t)={ A}_{\sigma (t)}{ x}(t)+{ C}_{\sigma (t)}{ w}(t),~~~~~{ w}(t)^T{ w}(t)\le d, \end{aligned}$$

(2.11)

is finite-time bounded with respect to $(c_1, c_2, d, { R}, T_f, \sigma )$, if the following conditions hold

$$\begin{aligned} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)\le c_1\Longrightarrow { x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t)< c_2, \end{aligned}$$

for $\forall t\in [t_0, T_f]$, where ${ R}>0, c_2>c_1>0, T_f>0$, $d\ge 0$.

3 Main Results

3.1 Finite-Time Stability

The sufficient condition for the FTS of the fractional-order switched singular continuous-time system (2.10) is derived in this subsection.

Theorem 1

Given the constants $\mu >0$ and $\lambda >1$, for any $i,j\in S, i\ne j$, if there exist nonsingular matrices ${ P}_i, { Z}_i>0$ such that the following inequalities hold

$$\begin{aligned}&\displaystyle {{ E}_i}^T{ P}_i={{ P}_i}^T{ E}_i \ge 0, \end{aligned}$$

(3.1a)

$$\begin{aligned}&\displaystyle {{ P}_i}^T{ A}_i+{{ A}_i}^T{ P}_i-\mu {{ E}_i}^T{ P}_i < 0,\end{aligned}$$

(3.1b)

$$\begin{aligned}&\displaystyle {{ \varPi }_i}^T{ E}_i^T{ P}_i{ \varPi }_i \le \lambda { E}_j^T{ P}_j, \end{aligned}$$

(3.1c)

and then system (2.10) is regular, impulse-free and finite-time stable with respect to $(c_1, c_2, { R}, T_f, \sigma )$ for an arbitrary switching signal satisfying the average dwell time

$$\begin{aligned} \tau _a>\tau ^*_a=\frac{\beta }{lnc_2\lambda _2-lnc_1\lambda _1-\gamma }, \end{aligned}$$

(3.2)

where ${{ E}_i}^T{ P}_i={{ E}_i}^T{ R}^\frac{1}{2}{ Z}_i{ R}^\frac{1}{2}{ E}_i,~\lambda _1=\max _{i\in S}(\lambda _{\max }({ Z}_i))$, $\lambda _2=\min _{i\in S}(\lambda _{\min }({ Z}_i)),$

$\beta =T_fln\lambda +\frac{\mu (1-\alpha )T_f}{\varGamma (\alpha +1)}$ and $\gamma =N_0ln\lambda +\frac{\mu (1-\alpha )(N_0+1)}{\varGamma (\alpha +1)}+\frac{\alpha \mu T_f}{\varGamma (\alpha +1)}$.

Proof

The proof of the theorem is divided into two steps. First, the regularity and impulse-free properties are solved. Second, the finite-time stability is studied.

First, for $\forall i\in S$, let

$$\begin{aligned} { M}_i^{-T}{ P}_i{ N}_i=\left[ \begin{array}{c@{\quad }c} { P}_{i11} &{} { P}_{i12} \\ { P}_{i21} &{} { P}_{i22} \\ \end{array} \right] ; \end{aligned}$$

thus, combining with Lemma 6, it follows that

$$\begin{aligned} { N}_i^{T}{ E}_i^T{ P}_i{ N}_i={ N}_i^{T}{ E}_i^T{ M}_i^T{ M}_i^{-T}{ P}_i{ N}_i=\left[ \begin{array}{c@{\quad }c} { P}_{i11} &{} { P}_{i12} \\ 0 &{} 0 \\ \end{array} \right] \ge 0, \end{aligned}$$

and similarly,

$$\begin{aligned} { N}_i^{T}{ P}_i^T{ E}_i{ N}_i={ N}_i^{T}{ P}_i^T{ M}_i^{-1}{ M}_i{ E}_i{ N}_i=\left[ \begin{array}{c@{\quad }c} { P}_{i11}^T &{} 0 \\ { P}_{i12}^T &{} 0 \\ \end{array} \right] \ge 0. \end{aligned}$$

As a result, it follows from (3.1a) that ${ P}_{i12}=0, { P}_{i11}= { P}_{i11}^T\ge 0$; then, we have

$$\begin{aligned} { M}_i^{-T}{ P}_i{ N}_i=\left[ \begin{array}{cc} { P}_{i11} &{} 0 \\ { P}_{i21} &{} { P}_{i22} \\ \end{array} \right] . \end{aligned}$$

Moreover, since ${ P}_i$ is nonsingular, ${ P}_{i11}$ and ${ P}_{i22}$ are nonsingular; thus, ${ P}_{i11}>0.$ In addition, it can also be derived from (3.1b) that

$$\begin{aligned}&{ N}_i^{T}{{ P}_i}^T{ A}_i{ N}_i+{ N}_i^{T}{{ A}_i}^T{ P}_i{ N}_i+\mu { N}_i^{T}{{ E}_i}^T{ P}_i{ N}_i\\&\quad ={ N}_i^{T}{{ P}_i}^T{ M}_i^{-1}{ M}_i{ A}_i{ N}_i+{ N}_i^{T}{{ A}_i}^T{ M}_i^T{ M}_i^{-T}{ P}_i{ N}_i+\mu { N}_i^{T}{ P}_i^T{ M}_i^{-1}{ M}_i{{ E}_i}{ N}_i\\&\quad =\left[ \begin{array}{cc} * &{} * \\ * &{} { A}_{i22}^T{ P}_{i22}+{ P}_{i22}^T{ A}_{i22} \\ \end{array} \right] <0, \end{aligned}$$

where $*$ symbolizes the elements that do not need to be known, which leads to ${ A}_{i22}^T{ P}_{i22}+{ P}_{i22}^T{ A}_{i22}<0$. Then, it follows from Lemma 5 that ${ A}_{i22}$ is nonsingular. By Lemma 6, $({ E}_i, { A}_i)$ is regular and impulse-free for any i, and then by Definition 3, the regularity and impulse-free properties of system (2.10) are derived.

Next, we need to prove the FTS of system (2.10). Choose the multiple Lyapunov functions as follows:

$$\begin{aligned} V_{\sigma (t)}=V_{\sigma (t)}(t,{ x}(t))={ x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t). \end{aligned}$$

It can be derived that $V_{\sigma (t)}\ge 0$ according to (3.1a). Suppose a switching sequence $0\le t_0<t_1<\cdots$; when $t\in [t_m, t_{m+1})$, it follows from Corollary 1 and (3.1b) that

$$\begin{aligned} _{t_0}^C{D}^\alpha _t{V_{\sigma (t)}(t, { x}(t))}\le & {} 2{ x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}~_{t_0}^C{D}^\alpha _t{ x}(t)\\= & {} 2{ x}^T(t){ P}_{\sigma (t)}^T{ E}_{\sigma (t)}~_{t_0}^C{D}^\alpha _t{ x}(t)\\= & {} 2{ x}^T(t){ P}_{\sigma (t)}^T{ A}_{\sigma (t)}{ x}(t)\\= & {} { x}^T(t)({ P}_{\sigma (t)}^T{ A}_{\sigma (t)}+{ A}_{\sigma (t)}^T{ P}_{\sigma (t)}){ x}(t)\\< & {} \mu { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)\\= & {} \mu V_{\sigma (t)}(t, { x}(t)). \end{aligned}$$

Taking the fractional integral $_{t_m}{D}^{-\alpha }_t$ and combining Property 3 and formula (2.1) of a fractional integral with $0<\alpha <1$, we have

$$\begin{aligned} V_{\sigma (t)}(t, { x}(t))-{V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}< & {} \mu ~_{t_m}{D}^{-\alpha }_tV_{\sigma (t)}(t, { x}(t))\\= & {} \frac{\mu }{\varGamma (\alpha )}\int _{t_{m}}^{t}(t-\tau )^{\alpha -1}V_{\sigma (t_m)}(\tau ,{ x}(\tau ))d\tau . \end{aligned}$$

Thus,

$$\begin{aligned} V_{\sigma (t)}(t, { x}(t))<{V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}+\frac{\mu }{\varGamma (\alpha )}\int _{t_{m}}^{t}(t-\tau )^{\alpha -1}V_{\sigma (t_m)}(\tau ,{ x}(\tau ))d\tau , \end{aligned}$$

for $t\in [t_m, t_{m+1})$. By Lemma 2, it follows that

$$\begin{aligned} V_{\sigma (t)}(t, { x}(t))< & {} {V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}\exp \left\{ \frac{\mu }{\varGamma (\alpha )}\int _{t_{m}}^{t}(t-\tau )^{\alpha -1}d\tau \right\} \\= & {} {V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}\exp \left\{ \frac{\mu }{\alpha \varGamma (\alpha )}(t-t_m)^{\alpha }\right\} \\= & {} {V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}\exp \left\{ \frac{\mu }{\varGamma (\alpha +1)}(t-t_m)^{\alpha }\right\} , \end{aligned}$$

for $t\in [t_m, t_{m+1})$. At the switching instant $t_m$, combining Lemma 7 and (3.1c),

$$\begin{aligned} V_{\sigma (t_m)}(t_m,{ x}(t_m))= & {} { x}^T(t_m){ E}_{\sigma (t_m)}^T{ P}_{\sigma (t_m)}{ x}(t_m)\\= & {} { x}^T(t_m^-){ \varPi }_{\sigma (t_m)}^T{ E}_{\sigma (t_m)}^T{ P}_{\sigma (t_m)}{ \varPi }_{\sigma (t_m)}{ x}(t_m^-)\\\le & {} \lambda V_{\sigma (t_m^-)}(t_m^-,{ x}(t_m^-)). \end{aligned}$$

Since $\exp \left\{ \frac{\mu }{\varGamma (\alpha +1)}(t-t_m)^{\alpha }\right\} >0$, by a similar method, this implies

$$\begin{aligned} V_{\sigma (t)}(t,{ x}(t))< & {} \lambda V_{\sigma (t_m^-)}(t_m^-,{ x}(t_m^-))\exp \left\{ \frac{\mu }{\varGamma (\alpha +1)}(t-t_m)^{\alpha }\right\} \\< & {} \lambda V_{\sigma (t_{m-1})}(t_{m-1},{ x}(t_{m-1}))\exp \left\{ \frac{\mu }{\varGamma (\alpha +1)}[(t-t_m)^{\alpha }+(t_m-t_{m-1})^{\alpha }]\right\} \\< & {} \cdots \\< & {} \lambda ^{N_\sigma (t_0,t)} V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{\mu }{\varGamma (\alpha +1)}[(t-t_m)^{\alpha }+\cdots +(t_1-t_0)^{\alpha }]\right\} . \end{aligned}$$

Using (2.9), Lemma 3 and Lemma 4, combined with $\lambda >1$,

$$\begin{aligned}&V_{\sigma (t)}(t,{ x}(t))\\&\quad<V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ ln\lambda ^{N_0+\frac{t-t_0}{\tau _a}}+\frac{\mu }{\varGamma (\alpha +1)}[(N_\sigma (t_0,t)+1)^{1-\alpha }(t-t_0)^{\alpha }]\right\} \\&\quad<V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{t-t_0}{\tau _a}ln\lambda +N_0ln\lambda \right. \\&\qquad \left. +\frac{\mu }{\varGamma (\alpha +1)}[(1-\alpha )(N_\sigma (t_0,t)+1)+{\alpha }(t-t_0)]\right\} \\&\quad<V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{t-t_0}{\tau _a}ln\lambda +N_0ln\lambda \right. \\&\qquad \left. +\frac{\mu }{\varGamma (\alpha +1)}\left[ (1-\alpha )\left( N_0+1+\frac{t-t_0}{\tau _a}\right) +{\alpha }(t-t_0)\right] \right\} \\&\quad =V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{t-t_0}{\tau _a}ln\lambda +\frac{\mu (1-\alpha )}{\varGamma (\alpha +1)}\frac{t-t_0}{\tau _a}+N_0ln\lambda \right. \\&\qquad \left. +\frac{\mu (1-\alpha )(N_0+1)}{\varGamma (\alpha +1)}+\frac{ \alpha \mu (t-t_0)}{\varGamma (\alpha +1)}\right\} \\&\quad <V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{1}{\tau _a} \left[ T_fln\lambda +\frac{\mu (1-\alpha )T_f}{\varGamma (\alpha +1)}\right] +N_0ln\lambda \right. \\&\qquad \left. +\frac{\mu (1-\alpha )(N_0+1)}{\varGamma (\alpha +1)}+\frac{ \alpha \mu T_f}{\varGamma (\alpha +1)}\right\} \\&\quad =V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{1}{\tau _a}\beta +\gamma \right\} . \end{aligned}$$

In addition, the following inequalities hold

$$\begin{aligned} V_{\sigma (t)}(t,{ x}(t))= & {} { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)\\= & {} { x}^T(t){ E}_{\sigma (t)}^T{ R}^{\frac{1}{2}}{ Z}_{\sigma (t)}{ R}^{\frac{1}{2}}{ E}_{\sigma (t)}{ x}(t)\\\ge & {} \lambda _2{ x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t).\\ V_{\sigma (t_0)}(t_0,{ x}(t_0))= & {} { x}^T(t_0){ E}_{\sigma (t_0)}^TP_{\sigma (t_0)}{ x}(t_0)\\= & {} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}^{\frac{1}{2}}{ Z}_{\sigma (t_0)}{ R}^{\frac{1}{2}}{ E}_{\sigma (t_0)}{ x}(t_0)\\\le & {} \lambda _1{ x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0). \end{aligned}$$

By utilizing ${ x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)\le c_1$ and condition (3.2), it follows that

$$\begin{aligned} { x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t)\le & {} \frac{1}{\lambda _2}V_{\sigma (t)}(t,{ x}(t))\\< & {} \frac{1}{\lambda _2}\exp \left\{ \frac{1}{\tau _a}\beta +\gamma \right\} V_{\sigma (t_0)}(t_0,{ x}(t_0))\\\le & {} \frac{\lambda _1}{\lambda _2}\exp \left\{ \frac{1}{\tau _a}\beta +\gamma \right\} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)\\\le & {} c_2. \end{aligned}$$

Then, by Definition 6, system (2.10) is finite-time stable with respect to $(c_1, c_2, { R}, T_f, \sigma )$. $\square$

Remark 1

If $\alpha =1$, then (3.2) is consistent with the condition of a switched singular continuous-time system [36], which shows that Theorem 1 is a generalization of integer-order switched singular continuous-time system.

Remark 2

In [28], the FTS of fractional-order impulsive switched nonlinear systems is considered in Theorem 4. The derived sufficient conditions are based on a fractional-order Lyapunov function and the average dwell time technique. However, there are no specific Lyapunov functions for FTS analysis or operative test conditions for FTS. Furthermore, the given conditions depend on the construction of the Lyapunov functions, which definitely increase the difficulties and conservatism of the results. In this paper, we find computationally appealing conditions that guarantee FTS by using LMI theory and present the specific multiple Lyapunov functions.

3.2 Finite-Time Boundedness

The FTB of the fractional-order switched singular continuous-time system (2.11) is investigated in this subsection.

Theorem 2

Given the constants $\mu >0$ and $\lambda >1$, for any $i,j\in S, i\ne j$, if there exist nonsingular matrices ${ P}_i, { Z}_i>0, { Q}_i>0$ such that the following inequalities hold

$$\begin{aligned}&\displaystyle {{ E}_i}^T{ P}_i={{ P}_i}^T{ E}_i \ge 0,\end{aligned}$$

(3.3a)

$$\begin{aligned}&\displaystyle \left[ \begin{array}{c@{\quad }c} {{ P}_i}^T{ A}_i+{{ A}_i}^T{ P}_i-\mu {{ E}_i}^T{ P}_i &{} { P}_i^T{ C}_i \\ { C}_i^T{ P}_i &{} -{ Q}_i \\ \end{array} \right] < 0,\end{aligned}$$

(3.3b)

$$\begin{aligned}&\displaystyle {{ \varPi }_i}^T{ E}_i^T{ P}_i{ \varPi }_i \le \lambda E_j^T{ P}_j, \end{aligned}$$

(3.3c)

then system (2.11) is regular, impulse-free and finite-time bounded with respect to $(c_1, c_2, d, { R}, T_f, \sigma )$ for an arbitrary switching signal satisfying the average dwell time

$$\begin{aligned} \tau _a>\tau ^*_a=\frac{\beta ^{'}}{lnc_2\lambda _2-ln(c_1\lambda _1+d)-\gamma ^{'}}, \end{aligned}$$

(3.4)

where ${{ E}_i}^T{ P}_i={{ E}_i}^TR^\frac{1}{2}{ Z}_iR^\frac{1}{2}{ E}_i,~\lambda _1=\max _{i\in S}(\lambda _{\max }({ Z}_i)),~\lambda _2=\min _{i\in S}(\lambda _{\min }({ Z}_i)),$

$\beta ^{'}=T_fln\lambda +\frac{\kappa (1-\alpha )T_f}{\varGamma (\alpha +1)}$ and $\gamma ^{'}=N_0ln\lambda +\frac{\kappa (1-\alpha )(N_0+1)}{\varGamma (\alpha +1)}+\frac{\alpha \kappa T_f}{\varGamma (\alpha +1)}$, and $\kappa =\max \{\mu , \eta \},~\eta =\max _{i\in S}(\lambda _{\max }({ Q}_i))$.

Proof

By the Schur complement, it is easy to check that inequality (3.3b) holds if and only if for $\forall i\in S$ the following inequality holds

$$\begin{aligned} {{ P}_i}^T{ A}_i+{{ A}_i}^T{ P}_i-\mu {{ E}_i}^T{ P}_i<0, \end{aligned}$$

then, together with (3.3a), according to the proof of Theorem 1, the regularity and impulse-free properties of system (2.11) can be obtained. Next, let us consider the FTB of system (2.11). Construct the multiple Lyapunov functions as follows

$$\begin{aligned} V_{\sigma (t)}=V_{\sigma (t)}(t,{ x}(t))={ x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)+d. \end{aligned}$$

It can be obtained that $V_{\sigma (t)}\ge 0$ according to (3.3a). Suppose a switching sequence $0\le t_0<t_1<\cdots$, when $t\in [t_m, t_{m+1})$. Then, it follows from Corollary 1 and (3.3b) that

$$\begin{aligned}&_{t_0}^C{D}^\alpha _t{V_{\sigma (t)}(t, { x}(t))}\\&\quad \le 2{ x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}~_{t_0}^C{D}^\alpha _t{ x}(t)\\&\quad =2{ x}^T(t){ P}_{\sigma (t)}^T{ E}_{\sigma (t)}~_{t_0}^C{D}^\alpha _t{ x}(t)\\&\quad =2{ x}^T(t){ P}_{\sigma (t)}^T({ A}_{\sigma (t)}{ x}(t)+{ C}_{\sigma (t)}{ w}(t))\\&\quad ={ x}^T(t)({ P}_{\sigma (t)}^T{ A}_{\sigma (t)}+{ A}_{\sigma (t)}^T{ P}_{\sigma (t)}){ x}(t)\\&\qquad +{ x}^T(t){ P}_{\sigma (t)}^T{ C}_{\sigma (t)}{ w}(t)+w^T(t){ C}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)\\&\quad =\left[ \begin{array}{cc} { x}^T(t) &{} { w}^T(t) \\ \end{array} \right] \left[ \begin{array}{cc} { P}_{\sigma (t)}^T{ A}_{\sigma (t)}+{ A}_{\sigma (t)}^T{ P}_{\sigma (t)} &{} { P}_{\sigma (t)}^T{ C}_{\sigma (t)} \\ { C}_{\sigma (t)}^T{ P}_{\sigma (t)} &{} 0 \\ \end{array} \right] \left[ \begin{array}{cc} { x}(t) \\ { w}(t) \\ \end{array} \right] \\&\quad <\left[ \begin{array}{cc} { x}^T(t) &{} { w}^T(t) \\ \end{array} \right] \left[ \begin{array}{cc} \mu { E}_{\sigma (t)}^T{ P}_{\sigma (t)} &{} 0 \\ 0 &{} { Q}_{\sigma (t)} \\ \end{array} \right] \left[ \begin{array}{cc} { x}(t) \\ { w}(t) \\ \end{array} \right] \\&\quad =\mu { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)+{ w}(t)^T{ Q}_{\sigma (t)}{ w}(t)\\&\quad \le \mu { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)+\eta { w}(t)^T{ w}(t)\\&\quad \le \mu { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)+\eta d\\&\quad \le \kappa V_{\sigma (t)}(t,{ x}(t)), \end{aligned}$$

where $\kappa =\max \{\mu , \eta \}$. By a similar method to the derivation of Theorem 1, it is easy to obtain

$$\begin{aligned} V_{\sigma (t)}(t,{ x}(t))<{V_{\sigma (t_{m})}(t_{m}, { x}(t_{m}))}\exp \left\{ \frac{\kappa }{\varGamma (\alpha +1)}(t-t_m)^{\alpha }\right\} , \end{aligned}$$

for $t\in [t_m, t_{m+1})$. At the switching instant $t_m$, combining Lemma 7 and (3.3c),

$$\begin{aligned} V_{\sigma (t_m)}(t_m,{ x}(t_m))\le \lambda V_{\sigma (t_m^-)}(t_m^-,{ x}(t_m^-)). \end{aligned}$$

By a similar method in Theorem 1, this implies

$$\begin{aligned}&V_{\sigma (t)}(t,{ x}(t))\\&\quad<\lambda V_{\sigma (t_m^-)}(t_m^-,{ x}(t_m^-))\exp \left\{ \frac{\kappa }{\varGamma (\alpha +1)}(t-t_m)^{\alpha }\right\} \\&\quad<\lambda V_{\sigma (t_{m-1})}(t_{m-1},{ x}(t_{m-1}))\exp \left\{ \frac{\kappa }{\varGamma (\alpha +1)}\left[ (t-t_m)^{\alpha }+(t_m-t_{m-1})^{\alpha }\right] \right\} \\&\quad<\cdots \\&\quad<\lambda ^{N_\sigma (t_0,t)} V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{\kappa }{\varGamma (\alpha +1)}\left[ (t-t_m)^{\alpha }+\cdots +(t_1-t_0)^{\alpha }\right] \right\} \\&\quad<V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ ln\lambda ^{N_0+\frac{t-t_0}{\tau _a}}+\frac{\kappa }{\varGamma (\alpha +1)}\left[ (N_\sigma (t_0,t)+1)^{1-\alpha }(t-t_0)^{\alpha }\right] \right\} \\&\quad<V_{\sigma (t_0)}(t_0,{x}(t_0))\exp \left\{ \frac{t-t_0}{\tau _a}ln\lambda +N_0ln\lambda \right. \\&\qquad \left. +\frac{\kappa }{\varGamma (\alpha +1)}\left[ (1-\alpha )(N_\sigma (t_0,t)+1)+{\alpha }(t-t_0)\right] \right\} \\&\quad<\cdots \\&\quad <V_{\sigma (t_0)}(t_0,{ x}(t_0))\exp \left\{ \frac{1}{\tau _a}\beta ^{'}+\gamma ^{'}\right\} , \end{aligned}$$

where $\beta ^{'}=T_fln\lambda +\frac{\kappa (1-\alpha )T_f}{\varGamma (\alpha +1)}$ and $\gamma ^{'}=N_0ln\lambda +\frac{\kappa (1-\alpha )(N_0+1)}{\varGamma (\alpha +1)}+\frac{\alpha \kappa T_f}{\varGamma (\alpha +1)}.$

In addition, the following inequalities hold

$$\begin{aligned} V_{\sigma (t)}(t,{ x}(t))= & {} { x}^T(t){ E}_{\sigma (t)}^T{ P}_{\sigma (t)}{ x}(t)+d\\\ge & {} { x}^T(t){ E}_{\sigma (t)}^T{ R}^{\frac{1}{2}}Z_{\sigma (t)}{ R}^{\frac{1}{2}}{ E}_{\sigma (t)}{ x}(t)\\\ge & {} \lambda _2{ x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t).\\ V_{\sigma (t_0)}(t_0,{ x}(t_0))= & {} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ P}_{\sigma (t_0)}{ x}(t_0)+d\\= & {} { x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}^{\frac{1}{2}}Z_{\sigma (t_0)}{ R}^{\frac{1}{2}}{ E}_{\sigma (t_0)}{ x}(t_0)+d\\\le & {} \lambda _1{ x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)+d. \end{aligned}$$

From ${ x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)\le c_1$ and condition (3.4), it follows that

$$\begin{aligned} { x}^T(t){ E}_{\sigma (t)}^T{ R}{ E}_{\sigma (t)}{ x}(t)\le & {} \frac{1}{\lambda _2}V_{\sigma (t)}(t,{ x}(t))\\< & {} \frac{1}{\lambda _2}\exp \left\{ \frac{1}{\tau _a}\beta ^{'}+\gamma ^{'}\right\} V_{\sigma (t_0)}(t_0,{ x}(t_0))\\\le & {} \frac{1}{\lambda _2}\exp \left\{ \frac{1}{\tau _a}\beta ^{'}+\gamma ^{'}\right\} \left\{ \lambda _1{ x}^T(t_0){ E}_{\sigma (t_0)}^T{ R}{ E}_{\sigma (t_0)}{ x}(t_0)+d\right\} \\\le & {} c_2. \end{aligned}$$

Then, by Definition 7, system (2.11) is finite-time bounded with respect to $(c_1, c_2, d, { R}, T_f, \sigma )$. $\square$

Remark 3

In fact, one of the interesting problems in switched systems is how to find less-conservative conditions to guarantee the stability of the systems for arbitrary switching laws. A powerful tool for this issue is the multiple Lyapunov functions approach, where an individual decrescent Lyapunov function is constructed for each subsystem. The multiple Lyapunov functions developed in Theorem 1 can be considered to be a trade-off between these conservative methodologies (using a single common Lyapunov function) and one that is less conservative but numerically difficult to check. In general, by choosing the same Lyapunov function in Theorem 1, the FTB of integer-order switched singular continuous-time systems is also be considered; meanwhile, the L-2 performance of the considered system can be derived.

Remark 4

However, if we directly choose the same Lyapunov function in Theorem 1 to study the FTB of the fractional-order switched singular continuous-time systems, there exist some difficulties in the computation and derivation of the inequalities due to the existence of the exogenous disturbance. Therefore, conservative multiple Lyapunov functions are chosen for system (2.11), but the advantage of this new multiple Lyapunov functions lies in the fact that it can be easily applied to solve the FTB of fractional-order switched singular continuous-time systems directly.

3.3 Finite-Time Stabilization

The finite-time stabilization for system (2.7) with ${ w}(t)=0$ is studied in this section. Here, we suppose that every state variable is available for state feedback. The main purpose of the following theorem is to design a state feedback controller for the system (2.7) with ${ w}(t)=0$ as

$$\begin{aligned} { u}(t)={ K}_{\sigma (t)}{ x}(t) \end{aligned}$$

(3.5)

such that the corresponding closed-loop system

$$\begin{aligned} { E}_{\sigma (t)} ~ _{t_0}^CD_t^\alpha { x}(t)=\bar{{ A}}_{\sigma (t)}{ x}(t) \end{aligned}$$

(3.6)

is finite-time stable, where $\bar{{ A}}_{\sigma (t)}={ A}_{\sigma (t)}+{ B}_{\sigma (t)}K_{\sigma (t)}$.

Theorem 3

Given the constants $\mu >0$ and $\lambda >1$, for any $i,j\in S, i\ne j$, if there exist nonsingular matrices ${ L}_i, { X}_i, { Z}_i>0$ such that the following inequalities

$$\begin{aligned}&\displaystyle {{ E}_i}{ X}_i={{ X}_i}^T{ E}_i^T \ge 0,\end{aligned}$$

(3.7a)

$$\begin{aligned}&\displaystyle {{ X}_i}^T{ A}_i^T+{ A}_i{ X}_i+{ L}_i^{T}{ B}_i^T+{ B}_i{ L}_i-\mu { X}_i^{T}{ E}_i^T < 0, \end{aligned}$$

(3.7b)

and (3.1c) hold, where ${ P}_i={ X}_i^{-1},$ then the closed-loop system (3.6) is finite-time stable with respect to $(c_1, c_2, { R}, T_f, \sigma )$ for an arbitrary switching signal satisfying the average dwell time

$$\begin{aligned} \tau _a>\tau ^*_a=\frac{\beta }{lnc_2\lambda _2-lnc_1\lambda _1-\gamma }. \end{aligned}$$

(3.8)

In this case, the gain matrix is ${ K}_i={ L}_i{ X}_i^{-1}$.

Proof

Pre- and post-multiplying (3.7a) and (3.7b) by ${ X}_i^{-T}$ and ${ X}_i^{-1}$, it can be obtained that

$$\begin{aligned}&\displaystyle {{ E}_i}^T{ P}_i={{ P}_i}^T{ E}_i \ge 0,\end{aligned}$$

(3.9)

$$\begin{aligned}&\displaystyle { A}_i^T{ P}_i+{ P}_i^{T}{ A}_i+{ K}_i^T{ B}_i^T{ P}_i+{ P}_i^{T}{ B}_i{ K}_i-\mu { E}_i^T{ P}_i < 0, \end{aligned}$$

(3.10)

and (3.10) is equivalent to

$$\begin{aligned} \bar{{ A}}_i^{T}{ P}_i+{ P}_i^{T}\bar{{ A}}_i^{T}-\mu { E}_i^T{ P}_i<0, \end{aligned}$$

(3.11)

where $\bar{{ A}}_i={ A}_i+{ B}_i{ K}_i$. Combining (3.9), (3.11) and (3.1c), using Theorem 1, the FTS of the corresponding closed-loop system (3.6) with the average dwell time scheme (3.8) can be obtained.

Next, the finite-time stabilization of system (2.7) via the state feedback controller defined by (3.5), such that the corresponding closed-loop system

$$\begin{aligned} { E}_{\sigma (t)} ~ _{t_0}^CD_t^\alpha { x}(t)=\bar{{ A}}_{\sigma (t)}{ x}(t)+{ C}_{\sigma (t)}{ w}(t) \end{aligned}$$

(3.12)

is finite-time bounded, will be investigated, where $\bar{{ A}}_{\sigma (t)}={ A}_{\sigma (t)}+{ B}_{\sigma (t)}{ K}_{\sigma (t)}$.

Theorem 4

Given the constants $\mu >0$ and $\lambda >1$, for any $i,j\in S, i\ne j$, if there exist nonsingular matrices ${ L}_i, { X}_i, {Z}_i>0, { Q}_i>0$ such that the following inequalities

$$\begin{aligned}&\displaystyle {{E}_i}{ X}_i={{ X}_i}^T{ E}_i^T \ge 0, \end{aligned}$$

(3.13a)

$$\begin{aligned}&\displaystyle \left[ \begin{array}{cc} {{ X}_i}^T{ A}_i^T+{ A}_i{ X}_i+{ L}_i^{T}{ B}_i^T+{ B}_i{ L}_i-\mu { X}_i^{T}{ E}_i^T &{} { C}_i \\ { C}_i^T &{} -{ Q}_i \\ \end{array} \right] < 0, \end{aligned}$$

(3.13b)

and (3.3c) hold, where ${ P}_i={ X}_i^{-1},$ then system (3.12) is finite-time bounded with respect to $(c_1, c_2, d, { R}, T_f, \sigma )$ for an arbitrary switching signal satisfying the average dwell time

$$\begin{aligned} \tau _a>\tau ^*_a=\frac{\beta ^{'}}{lnc_2\lambda _2-ln(c_1\lambda _1+d)-\gamma ^{'}}. \end{aligned}$$

(3.14)

In this case, the gain matrix is ${ K}_i={ L}_i{ X}_i^{-1}$.

Proof

By pre-multiplying (3.13a) by ${ X}_i^{-T}$ and post-multiplying by ${ X}_i^{-1}$, it can be obtained that

$$\begin{aligned} {{ E}_i}^T{ P}_i={{ P}_i}^T{ E}_i\ge 0, \end{aligned}$$

(3.15)

and by pre- and post-multiplying (3.13b) by

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} {{ X}_i}^{-T} &{} 0 \\ 0 &{} { I} \\ \end{array} \right] ,~~~~\left[ \begin{array}{c@{\quad }c} {{ X}_i^{-1}} &{} 0 \\ 0 &{} { I} \\ \end{array} \right] , \end{aligned}$$

it can be obtained that

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} { A}_i^T{ P}_i+{ P}_i^{T}{ A}_i+{ K}_i^T{ B}_i^T{ P}_i+{ P}_i^{T}{ B}_i{ K}_i-\mu { E}_i^T{ P}_i &{} { P}_i^{T}{ C}_i \\ { C}_i^T{ P}_i &{} -{ Q}_i \\ \end{array} \right] <0; \end{aligned}$$

(3.16)

(3.16) is equivalent to

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} \bar{{ A}}_i^{T}{ P}_i+{ P}_i^{T}\bar{{ A}}_i^{T}-\mu { E}_i^T{ P}_i &{} { P}_i^{T}{ C}_i \\ { C}_i^T{ P}_i &{} -{ Q}_i \\ \end{array} \right] <0, \end{aligned}$$

(3.17)

where $\bar{{ A}}_i={ A}_i+{ B}_i{ K}_i$; combining (3.15), (3.17) and (3.3c) and using Theorem 2, the FTB of system (3.12) can be obtained. $\square$

Remark 5

In Theorem 3 and Theorem 4, we mainly study the state feedback control law to guarantee the FTS and FTB of the closed-loop systems. This is a general and more convenient way to design the control law compared to most of the existing literature; however, it should be noted that not all states can be obtained in practical applications. Therefore, we will develop the output feedback control design in our future work.

Remark 6

From a computational point of view, the given conditions from Theorem 1 to Theorem 4 are all the standard linear matrix inequalities, which implies that these conditions can be solved by employing the LMI control toolbox in MATLAB. In future research, it will be interesting to employ the proposed method to discuss finite-time stabilization for repetitive control systems [37, 40].

Fig. 1

The switching signal $\sigma (t)$

Fig. 2

The trajectory of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$

Fig. 3

The trajectory of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$ under the state feedback controller

4 Numerical Example

It was analyzed in [11] that if an electrical circuit contains at least one mesh consisting of branches with only an ideal super capacitor and voltage sources or contains at least one node with branches with super coils, then its matrix E is singular since it has at least one zero row. This follows from the fact that the equation written using Kirchhoff’s voltage law or Kirchhoff’s current law is an algebraic equation. In this special case, the electrical circuit can be described as a singular fractional system governed by (6a) and (6b) in [11]. Then, in this paper, we consider a switching-type singular fractional-order circuit system with the following two subsystems, where $x_1(t)$ and $x_2(t)$ represent the voltages of different capacitances and u(t) represents the source voltage of the electrical circuit:

$$\begin{aligned} { E}_1= & {} \left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 0 \\ \end{array} \right] , { A}_1=\left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right] , { B}_1=\left[ \begin{array}{c@{\quad }c} 0 &{} 1 \\ 1 &{} 0 \\ \end{array} \right] ,\\ { E}_2= & {} \left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 0 \\ \end{array} \right] , { A}_2=\left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] , { B}_2=\left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] , \end{aligned}$$

and then, it can be obtained from Lemma 6 that two subsystems are regular and impulse-free. The corresponding parameters are specified as follows: $\alpha =0.5, c_1=1, c_2=100, T_f=2, { R}={ I}$ and $N_0=0$,

$$\begin{aligned} { \varPi }_1={ \varPi }_2=\left[ \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} 0 \\ \end{array} \right] . \end{aligned}$$

Applying Theorem 3 and setting $\mu =0.1, \lambda =1.1$, a feasible solution can be obtained

$$\begin{aligned} { X}_1= & {} \left[ \begin{array}{c@{\quad }c} 50.7555 &{} 0 \\ 0 &{} -0.4175 \\ \end{array} \right] ,\quad { X}_2=\left[ \begin{array}{c@{\quad }c} 50.7555 &{} 0 \\ 0 &{} 1.0066 \\ \end{array} \right] , \\ { L}_1= & {} \left[ \begin{array}{c@{\quad }c} 0 &{} -25.7953 \\ -73.5954 &{} 0 \\ \end{array} \right] ,\quad { L}_2=\left[ \begin{array}{c@{\quad }c} -73.5954 &{} 0 \\ 0 &{} -26.3844 \\ \end{array} \right] , \end{aligned}$$

and by a simple calculation, we have

$$\begin{aligned} { P}_1= & {} { X}_1^{-1}=\left[ \begin{array}{c@{\quad }c} 0.0197 &{} 0 \\ 0 &{} -2.3950 \\ \end{array} \right] ,\quad { P}_2={ X}_2^{-1}=\left[ \begin{array}{c@{\quad }c} 0.0197 &{} 0 \\ 0 &{} 0.9934 \\ \end{array} \right] ,\\ { Z}_1= & {} \left[ \begin{array}{c@{\quad }c} 0.0197 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] ,\quad { Z}_2=\left[ \begin{array}{c@{\quad }c} 0.0197 &{} 0 \\ 0 &{} 0.5 \\ \end{array} \right] , \end{aligned}$$

and thus, it can be obtained that the gain matrices are

$$\begin{aligned} { K}_1={ L}_1{ P}_1=\left[ \begin{array}{c@{\quad }c} 0 &{} 61.7786 \\ -1.45 &{} 0 \\ \end{array} \right] ,~~~~~~~ { K}_2={ L}_2{ P}_2=\left[ \begin{array}{c@{\quad }c} -1.45 &{} 0 \\ 0 &{} -26.2106 \\ \end{array} \right] , \end{aligned}$$

and then the closed-loop systems matrices are

$$\begin{aligned} { A}_1+{ B}_1{ K}_1=\left[ \begin{array}{c@{\quad }c} -0.45 &{} 0 \\ 0 &{} 60.7786 \\ \end{array} \right] ,~~~~~~~ { A}_2+{ B}_2{ K}_2=\left[ \begin{array}{c@{\quad }c} -0.45 &{} 0 \\ 0 &{} -25.2106 \\ \end{array} \right] . \end{aligned}$$

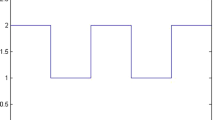
From Theorem 1, we can compute that $\lambda _1=1$ and $\lambda _2=0.0197,$ and from (3.8), $\tau _a^*=0.5966$. In fact, the value of $\tau _a$ only needs to satisfy $\tau _a>0.5966$, and without loss of generality, we can choose $\tau _a=0.6$; then, Fig. 1 shows the switching signal $\sigma (t)$.

First, a simulation was carried out for the system with ${ x}(0)=(1~0)^T$ and ${ u}(t)=0$. Figure 2 shows the trajectory of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$ under the average dwell time switching. It can be seen from Fig. 2 that the value of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$ exceeds the given threshold $c_2=100$, which means that the FTS of the system cannot be guaranteed with respect to $(1,100,{ I},2,\sigma )$.

Second, let us consider the finite-time stabilization through the proposed state feedback controller of the considered system. Figure 3 plots the trajectory of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$ of the corresponding closed-loop system over 0–2 s. From Fig. 3, we can conclude that for any switching signal $\sigma (t)$ with an average dwell time $\tau _a>0.5966$, the value of ${ x}^T(t){{ E}_{\sigma (t)}}^T{ R}{ E}_{\sigma (t)}{ x}(t)$ does not exceed $c_2$, which implies that the resulting closed-loop system (3.6) is finite-time stable with respect to $(1,100,{ I},2,\sigma )$.

As a result, with the help of a newly designed Caputo fractional-order differentiator in [25], a Simulink model can be constructed to present the simulations of the open-loop system and the corresponding closed-loop system under the given controller via Theorem 3. Hence, from the above discussions and simulations, the designed state feedback controller for a fractional-order switched singular system is effective.

5 Conclusion

The finite-time stability and stabilization of a class of fractional-order switched singular continuous-time systems with order $0<\alpha <1$ are investigated in this paper. First, definitions of FTS, FTB and consistent switching are introduced, and a consistent projector is given to guarantee the consistent switching of fractional-order switched singular systems. Second, by choosing suitable multiple Lyapunov functions, the sufficient conditions of FTS and FTB via the average dwell time technique are derived. Finally, LMI-based state feedback controllers are designed.