1 Introduction

According to ITRS reports [17], power consumption and reliability are the two major challenges eroding Moore’s law. Reliability is directly affected by noise and variation [6]. Therefore, noise margin (NM) is a fundamental concept in digital electronics, indicating how much a circuit is tolerant of noise. Literally, it determines the amount by which a signal exceeds the threshold for proper and acceptable logic values. Sensitivity to noise can be reduced by wider NMs; hence, the correct functionality of digital circuits will not be disrupted by small-amplitude noises.

The concept of noise tolerance is very important in binary digital circuits. It is an even more consequential issue in multiple-valued logic (MVL) circuits, where there are more than two logic levels. The importance is due to the fact that voltage levels come closer to one another and form narrower voltage zones. According to the comparisons in [40], a ternary inverter is more vulnerable to noise than a binary counterpart. Therefore, one must carefully consider proper NMs when designing MVL circuits. However, it seems that the deceptive simplicity of the subject has confused many researchers so far. The voltage transfer characteristic (VTC) of the most of the presented ternary [1, 2, 13, 18, 22, 23, 28, 31, 33, 34, 37, 42], quaternary [2, 10, 22, 29, 37], and quinary [2] inverters suffer from nonuniformity and reduced NMs. The problem becomes even more serious in today’s ongoing supply voltage reduction, and it is also widely influential both in combinational logic gates and in static random access memories (SRAMs).

Static noise margin (SNM) indicates the maximum tolerated amount of voltage noise by which the cross-coupled inverters within an SRAM do not flip the cell [5]. The SNM value is directly dependent upon the VTC curves of the cross-inverters. SRAMs with reduced SNMs, such as the ternary ones presented in [1, 24, 39, 43], do not provide sufficient reliability and stability [5, 32].

This paper aims to clarify the correct VTC shape of a multiple-valued inverter for higher noise tolerance capability in an analytical reviewing manner. The rest of the paper is organized as follows: A short study on the VTC and NM of a binary inverter is provided in Sect. 2. The necessary basic definitions are also given in this section to make the rest of the paper more comprehensible. Section 3 gives a full discussion about correct VTC of a ternary inverter, and the explanation is extended beyond ternary logic in Sect. 4. Section 5 contains a brief review on the most well-known ternary and quaternary inverters in the literature. Then, simulation results, comparisons, and investigations into the effects of process variation on NM are provided. Finally, Sect. 6 concludes the paper.

2 Noise Margin in Binary Logic

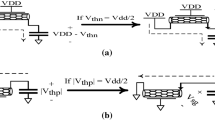
Binary inverter is the simplest logic gate. It is always considered as the reference circuit for studying the attributes of the integrated circuit logic families. As it is illustrated in Fig. 1, the VTC curve can model the behavioral characteristic of an inverter. There are five critical voltage points:

Fig. 1
figure 1

Typical VTC curve of a binary inverter

Full size image

  • VOH: The output voltage (Vout) at the first − 1 slope point (when Vin increases).

  • VOL: The output voltage (Vout) at the second − 1 slope point (when Vin increases).

  • VIL: The input voltage (Vin) at the first − 1 slope point (when Vin increases). It specifies the maximum input voltage, while the output is still High.

  • VIH: The input voltage (Vin) at the second − 1 slope point (when Vin increases). It specifies the minimum input voltage, while the output is still Low.

  • VM: The midpoint where Vout = Vin.

The Low and High states of NM, NML and NMH, can be defined by the following equations (Eqs. 1, 2):

$$ {\text{NM}}_{\text{L}} = \left| { \, V_{\text{IL}} {-} \, V_{\text{OL}} } \right| $$
(1)
$$ {\text{NM}}_{\text{H}} = \left| {V_{\text{OH}} {-} \, V_{\text{IH}} } \right| $$
(2)

Then, NM is the minimum of NML and NMH (Eq. 3):

$$ {\text{NM}} = \hbox{min} \left( {{\text{NM}}_{\text{L}} ,{\text{ NM}}_{\text{H}} } \right) $$
(3)

This is the basic definition of NM one can find in many VLSI text books [3]. However, the worst-case noise condition occurs when there are such noise sources on all inputs of an infinite chain of logic gates that intensify false voltage levels and upset logic values [14]. This condition is equivalent to a pair of cross-coupled inverters in such a way that the output of one inverter is the input of the other one (Fig. 2a) [14]. This situation is exactly similar to what happens in an SRAM cell. Figure 2b shows the overlapping transfer characteristics of the two cross-coupled inverters. It is also known as SRAM butterfly curve or eye diagram, expressing SNM, which is calculated by Eq. 4. The inscribed rectangles inside the loops (Fig. 2b) visually explain SNM properties:

Fig. 2
figure 2

Worst-case noise condition, a two cross-coupled inverters, and b their eye diagram

Full size image
  1. 1.

    Worst-case equal SNM happens if the rectangles become squares.

  2. 2.

    Worst-case single-sided SNM takes place when a rectangle becomes a vertical or horizontal line.

  3. 3.

    Worst-case symmetrical SNM occurs when the two rectangles have the same numerical area.

  4. 4.

    Worst-case uniform SNM happens when SNM is both equal and symmetrical as the same time.

    $$ {\text{SNM}} = \hbox{min} \left( {{\text{SNM}}_{1} ,{\text{ SNM}}_{2} ,{\text{ SNM}}_{3} ,{\text{ SNM}}_{4} } \right) $$
    (4)

In one case, two cross-inverters might make an equal, but not symmetrical condition (Fig. 3a). In another situation, two other ones with different voltage characteristics may create a symmetrical, but not equal condition (Fig. 3b). In order to have maximum noise endurance, uniform SNMs are required (Fig. 3c). One of the prime requisites for following this target in binary logic is that \( V_{\text{M}} \, = \,\frac{1}{2}V_{\text{DD}}\) for both inverters.

Fig. 3
figure 3

Static noise margins, a equal but not symmetrical, b symmetrical but not equal, and c uniform: equal and symmetrical

Full size image

3 Noise Margin in Ternary Logic

MVL is a popular subject among researchers. There is an international annual symposium about MVL (ISMVL), held for 48 years [16]. MVL is a propositional calculus in which there are more than two logic values. There are specifically three logic values in ternary logic, {0, 1, 2}3, implemented in digital electronics by the voltage levels 0 V, \( \frac{1}{2}V_{\text{DD}} \), and VDD, respectively [9]. The operation of negative (denoted by −), positive (denoted by +), and standard ternary inverters (NTI, PTI, and STI) is given in Table 1 [28]. Among them, STI, whose VTC is shown in Fig. 4, is the most common and practical. Although the functionality of an inverter is crystal clear and easy to understand, the accurate VTC curve of the standard ternary inverter seems to be a deceptive matter.

Table 1 Truth tables of PTI, NTI, and STI
Full size table
Fig. 4
figure 4

Typical VTC curve of a ternary inverter

Full size image

Several ternary inverters have recently been presented in the literature [1, 2, 13, 18, 22, 23, 28, 31, 33, 34, 37, 42]. Their behavioral characteristic is in a way that the entire voltage range is divided into three parts (Fig. 5a). In spite of its apparent logical division, this segmentation does not lead to full efficiency in terms of noise tolerance. The high number of inappropriate VTC curves in the literature indicates the importance of clarification on this subject. This paper exploits different ways to demonstrate that the input voltage range in the VTC curve must be divided into four parts (Fig. 5b), similar to the way that has been done in [7, 11, 21, 25, 26, 30, 38]. Unlike binary logic, NMs need to be calculated four times in ternary logic (Eqs. 5–8 [11]). These equations are the extended version of the ones required to calculate NM in binary logic.

$$ {\text{NM}}_{{{\text{L}},2 \to 1}} = \left| { \, V_{{{\text{IL}},2 \to 1}} {-} \, \left( {V_{{{\text{O}},1}} {-} \, \frac{1}{2}V_{\text{DD}} } \right)} \right| $$
(5)
$$ {\text{NM}}_{{{\text{H}},2 \to 1}} = \left| { \, \left( {V_{{{\text{O}},2}} {-} \, \frac{1}{2}V_{\text{DD}} } \right) \, {-} \, V_{{{\text{IH}},2 \to 1}} } \right| $$
(6)
$$ {\text{NM}}_{{{\text{L}},1 \to 0}} = \left| {\left( {V_{{{\text{IL}},1 \to 0}} {-} \, \frac{1}{2}V_{\text{DD}} } \right) \, {-} \, V_{{{\text{O}},0}} } \right| $$
(7)
$$ {\text{NM}}_{{{\text{H}},1 \to 0}} = \left| {V_{{{\text{O}},1}} {-} \, \left( {V_{{{\text{IH}},1 \to 0}} {-}\frac{1}{2}V_{\text{DD}} } \right)} \right| $$
(8)
Fig. 5
figure 5

VTC curve of a standard ternary inverter, a divided into three parts and b divided into four parts

Full size image

Then, NM is the minimum amount (Eq. 9):

$$ {\text{NM}}_{\text{Ternary}} = \, \hbox{min} \left( {{\text{NM}}_{{{\text{L}},2 \to 1}} ,{\text{ NM}}_{{{\text{H}},2 \to 1}} ,{\text{ NM}}_{{{\text{L}},1 \to 0}} ,{\text{ NM}}_{{{\text{H}},1 \to 0}} } \right) $$
(9)

In the above equations, VO,0, VO,1, and VO,2 are the output voltages indicating logic values ‘0,’ ‘1,’ and ‘2,’ respectively. Furthermore, \( {{V_{{{\text{IL}},2 \to 1}} } \mathord{\left/ {\vphantom {{V_{{{\text{IL}},2 \to 1}} } {V_{{{\text{IH}},2 \to 1}} }}} \right. \kern-0pt} {V_{{{\text{IH}},2 \to 1}} }} \) and \( {{V_{{{\text{IL}},1 \to 0}} } \mathord{\left/ {\vphantom {{V_{{{\text{IL}},1 \to 0}} } {V_{{{\text{IH}},1 \to 0}} }}} \right. \kern-0pt} {V_{{{\text{IH}},1 \to 0}} }} \) are the VIL/VIH parameters when the curve changes from ‘2’ to ‘1’ and from ‘1’ to ‘0,’ respectively. These critical voltage points are also depicted in Figs. 4 and 5. Figure 5 shows ideal curves in which the VIL and VIH points coincide with each other. Please note that taking this ideality into consideration does not affect the main point of this paper. According to Eqs. 5–8 and Table 2, the inverter with a VTC curve divided into four parts (Fig. 5b) has not only identical Low and High states of NM but also a higher NM than the one with three parts (Fig. 5a). Figure 5a and b has NMs equal to \( \frac{1}{6}V_{\text{DD}} \) and \( \frac{1}{4}V_{\text{DD}} \), respectively.

Table 2 Noise margin values of ternary inverters
Full size table

Although the numerical data in Table 2 clearly reveal the superiority of Fig. 5b, the advantage is also demonstrated visually in this paper. Figure 6 shows the two overlapping curves of Fig. 5a and b. As it is clear, the worst-case noise condition, SNM, is uniform in Fig. 6b. This will certainly bring about higher noise endurance. In Fig. 6a, a weak noise with low amplitude can cause malfunction and a change in logic when the input and output are at \( \frac{1}{2}V_{\text{DD}} \).

Fig. 6
figure 6

Static noise margin of a Fig. 5a and b Fig. 5b

Full size image

4 Noise Margin at Higher Radixes

This topic can cover other MVL inverters at higher radixes. In general, a standard r-valued (or radix r) inverter is defined by Eq. 10. The accurate VTC curve of a standard r-valued inverter must be divided into 2r − 2 parts, not into r parts. For instance, the VTC of a standard quaternary inverter (SQI) must be similar to what is shown in Fig. 7a with six parts. This results in the worst-case uniform SNM (Fig. 7b). In contrast with the mentioned proper segmentation, the curves in [10, 22, 29, 37] are divided into four parts (Fig. 8a). Consequently, the overlapping VTC curves (Fig. 8b) do not bring uniformity. As far as we know, there have been no quaternary inverters with entirely correct VTC in the literature yet. The available ones are not useful in practice because of their vanishing NMs.

$$ \bar{a} = (r - 1) - a $$
(10)
Fig. 7
figure 7

Behavioral characteristic of a standard quaternary inverter whose VTC is divided into six parts, a VTC curve and b overlapping VTC curves resulting in uniformity

Full size image
Fig. 8
figure 8

Behavioral characteristic of a standard quaternary inverter whose VTC is divided into four parts, a VTC curve and b overlapping VTC curves

Full size image

NM has to be calculated six times in quaternary logic (Eqs. 11–16), and the minimum amount as always represents NM.

$$ {\text{NM}}_{{{\text{L}},3 \to 2}} = \left| {V_{{{\text{IL}},3 \to 2}} {-} \, \left( {V_{{{\text{O}},2}} {-} \, \frac{2}{3}V_{\text{DD}} } \right)} \right| $$
(11)
$$ {\text{NM}}_{{{\text{H}},3 \to 2}} = \left| {\left( {V_{{{\text{O}},3}} {-} \, \frac{2}{3}V_{\text{DD}} } \right) \, {-} \, V_{{{\text{IH}},3 \to 2}} } \right| $$
(12)
$$ {\text{NM}}_{{{\text{L}},2 \to 1}} = \left| {\left( {V_{{{\text{IL}},2 \to 1}} {-} \, \frac{1}{3}V_{\text{DD}} } \right) \, {-} \, \left( {V_{{{\text{O}},1}} {-} \, \frac{1}{3}V_{\text{DD}} } \right)} \right| $$
(13)
$$ {\text{NM}}_{{{\text{H}},2 \to 1}} = \, \left| {\left( {V_{{{\text{O}},2}} {-} \, \frac{1}{3}V_{\text{DD}} } \right) \, {-} \, \left( {V_{{{\text{IH}},2 \to 1}} {-} \, \frac{1}{3}V_{\text{DD}} } \right)} \right| $$
(14)
$$ {\text{NM}}_{{{\text{L}},1 \to 0}} = \left| {\left( {V_{{{\text{IL}},1 \to 0}} {-} \, \frac{2}{3}V_{\text{DD}} } \right) \, {-} \, V_{{{\text{O}},0}} } \right| $$
(15)
$$ {\text{NM}}_{{{\text{H}},1 \to 0}} = \left| {V_{{{\text{O}},1}} {-} \, \left( {V_{{{\text{IH}},1 \to 0}} {-} \, \frac{2}{3}V_{\text{DD}} } \right)} \right| $$
(16)

Furthermore, NM can be calculated in a standard r-valued inverter by Eq. 17, where NMLs and NMHs are estimated r − 1 time(s).

$$ {\text{for}}\;i \, = \, 1\;{\text{to}}\;\left( {r - 1} \right)\;{\text{calculate:}} $$
(17)
$$ {\text{NM}}_{{{\text{L}},(r - i) \to (r - i - 1)}} = \left| {\left( {V_{{{\text{IL}},(r - i) \to (r - i - 1)}} - \frac{(r - 1) - (r - i)}{(r - 1)}V_{\text{DD}} } \right) - \left( {V_{{{\text{O}},(r - i - 1)}} - \frac{(r - 1) - (i)}{(r - 1)}V_{\text{DD}} } \right)} \right| $$
(17.1)
$$ {\text{NM}}_{{{\text{H}},(r - i) \to (r - i - 1)}} = \left| {\left( {V_{{{\text{O}},(r - i)}} - \frac{(r - 1) - (i)}{(r - 1)}V_{\text{DD}} } \right) - \left( {V_{{{\text{IH}},(r - i) \to (r - i - 1)}} - \frac{(r - 1) - (r - i)}{(r - 1)}V_{\text{DD}} } \right)} \right| $$
(17.2)

In the case of uniform arrangement of VTC, the Low and High states of NM become similar (the same as Table 2 for the ternary inverter of Fig. 5b). As a result, it is not required to calculate different NMs several times since all the NMLs and NMHs return the same value. In this situation, we can calculate NM only once by a single equation such as Eq. 18:

$$ {\text{NM}} = \left| {\left( {V_{{{\text{O}},(r - 1)}} - \frac{(r - 2)}{(r - 1)}V_{\text{DD}} } \right) - V_{{{\text{IH}},(r - 1) \to (r - 2)}} } \right| $$
(18)

Although uniformity is a necessary condition for maximizing NM, it is not sufficient. A uniform VTC is not necessarily an ideal one. In an ideal curve, the shaded areas are equally become as large as possible. In other words, the VIL and VIH points coincide with each other in an ideal VTC curve, whose NM can be calculated by Eq. 19. In the case of ideality, \( V_{{{\text{O}},r - 1}} \) would be VDD, \( V_{{{\text{IH}},(r - 1) \to (r - 2)}} \) would be \( \frac{{V_{\text{DD}} }}{ 2r - 2} \), and subsequently Eqs. 18 and 19 would be equal.

$$ {\text{NM}}_{\text{Ideal}} = \frac{{V_{\text{DD}} }}{2r - 2} $$
(19)

5 Literature Review and Simulation Results

5.1 Brief Review of MVL Inverters

Carbon nanotube field-effect transistor (CNTFET) is a popular technology for designing MVL circuits. Most of the recent works presented in the literature are based on this nanoscale emerging technology [1, 2, 7, 10, 11, 21,22,23,24,25, 28,29,30,31, 33, 34, 36, 37, 39, 42, 43]. Its popularity is mainly because of its flexibility in designing multi-threshold circuits, which is a definite necessity in MVL circuitry so as to detect different voltage levels. Unlike CNTFET, silicon transistors are inherently single-threshold devices [15]. Further explanations about CNTFET are beyond the aim of this paper, and one can find additional information in many references such as [8, 12, 27].

The designs in [23, 28] are the most successful and high-performance standard ternary inverters presented in the literature so far. The one in [23] is a CMOS-like structure, in which pull-up and pull-down networks connect the output node to power supply and ground, respectively (Fig. 9a). TP1 and TN1 are connected at the same time if the output value is to be ‘1.’ Then, two diode-connected transistors, TP3 and TN3, divide voltage to produce \( \frac{1}{2}V_{\text{DD}} \). In addition, TP2 and TN2 are, respectively, activated when the output value is supposed to be ‘2’ and ‘0.’

Fig. 9
figure 9

Standard ternary inverters presented in a [23], b [7], c [28], and d [30]

Full size image

The STI of [7] has the same structure as [23], but with some different transistor sizes (Fig. 9b). The diameter of carbon nanotubes (DCNT) determines threshold voltage (VTh) of transistor (Eq. 20) [8, 28]. DCNT of TP2 and TN2 has been reduced in [7] from 0.783 to 0.626 nm with the aim of improving SNM for the construction of a ternary SRAM. This is the only difference between the designs in [23] and its modified version in [7].

$$ V_{{{\text{Th,}}\;{\text{CNTFET}}}} \approx \frac{0.43}{{D_{\text{CNT}} ({\text{nanometer}})}} $$
(20)

The other well-known STI, presented in [28] (Fig. 9c), is based on the fact that STI is the average of PTI and NTI (Table 1). TP1 and TN1 generate the negative output value. TP2 and TN2 produce the positive output value. Afterward, TP3 and TN3, which are always ON, produce the average voltage level. Voltage division only occurs when PTI and NTI have different values.

The last inverter [30] (Fig. 9d) is the modified version of [28]. The authors have reduced DCNT from 0.783 to 0.626 nm for TP1 and TN2 with the purpose of increasing SNM. Different transistor sizes have been used to make the SRAM cell less vulnerable to noise. Moreover, two stacked transistors (TP4 and TN4) have been added to reduce static power consumption. The previous STIs have six CNTFETs each, whereas the one in [30] has eight ones. The modified STIs in [7, 30] are also selected in this paper to show how effective transistor sizing is in the subject of noise tolerance.

Additionally, Fig. 10 displays two high-performance standard quaternary inverters, which are in fact the extended versions of the STIs reviewed above. The main concept of the first SQI [29] (Fig. 10a) has been taken from the STI presented in [28]. The first three binary inverters, constructed by (TP1 and TN1) and (TP2 and TN2) and (TP3 and TN3), are, respectively, positive, neutral, and negative quaternary inverters (PQI, NeQI, and NQI), whose truth tables are depicted in Table 3. The final output is equal to their average amount. This is what happens in brief:

Fig. 10
figure 10

Standard quaternary inverters presented in a [29] and b [10]

Full size image
Table 3 Truth tables of PQI, NeQI, NQI, and SQI
Full size table

  • If the input value is ‘0,’ no voltage division occurs and the output node is only connected to VDD through TP7 and TP8.

  • If the input value becomes ‘1,’ TN8 is also activated. As a result, voltage division takes place through one n type (TN8) and two parallel p type (TP7 and TP8) transistors. The parallel p type transistors produce less equivalent resistance than the single n type one (\( R_{\rm PUN}\,=\,\frac{1}{2}R_{{\rm PDN}} \)). Therefore, the output voltage is \( \frac{2}{3}V_{\text{DD}} \).

  • If the input value becomes ‘2,’ TP7 turns off and TN7 switches on instead. As a result, voltage division takes place through one p type (TP8) and two parallel n type (TN7 and TN8) transistors. The parallel n type transistors produce less equivalent resistance than the single p type one (\( R_{\rm PDN}\,=\,\frac{1}{2}R_{{\rm PUN}} \)). In this case, the output voltage is equal to \( \frac{1}{3}V_{\text{DD}} \).

  • If the input value becomes ‘3,’ TP8 turns off. Consequently, the output node is only connected to the ground through TN7 and TN8.

The second SQI [10] (Fig. 10b) is the extended version of the STI presented in [23]. It has different pull-up and pull-down networks which are activated whenever needed. In short:

  • If the input value is ‘0,’ TP1 is activated and links the output node to the power supply. Please note that TP2 and TP3 are also ON in this case.

  • If the input value becomes ‘1,’ TP1 is deactivated. Instead, TN3 switches on. Voltage division occurs through one p type (TP5) and two n type (TN4 and TN5) diode-connected transistors. The n type ones are in series with more equivalent resistance than the single p type one (\( R_{\rm PUN}\,=\,\frac{1}{2}R_{{\rm PDN}} \)). Therefore, the output voltage equals \( \frac{2}{3}V_{\text{DD}} \) in this case. Although TP3 is also ON, it has no effect on voltage division since it is short-circuited by TP2.

  • If the input value becomes ‘2,’ TP2 is not activated any longer. This time, TN3 is short-circuited by TN2, which is ON now. Voltage division is caused by one n type (TN5) and two p type (TP4 and TP5) diode-connected transistors. The p type ones are in series producing more equivalent resistance than the single n type one (\( R_{\rm PDN}\,=\,\frac{1}{2}R_{{\rm PUN}} \)). As a result, the output voltage is \( \frac{1}{3}V_{\text{DD}} \) in this situation.

  • If the input value becomes ‘3,’ there are not any active p type transistors since TP3 also switches off. TN1 switches on and leads to the connection of the output node to the ground. TN2 and TN3 are also ON.

The first and second SQIs have 16 and 10 CNTFETs, respectively. Different voltage levels are detected in MVL circuits by proper threshold voltage adjustment for transistors. The diameters are also indicated in Figs. 9 and 10.

5.2 Simulation Results and Comparisons

VTC curve is the key element which quantifies NM and SNM. HSPICE DC sweep analysis is carried out to plot VTC. It performs a series of operating point analyses, changing the voltage of a selected source in some increasing steps, to give a DC transfer curve. The STIs and SQIs are simulated with the 32-nm Stanford CNTFET model [8, 41]. Simulations are carried out in 0.9 V power supply at room temperature. Since all of the STIs and SQIs have been designed with CNTFET in their original papers, the same technology has been used to run the simulations in this paper.

The VTC curves of the STIs are illustrated in Fig. 11. NM values are also presented in Table 4. The designs presented in [7, 30] have the largest NM because they maintain wider logic ‘1’ than the others. Similar to Fig. 5b, they divide the entire curve into four parts. As a result, they have about 38.1% higher NM than their former versions [23, 28]. NM improvement is simply achieved by a slight modification in transistor sizing. They have also 33.3% higher NM than the design in [28].

Fig. 11
figure 11

Voltage transfer characteristic (VTC) curves of standard ternary inverters (STIs)

Full size image
Table 4 Comparison of noise margin values in STIs
Full size table

The STI butterfly curves, indicating SNM, are depicted in Figs. 12, 13, 14, and 15. SNM values are also reported in Table 4. The largest SNM belongs to the STI in [30], whose curve is divided into four parts with sharp corners and steep drops. Among the rest, the design in [28] has the next-largest SNM although it does not divide the VTC curve properly. The reason is that it has steep drops and sharp corners around logic ‘1,’ which results in larger inscribed rectangles (or squares) in the butterfly curves. Moreover, a VTC with narrow transition width (TW) and wide logic swing (LS) is closer to the ideal form. TW is the amount of input voltage change (VTW) by which the output voltage changes from one state to another. There are two and three TWs in the standard ternary and quaternary inverters, respectively. VTWs can generally be calculated r − 1 times in radix r by Eq. 21, where \( 1 \le i \le r - 1 \).

$$ V_{{{\text{TW}},i \to (i - 1)}} = V_{{{\text{IH}},i \to (i - 1)}} - V_{{{\text{IL}},i \to (i - 1)}} $$
(21)
Fig. 12
figure 12

Worst-case noise condition of the STI in [23] a without process variation and b with process variation

Full size image
Fig. 13
figure 13

Worst-case noise condition of the STI in [7] (a) without process variation and (b) with process variation

Full size image
Fig. 14
figure 14

Worst-case noise condition of the STI in [28] a without process variation and b with process variation

Full size image
Fig. 15
figure 15

Worst-case noise condition of the STI in [30] a without process variation and b with process variation

Full size image

On the other hand, LS is the amount of voltage space (VLS) between two adjacent logic states. Ideally, the entire voltage range must be divided into r − 1 equal zones so that the voltage levels are situated the farthest apart from each other. Circuits with full voltage swings are always preferred. There are r − 1 LSs in a standard r-valued inverter, calculated by Eq. 22, where \( 1 \le i \le r - 1 \).

$$ V_{{{\text{LS}},i \to (i - 1)}} = V_{{{\text{O}},i}} - V_{{{\text{O}},(i - 1)}} $$
(22)

All of the STIs have the same LSs (Table 4). Nevertheless, the ones in [28, 30] have 10 mV narrower TWs than the other ones. As a result, the VIL and VIH points are closer to each other. This fact helps to inscribe more square-like, larger rectangles in the corresponding butterfly curves (Figs. 14, 15).

Despite its many great advantages, CNTFET is still in development and suffers from imperfect fabrication [4, 12]. Some manufacturing imperfections are the presence of metallic CNTs, chirality drift, CNT doping variations, and density fluctuations [4]. The most problematic issue regarding the topic of this paper is that the diameter of carbon nanotubes is subject to 0.04–0.2 nm variations [35]. Please note that CNTFET is not the only device which is sensitive to process variation. Fluctuations of electrical parameters are also significant in manufacturing of sub-45-nm CMOS devices [19, 20]. According to [19], 45-nm CMOS technology is under the influence of a number of variations such as random dopant fluctuation, line-edge and line-width roughness, and several variations in the gate dielectric.

The impact of process variation on NM of the selected STIs and SQIs is also studied in this section. Process variation may reduce circuit resistance against noise. Process variation analyses have been carried out by performing 100 Monte Carlo runs, in which the distribution of diameters is assumed as Gaussian with 6-sigma distribution. Moreover, the highest expected variability for each mean diameter, 0.2 nm, is brought up in measurements.

Noise analysis results with the consideration of process variation are also given in Table 4 and Figs. 12, 13, 14, and 15. As it is shown in Fig. 12b, SNM is zero for the STI of [23] because there is no room for a rectangle to be inscribed in the overlapping curves. Process variation affects NM and SNM disadvantageously. Since MVL circuits are usually based on CNTFETs, which are sensitive to process variation, the importance of appropriate NM adjustment becomes even more crucial.

The same investigations have been carried out for the two well-known standard quaternary inverters of [10, 29]. Their VTC and butterfly curves are plotted in Figs. 16, 17, and 18. Their NM and SNM values are also given in Table 5. The curves are divided into four parts in both circuits. However, the one in [29] has higher noise tolerance in the worst-case condition mainly because of its sharp corners and steep drops. As it is shown in Fig. 18b, SNM for the SQI of [10] disappears in the presence of process variation.

Fig. 16
figure 16

Voltage transfer characteristic (VTC) curves of standard quaternary inverters (SQIs)

Full size image
Fig. 17
figure 17

Worst-case noise condition of the SQI in [29] a without process variation and b with process variation

Full size image
Fig. 18
figure 18

Worst-case noise condition of the SQI in [10] a without process variation and b with process variation

Full size image
Table 5 Comparison of noise margin values in SQIs
Full size table

6 Conclusion

Many researchers have divided the behavioral characteristic of an r-valued inverter into r parts. This type of segmentation is not reliable and effective in practice. In this paper, the necessity of its division into 2r − 2 parts is shown; otherwise, reduced NM would be one of the major disadvantages. In addition, it shows that equality is not the only necessary and sufficient condition for the VTC of an MVL inverter. It also needs to be symmetrical so that NMs are properly set. Moreover, our investigations demonstrate that sharpness and steepness are other important qualities which can lead to higher noise endurance, especially in the worst-case condition. Besides, based on our studies, process variation reduces NM and SNM values. Thus, the accurate arrangement of the VTC curve is very crucial.

As far as we have searched, there are few entirely fitting MVL inverters in the literature. The ones with sharp corners and steep drops, such as [1, 2, 13, 28, 29, 31, 34, 37, 42], are not divided into the right number of parts. The ones with proper division, such as [7], do not have sharp corners. There are some MVL inverters which are neither sharp nor properly divided [10, 18, 22, 23, 33]. As shown in this paper, transistor sizing has a major impact on VTC. Circuit designers can simply reduce the vulnerability of their MVL circuits to noise with correct transistor sizing.

It is needed to mention that there are some successful examples in the literature as well. The STI in [30] is an example in which all of the factors have been observed regarding the topic of NM although it has two more transistors than its other famous competitors. The VTC curves of the ternary inverters in [11, 26] are also in accord with the required attributes mentioned in this paper. However, their structures are, respectively, based on dynamic logic and Differential Cascode Voltage Switch Logic (DCVSL), applications of which are somehow limited in digital electronics. In addition, the design in [26] depends on one extra supply voltage (\( \frac{1}{2}V_{{\rm DD}} \)) other than the power supply and ground. This requirement is in contrast with the main target of MVL, whose mission is to reduce interconnections inside a chip. The presented designs in [31, 37] have the same drawback. At last, in spite of suitable configuration, the designs in [25, 36] propose ternary and quaternary buffers, but not inverters.

Eventually, the VTC curves in [7, 30] have been ameliorated for the construction of SRAMs with higher SNM. Proper segmentation has also been taken into account for a special Low Standby-power Fast (LSF) circuit in [21] to build a ternary SRAM cell with improved stability. Nevertheless, SRAM is not the only application in which VTC matters. The behavioral characteristic of MVL inverters/buffers (and also other circuits) must be divided into the correct number of parts in all MVL applications including combinational logic gates, whose noise sensitivity is of importance as well.