1 Introduction and Motivation

Digital images are mostly noised in many ways during image transmission and capturing. Therefore, it is necessary to remove the unwanted noise from the captured image for improving visual quality. Basically, image noise is a random deviation of color information or unnecessary signals in the images. It can be incurred due to imperfect instruments and distortion in data acquisition process. Digital images may inherit different noises from different sources. Although the types of noise are very hard to identify exactly in some cases, there still have different models to address different types of noise in practice.

Denoising refers to the process of manipulating image data and eliminating noise from the original signal to produce a visually high-quality image. Undoubtedly, image denoising as a preprocessing scheme plays a vital role in digital image analysis. It becomes notable due to the need of denoised images before utilizing to the applications. The main objective of denoising is to remove unwanted noises as best as possible from the original image without losing true information. Over a period of time, different methods have been comprehensively studied to analyze and improve traditional denoising algorithms. So far, the most important concern for solving image denoising problems is maintaining a good balance between noise removal and image true details preservation. Therefore, denoising is still a challenging task for the researchers especially in the community of computer vision and pattern analysis.

To eliminate the unwanted noises as well as improving the performance, many denoising techniques have been proposed in scientific literature. The significant concerns for denoising have been noted in a number of diverse techniques including classical filtering-based methods [1, 32], relaxed median filtering [27], Laplacian-based filtering method [59], isotropic and anisotropic filtering models [33], based on anisotropic diffusion [63], the radial basis function (RBF)-based denoising method [69], maximum flow [12] and split Bregman [22, 25] are used in the applications. There are few other methods in image denoising domain also reported in the literature, such as adaptive soft-thresholding [43], Bayesian and wavelet-based [37, 56], wavelet thresholding-based [13, 17, 19], wavelet transform [57], speckle denoising method using monogenic wavelet transform and Bayesian framework [20], based on support vector machine (SVM) [26, 75], contourlet transforms [55], based on curvelet transform [2], fuzzy theory-based method [62], homogeneity and similarity-based [10, 58], nonlocal-based image denoising [18, 36, 41, 52, 66, 70, 72], nonlocal similarity and TV wavelet-based model [64], Laplacian and nonlocal low-rank approximation method [35], nonlocal-based sparse coding strategy [42], shearlet-based denoising method [15]. Empirical mode decomposition (EMD)-based method [40], dictionary learning-based methods [16, 39, 49, 74], correlation sparse representation and dictionary-based approach [5], the structural sparse representation (SSR) approach for image restoration [76], image deblurring method based on the choice of appropriate regularization parameters [73] and total generalized variation (TGV) method [6].

Recently, variational calculus becomes a powerful tool for model analysis and solutions. Therefore, variational and partial differential equation (PDE)-based methods have been used widely to tackle denoising concerns with a great influence to preserve image edges. PDE-based methods [3, 23, 45, 71] and variational approaches [9, 11, 11, 29,30,31, 44, 60, 61, 65, 68] are remarkable. In application, convex total variation (TV)-based approaches are extensively used in image denoising. The nonconvex approaches [28, 46, 50, 53, 78] are also reported in the literature. The nonconvex regularizer can restrain image details from oversmoothing. It has a significant influence to reduce staircase artifacts efficiently as well as protecting edges or boundary objects. A number of numerical methods [4, 8] have been proposed for solving total variation minimization problems. The aim of TV-denoising approach is to overcome the basic limitations of regularization algorithms. Many algorithms for TV-denoising have been designed, especially the algorithms based on duality [77], Newton-based method [51] and iteratively reweighting method [54]. The nonlocal-based algorithms such as BM3D [14] is incorporated with 3D transform collaborative filter for denoising and preserving image true details. In application, the nonlocal-based algorithms are quite efficient than local-based methods in case of image texture preservation. But nonlocal-based method is also computationally expensive because it involves in selecting similar blocks, group in 3D arrays, filtering and comparing many patch groups in implementation. Some of recently proposed denoising algorithms are also reported in image analysis domain such as: (a) proximal algorithms [34] as a domain-specific language and compiler for image optimization problems with different problem formulations and algorithm choices. The language uses proximal operators as basic building blocks and compiler to translate a problem formulation, as well as select the optimization algorithm for efficient implementation, (b) the algorithm based on color monogenic wavelet transform and trivariate shrinkage filter [21], (c) image enhancement algorithm based on contrast limited adaptive histogram equalization (CLAHE) [48], and (d) fixed-point algorithm [47] are also proposed in the recent literature. Moreover, TV-based image restoration models are broadly discussed by Rudin, Osher and Fatemi (ROF) in [60]. The ultimate goal of this model is preserving sharp discontinuities (edges) in an image while removing unwanted details. The ROF then extended to image deblurring in [61]. In [60], ROF proposed a time-marching approach in association with Euler–Lagrange equation for the solution of a parabolic PDE. Chambolle’s methods [7, 8] are well known and effective for minimizing the total variation of an image. The Chambolle’s projection algorithm in [7] is proved for regularizing noisy images without much isotropic affect of the boundary objects.

From the aforesaid discussion, it is observed that several denoising techniques have been applied till now, but the respective researches are still continuing toward better noise removal. Although few techniques are effective in some context, the solutions of these models are tough to be discussed in theoretical analysis. In estimation, the difficulty is choosing a reliably prior distribution and designing a regularizer to ensure a better trade-off with a given fidelity. Therefore, designing an appropriate regularizer for a given fidelity is mostly a challenging and sensitive issue in denoising . For example, the authors Rudin et al. in their work [60] use the classical convex total variation (TV) regularizer to preserve image edges. The advantage of ROF model [60] is the existence of unique solution due to the nature of its convexity. However, the numerical experiments of ROF model depict the isotropic influence for oversmoothing some important image details while increasing iteration. It is observed that the regularizer used in ROF model is certainly a limitation as it tends to blur important image information, especially when number of iteration increases. To overcome this limitation, Han et al. proposed a nonconvex regularizer in their works [28, 30]. They used nonconvex regularizer which can preserve image details from oversmoothing. In [30], they proved that the nonconvex regularizer is an ideal regularizer for removing noise and preserving image details simultaneously. In spite of improving performance, there still have some drawbacks of Han’s model. It cannot promise unique solution of the model because of its nonconvexity properties. In fact, the direct solution of their model is hard to prove and computationally much more expensive than other models. Moreover, the nonconvex regularizer in Han’s model considers the noise as image true details when it contains high-intensity noise, especially in homogeneous regions. As a remedy of this problem, we proposed a variational model in our previous work [38]. Even though the model performed well to address the problems and ensure edge preservation ability, it is still not effective enough for some benchmark problems.

Therefore, the objective of this work is to overcome the limitations of classical denoising methods and motivate to a research with a new approach, and substantially improving denoising performance both visually and quantitatively. Since edge preservation is a tricky issue during denoising process, this research also focuses on designing an appropriate regularizer in energy functional so that it can reduce the possibility of discontinuity and distortion of image edge details. For the purpose, we pull out our works and introduce a new denoising technique which utilizes the benefits of both convex and nonconvex regularizers. The proposed model encompasses with a novel weighted hybrid regularizer in variational framework to ensure a better trade-off between the noise removal and image details preservation.

Rest of the paper is divided as follows: Sect. 2 provides the preliminaries of image denoising techniques. The proposed model is presented in Sect. 3. Section 4 illustrates experimental studies. Performance evaluation of proposed technique is presented in Sect. 5. Finally, Sect. 6 concludes this paper.

2 Preliminaries

Images are a collection of pixel data or signal that carries information which can be incurred unwanted interference during acquisition. These unwanted interferences hinder the true images and form its degraded version. Let u(t) is the original clean image where \(u:\varOmega \subset {R^2} \rightarrow R\) and \(\varOmega \) refers to the image domain, \({u_0}(t)\) is the noisy image degraded with zero mean, and \(\eta (t)\) is the white Gaussian noise; then, the image with noise can be modeled mathematically as Eq. (1).

$$\begin{aligned} {u_0}(t) = u(t) + \eta \,(t). \end{aligned}$$
(1)

The aim is to recover the original image from its degraded version as shown in (1). To solve such a problem, it needs to reconstruct u from \({u_0}\). Assuming that \(\eta \) is additive white Gaussian noise uniformly distributed, i.e., independent and identical distributed (i.i.d.). An approximation to u can be found from the optimization problem (2).

$$\begin{aligned} \min {\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x. \end{aligned}$$
(2)

A regularization term as in Eq. (3) is needed to add to the energy signal as proposed in [67] to resolve the minimization problems (2):

$$\begin{aligned} {\mathscr {F}}(u) = {\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x\, + \,\lambda {\int _\varOmega {\left| {\nabla \left. u \right| } \right. } ^2}\mathrm{d}x. \end{aligned}$$
(3)

In Eq. (3), the first term refers the fidelity or data term and second term denotes the smoothing term that regularizes the problem. A real positive constant is \(\lambda \) which balances the trade-off between the smoothness and fidelity. The minimization problem (3) can promise a unique solution by dint of Euler–Lagrange equation as the following way:

$$\begin{aligned} u - {u_0} - \lambda \varDelta u\, = \,0 \end{aligned}$$
(4)

with the Neumann boundary conditions: \(\frac{{\delta u}}{{\delta M}} = 0\) on \(\partial \varOmega \), M is the outward normal to \(\partial \varOmega \). The solution of Eq. (4) is not a suitable candidate for the original restoration problem. Thus, the bounded variation (BV) regularization introduced by Rudin et al. in [60]. It uses the \({L^1}\) norm of \( {\nabla u} \) instead of \({L^2}\) in (4) which defines the smoothing term as a BV semi-norm; for smooth functions, it can be expressed as:

$$\begin{aligned} \lambda \int _\varOmega {\left| {\nabla \left. u \right| } \right. }. \end{aligned}$$
(5)

The term (5) denotes the total variation of u . Minimization of (5) is problematic for large gradients. Therefore, choosing an appropriate regularization term is important for the quality of the solution [67]. A common ROF denoising technique is a subject to minimize a functional of gradient as (6).

$$\begin{aligned} J(u) = \; \mathop {\min }\limits _u \left\{ \frac{1}{2}{\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x\, + \,\lambda {\int _\varOmega {\left| {\nabla \left. u \right| } \right. } ^{}}\mathrm{d}x\right\} . \end{aligned}$$
(6)

The regularization term in (6) is proposed by Rudian et al. [60] which can remove noise and ensure the existence of the unique solution. At the same time, it also removes some important image details (image edges) due to isotropic effect of its gradient operator with respect to iteration. As a solution of this problem, Han et al. [28, 30] proposed the nonconvex regularizer as (7).

$$\begin{aligned} \;{\int _\varOmega {\varPhi (\left| {\nabla \left. u \right| )} \right. } ^{}}\mathrm{d}x. \end{aligned}$$
(7)

The function \(\varPhi (s)\; = \;\frac{{\theta s}}{{1 + \;\theta s}}\), where \(\theta \) is a positive parameter. In practice, the nonconvex regularizer (7) is quite effective to restrain image details from high isotropic polishing effect. But it treats noise as the true details especially in the high-intensity image (edges) regions, and the model cannot ensure unique solution. To seek a solution of these problems, we investigate and experiment a variational approach on a set of samples images in our previous work [38]. Even though the model in [38] performs well to reduce noise as well as protect edge details, still it is not effective enough for some sample images.

Therefore, by incorporating the benefits of TV regularizer and nonconvex regularizer, we attempt to design an efficient and reliable weighted hybrid regularizer for much noise reduction while keeping the image true information during the denoising process.

3 Aspects of Proposed Model

In this work, we attempt to retrieve an image from its degraded version and produce a new image which would be visually close to the original image. In other word, the reconstructed image must be good quality in a technical sense that the variation between a pixel and its neighborhood keeps smaller as much as possible. As we noticed, designing an appropriate regularizer in variational framework is a crucial issue because of its significant influence on edge preservation ability during denoising. An efficient regularizer is always promising to reduce the discontinuity and distortion of edge details. It can also maintain a proper balance between noise reduction and oversmoothing in practice. Therefore, we propose a novel hybrid regularizer in association with convex and nonconvex TV regularizer as Eq. (8).

$$\begin{aligned} \int _\varOmega {\left| {\nabla \left. u \right| } \right. } \mathrm{d}x + \;\int _\varOmega {\varPhi (\left| {\nabla \left. u \right| )} \right. } \mathrm{d}x. \end{aligned}$$
(8)

In (8), convex TV regularizer mostly inherits the benefit of noise reduction and nonconvex regularizer influences to preserve edge details efficiently from oversmoothing. Therefore, our model encompasses both the convex and nonconvex regularizers as in the following form of functional (9).

$$\begin{aligned} \begin{aligned} J(u) =&\;\frac{1}{2}{\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x + \,\varepsilon \int _\varOmega {\left| {\nabla \left. u \right| } \right. } \mathrm{d}x \\&+ \;(1 - \varepsilon )\int _\varOmega {\varPhi (\left| {\nabla \left. u \right| )} \right. } \mathrm{d}x. \end{aligned} \end{aligned}$$
(9)

Comparing (6) and (7), we can see that \(\varepsilon \) in model (9) is a trade-off parameter between two different regularizers used in models (6) and (7). When \(\varepsilon = 1\), model (9) acts as ROF convex model (6), and when \(\varepsilon = 0\) it acts as Han’s nonconvex model (7). Thus, the proposed model (9) includes hybrid regularizer to inherit the benefits both from convex and nonconvex methods in practice. The technical merit of using these combined regularizers in variational framework is to ensure better generalization in aspect of removing noise and preserving edge details simultaneously. In model (9), the convex TV regularizer \( \int _\varOmega {\left| {\nabla \left. u \right| } \right. } \mathrm{d}x \) plays a vital role in much noise reduction from its given fidelity; on the other hand, the nonconvex regularizer \( \int _\varOmega {\varPhi (\left| {\nabla \left. u \right| )} \right. } ^{}\mathrm{d}x \) has a significant influence to reduce staircase artifacts efficiently as well as protecting edges or boundary objects from oversmoothing. The variational principles of our model rely on the solution of following minimization problem:

$$\begin{aligned} \mathop {\min }\limits _u \left\{ \begin{array}{l} \frac{1}{2}{\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x\, + \,\varepsilon {\int _\varOmega {\left| {\nabla \left. u \right| } \right. } ^{}}\mathrm{d}x\\ \;\;\;\;\;\;\;\;\;\;\;\; + \;(1 - \varepsilon ){\int _\varOmega {\varPhi (\left| {\nabla \left. u \right| )} \right. } ^{}}\mathrm{d}x \end{array} \right\} \;. \end{aligned}$$
(10)

But the direct solution of (10) is complicated due to nonconvex smoothing term used in the model. Therefore, instead of solving the minimization problem (10) directly, we turn to define the regularizer by iteratively reweighted method as:

$$\begin{aligned} \varPhi (\left| {\nabla \left. u \right| )} \right. \; = \;\left( \frac{{1 + \theta }}{{1 + \theta |\nabla u|}}\right) \left| {\nabla \left. u \right| } \right. = w\left| {\nabla \left. u \right| } \right. . \end{aligned}$$
(11)

In (11), we define weight w as:

$$\begin{aligned} w = \frac{{1 + \theta }}{{1 + \theta |\nabla u|}}, \end{aligned}$$
(12)

where \(\theta \) is a positive random parameter ranges [0.01, 0.09]. Thus, the model can be represented as (13).

$$\begin{aligned} J(u) = \;\frac{1}{2}{\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } ^2}\mathrm{d}x\, + \;\int _\varOmega ^{} {(\varepsilon + (1 - \varepsilon )w)\left| {\nabla \left. u \right| } \right. \mathrm{d}x}. \end{aligned}$$
(13)

Finally, the issue is to solve the model (13) as following minimization problem (14) for removing noise and reconstructing visually high-quality image:

$$\begin{aligned} \mathop {\min }\limits _u \left\{ {\frac{1}{2}{{\int _\varOmega {\left| {{u_0} - \left. u \right| } \right. } }^2}\mathrm{d}x\, + \,\int _\varOmega ^{} {(\varepsilon + (1 - \varepsilon )w)\left| {\nabla \left. u \right| } \right. \mathrm{d}x} \;} \right\} . \end{aligned}$$
(14)

The above model (13) is convex since w is given and the existence of the unique solution is promised. We introduce the Chambolle’s projection algorithm [7] to obtain the solution of the minimization problem (14), which is given as (15).

$$\begin{aligned} u_i^{} = \;u_{0i}^{} - \lambda \; \text {div}\;\mathbf p _i, \end{aligned}$$
(15)

where \(\text {div}\;\mathbf p \) is the divergence of the vector, \(\mathbf p :\varOmega \rightarrow R \times R\) represents a vector function, and \(\mathbf{p _i} \in {\ R}{^n}\) can be resolved by a fixed-point method: \({p^0} = 0\) given is an initial guess and let time-step=\(\tau \) , and then we iterate the following scheme (16):

$$\begin{aligned} p_i^{n + 1} = \;\frac{{p_i^n + \tau \nabla (\text {div}\;{p_i}^n - \;\;{u_{0i}})}}{{1 + (\tau /\varepsilon + (1 - \varepsilon )w)\left| {\text {div}\;{p_i}^n - \;\;{u_{0i}}} \right| }}. \end{aligned}$$
(16)

Based on calculus variation and some necessary assumptions, we can prove that the minimization problem has a unique minimizer. In practice, our proposed denoising method is more efficient because it not only complies much noise reduction ability, but also preserves image features or boundary objects effectively. In fact, this kind of weighted hybrid regularizer can inherit the benefit of both removing noise in homogeneous regions from the convex TV regularizer and protecting edge information from nonconvex regularizer simultaneously. In implementation, an algorithmic overview of the method is described as Algorithm 1.

Fig. 1
figure 1

a Original images and b their noisy version with intensity \(N = 25\) *Corresponding rows represent original and noisy images respectively

Full size image
Table 1 Quantitative performance evaluation [SNR (db), PSNR (db), time (s)] for different denoising methods (i.e., different models proposed in [30, 38, 60] and our proposed model)
Full size table

Algorithm 1. The weighted hybrid regularizer-based noise reduction

Input: Noised images N

Output: Denoised images D

1: Initialization: give parameters \(\lambda \), \(\epsilon \), \(\eta \), \(\tau >0\) and \(\theta \), \(p_i^0 = 0\) and set \(k = 0\)

2: repeat

3: update weight \({w_i}\) by formula (12) (inner loop is needed);

4: update \(u_0^{k}\) by formulas (15) (inner loop is needed);

5: update \(u_i^{k}\) by (15) and (16);

6: \(k = k+1 \);

7: until a stopping criterion is satisfied.

4 Experimental Studies

In this section, experimental results are presented to verify the effectiveness of different methods including the proposed method in this paper. For the efficient solution of the models, the corresponding algorithms are executed in MATLAB 10.0 simulation on a computer configured with core-i5 and 3.20 GHz. We carry out several experiments on a set of sample images and record the results to validate the denoising performance of different methods. During the evaluation process, the results generated by our proposed method are also compared with some classical methods, including the models proposed in [28, 30], the ROF model in [60] and our previous model in [38]. For each of these models, we discussed parameters selection criterion in Sect. 4.1.

Table 2 SSIM performance evaluation for different denoising methods (i.e., different models proposed in [30, 38, 60] and our proposed model)
Full size table
Fig. 2
figure 2

Denoising performance using different models, c model in [60], d model in [30], e model in [38], f proposed model

Full size image

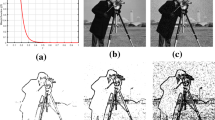
In order to measure the improvement in noise images, the performance indicated parameters must be estimated visually and quantitatively. For quantitative comparison, a set of reference original images are shown in (a) of Figs. 1, 4 and 5, respectively. During simulations, each of these images is degraded by different levels of noise intensity that are simulated by sampling from the Gaussian distributions. The parameter N is related to the standard deviation of noise \(\eta \). To minimize the length of our paper, we are mostly motivated to choose these noise parameters N from the set {15, 20, 25} in most of the cases. Furthermore, for few cases, we experimented our model on a large set of N ranges as {5, 10, 15, 20, 25, 30, 35, 40, 50} to validate the prospect and significance of our proposed method. It is noted that higher N means the intensity of the noise is stronger. The comparisons are generated based on noised and denoised images in terms of mean squared error (MSE), signal-to-noise ratio (SNR), peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) index . To reveal the superiority of the proposed approach, we used SNR, PSNR and SSIM as the evaluation indicators. These indicators are measured between clean and reconstructed images. Let \({\bar{u}}\) represent the image recovered from the noisy image \(u_o\) , and let \(\sigma _u^2\) represent the average variance of the clean image u. Then, we define the SNR indicator by formula (17).

$$\begin{aligned} \text {SNR}\; = \;10\;{\log _{10}}\;\left( \frac{{{\sigma _u}^2}}{{\text {MSE}}}\right) , \end{aligned}$$
(17)

where the value of MSE is computed as \(\text {MSE}=\frac{1}{{\left| \varOmega \right| }}\int _\varOmega {{{(u-{\bar{u}})}^2}}\mathrm{d}x\) and the PSNR is defined as (18).

$$\begin{aligned} \text {PSNR}\; = \;10\;{\log _{10}}\;\left( \frac{{{{\left| {\max \;u} \right| }^2}}}{{\text {MSE}}}\right) . \end{aligned}$$
(18)

We also used structural similarity (SSIM) as perceptual image quality indicator. The SSIM indicates the similarity between the clean image and denoised image. The value of SSIM index varies between 0 and 1. The high value indicates more structure similarity between the original image u and denoised image \({\bar{u}}\). It is measured between clean and reconstructed images. The SSIM is computed as formula (19).

$$\begin{aligned} \text {SSIM}\; = \;\frac{{\left( {2{\mu _u}{\mu _{{\bar{u}}}} + {v_1}} \right) \left( {2{\sigma _{u{\bar{u}}}} + {v_2}} \right) }}{{\left( {{\mu _u}^2 + {\mu _{{\bar{u}}}}^2 + {v_1}} \right) \;\left( {{\sigma _u}^2 + {\sigma _{{\bar{u}}}}^2 + {v_2}} \right) }}\;, \end{aligned}$$
(19)

where \({\mu _u}\) and \(\;{\mu _{{\bar{u}}}}\) are the mean values of the original and denoised image, respectively. Similarly, \({\sigma _u}\) and \({\sigma _{{\bar{u}}}}\) are the variance values of the original and denoised image, respectively. \({\sigma _{u{\bar{u}}}}\) is the covariance of images u and \({\bar{u}}\); \(v_1\) and \(v_2\) are two variables to stabilize the division with a weak denominator.

Fig. 3
figure 3

Performance comparison using different models and proposed model for denoising: model-a represents model in [60], model-b represents model in [30], model-c represents the model in [38]. a SNR values using Couple image. b PSNR values using Couple image. c SNR values using Canal-Mini image. d PSNR values using Canal-Mini image. e Total time of denoising for all images

Full size image

4.1 Parameters Selection Criterion

Parameter selection is an important issue for implementing algorithms as well as converging the corresponding models efficiently. To experiment the algorithms of all corresponding models, several parameters such as \(\lambda \), \(\epsilon \), \(\tau \) and \(\theta \) are needed to be initialized. The size of all images is needed to be normalized as \(256 \times 256\) before tuning the parameters. Then, it is necessary to adjust the image gray intensity ranges to be [1, 256]. As a trade-off parameter, \(\epsilon \) has a great influence on different regularizers in model (13). Through a lot of experiments, the best values of parameter \(\lambda \) can be chosen same as noise level. The parameter \(\epsilon \) is chosen from a fixed ranges [0, 0.6] as proposed in works [28, 30]. For our model, the parameter \(\epsilon \) can be selected randomly between [0, 1]. The parameters both \(\lambda \) and \(\epsilon \) play the important role in controlling the smoothness degree of the reconstructed image. The parameter \(\tau \) in (16) is the time-step of the iteration method. The parameter \(\tau \) has influence to make Chambolle’s algorithm converging. This parameter is proved to be smaller than \(\frac{1}{8}\) and equal to \(\frac{1}{15}\) as in the works [28] and [30], respectively. In our case, we fix it for any random value ranges \([0< \tau < 1]\) that can be a better choice to make a good trade-off between running time and the denoising performance. The value of \(\theta \) during this experiment is random and ranges [0.01, 0.09]. However, we do not mean that our denoising method only works in these intervals or suggested parameters. Through a lot of experiments, it is seen that these parameters and intervals initialization are more promising to reduce the searching time for achieving model convergence.

Fig. 4
figure 4

Denoising performance with different models a original image, b noise image having \(N=25\), c model in [60], d model in [30], e model in [38], f proposed model

Full size image
Fig. 5
figure 5

Denoising performance with different models a original image, b noise image having \(N=25\), c model in [60], d model in [30], e model in [38], f proposed model

Full size image
Fig. 6
figure 6

Enlarged denoising results: c model in [60], d model in [30], e model in [38], f proposed model

Full size image

5 Performance Evaluation

To evaluate denoising performance of different models, we implemented several experiments on a set of sample images and computed SNRs, PSNRs, SSIMs and CPUtimes as evaluation indicators. We recorded and compared the best SNRs, PSNRs and SSIM obtained from our proposed model as well as the models in [30, 38, 60]. The results in Tables 1 and 2 show the effectiveness of our approach. We also demonstrated different denoised results in (c)–(f) of Figs. 2, 4 and 5 for visual evaluation. Both the quantitative and visual results reveal the outstanding performance of our proposed method. From the evaluation indexes in Tables 1 and 2, it is seen that our approach averagely gets higher SNRs, PSNRs and SSIMs than the other approaches. Most of the cases, our model can produce better results except some running time penalties as shown in (e) of Fig. 3. The results in (a)–(e) of Fig. 3 demonstrated that the ROF model is quite faster, but has poor performance. The average CUP times on twenty-two images are calculated during denoising process. It is true that the proposed method is computationally little slower than ROF model since our model handles both convex and nonconvex cases. But in image denoising study, noise reduction, edge preservation ability, tackle overshooting artifacts and its trade-off are the fundamental concerns and tricky issues for performance evaluation. Denoising or edge preservation ability is always much more appreciative than some computational time penalty. In (e) of Fig. 3, even though our approach may outlay in running time than ROF model, it is still faster than the model in [30]. However, as a whole, the running time of our model is comparable and inexpensive than some other methods in the literature. For example, our method is computationally convenient than some nonlocal-based methods (e.g., BM3D [14]) because it is local-based approach in variational framework. Moreover, our proposed method can be generalized into nonlocal method using the nonlocal operator as proposed in [24] for more texture preservation. However, in this work we emphasize to inherit the benefits of both convex and nonconvex regularizers, as well as attain the better convergence using a novel weight function. The performance comparisons among the convex or nonconvex variational-based approaches are the ultimate target of this work. Here, we also explain how our proposed method is comparable and more influential than the methods [30, 38, 60] in order to clarify the context of our contributions. For all reference original images, the reconstructed images are shown in (c)–(f) of Figs. 2, 4 and 5. Comparing these denoising results, we can say that our method can remove much noise and protect image true details, especially in homogeneous regions. As for example, the denoised results in (c) of Figs. 2, 4 and 5 generated by the model in [60] still include some visible noise. The ROF model in [60] produced image oversmoothing while iteration increased. It mostly blurred the images due to its high isotropic polishing effects. The images recovered from Han’s model are shown in (d) of Figs. 2, 4 and 5. These results indicate that the noise is not well removed and the edge detail of the restored image also seems oversmoothed. In comparison with the results shown in (c)–(d) of Figs. 2, 4 and 5, the respective denoising results in (e) demonstrated that the model in [38] can achieve better noise-removing and edge-preserving ability than the models in [30, 60] except few samples with different levels of noise intensity. To verify the generalization of different models, we performed intensive experiments on Canal-Mini and Couple images with large ranges of noise intensities, and the corresponding results are shown in (a)–(d) of Fig. 3. In this figure, we observed that the performance of models in [30, 38, 60] fluctuates based on the levels of noise intensities. From Fig. 3, it is seen that the model in [30] cannot perform well at low noise intensities, whereas our proposed model can denoise efficiently at any level of noise intensities. In case of homogeneous regions of restored images, we observe that some image true details are also removed in (d) and oversmoothed in (c) than the image shown in (f) of Figs. 2, 4 and 5. In (f) of Figs. 2, 4 and 5, the reconstructed edges are much sharper and more image details are recovered. It means that the proposed model simultaneously can remove more noise in homogeneous regions and preserve edge details efficiently than the models in [30, 38, 60].

For visual performance improvement, we observe the significance of our proposed method for both noise reduction and edge preservation ability than the other methods [30, 38, 60]. As for reference, in Fig. 6, we include two enlarged denoising results for more precise analysis. From visual observation, we can find that the images restored from the proposed method (shown in Fig. 6(f) are better than those restored from models [30, 38, 60] as shown (c)–(e) in Fig. 6, respectively. In fact, Fig. 6(c) contains some visible noise; the model [38] generates better denoising results than model [30]. However, the models [30, 38] usually cannot make a good trade-off between smoothing homogeneous regions and image edges preservation, whereas the proposed model generates better denoising results whose details are well preserved, and at the same time noise is also well cleaned.

From the local reference enlarged results (shown in Fig. 6), we can conclude the performance more precisely as i) model [60]: noise not well cleaned in the white region and edge is oversmoothed; ii) model [30] and [38]: both noise and image details are preserved; iii) proposed method: noise is cleaned, and edges are preserved simultaneously. Thus, noise reduction and edge preservation ability, as well as better trade-off between fidelity and smoothing term make the proposed work more attractive than the works [30, 38, 60].

6 Conclusion

In this paper, we have investigated and incorporated a robust hybrid regularizer in variational framework for better trade-off between data fidelity and smoothing terms in functional minimization. This kind of hybrid regularizer incorporated with a novel designed weight in appropriate parameters estimation for protecting more geometric structural details of images from oversmoothing and removing more noise simultaneously. Our proposed method significantly inherited the benefits of both convex and nonconvex regularizers. Its efficiency is experimentally validated on a variety of images and noise levels. Numerical results on different benchmark images have depicted that our proposed method can effectively achieve the highest SNR, PSNR and SSIM values to ensure very competitive and promising denoising performance. The obtained results during the experimental simulation inspire us to draw a conclusion that our proposed approach is more efficient than some state-of-the-art denoising techniques i.e., both in quantitative and visual aspects especially in background smoothing and edge preservation from oversmoothing. The proposed approach can be extended and generalized to RGB images with different types of noises. Moreover, the findings of this work also encouraged us to generalize our model for comparing other non-variation-based methods in future works.