Breaking the Limits: Redefining the Instantaneous Frequency

Abstract

The Carson and Fry introduced the concept of variable frequency as a generalization of the constant frequency. The instantaneous frequency (IF) is the time derivative of the instantaneous phase, and it is well defined only when this derivative is positive. If this derivative is negative, the IF creates problem because it does not provide any physical significance. This study proposes a mathematical solution and eliminates this problem by redefining the IF such that it is valid for all monocomponent, multicomponent signals of nonlinear and nonstationary nature. This is achieved by using the property of the multivalued inverse tangent function that provides base to ensure that the instantaneous phase is an increasing function. The efforts and understanding of all the methods based on the IF would improve significantly by using this proposed definition of the IF. We also demonstrate that the decomposition of a signal, using zero-phase filtering based on the well-established Fourier and filter theory, into a set of desired frequency bands with proposed IF produces accurate time–frequency–energy (TFE) distribution that reveals true nature of signal. Simulation results demonstrate the efficacy of the proposed IF that makes zero-phase filter-based decomposition most powerful for the TFE analysis of a signal.

1 Introduction

The time domain representation and the frequency domain representation are two classical representations of a signal. In both domains, the time (t) and frequency (f) variables are mutually exclusive [4]. The time–frequency distributions (TFDs), on the other hand, provide localized signal information in time and frequency domain. The TFD provides insight into the complex structure of a signal consisting of several components. There exist many types of time–frequency analysis methods such as short-time Fourier transform (STFT), Gabor transform, wavelet transforms, Wigner–Ville distribution, and discrete orthonormal Stockwell transform (DOST) [39].

Carson and Fry [5] introduced the concept of variable frequency, required to the theory of frequency modulation (FM), as a generalization of the definition of constant frequency. Moreover, the nonstationary nature of the signals and nonlinear systems require the idea of instantaneous frequency (IF). The IF is the basis of the TFD or time–frequency–energy (TFE) representation and analysis of a signal. The IF is a practically important parameter of a signal which can reveal the underlying process, and provides explanations for physical phenomenon in many applications such as vibration, acoustic, speech signal analysis [32], meteorological and atmospheric applications [17], seismic [32], radar, sonar, solar physics, structural engineering, communications, health monitoring, biomedical and medical applications [7], mechanical systems analysis [41], TFE representation of cosmological gravity wave [1], financial market data analysis, imaging processing and classification [9, 14].

The IF is the time derivative of the instantaneous phase (IP), and it is well defined only when this derivative is positive. If this derivative is negative, it creates problem because it does not provide any physical significance. In order to avoid this problem, recently many nonlinear and nonstationary signal representation, decomposition and analysis methods, e.g., empirical mode decomposition (EMD) algorithms [17, 24, 25, 27,28,29,30, 40], synchrosqueezed wavelet transforms (SSWT) [8], variational mode decomposition (VMD) [10], eigenvalue decomposition (EVD) [19], empirical wavelet transform (EWT) [13], sparse time–frequency representation (STFR) [16], time-varying vibration decomposition (TVVD) [11], resonance-based signal decomposition (RSD) [26], Fourier decomposition methods (FDM) [31,32,33,34,35,36] based on the Fourier theory, are proposed. Fuzzy-based design and analysis of nonlinear systems are proposed in [20, 21]. The Fourier theory is the only tool for spectrum analysis of a signal, and the FDM [32] has established that it is a superior tool for nonlinear and nonstationary time series analysis. The main objective of all these methods is to obtain the signal representation such that the IF of a signal under study is always positive. A signal is defined as a monocomponent if the IF derived from its analytic representation is positive and well defined for all time. Notice that, traditionally, the IF is defined only for monocomponent signals [2, 3, 17]. Thus, the EMD and other related methods decompose a multicomponent signal into a set of monocomponent signals, termed as intrinsic mode functions (IMFs), which yield positive IF via the analytic signal representation using the Hilbert transform (HT).

Unlike these decomposition methods, the IF proposed in this study does not necessitate to decompose a signal into a set of monocomponent or narrow band components, which satisfy certain properties, to generate the TFE distribution of a signal. That is, without any decomposition the TFE distribution of a signal can be obtained by using the proposed IF. It also provides freedom and potential to decompose a signal into a set of desired, preferably orthogonal or linearly independent nonorthogonal yet energy preserving (LINOEP) [27], frequency bands by a zero-phase filtering approach to obtain TFE distribution of a signal. All these features are obtained by redefining the IF when it is negative and thus defining the IF for both monocomponent and multicomponent signals. In order to redefine the IF, we use the fact that inverse tangent is a multivalued (i.e., one-to-many mapping) function. So defined IF of a signal is always positive and valid for any signal.

There are two main paradoxes of the IF [6, 17, 22]: (1) The IF values may be different from the frequency in the spectrum of a signal, and (2) the spectrum of an analytic signal vanishes for negative frequencies; however, the IF may be negative. In this paper, we investigate and propose solutions to these problems. The first paradox is related to the uniqueness of the IF which can be eliminated by decomposing a signal into a set of narrowband components through a zero-phase filtering. The second paradox is the limitation of the traditional definition of the IF, which is fully eliminated in this study by redefining the conventional IF such that it is positive for any signal and for all the time. The main contributions as well as some important observations of this study are as follows:

• 1. We use the conventional definition of the IF when it is positive; if it is negative, then redefine the IF to make it positive such that it is limited to half of the sampling rate. Thus, the proposed IF is always positive and valid for all monocomponent as well as multicomponent signals, which can be nonstationary and nonlinear in nature.

• 2. Since many decades, there has been a general understanding in the literature, e.g., [2,3,4, 17, 19, 23, 25, 40], that the Fourier theory (due to linearity, periodicity, and stationarity) is not suitable for nonstationary signal analysis. This proposed IF provides an elegant way to use the Fourier and filter theory-based zero-phase filtering for the decomposition of a signal into a set of suitable bands with desired cutoff frequencies (e.g., divide complete bandwidth of a signal into a set of sub-bands of equal bandwidth or dyadic sub-bands). In order to validate this, in the study, we have used only the Fourier and finite impulse response (FIR) filter theory-based decomposition (except when comparing with EMD, wavelet transform, and conventional nonzero-phase FIR filtering) to obtain TFE analysis of a signal.

• 3. We propose two signal decomposition algorithms: first the zero-phase discrete Fourier transform (DFT) filter bank-based decomposition algorithm, as shown in Fig. 1, to obtain a set of orthogonal components, and second zero-phase FIR filter-based decomposition Algorithm 2 to obtain a set of LINOEP components. We demonstrate that it is more natural to obtain LINOEP components with second algorithm; moreover, both sets of orthogonal and LINOEP vectors preserve the energy in decomposition and present similar TFE distribution of a signal.

• 4. The proposed method, using the Hilbert spectrum, produces average frequencies in the TFE distribution with good time resolution when the envelope of signal is smooth. However, if envelope of a signal is fluctuating randomly and rapidly, e.g., the Gaussian white noise and Earthquake time series, the TFE plot presents good time and frequency resolution.

• 5. We demonstrate that the different decomposition methods are producing the different TFE distributions of a signal. Using the proposed method, when a signal is decomposed into a large numbers of orthogonal or LINOEP narrow bands, true frequencies present in the signal are revealed, frequency resolution also increases, while the time resolution reduces marginally.

Thus, this study presents a new paradigm for nonlinear and nonstationary data analysis. Moreover, this work independently and uniquely resolves some misconceptions that have grown with regard to the significance of the Fourier theory and its usefulness in the representation and analysis of nonstationary signal, and also supports the results of other related studies [32, 33]. This paper is organized as follows: The proposed methodology is presented in Sect. 2. Simulation results and discussion are presented in Sect. 3. Section 4 presents conclusion of the work.

Fig. 1

Block diagram of the DFT-based zero-phase filter bank (FDM) to decompose a signal x[n] into a set $\left\{ y_{1}[n], y_{2}[n], \ldots , y_{M}[n] \right\}$ of orthogonal desired frequency bands

2 Methods

The concept of variable frequency with application to the theory of FM is proposed in [5], and it is postulated that the notion of IF is a generalization of the definition of constant frequency. A definition of the IF by analyzing an expression for simple harmonic motion (SHM) is considered in [37] as

$$\begin{aligned} x_{\mathrm{SHM}}(t)=a \cos \left[ \int _{0}^{t} 2\pi f(t) \,\mathrm {d}t+ \theta \right] =a \cos (\psi (t)), \end{aligned}$$

(1)

where the argument of the cosine function is the phase $\psi (t)=\left[ \int _{0}^{t} 2\pi f(t) \,\mathrm {d}t+ \theta \right]$. This leads to the definition of IF [37]

$$\begin{aligned} f(t)=\frac{1}{2\pi } \frac{\,\mathrm {d}\psi (t)}{\,\mathrm {d}t}. \end{aligned}$$

(2)

The concept of IF was enhanced in [12] where a method for generating a unique complex signal z(t) from a real signal x(t) and its HT $\hat{x}(t)$ was proposed. This method obtains

$$\begin{aligned} z(t) =x(t)+j\hat{x}(t) = a(t)e^{j\phi (t)}, \end{aligned}$$

(3)

where

$$\begin{aligned} \left. \begin{aligned} a(t)&=\left[ x^2(t)+\hat{x}^2(t)\right] ^{1/2}\ge 0, \\ \phi (t)&=\tan ^{-1}[\hat{x}(t)/x(t)] \end{aligned}\right\} \end{aligned}$$

(4)

and z(t) is the Gabor’s complex signal (well known as the analytic signal) and $\hat{x}(t)$ is defined as

$$\begin{aligned} \hat{x}(t)= \text {p.v.} \int _{-\infty }^{\infty } \frac{x(\tau )}{\pi (t-\tau )} \,\mathrm {d}\tau = \text {p.v.} \left[ x(t)*\frac{1}{\pi t}\right] , \end{aligned}$$

(5)

where p.v. denotes the Cauchy principal value of the integral [15] and $*$ denotes convolution operation. The work done in [5, 12] was unified in [38] to define the IF of a signal $x(t) = a(t) \cos (\phi (t))$ as

$$\begin{aligned} \omega (t)= 2\pi f(t) =\frac{\,\mathrm {d}}{\,\mathrm {d}t} \left( \text {arg} [z(t)]\right) , \end{aligned}$$

(6)

where z(t) is the analytic signal given by (3) and $\text {arg} [z(t)]=\phi (t)$ as defined in (4). The IF defined in (6) provides physical meaning only if it is positive, and it becomes meaningless when it is negative [2, 3, 8, 10, 17, 19, 25, 27, 29, 31, 32, 40]. This is where we improve and provide the solution to make the IF positive for all time t. From (4) and (6), one can obtain the TFE distribution of a signal x(t) by 3-D plot of $\{t, f(t), a^2(t)\}$. However, it can be noted that the frequencies, of signal $x(t)=a(t)\cos (\phi (t))$, obtained by Fourier transform and Hilbert spectrum (6) are same only if a(t) is a constant; otherwise, Hilbert spectrum provides frequencies of signal $\cos (\phi (t))$ and not of signal x(t) as it excludes the frequencies of a(t).

Before evaluating the time derivative of phase in (6), phase unwrapping is necessary to ensure that all appropriate multiples of $2\pi$ have been included in phase $\phi (t)$. Phase unwrap operation corrects the radian phase angles by adding multiples of $\pm \,2\pi$ when absolute jumps between consecutive elements of a phase vector are greater than or equal to the default jump tolerance of $\pi$ radians [42]. This is being done for phase delay and IF determination by all the methods available in the literature.

As is well known that the tangent is a surjective (many-to-one mapping) function, the domain, range, and period of $\tan (x)$ are $\left\{ x|x\ne \frac{\pi }{2}+n\pi , \forall n \in \mathbb {Z}\right\}$, all real numbers $\mathbb {R}=(-\infty ,\infty )$ and $\pi$, respectively. The inverse tangent is the multivalued function. The domain of $\tan ^{-1}(x)$ is all real numbers, $\mathbb {R}$, and range is $\left( -\frac{\pi }{2},\frac{\pi }{2}\right)$. If $z=x+jy$, then the range of $\tan ^{-1}(y/x)$ is $(-{\pi },{\pi }]$, and sign of x and y is used to determine the specific quadrant.

In order to obtain the IF positive for all the time, we consider the discrete-time signal processing, with sampling frequency $F_\mathrm{s}$, which is the only practical way to process data by a digital processor. The discrete-time version of Eqs. (3), (4), (5) and (6) is [3, 31]

$$\begin{aligned} z[n]&=x[n]+j\hat{x}[n] = a[n]e^{j\phi [n]}, \end{aligned}$$

(7a)

$$\begin{aligned} a[n]&=\left[ x^2[n]+\hat{x}^2[n]\right] ^{1/2}\ge 0, \end{aligned}$$

(7b)

$$\begin{aligned} \phi [n]&=\tan ^{-1}\left( \hat{x}[n]/x[n]\right) ,\end{aligned}$$

(7c)

$$\begin{aligned} \hat{x}[n]&=x[n]*h[n],\end{aligned}$$

(7d)

$$\begin{aligned} \text { and } \omega [n]&=\phi _\mathrm{d}[n], \end{aligned}$$

(7e)

respectively, where the HT kernel [31, 32] defined as $h[n]=\left[ \frac{1-\cos (\pi n)}{\pi n}\right]$ is zero for n even and it is $\frac{2}{\pi n}$ for n odd. The differentiation of phase in discrete time, $\phi _\mathrm{d}[n]$, can be approximated by [3] forward finite difference (FFD), $\phi _\mathrm{d}[n]=\big (\phi [n+1] -\phi [n] \big )$, or backward finite difference (BFD), $\phi _\mathrm{d}[n]=\big (\phi [n] -\phi [n-1] \big )$ or central finite difference (CFD), $\phi _\mathrm{d}[n]=\big (\phi [n+1] -\phi [n-1] \big )/2$. It can be noted that the phase in (7c) is computed by the function, $\text {atan2}(\hat{x}[n],x[n])$, which produces the result in the range $(-\pi , \pi ]$ and also avoids the problems of division by zero. It is pertinent to notice that the IF defined by (2), (6), and (7e) is valid only for monocomponent signals because the so defined IF becomes negative in some time instants for multicomponent signals which does not provide any physical meaning [2, 3, 17].

By considering the phase unwrapping fact and multivalued nature of the inverse tangent function, we redefine the IF $\omega [n]$, which is defined in (7e) as a discrete-time version of (6), as

$$\begin{aligned} \omega [n] = {\left\{ \begin{array}{ll} \phi _\mathrm{d}[n], &{}\text {if}~ \phi _\mathrm{d}[n] \ge 0, \\ \phi _\mathrm{d}[n]+\pi , &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(8)

Definition (8) makes the IF positive (i.e., $0 \le \omega [n] \le \pi$ in radians/sample which corresponds to 0–${F_\mathrm{s}}/{2}$ in Hz) for all time n which is valid for all monocomponent as well as multicomponent signals. This small and trivial, but extremely important fact has been illusive for many decades. This IF would not only significantly improve the computational efforts (e.g., sifting process in EMD algorithms) and understanding of any method which uses the IF, but also provides an elegant solution in mathematical terms to use the Fourier and filter theory-based zero-phase filtering for nonstationary signal decomposition and TFE analysis. The mathematical validity of this solution can easily be seen by the fact that $\phi [n] =\tan ^{-1}\left( \hat{x}[n]/x[n]\right)$ and $\phi [n]+kn\pi =\tan ^{-1}\left( \hat{x}[n]/x[n]\right) , \forall k, n \in \mathbb {Z}$ [due to periodicity of tangent function, i.e., $\tan (\phi [n])=\tan (\phi [n]+kn\pi )$]. In solution (8), we have taken $k=0$ if $\phi _\mathrm{d}[n]\ge 0$; otherwise, $k=1$; thus, we can write

$$\begin{aligned} \omega [n]=\phi _\mathrm{d}[n]+k\pi . \end{aligned}$$

(9)

Equation (9) is also valid when $\phi [n]\in (-\pi ,\pi ]$ is a wrapped phase, and in this case we select the value of $k\in \mathbb {Z}$ such that $\omega [n]\in [0,\pi ]$. Thus, the proposed IF $\omega [n]$ in (8) or (9) is estimated by using the multivalued property of the inverse tangent function which provides basis to ensure that the instantaneous phase function $\phi [n]$ defined in (7c) is an increasing (or a nondecreasing) function, i.e., $\phi [n+1]\ge \phi [n], \forall n$.

A dual to IF (8), the group delay (GD) is defined as the negative frequency derivative of the phase in the Fourier domain. It measures the relative delay of different frequencies from the input to the output in a system. Thus, similar to (8), we can modify the GD definition to make it always positive and valid for all signals. The proposed definition of IF can easily be extended for multidimensional signals such as spatial data (image) and space–time data (3D wave equation).

A MATLAB implementation code of the proposed method is outlined in Algorithm 1. In order to avoid unnecessary variations in the IF, before estimating the IF, the mean and dominating low frequency component like trend present in the signal can be removed. These can be easily removed by any zero-phase low-pass filtering operation [32, 35]. Moreover, depending upon the requirements, signal can be decomposed into a set of desired frequency bands.

In the examples presented in the following section, to decompose a signal x[n] into a set of desired frequency bands, we have used the signal model

$$\begin{aligned} x[n]= c_0 + \displaystyle \sum _{i=1}^{M} y_{i}[n]=c_0 + \displaystyle \sum _{i=1}^{M} c_{i}[n], \end{aligned}$$

(10)

where $c_0$ is the mean value of signal x[n], and $\{y_{i}[n]\}_{i=1}^{M}$ and $\{c_{i}[n]\}_{i=1}^{M}$ are the M orthogonal and LINOEP components, respectively.

A simple block diagram of the DFT-based zero-phase filter bank (i.e., $H_i[k]\in \mathbb {R}_{\ge 0}$, $\forall i, k$) is shown in Fig. 1, which decomposes a signal x[n] into a set of orthogonal vectors $\{ y_{1}[n], y_{2}[n], \ldots , y_{M}[n] \}$. The frequency response of ith band of the DFT-based zero-phase filter bank can be defined by setting $H_i[k]=1$ at desired frequency band and zero otherwise, i.e.,

$$ \begin{aligned} \left. \begin{aligned} H_i[k]&=1, \qquad (K_{i-1}+1) \le k \le K_i \,\, \& \\&\quad (N-K_{i}) \le k \le (N-K_{i-1}-1),\\&=0, \qquad \text {otherwise} \end{aligned} \right\} \end{aligned}$$

(11)

where $i=1,2,\ldots , M$; $K_0=0$ and $K_M=N/2$ (or $K_M=(N-1)/2$ if N is odd). Using the inverse DFT (IDFT), component $y_{i}[n]$ can be computed as

$$\begin{aligned} y_{i}[n]=\displaystyle \sum _{k=0}^{N-1}\Big [H_i[k]X[k] \exp (j2\pi kn/N)\Big ], \end{aligned}$$

(12)

where $X[k]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]\exp (-j2\pi kn/N)$ is the DFT of signal x[n] of length N.

In this work, we propose to use noncausal finite impulse response (FIR) and infinite impulse response (IIR) filter to decompose a signal into a set of LINOEP vectors by the FDM algorithm as summarized in Algorithm 2. In this algorithm, for each iteration, ZPHPF$_i$ (ZPLPF$_i$) is zero-phase high (low)-pass filter (e.g., filtfilt function of MATLAB) with desired cutoff frequency $f_{ci}$, and value of $\alpha _i$ is obtained such that $\mathbf {c}_i \perp {\tilde{\mathbf {c}}}_{i+1}$. It can be noted that, in general, filter is not ideal (non brick wall frequency response), and therefore, ${\mathbf {c}_i} \not \perp {\mathbf {c}_l}$ for ${i,l=1,2,\ldots ,M-1}$ and only ${\mathbf {c}_{M-1} \perp \mathbf {c}_{M}}$. We use PART A (PART B) of algorithm to obtain $\{c_1,\ldots ,c_M\}$ in order of the highest to lowest (lowest to highest) frequency components. The FDM with proposed IF can easily be adapted for multichannel and multidimensional data decomposition into a set of AM–FM components.

We advocate to use zero-phase filtering (ZPF) because it preserves salient features such as minima and maxima in the filtered waveform exactly at the position where those features occur in the unfiltered waveform. It is pertinent to note that the conventional (i.e., non zero-phase) filtering shifts these features in the filtered waveform and therefore cannot be used to obtain a meaningful TFE distribution, which is clearly demonstrated in simulation results. The zero-phase filtering of a signal can be obtained by the DFT, discrete cosine transforms (DCTs) and discrete sine transforms (DSTs), short-time Fourier transform (STFT), discrete wavelet transform (DWT), noncausal FIR and IIR filters, or via other decomposition methods like FDM, VMD, EVD, EWT, SSWT, and EMD algorithms.

A comparison of the proposed method with the most widely used wavelet transform and EMD algorithm, for data analysis and TFE representation, is shown in Table 1. A study with first seven attributes (basis, frequency, uncertainty, nonlinear, nonstationary, Harmonics, and theoretical base) corresponding second and third column of this table is presented in [18, 32], and we have used all these attributes along with some other features to compare proposed method with wavelet transform and EMD–Hilbert approach.

Table 1 A comparison among wavelet transform, EMD–Hilbert, and ZPF-based approach (FDM) with proposed IF for TFE representation and data analysis

3 Simulation Results and Discussion

In this section, we consider a number of examples, which include both synthetic and real-life nonstationary data, that are mostly discussed in the literature to validate the efficacy of method under study. A complete MATLAB code of the proposed method is publicly available for download at [44].

3.1 Synthetic Nonstationary Data Analysis: IF and TFE Estimation

Example 1

In this example, we consider three nonstationary signals (a) linear chirp (unit amplitude and [1000–2000] Hz), (b) frequency modulated sinusoid (unit amplitude, carrier $f_c=780$ Hz and frequency deviation 200 Hz), and (c) mixture of a linear chirp and frequency modulated signals, i.e., sum of signals of cases (a) and (b). Figure 2 shows the TFE estimates of these three nonstationary signals [(a), (b) and (c)] obtained by using the proposed IF without decomposition. We observe that the frequencies in case (c), as shown in Fig. 2c, are average frequencies of the first two cases (a) and (b).

Figure 2d shows the IF and phase estimates of nonstationary signal, which is sum of linear chirp and FM signals, case (c) without decomposition: (1) top figure with conventional IF (7e) where both the positive and negative estimates of frequencies are present, and hence, it does not provide any physical meaning, (2) middle figure with proposed IF (8) that produces only positive and correct values of frequencies; thus, it easily reveals that the signal under analysis is a superposition of linear chirp and FM signals, (3) bottom figure shows: (1) phase (blue solid line) in radians corresponding to conventional IF (top figure) which is not an increasing function of time and (2) phase (red dashed line) corresponding to proposed IF (middle figure) which is an increasing function of time. This, clearly, demonstrates that the proposed definition of the IF is able to obtain correct values of frequencies at all times.

Figure 3 shows the TFE estimates of nonstationary signal, case (c), by this proposed method with decomposition: (a) into 2 bands of [0–1000, 1000–4000] Hz and (b) into 100 bands of equal bandwidth of 40 Hz (which is $F_{\max }/100$ where $F_{\max }$ is the highest frequency component present in the signal and it is equal to half of the sampling frequency, i.e., $F_{\max }=F_\mathrm{s}/2$). The proposed method is, clearly, able to track TFE distribution present in all these signals.

Figure 4 shows the TFE estimates of nonstationary signal, case (c), by this proposed IF: (a) with zero-phase FIR filter-based decomposition into 100 bands and (b) with conventional (non zero-phase) FIR filter-based decomposition into 100 bands of equal bandwidth, which is not able to detect and track true frequencies present in the signal.

Fig. 2

TFE analysis of nonstationary signals by this proposed method without decomposition: a linear chirp, b frequency modulated signal, c sum of linear chirp and FM signals. Plot d shows the IF estimates of nonstationary signal, which is sum of a linear chirp and FM signals, without decomposition: (top figure) with conventional IF (7e) and (middle figure) with proposed IF (8). Notice the both positive and negative frequencies with conventional IF, top figure in plot d, which does not provide any physical meaning; only positive and correct values of frequencies by the proposed IF, middle figure in plot d, which reveals that the signal under analysis is a superposition of a linear chirp and FM signals. The bottom figure of in plot d shows: phase in radians corresponding to conventional IF (blue solid line, not an increasing function); and phase corresponding to proposed IF (red dashed line, an increasing function) (Color figure online)

Fig. 3

TFE analysis of nonstationary signal, which is sum of linear chirp and FM signals, by this proposed method with DFT-based decomposition: a into 2 bands of [0–1000, 1000–4000] Hz and b into 100 bands of equal bandwidth, and in both cases true frequencies present in the signal are revealed

Fig. 4

TFE analysis of nonstationary signal, which is sum of linear chirp and FM signals, by this proposed method: a with zero-phase FIR filter-based decomposition into 100 bands which capture true frequencies of the signal and b with conventional (non zero-phase) FIR filter-based decomposition into 100 bands of equal bandwidth which is not bale to capture true nature of the signal under analysis

Example 2

We obtain a nonstationary signal by adding five unit amplitude linear chirps of frequencies [500–1500], [1000–2000], [1500–2500], [2000–3000] and [2500–3500] Hz. Figure 5 shows the TFE analysis of this nonstationary signal, which is sum of five linear chirp signals, by this proposed IF: (a) without decomposition that presents frequencies in the range of [1500–2500] Hz, which are average of frequencies present in five chirp signals; (b) with DFT-based decomposition into 10 bands; and (c) with DFT-based decomposition into 20 bands of equal bandwidth. These two, (b) and (c), figures clearly reveal the five chirp signals present in the signal under analysis.

The time–frequency and phase representations of signal considered in this example by the traditional and proposed methods are shown in Fig. 5d: (top figure) traditional IF which generates both positive and negative frequencies, (middle figure) proposed IF which yields only positive frequencies, (bottom figure) phase estimates with traditional IF (blue solid line) which is not an increasing function and phase estimates with proposed IF (red dashed line) which is an increasing function of time.

Figure 6 shows the TFE distribution of the nonstationary signal, which is the sum of five linear chirp signals: (a) by this proposed method with zero-phase FIR filter-based decomposition into 10 bands, (b) with conventional (non zero-phase) FIR filter-based decomposition into 10 bands of equal bandwidth, and (c) by the EMD algorithm. Clearly, the proposed method with zero-phase FIR filter-based decomposition reveals true frequencies of signal, whereas both the conventional FIR filter and EMD algorithm are not able to detect true frequencies present in the signal.

Fig. 5

TFE analysis of a nonstationary signal, which is sum of five linear chirp signals, by this proposed method: a without decomposition, b with DFT-based decomposition into 10 bands, and c with DFT-based decomposition into 20 bands of equal bandwidth which are clearly able to reveal true nature of the signal under analysis. Plot d shows the time–frequency estimates by: (top figure) traditional IF which generates both positive and negative frequencies, (middle figure) proposed IF which yields only positive frequencies, (bottom figure) phase estimates with traditional IF (blue solid line, not an increasing function), and phase estimates with proposed IF (red dashed line, an increasing function of time) (Color figure online)

Fig. 6

TFE analysis of a nonstationary signal, which is sum of five linear chirp signals (a) by the proposed method with zero-phase FIR filter-based decomposition into 10 bands, and b with conventional (non zero-phase) FIR filter-based decomposition into 10 bands of equal bandwidth, c by the EMD algorithm. Clearly, only proposed method reveals true frequencies

Example 3

In Fig. 7, we present the TFE analysis of the nonstationary signal, which is sum of the unit amplitude linear chirp signal [500–1500] Hz ([0–1] second chirp signal and [1–1.5] second no signal) and its delayed version ([0–0.5] second no signal and [0.5–1.5] second same chirp signal), by this proposed method. Figure 7a is obtained without decomposition that has three parts: (1) [0–0.5] s chirp signal frequencies, (2) [0.5–1] s average of overlapped chirp signals frequencies, and (3) [1–1.5] s chirp signal frequencies of delayed version. Figure 7b is obtained by DFT-based decomposition of signal into 10 bands of equal bandwidth, which clearly reveals that the signal under study is sum of a chirp signal and its delayed version.

Figure 8 shows the TFE distribution of the nonstationary signal (sum of the linear chirp signal and its delayed version) by this proposed IF: (a) with zero-phase FIR filter-based decomposition into 10 bands which is able track true frequencies of the signal, and (b) with conventional FIR filter-based decomposition into 10 bands of equal bandwidth, which clearly not able to reveal true frequencies present in the signal.

Fig. 7

TFE analysis of the nonstationary signal, which is the sum of the linear chirp signal and its delayed version, by this proposed method: a without decomposition and b with DFT-based decomposition into 10 bands of equal bandwidth which reveals true nature of the signal under analysis

Fig. 8

TFE analysis of a nonstationary signal, which is sum of a linear chirp signal and its delayed version, by this proposed method: a with zero-phase FIR filter-based decomposition into 10 bands and b with conventional FIR filter-based decomposition into 10 bands of equal bandwidth. Clearly, zero-phase FIR filter-based TFE analysis reveals true frequencies of the signal under analysis, whereas the conventional FIR filter-based TFE analysis is not able to catch true nature of signal

Discussion From Examples (1, 2, and 3), it is clear that the zero-phase DFT or zero-phase FIR filter-based decomposition is able to track TFE distribution present in a signal. However, conventional filtering cannot be used to obtain meaningful TFE distribution of a signal, which is clearly demonstrated in right figures in Figs. 4, 6 and 8.

Example 4

In this example, we consider the IF and TFE estimation of a delta function. The unit sample sequence (delta function) is defined as $x[n]=\delta [n-n_0]=1$ at $n=n_0$ and zero otherwise. Using the discrete-time Fourier transform (DTFT) $X(\omega )=\sum _{n=-\infty }^{\infty } x[n] \exp (-j\omega n)$, one can obtain the DTFT of unit sample sequence as $X(\omega )=\exp (-j\omega n_0) \Rightarrow |X(\omega )|=1$. Using the inverse DTFT (IDTFT), $x[n]=\frac{1}{2\pi }\int _{-\pi }^{\pi } X(\omega ) \exp (j\omega n) \,\mathrm {d}\omega$, one can represent the unit sample sequence as $x[n]=\frac{1}{2\pi }\int _{-\pi }^{\pi } \exp (j\omega (n-n_0)) \,\mathrm {d}\omega$. This representation demonstrates that it is a superposition of equal amplitude sinusoidal functions of all frequencies [0–$\pi$). The Nyquist frequency ($F_\mathrm{s}/2$) is the highest frequency that can be present at a given sampling rate, $F_\mathrm{s}$, in a discrete-time signal. The analytic representation of this signal is given by [32] $z[n] =\frac{\sin (\pi (n-n_0))+j[1-\cos (\pi (n-n_0))]}{\pi (n-n_0)}=a[n]\exp (j\phi [n])$, where $a[n] =\left|\frac{ \sin \left( \frac{\pi }{2} (n-n_0)\right) }{\frac{\pi }{2} (n-n_0))}\right|$, $\phi [n] =\frac{\pi }{2} (n-n_0)$, and real part of z[n] is the original signal as $\frac{\sin (\pi (n-n_0))}{\pi (n-n_0)}=\delta [n-n_0]$. Thus, frequency $\omega [n] =\phi [n+1]-\phi [n]=\frac{\pi }{2}$, which corresponds to half of the Nyquist frequency, i.e., $F_\mathrm{s}/4$. Figure 9 shows the TFE estimates of this signal (with $n_0 = 1999$, $F_\mathrm{s} = 1000$ Hz and length $N = 4000$) using the (a) EMD and (b) proposed method without decomposition. We observe that the frequency present in this TFE plot is the average frequency (because delta function contains equal amplitude sinusoids of all frequencies 0 to $F_\mathrm{s}/2$). This example also demonstrates that the TFE plot, obtained by the Hilbert spectrum, is not limited by uncertainty principle and signal can be highly concentrated in the time–frequency plane. However, it can be noted that this TFE plot is not providing the true frequencies of delta function.

Discussion In order to explain a average frequency effect in Figs. 2, 5, 7 and 9, let us consider a sum of sinusoids of equal amplitudes $x(t)=\sum _{k=1}^N A\cos (\omega _0 kt)$. Its analytic representation is given by $z(t)=\sum _{k=1}^N A\exp (j\omega _0 kt)=\frac{A\sin \left( \omega _0 \frac{N}{2}t \right) }{\sin (\omega _0 t/2)}\exp \left( j\omega _0\frac{N+1}{2}t \right) =a(t)\exp (j\phi (t))$ which implies phase $\phi (t)=\left( \omega _0\frac{N+1}{2}t\right)$, and hence, IF $f(t)=\frac{1}{2\pi }\omega _0\frac{N+1}{2}$ which is the average of frequencies $\{\omega _0,2\omega _0,\ldots , N\omega _0\}$. This is what we observe in these figures (especially Fig. 9b). Here, it is to be noted that if amplitudes of constituent sinusoids are not equal, then resultant IF would not be a constant (average) frequency, but it would be a variable one.

Fig. 9

TFE analysis of unit sample sequence $\delta [n-n_0]$ (with, $n_0 = 1999$, sampling frequency $F_\mathrm{s} = 1000$ Hz, length $N = 4000$) by a ensemble EMD (EEMD) and b the proposed method without decomposition. Proposed method produces TFE distribution which matches with theoretical result, whereas there is a energy spreading across a large range of frequencies by the EEMD method

Example 5

In this example, we consider the IF and TFE estimation of the White Gaussian noise data. Figure 10 shows the TFE analysis of a white Gaussian noise (with zero mean, unit variance, 10,240 samples and sampling frequency $F_\mathrm{s}=100$ Hz) obtained using (a) the EMD and (b) the proposed method without decomposition. It is clear that the energy in TFE plane is more concentrated at mid frequencies and almost randomly distributed across all the other frequency ranges by the proposed method. However, distribution of the energy in TFE plane is less random and concentration is weak at high frequencies by the EMD algorithm.

Fig. 10

TFE analysis of the Gaussian white noise with zero mean and unit variance (with sampling frequency $F_\mathrm{s} = 1000$ Hz, length $N =$ 10,240) by a the EMD and b the proposed method without decomposition

3.2 Real-Life Data Analysis: IF and TFE Estimation

In order to evaluate the effectiveness of the proposed method for real-life data analysis, we consider the Earthquake time series and Gravitational wave data in the following examples.

Example 6

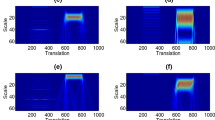
In this example, we consider the IF and TFE estimation of the Elcentro Earthquake time series. An Earthquake time series is a nonlinear and nonstationary data. The Elcentro Earthquake data (sampled at $F_\mathrm{s}= 50$ Hz) have been taken from [43] and are shown in Fig. 11a. The critical frequency range that matters in the structural design is less than 10 Hz, and the Fourier-based power spectral density (PSD), as shown in Fig. 11b, shows that almost all the energy in this Earthquake data is concentrated within 10 Hz, which is a critical frequency range for structural design. Figure 12 shows TFE distributions by the (a) continuous wavelet transform (CWT), (b) EMD, (c) FDM, (d) proposed method without decomposition, (e) proposed method with DFT-based decomposition into four bands [0–5, 5–10, 10–20, 20–25] Hz, and (f) proposed method with DFT-based decomposition into 25 bands of 1 Hz each. These TFE distributions indicate that the maximum energy concentration in the signal is around 2 s and 1.7 Hz. These TFE distributions provide details of how the different waves arrive from the epical center to the recording station, e.g., the compression waves of small amplitude, but higher frequency range of 10–20 Hz, the shear and surface waves of strongest amplitude and lower frequency range of below 5 Hz which does most of the damage, and other body shear waves which are present over the full duration of the data span.

Fig. 11

Elcentro Earthquake May 18, 1940 a North–South Component data and b Fourier-based power spectral density (PSD)

Fig. 12

TFE plot of the Elcentro Earthquake data using the: a CWT, b EMD, and c FDM, which has better time–frequency resolution and precision as compared to CWT and EMD, d proposed method without decomposition, e proposed method with DFT-based decomposition into four bands [0–5, 5–10, 10–20, 20–25] Hz, and f proposed method with DFT-based decomposition into 25 bands of 1 Hz each

Example 7

Finally, we consider the IF estimation and TFE representation of the Gravitational wave event GW150914 from a binary black hole merger [1]. The gravitational wave data used in this example are publicly available at [45]. The signal sweeps upwards in frequency from 35 to 250 Hz, and amplitude strain increases to a peak gravitational wave strain of $1.0 \times 10^{-21}$ [1]. An accurate IF estimation of the gravitational wave is important because it is the basis to calculate many parameters such as separation, velocity, luminosity distance, chirp mass, total mass, primary mass, secondary mass, and effective spin of binary black hole merger [1]. Figure 13 shows (a) the gravitational strain data GW150914, (b) the TFE representation of the data by proposed method which shows the signal frequency is increasing from 35 to 250 Hz, and (c) the TFE representation of the data by CWT. Thus, the TFE representation by the proposed method captures the real nature of the gravitational wave event and also provides better time and frequency resolution than the CWT approach.

Fig. 13

Gravitational wave event GW150914: a estimated numerical relativity waveform of data H1 strain [1], b the TFE representation of the data by the proposed IF without decomposition, and c TFE representation by the CWT

These examples clearly demonstrate the ability of the proposed method for TFE analysis of real-life signals such as seismic and gravitational wave data. This study is aimed to complement the current nonlinear and nonstationary data, e.g., seismic and gravitational time series, processing methods with the addition of the Fourier and zero-phase filter-based methods.

Discussion It is clear from the above examples that different methods are producing the different TFE distributions of a signal. So, before concluding anything one needs to be careful while performing the signal analysis. For example, frequencies present in the Fourier spectrum show that these frequencies are present all the time in a signal under analysis, which may not be true. Consider another example, as shown in Fig. 9 (right), of unit sample sequence which shows that this signal is concentrated in time (which is true) and also concentrated in frequency (which is not true). If this were true, then we could transmit delta function in almost zero time with zero bandwidth through any system or channel. Thus, we conclude that the TFE representation depends on the number of bands in which data have been divided. In order to further illustrate this point we divided the same unit sample sequence data, which is used in Fig. 9, by DFT-based zero-phase filtering into five and ten bands of equal bandwidth to obtain (a) and (b) plots in Fig. 14, respectively, which reveal many those frequencies of data which are not present in Fig. 9.

Fig. 14

TFE analysis of unit sample sequence $\delta [n-n_0]$ (with, $n_0 = 1999$, sampling frequency $F_\mathrm{s} = 1000$ Hz, length $N = 4000$) by proposed method with DFT-based decomposition into five (top figure) and ten (bottom figure) bands of equal bandwidth

From Figs. 2, 5, 7, 9 and 14, it is clear that the proposed method using the Hilbert spectrum produces average frequencies and good time resolution when the envelope of signal is smooth. However, if the envelope of a signal is fluctuating randomly or rapidly, e.g., consider the case of Gaussian white noise and Earthquake time series, the TFE plot has good time and frequency resolution as shown in Figs. 10 and 12d. It is also clear, from Figs. 3, 5, 7 and 14, that as the signal is decomposed into more number of narrow bands, true frequencies present in the signal under analysis are revealed, frequency resolution is also increasing while the time resolution is reducing marginally.

In the above simulation results, the TFE plots, as shown in Figs. 2, 5a, 7a, 9b, 10b, 12d and 13b, are obtained by the proposed IF (8) without decomposing the signals (i.e., zero computational complexity of decomposition). Moreover, these results are very interesting, physically significant as they reveal real nature of signal under analysis, and cannot be obtained by the traditional IF (7e).

4 Conclusion

The IF is an important parameter for the analysis of nonstationary signals and nonlinear systems. It is the basis of the TFE analysis of a signal. The IF is the time derivative of the instantaneous phase and, originally, it is well defined only when this derivative is positive. That is, the IF is valid only for monocomponent signals. If time derivative of instantaneous phase is negative, i.e., the IF is negative, then it does not provide any physical significance. This study proposed a mathematical solution and eliminates this problem by modifying the present definition of IF. This is achieved by using the property of the multivalued inverse tangent function that provides base to ensure that the instantaneous phase is an increasing (or a nondecreasing) function.

There are two fundamental and important conceptual innovations of this work. First is the extension of the conventional definition of IF by redefining it such that it is always positive. This proposed IF is valid for all types of signals such as monocomponent and multicomponent, narrowband and wideband, stationary and nonstationary signals generated by linear and nonlinear systems. The understanding of the TFE representation, by all the methods which are using the IF, would improve significantly by using this definition. Second, we have also demonstrated that the zero-phase filtering-based decomposition of a signal into a set of desired frequency bands with proposed IF accurately reveals the TFE distribution, whereas conventional (i.e., nonzero-phase) filtering-based decomposition cannot be used to obtain correct and meaningful TFE distribution. The Fourier and filter theory are well established, fully matured and developed; thus, the zero-phase filtering-based decomposition of a signal, i.e., the FDM, is the most powerful for analysis and TFE representation which presents full control over the number of bands with desired cutoff frequencies. This kind of control and features is difficult to achieve or may not be possible by the decomposition methods such as EMD algorithms, SSWT, VMD, EVD, time-varying vibration decomposition, resonance-based signal decomposition, EMD based on constrained optimization, and EWT available in the literature. Simulations and numerical results demonstrated the superiority, validity, and efficacy of the proposed IF for the TFE analysis of a signal as compared to other existing methods available in the literature.

In this study, we have considered many simulated signals and two real-life signals (an earthquake and a gravitational wave recordings generated by real-world phenomena) to demonstrate the efficacy of the proposed method. In order to reveal the underlying processes and provide explanations of physical phenomenon, the directions of future research would be (1) to apply the proposed method to a large class of nonstationary signals such as vibration, speech and acoustic signals, biomedical electrocardiogram (ECG) and electroencephalogram (EEG) signals, financial time series, radar, sonar, and communication signals analysis and (2) to use the proposed IF in all the decomposition methods such as EMD, SSWT, VMD, EVD, and EWT to obtain TFE distribution of a signal.