High-Performance 1-D and 2-D Inverse DWT 5/3 Filter Architectures for Efficient Hardware Implementation

Abstract

This paper presents high-performance and memory-efficient hardware architectures for one-dimensional (1-D) and two-dimensional (2-D) inverse discrete wavelet transform (DWT) 5/3 filters. The proposed 1-D filter architecture requires 33% less memory resources and 17% less logic resources than the best state-of-the-art solutions. The proposed 1-D filter architecture has 100% hardware utilization, which is defined as the ratio of the actual computation time to the total processing time, both expressed in numbers of clock cycles. It allows a 7% higher operational frequency and simultaneously has the lowest total power dissipation in comparison with the best state-of-the-art solutions. The proposed 2-D inverse DWT 5/3 architecture, based on the proposed 1-D inverse DWT filter design, provides medium total computing time and output latency, but outperforms the best state-of-the-art solutions for at least 20% in terms of required memory capacity.

1 Introduction

Discrete wavelet transform is widely used in many application areas. It has become a standard technique in signal processing, speech analysis, image coding, and video compression.

Some important research on wavelet transform were presented in [23, 24, 29, 31, 32]. The 2-D DWT has been adopted in JPEG 2000 still image compression standard [2]. The default reversible transformation in JPEG 2000 standard is implemented by using Le Gall’s 5/3 filter [17], since it allows perfect signal reconstruction and it has good compression performance for all classes of images, as well as a low computational complexity [3]. Difference equations (1) and (2) describe low- and high-pass forward DWT 5/3 filters, respectively, where x[n] represents the input signal samples, $y_0 [n]$ represents the output signal samples which are generated by forward low-pass filtering of input samples and $y_1 [n]$ represents the output signal samples which are generated by forward high-pass filtering of input samples.

$$\begin{aligned} y_0 [n]= & {} -\frac{1}{8}x[n]+\frac{1}{4}x[n-1]+\frac{3}{4}x[n-2]+\frac{1}{4}x[n-3]-\frac{1}{8}x[n-4] \end{aligned}$$

(1)

$$\begin{aligned} y_1 [n]= & {} -\frac{1}{2}x[n-1]+x[n-2]-\frac{1}{2}x[n-3] \end{aligned}$$

(2)

Difference equations (3) and (4) describe low- and high-pass inverse DWT 5/3 filters, respectively, where $w_0 [n]$ represents the output signal samples which are generated by inverse low-pass filtering of $y_0 [n]$ and $w_1 [n]$ represents the output signal samples which are generated by inverse high-pass filtering of $y_1 [n]$.

$$\begin{aligned} w_0 [n]= & {} \frac{1}{2}y_0 [n-1]+y_0 [n-2]+\frac{1}{2}y_0 [n-3] \end{aligned}$$

(3)

$$\begin{aligned} w_1 [n]= & {} -\frac{1}{8}y_1 [n]-\frac{1}{4}y_1 [n-1]+\frac{3}{4}y_1 [n-2]-\frac{1}{4}y_1 [n-3]-\frac{1}{8}y_1 [n-4] \end{aligned}$$

(4)

According to JPEG 2000 standard, DWT 5/3 filters typically support two filtering modes: a convolution-based mode and a lifting-based mode. In either mode, an input signal should be first periodically extended on all input signal boundaries for half-length of the filter, or the filter itself should be modified at input signal boundaries. Convolution-based filters perform a series of multiplications and additions between low-pass and high-pass filter coefficients. Lifting-based filtering consists of a sequence of alternative updating of signal samples with odd indexes with a weighted sum of signal samples with even indexes, and updating of signal samples with even indexes with a weighted sum of signal samples with odd indexes.

Convolution-based implementations of DWT are used in [9, 12, 28, 30, 34, 37]. These filter implementations usually require large use of memory and logic resources and a large number of arithmetic computations, and hence they are usually not suitable for low-power and high-speed signal and image processing applications.

Lifting-based implementations of DWT are used in [4, 8, 14, 15, 18,19,20, 22, 26]. These implementations usually have a simpler architecture, a lower power consumption, a lower computational complexity, and an efficient use of memory and logic resources.

Direct mapped architecture was proposed in [15, 22]. Even though this architecture is very simple and requires less logic and memory resources than convolution-based architecture, it still has only 50% hardware utilization. Also, for a single read port memory, the overall pipelined architecture is slowed down by 50%, since the odd and even samples are read serially in alternate clock cycles and buffered. Direct mapped architecture has been further improved in [18] where the new folded architecture was proposed. Improvement has been achieved by folding the last two pipeline stages into the first two stages, which increased the hardware utilization to 100%. However, no folded computing is necessary for 5/3 filter since it has only one stage for lifting-based operations. Generalized and highly programmable architecture has been proposed in [4]. This kind of lifting-based architecture can support a large set of different filters, including 5/3 filter. Flipping architecture has been proposed in [14] addressing the issue of long critical paths in DWT lifting-based architectures, but without pipelining which usually results in a significant increase in the number of registers. Another highly programmable architecture, based on multiply and accumulate structures, has been described in [8]. Recursive DWT architecture, which processes multiple DWT levels simultaneously, unlike the traditional DWT architectures, has been proposed in [19]. Dual-scan architecture for DWT, that achieves 100% hardware utilization for some special cases, by processing two independent data streams together, has been presented in [20]. Filter-independent DSP-type parallel DWT architecture, which can be programmed to support a wide range of filters, including 5/3 filter, has been described in [26]. Detailed comparison of all these lifting-based DWT architectures has been presented in [1]. The simplest implementations have the solutions proposed in [4, 15, 18, 22], while architectures described in [8, 14, 19, 20, 26] have a greater hardware complexity, but also a greater flexibility which includes the support for a wide range of different types of filters.

Several 2-D DWT hardware architectures have been recently proposed. SIMD array architecture was presented by Chakrabarti and Vishwanath [7]. A straightforward implementation of the 2-D DWT (so-called direct architecture), and the implementation which utilizes two systolic array filters and two parallel filters (so-called systolic-parallel architecture) have been suggested in [33]. A convolution-based, high-speed, and low-power pipelined architecture with four subbands transforms performed in parallel has been presented by Marino [25]. Already mentioned Chang et al.’s [8] filter design is also utilized in the appropriate programmable 2-D DWT architecture. Wu and Chen [34] employed their convolution-based filter design and created a line-based architecture for the 2-D DWT in which they used the coefficient folding technique and polyphase decomposition technique in order to decrease the total computing time and to increase the hardware utilization. Andra et al. [4] used their generalized filter design in order to develop a block-based implementation of four-processor 2-D DWT architecture which is highly programmable, but which uses a large embedded memory resources. The lifting-based 2-D DWT recursive architecture (RA) which simultaneously processes multiple levels of decomposition was proposed by Liao et al. [19]. Also, the 2-D DWT dual-scan architecture (DSA), which uses an interleaving scheme for multilevel decomposition with reduced memory size and reduced number of memory accesses, was described by Liao et al. [20]. A hybrid of level-by-level and line-based 2-D DWT architecture, which scans the image by the row processor in a raster format, was developed by Barua et al. [6]. An efficient pipeline architecture with critical path of only one multiplier achieved by merging predict and update stages was presented by Wu and Lin [35]. A high-speed 2-D DWT architecture (HA) which utilizes parallelism among four subband transforms was proposed by Xiong et al. [36]. The block-based 2-D DWT architecture without frame buffer, which, however, uses larger on-chip memory and has input interface units which cause significant overhead, was proposed by Mohanty and Meher [27]. Lifting-based parallel multilevel 2-D DWT architecture with a single processing unit which calculates both predict and update values was presented by Aziz and Pham [5]. Memory-efficient 2-D DWT architecture, with mixed column-wise and row-wise signal flow was designed by Hsia et al. [13]. A high-performance folded multilevel 2-D DWT architecture (FMA) and pipelined multilevel 2-D DWT architecture (PMA) which exploits dual-pixel scanning method with high operational frequency, low latency, and low power consumption were presented by Darji et al. [10].

2 Design of the Proposed 1-D Inverse DWT 5/3 Filter Architecture

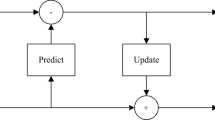
Block diagram of typical state-of-the-art 1-D forward and inverse DWT is shown in Fig. 1. On the analysis side of state-of-the-art 1-D DWT, input signal x[n] is low-pass-filtered with transfer function $H_0 (z)$ and decimated by a factor of two in the upper branch in Fig. 1, as well as high-pass-filtered with transfer function $H_1 (z)$ and decimated by a factor of two, in the lower branch in Fig. 1. Created data samples ${y}'_0 [n]$ which belong to low-pass subband, and ${y}'_1 [n]$ which belong to high-pass subband, are then transmitted through the transmission channel (typically after compression). On the synthesis side of block diagram in Fig. 1 (typically after decompression), transmitted samples ${y}'_0 [n]$ are interpolated by a factor of two and low-pass-filtered with transfer function $F_0 (z)$, in the upper branch in Fig. 1, creating $w_0 [n]$ samples, while transmitted samples ${y}'_1 [n]$ are interpolated by a factor of two and high-pass-filtered with transfer function $F_1 (z)$, in the lower branch in Fig. 1, creating $w_1 [n]$ samples. Samples $w_0 [n]$ and $w_1 [n]$ together create reconstructed signal w[n].

Fig. 1

Block diagram of state-of-the-art 1-D forward and inverse DWT

Each second sample in both branches is added during interpolation process on synthesis side, thus increasing memory and processing resources used for their generation. Such approach means that samples which are added by interpolators are also filtered by $F_0 (z)$ and $F_1 (z)$ filters, despite it is not necessary. Therefore, time, logic, and memory resources of $F_0 (z)$ and $F_1 (z)$ used for their filtering have been wasted.

The approach disclosed in this paper is based on the idea that time, logic and memory resources of inverse filters which are wasted in state-of-the-art approach, must be used only for filtering data samples which are not added by interpolators.

In the proposed concept, even time slots are used for filtering the low-pass signal components, while odd time slots are used for filtering the high-pass signal components. Therefore, the proposed 1-D inverse DWT 5/3 filter architecture utilizes time, logic, and memory resources which have been wasted in state-of-the-art solutions.

Additional savings of memory resources in the proposed 1-D inverse DWT 5/3 filter architecture, compared to state-of-the-art solutions, is obtained by using the same memory blocks (or registers) for the process of filtering low- and high-pass signal components, which is feasible since low- and high-pass signal components are filtered in different time slots. However, since the transfer function of a low-pass filter is different from the transfer function of a high-pass filter, the proposed approach requires using of non-stationary topology of the proposed 1-D inverse DWT 5/3 filter architecture. The first filter configuration should be applied during even time slots (when low-pass components of the signal are filtered), and the second filter configuration should be applied during odd time slots (when high-pass components of the signal are filtered). The change of configuration will be accomplished using the switches, while the same memory blocks (or registers) are reused for filtering low- and high-pass signal components due to feed-forward and feedback paths.

Schematic block diagram of the proposed 1-D inverse DWT 5/3 filter architecture is shown in Fig. 2. Control signal c controls four switches responsible for providing non-stationary filter topology. Time diagram of control signal c is shown in Fig. 3.

Fig. 2

Schematic block diagram of the proposed 1-D inverse DWT 5/3 filter architecture

Fig. 3

Time diagram of control signal c in the proposed 1-D inverse DWT 5/3 filter architecture

Whenever the control signal c is at low level $(c=0)$, for every input sample y[n] with even index $n=2p$, two upper switches are closed while two lower switches are opened, which leads to filter configuration shown in Fig. 4.

Fig. 4

Configuration of the proposed 1-D inverse DWT 5/3 filter architecture for $c=0$

Whenever the control signal c is at high level $(c=1)$, for every input sample y[n] with odd index $n=2p+1$, two upper switches are opened while two lower switches are closed, which leads to filter configuration shown in Fig. 5.

Fig. 5

Configuration of the proposed 1-D inverse DWT 5/3 filter architecture for $c=1$

The set of equations which describes the signals inside the proposed 1-D inverse DWT 5/3 filter architecture in time instances from $n=0$ to $n=5$ is shown in Table 1.

Table 1 Equations for signals inside the proposed 1-D inverse DWT 5/3 filter in time instances from $n=0$ to $n=5$

Based on the equations for time instance $n=5$, w[n] can be expressed as:

$$\begin{aligned} w[n]= & {} m\cdot u\cdot y[n]+u\cdot y[n-1]+(1+l\cdot m+k\cdot u)\cdot y[n-2]\nonumber \\&+\,l\cdot y[n-3]+k\cdot l\cdot y[n-4] \end{aligned}$$

(5)

From now on, this situation is being repeated periodically. For every odd index n, w[n] satisfies (5), while for every even index n, w[n] can be expressed as:

$$\begin{aligned} w[n]=m\cdot y[n-1]+y[n-2]+k\cdot y[n-3] \end{aligned}$$

(6)

In order to determine parameters k, l, m, u, we will use the fact that w[n] is actually a delayed replica of x[n], since the proposed 1-D inverse DWT 5/3 filter architecture should provide perfect reconstruction of samples previously filtered with the 1-D forward DWT 5/3 filter.

$$\begin{aligned} w[n]=x[n-\delta ] \end{aligned}$$

(7)

Parameter $\delta$ represents a delay introduced by cascaded connection of a 1-D forward DWT 5/3 filter and the proposed 1-D inverse DWT 5/3 filter architecture.

For every even index n, y[n] satisfies the difference equation (1) and for every odd index n, y[n] satisfies the difference equation (2). If we replace $y[n-1]$ and $y[n-3]$ from (6) with the corresponding Eq. (2) and $y[n-2]$ from (6) with the corresponding equation defined by (1), it yields:

$$\begin{aligned} w[n]= & {} -\frac{1}{2}m\cdot x[n-2]+m\cdot x[n-3]-\frac{1}{2}m\cdot x[n-4]-\frac{1}{8}\cdot x[n-2] \nonumber \\&+\,\frac{1}{4}x[n-3]+\frac{3}{4}x[n-4]+\frac{1}{4}x[n-5]-\frac{1}{8}x[n-6]-\frac{1}{2}k\cdot x[n-4]\nonumber \\&+\,k\cdot x[n-5]-\frac{1}{2}k\cdot x[n-6] \end{aligned}$$

(8)

Based on (8), w[n] can be expressed as:

$$\begin{aligned} w[n]= & {} \left( {-\frac{1}{2}m-\frac{1}{8}} \right) \cdot x[n-2]+\left( {m+\frac{1}{4}} \right) \cdot x[n-3]\nonumber \\&+\left( {-\frac{1}{2}m+\frac{3}{4}-\frac{1}{2}k} \right) \cdot x[n-4] \nonumber \\&+\left( {\frac{1}{4}+k} \right) \cdot x[n-5]+\left( {-\frac{1}{8}-\frac{1}{2}k} \right) \cdot x[n-6] \end{aligned}$$

(9)

It can be seen that coefficients of samples $x[n-2]$, $x[n-3]$, $x[n-5]$ and $x[n-6]$ disappear if we choose:

$$\begin{aligned} m=k=-\frac{1}{4} \end{aligned}$$

(10)

In that case Eq. (9) becomes simply:

$$\begin{aligned} w[n]=x[n-4] \end{aligned}$$

(11)

which means that perfect reconstruction is obtained for even indexes n.

If we replace m and k from (10) into the equation for w[n] with odd indexes n (5), it yields:

$$\begin{aligned} w[n]= & {} -\frac{1}{4}u\cdot y[n]+u\cdot y[n-1]+\left( 1-\frac{1}{4}l-\frac{1}{4}u\right) \cdot y[n-2]\nonumber \\&+\,l\cdot y[n-3]-\frac{1}{4}l\cdot y[n-4] \end{aligned}$$

(12)

If we replace y[n], $y[n-2]$ and $y[n-4]$ from (12) with the corresponding Eq. (2), and $y[n-1]$ and $y[n-3]$ from (12) with the corresponding equations defined by (1), we obtain:

$$\begin{aligned} w[n]= & {} \frac{1}{8}u\cdot x[n-1]-\frac{1}{4}u\cdot x[n-2]+\frac{1}{8}u\cdot x[n-3]-\frac{1}{8}u\cdot x[n-1] \nonumber \\&+\,\frac{1}{4}u\cdot x[n-2]+\frac{3}{4}u\cdot x[n-3]+\frac{1}{4}u\cdot x[n-4]-\frac{1}{8}u\cdot x[n-5]\nonumber \\&+\left( {-\frac{1}{2}+\frac{1}{8}l+\frac{1}{8}u} \right) \cdot x[n-3]+\left( {1-\frac{1}{4}l-\frac{1}{4}u} \right) \cdot x[n-4] \nonumber \\&+\left( {-\frac{1}{2}+\frac{1}{8}l+\frac{1}{8}u} \right) \cdot x[n-5]-\frac{1}{8}l\cdot x[n-3]+\frac{1}{4}l\cdot x[n-4]\nonumber \\&+\,\frac{3}{4}l\cdot x[n-5]+\frac{1}{4}l\cdot x[n-6]-\frac{1}{8}l\cdot x[n-7]\nonumber \\&+\,\frac{1}{8}l\cdot x[n-5]-\frac{1}{4}l\cdot x[n-6]+\frac{1}{8}l\cdot x[n-7] \end{aligned}$$

(13)

Based on (13), w[n] can be finally expressed as:

$$\begin{aligned} w[n]=\left( {u-\frac{1}{2}} \right) \cdot x[n-3]+x[n-4]+\left( {l-\frac{1}{2}} \right) \cdot x[n-5] \end{aligned}$$

(14)

It can be seen that coefficients of samples $x[n-3]$ and $x[n-5]$ disappear if we choose:

$$\begin{aligned} u=l=\frac{1}{2} \end{aligned}$$

(15)

In that case Eq. (14) becomes simply:

$$\begin{aligned} w[n]=x[n-4] \end{aligned}$$

(16)

which means that perfect reconstruction is also obtained for odd indexes n.

Therefore, the proposed 1-D inverse DWT 5/3 filter architecture, shown in Fig. 6, operates as low-pass filter for data samples y[n] with even indexes n, and operates as high-pass filter for data samples y[n] with odd indexes n.

Fig. 6

The proposed 1-D inverse DWT 5/3 filter architecture

Replacing obtained values for k and m (10) into Eq. (6), provides that input samples y[n] are low-pass-filtered within time slots with even indexes $n=2p$ without any need for upsampling by two, in order to produce output samples $w_0 [n]$, which actually represent output samples w[n] with even indexes $n=2p$ (17).

$$\begin{aligned} w_0 [n]=-\frac{1}{4}y[n-1]+y[n-2]-\frac{1}{4}y[n-3] \end{aligned}$$

(17)

Replacing obtained values for k, l, m, u (10) and (15) into Eq. (5), provides that input samples y[n] are high-pass-filtered within time slots with odd indexes $n=2p+1$ without any need for upsampling by two, in order to produce output samples $w_1 [n]$, which actually represent output samples w[n] with odd indexes $n=2p+1$ (18).

$$\begin{aligned} w_1 [n]=-\frac{1}{8}y[n]+\frac{1}{2}y[n-1]+\frac{3}{4}y[n-2]+\frac{1}{2}y[n-3]-\frac{1}{8}y[n-4] \end{aligned}$$

(18)

The difference equation (17) is different from Eq. (3), which is quite expected since Eq. (3) contains only data samples $y_0 [n]$ generated by forward low-pass filtering of input signal samples x[n], while Eq. (17) contains interleaved low-pass-filtered and high-pass-filtered signal components y[n] generated from input signal samples x[n].

Similarly, the difference equation (18) is different from Eq. (4), which is quite expected since Eq. (4) contains only data samples $y_1 [n]$ generated by forward high-pass filtering of input signal samples x[n], while Eq. (18) contains interleaved low-pass-filtered and high-pass-filtered signal components y[n] generated from input signal samples x[n].

However, both Eqs. (17) and (18) completely match corresponding equations for reconstructed signal samples $w_0 [n]$ and $w_1 [n]$ for lifting-based 1-D inverse DWT 5/3 filter architecture, since lifting filter architecture generates $w_0 [n]$ and $w_1 [n]$ based on interleaved low-pass-filtered and high-pass-filtered signal components y[n], i.e., in the same manner as it is the case of the proposed 1-D inverse DWT 5/3 filter architecture.

Finally, it can be concluded that the proposed 1-D inverse DWT 5/3 filter architecture provides perfect reconstructed signals at the output for both even indexes $n=2p$ and odd indexes $n=2p+1$, in an interleaved fashion, without any final addition operation (Fig. 7).

Fig. 7

Block diagram of the proposed 1-D inverse DWT 5/3 filter architecture

3 Comparison with Other 1-D Inverse DWT 5/3 Filter Designs

The proposed 1-D inverse DWT 5/3 filter architecture (Fig. 6) is compared with state-of-the-art convolution-based 1-D inverse DWT 5/3 filter architecture [9, 12, 28, 30, 34, 37] (shown in Fig. 8) and with the most efficient among the state-of-the-art lifting-based 1-D inverse DWT 5/3 filter architectures [4, 7, 15, 18, 22, 33] (shown in Fig. 9) in terms of hardware complexity, in order to illustrate the advantages of the proposed architecture. Even though the architecture [4] is a little bit more complex than it is shown in Fig. 9, it can be reduced to the form shown in Fig. 9 after removing pipeline registers. It has been shown in [1] that, as a price paid for a greater flexibility including the support for a wide range of different types of filters, lifting-based architectures [8, 14, 19, 20, 26] have a greater hardware complexity than those presented in [4, 7, 15, 18, 22, 33]. From that reason, comparison with architectures proposed in [8, 14, 19, 20, 26] is not included in this paper.

Fig. 8

State-of-the-art convolution-based 1-D inverse DWT 5/3 filter architecture

Fig. 9

State-of-the-art lifting-based 1-D inverse DWT 5/3 filter architecture

Table 2 provides the overview of used hardware components for aforementioned 1-D inverse DWT 5/3 filter architectures. Table 2 does not contain information about the number of used multipliers, since multipliers can be completely avoided in all realizations due to specific values of coefficients for multiplication. Namely, all coefficients for multiplication can be represented as a power of two (for state-of-the-art lifting-based architecture and the proposed architecture) or as a sum of numbers which are power of two (for state-of-the-art convolution-based architecture). Therefore, instead of multipliers in all realizations, permanently shifted hardware connections between output and input bit lines are used.

Table 2 Used hardware components for 1-D inverse DWT 5/3 filter architectures

It can be seen that the proposed 1-D inverse DWT 5/3 filter architecture has the simplest realization requiring the minimum number of used hardware components. Also, while state-of-the-art lifting-based 1-D inverse DWT 5/3 filter architecture requires additional logic for $w_0 [n]$ and $w_1 [n]$ output data combining, in cases when output samples with odd and even indexes have to be generated serially in alternate clock cycles, the proposed 1-D inverse DWT 5/3 filter architecture produces already interleaved data samples at the output without any additional logic. Therefore, in terms of simplicity and resource savings, the proposed 1-D inverse DWT 5/3 filter architecture represents the best solution.

4 Experimental Results for 1-D Inverse DWT 5/3 Filter Architectures

Functional verification of the proposed 1-D inverse DWT 5/3 filter architecture has been carried out through FPGA implementation of cascaded connection of a 1-D forward DWT 5/3 filter and the proposed 1-D inverse DWT 5/3 filter architecture (Fig. 10).

Fig. 10

Cascaded connection of a 1-D forward DWT 5/3 filter and the proposed 1-D inverse DWT 5/3 filter architecture for simulation and verification purposes

This cascaded structure has been implemented with 24-bit two’s complement fixed point number format, with 12 integer bits and 12 fractional bits using Altera Quartus II software (Fig. 11), since this data format ensures correct representation of generated data samples for at least four levels of DWT.

Fig. 11

Data format used for functional verification of the proposed 1-D inverse DWT 5/3 filter architecture

For verification purposes, an arbitrary sequence of input data x[n] has been used. A simulation of the cascaded structure has been carried out using Simulator Tool from Altera Quartus II, and simulation results confirmed the functional correctness of the proposed 1-D inverse DWT 5/3 filter architecture, since resulted data at the output w[n] were a delayed replica of input data x[n] (with four clock periods of delay).

Since hardware utilization can be defined as the ratio of the actual computation time to the total processing time, with time expressed in numbers of clock cycles, it can be concluded that the proposed 1-D inverse DWT 5/3 filter architecture has 100% hardware utilization.

Synthesis results for different 1-D inverse DWT 5/3 filter architectures obtained using Altera Quartus II 10.0 software in FPGA EP4CE115F29C7 are presented in Table 3. The second column of Table 3 contains data for state-of-the-art convolution-based 1-D inverse DWT 5/3 filter architecture [9, 12, 28, 30, 34, 37], the third column contains data for the most efficient state-of-the-art lifting-based 1-D inverse DWT 5/3 filter architecture [4, 7, 15, 18, 22, 33] without any additional logic for output data combining, while the fourth column contains data for the most efficient state-of-the-art lifting-based 1-D inverse DWT 5/3 filter architecture [4, 7, 15, 18, 22, 33] with additional logic for output data interleaving. Finally, the fifth column represents the synthesis results for the 1-D inverse DWT 5/3 filter architecture, proposed in this paper.

Synthesis results clearly show that in terms of used registers, the realization of the proposed 1-D inverse DWT 5/3 filter architecture is a 65% simpler than convolution-based 1-D inverse DWT 5/3 filter architecture and a 33% simpler than lifting-based 1-D inverse DWT 5/3 filter architecture with or without additional combining parts. In terms of used logic elements, the proposed 1-D inverse DWT 5/3 filter architecture is a 49% simpler than convolution-based 1-D inverse DWT 5/3 filter architecture, while has the same complexity as lifting-based 1-D inverse DWT 5/3 filter architecture without combining parts. However, in cases when additional logic for output data interleaving is necessary, the proposed 1-D inverse 5/3 filter architecture is a 17% simpler than lifting-based architecture in terms of used logic elements.

The proposed 1-D inverse 5/3 filter architecture and lifting-based 5/3 filter architecture with additional logic have the shortest critical path delay, convolution-based architecture has an 8% longer critical path delay, while lifting-based architecture without additional logic has a 64% longer critical path delay. Maximum operating frequency is a 7% higher for the proposed 1-D inverse 5/3 filter architecture in comparison with convolution-based 5/3 filter architecture and lifting-based 5/3 filter architecture with additional logic for output data interleaving, and a 40% higher in comparison with lifting-based architecture without additional logic for output data interleaving. Maximum operating frequencies for these implementations were determined under the worst case operating conditions—the highest working temperature ($85\,{^{\circ }}\hbox {C}$) and the slowest silicon on chip. Also, the proposed 1-D inverse DWT 5/3 filter architecture has the lowest total power dissipation, compared with other three filter architectures.

Table 3 1-D inverse DWT 5/3 filter performance in Altera FPGA EP4CE115F29C7

5 Utilization of the Proposed 1-D Inverse DWT 5/3 Filter Architecture within 2-D Inverse DWT 5/3 Architecture

The most important application of the proposed 1-D inverse DWT filter architecture is its utilization as a building block within 2-D inverse DWT 5/3 architecture. In this section, a high-performance and memory-efficient 2-D inverse DWT 5/3 architecture is proposed. Due to its simplicity, the proposed 1-D inverse DWT 5/3 filter architecture contributes to the efficient hardware implementation of the proposed 2-D inverse DWT 5/3 architecture.

The structure of the proposed 2-D inverse DWT 5/3 architecture with $J=7$ composition levels, which utilizes the proposed 1-D inverse 5/3 filter design described in Sect. 2, is shown in Fig. 12. The architecture which supports seven levels of composition is shown since this number of levels ensures the excellent compression and decompression quality for high-definition (HD) resolution images (1920 $\times$ 1080 pixels). However, this structure can easily be modified in order to support any other number of composition levels.

Input data for the proposed 2-D inverse DWT 5/3 architecture are the components of the decomposed signal $z_{HH}^{(j)} [m,n]$, $z_{HL}^{(j)} [m,n]$ and $z_{LH}^{(j)} [m,n]$ from level j ($j=1,2,\ldots ,7$) of composition, as well as the components of the decomposed signal $z_{LL}^{(7)} [m,n]$ from level 7 of composition.

Components $z_{HH}^{(j)} [m,n]$, $z_{HL}^{(j)} [m,n]$, $z_{LH}^{(j)} [m,n]$ and $z_{LL}^{(j)} [m,n]$ which belong to level j ($j=2,3,\ldots ,7$) subbands HH, HL, LH and LL, respectively, are received by appropriate “input register Level j” and then routed through a multiplexer, generating data samples $z_B [m,n]$:

$$\begin{aligned} z_B [m,n]=\left\{ {\begin{array}{l} z_{LH}^{(j)} [m,k],\;\mathrm{for}\;m=2l\;\mathrm{and}\;n=2k \\ z_{LL}^{(j)} [m,k],\;\mathrm{for}\;m=2l\;\mathrm{and}\;n=2k+1 \\ z_{HH}^{(j)} [m,k],\;\mathrm{for}\;m=2l+1\;\mathrm{and}\;n=2k \\ z_{HL}^{(j)} [m,k],\;\mathrm{for}\;m=2l+1\;\mathrm{and}\;n=2k+1 \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(19)

In this notation, the LL subband represents the result of forward low-pass filtering over rows and forward low-pass filtering over columns. The HL subband represents the result of forward low-pass filtering over rows and forward high-pass filtering over columns. The LH subband represents the result of forward high-pass filtering over rows and forward low-pass filtering over columns. The HH subband represents the result of forward high-pass filtering over rows and forward high-pass filtering over columns.

Fig. 12

The proposed 2-D inverse DWT 5/3 architecture

Data samples $z_B [m,n]$ are then vertically filtered by “Vertical Filter B”, producing the samples $y_B [m,n]$:

$$\begin{aligned} y_B [m,n]=\left\{ {\begin{array}{l} y_H^{(j)} [m,k],\;\mathrm{for}\;n=2k \\ y_L^{(j)} [m,k],\;\mathrm{for}\;n=2k+1 \\ \end{array}} \right. \end{aligned}$$

(20)

where $y_H^{(j)} [m,k]$ represent high-pass data components at level j ($j=2,3,\ldots ,7$) which are to be horizontally filtered, and $y_L^{(j)} [m,k]$ represent low-pass data components at level j ($j=2,3,\ldots ,7$) which are to be horizontally filtered. Data samples $y_B [m,n]$ are then routed through a demultiplexer and horizontally filtered by “Horizontal Filter Level j” ($j=2,3,\ldots ,7$), producing the components of the decomposed signal $z_{LL}^{(j-1)} [m,n]$ ($j=2,3,\ldots ,7$) which are later used for inverse filtering at level $j-$1. All horizontal filters are implemented as 1-D inverse DWT filters described in Sect. 2.

Components $z_{HH}^{(1)} [m,n]$, $z_{HL}^{(1)} [m,n]$, $z_{LH}^{(1)} [m,n]$ and $z_{LL}^{(1)} [m,n]$ which belong to level 1 subbands HH, HL, LH and LL, respectively, are received by appropriate “Input Register Level 1” and then routed through a multiplexer, generating data samples $z_A [m,n]$:

$$\begin{aligned} z_A [m,n]=\left\{ {\begin{array}{l} z_{LH}^{(1)} [m,k],\;\mathrm{for}\;m=2l\;\mathrm{and}\;n=2k \\ z_{LL}^{(1)} [m,k],\;\mathrm{for}\;m=2l\;\mathrm{and}\;n=2k+1 \\ z_{HH}^{(1)} [m,k],\;\mathrm{for}\;m=2l+1\;\mathrm{and}\;n=2k \\ z_{HL}^{(1)} [m,k],\;\mathrm{for}\;m=2l+1\;\mathrm{and}\;n=2k+1 \\ \end{array}} \right. \end{aligned}$$

(21)

Data samples $z_A [m,n]$ are then vertically filtered by “Vertical Filter A”, producing the samples $y_A [m,n]$:

$$\begin{aligned} y_A [m,n]=\left\{ {\begin{array}{l} y_H^{(1)} [m,k],\;\mathrm{for}\;n=2k \\ y_L^{(1)} [m,k],\;\mathrm{for}\;n=2k+1 \\ \end{array}} \right. \end{aligned}$$

(22)

where $y_H^{(1)} [m,k]$ represent high-pass data components at level 1 which are to be horizontally filtered, and $y_L^{(1)} [m,k]$ represent low-pass data components at level 1 which are to be horizontally filtered. Data samples $y_A [m,n]$ are then horizontally filtered by “Horizontal Filter Level 1”, producing the pixels w[m, n] of reconstructed image. “Horizontal Filter Level 1” is implemented as the 1-D inverse DWT filter described in Sect. 2.

The dynamics of the 2-D inverse filtering at the beginning of even lines (starting from 0) is presented on time diagram shown in Fig. 13. This time diagram shows the lines in first three levels of composition in case when lines at each presented level are even lines (since only even lines contain components of the decomposed signal from LL subbands, and these components are necessary for further inverse filtering at the next composition level). Only three levels of composition have been shown in order to reduce the diagram complexity, but the pattern shown in Fig. 13 can easily be extended to an arbitrary number of composition levels.

In this process of inverse vertical filtering, the components of the decomposed signal at level j, $z_{LH}^{(j)} [m^{(j)},n^{(j)}]$ and $z_{LL}^{(j)} [m^{(j)},n^{(j)}]$, alternately appear at the input of vertical filter. Appropriate high-pass signal components $y_H^{(j)} [m^{(j)},n^{(j)}]$ and low-pass signal components $y_L^{(j)} [m^{(j)},n^{(j)}]$ are alternately produced by vertical filter and routed to the input of horizontal filter at level j, and appropriate resulting signal components from level $j-1$ ($j>1)$ subband LL ($z_{LL}^{(j-1)} [m^{(j-1)},n^{(j-1)}])$ are produced at the output of this horizontal filter. After initial five signal components at level 3, the rest of them are filtered on every fourth time slot (starting from the time instance $n=10$). After initial five signal components at level 2, the rest of them are filtered on every second time slot (starting from the time instance $n=11$). Finally, signal components at level 1 are filtered on every time slot (starting from the time instance $n=8$), and the pixels of reconstructed image w[m, n] are successively produced at the output of horizontal filter at level 1, starting from the time instance $n=11$.

Starting time instance for the filtering of the first data sample at each level is chosen on the manner which allows appropriate interleaving of time slots when data samples are vertically filtered. This approach allows using one inverse vertical filter for level 1 (“Vertical Filter A”), and another inverse vertical filter for all other composition levels (“Vertical Filter B”), since any overlapping of time slots when “Vertical Filter B” is used has been avoided.

Fig. 13

The time diagram of the 2-D inverse DWT at the beginning of even lines

The described pattern of the 2-D inverse filtering at the beginning of even lines is also applied to all other levels of composition ($j=4, 5, 6$ and 7), which has not been shown in simplified Fig. 13. The inverse filtering of initial five signal components in the line at level j is performed after the inverse filtering of initial five signal components at level $j+1$, but before the inverse filtering of initial five signal components at level $j-1$. Time slots for the filtering of the sixth signal component at different levels is chosen so that the appropriate interleaving of time slots is achieved in order to allow utilization of the same vertical filter for levels from 2 to 7. All other signal components at level 4 are filtered on every eighth time slot, all other signal components at level 5 are filtered on every 16th time slot, all other signal components at level 6 are filtered on every 32nd time slot, etc.

The time diagram which illustrates the dynamics of the 2-D inverse filtering at the end of even lines of HD resolution images, for lines whose beginning is shown in Fig. 13, is presented in Fig. 14. Already-described pattern of filtering continues until the last signal component within the line for each level. The last pixel of reconstructed image (w[m, 1919]) is produced three time slots after the last signal component within the line is filtered at level 1.

Fig. 14

The time diagram of the 2-D inverse DWT at the end of even lines

Fig. 15

The time diagram of the 2-D inverse DWT at the beginning of odd lines (a) and at the end of odd lines (b)

The time diagram which illustrates the dynamics of the 2-D inverse filtering at the beginning of odd lines (starting from 0) is presented in Fig. 15a, while the diagram which illustrates the dynamics of the 2-D inverse filtering at the end of odd lines for HD resolution images is presented in Fig. 15b. The pattern of inverse filtering in this case is almost the same as in case of inverse filtering of even lines. Only two differences can be noticed. First, every even (starting from 0) signal component which appears at the input of vertical filter belongs to the subband HH ($z_{HH}^{(1)} [m^{(1)},n^{(1)}])$, while every odd signal component which appears at the input of vertical filter belongs to the subband HL ($z_{HL}^{(1)} [m^{(1)},n^{(1)}])$. Second, the first level of composition is always the only level of composition, since neither the signal components from HH subband nor the signal components from HL subband are generated based on signal components from previous levels of composition.

Fig. 16

The beginning of inverse line-wise filtering

The illustration of the beginning of line-wise filtering in the proposed 2-D inverse DWT architecture is shown in Fig. 16. In order to simplify the diagram, only three levels of composition have been shown.

Line 0 of signal components at level 3 at the input of “Vertical Filter B” contains signal components alternately from subbands LH and LL, i.e., notation “$z_{LH}^{(3)} [0,n^{(3)}],\;z_{LL}^{(3)} [0,n^{(3)}]$” from Fig. 16 represents the following sequence of signal components: $z_{LH}^{(3)} [0,0]$, $z_{LL}^{(3)} [0,0]$, $z_{LH}^{(3)} [0,1]$, $z_{LL}^{(3)} [0,1]$, $z_{LH}^{(3)} [0,2]$, $z_{LL}^{(3)} [0,2]$, etc. These components are vertically filtered by “Vertical Filter B”, and then horizontally filtered by “Horizontal Filter Level 3.” Line 1 of signal components at level 3 at the input of “Vertical Filter B” contains signal components alternately from subbands HH and HL, i.e., notation “$z_{HH}^{(3)} [1,n^{(3)}],\;z_{HL}^{(3)} [1,n^{(3)}]$” from Fig. 16 represents the following sequence of signal components: $z_{HH}^{(3)} [1,0]$, $z_{HL}^{(3)} [1,0]$, $z_{HH}^{(3)} [1,1]$, $z_{HL}^{(3)} [1,1]$, $z_{HH}^{(3)} [1,2]$, $z_{HL}^{(3)} [1,2]$, etc. These components are also vertically filtered by “Vertical Filter B”, and then horizontally filtered by “Horizontal Filter Level 3”. Line 2 of signal components at level 3 at the input of “Vertical Filter B” contains signal components alternately from subbands LH and LL ($z_{LH}^{(3)} [2,n^{(3)}],\;z_{LL}^{(3)} [2,n^{(3)}])$. After vertical filtering by “Vertical Filter B” and then horizontal filtering by “Horizontal Filter Level 3” of this line, signal components $z_{LL}^{(2)} [0,n^{(2)}]$ from level 2 subband LL are generated. The next line of signal components at level 3, which contains signal components alternately from subbands HH and HL, appears at the input of “Vertical Filter B” after one empty time slot of duration of one line. For all remaining lines at level 3 the following pattern continues: lines with signal components from subbands LH and LL and lines with signal components from subbands HH and HL alternately appear at the input of “Vertical Filter B,” with empty time slot of duration of three lines between successive lines. All these lines are vertically filtered by “Vertical Filter B,” and then horizontally filtered by “Horizontal Filter Level 3,” generating signal components from level 2 subband LL ($z_{LL}^{(2)} [m^{(2)},n^{(2)}])$, which are later used for inverse filtering at level 2.

Fig. 17

The end of inverse line-wise filtering

The filtering of line 0 at level 2 is interleaved with the filtering of line 2 at level 3. The pattern of line-wise filtering at level 2 is almost the same as for level 3. Only difference is that successive lines, starting from the line 2, appear at the input of “Vertical Filter B” with empty time slots of duration of one line between successive lines. All these lines are vertically filtered by “Vertical Filter B,” and then horizontally filtered by “Horizontal Filter Level 2,” generating signal components from level 1 subband LL $(z_{LL}^{(1)} [m^{(1)},n^{(1)}])$, which are later used for inverse filtering at level 1.

The filtering of line 0 at level 1 is interleaved with the filtering of line 2 at level 2. All lines at level 1 appear at the input of “Vertical Filter A” successively one after another without empty time slots between successive lines. All these lines are vertically filtered by “Vertical Filter A,” and then horizontally filtered by “Horizontal Filter Level 1,” generating the lines of reconstructed image. Line 0 of reconstructed image is interleaved with the filtering of line 2 at level 1.

The illustration of the end of line-wise filtering for HD resolution images in the proposed 2-D inverse DWT architecture is shown in Fig. 17. Already-described pattern of line-wise filtering continues until the last line of signal components for each level. Once all lines of signal components are filtered by appropriate inverse vertical and inverse horizontal filter, in the last two time slots of duration of one line per slot, “Vertical Filter B” or “Vertical Filter A” are used for processing the internal intermediate results “temp result 1” and “temp result 2.” These internal intermediate results from level j are used for generation of last two lines of resulting signal components from subband LL at level $j-1\,(j>1)$. Accordingly, two lines of internal intermediate results from level 1, are used for generation of the last two lines of reconstructed image.

The internal structure of “Vertical Filter A” and “Vertical Filter B” from Fig. 12 is shown in Fig. 18. Dependences between the input signal z[m, n] and the output signals for vertical filter blocks are described by equations represented in Table 4.

“Zero Line Block” and “First Line Block” receive data samples from the input line 0 and line 1, respectively, and generate the set of zeros at the output y[m, n].

When “Even Line Block” receives the input signal z[m, n] via the input line 2, it produces the output signal described with the equation which corresponds to the special form of low-pass Le Gall’s 5/3 inverse filter used for inverse vertical filtering near image boundaries, instead of symmetric extension of data samples at image boundaries. This output signal y[m, n] actually represents the line 0 of valid resulting data samples generated by inverse vertical filter. Otherwise, when “Even Line Block” receives the input signal z[m, n] via any even input line, except the input line 0 and input line 2, it generates the output signal described with the equation which corresponds to the low-pass Le Gall’s 5/3 inverse filter. This output signal y[m, n] actually represents any even line (starting from 0) of valid resulting data samples except the line 0 and the even line among the last three lines.

When “Odd Line Block” receives the input signal z[m, n] via input line 3, it produces the output signal y[m, n] described with the equation which corresponds to the special form of high-pass Le Gall’s 5/3 inverse filter used for inverse vertical filtering near image boundaries, instead of symmetric extension of data samples at image boundaries. This output signal y[m, n] actually represents the line 1 of valid resulting data samples generated by inverse vertical filter. Otherwise, when “Odd Line Block” receives the input signal z[m, n] via any odd input line, except the input line 1, input line 3 and the last input line, it generates the output signal described with the equation which corresponds to the high-pass Le Gall’s 5/3 inverse filter. This output signal y[m, n] actually represents any odd line (starting from 0) of valid resulting data samples except the line 1 and except the odd lines among the last three lines.

Fig. 18

The detailed structure of inverse vertical filter

Table 4 Relations between input and output signals for vertical filter blocks

In case when total number of lines within the image is even, “Last Line Block” receives the input signal z[m, n] via the last input line and produces the output signal y[m, n] described with the equation which corresponds to the high-pass Le Gall’s 5/3 inverse filter. “Last Plus 1 Line Block” is responsible for inverse vertical filtering of the remaining intermediate results IT0[m, n] and IT1[m, n]. The output signal y[m, n] of this block is described with the equation which corresponds to the low-pass Le Gall’s 5/3 inverse filter. Finally, “Last Plus 2 Line Block” is responsible for inverse vertical filtering of the remaining intermediate results IT1[m, n]. The output signal y[m, n] of this block is described with the equation which corresponds to the special form of high-pass Le Gall’s 5/3 inverse filter used for inverse vertical filtering near image boundaries, instead of symmetric extension of data samples at image boundaries. This output signal y[m, n] actually represents the last line of valid resulting data samples generated by inverse vertical filter.

Equations from Table 4 are derived with the respect to the fact that intermediate results T0[m, n] and T1[m, n] are stored in on-chip memory which produces the dependences:

$$\begin{aligned} IT0[m,n]= & {} T0[m-1,n] \nonumber \\ IT1[m,n]= & {} T1[m-1,n] \end{aligned}$$

(23)

On-chip memory used for the 2-D inverse DWT filtering is shown in Fig. 19. For successful inverse filtering and composition of $N\times N$ image, two lines of intermediate filtering results have to be stored in on-chip memory at each level of composition. The intermediate results from level 1 of composition are stored in “On-chip memory A” which contains one buffer with capacity of 2N data samples. The intermediate results from other levels of composition are stored in “On-chip memory B” which contains six buffers (in case of $J=7$ levels of composition) with capacity halved at every succeeding level, starting from capacity of N data samples at level 2. All these buffers represent FIFO memory.

Fig. 19

On-chip memory

6 Complexity and Performance Comparisons of Various 2-D Inverse DWT 5/3 Architectures

The proposed 2-D inverse DWT 5/3 architecture utilizes J FIFO buffers for storing the intermediate results T0[m, n] and T1[m, n], for J levels of composition of $N\times N$ image. The capacity of FIFO buffer for level 1 is 2N data samples, and the capacity of FIFO buffer for every succeeding level of composition is half of the capacity of FIFO buffer for the preceding level. Also, each level of composition requires four input registers for storing the signal components from LL, LH, HL and HH subbands, while each inverse horizontal filter itself contains two registers (delay elements). Therefore, the total on-chip memory used by the proposed 2-D inverse DWT 5/3 architecture can be calculated as follows:

$$\begin{aligned} 2N+N+\frac{N}{2}+\frac{N}{4}+\cdots +\frac{N}{2^{J-2}}+6J=4N\left( {1-2^{-J}} \right) +6J \end{aligned}$$

(24)

The proposed 2-D inverse DWT 5/3 architecture does not require off-chip memory at all. Since for all real image compression/decompression applications is $J\ll N$, the total used memory can be approximated as $4N(1-2^{-J})$.

Based on time diagrams shown in Figs. 13 and 14, it can be calculated that computing time per line is $N+4(J-1)+3$ clock cycles. Based on line-wise diagrams shown in Figs. 16 and 17, it can be concluded that the total number of time slots for line processing is $N+2J$. Therefore, the total computing time for the proposed 2-D inverse DWT 5/3 architecture can be expressed as:

$$\begin{aligned} \left( {N+4J-1} \right) \cdot \left( {N+2J} \right) \approx N^{2} \end{aligned}$$

(25)

Finally, based on Figs. 13 and 16, it can be concluded that the output latency for the proposed architecture is:

$$\begin{aligned} 2JN+4(J-1)+3\approx 2JN \end{aligned}$$

(26)

The capacity of total required memory is represented in number of data samples, while computing time and output latency are represented in number of clock cycles.

Table 5 shows the comparison of the performance of the proposed 2-D inverse DWT 5/3 architecture and architectures reported in [4,5,6,7,8, 10, 13, 19, 20, 25, 27, 33,34,35,36] in terms of required on-chip memory capacity, required off-chip memory capacity, computing time and output latency, for J levels of composition of $N\times N$ image.

Table 5 Comparison of various 2-D inverse DWT 5/3 architectures

Compared to other architectures, it can be noticed that the proposed architecture has medium computing time and medium output latency. However, the proposed architecture has the lowest total used memory in comparison to all other previously published architectures. For $J\rightarrow \infty$ levels of composition of $N\times N$ image, the proposed 2-D inverse DWT 5/3 architecture requires the total memory capacity of only 4N data samples, which is a 20% lower capacity than required capacity for the best state-of-the-art architecture.

The proposed 2-D inverse DWT 5/3 architecture is implemented on Xilinx Virtex-4 XC4VFX100 and Virtex-5 XC5VLX110T FPGA devices and the synthesis results are compared with the best available synthesis results of other 2-D DWT 5/3 architectures from the literature.

Table 6 FPGA synthesis results for the 2-D DWT 5/3 architectures

Table 7 Comparison of memory usage

Synthesis results for architectures with 16-bit word length are reported in Table 6. It can be seen that the proposed 2-D inverse DWT 5/3 architecture utilizes the lowest number of CLB slices in comparison to architecture [5] and PMA architecture [10]. The proposed architecture also utilizes a lower number of CLB slices than RMA architecture [10], even though the proposed architecture is implemented for $512\times 512$ image size and five levels of composition, while RMA architecture [10] is implemented for $256\times 256$ image size and only 3 levels of composition. However, since PMA architecture [10] uses the pipelined processor element in its design, it has the highest maximum operating frequency, while the proposed architecture has a higher maximum operating frequency than architecture [5].

Comparison of memory usage is presented in Table 7. For this purpose, the proposed architecture is implemented with 10-bit word length in order to make a proper comparison with the results available in [5]. Implementation results clearly show that the proposed 2-D inverse DWT 5/3 architecture requires the lowest memory size in comparison to other reported architectures, even though the proposed architecture is implemented for $512\times 512$ image size and five levels of composition, while architectures [4] and [11, 16, 21] are implemented for only one level of composition and some of them for smaller image size.

Table 8 Post-synthesis power analysis at 100 MHz (for Virtex-5 XC5VLX110T FPGA chip)

Table 8 compares the FPGA post-synthesis power analysis results at 100 MHz for image size $512\times 512$, 16-bit word length and Virtex-5 XC5VLX110T FPGA device. It can be seen that the proposed architecture has similar total power dissipation with architecture [5] and PMA architecture [10], even though the power dissipations for architectures [5] and PMA [10] are estimated for designs with only one level of composition, while the power dissipation for the proposed architecture is estimated for design with five levels of composition.

7 Conclusion

The proposed 1-D inverse DWT 5/3 filter architecture leads to simple filter design, receiving alternate low-pass- and high-pass-filtered signal components at the input, with even and odd data sample indexes, respectively. The advantages of the proposed 1-D inverse DWT 5/3 filter architecture are simplicity, minimization of memory and logic resources used in filter realization, high operating frequency, and low total power dissipation. The same filter components are reused for both low-pass and high-pass filtering as well as inherent interpolation.

Two-dimensional inverse DWT 5/3 architecture proposed in this paper, which utilizes the proposed 1-D inverse filter design, requires a lower storage capacity in comparison with other state-of-the-art architectures. Due to memory highly efficient solution, the proposed 2-D architecture does not require off-chip memory at all.