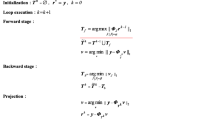1 Introduction

Compressed sensing deals with efficient representation and reconstruction of sparse (or more generally, compressible) signals. Most of the real-world signals are sparse or compressible in some basis. For example, natural images are known to be approximately sparse when represented in terms of Fourier or wavelet basis functions, giving rise to image compression algorithms like JPEG2000. Another example is the cognitive radio applications, which utilizes the spectrum holes to increase transmission efficiency in a high-bandwidth environment. In each case, if the classic Nyquist sampling rate is applied, several millions of pixels would be needed to represent a moderate-sized image or several gigasamples (per second) would be required to regenerate a transmission signal that has a much less total effective bandwidth.

In a compressed sensing framework, we are given a measurement matrix A of size \(M\hbox {x}N\) such that \(M < N\) and an observation vector y of length M such that y = Ax, where x is an unknown sparse vector of length N that has at most K nonzero elements placed in arbitrary locations where \(K \ll N\). If x is known to be sparse in some basis other than the measurement domain, then the observation vector can be expressed as \(\mathbf{y }= \mathbf{A}\varvec{\Phi }^{*}{} \mathbf{x}\) where \(\varvec{\Phi }\) is the matrix that consists of orthonormal sparsifying basis functions and \((^{*})\) denotes conjugate transpose. Throughout the paper, the signal is assumed to be sparse in the measurement domain and the \(\varvec{\Phi }\)-term is omitted.

Because \(M < N\), the problem setting defined by \(\mathbf{y }= \mathbf{Ax}\) is underdetermined and there is an infinite number of solutions. Some additional constraints utilizing the sparsity of x must be employed. Optimization methods utilizing \(\ell _{0}\)-norm or \(\ell _{1}\)-norm are extensively studied in the literature. \(\ell _{0}\)-minimization problem is in general NP-hard and computationally intractable [21]. \(\ell _{1}\)-minimization methods provide more tractable solutions that are supported by theoretical analysis using the restricted isometry property (RIP) [7, 11].

Because \(\ell _{1}\)-norm is a convex cost function, linear programming techniques can be used for reconstruction. Early studies on convex relaxation include interior-point methods that employ a primal–dual interior-point framework [6, 8, 18], the homotopy method [24], least absolute shrinkage and selection operator [28], and gradient methods [13, 15]. For more information, please see [30] and the references therein. More recently, coordinate descent methods [14, 37], a proximal gradient homotopy method [35], and active-set methods [17, 27] have been proposed among many others.

Although \(\ell _{1}\)-minimization provides strong theoretical guarantees for perfect sparse reconstruction, its computational complexity is too high to be used for most of the real-life scenarios. Noteworthy alternatives to speed up \(\ell _{1}\)-minimization include fast iterative shrinkage–threshold algorithm [2] and parallel coordinate descent method [5]. Also, in [34], screening tests and random projections are adopted in order to reduce the size of the problem and hence the computational cost.

Greedy algorithms, where one or more element(s) of the support of x are sought in each iteration, are widely applied for sparse signal reconstruction. In general, they have faster convergence speeds and more suited for large-scale problems than \(\ell _{1}\)-minimization methods. Arguably the most popular greedy algorithm is orthogonal matching pursuit (OMP) [26]. In OMP, the following steps are performed in each iteration: (i) Find the column (sometimes referred to as atom) of A which is maximally correlated with the residual, (ii) add the column index to the list, (iii) estimate the sparse vector using the current index list by orthogonal projection, and (iv) subtract its effect from the measurement vector to create a new residual. RIP-based theoretical bounds for OMP are given in [29] and [31].

A number of algorithms that improve the reconstruction performance and/or the processing time of OMP have been proposed. Regularized OMP (ROMP) chooses more than one column in each iteration based on a regularity measure [23]. Stagewise OMP (StOMP) does the same thing using a probabilistic model about the correlation coefficients [12]. Generalized OMP (gOMP) [32, 33] and the orthogonal super greedy algorithm [19] simply choose a multiple but constant number of columns in each iteration. In stagewise weak selection [4], all the elements that come within a factor of the largest inner product (coefficient correlation) are selected. Compressive sampling matching pursuit (CoSaMP) and forward–backward pursuit (FBP) first choose a bunch of columns and then apply a pruning step after orthogonal projection [16, 22]. In the pruning step, they remove a number of column indices which are least likely to be on the support of x from the estimated support set. Both the number of included and removed columns are constants for a given M or K. Two-stage algorithms have the ability to correct the errors made in the forward step, and hence, they have a potential of increased performance when compared to the single-stage methods. More recently, robust sparse approximation in the presence of impulsive noise [25, 38], multi-channel sparse signal recovery [3, 10], and nonnegative orthogonal matching pursuit [36] are proposed.

In this paper, a new OMP-type sparse signal reconstruction algorithm, namely data-driven forward–backward pursuit (DD-FBP), is presented. DD-FBP resembles the CoSaMP and FBP algorithms in the sense that it has a pruning step. In the forward step, after correlating the columns of A with the residual, the correlation values that are larger than a ratio of the maximum-valued one are chosen and the corresponding indices are included in the support set just like in [4]. Similarly, in the backward step, after the projection coefficients are calculated and among the newly included ones, the projection values that are smaller than a ratio of the maximum-valued one are chosen and their indices are removed from the support set. This way, the projection coefficients that have comparable magnitudes are not separated and are altogether included in the support set. Note that both FBP and CoSaMP use predefined constant number of indices for the inclusion and removal processes. The forward and backward steps are continued until the calculated residual error power falls below a certain value or the size of the estimated support exceeds M. The term “data-driven” comes from the fact that the threshold values used in the forward and backward steps are calculated using the correlation and projection coefficients, which are calculated from the signal or the data itself. In some respects, DD-FBP resembles wavelet thresholding methods for signal denoising in which the wavelet coefficients are thresholded in order to remove their noisy part [1].

The paper is organized as follows: In Sect. 2, OMP-type algorithms are described in some detail. In Sect. 3, threshold setting rules are defined and the DD-FBP algorithm is described. In Sect. 4, simulation results that show the superiority of DD-FBP in terms of performance and processing time are presented. Section 5 makes the conclusion.

2 OMP-Type Algorithms

A general framework for OMP-type sparse signal reconstruction algorithms is given below. More or less, all OMP-type methods conform to this framework with differences on implementation of some steps. Note that superscripts in parenthesis denote the iteration number.

Initialization       Residual: \(\mathbf{r}^{\left( 0 \right) }=\mathbf{y}\)

                           Index set: \({\varvec{\Lambda }}^{\left( 0 \right) }=\emptyset \)

                           Iteration number: \(t = 1\)

Algorithm

  1. 1.

    Correlation: Obtain a signal correlated with x such that \(\mathbf{c}^{\left( t \right) }=\mathbf{A}^{*}{} \mathbf{r}^{\left( {t-1} \right) }\). Columns of \(\mathbf{A} (\mathbf {a}_{1}, \mathbf {a}_{2}, {\ldots }, \mathbf {a}_{N})\) can be viewed as a dictionary as each measurement vector is a linear combination of just a small number of entries in the dictionary such that:

    $$\begin{aligned} \mathbf{y}=\mathbf{Ax}=\sum _{i=1}^K \mathbf{x}_{\varLambda _i} \mathbf{a}_{\varLambda _i } \end{aligned}$$
    (1)

    where \(\varvec{\Lambda } = (\varLambda _{1}, \varLambda _{2}, {\ldots }, \varLambda _{K})\) is the support of x. Multiplying this with \(\mathbf{A}^{*}\) in the first iteration yields:

    $$\begin{aligned} \mathbf{c}^{\left( t \right) }=\mathbf{A}^{*}{} \mathbf{Ax}=\left[ {\mathbf{x}_i \langle \mathbf{a}_i ,\mathbf{a}_i \rangle +\sum _{j=1,j\ne i}^N \mathbf{x}_j \langle \mathbf{a}_i ,\mathbf{a}_j\rangle } \right] _{i=1,\ldots ,N} \end{aligned}$$
    (2)

    If we assume that the columns of A are of unit length (which will be valid throughout the paper), then the correlation vector becomes \(\mathbf{c}^{\left( t \right) }=\mathbf{x}+\mathbf{e}\), where e can be regarded as a noise vector that occurred because of non-orthogonality of the columns of A.

  2. 2.

    Insertion: Using \(\mathbf{c}^{\left( t \right) }\), find the index values \(({\varvec{\lambda }}^{\left( t \right) })\) which are most likely from the support of x and add them to the index set: \({\varvec{\Lambda }}^{\left( t \right) }={\varvec{\Lambda }}^{\left( {t-1} \right) }\cup {\varvec{\lambda }}^{\left( t \right) }\). Exclude the previously chosen columns in the selection process. Selection of one or more indices that have relatively high correlation values seems plausible. This step can also be regarded as the forward step.

  3. 3.

    Estimation (orthogonal projection): Using the index set \({\varvec{\Lambda }}^{\left( t \right) }\), find an estimation \(\mathbf{x}^{\left( t \right) }\) that solves the least square problem \(\mathbf{x}^{\left( t \right) }=\hbox {argmin}_\mathbf{x} \parallel {\varvec{y}}-\mathbf{A}^{\left( t \right) }{} \mathbf{x}\parallel _2 \), where \(\mathbf{A}^{\left( t \right) }\) is created by taking the columns of A indexed by \({\varvec{\Lambda }}^{\left( t \right) }\). Note that \(\mathbf{x}^{\left( t \right) }\) can be found by

    $$\begin{aligned} \mathbf{x}^{\left( t \right) }=\left[ {\left( {\mathbf{A}^{\left( t \right) }} \right) ^{*}{} \mathbf{A}^{\left( t \right) }} \right] ^{-1}\left( {\mathbf{A}^{\left( t \right) }} \right) ^{*}\mathbf{y}. \end{aligned}$$
    (3)
  4. 4.

    Pruning: Shorten \({\varvec{\Lambda }}^{\left( t \right) }\) and \(\mathbf{x}^{\left( t \right) }\) by removing some of the indices chosen in the insertion step: \({\varvec{\Lambda }}^{\left( t \right) }={\varvec{\Lambda }}^{\left( t \right) }-{\varvec{\xi } }^{\left( t \right) } ({\varvec{\xi }}^{\left( t \right) }\) is the set of index values to be removed). This way, possible errors made by the insertion step are meant to be eliminated. Removing those that have relatively small values is reasonable. The number of indices pruned must be less than the number of indices inserted in order to make progress in each iteration. This step can be regarded as the backward step.

  5. 5.

    Residual update: Update the residual \(\mathbf{r}^{\left( t \right) }=\mathbf{y}-\mathbf{A}^{\left( t \right) }{} \mathbf{x}^{\left( t \right) }\).

  6. 6.

    Termination: Terminate if \(\parallel \mathbf{r}^{\left( t \right) }\parallel _2 <e_\mathrm{{max}} \) (some predefined threshold) OR \(t < t_\mathrm{max}\) (predefined maximum number of iterations) OR some other rule. Output \(\hat{\varvec{\Lambda }} ={\varvec{\Lambda }}^{\left( t \right) }\) and \(\hat{\mathbf{x}}=\mathbf{x}^{\left( t \right) }\). Else, increment t and go to step 1.

The OMP-type algorithms proposed in the literature differ from each other with respect to how and how many indices are selected in the insertion and pruning stages. The selection and removal rules used in some popular methods are given in Table 1. For the sake of completeness, the rules for DD-FBP are also included.

Table 1 Insertion and pruning rules for some OMP-type methods
Full size table

3 Data-Driven Forward–Backward Pursuit

DD-FBP is a two-stage sparse signal reconstruction algorithm with forward and backward steps. It resembles FBP in the sense that in the forward step, it chooses a number of atoms to be included in the support set, and in the backward step, some of the included indices are removed from the set. However, unlike FBP, the numbers are not pre-defined. For the inclusion step, the absolute correlation values that are higher than a threshold are selected. The threshold value is set to a ratio of the maximum absolute valued correlation coefficient:

$$\begin{aligned} c_\mathrm{f}^{\left( t \right) } =T_\mathrm{f} \hbox {max}\left| {\mathbf{c}^{\left( t \right) }} \right| \end{aligned}$$
(4)

\(T_{\mathrm{f}}\) is a pre-determined constant and its typical values are between 0.3 and 0.7. Note that while computing the forward threshold, the correlation values corresponding to the formerly selected indices must not be taken into consideration, i.e., the maximum value selection must be done among the indices that are not yet included in the estimated support set.

In the backward step, after the calculation of the projection coefficients, the indices whose corresponding absolute projection values are smaller than a threshold are removed from the estimated support. Similar to the forward step, the backward threshold value is set to a ratio of the maximum absolute valued projection coefficient:

$$\begin{aligned} x_\mathrm{b}^{\left( t \right) } =T_\mathrm{b} \hbox {max}\left| {\mathbf{x}^{\left( t \right) }} \right| \end{aligned}$$
(5)

\(T_{\mathrm{b}}\) is a pre-determined constant and its typical values range between 0.5 and 0.7. The maximum value selection must be done among the indices that are selected in the forward step of the current iteration.

Compared to FBP, it is expected that DD-FBP makes fewer mistakes and consumes less processing time. It utilizes the intuitive fact that in a set of clustered numbers, the ones that have similar or comparable values have a higher probability of belonging to the same cluster. A small numerical example will help understanding this concept. Let us assume that before the backward step, the newly included and sorted projection coefficients are 0.9, 0.8, 0.7, 0.2, 0.1, and so on. By eye inspection, we can deduce that it is highly probable that the first three indices are in the support set and the others are not. This is also the case for DD-FBP if \(T_{\mathrm{b}}\) is set to a reasonable value. But for FBP, unless \(\alpha \)– \(\beta \) is not preset to 3 coincidentally, more or less number of coefficients will be selected and it will result in erroneous inclusions or missed detections. Regarding DD-FBP, making more correct decisions in each iteration means less number of iterations on the average to converge and hence less processing time.

The theoretical complexity analysis of DD-FBP is hard to make, because in each step, the number of included indices is not constant, but it varies. Nevertheless, a comparative analysis with OMP can be made. The main differences between OMP and DD-FBP are that DD-FBP has a pruning step and it usually converges in \(C\hbox {log}(K)\) steps instead of K steps, where C is typically between 2 and 4. The pruning step has insignificant complexity, and hence, the proposed method is expected to be \(K/C\hbox {log}(K)\) times faster than OMP, which is roughly validated in the next section.

A disadvantage of DD-FBP is that for best performance, the forward and backward constants should be selected depending on the sparsity and noise levels. However, the dependence is not very strong, if the actual sparsity and noise levels are different than the assumed ones to some extent, the performance does not significantly change as explained in the next section.

For the reproducibility of the results that are presented in Sect. 4, the MATLAB source code of the method is given in Appendix. The iterations are terminated when the size of the estimated support reaches M or the power of the residual falls below a threshold. When the signal is noise free, the threshold is set to \(\Vert \mathbf{y}\Vert _{2}/100\), which corresponds to 40 dB SNR in y. Otherwise, the threshold value should be selected accordingly. Other implementation details can be recognized by examining the code.

4 Simulation Results

The simulation results for DD-FBP along with OMP, CoSaMP, StOMP, gOMP, and FBP using synthetic 1-D sparse signals and a 2-D real image are given in this section. DD-FBP is also compared to basis pursuit (BP), which is a convex relaxation method that uses linear programming and a primal–dual log-barrier algorithm [8]. The MATLAB code for BP is obtained from the Web site https://sparselab.stanford.edu. ROMP is excluded from the simulations to prevent the graphs from being more complex, because ROMP is reported to give similar (or even worse) results with OMP in some works [9, 32].

4.1 Simulation Setup

For 1-D signal simulation, exact reconstruction rates and runtimes are compared for the methods under consideration using several values of N, M, and K. The methods are executed 500 times for each (N, M, K) triple, and the success rate, which is the percentage of successful recovery, is recorded. For the noise-free case, “successful recovery” is defined such that signal-to-residual error (error present after recovery) ratio for the reconstructed sparse signal is above 40 dB. For noisy conditions, when the signal-to-residual error ratio is comparable to the initial signal-to-noise ratio (for instance, when it is a few decibels below), the signal is said to be successfully recovered. For each run, a new observation matrix, whose elements are drawn from a Gaussian random variable of zero mean and variance 1 / M, is created. Note that similar results are obtained when Bernoulli-type random matrices are involved. Two types of sparse 1-D signals are used in the simulations. The first type is created by placing constant-amplitude values \((\pm 1'\hbox {s})\) into K arbitrary locations and setting the others to zero. Such constant-amplitude random-sign distribution presents a challenging case for the reconstruction performances of matching pursuit-type algorithms [9, 20]. The sparse signals of the second type are drawn from a standard Gaussian random variable. To limit the total simulation time, N is fixed to 512 and a limited number of K values are used. The simulations are conducted on a laptop computer that has Windows 7 running on an Intel Core i7 2.10 GHz processor and 8 GB of RAM. In order to obtain fair runtimes, a similar implementation structure is used for each method.

4.2 Parameter Selection

For OMP, the only parameter to select is the total number of iterations, which is also the maximum size of the support set. Although it is mentioned that K iterations should suffice in [29], it is known that allowing the support size to exceed K gives better results. The idea of allowing larger than necessary supports comes from Lemma 3.1 of [12]. It states and proves that in the noiseless case, as long as the true support is covered, perfect recovery is possible if the size of the estimated support is smaller than or equal to the number of measurements (M). This allows for inclusion of false alarms to the estimated support. Hence, for OMP and any other method that iteratively expand the estimated support, it is reasonable not to stop at the sparsity level (K) and go on until the estimated support size reaches M. As the size grows larger (up to M), results become “better,” because there are probably more true detections in the estimated support, which in turn reduces the amount of the reconstruction error. The “best” results are obtained when the size reaches M, because making the size larger than M does not improve performance according to the Lemma above. Hence, the best results are obtained when the maximum support size is set to M with the cost of increased runtime especially in case of failure. For OMP, setting the value to \(\hbox {max}(K, M/3)\) gives significantly lower runtimes with minimal drop in performance, so it is adopted in the OMP implementation.

For FBP, choosing the forward parameter \(\alpha \) between 0.2M and 0.3M for \(\pm 1\) sparse signals brings about similar results with the latter having slightly lower runtimes, so \(\alpha =0.3M\) is used. Choosing the backward parameter \(\beta \) as \(\alpha -1\) gives the best recovery results, but the number of iterations, hence the runtime is very high. So, \(\beta \) is chosen as \(0.7\alpha \) with significant drop in runtimes and insignificant loss in performance. The maximum allowable support size is set to M.

Similar to the discussions above, the parameters for the other methods used in the comparisons are selected to give the best performance in terms of recovery rate and processing time for the corresponding signal type. For the repeatability of the simulation results, these parameters are given in Table 2. In the table, max \((\#{\varvec{\Lambda }})\) is the maximum allowable size of the support estimate, and \(t_{\mathrm{max}}\) is the maximum number of iterations. S is the number of expected iterations for StOMP, and G is the number of inclusions in each iteration for gOMP. \((\alpha ,\beta )\) are the forward and backward parameters for FBP, and \((T_{\mathrm{f}},T_{\mathrm{b}})\) are the forward and backward threshold values for DD-FBP. \(\varepsilon \) is the error tolerance for BP.

Table 2 Parameter settings
Full size table

In DD-FBP, the selection of the forward and backward threshold parameters, \(T_{\mathrm{f}}\) and \(T_{\mathrm{b}}\), is a little bit tricky. In Fig. 1, for \(\pm 1\) sparse signals, the number of observations (M) needed to have at least 50% successful reconstruction for different sparsity and noise levels is shown when \(T_{\mathrm{f}}\) and \(T_{\mathrm{b}}\) are varied between 0.1 and 0.9. As seen, the optimum values of the parameters, which correspond to the minimum points in the graphs, change with the sparsity and the noise levels. It is possible to adjust the parameters by using a priori information about the sparsity and the noise levels, but this is not a desired option. This situation seems like a major drawback of the method. Automatically adjusting the threshold parameters is left as a future work. The values used in the simulations for \(\pm 1\) sparse signals are given in Table 3. The good news is that in general, the performance of the method does not strictly depend on exact determination of the parameters, i.e., the sensitivity of the performance on the parameter values is low. This is evident in Fig. 1, where the minimum regions are kind of splayed instead of being sharp. This means that the \(T_{\mathrm{f}}\) and \(T_{\mathrm{b}}\) values can be changed to some degree without significant loss in performance. As a consequence, the performance of the method does not drop much when the sparsity and noise levels fluctuate from the assumed values. An exception occurs when both the sparsity and noise levels are high as seen in the last two graphs of Fig. 1b. In this case, small changes in \(T_{\mathrm{f}}\) seem to have a big impact on performance while the insensitivity to \(T_{\mathrm{b}}\) continues.

4.3 Simulation Results with Empirical Signals

The main purpose of the simulations in this part is to determine how many measurements M are necessary to correctly recover a K-sparse signal with high probability. In Fig. 2, out of the 500 trials, the percentage of correct reconstructions as a function of M for different sparsity levels when the sparse signal is composed of \(\pm 1'\hbox {s}\) and no noise is present is shown. DD-FBP outperforms every other OMP-based method especially for high sparsity levels. For low sparsity levels, it gives similar results with CoSaMP. It also performs comparably with BP for low sparsity levels.

Fig. 1
figure 1

Minimum number of measurements required for at least 50 % successful reconstruction for different sparsity levels, a clean case, b 20 dB SNR on the observation vector

Full size image
Table 3 Values of \(T_{\mathrm{f}}\) and \(T_{\mathrm{b}}\) used in the simulations
Full size table
Fig. 2
figure 2

Successful reconstruction rates as a function of the number of measurements for clean sparse signals

Full size image

In Fig. 3, average runtimes are exhibited as a function of M for different methods. Notice that DD-FBP consumes less processing time in nearly all of the cases due to the fact that more correct decisions and less false detections are made in each iteration. As a result, total number of iterations to converge is less on the average than the other methods. The runtime of BP is not shown, because it is 15 to 25 times larger than the runtime of DD-FBP. An observation that needs explanation is the “bump” in the graphs. For all methods, the runtime increases as M increases, then a drop occurs, and then it increases again. The drop occurs when M reaches the necessary amount of measurements for reliable successful reconstruction. Before that, because of insufficient M, erroneous decisions are made in each iteration and more iterations are needed for the algorithms to converge, if they converge at all. This results in larger average runtimes.

In Fig. 4, successful reconstruction rates when the observation vector is contaminated by noise are given. Here, by “successful,” we mean that after convergence, the energy of the residual is comparable with the energy of the actual noise. It is assumed that the noisy observation vector is \(\mathbf{y}_{\mathrm{noisy}} = \mathbf{y}+\mathbf{n}\), where n is an Mx1 noise vector whose elements are drawn from a zero-mean Gaussian random variable whose variance is selected such that the SNR is 20 dB. As observed in Fig. 4, DD-FBP and CoSaMP exhibit similar performances while seemingly CoSaMP is slightly better. But when one focuses on relatively large values of M for especially \(K=60\) and \(K=80\), it can be inferred that DD-FBP reaches the 100% reconstruction rate more rapidly than CoSaMP, i.e., less values of M are required for reliable successful reconstruction. As seen in the graphs, BP outperforms all of the OMP-type algorithms in the noisy case. Another observation is that two-stage algorithms (CoSaMP, FBP, DD-FBP) perform significantly better than the ones that do not have a backward stage (OMP, StOMP, gOMP) when noise is present. This can be attributed to the fact that the errors made in the forward step naturally tend to increase when the signal is noisy, and the two-stage algorithms have the ability to correct these errors while the others do not.

Fig. 3
figure 3

Average runtimes as a function of the number of measurements

Full size image
Fig. 4
figure 4

Successful reconstruction rates as a function of the number of measurements for noisy signals (SNR \(=\) 20 dB)

Full size image
Fig. 5
figure 5

Successful reconstruction rates as a function of the number of measurements for clean Gaussian sparse signals

Full size image

The results for Gaussian sparse signals are shown in Fig. 5. DD-FBP gives the best results, nearly edging FBP. The poor performances of CoSaMP and BP for Gaussian sparse signals are remarkable.

Fig. 6
figure 6

Successful reconstruction rates as a function of the number of measurements for a structured observation matrix

Full size image
Fig. 7
figure 7

Image reconstruction performance comparison

Full size image

In Fig. 6, simulation results using a structured observation matrix are shown. The observation matrix is formed by randomly selecting M rows of an \(N\hbox {x}N\) Hadamard matrix. The sparse signal is composed of \(\pm 1'\hbox {s}\) with no noise. The parameters of the algorithms are the same as the first row of Table 2. The results are not very different from the results of Fig. 2; DD-FBP generally outperforms other OMP-type algorithms while basis pursuit gives the best results with much more processing time.

4.4 Simulation Results with a Real Image

For a more realistic case, the methods are compared via their reconstruction performances of a real image. Images generally are not sparse in the spatial domain, and they are approximately sparse when represented in terms of some orthogonal basis such as DCT or Haar wavelet functions. The mandrill image (\(320\times 320\)) to be reconstructed, which is shown in Fig. 7a, is first decomposed into 16x16 sub-images in order to deal with manageable vector and matrix sizes. N, which is the total pixel number, is 256. Then, each sub-image is passed through the Haar wavelet transform to obtain an approximately sparse representation. The transformation is done by multiplying the vectorized sub-image with the Haar orthogonal transform matrix, which can be shown by \(\varvec{\Phi }\). In [16], a pre-processing is done on the sub-images to make them exactly sparse by keeping a number of largest wavelet coefficients and zeroing the others. This seems like an aberration from reality, so such pre-processing is not adopted here. The non-exact sparseness of real images can be considered as a noisy sparse reconstruction problem and presents a harder case for the reconstruction algorithms. After that, \(M=128\) observations are obtained by using an \(M\hbox {x}N\) observation matrix A whose entries are randomly drawn from a Gaussian random variable with zero mean and variance of 1 / M. Note that the composite matrix that will be used by the reconstruction methods becomes \(\mathbf{A} \varvec{\Phi }^{*}\). Then, the sub-images are recovered using the reconstruction method before combining into a single reconstructed \(320\times 320\) image. The results for the methods are shown in Fig. 7b–g along with the corresponding PSNR values. Note that the parameters used by the methods are adjusted to have the best visual quality and highest PSNR values (third row of Table 2). PSNR values suggest that the best result among the OMP-type methods is obtained by DD-FBP. By careful inspection, it can also be seen that DD-FBP manages to preserve the detailed regions of the image more accurately.

5 Conclusion and Future Work

In this work, a new sparse signal reconstruction method based on orthogonal matching pursuit, namely data-driven forward–backward pursuit, is proposed. It is a two-stage reconstruction algorithm that iteratively expands and shrinks the estimated support set. In each iteration, the expansion and shrinkage are not done by constant amounts like other methods, but they are dependent on the correlation and projection coefficients that are calculated in each iteration. Simulation results show that for all types of simulated sparse signals, DD-FBP generally provides better successful reconstruction rates with lower computational costs than the competing methods. It even outperforms the basis pursuit in some cases although the runtime of basis pursuit is several times higher.

A disadvantage of the method is that there are no automatic means of setting the forward and backward threshold values, and they must be pre-determined based on the sparsity and noise levels which are assumed to be known in advance. Nevertheless, this dependence is not very strong, and the values can be changed to some degree without significant loss in performance. Work is still being carried out to apply a probabilistic model in both correlation and projection coefficients to automatically set the forward and backward threshold parameters.

Among the two-stage OMP-type algorithms, subspace pursuit and CoSaMP provide theoretical analysis and guarantees [9, 22]. However, in their analysis, the support size is always fixed after the backward step in every iteration, and they make use of it in their analysis. For the proposed method, the support expands in each iteration, and the amount of expansion is not fixed. So, the theoretical analysis is more complex, and it is left as a future work.