A Class of Sequential Blind Source Separation Method in Order Using Swarm Optimization Algorithm

Abstract

We consider the problem of sequential, blind source separation in some specific order from a mixture of sub- and sup-Gaussian sources. Three methods of separation are developed, specifically, kurtosis maximization using (a) particle swarm optimization, (b) differential evolution, and (c) artificial bee colony algorithm, all of which produce the separation in decreasing order of the absolute kurtosis based on the maximization of the kurtosis cost function. The validity of the methods was confirmed through simulation. Moreover, compared with other conventional methods, the proposed method separated the various sources with greater accuracy. Finally, we performed a real-world experiment to separate electroencephalogram (EEG) signals from a super-determined mixture with Gaussian noise. Whereas the conventional methods separate simultaneously EEG signals of interest along with noise, the result of this example shows the proposed methods recover from the outset solely those EEG signals of interest. This feature will be of benefit in many practical applications.

1 Introduction

Recently, blind source separation (BSS), or blind signal separation, has received considerable attention in the fields of digital communications, biomedical engineering, speech processing, image processing, and robot navigation [2, 7, 9, 15, 19, 20]. The objective of BSS is to extract the original source signals from their mixtures using only the information of the observed signal with no or very limited knowledge about the source signals. Over the past few years, many methods have been developed to solve the BSS problem. They can be largely classified into two approaches. In the context of BSS, all the sources are simultaneously recovered or estimated from the observations, such as those based on the joint diagonalization cost function and the natural gradient [26], those based on temporal predictability and the differential search algorithm [3], and the nonlinear contract function-based BSS [31]. However, the different neurons of these BSS methods [3, 26] may converge to the same maximization, i.e., extracting the same sources from mixtures. The other class of algorithm is called blind source extraction (BSE). BSE is an extension of the BSS technique. Compared with these methods [3, 26, 31], the objective of BSE is to recover a single source or a part of a source from the observations one by one [6, 24], and this leads to low computation complexity and greater flexibility. This class of algorithms has a disadvantage in that the choice of nonlinearity has taken several directions because of the conflict between boundedness and analyticity. In this respect, Liouville’s theorem states that if a function is analytic and bounded in the plane, then it is a constant. Conventional BSS approaches do not ensure separation of source signals with a specified order in accordance with their stochastic properties. There are actually three types of source signals in [10, 16]; they are known as standard normal, sup-Gaussian, and sub-Gaussian. The kurtosis in [27, 32] is used to measure signals of the different distributions. This paper introduces a class of BSS methods based on swarm optimization, which is able to separate sup and sub-Gaussian sources from mixtures in decreasing order according to the absolute value of kurtosis. However, it requires the maximization of the cost function, which is nonlinear and multimodal. Indeed, the swarm optimization algorithm has yielded excellent performances in similar problems [17, 18, 21]. For these reasons, we believe it is necessary and certainly beneficial to study the application of swarm optimization algorithms in sequential BSS.

The paper is organized as follows. Sequential BSS is formulated in Sect. 2.1. Section 2.2 provides the description of the employed swarm intelligent algorithms: the particle swarm optimization, the differential evolution approach, and the artificial bee colony algorithm. Section 2.3 proposes a swarm intelligent optimization-based BSS. The performance of the proposed method is numerically evaluated in Sect. 3. Section 4 is devoted to concluding remarks.

2 Sequential Blind Source Separation Method in Order Using Swarm Optimization Algorithm

2.1 Problem Formulation

Consider the n unobservable components of a zero-mean vector $\mathbf{s}(t)=[s_{1}(t), s_{2}(t), {\ldots }, s_{n}(t)]^\mathrm{T}$, each component being mutually and statistically independent; here superscript T denotes transposition and $\mathbf{s}(t)\upvarepsilon \mathbf{R}^{n}$. The available sensor vector $\mathbf{x}(t)=[x_{1}(t), x_{2}(t),{\ldots }, x_{\mathrm{m}}(t)]^\mathrm{T}$, where m is the number of sensors and $\mathbf{x}(t)\upvarepsilon \mathbf{R}^{m}$, is given by

$$\begin{aligned} \mathbf{x}(t)=\mathbf{As}(t), \end{aligned}$$

(1)

where $\mathbf{A}\upvarepsilon \mathbf{R}^{m\times n}$ is a non-singular and unobservable matrix with a nonzero determinant, and its rank is n. Here, $t=0, 1,\ldots , N-1$ is the instant time of sampling. The objective of sequential BSS is to recover or estimate only a single source from the observations. The separated signal can be given by

$$\begin{aligned} y(t)=\mathbf{w}^\mathrm{T}\mathbf{x}(t)= \mathbf{w}^\mathrm{T}\mathbf{As}(t), \end{aligned}$$

(2)

where the extracted weighted vector w is a m column vector. Let $\mathbf{g}=\mathbf{w}^\mathrm{T} \mathbf{A}$; if only one element of g is nonzero while the others are zero, then y(t) is a recovery or estimate of $\mathbf{s}(t)$ with the same site being nonzero in g. $\mathbf{s}(t)$ is recovered using (2) n times.

Denote B as a whitening matrix and selected so as to sphere the observations, then $\mathbf{z}(t)=\mathbf{Bx}(t)$. We estimate each source, y(t), separately finding a vector w such that

$$\begin{aligned} y(t)=\mathbf{w}^{\mathrm{T}}\mathbf{z}(t). \end{aligned}$$

(3)

Without loss of generality, we make the typical assumption that the source signals have unit variance, i.e., $E[\mathbf{s}(t)\mathbf{s}(t)^{\mathrm{T}}]=\mathbf{I}$. It also means $E[y(t)^{2}]=1$, and hence we can rewrite $E[y(t)^{2}]$ as

$$\begin{aligned} E\left[ \mathbf{w}^{\mathrm{T}}\mathbf{z}(t)\mathbf{z}(t)^{\mathrm{T}}\mathbf{w}\right]= & {} \mathbf{w}^{\mathrm{T}}E\left[ \mathbf{z}(t)\mathbf{z}(t)^{\mathrm{T}}\right] \mathbf{w}\nonumber \\= & {} 1 \end{aligned}$$

(4)

From (4), we can obtain $\left\| \mathbf{w} \right\| ^{2}=1$, where $|\!|\cdot |\!|$ denotes the Frobenius norm.

In [27, 32], the kurtosis of a zero-mean random variable y(t) is defined as

$$\begin{aligned} K(y)\mathop =\limits ^\Delta \hbox {cum}[y(t),y(t),y(t),y(t)]. \end{aligned}$$

(5)

For Gaussian signals, the kurtosis is zero; for non-Gaussian signals, the kurtosis is nonzero. The kurtosis can be both positive and negative. Random variables that have positive kurtosis are called sup-Gaussian, and those with negative kurtosis are called sub-Gaussian. Non-Gaussianity is measured using the absolute value of kurtosis or the square of kurtosis in [17, 18, 21]. We use (5) to find an optimal w,

$$\begin{aligned} \mathbf{w}=\mathop {\arg \max }\limits _\mathbf{w} \left| {K(y)} \right| \qquad \hbox { s.t}. \left\| \mathbf{w} \right\| ^{2}=1. \end{aligned}$$

(6)

To justify the use of the optimization criterion in (6), we state the following theorem and give its proof.

Theorem

Assume that $\mathbf{z}(t)=\mathbf{BAs}(t)$ where B is the whitening matrix. Then, the local maxima (or minima) of K(y) under the constraint $\left\| \mathbf{w} \right\| ^{2}=1$ such that the corresponding independent components $s_{i}(t)$ satisfy $K(s_{i})>0$ (or $K(s_{i})< 0$).

Proof

We define a linear transformation $\mathbf{q}=(\mathbf{BA})^\mathrm{T}\mathbf{w}$. Without loss of generality, it is sufficient to analyze the stability of point $\mathbf{q}_i =[0,\ldots ,0, \delta _i, 0, \ldots ,0]^\mathrm{T}$ with $\left| {\delta _i } \right| =1$. At $\mathbf{q}_i$, we have $y(t)=\mathbf{q}_i ^\mathrm{T}\mathbf{s}(t)={\delta _{i}} s_{i}(t)$. Substituting it into (5), we then obtain

$$\begin{aligned} K(\mathbf{q})=E\left\{ [\mathbf{q}^{\mathrm{T}}\mathbf{s}(t)\mathbf{s}(t)^\mathrm{T}\mathbf{q}]^{2}\right\} -3\left\{ \mathbf{q}^{\mathrm{T}}E[\mathbf{s}(t)\mathbf{s}(t)^\mathrm{T}]\mathbf{q}\right\} ^{2}. \end{aligned}$$

(7)

Evaluating the first-order gradients and second order of $s_{i}(t)$ at optimal point $\mathbf{q}_i$ and using the independence of source signals, we obtain

$$\begin{aligned}&\left. {\frac{\partial K(\mathbf{q})}{\partial \mathbf{q}}} \right| _{\mathbf{q}=\mathbf{q}_i } =[0,\ldots , 0,4K(s_i )\delta _i ^{3},0, \ldots , 0]^{\mathrm{T}}, \end{aligned}$$

(8)

$$\begin{aligned}&\left. {\frac{\partial K(\mathbf{q})}{\partial \mathbf{q}\partial \mathbf{q}^\mathrm{T}}} \right| _{\mathbf{q}=\mathbf{q}_i } =\left[ {\begin{array}{c@{\quad }c@{\quad }c} 0, \ldots , 0,&{}\cdots \cdots ,&{}0, \ldots , 0 \\ \vdots &{}\cdots \cdots &{}\vdots \\ 0, \ldots , 0,&{} 12K(s_i )\delta _i ^{2},&{}0, \ldots , 0 \\ 0, \ldots , 0,&{}\cdots \cdots ,&{}0, \ldots , 0 \\ \vdots &{}\cdots \cdots &{}\vdots \\ 0, \ldots , 0,&{}\cdots \cdots ,&{}0, \ldots , 0 \\ \end{array}} \right] . \end{aligned}$$

(9)

Introducing a small perturbation $\Delta \mathbf{q}=[\Delta q_1,\Delta q_2, \ldots ,\Delta q_m ]^{\mathrm{T}}$ to $\mathbf{q}_i$. The difference between $K(\mathbf{q}_i +\Delta \mathbf{q})$ and $K(\mathbf{q}_i )$ to second order in a Taylor series expansion is

$$\begin{aligned}&K(\mathbf{q}_i +\Delta \mathbf{q})-K(\mathbf{q}_i ) \nonumber \\&\quad =\left[ {\left. {\frac{\partial K(\mathbf{q})}{\partial \mathbf{q}}} \right| _{\mathbf{q}=\mathbf{q}_i } } \right] ^{\mathrm{T}}\Delta \mathbf{q}+\left[ {\left. {\frac{1}{2}\Delta \mathbf{q}^{\mathrm{T}}\frac{\partial K(\mathbf{q})}{\partial \mathbf{q}\partial \mathbf{q}^{\mathrm{T}}}} \right| _{\mathbf{q}=\mathbf{q}_i } } \right] \Delta \mathbf{q}+o(\left\| {\Delta \mathbf{q}} \right\| ^{2}) \nonumber \\&\quad =2K(s_i )[2\delta _i ^{3}\Delta q_i +3\delta _{i}^{2}\Delta q_i^2 ]+o(\left\| {\Delta \mathbf{q}} \right\| ^{2}). \end{aligned}$$

(10)

From the constraint $\left\| {\mathbf{q}+\Delta \mathbf{q}} \right\| ^{2}=1$, we obtain $2\delta _i \Delta q_i =-\left\| {\Delta \mathbf{q}} \right\| ^{2}$, which implies that the higher-order terms in (10) are $o(\left\| {\Delta \mathbf{q}} \right\| ^{2})$ and can be neglected. Through a substitution, (10) can be simplified as

$$\begin{aligned} K(\mathbf{q}_i +\Delta \mathbf{q})-K(\mathbf{q}_i )=-2K(s_i )\left\| {\Delta \mathbf{q}} \right\| ^{2}+o(\left\| {\Delta \mathbf{q}} \right\| ^{2}), \end{aligned}$$

(11)

which clearly shows that $\mathbf{q}_i$ is an extremum and of the type implied by the conditions of the theorem.

According to the above analysis, it is clear that the blind separation in (6) would extract the dominant source with the highest absolute kurtosis value. However, it may be difficult to implement, because it requires the maximization of the cost function, which is nonlinear and multimodal. Inspired by nature, the swarm optimization algorithm is a technique of dynamic systems research, which endeavors to develop new computational tools for problem solving by simulating and mimicking natural behaviors of organisms, and may result in the design of novel computational systems [4]. Indeed, some swarm optimization algorithms have obtained excellent performances in similar problems [1, 8, 12]. Because of these reasons, we believe it is necessary and certainly beneficial to study the application of swarm optimization algorithms in sequential BSS. In the subsequent sections, we describe the details of particle swarm optimization, differential evolution, and the artificial bee colony algorithm used in this work.

2.2 Swarm Optimization Algorithms

2.2.1 Particle Swarm Optimization

The particle swarm optimization (PSO) is a population-based, self-adaptive search optimization technique first introduced by Kennedy and Eberhart [14]. The PSO algorithm emulates swarm behavior and the individuals represent points in the multidimensional space. A particle represents a possible potential solution. The swarm initially has a population of random solutions. Each particle is given a random velocity and is flown through the problem space. Each particle has a memory and keeps track of its previous optimal position, denoted $P_\mathrm{best}$, and corresponding fitness value. Each swarm remembers another value, denoted $G_\mathrm{best}$, which is the optimal solution achieved so far by a swarm. The velocity $V_{l}(d)$ and the position $\theta$ $_{l}(d)$ of the dth dimension of lth particle are updated by

$$\begin{aligned} V_l (d)= & {} \omega _k V_l (d)+c_1 r_1 (d)[P_{best,l} (d)-\theta _l (d)]+c_2 r_2 (d)[G_{best} (d)-\theta _l (d)], \end{aligned}$$

(12)

$$\begin{aligned} \omega _k= & {} \omega _{\max } -\frac{(\omega _{\max } -\omega _{\min } )}{k_{\max } }k, \end{aligned}$$

(13)

$$\begin{aligned} \theta _l (d)= & {} \theta _l (d)+V_l (d), \end{aligned}$$

(14)

where $d=1, 2, {\ldots }, D$ with D the dimension of the candidate solution; $P_{best,l}(d)$ and $G_\mathrm{best}(d)$ are the dth dimensional positions of $P_{\mathrm{best}}$ of the lth particle and $G_\mathrm{best}$, respectively; $r_{1}(d)$ and $r_{2}(d)$ are random numbers in the range [0, 1] and are different in different dimensions; k and $k_\mathrm{max}$ are the iteration number and total number of iterations, respectively, $k=1,2, {\ldots }, k_\mathrm{max}$; $c_{1}$ and $c_{2}$ are acceleration coefficients, and $\omega _{k }$ is the inertial weight, which plays the role of balancing the global search and local search. According to [29], $\omega _\mathrm{max}=0.9$, $\omega _\mathrm{min}=0.5$ and $c_{1}+c_{2} =4.\; l=1,2, {\ldots }, N_\mathrm{P}$, with $N_\mathrm{P}$ the particle population size.

Table 1 presents the pseudocode for the PSO algorithm that we employed in this work.

Table 1 Particle swarm optimization

2.2.2 Differential Evolution

The differential evolution (DE) was proposed by Storn and Price in 1995 [23, 25]. It is a population-based and directed-search method. Let us assume that ${\varvec{\uptheta }}_{l,k }(l=1,2, {\ldots },N_\mathrm{P})$ are candidate solution vectors in iteration k ($N_\mathrm{P}=\hbox {population}$ size). Successive populations are generated by adding the weighted difference of two randomly selected vectors into a third randomly selected vector. For classical DE, the mutation, crossover, and selection operators are defined straightforwardly as follows.

Mutation for each vector ${\varvec{\uptheta }}_{l,k}$ in iteration k, a mutant V $_{l,k }$ is defined by

$$\begin{aligned} \mathbf{V}_{l,k} ={\varvec{\uptheta }}_{r_1,k} +F({\varvec{\uptheta }}_{r_2,k} -{\varvec{\uptheta }}_{r_3,k} ), \end{aligned}$$

(15)

where $r_{1}$, $r_{2}$, and $r_{3 }$ are mutually different random integer indices selected from [1 $N_{\mathrm{p}}$]. Further, $r_{1}\ne r_{2} \ne r _{3}$. $F \upvarepsilon [0,2]$ is a real random constant that determines the amplification of the added differential variation of $({\varvec{\uptheta }}_{r_2,k} -{\varvec{\uptheta }}_{r_1,k} )$.

Crossover DE uses the crossover operation to generate new solutions by shuffling competing vectors and also to increase the diversity of the population. It defines the following trial vector:

$$\begin{aligned} \mathbf{U}_{l,k} =[U_{l1,k},U_{l2,k},\quad ,U_{lD,k}], \end{aligned}$$

(16)

where

$$\begin{aligned} U_{lj,k} =\left\{ \begin{array}{ll} V_{lj,k},&{}\quad \varphi \le C_\mathrm{R} \hbox { or }j=k \\ \theta _{lj,k},&{}\quad \hbox { otherwise} \end{array} \right. , \end{aligned}$$

(17)

$C _\mathrm{R} \upvarepsilon$[0,1] is the predefined crossover rate constant, $\varphi$ a uniform random number generator, and $k \upvarepsilon [1,D]$ a random parameter index, chosen once for each l to ensure that at least one parameter is always selected from the mutated vector $V_{lj,k}$.

Selection The approach must determine which vectors ${\varvec{\uptheta }}_{l,k }$ and $\mathbf{U}_{l,k}$ should be a next iteration ${\varvec{\uptheta }}_{l,k+1 }$ depending on their fitness value. Table 2 outlines the pseudocode of DE.

Table 2 Differential evolution

2.2.3 Artificial Bee Colony Algorithm

The artificial bee colony (ABC) is an algorithm that simulates the foraging behavior of a bee colony, and can be used to solve the multidimensional optimization problems. A honey bee swarm consists of three kinds of bees: employed bees, onlooker bees, and scout bees [13]. In the ABC algorithm, the position of a food source represents a possible solution to the optimization problem and the nectar amount of a food source corresponds to the object function of the associated solution. Let ${\varvec{\uptheta }}(l)$ represent the l-th food source in the population, $N _\mathrm{s}$ is the population size of food source. The units of the original ABC can be explained as follows:

Employed Bee Phase At this stage, each employed bee generates a new food source ${\varvec{\uptheta }}_\mathrm{EB}(l)$ in the neighborhood of its present position by

$$\begin{aligned} \theta _{\mathrm{EB}} (l,d)=\theta (l,d)+\varphi _{ld} [\theta (l,d)-\theta (r_1,d)], \end{aligned}$$

(18)

where $d=1, 2, {\ldots }, D$ and D is the dimension of candidate solution, $r _{1}$ is randomly chosen from [1, $N _\mathrm{F}$] and has to be different from l, i.e., $r _{1} \ne l$. $\varphi _{ld}$ is a random number in the range $[-1,1]$.

Once ${\varvec{\uptheta }}_\mathrm{EB}(l)$ is obtained, it is evaluated and compared with ${\varvec{\uptheta }}(l)$. If the fitness of ${\varvec{\uptheta }}_\mathrm{EB}(l)$ is better than that of ${\varvec{\uptheta }}(l)$, ${\varvec{\uptheta }}_\mathrm{EB}(l)$ replaces ${\varvec{\uptheta }}(l)$; otherwise if ${\varvec{\uptheta }}(l)$ is retained, then $k _\mathrm{count}(l)= k _\mathrm{count}(l)$+1. $k _\mathrm{count}(l)$ is a non-improvement number of the solution ${\varvec{\uptheta }}(l)$.

Onlooker Bee Phase After all worker bees complete their searches, they share in a dance their information related to the nectar amounts and the location of their sources with onlooker bees. An onlooker bee evaluates the nectar information given by each worker bee and chooses a food source site with a probability related to its nectar amount. This probability depends on the fitness values of the solutions in the population; it can be described as

$$\begin{aligned} p_l =\frac{F(l)}{\sum _{l=1}^{N_\mathrm{s} } {F(l)} }\quad l=\hbox {1, 2, }\ldots ,N_\mathrm{s}, \end{aligned}$$

(19)

where F(l) is the fitness function of lth candidate solution. Once the onlooker has selected her food source ${\varvec{\uptheta }}(l)$, she produces a modification on ${\varvec{\uptheta }}_\mathrm{OB}(l)$ using

$$\begin{aligned} \theta _{\mathrm{OB}} (l,d)=\left\{ {\begin{array}{ll} \theta (l,d)+\varphi _{ld} [\theta (l,d)-\theta (r_1,d)], &{}\quad p_l <MR \\ \theta (l,d),&{}\quad \hbox { otherwise} \\ \end{array}} \right. , \end{aligned}$$

(20)

where MR is a control parameter of the ABC algorithm in the range [0, 1], which controls the number of parameters to be modified. As in the phase of the worker bee, the onlooker bee produces a new position of the food source based on the fitness value. If the fitness of ${\varvec{\uptheta }}_\mathrm{OB}(l)$ is worse than that of ${\varvec{\uptheta }}(l)$, ${\varvec{\uptheta }}(l)$ is retained and $k _\mathrm{count}(l)= k _\mathrm{count}(l)$+1; otherwise ${\varvec{\uptheta }}_\mathrm{OB}(l)$ replaces ${\varvec{\uptheta }}(l)$.

Scout Bee Phase If a food source ${\varvec{\uptheta }}(l)$ cannot be further improved through a predetermined $k _\mathrm{limit}(l)$, it is abandoned. The food source abandoned by the bees is replaced with a new food source discovered by the scouts. The scout produces a food source randomly from the range of $[\theta _\mathrm{min}(d) \theta _\mathrm{max}(d)]$.

Pseudocode of ABC algorithm is given in Table 3.

Table 3 Artificial bee colony algorithm

2.3 Sequential Blind Source Separation Method in Order Using Swarm Optimization Algorithm

The idea of this paper is the application of the swarm optimization algorithm in sequential BSS. In other words, the swarm optimization algorithms were used to find the global optima of (6). As explained above, the upper and lower bounds of a candidate solution are assumed known in advance. Because of the constraint $\left\| \mathbf{w} \right\| ^{2}=1$, we can rewrite w as

$$\begin{aligned} \left[ {\begin{array}{c} w_1 \\ w_2 \\ \quad \vdots \\ w_{m-1} \\ w_m \\ \end{array}} \right] =\left[ {\begin{array}{c} \cos \alpha _1 \\ \sin \alpha _1 \cos \alpha _1 \\ \quad \vdots \\ \sin \alpha _1 \sin \alpha _2 \ldots \cos \alpha _{m-1} \\ \sin \alpha _1 \sin \alpha _2 \ldots \sin \alpha _{m-1} \\ \end{array}} \right] , \end{aligned}$$

(21)

where [$\alpha _{1}, \alpha _{2}, {\ldots }, \alpha _{m-1}] \upvarepsilon [0,2{\pi }]^{(m-1)}$, i.e., the upper and lower bounds of $\alpha _{i}(i=1,2,{\ldots }, m-1)$ are 0 and 2$\pi$, respectively.

The idea described in the above method aims at the extraction of one source having the highest absolute kurtosis value. However, it can also be used for recovering the remaining sources. After one source is extracted, we can remove it from the mixture. This can be achieved through a deflation procedure, in which the goal is to eliminate the contribution of the extracted y(t). Mathematically, this procedure is given by

$$\begin{aligned} \mathbf{x}(t) \quad \leftarrow \mathbf{x}(t)-\mathbf{h}y(t), \end{aligned}$$

(22)

where $\mathbf{h}=E[\mathbf{x}(t) y(t)]/E[y ^{2}(t)]$ is a vector that minimizes $E\{[\mathbf{x}(t)-\mathbf{h}y(t)]^{2}\}$.

As the outcome of the first deflation is a BSS problem with n mixtures and $n-1$ sources, we reduce the dimension of n via principle component analysis (PCA) [28] to obtain a $n-1$ model. Finally, the remaining sources can be extracted by repeating the same steps.

For clarity, the pseudocode of the proposed method is presented in Table 4.

Table 4 Procedural steps for sequential blind source separation used in the swarm optimization algorithm

3 Simulation Analysis

In this section, a detailed simulation is provided to investigate the performance of the proposed method. In all experiments, the elements of the mixing matrix A in (1) are randomly generated in accordance with a uniform distribution in $[-1, 1]$. The ABC parameters are used for the simulation as specified in (23), whereas the DE and PSO parameters are used for the simulation as given in (24) and (25), respectively. The simulation experiments were performed using the program MALAB ver.R2010b.

$$\begin{aligned}&\left\{ {\begin{array}{l} k_{\max } =200 \\ k_{\mathrm{limit}} =5 \\ N_\mathrm{F} =20 \\ \end{array}} \right. \end{aligned}$$

(23)

$$\begin{aligned}&\left\{ {\begin{array}{l} k_{\max } =200 \\ N_\mathrm{P} =20 \\ \omega _{\max } =0.9 \\ \omega _{\min } =0.4 \\ c_1 =c_2 =0.2 \\ \end{array}} \right. \end{aligned}$$

(24)

$$\begin{aligned}&\left\{ {\begin{array}{l} k_{\max } =200 \\ C_\mathrm{R} =0.5 \\ N_\mathrm{P} =20 \\ \end{array}} \right. \end{aligned}$$

(25)

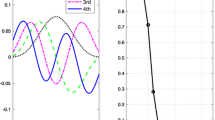
Experiment 1 In the first experiment, we consider the separation of sub-Gaussian signals. The source signals are shown in Fig. 1a; Fig. 1b shows the observation signal given by (1). Figure 2 shows the convergence curve of the different swarm optimization algorithms for first extraction of the signal. Table 5 shows the kurtosis of the estimated signals for a sub-Gaussian. The performance of the BSS algorithm can be evaluated using (26) and (27). A comparison of results obtained from different BSS methods for the sub-Gaussian signals is given in Table 6. Note that the simulation results were presented as average values of 30 independent runs. The method${}^{1}$ used in [11] is that the cost function $J(y)=\frac{1}{4}y(t)^{4}$ was maximized by the ABC algorithm of Sect. 2.

$$\begin{aligned} \hbox {SIR}_i= & {} 10\log \frac{\left\| {\mathbf{s}_i } \right\| ^2 }{\left\| {\mathbf{s}_i -\mathbf{y}_i} \right\| ^{2}} \quad i=1,2,\ldots ,n \end{aligned}$$

(26)

$$\begin{aligned} \hbox {SNR}= & {} \frac{1}{n}\sum _i {10\log \frac{\left\| {\mathbf{s}_i } \right\| ^{2} }{\left\| {\mathbf{s}_i -\mathbf{y}_i } \right\| ^{2} }} \end{aligned}$$

(27)

Table 5 Kurtosis of separated signal of sub-Gaussian nature

Table 6 Comparison of results from different BSS methods for a sub-Gaussian signal

Fig. 1

Signals of Experiment 1. a Source signals. b Observation signals

Fig. 2

Convergence curves for different swarm optimization algorithms for first extracted signals with sub-Gaussian nature

where the vector $\mathbf{y}_{i}$ is an estimation of $\mathbf{s}_{i}$. Clearly, $\hbox {SIR}_{i} \rightarrow \infty$ and $\hbox {SNR}\rightarrow \infty$ if perfect separation is achieved.

Experiment 2 In this experiment, the three speech signals in Fig. 3a are used. They are sup-Gaussian distributions and are available in [5]. Figure 3b shows the observation signal given by (1). Figure 4 shows the convergence curve of different swarm optimization algorithms for the first extracted signal. Table 7 gives the kurtosis of the estimated signals of the sub-Gaussian. A comparison of results from the different BSS methods for sup-Gaussian signals is shown in Table 8. The method${}^{2}$ used in [11] is that the cost function $J(y)=\frac{1}{a_1 }\exp [-a_1 y(t)^{2}/2]y(t)$ was maximized using the ABC algorithm given in Sect. 2, $a _{1} \approx ~1$.

Table 7 Kurtosis of the separated sup-Gaussian signals

Table 8 Comparison of results from different BSS methods for sup-Gaussian

Fig. 3

Signals of Experiment 2. a Source signals. b Observation signals

Fig. 4

Convergent curve of different swarm optimization algorithms for the first extracted sup-Gaussian signals

Experiment 3 This experiment exemplifies the separation of four source signals given in Fig. 5a; the observation signals are shown in Fig. 5b. Both $s _{1}(t)$ and $s _{2}(t)$ are speech signals of sup-Gaussian nature, whereas $s _{3}(t)$ and $s _{4}(t)$ are the communication signals of sub-Gaussian nature. The convergent curve for different swarm optimization algorithms for the first extraction of the signal is shown in Fig. 6. The kurtosis of the estimated signals (Table 9) and a comparison of results from different BSS methods (Table 10) are given for sup- and sub-Gaussian signals. The method$^{3}$ used in [11] maximizes the cost function $J(y)=\frac{1}{a_2 }\log \cosh [a_2 y(t)]$ using the ABC algorithm in Sect. 2, $1 \le a _{2}\le$ 2. The method${}^{1}$ in [26] maximizes the cost function in [26] using the DE algorithm in Sect. 2. The method$^{1}$ in [24] maximizes the cost function in [24] using the PSO algorithm in Sect. 2.

Fig. 5

Signals of Experiment 3. a Source signals. b Observation signals

Fig. 6

Convergent curve of different swarm optimization algorithms for first extracted signals with sub- and sup-Gaussian nature

Table 9 Kurtosis of separated signals of sub- and sup-Gaussian nature

Table 10 Comparison of results from different BSS methods for sub- and sup-Gaussian signals

From Figs. 2, 4, and 6, we observe that the ABC algorithm requires less iterations to achieve the fineness value compared with DE and PSO. A comparison of results from Tables 6, 8, and 10 shows that the ABC-BSS can separate sources of any distribution and has superior performance compared with DE-BSS and PSO-BSS. From Fig. 7 and Tables 5, 7, and 9, the proposed method is able to extract source signals (of sub-Gaussian and/or sup-Gaussian nature) one by one with decreasing order of absolute kurtosis. However, the results in Fig. 7d–f clearly demonstrate that method$^{3}$ in [11], method$^{1}$ in [26], and method$^{1}$ in [24] cannot extract source signals in the order specified by their stochastic properties. Compared with the proposed methods, the method in [11] separated sources with lower accuracy, especially for the mixed case of sub- and sup-Gaussians.

Fig. 7

Recovered signals in Experiment 3. a Recovered signals of ABC-BSS method. b Recovered signals of DE-BSS method. c Recovered signals of PSO-BSS method. d Recovered signals of the method${}^{3}$ in [11]. e Recovered signals using the method${}^{1}$ in [26]. f Recovered signals of the method${}^{1}$ in [24]

Experiment 4 To examine the noise impact of the separated performance of the proposed methods, in the last experiment, the four observation signals in Fig. 5b were added with different white Gaussian noise of varying signal-to-noise ratio (SNR) from 10 to 35 dB. Moreover, we verify the effectiveness of the proposed method by comparing it with the algorithms in [11, 24], and [26]. More details of the algorithm in [11] are available in [22]. The performance of the recovered signals is evaluated by (27). Figure 8 shows a comparison of results for five different BSS methods.

Fig. 8

Comparison of results of different BSS methods

As observed in Fig. 8, the separated performance of ABC-BSS, DE-BSS, and PSO-BSS is quite similar. The comparison of results also shows that our method can separate sources of sub- and sup-Gaussian nature with higher accuracy compared with other conventional methods.

Experiment 5 This class of BSS described in Sect. 2 could be essential in many applications, especially when the number of sources is large, and only some of them are interesting or useful signals buried in Gaussian noises. In this experiment, to further confirm the estimation performance of the proposed algorithms, we used a real-world example to compare the performance with those of the algorithm used in [24]. Figure 9 shows two electroencephalogram (EEG) signals that are available in [5], the kurtosis is positive and relatively large for the EEG signals (as also for clear heart, eye movement, and eye blinking artifacts); the kurtosis is zero or negative for noise. We mixed two EEG signals and one white Gaussian noise into four channels of an EEG. The mixed signals of the four channels are shown in Fig. 10. Figure 11 shows that we have employed different BSS methods to recover the EEG signals from the mixed signals; a comparison of the recovery performance is shown in Table 12. Table 11 shows the kurtosis of the estimated EEG signals. Note that m and n in this experiment are 4 and 3, respectively. Because the method in [26] uses an assumption that implies $m=n$, the method is not appropriate if $m > n$. Also, [11] makes the further assumption that the dimensions of x(t) and s(t) are equal.

Table 11 Kurtosis of separated EEG signals

Table 12 Comparison of results for the different BSS methods applied to the EEG signal

Fig. 9

EEG signals

Fig. 10

Mixed EEG signals of the four channels

Fig. 11

Recovered EEG signals of the different BSS methods. a Recovered EEG signals of the ABC-BSS method. b Recovered EEG signals of the DE-BSS method. c Recovered EEG signals of the DE-BSS method. d Recovered EEG signals of the method in [24]

As expected, Table 11 shows the proposed methods first recover those EEG signals of interest, whereas the method in [24] separated “useful” signals and “useless” noise simultaneously. Again, the superior performance of our method is confirmed by the results in Fig. 11 and Table 12. These features enable the proposed method to be of benefit in practice.

4 Conclusion

This paper introduced a class of sequential BSS methods that maximized the kurtosis cost function. They are able to extract the source signals of sub- and sup-Gaussian form one by one in a specific order determined according to their stochastic properties, specifically, in decreasing order of the absolute kurtosis. Simulation results demonstrated the excellent performance of the proposed method. Compared with previous methods, the methods introduced have the following merits: recovery of the original signals from a linear mixture of signals with higher accuracy and extraction of various sources in decreasing order according to the absolute value of the kurtosis. In addition, the proposed methods are suitable for $m \ge n$. These features make the methods suitable in many applications, especially when the number of sources is large and when only some signals are of interest or when useful signals are buried in white Gaussian noise.

Recently, complex-valued signals have arisen in many applications as diverse as wireless communications, radar, and functional magnetic resonance imaging. When processing has to be done in a transform domain such as Fourier space or complex wavelet domains, the data are again complex-valued. To perform BSS of such complex-valued signals, there are a number of options. For complex-valued signals, the Gaussianity implies zero kurtosis, sup-Gaussianity implies positive kurtosis, and sub-Gaussianity implies negative kurtosis [30]. The resolution of sequential BSS of various complex sources is one of the challenging problems of BSS. Future work may include developing sequential complex BSS algorithms that achieve the objective of extracting complex-valued signals one by one with specified order.