Further Criteria on Master–Slave Synchronization in Chaotic Lur’e Systems Using Delay Feedback Control

Abstract

This paper is concerned with designing delay feedback controllers of master–slave synchronization for Lur’e systems. Through dividing the delay interval into two parts and choosing two augmented Lyapunov–Krasovskii functionals, some delay-dependent synchronization criteria are formulated in terms of linear matrix inequalities (LMIs), in which the conservatism can be effectively reduced based on adjusting some useful parameters. The proposed conditions can be easily checked, and the controller gains can be achieved by solving the derived LMIs. Finally, two numerical examples are given to illustrate the presented results.

1 Introduction

In past decades, synchronization control of various chaotic systems has attracted considerable attention since the pioneering works of Pecora and Carroll were reported [5, 26], which shows that as some conditions are satisfied, a chaotic system (the slave system) may become synchronized to another identical one (the master system) if the master system sends some driving signals to the slave one. Presently, it is widely known that there exist many benefits of having synchronization in various engineering applications, such as teleoperation, secure communication, image processing, and harmonic oscillation generation. Moreover, there also exists synchronization in language emergence and development, which comes up with a common vocabulary, while agents’ synchronization in organization management will improve their work efficiency. Therefore, the problem on chaos synchronization has been widely investigated in recent years [1–4, 8, 16–19, 24, 25, 29, 31, 32, 38–40, 42].

Meanwhile, since Lur’e system can represent many nonlinear models as its special cases and exhibit some chaotic behaviors, its synchronization has received much attention and many elegant results have been proposed either [6, 7, 9–15, 20–22, 27, 28, 30, 33, 34, 36, 37, 41, 43, 44]. In [33], the finite-time master–slave synchronization has been discussed for uncertain Lur’e systems based on adaptive control. It is worth pointing out that time-delay is an inherent feature in physical processes, which may lead to instability or significantly deteriorate system’s performance. Thus, many works have dealt with the issue on chaotic synchronization of Lur’e systems [6, 7, 9–15, 20–22, 27, 28, 30, 34, 36, 37, 41, 43, 44]. In recent years, the design of delay feedback controllers for master–slave synchronization has been deeply studied. Based on several effective techniques, some elegant delay-dependent criteria have been obtained and formulated in terms of simple LMIs. In [10–12, 14, 20, 21, 28, 36, 41], through using free-weighting matrix, integral inequality, and Moon’s inequality, many significant results have been proposed with both constant and invariable delay included. In particular, the results in [6] were based on Lyapunov functional with quadratic form of some augmented vectors, in which the nonlinear functions were expressed as convex combinations and the derivative of state was also used in the controller. In [15], the synchronization of Lur’e systems was extended to singular case and the output feedback controller was used, in which the controller algorithm has been given in terms of nonlinear matrix inequalities.

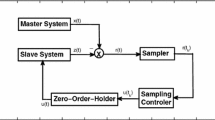
In many practical situations, digital controllers are more preferable than continuous ones since they allow for synchronization only by using the samples of the states in both the master system and slave one at discrete time instants. Thus, in [27, 30, 34, 43], the sampled-data controller was designed to discuss the master–slave synchronization and the controller gains could be obtained by solving the derived LMIs. Moreover, its application in secure communication was also involved in [30]. It should be noted that the synchronization schemes in [27, 30, 34, 43] were based on that there had been a perfect communication channel between the measurement of the system and the input of the controller. However, in networked environment, sampled signals are usually quantized before being transmitted. Thus, the quantizer can be regarded as a coder which converts the continuous signal into piecewise continuous one taking values in a finite set. Then quantization effect has been added into the master–slave synchronization problem [37, 44]. Presently, since the delay-partitioning idea was verified to be more effective in reducing the conservatism, it has been utilized to discuss chaotic synchronization [9, 22] and yet, their complicated results cannot be easily checked. Furthermore, though the synchronization in [13] has considered the presence of parameter mismatches, the concerning time-delay was constant.

Now based on the synchronization results in [7, 9, 13, 22, 27, 30, 34, 37, 43, 44], the issue on time-varying delay has been involved and many elegant techniques have been put forward, in which the information on bounds of both delay and its derivative has been deeply involved. Yet there still exists much room waiting for the improvements, which can be illustrated in what follows. On the one hand, since the restriction that the upper bound on derivative of time-varying delay was greater than 1 has been adopted, its negative effect could be somewhat removed by introducing some free-weighting matrices. However, in [9, 12, 14, 21, 22], as for Lyapunov term $\int _{t-\tau (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s$ with $\dot{\tau }(t)\ge 1$, its derivative could be obtained as

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \int _{t-\tau (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s\right) \\&\quad =\varepsilon ^T(t)Q_1\varepsilon (t) -[1-\dot{\tau }(t)]\varepsilon ^T(t-\tau (t))Q_1\varepsilon (t-\tau (t))\ge 0. \end{aligned}$$

It can be easily checked that even the free matrices were used, some conservatism still could be induced when estimating its upper bound and, thus, it is urgent to propose some new effective techniques. Though the work [35] has given some preliminary discussions on this point, there still exists some room for the further improvements. On the other hand, although the works [9, 13] divided delay interval into some uniform ones, they could not fully represent the inherent feature when time-delay took the values in each subinterval during choosing the LKF and estimating its derivative. Meanwhile, in recent years, the issue on time-delay also has been concerned during studying the various Lur’e systems [6, 7, 9–15, 20–22, 27–30, 34, 36, 37, 41, 43, 44]. Therefore, it still remains important and urgent to put forward some novel techniques to achieve the much less conservative results on chaotic synchronization for delay Lur’e systems, which constitutes the main focus of this work.

In this paper, the master–slave synchronization for Lur’e systems with time-varying delay will be further studied. Two augmented Lyapunov–Krasovskii functionals will be chosen based on the introduction of some adjusting parameters. Through employing combined convex technique, some novel conditions will be proposed owing to that the derived criteria can be presented in terms of LMIs and their feasibility can be easily checked by resorting to recently developed algorithms. Finally, the efficiency and reduced conservatism of the derived criteria will be demonstrated by utilizing two numerical examples.

Notation

$\mathbf {R}^{n\times m}$ is the set of all $n\times m$ real matrices. For the symmetric matrices $X,Y,X>Y$ (respectively, $X\ge Y$) means that $X-Y>0$ $(X-Y\ge 0)$ is a positive-definite (respectively, positive-semidefinite) matrix; $A^T$ stands for the transpose of matrix A; I represents the identity matrix of an appropriate dimension; and $*$ in a symmetric matrix denoting the symmetric term $Y^T$.

2 Model Descriptions and Preliminaries

Consider the master–slave synchronization scheme of Lur’e systems using delay-state feedback control

$$\begin{aligned}&\mathcal {M}: \left\{ \begin{array}{l} \dot{x}(t)=Ax(t)+B{h}(Ex(t)) \\ p(t)= Fx(t) \end{array}\right. \end{aligned}$$

(1)

$$\begin{aligned}&\mathcal {S}: ~\left\{ \begin{array}{l} \dot{z}(t)=Az(t)+B{h}(Ez(t))+u(t) \\ q(t)= Fz(t) \end{array}\right. \end{aligned}$$

(2)

$$\begin{aligned}&\mathcal {C}:\begin{array}{l} ~u(t)= K\left[ p(t)-q(t)\right] +L\left[ p(t-\tau (t))-q(t-\tau (t))\right] , \end{array} \end{aligned}$$

(3)

where $\mathcal {M}$ is master system, $\mathcal {S}$ is slave system, and $\mathcal {C}$ is controller; here $x(t),z(t)\in \mathbf {R}^n$ are the state vectors and the output vectors $p(t),q(t)\in \mathbf {R}^k$; $A=[a_{ij}]_{n\times n},B=[b_{ij}]_{n\times n_1}$, $E=[e_{ij}]_{n_1\times n}=[E_1^T,E_2^T,\ldots ,E_{n_1}^T]^T,F=[f_{ij}]_{k\times n}$ are constant matrices; moreover, ${h}(\cdot )=[h_1(\cdot ),h_2(\cdot ),\ldots ,h_{n_1}(\cdot )]^T$ denotes the nonlinear vector-valued function which satisfies global Lipschitz condition.

The following assumptions will be utilized throughout this paper.

H 1

$\tau (t)$ denotes the time-varying delay satisfying

$$\begin{aligned}&0\le \tau (t)\le \tau _m, \quad \mu _0\le \dot{\tau }(t)\le \mu _m, \end{aligned}$$

(4)

and we set $\bar{\mu }_m=\mu _m-\mu _0$.

H 2

There exist the constants $\sigma ^+_i,\sigma ^-_i~(i=1,\ldots ,n_1)$ such that the nonlinear function ${h}_{i}(\cdot )$ in (1)–(2) satisfies

$$\begin{aligned}&\left[ {h}_{i}(\xi )-\sigma ^+_i\xi \right] \left[ {h}_{i}(\xi )-\sigma ^-_i\xi \right] \le 0, \quad \forall ~ \xi \in \mathbf R . \end{aligned}$$

(5)

Here, we introduce $\bar{\Sigma }={\mathrm {diag}}(\sigma _1^+,\ldots ,\sigma _{n_1}^+)$, $\Sigma ={\mathrm {diag}}(\sigma _1^-,\ldots ,\sigma _{n_1}^-)$, and

$$\begin{aligned} \Sigma _1= & {} {\mathrm {diag}}\left( \sigma ^+_1\sigma ^-_1,\ldots ,\sigma ^+_{n_1}\sigma ^-_{n_1}\right) ,~\\ \Sigma _2= & {} {\mathrm {diag}}\left( \frac{\sigma ^+_1+\sigma ^-_1}{2},\ldots ,\frac{\sigma ^+_{n_1}+\sigma ^-_{n_1}}{2}\right) . \end{aligned}$$

Remark 1

In assumption H1, as for both bounds on the derivative of time-varying delay $\tau (t)$, the value $\mu _0$ is always less than 0 and the value $\mu _m$ is always greater than 0, which can help to guarantee $\tau (t)$ to be variable and bounded in $[0,\tau _m]$.

Letting the synchronization error state be $\varepsilon (t) = x(t)-z(t)$, then the error system can be obtained as

$$\begin{aligned}&\dot{\varepsilon }(t)=(A-KF)\varepsilon (t)+Bf(E\varepsilon (t))-LF \varepsilon (t-\tau (t)), \end{aligned}$$

(6)

where $f(E\varepsilon (t))={h}(Ex(t))-{h}(Ez(t))$ and $f_{i}(0)=0~(i=1,\ldots ,n_1)$. For any $\xi \in \mathbf R ^n$, it follows from H2 that

$$\begin{aligned}&\left[ f_{i}(E_i\xi )-\sigma ^+_iE_i\xi \right] \left[ f_{i}(E_i\xi )-\sigma ^-_iE_i\xi \right] \le 0.~ \end{aligned}$$

(7)

The purpose of this paper is to study the master–slave synchronization for the systems (1)–(2) and design the controller (3), i.e., to find the controller gains K, L such that the error system (6) is absolutely stable.

In order to obtain the less conservative conditions, two lemmas will be presented.

Lemma 1

[22] For any constant matrix ${\mathrm {X}}\in {\mathbf {R}}^{n\times n},$ ${\mathrm {X}}={\mathrm {X}}^T\ge 0$, two scalars $h_2\ge h_1\ge 0$, such that the following integrations are well defined, then

$$\begin{aligned} -(h_{2}-h_{1})\int _{t-h_{2}}^{t-h_{1}} {x}^T(s){\mathrm {X}}{x}(s)\hbox {d}s\le & {} -\left( \int _{t-h_{2}}^{t-h_{1}} {x}(s)\hbox {d}s\right) ^T {\mathrm {X}}\left( \int _{t-h_{2}}^{t-h_{1}} {x}(s)\hbox {d}s\right) , \\ -(h_{2}-h_{1})\int _{t-h_{2}}^{t-h_{1}} \dot{x}^T(s){\mathrm {X}}\dot{x}(s)\hbox {d}s\le & {} -\left[ x(t-h_{2})-x(t-h_{1})\right] ^T {\mathrm {X}}[x(t-h_{2})\\&-x(t-h_{1})]. \end{aligned}$$

Lemma 2

[23] For any vectors $\zeta _1,\zeta _2,$ constant matrices R, S, and two real scalars $\alpha \ge 0,\beta \ge 0$ satisfying $\left[ \begin{array}{cc} R &{}S \\ *&{} R \end{array} \right] \ge 0$ and $\alpha +\beta =1$, the following inequality can be true,

$$\begin{aligned} -\frac{1}{\alpha }\zeta _{1}^{TR}\zeta _{1}-\frac{1}{\beta }\zeta _{2}^{TR}\zeta _{2}~\le ~ -\left[ \begin{array}{cc} \zeta _1 \\ \zeta _{2} \end{array}\right] ^{T}\left[ \begin{array}{cc} R &{} S \\ *&{} R \end{array}\right] \left[ \begin{array}{cc} \zeta _1 \\ \zeta _{2} \end{array}\right] . \end{aligned}$$

3 Master–Slave Synchronization Results

In this section, we firstly propose some denotations, which will be essential in the following proof and theorems.

As for time-varying delay $0\le \tau (t)\le \tau$ and two scalars $0\le \delta ,\gamma \le 1$, we denote

$$\begin{aligned}&\omega \doteq \delta \tau ,\quad \nu \doteq (1-\delta ){\tau }=\tau -\omega ,\quad \varphi (t)\doteq \gamma \tau (t),\quad \varphi \doteq \gamma \tau ,\quad \phi =\tau -\varphi ; \end{aligned}$$

(8)

$$\begin{aligned}&e_i=\left\{ \begin{array}{c} \left[ \begin{array}{ccccccccccc} 0_{n\times (i-1)n} &{} I_n &{} 0_{n\times (6-i)n} &{}0_{n\times n_1} &{} \quad 0_{n\times 4n} \end{array}\right] ,\quad 1 \le i\le 6,\\ \left[ \begin{array}{ccccccccccc} 0_{n_1\times 6n} &{} I_{n_1} &{}0_{n_1\times 4n} \end{array}\right] ,\quad i=7,\\ \left[ \begin{array}{ccccccccccc} 0_{n\times 6n} &{}0_{n\times n_1} &{}0_{n\times (i-1-6n-n_1)n} &{}I_n &{}0_{n\times (10n+n_1-i)n} \end{array}\right] ,\quad 8\le i\le 11. \end{array}\right. \end{aligned}$$

(9)

Then based on (6)–(8), we will construct the following Lyapunov–Krasovskii functional (LKF):

$$\begin{aligned}&V(\varepsilon _t) ~=~ V_1(\varepsilon _t)+V_2(\varepsilon _t)+V_3(\varepsilon _t), \end{aligned}$$

(10)

where

$$\begin{aligned} V_1(\varepsilon _t)= & {} \varepsilon ^T(t)P\varepsilon (t)+2\sum \limits _{i=1}^{n_1}q_i\int _0^{E_i\varepsilon (t)}\left[ {f}_{i}(s) -\sigma _i^-s\right] \hbox {d}s\\&+2\sum \limits _{i=1}^{n_1}r_i\int _0^{E_i\varepsilon (t)}\left[ \sigma _i^+s-{f}_{i}(s)\right] \hbox {d}s \\&+ \left[ \begin{array}{cc} \int _{t-\omega }^{t}\varepsilon (s)\hbox {d}s \\ \int _{t-\tau }^{t-\omega }\varepsilon (s)\hbox {d}s \end{array}\right] ^T\left[ \begin{array}{ccc} P_1 &{} P_2 \\ *&{} P_3 \end{array}\right] \left[ \begin{array}{cc} \int _{t-\omega }^{t}\varepsilon (s)\hbox {d}s \\ \int _{t-\tau }^{t-\omega }\varepsilon (s)\hbox {d}s \end{array}\right] ,\\ V_2(\varepsilon _t)= & {} \int _{t-\varphi (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s+ \int _{t-\tau }^{t-\varphi (t)}\varepsilon ^T(s)Q_2\varepsilon (s)\hbox {d}s\\&+\int _{t-\omega }^{t}\varepsilon ^T(s)Q_3\varepsilon (s)\hbox {d}s+ \int _{t-\tau }^{t-\omega }\varepsilon ^T(s)Q_4\varepsilon (s)\hbox {d}s,\\ V_3(\varepsilon _t)= & {} \int _{-\omega }^{0}\int _{t+\theta }^t \omega \left[ \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_2{\varepsilon }(s)\right] \hbox {d}s\hbox {d}\theta \\&+\int _{-\tau }^{-\omega }\int _{t+\theta }^t \nu \left[ \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)+{\varepsilon }^T(s)R_4{\varepsilon }(s)\right] \hbox {d}s\hbox {d}\theta \\&+\int _{-\varphi }^{0}\int _{t+\theta }^t \varphi \dot{\varepsilon }^T(s)R_5\dot{\varepsilon }(s)\hbox {d}s\hbox {d}\theta +\int _{-\tau }^{-\varphi }\int _{t+\theta }^t \phi \dot{\varepsilon }^T(s)R_6\dot{\varepsilon }(s)\hbox {d}s\hbox {d}\theta \end{aligned}$$

with $n\times n$ matrices $P>0, Q_i>0~(i=1,2,3,4),R_i>0~(i=1,2,3,4,5,6)$, $2n\times 2n$ matrix $\left[ \begin{array}{ccc} P_1 &{} P_2 \\ *&{} P_3 \end{array}\right] >0$, and $n_1\times n_1$ diagonal matrices $Q={\mathrm {diag}}(q_1,\ldots ,q_{n_1})>0,R={\mathrm {diag}}(r_1,\ldots ,r_{n_1})>0$.

In what follows, we will give one novel delay-dependent stability criterion for the error system (6).

Theorem 1

For any given scalars $\tau \ge 0,\mu _0,\mu _m,1\ge \delta ,\gamma \ge 0$, the system (6) satisfying (4) and (7) has one equilibrium point and is absolutely stable, if there exist $n\times n$ matrices $P>0, P_1>0,P_2,P_3>0,Q_i>0~(i=1,2,3,4),R_j>0,Z_j~(i=1,2,3,4,5),R_6>0,N_1,N_2$ making $\left[ \begin{array}{ccc} P_1 &{} \quad P_2 \\ *&{} \quad P_3 \end{array}\right] >0,\left[ \begin{array}{ccc} R_j &{} \quad Z_j \\ *&{} \quad R_j \end{array}\right] >0~(j=1,2,3,4,5)$, $n_1\times n_1$ diagonal matrices $Q>0,R>0,U>0$ such that for $i=1,2,$ the matrix inequalities in (11)–(12) hold

$$\begin{aligned}&\varOmega +\left[ e^T_1Z_1e_6+e^T_6Z_1^Te_1\right] +\left[ e^T_1(R_1-Z_1)e_2+e^T_2(R_1-Z_1^T)e_1\right] \nonumber \\&\quad +\,\left[ e^T_2(R_1-Z_1)e_6+e^T_6(R_1-Z_1^T)e_2\right] \nonumber \\&\quad +\,\left[ e^T_3R_3e_6+e^T_6R_3e_3\right] -\left[ e^T_8Z_2e_9+e^T_9Z_2^Te_8\right] \nonumber \\&\quad +\,\,e^T_2(Z^T_1+Z_1-2R_1)e_2-e^T_9R_2e_9+\left[ e^T_9P_1e_1+e^T_1P_1e_9\right] \nonumber \\&\quad +\,\left[ e^T_6(P_2^T-P_1)e_9+e^T_9(P_2-P_1)e_6\right] \nonumber \\&\quad -\,\left[ e^T_3P_2^Te_9+e^T_9P_2e_3\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(11)

$$\begin{aligned}&\varOmega +\,\left[ e^T_1R_1e_6+e^T_6R_1e_1\right] +\left[ e^T_2(R_3-Z_3)e_3+e^T_3(R_3-Z_3^T)e_2\right] \nonumber \\&\quad +\,\left[ e^T_2(R_3-Z_3^T)e_6+e^T_6(R_3-Z_3)e_2\right] \nonumber \\&\quad +\,\left[ e^T_3Z_3^Te_6+e^T_6Z_3e_3\right] -\left[ e^T_9Z_4e_{10}+e^T_{10}Z_4^Te_{9}\right] \nonumber \\&\quad +\,e^T_2(Z^T_3+Z_3-2R_3)e_2-e^T_9R_4e_9+\left[ e^T_9P_2^Te_1+e^T_1P_2e_9\right] \nonumber \\&\quad +\,\left[ e^T_6(P_3-P_2)e_9+e^T_9(P_3-P_2^T)e_6\right] \nonumber \\&\quad -\,\left[ e^T_3P_3e_9+e^T_9P_3e_3\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(12)

where $e_i~(i=1,\ldots ,9)$ are defined in (9) and

$$\begin{aligned}&\varOmega =\left[ \begin{array}{cccccccccccccccc} \varOmega _{11} &{} \quad -N_1^TLF &{} 0 &{} \quad \varOmega _{14} &{} \quad Z_5 &{} 0 &{} \quad \varOmega _{17} &{} \quad P_1 &{} \quad 0 &{} \quad P_2 &{} \quad \varOmega _{1,11} \\ *&{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -(LF)^TN_2\\ *&{} \quad *&{} \quad \varOmega _{33} &{} \quad 0 &{} \quad 0 &{} \quad R_6 &{} \quad 0 &{} \quad -P_2^T &{} \quad 0 &{} \quad -P_3 &{} 0\\ *&{} \quad *&{} \quad *&{} \quad \varOmega _{44} &{} \quad \varOmega _{45} &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad -R_5 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad \varOmega _{66} &{} \quad 0 &{} \quad \varOmega _{68} &{} \quad 0 &{} \quad \varOmega _{6,10} &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -U &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad \varOmega _{7,11} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -R_2 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -R_4 &{} 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad \varOmega _{11,11} \\ \end{array}\right] \end{aligned}$$

with

$$\begin{aligned} \varOmega _{11}= & {} -R_1+Q_1+Q_3+\omega ^2R_2+\nu ^2R_4-R_5+N^T_1(A-KF)+(A-KF)^TN_1\\&-E^TU\Sigma _1E, \quad \varOmega _{14}=R_5-Z_5,\\ \varOmega _{17}= & {} N^T_1B+E^TU\Sigma _2, \varOmega _{1,11}=P+E^T({{\bar{\Sigma }R}}-{{\Sigma }} Q)E-N^T_1+(A-KF)^TN_2, \\ \varOmega _{33}= & {} -Q_2-Q_4-R_3-R_6,\quad \varOmega _{44}=(1-\gamma \mu _m)Q_1+(\gamma \mu _0-1)Q_2\\&+\,Z_5+Z_5^T-2R_5, \\ \varOmega _{45}= & {} R_5-Z_5,\quad \varOmega _{66}=Q_4-Q_3-R_1-R_3-R_6,\\ \varOmega _{68}= & {} P^T_2-P_1,\quad \varOmega _{6,10}=P_3-P_2,\\ \varOmega _{7,11}= & {} QE+B^TN_2-RE,\quad \varOmega _{11,11}=\omega ^2R_1+\nu ^2R_3+\varphi ^2R_5\\&+\,\phi ^2R_6-N^T_2-N_2. \end{aligned}$$

Proof

Firstly, for any appropriately dimensional matrices $N_i~(i=1,2)$ and diagonal one $U\ge 0$, it follows from (6) to (7) and methods in [9, 22, 32] that

$$\begin{aligned} 0= & {} 2\left[ \varepsilon ^T(t)N_1^T+\dot{\varepsilon }^T(t)N_2^T\right] \left[ -\dot{\varepsilon }(t)+(A-KF)\varepsilon (t)\right. \nonumber \\&\left. +Bf(E\varepsilon (t))-LF \varepsilon (t-\tau (t))\right] , \end{aligned}$$

(13)

$$\begin{aligned} 0\le & {} -\left[ \varepsilon ^T(t)E^TU\Sigma _1E\varepsilon (t)-2\varepsilon ^T(t)E^TU\Sigma _2f(E\varepsilon (t))+f^T(E\varepsilon (t))Uf(E\varepsilon (t))\right] .\nonumber \\ \end{aligned}$$

(14)

Now together with the denotations (8) and LKF (10), the derivative of ${V}_i(\varepsilon _t)~(i=1,2,3)$ along the system (6) can be directly computed out as

$$\begin{aligned} \dot{V}_1(\varepsilon _t)= & {} 2\varepsilon ^T(t)P\dot{\varepsilon }(t) +2\left[ {f}^T(E\varepsilon (t)) -\varepsilon ^T(t)E^T\Sigma \right] QE\dot{\varepsilon }(t)\nonumber \\&+\,2\left[ \varepsilon ^T(t)E^T\bar{\Sigma } -{f}^T(\varepsilon (t))\right] RE\dot{\varepsilon }(t)\nonumber \\&+\,\left[ \begin{array}{cc} \int _{t-\omega }^{t}\varepsilon (s)\hbox {d}s \\ \int _{t-\tau }^{t-\omega }\varepsilon (s)\hbox {d}s \end{array}\right] ^T\left( 2\cdot \left[ \begin{array}{cc} P_1 &{} \quad P_2 \\ *&{} \quad P_3 \end{array}\right] \right) \left[ \begin{array}{cc} \varepsilon (t)-\varepsilon (t-\omega ) \\ \varepsilon (t-\omega )-\varepsilon (t-\tau ) \end{array}\right] , \end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_2(\varepsilon _t)= & {} \varepsilon ^T(t)Q_1\varepsilon (t)-\left[ 1-\gamma \dot{\tau }(t)\right] \varepsilon ^T(t-\varphi (t))Q_1\varepsilon (t-\varphi (t))\nonumber \\&+ \left[ 1-\gamma \dot{\tau }(t)\right] \varepsilon ^T(t-\varphi (t))Q_2\varepsilon (t-\varphi (t)) \nonumber \\&-\,\varepsilon ^T(t-\tau )Q_2\varepsilon (t-\tau )+ \varepsilon ^T(t)Q_3\varepsilon (t)-\varepsilon ^T(t-\omega )Q_3\varepsilon (t-\omega )\nonumber \\&+\,\varepsilon ^T(t-\omega )Q_4\varepsilon (t-\omega ) -\varepsilon ^T(t-\tau )Q_4\varepsilon (t-\tau )\nonumber \\= & {} \varepsilon ^T(t)Q_1\varepsilon (t)-\varepsilon ^T(t-\tau )Q_2\varepsilon (t-\tau )\nonumber \\&+\,\varepsilon ^T(t)Q_3\varepsilon (t)-\varepsilon ^T(t-\omega )(Q_3-Q_4)\varepsilon (t-\omega )-\varepsilon ^T(t-\tau )Q_4\varepsilon (t-\tau ) \nonumber \\&+\,\varepsilon ^T(t-\varphi (t))\left[ (1-\gamma \mu _m)Q_1+(\gamma \mu _0-1)Q_2\right] \varepsilon (t-\varphi (t))\nonumber \\&+\,\varepsilon (t-\varphi (t))\gamma [\mu _m-\dot{\tau }(t)]Q_1\varepsilon (t-\varphi (t))\nonumber \\&+\,\varepsilon ^T(t-\varphi (t))\gamma [\dot{\tau }(t)-\mu _0]Q_2\varepsilon (t-\varphi (t)), \end{aligned}$$

(16)

$$\begin{aligned} \dot{V}_3(\varepsilon _t)= & {} \left[ \omega ^2\dot{\varepsilon }^T(t)R_1\dot{\varepsilon }(t)+ \omega ^2{\varepsilon }^T(t)R_2{\varepsilon }(t)\right] \nonumber \\&-\,\int _{t-\omega }^t \omega \left[ \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_2{\varepsilon }(s)\right] \hbox {d}s \nonumber \\&+\,\left[ \nu ^2\dot{\varepsilon }^T(t)R_3\dot{\varepsilon }(t)+ \nu ^2{\varepsilon }^T(t)R_4{\varepsilon }(t)\right] \nonumber \\&- \int _{t-\tau }^{t-\omega } \nu \left[ \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_4{\varepsilon }(s)\right] \hbox {d}s\nonumber \\&+\,\left[ \varphi ^2\dot{\varepsilon }^T(t)R_5\dot{\varepsilon }(t)+\phi ^2\dot{\varepsilon }^T(t)R_6\dot{\varepsilon }(t)\right] \nonumber \\&-\,\int _{t-\varphi }^{t} \varphi \dot{\varepsilon }^T(s)R_5\dot{\varepsilon }(s)\hbox {d}s - \int _{t-\tau }^{t-\varphi } \phi \dot{\varepsilon }^T(s)R_6\dot{\varepsilon }(s)\hbox {d}s. \end{aligned}$$

(17)

In what follows, as for (17), we will deal with two cases for delay subintervals, i.e., $[0,\omega ]\cup [\omega ,\tau ]=[0,\tau ]$. $\square$

Case I When $\tau (t)\in [0,\omega ]=[0,\delta \tau ]$, based on (8) and Lemmas 1–2 we can derive the following inequalities:

$$\begin{aligned} -\int _{t-\omega }^t \omega \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s= & {} -\omega \int _{t-\tau (t)}^t \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s -\omega \int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s \nonumber \\= & {} -\frac{\omega }{\tau (t)}\cdot \tau (t)\int _{t-\tau (t)}^t \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s\nonumber \\&-\frac{\omega }{\omega -\tau (t)}\cdot [\omega -\tau (t)]\int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s \nonumber \\\le & {} -\frac{\omega }{\tau (t)}\left( \int _{t-\tau (t)}^t \dot{\varepsilon }(s)\hbox {d}s\right) ^T R_1\left( \int _{t-\tau (t)}^t \dot{\varepsilon }(s)\hbox {d}s\right) \nonumber \\&- \frac{\omega }{\omega -\tau (t)} \left( \int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s\right) ^T R_1\left( \int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s\right) \nonumber \\\le & {} -\left[ \begin{array}{cc} \int _{t-\tau (t)}^t \dot{\varepsilon }(s)\hbox {d}s \\ \int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s \end{array}\right] ^T \left[ \begin{array}{cc} R_1 &{} \quad Z_1 \\ *&{} \quad R_1 \end{array}\right] \left[ \begin{array}{cc} \int _{t-\tau (t)}^t \dot{\varepsilon }(s)\hbox {d}s \\ \int _{t-\omega }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s \end{array}\right] \nonumber \\= & {} -\left[ {\varepsilon }(t)-{\varepsilon }(t-\tau (t))\right] ^TR_1\left[ {\varepsilon }(t)-{\varepsilon }(t-\tau (t))\right] \nonumber \\&-\left[ {\varepsilon }(t)-{\varepsilon }(t-\tau (t))\right] ^T (2Z_1)\left[ {\varepsilon }(t-\tau (t))-{\varepsilon }(t-\omega )\right] ^T \nonumber \\&-\left[ {\varepsilon }(t-\tau (t))-{\varepsilon }(t-\omega )\right] ^TR_1\left[ {\varepsilon }(t-\tau (t))-{\varepsilon }(t-\omega )\right] , \end{aligned}$$

(18)

$$\begin{aligned} -\int _{t-\omega }^t \omega {\varepsilon }^T(s)R_2{\varepsilon }(s)\hbox {d}s\le & {} -\left( \int _{t-\tau (t)}^t {\varepsilon }(s)\hbox {d}s\right) ^T R_2\left( \int _{t-\tau (t)}^t {\varepsilon }(s)\hbox {d}s\right) \nonumber \\&-\left( \int _{t-\tau (t)}^t {\varepsilon }(s)\hbox {d}s\right) ^T (2Z_2)\left( \int _{t-\omega }^{t-\tau (t)}{\varepsilon }(s)\hbox {d}s\right) \nonumber \\&-\left( \int _{t-\omega }^{t-\tau (t)} {\varepsilon }(s)\hbox {d}s\right) ^T R_2\left( \int _{t-\omega }^{t-\tau (t)} {\varepsilon }(s)\hbox {d}s\right) , \end{aligned}$$

(19)

$$\begin{aligned} -\int _{t-\tau }^{t-\omega } \nu \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)\hbox {d}s\le & {} -\left[ {\varepsilon }(t-\omega )-{\varepsilon }(t-\tau )\right] ^TR_3\left[ {\varepsilon }(t-\omega )-{\varepsilon }(t-\tau )\right] , \end{aligned}$$

(20)

$$\begin{aligned} -\int _{t-\tau }^{t-\omega } \nu {\varepsilon }^T(s)R_4{\varepsilon }(s)\hbox {d}s\le & {} -\left( \int _{t-\tau }^{t-\omega } {\varepsilon }(s) \hbox {d}s\right) ^T R_4\left( \int _{t-\tau }^{t-\omega } {\varepsilon }(s) \hbox {d}s\right) , \end{aligned}$$

(21)

$$\begin{aligned} -\int _{t-\varphi }^{t} \varphi \dot{\varepsilon }^T(s)R_5\dot{\varepsilon }(s)\hbox {d}s\le & {} -\left[ {\varepsilon }(t)-{\varepsilon }(t-\varphi (t))\right] ^TR_5\left[ {\varepsilon }(t)-{\varepsilon }(t-\varphi (t))\right] \nonumber \\&-\left[ {\varepsilon }(t)-{\varepsilon }(t-\varphi (t))\right] ^T(2Z_5)\left[ {\varepsilon }(t-\varphi (t))-{\varepsilon }(t-\varphi )\right] ^T \nonumber \\&-\left[ {\varepsilon }(t-\varphi (t))-{\varepsilon }(t-\varphi )\right] ^TR_5\left[ {\varepsilon }(t-\varphi (t))-{\varepsilon }(t-\varphi )\right] , \end{aligned}$$

(22)

$$\begin{aligned} - \int _{t-\tau }^{t-\varphi } \phi \dot{\varepsilon }^T(s)R_6\dot{\varepsilon }(s)\hbox {d}s\le & {} -\left[ {\varepsilon }(t-\varphi )-{\varepsilon }(t-\tau )\right] ^TR_6\left[ {\varepsilon }(t-\varphi )-{\varepsilon }(t-\tau )\right] . \end{aligned}$$

(23)

Now together with the denotations (8)–(9) and combining with the terms (13)–(23), we can easily derive

$$\begin{aligned}&\dot{V}(\varepsilon _t) ~\le ~ \xi ^T(t) \varXi _1(t) \xi (t), \end{aligned}$$

(24)

where

$$\begin{aligned} \varXi _1(t)= & {} \varOmega +\left[ e^T_1Z_1e_6+e^T_6Z_1^Te_1\right] +\left[ e^T_1(R_1-Z_1)e_2+e^T_2(R_1-Z_1^T)e_1\right] \\&+\left[ e^T_2\left( R_1-Z_1\right) e_6+e^T_6(R_1-Z_1^T)e_2\right] \\&+\left[ e^T_3R_3e_6+e^T_6R_3e_3\right] -\left[ e^T_8Z_2e_9+e^T_9Z_2^Te_8\right] \\&+e^T_2\left( Z^T_1+Z_1-2R_1\right) e_2-e^T_9R_2e_9\\&+\left[ e^T_9P_1e_1+e^T_1P_1e_9\right] -\left[ e^T_3P_2^Te_9+e^T_9P_2e_3\right] \\&+\left[ e^T_6(P_2^T-P_1)e_9+e^T_9\left( P_2-P_1\right) e_6\right] \\&+\gamma \left[ \mu _m-\dot{\tau }(t)\right] e^T_4Q_1e_4+\gamma \left[ \dot{\tau }(t)-\mu _0\right] e^T_4Q_2e_4,\\ \xi ^T(t)= & {} \Bigg [\varepsilon ^T(t)\quad \varepsilon ^T(t-\tau (t))\quad \varepsilon ^T(t-\tau )\quad \varepsilon ^T(t-\varphi (t))\quad \varepsilon ^T(t-\varphi )\quad \varepsilon ^T(t-\omega )\quad f^T(E\varepsilon (t)) \\&\qquad \left( \int _{t-\tau (t)}^{t}{\varepsilon }(s) \hbox {d}s\right) ^T\left( \int _{t-\omega }^{t-\tau (t)} {\varepsilon }(s) \hbox {d}s\right) ^T \quad \left( \int _{t-\tau }^{t-\omega } {\varepsilon }(s) \hbox {d}s\right) ^T\quad \dot{\varepsilon }^T(t)\Bigg ] \end{aligned}$$

with $\varOmega$ defined in (11)–(12). Then based on convex combination technique, the inequalities (11) can guarantee $\varXi _1(t)<0$ to be true since $\varXi _1(t)\mid _{\dot{\tau }(t)=\mu _0}<0$ and $\varXi _1(t)\mid _{\dot{\tau }(t)=\mu _m}<0$ hold simultaneously.

Case II When $\tau (t)\in [\omega ,\tau ]=[\delta \tau ,\tau ]$, by using Lemmas 1–2 we also can derive the following inequalities:

$$\begin{aligned} -\int _{t-\omega }^t \omega \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)\hbox {d}s\le & {} -\left[ {\varepsilon }(t)-{\varepsilon }(t-\omega )\right] ^TR_1\left[ {\varepsilon }(t)-{\varepsilon }(t-\omega )\right] , \end{aligned}$$

(25)

$$\begin{aligned} -\int _{t-\omega }^t \omega {\varepsilon }^T(s)R_2{\varepsilon }(s)\hbox {d}s\le & {} -\left( \int _{t-\omega }^{t} {\varepsilon }(s) \hbox {d}s\right) ^T R_2\left( \int _{t-\omega }^{t} {\varepsilon }(s) \hbox {d}s\right) , \end{aligned}$$

(26)

$$\begin{aligned} -\int _{t-\tau }^{t-\omega } \nu \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)\hbox {d}s= & {} -\nu \cdot \frac{\tau (t)-\omega }{\tau (t)-\omega }\int _{t-\tau (t)}^{t-\omega } \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)\hbox {d}s\nonumber \\&-\nu \cdot \frac{\tau -\tau (t)}{\tau -\tau (t)}\int _{t-\tau }^{t-\tau (t)} \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)\hbox {d}s \nonumber \\\le & {} -\frac{\nu }{\tau (t)-\omega }\left( \int _{t-\tau (t)}^{t-\omega } \dot{\varepsilon }(s)\hbox {d}s\right) ^T R_3\left( \int _{t-\tau (t)}^{t-\omega } \dot{\varepsilon }(s)\hbox {d}s\right) \nonumber \\&- \frac{\nu }{\omega -\tau (t)} \left( \int _{t-\tau }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s\right) ^T R_3\left( \int _{t-\tau }^{t-\tau (t)} \dot{\varepsilon }(s)\hbox {d}s\right) \nonumber \\\le & {} -\left[ \begin{array}{cc} \int _{t-\tau (t)}^{t-\omega }&{} \dot{\varepsilon }(s)\hbox {d}s \\ \int _{t-\tau }^{t-\tau (t)} &{} \dot{\varepsilon }(s)\hbox {d}s \end{array}\right] ^T \left[ \begin{array}{cc} R_3 &{} Z_3 \\ *&{} R_3 \end{array}\right] \left[ \begin{array}{cc} \int _{t-\tau (t)}^{t-\omega }&{} \dot{\varepsilon }(s)\hbox {d}s \\ \int _{t-\tau }^{t-\tau (t)} &{} \dot{\varepsilon }(s)\hbox {d}s \end{array}\right] \nonumber \\= & {} -\left[ {\varepsilon }(t-\omega )-{\varepsilon }(t-\tau (t))\right] ^TR_3[{\varepsilon }(t-\omega )\nonumber \\&-{\varepsilon }(t-\tau (t))] \nonumber \\&-\left[ {\varepsilon }(t-\omega )-{\varepsilon }(t-\tau (t))\right] ^T (2Z_3)[{\varepsilon }(t-\tau (t))\nonumber \\&-{\varepsilon }(t-\tau )] \nonumber \\&-\left[ {\varepsilon }(t-\tau (t))-{\varepsilon }(t-\tau )\right] ^TR_3[{\varepsilon }(t-\tau (t))\nonumber \\&-{\varepsilon }(t-\tau )],\end{aligned}$$

(27)

$$\begin{aligned} -\int _{t-\tau }^{t-\omega } \nu {\varepsilon }^T(s)R_4{\varepsilon }(s)\hbox {d}s\le & {} -\left( \int _{t-\tau (t)}^{t-\omega } {\varepsilon }(s)\hbox {d}s\right) ^T R_4\left( \int _{t-\tau (t)}^{t-\omega } {\varepsilon }(s)\hbox {d}s\right) \nonumber \\&-\left( \int _{t-\tau (t)}^{t-\omega } {\varepsilon }(s)\hbox {d}s\right) ^T (2Z_4)\left( \int _{t-\tau }^{t-\tau (t)}{\varepsilon }(s)\hbox {d}s\right) \nonumber \\&-\left( \int _{t-\tau }^{t-\tau (t)} {\varepsilon }(s)\hbox {d}s\right) ^T R_4\left( \int _{t-\tau }^{t-\tau (t)} {\varepsilon }(s)\hbox {d}s\right) . \end{aligned}$$

(28)

Combining the terms (13)–(17), (22), (23) with (25)–(28), we can easily obtain

$$\begin{aligned}&\dot{V}(\varepsilon _t) ~ \le ~\zeta ^T(t)\varXi _2(t)\zeta (t). \end{aligned}$$

(29)

where

$$\begin{aligned} \varXi _2(t)= & {} \varOmega +\left[ e^T_1R_1e_6+e^T_6R_1e_1\right] +\left[ e^T_2\left( R_3-Z_3\right) e_3+e^T_3(R_3-Z_3^T)e_2\right] \\&+\,\left[ e^T_2(R_3-Z_3^T)e_6+e^T_6\left( R_3-Z_3\right) e_2\right] \\&+\,\left[ e^T_3Z_3^Te_6+e^T_6Z_3e_3\right] -\left[ e^T_9Z_4e_{10}+e^T_{10}Z_4^Te_{9}\right] \\&+\,e^T_2\left( Z^T_3+Z_3-2R_3\right) e_2-e^T_9R_4e_9\\&+\,\left[ e^T_9P_2^Te_1+e^T_1P_2e_9\right] +\left[ e^T_6 \left( P_3-P_2\right) e_9+e^T_9(P_3-P_2^T)e_6\right] \\&-\,\left[ e^T_3P_3e_9+e^T_9P_3e_3\right] \\&+\,\gamma [\mu _m-\dot{\tau }(t)]e^T_4Q_1e_4+\gamma [\dot{\tau }(t)-\mu _0]e^T_4Q_2e_4,\\ \zeta ^T(t)= & {} \Bigg [\varepsilon ^T(t)\quad \varepsilon ^T(t-\tau (t))\quad \varepsilon ^T(t-\tau )\quad \varepsilon ^T(t-\varphi (t))\quad \varepsilon ^T(t-\varphi )\quad \varepsilon ^T(t-\omega )\\&\qquad f^T(E\varepsilon (t))\quad \left( \int _{t-\omega }^{t} {\varepsilon }(s) \hbox {d}s\right) ^T\left( \int _{t-\tau (t)}^{t-\omega } {\varepsilon }(s) \hbox {d}s\right) ^T ~~\\&\qquad \left( \int _{t-\tau }^{t-\tau (t)} {\varepsilon }(s) \hbox {d}s\right) ^T~~\dot{\varepsilon }^T(t)\Bigg ] \end{aligned}$$

with $\varOmega ,e_i~(i=1,\ldots ,9)$ defined in (9) and (11)–(12), respectively. Similar to Case I, through using convex combination technique, the inequalities (12) can guarantee $\varXi _2(t)<0$ to be true since $\varXi _2(t)\mid _{\dot{\tau }(t)=\mu _0}<0$ and $\varXi _2(t)\mid _{\dot{\tau }(t)=\mu _m}<0$ hold simultaneously. Therefore, together with the Cases I–II, it can be concluded that as the conditions (11)–(12) hold, the dynamics of Lur’e system (6) is absolutely stable.

Now based on Theorem 1, we are ready to address the issue on controller design (3). In order to show the design of the controller gain matrices K, L, a simple transformation is made to obtain the following theorem.

Theorem 2

For any given scalars $\tau \ge 0,\mu _0,\mu _m,1\ge \delta ,\gamma \ge 0,\upsilon >0$, the systems described by (1)–(3) achieve the master–slave synchronization, if there exist $n\times n$ matrices $P>0, P_1>0,P_2,P_3>0,Q_i>0~(i=1,2,3,4),R_j>0,Z_j~(j=1,2,3,4,5),R_6>0,N_1$ making $\left[ \begin{array}{ccc} P_1 &{} \quad P_2 \\ *&{} \quad P_3 \end{array}\right] >0,\left[ \begin{array}{ccc} R_j &{} \quad Z_j \\ *&{} \quad R_j \end{array}\right] >0~(j=1,2,3,4,5)$, $n_1\times n_1$ diagonal matrices $Q>0,$ $R>0,U>0$, and $n\times k$ matrices $F_i~(i=1,2)$ such that for $i=1,2,$ the LMIs in (30)–(31) hold

$$\begin{aligned}&\varXi +\left[ e^T_1Z_1e_6+e^T_6Z_1^Te_1\right] +\left[ e^T_1\left( R_1-Z_1\right) e_2+e^T_2 (R_1-Z_1^T)e_1\right] \nonumber \\&\quad +\,\left[ e^T_2\left( R_1-Z_1\right) e_6+e^T_6(R_1-Z_1^T)e_2\right] \nonumber \\&\quad +\, \left[ e^T_3R_3e_6+e^T_6R_3e_3\right] -\left[ e^T_8Z_2e_9+e^T_9Z_2^Te_8\right] \nonumber \\&\quad +\,e^T_2\left( Z^T_1+Z_1-2R_1\right) e_2-e^T_9R_2e_9\nonumber \\&\quad +\,\left[ e^T_9P_1e_1+e^T_1P_1e_9\right] -\left[ e^T_3P_2^Te_9+e^T_9P_2e_3\right] \nonumber \\&\quad +\,\left[ e^T_6(P_2^T-P_1)e_9+e^T_9\left( P_2-P_1\right) e_6\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(30)

$$\begin{aligned}&\varXi +\left[ e^T_1R_1e_6+e^T_6R_1e_1\right] +\left[ e^T_2\left( R_3-Z_3\right) e_3+e^T_3(R_3-Z_3^T)e_2\right] \nonumber \\&\quad +\,\left[ e^T_2(R_3-Z_3^T)e_6+e^T_6\left( R_3-Z_3\right) e_2\right] \nonumber \\&\quad +\,\left[ e^T_3Z_3^Te_6+e^T_6Z_3e_3\right] -\left[ e^T_9Z_4e_{10}+e^T_{10}Z_4^Te_{9}\right] \nonumber \\&\quad +\,e^T_2\left( Z^T_3+Z_3-2R_3\right) e_2-e^T_9R_4e_9\nonumber \\&\quad -\,\left[ e^T_9P_2^Te_1+e^T_1P_2e_9\right] +\left[ e^T_6\left( P_3-P_2\right) e_9+e^T_9(P_3-P_2^T)e_6\right] \nonumber \\&\quad -\,\left[ e^T_3P_3e_9+e^T_9P_3e_3\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(31)

where $e_i~(i=1,\ldots ,9)$ are defined in (9) and

$$\begin{aligned} \varXi =\left[ \begin{array}{cccccccccccccccc} \varXi _{11} &{} \quad \varXi _{12} &{} \quad 0 &{} \quad \varXi _{14} &{} \quad Z_5 &{} \quad 0 &{} \quad \varXi _{17} &{} \quad P_1 &{} \quad 0 &{} \quad P_2 &{} \quad \varXi _{1,11} \\ *&{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -\upsilon F^TF_2^T\\ *&{} \quad *&{} \quad \varXi _{33} &{} \quad 0 &{} \quad 0 &{} \quad R_6 &{} \quad 0 &{} \quad -P_2^T &{} \quad 0 &{} \quad -P_3 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad \varXi _{44} &{} \quad \varXi _{45} &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad \varXi _{55} &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad \varXi _{66} &{} \quad 0 &{} \quad \varXi _{68} &{} \quad 0 &{} \quad \varXi _{6,10} &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -U &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad \varXi _{7,11} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -R_2 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -R_4 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad \varXi _{11,11} \\ \end{array}\right] \end{aligned}$$

with

$$\begin{aligned} \varXi _{11}= & {} Q_1+Q_3+\omega ^2R_2+\nu ^2R_4-R_5+N^T_1A-F_1F+A^TN_1-F^TF_1^T\\&-\,E^TU\Sigma _1E-R_1, \quad \varXi _{12}=-F_2F,\\ \varXi _{14}= & {} R_{5}-Z_{5},\varXi _{17}=N^T_{1B}+E^{TU}\Sigma _2,\quad \varXi _{1,11}=P+E^T({{\bar{\Sigma }R}}-{{\Sigma }} Q)E\\&-\,N^T_1+\upsilon A^TN_1-\upsilon F^TF^T_1,\\ \varXi _{33}= & {} -Q_2-Q_4-R_3-R_6,~~\varXi _{44}=-2R_5+(1-\gamma \mu _m)Q_1\\&+\,(\gamma \mu _0-1)Q_2+Z_5+Z_5^T,\\ \varXi _{45}= & {} R_5-Z_5,~~ \varXi _{55}=-R_5 ,\quad \varXi _{66}=Q_4-Q_3-R_1-R_3-R_6, \\ \varXi _{68}= & {} P^T_2-P_1, ~~\varXi _{6,10}=P_3-P_2,~~\varXi _{7,11}=-RE+QE+\upsilon B^TN_1,\\ \varXi _{11,11}= & {} -\upsilon N^T_1-\upsilon N_1+\omega ^2R_1+\nu ^2R_3+\varphi ^2R_5. \end{aligned}$$

Moreover, the estimation gains can be derived as $K=N_1^{-T} F_1$ and $L=N_1^{-T} F_2$.

Proof

Based on Theorem 1, replacing $N_2$ in (11)–(12) by the term $\upsilon N_1$ and setting $F_1=N_1^{T} K,F_2=N_1^{T}L$, it is obvious to derive the theorem. The detailed proof is straightforward and omitted here. $\square$

In many present works, the lower bound $\mu _0$ of time-varying delay has not been involved, i.e., $\dot{\tau }(t)\le \mu _m$, such as [6, 10–12, 14, 15, 20, 21, 27, 28, 33, 34, 36, 41, 43]. Thus, as for this case, we can derive the following corollary.

Corollary 1

For any given scalars $\tau \ge 0,\mu _m,1\ge \delta ,\gamma \ge 0,\upsilon >0$, the systems described by (1)–(3) achieve the master–slave synchronization, if there exist $n\times n$ matrices $P>0, P_1>0,P_2,P_3>0,Q_i>0~(i=1,2,3,4),R_j>0,Z_j~(j=1,2,3,4,5),R_6>0,N_1$ making $\left[ \begin{array}{ccc} P_1 &{} P_2 \\ *&{} P_3 \end{array}\right] >0,\left[ \begin{array}{ccc} R_j &{} \quad Z_j \\ *&{} \quad R_j \end{array}\right] >0~(j=1,2,3,4,5)$, $n_1\times n_1$ diagonal matrices $Q>0,$ $R>0,U>0$, and $n\times k$ matrices $F_i~(i=1,2)$ such that the LMIs in (32)–(33) hold

$$\begin{aligned}&\varXi +\left[ e^T_1Z_1e_6+e^T_6Z_1^Te_1\right] +\left[ e^T_1\left( R_1-Z_1\right) e_2+e^T_2 (R_1-Z_1^T)e_1\right] \nonumber \\&\quad +\,\left[ e^T_2\left( R_1-Z_1\right) e_6+e^T_6(R_1-Z_1^T)e_2\right] \nonumber \\&\quad +\left[ e^T_3R_3e_6+e^T_6R_3e_3\right] -\left[ e^T_8Z_2e_9+e^T_9Z_2^Te_8\right] \nonumber \\&\quad +\,e^T_2\left( Z^T_1+Z_1-2R_1\right) e_2-e^T_9R_2e_9\nonumber \\&\quad +\,\left[ e^T_9P_1e_1+e^T_1P_1e_9\right] -\left[ e^T_3P_2^Te_9+e^T_9P_2e_3\right] \nonumber \\&\quad +\,\left[ e^T_6(P_2^T-P_1)e_9+e^T_9\left( P_2-P_1\right) e_6\right] <0, \end{aligned}$$

(32)

$$\begin{aligned}&\varXi +[e^T_1R_1e_6+e^T_6R_1e_1]+[e^T_2(R_3-Z_3)e_3+e^T_3(R_3-Z_3^T)e_2]\nonumber \\&\quad +\,[e^T_2(R_3-Z_3^T)e_6+e^T_6(R_3-Z_3)e_2]\nonumber \\&\quad +\,[e^T_3Z_3^Te_6+e^T_6Z_3e_3]-[e^T_9Z_4e_{10}+e^T_{10}Z_4^Te_{9}]\nonumber \\&\quad +\,e^T_2(Z^T_3+Z_3-2R_3)e_2-e^T_9R_4e_9\nonumber \\&\quad +\,[e^T_9P_2^Te_1+e^T_1P_2e_9]+[e^T_6(P_3-P_2)e_9+e^T_9(P_3-P_2^T)e_6]\nonumber \\&\quad -\,[e^T_3P_3e_9+e^T_9P_3e_3]<0, \end{aligned}$$

(33)

where the matrices $\varXi ,e_i~(i=1,\ldots ,9)$ are identical to the relevant ones in Theorem 2 except for two following terms

$$\begin{aligned}&\varXi _{44}=-2R_5-(1-\gamma \mu _m)Q_1+Z_5+Z_5^T,~~~\varXi _{55}=-Q_2-R_5. \end{aligned}$$

Moreover, the estimation gains can be derived as $K=N_1^{-T} F_1$ and $L=N_1^{-T} F_2$.

Proof

As for the term $V_2(\varepsilon _t)$ in (10), through replacing $\int _{t-\tau }^{t-\varphi (t)}\varepsilon ^T(s)Q_2\varepsilon (s)\hbox {d}s$ by $\int _{t-\tau }^{t-\varphi }\varepsilon ^T(s)Q_2\varepsilon (s)\hbox {d}s$ and using the similar methods to prove Theorem 2, the corollary can be derived and the detailed proof is omitted. $\square$

In what follows, we will consider the master-slave synchronization for more general systems as

$$\begin{aligned}&\mathcal {M}: \left\{ \begin{array}{l} \dot{x}(t)=Ax(t)+Cx(t-\tau (t))+B{h}(Ex(t)) \\ p(t)= Fx(t) \end{array}\right. \end{aligned}$$

(34)

$$\begin{aligned}&\mathcal {S}: ~\left\{ \begin{array}{l} \dot{z}(t)=Az(t)+Cz(t-\tau (t))+B{h}(Ez(t))+u(t) \\ q(t)= Fz(t) \end{array}\right. \end{aligned}$$

(35)

$$\begin{aligned}&\mathcal {C}:\begin{array}{l} ~u(t)= K\left[ p(t)-q(t)\right] +L\left[ p(t-\tau (t))-q(t-\tau (t))\right] . \end{array} \end{aligned}$$

(36)

Then through setting $\varepsilon (t)=x(t)-z(t)$, the synchronization error system can be derived as

$$\begin{aligned}&\dot{\varepsilon }(t)=(A-KF)\varepsilon (t)+(C-LF) \varepsilon (t-\tau (t))+Bf(E\varepsilon (t)). \end{aligned}$$

(37)

Theorem 3

For any given scalars $\tau \ge 0,\mu _0,\mu _m,1\ge \delta ,\gamma \ge 0,\upsilon >0$, the systems described by (34)–(36) achieve the master–slave synchronization, if there exist $n\times n$ matrices $P>0, P_1>0,P_2,P_3>0,Q_i>0~(i=1,2,3,4),R_j>0,Z_j~(j=1,2,3,4,5),R_6>0,N_1$ making $\left[ \begin{array}{ccc} P_1 &{} P_2 \\ *&{} P_3 \end{array}\right] >0,\left[ \begin{array}{ccc} R_j &{} \quad Z_j \\ *&{} \quad R_j \end{array}\right] >0~(j=1,2,3,4,5)$, $n_1\times n_1$ diagonal matrices $Q>0,$ $R>0,U>0$, and $n\times k$ matrices $F_i~(i=1,2)$ such that for $i=1,2,$ the LMIs in (38)–(39) hold

$$\begin{aligned}&\varXi +\left[ e^T_1Z_1e_6+e^T_6Z_1^Te_1\right] +\left[ e^T_1\left( R_1-Z_1\right) e_2+e^T_2(R_1-Z_1^T)e_1\right] \nonumber \\&\quad +\left[ e^T_2\left( R_1-Z_1\right) e_6+e^T_6(R_1-Z_1^T)e_2\right] \nonumber \\&\quad + \left[ e^T_3R_3e_6+e^T_6R_3e_3\right] -\left[ e^T_8Z_2e_9+e^T_9Z_2^Te_8\right] \nonumber \\&\quad +\,\, e^T_2\left( Z^T_1+Z_1-2R_1\right) e_2-e^T_9R_2e_9\nonumber \\&\quad + \left[ e^T_9P_1e_1+e^T_1P_1e_9\right] -\left[ e^T_3P_2^Te_9+e^T_9P_2e_3\right] \nonumber \\&\quad +\left[ e^T_6(P_2^T-P_1)e_9+e^T_9\left( P_2-P_1\right) e_6\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(38)

$$\begin{aligned}&\varXi +\left[ e^T_1R_1e_6+e^T_6R_1e_1\right] +\left[ e^T_2\left( R_3-Z_3\right) e_3+e^T_3 (R_3-Z_3^T)e_2\right] \nonumber \\&\quad +\left[ e^T_2(R_3-Z_3^T)e_6+e^T_6\left( R_3-Z_3\right) e_2\right] \nonumber \\&\quad +\left[ e^T_3Z_3^Te_6+e^T_6Z_3e_3\right] -\left[ e^T_9Z_4e_{10}+e^T_{10}Z_4^Te_{9}\right] \nonumber \\&\quad +\,\, e^T_2\left( Z^T_3+Z_3-2R_3\right) e_2-e^T_9R_4e_9\nonumber \\&\quad - \left[ e^T_9P_2^Te_1+e^T_1P_2e_9\right] +\left[ e^T_6\left( P_3-P_2\right) e_9+e^T_9(P_3-P_2^T)e_6\right] \nonumber \\&\quad -\left[ e^T_3P_3e_9+e^T_9P_3e_3\right] +\gamma \bar{\mu }_me^T_4Q_ie_4<0, \end{aligned}$$

(39)

where the matrices $\varXi ,e_i~(i=1,\ldots ,9)$ are identical to the relevant ones in Theorem 2 except for the following terms

$$\begin{aligned}&\varXi _{12}=N^T_1C-F_2F,~~~\varXi _{2,11}=\upsilon C^TN_1-\upsilon F^TF_2^T. \end{aligned}$$

Moreover, the estimation gains can be derived as $K=N_1^{-T} F_1$ and $L=N_1^{-T} F_2$.

Proof

Based on the proof of Theorem 2 and replacing the term (13) by the following equation

$$\begin{aligned} 0= & {} 2\left[ \varepsilon ^T(t)N_1^T+\dot{\varepsilon }^T(t)N_2^T\right] \left[ -\dot{\varepsilon }(t)+(A-KF)\varepsilon (t)\right. \nonumber \\&\left. +(C-LF) \varepsilon (t-\tau (t))+Bf(E\varepsilon (t))\right] , \end{aligned}$$

(40)

this theorem can be straightforwardly derived and its detailed proof is omitted here. $\square$

Remark 2

Though Theorems 2–3 and Corollary 1 in our work are not presented in terms of standard LMIs, it is still convenient to check their feasibility without tuning any parameters by resorting to the LMI in MATLAB Toolbox. Furthermore, through adjusting two useful parameters $\gamma ,\delta$, we can achieve the maximum allowable delay upper bound as large as possible.

Remark 3

Many existent works have used the LKF term $\int _{t-\tau (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s$ to derive the results. Yet as $\mu _m\ge \dot{\tau }(t)$ $>1$, this term’s derivative can be obtained as

$$\begin{aligned}&\frac{d}{dt}\left( \int _{t-\tau (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s\right) \\&\quad =\varepsilon ^T(t)Q_1\varepsilon (t) -[1-\dot{\tau }(t)]\varepsilon ^T(t-\tau (t))Q_1\varepsilon (t-\tau (t))\ge 0, \end{aligned}$$

which unavoidably played a negative role during estimating $\dot{V}(\varepsilon _t)<0$. Thus, in our paper, the LKF one $\int _{t-\gamma \tau (t)}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s$ has been used to get less conservative results via adjusting the parameter $\gamma$.

Remark 4

In many cases, the lower bound of time-delay may be greater than 0, i.e., it belongs to the interval $[\tau _0,\tau _m]$, which can be expressed as

$$\begin{aligned}&0\le \tau _0\le \tau (t)\le \tau _m, \quad \mu _0\le \dot{\tau }(t)\le \mu _m. \end{aligned}$$

(41)

Now as for two scalars $0\le \delta ,\gamma \le 1$, we can employ the following denotations

$$\begin{aligned}&\bar{\tau }_m\doteq \tau _m-\tau _0, \rho \doteq \delta \bar{\tau }_m, \quad \varrho \doteq \gamma \bar{\tau }_m, \quad \omega \doteq \tau _0+\delta \bar{\tau }_m=\tau _0+\rho , \end{aligned}$$

(42)

$$\begin{aligned}&\nu \doteq (1-\delta )\bar{\tau }_m=\tau _m-\omega , \quad \varphi (t)\doteq \gamma [\tau (t)-\tau _0]+\tau _0,\nonumber \\&\qquad \varphi \doteq \tau _0+\gamma \bar{\tau }_m=\tau _0+\varrho , \quad \phi \doteq \bar{\tau }_m-\varrho , \end{aligned}$$

(43)

and choose the following Lyapunov–Krasovskii functional as

$$\begin{aligned}&V(\varepsilon _t) ~=~ V_1(\varepsilon _t)+V_2(\varepsilon _t)+V_3(\varepsilon _t), \end{aligned}$$

(44)

where

$$\begin{aligned} V_1(\varepsilon _t)= & {} \varepsilon ^T(t)P\varepsilon (t)+2\sum \limits _{i=1}^{n_1}q_i\int _0^{E_i\varepsilon (t)}\left[ {f}_{i}(s) -\sigma _i^-s\right] \hbox {d}s\\&+2\sum \limits _{i=1}^{n_1}r_i\int _0^{E_i\varepsilon (t)}\left[ \sigma _i^+s-{f}_{i}(s)\right] \hbox {d}s +\int _{t-\tau _0}^{t}\varepsilon ^T(s)Q_1\varepsilon (s)\hbox {d}s\\&+\left[ \begin{array}{cc}\int _{t-\tau _0}^{t}\varepsilon (s)\hbox {d}s \\ \int _{t-\omega }^{t-\tau _0}\varepsilon (s)\hbox {d}s \\ \int _{t-\tau _m}^{t-\omega }\varepsilon (s)\hbox {d}s \end{array}\right] ^T\left[ \begin{array}{ccc} P_1 &{} \quad P_2 &{} \quad P_3\\ *&{} \quad P_4 &{} \quad P_5 \\ *&{} \quad *&{} \quad P_6 \end{array}\right] \left[ \begin{array}{cc} \int _{t-\tau _0}^{t}\varepsilon (s)\hbox {d}s \\ \int _{t-\omega }^{t-\tau _0}\varepsilon (s)\hbox {d}s \\ \int _{t-\tau _m}^{t-\omega }\varepsilon (s)\hbox {d}s \end{array}\right] , \\ V_2(\varepsilon _t)= & {} \int _{t-\varphi (t)}^{t-\tau _0}\varepsilon ^T(s)Q_2\varepsilon (s)\hbox {d}s+ \int _{t-\tau _m}^{t-\varphi (t)}\varepsilon ^T(s)Q_3\varepsilon (s)\hbox {d}s\\&+\int _{t-\omega }^{t-\tau _0}\varepsilon ^T(s)Q_4\varepsilon (s)\hbox {d}s + \int _{t-\tau _m}^{t-\omega }\varepsilon ^T(s)Q_5\varepsilon (s)\hbox {d}s,\\ V_3(\varepsilon _t)= & {} \int _{-\tau _0}^{0}\int _{t+\theta }^t \tau _0\left[ \dot{\varepsilon }^T(s)R_1\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_2{\varepsilon }(s)\right] \hbox {d}s\hbox {d}\theta \\&+\int _{-\omega }^{-\tau _0}\int _{t+\theta }^t \rho \left[ \dot{\varepsilon }^T(s)R_3\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_4{\varepsilon }(s)\right] \hbox {d}s\hbox {d}\theta \\&+\int _{-\tau _m}^{-\omega }\int _{t+\theta }^t \nu \left[ \dot{\varepsilon }^T(s)R_5\dot{\varepsilon }(s)+ {\varepsilon }^T(s)R_6{\varepsilon }(s)\right] \hbox {d}s\hbox {d}\theta \\&+\int _{-\varphi }^{-\tau _0}\int _{t+\theta }^t \varrho \dot{\varepsilon }^T(s)R_7\dot{\varepsilon }(s)\hbox {d}s\hbox {d}\theta +\int _{-\tau }^{-\varphi }\int _{t+\theta }^t \phi \dot{\varepsilon }^T(s)R_8\dot{\varepsilon }(s)\hbox {d}s\hbox {d}\theta \end{aligned}$$

with $n\times n$ matrices $P>0, Q_i>0~(i=1,2,3,4,5),R_i>0~(i=1,\ldots ,8)$, $3n\times 3n$ matrices $\left[ \begin{array}{ccc} P_1 &{} \quad P_2 &{} \quad P_3\\ *&{} \quad P_4 &{} \quad P_5 \\ *&{} \quad *&{} \quad P_6 \end{array}\right] >0$, and $n_1\times n_1$ diagonal matrices $Q={\mathrm {diag}}(q_1,\ldots ,q_{n_1})>0,R={\mathrm {diag}}(r_1,\ldots ,r_{n_1})>0$.

Remark 5

Though some novel techniques have been utilized in this work, the conditions of Theorems 1–3 are still rigorous and limited. Presently, delay-partitioning idea has been used to further reduce the conservatism [9, 22], which also can help to achieve less conservative conditions for the synchronization. Thus, in further research we will use and improve this approach to carry out the discussion. However, these techniques will add significantly to the complexities of proof procedure and theorems.

4 Numerical Examples

In order to show the effectiveness and less conservatism of the proposed criteria, we will consider two numerical examples and give the comparing results with some reported methods.

Example 1

As for $u(t)=L\left[ Fx(t-\tau )-Fy(t-\tau )\right]$, the following Chua’s circuit is considered to illustrate the master–slave synchronization criteria, which has been studied in [7, 9, 11, 12, 21, 22, 34]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=\alpha \left[ x_2-m_1x_1+h(x_1)\right] \\ \dot{x}_2=x_1-x_2+x_3 \\ \dot{x}_3=-\beta x_2 \end{array}\right. \end{aligned}$$

with $h(x_1)=\frac{1}{2}(m_1-m_0)(|x_1+c|-|x_1-c|)$ and parameters

$$\begin{aligned} m_0=-\frac{1}{7}, \quad m_1=\frac{2}{7}, \quad \alpha =9, \quad \beta =14.286, \quad c=1. \end{aligned}$$

Then the system can be represented in the form of Lur’e model (1) with

$$\begin{aligned}&A=\left[ \begin{array}{ccc} -\frac{18}{7} &{} \quad 9 &{} \quad 0\\ 1 &{} \quad -1 &{} \quad 1 \\ 0 &{} \quad -14.286 &{} \quad 0\\ \end{array}\right] ,\quad B=\left[ \begin{array}{ccc}\frac{27}{7}&{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0\\ 0 &{} \quad 0&{} 0\end{array}\right] , \quad E=\left[ \begin{array}{ccc} 1&\quad 0&\quad 0\end{array}\right] , \end{aligned}$$

and ${f}(\xi )=\frac{1}{2}(|\xi +1|-|\xi -1|)$ belonging to the sector [0, k] with $k=1$. Moreover, $F=\left[ \begin{array}{ccc}1&\quad 0&0\end{array}\right]$.

Since time-delay in u(t) is constant, one can check $\mu _0=\mu _m=0$. Then by resorting to LMI in the MATLAB Toolbox, we can obtain the feasible solutions to the LMIs in Theorem 2 based on setting $\nu =0.3$ and different $\delta ,\gamma$. Therefore, the corresponding gain matrix L can stabilize the error system (6) with different delay maximum allowable upper bounds (MAUB) $\tau _{\max }$, and the comparisons with some existent ones are shown in Table 1. Based on this table, one can clearly check that our criteria produce much less conservatism.

Table 1 The corresponding allowable bound $\tau _{\max }$ for various methods with $\mu _0=\mu _m=0$ and $\nu =0.3$

Example 2

Consider the master system (34) of delayed Lur’e model as follows:

$$\begin{aligned}&\dot{x}(t)=Ax(t)+Cx(t-\tau (t))+B{h}(Ex(t)), \end{aligned}$$

where

$$\begin{aligned} A= & {} \left[ \begin{array}{cc} -1 &{} \quad -0.4\\ -0.6&{} \quad -1 \end{array}\right] ,\quad C=\left[ \begin{array}{cc} 0.8&{} \quad 0.6 \\ 0.7 &{} \quad 0.8 \end{array}\right] ,\quad B=\left[ \begin{array}{cc} 2.1 &{} \quad -0.2\\ -5 &{} \quad 3 \end{array}\right] ,\\ E= & {} \left[ \begin{array}{cc} 1&{} \quad 0.8\\ 0.8&{} \quad 1 \end{array}\right] ,\quad F= \left[ \begin{array}{cc} 1 &{} \quad 1\\ 0 &{} \quad 1 \end{array}\right] . \end{aligned}$$

The nonlinear functions can be presented as ${h}_{i}(s)=\tanh (s)~(i=1,2)$. The corresponding slave system (35) can be given as

$$\begin{aligned}&\dot{z}(t)=Az(t)+C z(t-\tau (t))+B{h}(Ez(t))+u(t). \end{aligned}$$

Firstly, as a special case, through choosing time-delay as a constant, i.e., $\tau (t)=\tau$ with $\dot{\tau }(t)=0$, we will give some comparisons with two present works [13, 44] to illustrate the reduced conservatism. Through checking the LMIs in Theorem 3, our derived delay MAUBs $\tau _{\max }$ can be compared with the ones in [13, 44], which is listed in Table 2.

Table 2 The corresponding allowable bound $\tau _{\max }$ for various methods with $\mu _0=\mu _m=0$ and $\nu =0.3$

Furthermore, we consider the issue on time-varying delay. If $(\delta ,\gamma ,\nu )=(1,1,0.3)$ is set, we choose $\tau (t)=1.5+0.3\sin ^2(10t)+0.2\cos ^2(20t)$ and it is easy to check $\tau _m=2,\mu _0=-7,\mu _m=7$. Then we can verify the feasible solution to the LMIs in (30)–(31) and obtain the estimation gains K, L as

$$\begin{aligned}&K=L_1^{-T} F_1=\left[ \begin{array}{ccc}2.1803 &{} -8.2367\\ -3.9835 &{} 16.5365 \end{array}\right] , \quad L=L_1^{-T}F_2=\left[ \begin{array}{ccc} 0.8194 &{} \quad -0.2111\\ 0.7047 &{} \quad 0.1004 \end{array}\right] . \end{aligned}$$

Through choosing the initial conditions $[x_1(0),~x_2(0)]^T=[-2,~-1]^T$ and $[z_1(0),~z_2(0)]^T=[1,~2]^T$, the phase trajectories of master system and slave one are expressed in Fig. 1 and their state trajectories are, respectively, shown in Fig. 2, which helps illustrate the desired synchronization. In particular, in Fig. 3, the state trajectories of the error system also support the above results.

Fig. 1

Phase trajectories of the master system and slave system

Fig. 2

State trajectories of the master system and slave system

Fig. 3

State trajectories of the synchronization error system

In what follows, we choose time-varying delay as $\tau (t)=\alpha +0.3\sin ^2(20t)+0.2\cos ^2(70t)$, in which $\alpha$ is an alterable scalar and $\mu _0=-20,\mu _m=20$ can be easily checked. Now together with the LMIs in Theorem 3, we set $\nu =0.3$ and change the scalars $\delta ,\gamma$ to obtain the corresponding MAUBs $\tau _{\max }$, which can obtain the control gains K, L and guarantee the addressed synchronization.

Table 3 The maximum allowable bound $\tau _{\max }$ for various $\delta ,\gamma$, and $\mu _0=-20,\mu _m=20$

In particular, as for $(\delta ,\gamma ,\nu )=(0.1,0.1,0.3)$, when time-delay is chosen as $\tau (t)=30+0.3\sin ^2(20t)+0.2\cos ^2(70t)$, it is easy to check that $\tau _m=30.5,\mu _0=-20,\mu _m=20,$ which means that the delay satisfies Table 3. Then we can solve the LMIs in (30)–(31) and obtain the estimation gains K, L as

$$\begin{aligned}&K=L_1^{-T} F_1=\left[ \begin{array}{ccc}1.4563 &{} \quad -8.0323\\ -0.5763 &{} \quad 15.7886 \end{array}\right] ,~ L=L_1^{-T}F_2=\left[ \begin{array}{ccc} 0.7999 &{} \quad -0.2000\\ 0.6998 &{} \quad 0.1001 \end{array}\right] . \end{aligned}$$

Furthermore, if we choose the similar initial conditions in Figs. 1, 2 and 3, the phase trajectories of master system and slave one and their state trajectories are, respectively, shown in Figs. 4 and 5. In particular, based on the state trajectories of error system in Fig. 6, the desired synchronization can be achieved.

Fig. 4

Phase trajectories of the master system and slave system

Fig. 5

State trajectories of the master system and slave system

Fig. 6

State trajectories of the synchronization error system

5 Conclusions

In the paper, the problem on designing delay feedback controllers of master–slave synchronization has been considered for Lur’e systems and some novel criteria have been obtained. In order to reduce the conservatism, we have chosen two augmented LKFs and introducing some adjusting parameters, which were used to derive delay-dependent results. Together with stability criteria for synchronization error system, we have obtained several sufficient conditions on the existence of feedback controller and the controller gains can be computed out by solving a set of LMIs. Finally, two numerical examples have demonstrated that our results produced much less conservative than some reported ones.