Room Acoustics Analysis Using Circular Arrays: A Comparison Between Plane-Wave Decomposition and Modal Beamforming Approaches

Abstract

A complete room acoustics analysis requires not only measurements of the single-room impulse response, but also a rigorous analysis of the sound field’s spatial properties. Angle-dependent information for the direct and reflected waves is needed for a more complete sound field description than can be obtained with single microphone measurements. Analysis techniques based on uniform circular arrays (UCAs) have attracted a lot of attention in recent years. There is also active research on beamforming methods based on circular harmonic plane-wave sound field decomposition. However, to date, there has not been a comprehensive experimental study of the acoustics of real rooms that employs both techniques. In this paper, the UCA topology is used in a comparative study for plane-wave decomposition and enhanced modal beamforming techniques. As a result, room echograms can also be obtained by calculating a set of azimuth-steered impulse responses. Experiments in real and simulated rooms are compared and discussed, with an identification of strengths and weaknesses for both measurement methods. The results show the validity of the modal beamforming approach by comparing its performance with that of the plane-wave decomposition method.

1 Introduction

The acoustic design of amphitheaters and legendary concert halls has been mainly based on the knowledge and experience of the architects and engineers that contribute to their construction. Recent advances in the physics of sound have resulted in models for acoustic properties and behaviors [21], providing a more sophisticated framework for acoustic room design. Currently, the use of analysis methods in room acoustics is a consolidated field where well-known methodologies are applied to processes of acoustic measurements.

In room acoustics, the analysis and measurement of the room impulse responses (RIRs) are fundamental tasks in which many important parameters are extracted, such as the reverberation time and clarity [1, 14]. Spatial information contributes to important perceptive sensations such as the room size and shape, the apparent source width, or the locatedness properties of the room. However, this information is not encoded in the RIRs and their derived parameters, e.g., the distribution of early reflections in time, their direction of arrival, and their frequency characteristics. A classical alternative is to conduct measurements using a dummy head [13, 30], but this method is only optimized for human perception and is not applicable to physical descriptions or a reconstruction of the incident wavefield. As a result, directional acoustic properties cannot be extracted and other methods have to be applied for these purposes [17].

Acoustic measurements are typically acquired using a single microphone, but such measurements cannot provide spatial information regarding the whole room and multiple sound sources cannot be discriminated. To gather more information about the room, a microphone arrangement can be used instead that is capable of analyzing the directional and spatial variations in a reverberant sound field [10]. This will enable reflections and other distortions occurring in sound propagation to be accurately analyzed.

In this context, wavefield decomposition methods have received a lot of attention recently and have been used in investigations of benefits or possible defects and unwanted reflections within acoustic halls [6, 7, 11, 22]. In particular, plane-wave decomposition (PWD) is an effective method for the analysis of sound fields and can also be used to analyze the acoustic wavefield from a spatial point of view [28, 29]. The use of uniform circular microphone arrays (UCAs) with PWD has also been well studied [4]. These methods are based on the capture of multiple impulse responses with UCAs and the later decomposition of the sound field into plane waves using cylindrical harmonics [2, 15, 18, 26]. In order to analyze the acoustic wavefield from a spatial point of view, the Kirchhoff–Helmholtz and Rayleigh integrals must be applied, which greatly increases the mathematical complexity. It is considered that an equivalent process is to use the same circular array topology as employed in PWD, so that a beamforming method can be used that is able to point to different azimuth angles to obtain a RIR measurement in each direction.

Modal processing using UCAs has also received increased attention [16]. Methods based on circular harmonics beamforming (CHB) have been shown to perform better than classical beamforming approaches. In fact, CHB belongs to a more recent class of methods often referred to as eigenbeamforming [20, 24, 25]. In [27], it was shown that CHB achieves better resolution and side-lobe properties than delay-and-sum beamforming (DSB), as it selectively processes a different number of phase modes or spatial Fourier terms.

From these methods, we propose an implementation of the CHB approach to analyze the sound field in a room, similar to the methods based on PWD. The aim of this paper is to provide an alternative to acoustic field analyses that have lower computational cost and similar results. We also compare and discuss the performance of both methods through simulations and measurements in real rooms, demonstrating the validity of the CHB approach and how it performs relative to the PWD method.

The remainder of this paper is structured as follows. Section 2 introduces the theoretical backgrounds of the PWD and CHB methods applied to sound analysis. Section 3 describes the proposed detection method for both techniques in a room acoustics analysis. The experiments are described in Sect. 4, including the design of a circular microphone array, and different halls are measured in order to compare both methods. Finally, the results and conclusions are discussed in Sects. 5 and 6, respectively.

2 Theoretical Background

The implementation of the analysis methods carried out in this work needs the plane-wave decomposition and beamformer design using modal methods as starting points. These mathematical fundamentals are crucial to understand the acoustic field analysis once captured the RIRs. As mentioned above, one UCA was used in this paper which provides significant improvements in capturing the sound field [8, 12, 19]. Therefore, before discussing the resulting measurements, this section introduces the theoretical concepts of PWD and CHB methods.

2.1 Uniform Circular Array Geometry

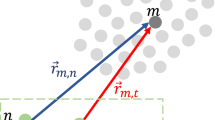
The coordinates, variables, and geometry used in the following are specified in Fig. 1.

Fig. 1

Geometry of the UCA with radius R and M elements at equidistant locations in the horizontal (x, y) plane

An UCA with radius R and M elements at equidistant locations is positioned in the horizontal (x, y) plane. Plane waves are considered incident on the array with azimuth angle $\theta$ and elevation angle $\phi$ (in degrees). Azimuth angle $\theta$ is relative to some reference point, chosen here $(x=R, y=0, z=0)$. Elevation angle $\phi$ is relative to the horizontal (x, y) plane. A microphone position on the array is specified by an angle $\theta _{m}=m\frac{2\pi }{M}$, also given in degrees relative to the reference point.

The location vector of each element in Cartesian coordinates is given by

$$\begin{aligned} {\mathbf {p}}_{m}=\left[ R\cos (\theta _{m}),\,R\sin (\theta _{m}),\,0\right] ^\mathrm{T},\quad m=0,1,\ldots ,M-1, \end{aligned}$$

(1)

where $(\cdot )^\mathrm{T}$ denotes transposition and the azimuth angle of each element is $\theta _{m}=m\frac{2\pi }{M}$.

An example of different plane waves (with directions $\theta _{i_1}={45}^{\circ },\, \theta _{i_2}={245}^{\circ }$ and $\theta _{i_3}={200}^{\circ }$) arriving with different intercept times (22, 44 and 78 ms) is shown in Fig. 2, where an array with $R=1.5$ m and $M= 288$ has been employed in the simulation.

Fig. 2

Array recording of three plane waves with directions $\theta _{i_1}={45}^{\circ },\, \theta _{i_2}={245}^{\circ }$ and $\theta _{i_3}={200}^{\circ }$ arriving with 22, 44, and 78 ms intercept times

The interelement distance can be calculated as

$$\begin{aligned} d=2R\sin \left( \frac{\pi }{M}\right) , \end{aligned}$$

(2)

and the above distance determines the spatial aliasing frequency, which is given by

$$\begin{aligned} f_{al}=\frac{c}{2d}. \end{aligned}$$

(3)

Assuming signals coming from the median plane ($\phi _{i}=\pi /2$), the steering vector for the UCA depends on the azimuth angle as follows:

$$\begin{aligned} {\mathbf {a}}(kR,\theta _{i})=\left[ \hbox {e}^{jkR\cos (\theta _{i}-\theta _{0})},\ldots ,\hbox {e}^{jkR\cos (\theta _{i}-\theta _{M-1})}\right] ^\mathrm{T}. \end{aligned}$$

(4)

where $kR = \frac{2\pi f r}{c}$, being f the frequency and c the speed of sound ($c \approx 342$ m/s).

2.2 Plane-Wave Decomposition Method

This section briefly describes the concepts of the application of the PWD method for sound field analysis using circular microphone arrays. For a complete description, please refer to Hulsebos et al. [11].

2.2.1 Cylindrical Harmonics Decomposition

Considering a continuous microphone array $(M\approx \infty )$, both pressure and the normal component of velocity are stored as $p(\theta ,\omega )$ and $v(\theta ,\omega )$ for each azimuth angle $\theta$, where $\omega$ is the angular frequency. With this dataset, the reconstruction of the sound field can be achieved by means of the Kirchhoff–Helmholtz integral equations in cylindrical coordinates [3]. Nevertheless, the Kirchhoff–Hermholtz integrals are not capable of reconstructing the sound field outside the array circle, and the decomposition into plane waves cannot be directly calculated. As a result, a preprocessing based on cylindrical harmonics decomposition is needed. The pressure on the circular microphone array is expressed as

$$\begin{aligned} p(\theta ,\omega )= & {} \sum _{k_\theta }{\mathcal {M}}^{(1)}(k_\theta ,\omega ){\mathcal {P}}_{k_\theta }^{(1)}(R,\theta ,\omega ) \end{aligned}$$

(5)

$$\begin{aligned}&+\, \sum _{k_\theta }{\mathcal {M}}^{(2)}(k_\theta ,\omega ){\mathcal {P}}_{k_\theta }^{(2)}(R,\theta ,\omega ) \end{aligned}$$

(6)

where $k = \omega /c$ is the wavenumber and ${\mathcal {M}}^{(1)}$ and ${\mathcal {M}}^{(2)}$ represent the expansion coefficients of the incoming and outgoing cylindrical harmonics ${\mathcal {P}}_{k_\theta }^{(1,2)}(r,\theta ,\omega ) = H_{k_\theta }^{(1,2)}(kr)\hbox {e}^{jk_\theta \theta }$ of order $k_\theta$. The expansion coefficients can be calculated as indicated in [12]. For sources located outside the circle ${\mathcal {M}} ^{(1)}={\mathcal {M}}^{(2)}$, so it is possible to consider a single set of expansion coefficients ${\mathcal {M}}=\frac{1}{2}({\mathcal {M}}^{(1)}+{\mathcal {M}}^{(2)})$. It can be shown that these coefficients can be calculated as follows:

$$\begin{aligned} {\mathcal {M}}(k_{\theta },\omega ) = \frac{\frac{1}{2}\left( P(k_{\theta },\omega )+\rho cV(k_{\theta },\omega )\right) }{\left( H_{k_{\theta }}^{(1)}(kR)+H_{k_{\theta }}^{(2)}(kR)-jH_{k_{\theta }}^{^{\prime }(1)}(kR)-jH_{k_{\theta }}^{^{\prime }(2)}(kR)\right) }. \end{aligned}$$

(7)

2.2.2 Plane-Wave Decomposition

Although, in general, pressure and normal velocity are needed to properly extrapolate the sound field, Eq. (7) suggests that a circular array with outward pointing cardioid microphones is sufficient for analyzing the sound field. This is due to the fact that the velocity term V (figure-of-eight microphone) combined with the pressure term P results in a cardioid pattern microphone, which is very convenient from a practical perspective [12]. Therefore, by taking the far-field approximation of the Hankel functions, the plane-wave decomposition of the sound field in terms of cylindrical harmonics becomes [12]:

$$\begin{aligned} S(\theta ,\omega )=\frac{1}{2\pi }\sum _{k_{\theta }}\hbox {e}^{-jk_{\theta }\pi /2} {\mathcal {M}}(k_{\theta },\omega )\hbox {e}^{jk_{\theta }\theta }. \end{aligned}$$

(8)

2.3 Modal Beamforming

2.3.1 Continuous Circular Aperture

The UCA shown in Fig. 1 can be considered as a spatially sampled (unbaffled) circular aperture using M sensors. Assuming a plane wave impinging from $(\theta _{i},\phi _{i}=\pi /2)$, the sound pressure at any point of a continuous circular aperture can be written in polar coordinates as

$$\begin{aligned} P(kR,\theta )=P_{0}\hbox {e}^{jkR\cos (\theta -\theta _{i})}, \end{aligned}$$

(9)

where $P_{0}$ is the amplitude of the impinging wave. Note that the temporal term $\hbox {e}^{-j\omega t}$ has been suppressed for simplicity. Expanding the above expression in a series of circular waves, and after some mathematical treatment [5], the incident pressure can be expressed as

$$\begin{aligned} P(kR,\theta )=P_{0}\sum _{n=-\infty }^{\infty }j^{n}J_{n}(kR)\hbox {e}^{jn(\theta -\theta _{i})}, \end{aligned}$$

(10)

where $J_{n}$ is a Bessel function of the first kind of order n. Note that the pressure in the aperture can be considered as a Fourier series, and therefore, it can be represented by

$$\begin{aligned} P(kR,\theta )=\sum _{n=-\infty }^{\infty }C_{n}\hbox {e}^{jn\theta }, \end{aligned}$$

(11)

with Fourier coefficients (or circular harmonics) given by

$$\begin{aligned} C_{n}(kR,\theta _{i})=P_{0}j^{n}J_{n}(kR)\hbox {e}^{-jn\theta _{i}}. \end{aligned}$$

(12)

In practice, continuous apertures must be sampled by means of a finite number of sensors. The next subsection describes the consequences of this sampling procedure.

2.3.2 Sampled Circular Aperture

The discretization of the continuous circular aperture by means of an UCA with M omnidirectional microphones results in the following Fourier coefficients:

$$\begin{aligned} \tilde{C}_{n}(kR)=\frac{1}{M}\sum _{m=0}^{M-1}\tilde{P}_{m}(kR)\hbox {e}^{-jn\theta _{m}}, \end{aligned}$$

(13)

where $\tilde{P}_{m}$ is the measured sound pressure at the mth microphone (placed at angle $\theta _{m}$). This sampling procedure implies an error in the Fourier coefficients [23].

Note that, according to Eq. (11), an infinite number of Fourier terms are needed to represent the sound pressure. In practice, the impinging wavefield must be decomposed into a maximum order L of circular harmonics and, thus, $M\ge 2L+1$. As a rule of thumb, $L\approx kR$ is usually chosen, since the value of a particular Bessel function is small when the order $n>0$ exceeds the argument. The selection of an appropriate number of Fourier terms is further discussed in Sect. 2.3.4.

2.3.3 Beamforming

Modal beamforming aims at combining the different circular harmonic components (or phase modes) to form a beam with appropriate spatial selective properties. Ideally, the beamformer response should have a maximum when the beamformer is steered toward the source direction $\theta _{i}$ and should be zero in all other directions. This ideal response can be represented as a delta function as follows:

$$\begin{aligned} G_{\text {ideal}}(kR,\theta )=P_{0}\delta (\theta -\theta _{i}). \end{aligned}$$

(14)

It can be shown that this ideal response is achieved by adding an infinite number of modes, so that the ideal beamformer can be written as [27]

$$\begin{aligned} G_{\text {ideal}}(kR,\theta )=\sum _{n=-\infty }^{\infty }\frac{ C_{n}(kR,\theta _{i})}{j^{n}J_{n}(kR)}\hbox {e}^{jn\theta }. \end{aligned}$$

(15)

As discussed previously, when using a real UCA the number of modes must be truncated to a maximum order L. Moreover, the modal coefficients correspond to those of a sampled circular aperture, resulting in the following response:

$$\begin{aligned} G_{\text {CHB}}(kR,\theta )=\sum _{n=-L}^{L}\frac{\tilde{C}_{n}(kR,\theta _{i}) }{j^{n}J_{n}(kR)}\hbox {e}^{jn\theta }. \end{aligned}$$

(16)

The output of the beamformer for a steering direction $\theta _{s}$ can be expressed as:

$$\begin{aligned} Y(kR,\theta _{s})=\frac{1}{2L+1}\sum _{n=-L}^{L}\tilde{C}_{n}(kR)B_{n}(kR)H_{n}(\theta _{s}), \end{aligned}$$

(17)

where $B_{n}$ is an equalization factor given by

$$\begin{aligned} B_{n}(kR)=j^{-n}J_{n}^{-1}(kR), \end{aligned}$$

(18)

and $H_{n}$ is a frequency-independent phase alignment factor

$$\begin{aligned} H_{n}(\theta _{s})=\hbox {e}^{jn\theta _{s}}. \end{aligned}$$

(19)

The normalization term, $1/(2L+1)$, is equal to the number of circular harmonics in the sum in order to keep unchanged the amplitude of the impinging plane-wave.

2.3.4 Mode Selection and Regularization

As mentioned in the last subsection, the filters $B_{n}(kR)$ are aimed at equalizing the responses of the individual eigenbeams, which depend on the Bessel function $J_{n}(kR)$. Figure 3 shows the magnitude of the four lowest-order $(n=0,\ldots ,3)$ Bessel functions of the first kind for different values of the argument kR. Note that for a given value of kR , there are only some orders (modes) with nonnegligible contribution.

Fig. 3

Magnitude of the four lowest-order Bessel functions of the first kind

As already explained, the rule of thumb is usually to select the maximum order L as

$$\begin{aligned} L=\left\lceil kR\right\rceil , \end{aligned}$$

(20)

where $\lceil \cdot \rceil$ is the ceiling function. Besides having orders with low magnitude, the different modes exhibit periodic zeros and, as a result, signals that carry components in the vicinity of the zeros cannot be completely resolved. To avoid this problem, the circular aperture can be mounted into a rigid cylindrical baffle as in [16, 23]. However, it must be emphasized that the array must be designed in this case to have a height-to-radius ratio greater than 2.8 for approximating an ideal infinite-length cylinder [23]. Note that this physical requirement can be an issue in some practical applications.

In order to avoid noise amplification due to large equalization values, Parthy et al. [16] proposed the use of Tikhonov-regularized filters. The use of regularization, besides improving white noise gain, produces a smoother beampattern and provides increased robustness. In fact, directivity and robustness are linked to the value of $\beta$ such that increasing $\beta$ improves robustness and decreases directivity.

Figure 4 shows a comparison between the broadband beampatterns provided by conventional DSB [9] and (regularized) CHB using a microphone array with $M = 13$ and $R = 0.12$ m steered to azimuth direction $\theta _{s}=\pi$. The regularization factor is $\beta =6.5\times 10^{-4}$ as in [16]. Note that CHB provides a narrower beampattern, although the effect of Bessel zeroes can be clearly seen in the response as vertical distortion lines around 1100, 1750, 2350 Hz, etc.

Fig. 4

Comparison between the broadband beampatterns provided by conventional DSB and CHB. a Conventional delay-and-sum broadband beampattern, b CHB broadband beampattern, and c transversal section for $f=1000$ Hz

3 Proposed Wave Event Detection

In the previous sections, all the mathematical background regarding the PWD and CHB has been described. In this section, we describe a method to detect plane waves on above representations by means of an alternative detection method which is based on cross-correlating a circularly shifted cosine-shaped mask with a binarized version of the original image [28]. In addition to the multi-trace impulse response which time–space matrix is formed by all the acquired impulse responses in the array (see Fig. 2), there are two main representations that appear when plotting the set of impulse measurements with UCAs. One useful representation of the sound field is the frequency–space decomposition, and the sound field can be easily interpreted as a summation of plane waves having different directions of arrival, Fig. 5a.

Fig. 5

Detection method representations for a frequency–space and b time–space

Another meaningful representation to be taken into account is the time–space decomposition representation where the different plane waves can be identified as sharp peaks corresponding to their original intercept times and azimuth directions, Fig. 5b.

The detection of main reflections from the measurements carried out in this paper has also been performed by applying other different wave-detection methods as “Manual detection,” “PWD detection,” and “CHB detection” that are explained below.

3.1 Manual Detection

Manually selected plane waves were obtained by visual analysis. To make the selection, eight different subjects familiarized with image signal processing were asked to identify visually the peaks they found more representative.

3.2 Plane-Wave and Modal Beamforming Detection Method

The detection of cosine-shaped curves is based on cross-correlating a circularly shifted cosine mask with the thresholded binary image resulting from the previous stage. The correlation mask must match the properties of the curves found in the multi-trace impulse response. To this end, the specific parameters of the array are used to build a cosine-shaped mask adapted to the processing parameters. If horizontal incidence is assumed, the curves found in the multi-trace impulse response are given by:

$$\begin{aligned} t_n(\tau _{i},\theta _{i}) = \left\lceil f_{s}\tau _{i} - f_{s}\frac{R}{c}\cos \left( \theta _{n}-\theta _{i}\right) \right\rceil , \end{aligned}$$

(21)

where $t_n(\tau _{i},\theta _{i})$ represents the time instant (in samples) at which a plane wave with DOA $\theta _{i}$ and intercept time $\tau _{i}$ arrives at each microphone n. Moreover, since cardioid microphones are used, the amplitude registered by each microphone can be modeled as

$$\begin{aligned} A_n(\theta _{i}) = 0.5 + 0.5\cos \left( \theta _{n}-\theta _{i}\right) . \end{aligned}$$

(22)

Therefore, the template correlation mask ${\mathbf {M}}$ will have dimensions $\left[ \lceil f_{s}\frac{2R}{c} \rceil ,\, N\right]$ and will be filled as follows:

$$\begin{aligned} M(t,n) = \left\{ { \begin{array}{ll} A_n(0) &{}\quad \text {if} \quad t = \left\lceil f_{s}\frac{R}{c}\left( 1 - \cos \theta _{l}\right) \right\rceil +1 \\ 0 &{}\quad \hbox {elsewhere} \end{array}} \right. \quad \forall t,n. \end{aligned}$$

(23)

The above mask is circularly shifted and cross-correlated with the thresholded binary image in the vertical direction to find matches of the shifted template at different time instants. The value of the resulting image $\mathbf {C}$ at pixel (u, v) will be given by

$$\begin{aligned} C(u,v) = \sum _{t,n} T(t,n)\cdot M^{(v-1)}(t-u-1,n), \end{aligned}$$

(24)

where $M^{(v-1)}$ denotes a circular template shift in the horizontal axis:

$$\begin{aligned} M^{(v-1)}(t,n) = M\left( t,(n-v+1)\,\text {mod}\, N\right) . \end{aligned}$$

(25)

3.3 PWD and CHB Detection

Wave events are automatically detected by applying amplitude thresholding and region selection over the PWD or CHB representations. Region labeling is performed for eight-connected neighboring pixels, and those regions with a considerable number of components are selected. The final selected values are those corresponding to the maximum values of the multi-trace impulse response in the surviving regions.

4 Experiments

In this section, we apply each method in an analysis of the spatial characteristics of room acoustics, in order to justify their viability and demonstrate the similarities between them. This section also presents the application of the above shape recognition methods to multi-trace impulse responses obtained with the PWD and CHB methods, measured in real rooms located at Castilla-La Mancha University. The validity of the CHB method as an alternative to the PWD method is then established through measurements in real rooms. First, a description of the analyzed rooms and the experimental setup is provided. Next, the obtained multi-trace impulse responses are processed to detect the main room reflections.

4.1 Analyzed Rooms

• 1. Multi-use room This room was chosen for being a conventional midsize meeting room having representative acoustic properties as shown in Fig. 6. Three walls are covered by wood panels and plaster, and the another is made with glasses. The measured reverberation time for the 1000 Hz band was approximately 0.55 s with the room empty.

• 2. Sport room It has a classical shoebox shape and its floor plan and dimensions are shown in Fig. 7. The measured reverberation time for the 1000 Hz band was approximately 1.23 s. The wall and floor materials are plaster and foam, respectively.

Fig. 6

A view on the “Sport Room” and its floorplan

Fig. 7

A view on the “Multi-use Room” and its floorplan

4.2 Setup Implementation

The measurements were taken with the same test loudspeaker positioned at the following ($x,\, y$) localizations, (5.75, 1.20) in the multi-use room and (21.28, 5.6) in the sport room. The array was positioned at (11.50, 3.17) in the multi-use room and (10.64, 5.6) in the sport room. All the rooms were kept empty and unaltered when taking the measurements. The array was composed of two condenser cardioid microphones attached to the end of a 2 m long rod on a circular sliding turntable. The array measurements were taken by carrying out automatically repeated captures for all the required microphone positions uniformly distributed over a circle of 2 m diameter placed within the listening area. Maximum length sequences (MLS) [28] were used as the sources of excitation (sampling frequency $f_{s}= 44{,}100$ Hz). The source test signal was controlled by means of a laptop computer with an M-Audio Fast Track Pro audio interface and processed with an ad hoc MATLAB program. Since the room conditions (temperature, humidity, etc.) did not change significantly during the measurements series, the results can be assumed to be the same as in the situation where all the impulses responses are measured simultaneously with a full array of $M=72$ microphones.

4.3 Measurements

The different multi-trace impulse responses and their corresponding template cross-correlation applied on time–space and frequency–space decompositions are shown in Figs. 8 and 9. The first column displays the impulse responses recorded for all neighboring receiver positions along the circular array where in spite of the fact that the sound field presents a complex structure due to interference and diffraction, many reflection events can still be discriminated for both figures. PWD and CHB representations (columns 3 and 4, respectively) provide high energy compaction at localized plane-wave reflections. The evolution with time of the spatial properties of the sound can be observed both in multi-trace impulse responses (columns 1 and 2), time–space PWDs (column 3), and time–space CHBs (column 4). Both first and late reflections can be identified in these representations, showing how the density of reflected waves coming from multiple directions increases significantly with time.

Fig. 8

Multi-trace impulse responses measured with PWD and CHB for multi-use room. a Manual detection. b Wave event detection algorithm. c PWD detection. d CHB detection

Fig. 9

Multi-trace impulse responses measured with PWD and CHB for sport room. a Manual detection. b Wave event detection algorithm. c PWD detection. d CHB detection

4.4 Events Detection

Regarding the detection of main reflections from the measured data, it has been performed by applying the different wave-detection methods explained in the Sect. 3.

4.4.1 Manual Detection

The white squares in the first column of Figs. 8 and 9 denote the final selected reflections, which are the ones that were commonly selected by, at least, 8 subjects. Despite not being a very accurate ground truth, these manually selected values will be used to compare the detection performance of the automatic detection methods.

4.4.2 Correlation-Based Detection

Wave events are automatically detected by following the image processing procedure described in Sect. 4. The detected reflections are shown as white circles in the second column of Figs. 8 and 9.

4.4.3 PWD and CHB Detection

Similarly, the detected reflections are shown as white circles in the third and fourth columns of Figs. 8 and 9 for PWD and CHB, respectively.

5 Results

The performances of the PWD and CHB methods are summarized in Table 1, showing the number of correctly detected wave events (Correct), the number of false negatives (FN), the number of false positives (FP), the mean absolute error on the time axis ($\hbox {MAE}_{t}$), and the mean absolute error on the angle axis ($\hbox {MAE}_{\theta }$) for the two analyzed rooms.

Table 1 Performance of the correlation-based (CB) method over the multi-trace impulse response and the PWD-based detection (PWD) and CHB-based detection (CHB)

The performance of the correlation-based (CB) method over the multi-trace impulse response and the PWD-based detection (PWD) and CHB-based detection (CHB) was studied by comparing the number of false negatives (undetected reflections) and false positives (badly detected reflections) with respect to manually selected events (Manual). We assume a given event is correctly detected when the distance to the closest manually selected event is less than ${10}^{\circ }$ in angle and 100 samples in time. Moreover, for the correctly detected reflections, the mean absolute errors on the time axis ($\hbox {MAE}_t$) and on the angle axis (MAE) were computed. In general, the correlation-based method provides a lower deviation in the angle dimension compared with the PWD- and CHB-based methods. As can be seen in Table 2, CB is capable of automatically detecting approximately 82 % of the events, and the PWD and CHB methods detect 75 and 42.85 %, respectively. However, the number of correctly detected waves, false positives, and false negatives is very dependent on the room being analyzed. In fact, the rate of false positives for all rooms is quite small when using CB (1 %), and although PWD seems to detect more reflections, some of them should be discarded (21.42 %). On the other hand, although the CHB method does not detect many reflections, almost all of them are correct (10.71 % should be false positives). Further work is needed to analyze the effects of the different parameters involved in the processing, the robustness as it depends on room type, the mean performance over larger datasets, and the use of more suitable models for characterizing plane-wave footprints with different heights.

Table 2 Relative percentages of correct values, false positives (FP) and false negatives (FN) for CB, PWD, and CHB methods

6 Conclusions

We implemented and compared two methods of room analysis. One method is based on the plane-wave decomposition with cylindrical harmonics, and the second is based on a modal beamforming technique. The objective was to verify that a decomposition of the data into cylindrical harmonics, combined with a wave-detection method based on cross-correlation, is capable of identifying and separating plane-wave events from impulse response measurements acquired with a circular array. Meaningful experiments were conducted to evaluate the performances of both methods in two real halls with different array and source positions. These experiments were carried out using an image processing technique based on the cross-correlation method and in the context of a sound field analysis using UCAs. Sound field representations have been shown to accurately describe the spatial characteristics of sound at the location of the listener. Although the accurate detection of every plane-wave reflection is very difficult, it has been shown that this method is capable of identifying many of the most meaningful echoes automatically in these representations, resulting in relatively small errors both in time and in angle. The analyzed techniques reveal the spatial coherence of neighboring responses, leading to far better insight into complex wavefields in enclosed spaces than can be obtained through an analysis of individual impulse responses. Therefore, the results also demonstrate the validity of the CHB approach in a room analysis and its use for analyzing the sound field, similar to the use of methods based on PWD.