Room in a Room: A Neglected Concept for Auralization

Abstract

The term Room in a Room describes an old technique which can be utilized for auralization purposes. Thereby the auralization procedure can be divided into an analysis- and a synthesis task, usually dependent of each other. The analysis recordings in the source room have to be made exactly at those directions where loudspeakers are physically placed in the target room. In doing so, the spatial separation, respectively, filtering will be realized by beamforming. The outputs of the different, fixed beamformers provide the signals for the loudspeakers in the target room, representing the synthesis of this auralization technique. Different methods of how such a beamformer can robustly be designed will be presented in this chapter.

1 Introduction

Auralization techniques have been an object of interest since a long time. They can be used to create an illusion of being acoustically in a desired room, whilst, in reality, sitting in a completely different one. If this illusion becomes authentic, such techniques can be utilized, for example, for acoustical documentation or virtual tuning purposes. Especially in automotive acoustics, such a tool is highly desired, since up to now the majority of prototype cars are still individually tuned by an acoustician, mostly by hand, which is very time consuming. At the same time, automotive companies constantly cut time frames for such tasks, since working time on the prototypes is expensive, as many people from different disciplines have to work on them. By using auralization techniques one could measure the car once and work, from this moment on, solely on this data, to get the car tuned. In doing so, valuable working time on a prototype can be reduced to a minimum, whilst at the same time; tuning time can be increased, eventually leading to a better acoustical result.

1.1 Background

There is a whole number of possibilities how auralization can be achieved, which can roughly be divided into two categories: headphone- and loudspeaker-based solutions. As representatives of the headphone solutions, a pure binaural recording and reproduction solution, as is more deeply described in [1], can be mentioned. Thereby the idea of the system, presented in [1], is to duplicate the binaural signal, as recorded directly at the eardrums within the source room by a headphone reproduction system. Thereby the headphones have to be adequately compensated, ideally with the inverse of the headphone transfer function, which can only be realized approximately, since this transfer function is usually not minimum phase. Despite its simplicity, this method is able to deliver a very authentic room impression. The BRS (Binaural Room Scanning) principle [2] is also based on binaural recordings, which are, in contrast to the before mentioned principle, not individualized. Due to the fact that BRS utilizes general HRTFs (Head Related Transfer Function) data, a head tracking system has to be applied in order to externalize the acoustic expression, or in other words to avoid in-the-head localizations. Thereby, the head tracker is able to measure the current head rotation. This information is then used to pick the most adequate, i.e., the two, in 2D applications, neighboring HRTFs out of a library, interpolate in between them and insert the result into a convolution machine. As a consequence an impression can be achieved that the stage does not move with the head during head rotations.

The topic of this chapter belongs to the category of loudspeaker-based auralization methods. There exist a number of different methods, from which only a few, which are considered to be the most promising ones, will briefly be mentioned in the following. In [3] the author utilized the inverse filter theory as three dimensional (=3D) sound reproduction technique. The aim of this technique is to compensate for any disturbing effects of the target room, by utilizing matrix inversion to calculate the necessary inverse filter matrix such, that in connection with the target room, a Dirac impulse, at the desired location within the target room, will ideally result. As soon as this task is successfully accomplished, it is easy to create any desired room impression by additionally inserting the room transfer matrix of the desired room into the system, which could, above all, be efficiently integrated into the already inevitable, inverse filter matrix. Despite its mathematical correctness, this principle suffers from diverse practical problems, such that the results are only valid at the location in the target room where the measurement had been applied but not at its close proximity. Furthermore, the acoustics are adversely affected by the inverse filter, as they usually show a great deal of pre-ringing. The term Ambisonics, as described, e.g., in [4], stands for an analysis and synthesis method able to measure and reproduce spherical harmonics of a sound field. Thereby, the main task consists of creating a gain or filter matrix, jointly maximizing the energy as well as the particle velocity vector. Since Ambisonic is based on free-field conditions, it can only auralize the desired wave field as expected, if the target room is free of reverberation and/or early reflections, which is the case if the target room is an anechoic chamber. This problem is tackled by the DirAC (Directional Audio Coding) system, as introduced in [5], which can be looked upon as an extension of the previously mentioned Ambisonic system. Here, in addition to the extraction of the azimuth and elevation information from the B-Format signal, which act as input, as is the case in the Ambisonic system, spatial parameters, like the diffuseness are extracted during analysis and used in synthesis, with the objective of creating a realistic spatial impression. This of course can only approximate spatial impressions. If one wants to replicate the “real” sound field by loudspeakers, probably the most accurate way is to utilize Wave Field Synthesis (WFS), as disclosed, e.g., in [6], or High Order Ambisonics (HOA) as introduced, e.g., in [7], despite the fact that here one has to deal with still unsolved problems too, such as spatial aliasing effects. Another negative aspect in this concern is the enormous effort necessary to successfully run a WFS or HOA system, since a great number of (closely spaced) loudspeakers and the accompanying signal processing are necessary to create the desired effect.

The aim of the Room in a Room method, as introduced in this chapter, is to create a realistic sound field in the target room, in an easy and efficient way, thereby circumventing diverse problems inherent in some of the above-mentioned principles.

This chapter is structured as follows. In Sect. 8.2 the principles of the Room in a Room method is presented. Then, in Sect. 8.3 the first utilized beamforming technique is reviewed. Thereby, the underlying 3D microphone array is presented, as well as a new concept of how superdirective beamformers can effectively be combined by utilization of the presented 3D microphone array , which forms the “heart” of the whole method. Section 8.4 presents simulations of the novel beamforming technique and reconsiders its outputs. In Sect. 8.5 measurements of the novel beamformer are discussed. Finally, Sect. 8.6 summarizes this chapter.

2 Room in a Room

As one can perceive in Fig. 8.1, a microphone array is placed in the source room at a desired position, which acoustic should eventually be reproduced at a certain position within the target room. Thereby two types of recordings are feasible. Firstly it is always possible to directly record the desired sound, picked up by all microphones, which we will subsequently refer to as signal-dependent recording. This is necessary if one wants to “document” the acoustics, e.g., of an opus at a specific location within an opera. Secondly, if the sound which should be reproduced stems from a sound system with a defined number and location of loudspeakers, as is the case in an automobile, it is reasonable to pick up the room impulse responses (RIR) from all S speakers to all M microphones of the microphone array in order to eventually create a signal-independent auralization system, which we will subsequently call room-dependent recording.

Fig. 8.1

Principle of the Room in a Room auralization method

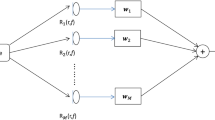
Independent of the type of recording, successively, based on the recorded data, beamforming filter will be applied, such that L beams, pointing exactly to the positions of the L loudspeakers, as located in the target room, will be created. Regarding a signal-dependent recording, further processing for the synthesis is not necessary. Figure 8.2 depicts all steps of the synthesis procedure, necessary for the room-dependent recording. In this process, based on the N input signals x, the driving signals for the S speakers (located in the target room) have to be calculated, by replication of the whole signal processing chain of the sound system, utilized in the target room. This may simply consist of a pure passive upmixing matrix ${\underset{\bar{\mkern6mu}}{\mathbf{M}}}_{N\times S}\left({e}^{j\omega}\right)$, broadcasting parts, combinations or originals of the N input signals to the S speakers. Afterwards, the influence of the transfer functions of the target room, stored in the RIR matrix ${\underset{\bar{\mkern6mu}}{\mathbf{H}}}_{S\times M}\left({e}^{j\omega}\right)$, will be considered during the course to create the M virtual microphone signals, as would be picked up by the microphone array if one were to play the desired input signal in the target room, utilizing its sound system and directly record these signals at a desired location by the M microphones of the microphone array. Finally, on grounds of these “virtual” microphone signals, L beams, pointing to the L loudspeakers, as located in the target room will be designed, whose output signals form their driving signals, the same as in the signal-dependent recording.

Fig. 8.2

Synthesis of room-dependent recordings

3 Beamforming

A microphone array consisting at least of two microphones, from which, at least one signal is filtered, with a successive filter, calculated such that a desired spatial filtering will eventually arise by combination of the processed microphone signals, is called a beamformer.

In the coordinate system, utilized for the design of a beamformer, as shown in Fig. 8.3, it is expected that all microphones are aligned along the x-axis. Furthermore, to design a beamformer with a beam pointing to a desired direction, e.g., as depicted by the vector u in Fig. 8.3, the direction of the beam will be assigned by its corresponding horizontal- (azimuth Θ) and vertical angle (elevation φ).

Fig. 8.3

Coordinate system utilized for the design of a beamformer

As revealed by Fig. 8.4, showing a beamformer, implemented in the spectral domain, the required signal processing can be divided into two parts, that is to say the so-called beamsteering on the one hand, which stands for a time delay compensation, necessary to ensure coherent, i.e., phase aligned addition of the microphone signals by ${e}^{j\omega {\tau}_i}$, and the filtering on the other hand by A(ω), which performs the intrinsic spatial filtering. It should be noted that in Fig. 8.4, it is expected that free-field conditions be met, i.e., signals picked up by the microphones differ in their phasing but not in their amplitude.

Fig. 8.4

Signal flow diagram of a beamformer, realized in the spectral domain

3.1 Design of Optimal Beamforming Filter

Optimal beamforming filter A(ω) can generally be calculated as follow:

$$ \mathbf{A}\left(\omega \right)=\frac{{\underset{\bar{\mkern6mu}}{\varphi}}_{NN}^{-1}\left(\omega \right)\mathbf{d}\left(\omega \right)}{{\mathbf{d}}^{\mathrm{H}}\left(\omega \right){\underset{\bar{\mkern6mu}}{\varphi}}_{NN}^{-1}\left(\omega \right)\mathbf{d}\left(\omega \right)} $$

(8.1)

where

A(ω)=Vector holding the beamforming filter

A(ω) = [A₁(ω), …, A_M(ω)]^T, where X ^T denotes the transpose of X,

${\underset{\bar{\mkern6mu}}{\varphi}}_{NN}\left(\omega \right)$=Power spectral density (PSD) matrix of the background noise N,

X ^H=Hermitian (conjugate transpose) of X,

ω=Angular frequency in $\left[\frac{1}{\mathrm{s}}\right]$ (ω = 2π f),

d(ω)=Steering vector d(ω) = [d₁(ω), …, d_M(ω)]^T,

with

$$ {\underset{\bar{\mkern6mu}}{\varphi}}_{NN}\left(\omega \right)=\left(\begin{array}{cccc}\hfill {\varphi}_{N_1{N}_1}\left(\omega \right)\hfill & \hfill {\varphi}_{N_1{N}_2}\left(\omega \right)\hfill & \hfill \cdots \hfill & \hfill {\varphi}_{N_1{N}_M}\left(\omega \right)\hfill \\ {}\hfill {\varphi}_{N_2{N}_1}\left(\omega \right)\hfill & \hfill {\varphi}_{N_2{N}_2}\left(\omega \right)\hfill & \hfill \cdots \hfill & \hfill {\varphi}_{N_2{N}_M}\left(\omega \right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill {\varphi}_{N_M{N}_1}\left(\omega \right)\hfill & \hfill {\varphi}_{N_M{N}_2}\left(\omega \right)\hfill & \hfill \cdots \hfill & \hfill {\varphi}_{N_M{N}_M}\left(\omega \right)\hfill \end{array}\right) $$

(8.2)

where

M=Number of microphones,

and

$$ d\left(\omega \right)={e}^{-j\frac{\omega \left(\frac{M+1}{2}-n\right)\;d \cos \left({\Theta}_0\right)}{c}} $$

(8.3)

where

n ∈ [1, …,M],

c=Speed of sound in $\left[\frac{\mathrm{m}}{\mathrm{s}}\right]\left(c=343\left[\frac{\mathrm{m}}{\mathrm{s}}\right]@\vartheta =20{}^{\circ}\mathrm{C}\right)$,

Θ₀=Main receive direction, respectively direction, where the beam points in [rad].

In case, the sound source resides in the near field, the beam steering vector d(ω) calculates to:

$$ d\left(\omega \right)=\left[{a}_0{e}^{-j\left(2\pi\;f\;{\tau}_0\right)},{a}_1{e}^{-j\left(2\pi\;f\;{\tau}_1\right)},\dots, {a}_{M-1}{e}^{-j\left(2\pi\;f\;{\tau}_{M-1}\right)}\right] $$

(8.4)

where

a ₀=Amplitude compensation value of the nth microphone signal,

τ _n =Time compensation value of the nth microphone signal,

with

$$ {a}_n=\frac{\left\Vert q-{p}_{ref}\right\Vert }{\left\Vert q-{p}_n\right\Vert }, $$

where

‖q − p _ref ‖=Distance between the sound source q and the reference microphone

p _ref in [m],

‖q − p _n ‖=Distance between the sound source q and nth microphone p _n in [m].

Regarding a rule of thumb, one talk about far-field conditions if the sound source is located at a distance from the microphone array, exceeding twice its dimension, which is usually always the case, hence, (8.4) usually does not apply in practical applications.

3.2 Practical Modifications

According to Fig. 8.4 one usually excludes the beam steering vector d(ω) from the design of the beamforming filter A(ω). The beam steering is usually applied upstream the actual beamforming filter, i.e., first one calculates the delays and phase shifts, necessary for all microphones of the array, combined in the beam steering vector d(ω), in order to let the resulting beam point to the desired direction, before the beamforming filter A(ω) takes place. Thus the steering vector d(ω) within (8.1) reduces to d(ω) = 1 = [1,1, …,1]^T.

In a further step, the cross-correlation matrix of the background noise ${\underset{\bar{\mkern6mu}}{\varphi}}_{NN}\left(\omega \right)$, which usually has to be measured continuously, or at least in situ, will be replaced by the complex coherence matrix of a diffuse noise field $\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)$, for which a closed solution exists. This modification can be conducted, since measurements showed, that spatially homogeneous noise fields, as approximately apparent in automobiles, closely resemble a diffuse noise field.

Taking all these modifications into account, the design of the beamforming filter converts to:

$$ \mathbf{A}\left(\omega \right)=\frac{{\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}}^{-1}\left(\omega \right)\mathbf{1}}{{\underset{\bar{\mkern6mu}}{{\mathbf{1}}^{\mathrm{H}}\boldsymbol{\Gamma}}}^{-1}\left(\omega \right)\mathbf{1}} $$

(8.5)

where

$\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)$=Complex coherence of a diffuse noise field,

1=Residual, respectively neutral steering vector $\mathbf{1}=\underset{M}{\underbrace{{\left[1,1,\dots, 1\right]}^T}}$.

After the beam steering has been carried out, the complex coherence matrix of the diffuse noise field $\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)$ calculates to:

$$ \underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)=\left(\begin{array}{llll}1\hfill & {\Gamma}_{X_1{X}_2}\left(\omega \right)\hfill & \cdots \hfill & {\Gamma}_{X_1{X}_M}\left(\omega \right)\hfill \\ {}{\Gamma}_{X_2{X}_1}\left(\omega \right)\hfill & 1\hfill & \cdots \hfill & {\Gamma}_{X_2{X}_M}\left(\omega \right)\hfill \\ {}\vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {}{\Gamma}_{X_M{X}_1}\left(\omega \right)\hfill & {\Gamma}_{X_M{X}_2}\left(\omega \right)\hfill & \cdots \hfill & 1\hfill \end{array}\right) $$

(8.6)

with

$$ {\Gamma}_{X_i{X}_j}\left(\omega \right)=\mathrm{sinc}\left(\frac{\omega\;{\mathrm{d}}_{\mathrm{ij}}}{\mathrm{c}}\right)\;{e}^{-j\frac{\omega\;{d}_{ij} \cos \left({\Theta}_0\right)}{c}} $$

(8.7)

where

i, j ∈ [1, …,M]_,

sinc(x)=Sinc function $\left(\frac{ \sin (x)}{x}\right)$,

d _ij =Element located at the ith row and jth column of the distance matrix $\underset{\bar{\mkern6mu}}{\mathbf{d}}$,

and

$$ \underset{\bar{\mkern6mu}}{\mathbf{d}}=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill d\hfill & \hfill \cdots \hfill & \hfill \left(M-1\right)\;d\hfill \\ {}\hfill -d\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \left(M-2\right)\;d\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill -\left(M-1\right)\;d\hfill & \hfill -\left(M-2\right)\;d\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right) $$

(8.8)

where

d=Inter-microphone distance in [m] of the equidistant microphone array.

3.3 Constrained Design

Both design rules, shown in (8.1) and (8.5) deliver the same, optimal beamforming filter A(ω), in a diffuse noise field. Unfortunately neither the one nor the other can be applied without any further modifications, considering inevitable, practical limits, such as manufacturing tolerances, or variations in the placement of the microphones. These incertitudes have been considered in [8] by the addition of a small scalar μ to the elements at the main diagonal of the cross-correlation matrix ${\underset{\bar{\mkern6mu}}{\varphi}}_{NN}\left(\omega \right)$, or as proposed in [9] to the coherence matrix of a diffuse noise field $\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)$. Another version, disclosed in [10], directly considers the inaccuracies in the design of the beamforming filter, leading to a constrained filter design as follows:

$$ \mathbf{A}\left(\omega \right)=\frac{{\left(\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)+\mu \left(\omega \right)\underset{\bar{\mkern6mu}}{\mathbf{I}}\right)}^{-1}\;\mathbf{d}\left(\omega \right)}{\mathbf{d}{\left(\omega \right)}^{\mathrm{H}}\;{\left(\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)+\mu \left(\omega \right)\underset{\bar{\mkern6mu}}{\mathbf{I}}\right)}^{-1}\;\mathbf{d}\left(\omega \right)} $$

(8.9)

where

d(ω)=Steering vector (=1, if previously applied),

$\underset{\bar{\mkern6mu}}{\mathbf{I}}$=Identity matrix in the size of $\underset{\bar{\mkern6mu}}{\boldsymbol{\Gamma}}\left(\omega \right)$,

μ(ω)=Regularization parameter.

The value of the regularization parameter μ(ω), which is now frequency dependent, and not a scalar as, e.g., in [8], depends on the MSE¹ of the imprecision of the placement of the microphones (=δ(ω)²) within the array, but mainly on the MSE of the inter-microphone tolerances (=ε(ω,Θ)²). The higher the quality of the microphone array, i.e., the lower the complete MSE (=Δ(ω,Θ)²), the smaller the value for the regularization parameter μ(ω) can be. Practical values reside within a range of: μ(ω) = [−40, …, 40] [dB].

The susceptibility K(ω) of a beamformer, given as:

$$ \mathrm{K}\left(\omega \right)=\frac{\mathbf{A}{\left(\omega \right)}^H\mathbf{A}\left(\omega \right)}{\left|\mathbf{A}{\left(\omega \right)}^{\mathrm{H}}\mathbf{d}\left(\omega \right)\right|}, $$

(8.10)

describes the sensitivity of a beamformer regarding tolerances of the corresponding microphone array. Aim of the constraint algorithm is to design a robust beamformer by limiting the susceptibility to a maximal value K _Max(ω). After [10], this upper limit K _Max(ω) directly results from the total MSE of the microphone array Δ(ω,Θ)² and the maximum tolerable deviations of the directional diagram ΔΨ(ω,Θ), with the directional diagram Ψ(ω,Θ) given as:

$$ \Psi \left(\omega, \Theta \right)=\frac{\varphi_{y,y}\left(\omega, \Theta \right)}{\varphi_{x_{ref},{x}_{ref}}\left(\omega, \Theta \right)}={\left|{\displaystyle \sum_{n=1}^M\;\mathbf{A}\left(\omega \right)\kern0.24em {e}^{j\frac{\omega\;d\;\left(\frac{\left(M+1\right)}{2}-n\right)\;\left( \cos \left({\Theta}_0\right)- \cos \left(\Theta \right)\right)}{c}}}\right|}^2 $$

(8.11)

where

φ _y,y (ω,Θ)=Auto power spectral density of the beamformer output signal y,

${\varphi}_{x_{ref},{x}_{ref}}\left(\omega, \Theta \right)$=Auto power spectral density of the reference microphone signal x _ref .

For the total MSE of the microphone array holds:

$$ \Delta {\left(\omega, \Theta \right)}^2=\varepsilon {\left(\omega, \Theta \right)}^2+\delta {\left(\omega \right)}^2 $$

(8.12)

with

$$ \varepsilon {\left(\omega, \Theta \right)}^2=E\left\{\frac{{\left|\Delta {H}_n^M\left(\omega, \Theta \right)\right|}^2}{{\left|{H}_0^M\left(\omega, \Theta \right)\right|}^2}\right\} $$

(8.13)

where

|H ^M₀ (ω,Θ)|²=Nominal, respectively mean transfer function of all microphones,

|ΔH ^M _n (ω,Θ)|²=Deviation of the transfer function of the nth microphone from the nominal transfer function,

E{.}=Expectation operator,

and

$$ \delta {\left(\omega \right)}^2={\left(\frac{\omega }{c}\right)}^2\;\frac{\sigma^2}{3} $$

(8.14)

where

σ=Variance of the zero-mean, normally distributed positioning error of the microphone, equal for each dimension, hence the scaling by $\frac{1}{3}$.

Tolerances in the microphone array can be considered in the directional diagram Ψ(ω,Θ) by addition of an error term, represented by ΔΨ(ω,Θ) to it, resulting in:

$$ E\left\{\;\tilde{\Psi}\left(\omega, \Theta \right)\right\}=\Psi \left(\omega, \Theta \right)+\Delta \Psi \left(\omega, \Theta \right) $$

(8.15)

with

$$ \Delta \Psi \left(\omega, \Theta \right)=\Delta {\left(\omega, \Theta \right)}^2\;K\left(\omega \right)\le {\Delta \Psi}_{\mathrm{Max}}\left(\omega, \Theta \right), $$

(8.16)

which must not exceed a certain threshold, provided by ΔΨ_Max(ω,Θ).

By inserting (8.12) and (8.14) in (8.16), it follows a maximally tolerable susceptibility K _Max(ω,Θ) of:

$$ {K}_{\mathrm{Max}}\left(\omega, \Theta \right)=\frac{{\Delta \Psi}_{\mathrm{Max}}\left(\omega, \Theta \right)}{\varepsilon {\left(\omega, \Theta \right)}^2+{\left(\frac{\omega }{c}\right)}^2\;\frac{\sigma^2}{3}} $$

(8.17)

The following practical simplifications can be applied to (8.17):

• Due to the fact that ε(ω,Θ)² hardly varies with Θ it suffices to determine ε(ω,Θ)² at a certain receive direction. Thereby the main receive direction Θ₀ is usually selected, which is Θ₀ = 90° in broadside and Θ₀ = 0° in endfire alignment of the beamformer.

• Inaccuracies in microphone placements, represented by δ(ω)², are much less probable then variations in the transfer functions of the array microphones, provided by ε(ω,Θ)². As such it suffices to consider mechanical deviations by a general value of, e.g., δ(ω)² = 1%.

• A dependency on Θ of ΔΨ_Max(ω,Θ) only makes sense, if one is interested in an exact reconstruction of the whole directional pattern, i.e., also of all side lobes, which is usually not the case. By taking a maximal, Θ-independent value ΔΨ_Max(ω), an almost perfect replication of the directional pattern in the main direction can still be obtained. Thereby, ΔΨ_Max(ω) can be determined by taking the maximum side lobe value of the ideal directional pattern. Furthermore, dependent on the use case, ΔΨ_Max(ω) could also be utilized as a frequency-independent threshold, e.g., ΔΨ _Max = 15[dB].

Taking all above-mentioned items into consideration, (8.17) simplifies to:

$$ {K}_{\mathrm{Max}}\left(\omega \right)=\frac{\Delta {\varPsi}_{\mathrm{Max}}\left(\omega \right)}{\varepsilon {\left(\omega \right)}^2+1\%} $$

(8.18)

with

$$ \varepsilon {\left(\omega \right)}^2\ge 1\% $$

(8.19)

Based on the previous findings, the following, iterative, constrained algorithm for the design of the beamforming filter A(ω), eventually leading to a robust, superdirective beamformer can be derived:

• 1. Preliminaries:

  • (a) Determine ΔΨ_Max(ω), based on the maximum values of the side lobes of the desired, ideal beamformer, over frequency (for M = 3: ΔΨ_Max(ω) ≈ − 9.5[dB]).

  • (b) Measure all transfer functions of the microphones H ^M _n (ω) at the desired main direction Θ₀. Afterwards, use (8.13) to calculate ε(ω)², thereby taking (8.19) into account.

• 2. Calculation of the maximum allowable susceptibility K _Max(ω), utilizing (8.18).

• 3. As initialization for the iteration, use μ(ω) = 1.

• 4. Calculation of the beamforming filter A(ω), utilizing (8.9).

• 5. Based on the beamforming filter A(ω), calculated in step 4, calculate the current susceptibility K(ω), utilizing (8.10).

• 6. Increase the regularization parameter μ(ω), if K(ω) > K _Max(ω), otherwise decrease μ(ω), e.g., by Δμ = 10^− 5.

• 7. Repeat steps 4–6 until K(ω) approaches K _Max(ω) as close as possible or if μ(ω) drops below a certain lower threshold, given, e.g., by μ _Min = 10^− 8, which is usually the case at higher frequencies $f\ge \frac{c}{2\;d}$.

4 Microphone Array

The susceptibility K(ω) of a beamformer mainly depends on the deviations of the inter-microphone transfer functions ε(ω)², as discussed in Sect. 8.3.3. To enhance the quality of the beamformer, these differences have to be kept as small as possible. Therefore, so called matched or paired microphones have been used during the construction of the microphone array, which frame, by the way, is shown in Fig. 8.1. For this purpose the transfer functions of 100 microphone capsules (Panasonic WM-62a) have been measured at Θ₀ = 0° in an anechoic chamber, from which the 7, best matching capsules have been chosen, as shown in Fig. 8.5.

Fig. 8.5

Bode diagram of the 7 best matching microphone capsules

Since the sensitivity of a beamformer against tolerances decreases with increasing frequency, a frequency-dependent weighting function, provided by a nonlinear smoothing filter (e.g., $\frac{1}{3}$ octave filter) has been applied during the selection process, prior to the calculation of the difference matrices.

An analysis of the inter-microphone differences revealed, that due to the selection process, the deviation could be decreased from primarily ± 3 [dB], as provided by the data sheet of the manufacturer, to ± 0.5 [dB], as shown in Fig. 8.6, corresponding to an value of ε(ω)² < 0.7%, which is already below the lower limit as noted in (8.19).

Fig. 8.6

Quadratic error ε(ω)² of all microphones (left figure) and of the 7 best matching microphones (right figure)

Due to the fact, that the beamformer ought be used in an auralization method, it should ideally be able to work throughout the whole audio frequency range: f ≈ [20, …,20000] [Hz]. With only one compact microphone array, this task cannot be accomplished. The best probable compromise for this purpose, had been found by utilizing a superdirective beamformer, ideally showing a frequency-independent directivity pattern up to the spatial aliasing frequency, which calculates to:

$$ f\le \frac{c}{2\;d} $$

(8.20)

As can be seen in (8.20), the spatial aliasing frequency solely depends on the inter-microphone spacing d, thus the dimension of the microphone array should be kept small to enlarge the frequency range of operation. Since the utilized capsules already have a diameter of Ø = 6[mm] and the fact that the frame cannot be made too small, to ensure a minimum of mechanical robustness, a inter-microphone distance of d = 1.25[cm] has been applied for the microphone array, leading to a spatial aliasing frequency of f = 13600[Hz] for an array in endfire orientation, which can be considered as sufficient for our purpose. In order to let the beam point in any room direction, a 3D² arrangement of the microphones was mandatory. For that reason, three linear microphone arrays, each consisting of three microphones, were arranged along the X, Y, and Z axes, each sharing the center microphone, resulting in an array with 7 microphones. Depending on the direction where the beam shall point at, a beamformer for each of the three linear arrays will be calculated, either in endfire or broadside orientation, resulting in the desired beamformer by combination of the three individual beamformers. Hence, considering (8.3) and (8.5), the final superdirective beamformer calculates to:

$$ {\mathbf{A}}_{\mathrm{Out}}\left(\omega \right)=\frac{1}{3}\left({\mathbf{A}}_x^T\left(\omega \right)\mathrm{diag}\left\{{\mathbf{d}}_{\mathrm{x}}\left(\omega \right)\right\}+{\mathbf{A}}_y^T\left(\omega \right)\mathrm{diag}\left\{{\mathbf{d}}_{\mathrm{y}}\left(\omega \right)\right\}+{\mathbf{A}}_z^T\left(\omega \right)\mathrm{diag}\left\{{\mathbf{d}}_{\mathrm{z}}\left(\omega \right)\right\}\right) $$

(8.21)

where

diag{X}=Diagonal matrix of vector X.

Because all beams of the three linear arrays, point as close as possible, to the desired direction, the resulting beam will completely point to this location, as depicted in Fig. 8.7.

Fig. 8.7

Polar diagram along the X/Y-plane of the three linear microphone arrays as well as of the resulting beamformer at f = 1[kHz], steered to φ = 0° and Θ = 45°

Each of the three beamformers exhibit a different aliasing pattern, which, as a matter of fact will also be combined, resulting in the positive effect, that the combined beamformer shows much less disturbing aliasing effects compared to each of the three individual beamformer, on which it is based on, as can be seen in Fig. 8.8.

Fig. 8.8

Top view of the X-, Y-, and Z- as well as of the resulting, superdirective beamformer at φ = 0° and Θ = 45°

Thereby the top plots of Fig. 8.8 affirm a spatial aliasing frequency of f = 13600[Hz] on the one hand and reveal that only at those regions in the spatial–spectral domain where the aliasing products of the individual beamformers overlap, the resulting beamformer shows aliasing too, which as a matter of fact appears enhanced. All other regions in the spatial–spectral domain have been suppressed during the overlapping process of the individual beamformer, as indicated by (8.20), leading to a final beamformer, exhibiting a higher spatial aliasing frequency, smaller aliasing regions within the spatial–spectral domain as well as a narrower beam width, as any of the underlying beamformers. With a mean squared error of the microphone transfer functions of ε(ω)² = 1%, which could, as previously shown, be achieved by sorting of the microphone capsules, a fix mean squared error of the microphone placement of δ(ω)² = 1% and a maximum deviation of the directivity pattern of ΔΨ _Max(ω) ≈ − 9.5[dB], for M = 3, a maximum susceptibility of K _Max(ω) ≈ 16.75 results, leading to a frequency from which on the beamformer can be considered as superdirective, of f ≈ 150[Hz], which is regarded as acceptable, since small rooms, such as the interiors of automobiles, behave more like a pressure chamber, leading to a distinct modal acoustical behavior up to a certain frequency. This transition frequency, known as Schröder frequency, given as:

$$ {f}_t=2000\;\sqrt{\frac{T}{V}} $$

(8.22)

with

f _t =Schröder, or transition frequency in [Hz],

T=Reverberation time [s] (usually T = T ₆₀),

V=Volume in the enclosure in [m³],

calculates for a typical medium-class car environment, with V ≈ 3.5[m³] and T ₆₀ ≈ 0.08[s] to:

$$ {f}_t=300\left[\mathrm{Hz}\right] $$

(8.23)

which is about twice the number of the previously determined, lower frequency bound of our final beamformer for superdirectivity. Hence it can be concluded that the novel, 3D microphone array , presents an adequate measuring device for broadband acoustical recordings.

5 Measurements

Measurements conducted in an anechoic chamber where used to verify the theory as described in the preceding chapters. Thereby, impulse responses from a broadband speaker with a membrane diameter of Ø = 10[cm], located 1[m] away from the center of the microphone array, to all 7 microphones had been gathered in the horizontal plane (φ = 0°) in 90° steps, i.e., for Θ = [0°, 90°, 180°, 270°], utilizing the exponential sine sweep technique as disclosed in [11].

In the first row of Fig. 8.9 one can see the behavior of the X beamformer, i.e., of a superdirective Beamformer in endfire direction, measured in four different orientations. At Θ = 0° its response should ideally follow the response of an omnidirectional microphone, represented by the reference microphone, located in the center of the microphone array, denoted as “RefMic” in Fig. 8.9, whereas at Θ = 180° the least amount of signal energy will be picked up. The second row shows the results of the Y beamformer, which forms a superdirective beamformer in broadside direction, measured at the same four orientations. Here one would expect equal responses with a maximum gain at Θ = [0°, 180°] and a minimum gain at Θ = [90°, 270°], with a gap, slowly increasing with frequency, which, in reality, is indeed the case.

Fig. 8.9

Magnitude frequency responses of the X-, Y-, and Z- as well as of the resulting, beamformer at φ = 0° and Θ = 0°

The Z beamformer also shows this characteristics but along the vertical axis. Along the horizontal axis, ideally no deviation should occur, which again holds true, as the measurements show. In the last row the behavior of the novel beamformer, resulting out of the overlap of the X, Y, and Z beamformer is shown. In principle it exhibits a similar behavior to the X beamformer, but with much less directivity in the low- and mid-frequency region, relativizing the practicability of the new beamforming technique.

6 Conclusions

With the novel beamforming structure a beam, pointing at any desired position in a room, can easily be formed. This can solely be accomplished via software, i.e., by utilization of different beamforming filter. Following the preluding example, Fig. 8.10 shows the result of the novel beamforming technique.

Fig. 8.10

Result of the novel beamforming technique, following the preluding example, i.e., beams pointing at φ = 0° and Θ = [0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°]

Unfortunately the final beam shows a directivity factor, which is, compared to a superdirectional beamformer, directly pointing to a desired direction, inferior, which is true, especially at low and mid-frequencies. Doubtless, there will be applications for the novel beamforming structure, but for auralization purposes it appears logical to use robustly designed superdirectional beamformer for each speaker, as located in the target room, instead. In our example with 8 speakers, regularly arranged in the target room, this would mean to measure the horizontal plane in the source room twice—one time with the X beam pointing at Θ = 0° and the other time oriented at Θ = 45°. Applicability of this method, especially regarding the introduced “Room in a Room” concept, remains a task for the future.