A Signal Decorrelation PNLMS Algorithm for Double-Talk Acoustic Echo Cancellation

Abstract

Acoustic echo cancellation (AEC) in voiced communication systems is used to eliminate the echo which corrupts the speech signal and reduces the efficiency of signal transmission. Usually, the performance of AEC system based on the adaptive filtering degrades seriously in the presence of speech issued from the near-end speaker (double-talk). In typical AEC scenarios, double-talk detector (DTD) must be added to AEC for improving speech quality. One of the main problems in AEC with DTD is that the DTD errors can result in either large residual echo or distorting the near-end input speech. Considering the strong correlation property of speech signals, this paper presents a novel proportionate decorrelation normalized least-mean-square (PDNLMS) adaptive AEC without DTD for echo cancellation as an interesting alternative to the typical AEC with DTDs. Unlike traditional AEC with a DTD, the proposed PDNLMS uses the difference of near-end speech as the residual error to update adaptive echo channel filter during the periods of double-talk, which can efficiently reduce the double-talk influence on the AEC adaptation process. The experimental results show that not only the proposed PDNLMS without DTD illustrate better stability and faster convergence rate, but it is also of a lower steady-state misalignment and better residual signal than current methods with DTDs at a lower computational cost.

1 Introduction

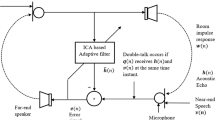
Acoustic echo cancellation (AEC) adaptive filters are commonly adopted in voiced communication systems. This kind of filter estimates the impulse response of echo channel between loudspeaker and microphone. A typical double-talk AEC system can be seen in Fig. 1a. Echo signal $y(n)$ is produced by filtering $x(n)$ through an echo channel $\varvec{w}(n)$. The microphone signal consists of echo $y(n)$, near-end speech $s(n)$ and system noise $v(n)$. An adaptive finite impulse response filter $\varvec{\hat{w}}(n)$ is modeled to obtain the replica of echo signal. Echo cancellation is accomplished by subtracting the replica $\hat{y}(n)$ from microphone signal. Even if this question is straightforward, the disturbance of near-end speech brings a great challenge for double-talk echo cancellation. For this reason, a DTD is introduced to sense this condition. Whenever double-talk condition is detected, the filter adaptation is slowed down or completely halted. Nevertheless, the filter may diverge since it works inefficiently during double-talk periods. This problem still remains to be solved.

Fig. 1

a A typical AEC system. b The proposed DTD echo cancellation

When no near-end signal is present, several conventional algorithms work well for AEC. The normalized least-mean-square (NLMS) algorithm in [15] achieves both fast convergence rate and low steady-state misadjustment. A number of variable step-size NLMS (VSS–NLMS) algorithms such as [2, 16, 22] are introduced to improve the performance of NLMS. Proportionate NLMS (PNLMS) in [6, 24] improves convergence rate on typical echo paths, and the PNLMS only entails a modest increase in computational complexity compared with NLMS. The affine projection algorithm (APA) and its different versions [10, 19, 21, 25] are attractive choices for acoustic echo cancellation. To improve the performance of APA, Paleologu [19] comes up with a variable step-size APA (VSS–APA). The proposed algorithm aims to recover near-end signal with the error signal and requires no priori information about the acoustic environment. The affine projection sign algorithm (APSA) [21] provides both good robustness and fast convergence. Proportionate APSA [25] designed for achieving a better performance under sparse channel is the combination of proportionate approach and APSA. The system [13] dealing with nonlinear acoustic channel is made up of a nonlinear module based on the polynomial Volterra filter and a standard linear module. In [14], a frequency domain postfilter is added to hands-free system. Meanwhile, a psychoacoustically motivated weighting rule is introduced. The new scheme [7] uses the least-mean-square (LMS) algorithm to update the parameters of sigmoid function and the recursive least-square (RLS) algorithm to determine the coefficient vector of the transversal filter. Literature [18] presents an overview about several approaches for the control of step size in adaptive echo cancellation.

However, the presence of near-end speech $s(n)$ disturbs the filter adaptation. As a consequence, the above algorithms fail to work properly. So DTDs in [11, 17, 20, 23] are introduced to stop the filter adaptation when double-talk is detected. Traditional DTD sets the threshold of a certain parameter between the far-end speech and near-end signal. By comparing this parameter with a defined threshold, a decision is made whether the adaptive filter works or should be frozen. Some well-known algorithms deal with the detection of near-end speech. They are mainly based on energy comparison and cross-correlation. The energy-based Geigel algorithm in [5] compares the magnitude of the mixed desire signal $d(n)$ with $M$ most recent samples of $x(n)$. Despite the superiority of being computationally simple, this algorithm does not always perform reliably. An algorithm based on the orthogonality principle is introduced in [3] . According to the idea, a cross-correlation vector between input vector and the scalar microphone output is considered to measure double-talk. In [1, 8, 9], the author proposed a normalized version which is called the normalized cross-correlation (NCR) algorithm. A low complexity version of NCR is presented in [12] for implementation on IP-enabled telephones. However, if the detection threshold is not chosen correctly, the adaptive filter will be influenced and achieves slow convergence rate. So a dynamic one based on signal envelopes is proposed in [23]. The results presented in this literature prove that the accuracy is higher than that in the Geigel algorithm and comparable to the correlation-based methods.

The main objective of this manuscript is to handle double-talk condition without DTDs. To achieve this goal, a signal decorrelation method is introduced to the proposed structure. The decorrelation in this paper is taking the difference of input sequences. In this way, the fluctuation of near-end sequences would not influence the adaptive filter since speech signals are strongly correlated. Adaptive filter keeps refreshing to match the latest echo channel during double-talk periods in the proposed structure. So the proposed algorithm obtains better recovered speech signals compared with its rival DTD algorithms and PNLMS. The paper is organized as follows. In Sect. 2, we present the PDNLMS algorithm designed for AEC applications. A brief convergence analysis is given in Sect. 3. Some simulation results are provided in Sect. 4 to support our point of view. Finally, Sect. 5 concludes this work.

2 Proposed Algorithm

In this section, we will state the model in Fig. 1b. Unlike traditional double-talk echo canceller, our proposed structure reduces the correlation of signals and focuses on minimizing the difference value of $e(n)$ and $e(n-1)$. This novel model removes the DTD to reduce complexity. The derivation of the algorithm will be presented below. All signals are real-valued.

Let $\varvec{w}(n)$ denotes the coefficient vector of an unknown echo system with length $M$, and $\varvec{\hat{w}}(n)$ represents the replica of $\varvec{w}(n)$

$$\begin{aligned} \varvec{w}(n)= & {} {[{w_0}(n){} ,{} {} {} {w_1}(n){} {} ,{} {} ...,{} {} {w_{M - 1}}(n)]^T} \end{aligned}$$

(1)

$$\begin{aligned} \varvec{\hat{w}}(n)= & {} {[{\hat{w}_0}(n){} ,{} {} {} {\hat{w}_1}(n){} {} ,{} {} ...,{} {} {\hat{w}_{M - 1}}(n)]^T} \end{aligned}$$

(2)

Superscript capital letter $T$ denotes transportation. Suppose $y(n)$ is the output signal of an unknown echo path.

$$\begin{aligned} y(n) = {\varvec{w}^T}(n)\varvec{x}(n)+ v(n) \end{aligned}$$

(3)

$\varvec{x}(n)$ contains $M$ recent samples of the far-end input signal. $v(n)$ is zero-mean Gaussian noise with variance $\sigma _v^2$. The system noise which corrupts the output of the unknown system is independent of the input sequences.

$$\begin{aligned} \varvec{x}(n) = {[{x(n)}{} ,{} {} {} {x(n-1)}{} {} ,{} {} ...,{} {} {x(n-M +1)}]^T} \end{aligned}$$

(4)

Let us define posteriori error signals at time $n$ and $n-1$, respectively

$$\begin{aligned} {e_p}(n)= & {} y(n) + s(n) - \varvec{\hat{w}}{{} ^T}(n + 1)\varvec{x}(n) \end{aligned}$$

(5)

$$\begin{aligned} {e_p}(n-1)= & {} y(n-1) + s(n-1) - \varvec{\hat{w}}{{} ^T}(n + 1)\varvec{x}(n-1) \end{aligned}$$

(6)

$\varvec{\hat{w}}(n)$ in (6) is replaced by $\varvec{\hat{w}}(n + 1)$ approximately. This assumption is reasonable because $\varvec{\hat{w}(n)}$ changes slowly at every iteration. The desired signal refers to $d(n) = y(n) + s(n)$. Inspired by our previous work [26, 27], let us consider the following constrain criteria

$$\begin{aligned} J(n) = {\left\| {\varvec{\hat{w}}(n + 1) - \varvec{\hat{w}}(n)} \right\| ^2} + \lambda *({e_p}(n) - \eta {e_p}(n - 1)) \end{aligned}$$

(7)

$\lambda$ is a Lagrange multiplier. Error difference parameter $\varDelta {e_p} = {e_p}(n) - \eta {e_p}(n - 1)$ helps minimize the distinction between ${e_p}(n)$ and its adjacent sample ${e_p}(n-1)$. If we take the partial derivative of (7) with respect to $\varvec{\hat{w}}(n + 1)$, by setting this derivative to zero the following equations are deduced

$$\begin{aligned} \frac{{\partial J(n)}}{{\partial \varvec{\hat{w}}(n + 1)}}= & {} 2\left( {\varvec{\hat{w}}(n + 1) - \varvec{\hat{w}}(n)} \right) - \lambda \left( {\varvec{x}(n) - \eta \varvec{x}(n - 1)} \right) = 0 \end{aligned}$$

(8)

$$\begin{aligned} \varvec{{\hat{w}}}(n + 1)= & {} \varvec{{\hat{w}}}(n) + \frac{\lambda }{2}\left( {\varvec{x}(n) -\eta \varvec{x}(n - 1)} \right) \end{aligned}$$

(9)

Assign $\varvec{D}(n) = \varvec{x}(n) - \eta \varvec{x}(n - 1)$ as the new input signal. $0 \le \eta < 1$ is called the decorrelation parameter which controls the degree of decorrelation. Obviously, if $\eta =0$, our algorithm will turn into NLMS. Combined (9) with $d(n - 1) = {\varvec{x}^T}(n - 1)\varvec{\hat{w}}{} (n + 1)$ and $d(n ) = {\varvec{x}^T}(n )\varvec{\hat{w}}{} (n + 1)$

$$\begin{aligned} \left\{ \begin{array}{l} d(n) = {\varvec{x}^T}(n)\left( {\varvec{\hat{w}}(n) + \frac{\lambda }{2}\varvec{D}(n)} \right) \\ \\ d(n - 1) = {\varvec{x}^T}(n - 1)\left( {\varvec{\hat{w}}(n) + \frac{\lambda }{2}\varvec{D}(n)} \right) \end{array} \right. \end{aligned}$$

(10)

$e(n) = d(n) - {\varvec{x}^T}(n)\varvec{\hat{w}}(n)$ and $e(n-1) = d(n-1) - {\varvec{x}^T}(n-1)\varvec{\hat{w}}(n)$ are defined as prior error sequences. From (10), we can obtain the solution of $\lambda$ as follows

$$\begin{aligned} \lambda = \frac{{2\left( {e(n) - \eta e(n - 1)} \right) }}{{{{\left\| {\varvec{D}(n)} \right\| }^2}}} \end{aligned}$$

(11)

Let $\varDelta e(n) = e(n) - \eta e(n - 1)$, so the update equation of filter coefficients can be rewritten as

$$\begin{aligned} \varvec{\hat{w}}(n + 1) = \varvec{\hat{w}}(n) + \frac{{\mu \varDelta e(n)\varvec{D}(n)}}{{{{\left\| {\varvec{D}(n)} \right\| }^2} + \delta }} \end{aligned}$$

(12)

where $\delta$ denotes a variable regularization parameter to avoid the divide-by-zero problem and $\mu$ is step-size constant.

The characteristic of echo channel should be taken into consideration before we apply the above algorithm to echo cancellation. Most transmission channels of acoustic echo cancellation are naturally sparse, so the coefficients are zero or close to zero. To accelerate the convergence rate of small coefficients and ensure the quality of recovered near-end speech, we combine the proportionate algorithm in [6] with our method. According to this idea, the update equation of our proportionate decorrelation method can be summarized as

$$\begin{aligned} \varvec{\hat{w}}(n + 1) = \varvec{\hat{w}}(n) + \frac{{\mu \varDelta e(n)\varvec{G}(n)\varvec{D}(n)}}{{{\varvec{D}^T}(n)\varvec{G}(n)\varvec{D}(n) + \delta }} \end{aligned}$$

(13)

Compared with (12), $\varvec{G}(n) = \mathrm{diag}[{g_0}(n),{g_1}(n),...,{g_{M - 1}}(n)]$ mainly controls the step size of each coefficients to achieve a faster convergence rate. The original definition of $\varvec{G}(n)$ can be specified in [6]

$$\begin{aligned} \left\{ \begin{array}{l} {\gamma _{\min }} = \rho \max ({\delta _p},|{{\hat{w}}_0}(n)|,...,|{{\hat{w}}_{M - 1}}(n)|) \\ {\gamma _l}(n) = \max ({\gamma _{\min }},|{{\hat{w}}_l}(n)|)\\ {g_l}(n) = {\gamma _l}(n)/\sum \nolimits _{i = 0}^{M - 1} {{\gamma _i}(n)} \end{array} \right. \end{aligned}$$

(14)

${\delta _p}$ prevents the system from stalling while any filter coefficient equals zero. $\rho$ sets the value of ${\gamma _{\min }}$ which controls the minimum adaption rate for each coefficient. For a filter with length $M=1024$, reasonable ${\delta _p}$ and $\rho$ both may be $0.01$.

3 Algorithm Analysis

We employ the tap-weight vector $\varvec{\hat{w}}(n)$ determined by our proposed adaptive filter to estimate echo system $\varvec{ w}(n)$. Define $\varvec{\varepsilon } (n) = \varvec{w}(n) - \varvec{\hat{w}}(n)$ as the mismatch between $\varvec{\hat{w}}(n)$ and $\varvec{ w}(n)$. Obviously, this parameter can be adopted to verify the performance and stability of our proposed algorithm. The following equation is obtained combining with (13)

$$\begin{aligned} \varvec{\varepsilon } (n + 1) = \varvec{\varepsilon } (n) - \frac{{\mu \varDelta e(n)\varvec{G}(n)\varvec{D}(n)}}{{{\varvec{D}^T}(n)\varvec{G}(n)\varvec{D}(n) + \delta }} \end{aligned}$$

(15)

Suppose that the input signal $x(n)$ is a zero-mean Gaussian signal with variance $\sigma _x^2$ which is independent with $s(n)$ and $v(n)$. This assumption has been widely adopted in NLMS-type analysis [6, 16]. Apparently, $D(n)$ is not an independent Gaussian process for that

$$\begin{aligned} \begin{aligned} E\{ D(n)D(n - 1)\}&= E\left\{ \left( {(x(n) - \eta x(n - 1)} \right) \left( {x(n - 1) - \eta x(n - 2)} \right) \right\} \\&=-\eta \sigma _x^2 \ne 0 \end{aligned} \end{aligned}$$

(16)

Similarly, we can easily obtain $E\{ {\varvec{D}^T}(n)\varvec{G}(n)\varvec{D}(n)\} = (1+\eta ^2) \sigma _x^2$. The denominator of (15) can be regarded as a constant according to [4, 6]. (15) will be rewritten as

$$\begin{aligned} \varvec{\varepsilon } (n + 1) = \varvec{\varepsilon } (n) - \frac{{\mu \varvec{G}(n)\varvec{D}(n)}}{{(1+\eta ^2) \sigma _x^2}}\left( {{\varvec{D}^T}(n)\varvec{\varepsilon } (n) + {v_\varDelta }(n) + s(n) - s(n - 1)} \right) \end{aligned}$$

(17)

${v_\varDelta }(n)$ applies white Gaussian distribution $(0,2\sigma _v^2)$ that is independent with $x(n)$. Let $\varvec{Z}(n) = E\{ \varvec{\varepsilon } (n)\}$, if we take the expectation of (17)

$$\begin{aligned} \varvec{Z}(n + 1) = \left( \varvec{I} - \frac{{\mu \varvec{G}(n){\varvec{R}_{DD}}}}{{(1+\eta ^2) \sigma _x^2}}\right) \varvec{Z}(n) \end{aligned}$$

(18)

$\varvec{R}_{DD}$ is the autocorrelation matrix of $\varvec{D}(n)$, $\varvec{R}_{DD}=E\left\{ {\varvec{D}(n){\varvec{D}^T}(n)} \right\}$. Suppose that $\varvec{Y}(n) = \left( {\varvec{I} - \mu \varvec{G}(n){\varvec{R}_{DD}}/(\sigma _x^2 + {\eta ^2}\sigma _x^2)} \right)$, then

$$\begin{aligned} \varvec{Y}(n) = \left( {\begin{array}{*{20}{c}} {1 - \mu {g_0}(n)}&{}{\frac{{\mu \eta }}{{1 + {\eta ^2}}}{g_0}(n)}&{}0&{} \cdots &{}0\\ {\frac{{\mu \eta }}{{1 + {\eta ^2}}}{g_1}(n)}&{}{1 - \mu {g_1}(n)}&{}{\frac{{\mu \eta }}{{1 + {\eta ^2}}}{g_1}(n)}&{} \cdots &{}0\\ 0&{}{\frac{{\mu \eta }}{{1 + {\eta ^2}}}{g_2}(n)}&{}{1 - \mu {g_2}(n)}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{}{\frac{{\mu \eta }}{{1 + {\eta ^2}}}{g_{M-1}}(n)}&{}{1 - \mu {g_{M-1}}(n)} \end{array}} \right) \end{aligned}$$

(19)

$\varvec{\hat{w}}(n) = \varvec{0}$ and $\mu =1$ are the initial values, so the equation (18) can be written as

$$\begin{aligned} \varvec{Z}(n + 1) = \prod \limits _{i = 0}^n {\varvec{Y}(i)\varvec{w}(n)} \end{aligned}$$

(20)

For any $0 \le \eta < 1$, consider the row norm of matrix $\varvec{Y}(n)$

$$\begin{aligned} {\left\| {\varvec{Y}(n)} \right\| _\infty } \le \max \left( 1 - \frac{{{{(1 - \eta )}^2}}}{{1 + {\eta ^2}}}{g_i}(n)\right) <1 \end{aligned}$$

(21)

And

$$\begin{aligned} {\left\| {\varvec{T}(n)} \right\| _\infty } = {\left\| {\prod \limits _{i = 0}^n \varvec{Y} (i)} \right\| _\infty } \le {\left\| {\varvec{Y}(0)} \right\| _\infty }{\left\| {\varvec{Y}(1)} \right\| _\infty } \cdots {\left\| {\varvec{Y}(n)} \right\| _\infty } \end{aligned}$$

(22)

Because ${\left\| {\varvec{Y}(n)} \right\| _\infty }$ is always smaller than 1, the limit of $\varvec{T}(n)$ keeps close to $\varvec{0}$. Actually, the proposed PDNLMS algorithm converges. According to (21), the parameter $\eta$ determines the convergence rate and misalignment. When $\eta$ equals 0, our algorithm turns into PNLMS. This characteristic can be verified in Sect. 4.

4 Simulations and Results

The simulations of the proposed algorithm are performed in a double-talk scenario. The input signal is either sinusoidal signal generated with a certain frequence or speech sequences. The echo channel with $M=1024$ can be found in Fig. 2. Two measurements are introduced to evaluate the performance of our PDNLMS algorithm. They are the system misalignment, $20{\log }(\left\| {\varvec{w}(n) - \varvec{\hat{w}}(n)} \right\| /\left\| {\varvec{w}(n)} \right\| )$ and speech attenuation (SA) during double-talk [20],

$$\begin{aligned} \mathrm{SA}= & {} \frac{1}{K}\sum \limits _{t = 1}^K {10\log \left[ {\frac{{E[s{^2}(t)]}}{{E[{e^2}(t)]}}} \right] } \end{aligned}$$

(23)

$$\begin{aligned} \mathrm{Misalignment}(n)= & {} 20\log \frac{{\sum \nolimits _{k = 0}^{N - 1} {\left\| {{\varvec{w}(n) - }{{\varvec{\widehat{w}}}_i}(n-k)} \right\| } }}{{N\left\| {\varvec{w}(n)} \right\| }} \end{aligned}$$

(24)

where $N$ is the number of samples used in the simulation. ${\varvec{\widehat{w}}_i}(n)$ represents the temporary filter coefficients at $i$th iteration. $K$ denotes the number of double-talk samples. From (24), the SA of a better recovered signal is always closer to 0.

Fig. 2

Acoustic echo channel adopted in the simulation

In this section, we compare PNLMS [6], Geigel-PNLMS [5], EPE-PNLMS [17], the SE-PNLMS [23] with our proposed PDNLMS algorithm. Both echo path and adaptive filters have the length of $M=1024$. All of our parameter settings can be found in the following Table 1.

Table 1 Simulation flow of PDNLMS and other comparing algorithms

4.1 Sinusoidal signal experiments

Firstly, a sinusoidal signal evaluation experiment is considered to test the performance of different systems. $y(n)$ is generated by filtering a speech signal $x(n)$ (sampling rate at 44.1 kHz) through the channel $\varvec{w(n)}$ with length $M=1024$. The speech comes from a part of an English dialogue. In terms of $s(n)$, sinusoidal signals with digital frequence $f=1/1500$ and amplitude 0.4 appear every 6000 samples to act as near-end speech. An example of the two signals can be seen in Fig. 3a. An independent Gaussian noise with 25 dB signal-to-noise ratio (SNR) is added to $y(n)$. The step size $\mu$ and regularization parameter $\delta$ equal to 1 and 0.001, respectively. Recovered near-end signal $e(n)$ is provided with $s(n)$ and $x(n)$ in Fig. 3b.

Fig. 3

a Far-end and near-end input, respectively. b Recovered near-end signals of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS, PDNLMS with sinusoidal near-end input

Figure 3b compares the recovered signals of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS and PDNLMS. It is observed that PNLMS fails to work properly, while other methods almost draw the outline of $s(n)$. But their results are not stable. PDNLMS produces the best-recovered signal which is the closest to near-end input $s(n)$. The residual signals in Fig. 4 clearly support our conclusion.

Fig. 4

Residual signals of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS, PDNLMS, respectively, with sinusoidal near-end input

Secondly, we replace the far-end input by zero-mean Gaussian AR1 process with variance 0.01 and a pole at 0.99. The SNR decreases from 25 to 10 dB between iteration number 15,000 and 24,000, then back to 25 dB after 24,000. All other conditions remain the same with the previous experiment. The misalignment performance of three parameters, where $\eta$ equals 0.5, 0.9, 0.99, respectively, is provided in Fig. 5. We can see that for different $\eta$, the stability and convergence rate get improved while $\eta$ approaches one. The misalignment curve of PDNLMS with $\eta =0.99$ outperforms its rival algorithms. In more detail, PNLMS diverges because of the fluctuation of $s(n)$. DTD-based methods achieve similar steady-state misalignment performance because adaptive filter is frozen once double-talk is detected. From Fig. 5, it is observed that our proposed algorithm is immune to the disturbance of near-end signal but a little sensitive to noise. This is because PDNLMS increases the variance of noise. However, the steady-state misalignment of PDNLMS still remains relatively low.

Fig. 5

Misalignment of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS, PDNLMS with sinusoidal near-end input. The far-end input is zero-mean Gaussian AR1 process with variance 0.01 and a pole at 0.99. $\eta$ equals 0.99, 0.9, 0.5, respectively

4.2 Real Speech Experiments

To investigate the efficiency of our proposed PDNLMS in speech applications, the following experiments are employed. Both far-end and near-end sources in our experiment are English recordings sampling at 44.1 KHz. The background is broadcast loudspeaker. The whole system works under the sparse channel in Fig. 2 with the filter length $M=1024$. White Gaussian noise is added to the echo signal with SNR=25 dB. $\mu$ and $\delta$ are fixed at 1 and 0.001, respectively, for all algorithms. Signals in Fig. 6a are short versions of the signal sources. Among the outputs in Fig. 6b, our PDNLMS fits the near-end input in Fig. 6a best. In Fig. 7, we introduce the residual signal $e(n)-s(n)$ to compare the performance of different algorithms. Obviously, PDNLMS still performs much better than the others.

Fig. 6

a Far-end and near-end input, respectively. b Recovered near-end signals of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS, PDNLMS with near-end speech

Fig. 7

Residual signals of PNLMS, Geigel-PNLMS, EPE-PNLMS, SE-PNLMS, PDNLMS, respectively, with near-end speech

A quantitative assessment of the PDNLMS is measured by SA. We test three groups of recordings from two male speakers and a female with the length of 20–35 s. Both near-end and far-end are English recordings. Since the value of $K$ can hardly be verified during a dialogue, we replace it by the length of whole samples. The average SAs of different SNR are recorded in Table 2. We can observe that the SAs of the proposed algorithm are better than those of the rival methods.

Table 2 Speech attenuation (dB) of PDNLMS and other comparing algorithms

5 Conclusion

In this study, the strong correlation of speech signals is taken into consideration to improve the performance of double-talk acoustic echo cancellation. It has been found that adjacent speech samples are quite similar, and the difference value of input sequence obtains small amplitude. Then, an improved structure based on the signal decorrelation is proposed to handle double-talk AEC without DTD. In this way, the new scheme is able to overcome interferences from near-end. In the proposed algorithm, adaptive filter keeps refreshing during double-talk periods which is different from DTD approaches. Moreover, the computational complexity is reduced by removing the double-talk detector in our algorithm. Simulations show that the architecture is more efficient than those with a DTD.

Nevertheless, our scheme still suffers some problems and need to be further addressed. First, PDNLMS increases the variance of noise so the performance may drop when SNR is low. And parameters of the algorithm should be further optimized to work better for low sampling rate signals. Solving these problems should be included in our further work.