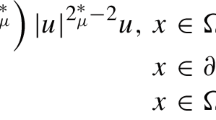Global existence and blow-up of weak solutions for a fourth-order parabolic equation with gradient nonlinearity

Abstract

This article deals with the behaviors of solutions to the initial-boundary value problem for a fourth-order parabolic equation with gradient nonlinearity. More precisely, we first get a threshold result for the solutions to exist globally or to blow up in finite time when the initial energy is subcritical and critical, and give an upper bound estimate of the lifespan. Furthermore, we derive the sufficient conditions for the existence of global and blow-up solutions for supercritical initial energy. Finally, we also give a lower bound estimate of the lifespan and obtain some estimates for blow-up rate. These results extend and improve some recent results.

Introduction

In this paper, we consider the following initial-boundary value problem for a fourth-order parabolic equation with gradient nonlinearity:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t+(- \Delta )^2 u=- \nabla \cdot (|\nabla u|^{p-2} \nabla u),~~&{}(x,t) \in \Omega \times (0,T),\\ \partial _\nu u = \partial _\nu \Delta u = 0,~~&{}(x,t) \in \partial \Omega \times (0,T),\\ u(x,0)=u_{0}(x),~~&{}x \in \Omega , \end{array}\right. } \end{aligned}$$

(1.1)

where $\Omega$ is a bounded domain in $\mathbb {R}^N (N\geqslant 2)$ with smooth boundary, $u_0 \in L^2(\Omega ),$ $T>0,$ and $\partial _\nu$ denotes the outer normal derivative to $\partial \Omega .$ Moreover, the parameter p satisfies one of the following conditions:

(H1) $2< p< \infty , ~\textrm{if}~ N =2; ~2< p < \frac{2N}{N-2}, ~\textrm{if}~ N > 2.$

(H2) $2< p < 2+\frac{4}{N+2}, N \ge 2.$

In recent years, the epitaxial growth of nanoscale thin films has attracted considerable attentions in materials science. To clarify such phenomena, we first sketch the lines along which the studied model is derived. Due to Zangwill in [14], for a spatial variable x in the domain $\Omega =[0,L]^2$, the continuum model for epitaxial thin-film growth reads

$$\begin{aligned} u_t=g-\nabla \cdot j+\eta , \end{aligned}$$

(1.2)

where u(x, t) denotes the height of a film in epitaxial growth with $g=g(x,t),~j=j(x,t)$ and $\eta =\eta (x,t)$ being the deposition flux, all processes of moving atoms along the surface and Gaussian noise, respectively. Purely phenomenologically, one can expand j(x, t) in a power series involving the surface slope $\nabla u$ and various powers and derivatives thereof. This simple case (to keep only “sensible” terms (see [14] for details)) is

$$\begin{aligned} j=A_1\nabla u+A_2\nabla (\Delta u)+A_3|\nabla u|^2\nabla u. \end{aligned}$$

(1.3)

The spatial derivatives in (1.3) have the following physical interpretations:

Hence, if we drop Gaussian noise, then Eq. (1.2) becomes

$$\begin{aligned} u_{t}+A_{1}\Delta u+A_{2}\Delta ^{2}u+A_{3}\nabla \cdot (|\nabla u|^{p-2}\nabla u)=g. \end{aligned}$$

(1.4)

Since these models describe the complex process of making a thin-film layer on a substrate by chemical vapor deposition, one of some interesting problems is to analyze these processes quantitatively on the correct scale so that we can deeply understand and optimize the particular properties of the film. These equations such as (1.4) under different initial and boundary conditions have been investigated extensively during the past few years. King et al. [7] studied the existence of global-in-time solutions and large time behavior of solutions to (1.4) in an appropriate function space for the case $A_{1}=A_{3}=1$ and $g = 0$. Later, Sandjo et al. [12] proved the local and global existence of solutions for similar problems. Recently, for the case $A_{1}=0,~A_{2}=1,~A_{3}=1$ and $g=0$, Ishige et al. [6] first obtained the local existence and singularity behavior on the whole space. Later, Miyake and Okabe [9] combined the well-known potential well method with the Galerkin method to derive the precise asymptotic behavior of global-in-time solution to problem (1.1) when the initial energy is subcritical. However, some problems are unsolved in [9].

$\bullet$ Whether or not will the advection term $\nabla \cdot (|\nabla u|^{p-2}\nabla u)$ cause the finite-time blow-up?

$\bullet$ Whether or not can the supercritical initial energy also cause the finite-time blow-up?

$\bullet$ If the finite-time blow-up happens, can we give some estimates for blow-up rate?

In this paper, we give a positive answer to the problems above. To be precise, we combine some energy estimates from [9] and the modified potential well method, which was first proposed by Payne and Sattinger [11, 13], with differential inequality arguments to prove that the solution globally exists when the initial energy starts from the stable set and fails to globally exist when the initial energy starts from the unstable set. For the high initial energy, to remedy the failure of potential well method, we borrow some ideas inspired by the study of dynamical system to prove that the functional $\int \limits _{\Omega }|u|^{2}dx$ is monotonically increasing with respect to time variable, which helps us establish a substitute for unstable sets. Meanwhile, we also obtain an upper bound of the lifespan. Finally, we obtain a lower bound estimate for the lifespan by constructing a first-order differential inequality. These results extended and improved some existing results [9].

This paper is organized as follows. In Sect. 2, we give some notations, definitions and lemmas concerning the basic properties of the related functionals and sets. Sections 3, 4 and 5 will be devoted to the cases $J(u_0) < d$, $J(u_0) = d$ and $J(u_0) > d$, respectively. In Sect. 6, we consider the lower bound estimate for the lifespan.

1 Preliminaries

In this section, we first introduce some notations and definitions that will be used throughout the paper. In what follows, we denote by $\Vert \cdot \Vert _r (r \ge 1)$ the norm in $L^r(\Omega )$ and by $(\cdot , \cdot )$ the $L^2(\Omega )$-inner product. C denotes a generic positive constant, which may differ at each appearance. In addition, we set

$$\begin{aligned} \mathscr {V}:= \left\{ \varphi \in H^1 \left( 0,T;L^2_{\mathscr {N}}(\Omega ) \right) \cap L^2\left( 0,T;H^2_{\mathscr {N}}(\Omega ) \right) |~\nabla \varphi \in \left( L^p \left( 0,T;L^p(\Omega ) \right) \right) ^N \right\} , \end{aligned}$$

where

$$\begin{aligned}{} & {} L^2_{\mathscr {N}}(\Omega ):= \left\{ v \in L^2(\Omega ) ~|~ \int \limits _{\Omega } v dx = 0 \right\} \subset L^2(\Omega ),\\{} & {} H^2_{\mathscr {N}}(\Omega ):= \left\{ v \in H^2(\Omega ) \cap L^2_{\mathscr {N}}(\Omega ) ~|~ \partial _\nu v = 0 ~\textrm{on}~ \partial \Omega \right\} \subset H^2(\Omega ). \end{aligned}$$

We mention several remarks on $L^2_{\mathscr {N}}(\Omega )$ and $H^2_{\mathscr {N}}(\Omega )$. As stated in [7], the map $\Delta : H^2_{\mathscr {N}}(\Omega ) \rightarrow L^2_{\mathscr {N}}(\Omega )$ is a homeomorphism and hence there exists a constant $c_1 = c_1(N) > 0$ such that

$$\begin{aligned} c_1^{-1}\sum _{k=0}^{2} \Vert \nabla ^k v\Vert ^2_2 \le \Vert v\Vert ^2_{H^2_{\mathscr {N}}} :=\Vert \Delta v\Vert _2^2, \quad v \in H^2_{\mathscr {N}}(\Omega ). \end{aligned}$$

Before stating our main results, we introduce the definition of weak solution to problem (1.1) in [9].

Definition 2.1

[9] Let $u_0 \in L^2_{\mathscr {N}}(\Omega )$ and $T>0$. We say that a function

$$\begin{aligned} u \in C \left( 0,T;L^2_{\mathscr {N}}(\Omega ) \right) \cap L^2\left( 0,T;H^2_{\mathscr {N}}(\Omega ) \right) \quad \textrm{with}\quad \nabla u \in \left( L^p \left( 0,T;L^p(\Omega ) \right) \right) ^N \end{aligned}$$

is a solution to problem (1.1) in $\Omega \times [0,T]$ if u satisfies

$$\begin{aligned} \int \limits _{\Omega }&\left[ u(T) \varphi (T)-u_0 \varphi (0)\right] dx\nonumber \\&-\int \limits _{0}^{T}\int \limits _{\Omega } u \partial _t \varphi dx dt + \int \limits _{0}^{T}\int \limits _{\Omega } \left[ \nabla u \nabla \varphi - |\nabla u|^{p-2} \nabla u \cdot \nabla \varphi \right] dx dt = 0, \end{aligned}$$

(2.1)

for all $\varphi \in \mathscr {V}$. Moreover, we say that u is a global-in-time solution to problem (1.1) if u is a solution to problem (1.1) in $\Omega \times [0, T']$ for all $T' > 0$.

2 The case $J(u_0) < d$

In this section, on the basis of reference [9], we continue to study the blow-up properties of solutions to problem (1.1) under the condition that $J(u_0) < d$, and we will give the threshold result of solutions to exist globally or to blow up in finite time. First, we give the definition of the solution blow-up in finite time.

Definition 3.1

Let u(t) be a weak solution to problem (1.1), define the maximal existence time of u(t) by

$$\begin{aligned} T^* = \sup \{T > 0: u = u(t) ~\text{ exists } \text{ on }~ [0, T]\}. \end{aligned}$$

We say that u(t) blows up at a finite time $T^* < \infty$ provided that

$$\begin{aligned} \lim \limits _{t \rightarrow T^*}\Vert u\Vert _2^2=+\infty . \end{aligned}$$

In order to investigate the blow-up properties of solutions to problem (1.1), we introduce the following functionals. For $u \in H^2_{\mathscr {N}}(\Omega )$, define the energy functional associated with problem (1.1)

$$\begin{aligned} J(u)=\frac{1}{2}\Vert \Delta u\Vert _2^2-\frac{1}{p}\Vert \nabla u\Vert _p^p,\quad \forall \; t \ge 0. \end{aligned}$$

(3.1)

By a simple calculation and density argument, it is not hard to verify that J(u) is a nonincreasing function on $[0,+\infty )$ and satisfies

$$\begin{aligned} \frac{d}{{dt}}J(u)= -\Vert u_t\Vert _2^2 \le 0,\quad \forall \; t \ge 0, \quad \mathrm{i.e.,}\quad J(u_0)=J(u)+\int \limits _{0}^{t} \Vert u_s\Vert _2^2 \;ds, \end{aligned}$$

(3.2)

where

$$\begin{aligned} J(u_0)=\frac{1}{2}\Vert \Delta u_0\Vert _2^2-\frac{1}{p}\Vert \nabla u_0\Vert _p^p. \end{aligned}$$

Further, we also define Nehari functional

$$\begin{aligned} I(u)=<J'(u),u>=\Vert \Delta u\Vert _2^2 -\Vert \nabla u\Vert _p^p, \end{aligned}$$

(3.3)

and the Nehari manifold

$$\begin{aligned} \mathcal {N}=\{u\in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}~|~I(u)=0\}. \end{aligned}$$

Owing to $p\le 2^*$, it is obvious to find that both J(u) and I(u) are well defined. So we define

$$\begin{aligned} W= & {} \{u\in H^2_{\mathscr {N}}(\Omega )~|~J(u)<d, I(u)>0 \}\cup \{0\},\\ V= & {} \{u\in H^2_{\mathscr {N}}(\Omega )~|~J(u)<d, I(u)<0 \}, \end{aligned}$$

where

$$\begin{aligned} d=\inf \limits _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \sup \limits _{\lambda \ge 0 } J(\lambda u) =\inf \limits _{u \in \mathcal {N}} J(u) \end{aligned}$$

is the depth of the potential well W.

Next, we state some existing results of the precise asymptotic behavior [9].

Theorem 3.1

[9] Let (H1) hold and $u_0 \in W$. Then problem (1.1) possesses the unique global-in-time solution u satisfying

$$\begin{aligned} \Vert \Delta u\Vert _2 = O\left( e^{-\mu _1^2 t} \right) \quad {\text {as}}\quad t \rightarrow \infty . \end{aligned}$$

Obviously, when $u_0 \in V$, there are seldom any results. Subsequently, we give the main result about the blow-up properties of solutions to problem (1.1).

Theorem 3.2

Let (H1) hold and u be a weak solution of problem (1.1) with $u_0 \in L^2_{\mathscr {N}}(\Omega )$. If $u_0\in V$, then there exists a finite time $T^*$ such that u blows up at $T^*$. Moreover, $T^*$ can be estimated from above as follows

$$\begin{aligned} T^* \le \frac{pd}{(p-2)^2 B^p (d-J(u_0)) \Vert u_0\Vert _2^{p-2} }. \end{aligned}$$

Proofs of Theorem 3.2 begin with the following two important lemmas.

Lemma 3.1

The potential depth d is positive.

Proof

From the definition of d, we obtain

$$\begin{aligned} d&=\inf _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \sup _{\lambda \ge 0} J(\lambda u) = \inf _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \left\{ \frac{\lambda _0^2}{2} \Vert \Delta u\Vert _2^2- \frac{\lambda _0^p}{p} \Vert \nabla u\Vert _p^p \right\} \nonumber \\&= \inf _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \left\{ \frac{1}{2} \left( \frac{\Vert \Delta u\Vert _2^2}{\Vert \nabla u\Vert _p^p} \right) ^{\frac{2}{p-2}}\Vert \Delta u\Vert _2^2- \frac{1}{p} \left( \frac{\Vert \Delta u\Vert _2^2}{\Vert \nabla u\Vert _p^p} \right) ^{\frac{p}{p-2}}\Vert \nabla u\Vert _p^p \right\} \nonumber \\&= \frac{p-2}{2p} \inf _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \left( \frac{\Vert \Delta u\Vert _2^2}{\Vert \nabla u\Vert _p^2} \right) ^{\frac{p}{p-2}} = \frac{p-2}{2p} S_p^{\frac{p}{p-2}} >0, \end{aligned}$$

(3.4)

where

$$\begin{aligned} S_p = \inf _{u \in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}} \frac{\Vert \Delta u\Vert _2^2}{\Vert \nabla u\Vert _p^2},\quad \mathrm{i.e.,}\quad S_p \Vert \nabla u\Vert _p^2 \le \Vert \Delta u\Vert _2^2. \end{aligned}$$

$\square$

The following lemma shows that the set V is invariant under the semi-flow of problem (1.1). Meanwhile, as a by-product, we also establish the precise relation between $\min \Big \{\Vert \nabla u\Vert ^{p}_{p},\Vert \Delta u\Vert _{2}^{2}\Big \}$ and the depth d.

Lemma 3.2

Assume that (H1) holds and $u_0\in V$. Then $u(t)\in V$ for all $t\in [0,T^*)$ and

$$\begin{aligned} d < \frac{p-2}{2p} \min \left\{ \Vert \nabla u\Vert _p^p, \Vert \Delta u\Vert _2^2 \right\} . \end{aligned}$$

(3.5)

Proof

We first prove $u(t)\in V$ for all $t\in [0,T^*)$ by arguing by contradiction. If there exists $t'>0$ such that $u(t')\not \in V$, then from $I(u_0)<0$ and the continuity of I(u(t)) with respect to time variable t, we know that there exists a $t_0\in [0,T^*)$ such that $I(u(t))<0$ for all $t\in [0,t_0)$ and $I(u(t_0))=0$, then $u(t_0)\in \mathcal {N}$.

On the one hand, the fact $u(t_0)\in \mathcal {N}$ and the definition of d show

$$\begin{aligned} J(u(t_0))\ge d. \end{aligned}$$

(3.6)

On the other hand, due to the monotonicity of J(u), we get $J(u)\le J(u_0)<d$ for all $t\in [0,T^*)$, which contradicts with (3.6). Consequently, we prove that $u(t) \in V$ for all $t\in [0,T^*)$.

Next, we will prove (3.5). According to $u(t)\in V$ for all $t\in [0,T^*)$, we know $I(u)<0,$ which implies $\Vert \Delta u\Vert _2^2 < \Vert \nabla u\Vert _p^p.$ Then, to utilize the embedding inequality $S_p \Vert \nabla u\Vert _p^2 \le \Vert \Delta u\Vert _2^2$ and the definition of d, we obtain (3.5). $\square$

Proof of Theorem 3.2.

Let

$$\begin{aligned} F_1(t)= \frac{1}{2} \int \limits _{\Omega } |u|^2 dx. \end{aligned}$$

Taking a derivative of $F_1(t)$, and combining with problem (1.1), Green formula, Lemma 3.2 and embedding inequality, we obtain

$$\begin{aligned} F_1'(t)= \int \limits _{\Omega } u u_t dx&= \int \limits _{\Omega } u\left( -\Delta ^2 u -\Delta _p u\right) dx = - \int \limits _{\Omega } |\Delta u|^2dx +\int \limits _{\Omega } |\nabla u|^pdx \nonumber \\&= \frac{p-2}{p} \int \limits _{\Omega } |\nabla u|^pdx - 2J(u) > \left( 1- \frac{J(u_0)}{d} \right) \frac{p-2}{p} \int \limits _{\Omega } |\nabla u|^pdx \nonumber \\&\ge B^p \left( 1- \frac{J(u_0)}{d} \right) \frac{p-2}{p} \left( \int \limits _{\Omega } |u|^2 dx\right) ^{\frac{p}{2}} \nonumber \\&= \left( \sqrt{2} B\right) ^p \left( 1- \frac{J(u_0)}{d} \right) \frac{p-2}{p} F_1^{\frac{p}{2}}(t):= CF_1^{\frac{p}{2}}(t),\quad \forall \; t\in [0,T^*), \end{aligned}$$

(3.7)

where $B\Vert u\Vert _2 \le \Vert \nabla u\Vert _p \mathrm{~and~} C= \left( \sqrt{2} B\right) ^p \left( 1- \frac{J(u_0)}{d} \right) \frac{p-2}{p}.$

A simple integration of (3.7) over (0, t) is easy to calculate that

$$\begin{aligned} \Vert u\Vert _2^2 \ge \frac{2}{ \left[ \left( \frac{1}{2}\Vert u_0\Vert _2^2 \right) ^{1-\frac{p}{2}} - \frac{p-2}{2} Ct \right] ^ \frac{2}{p-2} }. \end{aligned}$$

(3.8)

Therefore,

$$\begin{aligned} \lim \limits _{t \rightarrow \frac{2}{C(p-2)}\left( \frac{1}{2}\Vert u_0\Vert _2^2 \right) ^{1-\frac{p}{2}} } \Vert u\Vert _2^2 =+\infty . \end{aligned}$$

(3.9)

At the same time, it is easy to see that the upper bound for the blow-up time $T^*$ satisfies

$$\begin{aligned} T^* \le \frac{pd}{(p-2)^2 B^p (d-J(u_0)) \Vert u_0\Vert _2^{p-2}}. \end{aligned}$$

(3.10)

The proof of Theorem 3.2 is complete. $\square$

To sum up, we may obtain the following sharp results for the subcritical case.

Remark 3.1

(Sharp condition for $J(u_0) < d$.) Let (H1) hold and $u_0 \in H^2_{\mathscr {N}}(\Omega )$. Assume that $J(u_0) < d$. If $I(u_0) > 0$, then problem (1.1) admits a global weak solution; if $I(u_0) < 0$, then the solution to problem (1.1) blows up in finite time.

3 The case $J(u_0) = d$

For the critical case $J(u_0) = d$, the invariance of W cannot be true in general. To overcome this difficulty, we borrow some ideas from [8]; we find out a substitute for unstable sets to obtain similar results as the subcritical case. First, we give a key lemma.

Lemma 4.1

Let (H1) hold. Then for any $u\in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}$, we have

(i) $\lim \limits _{\lambda \rightarrow 0^+} J(\lambda u)=0$, $\lim \limits _{\lambda \rightarrow +\infty } J(\lambda u)=-\infty$.

(ii) There exists a unique $\lambda ^* = \lambda ^*(u) > 0$ such that $\frac{{d}}{dt} J(\lambda u)|_{\lambda =\lambda ^*} = 0$. $J(\lambda u)$ is increasing on $0 < \lambda \le \lambda ^*$, decreasing on $\lambda ^* \le \lambda < +\infty$ and takes its maximum at $\lambda = \lambda ^*$.

(iii) $I(\lambda u) > 0$ on $0< \lambda < \lambda ^*$, $I(\lambda u) < 0$ on $\lambda ^*< \lambda < +\infty$ and $I(\lambda ^* u) = 0$.

Since the proof is standard, we will omit more details here. The interested readers may refer to [3, 4, 8, 15]. The forthcoming theorem deals with the critical case.

Theorem 4.1

(Global Existence for $J(u_0) = d$.) Let (H1) hold and $u_0 \in H^2_{\mathscr {N}}(\Omega )$. If $J(u_0) = d$ and $I(u_0) \ge 0$, then problem (1.1) admits a global weak solution.

Proof

Let $\lambda _k = 1-\frac{1}{k}, k = 1, 2, \ldots$. Consider the following initial boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t+(- \Delta )^2 u=- \nabla \cdot (|\nabla u|^{p-2} \nabla u),~~&{}(x,t) \in \Omega \times (0,T),\\ \partial _\nu u = \partial _\nu \Delta u = 0,~~&{}(x,t) \in \partial \Omega \times (0,T),\\ u(x,0)=\lambda _ku_{0}(x)\triangleq u_{0}^k,~~&{}x \in \Omega . \end{array}\right. } \end{aligned}$$

(4.1)

Noticing that $I(u_0) \ge 0$, by Lemma 4.1(iii) we can deduce that there exists a unique $\lambda ^*=\lambda ^* (u_0) \ge 1$ such that $I(\lambda ^* u_0) = 0$. Then from $0< \lambda _k < 1 \le \lambda ^*$ and Lemma 4.1(ii), we get $I(u^k_0) = I( \lambda _k u_0) > 0$ and $J(u^k_0) = J(\lambda _k u_0) < J(u_0) = d$. In view of Theorem 3.1 in [9], it follows that for each k problem (4.1) admits a global weak solution $u^k \in C \left( 0,T;L^2_{\mathscr {N}}(\Omega ) \right) \cap L^2\left( 0,T;H^2_{\mathscr {N}}(\Omega ) \right)$ with $\nabla u^k \in \left( L^p \left( 0,T;L^p(\Omega ) \right) \right) ^N$ and $u^k \in W$ for $0 \le t < \infty$ satisfying

$$\begin{aligned} \int \limits _{0}^{t} \Vert u_s^k\Vert _2^2 \;ds +J(u^k)=J(u^k_0)<d. \end{aligned}$$

Applying the arguments similar to those in Theorem 3.1, we see that there exist a subsequence of $\{u^k\}$ and a function u such that u is a weak solution of problem (1.1) with $I(u) \ge 0$ and $J(u) \le d$ for $0 \le t < \infty$.

$\square$

Theorem 4.2

(Blow-up for $J(u_0) = d$.) Let (H1) hold and u be a weak solution of problem (1.1) with $u_0 \in H^2_{\mathscr {N}}(\Omega )$. If $J(u_0) = d$ and $I(u_0) < 0$, then there exists a finite time $T^*$ such that u blows up at $T^*$.

Proof

Similarly to the proof of Theorem 3.2, we can get

$$\begin{aligned} F_1'(t)\ge \frac{p-2}{p} \int \limits _{\Omega } |\nabla u|^pdx - 2J(u). \end{aligned}$$

Since $J(u_0) = d$, $I(u_0) < 0$, by the continuity of J(u) and I(u) with respect to t, there exists a $t_0 > 0$ such that $J(u(x,t)) > 0$ and $I(u(x,t)) < 0$ for $0 < t \le t_0$. From $(u_t, u) = -I(u)$, we have $u_t \not \equiv 0$ for $0 < t \le t_0$. Furthermore, we have

$$\begin{aligned} J(u(t_0))\le d-\int \limits _{0}^{t_0} \Vert u_s\Vert _2^2 \;ds<d. \end{aligned}$$

Taking $t = t_0$ as the initial time and by Lemma 3.2, we know that $u(x,t) \in V$ for $t>t_0$. The reminder of the proof is almost the same as that of Theorem 3.2 and hence is omitted. $\square$

In short, we also have the following conclusions.

Remark 4.1

(Sharp condition for $J(u_0) = d$.) Let (H1) hold and $u_0 \in H^2_{\mathscr {N}}(\Omega )$. Assume that $J(u_0) = d$. If $I(u_0) \ge 0$, then problem (1.1) admits a global weak solution; if $I(u_0) < 0$, then problem (1.1) admits no global weak solution.

4 The case $J(u_0) > d$

In this section, inspired by some ideas from [4], we will investigate the conditions to ensure the existence of global solutions or blow-up solutions to problem (1.1) with $J(u_0) > d$. Before moving on to our result, let us pause to give some pivotal sets and functionals.

$$\begin{aligned}{} & {} \mathcal {N}_+=\{u\in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}~|~I(u)>0\}, ~~\mathcal {N}_-=\{u\in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}~|~I(u)<0\},\\{} & {} J^\alpha = \left\{ u\in H^2_{\mathscr {N}}(\Omega ) \backslash \{0\}~|~ J(u)< \alpha \right\} ,\\{} & {} \mathcal {N}^\alpha = \mathcal {N} \cap J^\alpha = \left\{ u\in \mathcal {N} ~|~ J(u) < \alpha \right\} , \quad \forall \; \alpha >d. \end{aligned}$$

Also define

$$\begin{aligned} \lambda _\alpha = \inf \left\{ \Vert u\Vert _2^2 ~|~u \in \mathcal {N}^\alpha \right\} , \quad \Lambda _\alpha = \sup \left\{ \Vert u\Vert _2^2 ~|~u \in \mathcal {N}^\alpha \right\} . \end{aligned}$$

(5.1)

It is clear that $\lambda _\alpha ~(\Lambda _\alpha )$ is nonincreasing (nondecreasing) with respect to $\alpha$. In addition, we introduce the following three sets:

$$\begin{aligned}&\mathcal {B}= \left\{ u_0 \in H^2_{\mathscr {N}}(\Omega ) ~|~ \mathrm{the~ solution~} u = u(t) \mathrm{~of~ (1.1) ~blows~ up~ in~ finite~ time~} \right\} , \\&\mathcal {G}= \left\{ u_0 \in H^2_{\mathscr {N}}(\Omega ) ~|~ \mathrm{the~ solution~} u = u(t) \mathrm{~of~ (1.1) ~exists~ for~ all~ } t > 0 \right\} ,\\&\mathcal {G}_0= \left\{ u_0 \in H^2_{\mathscr {N}}(\Omega ) ~|~ u(t) \rightarrow 0 \mathrm{~in ~ H^2_{\mathscr {N}}(\Omega ) ~as~} t~ \rightarrow \infty \right\} . \end{aligned}$$

To better analyze the behavior of the solutions to problem (1.1) with high energy level, we first present some useful lemmas.

Lemma 5.1

Let (H1) hold. Then

(i) 0 is away from both $\mathcal {N}$ and $\mathcal {N}_-,$ i.e., dist$(0, \mathcal {N})>0$, dist$\mathrm{(0, \mathcal {N}_-)} > 0$.

(ii) For any $\alpha > 0$, the set $J^\alpha \cap \mathcal {N}_+$ is bounded in $H^2_{\mathscr {N}}(\Omega )$.

Proof

(i) For any $u \in \mathcal {N},$ according to the definition of d and I(u), we have

$$\begin{aligned} d \le J(u) = \frac{1}{2}\Vert \Delta u\Vert _2^2-\frac{1}{p}\Vert \nabla u\Vert _p^p =\frac{p-2}{2p}\Vert \Delta u\Vert _2^2, \end{aligned}$$

(5.2)

which implies

$$\begin{aligned} \Vert \Delta u\Vert _2^2 \ge \frac{2pd}{p-2}. \end{aligned}$$

Therefore, we know that $dist \mathrm{(0, \mathcal {N})}= \inf \limits _{u \in \mathcal {N}}\Vert u\Vert _{H^2_{\mathscr {N}}}=\inf \limits _{u \in \mathcal {N}}\Vert \Delta u\Vert _2 >0.$

For any $u \in \mathcal {N}_-$, from the embedding inequality, we have

$$\begin{aligned} \Vert \Delta u\Vert _2^2 <\Vert \nabla u\Vert _p^p \le S_p^{-\frac{p}{2}} \Vert \Delta u\Vert _2^p, \end{aligned}$$

(5.3)

which implies

$$\begin{aligned} \Vert \Delta u\Vert _2^2 \ge S_p^{\frac{p}{p-2}}, \end{aligned}$$

where $S_p > 0$ is given in Lemma 3.1. Thus, $dist \mathrm{(0, \mathcal {N}_-)}= \inf \limits _{u \in \mathcal {N}_-}\Vert u\Vert _{H^2_{\mathscr {N}}} =\inf \limits _{u \in \mathcal {N}_-}\Vert \Delta u\Vert _2 >0.$

(ii) For any $u \in J^\alpha \cap \mathcal {N}_+$, we obtain

$$\begin{aligned} \alpha \ge J(u) = \frac{1}{p} I(u) + \frac{p-2}{2p} \Vert \Delta u\Vert _2^2 > \frac{p-2}{2p} \Vert \Delta u\Vert _2^2, \end{aligned}$$

(5.4)

which yields

$$\begin{aligned} \Vert u\Vert _{H^2_{\mathscr {N}}}^2 = \Vert \Delta u\Vert _2^2 < \frac{2p \alpha }{p-2}. \end{aligned}$$

Therefore, the set $J^\alpha \cap \mathcal {N}_+$ is bounded in $H^2_{\mathscr {N}}(\Omega )$. $\square$

Next, we discuss the properties of $\lambda _\alpha$ and $\Lambda _\alpha$.

Lemma 5.2

Let (H1) hold. Then for any $\alpha >d$, $\lambda _\alpha$ and $\Lambda _\alpha$ defined in (5.1) satisfy $0 < \lambda _\alpha$ $\le \Lambda _\alpha \le M_\alpha < +\infty$.

Proof

First, we prove $\Lambda _\alpha \le M_\alpha < +\infty$, where $\Lambda _\alpha = \sup \left\{ \Vert u\Vert _2^2 ~|~u \in \mathcal {N}^\alpha \right\} .$ For any $u \in \mathcal {N}^\alpha ,$

$$\begin{aligned} J(u)= \frac{1}{2} I(u) + \frac{p-2}{2p}\Vert \nabla u\Vert _p^p = \frac{p-2}{2p}\Vert \nabla u\Vert _p^p \le \alpha , \end{aligned}$$

(5.5)

which implies

$$\begin{aligned} \Vert \nabla u\Vert _p^p \le \frac{2p \alpha }{p-2}. \end{aligned}$$

Then from embedding inequality, we have

$$\begin{aligned} \Vert u\Vert _2^2 \le B^{-2}\Vert \nabla u\Vert _p^2 \le B^{-2}\left( \frac{2p \alpha }{p-2} \right) ^{\frac{2}{p}}:= M_\alpha . \end{aligned}$$

Therefore, we get $\Lambda _\alpha \le M_\alpha < +\infty$.

Next, we prove $\lambda _\alpha > 0,$ where $\lambda _\alpha = \inf \left\{ \Vert u\Vert _2^2 ~|~u \in \mathcal {N}^\alpha \right\} .$ The Gagliardo–Nirenberg inequality indicates that there exists a positive constant $B_2$ such that

$$\begin{aligned} \Vert \nabla u\Vert _p \le B_2 \Vert \Delta u\Vert _2^\theta \Vert u\Vert _2^{1-\theta }, \end{aligned}$$

where $\theta = \frac{1}{2} + \frac{N(p-2)}{4p} \in \left( \frac{1}{2}, 1 \right)$. Moreover, noticing that $u \in \mathcal {N} \Rightarrow \Vert \Delta u\Vert _2^{\frac{2}{p}} = \Vert \nabla u\Vert _p$, we have

$$\begin{aligned} \Vert u\Vert _2^2 \ge B_2^{-\frac{2}{1-\theta }} \left( \Vert \Delta u\Vert _2^2 \right) ^{\frac{1}{1-\theta }\left( \frac{2}{p}-\theta \right) }. \end{aligned}$$

Obviously, by Lemma 5.1(i) and the definition of $\mathcal {N}^\alpha$, the right-hand side of the above inequality remains bounded away from 0 no matter what the sign of $\frac{2}{p}-\theta$ is. Therefore, $\lambda _\alpha > 0$. $\square$

In the following, we give a criterion for the existence of global solutions that tend to 0 as t tends to $\infty$ or finite-time blow-up solutions in terms of $\lambda _\alpha$ and $\Lambda _\alpha$ for supercritical initial energy, i.e., $J(u_0) > d$. Noticing that $\lambda _{J(u_0)} > 0$, Theorem 5.1(i) is nontrivial. Our main results are as follows:

Theorem 5.1

Let (H1) hold and $J(u_0) >d$. Then we have

(1) If $u_0 \in \mathcal {N}_+$ and $\Vert u_0\Vert _2^2 \le \lambda _{J(u_0)}$, then $u_0 \in \mathcal {G}$. That is, the weak solution u of problem (1.1) exists globally and $u(t) \rightarrow 0$ as $t \rightarrow +\infty$.

(2) If $u_0 \in \mathcal {N}_-$ and $\Vert u_0\Vert _2^2 \ge \Lambda _{J(u_0)}$, then $u_0 \in \mathcal {B}$. That is, the weak solution u of problem (1.1) blows up in finite time.

Proof

We denote by $\omega (u_0) = \cap _{t\ge 0} \overline{\left\{ u(s): s \ge t \right\} }$ the $\omega -$limit of $u_0$. And as shown by Definition 3.1, $T^*$ represents the maximum existence time of the solution.

(1) If $u_0 \in \mathcal {N}_+$ and $\Vert u_0\Vert _2^2 \le \lambda _{J(u_0)}$.

First, we claim that $u \in \mathcal {N}_+,$ for all $t \in [0,T^*)$. By contradiction, there exists a $t_0 \in (0,T^*)$ such that $u \in \mathcal {N}_+$ for $t\in [0,t_0)$ and $u(t_0) \in \mathcal {N}$. Taking $\varphi = u$ in the definition of weak solution (2.1), we obtain

$$\begin{aligned} \frac{d}{dt} \Vert u\Vert _2^2 = 2(u,u_t) = -2I(u) <0,\quad \forall \; t \in [0, t_0). \end{aligned}$$

(5.6)

Then, we have

$$\begin{aligned} \Vert u(t_0)\Vert _2^2 < \Vert u_0\Vert _2^2 \le \lambda _{J(u_0)}. \end{aligned}$$

(5.7)

On the other hand, (5.6) implies that $u_t \not \equiv 0$ for $(x, t) \in \Omega \times (0, t_0).$ It follows from (3.2) that $J(u(t_0)) < J(u_0)$, which yields $u(t_0) \in J^{J(u_0)}$. Therefore, $u(t_0)\in \mathcal {N}^{ J(u_0)}.$ By the definition of $\lambda _{J(u_0)}$, we obtain

$$\begin{aligned} \Vert u(t_0)\Vert _2^2 \ge \lambda _{J(u_0)}, \end{aligned}$$

(5.8)

which contradicts (5.7). Therefore, $u \in \mathcal {N}_+,$ for all $t \in [0,T^*)$. Further, we know that $u \in \mathcal {N}_+ \cap J^{J(u_0)}$ for all $t \in [0,T^*)$.

Next, Lemma 5.1(ii) shows that the orbit u(t) remains bounded in $H^2_{\mathscr {N}}(\Omega )$ for $t \in [0,T^*)$ so that $T^*= \infty$.

Finally, we prove $\omega (u_0)={0}$, i.e., $u(t) \rightarrow 0$ when $t \rightarrow +\infty .$ For any $\omega \in \omega (u_0)$, from (5.6) and the hypothesis, we can infer that

$$\begin{aligned} \Vert \omega \Vert _2^2 <\Vert u_0\Vert _2^2 \le \lambda _{J(u_0)}. \end{aligned}$$

(5.9)

In addition, according to (3.2), we can deduce $\omega \in J^{J(u_0)}$ from $J(\omega ) < J(u_0)$. Notice that (5.9) and $\lambda _{J(u_0)}= \inf \left\{ \Vert u\Vert _2^2 ~|u \in \mathcal {N}^{J(u_0)} \right\}$, we obtain $\omega \notin \mathcal {N}^{J(u_0)}$, further $\omega \notin \mathcal {N}$. Thus, $\omega (u_0) \cap \mathcal {N} = \emptyset$, which indicates $\omega (u_0) = \{0\}$. Therefore, the weak solution u of problem (1.1) exists globally and $u(t) \rightarrow 0$ as $t \rightarrow +\infty$.

(2) If $u_0 \in \mathcal {N}_-$ and $\Vert u_0\Vert _2^2 \ge \Lambda _{J(u_0)}$.

We first claim that $u \in \mathcal {N}_-,$ for all $t \in [0,T^*)$. By contradiction, there exists a $t_0 \in (0,T^*)$ such that $u \in \mathcal {N}_-$ for $t\in [0,t_1)$ and $u(t_1) \in \mathcal {N}$. Similar to case (1), we get $u(t_1) \in \mathcal {N}^{J(u_0)}$. Review the definition of $\Lambda _{J(u_0)}$, we get

$$\begin{aligned} \Vert u(t_1)\Vert _2^2 \le \Lambda _{J(u_0)}. \end{aligned}$$

(5.10)

Moreover, noticing that $I(u(t)) < 0$ for $t \in [0, t_1)$, it follows from (5.6) that

$$\begin{aligned} \frac{d}{dt} \Vert u\Vert _2^2 = 2(u,u_t) = -2I(u) > 0,\quad \forall \; t \in [0, t_1). \end{aligned}$$

(5.11)

Then, we have

$$\begin{aligned} \Vert u(t_1)\Vert _2^2 > \Vert u_0\Vert _2^2 \ge \Lambda _{J(u_0)}, \end{aligned}$$

(5.12)

which contradicts (5.10). Therefore, $u \in \mathcal {N}_-$ for all $t \in [0,T^*)$. Further, we obtain $u \in \mathcal {N}_- \cap J^{J(u_0)}$ for all $t \in [0,T^*)$.

Next, we prove that $\omega (u_0) \cap \mathcal {N} = \emptyset$, $T^* < +\infty$. If not, suppose $T^* = +\infty$, then for any $\omega \in \omega (u_0)$, we have

$$\begin{aligned} \Vert \omega \Vert _2^2 > \Vert u_0\Vert _2^2 \ge \Lambda _{J(u_0)}, \end{aligned}$$

(5.13)

and $J(\omega ) < J(u_0)$ from (5.11) and (3.2), respectively. The second inequality implies $\omega \in J^{J(u_0)}$. Noting that the definition of $\Lambda _{J(u_0)}$ and (5.13), we derive $\omega \notin \mathcal {N}^{J(u_0)}$, further $\omega \notin \mathcal {N}$. Thus, $\omega (u_0) \cap \mathcal {N} = \emptyset$, which indicates $\omega (u_0) = \{0\}$, which is contradictive with Lemma 5.1(i). Hence, $\omega (u_0) = \emptyset$, $T^* < +\infty$. That is, the weak solution u of problem (1.1) blows up in finite time.

Based on the above discussion, we have completed the proof of Theorem 5.1. $\square$

Proposition 5.1

If $J(u_0)$ satisfies $d< J(u_0) < \frac{p-2}{2p} B^p \Vert u_0\Vert _2^p$, then $u_0 \in \mathcal {N}_- \cap \mathcal {B}$. That is, the weak solution u of problem (1.1) blows up in finite time.

Proof

From (3.3), (3.1) and embedding inequality, we obtain

$$\begin{aligned} J(u_0) = \frac{1}{2} I(u_0) + \frac{p-2}{2p} \Vert \nabla u_0\Vert _p^p \ge \frac{1}{2} I(u_0) + \frac{p-2}{2p} B^p \Vert u_0\Vert _2^p. \end{aligned}$$

Combining the above inequality with the given assumption, we can obtain $I(u_0) < 0$, i.e., $u_0 \in \mathcal {N}_-$. In addition, according to the assumption and Lemma 5.2, we know that

$$\begin{aligned} \Vert u_0\Vert _2^2 > B^{-2}\left( \frac{2p J(u_0) }{p-2} \right) ^{\frac{2}{p}} = M_{J(u_0)} \ge \Lambda _{J(u_0)}. \end{aligned}$$

Finally, by utilizing Theorem 5.1, it is easy to derive the conclusion of Proposition 5.1. $\square$

Theorem 5.2

For any $M > d$, there exists initial value $u_M \in \mathcal {N}_-$ such that $J(u_M) \ge M$ and $u_M \in \mathcal {B}$.

Proof

Assume that $M > d$ and $\Omega _1, \Omega _2$ are two arbitrary disjoint open subdomains of $\Omega$. Furthermore, we assume that $\nu \in H^2_{\mathscr {N}}(\Omega _1)$ is an arbitrary nonzero function. Then, we take $\xi >0$ large enough such that

$$\begin{aligned} J(\xi u)=\frac{\xi ^2}{2}\Vert \Delta u\Vert _2^2-\frac{\xi ^p}{p}\Vert \nabla u\Vert _p^p\le 0,\quad M < \frac{p-2}{2p} B^p \Vert \xi \nu \Vert _2^p. \end{aligned}$$

We fix such a number $\xi >0$ and choose a function $\mu \in H^2_{\mathscr {N}}(\Omega _2)$ satisfying $M = J(\mu ) + J(\xi \nu )$. Extend $\nu$ and $\mu$ to be 0 in $\Omega \backslash \Omega _1$ and $\Omega \backslash \Omega _2$, respectively, and set $u_M = \mu + \xi \nu$, then $J(u_M) = J(\mu ) + J(\xi \nu ) = M$, and it follows that

$$\begin{aligned} \frac{p-2}{2p} B^p \Vert u_M\Vert _2^p\ge \frac{p-2}{2p} B^p \Vert \xi \nu \Vert _2^p> M = J(u_M) > d. \end{aligned}$$

By Proposition 5.1 it is seen that $u_M \in \mathcal {N}_- \cap \mathcal {B}$. $\square$

5 Lower bound for the lifespan

We all know that the upper bound guarantees blowing up of the solution and the importance of the lower bound is that it may provide us a safe time interval for operation if we use problem (1.1) to model a physical process. In this section, we mainly give the lower bound estimate for the lifespan.

Theorem 6.1

If $T^{*}$ is blow-up time, then $T^{*}$ satisfies the following estimate

$$\begin{aligned} T^{*}\ge \frac{\Vert u_0\Vert _2^{-2\kappa } }{B_2^{\frac{2p \kappa }{p-2}} \kappa }, \quad 2<p\le p_*, ~N\ge 2, \end{aligned}$$

where $\kappa = \frac{4(p-2)}{8-2p-N(p-2)}$ and $p_* = 2+ \frac{4}{N+2}$.

Proof

Set

$$\begin{aligned} F_{2}(t) = \int \limits _{\Omega }|u|^2dx. \end{aligned}$$

Taking the first derivative of $F_{2}(t)$, then using Gagliardo–Nirenberg inequality, we have

$$\begin{aligned} F_{2}'(t) =\int \limits _{\Omega }uu_{t}dx&=\int \limits _{\Omega }u \left( - \Delta ^2 u -\Delta _p u \right) dx\nonumber \\&= -\Vert \Delta u\Vert ^2_2 +\Vert \nabla u\Vert _p^p\nonumber \\&\le -\Vert \Delta u\Vert ^2_2 + B_2^p \Vert \Delta u\Vert _2^{\theta p} \Vert u\Vert _2^{(1-\theta )p}, \end{aligned}$$

(6.1)

where $\theta p = \frac{N(p-2)}{4} + \frac{p}{2}$. Since $2<p\le p_*$, this shows $\theta p>2$. Then, together with the $\varepsilon$-Young’s inequality, we have

$$\begin{aligned} F_{2}'(t) \le -\Vert \Delta u\Vert ^2_2 + B_2^p \left( \varepsilon ^\beta \Vert \Delta u\Vert ^2_2 + \varepsilon ^ {-\beta '} \Vert u\Vert _2^{(1-\theta )p \beta '} \right) , \end{aligned}$$

(6.2)

where $\beta = \frac{2}{\theta p}$ and $\beta ' = \frac{2}{2- \theta p}$. Next, we choose $\varepsilon$, such that $B_2^p \varepsilon ^\beta = 1$, which implies $B_2^p \varepsilon ^ {-\beta '} = B_2^{p \beta '}$ by virtue of $\frac{1}{\beta } + \frac{1}{\beta '} = 1$. Then (6.2) can be reduced to

$$\begin{aligned} F_{2}'(t) \le B_2^{p \beta '} F_{2}^{\frac{(1-\theta )p \beta '}{2}}(t). \end{aligned}$$

(6.3)

A simple integration of (6.3) over (0, t) is easy to calculate that

$$\begin{aligned} \Vert u\Vert _2^2 \le \left[ \frac{1}{\Vert u_0\Vert _2^{-2\kappa } - B_2^{p \beta '}\kappa t } \right] ^{\frac{1}{\kappa }}. \end{aligned}$$

(6.4)

Therefore,

$$\begin{aligned} \lim \limits _{t \rightarrow \kappa ^{-1} B_2^{-p \beta '} \Vert u_0\Vert _2^{-2\kappa } } \Vert u\Vert _2^2 =+\infty . \end{aligned}$$

(6.5)

In other words, we also obtain some estimate for the upper bound of the blow-up time $T^*$

$$\begin{aligned} T^{*}\ge \kappa ^{-1} B_2^{\frac{2p \kappa }{2-p}} \Vert u_0\Vert _2^{-2\kappa },\quad 2<p\le p_*, ~N\ge 2, \end{aligned}$$

(6.6)

where $\kappa = \frac{4(p-2)}{8-2p-N(p-2)}$. $\square$

Remark 6.1

From the above analysis, it is not difficult to find, if all the assumptions in Theorems 3.2 and 6.1 hold, then the following blow-up rate holds

$$\begin{aligned} C_1 \left( T^*_1 -t \right) ^{-\frac{2}{p-2}} \le \Vert u\Vert _2^2 \le C_2 \left( T^*_2 -t \right) ^{-\frac{2}{p-2}}, \quad 2<p\le 2+ \frac{4}{N+2}, N\ge 2, \end{aligned}$$

where $T^*_1 = \frac{pd}{(p-2)^2 B^p (d-J(u_0) ) \Vert u_0\Vert _2^{p-2} }$, $T^*_2 = \kappa ^{-1} B_2^{\frac{2p \kappa }{2-p}} \Vert u_0\Vert _2^{-2\kappa }$, $\kappa = \frac{4(p-2)}{8-2p-N(p-2)}$.