Global well-posedness and optimal decay rates for a transmission problem of viscoelastic wave equations with degenerate nonlocal damping

Abstract

This paper investigates a transmission problem of viscoelastic wave equations with degenerate nonlocal damping. We prove the global well-posedness of the problem with the aid of Faedo–Galerkin technique and the multiplier method. Meantime, by introducing a new Lyapunov functional, we establish the optimal explicit and general energy decay results.

1 Introduction

We consider a transmission problem of viscoelastic wave equations with degenerate nonlocal internal (frictional) damping

$$\begin{aligned}&u_{tt}-\Delta u+\int \limits _{0}^{t}g(t-s)\Delta u(s){\textrm{d}}s+\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }u_{t}+f_{1}(u)=0,\;\;(x,t)\in \Omega _{1}\times (0,+\infty ), \end{aligned}$$

(1.1)

$$\begin{aligned}&v_{tt}-\Delta v+f_{2}(v)=0,\;\;(x,t)\in \Omega _{2}\times (0,+\infty ), \end{aligned}$$

(1.2)

subject to the boundary and transmission conditions

$$\begin{aligned}&\frac{\partial u}{\partial \nu }-\int \limits _{0}^{t}g(t-s)\frac{\partial u(s)}{\partial \nu }{\textrm{d}}s+u_{t}=0, \;\;(x,t)\in \Gamma _{2}\times (0,+\infty ), \end{aligned}$$

(1.3)

$$\begin{aligned}&v=0,\;\;(x,t)\in \Gamma _{0}\times (0,+\infty ), \end{aligned}$$

(1.4)

$$\begin{aligned}&u=v,\;\;\frac{\partial u}{\partial \nu }-\int \limits _{0}^{t}g(t-s)\frac{\partial u(s)}{\partial \nu }{\textrm{d}}s=\frac{\partial v}{\partial \nu }, \;\;(x,t)\in \Gamma _{1}\times (0,+\infty ), \end{aligned}$$

(1.5)

and initial conditions

$$\begin{aligned}&u(x,0)=u_{0}(x),\;\;u_{t}(x,0)=u_{1}(x),\;\;x\in \Omega _{1}, \end{aligned}$$

(1.6)

$$\begin{aligned}&v(x,0)=v_{0}(x),\;\;v_{t}(x,0)=v_{1}(x),\;\;x\in \Omega _{2}, \end{aligned}$$

(1.7)

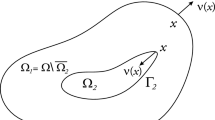
where $\beta \ge 1$, $\Omega \subset {\mathbb {R}}^{N}$($N\ge 2$) is a bounded domain with smooth boundary $\partial \Omega =\Gamma _{0}\cup \Gamma _{2}$, $\overline{\Gamma _{0}}\cap \overline{\Gamma _{2}}=\emptyset$. $\Gamma _{0}$ is the boundary of small ball $B(x_{0})$ containing $x_{0}$ in $\Omega$, $\Omega _{2}\subset \Omega$ is a subdomain with smooth boundary $\Gamma _{0}\cup \Gamma _{1}$ in the outside of $B(x_{0})$, and $\Omega _{1}=\Omega \setminus (\overline{\Omega _{2}}\cup B(x_{0}))$ is a subdomain with smooth boundary $\Gamma _{2}\cup \Gamma _{1}$. $\nu$ denotes the unit outer normal vector pointing toward the exterior of $\Omega _{1}$, and there exists $\delta >0$, such that $m\cdot \nu \ge \delta >0$ on $\Gamma _{2}$, where $m:=m(x)=x-x_{0}$ (see Fig. 1 for an example). Moreover, the relaxation function g and nonlinearities $f_{i}$ ($i=1,2$) satisfy appropriate conditions.

Fig. 1

An example of $\Omega$

The phenomenon that several kinds of materials with different elastic properties connect together over the whole surface appears frequently in the applications of engineering technology, material science, and so on. The wave propagations among different materials are called transmission problem. In view of mathematics, the transmission problem for wave propagation is related to the problem of a hyperbolic equation where the coefficient of the elliptic operator is discontinuous, which causes difficulties on the studies of well-posedness, regularity and qualitative properties.

There have been fruitful results on the existence, regularity, controllability and decay estimates of solutions for the transmission problem without delay and memory, see [1,2,3] and references therein. For example, Marzocchi [1] proved that the solution for a semilinear transmission problem in one-dimensional space between an elastic and thermoelastic material decays exponentially. This result was extended to N-dimensional space by Marzocchi and Naso [2]. For the transmission problem with frictional damping, Bastos and Raposo [3] proved the well-posedness and exponential stability of the total energy.

For the researches on transmission problems with viscoelastic dampings, Rivera and Oquendo [4] considered the transmission problem between viscoelastic part and elastic part in one-dimensional space

$$\begin{aligned}&\rho _{1}u_{tt}(x,t)-au_{xx}(x,t)=0,\quad (x,t)\in (0,L_{1})\times (0,+\infty ),\\&\rho _{2}v_{tt}(x,t)-bv_{xx}(x,t)+\int \limits _{0}^{t}g(t-s)v_{xx}(x,s){\textrm{d}}s=0,\quad (x,t)\in (L_{1},L_{2})\times (0,+\infty ), \end{aligned}$$

and obtained that the energy decays exponentially provided g decays exponentially. Andrade et al. [5] studied the following nonlinear transmission problem

$$\begin{aligned}&\rho _{1}u_{tt}(x,t)-\gamma _{1}\Delta u(x,t)+f(u)=0,\quad (x,t)\in \Omega _{1}\times (0,+\infty ),\\&\rho _{2}v_{tt}(x,t)-\gamma _{2}\Delta v(x,t)+f(v)=0,\quad (x,t)\in \Omega _{2}\times (0,+\infty ), \end{aligned}$$

with a memory condition on a part of the boundary

$$\begin{aligned} u(x,t)+\int \limits _{0}^{t}g(t-s)\frac{\partial u(x,s)}{\partial \nu }{\textrm{d}}s=0,\quad (x,t)\in \Gamma _{1}\times (0,+\infty ). \end{aligned}$$

They proved the global existence of solutions and showed that the solutions had the same decay rates provided the relaxation function decays exponentially or polynomially. Later, Alves et al. [6] investigated the transmission problem for nonlinear Timoshenko beam system with internal memory in one-dimensional space and derived some similar results to [5]. Moreover, the authors of this article investigated the wave transmissions with boundary memory sources, the transmission problems of (weak) viscoelastic wave equations with linear or nonlinear delay terms and transmission problem of viscoelastic Timoshenko systems and derived general and optimal decay estimates; one can see [7,8,9,10,11].

Recently, we are particularly concerned with the issue on optimal decay estimate for scalar viscoelastic equations, and the advances on decay estimate on wave equations with nonlocal damping terms. For example, Mustafa [12] considered the viscoelastic wave equation

$$\begin{aligned} u_{tt}-\Delta u+\int \limits _{0}^{t}g(t-s)\Delta u(s){\textrm{d}}s=0,\quad (x,t)\in \Omega \times (0,+\infty ). \end{aligned}$$

Under the homogeneous Dirichlet boundary condition, they presented the optimal decay estimate of the energy with the general decay assumption on memory kernel, which is $g'(t)\le -\xi (t)H\left( g(t)\right)$, $\forall t>0$. Lange and Menzala [13] studied firstly the beam equation with nonlocal damping

$$\begin{aligned} u_{tt}+\Delta ^{2} u+M\left( \Vert \nabla u\Vert _{2}^{2}\right) u_{t}=0,\quad (x,t)\in {\mathbb {R}}^{N}\times (0,+\infty ), \end{aligned}$$

where $M:[0,+\infty )\rightarrow [1,+\infty )$ is a function of $C^{1}$-class with $M(s)\ge 1+s$, $\forall s\ge 0$, in which the nonlocal damping term $M\left( \Vert \nabla u\Vert _{2}^{2}\right) u_{t}$ represented the friction mechanism depended on the average of u. They pointed out that this model is closely related to a nonlinear Schrödinger equation with a time-dependent dissipation and obtained the uniform decay estimate of the energy. Later, Cavalcanti et al. [14] considered the equation with viscoelastic damping. Zhang et al. [15] investigated the Dirichlet initial boundary problem of wave equation with degenerate nonlocal damping and nonlinear source

$$\begin{aligned} u_{tt}-\Delta u+M\left( \Vert \nabla u\Vert _{2}^{2}\right) g\left( u_{t}\right) =f(u),\quad (x,t)\in \Omega \times (0,+\infty ). \end{aligned}$$

By the theory of potential well, they showed the asymptotic stability of energy and derived some sufficient conditions leading to finite time blowup. In addition, for the advances on long-time dynamic behavior of Kirchhoff-type wave equation with nonlocal weak damping (including the cases of fourth and second order) and the infinite blow-up phenomenon of Kirchhoff-type wave equation with strong damping, we refer to [16,17,18,19,20,21,22,23] and the references therein.

In view of the works mentioned above, one can find that the studies on transmission problem of viscoelastic wave equations with degenerate nonlocal internal (fractional) damping have not been started. The main difficulties lie in seeking the influence caused by the competition between internal viscoelastic dissipation, degenerate nonlocal internal damping and nonlinearities on the asymptotic behavior of the solution. Motivated by these observations, we establish the global well-posedness of the solution by Faedo–Galerkin technique and the multiplier method and derive the general and optimal decay rates of the energy by introducing a new Lyapunov functional.

The remainder of this paper is organized as follows. In Sect. 2, we introduce some material needed in the proof of our results and state the main results. In Sect. 3, we establish the global well-posedness of the solution. Finally, we derive the general and optimal decay rates in Sect. 4.

2 Preliminaries and main results

Throughout this paper, we will use c and C to denote various constants. Define

$$\begin{aligned}{} & {} H_{\Gamma }^{1}(\Omega _{2}):=\{v\in H^{1}(\Omega _{2}):v=0\;\textrm{on}\;\Gamma _{0}\}, \\{} & {} V:=\{(u,v)\in H^{1}(\Omega _{1})\times H_{\Gamma }^{1}(\Omega _{2}):u=v\;\textrm{on}\;\Gamma _{1}\}, \\{} & {} (u,v)_{\Omega _{i}}:=\int \limits _{\Omega _{i}}u(x)v(x){\textrm{d}}x,\;i=1,2,\quad (u,v)_{\Gamma _{j}}:=\int \limits _{\Gamma _{j}}u(x)v(x){\textrm{d}}x,\;j=1,2. \end{aligned}$$

For a Banach space X, $\Vert \cdot \Vert _{X}$ represents the norm of X. For simplicity, we will use $\Vert \cdot \Vert _{\Omega _{i}}$ and $\Vert \cdot \Vert _{\Gamma _{j}}$ to denote $\Vert \cdot \Vert _{L^{2}(\Omega _{i})}$ and $\Vert \cdot \Vert _{L^{2}(\Gamma _{j})}$, respectively. Moreover, $L_{1}(t)\sim L_{2}(t)$ means that there exist constants $c_{1},c_{2}>0$ such that

$$\begin{aligned} c_{1}L_{1}(t)\le L_{2}(t)\le c_{2}L_{1}(t), \end{aligned}$$

and we denote

$$\begin{aligned} (g\diamond u)(t):=\int \limits _{0}^{t}g(t-s)\Vert u(t)-u(s)\Vert _{\Omega _{1}}^{2}{\textrm{d}}s. \end{aligned}$$

Now, we present some reasonable assumptions.

• ${{\textbf {(H1)}}}$$g:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$ is a nonincreasing differentiable $C^{1}$-function satisfying

  $$\begin{aligned} g(0)>0,\;l:=1-\int \limits _{0}^{+\infty }g(s){\textrm{d}}s>0. \end{aligned}$$

  (2.1)

  Meantime, there exists a $C^{1}$-function $H:(0,+\infty )\rightarrow (0,+\infty )$ which is a linear function or a strictly increasing and strictly convex $C^{2}$-function on (0, r], $r\le g(0)$ with $H(0)=H'(0)=0$, such that

  $$\begin{aligned} g'(t)\le -\xi (t)H\left( g(t)\right) ,\quad \forall t\ge 0, \end{aligned}$$

  (2.2)

  where $\xi (t)>0$ is a nonincreasing and differentiable positive functions.

• ${{\textbf {(H2)}}}$ Nonlinearities $f_{1},\;f_{2}\in C^{1}({\mathbb {R}})$ satisfy

  $$\begin{aligned} f_{i}(s)s\ge 0,\quad \forall s\in {\mathbb {R}},\;i=1,2. \end{aligned}$$

  Moreover, $f_{1}$ and $f_{2}$ are superlinear, that is

  $$\begin{aligned} f_{i}(s)s\ge (2+\mu _{i})F_{i}(s),\;F_{i}(s):=\int \limits _{0}^{s}f_{i}(\tau ){\textrm{d}}\tau ,\quad \forall s\in {\mathbb {R}},\;i=1,2, \end{aligned}$$

  (2.3)

  for some $\mu _{i}>0$ with the following growth condition:

  $$\begin{aligned} \left| f_{i}(x)-f_{i}(y)\right| \le \gamma \left( 1+|x|^{\rho -1}+|y|^{\rho -1}\right) |x-y|,\quad \forall x,y\in {\mathbb {R}}, \end{aligned}$$

  (2.4)

  where $\gamma >0$ and

  $$\begin{aligned} \left\{ \begin{array}{ll} 1\le \rho \le \frac{N}{N-2},&{}\quad N\ge 3,\\ 1\le \rho <+\infty ,&{}\quad N=1,2. \end{array} \right. \end{aligned}$$

  (2.5)

By virtue of the technique of Faedo–Galerkin approximation and some energy estimates, we obtain the following result on the well-posedness of problem (1.1)–(1.7).

Theorem 2.1

Suppose that (H1) and (H2) hold and initial data $(u_{0},v_{0})\in (H^{2}(\Omega _{1})\times H^{2}(\Omega _{2}))\cap V$, $(u_{1},v_{1})\in V$ satisfy the compatibility conditions

$$\begin{aligned}{} & {} \frac{\partial u_{0}}{\partial \nu }+u_{1}=0,\; \textrm{on}\;\Gamma _{2},\;v_{0}=0, \textrm{on}\;\Gamma _{0}, \\{} & {} u_{0}=v_{0},\;\frac{\partial u_{0}}{\partial \nu }=\frac{\partial v_{0}}{\partial \nu },\;\textrm{on}\;\Gamma _{1}, \end{aligned}$$

then there exists a unique solution (u, v) of problem (1.1)–(1.7) in the class

$$\begin{aligned}{} & {} (u,v)\in C\left( (0,+\infty );(H^{2}(\Omega _{1})\times H^{2}(\Omega _{2}))\cap V\right) , \\{} & {} (u_{t},v_{t})\in L^{2}\left( (0,+\infty );L^{2}(\Omega _{1})\times L^{2}(\Omega _{2})\right) . \end{aligned}$$

In order to describe the estimate of energy, we define the energy functional as

$$\begin{aligned} E(t):=\,&\frac{1}{2}\left[ \Vert u_{t}\Vert _{\Omega _{1}}^{2}+\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \Vert \nabla u\Vert _{\Omega _{1}}^{2}+(g\diamond \nabla u)(t)\right] +\int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x\nonumber \\&+\frac{1}{2}\left( \Vert v_{t}\Vert _{\Omega _{2}}^{2}+\Vert \nabla v\Vert _{\Omega _{2}}^{2}\right) +\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x, \end{aligned}$$

(2.6)

Then, taking the derivative directly to derive

$$\begin{aligned} \frac{{\textrm{d}}E(t)}{{\textrm{d}}t}=&-\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}-\Vert u_{t}\Vert _{\Gamma _{2}}^{2}+\frac{1}{2}(g'\diamond \nabla u)(t)-\frac{1}{2}\int \limits _{0}^{t}g(s){\textrm{d}}s\Vert \nabla u\Vert _{\Omega _{1}}^{2}. \end{aligned}$$

(2.7)

We derive the following decay estimate of the energy:

Theorem 2.2

Let (u, v) be the solution of (1.1)–(1.7) given in Theorem 2.1 and assume (H1)–(H2) hold. If the additional condition is imposed on $\Gamma _{1}$, that is,

$$\begin{aligned} m\cdot \nu \le 0\;\textrm{and}\; F_{1} \le F_{2} \;on\;\Gamma _{1}, \end{aligned}$$

(2.8)

then for $t_{1}>0$ large enough, there exist constants $c_{1},\;c_{2}>0$ such that

$$\begin{aligned} E(t)\le c_{1}{\mathcal {H}}^{-1}\left( c_{2}\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s\right) ,\; \forall t\ge t_{1}, \end{aligned}$$

where ${\mathcal {H}}(t):=\int \limits _{t}^{r}\frac{1}{sH'(s)}{\textrm{d}}s$.

Remark 2.1

The decay rate of the energy in Theorem 2.2 is optimal. In fact, similar to [12], it follows from (2.2) that

$$\begin{aligned} g'(t)\le -\xi (t)H\left( g(t)\right) \Rightarrow \int \limits _{g(t)}^{r}\frac{{\textrm{d}}s}{H\left( s\right) }=\int \limits _{g^{-1}(r)}^{t}\frac{-g'(s)}{H\left( g(s)\right) }{\textrm{d}}s \ge \int \limits _{g^{-1}(r)}^{t}\xi (s){\textrm{d}}s. \end{aligned}$$

Therefore, if we denote ${\mathcal {H}}_{0}(t):=\int \limits _{t}^{r}\frac{{\textrm{d}}s}{H\left( s\right) }$, then ${\mathcal {H}}_{0}(t)$ is strictly increasing and strictly convex on (0, r] and satisfying $\lim \nolimits _{t\rightarrow 0^{+}}{\mathcal {H}}_{0}(t)=+\infty$ and ${\mathcal {H}}_{0}\left( g(t)\right) \ge \int \limits _{g^{-1}(r)}^{t}\xi (s){\textrm{d}}s$, which imply that

$$\begin{aligned} g(t)\le {\mathcal {H}}_{0}^{-1}\left( \int \limits _{g^{-1}(r)}^{t}\xi (s){\textrm{d}}s\right) ,\;\forall t\ge g^{-1}(r). \end{aligned}$$

On the other hand, by the properties of H, ${\mathcal {H}}$ and ${\mathcal {H}}_{0}$, we can see that

$$\begin{aligned} {\mathcal {H}}(t)=\int \limits _{t}^{r}\frac{1}{sH'(s)}{\textrm{d}}s\le \int \limits _{t}^{r}\frac{1}{H(s)}{\textrm{d}}s={\mathcal {H}}_{0}(t) \Rightarrow {\mathcal {H}}^{-1}(t)\le {\mathcal {H}}_{0}^{-1}(t). \end{aligned}$$

Thus, Theorem 2.2 presents an optimal decay estimate of the energy.

Remark 2.2

We present some examples in the following to illustrate the result of Theorem 2.2:

• $\mathrm{(I)}$ Let $g(t)=a(1+t)^{-p}$ with $p>1$, and $a>0$ is an appropriate constant such that (2.1) hold. Computing directly we can see that the (2.2) holds by taking

  $$\begin{aligned} \xi (t)=pa^{-\frac{1}{p}},\;\;H(s)=s^{1+\frac{1}{p}}. \end{aligned}$$

  Then, it follows from Theorem 2.2 that

  $$\begin{aligned} E(t)\le c(1+t)^{-p},\quad \forall t>t_{1}. \end{aligned}$$

• $\mathrm{(II)}$ Let $g(t)=a\exp \left( -t^{q}\right)$ with $0<q<1$, and $a>0$ is an appropriate constant such that (2.1) hold. Computing directly we can see that (2.2) holds by taking

  $$\begin{aligned} \xi (t)=1,\;\;H(s)=\frac{qs}{\left[ \ln \left( \frac{a}{s}\right) \right] ^{\frac{1}{q}}}. \end{aligned}$$

  Since

  $$\begin{aligned} H'(s)=\frac{(1-q)+q\ln \left( \frac{a}{s}\right) }{\left[ \ln \left( \frac{a}{s}\right) \right] ^{\frac{1}{q}}},\;\textrm{and}\; H''(s)=\frac{(1-q)\left[ \ln \left( \frac{a}{s}\right) +\frac{1}{q}\right] }{\left[ \ln \left( \frac{a}{s}\right) \right] ^{\frac{1}{q}+1}}, \end{aligned}$$

  then H satisfies (H1) in (0, r] for $\forall 0<r<a$. Moreover,

  $$\begin{aligned}&{\mathcal {H}}(t)=\int \limits _{t}^{r}\frac{1}{sH'(s)}{\textrm{d}}s=\int \limits _{t}^{r}\frac{\left[ \ln \left( \frac{a}{s}\right) \right] ^{\frac{1}{q}}}{s\left[ (1-q)+q\ln \left( \frac{a}{s}\right) \right] }{\textrm{d}}s \le \left[ \ln \left( \frac{a}{t}\right) \right] ^{\frac{1}{q}}\Rightarrow {\mathcal {H}}^{-1}(t)\le a\exp \left( -t^{q}\right) . \end{aligned}$$

  Therefore, it follows from Theorem 2.2 that

  $$\begin{aligned} E(t)\le ac_{1}\exp \left( -c_{2}t^{q}\right) ,\quad \forall t>t_{1}. \end{aligned}$$

• $\mathrm{(III)}$ Let $g(t)=\frac{a}{(t+e)\left[ \ln (t+e)\right] ^{p}}$ with $p>1$, and $a>0$ is an appropriate constant such that (2.1) hold. Computing directly we can see that (2.2) holds by taking

  $$\begin{aligned} \xi (t)=\frac{\left[ \ln (t+e)+p\right] }{a^{\frac{1}{p}}(t+e)^{1-\frac{1}{p}}},\;\;H(s)=s^{1+\frac{1}{p}}. \end{aligned}$$

  Then, it follows from Theorem 2.2 that

  $$\begin{aligned} E(t)\le c_{1}\left( 1+\int \limits _{0}^{t}\frac{\ln (s+e)+p}{a^{\frac{1}{p}}(s+e)^{1-\frac{1}{p}}}{\textrm{d}}s\right) ^{-p} \le \frac{c}{(t+e)\left[ \ln (t+e)\right] ^{p}}, \end{aligned}$$

  for $t>t_{1}$ large enough.

3 Global well-posedness

In this section, we obtain some prior estimates of the energy and then establish the global well-posedness of (1.1)–(1.7) by virtue of the technique of Faedo–Galerkin approximation and the method of multiplier.

Proof of Theorem 2.1

We divide the proof into 4 steps.

Step1. Approximation problem. Let $\{(\varphi _{j},\psi _{j})\}_{j\in {\mathbb {N}}}$ be a basis in $(H^{2}(\Omega _{1})\times H^{2}(\Omega _{2}))\cap V$, which is orthogonal in $L^{2}(\Omega _{1})\times L^{2}(\Omega _{2})$. For $\forall n\ge 1$, denoting

$$\begin{aligned} V_{n}:=\textrm{span}\left\{ (\varphi _{1},\psi _{1}),(\varphi _{2},\psi _{2}),\ldots ,(\varphi _{n},\psi _{n})\right\} . \end{aligned}$$

We define the approximations:

$$\begin{aligned} \left( u^{(n)}(x,t),v^{(n)}(x,t)\right) :=\sum _{j=1}^{n}b_{jn}(t)(\varphi _{j}(x),\psi _{j}(x)), \end{aligned}$$

where $\left( u^{(n)},v^{(n)}\right)$ are solutions to the following Cauchy problem:

$$\begin{aligned}&\big (u_{tt}^{(n)},\varphi _{j}\big )_{\Omega _{1}}+\big (\nabla u^{(n)},\nabla \varphi _{j}\big )_{\Omega _{1}} -\left( \int \limits _{0}^{t}g(t-s)\nabla u^{(n)}(s){\textrm{d}}s,\nabla \varphi _{j}\right) _{\Omega _{1}} +\Vert \nabla u^{(n)}\Vert _{\Omega _{1}}^{2\beta }\big (u_{t}^{(n)},\varphi _{j}\big )_{\Omega _{1}}\nonumber \\&\quad +\big (f_{1}(u^{(n)}),\varphi _{j}\big )_{\Omega _{1}}+\big (u_{t}^{(n)},\varphi _{j}\big )_{\Gamma _{2}}+\big (v_{tt}^{(n)},\psi _{j}\big )_{\Omega _{2}} +\big (\nabla v^{(n)},\nabla \psi _{j}\big )_{\Omega _{2}} +\big (f_{2}(v^{(n)}),\psi _{j}\big )_{\Omega _{2}}=0, \end{aligned}$$

(3.1)

$$\begin{aligned}&\big (u^{(n)}(0),v^{(n)}(0)\big )=\left( u_{0n},v_{0n}\right) =\sum _{j=1}^{n}b_{jn}(0)\left( \varphi _{j},\psi _{j}\right) \rightarrow \big (u_{0},v_{0}\big ),\;\textrm{in}\;(H^{2}(\Omega _{1})\times H^{2}(\Omega _{2}))\cap V, \end{aligned}$$

(3.2)

$$\begin{aligned}&\big (u_{t}^{(n)}(0),v_{t}^{(n)}(0)\big )=\big (u_{1n},v_{1n}\big )=\sum _{j=1}^{n}b'_{jn}(0)\left( \varphi _{j},\psi _{j}\right) \rightarrow \left( u_{1},v_{1}\right) ,\;\textrm{in}\;V. \end{aligned}$$

(3.3)

According to the standard theory of ordinary differential equations, problem (3.1)–(3.3) has a unique solution $b_{jn}(t)$ defined on $[0,T_{n})$, $T_{n}>0$. The extension of these solutions to the whole interval [0, T], for all $T>0$, is a consequence of the first estimate which we are going to prove below.

Step 2. Energy estimates.

A prior estimate I: Multiplying (3.1) by $b'_{jn}(t)$ and summing on j, we can see

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}E^{(n)}(t)&=-\left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2\beta }\left\| u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}-\left\| u^{(n)}_{t}\right\| _{\Gamma _{2}}^{2} +\frac{1}{2}\big (g'\diamond \nabla u^{(n)}\big )(t)-\frac{1}{2}\int \limits _{0}^{t}g(s){\textrm{d}}s\left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} E^{(n)}(t):=\,&\frac{1}{2}\left[ \left\| u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}+\left\| v^{(n)}_{t}\right\| _{\Omega _{2}}^{2} +\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2}+\left\| \nabla v^{(n)}\right\| _{\Omega _{2}}^{2}\right] \nonumber \\&+\frac{1}{2}\big (g\diamond \nabla u^{(n)}\big )(t)+\int \limits _{\Omega _{1}}F_{1}\big (u^{(n)}\big ){\textrm{d}}x +\int \limits _{\Omega _{2}}F_{2}\big (v^{(n)}\big ){\textrm{d}}x. \end{aligned}$$

(3.5)

It follows from the nondecreasing property of g, Gronwall’s inequality and (3.2)–(3.3) that

$$\begin{aligned}&\left\| u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}+\left\| v^{(n)}_{t}\right\| _{\Omega _{2}}^{2} +\left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2}+\left\| \nabla v^{(n)}\right\| _{\Omega _{2}}^{2}+\int \limits _{0}^{t}\left\| u^{(n)}_{s}(s)\right\| _{\Gamma _{2}}^{2}{\textrm{d}}s\nonumber \\&\quad +\int \limits _{0}^{t}\left\| \nabla u^{(n)}(s)\right\| _{\Omega _{1}}^{2\beta }\left\| u^{(n)}_{s}(s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s \le L_{1},\;\forall n\in {\mathbb {N}}_{+}, \end{aligned}$$

(3.6)

where $L_{1}>0$ is a constant independent of n.

A prior estimate II: Differentiating (3.1) with respect to t and multiplying it by $b''_{jn}(t)$, and summing on j, we have

$$\begin{aligned}&\frac{1}{2}\frac{{\textrm{d}}}{{\textrm{d}}t}\left[ \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2}+\left\| v^{(n)}_{tt}\right\| _{\Omega _{2}}^{2} +\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}+\left\| \nabla v^{(n)}_{t}\right\| _{\Omega _{2}}^{2} \right] \nonumber \\&\qquad +\frac{1}{2}\big (g\diamond \nabla u^{(n)}_{t}\big )(t)+\left\| u^{(n)}_{tt}\right\| _{\Gamma _{2}}^{2}\nonumber \\&\quad \le -2\beta \left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2(\beta -1)} \int \limits _{\Omega _{1}}\nabla u^{(n)}\cdot \nabla u^{(n)}_{t}{\textrm{d}}x\int \limits _{\Omega _{1}} u^{(n)}_{t} u^{(n)}_{tt}{\textrm{d}}x-g(t)\int \limits _{\Omega _{1}}u^{(n)}_{tt}\Delta u_{n0}{\textrm{d}}x\nonumber \\&\qquad -\int \limits _{\Omega _{1}}f'_{1}\big (u^{(n)}\big )u^{(n)}_{t} u^{(n)}_{tt}{\textrm{d}}x -\int \limits _{\Omega _{2}}f'_{2}\big (v^{(n)}\big )v^{(n)}_{t} v^{(n)}_{tt}{\textrm{d}}x, \end{aligned}$$

(3.7)

where we have used the nonincreasing property and the following equality

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\int \limits _{0}^{t}g(t-s)\nabla u^{(n)}(s){\textrm{d}}s=\int \limits _{0}^{t}g(t-s)\nabla u^{(n)}_{s}(s){\textrm{d}}s+g(t)\nabla u_{n0}. \end{aligned}$$

It follows from Young’s inequality that

$$\begin{aligned}&-g(t)\int \limits _{\Omega _{1}}u^{(n)}_{tt}\Delta u_{n0}{\textrm{d}}x\le \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2} +\frac{g^{2}(0)}{4}\left\| \Delta u_{n0}\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(3.8)

$$\begin{aligned}&-2\beta \left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2(\beta -1)} \int \limits _{\Omega _{1}}\nabla u^{(n)}\cdot \nabla u^{(n)}_{t}{\textrm{d}}x\int \limits _{\Omega _{1}} u^{(n)}_{t} u^{(n)}_{tt}{\textrm{d}}x\nonumber \\&\quad \le 2\beta \left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{2\beta -1}\left\| u^{(n)}_{t}\right\| _{\Omega _{1}} \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}\left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}\nonumber \\&\quad \le \beta L_{1}^{\beta }\left( \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2}+\left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}\right) , \end{aligned}$$

(3.9)

$$\begin{aligned}&-\int \limits _{\Omega _{1}}f'_{1}\big (u^{(n)}\big )u^{(n)}_{t} u^{(n)}_{tt}{\textrm{d}}x\nonumber \\&\quad \le c\int \limits _{\Omega _{1}}\left( 1+2\left| u^{(n)}\right| ^{\rho -1}\right) u^{(n)}_{t} u^{(n)}_{tt}{\textrm{d}}x\nonumber \\&\quad \le c\left[ \,\,\int \limits _{\Omega _{1}}\left( 1+2\left| u^{(n)}\right| ^{\rho -1}\right) ^{N}{\textrm{d}}x\right] ^{\frac{1}{N}} \left( \,\,\int \limits _{\Omega _{1}}\left| u^{(n)}_{t}\right| ^{\frac{2N}{N-2}}{\textrm{d}}x\right) ^{\frac{N-2}{2N}} \left( \,\,\int \limits _{\Omega _{1}}\left| u^{(n)}_{tt}\right| ^{2}{\textrm{d}}x\right) ^{\frac{1}{2}}\nonumber \\&\quad \le c\max \left\{ 1,\;2^{N-1}\right\} \left[ |\Omega _{1}|+2^{N}\left\| \nabla u^{(n)}\right\| _{\Omega _{1}}^{N(\rho -1)}\right] ^{\frac{1}{N}} \left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}} \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}\nonumber \\&\quad \le c\left( \left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}+ \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2}\right) . \end{aligned}$$

(3.10)

Similarly, we can obtain

$$\begin{aligned} -\int \limits _{\Omega _{2}}f'_{2}\big (v^{(n)}\big )v^{(n)}_{t} v^{(n)}_{tt}{\textrm{d}}x \le c\left( \left\| \nabla v^{(n)}_{t}\right\| _{\Omega _{2}}^{2}+ \left\| v^{(n)}_{tt}\right\| _{\Omega _{2}}^{2}\right) . \end{aligned}$$

(3.11)

Substituting (3.8)–(3.11) into (3.7) and combining (3.2)–(3.3) to derive

$$\begin{aligned}&\frac{1}{2}\frac{{\textrm{d}}}{{\textrm{d}}t}\left[ \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2} +\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2}+\big (g\diamond \nabla u^{(n)}_{t}\big )(t) \right. \\&\qquad \left. +\left\| v^{(n)}_{tt}\right\| _{\Omega _{2}}^{2}+\left\| \nabla v^{(n)}_{t}\right\| _{\Omega _{2}}^{2}\right] +\left\| u^{(n)}_{tt}\right\| _{\Gamma _{2}}^{2}\\&\quad \le C_{1}\left[ \left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2} +\left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2} +\left\| v^{(n)}_{tt}\right\| _{\Omega _{2}}^{2} +\left\| \nabla v^{(n)}_{t}\right\| _{\Omega _{2}}^{2}\right] +C_{2}. \end{aligned}$$

By virtue of Gronwall’s inequality, we can see

$$\begin{aligned}&\left\| u^{(n)}_{tt}\right\| _{\Omega _{1}}^{2} +\left\| \nabla u^{(n)}_{t}\right\| _{\Omega _{1}}^{2} +\left\| v^{(n)}_{tt}\right\| _{\Omega _{2}}^{2} +\left\| \nabla v^{(n)}_{t}\right\| _{\Omega _{2}}^{2}+\int \limits _{0}^{t}\left\| u^{(n)}_{ss}(s)\right\| _{\Gamma _{2}}^{2}{\textrm{d}}s \le L_{2},\;\forall n\in {\mathbb {N}}_{+}, \end{aligned}$$

(3.12)

where $L_{2}>0$ is a constant independent of n.

Step 3. Passing to the limit.

It follows from the first prior estimate (3.6) and second prior estimate (3.12) that there exist subsequences of $\left\{ \left( u^{(n)},\;v^{(n)}\right) \right\} _{n=1}^{\infty }$ (we still denote the subsequences by $\left\{ \left( u^{(n)},\;v^{(n)}\right) \right\} _{n=1}^{\infty }$ for convenience) such that

$$\begin{aligned}&\left( u^{(n)},\;v^{(n)}\right) \rightarrow (u,v)\;\mathrm{weakly \;star\; in}\; L^{\infty }(0,T;V), \end{aligned}$$

(3.13)

$$\begin{aligned}&\left( u^{(n)}_{t},\;v^{(n)}_{t}\right) \rightarrow (u_{t},v_{t})\;\mathrm{weakly \;star\; in}\; L^{\infty }(0,T;V), \end{aligned}$$

(3.14)

$$\begin{aligned}&\left( u^{(n)}_{tt},\;v^{(n)}_{tt}\right) \rightarrow (u_{tt},v_{tt})\;\mathrm{weakly \; in}\; L^{2}\left( 0,T;L^{2}(\Omega _{1})\times L^{2}(\Omega _{2})\right) , \end{aligned}$$

(3.15)

$$\begin{aligned}&u^{(n)}_{t}\rightarrow u_{t}\;\mathrm{weakly \; in}\; L^{2}\left( 0,T;\Gamma _{2}\right) , \end{aligned}$$

(3.16)

$$\begin{aligned}&u^{(n)}_{tt}\rightarrow u_{tt}\;\mathrm{weakly \; in}\; L^{2}\left( 0,T;\Gamma _{2}\right) . \end{aligned}$$

(3.17)

According to Arzela–Ascoli theorem and (3.13)–(3.14), we have

$$\begin{aligned}&\left( u^{(n)},\;v^{(n)}\right) \rightarrow (u,v)\;\mathrm{strongly\; in}\; C(0,T;V), \end{aligned}$$

(3.18)

Moreover, by (3.7) and the continuity of trace operator ${\mathcal {T}}:H^{1}(\Omega _{1})\rightarrow H^{\frac{1}{2}}(\Gamma _{2})$, we can obtain

$$\begin{aligned}&\left\{ u^{(n)}\right\} \;\mathrm{is\;bounded\;in}\;L^{2}(0,T;H^{\frac{1}{2}}(\Gamma _{2})),\\&\left\{ u_{t}^{(n)}\right\} \;\mathrm{is\;bounded\;in}\;L^{2}(0,T;H^{\frac{1}{2}}(\Gamma _{2})),\\&\left\{ u_{tt}^{(n)}\right\} \;\mathrm{is\;bounded\;in}\;L^{2}(0,T;L^{2}(\Gamma _{2})). \end{aligned}$$

Using Aubin–Lions theorem, we can get

$$\begin{aligned}&\left( u^{(n)},\;v^{(n)}\right) \rightarrow (u,v)\;\mathrm{a.e.\;on}\; (\Omega _{1},\Omega _{2})\times (0,T), \end{aligned}$$

which implies

$$\begin{aligned}&f_{1}\left( u^{(n)}\right) \rightarrow f_{1}(u)\;\mathrm{a.e.\;on}\; \Omega _{1}\times (0,T),\\&f_{2}\left( v^{(n)}\right) \rightarrow f_{2}(v)\;\mathrm{a.e.\;on}\; \Omega _{2}\times (0,T),\\&\Vert \nabla u^{(n)}\Vert _{\Omega _{1}}^{2\beta }u_{t}^{(n)}\rightarrow \Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }u_{t}\;\textrm{in}\; C\left( 0,T;L^{2}(\Omega _{1})\right) . \end{aligned}$$

Since $\left( u,\;v\right) ,\;\left( u_{tt},\;v_{tt}\right) \in L^{2}_{\textrm{loc}}\left( 0,+\infty ;L^{2}(\Omega _{1})\times L^{2}(\Omega _{2})\right)$, then we can pass the limit in (3.1) to obtain

$$\begin{aligned}&u_{tt}-\Delta u+\int \limits _{0}^{t}g(t-s)\Delta u(s){\textrm{d}}s+\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }u_{t}+f_{1}(u)=0,\;\textrm{in}\; L^{2}_{\textrm{loc}}\left( 0,+\infty ;L^{2}(\Omega _{1})\right) , \\&v_{tt}-\Delta v+f_{2}(v)=0,\;\;\textrm{in}\; L^{2}_{\textrm{loc}}\left( 0,+\infty ;L^{2}(\Omega _{2})\right) . \end{aligned}$$

Returning to the approximating problem and using Green identity, we have

$$\begin{aligned}&v=0,\;\textrm{on}\;\Gamma _{0},\\&u=v,\;\;\frac{\partial u}{\partial \nu }-\int \limits _{0}^{t}g(t-s)\frac{\partial u(s)}{\partial \nu }{\textrm{d}}s=\frac{\partial v}{\partial \nu }, \;\textrm{on}\;\Gamma _{1}. \end{aligned}$$

Since $u,u_{t}\in L^{2}_{\textrm{loc}}\left( 0,+\infty ;H^{\frac{1}{2}}(\Gamma _{2})\right)$, we have

$$\begin{aligned}&\frac{\partial u}{\partial \nu }-\int \limits _{0}^{t}g(t-s)\frac{\partial u(s)}{\partial \nu }{\textrm{d}}s+u_{t}=0, \;\textrm{on}\; L^{2}_{\textrm{loc}}\left( 0,+\infty ;H^{\frac{1}{2}}(\Gamma _{2})\right) . \end{aligned}$$

This completes the proof of the existence of solutions for problem (1.1)–(1.7).

Step 4. Uniqueness.

Let $({\overline{u}},{\overline{v}})$ and $({\widetilde{u}},{\widetilde{v}})$ be two solutions of problem (1.1)–(1.7). Then, $({\widehat{u}},{\widehat{v}})=({\overline{u}}-{\widetilde{u}},{\overline{v}}-{\widetilde{v}})$ verifies

$$\begin{aligned}&\left( {\widehat{u}}_{tt},\varphi \right) _{\Omega _{1}}+\left( \nabla {\widehat{u}},\nabla \varphi \right) _{\Omega _{1}} -\left( \int \limits _{0}^{t}g(t-s)\nabla {\widehat{u}}(s){\textrm{d}}s,\nabla \varphi \right) _{\Omega _{1}} +\big ({\widehat{u}}_{t},\varphi \big )_{\Gamma _{2}}\nonumber \\&\quad +\left( \Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2\beta }{\overline{u}}_{t}- \Vert \nabla {\widetilde{u}}\Vert _{\Omega _{1}}^{2\beta }{\widetilde{u}}_{t},\varphi \right) _{\Omega _{1}} +\left( f_{1}\left( {\overline{u}}\right) -f_{1}\left( {\widetilde{u}}\right) ,\varphi \right) _{\Omega _{1}}\nonumber \\&\quad +\left( {\widehat{v}}_{tt},\psi \right) _{\Omega _{2}}+\left( \nabla {\widehat{v}},\nabla \psi \right) _{\Omega _{2}} +\left( f_{2}\left( {\overline{v}}\right) -f_{2}\left( {\widetilde{v}}\right) ,\psi \right) _{\Omega _{2}}=0, \end{aligned}$$

(3.19)

$$\begin{aligned}&{\widehat{u}}(x,0)=0,\;\;{\widehat{u}}_{t}(x,0)=0,\;\;x\in \Omega _{1}, \end{aligned}$$

(3.20)

$$\begin{aligned}&{\widehat{v}}(x,0)=0,\;\;{\widehat{v}}_{t}(x,0)=0,\;\;x\in \Omega _{2}. \end{aligned}$$

(3.21)

Taking $\varphi ={\widehat{u}}_{t}$ and $\psi ={\widehat{v}}_{t}$ in (3.19) to derive

$$\begin{aligned}&\frac{1}{2}\frac{{\textrm{d}}}{{\textrm{d}}t}\bigg [\left\| {\widehat{u}}_{t}\right\| _{\Omega _{1}}^{2} +\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \left\| \nabla {\widehat{u}}\right\| _{\Omega _{1}}^{2}+\left( g\diamond \nabla {\widehat{u}}\right) (t)+\left\| {\widehat{v}}_{t}\right\| _{\Omega _{2}}^{2}+\left\| \nabla {\widehat{v}}\right\| _{\Omega _{2}}^{2}\bigg ]\nonumber \\&\quad \le -\left\| {\widehat{u}}_{t}\right\| _{\Gamma _{2}}^{2} -\int \limits _{\Omega _{1}}\left( \Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2\beta }{\overline{u}}_{t}- \Vert \nabla {\widetilde{u}}\Vert _{\Omega _{1}}^{2\beta }{\widetilde{u}}_{t}\right) {\widehat{u}}_{t}{\textrm{d}}x\nonumber \\&\qquad -\int \limits _{\Omega _{1}}\left[ f_{1}\left( {\overline{u}}\right) -f_{1}\left( {\widetilde{u}}\right) \right] {\widehat{u}}_{t}{\textrm{d}}x -\int \limits _{\Omega _{2}}\left[ f_{2}\left( {\overline{v}}\right) -f_{2}\left( {\widetilde{v}}\right) \right] {\widehat{v}}_{t}{\textrm{d}}x\nonumber \\&\quad =-\left\| {\widehat{u}}_{t}\right\| _{\Gamma _{2}}^{2}-\Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2\beta }\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}^{2} +\int \limits _{\Omega _{1}}\left( \Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2\beta }- \Vert \nabla {\widetilde{u}}\Vert _{\Omega _{1}}^{2\beta }\right) {\widetilde{u}}_{t}{\widehat{u}}_{t}{\textrm{d}}x\nonumber \\&\qquad -\int \limits _{\Omega _{1}}\left[ f_{1}\left( {\overline{u}}\right) -f_{1}\left( {\widetilde{u}}\right) \right] {\widehat{u}}_{t}{\textrm{d}}x -\int \limits _{\Omega _{2}}\left[ f_{2}\left( {\overline{v}}\right) -f_{2}\left( {\widetilde{v}}\right) \right] {\widehat{v}}_{t}{\textrm{d}}x. \end{aligned}$$

(3.22)

Applying Young’s inequality to the 3rd term on the right side of (3.22), we get

$$\begin{aligned}&\int \limits _{\Omega _{1}}\left( \Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2\beta }- \Vert \nabla {\widetilde{u}}\Vert _{\Omega _{1}}^{2\beta }\right) {\widetilde{u}}_{t}{\widehat{u}}_{t}{\textrm{d}}x\nonumber \\&\quad \le 2c\beta \left( \Vert \nabla {\overline{u}}\Vert _{\Omega _{1}}^{2}+ \Vert \nabla {\widetilde{u}}\Vert _{\Omega _{1}}^{2}\right) ^{\frac{1}{2}}\Vert \nabla {\widetilde{u}}_{t}\Vert _{\Omega _{1}} \Vert \nabla {\widehat{u}}\Vert _{\Omega _{1}}\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}\nonumber \\&\quad \le c\left( \Vert \nabla {\widehat{u}}\Vert _{\Omega _{1}}^{2}+\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}^{2}\right) . \end{aligned}$$

(3.23)

Similar to the procedure of (3.10)–(3.11), we can derive

$$\begin{aligned}&-\int \limits _{\Omega _{1}}\left[ f_{1}\left( {\overline{u}}\right) -f_{1}\left( {\widetilde{u}}\right) \right] {\widehat{u}}_{t}{\textrm{d}}x \le c\left( \Vert \nabla {\widehat{u}}\Vert _{\Omega _{1}}^{2}+\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}^{2}\right) , \end{aligned}$$

(3.24)

$$\begin{aligned}&-\int \limits _{\Omega _{2}}\left[ f_{2}\left( {\overline{v}}\right) -f_{2}\left( {\widetilde{v}}\right) \right] {\widehat{v}}_{t}{\textrm{d}}x \le c\left( \Vert \nabla {\widehat{v}}\Vert _{\Omega _{2}}^{2}+\Vert {\widehat{v}}_{t}\Vert _{\Omega _{2}}^{2}\right) . \end{aligned}$$

(3.25)

Substituting (3.23)–(3.25) into (3.22) to obtain

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\bigg [\left\| {\widehat{u}}_{t}\right\| _{\Omega _{1}}^{2} +\big (1-\int \limits _{0}^{t}g(s){\textrm{d}}s\big )\left\| \nabla {\widehat{u}}\right\| _{\Omega _{1}}^{2}+\left( g\diamond \nabla {\widehat{u}}\right) (t)+\left\| {\widehat{v}}_{t}\right\| _{\Omega _{2}}^{2}+\left\| \nabla {\widehat{v}}\right\| _{\Omega _{2}}^{2}\bigg ]\nonumber \\&\quad \le c\left( \Vert \nabla {\widehat{u}}\Vert _{\Omega _{1}}^{2}+\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}^{2} +\Vert \nabla {\widehat{v}}\Vert _{\Omega _{2}}^{2}+\Vert {\widehat{v}}_{t}\Vert _{\Omega _{2}}^{2}\right) . \end{aligned}$$

(3.26)

Now, by means of Gronwall’s inequality, we can deduce

$$\begin{aligned} \Vert \nabla {\widehat{u}}\Vert _{\Omega _{1}}^{2}+\Vert {\widehat{u}}_{t}\Vert _{\Omega _{1}}^{2} +\Vert \nabla {\widehat{v}}\Vert _{\Omega _{2}}^{2}+\Vert {\widehat{v}}_{t}\Vert _{\Omega _{2}}^{2}=0, \end{aligned}$$

and uniqueness follows. Therefore, Theorem 2.1 is proved completely.

$\square$

4 Optimal decay rates

In this section, we investigate the general and optimal decay of the energy to problem (1.1)–(1.7). In order to prove our main result, we introduce some lemmas firstly.

Define

$$\begin{aligned} \Phi (t):=\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x+\int \limits _{\Omega _{2}}\left[ (m\cdot \nabla v)+\left( \frac{N}{2}-\theta \right) v\right] v_{t}{\textrm{d}}x, \end{aligned}$$

where $w(t):=u(t)-\int \limits _{0}^{t}g(t-s)u(s){\textrm{d}}s$ and $0<\theta <\min \left\{ 1,\;\frac{N\mu _{i}}{2\left( \mu _{i}+2\right) }\right\}$, $i=1,2$ is a constant which will be determined later.

Lemma 4.1

Let (u, v) be the global solution of problem (1.1)–(1.7). If the additional condition (2.8) holds, then there exist time $t_{1}>0$ and constants $C_{1},C_{2},C_{3}>0$ such that

$$\begin{aligned} \frac{{\textrm{d}}\Phi (t)}{{\textrm{d}}t}&\le -\frac{\theta }{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2} -\frac{(1-\theta )l}{2}\Vert \nabla u\Vert _{\Omega _{1}}^{2}+C_{1}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}+C_{2}\Vert u_{t}\Vert _{\Gamma _{2}}^{2}\\&\quad +C_{3}(1+C_{\alpha })(h\diamond \nabla u)(t)-\left[ \frac{N\mu _{1}}{2}-\theta (2+\mu _{1})\right] \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x\\&\quad -\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}-(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2} -\left[ \frac{N\mu _{2}}{2}-\theta (2+\mu _{2})\right] \int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x, \end{aligned}$$

for $\forall t>t_{1}$, where $R:=\max \{|x-x_{0}|:x\in {\overline{\Omega }}\}$ and

$$\begin{aligned} C_{\alpha }:=\int \limits _{0}^{+\infty }\frac{g^{2}(s)}{\alpha g(s)-g'(s)}{\textrm{d}}s,\; \;h(t):=\alpha g(t)-g'(t), \end{aligned}$$

(4.1)

for $\forall \alpha \in (0,1).$

Proof

By (1.1) and Green’s formula, we obtain

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x\nonumber \\&\quad =\int \limits _{\Omega _{1}}(m\cdot \nabla u_{t})u_{t}{\textrm{d}}x+\int \limits _{\Omega _{1}}u_{t}\int \limits _{0}^{t}g'(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\qquad -g(t)\int \limits _{\Omega _{1}}(m\cdot \nabla u)u_{t}{\textrm{d}}x-\int \limits _{\Omega _{1}}\nabla (m\cdot \nabla w)\cdot \nabla w{\textrm{d}}x\nonumber \\&\qquad +\left( \frac{N}{2}-\theta \right) \Vert u_{t}\Vert _{\Omega _{1}}^{2}-\left( \frac{N}{2}-\theta \right) \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \Vert \nabla u\Vert _{\Omega _{1}}^{2}\nonumber \\&\qquad -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}\nabla u(t)\cdot \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s{\textrm{d}}x\nonumber \\&\qquad +\int \limits _{\partial \Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] \frac{\partial w}{\partial \nu }{\textrm{d}}\Gamma \nonumber \\&\qquad -\int \limits _{\Omega _{1}}f_{1}(u)\int \limits _{0}^{t}g(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\qquad -\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \int \limits _{\Omega _{1}}(m\cdot \nabla u)f_{1}(u){\textrm{d}}x -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}uf_{1}(u){\textrm{d}}x\nonumber \\&\qquad -\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x. \end{aligned}$$

(4.2)

Noting that

$$\begin{aligned}&\int \limits _{\Omega _{1}}(m\cdot \nabla u_{t})u_{t}{\textrm{d}}x=-\frac{N}{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2}+\frac{1}{2}\int \limits _{\partial \Omega _{1}}(m\cdot \nu )|u_{t}|^{2}{\textrm{d}}\Gamma , \end{aligned}$$

(4.3)

$$\begin{aligned}&\qquad -\int \limits _{\Omega _{1}}\nabla (m\cdot \nabla w)\cdot \nabla w{\textrm{d}}x\nonumber \\&\quad =-\int \limits _{\Omega _{1}}\Sigma _{i,j=1}^{N}\left[ \frac{\partial }{\partial x_{i}}\left( m_{j}\frac{\partial w}{\partial x_{j}}\right) \frac{\partial w}{\partial x_{i}}\right] {\textrm{d}}x\nonumber \\&\quad =-\int \limits _{\Omega _{1}}\Sigma _{i,j=1}^{N}\frac{\partial w}{\partial x_{i}}\frac{\partial w}{\partial x_{j}}\frac{\partial m_{j}}{\partial x_{i}}{\textrm{d}}x-\frac{1}{2}\int \limits _{\Omega _{1}}\Sigma _{i,j=1}^{N}\frac{\partial }{\partial x_{j}}\left( \frac{\partial w}{\partial x_{i}}\right) ^{2}m_{j}{\textrm{d}}x\nonumber \\&\quad =\left( \frac{N}{2}-1\right) \Vert \nabla w\Vert _{\Omega _{1}}^{2}-\frac{1}{2}\int \limits _{\partial \Omega _{1}}(m\cdot \nu )|\nabla w|^{2}{\textrm{d}}\Gamma , \end{aligned}$$

(4.4)

and

$$\begin{aligned} \int \limits _{\Omega _{1}}(m\cdot \nabla u)f_{1}(u){\textrm{d}}x=N\int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x -\int \limits _{\partial \Omega _{1}}(m\cdot \nu )F_{1}(u){\textrm{d}}\Gamma . \end{aligned}$$

(4.5)

Substituting (4.3)–(4.5) into (4.2), we conclude that

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x\nonumber \\&\quad =-\theta \Vert u_{t}\Vert _{\Omega _{1}}^{2}-\left( \frac{N}{2}-\theta \right) \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \Vert \nabla u\Vert _{\Omega _{1}}^{2} +\left( \frac{N}{2}-1\right) \Vert \nabla w\Vert _{\Omega _{1}}^{2}\nonumber \\&\qquad -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}\nabla u(t)\cdot \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s{\textrm{d}}x\nonumber \\&\qquad -\int \limits _{\Omega _{1}}f_{1}(u)\int \limits _{0}^{t}g(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\qquad +\int \limits _{\partial \Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] \frac{\partial w}{\partial \nu }{\textrm{d}}\Gamma \nonumber \\&\qquad +\int \limits _{\partial \Omega _{1}}(m\cdot \nu )\left[ \frac{1}{2}\left( \left| u_{t}\right| ^{2}-\left| \nabla w\right| ^{2}\right) -\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) F_{1}(u)\right] {\textrm{d}}\Gamma \nonumber \\&\qquad +\int \limits _{\Omega _{1}}u_{t}\int \limits _{0}^{t}g'(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x -g(t)\int \limits _{\Omega _{1}}(m\cdot \nabla u)u_{t}{\textrm{d}}x\nonumber \\&\qquad +N\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}uf_{1}(u){\textrm{d}}x\nonumber \\&\qquad -\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x. \end{aligned}$$

(4.6)

Similarly, by virtue of (1.2) and Green’s formula, we get

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\int \limits _{\Omega _{2}}\left[ (m\cdot \nabla v)+\left( \frac{N}{2}-\theta \right) v\right] v_{t}{\textrm{d}}x\nonumber \\&\quad =-\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}-(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2} +N\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x-\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{2}}vf_{2}(v){\textrm{d}}x\nonumber \\&\qquad +\int \limits _{\partial \Omega _{2}}\left[ (m\cdot \nabla v)+\left( \frac{N}{2}-\theta \right) v\right] \frac{\partial v}{\partial {\widetilde{\nu }}}{\textrm{d}}\Gamma +\int \limits _{\partial \Omega _{2}}(m\cdot {\widetilde{\nu }})\left[ \frac{1}{2}\left( \left| v_{t}\right| ^{2}-\left| \nabla v\right| ^{2}\right) -F_{2}(v)\right] {\textrm{d}}\Gamma , \end{aligned}$$

(4.7)

where ${\widetilde{\nu }}$ denotes the normal vector pointing out of $\Omega _{2}$.

Adding (4.6) to (4.7) and using the boundary and transmission conditions (1.3)–(1.5), according to the fact that and ${\widetilde{\nu }}=-\nu$ on $\Gamma _{1}$, we see that

$$\begin{aligned} \frac{{\textrm{d}}\Phi (t)}{{\textrm{d}}t}&=-\theta \Vert u_{t}\Vert _{\Omega _{1}}^{2}-\left( \frac{N}{2}-\theta \right) \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \Vert \nabla u\Vert _{\Omega _{1}}^{2} +\left( \frac{N}{2}-1\right) \Vert \nabla w\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}\nabla u(t)\cdot \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s{\textrm{d}}x\nonumber \\&\quad -\int \limits _{\Omega _{1}}f_{1}(u)\int \limits _{0}^{t}g(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\quad +\int \limits _{\Gamma _{2}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}\Gamma \nonumber \\&\quad +\int \limits _{\Gamma _{2}}(m\cdot \nu )\left[ \frac{1}{2}\left( \left| u_{t}\right| ^{2}-\left| \nabla w\right| ^{2}\right) -\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) F_{1}(u)\right] {\textrm{d}}\Gamma \nonumber \\&\quad +\int \limits _{\Omega _{1}}u_{t}\int \limits _{0}^{t}g'(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x -g(t)\int \limits _{\Omega _{1}}(m\cdot \nabla u)u_{t}{\textrm{d}}x \nonumber \\&\quad +N\left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}uf_{1}(u){\textrm{d}}x \nonumber \\&\quad -\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x \nonumber \\&\quad -\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}-(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2} +N\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x-\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{2}}vf_{2}(v){\textrm{d}}x \nonumber \\&\quad -\int \limits _{\Gamma _{1}}(m\cdot \nu )\left[ \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) F_{1}(u)-F_{2}(u)\right] {\textrm{d}}\Gamma \nonumber \\&\quad +\int \limits _{\Gamma _{0}}(m\cdot \nabla v)\frac{\partial v}{\partial {\widetilde{\nu }}}{\textrm{d}}\Gamma -\frac{1}{2}\int \limits _{\Gamma _{0}}(m\cdot {\widetilde{\nu }})\left| \nabla v\right| ^{2}{\textrm{d}}\Gamma . \end{aligned}$$

(4.8)

It follows from $1-\int \limits _{0}^{t}g(s){\textrm{d}}s\le 1$ and (2.8) that

$$\begin{aligned} -\int \limits _{\Gamma _{1}}(m\cdot \nu )\left[ \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) F_{1}(u)-F_{2}(u)\right] {\textrm{d}}\Gamma \le -\int \limits _{\Gamma _{1}}(m\cdot \nu )\left[ F_{1}(u)-F_{2}(u)\right] {\textrm{d}}\Gamma \le 0. \end{aligned}$$

(4.9)

For the last two terms on the right side of (4.8), we have

$$\begin{aligned}&-\frac{1}{2}\int \limits _{\Gamma _{0}}(m\cdot {\widetilde{\nu }})|\nabla v|^{2}{\textrm{d}}\Gamma +\int \limits _{\Gamma _{0}}(m\cdot \nabla v)\frac{\partial v}{\partial {\widetilde{\nu }}}{\textrm{d}}\Gamma \nonumber \\&\quad =-\frac{1}{2}\int \limits _{\Gamma _{0}}(m\cdot {\widetilde{\nu }})|\nabla v|^{2}{\textrm{d}}\Gamma +\int \limits _{\Gamma _{0}}(m\cdot \nabla v)(\nabla v\cdot {\widetilde{\nu }}){\textrm{d}}\Gamma \nonumber \\&\quad =\frac{1}{2}\int \limits _{\Gamma _{0}}|m||\nabla v|^{2}{\textrm{d}}\Gamma -\int \limits _{\Gamma _{0}}\frac{1}{|m|}|m\cdot \nabla v|^{2}{\textrm{d}}\Gamma \nonumber \\&\quad =-\frac{1}{2}\int \limits _{\Gamma _{0}}|m||\nabla v|^{2}{\textrm{d}}\Gamma \le 0, \end{aligned}$$

(4.10)

where we have used the fact that $\Gamma _{0}$ is the boundary of ball $B(x_{0})$, which means ${\widetilde{\nu }}=-\frac{x-x_{0}}{|x-x_{0}|}=-\frac{m}{|m|}$ on $\Gamma _{0}$ and the direction of $\nabla v$ is consistent with $-m$ on $\Gamma _{0}$. In addition, it follows from Young’s inequality that

$$\begin{aligned} \Vert \nabla w\Vert _{\Omega _{1}}^{2}&=\int \limits _{\Omega _{1}}\left[ \nabla u(t)-\int \limits _{0}^{t}g(t-s)\nabla u(s){\textrm{d}}s\right] ^{2}{\textrm{d}}x\nonumber \\&=\int \limits _{\Omega _{1}}\left[ \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) \nabla u(t)+\int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right] ^{2}{\textrm{d}}x \nonumber \\&\le \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s+\eta _{1}\right) \Vert \nabla u\Vert _{\Omega _{1}}^{2}+\left( 1+\frac{1}{\eta _{1}}\right) \left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(4.11)

$$\begin{aligned}&\quad -\left( \frac{N}{2}-\theta \right) \int \limits _{\Omega _{1}}\nabla u(t)\cdot \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s{\textrm{d}}x\nonumber \\&\le \eta _{2}\Vert \nabla u\Vert _{\Omega _{1}}^{2}+ \frac{1}{4\eta _{2}}\left( \frac{N}{2}-\theta \right) ^{2} \left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(4.12)

$$\begin{aligned}&\quad -\int \limits _{\Omega _{1}}f_{1}(u)\int \limits _{0}^{t}g(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\le \eta _{3}\int \limits _{\Omega _{1}}\left| f_{1}(u)\right| ^{2}{\textrm{d}}x +\frac{R^{2}}{4\eta _{3}} \left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}\nonumber \\&\le \gamma C_{S}\eta _{3}\Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{R^{2}}{4\eta _{3}} \left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(4.13)

$$\begin{aligned}&\quad \int \limits _{\Gamma _{2}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}\Gamma \nonumber \\&\le \eta _{4}R^{2}\Vert \nabla w\Vert _{\Gamma _{2}}^{2}+\eta _{4}\left( \frac{N}{2}-\theta \right) ^{2}\Vert u\Vert _{\Gamma _{2}}^{2} +\frac{1}{2\eta _{4}}\Vert u_{t}\Vert _{\Gamma _{2}}^{2}\nonumber \\&\le \eta _{4}R^{2}\Vert \nabla w\Vert _{\Gamma _{2}}^{2}+\eta _{4}\left( \frac{N}{2}-\theta \right) ^{2}C_{T}\Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{4}}\Vert u_{t}\Vert _{\Gamma _{2}}^{2}, \end{aligned}$$

(4.14)

$$\begin{aligned}&\quad \int \limits _{\Omega _{1}}u_{t}\int \limits _{0}^{t}g'(t-s)m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&=\int \limits _{\Omega _{1}}u_{t}\int \limits _{0}^{t}[\alpha g(t-s)-h(t-s)]m\cdot \left[ \nabla u(t)-\nabla u(s)\right] {\textrm{d}}s{\textrm{d}}x\nonumber \\&\le \eta _{5}\Vert u_{t}\Vert _{\Omega _{1}}^{2}+\frac{R^{2}}{2\eta _{5}}\int \limits _{0}^{t}h(s){\textrm{d}}s(h\diamond \nabla u)(t)+\frac{R^{2}}{2\eta _{5}}\left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(4.15)

$$\begin{aligned}&\quad -g(t)\int \limits _{\Omega _{1}}(m\cdot \nabla u)u_{t}{\textrm{d}}x \le \frac{R}{2}g(t)\Vert u_{t}\Vert _{\Omega _{1}}^{2}+\frac{R}{2}g(t)\Vert \nabla u\Vert _{\Omega _{1}}^{2}, \end{aligned}$$

(4.16)

$$\begin{aligned}&\quad -\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\int \limits _{\Omega _{1}}\left[ (m\cdot \nabla w)+\left( \frac{N}{2}-\theta \right) u\right] u_{t}{\textrm{d}}x\nonumber \\&\le \eta _{6}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\left[ R^{2}\Vert \nabla w\Vert _{\Omega _{1}}^{2} +\left( \frac{N}{2}-\theta \right) ^{2}\Vert u\Vert _{\Omega _{1}}^{2}\right] +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\le \eta _{6}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\left[ 2R^{2}+\left( \frac{N}{2}-\theta \right) ^{2}C_{S}\right] \Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad +2R^{2}\eta _{6}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}\nonumber \\&\le \eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\left[ 2R^{2}+\left( \frac{N}{2}-\theta \right) ^{2}C_{S}\right] \Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad +2R^{2}\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}, \end{aligned}$$

(4.17)

where we have used (2.4) to derive (4.13), $\eta _{i}$, $i=1,2,\ldots ,6$ are small positive constants to be determined later, and $C_{S}$ and $C_{T}$ are Sobolev embedding constant and trace embedding constant, respectively.

Now, we substitute (4.9)–(4.17) into (4.8) and utilize (2.3) to arrive at

$$\begin{aligned} \frac{{\textrm{d}}\Phi (t)}{{\textrm{d}}t}&\le -\left[ \theta -\eta _{5}-\frac{R}{2}g(t)\right] \Vert u_{t}\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2} \nonumber \\&\quad -\left\{ \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) (1-\theta )-\left( \frac{N}{2}-1\right) \eta _{1}-\eta _{2}-\gamma C_{S}\eta _{3}\right. \nonumber \\&\quad \left. -\eta _{4}\left( \frac{N}{2}-\theta \right) ^{2}C_{T} -\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\left[ 2R^{2}+\left( \frac{N}{2}-\theta \right) ^{2}C_{S}\right] \right\} \Vert \nabla u\Vert _{\Omega _{1}}^{2} \nonumber \\&\quad +\left\{ \left( 1+\frac{1}{\eta _{1}}\right) \left( \frac{N}{2}-1\right) +\frac{1}{4\eta _{2}}\left( \frac{N}{2}-\theta \right) ^{2} +\frac{R^{2}}{4\eta _{3}}+\frac{R^{2}}{2\eta _{5}}\right. \nonumber \\&\quad \left. +2R^{2}\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\right\} \left\| \int \limits _{0}^{t}g(t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2} \nonumber \\&\quad +\frac{R^{2}}{2\eta _{5}}\int \limits _{0}^{t}h(s){\textrm{d}}s(h\diamond \nabla u)(t) -\left( \frac{\delta }{2}-R^{2}\eta _{4}\right) \Vert \nabla w\Vert _{\Gamma _{2}}^{2} \nonumber \\&\quad +\left( \frac{1}{2\eta _{4}}+\frac{R}{2}\right) \Vert u_{t}\Vert _{\Gamma _{2}}^{2} -\left[ \frac{N}{2}\mu _{1}-\theta (2+\mu _{1})\right] \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x-\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}\nonumber \\&\quad -(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2}-\left[ \frac{N}{2}\mu _{2}-\theta (2+\mu _{2})\right] \int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x. \end{aligned}$$

(4.18)

Next, we deal with the 4th term on the right side of (4.18). It follows from Cauchy–Schwarz inequality that

$$\begin{aligned}&\left\| \int \limits _{0}^{t}g (t-s)[\nabla u(t)-\nabla u(s)]{\textrm{d}}s\right\| _{\Omega _{1}}^{2}\nonumber \\&\le \left( \int \limits _{0}^{t}g (t-s)\Vert \nabla u(t)-\nabla u(s)\Vert _{\Omega _{1}}{\textrm{d}}s\right) ^{2}\nonumber \\&=\left( \int \limits _{0}^{t}\frac{g (t-s)}{\sqrt{\alpha g (t-s)-g' (t-s)}}\sqrt{\alpha g (t-s)-g' (t-s)}\Vert \nabla u(t)-\nabla u(s)\Vert _{\Omega _{1}}{\textrm{d}}s\right) ^{2}\nonumber \\&\le \left( \int \limits _{0}^{t}\frac{g ^{2}(s)}{\alpha g (s)-g' (s)}{\textrm{d}}s\right) \int \limits _{0}^{t}[\alpha g (t-s)-g' (t-s)]\Vert \nabla u(t)-\nabla u(s)\Vert _{\Omega _{1}}^{2}{\textrm{d}}s\nonumber \\&\le C_{\alpha }(h\diamond \nabla u)(t). \end{aligned}$$

(4.19)

Combining (4.18) and (4.19), we can see

$$\begin{aligned} \frac{{\textrm{d}}\Phi (t)}{{\textrm{d}}t}&\le -\left[ \theta -\eta _{5}-\frac{R}{2}g(t)\right] \Vert u_{t}\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad -\left\{ \left( 1-\int \limits _{0}^{t}g(s){\textrm{d}}s\right) (1-\theta )-\left( \frac{N}{2}-1\right) \eta _{1}-\eta _{2}-\gamma C_{S}\eta _{3}\right. \nonumber \\&\quad \left. -\eta _{4}\left( \frac{N}{2}-\theta \right) ^{2}C_{T} -\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\left[ 2R^{2}+\left( \frac{N}{2}-\theta \right) ^{2}C_{S}\right] \right\} \Vert \nabla u\Vert _{\Omega _{1}}^{2} \nonumber \\&\quad +\left\{ \left[ \left( 1+\frac{1}{\eta _{1}}\right) \left( \frac{N}{2}-1\right) +\frac{1}{4\eta _{2}}\left( \frac{N}{2}-\theta \right) ^{2} +\frac{R^{2}}{4\eta _{3}}+\frac{R^{2}}{2\eta _{5}}\right. \right. \nonumber \\&\quad +\left. \left. 2R^{2}\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\right] C_{\alpha } +\frac{R^{2}}{2\eta _{5}}\int \limits _{0}^{t}h(s){\textrm{d}}s\right\} (h\diamond \nabla u)(t)\nonumber \\&\quad -\left( \frac{\delta }{2}-R^{2}\eta _{4}\right) \Vert \nabla w\Vert _{\Gamma _{2}}^{2}+\left( \frac{1}{2\eta _{4}}+\frac{R}{2}\right) \Vert u_{t}\Vert _{\Gamma _{2}}^{2}\nonumber \\&\quad -\left[ \frac{N}{2}\mu _{1}-\theta (2+\mu _{1})\right] \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x-\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}-(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2}\nonumber \\&\quad -\left[ \frac{N}{2}\mu _{2}-\theta (2+\mu _{2})\right] \int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x. \end{aligned}$$

(4.20)

choosing $\eta _{i}(i=1,2,\ldots ,6)$ sufficiently such that

$$\begin{aligned}&\eta _{1}<\frac{(1-\theta )l}{10(N-2)},\;\eta _{2}<\frac{(1-\theta )l}{20},\; \eta _{3}<\frac{(1-\theta )l}{20\gamma C_{S}},\\&\eta _{4}<\min \left\{ \frac{(1-\theta )l}{5(N-2\theta )^{2}\gamma C_{T}},\;\frac{\delta }{2R^{2}}\right\} ,\; \eta _{5}<\frac{\theta }{4},\\&\eta _{6}<\frac{(1-\theta )l}{20\left( \frac{2E(0)}{l}\right) ^{\beta }\left[ 2R^{2}+\left( \frac{N}{2}-\theta \right) ^{2}C_{S}\right] }. \end{aligned}$$

Meantime, since $\lim \nolimits _{t\rightarrow +\infty }g(t)=0$, then there exists a time $t_{1}>0$ such that

$$\begin{aligned} g(t)<\min \left\{ \frac{\theta }{8R},\;\frac{(1-\theta )l}{8R}\right\} ,\;\forall t>t_{1}. \end{aligned}$$

Therefore, (4.20) can be rewritten as

$$\begin{aligned} \frac{{\textrm{d}}\Phi (t)}{{\textrm{d}}t}&\le -\frac{\theta }{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2} -\frac{(1-\theta )l}{2}\Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{1}{2\eta _{6}}\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad +\left\{ \left[ \left( 1+\frac{1}{\eta _{1}}\right) \left( \frac{N}{2}-1\right) +\frac{1}{4\eta _{2}}\left( \frac{N}{2}-\theta \right) ^{2} +\frac{R^{2}}{4\eta _{3}}+\frac{R^{2}}{2\eta _{5}}\right. \right. \nonumber \\&\quad \left. \left. +2R^{2}\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta }\right] C_{\alpha } +\frac{R^{2}}{2\eta _{5}}\int \limits _{0}^{t}h(s){\textrm{d}}s\right\} (h\diamond \nabla u)(t)\nonumber \\&\quad +\left( \frac{1}{2\eta _{4}}+\frac{R}{2}\right) \Vert u_{t}\Vert _{\Gamma _{2}}^{2} -\left[ \frac{N}{2}\mu _{1}-\theta (2+\mu _{1})\right] \int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x-\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}\nonumber \\&\quad -(1-\theta )\Vert \nabla v\Vert _{\Omega _{2}}^{2} -\left[ \frac{N}{2}\mu _{2}-\theta (2+\mu _{2})\right] \int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x. \end{aligned}$$

(4.21)

Then, we can derive the conclusion of Lemma 4.1 by denoting

$$\begin{aligned} C_{1}&=\frac{1}{2\eta _{6}},\;C_{2}=\frac{1}{2\eta _{4}}+\frac{R}{2},\\ C_{3}&=\max \left\{ \left( 1+\frac{1}{\eta _{1}}\right) \left( \frac{N}{2}-1\right) +\frac{1}{4\eta _{2}}\left( \frac{N}{2}-\theta \right) ^{2} +\frac{R^{2}}{4\eta _{3}}+\frac{R^{2}}{2\eta _{5}}\right. \\&\quad \left. +2R^{2}\eta _{6}\left( \frac{2E(0)}{l}\right) ^{\beta },\;\frac{R^{2}}{2\eta _{5}}\int \limits _{0}^{t}h(s){\textrm{d}}s\right\} . \end{aligned}$$

Therefore, Lemma 4.1 is proved completely. $\square$

Let

$$\begin{aligned} L(t):=M_{0}E(t)+M_{1}\Phi (t), \end{aligned}$$

where $M_{0}$ and $M_{1}$ are positive constants to be determined later. Then, we have the following estimate:

Lemma 4.2

Let (u, v) be the global solution of problem (1.1)–(1.7) and (H1)–(H2) hold, then there exists time $t_{1}>0$ such that

$$\begin{aligned} \frac{{\textrm{d}}L(t)}{{\textrm{d}}t}&\le -\frac{M_{1}\theta }{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2} -4(1-l)\Vert \nabla u\Vert _{\Omega _{1}}^{2} +\frac{1}{4}(g\diamond \nabla u)(t)\nonumber \\&\quad -\left[ \frac{N\mu _{1}}{2}-\theta (2+\mu _{1})\right] M_{1}\int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x-M_{1}\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}\nonumber \\&\quad -(1-\theta )M_{1}\Vert \nabla v\Vert _{\Omega _{2}}^{2}-\left[ \frac{N\mu _{2}}{2}-\theta (2+\mu _{2})\right] M_{1}\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x,\;\forall t>t_{1}, \end{aligned}$$

(4.22)

where $M_{1}:=\frac{8(1-l)}{(1-\theta )l}$.

Proof

Combining (2.7), Lemma 4.1 and $g'=\alpha g-h$ to deduce

$$\begin{aligned} \frac{{\textrm{d}}L(t)}{{\textrm{d}}t}&\le -\frac{M_{1}\theta }{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2} -\frac{(1-\theta )lM_{1}}{2}\Vert \nabla u\Vert _{\Omega _{1}}^{2} +(M_{0}-M_{1}C_{1})\Vert \nabla u\Vert _{\Omega _{1}}^{2\beta }\Vert u_{t}\Vert _{\Omega _{1}}^{2}\nonumber \\&\quad +\frac{M_{0}\alpha }{2}(g\diamond \nabla u)(t) -\left[ \frac{M_{0}}{2}-M_{1}C_{3}\left( 1+C_{\alpha }\right) \right] (h\diamond \nabla u)(t)\nonumber \\&\quad +(M_{0}-M_{1}C_{2})\Vert u_{t}\Vert _{\Gamma _{2}}^{2} -\left[ \frac{N}{2}\mu _{1}-\theta (2+\mu _{1})\right] M_{1}\int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x\nonumber \\&\quad -M_{1}\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}-(1-\theta )M_{1}\Vert \nabla v\Vert _{\Omega _{2}}^{2} -\left[ \frac{N}{2}\mu _{2}-\theta (2+\mu _{2})\right] M_{1}\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x. \end{aligned}$$

(4.23)

Meanwhile, since $\frac{\alpha g^{2}(s)}{\alpha g(s)-g'(s)}<g(s)$, it is easy to show, by virtue of Lebesgue dominated convergence theorem, that

$$\begin{aligned} \alpha C_{\alpha }=\int \limits _{0}^{+\infty }\frac{\alpha g^{2}(s)}{\alpha g(s)-g'(s)}{\textrm{d}}s\rightarrow 0,\;\textrm{as}\;\alpha \rightarrow 0, \end{aligned}$$

and there exists $0<\alpha _{0}<1$ such that

$$\begin{aligned} \alpha C_{\alpha }<\frac{1}{8M_{1}C_{3}}, \end{aligned}$$

(4.24)

when $\alpha <\alpha _{0}$. Now, we can choose $M_{0}>0$ large enough such that

$$\begin{aligned} M_{0}>\max \left\{ M_{1}C_{1},\;M_{1}C_{2},\;2M_{1}C_{3}\right\} \end{aligned}$$

and take

$$\begin{aligned} \alpha =\frac{1}{2M_{0}}<\alpha _{0}. \end{aligned}$$

Then, it follows from (4.24) that

$$\begin{aligned} \frac{M_{0}}{2}-M_{1}C_{3}\left( 1+C_{\alpha }\right) >0, \end{aligned}$$

which implies the result and Lemma 4.2 is proved completely. $\square$

Next, we introduce the functional

$$\begin{aligned} \Lambda (t):=\int \limits _{0}^{t}G(t-s)\Vert \nabla u(s)\Vert _{\Omega _{1}}^{2}{\textrm{d}}s, \end{aligned}$$

where $G(t):=\int \limits _{t}^{+\infty }g(s){\textrm{d}}s$.

Lemma 4.3

([7]) Suppose that (H1) holds, then we have

$$\begin{aligned} \frac{{\textrm{d}}\Lambda (t)}{{\textrm{d}}t}\le -\frac{1}{2}(g\diamond \nabla u)(t)+3(1-l)\Vert \nabla u\Vert _{\Omega _{1}}^{2}. \end{aligned}$$

Now, we give the proof of Theorem 2.2 in detail.

Proof of Theorem 2.2

First of all, it follows from the continuity of g and $\xi$ that

$$\begin{aligned} \left\{ \begin{array}{l} 0<g(t_{1})\le g(t)\le g(0),\\ 0<\xi (t_{1})\le \xi (t)\le \xi (0), \end{array} \right. \quad \forall t\in [0, t_{1}]. \end{aligned}$$

Moreover, by the fact that H is an positive continuous function, there exist constants $a,{\overline{a}}>0$ such that

$$\begin{aligned} a\le \xi (t)H\left( g(t)\right) \le {\overline{a}},\quad \forall t\in [0, t_{1}]. \end{aligned}$$

Thus,

$$\begin{aligned} g'(t)\le -\xi (t)H\left( g(t)\right) \le -a=-\frac{a}{g(0)}g(0)\le -\frac{a}{g(0)}g(t),\quad \forall t\in [0, t_{1}], \end{aligned}$$

which implies

$$\begin{aligned}&\int \limits _{0}^{t_{1}}g(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s\nonumber \\&\le -\frac{g(0)}{a}\int \limits _{0}^{t_{1}}g'(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s\le -cE'(t). \end{aligned}$$

(4.25)

Combining (4.22) and (4.25), we can see

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}L(t)&\le -Q_{1}E'(t)-Q_{2}E(t)-Q_{3}\int \limits _{t_{1}}^{t}g(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s,\quad \forall t>t_{1}, \end{aligned}$$

that is,

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}L_{1}(t)&\le -Q_{2}E(t)-Q_{3}\int \limits _{t_{1}}^{t}g(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s,\quad \forall t>t_{1}, \end{aligned}$$

(4.26)

where $L_{1}(t):=L(t)+Q_{1}E(t)\sim E(t)$ and $Q_{1},Q_{2},Q_{3}>0$ are constants.

Now, we consider the following two cases:

(i) H is a linear function: Multiplying (4.26) by $\xi (t)$ and using the nonincreasing property of $\xi$, we can obtain

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\left[ \xi (t)L_{1}(t)\right]&\le -Q_{2}\xi (t)E(t)-Q_{3}\xi (t)\int \limits _{t_{1}}^{t}g(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s\\&\le -Q_{2}\xi (t)E(t)+Q_{3}\int \limits _{t_{1}}^{t}g'(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s\\&\le -Q_{2}\xi (t)E(t)-2Q_{3}E'(t),\quad \forall t>t_{1}. \end{aligned}$$

Define the Lyapunov functional as

$$\begin{aligned} {\mathcal {L}}_{1}(t):=\xi (t)L_{1}(t)+2Q_{3}E(t),\quad t>t_{1}. \end{aligned}$$

It is clear that ${\mathcal {L}}_{1}(t)\sim E(t)$ and

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}{\mathcal {L}}_{1}(t)\le&-Q_{2}\xi (t)E(t),\quad t>t_{1}. \end{aligned}$$

Integrating the inequality above over $(t_{1},t)$, we find that there exist $c_{1},c_{2}>0$ such that

$$\begin{aligned} {\mathcal {L}}_{1}(t)\le&\, c_{1}\exp \left\{ -c_{2}\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s\right\} \\&= c_{1}{\mathcal {H}}^{-1}\left( c_{2}\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s\right) ,\quad \forall t>t_{1}. \end{aligned}$$

Then, we can obtain the result by ${\mathcal {L}}_{1}(t)\sim E(t)$.

(ii) H is a nonlinear function: We define a functional

$$\begin{aligned} L_{2}(t):=L (t)+\Lambda (t) \end{aligned}$$

and utilize Lemma 4.2 and Lemma 4.3 to get

$$\begin{aligned} \frac{{\textrm{d}}L_{2}(t)}{{\textrm{d}}t}&\le -\frac{M_{1}\theta }{2}\Vert u_{t}\Vert _{\Omega _{1}}^{2} -(1-l)\Vert \nabla u\Vert _{\Omega _{1}}^{2} -\frac{1}{4}(g\diamond \nabla u)(t)\\&\quad -\left[ \frac{N\mu _{1}}{2}-\theta (2+\mu _{1})\right] M_{1}\int \limits _{\Omega _{1}}F_{1}(u){\textrm{d}}x-M_{1}\theta \Vert v_{t}\Vert _{\Omega _{2}}^{2}\\&\quad -(1-\theta )M_{1}\Vert \nabla v\Vert _{\Omega _{2}}^{2}-\left[ \frac{N\mu _{2}}{2}-\theta (2+\mu _{2})\right] M_{1}\int \limits _{\Omega _{2}}F_{2}(v){\textrm{d}}x\\&\le bE(t),\quad \forall t>t_{1}, \end{aligned}$$

where b is a positive constant. Integrating the inequality above over $(t_{1},t)$, we see that

$$\begin{aligned} b\int \limits _{t_{1}}^{t}E(s){\textrm{d}}s\le L_{2}(t_{1})-L_{2}(t)\le L_{2}(t_{1}),\;\textrm{and}\;\int \limits _{0}^{+\infty }E(s){\textrm{d}}s<+\infty . \end{aligned}$$

Thus, we can choose $0<q<1$ such that

$$\begin{aligned} I(t):=q\int \limits _{0}^{t}\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\le C \int \limits _{0}^{t}E(s){\textrm{d}}s<1,\; \forall t>t_{1}. \end{aligned}$$

(4.27)

Without loss of generality, we assume $t_{1}>0$ large enough so that

$$\begin{aligned} I(t)>0, \;\forall t>t_{1}. \end{aligned}$$

Next, we introduce the functional

$$\begin{aligned} \lambda (t):=-\int \limits _{t_{1}}^{t}g'(s)\int \limits _{\Omega _{1}}\left| \nabla u(t)-\nabla u(t-s)\right| ^{2}{\textrm{d}}x{\textrm{d}}s, \end{aligned}$$

It is easy to see that $\lambda (t)\le -2E'(t)$. Meantime, we can know from H, strictly convex on (0, r], that

$$\begin{aligned} H(\kappa x)\le \kappa H(x), \;\forall x\in (0,r], \end{aligned}$$

(4.28)

for $0<\kappa <1$, from which we can use Jensen’s inequality to obtain

$$\begin{aligned} \lambda (t) =&\,\frac{1}{qI(t)}\int \limits _{t_{1}}^{t}I(t)\left( -g'(s)\right) q\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\nonumber \\ \ge&\,\frac{1}{qI(t)}\int \limits _{t_{1}}^{t}I(t)\xi (s)H\left( g(s)\right) q\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\nonumber \\ \ge&\,\frac{\xi (t)}{qI(t)}\int \limits _{t_{1}}^{t}H\left( I(t)g(s)\right) q\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\nonumber \\ \ge&\,\frac{\xi (t)}{q}H\left[ \frac{1}{I(t)}\int \limits _{t_{1}}^{t}I(t)g(s)q\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\right] \nonumber \\ =&\,\frac{\xi (t)}{q}H\left[ q\int \limits _{t_{1}}^{t}g(s)\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\right] \nonumber \\ =&\,\frac{\xi (t)}{q}{\overline{H}}\left[ q\int \limits _{t_{1}}^{t}g(s)\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s\right] . \end{aligned}$$

(4.29)

where ${\overline{H}}$ is the extension of H, which is a strictly increasing and strictly convex $C^{2}$-function on ($0, +\infty )$. This implies

$$\begin{aligned} \int \limits _{t_{1}}^{t}g(s)\left\| \nabla u(t)-\nabla u(t-s)\right\| _{\Omega _{1}}^{2}{\textrm{d}}s \le \frac{1}{q}{\overline{H}}^{-1}\left( \frac{q\lambda (t)}{\xi (t)}\right) , \end{aligned}$$

(4.30)

and (4.26) can be rewritten as

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}L_{1}(t)\le&-Q_{2}E(t) -\frac{Q_{3}}{q}{\overline{H}}^{-1}\left( \frac{q\lambda (t)}{\xi (t)}\right) ,\;\forall t>t_{1}, \end{aligned}$$

(4.31)

For $\varepsilon <r$, multiplying (4.31) by ${\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right)$ and using the fact that $E'\le 0$, ${\overline{H}}'>0$, ${\overline{H}}''>0$, we can obtain

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\left[ {\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) L_{1}(t)\right]&\le -Q_{2}{\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) E(t)-\frac{Q_{3}}{q}{\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) {\overline{H}}^{-1}\left( \frac{q\lambda (t)}{\xi (t)}\right) . \end{aligned}$$

(4.32)

In order to deal with the last term on the right side of (4.32), we utilize the argument of Legendre transform in [24]. Denote $B^{*}$ as the conjugate function of B, i.e., $B^{*}=\sup \limits _{t\in {\mathbb {R}}^{+}}\left[ st-B(t)\right]$. Then, $B^{*}$ is the Legendre transform of B given by

$$\begin{aligned} B^{*}(s):=s\left( B'\right) ^{-1}(s)-B\left[ \left( B'\right) ^{-1}(s)\right] , \end{aligned}$$

(4.33)

and satisfying

$$\begin{aligned} ab\le B^{*}(a)+B(b),\;\forall a,b\ge 0. \end{aligned}$$

(4.34)

We set $a={\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right)$ and $b={\overline{H}}^{-1}\left( \frac{q\lambda (t)}{\xi (t)}\right)$ in (4.34), and then, (4.32) becomes

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}t}\left[ {\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) L_{1}(t)\right]&\le -\left[ Q_{2}E(0)-\frac{Q_{3}\varepsilon }{q}\right] {\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) \frac{E(t)}{E(0)}+Q_{3}\frac{\lambda (t)}{\xi (t)},\;\forall t>t_{1}. \end{aligned}$$

(4.35)

Meantime, it follows from $\varepsilon \frac{E(t)}{E(0)}\le \varepsilon <r$ that ${\overline{H}}'\left( \varepsilon \frac{E(t)}{E(0)}\right) =H'\left( \varepsilon \frac{E(t)}{E(0)}\right)$. Multiplying (4.35) by $\xi (t)$ and using the nonincreasing property of $\xi$ to derive

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}\left[ \xi (t)H'\left( \varepsilon \frac{E(t)}{E(0)}\right) L_{1}(t)\right] \nonumber \\&\le -\xi (t)\left[ Q_{2}E(0)-\frac{Q_{3}\varepsilon }{q}\right] H'\left( \varepsilon \frac{E(t)}{E(0)}\right) \frac{E(t)}{E(0)} +Q_{3}\lambda (t)\nonumber \\&\le -\xi (t)\left[ Q_{2}E(0)-\frac{Q_{3}\varepsilon }{q}\right] H'\left( \varepsilon \frac{E(t)}{E(0)}\right) \frac{E(t)}{E(0)} -2Q_{3}E'(t),\;\forall t>t_{1}. \end{aligned}$$

(4.36)

Choosing $\varepsilon <\min \left\{ r,\;\frac{qQ_{2}E(0)}{2Q_{3}}\right\}$ and setting

$$\begin{aligned} {\mathcal {L}}_{2}(t):=\xi (t)H'\left( \varepsilon \frac{E(t)}{E(0)}\right) L_{1}(t)+2Q_{3}E(t),\;\forall t>t_{1}. \end{aligned}$$

It is clear that $\overline{{\mathcal {L}}}_{2}(t)\sim E(t)$; that is, there exist constants $c_{1},c_{2}>0$ such that

$$\begin{aligned} c_{1}{\mathcal {L}}_{2}(t)\le E(t)\le c_{2}{\mathcal {L}}_{2}(t), \end{aligned}$$

(4.37)

and

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}{\mathcal {L}}_{2}(t) \le -c\xi (t)H'\left( \varepsilon \frac{E(t)}{E(0)}\right) \frac{E(t)}{E(0)} =-c\xi (t){\mathcal {H}}_{0}\left( \varepsilon \frac{E(t)}{E(0)}\right) ,\;\forall t>t_{1}, \end{aligned}$$

where ${\mathcal {H}}_{0}(t)=tH'(\varepsilon t)$ and by ${\mathcal {H}}'_{0}(t)=H'(\varepsilon t)+\varepsilon t H''(\varepsilon t)$ and the fact that H is strictly convex on (0, r], we can see that ${\mathcal {H}}_{0}(t)>0$ and ${\mathcal {H}}'_{0}(t)>0$. Let

$$\begin{aligned} R(t):=\frac{c_{1}{\mathcal {L}}_{2}(t)}{E(0)}. \end{aligned}$$

(4.38)

Then, it is easy to show $R(t)\sim E(t)$ and

$$\begin{aligned}&\frac{{\textrm{d}}}{{\textrm{d}}t}R(t) \le -c\xi (t){\mathcal {H}}_{0}\left( R(t)\right) ,\;\forall t>t_{1}, \end{aligned}$$

Integrating the inequality above over $(t_{1},t)$, we can deduce

$$\begin{aligned} \int \limits _{t_{1}}^{t}\frac{-R'(s)}{{\mathcal {H}}_{0}\left( R(s)\right) }{\textrm{d}}s\ge c\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s&\Rightarrow \int \limits _{\varepsilon R(t)}^{\varepsilon R(t_{1})}\frac{1}{sH'(s)}{\textrm{d}}s\ge c\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s\nonumber \\&\Rightarrow R(t)\le \frac{1}{\varepsilon }{\mathcal {H}}^{-1}\left( c\int \limits _{t_{1}}^{t}\xi (s){\textrm{d}}s\right) ,\;\forall t>t_{1}, \end{aligned}$$

(4.39)

where ${\mathcal {H}}(t)=\int \limits _{t}^{r}\frac{1}{sH'(s)}{\textrm{d}}s$; then, we can derive the result by $R(t)\sim E(t)$ and Theorem 2.2 is proved completely.

$\square$