Abstract
In this paper, we derive a nonlocal theory for porous elastic materials in the context of Mindlin’s strain gradient model. The second gradient of deformation and the second gradient of volume fraction field are added to the set of independent constitutive variables by taking into account the nonlocal length scale parameters effect. The obtained system of equations is a coupling of a two hyperbolic equations with higher gradients terms due to the strain gradient length scale parameter l and the elastic nonlocal parameter \(\varpi \). This poses some new mathematical difficulties due to the lack of regularity. Under quite general assumptions on nonlinear sources terms and based on nonlinear semigroups and the theory of monotone operators, we establish existence and uniqueness of weak and strong solutions to the one dimensional nonlinear problem. By an approach based on the Gearhart–Herbst–Prüss–Huang Theorem, we prove that the semigroup associated with the derived model is not analytic in general (\(\varpi =0\) or not). A frictional damping for the elastic component, whose form depends on the elastic nonlocal parameter (\(\varpi =0\) or not), is shown to lead to exponential stability at a rate of decay determined explicitly. Without frictional damping, the derived system can be exponentially stable only in the absence of body forces and under the condition of equal wave speeds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recently, an increasing attention is being devoted to the effect of material length scales in the study of mechanics of solids at micro- and/or nano-scales. Examples of such materials are provided by nematic elastomers and carbon nanotubes (see, e.g., [19, 20]). Thus, there is a need to model the mechanical response of the new class of materials by bringing the length scales into the structural theories. Although the classical continuum elastic models are able to analyze the mechanical behaviors of porous elastic materials, they fail to describe satisfactorily some phenomena related to nanoscale size effect. This is due to the absence of the material constants related to structural scale parameters in the constitutive relations (see, e.g., [32, 37]). Since material properties are size-dependent at nanoscale, the study of size effect on mechanical properties of porous elastic becomes an important area of interest. It is necessary to improve the classical continuum theory to deal with size-dependent material properties. New mathematical models for nonlocal continuum elastic materials have been proposed in the last years to overcome this limitation. One of the most interesting approach for such size effect is the nonlocal continuum elastic stress field approach first proposed by Eringen (see, e.g., [10,11,12]) and another deals with the strain gradient theories [23, 24, 38]. In nonlocal theory of elasticity, the stress at any reference point \(\mathbf{x} \) within a continuous body depends not only on the strain at that point, but also influenced by the strains at all other points \(\mathbf{x} '\) in the domain through a nonlocal attenuation function in an integrated sense. Thus, the nonlocal stress forces act as a remote action forces. These types of forces are frequently encountered in atomic theory of lattice dynamics. Hence, the cohesive forces at long range between atoms or molecules can be included in the continuum mechanics framework by nonlocal formulation. It turns out that the nonlocal continuum theory potentially plays a useful role in the analyses related to size dependent mechanical behavior for porous elastic materials. The concept of nonlocality has been extended to various other fields by Biswas [6], Eringen [13,14,15]), Lim et al. [20], McCay and Narsimhan [22], Narsimhan and McCay [26], Singh et al. [36], etc.
Nonlocal elastic models can only account for softening stiffness with increasing nanoscale parameter; however, the stiffness enhancement effect noticed from experimental observation and as well as the gradient elasticity (or modified couple stress) theories cannot be characterized. The strain gradient elastic theories provide extensions of the classical equations of elasticity with additional higher-order strain gradient terms based on the assumption that the materials cannot be modeled as collections of points. The strain gradient elasticity theories have been extensively explored since the works by Mindlin [23, 24] and Toupin [38]. Most of the earlier researches devoted to elaborate mathematically complete gradient theories rather than paying attention to the practical applications of interpreting physical phenomena of interest.
The theory of porous elastic materials (called also elastic materials with voids) developed by Cowin and his co-worker [8, 27, 30] is a beautiful extension of the classical theory of elasticity. In their theory, the strain and the change in void volume fraction are considered as independent kinematic variables. In local models, Ieşan [17, 18] was recently extended the theory of elastic materials with voids in the frame of the second gradient theory. He derived in [18] the theory of “grade consistency” by supposing that the second-order derivatives for the displacement could exist in the constitutive equation for the hyperstress, but only first-order derivatives in the gradient of the volume fraction. Recently, Ieşan [17] derived the strain gradient theory for porous elastic materials where the second gradient of deformation and the second gradient of volume fraction field are added to the set of independent constitutive variables. Aouadi et al. [1, 2] extended some local porous thermoelastic theory to Form II Mindlin’s strain gradient where the characteristic length of the material structure is taken into account. In nonlocal models, the constitutive relations and field equations for porous elastic materials were derived by Singh et al. [36] (without considering the strain gradient model) and by Biswas [6] (by considering the strain gradient model) under the Green–Naghdi model of type III for thermal transmission.
The present paper aims to establish the fact that the length scales present in nonlocal elasticity and strain gradient theory describe two entirely different physical characteristics for porous elastic materials. The paper presents a theory which relates the nonlocal elasticity and the strain gradient theory, and it results in a higher-order nonlocal strain gradient theory. In this theory, a higher-order nonlocal strain gradient elasticity system which considers higher-order stress gradients and strain gradient nonlocality is proposed. This theory intends to generalize the classical strain gradient local porous elasticity (see, e.g., [17, 18]) and the classical nonlocal porous elasticity (see, e.g., [6, 36]) by introducing the nonlocal effects of the strain field and the second gradient strain field together. Consequently, two additional kinds of parameters, the strain gradient length scale parameter l and the elastic nonlocal parameter \(\varpi \), are introduced.
One of the important questions to be answered for any model is the decay rate of the solutions of the proposed system of equations when certain dissipation mechanisms are taken into account. This frictional damping will play an important role in the dissipative nature of the problem. Without trying to be exhaustive, let us refer to some studies carried out for porous elastic materials in classical local models (see, e.g., [4, 21, 25, 28, 33,34,35] among others). Of course, the question arises to know the effects of both length scales of nonlocal and strain gradient model derived here on well-posedness, analyticity and stability issues. We find that both length scales play an important role especially in choosing the damped term leading to exponential stability. These results confirm those obtained previously in the context of local Mindlin’s strain gradient model (see, e.g., [1, 2]). In this article, we limit our attention to the one-dimensional setting since the well-posedness, analyticity and stability issues for this new model have not been studied before.
The rest of the paper is organized as follows. In Sect. 2, we derive the constitutive relations and field equations for porous elastic materials based on the nonlocal strain gradient theory. Under quite general assumptions on nonlinear sources terms presented in Sect. 3 and based on nonlinear semigroups and the theory of monotone operators, we prove in Sect. 4 the well-posedness of the one-dimensional nonlinear problem. In Sect. 5, by an approach based on the Gearhart–Herbst–Prüss–Huang Theorem, we prove that the semigroup associated with the derived model is not analytic in general (\(\varpi =0\) or not). Then, in Sect. 6, to increase the dissipative nature of the problem, we add in the system a frictional damping for the elastic component whose form depends on the elastic nonlocal parameter (\(\varpi =0\) or not). By using the multipliers technique, we construct appropriate functionals leading to the exponential stability at a rate of decay determined explicitly in terms of the physical parameters. Without frictional damping, the derived system can be exponentially stable only in the absence of body forces and under the condition of equal wave speeds.
2 Derivation of the field equations
Consider a porous elastic material having volume V, bounded by the surface S and occupying region B in \(\mathbb {R}^3\) at time \(t_0\) of reference configuration. Let the position of a typical point of B in undeformed state be \({X}_i\) and the position of the corresponding point in the deformed state be \({x}_i\). We consider a reference configuration which is free from stresses. The basic idea in porous elastic materials is that the mass density \(\rho \) is written as a product of matrix density \(\gamma \) and void volume fraction \(\nu \) \((0 < \nu \le 1)\). The void volume fraction is a measure of volume change of bulk material arising from void compaction and distension. This enables to introduce a new independent kinematic variable \(\phi \) corresponding to change in volume fraction which depends on spatial coordinate x and time t. We assume that the deformations and the changes of the volume fraction and temperature are very small with respect to the reference configuration in such way that, if \(\nu _0\) is the (constant) volume fraction field in the reference configuration, we can write
where \(\varepsilon \) is a constant small enough for squares and higher powers to be neglected, and \( u'_i\) and \( \phi '\) are independent on \(\varepsilon \). Under these hypotheses, the strain tensor is approximated with
where a comma (, ) in the subscript represents the spatial partial derivative. Within the context of linear theory, and assuming that the initial body is free from stresses and has zero intrinsic equilibrated force, we take the set of basic variables at points \(\mathbf{x} \) and \(\mathbf{x} '\), respectively, as:
To obtain a nonlocal linear theory for centro-symmetric materials, we consider the free energy \(\Psi \) function in the quadratic approximation
where \(A_{ijkl}\) is the tensor of elastic constants, \(A_{ij}\), \(B_{ij}\) and \(\xi \) are functions which are typical in porous theories. All these constitutive coefficients are prescribed functions of \(\mathbf{x} \) and \(\mathbf{x} '\).
Following Eringen [10], the constitutive relations are obtained from
where the superscript ‘s’ represents the symmetry of that quantity with respect to interchange of \(\mathbf{x} \) and \(\mathbf{x} '\). The set \(\Gamma = \{\tau _{ij}, h_i,F+\text {g}\}\) is an ordered set with the set Y. Here, \(\tau _{ij}\) is the force stress tensor, \(h_i\) is the equilibrated stress components, \(\text {g}\) is the equilibrated force and F is a dissipation function given by
where the non-negative coefficient \(\tau \) is a constitutive coefficient and superposed dot denotes the time derivative.
Thus, the force stress tensor \(\tau _{ij}\) , equilibrated stress components \(h_i\) and the equilibrated force \(\text {g}\) are obtained from relations (2.1)–(2.3), for centrosymmetric materials, as [10]
where \(\text {g}\) in (2.5)\(_3 {\text { is actually }} F+\text{ g }\)). The constitutive coefficients in (2.5) satisfy the following symmetries relations:
For a centro-symmetric isotropic material, the constitutive coefficients reduce to
where \(\delta _{ik}\) is the Kronecker delta function, the coefficients \(\lambda ,\ \mu ,\ \gamma ,\ b,\ \tau \) and \(\xi \) are functions of \(|\mathbf{x} - \mathbf{x} '|\), that is, \(\lambda = \lambda (|\mathbf{x} - \mathbf{x} '|),\ \mu = \mu (|\mathbf{x} - \mathbf{x} '|)\), etc. Thus, the constitutive relations (2.5) become
For most of the materials, the cohesive zone is very small, and within that zone the intermolecular forces decrease rapidly with distance from the reference point. Hence, we consider that all constitutive coefficients attenuate with distance [12], e.g.,
We also consider that all the constitutive coefficients attenuate the same degree and they attain their maxima at \(\mathbf{x} = \mathbf{x} '\). Therefore, we can take the following relations between nonlocal and local coefficients:
Here, the quantities in the denominator are constant coefficients. The \(\lambda _0,\ \mu _0\) are the well-known Lame’s constants, \(\gamma _0,\ b_0,\ \tau _0\) and \(\xi _0\) are constants corresponding to voids and the function \(\mathscr {G}(|\mathbf{x} - \mathbf{x} '|)\) is a nonlocal kernel representing the effect of distant interactions of material points between \(\mathbf{x} \) and \( \mathbf{x} '\). Also, the integral of nonlocal kernel \(\mathscr {G}(|\mathbf{x} - \mathbf{x} '|)\) over the domain of integration is unity [12], i.e.,
Hence, the kernel function \(\mathscr {G}\) behaves as a Dirac-delta function over the domain of influence. The function \(\mathscr {G}\) attains its peak at \(|\mathbf{x} - \mathbf{x} '| = 0\) and generally decays with increasing \(|\mathbf{x} - \mathbf{x} '|\). Eringen [12] has already shown that the function \(\mathscr {G}\) satisfies the relation
where I is the identity operator and \(\nabla ^2\) is the Laplacian operator, \(\varpi = e_0\varsigma \) is a nonlocal parameter [10, 12], \(\varsigma \) being the internal characteristic length and \(e_0\) is a material constant. The internal characteristic length \(\varsigma \) is the interatomic distance, e.g., length of \(C-C\) bond (0.142 mm in carbon nanotube) [6, 20, 36].
Using Mindlin’s strain gradient theory (see Mindlin [23, 24]) and applying the operator \(({I} -\varpi ^2\nabla ^2)\) on the constitutive relations (2.6), owing to the relation (2.7) and the property (2.8), we obtain (after suppressing the subscript ‘0’ from the constitutive coefficients)
wherein the formula
has been employed. The quantities \(\tau ^l_{ ij},\ h^l_i\) and \(\text {g}^l\) correspond to the local porous elastic materials. In Mindlin’s strain gradient theory, l is the material length scale parameter introduced to account for the effect of the strain gradient field [20, 23, 24].
Note that a correction pointed out by Puri and Cowin [30] has been taken care here.
Equations of motion for a nonlocal isotropic porous elastic materials are given by [8, 30]
where \(G_i\) is the body force, J is the extrinsic equilibrated body force, \(\chi \) is the equilibrated inertia, and \(\rho \) is the bulk density. Superposed dots represent the double time derivative.
Plugging the constitutive relations (2.9) into (2.10) and retaining only the terms of \(O(\nabla ^2)\) order, we obtain the following equations:
These are the governing equations of nonlocal isotropic porous elastic materials in the context of strain gradient theory. Note that in the absence of strain gradient effects, that is, when \(l = 0\), these equations reduce to those derived by Singh et al. [36] for nonlocal elastic solid with voids. When the elastic nonlocal parameter \(\varpi = 0\), our equations are equivalent to those derived by Ieşan [17, 18] in the frame of the classical local strain gradient porous elasticity. However, in the absence of nonlocality, that is, when \( \varpi = l = 0\), these equations reduce to those of local isotropic porous elastic materials earlier derived by Puri and Cowin [30].
Without loss of generality, we set \(\rho =\chi =1\). In the one dimensional setting, the system (2.11) can be written in the domain \(\Omega =(0,L)\times \mathbb {R}^+\):
where \(a=\lambda +2\mu \), and \(f_1=-(1-\varpi ^2\partial _{xx}) G_1\) and \(f_2=-(1-\varpi ^2\partial _{xx}) J\) are nonlinear sources forces. We assume the following initial conditions for \(x \in (0, L)\)
For boundary conditions, we consider one of the following cases:
-
1.
hinged-hinged boundary conditions:
$$\begin{aligned} u(x,t)= u_{xx}(x,t) =\phi (x,t)=\phi _{xx}(x,t)=0,\quad x=0,L,\quad t>0.\end{aligned}$$(2.14) -
2.
or hinged-clamped boundary conditions:
$$\begin{aligned} u(x,t)= u_{xx}(x,t)=\phi (x,t)=\phi _{x}(x,t)=0,\quad x=0,L,\quad t>0.\end{aligned}$$(2.15) -
3.
or clamped-hinged boundary conditions:
$$\begin{aligned} u(x,t)= u_{x}(x,t) =\phi (x,t)=\phi _{xx}(x,t)=0,\quad x=0,L,\quad t>0.\end{aligned}$$(2.16) -
4.
or clamped-clamped boundary conditions:
$$\begin{aligned} u(x,t)= u_{x}(x,t)=\phi (x,t)=\phi _{x}(x,t)=0,\quad x=0,L,\quad t>0.\end{aligned}$$(2.17)
Our purpose in this work is to investigate the well-posedness, analyticity and stability issues of the solutions to system (2.12), with the initial conditions (2.13) and the boundary conditions (2.14) or (2.15) or (2.16) or (2.17).
Remark 2.1
-
1.
The term \(\tau \phi _t\) in (2.12)\(_2\) models the porous dissipation (called viscoporosity); however, in the local porous thermoelastic model derived by Ieşan [16] such a term does not appear. In our case, the dissipative term \(\tau \phi _t\) appears naturally because we have replaced the response function \(\text {g}\) by \( F+\text {g}\) (see (2.4)).
-
2.
When the coupling is considered b must be different from zero, but its sign does not matter in the analysis we propose. The internal energy and the dissipation of the system will have the form:
$$\begin{aligned} 2\mathscr {W}= & {} a |u_x|^2 +a l^2 |u_{xx}|^2 +(\gamma +\xi l^2) |\phi _x|^2 +\gamma l^2 |\phi _{xx}|^2 + \xi |\phi |^2 \nonumber \\+ & {} 2b \Re e \langle u_x, \phi \rangle + 2b l^2 \Re e \langle u_{xx}, \phi _x\rangle \end{aligned}$$and
$$\begin{aligned} \mathscr {V} = \tau |\phi _t|^2+\tau l^2 | \phi _{xt}|^2, \end{aligned}$$where \( \langle \cdot ,\cdot \rangle \) denotes the inner product in \(L^2(0,L)\). We also assume the positivity of the internal energy. That is, there exists a positive constant M such that
$$\begin{aligned} \mathscr {W} \ge M\Big ( a |u_x|^2 +a l^2 |u_{xx}|^2 +(\gamma +\xi l^2) |\phi _x|^2 +\gamma l^2 |\phi _{xx}|^2 + \xi |\phi |^2\Big ). \end{aligned}$$ -
3.
Therefore, when we assume that the internal energy is positive (which is related with the elastic stability) we have to assume that
$$\begin{aligned} a> 0,\quad \gamma> 0,\quad a\xi > b^2 \end{aligned}$$(2.18)meanwhile if we assume that the dissipation is positive we need to impose that
$$\begin{aligned} \tau > 0. \end{aligned}$$(2.19)
3 Preliminaries
Throughout this paper, we use the standard Lebesgue space \(L^2(0, L)\) and the Sobolev spaces \(H^m (0, L)=W^{m,2}\) \((1\le m\le \infty )\) with their usual scalar products and norms. Let \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert \) denote the \(L^2-\) inner product and \(L^2-\) norm, respectively. As usual, \(C >0\) will denote a generic constant depending only on the structural quantities of the problem. We recall the Poincaré’s inequality
where \(\lambda _{0}= L^2/\pi ^{2}\). Let us introduce the inertia operator \(R_{\epsilon }=1-\epsilon ^2 \partial _{xx}\) with the domain \(\mathscr {D}(R_\epsilon ) = H^2(0,L)\cap H^1_0(0,L)\) when \(\epsilon \not = 0\) and \(L^2(\Omega )\) otherwise. Observe in our case \(\epsilon =\varpi \) or \(\epsilon =l\). In the following, we limit ourselves to the cases \(\varpi \not = 0\) or \(\varpi = 0\) and \(l\not = 0\). We could also consider the case \(\varpi =l = 0\). As this case has already been studied (see, e.g., [21, 25] among others) and is not essential to the analysis of the article, will not be taken into account. Then, one has
with the inner products and norms
respectively. Let \(V_{\epsilon }'\) stand for the dual space of \(V_\epsilon \)
For every \(\epsilon \not = 0\), we recall that \(R_\epsilon \ :\ H^{1}_0(0,L)\rightarrow H^{-1}(0,L)\) is an isometrical bijection with respect to the norm (3.2). Note that when \(\epsilon = 0\), \(R_0 = I\ :\ L^{2}(0,L)\rightarrow L^{2}(0,L)\). The obvious \(H^{1}_0(0,L)\)-ellipticity of \(R_{\epsilon }\) and Lax–Milgram theorem give that \(R_{\varpi }\) is boundedly invertible, i.e., \(R_\epsilon ^{-1} \in \mathscr {L}(H^{-1}(0,L),H^1_0(0,L))\). Thus, for \(\epsilon \not =0\), we have
Now we consider the following assumptions on \(f_i\) for \(i = 1, 2\):
\(f_i\ :\ \mathbb {R}^2 \rightarrow \mathbb {R}\) is locally Lipschitz continuous on each of its arguments, namely there exist \(p \ge 1\) and \(C>0\) such that, for \(i = 1, 2\),
There exists a nonnegative \(C^2\) function \(F :\ \mathbb {R}^2 \rightarrow \mathbb {R}\) satisfying
and there exists a small positive constant \(\beta \) such that for any \( p,\ q \in \mathbb {R}\)
Moreover, we assume that
Remark 3.1
A typical example of F satisfying (3.5)–(3.7) is
where \(\beta \) is a small positive constant.
4 Well-posedness
By using the nonlinear semigroups theory and monotone operators [5, 7], we study in this section the well-posedness of the problem (2.12), (2.13) and (2.14) or ((2.15) or (2.16) or (2.17)). First, we set \(v=u_t\) and \(\psi =\phi _t\). Then, we consider the following Hilbert spaces:
where the phrase “B.C’s” means that u and \( \phi \) satisfy the relevant boundary conditions.
In these Hilbert spaces, we define the inner product

where \({U}=(u,\phi ,v,\psi )\), \({U}^*=(u^*,\phi ^*,v^*,\psi ^*)\). The corresponding norm in \(\mathscr {H_\varpi }\) is given by

Note that (2.18)\(_3\) leads to
Consequently,  is nonnegative. Moreover, the induced norm
is nonnegative. Moreover, the induced norm  is equivalent to the usual norm in the Hilbert space \(\mathscr {H_\varpi }\),
is equivalent to the usual norm in the Hilbert space \(\mathscr {H_\varpi }\),
with positive constants \(C_1\) and \(C_2\). While the estimate from below is obvious, the estimate from above can be obtained by choosing \(\varepsilon > 0\) sufficiently small such
and then
In particular, there exists a positive constant \(\varrho \) such that

where
Problem (2.12), (2.13) and (2.14) or ((2.15) or (2.16) or (2.17)) can be written as a Cauchy problem
where \(\mathscr {A_\varpi }:\mathcal {D}(\mathscr {A_\varpi })\subset \mathscr {H_\varpi } \rightarrow \mathscr {H_\varpi }\) and \(\mathscr {B}:\mathcal {D}(\mathscr {B})\subset \mathscr {H_\varpi } \rightarrow \mathscr {H_\varpi }\) are defined by
and \(\mathcal {F}\ :\ \mathscr {H_\varpi } \rightarrow \mathscr {H_\varpi }\) is defined by
with the domains for \(l\not = 0\) and \(\varpi \not = 0\)
For \(l\not = 0\) and \(\varpi = 0\), we obtain \( \mathcal {D}(\mathscr {A}_0) \) by replacing in (4.11) \( H^{3}(0, L)\) by \( H^{4}(0, L)\).
We start by proving two auxiliary results (Lemmas 4.1 and 4.2) which will be used in the sequel.
Lemma 4.1
The operator \(\mathscr {A_\varpi } + \mathscr {B}\) is maximal monotone in \(\mathscr {H_\varpi }\).
Proof
We divide the proof into two steps.
Step 1: \(\mathscr {A_\varpi }\) is maximal monotone. Let us denote \(U = (u,\phi ,v,\psi )\), \({\widetilde{U}} = (\widetilde{u},{{\widetilde{\phi }}},{\widetilde{v}},{{\widetilde{\psi }}})\in \mathcal {D}(\mathscr {A_\varpi })\). Using integration by parts and the boundary conditions, we obtain
and thereby \(\mathscr {A_\varpi }\) is monotone. In order to prove that \(\mathscr {A_\varpi }\) is maximal monotone, we need to prove that \(\text{ Range } ({I}+\mathscr {A_\varpi })=\mathscr {H_\varpi }\). We must prove that
has a solution \(U=(u,\phi ,v,\psi ) \in \mathcal {D}(\mathscr {A_\varpi })\) for any \(U^{*}=(u^{*},\phi ^{*},v^{*},\psi ^{*}) \in \mathscr {H_\varpi }\). This equation leads to the system
Replacing (4.12)\(_{1}\) and (4.12)\(_{2}\) into (4.12)\(_{3}\) and (4.12)\(_{4}\), respectively, we obtain the following system:
where \(V'_\epsilon \) is defined by (3.3). We define
Consequently, for any \((u,\phi ) \in \Lambda \), problem (4.13) is equivalent to
where the bilinear form \(B\ :\ \Lambda \times \Lambda \rightarrow \mathbb {R}\) and the linear form \(L\ :\ \Lambda \rightarrow \mathbb {R}\) are defined by
for any \((w, \varphi )\in \Lambda \). The bilinear form \(B (\cdot , \cdot )\) is bounded since for any \((u, \phi )\) and \((w, \varphi )\in \Lambda \), we have
From (4.5), we obtain for any \((u, \phi )\in \Lambda \)
By assuming \( a\varsigma -b^2> 0\), we get
then there exists a positive constant \( M_0\) such that for any \((u, \phi )\in \Lambda \), we have
Thus, B is coercive. Since L is continuous, from the Lax–Milgram Theorem, problem (4.15) admits a unique solution \((u, \phi ) \in \Lambda \) for all \((w, \varphi ) \in \Lambda \). From (4.12\(_{1,2}\)), we get
Then, by (4.13), we have for \(l\not =0,\)
If \(\varpi =0\), by the definition of weak derivatives, \(u_{xxxx}\) and \(\phi _{xxxx} \) belong to \(L^2 (0, L)\), hence \(u,\phi \in H^4 (0, L)\).
If \(\varpi \not =0\), by the definition of weak derivatives, \(u_{xxxx}\) and \(\phi _{xxxx} \) belong to \(H^1_0 (0, L)\), hence \(u,\phi \in H^3 (0, L)\).
Finally, the vector \((u,\phi ,u_{t},\phi _{t}) \in \mathcal {D}(\mathscr {A_\varpi })\). Therefore, \(\text{ Range } ({I}+\mathscr {A_\varpi })=\mathscr {H_\varpi }\). This complete the proof of the maximal monotonicity of \(\mathscr {A_\varpi }\).
Step 2: \(\mathscr {B}\) is maximal monotone. To prove that \(\mathscr {B}\) is maximal monotone, by Theorem 2.4 of [5] we only need to prove that \(\mathscr {B}\) is monotone and hemicontinuous. For any \(U=(u,\phi ,u_{t},\phi _{t}),\ {\widetilde{U}} = ({\widetilde{u}},{{\widetilde{\phi }}},{\widetilde{u}}_t,{{\widetilde{\phi }}}_{t})\in \mathscr {H_\varpi }\), by using (2.19), (3.4) and (4.9)\(_2\) we have
which implies that \(\mathscr {B}\) is monotone. We observe that
which yields that
Therefore, \(\mathscr {B}\) is hemicontinuous and the maximal monotonicity follows.
Now, since \(\mathscr {A_\varpi }\) and \(\mathscr {B}\) are both maximal monotone and \({\text {int}}(\mathcal {D}(\mathscr {A_\varpi })) \cap \mathcal {D}(\mathscr {B}) \ne \varnothing \), by [5, Theorem 2.6] we conclude that \(\mathscr {A_\varpi } + \mathscr {B}\) is maximal monotone. \(\square \)
Lemma 4.2
We assume that assumptions (3.5)–(3.7) and (4.7) hold. Let \((u,\phi ,u_{t},\phi _{t})\) a strong solution to problem (2.12), (2.13) and (2.14) or ((2.15) or (2.16) or (2.17)) and the total energy defined by

(1) The total energy satisfies
(2) Moreover, there exists a positive constant \(\beta _{0}\) such that
Proof
(1) We multiply the first equation of the system (2.12) by \(u_{t}\) and the second equation by \(\phi _{t}\), integrate over (0, L) and using integration by part and the boundary conditions (2.14) or ((2.15) or (2.16) or (2.17)), we get (4.19).
(2) By (4.6) and (3.6), we have
Substituting (4.21) in (4.18), it follows that
From (4.7), we obtain (4.20) with
\(\square \)
We are now in a position to give the definitions of mild solutions, strong solutions (according to [29], Chapter 6) and weak solutions to problem (2.12), (2.13) and (2.14). Similar definitions can be formulated for the boundary conditions (2.15), (2.16) or (2.17).
Definition 4.1
-
(i)
Given \(T > 0\). A solution \(U (t) \in C([0,T];\mathscr {H}_\varpi )\) to the integral equation
$$\begin{aligned} U(t) = e^{-(\mathscr {A}_\varpi +\mathscr {B})t}U(0)+\int \limits _0^t e^{-(\mathscr {A}_\varpi +\mathscr {B})(t-s)}\mathcal {F}(U(s))ds \end{aligned}$$(4.24)is called a mild solution to problem (2.12)–(2.14) on the interval [0, T].
-
(ii)
Given \(T > 0\). A function \(U : [0, T) \rightarrow \mathscr {H}_\varpi \) is called strong solution to (2.12)–(2.14) on \([0, T),\ T > 0\), if U is continuous on [0, T), continuously differentiable on (0, T), with \(U(t) \in \mathcal {D}(\mathscr {A}_\varpi +\mathscr {B})\) for \(t \in (0, T)\), and (2.12)–(2.14) is satisfied on [0, T) almost everywhere.
-
(iii)
Given \(T > 0\) and initial data \(( u_0, \phi _0, u_1, \phi _1)\in \mathscr {H}_\varpi \). We say that a set of functions \(( u, \phi , u_t, \phi _t)\) is a weak (or generalized) solution to (2.12)–(2.14) if
$$\begin{aligned} ( u, \phi , u_t, \phi _t)\in C([0,T),\mathscr {H}_\varpi ) \end{aligned}$$satisfies (2.13) and the following identity in the sense of distributions
$$\begin{aligned}&\frac{d}{dt}\langle u,w \rangle _\varpi -\langle a u_{xx}+b \phi _x ,w\rangle _l+ \langle f_1(u,\phi ),w\rangle +\frac{d}{dt}\langle \phi ,\varphi \rangle _\varpi \nonumber \\&-\quad \langle \gamma \phi _{xx}-\xi \phi -b u_{x}-\tau \phi _t,\varphi \rangle _l+\langle f_2(u,\phi ),\varphi \rangle =0, \end{aligned}$$in \([0,L]\times [0,T]\) and for all \(w,\varphi \in H^2(0,L)\cap H_0^1 (0,L)\).
To prove the existence of global solutions, we need first to show two energy estimates.
We are now in a position to give the main result of this section.
Theorem 4.1
We assume that assumptions (3.5)–(3.7) and (4.7) hold.
-
(i)
Given \(U_0 = ( u_0,\phi _0, u_1, \phi _1) \in {\mathscr {H}_\varpi }\), then problem (4.8) has a unique global mild solution satisfying \(U (t) \in C([0,\infty );{\mathscr {H}_\varpi })\) given by (4.24).
-
(ii)
The weak solutions depend continuously on the initial data in \({\mathscr {H}_\varpi }\). More precisely, given any two weak solutions \(U^1\) and \(U^2\) are two mild solutions to problem (4.8), then there exists a positive constant C depending on \(U^1(0)\) and \(U^2(0)\), such that
$$\begin{aligned} \Vert U^1(t)-U^2(t)\Vert _{{\mathscr {H}_\varpi }}\le e^{C T}\Vert U^1(0)-U^2(0)\Vert _{{\mathscr {H}_\varpi }},\qquad 0\le t\le T.\end{aligned}$$(4.25) -
(iii)
If \(U_0 = ( u_0,\phi _0, u_1, \phi _1) \in \mathcal {D}(\mathscr {A}_\varpi +\mathscr {B})\), then the corresponding mild solution is strong, that is, it is continuously differentiable, it takes values in \(\mathcal {D}(\mathscr {A}_\varpi +\mathscr {B})\) and it satisfies (4.8) in \({\mathscr {H}_\varpi }\) for almost all \(t \in [0,T]\).
Proof
-
(i)
We need to prove first that \(\mathcal {F}(U)=(0,0,-R_\varpi ^{-1}f_1(u,\phi ),-R_\varpi ^{-1}f_2(u,\phi ))\) defined in (4.10) is locally Lipschitz in \({\mathscr {H}_\varpi }\). Let us denote \(U^1 = (u^1,\phi ^1,u^1_{t},\phi ^1_{t}) \in \mathscr {H_\varpi }\) and \( U^2 = ( u^2, \phi ^2, u^2_{t},\phi ^2_{t})\in \mathscr {H_\varpi }\), such that
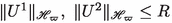 , where \(R>0\) is a constant. The quantities to control are $$\begin{aligned} \Vert \mathcal {F}(U^1)-\mathcal {F}(U^2)\Vert _{{ {\mathscr {H}_\varpi }}}= & {} \Vert R_\varpi ^{-1}(f_1(u^1,\phi ^1)-f_1({u}^2,{\phi }^2))\Vert _{\varpi }\nonumber \\&+\Vert R_\varpi ^{-1}(f_2(u^1,\phi ^1)-f_2({u}^2,{\phi }^2))\Vert _{\varpi }\nonumber \\= & {} \Vert f_1(u^1,\phi ^1)-f_1({u}^2,{\phi }^2)\Vert \nonumber \\&+\Vert f_2(u^1,\phi ^1)-f_2({u}^2,{\phi }^2)\Vert . \end{aligned}$$(4.26)
, where \(R>0\) is a constant. The quantities to control are $$\begin{aligned} \Vert \mathcal {F}(U^1)-\mathcal {F}(U^2)\Vert _{{ {\mathscr {H}_\varpi }}}= & {} \Vert R_\varpi ^{-1}(f_1(u^1,\phi ^1)-f_1({u}^2,{\phi }^2))\Vert _{\varpi }\nonumber \\&+\Vert R_\varpi ^{-1}(f_2(u^1,\phi ^1)-f_2({u}^2,{\phi }^2))\Vert _{\varpi }\nonumber \\= & {} \Vert f_1(u^1,\phi ^1)-f_1({u}^2,{\phi }^2)\Vert \nonumber \\&+\Vert f_2(u^1,\phi ^1)-f_2({u}^2,{\phi }^2)\Vert . \end{aligned}$$(4.26)Using (3.5), we have
$$\begin{aligned} \begin{aligned} \left| f_i(u^1,\phi ^1)-f_i({u}^2,{\phi }^2)\right| ^{2}&=\left| \nabla f_{i}(\theta (u^1,\phi ^1)+(1-\theta )({u}^2,{\phi }^2))\right| ^{2}|({u}^1,{\phi }^1)-({u}^2,{\phi }^2)|^{2} \\&\le C_f\left( |u^1|^{p-1}+| u^2|^{p-1}+|\phi ^1|^{p-1}+|{\phi }^2|^{p-1}+1\right) ^{2} \\&.\left( |u^1-{u}^2|^{2}+|\phi ^1-{\phi }^2|^{2}\right) \end{aligned} \end{aligned}$$(4.27)where \(0 \le \theta \le 1\) and \(C_f > 0\) is a constant depending on the initial data. For the boundary conditions (2.14), it follows from (4.27) and the embedding \(H^{2} (0, L)\cap H^{1}_0 (0, L)\hookrightarrow H^{1}_0 (0, L) \hookrightarrow L^\infty (0, L)\) that there exist a constant \(C_{R}>0\) such that
$$\begin{aligned} \int \limits _0^{L}\left| f_i(u^1,\phi ^1)-f_i({u}^2,{\phi }^2)\right| ^{2} d x \le C_{R}\left\| ({u}^1,{\phi }^1)-({u}^2,{\phi }^2)\right\| ^{2} \le C_{R}\Vert U^1- U^2\Vert _{\mathscr {H_\varpi }}^{2} \end{aligned}$$(4.28)for \( i=1,2\). Substituting the last estimate in (4.26), we conclude that there exists \(L_R > 0\) such that
$$\begin{aligned} \Vert \mathcal {F}(U^1)-\mathcal {F}(U^2)\Vert ^{2} \le L_{R}\Vert U^1- U^2\Vert _{\mathscr {H_\varpi }}^{2}. \end{aligned}$$Therefore, \(\mathcal {F}\) satisfying the local Lipschitz condition. We obtain the same result for the other boundary conditions (2.15), (2.16) or (2.17). Since \(\mathscr {A_\varpi } + \mathscr {B}\) is maximal monotone and, for each \(t \in [0, \infty )\) fixed, \(\mathcal {F}(\cdot ): \mathscr {H_\varpi } \rightarrow \mathscr {H_\varpi }\) is locally Lipschitz. Then, by [7, Theorem 7.2], for all \(U_{0} \in \mathcal {D}(\mathscr {A_\varpi } + \mathscr {B})\), there exists \(t_{\max } \le \infty \) and a unique strong solution U for (4.8) defined on the interval \(\left[ 0, t_{\max }\right) \). Moreover, if \(U_{0} \in \mathscr {H_\varpi }\), then (4.8) has a unique weak solution \(U \in C\left( \left[ 0, t_{\max }\right) , \mathscr {H_\varpi }\right) \), and such solutions satisfy \(\lim \sup _{t \rightarrow t_{\max }}\Vert U(t)\Vert _{\mathscr {H_\varpi }}=\infty \), provided \(t_{\max }<\infty \). Next we prove that the solution is global, that is, \(t_{max} = \infty \). From (4.20), we have
$$\begin{aligned} \Vert U(t)\Vert _{\mathscr {H_\varpi }}^{2} \leqslant \frac{1}{\beta _0} \mathcal {E}_\varpi (t), \quad \forall t \geqslant 0. \end{aligned}$$(4.29)Hence, by (4.29), we conclude
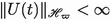 for any \(t \geqslant 0\), which implies that \(t_{\max }=\infty \). This concludes the proof of item (i) of Theorem 4.1.
for any \(t \geqslant 0\), which implies that \(t_{\max }=\infty \). This concludes the proof of item (i) of Theorem 4.1. -
(ii)
On the other hand, given \(T > 0\) and any \( t \in (0, T)\), we consider two mild solutions \(U^1(t)\) and \(U^2(t)\) with initial data \(U^1(0)\) and \(U^2(0)\), respectively. Let us also assume that \(\Vert U^i\Vert _{\mathscr {H}_\varpi }\le R\). Then, using (4.24),
$$\begin{aligned} \Big \Vert U^1(t)-U^2(t)\Big \Vert _{\mathscr {H}_\varpi }\le & {} \Big \Vert e^{-(\mathscr {A}_\varpi +\mathscr {B})t}(U^1(0)-U^2(0))\Big \Vert _{\mathscr {H}_\varpi }\nonumber \\&+\int \limits _0^t \Big \Vert e^{-(\mathscr {A}_\varpi +\mathscr {B})(t-s)}\Big (\mathcal {F}(U^1(s))-\mathcal {F}(U^2(s))\Big )\Big \Vert _{\mathscr {H}_\varpi }ds.\end{aligned}$$Using the local Lipschitz property of \(\mathcal {F}\) and (4.29), we obtain
$$\begin{aligned} \Vert U^1(t)-U^2(t)\Vert _{\mathscr {H}_\varpi }\le \Vert U^1(0)-U^2(0)\Vert _{\mathscr {H}_\varpi }+C_{R,T}\int \limits _0^t \Vert U^1(s)-U^2(s)\Vert _{\mathscr {H}_\varpi }ds. \end{aligned}$$Then, the Gronwall’s lemma gives
$$\begin{aligned} \Vert U^1(t)-U^2(t)\Vert _{\mathscr {H}_\varpi }\le e^{C_{R,T}}\Vert U^1(0)-U^2(0)\Vert _{\mathscr {H}_\varpi },\qquad 0\le t\le T, \end{aligned}$$which implies (4.25) and the continuous dependence of the mild solution on the initial data. This concludes the proof of item (ii) of Theorem 4.1.
-
(iii)
Finally, as noticed above, from an abstract result [29, Theorem 6.1.5] any mild solution with initial data in \(\mathcal {D}(\mathscr {A}_\varpi +\mathscr {B})\) is strong. This proves the item (iii) of Theorem 4.1. The proof is complete.
\(\square \)
5 Lack of exponential stability and analyticity
In this section, we prove that the viscoelastic term, \(-\tau R_l \phi _t\), is not strong enough to bring the solutions of (2.12) to exponential stability when \(\varpi \not =0\) or analyticity when \(\varpi =0\). To show the lack of exponential decay, we use the following well-known result due to Gearhart–Herbst–Prüss–Huang for dissipative systems, from semigroup theory (see, e.g., [9, 31]).
Theorem 5.1
Let \(S(t)=e^{\mathcal {A}t}\) be a \(C_0\)–semigroup of contractions on Hilbert space \(\mathcal {H}\). Then, S(t) is exponentially stable if and only if
where \(\alpha \in \mathbb {R}\) and \(\rho (\mathcal {A})\) is the resolvent set of the differential operator \(\mathcal {A}\).
On the other hand, we use the following characterization of analytic semigroups (see, e.g., [9, 31]).
Theorem 5.2
Let \(S(t)=e^{\mathcal {A}t}\) be a \(C_0\)–semigroup of contractions on Hilbert space \(\mathcal {H}\). Then, S(t) is of analytic type if and only if
For the rest, we need to prove the following
Lemma 5.1
The operator \((\mathscr {A_\varpi }+\mathscr {B})^{-1} :\mathscr {H}_\varpi \rightarrow \mathscr {H}_\varpi \) is compact.
Proof
Let us consider \((F_n)\) a bounded sequence in \(\mathscr {H}_\varpi \) and \(({U}_n)\) the sequence in \(\mathcal {D}(\mathscr {A_\varpi }+\mathscr {B})\) such that \(F_n = (\mathscr {A_\varpi }+\mathscr {B}) {U}_n,\ U_n=(u_n,\phi _n, v_n, \psi _n)\). Since \((\mathscr {A_\varpi }+\mathscr {B})^{-1} \in \mathscr {L(\mathscr {H}_\varpi )}\), there exists a positive constant C such that
From (5.3), we conclude that \((u_n,\phi _n, v_n, \psi _n)\) is bounded in \(\mathcal {D}(\mathscr {A_\varpi }+\mathscr {B})\). Since the embedding of \(H^m(0,L)\) in \(H^j(0,L),\ m > j\), is compact, there exists a subsequence \((u_\nu ,\phi _\nu , v_\nu , \psi _\nu )\) and functions \((u,\phi ,v,\psi )\) such that
that is, the subsequence \(((\mathscr {A_\varpi }+\mathscr {B})^{-1} F_\nu )\) converges in \(\mathscr {H}_\varpi \).\(\square \)
Lemma 5.2
The operator \(\mathscr {A_\varpi }+\mathscr {B}\) satisfies (5.1)\(_1\).
Proof
We only need to show that there is no point spectrum on the imaginary axis, i.e., \(i\mathbb {R}\cap \sigma _p(\mathscr {A_\varpi }+\mathscr {B})=\emptyset \).
Let us suppose that \(i\mathbb {R}\cap \rho (\mathscr {A_\varpi }+\mathscr {B})\) is not true. Since \(0 \in \rho (\mathscr {A_\varpi }+\mathscr {B})\) (see Lemma 4.1), then there exists \( \chi \in \mathbb {R}\), with \(\Vert (\mathscr {A_\varpi }+\mathscr {B})^{-1}\Vert ^{-1} \le |\chi | < \infty \), such that \(\{i\alpha \ :\ |\alpha | < |\chi |\} \subset \rho (\mathscr {A_\varpi }+\mathscr {B})\) and \(\sup \{\Vert (i\alpha I - (\mathscr {A_\varpi }+\mathscr {B})) ^{-1}\Vert : |\alpha | < |\chi |\} = \infty .\) Since \((\mathscr {A_\varpi }+\mathscr {B})^{-1}\) is compact, there exists a sequence of real numbers \(\alpha _n\), with \(\alpha _n \rightarrow \chi \), \(|\alpha _n|<|\chi |\) when \(n\rightarrow \infty \), and a sequence of unit norm vectors in the domain of \(\mathscr {A_\varpi }+\mathscr {B}\), \({U}_n=({u}_n,{\phi }_n, {v}_n, \psi _n)\), such that
Writing (5.4) term by term we get
Since
we infer from (3.2) that \(\psi _n,\ \psi _{nx}\rightarrow 0\) in \(L^2(0,L)\). By (5.5)\(_{2}\), we have \(\phi _n,\ \phi _{nx}\rightarrow 0\) in \(L^2(0,L)\).
Considering the inner product of (5.5)\(_{4}\) times \(\phi _n\) and removing the terms that tend to zero, yields
Hence, having in mind that \(\phi _n,\ \phi _{nx}\rightarrow 0\) in \(L^2(0,L)\) and the fact that \(\Vert u_{nx}\Vert _l\) is bounded, we get
Then, \(\phi _{nxx}\rightarrow 0\) in \(L^2(0,L)\) and by (5.5)\(_2\) \(\psi _{nxx}\rightarrow 0\) in \(L^2(0,L)\).
Next, we take the inner product of (5.5)\(_{4}\) with \( u_{nx}\) to obtain that
As \( \psi _{n},\ \psi _{nx}\rightarrow 0\) in \(L^2(0,L)\) and \(u_{nx}\) and \(u_{nxx}\) are bounded (because of (5.5)\(_{3,4}\)), we get after applying integration by parts of the second term of the aforementioned equation,
As \( \phi _{nx},\ \phi _{nxx}\rightarrow 0\) in \(L^2(0,L)\) and \(u_{nxx}\) and \(u_{nxxx}\) are bounded (because of (5.5)\(_{3,4}\)), we have
The first and second boundary terms of the equation mentioned above vanish for the boundary conditions (2.15) and (2.16), while the first term vanishes for the boundary conditions (2.17) and the second one vanishes for the boundary conditions (2.14). To eliminate the first term, for the boundary conditions (2.14), we use the Gagliardo–Nirenberg inequality,
and
The same procedure can be applied in case of the boundary conditions (2.17). We then conclude that
and therefore
Then, we take the inner product of (5.5)\(_{3}\) with \(u_{n}\), we obtain
Using (5.5)\(_{1}\) and previous results, it is clear that
Thus, we have a contradiction since \(U_n\) cannot be of unit norm and, in consequence, the first condition of Theorem 5.1 holds.\(\square \)
Often and in particular in one-dimensional setting, the non-uniform boundedness of the resolvent operator is shown by giving an explicit sequence of exact solutions of the system. This requires adequate boundary conditions. As the method used here is not adequate for any of the considered boundary conditions, we will consider the particular case \(\gamma =0\) to consider the following boundary conditions:
which is more adapted to the method we are going to apply.
Under the boundary conditions (5.9), the problem is well-posed and is governed by a \(C_0-\)contraction semigroup S(t) on \(\mathscr {K}_\varpi = (H^2(0,L)\cap H_0^1 (0,L))\times H_*^1 (0,L)\times V_\varpi \times V_\varpi ^*\), where
and
The corresponding norm in \(\mathscr {K_\varpi }\) will be given by (4.3) with \(\gamma = 0\).
5.1 Lack of exponential decay when \(\varpi \not =0\).
The lack of exponential stability is based on the well-known criterion for contraction semigroups, which states that the semigroup is exponentially stable if and only if the imaginary axis belongs to the resolvent set (see assertion (5.1)\(_1\) of Theorem 5.1) and the resolvent operator is uniformly bounded on the imaginary axis (see assertion (5.1)\(_2\)).
Lemma 5.3
Let \(S(t) = e^{-(\mathscr {A}_\varpi +\mathscr {B})t}\) the \(C_0-\)semigroup of contraction on Hilbert space \(\mathscr {K}_\varpi \) associated with the problem (2.12), (2.13) and (5.9) with \(\gamma =0\) and \(\varpi \not =0\). Then, S(t) is not exponentially stable.
Proof
Because of Theorem 5.1 and Lemma 5.2, we have to prove that (5.1)\(_2\) does not hold. To prove this result we will argue by contradiction, that is, we will show that there exists a sequence of imaginary number \(\alpha _n\) with \(\lim _{n \rightarrow \infty } |\alpha _n| = \infty \) and \({U}_{n}=(u_n, \phi _n, v_n, \psi _n)^T\in \mathcal {D}(\mathscr {A}_\varpi +\mathscr {B})\) for \(F_n=(f_{1n}, f_{2n}, f_{3n}, f_{4n})^T\in {\mathscr {K}_\varpi }\) with \(\Vert F_n\Vert _{{\mathscr {K}_\varpi }}<1\) such that
where \(F_n\) is bounded in \({\mathscr {K}_\varpi }\), but \(\Vert U_n\Vert _{\mathscr {K}_\varpi }\) tends to infinity. Rewriting the above spectral equation in term of its components, we have
We choose for all \(n\in \mathbb {N}\), \(F_{n}=(0,0,\sin (n\nu x),0)\). Then, \(F_n\) is bounded in \({\mathscr {K}_\varpi }\). On the basis of the boundary conditions (5.9), we can try solutions of the type
where \(\nu =\frac{\pi }{L}\), \(A_{n}\) and \(B_{n}\) are unknown functions. Substituting (5.12) in (5.11), we find that \(A_{n}\) and \(B_{n}\) satisfy
where \(\Xi _\epsilon =1+\epsilon ^2 n^{2}\nu ^2\). We choose \(\alpha _{n} \) so that \(-\alpha _{n} ^{2}(1+\varpi ^2 n^{2}\nu ^2)+a(1+l^2 n^{2}\nu ^2) n^{2}\nu ^2=0\) which implies that \(\alpha _{n} =\pm n\nu \sqrt{a}\sqrt{\frac{1+l^2 n^{2}\nu ^2}{1+\varpi ^2 n^{2}\nu ^2}}.\) Moreover, (5.13)\(_1\) leads to
The asymptotic behavior of the coefficient \(B_{n}\) will give us \(B_{n}\sim - \frac{\varpi ^2}{bl^2 n \nu }\) as \(n\rightarrow \infty .\) This gives \(\phi _n (x) \sim -\frac{\varpi ^2}{bl^2 n \nu } \cos ( n \nu x)\) and \(\psi _n (x) \sim \pm i \frac{\varpi \sqrt{a}}{bl} \cos ( n \nu x)\) as \(n\rightarrow \infty .\) On the other hand, as \(n\rightarrow \infty \), we have
from where it follows that
which proves the lack of exponential stability. \(\square \)
5.2 Lack of analyticity when \(\varpi =0\)
Lemma 5.4
Let \(S(t) = e^{-(\mathscr {A}_0+\mathscr {B})t}\) the \(C_0-\)semigroup of contraction on Hilbert space \(\mathscr {K}_0\) associated with the problem (2.12), (2.13) and (5.9) with \(\gamma =0\) and \(\varpi =0\). Then, S(t) is not analytic.
Proof
Taking into account Theorem 5.2 and Lemma 5.2, to prove our statement, we will argue by contradiction, that is, we will show that there exists a sequence of real number \(\alpha _n\) with \(\lim _{n \rightarrow \infty } |\alpha _n| =\infty \) and \({U}_{n}=(u_n, \phi _n, v_n, \psi _n)^T\in \mathcal {D}(\mathscr {A}_0+\mathscr {B})\) for \(F_{n}=(0,0,\sin (n\nu x),0)^T\in {\mathscr {K}_0}\) with \(\Vert F_n\Vert _{{\mathscr {K}}_0}<1\) such that (5.10) holds, where the vector \(F_n\) is bounded in \({\mathscr {K}_0}\), but \(\Vert U_n\Vert _{\mathscr {K}_0}\) tends to infinity. Repeating the same previous procedure and choosing the same type solution (5.12), the system (5.13) becomes
By choosing \(\alpha _{n} =\pm n\nu \sqrt{a(1+l^2 n^{2}\nu ^2)}\), we obtain the following asymptotic behavior:
This gives \(u_n (x) \sim -\frac{\sqrt{a}(\sqrt{a}\pm i\tau l )}{b^2l^2 n^{2}\nu ^2} \sin ( n \nu x)\) as \(n\rightarrow \infty .\) On the other hand, we have
Thus, we obtain
which completes the proof of the theorem. \(\square \)
Remark 5.1
-
1.
The solutions are not analytic in general. In fact, they are not analytic when \(\varpi =0\) and not exponentially stable when \(\varpi \not =0\), which means that the corresponding semigroup is not analytic.
-
2.
The case \( \gamma = 0 \) is considered here only to use the boundary conditions (5.9) which is more adapted to the above method than the considered boundary conditions. Note that, in these cases, we cannot apply the procedure used previously, because we do not have appropriate solutions (satisfying boundary conditions) to solve system (2.12). Explicitly speaking, the lack of exponential stability or the lack of analyticity of the semigroups associated to system (2.12) with boundary conditions (2.14)–(2.17) is an open problem.
6 Exponential decay
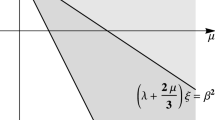
In this section, we show that the presence of frictional damping in the elastic component, whose form depends on the elastic nonlocal parameter (\(\varpi =0\) or not), leads to exponential stability. Without frictional damping, the exponential stability can only obtained in the absence of nonlinear body forces and under the well-known condition of equal speed waves propagation, which can be written here as:
An approach based on the construction of a Lyapunov functional is applied to obtain the optimal rate of decay of solutions in terms of the physical parameters.
6.1 Case \(\varpi =0\)
In this subsection, we prove that when \(\varpi =0\), we need to add a frictional damping for the elastic component characterized by \(\alpha u_{t}\) where \(\alpha >0\), to get exponential stability of the nonlinear problem. This leads to the following:
subjected to the initial conditions (2.13) and the boundary conditions (2.14).
From Theorem 4.1, the problem (6.2) subjected to the initial conditions (2.13) and the boundary conditions (2.14) is well-posed and is governed by a \(C_0-\)contraction semigroup S(t) on the Hilbert space \( \mathscr {H}_0:= \left( H^2(0,L)\cap H_0^1 (0,L)\right) ^2\times \left( L^2 (0,L)\right) ^2\).
Lemma 6.1
Suppose that assumptions (3.5)–(3.7) and (4.7) hold and \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.2), (2.13) and (2.14). Then, there exists a positive constant \(\epsilon \) defined by (6.14) such that
where \(\mathcal {E}_0(t)\) is the total energy of the problem (6.2), (2.13) and (2.14), defined by
Proof
In this case, the total energy defined by (6.4) satisfies
For each \(\epsilon >0\), we shall define the perturbed energy by
where
Firstly, let us prove that there exists \(\epsilon _{0}>0\) such that
Indeed, by Young’s inequality, we have that
Choosing
then the inequality (6.7) holds. Now, we want to get
where
Let us multiply the first equation of (6.2) by u and the second one by \(\phi \), we obtain
By adding and subtracting (6.4) to (6.11), we get
By plugging (6.13) into (6.12) and using the fact that \(\Vert \phi _{t}\Vert ^{2}\le \Vert \phi _{t}\Vert ^2_l\), (6.9) follows immediately.
From (4.7) and (4.23), we infer that \(1-\frac{\beta \varrho }{\beta _0}>0\).
Finally, we shall prove that inequality (6.3) holds. Now substituting (6.5) and (6.9) in (6.6), we get
By choosing
yields
Using the second inequality in (6.7), we conclude that
Integrating from 0 to t, yields
Combining the inequalities (6.15) together with (6.7), it follows that (6.3) holds. The proof is complete.
\(\square \)
6.2 Case \(\varpi \not =0\)
When \(\varpi \not =0\), we need to add a frictional damping for the elastic component characterized by \(-\alpha u_{xxt}\) where \(\alpha >0\), to get exponential stability of the nonlinear problem. This leads to the following:
subjected to the initial conditions (2.13) and the boundary conditions (2.14).
Lemma 6.2
Suppose that assumptions (3.5)–(3.7) and (4.7) hold and \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.16), (2.13) and (2.14). Then, there exists a positive constant \(\epsilon \) defined by (6.26) such that
where \( \mathcal {E}_\varpi (t)\) is the total energy of the problem (6.16), (2.13) and (2.14) defined by (4.18).
Proof
In this case, the total energy defined by (4.18) satisfies
For each \(\epsilon >0\), we shall define the perturbed energy by
where
Following the previous argument, one can prove that there exists \(\epsilon _{0}>0\) such that
Now, we want to get
Let us multiply the first equation of (6.16) by u and the second one by \(\phi \), we obtain
where \(\Upsilon \) is given by (6.10). By adding and subtracting (4.18) to (6.22), we get
Similar to (6.13), we have
Substituting (6.24) in (6.23) and using the fact that \(\Vert u_{t}\Vert ^{2}\le \lambda _0\Vert u_{xt}\Vert ^2\) (see (3.1)), we conclude that (6.21) holds.
Finally, we shall prove that inequality (6.17) holds. Substituting (6.18) and (6.21) in (6.19), we obtain
By choosing
and following the previous arguments, we arrive at (6.17). The proof is complete. \(\square \)
Remark 6.1
-
1.
We consider here the hinged-hinged boundary conditions (2.14), since they provide a lot of symmetry due to the commutativity of the operators \(R_\epsilon \partial _{xx}\). But in both cases (\(\varpi =0\) or not), the obtained results can be extended to the other boundary conditions (2.15), (2.16) or (2.17) with some little modifications.
-
2.
It is worth mentioning that Magaña and Quintanilla in [21] used the Routh–Hurwitz theorem to prove the lack of exponential decay of system (6.2) without nonlocality (\(\varpi =l=0\)), viscoporosity (\(\tau =0\)) and body forces (\(f_1=f_2=0\)). However, they showed that the presence of both viscoporosity (\(\tau \not =0\)) and viscoelasticity (\(\alpha \not =0\)) stabilized the system exponentially. Rivera and Quintanilla [25] proved that the solutions to the same system (studied in [21]) decays polynomially by a rate decay of type \(\frac{1}{t}\).
6.3 Case \(f_1=f_2=0\) and \(\gamma =a\)
The aim of this subsection is to prove that the problem (2.12) (when \(\gamma =a\)), (2.13) and (2.17) is exponentially stable in the absence of body forces and under the condition of equal wave speeds (6.1). For this, we consider in this section the following system:
subjected to the initial conditions (2.13) and the clamped-clamped boundary conditions (2.17).
From Theorem 4.1, the problem (6.27), (2.13) and (2.17) is well-posed and is governed by a \(C_0-\)contraction semigroup S(t) on \(\mathscr {H}_\varpi = (H_0^2(0,L))^2\times (V_\varpi )^2\).
Lemma 6.3
Suppose that \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.27), (2.13) and (2.17) with \(\gamma =a\). Then, there exists a positive constant \(\delta \) (given by (6.38)\(_3\)) such that
where
Proof
The time derivative of (6.29) gives
By the Cauchy–Schwarz inequality, it is clear that
Estimate (6.28) follows by combining the two inequalities above and using \(\xi -\frac{b^2}{a}>0\) (see (2.18)\(_3\)).\(\square \)
Lemma 6.4
Suppose that \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.27), (2.13) and (2.17) with \(\gamma =a\). Then, we have
where
Proof
The time derivative of (6.32) gives
Since \(\gamma =a\), we obtain (6.31) after using Young’s inequality together with (3.1). \(\square \)
Lemma 6.5
Suppose that \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.27), (2.13) and (2.17) with \(\gamma =a\). Then, we have
where
Proof
The time derivative of (6.32) gives
Using an integration by parts and Young’s inequality, we obtain (6.33).\(\square \)
Lemma 6.6
Suppose that \((u,\phi , u_t, \phi _t)\) be a solution to the problem (6.27), (2.13) and (2.17) with \(\gamma =a\). Then, there exists two positive constants \(d_1\) and \(d_2\) such that
where \( \mathcal {E}_\varpi (t)\) is defined by (4.18) with \(F=0\) and satisfies (4.19).
Proof
For each \(\epsilon >0\), we shall define the perturbed energy by
where \(\epsilon \), \(\epsilon _1\) and \(\epsilon _2\) are positive constants to be properly chosen later.
Exploiting Young’s and Poincaré’s inequalities, we obtain
where \(0<c<\epsilon \). Consequently, we obtain
that is
Using Lemmas 6.3-6.5, we obtain
We choose \(\epsilon _1\), \(\epsilon _2\), \(\delta \) and \(\epsilon \) such that
and by following the previous arguments, we arrive at (6.36). The proof is complete.\(\square \)
7 Conclusion
We summarize the obtained results as follows:
(i) In this paper, we have derived a nonlocal theory for porous elastic materials in the context of Mindlin’s strain gradient model. By comparison with other nonlocal [6, 20, 36] or local [17, 18] theories, the model proposed in this paper is more reasonable in predicting the propagation of porous elastic waves. This work, which has not been obtained in any reference yet, represents a first step towards understanding the fundamental limits of porous elastic waves propagation in nonlocal Mindlin’s strain gradient materials. In fact we have obtained two nonlocal hyperbolic equations for displacement and void volume fraction propagating with finite waves speeds. When the elastic nonlocal parameter \(\varpi =0\), our equations propagate with infinite waves speeds. This has a great impact on the general dynamics of the solutions as we can see.
(ii) By means of nonlinear semigroups and the theory of monotone operators, the well-posedness of the nonlocal Mindlin’s strain gradient porous elasticity for a one-dimensional nonlinear problem was proved. The exponential stability and analyticity issues were discussed as well. By an approach based on the Gearhart–Herbst–Prüss–Huang Theorem, we prove that the semigroup associated with the derived model is not exponentially stable when \(\varpi \not =0\) and is not analytic when \(\varpi =0\). We have proved that a frictional damping for the elastic component, whose form depends on the elastic nonlocal parameter (\(\varpi =0\) or not), is shown to lead to exponential stability. Without frictional damping, the derived system can be exponentially stable only in the absence of body forces and under the condition of equal wave speeds. These results confirm our previous results obtained in [1,2,3] in the frame local Mindlin’s strain gradient model.
(iii) In comparison with plates and beams theory in classic elasticity, the elastic nonlocal parameter of our model \(\varpi \), represents the rotational inertia parameter related with the thickness of the plate. From the literature, we know that if the rotational inertia parameter is different from zero, then the corresponding problem is of hyperbolic-like dynamics with finite speed of propagation. The corresponding semigroup is not analytic, but the exponential stability of solutions is kept. Without the rotational inertia parameter, the dynamics has infinite speed of propagation and the corresponding semigroup is analytic. In our case, the solutions are generally not analytic. This lack of analyticity is due to the nonlocality and the strain gradient effects which cause a lack of regularity.
(iv) The importance of the multi-dimensional counterpart of these results is clear, but this question is difficult from a mathematical point of view. The important question is whether or not this exponential stability will be preserved in multi-dimensional problem. From [1,2,3] and this study, one would expect that a frictional damping for the elastic component of the form \(-\alpha _{ij} \dot{u}_j\) when \(\varpi =0\) or characterized by \(\alpha \Delta \dot{u}_i\) when \(\varpi \not =0\), can lead to exponential stability in a multi-dimensional setting for \(\alpha >0\).
(v) The study presented in this paper should prove useful for researchers working on qualitative properties of materials or designers of nonlocal strain gradient models. In particular, it will be useful in predicting and better understanding the mathematical and mechanical responses of nonlocal materials comparing to local one.
References
Aouadi, M., Passarella, F., Tibullo, V.: Exponential stability in Mindlin’s Form II gradient thermoelasticity with microtemperatures of type III. Proc. R. Soc. A 476, 20200459 (2020)
Aouadi, M., Amendola, A., Tibullo, V.: Asymptotic behavior in Form II Mindlin’s strain gradient theory for porous thermoelastic diffusion materials. J. Therm. Stresses 59, 191–209 (2020)
Aouadi, M., Copetti, M.I.M.: Exponential stability and numerical analysis of a thermoelastic diffusion beam with rotational inertia and second sound. Math. Comput. Simul. 187, 586–613 (2021)
Apalara, T.A.: Exponential decay in one-dimensional porous dissipation elasticity. Quart. J. Mech. Appl. Math. 70, 363–372 (2017)
Barbu, V.: Nonlinear Differential Equations of Monotone Types in Banach Spaces. Springer Monographs in Mathematics, vol. 190. Springer, New York (2010)
Biswas, S.: The propagation of plane waves in nonlocal visco-thermoelastic porous medium based on nonlocal strain gradient theory. Waves Random Complex Media (2021). https://doi.org/10.1080/17455030.2021.1909780
Chueshov, I., Eller, M., Lasiecka, I.: On the attractor for a semilinear wave equation with critical exponent and nonlinear boundary dissipation. Commun. Partial Diff. Equ. 27, 1901–1951 (2002)
Cowin, S.C., Nunziato, J.W.: Linear elastic materials with voids. J. Elast. 13(125–147), 22 (1983)
Gearhart, L.: Spectral theory for contraction semigroups on Hilbert space. Trans. Am. Math. Soc. 236, 385–385 (1978)
Eringen, A.C.: Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 10, 425–435 (1972)
Eringen, A.C.: On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54, 4703–4710 (1983)
Eringen, A.C.: Nonlocal Continuum Field Theories. Springer, London (2002)
Eringen, A.C.: Nonlocal polar elastic continua. Int. J. Eng. Sci. 10, 1–16 (1972)
Eringen, A.C.: On nonlocal fluid mechanics. Int. J. Eng. Sci. 10, 561–575 (1972)
Eringen, A.C.: Nonlocal continuum theory of liquid crystals. Mol. Cryst. Liq. Cryst. 75, 321–343 (1981)
Ieşan, D.: Thermoelastic Models of Continua. Springer, London (2004)
Ieşan, D.: A gradient theory of porous elastic solids. Z. Angew. Math. Mech. 100, 1–18 (2020)
Ieşan, D.: On the grade consistent theories of micromorphic solids. Am. Inst. Phys. Conf. Proc. 1329, 130–149 (2011)
Kaempgen, M., Duesberg, G.S., Roth, S.: Transparent carbon nanotube coatings. Appl. Surface Sci. 252, 425–429 (2005)
Lim, C.W., Zhang, G., Reddy, J.N.: A Higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 78, 298–313 (2015)
Magaña, A., Quintanilla, R.: On the time decay of solutions in one-dimensional theories of porous materials. Int. J. Solids Struct. 43, 3414–3427 (2006)
McCay, B.M., Narsimhan, M.L.N.: Theory of nonlocal electromagnetic fluids. Arch. Mech. 33, 365–384 (1981)
Mindlin, R.: Micro-structure in linear elasticity. Arch. Rat. Mech. Anal. 16, 52–78 (1964)
Mindlin, R.: Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1, 414–438 (1965)
Muñoz, R.J.E., Quintanilla, R.: On the time polynomial decay in elastic solids with voids. J. Math. Anal. Appl. 338, 1296–1309 (2008)
Narsimhan, M.L.N., McCay, B.M.: Dispersion of surface waves in nonlocal dielectric fluids. Arch. Mech. 33, 385–400 (1981)
Nunziato, J.W., Cowin, S.C.: A non linear theory of elastic materials with voids. Arch. Ration. Mech. Anal. 72, 175–201 (1979)
Pamplona, P.X., Muñoz Rivera, J.E., Quintanilla, R.: On the decay of solutions for porous elastic systems with history. J. Math. Anal. Appl. 379, 682–705 (2011)
Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, vol. 44. Springer-Verlag, New York (1983)
Puri, P., Cowin, S.C.: Plane waves in linear elastic materials with voids. J. Elast. 15, 167–183 (1985)
Prüss, J.: On the spectrum of \(C_0-\)semigroups. Trans. Am. Math. Soc. 284, 847–847 (1984)
Reddy, J.N., Srinivasa, A.R.: Nonlinear theories of beams and plates accounting for moderate rotations and material length scales. Int. J. Non-Linear Mech. 66, 43–53 (2014)
Santos, M.L., Jùnior, D.A.: On porous-elastic system with localized damping. Z. Angew. Math. Phys. 67, 1–18 (2016)
Santos M.L., Campelo, A.D.S., Almeida Jùnior, D.S.: Rates of decay for porous elastic system weakly dissipative. Acta Appl. Math. 151, 1–16 (2017)
Santos, M.L., Campelo, A.D.S., Almeida Jùnior, D.S.: On the decay rates of porous elastic systems. J. Elast. 127, 79–101 (2017)
Singh, D., Kaur, G., Tomar, S.K.: Waves in nonlocal elastic solid with voids. J. Elast. 128, 85–114 (2017)
Srinivasa, A.R., Reddy, J.N.: A model for a constrained, finitely deforming, elastic solid with rotation gradient dependent strain energy, and its specialization to von Kármán plates and beams. J. Mech. Phys. Solids 61, 873–885 (2013)
Toupin, R.: Elastic materials with couple-stresses. Arch. Rat. Mech. Anal. 11, 385–414 (1962)
Acknowledgements
The author would like to thank the Editor Prof. Laurent Chupin and the anonymous reviewers for their recommendations and remarks aiming at improving the manuscript in terms of clarity.
ORCID Moncef Aouadi http://orcid.org/0000-0003-3400-5670
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Aouadi, M. Well-posedness, lack of analyticity and exponential stability in nonlocal Mindlin’s strain gradient porous elasticity. Z. Angew. Math. Phys. 73, 111 (2022). https://doi.org/10.1007/s00033-022-01764-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-022-01764-2



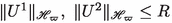 , where
, where 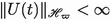 for any
for any