Variable-coefficient symbolic computation approach for finding multiple rogue wave solutions of nonlinear system with variable coefficients

Abstract

In this paper, a variable-coefficient symbolic computation approach is proposed to solve the multiple rogue wave solutions of nonlinear equation with variable coefficients. As an application, a ($2+1$)-dimensional variable-coefficient Kadomtsev–Petviashvili equation is investigated. The multiple rogue wave solutions are obtained and their dynamic features are shown in some 3D and contour plots.

1 Introduction

In this paper, the following (2+1)-dimensional variable-coefficient Kadomtsev–Petviashvili (vcKP) equation is investigated [1]

$$\begin{aligned} \alpha (t) u_x^2+\alpha (t) u u_{xx}+\beta (t) u_{xxxx}-\gamma (t) u_{yy}+u_{xt}=0, \end{aligned}$$

(1)

where $u=u(x,y,t)$ describes amplitude of the long wave of two-dimensional fluid domain on varying topography or in turbulent flow over a sloping bottom. $\alpha (t)$, $\beta (t)$ and $\gamma (t)$ are arbitrary real functions. The solitonic solution [1], Wronskian and Gramian solutions [2], Bäcklund transformation [3], breather wave solutions [4], lump and interactions solutions [5, 6] of Eq. (1) have been studied.

Rogue wave has important applications in ocean’s waves [7], optical fibers [8], Bose–Einstein condensates [9] and other fields. Rogue wave solutions of many integrable equations have been investigated [10,11,12,13,14,15,16,17]. Recently, a symbolic computation approach to obtain the multiple rogue wave solutions is proposed by Zhaqilao [18]. But the main application of this method is constant-coefficient integrable equation [19,20,21], which is not suitable for variable-coefficient integrable equation. So, we give an improved method named variable-coefficient symbolic computation approach (vcsca) to solve this problem and apply this method to Eq. (1), which will be the main work of our paper.

The organization of this paper is as follows. Section 2 proposes a vcsca; Sect. 3 gives the 1-rogue wave solutions; Sect. 4 obtains the 3-rogue wave solutions; Sect. 5 presents the 6-rogue wave solutions; and Sect. 6 gives this conclusions.

2 Modified symbolic computation approach

Here, we present a vcsca to find the multiple rogue wave solutions of variable-coefficient integrable equation

Step 1. Instead of the traveling wave transformation in Ref. [18], we make a non-traveling wave transformation $\upsilon =x-\omega (t)$ in the following nonlinear system with variable coefficients

$$\begin{aligned} \varXi (u, u_t, u_x, u_y, u_{xy}, \ldots )=0, \end{aligned}$$

(2)

and Eq. (2) is reduced to a (1+1)-dimensional equation

$$\begin{aligned} \varXi (u, u_\upsilon , u_y, u_{\upsilon y}, \ldots )=0. \end{aligned}$$

(3)

Step 2. By Painlevé analysis, we make the following transformation

$$\begin{aligned} u(\upsilon , y)=\frac{\partial ^n}{\partial \upsilon ^m}ln\xi (\upsilon , y). \end{aligned}$$

(4)

m can be derived by balancing the order of the highest derivative term and nonlinear term.

Step 3. Assuming

$$\begin{aligned} \xi (\upsilon , y)=F_{n+1}(\upsilon , y)+2 \nu y P_n(\upsilon , y)+2 \mu \upsilon Q_n(\upsilon , y)+(\mu ^2+\nu ^2) F_{n-1}(\upsilon , y), \end{aligned}$$

(5)

with

$$\begin{aligned} F_n(\upsilon , y)= & {} \sum ^{n(n+1)/2}_{k=0}\sum ^{k}_{i=0}a_{n(n+1) -2k,2i}y^{2i}\upsilon ^{n(n+1)-2k},\\ P_n(\upsilon , y)= & {} \sum ^{n(n+1)/2}_{k=0}\sum ^{k}_{i=0}b_{n(n+1) -2k,2i}\upsilon ^{2i}y^{n(n+1)-2k},\\ Q_n(\upsilon , y)= & {} \sum ^{n(n+1)/2}_{k=0}\sum ^{k}_{i=0}c_{n(n+1) -2k,2i}y^{2i}\upsilon ^{n(n+1)-2k}, \end{aligned}$$

$F_0=1, F_{-1}=P_0=Q_0=0$, where $a_{m,l}$, $b_{m,l}$ and $c_{m,l}$($m, l\in {[0, 2,4, \ldots , n(n+1)]}$) are unknown constants, $\mu$ and $\nu$ are the wave center.

Step 4. Substituting Eqs. (4) and (5) into Eq. (3) and equating all the coefficients of the different powers of $\upsilon$ and y to zero, we can know $a_{m,l}$, $b_{m,l}$ and $c_{m,l}$($m, l\in {[0, 2,4, \ldots , n(n+1)]}$). The corresponding multiple rogue wave solutions can be presented.

3 1-Rogue wave solutions

Based on the vcsca, set

$$\begin{aligned} \alpha (t)=\frac{6 \beta (t)}{\varTheta _0}, \upsilon =x-\omega (t), u=2 \varTheta _0\,[ln\xi (\upsilon ,y)]_{\upsilon \upsilon }, \end{aligned}$$

(6)

and Eq. (1) can be changed as

$$\begin{aligned}&6 \xi _\upsilon ^2 [\xi [3 \beta (t) \xi _{\upsilon \upsilon \upsilon \upsilon }-2 \omega '(t) \xi _{\upsilon \upsilon }]+3 \beta (t) \xi _{\upsilon \upsilon }^2]+2 \xi ^2 \xi _\upsilon [2 \omega '(t) \xi _{\upsilon \upsilon \upsilon }\nonumber \\&\quad -3 \beta (t) \xi _{\upsilon \upsilon \upsilon \upsilon \upsilon }]+\xi [\xi [-3 \beta (t) \xi _{\upsilon \upsilon \upsilon \upsilon } \xi _{\upsilon \upsilon }+2 \beta (t) \xi _{\upsilon \upsilon \upsilon }^2+3 \omega '(t) \xi _{\upsilon \upsilon }^2]\nonumber \\&\quad +\xi ^2 [\beta (t) \xi _{\upsilon \upsilon \upsilon \upsilon \upsilon \upsilon }-\omega '(t) \xi _{\upsilon \upsilon \upsilon \upsilon }]-6 \beta (t) \xi _{\upsilon \upsilon }^3]-24 \beta (t) \xi _{\upsilon \upsilon \upsilon } \xi _\upsilon ^3\nonumber \\&\quad +\gamma (t) [[6 \xi _\upsilon ^2-2 \xi \xi _{\upsilon \upsilon }] \xi _y^2+2 \xi [\xi \xi _{\upsilon \upsilon y}-4 \xi _\upsilon \xi _{\upsilon y}] \xi _y+\xi [\xi _{yy} [\xi \xi _{\upsilon \upsilon }-2 \xi _\upsilon ^2]\nonumber \\&\quad +\xi [2 \xi _{\upsilon y}^2+2 \xi _\upsilon \xi _{\upsilon yy}-\xi \xi _{\upsilon \upsilon yy}]]] +6 \omega '(t) \xi _\upsilon ^4. \end{aligned}$$

(7)

According to Eq. (5), we have

$$\begin{aligned} \xi (\upsilon ,y)=(\upsilon -\mu )^2+\zeta _1 (y-\nu )^2+\zeta _0, \end{aligned}$$

(8)

where $\mu$, $\nu$, $\zeta _0$ and $\zeta _1$ are unknown real constants. Substituting Eq. (8) into Eq. (7) and equating the coefficients of all powers $\upsilon$ and y to zero, we obtain

$$\begin{aligned} \gamma (t)=\frac{3 \beta (t)}{\zeta _0 \zeta _1}, \omega '(t)=\zeta _1 \gamma (t). \end{aligned}$$

(9)

Substituting Eqs. (8) and (9) into Eq. (6), the 1-rogue wave solutions for Eq. (1) can be read as

$$\begin{aligned} u=\frac{4 \varTheta _0 [-(\mu -\upsilon )^2+\zeta _1 (y-\nu )^2 +\zeta _0]}{[(\mu -\upsilon )^2+\zeta _1 (y-\nu )^2+\zeta _0]{}^2}. \end{aligned}$$

(10)

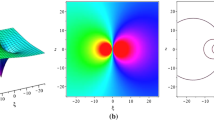
When $\zeta _0>0$, rogue wave (10) has three extreme value points $(\mu , \nu )$, $(\mu \pm \sqrt{3} \sqrt{\zeta _0}, \nu )$. When $\zeta _0< 0, \zeta _1> 0$, rogue wave (10) has three extreme value points $(\mu , \nu )$, $(\mu , \nu \pm \frac{\sqrt{-\zeta _0}}{\sqrt{\zeta _1}})$. Figures 1 and 2 describe the dynamic features of rogue wave (10) when $\zeta _0$ and $\zeta _1$ select different values.

Fig. 1

Rogue wave (10) with $\mu =\nu =0$, $\varTheta _0=1$, $\zeta _0=-10$, $\zeta _1=2$, a 3D graphic, b contour plot

Fig. 2

Rogue wave (10) with $\mu =\nu =0$, $\varTheta _0=1$, $\zeta _0=1$, $\zeta _1=2$, a 3D graphic, b contour plot

4 3-Rogue wave solutions

In order to look for the 3-rogue wave solutions, we set

$$\begin{aligned} \xi (\upsilon ,y)= & {} \mu ^2+\nu ^2+\upsilon ^6+y^6 \zeta _{17}+y^4 \zeta _{16}+2 \mu \upsilon \left( y^2 \zeta _{23}+\upsilon ^2 \zeta _{24}+\zeta _{22}\right) \nonumber \\&+2 \nu y \left( y^2 \zeta _{20}+\upsilon ^2 \zeta _{21} +\zeta _{19}\right) +\upsilon ^4 y^2 \zeta _{11}+y^2\zeta _{15}\nonumber \\&+\upsilon ^2 \left( y^4 \zeta _{14}+y^2 \zeta _{13} +\zeta _{12}\right) +\upsilon ^4 \zeta _{10}+\zeta _{18}, \end{aligned}$$

(11)

Fig. 3

Rogue wave (13) with $\mu =\nu =0$, $\varTheta _0=1$, $\zeta _{11}=\zeta _{13}=\zeta _{21}=\zeta _{24}=1$, a 3D graphic, b contour plot

Fig. 4

Rogue wave (13) with $\mu =10, \nu =0$, $\zeta _{11}=\zeta _{13}=\zeta _{21}=\zeta _{24}=1$, $\varTheta _0=1$, a 3D graphic, b contour plot

Fig. 5

Rogue wave (13) with $\mu =0, \nu =10$, $\zeta _{11}=\zeta _{13}=\zeta _{21}=\zeta _{24}=1$, $\varTheta _0=1$, a 3D graphic, b contour plot

Fig. 6

Rogue wave (13) with $\mu =\nu =10$, $\zeta _{11}=\zeta _{13}=\zeta _{21}=\zeta _{24}=1$, $\varTheta _0=1$, a 3D graphic, b contour plot

Fig. 7

Rogue wave (16) with $\mu =\nu =0$, $\varTheta _0=1$, $\zeta _0=\zeta _1=\zeta _{28}=1$, $\zeta _{26}=2$, a 3D graphic, b contour plot

Fig. 8

Rogue wave (16) with $\mu =10, \nu =0$, $\varTheta _0=1$, $\zeta _0=\zeta _1=\zeta _{28}=1$, $\zeta _{26}=2$, a 3D graphic, b contour plot

Fig. 9

Rogue wave (16) with $\mu =0, \nu =10$, $\varTheta _0=1$, $\zeta _0=\zeta _1=\zeta _{28}=1$, $\zeta _{26}=2$, a 3D graphic, b contour plot

Fig. 10

Rogue wave (16) with $\mu =\nu =30$, $\varTheta _0=1$, $\zeta _0=\zeta _1=\zeta _{28}=1$, $\zeta _{26}=2$, a 3D graphic, b contour plot

Fig. 11

Rogue wave (17) with $\mu =\nu =\varTheta _0=1$, $x=0$, $\zeta _0=-1$, $\zeta _1=2$, $\beta (t)=1$ in a, d, $\beta (t)=t$ in b, e and $\beta (t)=\cos t$ in c, f

where $\zeta _i (i=10,\ldots , 24)$ is unknown real constant. Substituting Eq. (11) into Eq. (7) and equating the coefficients of all powers $\upsilon$ and y to zero, we get

$$\begin{aligned} \gamma (t)= & {} \frac{90 \beta (t)}{\zeta _{13}}, \omega '(t) =\frac{30 \zeta _{11} \beta (t)}{\zeta _{13}}, \zeta _{14}=\frac{\zeta _{11}^2}{3}, \zeta _{16} =\frac{17 \zeta _{11} \zeta _{13}}{270},\nonumber \\ \zeta _{20}= & {} -\frac{1}{9} \zeta _{11} \zeta _{21}, \zeta _{17}=\frac{\zeta _{11}^3}{27}, \zeta _{15} =\frac{19\zeta _{13}^2}{108 \zeta _{11}}, \zeta _{23}=-\zeta _{11}\zeta _{24},\nonumber \\ \zeta _{22}= & {} -\frac{\zeta _{13} \zeta _{24}}{30 \zeta _{11}}, \zeta _{12}=-\frac{5 \zeta _{13}^2}{36 \zeta _{11}^2}, \zeta _{10}=\frac{5 \zeta _{13}}{6 \zeta _{11}}, \zeta _{19} =\frac{\zeta _{13} \zeta _{21}}{18 \zeta _{11}},\nonumber \\ \zeta _{18}= & {} -\mu ^2-\nu ^2+\mu ^2 \zeta _{24}^2 +\frac{\nu ^2 \zeta _{21}^2}{3 \zeta _{11}} +\frac{5 \zeta _{13}^3}{72 \zeta _{11}^3}. \end{aligned}$$

(12)

Substituting Eqs. (11) and (12) into Eq. (6), the 3-rogue wave solutions for Eq. (1) can be read as

$$\begin{aligned} u= & {} [24 \varTheta _0 \zeta _{11} [5 [12 y^4 \zeta _{11}^4+36 \zeta _{11}^2 \left( 15 \upsilon ^4+y^2 \zeta _{13}+2 \nu y \zeta _{21}+6 \mu \upsilon \zeta _{24}\right) \nonumber \\&+216 \upsilon ^2 y^2 \zeta _{11}^3+180 \upsilon ^2 \zeta _{13} \zeta _{11}-5 \zeta _{13}^2] [40 y^6 \zeta _{11}^6 +360 \upsilon ^2 y^4 \zeta _{11}^5\nonumber \\&+2 \zeta _{11}^2 [95 y^2 \zeta _{13}^2+6 \zeta _{13} \left( 75 \upsilon ^4+10 \nu y \zeta _{21}-6 \mu \upsilon \zeta _{24}\right) +180 \nu ^2 \zeta _{21}^2]\nonumber \\&+4 y^2 \zeta _{11}^4 [y \left( 17 y \zeta _{13}-60 \nu \zeta _{21}\right) +270 \upsilon \left( \upsilon ^3-2 \mu \zeta _{24}\right) ] +1080 \zeta _{11}^3 [\upsilon ^2 y^2 \zeta _{13}\nonumber \\&+2 \nu \upsilon ^2 y \zeta _{21} +\left( \upsilon ^3+\mu \zeta _{24}\right) {}^2] -150 \upsilon ^2 \zeta _{13}^2 \zeta _{11}+75 \zeta _{13}^3] -12 \zeta _{11} [60 \upsilon y^4 \zeta _{11}^4\nonumber \\&+180 \upsilon \zeta _{11}^2 \left( 3 \upsilon ^4+y^2 \zeta _{13} +2 \nu y \zeta _{21}+3 \mu \upsilon \zeta _{24}\right) +180 y^2 \zeta _{11}^3 \left( 2 \upsilon ^3-\mu \zeta _{24}\right) \nonumber \\&+6 \zeta _{13} \zeta _{11} \left( 50 \upsilon ^3-\mu \zeta _{24}\right) -25 \upsilon \zeta _{13}^2]{}^2]]/[[40 y^6 \zeta _{11}^6+360 \upsilon ^2 y^4 \zeta _{11}^5\nonumber \\&+2 \zeta _{11}^2 [95 y^2 \zeta _{13}^2+6 \zeta _{13} \left( 75 \upsilon ^4+10 \nu y \zeta _{21}-6 \mu \upsilon \zeta _{24}\right) +180 \nu ^2 \zeta _{21}^2]\nonumber \\&+4 y^2 \zeta _{11}^4 [y \left( 17 y \zeta _{13}-60 \nu \zeta _{21}\right) +270 \upsilon \left( \upsilon ^3-2 \mu \zeta _{24}\right) ] +1080 \zeta _{11}^3 [\upsilon ^2 y^2 \zeta _{13}\nonumber \\&+2 \nu \upsilon ^2 y \zeta _{21}+\left( \upsilon ^3+\mu \zeta _{24}\right) {}^2] -150 \upsilon ^2 \zeta _{13}^2 \zeta _{11}+75 \zeta _{13}^3]{}^2], \end{aligned}$$

(13)

where $\zeta _{11}$, $\zeta _{13}$, $\zeta _{21}$ and $\zeta _{24}$ are unrestricted. Dynamic features of 3-rogue wave solutions are displayed in Figs. 3, 4, 5 and 6 when $(\mu ,\nu )$ selects different values, we can see that three rogue waves break apart and form a set of three 1-rogue waves in Figs. 3, 4, 5 and 6.

5 6-Rogue wave solutions

To present the 6-rogue wave solutions, we assume

$$\begin{aligned} \xi (\upsilon ,y)= & {} \upsilon ^{12}+y^8 \zeta _{48}+y^6 \zeta _{47}+y^4 \zeta _{46}+\upsilon ^{10} \left( y^2 \zeta _{26}+\zeta _{25}\right) \nonumber \\&+y^2 \zeta _{45}+\upsilon ^8 \left( y^4 \zeta _{29}+y^2 \zeta _{28} +\zeta _{27}\right) +2 \mu \upsilon [\upsilon ^6+y^6 \zeta _{64}+y^4 \zeta _{63}\nonumber \\&+\upsilon ^4 \left( y^2 \zeta _{69}+\zeta _{68}\right) +y^2 \zeta _{62}+\upsilon ^2 \left( y^4 \zeta _{67}+y^2 \zeta _{66}+\zeta _{65}\right) +\zeta _{61}]\nonumber \\&+2 \nu y [y^6+y^4 \left( \upsilon ^2 \zeta _{57}+\zeta _{56}\right) +y^2 \left( \upsilon ^4 \zeta _{55}+\upsilon ^2 \zeta _{54}+\zeta _{53}\right) +\upsilon ^6 \zeta _{60}\nonumber \\&+\upsilon ^4 \zeta _{59}+\upsilon ^2 \zeta _{58}+\zeta _{52}]+\upsilon ^6 \left( y^6 \zeta _{33}+y^4 \zeta _{32}+y^2 \zeta _{31}+\zeta _{30}\right) \nonumber \\&+\upsilon ^4 \left( y^8 \zeta _{38}+y^6 \zeta _{37}+y^4 \zeta _{36}+y^2 \zeta _{35} +\zeta _{34}\right) +\upsilon ^2 (y^{10} \zeta _{44}+y^8 \zeta _{43}\nonumber \\&+y^6 \zeta _{42}+y^4 \zeta _{41}+y^2 \zeta _{40}+\zeta _{39})+\zeta _{51} +y^{12} \zeta _{50}+y^{10} \zeta _{49}\nonumber \\&+\left( \mu ^2+\nu ^2\right) [\upsilon ^2+y^2 \zeta _1+\zeta _0], \end{aligned}$$

(14)

where $\zeta _i (i=25,\ldots , 69)$ is unknown real constant. Substituting Eq. (14) into Eq. (7) and equating the coefficients of all powers $\upsilon$ and y to zero, we obtain

$$\begin{aligned} \gamma (t)= & {} \frac{690 \beta (t)}{\zeta _{28}}, \omega '(t) =\frac{1}{6} \zeta _{26} \gamma (t), \zeta _{29}=\frac{5 \zeta _{26}^2}{12}, \zeta _{33}=\frac{5 \zeta _{26}^3}{54},\nonumber \\ \zeta _{32}= & {} \frac{77 \zeta _{26} \zeta _{28}}{207}, \zeta _{31}=\frac{1862 \zeta _{28}^2}{7935 \zeta _{26}}, \zeta _{37}=\frac{73 \zeta _{26}^2 \zeta _{28}}{1242}, \zeta _{36}=\frac{749 \zeta _{28}^2}{9522},\nonumber \\ \zeta _{55}= & {} -\frac{180}{\zeta _{26}^2}, \zeta _{38} =\frac{5 \zeta _{26}^4}{432}, \zeta _{35} =\frac{294 \zeta _{28}^3}{12167 \zeta _{26}^2}, \zeta _{43} =\frac{19 \zeta _{26}^3 \zeta _{28}}{4968},\nonumber \\ \zeta _{42}= & {} \frac{77 \zeta _{26} \zeta _{28}^2}{6210}, \zeta _{41}=-\frac{49 \zeta _{28}^3}{182505 \zeta _{26}}, \zeta _{52}=\frac{271656 \zeta _{28}^3}{304175 \zeta _{26}^6},\nonumber \\ \zeta _{54}= & {} -\frac{1368 \zeta _{28}}{23 \zeta _{26}^3}, \zeta _{44}=\frac{\zeta _{26}^5}{1296}, \zeta _{57}=-\frac{54}{\zeta _{26}}, \zeta _{40} =\frac{3773 \zeta _{28}^4}{6996025 \zeta _{26}^3},\nonumber \\ \zeta _{50}= & {} \frac{\zeta _{26}^6}{46656}, \zeta _{49} =\frac{29 \zeta _{26}^4 \zeta _{28}}{447120}, \zeta _{48}=\frac{289 \zeta _{26}^2 \zeta _{28}^2}{1142640},\nonumber \\ \zeta _{64}= & {} \frac{5 \zeta _{26}^3}{216}, \zeta _{47} =\frac{39949\zeta _{28}^3}{49276350}, \zeta _{27}=\frac{147 \zeta _{28}^2}{2645 \zeta _{26}^2},\nonumber \\ \zeta _{67}= & {} -\frac{5 \zeta _{26}^2}{36}, \zeta _{63}=\frac{\zeta _{26} \zeta _{28}}{92}, \zeta _{66}=-\frac{\zeta _{28}}{3},\nonumber \\ \zeta _{25}= & {} \frac{98 \zeta _{28}}{115 \zeta _{26}}, \zeta _{56}=-\frac{42 \zeta _{28}}{115 \zeta _{26}^2}, \zeta _{46}=\frac{655669 \zeta _{28}^4}{755570700 \zeta _{26}^2},\nonumber \\ \zeta _{53}= & {} -\frac{1764 \zeta _{28}^2}{2645 \zeta _{26}^4}, \zeta _{60}=\frac{1080}{\zeta _{26}^3}, \zeta _{69} =-\frac{3 \zeta _{26}}{2}, \zeta _{65} =-\frac{49 \zeta _{28}^2}{2645 \zeta _{26}^2},\nonumber \\ \zeta _{30}= & {} \frac{15092 \zeta _{28}^3}{912525 \zeta _{26}^3}, \zeta _{39}=-\nu ^2+\frac{279936 \nu ^2}{\zeta _{26}^7} +\frac{6391462\zeta _{28}^5}{2413628625 \zeta _{26}^5},\nonumber \\ \zeta _{34}= & {} -\frac{41503 \zeta _{28}^4}{4197615 \zeta _{26}^4}, \zeta _{68}=\frac{13 \zeta _{28}}{115 \zeta _{26}}, \zeta _{58}=-\frac{28728 \zeta _{28}^2}{2645 \zeta _{26}^5},\nonumber \\ \zeta _{45}= & {} -\zeta _1 \left( \mu ^2+\nu ^2\right) +\frac{\mu ^2 \zeta _{26}}{6}+\frac{46656 \nu ^2}{\zeta _{26}^6} +\frac{1203587 \zeta _{28}^5}{1448177175 \zeta _{26}^4},\nonumber \\ \zeta _{62}= & {} \frac{107 \zeta _{28}^2}{15870 \zeta _{26}}, \zeta _{61}=\frac{2401 \zeta _{28}^3}{912525 \zeta _{26}^3}, \zeta _{59}=\frac{4536 \zeta _{28}}{23 \zeta _{26}^4},\nonumber \\ \zeta _{51}= & {} \frac{3 \zeta _{28} \left( 279936 \nu ^2+\mu ^2 \zeta _{26}^7\right) }{115 \zeta _{26}^8}-\zeta _0 \left( \mu ^2+\nu ^2\right) +\frac{35153041 \zeta _{28}^6}{832701875625 \zeta _{26}^6}. \end{aligned}$$

(15)

Substituting Eqs. (14) and (15) into Eq. (6), the 6-rogue wave solutions for Eq. (1) can be written as

$$\begin{aligned} u=2 \varTheta _0 \left( \frac{\xi _{\upsilon \upsilon }}{\xi } -\frac{\xi _\upsilon ^2}{\xi ^2}\right) , \end{aligned}$$

(16)

where $\xi$ satisfies Eq. (14) and Eq. (15), $\zeta _{26}$ and $\zeta _{28}$ are unrestricted. Dynamic features of 6-rogue wave solutions are shown in Figs. 7, 8, 9 and 10 when $(\mu ,\nu )$ selects different values, we can see that sixrogue waves break apart and form a set of six 1-rogue waves in Figs. 7, 8, 9 and 10.

6 Conclusion

In the paper, a variable-coefficient symbolic computation approach is proposed. The main difference between this method and the previous one in Ref. [18] is that we replace the traveling wave transformation with the non-traveling wave transformation, making it suitable for solving the multiple rogue wave solution of the nonlinear system with variable coefficients. This change has not been seen in other literatures. Applied the vcsca to the (2+1)-dimensional vcKP equation, the 1-rogue wave solutions, 3-rogue wave solutions and 6-rogue wave solutions are present. By setting different values of $(\mu , \nu )$, their dynamic features are displayed in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. All the obtained solutions have been verified to be correct.

Substituting $\upsilon =x-\omega (t)$ in rogue wave solution (10), we have

$$\begin{aligned} u(x,y,z,t)=\frac{4 \varTheta _0 \left[ -\left[ \mu +\frac{3 \int \beta (t) \, dt}{\zeta _0}-x\right] {}^2 +\zeta _1 (y-\nu )^2+\zeta _0\right] }{\left[ \left[ \mu +\frac{3 \int \beta (t) \, dt}{\zeta _0}-x\right] {}^2 +\zeta _1 (y-\nu )^2+\zeta _0\right] {}^2}. \end{aligned}$$

(17)

When variable-coefficient $\beta (t)$ chooses different function, the rogue wave (17) shows different dynamic features in Fig. 11.

In addition to this (2+1)-dimensional vcKP equation, this vcsca can also be applied to the (3+1)-dimensional generalized KP equation with variable coefficients [22], the generalized (3 + 1)-dimensional variable-coefficient nonlinear wave equation [23] based on the symbolic computation [24,25,26,27,28,29,30,31,32,33,34,35,36].