Green’s functions and integral representation of generalized continua: the case of orthogonal pantographic lattices

Abstract

This paper shows how the classical representation techniques for the solution of elasticity problems, based on the Green’s functions, can be generalized to second-gradient continua focusing on the specific case of pantographic lattices. As these last are strongly anisotropic, the fundamental solutions of isotropic second-gradient continua involving bi-Helmholtz-type operators are not applicable. More specifically we establish the analytical fundamental solution for the linearized equations governing the equilibrium of pantographic 2D continua in the neighbourhood of the reference configuration. Moreover, by means of found novel Green’s functions, it is shown that it is possible to solve aforesaid equilibrium equations by using Fredholm integral equations. It is seen that an approximated analytical solution for the standard bias test for pantographic 2D continua can be found by using judiciously the found analytical fundamental solutions. The micro-macro-asymptotic identification allows for a clear and satisfactory physical interpretation of the obtained analytical results.

1 Introduction

First, gradient continuum models, as developed by Cauchy, were conceived as models in which the considered deformable bodies can interact with their external world by means of two kinds of interactions: (i) forces distributed per unit volume (interactions acting at a distance) and (ii) forces distributed per unit surface (contact interactions between the external surface of the body and its external world). It is clear that this kind of interactions do not exhaust all the logical possibilities. For instance, it does not include forces distributed on curves or concentrated on points, nor momentum distributed on surfaces. There is no reason for which mathematical physics should not introduce also these concepts in its effort to model physical reality.

As a matter of fact, classical elasticity shows that in the presence of interactions concentrated on lines or points, the displacement field becomes infinite in the points where these forces are applied. In fact, this kind of externally applied forces can be a useful conceptual tool in two kinds of circumstances: (i) when one looks for models capable to describe the deformation induced on physical bodies when a small region of their contact surface is interacting with the external world and one does not want to describe in detail how this force is distributed inside this small region or (ii) when one wants to “decompose” the external interactions into its “basic” components and apply, in the case of linearized systems, the principle of superposition of effects. While the first circumstance refers to a specific modelling problem, as it is relative to the choice of the most adapted model to be used to describe a specific deformation phenomenon, the second one refers to a specific mathematical method, to be used for calculating the solutions of a boundary value problems.

This specific last method is often called the method of Green’s functions: it is, indeed, based on the search of the deformation field consequent to the application of a force concentrated in a point, in order to represent the general solution of a generic boundary problem, in linearized theories. This representation is possible notwithstanding the singularity shown, in the point where the concentrated force is applied, by calculated Green’s functions. Intuitively we can say that the ‘power of the idea’ is based on its simplicity: to reconstruct every specific deformation field as superposition of the deformation fields caused by a family of concentrated force. In fact (see e.g. [12]) by using the method of Green’s function the most general boundary value problem in isotropic (and some types of anisotropic) first gradient linear elasticity can be solved by finding the solution of suitable Fredholm integral equations of first or second type. In these integral equations, the unknowns are the fields ‘dual in work’ with the fields that are assigned on the boundary. In the case of first gradient linear elasticity, the fields assigned on the boundary can be the displacement field (in the case of so-called essential boundary conditions) or the field of externally applied contact forces (in the case of so-called natural boundary conditions). The ‘dual in work’ field of assigned displacement is the corresponding constraint force exerted by the applied kinematical constraint while the dual in work of the external force assigned on a certain material particle P of the external surface of the body is the corresponding displacement of P necessary to reach the equilibrium configuration.

Actually, the just described structure of first gradient linear elasticity is consistent with the Postulation approach to Continuum Mechanics as presented by Cauchy and based on balance laws. In fact, the development of continuum theories as conceived by Cauchy is based on the famous tetrahedron argument, on the postulation of balance of forces and moment of forces and on the hypothesis that only the contact surface and volume (at a distance) interactions are applicable to the continuum. Here it is essential to note that the set of assumptions used by Cauchy is, in facts, completely equivalent to assume that deformation energy depends on the first gradient of displacement only [21].

Now, basing the Postulate of Continuum Mechanics on the Principle of Virtual Work, we can consider media whose deformation energy depends on both the first and the second gradient of displacement as already clarified by Gabrio Piola (see [21]) and then clearly stated by R. Toupin and P. Germain when dealing with elasticity, see [25, 32]. And once continuum mechanics is suitably generalized, it is possible to consider continua capable to support, at their boundaries, much more general kinds of external interactions. In a sense, it is possible to state that second gradient continua are the ‘simplest’ model generalizing standard Cauchy continua: the reader will recall that in generalized continua some extra kinematical descriptors are often introduced, beyond the displacement field, and that the deformation energy may depend of several (all)order gradients of all considered kinematical descriptors.

As the whole set of assumptions used by Cauchy in his Postulation of Continuum Mechanics is, as a matter of facts, mixing constitutive assumptions and basic principles in such a way that they cannot be clearly distinguished, it has been recognized that variational principles are a suitable tool for formulating such generalized models [21].

The variational approach has the advantage of providing a rigorous formal theoretical framework, but its application is confronted with the fact that they do not explicitly link the micro-morphology of the medium to the effective parameters of the equivalent generalized continuous medium. The limitation is lifted by the methods of asymptotic homogenization [30], developed at higher orders [5] or recasted for highly contrasted media see e.g. [6, 8]. The asymptotic method underlines the key role played by the scale separation between the morphological cell and the phenomenon. In particular, it highlights the conditions under which a description of Cauchy is sufficient or insufficient to describe the actual behaviour and shows that strictly homogeneous media are relevantly described by Cauchy’s continua.

To find a conclusive argument in supporting the need of developing higher gradient continuum models, more recently it has been shown that it is possible to conceive some micro-architectures whose macroscopic behaviour is suitably modelled by a particular class of second-gradient continua. We specifically refer to the so-called 2D pantographic micro-architectures, see e.g. [23]. Pantographic 2D continua are in sense incomplete, or singular: in facts there are some second-order derivatives in the displacement on which their deformation energy does not depend. Therefore, for pantographic continua the standard strong ellipticity arguments cannot be immediately applied: the necessary modification of the standard treatment to prove some existence and uniqueness results are presented in [13]. The peculiar mechanical behaviour of pantographic continua has been investigated both from the theoretical point of view and experimentally. Conceived experiments were based on a careful design aimed to build micro-architectures whose macroscopic behaviour could not be effectively described without the introduction of second-gradient continuum models [24].

It has to be remarked that the theoretically designed properties of pantographic continua could be verified experimentally by exploiting the 3D printing techniques and that one can conclude that it is possible to actually construct ‘real’ metamaterials having their most desired properties (for an exhaustive presentation of the state of the art in metamaterial design see [2]).

The study of their linearized elastic behaviour led to some interesting results: this study was made easier by the identification of the constitutive parameters for the linearized homogenized macro-model in terms of the relevant micro-mechanical properties and micro-architecture geometry. Mentioned identification was made possible by applying judiciously the asymptotic homogenization method of discrete periodic media see [10, 20], to pantographic micro-architectures, albeit the obtained macro-model results to be highly anisotropic. It is possible to say that, at least in the particular case of linearized elasticity, every macroscopic kinematical or constitutive parameter for pantographic continua can be precisely associated to specific micro-geometry and micro-mechanical properties [7], and therefore that a full mechanical understanding of the obtained macro-second-gradient model has been obtained. This understanding can be applied to the description of real pantographic sheets, that are constituted by a finite number of beams. In fact, it has to be remarked, in this context, that the range of applicability of homogenized models seems to be larger than expected [31].

In this paper, also by exploiting the mentioned mechanical interpretation of macro-constitutive parameters, it is shown how the method of representation by means of Green’s functions is applicable to find the linearized equilibrium configurations of pantographic continua.

The results available, in the literature, for isotropic second gradient continua could not be applied in the considered instance, because (i), unlike the micro-heterogeneous materials most frequently studied, the second-gradient effect is not here a perturbating effect but an effect of the same order as that of the simple gradient, and (ii) because of the strong anisotropy of introduced deformation energy, that does not depend on (bi-)Laplacian of displacement field. In fact in the case of the particular class of isotropic second-gradient materials considered in [27], the analysis is made possible by the use of the properties of Helmholtz operators slightly corrected by bi-Helmholtz-type operators. The aforesaid differential operators do not appear in the volume linear balance equations for 2D pantographic continua.

To be more precise, we find explicitly here the analytical expression for the fundamental solution of the mentioned volume equations. The found Green’s functions, as theoretically expected, have a less ‘sharp’ singularity in the neighbourhood of the applied concentrated point forces, than the Green’s functions of non-pantographic reticulated media (of similar morphology but having stiff instead hinged internal connexion) described by single-gradient anisotropic continuum. This property had to be expected, and it is obviously related to the capacity of second-gradient 2D continua to ‘support’ concentrated boundary contact forces. It is very interesting to check that by combining four of the found fundamental solutions it is possible to find an analytical approximate solution for the standard bias extension test for pantographic 2D continua.

Finally, based on the found expression for the novel Green’s function introduced, it is shown how one can, in principle, solve the aforesaid equilibrium problem by using a suitably formulated boundary elements method, whose formulation is based on the solution of calculated Fredholm integral equations. The latter involves the classical integral of the first and second type.

All found analytical results can be physically interpreted by exploiting the micro-macro asymptotic identification results previously obtained in [7]: these identification results, on the other hand, were a guidance in the deduction of presented analytical results and gave the possibility to verify and justify heuristically every results presented.

2 Setting of the problem

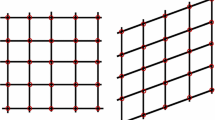
We consider orthogonal pantographic lattices of periodic cell $\ell _x \times \ell _y$ with $\ell _x/\ell _y = O(1)$, made of x- and y -fibers of respective axial and bending stiffnesses $E_xA_x$, $E_yA_y$; $E_xI_x$, $E_yI_y$. $\ell _x/\ell _y = O(1)$, The properties of the x- and y fibers are of the same order, i.e. $E_xA_x/(E_yA_y) = O(1)$ and $E_xI_x/(E_yI_y) = O(1)$. The specificity of the pantographic lattice lies in the fact that the orthogonal fibers are connected by pivots that realize a perfect connexion for the forces but a vanishing connexion for the moments of the orthogonal fibers (Fig. 1).

Fig. 1

Orthogonal pantographic sheet of periodic cell $\ell _x \times \ell _y$. The lattice is made of orthogonal fibers (blue and grey lines) connected by pivots (red points). The latter realizes a perfect connexion for force and a vanishing connexion for moments. On the right, a picture of a pantographic lattice with $\ell _x = \ell _y$ realized by 3D printing (Color figure online)

2.1 The differential operator of orthogonal pantographic lattices

The homogenization approach has made it possible to establish that in orthogonal pantographic lattices, the axial force in a fibre varies in its length due to the transverse forces that arise by bending in the orthogonal fibres to which it is connected, see [7]. This situation resulting from the pivot connections is accompanied by the fact that the axial deformations of the fibres are much smaller than the distortions (transverse gradient of the axial displacement). Thus, when projecting along $\mathbf {e}_x$ and $\mathbf {e}_y$ the balance equations that govern the mechanical behaviour of considered orthogonal pantographic lattices, in absence of body force and in small deformations regime, (see [7]) one gets:

$$\begin{aligned} \begin{pmatrix} \mathcal {D}_x&{} &{} 0\\ 0&{} &{} \mathcal {D}_y \end{pmatrix} \begin{pmatrix} u_x\\ u_y \end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \end{aligned}$$

(2.1)

where the differential operators $\mathcal {D}_x$, $\mathcal {D}_y$ are given by:

$$\begin{aligned} \mathcal {D}_x = \frac{E_xA_x}{\ell _y}\partial ^2_{xx}- \frac{E_yI_y}{\ell _x} \partial ^4_{yyyy}\qquad ;\qquad \mathcal {D}_y = \frac{E_yA_y}{\ell _x}\partial ^2_{yy}- \frac{E_xI_x }{\ell _y}\partial ^4_{xxxx} \end{aligned}$$

(2.2)

To make writing lighter, let’s introduce (i) the coefficients:

$$\begin{aligned} K_x^e = \frac{E_xA_x}{\ell _y}>0,\quad K_{x}^b = \frac{E_xI_x}{\ell _y}>0 \qquad ;\qquad K_y^e = \frac{E_yA_y}{\ell _x}>0,\quad K_{y}^b = \frac{E_yI_y}{\ell _x} >0 \end{aligned}$$

related, respectively, to the extensional and bending stiffnesses of the x- and y- fibers at the interpivot scale, (ii) the intrinsic lengths $\eta _x$, $\eta _y$ that relates the bending parameters of fibers a given direction and the tension parameters of fibers the orthogonal direction:

$$\begin{aligned} \eta _x^2 =\frac{ E_yI_y}{E_xA_x}\frac{\ell _y}{\ell _x} = \frac{K_y^b }{K_x^e } \quad&;&\quad \eta _y^2 =\frac{ E_xI_x}{E_yA_y}\frac{\ell _x}{\ell _y} = \frac{K_x^b }{K_y^e } \end{aligned}$$

(2.3)

and (iii) the normalized differential operators $\mathcal {D}^*_x$, $\mathcal {D}^*_y$ defined as follows:

$$\begin{aligned} \mathcal {D}^*_x = \partial ^2_{xx}-\eta ^2_x \partial ^4_{yyyy} = \frac{1}{K_x^e} \mathcal {D}_x \quad&;&\quad \mathcal {D}^*_y = \partial ^2_{yy}-\eta ^2_y\partial ^4_{xxxx} = \frac{1}{K_y^e} \mathcal {D}_y \end{aligned}$$

(2.4)

Then, the balance equations reads:

$$\begin{aligned} K_x^e\mathcal {D}^*_x (u_x)\mathbf {e}_x + K_y^e\mathcal {D}^*_y (u_y)\mathbf {e}_x =0\end{aligned}$$

that produces the following normalized equations in each direction:

$$\begin{aligned} \mathcal {D}^*_x (u_x) = u_{x,xx}-\eta _x^2 u_{x,yyyy}= & {} 0\, \text{: } \text{ force } \text{ balance } \text{ along } \mathbf {e}_x \hbox { normalized by} \, K_x^e \end{aligned}$$

(2.5)

$$\begin{aligned} \mathcal {D}^*_y (u_x) = u_{y,xx}-\eta _y^2 u_{y,xxxx}= & {} 0\, \text{: } \text{ force } \text{ balance } \text{ along } \mathbf {e}_y \hbox { normalized by} \, K_y^e \end{aligned}$$

(2.6)

Since the equations for the variables $u_x$ and $u_y$ are uncoupled, they can be treated independently. Focusing on the equilibrium along $\mathbf {e}_x$, the Eq. (2.5)-a can be rewritten as:

$$\begin{aligned} \mathcal {D}^*_x (u_x) = (\partial ^2_{xx}-\eta ^2_x \partial ^4_{yyyy})u_{x}= (\partial _{x}-\eta _x \partial ^2_{yy})(\partial _{x}+\eta _x \partial ^2_{yy})u_x = (\partial _{x}+\eta _x \partial ^2_{yy})(\partial _{x}-\eta _x \partial ^2_{yy})u_x= 0\nonumber \\ \end{aligned}$$

(2.7)

or equivalently:

$$\begin{aligned} \mathcal {D}^*_x(u_x)= \mathcal {D}_x^-\mathcal {D}_x^+(u_x) = \mathcal {D}_x^+\mathcal {D}_x^-(u_x) = 0 \end{aligned}$$

where $\mathcal {D}^*_x$ is decomposed into the two differential operators $\mathcal {D}_x^+$, $\mathcal {D}_x^-$ defined below:

$$\begin{aligned} \mathcal {D}_x^+ = \partial _{x}+\eta _x \partial ^2_{yy}\qquad \text{; }\qquad \mathcal {D}_x^- = \partial _{x}-\eta _x \partial ^2_{yy} \end{aligned}$$

2.2 Analogies with diffusion processes

The operators $\mathcal {D}_x^+$ and $\mathcal {D}_x^-$ are analogous to the transient 1-D diffusion differential operator $\partial _{t}+\eta \partial ^2_{yy}$, where the time variable t is replaced by the space variable x. Thus, $\mathcal {D}_x^-$ would correspond to a physical diffusion (e.g. thermal) process with positive diffusivity $\eta _x$, while $\mathcal {D}_x^+$ would correspond to a non-physical (because it is non-causal) diffusion process with negative diffusivity $-\eta _x$. The temporal causality requirements do not apply to the spatial domain, and the two operators $\mathcal {D}_x^+$ and $\mathcal {D}_x^-$ are physically acceptable for the problem under study.

Note also the direct analogy of $\mathcal {D}_x^+$ and $\mathcal {D}_x^-$ with the 2D-steady state diffusion-advection problems of operator $\pm v\partial _{x} + D\partial ^2_{yy}$, where the diffusion coefficient D is replaced here by the bending parameter $K^b_y$ of the y-fibers and operates in the y-direction, while the advection of velocity $\pm v$ becomes the extensional parameter $K^e_x$ of the x-fibers, which operates in the $+x$-direction for $\mathcal {D}_x^-$, and in the$-x$-direction for $\mathcal {D}_x^+$.

3 Green’s functions

The Green’s function $G_x(x,y)\mathbf {e}_x$ associated with the normalized $\mathbf {e}_x$-balance Eq. (2.7) is the displacement oriented along $\mathbf {e}_x$ for a point force normalized by $K_x^e$ located at the origin ($x=y=0$) and oriented along $\mathbf {e}_x$. Hence, by definition:

$$\begin{aligned} \mathcal {D}^*_x (G_x)\mathbf {e}_x + \delta (x,y)\mathbf {e} _x = 0 \quad \text{ i.e. } \quad G_{x,xx }-\eta _x^2 G_{x,yyyy} + \delta (x,y) =0 \end{aligned}$$

(3.1)

where $\delta (x,y) = \delta (x) \delta (y)$ is the 2D Dirac distribution. In terms of distribution, (3.1) reads ($*$ stands for the convolution):

$$\begin{aligned} \big (\mathcal {D}^*_x(\delta )\big )*G_x +\delta = 0 \end{aligned}$$

(3.2)

that means that $G_x$ is the inverse of convolution of the distribution $\mathcal {D}^*_x(\delta ) = \delta _{,xx}-\eta _x^2\delta _{,yyyy}$.

Similarly the Green’s function $G_y(x,y)\mathbf {e}_y$ associated with the $\mathbf {e}_y$-balance is the displacement oriented along $\mathbf {e}_y$ resulting from a point force (normalized by $K_y^e$) located at the origin ($x=y=0$) and oriented along $\mathbf {e}_y$, so that:

$$\begin{aligned} \mathcal {D}^*_y (G_y)\mathbf {e}_y + \delta \mathbf {e} _y = 0 \quad \text{ i.e. } \quad \big (\mathcal {D}^*_y(\delta )\big )*G_y+\delta = 0 \end{aligned}$$

(3.3)

3.1 Green’s functions for doublet of force and doublet of moment

As a first step in the determination of the Green’s functions $G_x(x,y)$ solution of (3.1), let us consider the intermediary problem that consists in identifying the functions $g_x^+(x,y)$ and $g_x^-(x,y)$, respectively, solution of:

$$\begin{aligned} \mathcal {D}_x^+(g_x^+) + \delta (x,y) = 0 \qquad \text{ and }\qquad \mathcal {D}_x^-(g_x^-) + \delta (x,y) = 0 \end{aligned}$$

According to the classical expression of the spatio-temporal Green’s function of the heat equation, $g_x^-$ reads as follows, see e.g. [11], where H(x) is the step function:

$$\begin{aligned} g_x^-(x,y) = H(x)\frac{\exp (\frac{-y^2}{4\eta _x x})}{\sqrt{4\pi \eta _x x}} = H(x)\frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}}\qquad \text{ so } \text{ that }\qquad g_x^-(x,y) = 0 \quad \text{ for }\quad x < 0 \end{aligned}$$

As for $g_x^+(x,y)$, one notices that:

$$\begin{aligned} - \mathcal {D}^+(g_x^+) = -(\partial _{x} + \eta _x \partial ^2_{yy})(g_x^+(x,y)) = \delta (x,y) \end{aligned}$$

Thus, changing x into $-x$ yields:

$$\begin{aligned} -(-\partial _{x} + \eta _x \partial ^2_{yy})(g_x^+(-x,y)) = \mathcal {D}^-(g_x^+(-x,y)) = \delta (-x,y) = \delta (x,y) \end{aligned}$$

so that: $g_x^+(-x,y) = - g_x^-(x,y)$ and consequently:

$$\begin{aligned} g_x^+(x,y) = -H(-x)\frac{\exp (\frac{y^2}{4\eta _x x})}{\sqrt{-4\pi \eta _x x}} = -H(-x)\frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}} \qquad \text{ so } \text{ that }\qquad g_x^+(x,y) = 0 \quad \text{ for }\quad x > 0 \end{aligned}$$

Now, consider the linear combination $\alpha ^+ g_x^+ + \alpha ^- g_x^-$. By construction:

$$\begin{aligned} \mathcal {D}^*_x ( \alpha ^+ g_x^+ + \alpha ^- g_x^-)= & {} \mathcal {D}_x^-\mathcal {D}_x^+( \alpha ^+ g_x^+ + \alpha ^- g_x^-) \\= & {} \alpha ^+ \mathcal {D}_x^-\mathcal {D}_x^+(g_x^+)+\alpha ^- \mathcal {D}_x^+\mathcal {D}_x^-(g_x^-) = \alpha ^+ \mathcal {D}_x^- (\delta (x,y))+\alpha ^- \mathcal {D}_x^+(\delta (x,y)) \end{aligned}$$

Consequently:

$$\begin{aligned} \mathcal {D}^*_x (g_x) = ( \alpha ^+ +\alpha ^- )\partial _{x}\delta -\eta _x ( \alpha ^+ -\alpha ^- )\partial ^2_{yy}\delta \end{aligned}$$

Therefore, considering $g_x = (g_x^+ + g_x^-)/2$ yields:

$$\begin{aligned} \mathcal {D}^*_x (g_x ) + \partial _{x}\delta = 0 \qquad ;\qquad g_x (x,y) = \frac{\mathrm {sgn}(x)}{2} \frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}} \end{aligned}$$

(3.4)

Similarly, considering $h_x = (-g_x^+ + g_x^-)/2$ gives:

$$\begin{aligned} \mathcal {D}^*_x (h_x ) + \partial _{yy}\delta =0 \qquad ;\qquad h_x(x,y) = -\frac{1}{2\eta _x} \frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}} \end{aligned}$$

(3.5)

Recalling that we focus on the balance along $\mathbf {e}_x$:

• $g_x \mathbf {e}_x$ is the displacement resulting from the normalized loading $\partial _{x}\delta \mathbf {e}_x$. The derivative of the Dirac along x describes a doublet of opposite normalized $\mathbf {e}_x$-point forces applied at the origin in the x-direction.

• $h_x \mathbf {e}_x$ is the displacement resulting from the normalized loading $\partial _{yy}\delta \mathbf {e}_x$. The double derivative of the Dirac along y describes a doublet of opposite normalized in-plane point moments applied at the origin.

At this stage, we have established the response of the pantographic lattice to particular doublet of point loadings. As the problem treated is linear (linear behaviour and small deformation), the principle of superposition applies. Therefore, by integration, we can deduce the Green’s function for a normalized point force $G_x$ and a normalized in-plane point moment, $H_x$.

3.2 Normalized Green’s functions

3.2.1 Green’s function $G_x (x,y)\mathbf {e}_x$ for a normalized point force $\delta \mathbf {e}_x$

The Green’s function $G_x$ is associated with the normalized force $\delta \mathbf {e}_x$, applied at the origin and satisfies:

$$\begin{aligned} \mathcal {D}^*_x (G_x ) + \delta = 0 \end{aligned}$$

(3.6)

On the other hand, we know that $g_x$ is associated with the doublet of normalized forces $\partial _{x}\delta \mathbf {e}_x$ applied at the origin. Consequently, comparing (3.4) and (3.6) one deduces by linearity that $g_x$ and $G_x$ are related by ($\pm \mathrm {d}X$ denotes the position of the opposite forces of the doublets):

$$\begin{aligned} g_x (x,y) = \lim _{\mathrm {d}X\rightarrow 0}\frac{G_x (x - \mathrm {d}X,y) - G_x (x +\mathrm {d}X,y)}{2\mathrm {d}X} = -\partial _xG_x(x,y) \end{aligned}$$

(3.7)

which means that the x-displacement $G_x$ is obtained by integrating $-g_x$. It seems a priori natural to impose a zero displacement for $x \rightarrow -\infty$. That yields:

$$\begin{aligned} G_x^{\infty }(x,y) = -\int _{-\infty }^{x}g_x (u,y) \mathrm {d}u \end{aligned}$$

(3.8)

which can be rewritten as follows, as $g_x (x,y)$ is odd with respect of the variable x,

$$\begin{aligned} G_x^{ \infty }(x,y) = \int ^{\infty }_{-x}g_x (u,y) \mathrm {d}u = \int ^{|x|}_{-x}g_x (u,y) \mathrm {d}u+ \int _{|x|}^{\infty } g_x (u,y) \mathrm {d}u = \int _{|x|}^{\infty } g_x (u,y) \mathrm {d}u \end{aligned}$$

Hence, $G_x^{ \infty }(x,y)$ takes the following expression that is even with respect to both x and y variables:

$$\begin{aligned} G_x^{ \infty }(x,y) = \frac{1}{2} \int ^{\infty }_{|x|}\frac{\exp (\frac{-y^2}{4\eta _x u})}{\sqrt{4\pi \eta _x u}}\mathrm {d}u \end{aligned}$$

(3.9)

However, $G_x^{\infty }$ is difficult to handle as it is not bounded. This feature is consistent with the fact that we consider an infinite domain and that the deformation is O($\mathrm {sgn}(x)/\sqrt{ |x|}$) for large |x|. This leads to replace the condition at infinity, by the condition of zero x-displacement on $x = - L < 0$ (and consequently the x-displacement is also null on $x = L$ as $g_x$ is odd). From similar calculations:

$$\begin{aligned} G_x^{ L}(x,y) = \frac{1}{2} \int ^{L}_{|x|}\frac{\exp (\frac{-y^2}{4\eta _x u})}{\sqrt{4\pi \eta _x u}}\mathrm {d}u \end{aligned}$$

(3.10)

which takes finite values for any finite |x|. As any L can be chosen, one can take $L=0$ which avoid the introduction of the arbitrary constant L. Then we set:

$$\begin{aligned} G_x (x,y) = - \frac{1}{2} \int _{0} ^{|x|} \frac{\exp (\frac{-y^2}{4\eta _x u})}{\sqrt{4\pi \eta _x u}}\mathrm {d}u \end{aligned}$$

(3.11)

and obviously, $G_x^{ L}(x,y) = G_x (x,y) - G_x (L,y)$. Furthermore, $G_x$ has the following explicit expression¹:

$$\begin{aligned} G_x (x,y) = -\sqrt{\frac{|x|}{4\pi \eta _x} }\exp \big (\frac{-y^2}{4\eta _x |x|}\big ) +\frac{|y|}{4\eta _x } \mathrm {erfc }\big (\frac{|y|}{\sqrt{4\eta _x |x|}} \big ) \end{aligned}$$

(3.12)

or equivalently:

$$\begin{aligned} G_x (x,y) = \frac{|y|}{4\eta _x } \Big (-\frac{\exp (- \xi _x^2)}{\sqrt{\pi } |\xi _x| }+\mathrm {erfc }(|\xi _x|) \Big ) \end{aligned}$$

(3.13)

where we use the notations:

$$\begin{aligned} \xi _x =\frac{y}{\sqrt{4\eta _x |x|}} \qquad ;\qquad \mathrm {erf}(u) = \frac{2}{\sqrt{\pi }}\int _0^u\exp (-u^2)\mathrm {d}u \qquad ;\qquad \mathrm {erfc}(u) = 1- \mathrm {erf}(u) \end{aligned}$$

The Green’s function $G_x(x,y)$, (3.13), in the infinite pantographic sheet, is such that the displacement $G_x\mathbf {e}_x$ vanishes on the fiber $x = 0$. This corresponds to the situation where the x-displacement of the lattice is prevented on the line $x=0$, i.e. on the y-fiber that crosses the point of application of the normalized point force $\delta \mathbf {e}_x$ and is orthogonal to it.

For a normalized $\mathbf {e}_x$-point force located on M(X, Y), the displacement will be given by $G_x (x-X,y-Y)\mathbf {e}_x$, with a null x-displacement along the line $x= X$.

By the superposition principle, the field of displacement for two normalized point x-forces $f_P\delta _P\mathbf {e}_x$ and $f_Q\delta _Q\mathbf {e}_x$, respectively, located on the points $P(X_P,Y_P)$ and $Q(X_Q,Y_Q)$, is given by:

$$\begin{aligned} \mathbf {u}(x,y) = \left( f_PG_x(x-X_P, y-Y_P) + f_QG_x(x-X_Q, y-Y_Q)\right) \mathbf {e}_x \end{aligned}$$

and $\mathbf {u}(x,y) -\mathbf {u}(X_A,Y_A )$ yields a a zero x-displacement on the point $A(X_A ,Y_A )$.

3.2.2 Green’s function $G_y (x,y)\mathbf {e}_y$ for a normalized point force $\delta \mathbf {e}_y$

The case of a normalized point force in the y-direction can be treated similarly by inverting x and y and replacing $\eta _x, E_xA_x$ by $\eta _y, E_yA_y$. Thus, the Green’s function for a normalized point force $\delta \mathbf {e_y}$ is the y-displacement $G_y^{F}\mathbf {e_y}$ defined by:

$$\begin{aligned} G_y (x,y) = \frac{|x|}{4\eta _y } \Big (-\frac{\exp (- \xi _y^2)}{\sqrt{\pi } |\xi _y| }+\mathrm {erfc }(|\xi _y|) \Big ) \qquad ;\qquad \xi _y =\frac{x}{\sqrt{4\eta _y |y|}} \end{aligned}$$

(3.14)

solution of:

$$\begin{aligned} \mathcal {D}^*_y (G_y ) + \delta = 0 \end{aligned}$$

(3.15)

and such that the y-displacement of the lattice vanishes on the line $y=0$.

3.2.3 Green’s matrix $\underline{\underline{ \mathbb {G}}}$

If a physical (i.e. non-normalized) point force $\mathbf {F} = F_x\delta \mathbf {e}_x + F_y\delta \mathbf {e}_y$ is applied at the origin, the vectorial field of displacement such that the x-displacement vanishes on the line $x= 0$ and the y-displacement vanishes on the line $y= 0$, reads:

$$\begin{aligned} \mathbf {U}_G(x,y) = \frac{ F_x}{K_x^e}G_x \mathbf {e}_x + \frac{ F_y}{K_y^e}G_y \mathbf {e}_x \end{aligned}$$

or under matrix form, that highlights the diagonal character of the Green’s matrix $\underline{\underline{\mathbb {G}}}$

$$\begin{aligned} \mathbf {U}_G = \underline{\underline{ \mathbb {G}}} . \mathbf {F}\qquad ;\qquad \underline{\underline{\mathbb {G}}} =\begin{pmatrix} \mathbb {G}_x = \frac{ 1}{K_x^e}G_x &{}{}; &{}{} 0 \\ 0 &{}{};&{}{} \mathbb {G}_y = \frac{ 1}{K_y^e}G_y \end{pmatrix} \end{aligned}$$

(3.16)

Remark

$\mathbf {U}_G(x,y) -\mathbf {U}_G(X,y)\mathbf {e}_x - \mathbf {U}_G(x,Y)\mathbf {e}_x + \mathbf {U}_G(X,Y)\mathbf {e}_x$ yields a field of zero x-displacement on the line $x= X$ and of zero y-displacement on the line $y= Y$

3.3 Features of the Green’s function $G_x (x,y)\mathbf {e}_x$ and $G_y (x,y)\mathbf {e}_x$

Since $G_x (x,y)\mathbf {e}_x$ is the field of displacement, then $\partial _xG_x (x,y) = -g_x (x,y)$ describes the field of extension/contraction of the x-fibers, (and, multiplied by the axial stiffness of the x-fibers it gives the field of tension/compression in these fibers). Thus:

$$\begin{aligned} \varepsilon _{_xxx}^F(x,y) =- g_x (x,y) = -\frac{\mathrm {sgn}(x)}{2} \frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}}\qquad ;\qquad \varepsilon _{_xxx}^F(x,0) =-\frac{\mathrm {sgn}(x)}{2 \sqrt{4\pi \eta _x |x|}} \end{aligned}$$

(3.17)

Expressions (3.17) show that the tension of the fiber $y=0$ presents a singularity at the origin where the force is applied. In contrast, there is no singularity at $x=0$ for any other fibers $y\ne 0$. Besides, apart from the origin, the extension of the fibers $y\ne 0$ becomes close to that of the fiber $y=0$ provided that $|x|\gg y^2/(4\eta _x)$.

These features result from the bending stiffness of the constitutive beam elements that enables to distribute within the whole pantographic array the response to the point force. Indeed, in the case of null bending stiffness, then the single fiber $y=0$ would undergo the force. Thus, it would experience a uniform extension (or compression) opposite on each side of the loading point with a step singularity on this point. Unlike standard elastic media where the singularity arises in any directions around the loading, it is focused here in the single direction corresponding to the common orientation of the fiber and of the loading.

Note also that $\partial _{yy} G_x$ gives the curvature $^y\kappa ^F_x$ of the y-oriented fibers induced by the normalized force $\delta \mathbf {e}_x$, (and the moment that they undergo when multiplied by their bending stiffness constant). It’s expression can be obtained either by double y-derivation or observing that as $G_x$ is solution of (3.6), then $\partial _{yy} G_x$ satisfies Eq. (3.5) whose the solution is $h_x (x,y)$. Consequently:

$$\begin{aligned} ^y \kappa ^F_x(x,y) = \partial _{yy} G_x (x,y) = -\frac{1}{2\eta _x } \frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|} }= h_x(x,y) \end{aligned}$$

(3.18)

Similarly, under a normalized $\mathbf {e}_y$-point force, the deformation in extension of the y-fibers and the curvature of the y-fibers are, respectively, given by $\varepsilon _{_yyy}^F =- g_y$ and $^x \kappa ^F_y = \partial _{xx} G_y$.

Knowing the deformation in extension of the x-fibers and the curvature of the y-fibers, one deduces the density of elastic energy of deformation $w^F$ developed by a normalized point force:

$$\begin{aligned} w^F = K_x^e (\varepsilon _{_xxx}^F)^2 +K_x^b (^y\kappa ^F_x)^2 = K_x^e\big ((\varepsilon _{_xxx}^F)^2 + \eta _x^2 (^y\kappa ^F_x)^2 \big ) \end{aligned}$$

(3.19)

and from (3.17) and (3.18) one notices that the energy is equally distributed between the tension of the x-fibers and the bending of the y-fibers, independently of the fact that the x- and y-fibers have distinct properties. The density of energy $w^F$ and $W^F$ for a normalized point force and, respectively, a physical point force $F_x\delta \mathbf {e}_x$ reads:

$$\begin{aligned} w^F(x,y) = \frac{K_x^e}{2} \frac{\exp (\frac{-y^2}{2\eta _x |x|})}{4\pi \eta _x |x|}\qquad ;\qquad W^F(x,y) = \frac{F_x^2}{2K_x^e} \frac{\exp (\frac{-y^2}{2\eta _x |x|})}{4\pi \eta _x |x|} \end{aligned}$$

(3.20)

Fig. 2

Green’s function $G_x$ for a normalized $\mathbf {e}_x$ point-force applied on the origin of an infinite pantographic sheet. Left: field of displacement $G_x$, Center: field of extension of the x-fibers $\varepsilon _{_xxx}^F$ Right: density of elastic energy of deformation by extension of the x-fibers and by bending of the y-fibers, $w^F$. The plot displays the square zone [$50\eta _x \times 50\eta _x$]

In Fig. 2, the Green’s function $G_x$ and the associated fields of deformation $\varepsilon _{_xxx}^F$ and of energy $w^F$ are displayed. One notices the strong directionality of the response along the loaded fiber together with the perpendicular “parabolic” diffusion smoothing related to the bending of the orthogonal fibers.

3.4 Green’s function $H_x (x,y)$ for a normalized point moment $\partial _{y}\delta \mathbf {e}_x$

The Green’s function $h_x \mathbf {e}_x$ associated with the doublet of normalized moments $\partial _{yy}\delta \mathbf {e}_x$ and the Green’s function $H_x \mathbf {e}_x$ associated with a normalized moment $\partial _{y}\delta \mathbf {e}_x$ are related by ($\pm \mathrm {d}Y$ denotes the position of the opposite moments):

$$\begin{aligned} h_x (x,y) = \lim _{\mathrm {d}Y\rightarrow 0}\frac{H_x (x ,y - \mathrm {d}Y) - H_x (x ,y +\mathrm {d}Y)}{2\mathrm {d}Y} = -\partial _yH_x (x,y) \end{aligned}$$

Consequently, imposing a zero x-displacement on the line $y=0$ yields:

$$\begin{aligned} H_x (x,y) = -\int _{0}^{y}h_x (x,y) \mathrm {d}y = \frac{1}{2\eta _x} \int _{0}^{y} \frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}} \mathrm {d}y = \frac{1}{4\eta _x}\mathrm {erf}\bigg (\frac{y}{\sqrt{4\eta _x|x|}} \bigg ) \end{aligned}$$

(3.21)

Thus, the x-component of the displacement is bounded and reach $\pm 1/(4\eta _x)$ when $y\rightarrow \pm \infty$. Besides, $\varepsilon _{_xxx}^M = \partial _{x} H_x$ and $^y \kappa ^M_x =\partial _{yy} H_x$ are, respectively, the extension of the x-fibers and the curvature of the y-oriented fibers induced by the normalized moment $\partial _{y}\delta \mathbf {e}_x$, and, multiplied by the corresponding stiffness constants, the tension and the moment that they undergo. Their expressions are

$$\begin{aligned} \varepsilon _{_xxx}^M = \partial _{x} H_x = -\frac{1}{4\eta _x}\frac{y}{ x}\frac{\exp (\frac{-y^2}{4\eta _x |x|})}{\sqrt{4\pi \eta _x |x|}} \qquad ;\qquad ^y \kappa ^M_x =\partial _{yy} H_x =\eta _x^{-1}\varepsilon _{_xxx}^M \end{aligned}$$

Hence, as with a point-force, the energy of deformation for a point-moment is equally distributed between the tension of the x-fibers and the bending of the y-fibers.

Note that two types of moments must be considered depending on the fact that they act either on the x- or on the y-fibers. Thus, we have similarly $H_y (x,y) = \frac{1}{4\eta _y}\mathrm {erf}\big (\frac{x}{\sqrt{4\eta _y|y|}} \big )$.

3.5 Synthesis of obtained results

1) organize in a common pattern the four herebelow equation (3.22 to 3.25) 2) introduce in each case a larger space after ‘=0’, we have the following explicit solutions for the displacement field $\mathbf {u} =u_x\mathbf {e}_x$ governed by the $\mathbf {e}_x$-force balance with different $\mathbf {e}_x$ point source distributions normalized by $K_x^e$:

$$\begin{aligned}&\mathbf {e}_x-\text{ force } \nonumber \\&\mathcal {D} (G_x ) + \delta =0, \qquad G_x (x,y) = - \frac{|y|}{4\eta _x } \left( -\frac{\exp (-\xi _x^2)}{\sqrt{ \pi }|\xi _x|}+\mathrm {erfc }(|\xi _x|) \right) \end{aligned}$$

(3.22)

$$\begin{aligned}&\text{ Moment } \text{ of } \mathbf {e}_x-\text {force} \nonumber \\&\mathcal {D} (H_x ) + \partial _{y}\delta =0,\qquad H_x (x,y) = \frac{1}{4}\mathrm {erf}(\xi _x) \end{aligned}$$

(3.23)

$$\begin{aligned}&\text{ x-Doublet } \text{ of } \mathbf {e}_x-\text {force} \nonumber \\&\mathcal {D} (g_x ) + \partial _{x}\delta = 0,\qquad g_x (x,y) = \frac{\mathrm {sgn}(x)}{2} \frac{\exp (-\xi _x^2)}{\sqrt{4\pi \eta _x |x|}} \qquad ;\qquad \xi _x =\frac{y }{\sqrt{4\eta _x |x|}}\end{aligned}$$

(3.24)

$$\begin{aligned}&\text{ y-Doublet } \text{ of } \text{ Moment } \text{ of } \mathbf {e}_x-\text {force} \nonumber \\&\mathcal {D} (h_x ) + \partial ^2_{yy}\delta =0, \qquad h_x (x,y) = -\frac{1}{2\eta _x} \frac{\exp (-\xi _x^2)}{\sqrt{4\pi \eta _x |x|}} \end{aligned}$$

(3.25)

These solutions are linked by the following relations:

$$\begin{aligned} H_x = -\partial _yG_x \quad ;\quad g_x = -\partial _xG_x \quad ;\quad h_x = -\partial _yH_x = \partial ^2_{yy}G_x \quad ;\quad \partial _{y}g_x = \partial _{x}H_x \end{aligned}$$

Similar expressions are obtained for $\mathbf {e}_y$ point source distributions normalized by $K_y^e$, by inverting x and y, so that $\eta _x$ and $\xi _x$ become $\eta _y$ and $\xi _y$.

4 Some loading simulations of pantographic sheet

Consider an infinite pantographic sheet of square period ($\ell _x =\ell _y$) with identical x- and y-fibers, hence $\eta _x =\eta _y$. In that case $G_x (x,y) = G_y (y,x)$.

4.1 Equal-axis opposite forces

Consider the case of two opposite normalized point-forces (Fig. 3-1), namely $\delta (x+d)\delta (y)\mathbf {e}_x -\delta (x-d)\delta (y)\mathbf {e}_x$, that are applied on the same fiber $y=0$ and applied at a distance 2d. The field of displacement and of energy of deformations read:

$$\begin{aligned} \mathbf {u}(x,y) =\left( G _x(x-d,y) - G _x(x+d,y)\right) \mathbf {e}_x \qquad ;\qquad W(x,y) = \left( w^{F}_x(x-d,y) +w^{F}_x(x+d,y)\right) \end{aligned}$$

These expressions are displayed in Fig. 4 for forces distant $2d = 20\eta _x$.

As expected, the strong directionality of the response is observed with a low lateral spread. Displacements at infinity tend towards zero. The deformation is in extension between the two loading points and in contraction outside. The deformation energy is concentrated in the vicinity of the loading points.

Fig. 3

Different forces loadings. From left to right. Equal axis loadings: opposite x-forces (see also Fig. 4); opposed uniform axial loading (see also Fig. 5); Bias loading (see also Fig. 7)

Fig. 4

Infinite pantographic sheet loaded by two opposite point-forces applied on the same fiber $y=0$ and applied at the distance $2d = 20\eta _x$. Left: displacement, Center: extension of the x-fibers Right: density of energy. The plot displays the square zone [$50\eta _x \times 50\eta _x$]

4.2 Uniform extension along the fiber direction

On the infinite sheet, one isolates mentally a rectangular strip of width 2a in the direction $\overrightarrow{E}_1 = (\mathbf {e}_x-\mathbf {e}_y)/\sqrt{2}$ diagonal to the fibers, and of length 2h in the second diagonal direction $\overrightarrow{E}_2 = (\mathbf {e}_x+\mathbf {e}_y)/\sqrt{2}$. In the $(\mathbf {e}_x, \mathbf {e}_y)$ frame, the position of the four corners $A, A', B, B'$ of the strip are:

$$\begin{aligned} \overrightarrow{OA} = X\mathbf {e}_x+ Y\mathbf {e}_y\quad ;\quad \overrightarrow{OA'} = Y\mathbf {e}_x+ X\mathbf {e}_y \quad ;\quad \overrightarrow{OB'} = -X\mathbf {e}_x- Y\mathbf {e}_y \quad ;\quad \overrightarrow{OB} = -Y\mathbf {e}_x-X\mathbf {e}_y \end{aligned}$$

with $X = (h+a)/\sqrt{2}$ and $Y= (h-a)/\sqrt{2}$. In the following numerical examples of this section $X = 50\eta _x$ and $Y= 30\eta _x$ which corresponds to a strip with $h = 4a$ and $a = 10\sqrt{2}\eta _x$.

The uniform loading corresponds to opposite $\mathbf {e}_x$ normalized point-forces distant from the distance 2d and applied uniformly in between the fibers $-b<y<b$ (Fig. 3-2). The field of displacement and of energy of deformations read:

$$\begin{aligned} \mathbf {u}(x,y) =\mathbf {e}_x \int _{-b}^{b}\big (G _x(x-d,y +v) - G _x(x+d,y +v)\big )\mathrm {d}v \\ W(x,y) = \int _{-b}^{b}\big (w^{F}_x(x-d,y+u) +w^{F}_x(x+d,y+u)\big ) \mathrm {d}v \end{aligned}$$

These expressions are displayed in Fig. 5 (to be compared with Fig. 4) for forces distant of $2d = 20\eta _x$ and a loading zone $2b = 40\eta _x$. On notices the quasi-uniform extension inside the loading zone and the fast vanishing of the deformation perpendicularly to the force direction.

4.3 Diagonal point-force

For a point-force oriented along the diagonal of the square lattice, i.e. $\delta (\mathbf {e}_x+\mathbf {e}_y)/\sqrt{2}$ the field of displacement and the energy of deformation are given by

$$\begin{aligned} \mathbf {u}(x,y) =F\left( G _x(x,y)\mathbf {e}_x + G _y(x,y)\mathbf {e}_y\right) /\sqrt{2};\; W(x,y) =F\bigg (w^{F}_x(x,y) +w^{F}_y(x,y)\bigg ) \end{aligned}$$

These fields are displayed in Fig. 6. Although the point force is oriented diagonally to the fibres, its effect is essentially transmitted in the directions of the fibres with low bending diffusion, perpendicular to the fibres. Comparison with the Fig. 2 clearly shows that the effect of the diagonal force is simply the sum of the effects of its two components in the direction of the fibres.

Fig. 5

Uniform tension test (details in the text). Same legend as in Fig. 4

Fig. 6

Infinite pantographic sheet loaded by a diagonal point-force $\mathbf {F} = F(\mathbf {e}_x+\mathbf {e}_y)/\sqrt{2}$. Left: modulus of the displacement, Center: quadratic mean of the extension of the x-fibers and y-fibers. Right: density of energy. The plot displays the square zone [$50\eta _x \times 50\eta _x$]

Fig. 7

Discrete bias loading (details in the text). Left: modulus of the displacement within the zone [$100\eta _x \times 100\eta _x$], Center: the same, zoomed on [$50\eta _x \times 50\eta _x$]. Right: density of energy on the zone [$100\eta _x \times 100\eta _x$]

4.4 Discrete bias extension loading

The discrete bias loading is realized through four normalized point-forces distributed as follows (Fig. 3-3). On the points $A, A'$ one applies a point-force oriented in the diagonal direction $\overrightarrow{E}_2 = F(\mathbf {e}_x+\mathbf {e}_y)/\sqrt{2}$ and on points $B, B'$ one applies a point-force in the opposite direction $- \overrightarrow{E}_2$.

Decomposing the forces according to the fibers directions, the displacement field is given by:

$$\begin{aligned} \mathbf {u}(x,y)= & {} \frac{\mathbf {e}_x}{\sqrt{2}} \bigg (G _x(x-X,y-Y) + G _x(x-Y,y-X) - G _x(x+X,y+Y) -G _x(x+Y,y+X)\bigg ) \nonumber \\&+ \frac{\mathbf {e}_y}{\sqrt{2}} \bigg (G _y(x-X,y-Y) + G _y(x-Y,y-X) - G _y(x+X,y+Y) - G _y(x+Y,y+X)\bigg )\nonumber \\ \end{aligned}$$

(4.1)

By construction, $\mathbf {u}(0,0)= \mathbf {0}$; by symmetry, the displacement on the line $x=y$ is along the direction $\overrightarrow{E}_1 = (\mathbf {e}_x-\mathbf {e}_y)/\sqrt{2}$ and the displacement on the line $x= -y$ is along the direction $\overrightarrow{E}_2 = (\mathbf {e}_x-\mathbf {e}_y)/\sqrt{2}$. Figure 7 shows the distribution of the modulus of displacement and of the energy corresponding to such a type of loading. The observed displacement and deformation is determined by the fact that each diagonal force is mainly transferred in the direction of the two orthogonal fibres. The energy is concentrated around the point of application of the forces.

5 Pantographic array versus rigidly connected array

The highly anisotropic second-gradient behaviour of pantographic lattices results from two features, namely the strong (bi-)directionality related to the fiber orientations and the pivot connexions between fibers. As demonstrated in [16, 20], if the pivots are replaced by rigid connexions then the arrays are highly anisotropic and behaves as simple gradient medium ruled by the classical Cauchy stresses. Pivots are introduced in the design of pantographic metamaterials in order to have an high contrast in the mechanical properties of the micro-architectures: extremely soft and extremely stiff micro-deformations modes of the periodic cell are the cause of a second-gradient macro-behaviour (for further details see [7, 18]).

A simple way to highlight the paramount importance of the nature of the connexions is to compare the Green’s functions of two identical orthogonal fiber array, one having pivot connexions, the other having rigid connexions.

To this aim, let us consider again the orthogonal $\ell _x \times \ell _y$-periodic lattice made of x- and y-fibers of respective axial and bending stiffnesses $E_xA_x$, $E_yA_y$; $E_xI_x$, $E_yI_y$ with $E_xA_x/(E_yA_y) = O(1)$ and $E_xI_x/(E_yI_y) = O(1)$. However, in contrast to the pantographic array the x- and y-fibers are rigidly connected at there crossing points. In small deformations, the effective constitutive law of such lattice reads as follows, [16, 20], where $\sigma _{xx}$, $\sigma _{xy}$, $\sigma _{yy}$ are the components of the 2D symmetric stress tensor $\underline{\underline{\sigma }}$ expressed in the $(\mathbf {e}_x,\mathbf {e}_y)$ frame and $u_x$, $u_y$ the component of the displacement $\mathbf {u}$ in the same frame:

$$\begin{aligned} \sigma _{xx} = K^e_x u_{x,x} ;\qquad \sigma _{yy} = K^e_y u_{y,y} ;\qquad \sigma _{xy} = \sigma _{yx} =M (u_{x,y}+u_{x,y})/2 \end{aligned}$$

(5.1)

The shear parameters are given by:

$$\begin{aligned}&\frac{1}{M } = \frac{1}{M _x}+ \frac{1}{M _y}\,;\qquad M _x = \frac{12}{\ell _x^2}K^b_x\,;\qquad M _y = \frac{12}{\ell _y^2}K^b_y \end{aligned}$$

(5.2)

$K^e_x$ and $K^e_y$ are directly related to the tension of the fiber, while the effective shear modulus M encapsulates the combined local bending of the fibers in both directions. Consequently, the shear modulus is much smaller than the axial moduli. Indeed, dropping the $_x$ or $_y$ indices, $M/K^e = O(\frac{I}{A\ell ^2}) = O(\frac{A}{\ell ^2}) \ll 1$ since $\frac{\sqrt{A}}{\ell }$ is nothing but the inverse of the slenderness ratio of the fiber taken over the cell length $\ell$. In absence of body force, the balance equation of the array reads: $\mathbf {\mathrm {div}}(\underline{\underline{\sigma }}) = \mathbf {0}$. Now, in presence of a point force $\mathbf {F}\delta (x,y)$ located at the origin, one has $\mathbf {\mathrm {div}}(\underline{\underline{\sigma }}) = \mathbf {F}\delta (x,y)$, that yields the following differential system to be compared with (2.1):

$$\begin{aligned} \begin{pmatrix} K^e_x\partial ^2_{xx} + M \partial ^2_{yy} &{}; &{} M \partial ^2_{xy} \\ M \partial ^2_{xy} &{};&{} K^e_y\partial ^2_{yy} + M \partial ^2_{xx} \end{pmatrix} \begin{pmatrix} U_{Gx}\\ U_{Gy} \end{pmatrix} + \begin{pmatrix}F_{x}\\ F_{y} \end{pmatrix} \delta (x,y)= 0 \end{aligned}$$

(5.3)

Unlike the pantographic array, the variables $U_{Gx}$ and $U_{Gy}$ are coupled, and the balance equations in the two directions must be treated conjointly. The coupling results from the shear parameter M inherited from the local bending. For the pantographic array, the free connection for the moments makes that the shear coupling disappears. However, because of the stiff connection for the forces, the bending effect remains on the usual form of a fourth derivative term in the balance equation in both fiber directions.

The set (5.3) corresponds to the balance equations of a specific 2D orthotropic medium, in which, using the Voigt’s notations, $C_{11} = K^e_x$, $C_{22} = K^e_y$, $C_{66} = M$ and $C_{12} = 0$. The Green’s functions have been already established in the general case where $C_{12} \ne 0$, [19, 28]. Introducing the simplification due to $C_{12} = 0$ yields the following symmetric Green’s matrix $\underline{\underline{\mathcal {G}}}$:

$$\begin{aligned} \mathbf {U}_G = \underline{\underline{\mathcal {G}}}.\mathbf {F} \quad ;\quad \underline{\underline{\mathcal {G}}}= \frac{1}{2 (a_1-a_2)} \begin{pmatrix} -\frac{a_1}{b_1}\ln \left( \rho _1^2\right) + \frac{a_2}{b_2}\ln \left( \rho _2^2\right) &{}; &{} \arctan (\frac{yb_1}{x}) - \arctan (\frac{y b_2}{x}) \\ \arctan (\frac{yb_1}{x}) - \arctan (\frac{y b_2}{x}) &{};&{} -\frac{b_2}{a_2}\ln \left( \rho _2^2\right) + \frac{b_1}{a_1}\ln \left( \rho _1^2\right) \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \rho _i^2 = \frac{x^2}{b_i} + y^2b_i\,;\qquad b_i = \root 4 \of {\frac{K^e_x a_i }{K^e_y }} \end{aligned}$$

and $a_1$ and $a_2$ are the roots of the second-degree equation:

$$\begin{aligned} a^2+(2-\frac{K^e_x K^e_y}{M^2})a +1 =0 \quad \text{ therefore }\quad a_1a_2 =1 \end{aligned}$$

Then, for $i= 1,2$

$$\begin{aligned} a_i = \frac{K^e_x K^e_y}{2M^2}\bigg ( 1-\frac{2M^2}{K^e_x K^e_y} + (-1)^{i+1} \sqrt{1-\frac{4M^2}{K^e_x K^e_y}}\bigg ) \,;\quad \sqrt{a_i} = \frac{\sqrt{K^e_x K^e_y}}{2M}\bigg (1 + (-1)^{i+1} \sqrt{1-\frac{4M^2}{K^e_x K^e_y}}\bigg )\nonumber \\ \end{aligned}$$

(5.4)

The salient features of the fundamental solutions given by the Green’s matrix are identical whatever the parameters $a_i$. Thus, to facilitate the comparison with the Green’s matrix of the pantographic array (3.13)–(3.14)–(3.16) we focus on the case where the lattice is square, i.e. $\ell _x = \ell _y = \ell$, the x- and y-fibers are identical, i.e. $\eta _x = \eta _y = \eta$ and $K^e_x = K^e_y = K^e$, so that, referring to the intrinsic length of the pantographic array, ${{M}/{K^e}}= \eta ^2/(6\ell ^2)$. Using limit expressions that corresponds to $M\ll K^e$, we have in that case:

$$\begin{aligned}&\sqrt{a_1} \approx \frac{K^e}{M} \gg 1\quad ;\quad \sqrt{a_2} \approx \frac{M}{K^e}\ll 1\quad ;\quad b_i \approx \root 4 \of { a_i }\\&\rho _1^2 \approx \sqrt{\frac{M}{K^e}}x^2 + \sqrt{ \frac{K^e}{M}}y^2\quad ;\quad \rho _2^2 \approx \sqrt{ \frac{K^e}{M}}x^2 + \sqrt{\frac{M}{K^e}}y^2 \end{aligned}$$

and

$$\begin{aligned} \underline{\underline{\mathcal {G}}} \approx \frac{M}{2\pi (K^e)^2} \begin{pmatrix} -(\frac{K^e}{M})^{3/2}\ln (\rho _1^2 ) + (\frac{M}{K^e})^{3/2}\ln (\rho _2^2 ) &{}; &{} \arctan (\frac{y}{x}\sqrt{\frac{K^e}{M}}) - \arctan (\frac{y}{x}\sqrt{ \frac{M}{K^e}}) \\ \arctan (\frac{y}{x}\sqrt{\frac{K^e}{M}}) - \arctan (\frac{y}{x}\sqrt{ \frac{M}{K^e}}) &{};&{} (\frac{M}{K^e})^{3/2}\ln (\rho _1^2) - (\frac{K^e}{M})^{3/2}\ln (\rho _2^2) \end{pmatrix} \end{aligned}$$

Considering the response under a $\mathbf {e}_x$-point force, one notices that the y-component of the displacement is not null but bounded, while the x-component presents a logarithmic singularity in any direction around the loading. Beside, the strain tensor reads:

$$\begin{aligned} \underline{\underline{\epsilon }} \approx \frac{M}{2\pi (K^e)^2} \begin{pmatrix} -\frac{K^e}{M}\frac{2x}{ \rho _1^2} + \frac{M}{K^e}\frac{2x}{ \rho _2^2} &{}; &{} -(1+ 2(\frac{K^e}{M})^2)\frac{y}{ \rho _1^2} + (1+ 2(\frac{M}{K^e})^2)\frac{y}{ \rho _2^2} \\ -(1+ 2(\frac{K^e}{M})^2)\frac{y}{ \rho _1^2} + (1+ 2(\frac{M}{K^e})^2)\frac{y}{ \rho _2^2} ) &{};&{} \frac{x}{ \rho _1^2} - \frac{x}{ \rho _2^2} \end{pmatrix} \end{aligned}$$

Fig. 8

Field of deformation in a rigidly connected array undergoing a $\mathbf {e}_x$-point force. Left: $\epsilon _{xx}$, Center: $\epsilon _{xy}$, Right: $\epsilon _{yy}$. The plot is drawn for $K^e/M= 5$

The high anisotropy of the response is evidenced in Fig. 8 where the three terms $\epsilon _{xx}$, $\epsilon _{xy}$, $\epsilon _{yy}$, are displayed and show a strong $\mathbf {e}_x$-directivity. It is worth mentioning that the axial deformation $\epsilon _{xx}$ along the force direction significantly differs from that of the pantographic array, cf. (3.17). Indeed, the tension of any fiber presents a singularity O(1/x) instead of the singularity $O(1/\sqrt{|x|})$ for the single fiber $y= 0$. Thus, meanwhile the rigidly connected array is highly anisotropic, the effect of directionality is even magnified in pantographic arrays. Furthermore, the pivots smoothen the singularity in two manner, i.e. by reducing O(1/x) into $O(1/\sqrt{|x|})$, and by limiting drastically its spatial distribution. The smoothening in magnitude is well known for isotropic second-gradient material but, up to our knowledge, the spatial effect was not yet evidenced.

6 Integral representation for pantographic array

The advantage of Green’s functions, apart from providing exact solutions for particular loads, is that it gives access to exact integral representations of the fields. These formulations, which only involve boundary values, allow numerical solutions to boundary problems by solving integral equations. This approach has two advantages. On one hand, as the analytical approach to the problem is preserved since the local equations are already integrated, the only approximations appear at the boundary. This difference with respect to finite elements where the equations are solved at any point of the discretized medium is particularly interesting for complex media for which the problems can be ill-conditioned. On the other hand, the resolution only requires the discretization on the boundary. The computational burden involved in considered numerical problem is therefore greatly reduced.

The aim of this section is to establish the integral representation for pantographic 2D continua.

Taking into account that the components $u_x$ and $u_y$ are uncoupled, as well as the $\mathbf {e}_x$ and $\mathbf {e}_y$ balance equations, we can focus on the field $u_x$ governed by the balance along $\mathbf {e}_x$; $u_y$ could be treated similarly considering the balance along $\mathbf {e}_y$. Here we will use the non-normalized equations of equilibrium that allow the physical sense to appear more easily.

6.1 Setting the problem in the framework of distributions theory

In a finite pantographic sheet, we specify a domain $\Omega$ having a smooth border $\Gamma = \partial \Omega$. Let us consider that the domain $\Omega$ undergoes an $\mathbf {e}_x$-balanced non-null continuous twice derivable field $u_x$, whilst outside of $\Omega$ the field is null, i.e. $u_x(P') =0$ for $P'\notin \Omega$. In addition, we assume for simplicity that the sheet is free of internal loading (this assumption alleviates the developments but is not essential). Now, on the boundary $\Gamma$ the field $u_x$ is generally not continuous, then its derivatives has to be considered in the sense of distributions. This leads us to introduce the distribution $U_x(x,y)$ defined by

$$\begin{aligned} U_x(P)= u_x(P) \quad \text{ for } P\,\in \Omega ;\qquad U_x(P')= 0 \quad \text{ for } \,P'\notin \Omega \end{aligned}$$

The differential equation $\mathcal {D}_x(u_x) = 0$ rewritten in the framework of distributions reads:

$$\begin{aligned} \mathcal {D}_x(\delta )*U_x = \mathcal {D}_x(\delta )*u_x = \mathcal {D}_x(u_x) = 0 \quad \text { in } \quad \Omega \qquad ;\qquad \mathcal {D}_x(\delta )*U_x = \mathcal {D}_x(\delta )*0 = 0 \quad \text { out } \quad \Omega \end{aligned}$$

However, the distribution $\mathcal {D}_x(\delta )*U_x$ does not vanish on the boundary and must be determined.

To this purpose, let us recall that on any point Q of $\Gamma$, the x-derivative of the discontinuous distribution U through $\Gamma$ of outward normal $\mathbf {n}_Q$ reads:

$$\begin{aligned} \forall Q\in \Gamma \qquad \partial _x\delta *U_Q = \partial _xU_Q = [U]_Q \mathbf {n}_Q.\mathbf {e}_x\delta _\Gamma + (\partial _xu)_Q \end{aligned}$$

where $\delta _\Gamma$ is the line distribution of Dirac over $\Gamma$, and $[U]_Q$ is the jump through $\Gamma$ taken in the direction of the outward normal, hence $[U]_Q = 0 - u_Q$. Consequently, denoting unambiguously $\mathbf {n}_Q.\mathbf {e}_x$ by $n_x$:

$$\begin{aligned} \partial _xU_x = -u_xn_x \delta _\Gamma + \partial _xu_x \end{aligned}$$

Applying the same rule for the second derivative yields:

$$\begin{aligned} \partial ^2_{xx}U_x= & {} \partial _x\left( -u_x n_x\delta _\Gamma + \partial _{x}u\right) = S^e_{x} +\partial ^2_{xx}u_x \end{aligned}$$

(6.1)

$$\begin{aligned} S^e_{x}= & {} -( u_{x} \delta _{\Gamma ,x} + u_{x,x} \delta _\Gamma ) n_x \end{aligned}$$

(6.2)

where $S^e_{x}$ is a line distribution defined over the border $\Gamma$. Similarly, introducing the line distribution $S^b_{y}$ over $\Gamma$ ($n_y$ stands for $\mathbf {n}_Q.\mathbf {e}_y$):

$$\begin{aligned} \partial ^4_{yyyy}U_x= & {} S^b_{y} +\partial ^4_{yyyy}u_x \end{aligned}$$

(6.3)

$$\begin{aligned} S^b_{y}= & {} - ( u_{x}\delta _{\Gamma ,yyy} + u_{x,y} \delta _{\Gamma ,yy} + u_{x,yy}\delta _{\Gamma ,y} + u _{x,yyy} \delta _\Gamma )n_y \end{aligned}$$

(6.4)

Bringing these results together yields:

$$\begin{aligned} \mathcal {D}(\delta )*U_x = K^e_x\partial ^2_{xx}U_x - K^b_y \partial ^4_{yyyy}U_x = K^e_x S^e_{x} - K^b_y S^b_{y} + K^e_x \partial ^2_{xx}u_x - K^b_y \partial ^4_{yyyy}u_x \end{aligned}$$

Furthermore, $\partial ^2_{xx}u_x$ and $\partial ^4_{yyyy}u_x$ are values inside $\Omega$ taken on the border and as such $K^e_x \partial ^2_{xx}u_x - K^b_y \partial ^4_{yyyy}u_x = \mathcal {D}(u) = 0$. Thus, $\mathcal {D}_x(\delta ) *U_x$ is the singular distribution on $\Gamma$ given by:

$$\begin{aligned} \mathcal {D}_x(\delta )*U_x = K^e_x S^e_{x } - K^b_y S^b_{y } \end{aligned}$$

(6.5)

Expliciting $S^e_{x }$ and $S^b_{y }$, this expression is reworded as follows:

$$\begin{aligned}&\mathcal {D}_x(\delta )*U_x = u_{x} (- K^e_x \delta _{\Gamma {,x}} n_x + K^b_y \delta _{\Gamma ,yyy} n_y ) + (-K^e_x u _{x,x}n_x + K^b_y u _{x,yyy}n_y )\delta _\Gamma \nonumber \\&\quad + K^b_y u _{x,y}n_y \delta _{\Gamma ,yy}+ K^b_y u_{x,yy}n_y \delta _{\Gamma {,y}} \end{aligned}$$

(6.6)

6.2 Integral representation

The non-normalized Green’s function $\mathbb {G}_x$, is by construction the inverse of convolution of the distribution $\mathcal {D}_x(\delta )$. Therefore, we have, using the commutativity and associativity of the convolution:

$$\begin{aligned} \mathbb {G}_x*\big (\mathcal {D}_x(\delta )*U_x\big ) = \big (\mathbb {G}_x*\mathcal {D}_x(\delta )\big )*U_x = \big (\mathcal {D}_x(\delta )*\mathbb {G}_x\big )*U_x = - \delta * U_x = - U_x \end{aligned}$$

Consequently, using the expression (6.5) of $\mathcal {D}_x(\delta ) *U_x$:

$$\begin{aligned} U_x = - \mathbb {G}_x*( K^e_x \mathcal {S}^e_{x} - K^b_y S^b_{y} ) = -( K^e_x S^e_{x} - K^b_y Sb_{y } )*\mathbb {G}_x \end{aligned}$$

(6.7)

and since $S^e_{x}$ and $S^b_{y}$ are singular distributions on $\Gamma$ one obtains from the definition of $U_x$ inside and outside $\Omega$:

$$\begin{aligned}&\forall P\,\in \Omega \qquad u_x(P) = -\int _{Q\in \Gamma } \left( K^e_xS^e_{{x}{(Q)}}\mathbb {G}_{x{(P-Q)}} - K^b_y S^b_{{y}{(Q)}} \mathbb {G}_{x{(P-Q) }}\right) \mathrm {d}l \nonumber \\ {}&\forall P'\,\notin \Omega \qquad 0 = -\int _{Q\in \Gamma } \left( K^e_x S^e_{{x}{(Q)}}\mathbb {G}_{x{(P'-Q)}} - K^b_yS^b_{{y}{(Q)}}\mathbb {G}_{x{(P'-Q) }} \right) \mathrm {d}l \end{aligned}$$

(6.8)

The integral representation can be interpreted according to the Huygens–Fresnel principle: the response in any internal or external point of $\Omega$ results from a density of fictitious source located on the boundary $\Gamma$. The physical meaning of these sources appears clearer by inserting the expressions of different terms as given by (6.6):

$$\begin{aligned} \forall P\,\in \Omega \quad u_x(P)= & {} \int _{Q\in \Gamma } \bigg (- ( u_{x}n_x)_{(Q)} (K^e_x \mathbb {G}_{,x})_{(P-Q) } + ( u_{x}n_y)_{(Q)} (K^b_y \mathbb {G}_{ x,yyy}) _{(P-Q)}\bigg ) \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } \big ( K^e_xu_{x,x} n_x - K^b_y u_{x,yyy} n_y\big )_{(Q)} \mathbb {G}_{x{(P-Q)}} \mathrm {d}l \nonumber \\&- \int _{Q\in \Gamma } ( u_{x,y}n_y)_{(Q)} \big (K^b_y \mathbb {G}_{ x,yy} \big )_{(P-Q)} \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } K^b_y (u_{x,yy} n_y)_{(Q)} (\mathbb {G}_{x,y})_{(P-Q) } \mathrm {d}l \end{aligned}$$

(6.9)

Recalling that for a pantographic array, the boundary conditions related to the $\mathbf {e}_x$-balance and the $u_x$ component, are of four different types:

• The two kinematic conditions consisting in the displacement $u_x$ and its transverse gradient $u_{x,y}$,

• The two “static” dual variables consisting in (i) the $\mathbf {e}_x$-force $K^e_x u_{x,x} n_x - K^b_y u_{x{,yyy}} n_y$, which cumulates the tension of the x-fiber and the shear force for the y-fiber, and (ii) the moment $K^b_y u_{x,yy}n_y$ in the x-fiber [7].

One recognizes in the four different integrals of (6.9) a combination of the boundary conditions that acts as sources terms, and of their proper radiation functions derived from the Green’s function. Namely:

• the displacement $u_x$ is radiated by the two terms, $K^e_x \mathbb {G}_{x,x}$ for $u_x n_x$ and $- K^b_y \mathbb {G}_{x,yyy}$ for $u_x n_y$,

• the projected rotation $u_{x{,y}} n_y$ is radiated $K^b_y \mathbb {G}_{x,yy}$,

• the force $K^e_x u_{x,x} n_x - K^b_y u_{x{,yyy}} n_y$ is radiated by $\mathbb {G}_x$,

• the force $K^b_y u_{x,yy}n_y$ is radiated by $\mathbb {G}_{x,y}$.

If instead of the $\mathbf {e}_x$-balance and $u_x$, one considers the $\mathbf {e}_y$-balance and $u_y$ we get an equation similar to (6.8) or (6.9) except that the roles of x and y are inverted.

Equation (6.9) allows to calculate the field at any point of the domain as soon as every boundary radiating fields is known. However, only part of these fields can be imposed as boundary conditions, the others (i.e. those dual in work to the assigned boundary conditions) result from the response of the loaded medium and are to be found as a part of the equilibrium problem. To be able to use the method of boundary integral equations, it is thus necessary to calculate the missing dual boundary fields. Generalizing the standard procedure presented in classical elasticity, for doing so we introduce the integral equations that are determined in the next section .

6.3 The two integral equations

Unlike first-gradient elastic media, for which a single integral equation is sufficient, for second-gradient pantographic media, whose deformation energy depends on first and second gradient of displacement and for which two independent boundary conditions must be given, it is necessary to establish two integrals equations.

6.3.1 Integral equation for displacement $u_x$

The integral representation (6.9) applies in the whole space and then also on $\Gamma$. This leads to the integral equation in the x-direction:

$$\begin{aligned} \forall Q_0\,\in \Gamma \quad u_x(Q_0)= & {} -\int _{Q\in \Gamma } \left( K^e_xS^e_{{x}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}} - K^b_y S^b_{{y}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}}\right) \mathrm {d}l \nonumber \\= & {} \int _{Q\in \Gamma } \big (- ( u_{x}n_x)_{(Q)} (K^e_x \mathbb {G}_{,x})_{(Q_{0}-Q) } + ( u_{x}n_y)_{(Q)} (K^b_y \mathbb {G}_{ x,yyy})_{(Q_0-Q)}\big ) \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } \big ( K^e_{xu{x,x}} n_x - K^b_y u_{x,yyy} n_y\big )_{(Q)} \mathbb {G}_{x {(Q_0-Q)}} \mathrm {d}l \nonumber \\&- \int _{Q\in \Gamma } ( u_{x,y}n_y)_{(Q)} \big (K^b_y \mathbb {G}_{x,yy} \big )_{(Q_0-Q)} \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } K^{b}_{y} (u_{x,yy} n_y)_{(Q)} (\mathbb {G}_{x,y})_{(Q_0-Q)} \mathrm {d}l \end{aligned}$$

(6.10)

This equation associates the values of the physical variables at the boundary as well as the function $\mathbb {G}_x$ and its derivatives. The physical variables are regular, but the function $\mathbb {G}_x$ and its derivatives can introduce singularities on $Q = Q_0$. Thus, in order to evaluate integrals, singularities must be identified and resolved. For this purpose, let us consider a slightly modified $\Gamma ^*$ boundary around $Q_0$ so that $Q_0$ is inside the integration domain and then takes the limit when $\Gamma ^*$ to $\Gamma$. Doing so:

$$\begin{aligned} u(Q_0) = \lim _{\Gamma ^*\rightarrow \Gamma } \int _{Q\in \Gamma ^*} -\left( K^e_xS^e_{{x}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}} - K^b_y S^b_{{y}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}}\right) \mathrm {d}l \end{aligned}$$

(6.11)

One assumes that $\Gamma$ is regular at $Q_0$ of coordinates $(x_0,y_0)$, and that its tangent makes an angle $\theta$ with the x-axis. The disturbed boundary $\Gamma ^*$ is constructed as follows, see Fig. 9. Isolating a small portion $\sigma _\theta$ of $\Gamma$ centered on $Q_0$, one has $\Gamma = \Gamma '\cup \sigma _\theta$. Then replace $\sigma _\theta$ by $\sigma _0 \cup \sigma _{\pi /2}$, where $\sigma _0$ and $\sigma _{\pi /2}$ are the two parts of the disturbed border, respectively, parallel to x and y, that forms a rectangular triangle with $\sigma _\theta$. The disturbed boundary $\Gamma ^*$ is $\Gamma ^* = \Gamma '\cup \sigma _0 \cup \sigma _{\pi /2}$, the normal of $\sigma _0$ is $\mathbf {n}_0 = \mathbf {e}_y$ and that of $\sigma _0$ is $\sigma _{\pi /2}$ is $\mathbf {n}_{\pi /2}= \mathbf {e}_x$.

Fig. 9

The boundary $\Gamma$ and the disturbed boundary $\Gamma ^*$

Over $\Gamma '$ there is no singularity, since $Q_0 \notin \Gamma '$. On the disturbated path $\sigma _0 \cup \sigma _{\pi /2}$, the integrals involving $K^e_xn_x$ taken over $\sigma _0$ vanishes as $\mathbf {n}_0 =\mathbf {e}_y$, and similarly the integrals involving $K^b_yn_y$ taken over $\sigma _{\pi /2}$ vanishes as $\mathbf {n}_{\pi /2}= -\mathbf {e}_x$. Thus:

$$\begin{aligned}&\int _{ \sigma _0\cup \sigma _{\pi /2}} - \left( K^e_xS^e_{{x}{(Q)}}\mathbb {G}_{x{(Q_0-Q) }} - K^b_y S^b_{{y}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}}\right) \mathrm {d}l \nonumber \\&\quad = - \int _{\sigma _{\pi /2}} K^e_xS^e_{{x}{(Q)}}\mathbb {G}_{x{(Q_0-Q) }} \mathrm {d}l + \int _{ \sigma _0}K^b_y S^b_{{y}{(Q)}}\mathbb {G}_{x{(Q_0-Q)}} \mathrm {d}l \end{aligned}$$

(6.12)

Furthermore, denoting by 2a the small lenght of $\sigma _\theta$, the lengths of $\sigma _0$ and $\sigma _{\pi /2}$ are, respectively, $2a_x = 2a\cos (\theta )$, $2a_y =2a\sin (\theta )$. Hence, introducing $x' =x - x_{0}$ and $y' =y- y_{0}$, the integration over $\sigma _0$ is performed on $x'$, with $y' = a_y$, and the integral over $\sigma _{\pi /2}$ is performed on $y'$, with $x' = -a_x$. Consequently, the integral over $\sigma _0\cup \sigma _{\pi /2}$ simplifies into (on $\sigma _{\pi /2}$, $n_x =-1$):

$$\begin{aligned}&+\int _{-a_y}^{a_y} u_{{x}{(x_0-a_x, y_0+ y' )}} K^e_x \mathbb {G}_{{x,x}{(a_x, -y')}} \mathrm {d}y' + \int _{-a_x}^{a_x} u_{{x}{(x_0+x', y_0 +a_y)}}K^b_y \mathbb {G}_{{x,yyy}{(-x', -a_y)}} \mathrm {d}x' \nonumber \\&- \int _{-a_y}^{a_y} K^e_{x} u_{{x,x}{(x_0-a_x, y_0 +y')}}\mathbb {G}_{x{(a_x, - y')}} \mathrm {d}y' -\int _{-a_x}^{a_x}K^b_y u_{{x,yyy} {(x_0+x', y_0 +a_y)}} \mathbb {G}_{x{(-x', -a_y)}} \mathrm {d}x' \nonumber \\&- \int _{-a_x}^{a_x} u_{{x,y}{(x_0+x', y_0 +a_y)}} K^b_y \mathbb {G}_{{x,yy}{(-x', -a_y)}} \mathrm {d}x' + \int _{-a_x}^{a_x} K^b_y u_{{x,yy}{(x_0+x', y_0 +a_y)}} \mathbb {G}_{{x,y}{(-x', -a_y)}} \mathrm {d}x' \end{aligned}$$

(6.13)

Since $u_x$ and its derivatives are regular, one deduces, from the expressions of the Green’s function and their derivatives (cf. Sect. 3.5), that:

$$\begin{aligned} \int _{-a_y}^{a_y} u_{{x,x}{(x_0-a_x, y_0 +y')}}\mathbb {G}_{x{(a_x,- y')}} \mathrm {d}y'= & {} O\left( a^{3/2}\, \partial _{x}u_{x(Q_0)} \right) \underset{a\rightarrow 0}{\rightarrow 0}\\ \int _{-a_x}^{a_x} u_{{x,yyy}{(x_0+x', y_0 +a_y)}} \mathbb {G}_{x{(-x', -a_y)}} \mathrm {d}x'= & {} O\left( a^{3/2}\,\partial ^3_{yyy}u_{x(Q_0)} \right) \underset{a\rightarrow 0}{\rightarrow 0}\\ \int _{-a_x}^{a_x} u_{{x,y}{(x_0+x', y_0 +a_y)}} \mathbb {G}_{{x,yy}{(-x', -a_y)}} \mathrm {d}x'= & {} O\left( \sqrt{a}\,\partial _{y}u_{x(Q_0)} \right) \underset{a\rightarrow 0}{\rightarrow 0}\\ \int _{-a_x}^{a_x} u_{{x,yy}{(x_0+x', y_0 +a_y)}} \mathbb {G}_{{x,y}{(-x', -a_y)}} \mathrm {d}x'= & {} O\left( \sqrt{a}\,\partial ^2_{yy}u_{x(Q_0)} \right) \underset{a\rightarrow 0}{\rightarrow 0} \end{aligned}$$

Thus, it remains to evaluate the “self-influence” term:

$$\begin{aligned}&+ \int _{-a_y}^{a_y} u_{{x}{(x_0-a_x, y_0+ y' )}} K^e_x \mathbb {G}_{{x,x}{(a_x, -y')}} \mathrm {d}y' + \int _{-a_x}^{a_x} u_{{x}{(x_0+x', y_0 +a_y)}}K^b_y \mathbb {G}_{{x,yyy}{(-x', -a_y)}} \mathrm {d}x' \\&\approx u_{{x}{(x_0, y_0 )}} \left( \int _{-a_y}^{a_y} K^e_x \mathbb {G}_{{x,x}{(a_x, y')}} \mathrm {d}y' - \int _{-a_x}^{a_x} K^b_y \mathbb {G}_{{ x,yyy}{( x',a_y)}} \mathrm {d}x' \right) = u_{x(Q_0)} J \end{aligned}$$

where the approximation is obtained by expanding $u_{x(Q)}$ around $Q_0$, keeping $u_{x(Q_0)}$ and neglecting the rest (that results in terms $O\left( \sqrt{a}\,u_{x(Q_0)} \right)$ leading to vanishing terms). Now, $\mathbb {G}_x$ being the Green’s function:

$$\begin{aligned} K^e_x\mathbb {G}_{{x,xx}{(Q-Q_0)}} - K^b_y \mathbb {G}_{{x,yyyy}{(Q-Q_0)}} = -(K^e_x\mathbb {G}_{{x,xx}{(Q_0-Q)}} - K^b_y \mathbb {G}_{{x,yyyy}{(Q_0-Q)}}) = -\delta _{(Q_0)} \end{aligned}$$

Consequently, integrating over the rectangle $|x'| \le a_x$, $|y'| \le a_y$ yields:

$$\begin{aligned} \int _{-a_x}^{a_x} \int _{-a_y}^{a_y} (K^e_x\mathbb {G} _{x,xx} -K^b_y\mathbb {G}_{x,yyyy})_{(Q_0-Q)} \mathrm {d}x'\mathrm {d}y' = 1 \end{aligned}$$

that gives by partial integrations and taking into account that $\mathbb {G}_{x}$ is even with respect to x and y (implying that $\mathbb {G}_{x,x}$ is an odd function with respect to x and $\mathbb {G}_{x,yyy}$ an odd function with respect to y):

$$\begin{aligned} 1 =2K^e_x\int _{-a_y}^{a_y} \mathbb {G}_{{x,x}{(a_x, y')}} \mathrm {d}y' -2K^b_y \int _{-a_x}^{a_x} \mathbb {G}_{{x,yyy}{(x', a_y)}} \mathrm {d}x' ) = 2J \end{aligned}$$

Remark

At a point where the surface is not smooth, the value of the self-influence term J depends on the angle and orientation of the corner of the material. The value of J is between 0 ($J \approx 0$ corresponds to a quite obtuse angle ($\approx 2\pi$)) and 1 ($J \approx 1$ corresponds to an acute angle ($\approx 0$) ) and generally differs from 1/2.

To sum up, by taking the limit $a\rightarrow 0$, Eq.  (6.11) can be rewritten in the following form:

$$\begin{aligned} u_x(Q_0)= & {} \int _{Q\in \Gamma ^*} \left( K^e_xS_{xxQ}\mathbb {G}_{x{(Q_0-Q) }} - K^b_y S_{yyyyQ}\mathbb {G}_{x{(Q_0-Q) }}\right) \mathrm {d}l \nonumber \\= & {} \underset{for \,u}{P.V.} \int _{Q\in \Gamma } \left( K^e_xS_{xxQ}\mathbb {G}_{x{(Q_0-Q) }} - K^b_y S_{yyyyQ}\mathbb {G}_{x{(Q_0-Q) }}\right) \mathrm {d}l+\frac{1}{2}u_x(Q_0) \end{aligned}$$

(6.14)

in which the notation $\underset{for \,u}{P.V.}$ indicates that in the integral, the terms involving u have to be integrated in the sense of the Cauchy principal value. Finally, for a smooth boundary, the integral equation in the x-direction reads:

$$\begin{aligned} \frac{1}{2}u_x(Q_0)= & {} {P.V.} \int _{Q\in \Gamma } u_{xQ} \big (K^e_x \mathbb {G}_{x,x} n_x - K^b_y \mathbb {G}_{ x,yyy} n_y\big )_{(Q_0-Q) } \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } \big ( K^e_x(u_{xQ})_{,x} n_x - K^b_y (u_{{xQ}){,yyy}} n_y\big )\mathbb {G}_{x{(Q_0-Q) } } \mathrm {d}l \nonumber \\&- \int _{Q\in \Gamma } (u_{xQ})_{,y} n_y \big (K^b_y \mathbb {G}_{ x,yy} \big )_{(Q_0-Q)} \mathrm {d}l - \int _{Q\in \Gamma } K^b_y (u_{xQ})_{,yy} n_y (\mathbb {G}_{x,y})_{(Q_0-Q) } \mathrm {d}l \end{aligned}$$

(6.15)

Obviously, a similar equation is satisfied by $u_y$ provided that the roles of x and y are reversed.

6.3.2 Integral representation and integral equation for rotation $u_{x,y}$

In order to establish the integral equation for the second kinematic descriptor, namely the rotation $u_{x,y}$, we must first give the integral representation for this field inside the body and at its boundary. To do this, we start from (6.9) and use a mathematical property which is established in the theory of distribution: to calculate a convolution product, it is sufficient to derive one of the two convoluted functions. In our case, the choice to derive one of the two convoluted function is dictated by the fact that (i) the equation should only involve the same physical (natural or essential) boundary conditions, (ii) the level of singularity cannot be increased to ensure the convergence of the integrals. These considerations lead to express $u_{x, y}$ as follows:

$$\begin{aligned} \forall P\,\in \Omega \qquad u_{x, y}(P)=&{} \int _{Q\in \Gamma } \bigg (- ( u_{x}n_x)_{{,y}{(Q)}} (K^e_x \mathbb {G}_{x,x})_{(P-Q) } + ( u_{x}n_y)_{{,y}{(Q)}} (K^b_y \mathbb {G}_{ x,yyy}) _{(P-Q)}\bigg ) \mathrm {d}l \nonumber \\ {}&+ \int _{Q\in \Gamma } \big ( K^e_{xu{x,x}} n_x - K^b_y u_{x,yyy} n_y\big )_{(Q)} \mathbb {G}_{{x,y}{(P-Q) }} \mathrm {d}l \nonumber \\ {}&- \int _{Q\in \Gamma } ( u_{x,y}n_y)_{{,y}{(Q)}} \big (K^b_y \mathbb {G}_{ x,yy} \big )_{(P-Q)} \mathrm {d}l \nonumber \\ {}&+ int_{Q\in \Gamma } K^b_y (u_{x,yy} n_y)_{(Q)} (\mathbb {G}_{x,yy}) _{(P-Q) } \mathrm {d}l\end{aligned}$$

(6.16)

This expression is issued from the y-derivation of (6.9), where we have derived the functions $u_xn_x$ and $u_xn_y$ in the first integral, and the function $\mathbb {G}_x$ in the second integral, $u_{x,y}n_y$ in the third integral, and $\mathbb {G}_{x,y}$ in the last one. After developing the terms $(u_xn_x)_{,y}$, $(u_xn_y)_{,y}$ and $(u_{x,y}n_y)_{,y}$ and simplifying, we get:

$$\begin{aligned} u_{x, y}(P)= & {} \int _{Q\in \Gamma } \bigg (- ( u_{x,y}n_x)_{(Q)} (K^e_x \mathbb {G}_{x,x})_{(P-Q) } + ( u_{x,y}n_y) _{(Q)} (K^b_y \mathbb {G}_{ x,yyy}) _{(P-Q)}\bigg ) \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } \big ( K^e_xu_{x,x} n_x - K^b_y u_{x,yyy} n_y\big )_{(Q)} \mathbb {G}_{{x,y}{(P-Q) }} \mathrm {d}l \nonumber \\&+ \int _{Q\in \Gamma } \bigg (- ( u_{x}n_{x{,y}})_{(Q)} (K^e_x \mathbb {G}_{x,x})_{(P-Q) } + ( u_{x}n_{y{,y}}) _{(Q)} (K^b_y \mathbb {G}_{ x,yyy}) _{(P-Q)}\bigg ) \mathrm {d}l \nonumber \\&- \int _{Q\in \Gamma } ( u_{x,y}n_{y{,y}})_{(Q)} \big (K^b_y \mathbb {G}_{ x,yy} \big )_{(P-Q)} \mathrm {d}l \end{aligned}$$

(6.17)

The rotation $u_{x,y}$ results on one hand from the boundary terms that are radiated as follows:

• the rotation $u_{x{,y}}$ is radiated by the two terms, $K^e_x \mathbb {G}_{x,x}$ for $u_{x{,y}} n_x$ and $- K^b_y \mathbb {G}_{x,yyy}$ for $u_{x{,y}} n_y$,

• the force $K^e_x u_{x,x} n_x - K^b_y u_{x{,yyy}} n_y$ is radiated by $\mathbb {G}_{x,y}$,

and on the other hand by terms due to the curvature of the border which appears through $n_{x{,y}}$ and $n_{y{,y}}$:

• $u_{x}n_{x{,y}}$ et $u_{x}n_{y{,y}}$ are, respectively, radiated by $K^e_x \mathbb {G}_{x,x}$ and $K^b_y \mathbb {G}_{ x,yyy}$

• $u_{x,y}n_{y{,y}}$ is radiated by $K^b_y \mathbb {G}_{ x,yy}$.

Considering the $\mathbf {e}_y$-balance and $u_{y,x}$, one gets an equation similar to (6.16–6.17) by inverting the roles of x and y.

The representation (6.16–6.17) applies in the whole space and then also on $\Gamma$. Replacing in (6.16) P by $Q_0\,\in \Gamma$ provides the integral equation satisfied by $u_{x,y}$.

Since the radiation functions are the same as for the displacement integral Eq. (6.15), the discussion on singularities can be conducted similarly.

Thus, the first integral must be taken as the Cauchy principal value with a self-influence term of -1/2 for a smooth surface. Furthermore, as examined above, $\mathbb {G}_{x,y}$ and $\mathbb {G}_{ x,yy}$ are regular enough to be integrable. It only remains to examine the integral where the curvature and the displacement occurs, i.e.:

$$\begin{aligned} \mathcal { J} = \int _{Q\in \Gamma } \bigg (- ( u_{x}n_{x{,y}})_{(Q)} (K^e_x \mathbb {G}_{x,x})_{(Q_0-Q) } + ( u_{x}n_{y{,y}}) _{(Q)} (K^b_y \mathbb {G}_{ x,yyy})_{(Q_0-Q)}\bigg ) \mathrm {d}l \end{aligned}$$

Let us consider again the integration on the perturbed geometry $\Gamma ^*$. We note that on both sides $\sigma _0$ and $\sigma _{\pi /2}$ the normal is constant, i.e., $n_{x{,y}}=n_{y{,y}}= 0$ and that the set of points where the normal is undefined is of null measure. The integral on $\sigma _0 \cup \sigma _{\pi /2}$ is therefore identically null. Taking the limit $\Gamma ^*\rightarrow \Gamma$, this ensures the convergence of $\mathcal { J}$. Therefore, for a smooth surface the integral equation associated with rotation is given by:

$$\begin{aligned} \forall Q_0\,\in \Gamma \qquad \frac{1}{2}u_{x, y}(Q_0)=&{} P.V. \int _{Q\in \Gamma } \bigg (- ( u_{x,y}n_x)_{(Q)} (K^e_x \mathbb {G}_{x,x})_{(Q_0-Q) } + ( u_{x,y}n_y) _{(Q)} (K^b_y \mathbb {G}_{ x,yyy}) _{(Q_0-Q)}\bigg ) \mathrm {d}l \nonumber \\ {}&+ \int _{Q\in \Gamma } \big ( K^e_xu_{x,x} n_x - K^b_y u_{x,yyy} n_y\big )_{(Q)} \mathbb {G}_{{x,y}{(Q_0-Q) }} \mathrm {d}l \nonumber \\ {}&+ \int _{Q\in \Gamma } \bigg (- ( u_{x}n_{x{,y}})_{(Q)} (K^e_x \mathbb {G}_{x,x})_{(Q_0-Q) } + ( u_{x}n_{y{,y}}) _{(Q)} (K^b_y \mathbb {G}_{ x,yyy}) _{(Q_0-Q)}\bigg ) \mathrm {d}l \nonumber \\ {}&- \int _{Q\in \Gamma } ( u_{x,y}n_{y{,y}})_{(Q)} \big (K^b_y \mathbb {G}_{ x,yy} \big )_{(Q_0-Q)} \mathrm {d}l\end{aligned}$$

(6.18)

Again, a similar equation is satisfied by $u_{x,y}$ provided that the roles of x and y are reversed.

6.4 Solving boundary value problems

From the set of $\mathbf {e}_x$-equations (6.9), (6.16), (6.15), (6.18), and their equivalent in the y-direction, a numerical procedure for solving boundary value problems can be developed by following and adjusting the classical techniques used for problems governed by second-order differential equations [9]. As demonstrated in [13], in order to get a well-posed equilibrium problem for pantographic 2D continua, the prescribed boundary conditions may be of different nature over different regions of the boundary, but when a kinematic (essential boundary) condition (concerning either the displacement or the rotation is imposed, the dual static variable (giving the natural boundary condition) must be considered as unknown and vice versa. Specifically, of the four (eight if one considers the two directions) types of boundary conditions, two must be imposed and the other two are to be determined by imposing equilibrium conditions. For instance, if on some part of the boundary the x-component of the displacement $u_x$ is imposed, then the x-component of the force $\left( K_x^e\partial _xu_x n_x -K_y^b\partial ^3_{yyy}u_y n_y\right)$, cannot be prescribed, or if the moment $K_y^b\partial ^2_{yy}u_xn_y$ is imposed the rotation $\partial _{y}u_x$ is undetermined, etc..

Let us discretize the boundary $\Gamma$ into N boundary elements. In this way, we can transform any boundary integral appearing in the integral Eqs. (6.15), (6.18), into a discrete sum of N terms. Each of these terms corresponds to a given boundary element and is composed of a radiation factor (calculable since Green’s functions are known) and a boundary condition (known or unknown). The two discretized integral Eqs. (6.15), (6.18), expressed for each of the N boundary elements provide 2N discrete equations. Each of these equations implies the radiation factors and the 4N boundary conditions, 2N being known and 2N being unknown. We therefore have a system of 2N linear equations for 2N unknowns. The resolution of this system leads to the determination of the 2N boundary conditions which were initially undetermined. Considering the two directions yields a set of 4N linear equations for 4N unknowns.

Once this step is completed, all the terms are known on the boundary. Then we can transfer the 4N boundary conditions (8N for the two directions) into the integral representations (6.9), (6.16). This allows us to calculate the displacement and rotation field at any point of the domain. Finally, from these kinematic fields, we can reconstruct the field of forces and moment by exploiting the constitutive laws.

A description in more details of this method and its numerical implementation are behind the scope of the present paper and will be developed in a forthcoming work. We explicit remark here that the set of integral equations, found in the previous section for determining the unknown boundary fields in terms of the assigned boundary conditions, form a system of first- and second-type Fredholm equations, for which an alternative theorem is envisageable.

7 Conclusion

In order to solve the problem of the synthesis of metamaterials ‘capable to undergo planar large deformations in elastic regime’, the pantographic microarchitecture has been proposed and extensively studied, see the reviews [23, 24], as exhaustively discussed in the introduction. Once it has been theoretically accepted the use, in the micro-structure synthesis, of perfect pivots, the micro-scale relative rotations permitted to the micro-beams constituting synthesized micro-architecture allowed for the demanded macro-behaviour. The possibility of using 3D printing technology did allow for the subsequent experimental validation of such synthesis concept.

By tailoring the asymptotic homogenization of discrete beam lattices [10, 20] to the pantographic context, it has been possible to provide, in the framework of small in-plane deformations and linear elasticity a consistent macro-description of the pantographic sheet [7]. The latter explicitly discloses the second-gradient nature of such media and clearly relates the effective parameters to the micro-structure. Such a micro-macro-identification process enables a straightforward physical interpretation of the analytical Euler-Lagrange equilibrium conditions, together with the corresponding essential and natural boundary conditions. Indeed, this approach allows for the identification of contact couples and contact forces in the pantographic continua, as originated by the contact forces and couples acting in the beams constituting the subjacent pantographic micro-structure. Furthermore, it was demonstrated by a classical argument of integration by parts, that this description is consistent with the minimum energy principle. In this way, this physical interpretation supplies an important check of obtained mathematical results postulating the minimum energy principle. In addition, it gives a useful hint for the further steps in the mathematical study of pantographic continua which is presented in this paper. Well-posedness of the linearized deformation problem has been proven, for pantographic continua that are the object of the present work [13].

In fact, considering the deformation field produced by forces and couples concentrated in a point of an infinite 2D pantographic planar continuum, in this paper we show how it is possible to get the Green’s functions for the considered equilibrium problem. Using the introduced Green’s functions for solving the equilibrium boundary problem, one can reduce its solution to the solution of a system of two Fredholm equations into two unknown functions defined on the boundary of the considered continuum. In other words, in this paper it is formulated for 2D pantographic continua the method of boundary elements for the solution of equilibrium problems. Finally, by using four Green’s functions concentrated in the corner of a rectangular specimen undergoing a bias extensional test, we show how an approximated solution, in analytical form, can be found that is very close to those previously computer by means of numerical methods.

Beyond the particular case represented by pantographic media extensively studied, this result provides a first example of an analytical Green’s function for anisotropic second-gradient media not reducible to Cauchy media. It also paves the way for formulations in integral representation of generalized continua. In particular, it shows that the use of distributions is particularly convenient and adapts without major difficulty to the development of integral representation associated with differential operators of order higher than two, such as those of generalized continuous media. This type of representation presents a double interest for the calculation of this type of material: on the one hand, the reduction in dimension of the numerical problem, on the other hand the exhaustive exploitation of the analytical formulation of Green’s functions which encapsulates all the physical complexity of the micro-structure and allows to better tackle poorly conditioned problems.

The future perspectives opened by the presented results seem rather interesting.

• From the mathematical and numerical point of view, it seems interesting to consider the study of the first and second kind Fredholm equations that we have introduced to solve the generic deformation boundary problem for 2D pantographic continua. Fixed point theorems and the theorem of alternative seem applicable; however, a careful analysis of the new kernels may deserve some attention.

• It is very interesting to explore the possibility to extend the presented results to the problems of linearized deformation of bi-pantographic 2D planar continua see [3], and to complete second-gradient 2D continua. These problems are challenging as natural boundary conditions include not only forces and couples, but also double forces. Therefore, another class of Green’s functions seem needed.

• The study of out-of-plane displacements of 2D pantographic continua will also be of interest, see e.g. [17].

• The method used in the present paper for studying linear equilibrium solutions can allow for the application of Euler standard methods for determining the loss of stability of pantographic sheets and consequent post-buckling behaviour, that may deserve many surprises (see [1, 14])

• The Green’s function method and the associated boundary element method may be very useful also in studying multi-physics pantographic sheets as those studied in [15] and help in unveiling their peculiar behaviour.

  Probably, once having linearized the corresponding equilibrium equations, some generalization of the Green’s functions presented here is possible.

To conclude, we are aware that in a generalized continua, the determination of the analytical expression of functions can be very complex (if not impossible). A possible alternative would then be to look for a numerical approximation (framed by theoretical considerations) which could be used as a data library and exploited to carry out calculations through boundary element method.