1 Introduction

The analysis of heat transport, both in laminar and in turbulent regimes, in channels and devices using superfluid helium has much practical interest in cryogenics [1], and it is challenging from the point of view of transport theory and non-equilibrium thermodynamics [2]. Indeed, heat transport in helium has particularly outstanding aspects that much differ from usual transport described by Fourier’s law. Not only the superfluid material properties are relevant, but also the geometrical characteristics of the devices. Indeed, the effective thermal conductivity of superfluid helium strongly depends, for instance, on the size and on the form of channels, instead of being a purely material quantity.

The simplest situation refers to counterflow heat transfer (i.e., heat transfer without net mass transfer) in laminar regime along a cylindrical channel, or between two parallel plates. A natural extension of the former situation is to consider heat transport through a layer with a number N of parallel pores of radius R per unit area of the layer, in the laminar regime. It may be obtained in an easy way, starting from Landau–Lifshitz expression for counterflow heat transfer in a cylindrical channel [2,3,4]. Such expression is:

$$\begin{aligned} {\dot{Q}} = \frac{N \pi R^4 S^2 {\overline{T}}}{8 \eta } \left( \frac{T_1 - T_2}{L}\right) , \end{aligned}$$
(1)

with S the entropy density of the normal component, \(\eta \) the viscosity of the normal component, \(T_1\) and \(T_2\) the temperatures of the superfluid at both sides of the layer, \({\overline{T}}\) the average temperature inside the channel, L the thickness of the layer (which corresponds to the length of the channels), and \({\dot{Q}}\) the heat flow through the layer per unit area of the layer and unit time. Note that, in contrast to Fourier’s law, in which \({\dot{Q}}\) should be proportional to \(N \pi R^2\), the total transversal area of the several pores, it depends on \(N \pi R^4\). This is a characteristic feature of the so-called hydrodynamic heat transfer.

Fig. 1
figure 1

Heat flux flowing through a layer with N parallel pores of radius R, with length L. The dependence of the total heat flow per unit area \({\dot{Q}}\) on \(\Delta T \equiv T_1 - T_2\), L and R is considerably different for \(R \gg l\) and \(R \ll l\), being l phonon mean free path, and for \(L \gg L_\mathrm{entrance}\) and \(L \ll L_\mathrm{entrance}\), \(L_\mathrm{entrance}\) being entrance length

Full size image

In the present paper, we aim to generalize expression (1) to the case of thin layers and of narrow pores and to incorporate the effects of possible quantized vortices at the exit of the pores. Indeed, expression (1) is valid for sufficiently long channels allowing a fully developed Poiseuille parabolic profile along most of their length, and with non-slip condition at the walls, i.e., assuming that the relative velocity of the normal component on the wall is zero. These hypotheses are not valid when the diameter of the cylinders becomes comparable to the phonon mean free path, or when the cylinder length is comparable to the so-called entrance length, which is the length necessary to achieve the parabolic velocity profile starting from a flat velocity profile at the entrance of a cylindrical tube. Thus, we consider how both restrictions of (1) could be overcome (Fig. 1). Both topics are of interest but they have not yet received sufficient attention up to now, though they become especially relevant for the cryogenics of small systems. In Sect. 2 we deal with thin layers (relevant effects of the entrance length) in the corresponding short channels, and in Sect. 3, we study the appearance of a layer of quantized vortices past the wall and their contribution to the total thermal resistance. In Sect. 4, we deal with narrow pores (transition to slip flow).

2 Short pores: influence of the entrance length

Heat transport in superfluid \(^4\)He follows very different laws than heat transport in other materials, both in the laminar and in the turbulent regimes [2]. Instead of being given by Fourier’s law \(\mathbf{q} = - \lambda \nabla T\), with \(\lambda \) the thermal conductivity, it is described, in the steady state, by the equation [1,2,3, 5, 6]:

$$\begin{aligned} \frac{ \eta }{{\overline{T}} S^2} \nabla ^2 \mathbf{q} =\nabla T. \end{aligned}$$
(2)

Here \(\eta \) is the viscosity of the normal component, \({\overline{T}}\) the average temperature of superfluid helium, and S the entropy density per unit volume.

Remembering the equation of a viscous fluid in steady state along a straight channel, namely:

$$\begin{aligned} \eta \nabla ^2 \mathbf{v} = \nabla p, \end{aligned}$$
(3)

with \(\mathbf{v}\) the velocity and p the pressure, Eq. (2) is analogous to Eq. (3) for a steady rectilinear viscous flow along a channel, with \(\nabla T\) instead of the pressure gradient \(\nabla P\), \(\mathbf{q} (r)\) instead of the barycentric velocity \(\mathbf{v}(r)\), and \(\eta / T S^2\) instead of \(\eta / \rho \). Because of this analogy, this regime of heat transfer is known as hydrodynamic heat transport [7,8,9,10,11,12].

Equation (2) may be solved for the flow of \(\mathbf{q}\) along a cylindrical channel of radius R and length L, leading for q(r) to the parabolic profile:

$$\begin{aligned} \mathbf{q}(r) = - \frac{{\overline{T}} S^2}{4 \eta } \left[ R^2 - r^2 \right] \nabla T, \end{aligned}$$
(4)

where it has been assumed the non-slip condition on the wall, implying \(\mathbf{v} = 0\) at \(r=R\). Integration of (4) over a transversal cross section leads to:

$$\begin{aligned} {\dot{Q}}_1 = \frac{\pi R^4 S^2 {\overline{T}}}{8 \eta } \left( \frac{T_1 - T_2}{L}\right) , \end{aligned}$$
(5)

where \({\dot{Q}}_1\) is the total heat flow along the cylinder. If one considers a layer with N cylindrical parallel pores per unit area (see Fig. 1), the total heat flow per unit time and area \({\dot{Q}} = N {\dot{Q}}_1\) will be the same of expression (1).

Equation (2), and therefore solution (4) with parabolic profile, is valid when the flow is sufficiently developed, i.e., for long pores, but in the entrance of the pore \(\mathbf{q}\) as a function of r (the radial position) usually has a flat profile. The region from the flat profile to the well-developed parabolic profile q(r) (4) is known as entrance region [3, 13]. In such region \(\mathbf{q}\) depends on r and x, i.e., \(\mathbf{q}(r,x)\), and the rearrangement of the q(r) profile implies that there is a radial flow \(q_r\) besides the longitudinal flow \(q_x\). In this case, terms of the form \(\mathbf{q} \cdot \nabla \mathbf{q}\) (or more complicated terms [14, 15]) would also appear on the left-hand side of (2), analogous to the convective terms appearing in the Navier–Stokes equation (6) presented below. Such terms vanish when \(\mathbf{q}\) has only the longitudinal component and depends only on the radial coordinate r, but it does not vanish when \(\mathbf{q}\) has also a radial component. Thus, in the entrance region, nonlinear effects become relevant and require a more complicated analysis than (2).

There are not many studies of the effects of entrance length [16,17,18] in heat transport in helium II. Recently [18], this topic has been dealt by comparing the entrance length for normal component and for superfluid component. It has been found that at the hot end of the channel the entrance length for the normal fluid behaves in a classical way and increases linearly with the Reynolds number. However, at the cool end, the entrance length (or exit length) for the superfluid is one magnitude longer than for the normal component. This has been attributed to the large-scale superfluid vortices produced in the cool bath and which partially reenter in the pipe along the layers. Thus, there is much interesting physics in this phenomenon. In this section we consider a pure laminar flow without vortices at the end, so that the sophisticated effects in [18] are not expected to influence the result. Later, we will consider the appearance of vortices.

In viscous fluids, in such region, Eq. (3) is no longer satisfactory, but the full Navier–Stokes equation must be used, namely:

$$\begin{aligned} \frac{\partial \mathbf{v}}{\partial t} + \mathbf{v} \cdot \nabla \mathbf{v} = - \frac{1}{\rho } \nabla \mathbf{p} + \frac{\eta }{\rho } \nabla ^2 \mathbf{v}, \end{aligned}$$
(6)

in the entrance region, the nonlinear term \(\mathbf{v} \cdot \nabla \mathbf{v} \) plays a very relevant role. The analytical solution of (6) is very challenging [13].

The characteristic entrance length for viscous fluids in a cylindrical channel of diameter \(d= 2R\) is of the order of [3, 13]:

$$\begin{aligned} L_\mathrm{entrance} \approx d \mathrm{Rey}, \end{aligned}$$
(7)

with \(\mathrm{Rey}\) the Reynolds number given by:

$$\begin{aligned} \mathrm{Rey}= \frac{ \rho {\mathcal {U}}}{\eta } d, \end{aligned}$$
(8)

with \({\mathcal {U}}\) the average barycentric speed of the fluid in the channel. For channels of length comparable to \(L_\mathrm{entrance}\), the Poiseuille law:

$$\begin{aligned} {\dot{V}}= \pi R^2 {\mathcal {U}} = \frac{\pi R^4}{8 \eta } \frac{(p_1 - p_2)}{L}, \end{aligned}$$
(9)

where \({\dot{V}}\) is the volume rate along the cylinder, valid for channels much longer than \(L_\mathrm{entrance}\), must be generalized to account for entrance length effects.

Though the accurate mathematical solution of (6) is very cumbersome [13], there are several approximate expressions. In [19], Shah and London made a simplified analysis of the factors influencing the entrance region in a viscous fluid and they found that \(\Delta p\), the difference of pressure between the ends of the channel, in a tube of length L may be approximated by the following expression:

$$\begin{aligned} \Delta p = \frac{\rho {\mathcal {U}}^2}{2} \left[ A_1 X^{\frac{1}{2}} + \frac{A_2 + 64 X - A_1 X^{\frac{1}{2}}}{1+A_3 X^{-2}} \right] , \end{aligned}$$
(10)

with coefficients \(A_i\) as in Table 1, and X a dimensionless parameter, given by:

$$\begin{aligned} X = \frac{L}{d^2 {\mathcal {U}}} \frac{\eta }{\rho }\equiv \frac{L}{d} \frac{1}{\mathrm{Rey}}. \end{aligned}$$
(11)
Table 1 Values of coefficients \(A_i\) in expression (10) as obtained by Shah and London in [19]
Full size table

High values of X correspond to long channels. One may consider \(L_\mathrm{entrance}\) as the L for which \(X =1\) [in this case we recover expression (7)]. Recall that for \(\mathrm{Rey} > 1000\) the flow becomes turbulent; thus, high values of X (small \(\mathrm{Rey}\)) will usually correspond to laminar flows. Here we consider laminar flows.

For \(X \ll 1\) (short channels) the right-hand side of (10) reduces to its first term \(A_1 X^{\frac{1}{2}}\), which fits well the experimental results (thus, it includes both entrance effects as exit effects). For \(X \gg 1\), (10) yields \(A_2 + 64 X\) for X high. The latter term corresponds to the well-developed Poiseuille flow in long channels, plus the contribution \(A_2\), that approximates better the observed results. Thus, (10) provides an interpolation between \(A_1 X^{\frac{1}{2}}\) and \(A_2 + 64 X\), of the form \(A_1 X^{\frac{1}{2}} + \frac{A_2 + 64 X -A_1 X^{\frac{1}{2}}}{1+A X^{-n}}\), with A obtained by Bender in [20] and n by Shah in [21].

In [22, 23] it was proposed to use (10) as the basis to generalize (1) to short channels, using the Gibbs–Duhem relation at constant chemical potential, namely \(\Delta p = S \Delta T\), and the relation \( S {\overline{T}} \pi R^2 {\mathcal {U}}_1 = {\dot{Q}}/N\) (where \({\mathcal {U}}_1\) is the average velocity in one channel and \({\dot{Q}}/N\) the heat transmitted per unit time along one channel) [22]. Making these changes, expression (10) may be adapted to heat flux as:

$$\begin{aligned} {\dot{Q}} = \frac{N \pi R^4 S^2 {\overline{T}}}{8 \eta } \left[ B_1 X^{-\frac{1}{2}} + \frac{B_2 X^{-1} + 1 - B_1 X^{-\frac{1}{2}}}{1 + A_3 X^{-2}} \right] ^{-1} \frac{T_1 - T_2}{L}, \end{aligned}$$
(12)

where \(B_i = A_i/ 64 \) and

$$\begin{aligned} X\equiv \frac{\eta \pi S {\overline{T}} L }{4 \rho ({\dot{Q}}/N)}. \end{aligned}$$
(13)

In strict terms, to be able of using (12)—the analogous of Eq. (10) for the superfluid case—the evolution equation for the heat flux should be the analogous to the Navier–Stokes equation (6). Then in Eq. (2) we have to incorporate convective terms of the form \(\mathbf{q} \cdot \nabla \mathbf{q}\), that in the two-fluid model for helium II are related to terms of the form \(\mathbf{v}_\mathrm{n} \cdot \nabla \mathbf{v}_\mathrm{s}\) and \(\mathbf{v}_\mathrm{s} \cdot \nabla \mathbf{v}_\mathrm{n}\), and that take into account the interaction between normal and superfluid component (see [14, 24]). Complicated nonlinear terms could also appear [14, 15], in which case the analysis of the entrance region would be more complicated than that using the analogy with (10).

In summary, we propose using (12) as a suitable generalization of (1), but one must keep in mind that this is conditioned to the validity of the equation chosen for the heat flux and, if a different equation should be used for \(\mathbf{q}\), the numerical coefficients \(B_1\) and \(A_3\) of the terms in \(X^{-\frac{1}{2}}\) and in \(X^{-2}\) should probably take other values. Anyway, more relevant than the concrete values of the coefficients in (13) is the scaling of the heat flux with L. Accurate experiments on superfluid flow through thin porous layers with known values of the pore radii would be very useful to compare experimental results with those following from different nonlinear models. In this sense, our analysis corresponds to the simple model analogous to nonlinear Navier–Stokes equation.

According to (12), for \(X=1\), \({\dot{Q}}= 0.98 \, {\dot{Q}}_\mathrm{Pois.}\) and therefore the Poiseuille expression (5) is considerably accurate. However, for shorter channels (5) becomes less accurate: for \(X=0.5\), one has \({\dot{Q}}= 0.96 \, {\dot{Q}}_\mathrm{Pois.}\), and for \(X=0.1\), \({\dot{Q}}\) becomes \({\dot{Q}}= 0.85 \, {\dot{Q}}_\mathrm{Pois.}\), which indicates errors of Poiseuille expression (5) with respect to the observed flow of the order of \(4\%\) and \(15\%\) respectively, and the difference is remarkable.

For \(X \gg 1\) (L long or \({\dot{Q}}\) small) expression (12) reduces to:

$$\begin{aligned} {\dot{Q}} = \frac{N \pi R^4 S^2 {\overline{T}}}{8 \eta } \left[ 1 + B_2 X^{-1} \right] ^{-1} \frac{T_1 - T_2}{L}, \end{aligned}$$
(14)

which yields (1) for \(X \rightarrow \infty \), and gives first-order corrections to (1) in \(X^{-1}\) for long but finite channels.

In the opposite limit of \(X \ll 1\) (L short or \({\dot{Q}}\) high), expression (12) reduces to:

$$\begin{aligned} {\dot{Q}} = \frac{N \pi R^4 S^2 {\overline{T}}}{8 B_1 \eta } X^{\frac{1}{2}}\frac{T_1 - T_2}{L}, \end{aligned}$$
(15)

namely, using (13) for X,

$$\begin{aligned} {\dot{Q}}^{\frac{3}{2}} = \frac{N^{\frac{3}{2}} \pi R^4 S^2 {\overline{T}}}{8 B_1 \eta } \left( \frac{\eta \pi S {\overline{T}} L}{4 \rho } \right) ^{\frac{1}{2}}\frac{T_1 - T_2}{L}. \end{aligned}$$
(16)

It is indeed seen from (15) that for short L or high \({\dot{Q}}\), the relation between \(\Delta T=T_1 - T_2\) and \({\dot{Q}}\) is no longer linear, but \({\dot{Q}}\) becomes

$$\begin{aligned} {\dot{Q}} \propto L^{\frac{1}{3}} \left( \frac{\Delta T}{L}\right) ^{\frac{2}{3}} = L^{-\frac{1}{3}} \Delta T^{\frac{2}{3}}. \end{aligned}$$
(17)

(see Fig. 2).

This dependence of \({\dot{Q}}\) on L and \(\Delta T\) is different from that of the Gorter–Mellink nonlinear law in superfluid turbulence, in which [1, 2, 16]

$$\begin{aligned} {\dot{Q}} \propto L^{-\frac{1}{3}} \Delta T^{\frac{1}{3}}. \end{aligned}$$
(18)

Instead the dependence of \({\dot{Q}}\) as a function of 1/L at constant \(\Delta T\) is the same in (16) and (17). Of course, the phenomenon analyzed here is very different than the turbulent regime considered in (18), and it is not expected that the dependence of \({\dot{Q}}\) with \( \Delta T / L \) is the same in both cases. It is interesting to note that a marked separation from the linear dependence of \({\dot{Q}}\) with \(\Delta T / L \) is found in short channels despite that the helium flow is laminar.

Fig. 2
figure 2

In the figure is plotted \(\frac{{\dot{Q}}}{N \pi R^2}\) versus 1/L for constant \(\Delta T\). In the region of long L (small 1/L) the black line corresponds to Eq. (1); in this case the channel is sufficiently long to have a fully developed parabolic profile almost everywhere and \(\frac{{\dot{Q}}}{N \pi R^2}\) is linear in 1/L. Instead, the blue line describes Eq. (16) for short channel; the dependence on 1/L is no longer linear, but it goes as \((1/L)^{1/3}\) according to (17). In this figure we have considered \(R=0.05\) cm as in the experiments of [25]. The dotted line indicatively shows the cross-over region between both behaviors

Full size image

The effective thermal resistance per unit area of the layer, is defined as:

$$\begin{aligned} \mathrm{Th.Res.} \equiv \frac{\Delta T}{{\dot{Q}}}, \end{aligned}$$
(19)

and for short pores, according to Eq. (16), is:

$$\begin{aligned} \mathrm{Th.Res.}_\mathrm{short-ch.} \equiv \frac{\Delta T}{{\dot{Q}}}= \frac{16 B_1 (\rho \eta L {\dot{Q}})^{\frac{1}{2}} }{(N \pi {\overline{T}})^{\frac{3}{2}} R^4 S^{\frac{5}{2}}}. \end{aligned}$$
(20)

We may estimate the order of magnitude of \(L_\mathrm{entrance}\) for hydrodynamic heat transfer in superfluid \(^4\)He by setting \(X \approx 1\) in (13), and therefore:

$$\begin{aligned} L_\mathrm{entrance} \approx \frac{4 \rho }{ \eta \pi S {\overline{T}}} \frac{{\dot{Q}}}{N}. \end{aligned}$$
(21)

So that, for \(T=1.7\) K, after using the values of \(\rho \) and S [26] at this temperature, we have:

$$\begin{aligned} L_\mathrm{entrance} \text {(cgs units)} \approx 0.014 \,{\dot{Q}}/N \text {(cgs unit)}. \end{aligned}$$
(22)

This means that for \({\dot{Q}}/N = 10^2 \text {erg/s}\) or \({\dot{Q}}/N = 10^3 \text {erg/s}\), the entrance length will be of the order of 1.4 cm or 14 cm respectively. In Table 2 are reported some values of L, X (for \(\dot{Q_1}= 10^2\) erg/ (\(\hbox {cm}^2\) s) and \(L_\mathrm{entrance} = 1.4\) cm), the relative error of Poiseuille flow \(\epsilon _Q = {\dot{Q}} - {\dot{Q}}_P \) [where \({\dot{Q}}_P\) is the Poiseuille flow calculated by (1)], and the relative error of the thermal resistance, \(\epsilon _{ThR}\) due to the error of the Poiseuille flow, i.e., \(\mathrm{Th.Res.}_\mathrm{short-por}= \frac{\Delta T}{{\dot{Q}}} \frac{1}{1 + \epsilon _Q}\).

Table 2 For \(\dot{Q_1}= 10^2\) erg/ (\(\hbox {cm}^2\) s) and \(L_\mathrm{entrance} = 1.4\) cm in the table are evaluated the values of X, the error of Poiseuille flow \(\epsilon _Q\), and the error on the thermal resistance, \(\epsilon _{ThR}\), due to the error in the Poiseuille flow
Full size table

If we want to make explicit the role of the radius R of the pores in the value of the entrance length, we may write (22) in terms of \(\mathbf{q}_\mathrm{pores} \equiv {\dot{Q}} (N \pi R^2)^{-1}\), as:

$$\begin{aligned} L_\mathrm{entrance} \text {(cgs units)} = 0.043 \, \mathbf{q}_\mathrm{pores} R^2 \text {(cgs units)} \end{aligned}$$
(23)

It is seen that for a given value of \(\mathbf{q}_\mathrm{pores}\) (the average heat flux in a single pore) \(L_\mathrm{entrance}\) goes as \(R^2\).

3 Influence of vortices beyond the layer

In Sects. 4 and 2, we have assumed that neither in the channels nor outside the channels there is turbulence. Quantum turbulence arises when the quantum Reynolds number:

$$\begin{aligned} \mathrm{Rey}_{q} \equiv \frac{\mathbf{q}}{{\overline{T}} S} \frac{d}{\kappa }, \end{aligned}$$
(24)

with d the diameter of the pores, and \(\kappa \) the quantum of circulation given by \(\kappa = h/m\), being h the Planck’s constant and m the mass of helium atom, is higher than some critical value, of the order of \(10^{2}\) (in fact, such a value depends on temperature; in terms of \(\mathbf{V}_\mathrm{ns} d / \kappa \), the critical value is 127 at \(T=1.5\) K, 112 at \(T=1.6\) K and 96 at \(T=1.7\) K [25]). For a discussion on these critical Reynolds numbers, see [18], where is pointed out that for short channels there is a relatively wide scatter of values of the critical Reynolds numbers, in contrast to long channels, probably because of entrance effects.

Note that \(\mathbf{q}/ {\overline{T}} S\) has dimensions of velocity and \(\kappa \) has the dimension of (length)\(^2\)/time, the same as the kinematical viscosity \(\nu = \eta /\rho \). Thus, (24) is the thermal quantum analog of the classical hydrodynamical Reynolds number. The physical basis of (24) is that the velocity circulation in a quantum fluid is quantized, and it must be an integer multiple of \(\kappa \). (This is a consequence of the quantum macroscopic behavior of the fluid.) Since the minimum value of the circulation inside the channel is of the order of \((\mathbf{q}/T S)R\), this means that \((\mathbf{q}/T S) R\) should be higher than \(\kappa \) in order that a quantized vortex may appear.

Fig. 3
figure 3

In the left \(\mathrm{Rey}_{q} < \mathrm{Rey}_\mathrm{crit}\), in the middle \(\mathrm{Rey}_{q} > \mathrm{Rey}_\mathrm{crit}\) and in the right \(\mathrm{Rey}_{q} \gg \mathrm{Rey}_\mathrm{crit}\). The vector is the heat flux \(\mathbf{q}\), in a channel; the separation between neighboring channels is \(L'\)

Full size image

In this sketch, we have assumed that the vortices are out of the channel and do not influence the flow in the channel. However, for sufficiently wide channels, the vortex flow is expected to have deeper influence on the flow near the channel outlet. Such effects have been pointed out recently in [18] and we aim to consider them in future works.

3.1 Formation of vortices beyond the layer

If the radius R is small, the critical value of \(\mathbf{q}\) according to (8) will be high inside the channel. However, turbulence could arise at the exit of the channels (Fig. 3) if:

$$\begin{aligned} \mathrm{Rey}_{q} \equiv \frac{\mathbf{q}}{{\overline{T}} S} \frac{L'}{\kappa }, \end{aligned}$$
(25)

with \(L'\) the average separation between neighboring channels, is higher than the critical value. Note that \(L'\) may be expressed in terms of N (the number of channels per unit area) as \(L' = (1/N)^{\frac{1}{2}}\) (thus if \(N= 100\) channels/\(\hbox {cm}^2\), \(L' = 0.1\) cm, for instance). Since \(L'\) may be much higher than R, it could be that vortices may form at the exit of the channel.

The value of the heat flux \(\mathbf{q}\) in the channel and just at the exit of the channel is \(\mathbf{q}_{ch}= \frac{{\dot{Q}}}{N \pi R^2}\). In fact, in confined geometries (small orifices), superfluid hydrodynamic effects may be observed which are the analogous of the well-known Josephson effects in superconductors, related to the nucleation of a small number of quantized vortices and manifested as discrete quantized dissipation events, being multiplies of \(\kappa J_\mathrm{c}\), with \(J_\mathrm{c}\) the critical mass flow rate (something similar could be observed for the critical heat flow rate in the case of counterflow) [27]. In the case of heat flux, the elementary energy related to the vortices would be of the order of \(\kappa ^{-1} q_\mathrm{c}\).

When separating from the exit of the pores, the heat flux will become distributed in a wider area of the order of \(L'^2\) beyond some length \(D'\) (Fig. 4). The average flux there will be of the order of \(\mathbf{q}_{D'} \approx \mathbf{q}_{ch} \frac{\pi R^2 }{(L'/2)^2}\), and will be considerably reduced as compared to the heat flux in a single channel \(\mathbf{q}_{ch}\).

Fig. 4
figure 4

When the heat flux is high enough (namely, when the value of (24) is higher than the critical value of the order of 100), vortices appear beyond the porous layer. \(D'\) is the width of the layer occupied by vortices near the wall, \(L^{''}\) the width of the wider channel beyond the layer. In this situation, one can observe three regions, the channels, the vortex layer with thickness \(D'\), and a third one in which the turbulence depends on the full width of the wide channel

Full size image

At such position \(D'\), the Reynolds number will be:

$$\begin{aligned} \mathrm{Rey}_{q}= \frac{\mathbf{q}_{D'}}{{\overline{T}} S} \frac{L^{''}}{\kappa }= \frac{\mathbf{q}_{ch}}{{\overline{T}} S} \frac{\pi R^2 }{L'^2} \frac{L^{''}}{\kappa ,} \end{aligned}$$
(26)

with \(L^{''}\) the width of the wider channel beyond the layer. The length \(D'\) may be estimated from the theory of jets in a viscous fluid [28,29,30,31]. If such value is lower than the critical one, vortices disappear at \(D'\). Otherwise, vortices will occupy the whole channel.

To get a rough estimate of the length \(D'\), we consider that the diffusive lateral broadening \(\Delta R\) of the jet will be of the order of \((\Delta R)^2 \simeq (4 \eta /\rho )t\), with \(\eta /\rho \) the diffusive coefficient for velocity (being \(\eta \) the viscosity and \(\rho \) the density), and t the time elapsed since the jet has left the channel. Then, the time to reach \(\Delta R \approx L'/2\) (characterizing the full homogeneous redistribution of \(\mathbf{q}\) across the total width of the channel) will be of the order of \(t' \simeq \frac{L'^2}{16 \eta /\rho }\). The speed at which the jet is flowing is of the order of \(\mathbf{v}_\mathrm{ns}= |\mathbf{v}_\mathrm{n} - \mathbf{v}_\mathrm{s}|\), which is related to the heat flux as \(\mathbf{v}_\mathrm{ns} = \mathbf{q}_{ch} (S {\overline{T}})^{-1}\). Therefore, the distance \(D'\) may be estimated as:

$$\begin{aligned} D' = \overline{\mathbf{v}_\mathrm{ns}} t' = \frac{\mathbf{q}_{ch} - \mathbf{q}_{D'}}{2 S {\overline{T}} } \frac{L'^2}{16 \eta /\rho }. \end{aligned}$$
(27)

If we assume \(\mathbf{q}_{D'} \ll \mathbf{q}_{ch}\), \(D'\) may be estimated as:

$$\begin{aligned} D' (\text {cm}) = \frac{\mathbf{q}_{ch}}{2 S {\overline{T}}} \frac{1}{16 \eta /\rho } \frac{1}{N} = \frac{{\dot{Q}}}{N^2} \frac{1}{\pi R^2} \frac{\rho }{32 \eta S {\overline{T}} }, \end{aligned}$$
(28)

because \({\dot{Q}} = \mathbf{q}_{ch} N \pi R^2\). Here we have assumed that the average separation \(L'\) between close neighbor pores is \(L' \approx N^{-\frac{1}{2}}\). For \({\overline{T}}=1.7\) K, \(D' (\text {cm}) \simeq 10^{-4} \frac{{\dot{Q}}}{N^2} \frac{1}{ R^2} \) (cgs units). Concrete values of \(D'\) are given in Table 3 for different values of \({\dot{Q}}\), R and N.

3.2 Contribution of the vortices to the thermal resistance

If vortices appear, their contribution to the total thermal resistance should be taken into account. The thermal resistance per unit area of the layer of vortices in terms of the vortex length density \({\mathcal {L}}\) is [2, 4]:

$$\begin{aligned} \mathrm{Th.Res.}_\mathrm{vort.} = \frac{K}{\zeta } {\mathcal {L}} D', \end{aligned}$$
(29)

with K a coefficient which in the two-fluid model is interpreted as the mutual friction coefficient between normal component and quantized vortex lines [32,33,34], \(\zeta \) is related to second sound speed \(V_2\) as \(\zeta = \rho c V_2^2\), and \(D'\) is the thickness of the layer occupied by vortices near the wall (if vortices occupy the whole length of the channel, such whole length should be considered).

Relating \({\mathcal {L}}\) to \({\dot{Q}}\) is important. Usually, \({\mathcal {L}}\) is related to \(\mathbf{q}\) in terms of the Vinen’s equation [2, 32,33,34]:

$$\begin{aligned} \frac{\mathrm{d} {\mathcal {L}}}{\mathrm{d} t} = \alpha \mathbf{v}_\mathrm{ns} {\mathcal {L}}^{\frac{3}{2}} - \beta \kappa {\mathcal {L}}^2, \end{aligned}$$
(30)

with \(\alpha \) and \(\beta \) temperature dependent coefficients describing the local rate of vortex production and of vortex destruction per unit volume. We use here this equation for the sake of simplicity of illustration, but it should be kept in mind that more complicated equations are needed to incorporate the effects of the walls [4], of the anisotropy of the tangle [35], and of non-uniformity fields of velocity [35,36,37]. Before incorporating these complex effects, it seems useful to begin the study by considering the simplest situation.

The steady-state solution of (30) is:

$$\begin{aligned} {\mathcal {L}}^{\frac{1}{2}}= \frac{\alpha }{\beta \kappa } \mathbf{v}_\mathrm{ns} = \frac{\alpha }{\beta \kappa } \frac{\mathbf{q}}{S {\overline{T}}} \frac{\rho }{\rho _\mathrm{s}}. \end{aligned}$$
(31)

As a first approximation, we propose using (30) and taking (31) for the average vortex length density in the vortex layer beyond the wall:

$$\begin{aligned} \overline{{\mathcal {L}}}= \frac{\alpha ^2}{\beta ^2 \kappa ^2} \frac{\mathbf{q}_{ch}^2}{4 (S {\overline{T}})^2} \frac{\rho ^2}{\rho _\mathrm{s}^2}. \end{aligned}$$
(32)

Combining (28) for \(D'\), (32) for \({\mathcal {L}}\) and (29), the total contribution of the vortex layer to the total thermal resistance will be:

$$\begin{aligned} \mathrm{Th.Res.}_\mathrm{vort.} = \frac{K}{\zeta } \frac{\rho }{16 \eta } \frac{\alpha ^2}{\beta ^2 \kappa ^2} \frac{\rho ^2}{\rho _\mathrm{s}^2} \frac{1}{N} \frac{1}{(N \pi R^2)^3} \left( \frac{{\dot{Q}} }{2 S {\overline{T}}}\right) ^3 . \end{aligned}$$
(33)
Table 3 Thickness \(D'\) of the turbulent layer of vortices produced at the end of the channel for different values of \({\dot{Q}}/N\), N and R. In the last two columns are reported the thermal resistance due to the vortices from (33) and the thermal resistance due only to the channel in the Landau approximation from (41), with \(L=10\) cm and \({\overline{T}} = 1.7 \) K
Full size table

Expression (33) has a dependence in \({\dot{Q}}^3\), a factor \({\dot{Q}}^2\) comes from \({\mathcal {L}}\), and another factor \({\dot{Q}}\) comes from the estimation of \(D'\). If vortices are occupying the whole channel, the thermal resistance will become proportional to \({\dot{Q}}^2\), as in the Gorter–Mellink expression (18) [1, 2, 16]. In Table 3, we estimate the contributions of the channels and of the vortex layer to the thermal resistance, for a few indicative values of \(\frac{{\dot{Q}}}{N}\), N, and R, in the range of validity of the usual Eq. (1) for the heat flux in the channel. Other analysis could be made for thin layers and narrow channels. Table 3 shows that for \(\frac{{\dot{Q}}}{N} = 10^2\) (erg/s) the contribution of the vortex layer is small as compared with that of the channel, but that for \(\frac{{\dot{Q}}}{N}=10^4\) (erg/s) the thermal resistance of the vortex layer is dominating.

4 Narrow pores: transition from hydrodynamic flow to slip flow

Equation (2) is valid when the phonon mean free path is much shorter than the radius of the channel. But, the phonon mean free path in liquid helium becomes longer than \(4 \times 10^{-4}\) m for temperatures lower than 1 K, and increases for lower temperatures, as it behaves as \(T^{- \frac{4}{3}}\)[38]. Thus, channels of diameter of the order of 1 mm or smaller must be considered as truly narrow channels, where phonons flow in a ballistic way at low temperature (i.e., their collisions with the walls are dominant over their mutual collisions inside the fluid).

In this situation the usual non-slip condition \(\mathbf{q}=0\) along the wall must be modified as it happens in the flow of rarefied viscous gases [39,40,41,42,43]. In rarefied gases, the non-slip condition for the velocity along the wall is replaced by: \(\mathbf{v} = - C' l (\partial \mathbf{v} / \partial r)\), with l the mean free path and \(C'\) a coefficient depending on temperature. An analogous of such equation has been proposed for heat flow in [7, 8, 44, 45], namely:

$$\begin{aligned} q (r=R) = - C l \frac{\partial q(r)}{\partial r}_{\left| r=R\right. }, \end{aligned}$$
(34)

where l is the average phonon mean free path [8]. The coefficient C is a constant dependent on the wall properties, and it may be interpreted as \(C= (2- f)/f\), f being the fraction of phonons which undergo diffusive scattering with the walls, and \((1-f)\) the fraction undergoing specular scattering. In superfluid helium, the boundary conditions for slip flow of velocity and of heat flux could be related by the boundary condition, proposed in [6], \( v_t- \frac{1}{T S} q_t =0\), where the underscript t denotes the tangential component of the vectors along the wall.

The solution of (2) has the general form:

$$\begin{aligned} \mathbf{q}(r)= c_1 r^2 + c_2 r + c_3. \end{aligned}$$
(35)

Imposing the boundary condition (34), and that the maximum of heat flux is at the center of the channel (i.e., \(\frac{\partial q(r)}{\partial r}_{\left| r=0\right. }=0\)), we obtain the coefficients:

$$\begin{aligned} c_1 = \frac{{\overline{T}} S^2}{4 \eta } \nabla T, \quad c_2 = 0, \quad c_3 = - \frac{{\overline{T}} S^2 }{4 \eta }R^2\nabla T \left[ 1 + 2 C \frac{l}{R}\right] . \end{aligned}$$
(36)

Then the solution (35) becomes:

$$\begin{aligned} \mathbf{q}(r) = - \frac{{\overline{T}} S^2}{4 \eta } \left[ R^2 \left( 1 + 2 C \frac{l}{R}\right) - r^2 \right] \nabla T. \end{aligned}$$
(37)

The corresponding total heat flux, obtained by integration of (4) over a cross section of the channel, becomes:

$$\begin{aligned} {\dot{Q}}_1 = \int \limits _0^R 2 \pi r q(r) \mathrm{d}r =\frac{\pi R^4 S^2 {\overline{T}}}{8 \eta } \left[ 1 + 4 C \frac{l}{R} \right] \frac{T_1 - T_2}{L}. \end{aligned}$$
(38)

This value is higher than that considered in (1) in a factor \((1 + 4 C l / R )\), whose second term yields the contribution of the slip flow described by (34). When \(l\ll R \) one recovers expression (1). Expression (38) remains valid when the diameter of the cylinders becomes comparable to the phonon mean free path. For \( R \ll l\) expression (38) yields:

$$\begin{aligned} {\dot{Q}}_1= \frac{ \pi R^3 S^2 {\overline{T}} C l}{2 \eta } \quad \frac{T_1 - T_2 }{L}. \end{aligned}$$
(39)

For N parallel pores, the heat flux per unit area and unit time will be:

$$\begin{aligned} {\dot{Q}} = N {\dot{Q}}_1= \frac{ N \pi R^3 S^2 {\overline{T}} C l}{2 \eta } \quad \frac{T_1 - T_2 }{L}. \end{aligned}$$
(40)

Thus, in the ballistic regime \({\dot{Q}}\) becomes proportional to \(R^3 l\) instead of to \(R^4\); since in this regime \(l \gg R\), this means a relative increase of heat transport with respect to (1), because of the contribution of the slip flow (34). For a single cylindrical channel, the transition from \(R^4\) to \(R^3 l\) regime was experimentally observed in [38, 44].

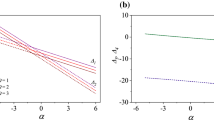
In Fig. 5 we plot \(\frac{{\dot{Q}}}{N \pi R^2}\) as a function of R, for constant \(\Delta T\), which is linear at small values of R (shorter than l) according to (40) and quadratic at \(R \gg l\), according to (1).

Fig. 5
figure 5

In the figure is plotted \(\frac{{\dot{Q}}}{N \pi R^2}\) versus R for constant \(\Delta T\). The dashed blue line corresponds to Eq. (38), the black line to the Landau–Lifshitz expression (1). For high values of R Eq. (38) tends to Eq. (1) as shown in the figure on the left. On the right, we have zoomed on the region for very small values of R, i.e., when the radius is smaller than the mean free path of phonons and Eq. (38) reduces to Eq. (40). On the figure on the right it is apparent that \({\dot{Q}}/ N \pi R^2\) is linear in R in this region, in contrast to the behavior in \(R^2\) shown for wider pores as plotted on the left figure. The data for \(\Delta T / L\), \(C=2\) and \(l=1.53*10^{-2}\)cm are extracted from [46] at \({\overline{T}}= 1.7\) K. The values of the other coefficients are extracted from [26]

Full size image

In wide channels, the corresponding thermal resistance, according to (19), is (\(R \gg l\)):

$$\begin{aligned} \mathrm{Th.Res.} = \frac{8 \eta L}{S^2 {\overline{T}} N \pi R^4}, \end{aligned}$$
(41)

according to (1) and for narrow channels (\(R \ll l\)), namely, in the slip regions, is:

$$\begin{aligned} \mathrm{Th.Res.}_{ballistic} = \frac{2 \eta L}{N \pi S^2 {\overline{T}} C R^3 l}, \end{aligned}$$
(42)

and in the transition regime from hydrodynamic to ballistic heat flow may be obtained from [46].

For short (\(L < L_\mathrm{entrance}\)) and narrow (\(R < l\)) channels, we tentatively generalize the expression (12) for short channels by multiplying it times the correction for narrow channels \((1 + 4 C l/R)\), to recover (38) in the small \({\dot{Q}}/N\) limit. In the limit of small X and of small R, this generalization of (12) leads to:

$$\begin{aligned} {\dot{Q}} = \frac{N \pi R^3 C l S^2 {\overline{T}}}{0.43 \eta } X^{\frac{1}{2}} \frac{T_1 - T_2}{L}, \end{aligned}$$
(43)

instead of (15). Using expression (13) for X and the definition (19), we are led to:

$$\begin{aligned} \mathrm{Th.Res.}_\mathrm{short-ch.} \equiv \frac{\Delta T}{{\dot{Q}}}= \frac{0.86 (\rho \eta L {\dot{Q}})^{\frac{1}{2}} }{(N \pi {\overline{T}})^{\frac{3}{2}} R^3 l C S^{\frac{5}{2}}}. \end{aligned}$$
(44)

In fact, it would be desiderable to know a more detailed expression generalizing (12) for short channels, but this is not yet known to our knowledge.

5 Conclusions

We have obtained the thermal resistance per unit area of a porous layer (with N pores of radius R per unit area of the layer and length L, given by the thickness of the layers) and of the adjacent layer of quantized vortices formed at the exit of the pores of characteristic thickness \(D'\) [given by (27)]. Beyond this distance, the effects of the discrete channels are not visible, because the heat flux has become homogeneous in the directions parallel to the layer (and perpendicular to the channels).

The main results in the several situations considered in this paper have been the following ones, which exhibit the contribution of the channels (first term) plus that of the layer of vortices at the exit of the channels (second term). Concerning the contribution of the walls, the first result is well known, but the other one has been obtained here. Furthermore, we are not aware of previous situations of the width \(D'\) of the vortex layer beyond the wall, nor of its contribution to thermal resistance, because usual result in this field directly use the Gorter–Mellink expression for fully developed turbulent flows.

  • For thick layers (\(L \gg L_\mathrm{entrance}\)) and wide pores (\(R \gg l\)) [from Eqs. (41) and (33)]:

    $$\begin{aligned} \mathrm{Th.Res.}\,(\mathrm{total})(L, R, N, {\dot{Q}}) \, \sim \frac{L}{N R^4} + f(T) \frac{{\dot{Q}}^3 }{N^4 R^6}. \end{aligned}$$
    (45)

  • For thick layers (\(L \gg L_\mathrm{entrance}\)) and narrow pores (\(R \ll l\)) [from Eqs. (42) and (33)]:

    $$\begin{aligned} \mathrm{Th.Res.}\,(\mathrm{total})(L, R, N, {\dot{Q}}) \, \sim \frac{L}{N R^3 C l} + f(T) \frac{{\dot{Q}}^3 }{N^4 R^6}. \end{aligned}$$
    (46)

  • For thin layers (\(L \ll L_\mathrm{entrance}\)) and wide pores (\(R \gg l\)) [from Eqs. (20) and (33)]:

    $$\begin{aligned} \mathrm{Th.Res.}\,(\mathrm{total})(L, R, N, {\dot{Q}})\, \sim \frac{{\dot{Q}}^{\frac{1}{2}}L^{\frac{1}{2}}}{N R^4} + f(T) \frac{{\dot{Q}}^3 }{N^4 R^6}. \end{aligned}$$
    (47)

  • For thin layers (\(L \ll L_\mathrm{entrance}\)) and narrow pores (\(R \ll l\)) [from Eqs. (44) and (33)]:

    $$\begin{aligned} \mathrm{Th.Res.}\,(\mathrm{total})(L, R, N, {\dot{Q}}) \, \sim \frac{{\dot{Q}}^{\frac{1}{2}}L^{\frac{1}{2}}}{N R^3 C l} + f(T) \frac{{\dot{Q}}^3 }{N^4 R^6}. \end{aligned}$$
    (48)

In previous expressions, f(T) comes from (33) and it is \(\frac{K}{\zeta } \frac{\rho }{16 \eta } \frac{\alpha ^2}{\beta ^2 \kappa ^2} \frac{1 }{(2 \pi S {\overline{T}})^3} \). Recall that according to the estimation based on (22), and for \({\dot{Q}}= 10^2\) erg/s, and \(N =100\)\(\hbox {cm}^{-2}\), thick layers means \(L \gg 0.01\) cm and narrow pores \(L \ll 0.01\) cm [the result for intermediate L may be obtained from (12)].

In these expressions we have emphasized the respective dependence of the thermal resistance on N, R, L, and \({\dot{Q}}\). Note that for thick layers (channels much longer than the entrance length) the resistance does not depend on \({\dot{Q}}\) and depends on \(L R^{-4}\) for wide channels and \(L R^{-3}\) for narrow channels, whereas for thin layers (channels comparable to the entrance length) it depends on \({\dot{Q}}^{\frac{1}{2}} L^{\frac{1}{2}} R^{-4}\) for wide pores and \({\dot{Q}}^{\frac{1}{2}} L^{\frac{1}{2}} R^{-3}\) for narrow pores.

The contribution of the turbulent layer beyond the wall has the same form in all situations, and \(L'\) the average separation of neighboring pores has be taken as \(N^{-\frac{1}{2}}\), for a given area of the layer. Note that this part depends on N and R in a stronger way than the contribution of the pores. As seen in Table 3, for sufficiently, high values of \(\frac{{\dot{Q}}}{N}\), the contribution of the vortex layer is dominating over the contribution of the pores.