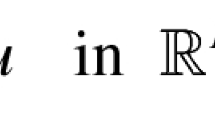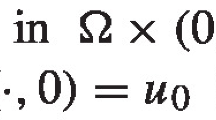New critical exponents, large time behavior, and life span for a fast diffusive p-Laplacian equation with nonlocal source

Abstract

This paper mainly investigate positive solutions of the Cauchy problem for a fast diffusive p-Laplacian equation with nonlocal source

$$\begin{aligned} u_{t}=\Delta _pu+\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q(y,t)\mathrm{d}y\right) ^{\frac{r-1}{q}}u^{s+1},\quad (x,t)\in {\mathbb {R}}^N\times (0,T), \end{aligned}$$

where $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, $r\ge 1$, $0\le s<\left( 1+\frac{1}{N}\right) p-2$ and $r+s>1$. We obtain the new critical Fujita exponent by virtue of the auxiliary function method and forward self-similar solution, and then determine the second critical exponent to classify global and non-global solutions of the problem in the coexistence region via the decay rates of an initial data at spatial infinity. Moreover, the large time behavior of global solution and the life span of non-global solution are derived.

1 Introduction

We consider a Cauchy problem for a fast diffusive p-Laplacian equation with nonlocal source

$$\begin{aligned}&u_{t}=\Delta _pu+\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q(y,t)\mathrm{d}y\right) ^{\frac{r-1}{q}}u^{s+1},\quad (x,t)\in {\mathbb {R}}^N\times (0,T), \end{aligned}$$

(1.1)

$$\begin{aligned}&u(x,0)=u_0(x),\quad x\in {\mathbb {R}}^N, \end{aligned}$$

(1.2)

where $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, $r\ge 1$, $0\le s<(1+\frac{1}{N})p-2$, $r+s>1$, and the initial data $u_0(x)$ is a nonnegative, continuous and nontrivial function. Then problems (1.1)–(1.2) have a unique continuous solution in the sense of distribution, and the comparison principle is valid (see [1, 2]).

Nonlocal model (1.1) describes many natural phenomena, such as the non-Newton flux in the mechanics of fluid, population of biological species and filtration; see [3,4,5] and references therein. In the non-Newtonian fluids, the quantity p is a characteristic of the medium. Media with $p>2$ are called dilatant fluids, while $p<2$ are called pseudo-plastics. If $p=2$, they are Newtonian fluids. Meanwhile, in the nonlinear diffusion theory, there exist obvious differences among the situations of slow ($p>2$), fast ($1<p<2$), and linear ($p=2$) diffusions. For example, there is a finite speed propagation in the slow and linear diffusion situations, whereas an infinite speed propagation exists in the fast diffusion situation.

It is well known that the Cauchy problem for the local diffusion equation with power type source

$$\begin{aligned} u_t=\Delta _pu+u^{s+1},\quad (x,t)\in {\mathbb {R}}^N\times (0,T), \end{aligned}$$

(1.3)

possesses the critical Fujita exponent $s_c=p-2+\frac{p}{N}$, namely any nontrivial solutions blow up in finite time when $0<s\le s_c$, and there are both global and non-global solutions if $s>s_c$, depending on the size of initial data (see Fujita et al. [6,7,8] for $p=2$, Galaktionov et al. [9, 10] for $p>2$, and Qi and Wang [11] for $\frac{2N}{N+1}<p<2$). Thus, the number $s_c$ is the cutoff between the blow-up case and the global existence case, and it is called the critical Fujita exponent. For the study of the Cauchy problems for nonlocal diffusion equations with nonlocal sources, Galaktionov and Levine [12] firstly considered positive solutions of a Cauchy problem for the following parabolic equation with weighted nonlocal sources

$$\begin{aligned} u_{t}=\Delta _pu +\left( \,\,\int \limits _{{\mathbb {R}}^N}K(y)u^q(y,t)\mathrm{d}y\right) ^{\frac{r-1}{q}}u^{s+1},\quad (x,t)\in {\mathbb {R}}^N\times (0,T), \end{aligned}$$

(1.4)

where $p\ge 2$, $q,r\ge 1$, $s\ge 0$ and $r+s>1$. They obtained the critical Fujita exponent by the parameter r to classify solutions of the equation. When $p=2$ and the nonnegative weight function $K(x)\in L^1({\mathbb {R}}^N)$, the critical Fujita exponent is $r_c=1+\frac{2}{N}-s$, while if $K(x)\notin L^1({\mathbb {R}}^N)$ and $K(x)\sim |x|^{-\sigma }$ for |x| large enough, the critical Fujita exponent is $r_c=1+\frac{2q(1-\frac{Ns}{2})}{N(q-1)+\sigma }$ for $\frac{Ns}{2}<1$, which is included in blow-up case. Moreover, they derived the critical Fujita exponent $r_c=p-1-s+\frac{p-2}{q}+\frac{p}{N}$ for $s<\frac{p-2}{q}+\frac{p}{N}$ when $p>2$ and $K(x)\in L^1({\mathbb {R}}^N)$, which is included in blow-up case. Afterward, Afanas’eva and Tedeev [13] obtained the critical Fujita exponent $s_c=p-2+\frac{p}{N}-(\sigma +N(q-1))\frac{r-1}{Nq}$ with respect to the parameter s when $p>2$, $K(x)=(1+|x|)^{-\sigma }$ and $-N(q-1)<\sigma <N$, but they did not show whether the critical case $s=s_c$ belongs to blow-up case.

Note that for the critical Fujita exponent, the region satisfying $s>s_c$ or $r>r_c$ is a coexistence region of global and non-global solutions for the Cauchy problem. To identify the global and non-global solutions in the coexistence region, Lee and Ni [14] introduced a new second critical exponent $\alpha ^*=\frac{2}{s}$ for problem (1.3) with $p=2$ by virtue of the slow decay behavior of the initial data at spatial infinity. More precisely, with initial data $u_0(x)=\lambda \phi (x)$ and $s>s_c=\frac{2}{N}$, there exist constants $\mu ,\Lambda ,\Lambda _0$ such that the solution blows up in finite time whenever $\liminf _{|x|\rightarrow \infty }|x|^{\alpha ^*}\phi (x)>\mu >0$ and $\lambda >\Lambda$, or exists globally if $\limsup _{|x|\rightarrow \infty }|x|^{\alpha }\phi (x)<\infty$ with $\alpha \ge \alpha ^*$ and $\lambda <\Lambda _0$. Afterward, Mu et al. [15] and Yang et al. [16] considered the slow and fast diffusion cases of Cauchy problem (1.3), respectively, and they all derived a new second critical exponent $\alpha ^*=\frac{p}{s+2-p}$ when $s>s_c=p-2+\frac{p}{N}$. Moreover, the life span of non-global solution is obtained. On the nonlocal diffusion equation (1.4), recently, Yang et al. [17] studied the linear diffusion case with $r>r_c$, $K(x)\in L^\infty ({\mathbb {R}}^N)\cap C({\mathbb {R}}^N)$ and $K(x)\sim |x|^{-\sigma }$ for |x| large, and they found a new second critical exponent $\alpha ^*=\frac{2q+(r-1)(N-\sigma )_+}{q(r+s-1)}$. Lately, Ma and Fang [18] derived a new second critical exponent $\alpha ^*=\frac{pq+(r-1)(N-\sigma )_+}{q(r+s+1-p)}$ with $r>r_c$ when $p>2$, $K(x)\in L^1({\mathbb {R}}^N)$ and $K(x)\sim |x|^{-\sigma }$ for |x| large enough. Moreover, they also found a second critical exponent $\alpha ^*=\frac{pq+(r-1)(N-\sigma )}{q(r+s+1-p)}$ classified by the parameter s with $s>s_c$ when $p>2$, $K(x)=(1+|x|)^{-\sigma }$ and $0\le \sigma <N$ in [19], where $r_c$ and $s_c$ are given in [12, 13]. Meanwhile, they obtained the large time behavior of the global solution and the life span of the non-global solution.

To the best of our knowledge, the research on the critical exponents for the Cauchy problem (1.1)–(1.2) of a fast situation has not been proceeded yet. Our main difficulty lies in finding the effects of the fast diffusive p-Laplace operator, nonlocal source and the behavior of initial data at spatial infinity on the global existence and nonexistence of solutions. Motivated by these observations, we establish the critical Fujita exponent by means of the auxiliary function method and forward self-similar solution, and by virtue of the decay rates of an initial data at spatial infinity to seek a new second critical exponent. Moreover, we derive the large time behavior of global solution as well as a life span of non-global solution.

Throughout the rest of this paper, we denote by $C_b({\mathbb {R}}^N)$ the space of all bounded continuous functions in ${\mathbb {R}}^N$, and define

$$\begin{aligned} \Pi _\alpha:= & {} \{\psi \in C_b({\mathbb {R}}^N)|\psi (x)\ge 0,\liminf _{|x|\rightarrow \infty }|x|^\alpha \psi (x)>0\},\\ \Pi ^\alpha:= & {} \{\psi \in C_b({\mathbb {R}}^N)|\psi (x)\ge 0,\limsup _{|x|\rightarrow \infty }|x|^\alpha \psi (x)<\infty \}. \end{aligned}$$

Moreover, let

$$\begin{aligned} r_c:=1+\frac{q[p-N(s+2-p)]}{N(q-1)},\;\, \alpha ^*:=\frac{pq+N(r-1)}{q(r+s+1-p)}, \end{aligned}$$

and u(x, t) denotes the solution of problem (1.1)–(1.2). Our main results are summarized as follows.

• If $1<r\le r_c$, then every nontrivial solution u(x, t) blows up in finite time.

• If $r>r_c$, then there exists a global solution u(x, t) for small initial data $u_0(x)$, and a non-global solution for large initial data.

• Suppose $r>r_c$ and $u_0=\lambda \phi (x)$, $\lambda >0$.

• (1) If $\phi (x)\in \Pi _\alpha$ and $0<\alpha <\alpha ^*$ or $\alpha \ge \alpha ^*$ with $\lambda$ large enough, then u(x, t) blows up in finite time;

• (2) If $\phi (x)\in \Pi ^\alpha$ and $\alpha ^*<\alpha <N$, then there exist positive constants $\lambda _0=\lambda _0(\phi )$ and C such that u(x, t) exists globally for $\lambda \in (0,\lambda _0)$ satisfying

  $$\begin{aligned} \Vert u(x,t)\Vert _{L^\infty ({\mathbb {R}}^N)}\le Ct^{-\alpha \beta }\;\,\text {for all}\;\,t>0, \end{aligned}$$

  where $\beta =\frac{1}{p-\alpha (2-p)}$. Furthermore, if $\lim _{|x|\rightarrow \infty }|x|^\alpha \phi (x)=M>0$, then u(x, t) satisfies

  $$\begin{aligned} t^{\alpha \beta }|u(x,t)-U_{\lambda ,M,\alpha }(x,t)|\rightarrow 0\;\,\text {as}\;\, t\rightarrow \infty \end{aligned}$$

  uniformly in compact set of ${\mathbb {R}}^N$ for $\lambda \in (0,\lambda _0)$, where $U_{\lambda ,M,\alpha }(x,t)$ is the solution of the following Cauchy problem

  $$\begin{aligned} {\left\{ \begin{array}{ll} U_t=\mathrm{div}(|\nabla U|^{p-2}\nabla U),\quad x\in {\mathbb {R}}^N,t>0,\\ U(x,0)=\lambda M|x|^{-\alpha },\quad x\in {\mathbb {R}}^N. \end{array}\right. } \end{aligned}$$

• Let u(x, t) is a solution of problem (1.1)–(1.2) with initial data $u_0=\lambda \phi (x)$ which blows up at finite time T, and $\Vert \phi \Vert _{L^\infty ({\mathbb {R}}^N)}=\lim _{|x|\rightarrow \infty }\phi =\phi _\infty$. Then the life span of u(x, t) satisfies

  $$\begin{aligned} \frac{c_4}{r+s-1}(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)}\le T\le \frac{c_5}{r+s-1}(\lambda \phi _\infty )^{-(r+s-1)}, \end{aligned}$$

  where $c_4,c_5$ are the positive constants given below.

Note that the new critical Fujita exponent $r_c=1+\frac{q[p-N(s+2-p)]}{N(q-1)}$ and the second critical exponent $\alpha ^*=\frac{pq+N(r-1)}{q(r+s+1-p)}$ established in this paper are in full accord with the conclusions in the previous studies [10,11,12, 14,15,16,17]. Indeed, by simple calculations, one can see that the critical Fujita exponent $r_c$ classified by parameter r is equivalent to the critical Fujita exponent $s_c:=p-2+\frac{p}{N}-\frac{(r-1)(q-1)}{q}$ classified by parameter s. Take $r=1$ in $s_c$ and $\alpha ^*$, we can derive the critical exponents of local diffusion equation in [10, 11, 14,15,16]. Let $p\rightarrow 2^-$ in $r_c$ and $\alpha ^*$, then the critical exponents are consistent with [12, 17] when $K(x)\notin L^1({\mathbb {R}}^N)$ and $\sigma =0$.

The rest of this paper is organized as follows. In Sects. 2 and 3, we establish the new critical Fujita exponent and a second critical exponent for problem (1.1)–(1.2). In Sect. 4, we derive the large time behavior of the global solution and a life span of the non-global solution of problem (1.1)–(1.2).

2 Critical Fujita exponent

In this section, we are devoted to seek the new critical Fujita exponent for problem (1.1)–(1.2) by virtue of the auxiliary function method and forward self-similar solution.

Firstly, we try to construct an appropriate auxiliary function to guarantee that the solution u(x, t) blows up in finite time.

Theorem 2.1

For $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, and $0\le s<(1+\frac{1}{N})p-2$, suppose that $1<r\le r_c$, then every nontrivial solution u(x, t) of Cauchy problem (1.1)–(1.2) blows up in finite time.

Proof

Let $\varphi (x)=\varphi (|x|)$ be a smooth, radially symmetric and non-increasing function such that

$$\begin{aligned} 0\le \varphi (x)\le 1,\;\,\varphi (x)\equiv 1\;\,\text {for}\;\,|x|\le 1,\;\,\text {and}\;\, \varphi (x)\equiv 0\;\,\text {for}\;\,|x|\ge 2. \end{aligned}$$

Define $\varphi _R(x)=\varphi (\frac{x}{R})$, then for $R\ge 1$, $\varphi _R(x)$ is a smooth, radially symmetric, and non-increasing function, which satisfies

$$\begin{aligned} 0\le \varphi _R(x)\le 1,\;\,\varphi _R(x)\equiv 1\;\,\text {for}\;\,|x|\le R,\;\,\text {and}\;\,\varphi _R(x)\equiv 0\;\,\text {for}\;\,|x|\ge 2R. \end{aligned}$$

Moreover, let $\varphi _0(x)=\varphi _0(|x|)$ be a smooth, radially symmetric, and non-decreasing function satisfying

$$\begin{aligned} 0\le \varphi _0(x)\le 1,\;\,\varphi _0(x)\equiv 0\;\,\text {for}\;\,|x|\le 1,\;\,\text {and}\;\, \varphi _0(x)\equiv 1\;\,\text {for}\;\,|x|\ge 2. \end{aligned}$$

Then we set $\phi _R(x)=\varphi _0(x)\varphi _R(x)$, it follows that $\phi _R(x)$ is a smooth and radially symmetric function which satisfies for $R>2$,

$$\begin{aligned}&0\le \phi _R(x)\le 1,\;\,\phi _R(x)\equiv 0\;\,\text {for}\;\,|x|\le 1,\\&\phi _R(x)\equiv 1\;\,\text {for}\;\,2\le |x|\le R,\;\,\phi _R(x)\equiv 0\;\,\text {for}\;\,|x|\ge 2R, \end{aligned}$$

and $\phi _R(x)$ is non-decreasing for $1\le |x|\le 2$ and non-increasing for $R\le |x|\le 2R$.

Next, we introduce the auxiliary function

$$\begin{aligned} \Theta _R(t)=\int \limits _\Omega u\phi _R(x)\mathrm{d}x, \end{aligned}$$

(2.1)

where $\Omega ={\mathbb {R}}^N\backslash B_{1/2}$ with $B_{1/2}$ being the ball with radius 1 / 2 and center at the origin. Without loss of generality, we may assume u is radially symmetric and non-increasing in $r=|x|$. Indeed, similar to the argument in [11, Section 1, Remark], by the comparison principle we need only consider that $u_0(x)$ is radially symmetric and non-increasing, i.e., $u_0(x)=u_0(r)$ and $u_0(r)$ non-increasing in r, and the solution u of (1.1)–(1.2) is also radially symmetric and non-increasing in $r=|x|$. Therefore, $\Theta _R$ is an increasing function of R.

Firstly, differentiating $\Theta _R(t)$, using (1.1) and Green’s formula, we obtain

$$\begin{aligned} \Theta _R'(t)&=-\int \limits _\Omega |\nabla u|^{p-2}\nabla u\cdot \nabla \phi _R\mathrm{d}x+\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}} \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x \nonumber \\&=-\omega _N\int \limits _1^{2R}|u'|^{p-2}u'\phi _R'\tau ^{N-1}\mathrm{d}\tau +\left( \,\,\int \limits _{{\mathbb {R}}^N} u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\nonumber \\&=\omega _N\int \limits _1^{2R}|u'|^{p-1}\phi _R'\tau ^{N-1}\mathrm{d}\tau +\left( \,\,\int \limits _{{\mathbb {R}}^N} u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\nonumber \\&\ge -\omega _N\int \limits _1^{2R}|u'|^{p-1}|\phi _R'|\tau ^{N-1}\mathrm{d}\tau +\left( \,\,\int \limits _{{\mathbb {R}}^N} u^q\phi _R\mathrm{d}x\right) ^{\frac{r-1}{q}}\Vert \phi _R\Vert _{L^\infty ({\mathbb {R}}^N)} ^{-\frac{r-1}{q}}\int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x, \end{aligned}$$

(2.2)

where $\omega _N$ is the area of the unit sphere in ${\mathbb {R}}^N$.

Thanks to the calculation in [11], we get the inequality

$$\begin{aligned} \int \limits _1^{2R}|u'|^{p-1}|\phi _R'|\tau ^{N-1}\mathrm{d}\tau \le c_0R^{(2-p)(N-1)}\left( \int \limits _\Omega u|\Delta \phi _R|\mathrm{d}x\right) ^{p-1}, \end{aligned}$$

(2.3)

where $c_0$ is independent of R. Thus, substituting (2.3) into (2.2), we have

$$\begin{aligned} \Theta _R'(t)&\ge -c_0R^{(2-p)(N-1)}\left( \int \limits _\Omega u|\Delta \phi _R|\mathrm{d}x\right) ^{p-1} \nonumber \\&\quad +\left( \,\,\int \limits _{{\mathbb {R}}^N} u^q\phi _R\mathrm{d}x\right) ^{\frac{r-1}{q}}\Vert \phi _R\Vert _{L^\infty \left( {\mathbb {R}}^N\right) } ^{-\frac{r-1}{q}}\int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x. \end{aligned}$$

(2.4)

Let us estimate each integral on the right side of (2.4) by H$\ddot{o}$ldre’s inequality, we derive

$$\begin{aligned} \left( \int \limits _\Omega u|\Delta \phi _R|\mathrm{d}x\right) ^{p-1}&\le \left( \int \limits _\Omega |\Delta \phi _R|^{\frac{s+1}{s}}\phi _R^{-\frac{1}{s}}\mathrm{d}x\right) ^{\frac{s(p-1)}{s+1}} \left( \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\right) ^{\frac{p-1}{s+1}} \nonumber \\&\le R^{(\frac{Ns}{s+1}-2)(p-1)}\Vert |\Delta \phi _1|\phi _1^{-\frac{1}{s+1}}\Vert _{L^{\frac{s+1}{s}}(\Omega )}^{p-1}\left( \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\right) ^{\frac{p-1}{s+1}}, \end{aligned}$$

(2.5)

$$\begin{aligned} \left( \int \limits _{{\mathbb {R}}^N}u^q\phi _R\mathrm{d}x\right) ^{\frac{r-1}{q}}&\ge \Vert \phi _R\Vert _ {L^1({\mathbb {R}}^N)}^{-\frac{(r-1)(q-1)}{q}}\Theta _R^{r-1}(t) \nonumber \\&=R^{-\frac{N(r-1)(q-1)}{q}} \Vert \phi _1\Vert _ {L^1({\mathbb {R}}^N)}^{-\frac{(r-1)(q-1)}{q}}\Theta _R^{r-1}(t), \end{aligned}$$

(2.6)

and

$$\begin{aligned} \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x&\ge \Vert \phi _R\Vert _{L^1(\Omega )}^{-s} \Theta _R^{s+1}(t) \nonumber \\&=R^{-Ns}\Vert \phi _1\Vert _{L^1(\Omega )}^{-s} \Theta _R^{s+1}(t). \end{aligned}$$

(2.7)

Therefore, substituting (2.5)–(2.7) into (2.4), one can deduce the inequality

$$\begin{aligned} \Theta _R'(t)&\ge -c_1R^{(2-p)(N-1)+(\frac{Ns}{s+1}-2)(p-1)}\left( \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\right) ^{\frac{p-1}{s+1}} \nonumber \\&\quad +c_2R^{-\frac{N(r-1)(q-1)}{q}}\Theta _R^{r-1}(t)\int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\nonumber \\&\ge R^{-\frac{N(r-1)(q-1)}{q}-\frac{Ns(s+2-p)}{s+1}}\left( \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\right) ^{\frac{p-1}{s+1}}\Theta _R^{r+s+1-p}(t)\nonumber \\&\quad \times [c_2-c_1 R ^{2N-(1+N)p+\frac{N(r-1)(q-1)}{q}+Ns}\Theta _R^{-(r+s+1-p)}(t)], \end{aligned}$$

(2.8)

where $c_1=c_0\Vert |\Delta \phi _1|\phi _1^{-\frac{1}{s+1}}\Vert _{L^{\frac{s+1}{s}}(\Omega )}^{p-1}$, $c_2=\Vert \phi _1\Vert _{L^1({\mathbb {R}}^N)}^{-\frac{(r-1)(q-1)}{q}} \Vert \phi _R\Vert _{L^\infty ({\mathbb {R}}^N)} ^{-\frac{r-1}{q}}\Vert \phi _1\Vert _{L^1(\Omega )}^{-s}$.

For $1<r<r_c$ , we have $2N-(1+N)p+\frac{N(r-1)(q-1)}{q}+Ns<0$. Because of

$$\begin{aligned} \Theta _R(0)=\int \limits _\Omega u_0\phi _R(x)\mathrm{d}x\ge \epsilon >0 \end{aligned}$$

for some $\epsilon >0$. Thus, we see from (2.8) that there exist a large $R_0$ and $C_0$ such that

$$\begin{aligned} \Theta _R'(t)\ge C_0\Theta _R^{r+s}(t)\;\,\text {for}\;\,R>R_0,\,t>0. \end{aligned}$$

Consequently, $\Theta _R(t)$ blows up in finite time by the fact that $r+s>1$.

For $r=r_c$ , we have $2N-(1+N)p+\frac{N(r-1)(q-1)}{q}+Ns=0$. Now, we give the proof by contradiction. Suppose $\Theta _R(t)$ cannot blow up in finite time. According to (2.8), there must be

$$\begin{aligned} \Theta _R(t)\le (\frac{c_1}{c_2})^{\frac{1}{r+s+1-p}}. \end{aligned}$$

(2.9)

On the other hand, making use of (2.4), (2.6) and (2.7), we deduce

$$\begin{aligned} \Theta _R(t)&\ge -c_0R^{2N-(1+N)p}C(R)+c_2R^{2N-(1+N)p}\Theta _R^{r+s}(t) \nonumber \\&=R^{2N-(1+N)p}(c_2\Theta _R^{r+s}(t)-c_0C(R)), \end{aligned}$$

(2.10)

where $C(R)=(\int \limits _\Omega u|\Delta \phi _R|\mathrm{d}x)^{p-1}$. Combining with (2.9) and the definition of $\phi _R(x)$ yields

$$\begin{aligned} C(R)\rightarrow 0\;\,\text {as}\;\,R\rightarrow \infty , \end{aligned}$$

and therefore, there exists a sufficient large $R_1$ to satisfy

$$\begin{aligned} C(R)<\frac{c_2}{2c_0}\Theta _R^{r+s}(t)\;\,\text {for}\;\,R>R_1. \end{aligned}$$

(2.11)

It follows from (2.10) and (2.11) that

$$\begin{aligned} \Theta _R'(t)\ge \frac{c_2}{2}R^{2N-(1+N)p}\Theta _R^{r+s}(t). \end{aligned}$$

Hence, $\Theta _R(t)$ blows up at $t=T=\frac{2R^{-2N+(1+N)p}}{c_2(r+s-1)}\Theta _R^{-(r+s-1)}(0)$ due to $r+s>1$, which contradicts with our assumption. $\square$

Next, we show that there exists a global solution utilizing the forward self-similar solution.

Theorem 2.2

For $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, and $0\le s<(1+\frac{1}{N})p-2$, suppose that $r>r_c$, then there exists a global solution u(x, t) of Cauchy problem (1.1)–(1.2) for small initial data $u_0(x)\le V(|x|)$, and a non-global solution u(x, t) for large initial data $u_0(x)$ satisfying $\Theta _R(0)\ge c$, where $\Theta _R(0)$, V(|x|) and c are defined by (2.1), (2.13) and (2.20), respectively.

Proof

We first show that there exists a global solution for small initial data. To this end, consider the forward self-similar solution of problem (1.1)–(1.2). It takes the form

$$\begin{aligned} u(x,t)=(1+t)^{-a}v\left( \frac{|x|}{(1+t)^b}\right) , \end{aligned}$$

where

$$\begin{aligned} a=\frac{pq+N(r-1)}{pq(r+s-1)-N(2-p)(r-1)},\; b=\frac{q(r+s+1-p)}{pq(r+s-1)-N(2-p)(r-1)}. \end{aligned}$$

Set $\eta =\frac{|x|}{(1+t)^b}$, after an appropriate scaling, the resulting ODE for v is

$$\begin{aligned} {\left\{ \begin{array}{ll} (p-1)|v'|^{p-2}v''+\frac{N-1}{\eta }|v'|^{p-2}v'+av+b\eta v'+Jv^{s+1}=0,\\ v(0)=\zeta >0,\;\,|v'|^{p-2}v'(0)=-\lim _{\eta \rightarrow 0^+}\frac{J\eta v^{s+1}(\eta )}{N}, \end{array}\right. } \end{aligned}$$

where $J=(\int \limits _{{\mathbb {R}}^N}v^q(|x|)\mathrm{d}x)^{\frac{r-1}{q}}.$

We observe that a function ${\bar{u}}(x,t)=(1+t)^{-a}V(\frac{|x|}{(1+t)^b})$ is a supersolution of problem (1.1)–(1.2) if and only if $V(\eta )$ satisfies the inequality

$$\begin{aligned} (p-1)|V'|^{p-2}V''+\frac{N-1}{\eta }|V'|^{p-2}V'+aV+b\eta V'+JV^{s+1}\le 0,\;\; \eta >0. \end{aligned}$$

(2.12)

Next, we try to find a positive solution of (2.12). Choosing

$$\begin{aligned} V(\eta )=\varepsilon (1+B\eta ^k)^{-A}, \end{aligned}$$

(2.13)

where $k=\frac{p}{p-1}$, $A=\frac{p-1}{2-p}$, and $\varepsilon$ and B are positive constants to be determined later. A serial computation shows that $V(\eta )$ satisfies (2.12) if and only if

$$\begin{aligned}&\varepsilon ABk[\varepsilon ^{p-2}(ABk)^{p-1}-b]\eta ^k(1+B\eta ^k)^{-A-1} \nonumber \\&\quad +\varepsilon (a-N\varepsilon ^{p-2}(ABk)^{p-1})(1+B\eta ^k)^{-A}\nonumber \\&\quad +\varepsilon ^{r+s}\left( \int \limits _{{\mathbb {R}}^N}(1+B|x|^k)^{-Aq}\mathrm{d}x\right) ^{\frac{r-1}{q}}(1+B\eta ^k)^{-A(s+1)}\le 0. \end{aligned}$$

(2.14)

Since $Akq=\frac{pq}{2-p}>1$ and $As=\frac{(p-1)s}{2-p}>0$, there exist $C_1,C_2>0$ such that

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}(1+B|x|^k)^{-Aq}\mathrm{d}x\le C_1, \end{aligned}$$

(2.15)

and

$$\begin{aligned} (1+B\eta ^k)^{-As}\le C_2\;\,\text {for all}\;\,\eta \ge 0. \end{aligned}$$

(2.16)

Then, we pick $B=B(\varepsilon )$ to satisfy

$$\begin{aligned} \varepsilon ^{p-2}(ABk)^{p-1}=b,\;\,\text {i.e.}\;\, B=\varepsilon ^{\frac{2-p}{p-1}}b^{\frac{1}{p-1}}(Ak)^{-1}. \end{aligned}$$

For this choice of B, and in view of (2.15) and (2.16), (2.14) is equivalent to

$$\begin{aligned} a-Nb+C\varepsilon ^{r+s-1}\le 0, \end{aligned}$$

(2.17)

where C is a positive constant. Throughout this paper, we assume that C denotes a positive constant that is independent of x and t for convenience, which may be different from line to line.

Note that $r>r_c$, it implies

$$\begin{aligned} a=\frac{pq+N(r-1)}{q(r+s+1-p)}b <\left( \frac{N(q-1)(p-\frac{N}{q}(s+2-p))}{pq-N(s+2-p)}+\frac{N}{q}\right) b =Nb. \end{aligned}$$

Therefore, there exists $\varepsilon _0$ such that (2.17) holds for all $\varepsilon \in (0,\varepsilon _0]$. These arguments show that $V(\eta )=\varepsilon (1+B\eta ^k)^{-A}$ satisfies (2.12) for all $\varepsilon \in (0,\varepsilon _0]$. Using the comparison principle ([2]) we see that the solution u(x, t) of problem (1.1)–(1.2) exists globally provided that $u_0(x)\le V(|x|)$.

Next, we prove that the solution u(x, t) of problem (1.1)–(1.2) blows up in finite time for large initial data when $r>r_c$. Recalling (2.8) in the proof of Theorem 2.1, we have

$$\begin{aligned} \Theta _R'(t)&\ge R^{2N-(1+N)p+Ns-\frac{Ns(s+2-p)}{s+1}}\left( \int \limits _\Omega u^{s+1}\phi _R\mathrm{d}x\right) ^{\frac{p-1}{s+1}} \nonumber \\&\quad \times (c_2R^{-2N+(1+N)p-\frac{N(r-1)(q-1)}{q} -Ns}\Theta _R^{r+s+1-p}(t)-c_1)\nonumber \\&\ge \frac{1}{2}c'\Theta _R^{r+s}(t), \end{aligned}$$

(2.18)

with $c'=c_2R^{-\frac{N(r-1)(q-1)}{q}-Ns}$, as long as

$$\begin{aligned} \frac{1}{2}c_2R^{-2N+(1+N)p-\frac{N(r-1)(q-1)}{q} -Ns}\Theta _R^{r+s+1-p}(t)\ge c_1\;\text {for all}\;t\in [0,T). \end{aligned}$$

(2.19)

By virtue of (2.19), we are led to

$$\begin{aligned} \Theta _R(t)\ge \left( \frac{2c_1}{c_2}R^{2N-(1+N)p+\frac{N(r-1)(q-1)}{q} +Ns}\right) ^{\frac{1}{r+s+1-p}}. \end{aligned}$$

Note that $r>r_c$ implies $2N-(1+N)p+\frac{N(r-1)(q-1)}{q} +Ns>0$. Therefore, if $\Theta _R(0)$ satisfies

$$\begin{aligned} \Theta _R(0)\ge \left( \frac{2c_1}{c_2}R^{2N-(1+N)p+\frac{N(r-1)(q-1)}{q} +Ns}\right) ^{\frac{1}{r+s+1-p}}:=c, \end{aligned}$$

(2.20)

then $\Theta _R(t)$ increases and is bounded below by c for all $t\in [0,T)$. Making use of (2.18) and the fact that $r+s>1$, we conclude that u(x, t) blows up in finite time for large enough initial data $u_0(x)$. $\square$

3 Second critical exponent

In this section, by means of the slow decay behavior of an initial data at spatial infinity, we find a second critical exponent using test function method and comparison principle. Note that the case $r>r_c$ results in $\alpha ^*<N.$

First of all, we derive a sufficient condition to guarantee that the solution u(x, t) blows up at finite time in the coexistence region.

Theorem 3.1

For $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, $0\le s<(1+\frac{1}{N})p-2$, $r>r_c$ and $u_0=\lambda \phi (x)$, $\lambda >0$. If $\phi (x)\in \Pi _\alpha$ and $0<\alpha <\alpha ^*$ or $\alpha \ge \alpha ^*$ with $\lambda$ large enough, then the solution u(x, t) of Cauchy problem (1.1)–(1.2) blows up in finite time.

Proof

We define the following test function

$$\begin{aligned} \psi _\epsilon (x)=D_\varepsilon e^ {-\varepsilon |x|},\quad \varepsilon >0, \end{aligned}$$

where $D_\varepsilon =\frac{1}{\int \limits _{{\mathbb {R}}^N}e^ {-\varepsilon |x|}\mathrm{d}x}=\frac{\varepsilon ^N}{\int \limits _{\omega ^N}\int \limits _0^\infty e^{-\tau }\tau ^{N-1}\mathrm{d}\tau \mathrm{d}s}$. Then it is not difficult to verify that

$$\begin{aligned} \nabla \psi _\varepsilon (x)=-\varepsilon \psi _\varepsilon (x)\frac{x}{|x|}, \end{aligned}$$

(3.1)

and

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}\psi _\varepsilon (x)\mathrm{d}x=1. \end{aligned}$$

(3.2)

Next, we introduce the auxiliary function

$$\begin{aligned} \Phi (t)=\frac{1}{\sigma }\int \limits _{{\mathbb {R}}^N}u^\sigma \psi _\varepsilon (x)\mathrm{d}x, \end{aligned}$$

where $2-p<\sigma <\frac{1}{p}$. Firstly, differentiating $\Phi (t)$, using (3.1) and Green’s formula, we obtain

$$\begin{aligned} \Phi '(t)&=\int \limits _{{\mathbb {R}}^N}u^{\sigma -1}\psi _\varepsilon \mathrm{div}(|\nabla u|^{p-2}\nabla u)\mathrm{d}x+\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _{{\mathbb {R}}^N}u^{\sigma +s} \psi _\varepsilon \mathrm{d}x \nonumber \\&=-(\sigma -1)\int \limits _{{\mathbb {R}}^N}u^{\sigma -2}\psi _\varepsilon |\nabla u|^p\mathrm{d}x+\varepsilon \int \limits _{{\mathbb {R}}^N}u^{\sigma -1}\psi _\varepsilon \frac{|\nabla u|^{p-2}}{|x|}\nabla u\cdot x\mathrm{d}x \nonumber \\&\quad +\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _{{\mathbb {R}}^N}u^{\sigma +s} \psi _\varepsilon \mathrm{d}x \nonumber \\&\ge (1-\sigma )\int \limits _{{\mathbb {R}}^N}u^{\sigma -2}\psi _\varepsilon |\nabla u|^p\mathrm{d}x-\varepsilon \int \limits _{{\mathbb {R}}^N}u^{\sigma -1}\psi _\varepsilon |\nabla u|^{p-1}\mathrm{d}x \nonumber \\&\quad +\left( \,\,\int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _{{\mathbb {R}}^N}u^{\sigma +s} \psi _\varepsilon \mathrm{d}x. \end{aligned}$$

(3.3)

Afterward, using Young’s inequality to the second term in the right side of (3.3), we get

$$\begin{aligned} \varepsilon \int \limits _{{\mathbb {R}}^N}u^{\sigma -1}\psi _\varepsilon |\nabla u|^{p-1}\mathrm{d}x\le \frac{p-1}{p}\int \limits _{{\mathbb {R}}^N}u^{\sigma -2}\psi _\varepsilon |\nabla u|^p\mathrm{d}x+\frac{\varepsilon ^p}{p}\int \limits _{{\mathbb {R}}^N}u^{\sigma +p-2}\psi _\varepsilon \mathrm{d}x. \end{aligned}$$

(3.4)

Thus, substituting (3.4) into (3.3) and by the fact that $2-p<\sigma <\frac{1}{p}$ yields the following inequality

$$\begin{aligned} \Phi '(t)\ge \left( \int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}}\int \limits _{{\mathbb {R}}^N} u^{\sigma +s}\psi _\varepsilon \mathrm{d}x-\frac{\varepsilon ^p}{p}\int \limits _{{\mathbb {R}}^N}u^{\sigma +p-2}\psi _\varepsilon \mathrm{d}x. \end{aligned}$$

(3.5)

Then applying H$\ddot{o}$lder’s inequality to the last term in the right side of (3.5), and by (3.2), we see

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}u^{\sigma +p-2}\psi _\varepsilon \mathrm{d}x=\int \limits _{{\mathbb {R}}^N}u^{\sigma +p-2}\psi _\varepsilon ^{\frac{\sigma +p-2}{\sigma +s}} \psi _\varepsilon ^{\frac{s+2-p}{\sigma +s}}\mathrm{d}x\le \left( \int \limits _{{\mathbb {R}}^N}u^{\sigma +s} \psi _\varepsilon \mathrm{d}x\right) ^{\frac{\sigma +p-2}{\sigma +s}}. \end{aligned}$$

(3.6)

In view of $2-p<\sigma <\frac{1}{p}$, $\frac{2N}{N+1}<p<2$ and $0\le s<(1+\frac{1}{N})p-2$, it follows that $\frac{\sigma +p-2}{\sigma +s}\in (0,1)$. Hence, substituting (3.6) into (3.5), we deduce

$$\begin{aligned} \Phi '(t)\ge \left( \int \limits _{{\mathbb {R}}^N}u^{\sigma +s}\psi _\varepsilon \mathrm{d}x\right) ^{\frac{\sigma +p-2}{\sigma +s}}\left[ \left( \int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\right) ^{\frac{r-1}{q}} \left( \int \limits _{{\mathbb {R}}^N}u^{\sigma +s}\psi _\varepsilon \mathrm{d}x\right) ^{\frac{s+2-p}{\sigma +s}}-\frac{\varepsilon ^p}{p}\right] . \end{aligned}$$

(3.7)

Then we estimate each integral in the right side of (3.7) by virtue of inverse H$\ddot{o}$lder’s inequality, one can see that

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}u^{\sigma +s}\psi _\varepsilon \mathrm{d}x\ge & {} \left( \,\,\int \limits _{{\mathbb {R}}^N}u^{\sigma }\psi _\varepsilon \mathrm{d}x\right) ^{\frac{\sigma +s}{\sigma }}=(\sigma \Phi (t))^{\frac{\sigma +s}{\sigma }}, \end{aligned}$$

(3.8)

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}u^q\mathrm{d}x\ge & {} \left( \,\,\int \limits _{{\mathbb {R}}^N}u^{\sigma }\psi _\varepsilon \mathrm{d}x\right) ^{\frac{q}{\sigma }}\left( \int \limits _{{\mathbb {R}}^N}\psi _\varepsilon ^{\frac{q}{q-\sigma }} \mathrm{d}x\right) ^{-\frac{q-\sigma }{\sigma }}, \end{aligned}$$

(3.9)

and calculate

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}\psi _\varepsilon ^{\frac{q}{q-\sigma }} \mathrm{d}x=C\varepsilon ^{\frac{Nq}{q-\sigma }}\int \limits _{{\mathbb {R}}^N}e^{-\frac{q}{q-\sigma } \varepsilon |x|} \mathrm{d}x=C\varepsilon ^{\frac{N\sigma }{q-\sigma }}\int \limits _{{\mathbb {R}}^N} e^{-\frac{q}{q-\sigma }|y|}\mathrm{d}y\le C\varepsilon ^{\frac{N\sigma }{q-\sigma }}. \end{aligned}$$

(3.10)

Now, combining with (3.7)–(3.10) gives

$$\begin{aligned} \Phi '(t)&\ge (\sigma \Phi (t))^{\frac{\sigma +p-2}{\sigma }}\left[ C\varepsilon ^ {-\frac{N(r-1)}{q}}(\sigma \Phi (t))^{\frac{r+s+1-p}{\sigma }}-\frac{\varepsilon ^p}{p}\right] \\&\ge \frac{c_3}{2}(\Phi (t))^{\frac{r+s+\sigma -1}{\sigma }}, \end{aligned}$$

with $c_3=C\sigma ^{\frac{r+s+\sigma -1}{\sigma }}\varepsilon ^ {-\frac{N(r-1)}{q}}$, as long as

$$\begin{aligned} \frac{1}{2}C\varepsilon ^ {-\frac{N(r-1)}{q}}(\sigma \Phi (t))^{\frac{r+s+1-p}{\sigma }} \ge \frac{\varepsilon ^p}{p}, \end{aligned}$$

which yields

$$\begin{aligned} \Phi (t)\ge \frac{1}{\sigma }\left( \frac{2}{Cp}\right) ^{\frac{\sigma }{r+s+1-p}} \varepsilon ^{(p+\frac{N(r-1)}{q})\frac{\sigma }{r+s+1-p}}. \end{aligned}$$

Thus, if $\Phi (0)$ satisfies

$$\begin{aligned} \Phi (0)\ge \frac{1}{\sigma }\left( \frac{2}{Cp}\right) ^{\frac{\sigma }{r+s+1-p}} \varepsilon ^{(p+\frac{N(r-1)}{q})\frac{\sigma }{r+s+1-p}}, \end{aligned}$$

(3.11)

then $\Phi (t)$ blows up in finite time follows from $\frac{r+s+\sigma -1}{\sigma }>1$.

It remains to verify the blow-up condition (3.11). Since $\phi (x)\in \Pi _\alpha$ and $0<\alpha <\alpha ^*$, then there exist constants $C_3$ and $R_2$ such that $\phi (x)\ge C_3|x|^{-\alpha }$ for all $|x|\ge R_2$. We compute that

$$\begin{aligned} \Phi (0)&=\frac{1}{\sigma }\int \limits _{{\mathbb {R}}^N}u_0^\sigma \psi _\varepsilon (x)\mathrm{d}x \nonumber \\&\ge \frac{\lambda ^\sigma C_3^\sigma }{\sigma }\varepsilon ^N\int \limits _{|x|\ge R_2}|x|^{-\alpha \sigma }e^{-\varepsilon |x|}\mathrm{d}x \nonumber \\&=\frac{\lambda ^\sigma C_3^\sigma }{\sigma }\varepsilon ^{\alpha \sigma }\int \limits _{|y|\ge \varepsilon R_2}|y|^{-\alpha \sigma }e^{-|y|}\mathrm{d}y. \end{aligned}$$

(3.12)

Comparing (3.11) with (3.12), when $0<\alpha <\alpha ^*=\frac{pq+N(r-1)}{q(r+s+1-p)}$, we have

$$\begin{aligned} \alpha \sigma <\left( p+\frac{N(r-1)}{q}\right) \frac{\sigma }{r+s+1-p}=\frac{pq+N(r-1)}{q(r+s+1-p)}\sigma , \end{aligned}$$

then we may choose $\varepsilon >0$ so small that (3.11) holds. If $\alpha \ge \alpha ^*$, there exists $\lambda _\varepsilon >0$ for any fixed $\varepsilon >0$ such that (3.11) holds for all $\lambda >\lambda _\varepsilon$. $\square$

Next, we prove the existence of the global solution by constructing an upper solution of the problem (1.1)–(1.2).

Theorem 3.2

For $N\ge 1$, $\frac{2N}{N+1}<p<2$, $q>1$, $0\le s<(1+\frac{1}{N})p-2$, $r>r_c$ and $u_0=\lambda \phi (x)$, $\lambda >0$. If $\phi (x)\in \Pi ^\alpha$ and $\alpha ^*<\alpha <N$, then there exist positive constants $\lambda _0=\lambda _0(\phi )$ and C such that the solution u(x, t) of Cauchy problem (1.1)–(1.2) exists globally for $\lambda \in (0,\lambda _0)$, and satisfies

$$\begin{aligned} \Vert u(x,t)\Vert _{L^\infty ({\mathbb {R}}^N)}\le Ct^{-\alpha \beta }\;\,for\;all\;\,t>0, \end{aligned}$$

where $\beta =\frac{1}{p-\alpha (2-p)}$.

Proof

Since $\phi (x)\in \Pi ^\alpha$ and $\alpha ^*<\alpha <N$, there exists a positive constant $C_4$ such that $\phi (x)\le C_4(1+|x|)^{-\alpha }$ for all $x\in {\mathbb {R}}^N$. Choosing $M>C_4$ and considering the following Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} U_t={\mathrm{div}}(|\nabla U|^{p-2}\nabla U),\quad x\in {\mathbb {R}}^N,t>0,\\ U(x,0)=M|x|^{-\alpha },\quad x\in {\mathbb {R}}^N. \end{array}\right. } \end{aligned}$$

(3.13)

It is known that the existence and uniqueness of the solution of (3.13) have been well established and the radially symmetric self-similar solution

$$\begin{aligned} U_{M,\alpha }(x,t)=t^{-\alpha \beta }f_M(\frac{|x|}{t^\beta }) \end{aligned}$$

(3.14)

was given in [20, 21], where $\beta =\frac{1}{p-\alpha (2-p)}$ and the positive function $f_M$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} (|f_M'|^{p-2}f')'+\frac{N-1}{\xi }|f_M'|^{p-2}f'(\xi )+\beta \xi f_M'(\xi )+\alpha \beta f_M(\xi )=0,\quad \xi >0,\\ f_M\ge 0,\xi \ge 0,\quad f_M'(0)=0,\quad \lim _{\xi \rightarrow \infty }\xi ^\alpha f_M(\xi )=M. \end{array}\right. } \end{aligned}$$

Note that $\beta >0$, since $\frac{2N}{N+1}<p<2$ and $\alpha <N$. Then by $\lim _{\xi \rightarrow \infty }\xi ^\alpha f_M(\xi )=M>C_4$, there is a positive constant $R_3$ such that

$$\begin{aligned} \xi ^\alpha f_M(\xi )>C_4\;\,\text {for any}\;\,\xi \ge R_3. \end{aligned}$$

Let $\gamma =f_M(R_3)=\min \{f_M(\xi )|\xi \in [0,R_3]\}>0$, it is not difficult to verify that

$$\begin{aligned} \phi (x)\le U_{M,\alpha }(x,t_0)\;\,\text {for all}\;\,x\in {\mathbb {R}}^N, \end{aligned}$$

where $t_0\in (0,1)$ and $t_0^{-\alpha \beta }\gamma >\Vert \phi \Vert _\infty$.

Next, through a simple calculation, we obtain

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}U_{M,\alpha }^q(x,t+t_0)\mathrm{d}x&=(t+t_0)^{-\alpha \beta q}\int \limits _{{\mathbb {R}}^N}f_M^q\left( \frac{|x|}{(t+t_0)^\beta }\right) \mathrm{d}x \nonumber \\&=(t+t_0)^{\beta (N-\alpha q)}\int \limits _{{\mathbb {R}}^N}f_M^q(|y|)\mathrm{d}y\nonumber \\&\le C(t+t_0)^{\beta (N-\alpha q)}. \end{aligned}$$

(3.15)

Now, let h(t) be the solution of the following ordinary differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} h'(t)=C\lambda ^{r+s-1}(t+t_0)^{-\theta }h^{r+s}(t),\quad t>0,\\ h(0)=1, \end{array}\right. } \end{aligned}$$

(3.16)

where $\theta >1$. The local existence and uniqueness of solution h(t) for (3.16) follow from the standard theory of initial value problem on ordinary differential equation.

Afterward, we claim that there exists $\lambda _0=\lambda _0(\phi )>0$ such that h(t) is bounded in $[0,+\infty )$ for all $\lambda \in [0,\lambda _0)$. Integrating (3.16) over [0, t] to compute

$$\begin{aligned} 1-h^{-(r+s-1)}(t)=C(r+s-1)\lambda ^{r+s-1}\int \limits _0^t(\tau +t_0)^{-\theta }\mathrm{d}\tau \le \frac{C(r+s-1)\lambda ^{r+s-1}t_0^{-\theta +1}}{\theta -1}. \end{aligned}$$

Let $\lambda _0=\lambda _0(\phi )>0$ satisfies $\frac{C(r+s-1)\lambda _0^{r+s-1}t_0^{-\theta +1}}{\theta -1}=1$, and define

$$\begin{aligned} C_\lambda =\frac{C(r+s-1)\lambda ^{r+s-1}t_0^{-\theta +1}}{\theta -1},\quad h_\lambda =(\frac{1}{1-C_\lambda })^{\frac{1}{r+s-1}}, \end{aligned}$$

for $\lambda \in [0,\lambda _0)$. It is easy to verify that $h(t)\le h_\lambda$ in $[0,+\infty )$.

Then, we construct the following global solution

$$\begin{aligned} {\bar{u}}(x,t)=\lambda h(t)U_{M,\alpha }(x,t+t_0), \end{aligned}$$

where $U_{M,\alpha }(x,t+t_0)$ is the solution of (3.13) and h(t) solves (3.16) with $\theta =\frac{\alpha qs-(N-\alpha q)(r-1)}{pq-\alpha q(2-p)}$. Note that $\theta >1$ for $\alpha >\alpha ^*=\frac{pq+N(r-1)}{q(r+s+1-p)}$. Combining with (3.15), it is easy to verify that

$$\begin{aligned}&{\bar{u}}_t-\mathrm{div}(|\nabla {\bar{u}}|^{p-2}\nabla {\bar{u}})- \left( \int \limits _{{\mathbb {R}}^N}{\bar{u}}^q(x,t)\mathrm{d}x\right) ^{\frac{r-1}{q}}{\bar{u}}^{s+1} \nonumber \\&\quad =\lambda h'(t)U_{M,\alpha }-\lambda ^{r+s}h^{r+s}(t) \left( \int \limits _{{\mathbb {R}}^N}U_{M,\alpha }^q(x,t+t_0)\mathrm{d}x\right) ^{\frac{r-1}{q}}U_{M,\alpha }^{s+1}\nonumber \\&\quad \ge \lambda U_{M,\alpha }[h'(t)-C\lambda ^{r+s-1}(t+t_0)^{\frac{\beta (N-\alpha q)(r-1)}{q}}h^{r+s}(t)\Vert U_{M,\alpha }\Vert _\infty ^s]\nonumber \\&\quad =\lambda U_{M,\alpha }[h'(t)-C\lambda ^{r+s-1}(t+t_0)^{-(\theta -\alpha \beta s)}h^{r+s}(t)\Vert U_{M,\alpha }\Vert _\infty ^s]\nonumber \\&\quad \ge \lambda U_{M,\alpha }[h'(t)-C\lambda ^{r+s-1}(t+t_0)^{-\theta }h^{r+s}(t)]\nonumber \\&\quad =0. \end{aligned}$$

(3.17)

Moreover, the initial data ${\bar{u}}(x,0)$ satisfy

$$\begin{aligned} {\bar{u}}(x,0)=\lambda U_{M,\alpha }(x,t_0)\ge \lambda \phi (x)=u_0. \end{aligned}$$

(3.18)

Therefore, it follows from (3.17) and (3.18) that ${\bar{u}}(x,t)$ is a global supersolution of Cauchy problem (1.1)–(1.2). Furthermore, we derive the decay estimate for the solution u(x, t) as follows

$$\begin{aligned} \Vert u(x,t)\Vert _{L^\infty ({\mathbb {R}}^N)}\le \lambda h_\lambda \Vert U_{M,\alpha }(x,t)\Vert _{L^\infty ({\mathbb {R}}^N)}\le Ct^{-\alpha \beta }, \end{aligned}$$

(3.19)

for all $t>0$. $\square$

4 Large time behavior and life span

In this section, we give the large time behavior of the global solution and a life span of the non-global solution by the scaling technique and constructing a blow-up supersolution of problem (1.1)–(1.2).

Firstly, the large time behavior of the global solution is represented in the following theorem.

Theorem 4.1

Suppose that the conditions in Theorem 3.2 hold, and $\lim _{|x|\rightarrow \infty }|x|^\alpha \phi (x)=M>0$, then the solution u(x, t) of Cauchy problem (1.1)–(1.2) satisfies

$$\begin{aligned} t^{\alpha \beta }|u(x,t)-U_{\lambda ,M,\alpha }(x,t)|\rightarrow 0\;\,as\;\, t\rightarrow \infty \end{aligned}$$

uniformly in compact set of ${\mathbb {R}}^N$ for $\lambda \in (0,\lambda _0)$, where $\lambda _0,\beta$ are same as in Theorem 3.2, and $U_{\lambda ,M,\alpha }(x,t)$ is the solution of the following Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} U_t=\mathrm{div}(|\nabla U|^{p-2}\nabla U),\quad x\in {\mathbb {R}}^N,t>0,\\ U(x,0)=\lambda M|x|^{-\alpha },\quad x\in {\mathbb {R}}^N. \end{array}\right. } \end{aligned}$$

Proof

We define $u_k(x,t)=k^\alpha u(kx,k^{p-\alpha (2-p)}t)$ with $k>1$. Then $u_k(x,t)$ solves

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{kt}=\mathrm{div}(|\nabla u_k|^{p-2}\nabla u_k) +k^{p-\alpha (r+s+1-p)}(\int \limits _{{\mathbb {R}}^N}u_k^q\mathrm{d}x)^{\frac{r-1}{q}}u_k^{s+1},\;\; x\in {\mathbb {R}}^N,t>0,\\ u_k(x,0)=\lambda k^\alpha \phi (kx),\;\; x\in {\mathbb {R}}^N. \end{array}\right. } \end{aligned}$$

(4.1)

Applying the decay estimate (3.19) for the global solution u(x, t), we have

$$\begin{aligned} \Vert u_k(x,t)\Vert _{L^\infty ({\mathbb {R}}^N)} =k^\alpha \Vert u(kx,k^{p-\alpha (2-p)}t)\Vert _{L^\infty ({\mathbb {R}}^N)} \le Ct^{-\alpha \beta }. \end{aligned}$$

Thus, $\{u_k(x,t)\}$ is uniformly bounded in ${\mathbb {R}}^N\times [\delta ,\infty )$ for any $\delta >0$. As was shown in [2], we conclude that ${u_k(x,t)}$ is relatively compact in $L_{loc}^\infty ({\mathbb {R}}^N\times (0,\infty ))$. Then using the Ascoli–Arzela theorem and a diagonal sequence method in $\delta$, we see that for any sequence $k_j\rightarrow \infty$, there exist a subsequence $k_j'\rightarrow \infty$ and a function $\omega (x,t)\in C({\mathbb {R}}^N\times (0,\infty ))$ such that

$$\begin{aligned} u_{k_j'}(x,t)\rightarrow \omega (x,t)\;\,\text {as}\;\,k_j'\rightarrow \infty \end{aligned}$$

local uniformly in ${\mathbb {R}}^N\times (0,\infty )$.

Next, we show that $\omega (x,t)=U_{\lambda ,M,\alpha }(x,t)$. Firstly, the weak solution $u_k(x,t)$ satisfies (4.1) in the distribution sense

$$\begin{aligned}&\int \limits _{{\mathbb {R}}^N}u_k(x,t)\psi (x,t)\mathrm{d}x-\int \limits _{{\mathbb {R}}^N}u_k(x,0)\psi (x,0)\mathrm{d}x =\int \limits _0^t\int \limits _{{\mathbb {R}}^N}u_k\psi _\tau \mathrm{d}x\mathrm{d}\tau \nonumber \\&\quad -\int \limits _0^t\int \limits _{{\mathbb {R}}^N}|\nabla u_k|^{p-2}\nabla u_k\cdot \nabla \psi +k^{p-\alpha (r+s+1-p)}\left( \int \limits _{{\mathbb {R}}^N}u_k^q\mathrm{d}x\right) ^ {\frac{r-1}{q}}u_k^{s+1}\psi \mathrm{d}x\mathrm{d}\tau , \end{aligned}$$

(4.2)

for any nonnegative function $\psi (x,t)\in C_0^\infty ({\mathbb {R}}^N\times [0,\infty ))$. Then by virtue of the assumption $\lim _{|x|\rightarrow \infty }|x|^\alpha \phi (x)=M>0$, it follows that

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}u_k(x,0)\psi (x,0)\mathrm{d}x&=\int \limits _{{\mathbb {R}}^N}\lambda k^\alpha \phi (kx)\psi (x,0) \nonumber \\&\rightarrow \lambda M\int \limits _{{\mathbb {R}}^N}|x|^{-\alpha }\psi (x,0)\mathrm{d}x \end{aligned}$$

(4.3)

as $k=k_j'\rightarrow \infty$. On the other hand, using variable transformation to the last term on the right side of (4.2), we deduce that

$$\begin{aligned}&\int \limits _0^t\int \limits _{{\mathbb {R}}^N}k^{p-\alpha (r+s+1-p)}\left( \int \limits _{{\mathbb {R}}^N}u_k^q\mathrm{d}x\right) ^ {\frac{r-1}{q}}u_k^{s+1}\psi \mathrm{d}x\mathrm{d}\tau \nonumber \\&\quad =\int \limits _0^{k^{p-\alpha (2-p)}t}\left( \int \limits _{{\mathbb {R}}^N}u^q(kx,\tau )\mathrm{d}x\right) ^{\frac{r-1}{q}} \int \limits _{{\mathbb {R}}^N}k^\alpha u^{s+1}(kx,\tau )\psi (x,k^{-p+\alpha (2-p)}\tau )\mathrm{d}x\mathrm{d}\tau . \end{aligned}$$

(4.4)

We know from the proof of Theorem 3.2 that ${\bar{u}}(x,t)$ is a supersolution of Cauchy problem (1.1)–(1.2), and the condition $\lim _{\xi \rightarrow \infty }\xi ^\alpha f_M(\xi )=M$, then we get

$$\begin{aligned}&k^\alpha u^{s+1}(kx,t)\le k^\alpha {\bar{u}}^{s+1}(kx,t)=k^\alpha \lambda ^{s+1}h^{s+1}(t)(t+t_0)^{-\alpha \beta (s+1)} f_M^{s+1}\left( \frac{|kx|}{(t+t_0)^\beta }\right) \nonumber \\&\quad =k^{-\alpha s}\lambda ^{s+1}|x|^{-\alpha (s+1)}h^{s+1}(t)\left[ \left( \frac{|kx|}{(t+t_0)^\beta }\right) ^\alpha f_M\left( \frac{|kx|}{(t+t_0)^\beta }\right) \right] ^{s+1}\rightarrow 0 \end{aligned}$$

(4.5)

as $k=k_j'\rightarrow \infty$. Similarly, we have

$$\begin{aligned} u^q(kx,t)\rightarrow 0\;\,\text {as}\;\,k=k_j'\rightarrow \infty . \end{aligned}$$

(4.6)

Thus, by (4.5), (4.6) and the Lebesgue-dominated convergence theorem, (4.4) turns into

$$\begin{aligned} \int \limits _0^t\int \limits _{{\mathbb {R}}^N}k^{p-\alpha (r+s+1-p)}\left( \int \limits _{{\mathbb {R}}^N}u_k^q\mathrm{d}x\right) ^ {\frac{r-1}{q}}u_k^{s+1}\psi \mathrm{d}x\mathrm{d}\tau \rightarrow 0 \end{aligned}$$

(4.7)

as $k=k_j'\rightarrow \infty$. Let $k=k_j'\rightarrow \infty$ in (4.2), it follows from (4.3) and (4.7) that

$$\begin{aligned}&\int \limits _{{\mathbb {R}}^N}\omega (x,t)\psi (x,t)\mathrm{d}x-\lambda M\int \limits _{{\mathbb {R}}^N}|x|^{-\alpha }\psi (x,0)\mathrm{d}x \nonumber \\&\quad =\int \limits _0^t\int \limits _{{\mathbb {R}}^N}\omega \psi _\tau -|\nabla \omega |^{p-2}\nabla \omega \cdot \nabla \psi \mathrm{d}x\mathrm{d}\tau . \end{aligned}$$

(4.8)

This implies that $\omega (x,t)$ is the weak solution to the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega _t=\mathrm{div}(|\nabla \omega |^{p-2}\nabla \omega ),\quad x\in {\mathbb {R}}^N,t>0,\\ \omega (x,0)=\lambda M|x|^{-\alpha },\quad x\in {\mathbb {R}}^N, \end{array}\right. } \end{aligned}$$

(4.9)

then by the uniqueness of the weak solution of (4.9), we deduce that $\omega (x,t)=U_{\lambda ,M,\alpha }(x,t)$. Thus, we have proved that

$$\begin{aligned} u_k(x,t)\rightarrow U_{\lambda ,M,\alpha }(x,t)\;\,\text {as}\;\,k\rightarrow \infty \end{aligned}$$

(4.10)

uniformly in compact set of ${\mathbb {R}}^N\times (0,\infty )$. Let $t=1$ in (4.10), we obtain

$$\begin{aligned} u_k(x,1)\rightarrow U_{\lambda ,M,\alpha }(x,1)\;\,\text {as}\;\,k\rightarrow \infty , \end{aligned}$$

that is

$$\begin{aligned} k^\alpha u(kx,k^{p-\alpha (2-p)})\rightarrow f_{\lambda ,M}(|x|)\;\,\text {as}\;\,k\rightarrow \infty \end{aligned}$$

(4.11)

uniformly in compact set of ${\mathbb {R}}^N$. Setting $y=kx$ and $\tau =k^{p-\alpha (2-p)}$ in (4.11), then we get

$$\begin{aligned} \tau ^{\frac{\alpha }{p-\alpha (2-p)}}u(y,\tau )\rightarrow f_{\lambda ,M}\left( \frac{|y|}{\tau ^{\frac{1}{p-\alpha (2-p)}}}\right) \;\,\text {as}\;\,\tau \rightarrow \infty . \end{aligned}$$

Therefore, we conclude from (3.14) that

$$\begin{aligned} t^{\alpha \beta }|u(x,t)-U_{\lambda ,M,\alpha }(x,t)|\rightarrow 0\;\,\text {as}\;\,t\rightarrow \infty \end{aligned}$$

uniformly in compact set of ${\mathbb {R}}^N$, where $\beta =\frac{1}{p-\alpha (2-p)}.$ $\square$

Finally, we give a life span of the non-global solution by constructing a blow-up supersolution of problem (1.1)–(1.2).

Theorem 4.2

Suppose that u(x, t) is a solution of problem (1.1)–(1.2) under the conditions of Theorem 3.1, which blows up at finite time T, and $\Vert \phi \Vert _{L^\infty ({\mathbb {R}}^N)}=\lim _{|x|\rightarrow \infty }\phi =\phi _\infty$. Then the life span of u(x, t) satisfies

$$\begin{aligned} \frac{c_4}{r+s-1}(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)}\le T\le \frac{c_5}{r+s-1}(\lambda \phi _\infty )^{-(r+s-1)}, \end{aligned}$$

where

$$\begin{aligned}&c_4\le \min \left\{ \frac{3}{c_6( (2-p)L_4+L_3)L_2^{p-2}}, \frac{3}{2(p-1)L_2^p}, \frac{3}{(\int \limits _{{\mathbb {R}}^N}(1+\phi )^{-q}\mathrm{d}x)^{\frac{r-1}{q}}},c_5\right\} ,\\&c_5=\frac{2\sigma ^{\frac{r+s+\sigma -1}{\sigma }}}{c_3},\\&c_6=\max \{1,(1+L_1)^{3-2p}\},\\&L_1=\max \phi ,\;L_2=\max |\nabla \phi |,\;L_3=\max |\Delta \phi |,\;L_4=\max |D^2\phi |. \end{aligned}$$

Proof

Firstly, in the proof of Theorem 3.1, we have already obtained an upper bound of the blow-up time for u(x, t) in the measure of $\Phi (t)$ as follows

$$\begin{aligned} T\le \frac{2\sigma }{c_3(r+s-1)}\left( \frac{\lambda ^\sigma }{\sigma } \int \limits _{{\mathbb {R}}^N}\phi ^\sigma \psi _\varepsilon \mathrm{d}x\right) ^{-\frac{r+s-1}{\sigma }}. \end{aligned}$$

Then, it follows from $\Vert \phi \Vert _{L^\infty ({\mathbb {R}}^N)}=\lim _{|x|\rightarrow \infty }\phi =\phi _\infty$ that there exists $R_4$ such that $|\phi -\phi _\infty |<\varepsilon$ for $|x|>R_4$ and any $\varepsilon >0$. Meanwhile, by the definition of test function $\psi _\varepsilon (x)$, we have

$$\begin{aligned} T\le \frac{2\sigma }{c_3(r+s-1)}\left( \frac{\lambda ^\sigma }{\sigma } (\phi _\infty -\varepsilon )^\sigma \right) ^{-\frac{r+s-1}{\sigma }} \end{aligned}$$

for $R_2>R_4$. Thus, from the arbitrariness of $\varepsilon$, let $\varepsilon \rightarrow 0$ can yield that

$$\begin{aligned} T\le \frac{c_5}{r+s-1}(\lambda \phi _\infty )^{-(r+s-1)}, \end{aligned}$$

(4.12)

where $c_5=\frac{2\sigma ^{\frac{r+s+\sigma -1}{\sigma }}}{c_3}$.

On the other hand, in order to estimate T from below, we shall construct a suitable supersolution of (1.1)–(1.2). To this end, we consider the following ordinary differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} z'(t)=\frac{1}{c_4}z^{r+s}(t),\quad t>0,\\ z(0)=\lambda \phi _\infty (1+\lambda \phi _\infty )+1. \end{array}\right. } \end{aligned}$$

(4.13)

By a direct calculation, one can see that the solution z(t) of (4.13) is given by

$$\begin{aligned} z(t)=[(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)} -\frac{r+s-1}{c_4}t]^{-\frac{1}{r+s-1}}, \end{aligned}$$

and $z(t)>1$ for all $0<t<\frac{c_4}{r+s-1}(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)}$.

Next, we define

$$\begin{aligned} w(x)=\frac{1}{1+\phi (x)}, \end{aligned}$$

and let

$$\begin{aligned} L_1=\max \phi ,\;L_2=\max |\nabla \phi |,\; L_3=\max |\Delta \phi |,\; \mathrm{and}\;L_4=\max |D^2\phi |. \end{aligned}$$

Now, we construct the following blow-up supersolution

$$\begin{aligned} {\bar{u}}(x,t)=z(t)w(x). \end{aligned}$$

Since $z(t)>1$, $0<w(x)\le 1$ and $r+s>1$, we then deduce

$$\begin{aligned}&{\bar{u}}_t-\mathrm{div}\left( |\nabla {\bar{u}}|^{p-2}\nabla {\bar{u}}\right) - \left( \int \limits _{{\mathbb {R}}^N}{\bar{u}}^q\mathrm{d}x\right) ^{\frac{r-1}{q}}{\bar{u}}^{s+1} \\&\quad =z'w+z^{p-1}\mathrm{div}\left( |\nabla \phi |^{p-2}\nabla \phi w^{2(p-1)}\right) -z^{r+s} \left( \int \limits _{{\mathbb {R}}^N}w^q\mathrm{d}x\right) ^{\frac{r-1}{q}}w^{s+1}\\&\quad \ge \frac{1}{c_4}z^{r+s}w-\left( (2-p)L_4+L_3\right) L_2^{p-2}z^{p-1}w^{2(p-1)}-2(p-1)L_2^pz^{p-1}w^{2p-1}\\&\qquad -z^{r+s} \left( \int \limits _{{\mathbb {R}}^N}w^q\mathrm{d}x\right) ^{\frac{r-1}{q}}w^{s+1}\\&\quad \ge \left( \frac{3}{c_4}-c_6( (2-p)L_4+L_3)L_2^{p-2}\right) z^{p-1}w+ \left( \frac{3}{c_4}-2(p-1)L_2^p\right) z^{p-1}w\\&\qquad +\left( \frac{3}{c_4}- \left( \int \limits _{{\mathbb {R}}^N}(1+\phi )^{-q}\mathrm{d}x\right) ^{\frac{r-1}{q}}\right) z^{r+s}w \end{aligned}$$

by a simple calculation, where $c_6=\max \{1,(1+L_1)^{3-2p}\}$. Therefore, applying the comparison principle ([2]) and

$$\begin{aligned} c_4\le \min \left\{ \frac{3}{c_6( (2-p)L_4+L_3)L_2^{p-2}}, \frac{3}{2(p-1)L_2^p}, \frac{3}{(\int \limits _{{\mathbb {R}}^N}(1+\phi )^{-q}\mathrm{d}x)^{\frac{r-1}{q}}}\right\} , \end{aligned}$$

it can be easily shown that ${\bar{u}}(x,t)=z(t)w(x)$ is a supersolution of problem (1.1)–(1.2). We then obtain a lower bound of the blow-up time, i.e.,

$$\begin{aligned} T\ge \frac{c_4}{r+s-1}(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)}. \end{aligned}$$

(4.14)

Therefore, combining (4.12), (4.14) and $c_4\le c_5$ , we get the life span of the non-global solution for problem (1.1)–(1.2) as follows

$$\begin{aligned} \frac{c_4}{r+s-1}(\lambda \phi _\infty (1+\lambda \phi _\infty )+1)^{-(r+s-1)}\le T\le \frac{c_5}{r+s-1}(\lambda \phi _\infty )^{-(r+s-1)}. \end{aligned}$$

$\square$