Abstract
We show that any Abelian module category over the (degenerate or quantum) Heisenberg category satisfying suitable finiteness conditions may be viewed as a 2-representation over a corresponding Kac–Moody 2-category (and vice versa). This gives a way to construct Kac–Moody actions in many representation-theoretic examples which is independent of Rouquier’s original approach via “control by \(K_0\).” As an application, we prove an isomorphism theorem for generalized cyclotomic quotients of these categories, extending the known isomorphism between cyclotomic quotients of type A affine Hecke algebras and quiver Hecke algebras.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The field of higher representation theory has both benefitted and suffered from a multiplicity of perspectives. One such juncture is in the definition of a categorical action of a Kac–Moody algebra, which was developed independently by Rouquier [34] and Khovanov and Lauda [27]. Both of these works introduced a remarkable new 2-category, the Kac–Moody 2-category \({{\mathfrak {U}}}(\mathfrak {g})\) associated to a symmetrizable Kac–Moody algebra \(\mathfrak {g}\), although it took several more years before the distinct approaches taken in [27, 34] were reconciled with one another; see [3]. The object set of \({{\mathfrak {U}}}(\mathfrak {g})\) is the weight lattice X of the underlying Kac–Moody algebra. Then a categorical action of \(\mathfrak {g}\) on a family of categories \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) is the data of a strict 2-functor from \({{\mathfrak {U}}}(\mathfrak {g})\) to the 2-category \(\mathfrak {Cat}\) of categories sending \(\lambda \) to \({{\mathcal {R}}}_\lambda \) for each \(\lambda \in X\). This means that there are functors \(E_i:{{\mathcal {R}}}_\lambda \rightarrow {{\mathcal {R}}}_{\lambda +\alpha _i}\), \(F_i:{{\mathcal {R}}}_{\lambda +\alpha _i}\rightarrow {{\mathcal {R}}}_{\lambda }\) corresponding to the Chevalley generators \(e_i, f_i\,(i \in I)\) of \(\mathfrak {g}\) (where \(\alpha _i\) is the ith simple root), and there are natural transformations between these functors satisfying relations paralleling the 2-morphisms in \({{\mathfrak {U}}}(\mathfrak {g})\). These relations are recorded in Sect. 3.3 below. They imply that
-
(KM1)
there are prescribed adjunctions \((E_i, F_i)\) for all \(i \in I\);
-
(KM2)
for \(d \ge 0\) there is an action of the quiver Hecke algebra \(QH_d\) of the same Cartan type as \(\mathfrak {g}\) on the dth power of the functor \(E := \bigoplus _{i \in I} E_i\);
-
(KM3)
there is an explicit isomorphism of functors lifting the familiar Chevalley relation \([e_i, f_j] = \delta _{i,j} h_i\) in the Lie algebra \(\mathfrak {g}\); see (3.56)–(3.58).
In this article, we will only consider categorical actions on Abelian categories satisfying certain finiteness properties, which are needed to ensure that the relevant morphism spaces are finite-dimensional vector spaces. More precisely, all categories considered will either be locally finite Abelian or Schurian \(\Bbbk \)-linear categories for a fixed algebraically closed field \(\Bbbk \); see Sect. 2.2 for these definitions. All functors between such categories will be assumed to be \(\Bbbk \)-linear without further mention.
In Cartan type A, Rouquier also introduced a related notion of \(\mathfrak {sl}'_I\)-categorification, which was based in part on his previous work with Chuang [17] treating the case of \(\mathfrak {sl}_2\). Instead of the tower of quiver Hecke algebras mentioned in the previous paragraph, the definition of \(\mathfrak {sl}'_I\)-categorification involves a tower of affine Hecke algebras of type A (either quantum or degenerate). In more detail, assume that we are given \(z=q-q^{-1} \in \Bbbk \). Let \(AH_d\) be the affine Hecke algebra corresponding to the symmetric group \(\mathfrak {S}_d\) with defining parameter q if \(z \ne 0\), or its degenerate analog if \(z=0\). Let I be a subset of \(\Bbbk \) closed under the automorphisms \(i \mapsto i^\pm \) defined by
assuming moreover that \(0 \notin I\) in the quantum case. The map \(i \mapsto i^+\) defines edges making the set I into a quiver with connected components of type \(\mathrm A_\infty \) if \(p= 0\) or \(\mathrm A_{p-1}^{(1)}\) if \(p\ne 0\), where \(p\) is the (not necessarily prime!) quantum characteristic, that is, the smallest positive integer such that \(q^{p-1}+q^{p-3}+\cdots +q^{1-p}=0\) or 0 if no such integer exists. Let \(\mathfrak {g} = \mathfrak {sl}_I'\) be the corresponding (derived) Kac–Moody algebra. To have an \(\mathfrak {sl}'_I\)-categorification on a locally finite Abelian or Schurian \(\Bbbk \)-linear category \({{\mathcal {R}}}\), one needs:
-
(SL1)
an adjoint pair (E, F) of endofunctors of \({{\mathcal {R}}}\) such that F is also left adjoint to E;
-
(SL2)
endomorphisms \(x:E \Rightarrow E\) and \(\tau :E^2 \Rightarrow E^2\) inducing an action of \(AH_d\) on the dth power \(E^d\) for all \(d \ge 0\).
Assume moreover that all eigenvalues of \(x:E \Rightarrow E\) belong to the given set I so that, by taking generalized eigenspaces, one obtains decompositions of E and its adjoint F into eigenfunctors: \(E = \bigoplus _{i \in I} E_i\), \(F = \bigoplus _{i \in I} F_i\). Then, we require that
-
(SL3)
the induced maps \(e_i := [E_i]\) and \(f_i := [F_i]\) make the complexified Grothendieck group \({{\mathbb {C}}}\otimes _{{{\mathbb {Z}}}} K_0({{\mathcal {R}}})\) into an integrable representation of the Lie algebra \(\mathfrak {g}\), with the Grothendieck group of each block of \({{\mathcal {R}}}\) giving rise to an isotypic representation of the Cartan subalgebra \(\mathfrak {h}\) of \(\mathfrak {g}\).
Under these hypotheses, there is an induced categorical action of \(\mathfrak {g}\) on \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) in the sense defined in the previous paragraph, for Serre subcategories \({{\mathcal {R}}}_\lambda \) of \({{\mathcal {R}}}\) defined so that \({{\mathbb {C}}}\otimes _{{\mathbb {Z}}}K_0({{\mathcal {R}}}_\lambda )\) is the \(\lambda \)-weight space of \({{\mathbb {C}}}\otimes _{{\mathbb {Z}}}K_0({{\mathcal {R}}})\). This fundamental result is known as “control by \(K_0\);” see [34, Theorem 5.30] in the locally finite Abelian case and [8, Theorem 4.27] for the extension to the Schurian case. In its proof, the property (SL1) obviously implies (KM1), and (SL2) implies (KM2) due to the isomorphism \({\widehat{AH}}_d \cong {\widehat{QH}}_d\) between completions of affine Hecke algebras and quiver Hecke algebras discovered in [10, 34]. Finally, and most interesting, to pass from (SL3) (which involves relations at the level of the Grothendieck group) to (KL3) (which involves “higher” relations), Rouquier applies the sophisticated structure theory developed in [17], thereby reducing the proof to minimal \(\mathfrak {sl}_2\)-categorifications which are analyzed explicitly.
In the current literature, almost all examples of categorical actions of Kac–Moody algebras of Cartan type A on Abelian categories are constructed via this “control by \(K_0\)” theorem. In this article, we develop a new approach to constructing such Kac–Moody actions based instead on the Heisenberg category \(\mathcal {H}eis_k\) of central charge \(k \in {{\mathbb {Z}}}\). This is a monoidal category that is constructed from affine Hecke algebras in a way that is entirely analogous to the construction of the Kac–Moody 2-category from quiver Hecke algebras. It comes in two forms, degenerate or quantum, depending on the parameter \(z=q-q^{-1}\) as fixed above. In the special case \(k=-1\), the Heisenberg category was defined originally in the degenerate case by Khovanov [25] and in the quantum case by Licata and the second author [28]. The appropriate extension of the definition to arbitrary central charge was worked out much more recently; see [4, 30] in the degenerate case and [13] in the quantum case. A categorical Heisenberg action on a category \({{\mathcal {R}}}\) is the data of a strict monoidal functor \(\mathcal {H}eis_k \rightarrow \mathcal {E}nd({{\mathcal {R}}})\), where \(\mathcal {E}nd({{\mathcal {R}}})\) is the strict monoidal category consisting of endofunctors and natural transformations. In view of the defining relations of \(\mathcal {H}eis_k\) recorded in Sects. 3.1 and 3.2 below, this means that there are endofunctors \(E, F:{{\mathcal {R}}}\rightarrow {{\mathcal {R}}}\) and natural transformations such that
-
(H1)
there is a prescribed adjunction (E, F);
-
(H2)
for \(d \ge 0\) there is an action of \(AH_d\) on \(E^d\);
-
(H3)
there is an explicit isomorphism of functors lifting the relation \([e,f] = k\) in the Heisenberg algebra of central charge k; see (3.9) and (3.10) in the degenerate case and (3.33) and (3.34) in the quantum caseFootnote 1.
The properties (H1)–(H3) exactly parallel (KM1)–(KM3), unlike (SL1)–(SL3). Now we can formulate our first main theorem; see Theorem 4.11 below for a more precise statement. The idea of the proof is to upgrade the homomorphism \({\widehat{QH}}_d \rightarrow {\widehat{AH}}_d\) constructed in [10, 34] to the entire 2-category \({{\mathfrak {U}}}(\mathfrak {g})\).
Theorem A
Let \({{\mathcal {R}}}\) be either a locally finite Abelian or a Schurian \(\Bbbk \)-linear category equipped with a categorical Heisenberg action. Let I be the spectrum of \({{\mathcal {R}}}\), that is, the set of eigenvalues of the given endomorphism \(x:E \Rightarrow E\). This set is closed under the maps \(i \mapsto i^{\pm }\) defined above. Let \(\mathfrak {g} = \mathfrak {sl}_I'\) be the corresponding Kac–Moody algebra with weight lattice X. For each \(\lambda \in X\), there is a Serre subcategory \({{\mathcal {R}}}_\lambda \) of \({{\mathcal {R}}}\) defined explicitly in Sect. 4.2 below in terms of the action of \({{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1})\) (“bubbles”). Moreover, there is a canonically induced categorical action of \(\mathfrak {g}\) on \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) in the sense of (KM1)–(KM3).
This theorem considerably simplifies the construction of the most important examples of categorical Kac–Moody actions. In these examples, the existence of a Heisenberg action is straightforward to demonstrate, so that Theorem A can be applied without any need to develop the theory to the point of being able to check relations on the Grothendieck group. Of course it is still important to investigate such aspects, but it is helpful to have the rich structure theory of a categorical Kac–Moody action in place from the outset. For example, one often wants to compute the spectrum I exactly, or to find an explicit combinatorial description of the underlying crystal structure on the set \(\mathbf{B} \) of isomorphism classes of irreducible objects. The answers to these sorts of more intricate combinatorial questions tend to vary in a discontinuous fashion as parameters change, whereas the existence of a Heisenberg action is more robust.
1.1 Representations of symmetric groups and related Hecke algebras
The original motivating example comes from the representation theory of the symmetric groups \(\mathfrak {S}_d\). As observed in [17, \(\S \)7.1], the classical representation theory of symmetric groups (Specht modules, branching rules, blocks, etc...) implies that \({{\mathcal {R}}}:= \bigoplus _{d \ge 0} \Bbbk \mathfrak {S}_d\text {-}{\text {mod}}_{{\text {fd}}}\) admits the structure of an \(\mathfrak {sl}_I'\)-categorification with E given by induction and F by restriction. The set I (which is the spectrum in our language) is the image of \({{\mathbb {Z}}}\) in \(\Bbbk \), so that \(\mathfrak {sl}_I'\) is \(\mathfrak {sl}_\infty ({{\mathbb {C}}})\) if \(p= 0\) or \(\widehat{\mathfrak {sl}}_p({{\mathbb {C}}})'\) if \(p> 0\). Applying “control by \(K_0\)” it follows that there is an induced categorical action of \(\mathfrak {g}=\mathfrak {sl}_I'\); the Grothendieck group \(K_0({{\mathcal {R}}})\) is a \({{\mathbb {Z}}}\)-form for the basic representation of \(\mathfrak {g}\) (e.g., see [11, Theorem 4.18]). Subsequently, Khovanov [25] used this example to motivate his definition of the degenerate Heisenberg category \(\mathcal {H}eis_{-1}\), making the existence of a categorical Heisenberg action on \({{\mathcal {R}}}\) almost tautological: the conditions (H1) and (H2) are immediate while (H3) follows from the Mackey isomorphism \(F \circ E \cong E \circ F\oplus {\text {Id}}\). So now Theorem A gives a new proof of the existence of a categorical action of \(\mathfrak {g}\), without any need to appeal to combinatorial facts from the representation theory of symmetric groups. (See also [32] for a different point of view.)
There are many much-studied variations on this example, in which one replaces \(\Bbbk \mathfrak {S}_d\) by higher level cyclotomic quotients of (degenerate or quantum) affine Hecke algebras or quiver Hecke algebras; see [1, 11, 23]. The Grothendieck groups in these cases give \({{\mathbb {Z}}}\)-forms for the other integrable highest or lowest weight representations. Another closely related situation is the category \(\mathcal {O}\) for rational Cherednik algebras of types \(G(\ell ,1,d)\) for \(d \ge 0\), which categorifies Fock space; see [21, 36]. This also includes categories of modules over cyclotomic q-Schur algebras as a special case. We refer the reader to [13, \(\S \S \)6–7] for further discussion of this from the perspective of the quantum Heisenberg category; our approach does not require any integrality assumptions unlike much of the existing literature.
1.2 Representations of the general linear group and related algebras
There are many variants of the representation theory of the general linear group, including
-
rational representations of the algebraic group \(GL_n\) over \(\Bbbk \);
-
representations of the Lie algebra \(\mathfrak {gl}_n({{\mathbb {C}}})\) in the BGG category \({\mathcal {O}}\);
-
analogous categories for the general linear supergroup \(GL_{m|n}\) and its Lie superalgebra;
-
finite-dimensional representations of restricted enveloping algebras arising from the Lie algebra \(\mathfrak {gl}_n(\Bbbk )\) over a field of positive characteristic;
-
analogous categories for the quantized enveloping algebra \(U_q(\mathfrak {gl}_n)\), including situations in which q is a root of unity.
Each of these gives rise to a locally finite Abelian category \({{\mathcal {R}}}\) admitting a categorical Heisenberg action of central charge zero, either degenerate in the classical cases or quantum when \(U_q(\mathfrak {gl}_n)\) is involved. The endofunctors E and F are defined by tensoring with the n-dimensional defining representation V and its dual \(V^*\), respectively. The endomorphism \(x:E \Rightarrow E\) arises from the action of the Casimir tensor, while \(\tau :E^2 \Rightarrow E^2\) comes from the tensor flip classically, or its braided analog defined by the R-matrix in the quantum case. The relations (H1)–(H3) are all easy to check, with (H3) amounting to the existence of a particular isomorphism \(V \otimes V^* \cong V^* \otimes V\). On applying Theorem A, we obtain a uniform proof of the existence of a categorical Kac–Moody action on each of these categories. In most cases, this action has already been constructed in the literature via “control by \(K_0\);” e.g. see [17, \(\S \)7.4] and [33, \(\S \)6.4] for rational representations of \(GL_n\), [17, \(\S \)7.5] and [9, \(\S \)4.4] for category \({\mathcal {O}}\), [38, \(\S \S \)6–7] and [13, \(\S \)5] for the quantum analogs, and [16, \(\S \)5.1] and [12, \(\S \)3.2] for the super analogs. In particular, for rational representations of \(GL_n\), the complexified Grothendieck group may be identified with \(\bigwedge ^n {\text {Nat}}_p\), where \({\text {Nat}}_p\) is a natural level zero representation of \(\widehat{\mathfrak {sl}}_p(\mathbb {C})'\), while for integral blocks of category \({\mathcal {O}}\) for \(\mathfrak {gl}_{m|n}(\mathbb {C})\) the complexified Grothendieck group is \({\text {Nat}}_+^{\otimes m} \otimes {\text {Nat}}_-^{\otimes n}\) where \({\text {Nat}}_{\pm }\) are the natural and dual natural representations of \(\mathfrak {sl}_\infty (\mathbb {C})\). As well as establishing the existence of a categorical Kac–Moody action in all of these previously known cases, our approach encompasses several new situations involving quantum groups at roots of unity and restricted enveloping algebras in positive characteristic; for the latter we are only aware of [31, Theorem 3.12] in the existing literature, which treats a special case by explicitly checking relations at the level of \(K_0\).
1.3 Generalized cyclotomic quotients
We have already mentioned cyclotomic quotients of the affine Hecke algebras \(AH_d\). The isomorphism theorem of [10] shows that these are isomorphic to corresponding cyclotomic quotients of the quiver Hecke algebras \(QH_d\). Both of these families of cyclotomic quotients can also be obtained in a Morita equivalent form by taking cyclotomic quotients of the Heisenberg category \(\mathcal {H}eis_k\) or of the Kac–Moody 2-category \({{\mathfrak {U}}}(\mathfrak {g})\). This was first realized by Rouquier in the Kac–Moody setting, indeed, it is the key to Rouquier’s definition of universal categorifications of integrable highest weight modules; see [35, Theorem 4.25]. The analogous theorem in the Heisenberg setting is [4, Theorem 1.7]. This point of view leads naturally to many more examples which we refer to as generalized cyclotomic quotients; these were first considered in the Kac–Moody setting in [39, Proposition 5.6] and categorify tensor products of an integrable lowest weight and an integrable highest weight representation of \(\mathfrak {g}\). In the final section of this article, we apply Theorem A, this time with \({{\mathcal {R}}}\) being a Schurian category, to prove the following result (see Theorem 5.19).
Theorem B
Consider the generalized cyclotomic quotients \(H_Z(\mu |\nu )\) of the Kac–Moody 2-category as defined in Sect. 5.2 and \(H_Z(m|n)\) of the (degenerate or quantum) Heisenberg category as defined in Sect. 5.3. Assuming the defining parameters are chosen so that (5.29) and (5.30) hold, these algebras are isomorphic via an explicit isomorphism.
The data needed to define generalized cyclotomic quotients in the most general form includes a finite-dimensional, commutative, local algebra Z, but generalized cyclotomic quotients are already interesting when Z is simply taken to be equal to the ground field \(\Bbbk \). Assuming this and taking the parameter n (which in general is a monic polynomial \(n(u) \in Z[u]\)) to be of degree zero, the generalized cyclotomic quotient \(H_Z(m|n)\) is the usual cyclotomic quotient of \(\mathcal {H}eis_k\) associated to m (which in general is a monic polynomial \(m(u) \in Z[u]\)) for \(k = -\deg m(u)\). Then Theorem B specializes to the isomorphism theorem between cyclotomic quotients of affine Hecke algebras and quiver Hecke algebras of type A already mentioned.
Another example of a generalized cyclotomic quotient “in nature” arises by taking \(Z= \Bbbk = {{\mathbb {C}}}\), and either \(m(u) = u\) and \(n(u) = u+d\) in the degenerate case, or \(m(u) = u-1\) and \(n(u) = u-q^{-2d}\) in the quantum case for q that is not a root of unity. Under these assumptions, the generalized cyclotomic quotient \(H_Z(m|n)\) is the locally unital algebra underlying the oriented Brauer category denoted \(\mathcal {OB}(d)\) in [7] in the degenerate case, or the HOMFLY-PT skein category denoted \(\mathcal {OS}(z,q^d)\) in [5] in the quantum case. The additive Karoubi envelopes of these monoidal categories are the Deligne categories \(\underline{{\text {Re}}}\!{\text {p}} GL_d\) and \(\underline{{\text {Re}}}\!{\text {p}} U_q(\mathfrak {gl}_d)\), respectively. Assuming that \(d \in {{\mathbb {Z}}}\) (so that the spectrum I is \({{\mathbb {Z}}}\) in the degenerate case or \(q^{2{{\mathbb {Z}}}}\) in the quantum case), Theorem B implies that both of these categories are equivalent as \(\Bbbk \)-linear categories to the additive Karoubi envelope of the corresponding generalized cyclotomic quotient of \({{\mathfrak {U}}}(\mathfrak {sl}_\infty )\). This was proved originally using “control by \(K_0\)” in [5]. (See also [19, Theorem 10.2.7] for a related uniqueness result.)
Due to their universal nature, generalized cyclotomic quotients also play an important role in the proof of the final theorem of the article, Theorem 5.22, which explains how to construct a categorical Heisenberg action starting from a suitable Kac–Moody action. This result gives a converse to Theorem A, further clarifying the relationship between the three formulations (KM1)–(KM3), (SL1)–(SL3) and (H1)–(H3) of the notion of categorical action discussed in this introduction.
The equivalence of Heisenberg and Kac–Moody actions revealed by this paper seems to be a feature of categorical actions which does not persist at the decategorified level. For the degenerate Heisenberg category and assuming that the ground field \(\Bbbk \) is of characteristic zero, [14, Theorem 1.1] shows that the Grothendieck ring \(K_0({\text {Kar}}(\mathcal {H}eis_k))\) of the additive Karoubi envelope of \(\mathcal {H}eis_k\) is isomorphic to a certain \({{\mathbb {Z}}}\)-form for the universal enveloping algebra of the infinite-dimensional Heisenberg Lie algebra specialized at central charge k. In this case, we expect that the passage from categorical Kac–Moody action to categorical Heisenberg action arising from Theorem 5.22 is related at the level of complexified Grothendieck groups to restriction from \(\mathfrak {sl}_\infty (\mathbb {C})\) (suitably completed) to its principal Heisenberg subalgebra.
2 Preliminaries
Throughout the article, \(\Bbbk \) is an algebraically closed field and \(z \in \Bbbk \) is a parameter. We refer to the cases \(z\ne 0\) and \(z = 0\) as the quantum and degenerate cases, respectively. For use in the quantum case, we choose a root q of the polynomial \(x^2-zx-1\), so that \(z=q - q^{-1}\). We also have in mind some fixed integer k, which we call the central charge.
2.1 Generating functions
We will often use generating functions when working with elements of an algebra A. This means that we will work with formal Laurent series \(f(u) \in A(\!(u^{-1})\!)\) in an indeterminate u (or v, w, ...). We write \(\left[ f(u)\right] _{u^r}\) for the \(u^r\)-coefficient of such a series, \(\left[ f(u)\right] _{u^{< 0}}\) for \(\sum _{r < 0} \left[ f(u)\right] _{u^r} u^r\), \(\left[ f(u)\right] _{u^{\ge 0}}\) for \(\sum _{r \ge 0} \left[ f(u)\right] _{u^r} u^r\) (which is a polynomial), and so on. To give an example, suppose that
for some \(f_r \in A\). Then we can define new elements \(g_r \in A\) by declaring that
is the inverse of the formal Laurent series f(u). In fact, setting \(f_r := 0\) for \(r < 0\), we have that
This identity is valid even if A is non-commutative providing the determinant is interpreted as a suitably ordered Laplace expansion. The best known instance of it arises in the algebra of symmetric functions \({\text {Sym}}\), in which the generating functions \(e(u) = \sum _{r \ge 0} e_r u^{-r}\) and \(h(u) = \sum _{r \ge 0} h_r {u^{-r}}\) for the elementary and complete symmetric functions are related by the identity \(e(u) h(-u) = 1\). The determinantal formula from [29, (I.2.6)] is then equivalent to (2.1).
2.2 Locally finite Abelian and Schurian categories
We will be studying categorical actions on \(\Bbbk \)-linear Abelian categories \({{\mathcal {R}}}\) satisfying certain finiteness conditions, following [15, \(\S \)2]. The nicest condition to impose is that \({{\mathcal {R}}}\) is a locally finite Abelian category. This means that \({{\mathcal {R}}}\) is Abelian, all objects are of finite length, and the space of morphisms between any two objects is finite-dimensional. By a theorem of Takeuchi, an (essentially small) \(\Bbbk \)-linear category \({{\mathcal {R}}}\) is a locally finite Abelian category in this sense if and only if it is equivalent to the category \({\text {comod}}_{{\text {fd}}}\text {-}C\) of finite-dimensional right C-comodules for a coalgebra C; e.g., see [20, Theorem 1.9.15].
Special cases of locally finite Abelian categories include finite Abelian categories, that is, categories equivalent to \(A\text {-}{\text {mod}}_{{\text {fd}}}\) for a finite-dimensional algebra A, and essentially finite Abelian categories in the sense of [15, \(\S \)2.4]Footnote 2, that is, the locally finite Abelian categories that have enough projectives and injectives. An (essentially small) \(\Bbbk \)-linear category \({{\mathcal {R}}}\) is an essentially finite Abelian category if and only if it is equivalent to the category \(A\text {-}{\text {mod}}_{{\text {fd}}}\) of finite-dimensional left A-modules for some essentially finite-dimensional locally unital algebra A. Here, a locally unital algebra is an associative algebra equipped with a local unit, that is, a system \(\{1_a\,|\,a \in {\mathbb {A}}\}\) of mutually orthogonal idempotents such that
We say that A is essentially finite-dimensional if both \(\dim 1_a A < \infty \) and \(\dim A 1_a< \infty \) for all \(a \in {\mathbb {A}}\). A left A-module means a left module V as usual such that \(V = \bigoplus _{a \in {\mathbb {A}}} 1_a V\).
The other sort of Abelian categories with which we will be concerned are the so-called Schurian categories. Although a well-known concept, the language is not standard. The idea was discussed in detail in [8, \(\S \)2]Footnote 3, but actually we will follow the conventions of [15, \(\S \)2.3], according to which a Schurian category is a category \({{\mathcal {R}}}\) that is equivalent to the category \(A\text {-}{\text {mod}}_{{\text {lfd}}}\) of locally finite-dimensional left A-modules for a locally finite-dimensional locally unital algebra A. Here, a locally unital algebra A (resp., a left A-module V) is called locally finite-dimensional if \(\dim 1_a A 1_{a'} < \infty \) (resp., \(\dim 1_a V < \infty \)) for all \(a,a' \in {\mathbb {A}}\). Care is needed since an object V in a Schurian category \({{\mathcal {R}}}\) is not necessarily of finite length, although all such modules have finite composition multiplicities. Also for \(V,W \in {{\mathcal {R}}}\) the morphism space \({\text {Hom}}_{{{\mathcal {R}}}}(V,W)\) is not necessarily finite-dimensional, although it is if V is finitely generated. We refer the reader to [8, 15] for further discussion.
To give a sense of the difference between locally finite Abelian categories and Schurian categories, we formulate the appropriate notion of Grothendieck group which should be used in the two settings. If \({{\mathcal {R}}}\) is a locally finite Abelian category, the Grothendieck group \(K_0({{\mathcal {R}}})\) is the free Abelian group generated by isomorphism classes [V] of modules subject to relations \([V]=[V_1]+[V_2]\) for all short exact sequences \(0 \rightarrow V_1 \rightarrow V \rightarrow V_2 \rightarrow 0\). If \({{\mathcal {R}}}\) is a Schurian category, the Grothendieck group \(K_0({{\mathcal {R}}})\) is the free Abelian group generated by isomorphism classes [P] of finitely-generated projective modules subject to relations \([P]=[P_1]+[P_2]\) if \(P \cong P_1 \oplus P_2\).
Suppose that \({{\mathcal {R}}}\) is either locally finite Abelian or Schurian. As our ground field is algebraically closed, we have that \({{\text {End}}}_{{\mathcal {R}}}(L)\cong \Bbbk \) for any irreducible object \(L \in {{\mathcal {R}}}\). By a sweet endofunctor of \({{\mathcal {R}}}\), we mean a \(\Bbbk \)-linear functor \(F:{{\mathcal {R}}}\rightarrow {{\mathcal {R}}}\) that possesses both a left adjoint and a right adjoint, with the two adjoints being isomorphic functors. Such a functor is automatically additive and exact, so it induces an endomorphism [F] of the Grothendieck ring \(K_0({{\mathcal {R}}})\). Also, such a functor sends finitely generated objects to finitely generated objects. In the Schurian case, some further properties of sweet endofunctors are discussed in [8, \(\S \)2.4], including the following:
Lemma 2.1
([8, Lemma 2.12]) Suppose that F and G are sweet endofunctors of a Schurian category \({{\mathcal {R}}}\), and that \(\eta :F \Rightarrow G\) is a natural transformation such that \(\eta _L:FL \rightarrow GL\) is an isomorphism for each irreducible \(L \in {{\mathcal {R}}}\). Then \(\eta \) is an isomorphism.
For finitely generated \(V \in {{\mathcal {R}}}\), the functor \({\text {Hom}}_{{\mathcal {R}}}(V, -):{{\mathcal {R}}}\rightarrow \mathcal {V}ec_{{\text {fd}}}\) has a left adjoint
To make an explicit choice for this functor, one needs to pick a basis for each finite-dimensional vector space W. Then \(V \otimes W := V^{\oplus \dim W}\) and, for a linear map \(f:W \rightarrow W'\), the morphism \(V \otimes f:V \otimes W \rightarrow V \otimes W'\) is the morphism \(V^{\oplus \dim W} \rightarrow V^{\oplus \dim W'}\) defined by the matrix of f with respect to the fixed bases.
2.3 Diagrammatics
We will use the string calculus for strict monoidal categories and strict 2-categories as explained in [37, Chapter 2]. We will also use analogous diagrammatic formalism when working with module categories and 2-representations.
To give a brief review, let \({{\mathcal {A}}}\) be a strict \(\Bbbk \)-linear monoidal category. A (strict) module category over \({{\mathcal {A}}}\) is a \(\Bbbk \)-linear category \({{\mathcal {R}}}\) plus a \(\Bbbk \)-linear functor \(-\otimes -:{{\mathcal {A}}}\boxtimes {{\mathcal {R}}}\rightarrow {{\mathcal {R}}}\) satisfying associativity and unity axioms. Here, \({{\mathcal {A}}}\boxtimes {{\mathcal {R}}}\) is the \(\Bbbk \)-linearization of the Cartesian product \({{\mathcal {A}}}\times {{\mathcal {R}}}\). Equivalently, a module category is a \(\Bbbk \)-linear category \({{\mathcal {R}}}\) together with a strict \(\Bbbk \)-linear monoidal functor \(\texttt {R}:{{\mathcal {A}}}\rightarrow \mathcal {E}nd_\Bbbk ({{\mathcal {R}}})\), where \(\mathcal {E}nd_\Bbbk ({{\mathcal {R}}})\) denotes the strict \(\Bbbk \)-linear monoidal category with objects that are \(\Bbbk \)-linear endofunctors of \({{\mathcal {R}}}\) and morphisms that are natural transformations. We usually suppress the monoidal functor \(\texttt {R}\), using the same notation \(f:E \rightarrow F\) both for a morphism in \({{\mathcal {A}}}\) and for the natural transformation between endofunctors of \({{\mathcal {R}}}\) that is its image under \(\texttt {R}\). The evaluation \(f_V:EV \rightarrow FV\) of this natural transformation on an object \(V \in {{\mathcal {R}}}\) will be represented diagrammatically by drawing a line labelled by V on the right-hand side of the usual string diagram for f:

This line represents the identity endomorphism of the object V. Another morphism \(g:V \rightarrow W\) in \({{\mathcal {A}}}\) can be represented by placing a coupon labelled by g on it. For example, the following depicts \((f \otimes W) \circ (E \otimes g) = f \otimes g = (F \otimes g) \circ (f \otimes V)\):

The equality of these morphisms is the interchange law for module categories.
Suppose instead that \({{\mathfrak {A}}}\) is a strict \(\Bbbk \)-linear 2-category. A (strict) 2-representation of \({{\mathfrak {A}}}\) is a family \(({{\mathcal {R}}}_\lambda )_{\lambda \in {{\mathfrak {A}}}}\) of \(\Bbbk \)-linear categories indexed by the objects of \({{\mathfrak {A}}}\), plus \(\Bbbk \)-linear functors \(\mathcal {H}om_{{{\mathfrak {A}}}}(\lambda ,\mu ) \boxtimes {{\mathcal {R}}}_\lambda \rightarrow {{\mathcal {R}}}_\mu \) for \(\lambda ,\mu \in {{\mathfrak {A}}}\) satisfying associativity and unity axioms. Equivalently, letting \(\mathfrak {Cat}_\Bbbk \) be the strict \(\Bbbk \)-linear 2-category of \(\Bbbk \)-linear categories, a 2-representation is a family \(({{\mathcal {R}}}_\lambda )_{\lambda \in {{\mathfrak {A}}}}\) of \(\Bbbk \)-linear categories together with a strict \(\Bbbk \)-linear 2-functor \(\mathbf{R} :{{\mathfrak {A}}}\rightarrow \mathfrak {Cat}_\Bbbk \) such that \(\mathbf{R} (\lambda ) = {{\mathcal {R}}}_\lambda \) for each \(\lambda \in {{\mathfrak {A}}}\). As with module categories, when working with a 2-representation we will usually drop the 2-functor \(\mathbf{R} \) from our notation. The string calculus can be used in this setting too. For example, a 1-morphism \(F 1_\lambda :\lambda \rightarrow \mu \) in \({{\mathfrak {A}}}\) gives rise to a functor \(F|_{{{\mathcal {R}}}_\lambda }:{{\mathcal {R}}}_\lambda \rightarrow {{\mathcal {R}}}_\mu \); the diagram

depicts the morphism in \({{\mathcal {R}}}_\mu \) obtained by applying this to morphism \(g:V \rightarrow W\) in \({{\mathcal {R}}}_\lambda \). We say that \(({{\mathcal {R}}}_\lambda )_{\lambda \in {{\mathfrak {A}}}}\) is a locally finite Abelian or a Schurian 2-representation if each of the categories \({{\mathcal {R}}}_\lambda \) is a locally finite Abelian category or a Schurian category, respectively.
2.4 A version of Hensel’s lemma
Let Z be a finite-dimensional, commutative, local \(\Bbbk \)-algebra with unique maximal ideal \(J = J(Z)\). As \(\Bbbk \) is algebraically closed, we may naturally identify the quotient Z/J with \(\Bbbk \). Note that two polynomials \(g(u), h(u) \in Z[u]\) are relatively prime if and only if their images in \(\Bbbk [u]\) are relatively prime. Equivalently, there exist \(a(u), b(u) \in Z[u]\) such that \(a(u)g(u)+b(u)h(u) = 1\). The following is well known but we could not find a suitable reference.
Lemma 2.2
Suppose that I is a proper ideal of Z such that \(I^2 = 0\). Let \({\bar{Z}} := Z / I\).
-
(1)
Suppose that we are given a monic polynomial \({{\bar{f}}}(u) \in {\bar{Z}}[u]\) and some choice of \({\hat{f}}(u) \in Z[u]\) lifting \(\bar{f}(u)\). Then there is a unique monic lift f(u) of \({{\bar{f}}}(u)\) such that \({{\hat{f}}}(u) = f(u) q(u)\) for \(q(u) \in 1 + I[u]\). Moreover, \(\deg f(u) = \deg {{\bar{f}}}(u)\).
-
(2)
For a monic lift f(u) of \({{\bar{f}}}(u)\) as in (1), suppose in addition that we are given relatively prime monic polynomials \({{\bar{g}}}(u), {{\bar{h}}}(u) \in {\bar{Z}}[u]\) such that \({{\bar{f}}}(u) = {{\bar{g}}}(u) {{\bar{h}}}(u)\). There exist monic lifts g(u) of \({{\bar{g}}}(u)\) and h(u) of \({{\bar{h}}}(u)\) such that \(f(u) = g(u) h(u)\).
-
(3)
The monic lifts g(u) and h(u) in (2) are unique.
Proof
-
(1)
Let p(u) be any monic lift of \({{\bar{f}}}(u)\). It is automatically of the same degree. By the division algorithm, we have that \({{\hat{f}}}(u) = p(u) q(u)+r(u)\) for r(u) with \(\deg r(u) < \deg p(u)\). On reducing coefficients modulo I, we see that \(q(u) \in 1 + I[u]\) and \(r(u) \in I[u]\). Since \(I^2 = 0\) it follows that \(r(u) = r(u) q(u)\). Hence, we have that \({{\hat{f}}}(u) = f(u)q(u)\) for \(f(u) := p(u)+r(u)\), which is another monic lift of \({{\bar{f}}}(u)\). Uniqueness is obvious.
-
(2)
Let \({{\hat{g}}}(u)\) and \({{\hat{h}}}(u)\) be any lifts of \({{\bar{g}}}(u)\) and \({{\bar{h}}}(u)\). Since \({{\bar{g}}}(u), {{\bar{h}}}(u)\) are relatively prime, there exist \(a(u), b(u) \in Z[u]\) such that \(a(u) {{\hat{g}}}(u) + b(u) {{\hat{h}}}(u)=1\). Applying (1) to the lift \({{\hat{g}}}(u) + (f(u)-{{\hat{g}}}(u) {{\hat{h}}}(u))b(u)\) of \({{\bar{g}}}(u)\), we see that there exists a monic lift g(u) of \({{\bar{g}}}(u)\) and \(p(u)\in 1+I[u]\) such that \(g(u) p(u) = {{\hat{g}}}(u)+(f(u)-{{\hat{g}}}(u){{\hat{h}}}(u))b(u)\). Similarly there is a monic lift h(u) of \({{\bar{h}}}(u)\) and \(q(u) \in 1+I[u]\) such that \(h(u) q(u) = {{\hat{h}}}(u) + (f(u)-{{\hat{g}}}(u){{\hat{h}}}(u)) a(u)\). Using the assumption \(I^2=0\), it is easy to check that \(f(u) = g(u) h(u) p(u) q(u)\). Moreover since f(u) and g(u)h(u) are monic and \(p(u) q(u) \in 1+I[u]\), we must actually have that \(p(u) q(u) = 1\).
-
(3)
Suppose that we have two such factorizations \(f(u) = g(u) h(u) = g'(u) h'(u)\). Then \(g'(u) = g(u) + s(u)\) and \(h'(u) = h(u) + t(u)\) for \(s(u), t(u) \in I[u]\), and we deduce that \(g(u) t(u) + h(u) s(u) = 0\). Again we choose \(a(u), b(u) \in Z[u]\) so that \(a(u) g(u) + b(u) h(u) = 1\). Then we have that
$$\begin{aligned} (1-b(u)h(u)) t(u) + a(u) h(u) s(u) = a(u) g(u) t(u) + a(u) h(u) s(u) = 0. \end{aligned}$$Hence, \(t(u) = (b(u)t(u) - a(u) s(u)) h(u)\) and \(h'(u) = (1 + b(u)t(u)-a(u)s(u)) h(u)\). But h(u) and \(h'(u)\) are both monic and \(b(u)t(u)-a(u)s(u) \in I[u]\), which implies that \(b(u)t(u)-a(u)s(u) = 0\), i.e., \(h'(u) = h(u)\). Similarly, \(g'(u) = g(u)\).
\(\square \)
Corollary 2.3
Suppose that \(f(u) \in Z[u]\) is a monic polynomial whose reduction modulo J is \({{\bar{f}}}(u) \in \Bbbk [u]\). Suppose that we are given a factorization \({{\bar{f}}}(u) = {{\bar{g}}}(u) \bar{h}(u)\) for relatively prime monic polynomials \({{\bar{g}}}(u), {{\bar{h}}}(u) \in \Bbbk [u]\). There exist unique monic lifts \(g(u), h(u) \in Z[u]\) of \(\bar{g}(u), {{\bar{h}}}(u)\) such that \(f(u) = g(u) h(u)\).
Proof
This follows from the lemma by induction on the nilpotency degree of J. \(\square \)
Corollary 2.4
Suppose that \(f(u) \in Z[u]\) is a monic polynomial. Let \(p_i\) be the multiplicity of \(i \in \Bbbk \) as a root of \({{\bar{f}}}(u) \in \Bbbk [u]\), i.e., \({{\bar{f}}}(u) = \prod _{i \in I} (u-i)^{p_i}\) for some subset I of \(\Bbbk \). Then there exist unique monic polynomials \(f_i(u) \in u^{p_i}+J[u]\) such that \(f(u) = \prod _{i \in I} f_i(u-i)\).
Proof
This follows from the previous corollary by induction on \(\deg f(u)\). (Note the assumption that \(f_i(u)\) is monic and belongs to \(u^{p_i}+J[u]\) is equivalent to the assertion that \(f_i(u-i)\) is a monic lift of \((u-i)^{p_i} \in \Bbbk [u]\).) \(\square \)
3 Three diagrammatic categories
In this section, we review the definitions of the three diagrammatic categories that are the subject of the paper: the degenerate Heisenberg category, the quantum Heisenberg category, and the Kac–Moody 2-category of type A. We also explain how to recast the defining relations in terms of generating functions.
3.1 The degenerate Heisenberg category
The Heisenberg category \(\mathcal {H}eis_k\) is a strict \(\Bbbk \)-linear monoidal category defined by generators and relations. In this subsection, we review the definition in the degenerate case \(z=0\). This was worked out originally by Khovanov [25] for central charge \(k=-1\) (our convention), then extended to all negative central charges in [30]. We instead follow the approach of [4, Theorem 1.2], which simplified the presentation and incorporated also the non-negative central charges, with \(\mathcal {H}eis_0\) being the affine oriented Brauer category from [7]. In this approach, the degenerate Heisenberg category \(\mathcal {H}eis_k\) is the strict \(\Bbbk \)-linear monoidal category generated by objects \(E=\uparrow \) and \(F=\downarrow \) and morphisms


subject to certain relations. To record these, we denote \(n\ge 0\) dots on a string instead by labelling a single dot with the multiplicity n. Also introduce the sideways crossings

and the negatively dotted bubbles

Then the relations are as follows:






In fact, one only needs to impose one of the adjunction relations (3.4) or (3.5), then the other one follows automatically. Moreover, \(\mathcal {H}eis_k\) is strictly pivotal, i.e., the following relations hold:

These assertions are established in [4, Theorem 1.3].
The category \(\mathcal {H}eis_k\) has an alternative presentation which is often useful when constructing \(\mathcal {H}eis_k\)-module categories since it involves fewer generators and relations. In this approach, which is [4, Definition 1.1], one just needs the generating morphisms  ,
,  ,
,  and
and  (hence, we also have the rightwards crossing defined as above), subject to the relations (3.3) and (3.4) together with the omnipotent inversion relation, namely, that the following is an isomorphism in the additive envelope:
(hence, we also have the rightwards crossing defined as above), subject to the relations (3.3) and (3.4) together with the omnipotent inversion relation, namely, that the following is an isomorphism in the additive envelope:


The resulting category then contains unique morphisms  and
and  such that the other relations (3.6)–(3.8) hold; see [14, Lemma 5.2].
such that the other relations (3.6)–(3.8) hold; see [14, Lemma 5.2].
The following additional relations are also derived in [4, Theorem 1.3]: the infinite Grassmannian relation

for any \(n \in {{\mathbb {Z}}}\), the alternating braid relation

the curl relations

for all \(n \ge 0\), and the bubble slides

for \(n \in {{\mathbb {Z}}}\). It seems to be most convenient to work with these relations in terms of generating functions as in Sect. 2.1. In order to do this, we switch henceforth to using the notation  instead of
instead of  to denote a dot of multiplicity n; we do this also for negatively dotted bubbles using negative values of n. Then we can represent linear combinations of monomials by labelling dots by polynomials in x too. Viewing the power series
to denote a dot of multiplicity n; we do this also for negatively dotted bubbles using negative values of n. Then we can represent linear combinations of monomials by labelling dots by polynomials in x too. Viewing the power series

as a generating function for multiple dots on a string, the dot sliding relation implies the following:

To write the other relations in this form, we use the following generating functions for the dotted bubbles:


Then the infinite Grassmannian relation implies that

This puts us in the situation of (2.1), which explains the origin of the determinantal formulae used to define the negatively dotted bubbles above. In terms of generating functions, the other relations involving bubbles translate into the following:




To understand the last relation, it is helpful to note that \(1-(u-x)^{-2} = \frac{(u-(x+1))(u-(x-1))}{(u-x)^2}\).
Lemma 3.1
For a polynomial \(p(u) \in \Bbbk [u]\), we have that



Proof
By linearity, it suffices to prove (3.19) and (3.20) in the case that \(p(u) = u^r\) for \(r \ge 0\), and in that case they follow easily on computing the \(u^{-1}\)-coefficient on the right-hand side, recalling also the definitions (3.12) and (3.13). To deduce (3.21), rewrite the left-hand side using (3.19), then apply the curl relation (3.17). \(\square \)
Finally, let us justify the terminology “Heisenberg category” in more detail. Let \({\text {Kar}}(\mathcal {H}eis_k)\) be the additive Karoubi envelope of \(\mathcal {H}eis_k\), and \(K_0({\text {Kar}}(\mathcal {H}eis_k))\) be the Grothendieck ring of that monoidal category. When the characteristic of the ground field is zero, \(K_0({\text {Kar}}(\mathcal {H}eis_k))\) is isomorphic to the Heisenberg ring \(\mathrm {Heis}_k\), that is, the ring generated by elements \(\{h_n^+, e_n^-\,|\,n \ge 0\}\) subject to the relations
This ring is a \({{\mathbb {Z}}}\)-form for the universal enveloping algebra of the infinite-dimensional Heisenberg Lie algebra specialized at central charge k. The existence of an isomorphism \(K_0({\text {Kar}}(\mathcal {H}eis_k)) \cong \mathrm {Heis}_k\) was conjectured originally by Khovanov in [25] for \(k=-1\) and it was proved in general in [14, Theorem 1.1]. Under the isomorphism, the classes \([E], [F] \in K_0({\text {Kar}}(\mathcal {H}eis_k))\) correspond to \(h_1^+, e_1^- \in \mathrm {Heis}_k\); more generally \(h_n^+, e_n^-\) correspond to summands of \(E^n\) and \(F^n\) defined by idempotents that correspond to the trivial and sign representations of the symmetric group \(\mathfrak {S}_n\). When \(\Bbbk \) is of positive characteristic, the category \({\text {Kar}}(\mathcal {H}eis_k)\) does not have enough indecomposable objects for there to be any chance of an analogous isomorphism; in this case, we expect that one should really work with a “thickened” version of \(\mathcal {H}eis_k\) which incorporates generators of the affine Schur algebra. However, for the purposes of the present article, the category \(\mathcal {H}eis_k\) as defined above is exactly the right object.
3.2 The quantum Heisenberg category
In the quantum case \(z \ne 0\), the category \(\mathcal {H}eis_k\) was introduced in [13, Definition 4.1], building on the earlier work [28] which produced a different (but closely related) deformation of Khovanov’s Heisenberg category. In fact, in the quantum case, there is an additional invertible parameter t which we will treat here as an indeterminate (although in applications one usually specializes t to a scalar in \(\Bbbk ^\times \)). Thus, in the quantum case, we will work over the ground ring
and define the quantum Heisenberg category \(\mathcal {H}eis_k\) to be the strict \(\mathbb {K}\)-linear monoidal category generated by objects \(E=\uparrow \) and \(F=\downarrow \) and the following morphisms:


The generators on the left of (3.24) and (3.25), the dot and the positive crossing, are required to be invertible. The invertibility of the dot means that now it makes sense to label dots by an arbitrary integer, rather than just by \(n \in {{\mathbb {N}}}\). We denote the inverse of the positive crossing by

and call this the negative crossing. Thus, we have that

We also introduce the sideways crossings, both positive and negative,

and the \((+)\)-bubblesFootnote 4

The other defining relations are as follows:






As in the degenerate case, one actually only needs to impose one of the adjunction relations (3.28) or (3.29), after which the other one may be deduced as a consequence of the other relations. Moreover, the quantum Heisenberg category is strictly pivotal, so that one can introduce the downward dot and the downward positive and negative crossings by taking left and/or right mates of the upward ones.
Again like the degenerate case, there are also some alternative presentations involving an inversion relation; see [13, Definitions 2.2 and 3.1]. To formulate a version of this, one just needs the generating morphisms  ,
,  ,
,  and
and  , the first two of which are required to be invertible (hence, we also get negative upwards and positive/negative rightwards crossings as above), subject to the relations (3.27) and (3.28) plus the inversion relation asserting that the following is invertible:
, the first two of which are required to be invertible (hence, we also get negative upwards and positive/negative rightwards crossings as above), subject to the relations (3.27) and (3.28) plus the inversion relation asserting that the following is invertible:


The situation is slightly more delicate than in the degenerate case as it is also necessary to impose one additional relation:
-
If \(k > 0\) we require that
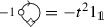 where
where  is the last entry of the inverse of the matrix (3.33).
is the last entry of the inverse of the matrix (3.33). -
If \(k < 0\) we require that
 where
where  is the last entry of the inverse of the matrix (3.34).
is the last entry of the inverse of the matrix (3.34). -
If \(k=0\) there are two equivalent presentations here: if one picks (3.33) the additional relation is
 where
where  , while for (3.34) it is
, while for (3.34) it is  where
where  .
.
The resulting category then contains unique morphisms  and
and  such that the other relations (3.30)–(3.32) hold; see [13, Lemma 4.3].
such that the other relations (3.30)–(3.32) hold; see [13, Lemma 4.3].
Remark 3.2
The alternative presentation of \(\mathcal {H}eis_k\) just formulated only involves even powers of t, so that using it the category could be defined over \(\Bbbk [t^2,t^{-2}]\) rather than the algebra \(\mathbb {K}\) from (3.23). The square root t of \(t^2\) is needed in order for there to exist leftwards cups and caps satisfying the earlier relations. The specific normalization of these leftwards cups and caps was chosen originally in [13] so as to match the usual normalization in the HOMFLY-PT skein category; see [5].
In [13, \(\S \S \)2–4], many additional relations are derived from the defining relations, including counterparts of the infinite Grassmannian, alternating braid, curl, and bubble slide relations. Again, all of these relations can be reformulated quite compactly in terms of generating functions. We do this here just for the infinite Grassmannian relation, the curl relation and the bubble slides, since actually those are the only ones we will need later on. Like we did in the previous subsection, we switch from now onwards to labelling dots by polynomials, now possibly in \(\Bbbk [x,x^{-1}]\), instead of by integers. We also assemble the \((+)\)-bubbles into the following generating functions:


Here, we are using slightly different notation from [13], where these were denoted  . Then we have the following, which are equivalent to [13, Lemmas 3.4, 4.4 and 4.6]:
. Then we have the following, which are equivalent to [13, Lemmas 3.4, 4.4 and 4.6]:



For the last relation, we note that \(1-z^2xu(u-x)^{-2} = \frac{(u-q^2x)(u-q^{-2}x)}{(u-x)^2}\).
Lemma 3.3
For a polynomial \(p(u) \in \Bbbk [u]\), we have that



Proof
This is almost the same as the proof of Lemma 3.1, using (3.35) and (3.36) and (3.38) instead of (3.12) and (3.13) and (3.17). For (3.41), one also needs to know that  and
and  due to [13, (2.18), (3.12)]. \(\square \)
due to [13, (2.18), (3.12)]. \(\square \)
In the quantum case for q not a root of unity, it is conjectured that \(K_0({\text {Kar}}(\mathcal {H}eis_k))\) is isomorphic to the Heisenberg ring \(\mathrm {Heis}_k\), just like in the degenerate case.
3.3 The Kac–Moody 2-category
Last, but by no means least, we have the Kac–Moody 2-category. This was defined by Khovanov and Lauda [27] and Rouquier [34]. In fact, there is such a category associated to any symmetrizable Cartan matrix, but in this paper we are only interested in the ones of Cartan type A, so we specialize to that right away. Our exposition is based on [3], which unified the different approaches of Khovanov–Lauda and Rouquier, and [8, \(\S \)3], which incorporated some renormalizations of the bubbles following the idea of [2] in order to make the strictly pivotal structure apparent.
Assume that I is a set equipped with a fixed-point-free automorphism \(I \rightarrow I, i \mapsto i^+\). Let \(i \mapsto i^-\) be the inverse function. This can also be interpreted as the data of a quiver whose connected components are of types \(A_\infty \) or \(A_{p-1}^{(1)}\) for \(p\ge 2\). There is an associated generalized Cartan matrix \((a_{i,j})_{i,j \in I}\) with \(a_{i,i} := 2\) for each \(i \in I\), and \(a_{i,j}:=-\delta _{i^+,j}-\delta _{i,j^+}\) for each \(i \ne j\). Let \(\mathfrak {g}\) be the Kac–Moody Lie algebra over \({{\mathbb {C}}}\) generated by \(\{e_i, f_i, h_i\,|\,i \in I\}\) subject to the Serre relations defined from the Cartan matrix \((a_{i,j})_{i, j \in I}\). Note \(\mathfrak {g}\) is a direct sum of Kac–Moody Lie algebras of types \(\mathfrak {sl}_\infty ({{\mathbb {C}}})\) (the infinite components in the quiver) or \(\widehat{\mathfrak {sl}}_{p}({{\mathbb {C}}})'\) (finite components with \(p\) vertices).
Let \(\mathfrak {h}\) be the Cartan subalgebra of \(\mathfrak {g}\) with basis \(\{h_i\,|\,i \in I\}\). The weight lattice X of \(\mathfrak {g}\) is the Abelian subgroup of \(\mathfrak {h}^*\) generated by the fundamental weights \(\{\Lambda _j\,|\,j \in I\}\) defined from \(\langle h_i,\Lambda _j \rangle = \delta _{i,j}\). We have the set of dominant weights
Let \(\alpha _i := \sum _{j \in I} a_{i,j} \Lambda _j \in X\) be the ith simple root. Unlike the fundamental weights, these are not necessarily linearly independent, indeed, we have that \(\sum _{i \in I_0} \alpha _i = 0\) for each finite component \(I_0\) of I, due to the fact that we have not extended by scaling elements. Let \(Y := \sum _{i \in I} {{\mathbb {Z}}}\alpha _i \subseteq X\).
Finally, we choose signs \(\{\sigma _{i}(\lambda )\,|\,\lambda \in X, i \in I\}\) so that \(\sigma _{i}(\lambda )\sigma _{i}(\lambda +\alpha _j) = (-1)^{\delta _{i,j^+}}\) for each \(j \in I\). There is a unique such choice satisfying \(\sigma _{i}(\lambda ) = 1\) for each \(i \in I\) and each \(\lambda \) lying in a set of X/Y-coset representatives.
Then the Kac–Moody 2-category \({{\mathfrak {U}}}(\mathfrak {g})\) is the strict \(\Bbbk \)-linear 2-category with objects X, generating 1-morphisms  and
and  for \(i \in I\) and \(\lambda \in X\), and generating 2-morphisms
for \(i \in I\) and \(\lambda \in X\), and generating 2-morphisms


This time, the sideways crossings are defined from

and there are negatively dotted bubbles defined by

The generating 2-morphisms are subject to the following relations:











As with the Heisenberg category, one only needs to impose one of the relations (3.48) or (3.49), then the other follows as a consequence. Moreover, \({{\mathfrak {U}}}(\mathfrak {g})\) is strictly pivotal, so that we can again introduce downward dots and crossings by taking right and/or left mates of the upward ones.
The presentation described in the previous paragraph is similar to the original approach of Khovanov and Lauda. Rouquier’s approach was based instead on an inversion relation. To formulate it, we need the generating morphisms  ,
,  ,
,  and
and  (hence, we also have the rightwards crossings), subject to the relations (3.45)–(3.48) plus the inversion relation asserting that the following are isomorphisms:
(hence, we also have the rightwards crossings), subject to the relations (3.45)–(3.48) plus the inversion relation asserting that the following are isomorphisms:



Lemma 3.4
Let \({{\mathfrak {A}}}\) be a strict \(\Bbbk \)-linear 2-category containing objects \(\{o_\lambda \,|\,\lambda \in X\}\), 1-morphisms \(E_i 1_\lambda :o_\lambda \rightarrow o_{\lambda +\alpha _i}\) and \(F_i 1_\lambda :o_\lambda \rightarrow o_{\lambda -\alpha _i}\), and 2-morphisms  ,
,  and
and  satisfying (3.45)–(3.48). If \({{\mathfrak {A}}}\) contains 2-morphisms
satisfying (3.45)–(3.48). If \({{\mathfrak {A}}}\) contains 2-morphisms  and
and  for all \(i\in I\) and \(\lambda \in X\) such that the relations (3.50)–(3.55) all hold (for the sideways crossings and negatively dotted bubbles defined as above), then these 2-morphisms are uniquely determined.
for all \(i\in I\) and \(\lambda \in X\) such that the relations (3.50)–(3.55) all hold (for the sideways crossings and negatively dotted bubbles defined as above), then these 2-morphisms are uniquely determined.
Proof
Fix \(i \in I\) and \(\lambda \in X\). Let M be the matrix (3.57) if \(\langle h_i, \lambda \rangle \ge 0\) or the matrix (3.58) if \(\langle h_i, \lambda \rangle < 0\), viewed as a 2-morphism in the additive envelope \({\text {Add}}({{\mathfrak {A}}})\). The assumed relations (3.45)–(3.48) and (3.50)–(3.55) imply that M is invertible. Moreover the first entry of the inverse matrix \(M^{-1}\) is  . Thus, this 2-morphism is uniquely determined in \({{\mathfrak {A}}}\) independent of the choices of the leftwards cups and caps. Also if \(\langle h_i, \lambda \rangle > 0\) (resp., \(\langle h_i, \lambda \rangle < 0\)) then the last entry of \(M^{-1}\) is
. Thus, this 2-morphism is uniquely determined in \({{\mathfrak {A}}}\) independent of the choices of the leftwards cups and caps. Also if \(\langle h_i, \lambda \rangle > 0\) (resp., \(\langle h_i, \lambda \rangle < 0\)) then the last entry of \(M^{-1}\) is  (resp.,
(resp.,  ). So these 2-morphisms are uniquely determined. Finally, using (3.50) and (3.51), one sees that
). So these 2-morphisms are uniquely determined. Finally, using (3.50) and (3.51), one sees that

This means these morphisms are uniquely determined too. \(\square \)
Again, one can introduce generating functions and work with the defining relations in those terms; this technique was pioneered in [40]. We just write down the counterparts of (3.14), (3.17) and (3.18) and (3.37)–(3.39). Let


Switching from now on to labelling dots by polynomials rather than integers in the same way as we did when working with the Heisenberg category, but using the variable y in place of x to avoid possible confusion later on, we have that



The following is proved in exactly the same way as Lemma 3.1.
Lemma 3.5
For a polynomial \(p(u) \in \Bbbk [u]\), we have that



Finally, we outline the precise connection between \({{\mathfrak {U}}}(\mathfrak {g})\) and the quantized enveloping algebra \(U_q(\mathfrak {g})\) associated to \(\mathfrak {g}\). To do this, one needs to introduce a \({{\mathbb {Z}}}\)-grading on 2-morphisms, thereby making \({{\mathfrak {U}}}(\mathfrak {g})\) into a 2-category enriched in graded vector spaces. From that, one obtains a graded 2-category \({{\mathfrak {U}}}_q(\mathfrak {g})\) by formally adjoining grading shift operators to the 1-morphism categories. The Grothendieck ring \(K_0({\text {Kar}}({{\mathfrak {U}}}_q(\mathfrak {g})))\) of the additive Karoubi envelope of this graded 2-category is then a \({{\mathbb {Z}}}[q,q^{-1}]\)-algebra with q acting by the grading shift. This Grothendieck ring is isomorphic to the \({{\mathbb {Z}}}[q,q^{-1}]\)-form of Lusztig’s idempotented form for the quantized enveloping algebra of \(\mathfrak {g}\). This was proved for \(\mathfrak {sl}_\infty ({{\mathbb {C}}})\) in [27], and in general in [41]. Since we will not need these results here, we omit the detailed constructions.
4 Heisenberg module categories
This section is the heart of the article. Let \(\mathcal {H}eis_k\) be the Heisenberg category, either degenerate or quantum according to the choice of \(z \in \Bbbk \). Suppose that we are given a (\(\Bbbk \)-linear) \(\mathcal {H}eis_k\)-module category \({{\mathcal {R}}}\) which is either locally finite Abelian or Schurian. We are going to show that \({{\mathcal {R}}}\) can be given the structure of a Kac–Moody 2-representation.
4.1 Eigenfunctors
The endofunctors E and F of \({{\mathcal {R}}}\) defined by the generating objects of \(\mathcal {H}eis_k\) are biadjoint, with adjunctions (E, F) and (F, E) defined by the rightwards cups/caps and the leftwards cups/caps, respectively. Hence, both E and F are sweet endofunctors. For \(i \in \Bbbk \), let \(E_i\) and \(F_i\) be the subfunctors of E and F defined on \(V \in {{\mathcal {R}}}\) by declaring that \(E_i V\) and \(F_i V\) are the generalized i-eigenspaces of the endomorphisms  and
and  , respectively.
, respectively.
Let us spell this definition out in more detail. In the Schurian case, any object is the direct limit of its compact (\(=\) finitely presented) subobjects by [15, Lemma 2.6], so in view of the exactness of E and F it suffices to define \(E_i V\) and \(F_i V\) under the assumption that V is finitely generated. Assuming this (which is no restriction at all in the locally finite Abelian case), the objects EV and FV are finitely generated too, hence, their endomorphism algebras \({{\text {End}}}_{{{\mathcal {R}}}}(EV)\) and \({{\text {End}}}_{{{\mathcal {R}}}}(FV)\) are finite-dimensional. So we can define \(m_V(u), n_V(u) \in \Bbbk [u]\) to be the (monic) minimal polynomials of the endomorphisms  and
and  , respectively. Then there are injective homomorphisms
, respectively. Then there are injective homomorphisms

Also let \({\varepsilon }_i(V)\) and \(\phi _i(V)\) denote the multiplicities of \(i \in \Bbbk \) as a root of the polynomials \(m_V(u)\) and \(n_V(u)\), respectively. By the Chinese remainder theorem, we have that
There are corresponding decompositions \(1 = \sum _{i \in \Bbbk } e_i\) of and \(1 = \sum _{i \in \Bbbk } f_i\) of the identity elements of these algebras as a sum of mutually orthogonal idempotents. We define \(E_i V\) and \(F_i V\) to be the summands of EV and FV, respectively, defined by the images of the idempotents \(e_i\) and \(f_i\) under (4.1).
We will represent the identity endomorphisms of the functors \(E_i\) and \(F_i\) by vertical strings colored by i, see the first pair of diagrams below. The inclusions \(E_i \hookrightarrow E\) and \(F_i \hookrightarrow F\) are depicted by the second pair of diagrams below. The projections \(E \twoheadrightarrow E_i\) and \(F \twoheadrightarrow F_i\) are the final pair.

To illustrate the notation, the natural transformation is the projection of E onto its summand \(E_i\), while

It is also clear from the definition that the endomorphisms of E and F defined by the dots restrict to endomorphisms of the summands \(E_i\) and \(F_i\). Representing these restrictions simply by drawing the dots on a string colored by i, we have that

Since the downwards dot is both the left and right mate of the upwards dot, the adjunctions (E, F) and (F, E) induce adjunctions \((E_i, F_i)\) and \((F_i, E_i)\) for all \(i \in I\). We draw the units and counits of these adjunctions using cups and caps colored by i. Again, the various inclusions and projections commute with these morphisms:

The situation with crossings is more interesting. For \(i,j,i',j' \in \Bbbk \), define

Thus, these natural transformation are defined by first including the summand \(E_j E_i\) into EE, then applying natural transformation \(EE \Rightarrow EE\) defined by the usual crossing (positive or negative in the quantum case), then projecting EE onto the summand \(E_{j'} E_{i'}\). The defining relations plus (4.4) imply that

in the degenerate case, or

in the quantum case. There are also sideways and downwards versions of the new crossings which may be defined in a similar way, or equivalently by “rotating” the upwards ones using (4.5). The following lemma is well known but essential.
Lemma 4.1
If \(\{i,j\}\ne \{i',j'\}\) then the natural transformation (4.6) is zero. The same holds for the rotated versions of these crossings.
Proof
For the rotated crossings the lemma follows from the upwards case using also (4.5). To prove the result for the upwards crossing, we just explain in the degenerate case; the quantum case is similar using (4.8) in place of (4.7). If \(\{i,j\}\ne \{i',j'\}\) then one of the following holds: \(i \notin \{i',j'\}, j \notin \{i',j'\}, i' \notin \{i,j\}\) or \(j' \notin \{i,j\}\). Suppose first that \(j \notin \{i',j'\}\) or \(i' \notin \{i,j\}\). It suffices to show that the natural transformation vanishes on every finitely generated \(V \in {{\mathcal {R}}}\). We can find polynomials \(f(u), g(u) \in \Bbbk [u]\) so that \(f(u) (u-j)^{{\varepsilon }_j(E_i V)} + g(u) (u-i')^{{\varepsilon }_{i'}(V)}= 1\). Letting \(p(u) := g(u) (u-i')^{{\varepsilon }_{i'}(V)}\), we then use (4.7) to see that

A similar argument with the dot on the other string treats the cases \(i \notin \{i',j'\}\) or \(j' \notin \{i,j\}\). \(\square \)
Now we come to an extremely useful diagrammatic convention. On any finitely generated \(V \in {{\mathcal {R}}}\), the endomorphism is nilpotent, hence, the notation  makes sense for power series \(p(x) \in \Bbbk [\![x-i]\!]\) rather than merely for polynomials. Since any object of \({{\mathcal {R}}}\) is a direct limit of finitely generated objects, it follows that there is a well-defined natural transformation
makes sense for power series \(p(x) \in \Bbbk [\![x-i]\!]\) rather than merely for polynomials. Since any object of \({{\mathcal {R}}}\) is a direct limit of finitely generated objects, it follows that there is a well-defined natural transformation

for any \(i \in \Bbbk \) and any \(p(x) \in \Bbbk [\![x-i]\!]\). The same definition can be made for dots on downward strings too. More generally, suppose that we are given some more complicated string diagram for a natural transformation between some endofunctors of \({{\mathcal {R}}}\), together with a sequence of n points \(P_1,\dots ,P_n\) on strings colored \(i_1,\dots ,i_n \in \Bbbk \) in this diagram. Then for any \(p(x_1,\dots ,x_n) \in \Bbbk [\![x_1-i_1,\dots ,x_n-i_n]\!]\) there is a well-defined natural transformation represented diagrammatically by drawing a dot on each of the given points in the given diagram then joining them up with a dotted arrow directed from \(P_1\) to \(P_n\) labelled by the power series \(p(x_1,\dots ,x_n)\). Thus, \(x_1\) indicates x labelling the first dot (the one nearest the tail of the arrow) and \(x_n\) indicates x labelling the last dot (the one nearest the head). To give an example, suppose that \(n = 2\) and \(i_1 \ne i_2\). Set \(c := (i_2-i_1)^{-1}\) so that \((x_2-x_1)^{-1} \in \Bbbk [\![x_1-i_1,x_2-i_2]\!]\) has power series expansion \(c -c^2(x_1-i_1) + c^2(x_2-i_2) +\) (higher order terms). Then we have defined the natural transformations

These natural transformations appear in the following lemma.
Lemma 4.2
For \(j \ne i\), we have that

Proof
It suffices to prove this when the natural transformations are evaluated on a finitely generated object \(V \in {{\mathcal {R}}}\). We have to prove that

is zero in the finite-dimensional algebra \(A := {{\text {End}}}_{{{\mathcal {R}}}}(E_j E_i V)\). Let \(L:A \rightarrow A\) be the linear map defined by left multiplication (diagrammatically, this is vertical composition on the top) by , let \(R:A \rightarrow A\) be the linear map defined by right multiplication (diagrammatically, this is vertical composition on the bottom) by , and let \(I:A \rightarrow A\) be the identity map. We have that \((L-jI)^{{\varepsilon }_j(E_i V)} = 0\) and \((R - i I)^{{\varepsilon }_i(V)} = 0\). Hence, for sufficiently large N, we have that
Now observe that \((L-R)(\phi ) = 0\) by the relations (4.7) and (4.8). Hence, we have shown that \((i-j)^N \phi = 0\). Since \(i \ne j\) this implies that \(\phi = 0\). \(\square \)
4.2 Bubbles and central characters
Any dotted bubble in \(\mathcal {H}eis_k\) defines an endomorphism of the identity functor \({\text {Id}}_{{{\mathcal {R}}}}\), i.e., an element of the center of the category \({{\mathcal {R}}}\). In particular, for \(V \in {{\mathcal {R}}}\), dotted bubbles evaluate to elements of the center \(Z_V\) of the endomorphism algebra \({{\text {End}}}_{{\mathcal {R}}}(V)\). It is convenient to work with all of these endomorphisms at once in terms of the generating function

Recalling (3.12) and (3.35), we have \(\mathbb {O}_V(u) \in u^k + u^{k-1} Z_V[\![u^{-1}]\!]\). In the quantum case, there is also a distinguished element \(t_V \in Z_V^\times \) define by the action of \(t 1_{\mathbb {1}}\). In the following lemma, given a polynomial \(p(u) = \sum _{s=0}^r z_s u^{r-s} \in Z_V[u]\), we let

Lemmas 3.1 and 3.5 obviously extend to the setting of coefficients in \(Z_V\).
Lemma 4.3
Let \(V \in {{\mathcal {R}}}\) be any object.
-
(1)
If \(f(u) \in Z_V[u]\) is a monic polynomial such that
 , then \(g(u) := \mathbb {O}_V(u) f(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg f(u)+k\) such that
, then \(g(u) := \mathbb {O}_V(u) f(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg f(u)+k\) such that  .
. -
(2)
If \(g(u) \in Z_V[u]\) is a monic polynomial such that
 , then \(f(u) := \mathbb {O}_V(u)^{-1} g(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg g(u)-k\) such that
, then \(f(u) := \mathbb {O}_V(u)^{-1} g(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg g(u)-k\) such that 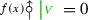 .
.
In the quantum case, we also have that \(f(0) = t_V^2 g(0)\) in both situations.
Proof
We just consider (1), since (2) is similar. To show that g(u) is a polynomial, we must show that \([g(u)]_{u^{-r-1}}=0\) for \(r \ge 0\). Let \(p(u) := u^r f(u)\) in the degenerate case or \(p(u) := t_V^{-1} z u^{r+1} f(u)\) in the quantum case. Applying (3.20) or (3.41), we have that

This is zero as  . Hence, g(u) is a polynomial in u. Moreover, in the quantum case the same argument with \(r=-1\) gives that \(g(0) = t_V^{-2} f(0)\).
. Hence, g(u) is a polynomial in u. Moreover, in the quantum case the same argument with \(r=-1\) gives that \(g(0) = t_V^{-2} f(0)\).
It remains to show that  . In the degenerate case, this follows by (3.19) and (3.21):
. In the degenerate case, this follows by (3.19) and (3.21):

The proof in the quantum case is similar, using (3.40) and (3.42) instead. \(\square \)
If \(L \in {{\mathcal {R}}}\) is irreducible then of course \(\mathbb {O}_L(u) \in \Bbbk (\!(u^{-1})\!)\). The following relates the central character information encoded in this generating function to the minimal polynomials \(m_L(u)\) and \(n_L(u)\) introduced earlier.
Lemma 4.4
For an irreducible object \(L \in {{\mathcal {R}}}\), we have that
Moreover, in the quantum case, the (invertible!) constant terms of the polynomials \(m_L(u)\) and \(n_L(u)\) satisfy \(t_L^2 = m_L(0) / n_L(0)\).
Proof
Applying Lemma 4.3(1) with \(f(u) = m_L(u)\) shows that \(\mathbb {O}_L(u) m_L(u)\) is a monic polynomial of degree \(\deg m_L(u) + k\) which is divisible by \(n_L(u)\). Hence, \(\deg n_L(u) \le \deg m_L(u)+k\). Applying Lemma 4.3(2) with \(g(u) = n_L(u)\) shows that \(\mathbb {O}_L(u)^{-1} n_L(u)\) is a monic polynomial of degree \(\deg n_L(u)-k\) that is divisible by \(m_L(u)\). Hence, \(\deg m_L(u) \le \deg n_L(u)-k\). We deduce that both inequalities are equalities, and we actually have that \(n_L(u) = \mathbb {O}_L(u) m_L(u)\). The assertion about the constant terms follows from the final part of Lemma 4.3. \(\square \)
For \(i \in \Bbbk \), define \(i^\pm \) as in the introduction.
Lemma 4.5
Suppose that \(L \in {{\mathcal {R}}}\) is an irreducible object and let K be an irreducible subquotient of \(E_i L\) for some \(i \in \Bbbk \). Then
Proof
This follows from the bubble slides (3.18) and (3.39). For example, in the degenerate case, we have by (3.18) that

When we pass to the irreducible subquotient K of \(E_i L\), we can replace the occurences of x in the expression on the right-hand side here with i, and the lemma follows. \(\square \)
Now we define the spectrum I of \({{\mathcal {R}}}\) to be the union of the sets of roots of the minimal polynomials \(m_L(u)\) for all irreducible \(L \in {{\mathcal {R}}}\). Noting that i is a root of \(m_L(u)\) if and only if \(E_i L \ne 0\), we have equivalently that I is the set of all \(i \in \Bbbk \) such that \(E_i L \ne 0\) for some irreducible \(L \in {{\mathcal {R}}}\). In view of the exactness of \(E_i\), we can drop the word “irreducible” in this characterization: the spectrum I is the set of all \(i \in \Bbbk \) such that \(E_i\) is a non-zero endofunctor of \({{\mathcal {R}}}\). By adjunction, it follows that I is the set of all \(i \in \Bbbk \) such that the endofunctor \(F_i\) is non-zero, hence, I could also be defined as the union of the sets of roots of the polynomials \(n_L(u)\) for all irreducible \(L \in {{\mathcal {R}}}\). This discussion shows that
with each of the endofunctors \(E_i\) and \(F_i\) written here being non-zero.
Lemma 4.6
We have that \(i \in I\) if and only if \(i^+ \in I\). Moreover, in the quantum case, we have that \(0 \notin I\).
Proof
The fact that \(0 \notin I\) in the quantum case follows from the invertibility of the dot. For the first part, it suffices to show for \(i \in I\) that \(i^+\) and \(i^-\) both belong to I. Let \(j:= i^\pm \) for some choice of the sign. As \(i \in I\), there is an irreducible \(L \in {{\mathcal {R}}}\) such that \(E_i L \ne 0\). Let K be an irreducible subquotient of \(E_i L\). By (4.11), we have that \(\mathbb {O}_K(u) (u-i^+)(u-i^-) = \mathbb {O}_L(u) (u-i)^2\). Using Lemma 4.4, we deduce that
Thus \((u-j)\) divides either \(m_K(u)\) or \(n_L(u)\), so either \(E_j K \ne 0\) or \(F_j L \ne 0\). This shows that \(E_j \ne 0\) or \(F_j \ne 0\), hence, \(j \in I\). \(\square \)
In view of Lemma 4.6, the map \(i \mapsto i^+\) defines a fixed-point-free automorphism of I. This puts us in the situation of Sect. 3.3, so we can associate a Kac–Moody Lie algebra \(\mathfrak {g}\) with weight lattice X, fundamental weights \(\{\Lambda _i\,|\,i \in I\}\), etc. For an irreducible object \(L \in {{\mathcal {R}}}\), let
In other words, due to the definition preceeding (4.2) and Lemma 4.4, \(\langle h_i, {{\text {wt}}}(L)\rangle \in {{\mathbb {Z}}}\) is the multiplicity of \(u=i\) as a zero or pole of the rational function \(\mathbb {O}_L(u) \in \Bbbk (u)\) for each \(i \in I\). Then for \(\lambda \in X\) we let \({{\mathcal {R}}}_\lambda \) be the Serre subcategory of \({{\mathcal {R}}}\) consisting of the objects V such that every irreducible subquotient L of V satisfies \({{\text {wt}}}(L) = \lambda \). The point of this definition is that irreducible objects \(K, L \in {{\mathcal {R}}}\) with \({{\text {wt}}}(K) \ne {{\text {wt}}}(L)\) have different central characters. Using also the general theory of blocks in our two sorts of Abelian category, it follows that
We refer to this as the weight space decomposition of \({{\mathcal {R}}}\).
Lemma 4.7
For \(\lambda \in X\) and \(i \in I\), the restrictions of \(E_i\) and \(F_i\) to \({{\mathcal {R}}}_\lambda \) give functors
Proof
For \(E_i\), this follows from Lemma 4.5. Then it follows for \(F_i\) by adjunction. \(\square \)
4.3 The main isomorphism
The next lemma is quite trivial but serves as a good warm-up exercise for the one that follows.
Lemma 4.8
For \(i,j \in I\) with \(j \ne i\), the natural transformations

are mutually inverse isomorphisms. (Here, we have drawn the crossings in the degenerate case; in the quantum case they should be interpreted as positive or negative crossings, it does not matter which is chosen.)
Proof
Check that the compositions both ways around are the identities. For example, one way in the degenerate case gives

using Lemma 4.1 (the sideways crossing version!) for the first equality, the relation (3.8) for the second, and (4.3)–(4.5) for the final one. The other cases are similar. \(\square \)
Now we come to what is really the main step. In the statement of the following two lemmas, the restrictions \(F_i E_i|_{{{\mathcal {R}}}_\lambda }\) and \(E_i F_i|_{{{\mathcal {R}}}_\lambda }\) are endofunctors of \({{\mathcal {R}}}_\lambda \) due to Lemma 4.7.
Lemma 4.9
Given \(\lambda \in X\) and \(i \in I\) such that \(\langle h_i, \lambda \rangle \le 0\), the natural transformation

is an isomorphism. (This time, we have drawn the crossing in the quantum case; in the degenerate case it should be replaced by the degenerate crossing.)
Proof
We just prove this in the quantum case; the degenerate case is similar. It suffices to prove that the natural transformation in the statement of the lemma defines an isomorphism on every irreducible object \(L \in {{\mathcal {R}}}_\lambda \); in the Schurian case one needs to apply Lemma 2.1 to make this reduction. So take an irreducible \(L \in {{\mathcal {R}}}_\lambda \). We have that \(m:= {\varepsilon }_i(L)-\phi _i(L)=-\langle h_i,\lambda \rangle \ge 0\). Let \(P := \Bbbk [u] / (m_L(u))\) and \(Q := \Bbbk [u] / (n_L(u))\). Let \(P_i\) and \(Q_i\) be the summands of P and Q that are isomorphic to \(\Bbbk [u] \big / \big ((u-i)^{{\varepsilon }_i(L)}\big )\) and \(\Bbbk [u] \big / \big ((u-i)^{\phi _i(L)}\big )\) in the CRT decomposition (4.2). To be explicit, let f(u) and g(u) be polynomials such that
Then the identity elements \(e_i \in P_i\) and \(f_i \in Q_i\) are the images of \(f(u) m_L(u) / (u-i)^{{\varepsilon }_i(L)}\) and \(g(u) n_L(u) / (u-i)^{\phi _i(L)}\) in P and Q, respectively. Moreover, f(u) is invertible in \(P_i\), so \(P_i\) can be described equivalently as the ideal of P generated by \(m_L(u) / (u-i)^{{\varepsilon }_i(L)}\). Similarly, \(Q_i\) is the ideal of Q generated by \(n_L(u) / (u-i)^{\phi _i(L)}\). There is an injective \(\Bbbk [u]\)-module homomorphism
Its image has basis \((u-i)^m e_i, (u-i)^{m+1} e_i,\dots , (u-i)^{{\varepsilon }_i(L)-1} e_i\). Let \(C_i\) be the subspace of \(P_i\) with basis \(e_i, (u-i) e_i,\dots , (u-i)^{m-1} e_i\). This is a linear complement to \(\mu (Q_i)\) in \(P_i\).
The composition of the algebra embeddings (4.1) with the adjunction isomorphisms \({{\text {End}}}_{{{\mathcal {R}}}}(EL) \cong {\text {Hom}}_{{{\mathcal {R}}}}(L, FEL)\) and \({{\text {End}}}_{{{\mathcal {R}}}}(FL) \cong {\text {Hom}}_{{{\mathcal {R}}}}(L, EFL)\) give us linear embeddings \(\vec {\beta }:P \hookrightarrow {\text {Hom}}_{{{\mathcal {R}}}}(L, FEL)\) and  , respectively. So:
, respectively. So:

Recalling (2.3), the linear maps \(\vec {\beta }\) and  induce morphisms
induce morphisms

For example, if \(v_1,\dots ,v_n\) is the fixed basis for P then \(\vec {\gamma }\) is the morphism \(L^{\oplus n} \rightarrow FEL\) defined by the matrix \(\left[ \vec {\beta }(v_1)\,\cdots \,\vec {\beta }(v_n)\right] \). As the morphisms \(\vec {\beta }(v_1),\dots ,\vec {\beta }(v_n):L \rightarrow FEL\) are linearly independent and L is irreducible, \(\vec {\gamma }\) is a monomorphism. Similarly, so is  . As \(\vec {\beta }(e_i)\) maps L into the summand \(F_i E_i L\) of FEL, we have that \(\vec {\gamma }(L \otimes P_i) \subseteq F_i E_i L\). Similarly,
. As \(\vec {\beta }(e_i)\) maps L into the summand \(F_i E_i L\) of FEL, we have that \(\vec {\gamma }(L \otimes P_i) \subseteq F_i E_i L\). Similarly,  . Finally, let
. Finally, let

We are trying to prove that the morphism
is an isomorphism. Equivalently, using the basis \(e_i, (u-i) e_i,\dots ,(u-i)^{m-1} e_i\) for \(C_i\) to identify \(L \otimes C_i\) with \(L^{\oplus m}\), we must show that
is an isomorphism. This follows from the following series of claims.
\(\underline{\hbox {Claim }1}\):  . To justify this, take \(p(u) \in P_i\), we have that
. To justify this, take \(p(u) \in P_i\), we have that

Using the defining relations, p(x) can now be commuted past the crossing and the curl can be “straightened.” The resulting morphism clearly has image in  .
.
\(\underline{\hbox {Claim }2}\):  . Take a polynomial \(p(u) \in \Bbbk [u]\) representing an element of \(Q_i\), i.e., a polynomial divisible by \(n_L(u) / (u-i)^{\phi _i(L)}\). Let \(q(u) := t_L^{-1} p(u) m_L(u) / n_L(u) \in \Bbbk [u]\). This is a representative for the image of p(u) under \(\mu :Q_i \rightarrow P_i\). Using Lemmas 3.3 and 4.4, we have that
. Take a polynomial \(p(u) \in \Bbbk [u]\) representing an element of \(Q_i\), i.e., a polynomial divisible by \(n_L(u) / (u-i)^{\phi _i(L)}\). Let \(q(u) := t_L^{-1} p(u) m_L(u) / n_L(u) \in \Bbbk [u]\). This is a representative for the image of p(u) under \(\mu :Q_i \rightarrow P_i\). Using Lemmas 3.3 and 4.4, we have that

The claim follows from this using the definitions of \(\vec {\gamma }\) and  .
.
\(\underline{\hbox {Claim }3}\): We have that  for some morphism \(\phi :F_i E_i L \rightarrow F_i E_i L\) whose image is contained in \(\vec {\gamma }(L \otimes P_i)\). Similarly,
for some morphism \(\phi :F_i E_i L \rightarrow F_i E_i L\) whose image is contained in \(\vec {\gamma }(L \otimes P_i)\). Similarly,  for some morphism \(\phi :E_i F_i L \rightarrow E_i F_i L\) whose image is contained in
for some morphism \(\phi :E_i F_i L \rightarrow E_i F_i L\) whose image is contained in  . We just explain in the first case. We have that
. We just explain in the first case. We have that

The second, third and fourth terms on the right-hand side are morphisms whose image is contained in \(\vec {\gamma }(L \otimes P_i)\). It just remains to see that the final term consists of such morphisms too. Take \(j \ne i\). Like in the proof of Lemma 4.1, we can find a polynomial \(p(u) \in \Bbbk [u]\) divisible by \((u-j)^{\phi _j(L)}\) so that \(p(u)\equiv 1 \pmod {(u-i)^{\phi _i(E_i L)}}\). We have that

Now using the commutation relations (4.8), we commute p(x) past the crossing to produce a term that is zero as p(x) is divisible by a sufficiently large power of \((x-j)\), plus correction terms all of which are morphisms with image lying in \(\vec {\gamma }(L \otimes P_i)\).
\(\underline{\hbox {Claim }4}\): \(\theta \) is an epimorphism. Note by the first assertion from Claim 3 that \(F_i E_i L \subseteq \vec {\chi }(E_i F_i L) + \vec {\gamma }(L \otimes P_i)\). Claim 2 implies that  . Since \(P_i = \mu (Q_i) \oplus C_i\), we deduce that \(F_i E_i L \subseteq \vec {\chi }(E_i F_i L) + \vec {\gamma }(L \otimes C_i)\) as required.
. Since \(P_i = \mu (Q_i) \oplus C_i\), we deduce that \(F_i E_i L \subseteq \vec {\chi }(E_i F_i L) + \vec {\gamma }(L \otimes C_i)\) as required.
\(\underline{\hbox {Claim }5}\): \(\theta \) is a monomorphism. Let K be its kernel. Of course, K is contained in the kernel of the composition  Using the second assertion from Claim 3 together with Claim 1, we deduce that
Using the second assertion from Claim 3 together with Claim 1, we deduce that  . Hence, it suffices to show that
. Hence, it suffices to show that  is a monomorphism. Using Claim 2 again, this follows because both \(L \otimes \mu \) and \(\vec {\gamma } = \left[ \vec {\gamma }|_{\mu (Q_i)\otimes L} \quad \vec {\gamma }|_{L \otimes C_i}\right] \) are monomorphisms. \(\square \)
is a monomorphism. Using Claim 2 again, this follows because both \(L \otimes \mu \) and \(\vec {\gamma } = \left[ \vec {\gamma }|_{\mu (Q_i)\otimes L} \quad \vec {\gamma }|_{L \otimes C_i}\right] \) are monomorphisms. \(\square \)
Lemma 4.10
Given \(\lambda \in X\) and \(i \in I\) such that \(\langle h_i, \lambda \rangle \ge 0\), the natural transformation

is an isomorphism. (Again, we have just drawn the crossing in the quantum case.)
Proof
Let \((\mathcal {H}eis_k)^{{{\text {op}}}}\) be the opposite category viewed as a monoidal category with the same horizontal composition law as in \(\mathcal {H}eis_k\). Let \(\mathcal {H}eis_{-k}'\) be the \(\Bbbk \)-linear category \(\mathcal {H}eis_{-k}\) in the degenerate case, or the \(\mathbb {K}\)-linear category defined in the same way as \(\mathcal {H}eis_{-k}\) but with t replaced by \(t^{-1}\) in the quantum case. By [4, Lemma 2.1] or [13, Theorem 3.2], there is a \(\Bbbk \)-linear isomorphism \(\Omega :\mathcal {H}eis_{-k}{\mathop {\rightarrow }\limits ^{\sim }} (\mathcal {H}eis'_k)^{{{\text {op}}}}\) defined by reflecting diagrams in a horizontal plane, then multiplying by \((-1)^{x+y}\) where x is the total number of crossings and y is the total number of leftward cups and caps in the diagram. Saying that \({{\mathcal {R}}}\) is a module category over \(\mathcal {H}eis_k\) is equivalent to saying that \({{\mathcal {R}}}^{{{\text {op}}}}\) is a module category over \((\mathcal {H}eis_k)^{{{\text {op}}}}\). Note moreover that \({{\mathcal {R}}}^{{{\text {op}}}}\) is an Abelian category of the same type (locally finite Abelian or Schurian) as \({{\mathcal {R}}}\) itself due to [15, (2.2), (2.10)]. Its pull-back through the isomorphism \(\Omega \) gives us a \(\mathcal {H}eis_{-k}'\)-module category \(\Omega ^*({{\mathcal {R}}}^{{{\text {op}}}})\). Moreover
This follows from (4.13) since \(\Omega \) switches E and F. Now we take \(\lambda \in X\) with \(\langle h_i, \lambda \rangle \ge 0\) and consider the natural transformation between endofunctors of \({{\mathcal {R}}}_\lambda \) from the statement of the lemma. This natural transformation can be viewed instead as a natural transformation \(F_i E_i|_{({{\mathcal {R}}}_\lambda )^{{\text {op}}}} \oplus {\text {Id}}_{({{\mathcal {R}}}_\lambda )^{{\text {op}}}}^{\oplus \langle h_i, \lambda \rangle } \Rightarrow E_i F_i|_{({{\mathcal {R}}}_\lambda )^{{\text {op}}}}\) between endofunctors of \(({{\mathcal {R}}}_\lambda )^{{\text {op}}}\). This is just the same as the natural transformation \(E_i F_i|_{(\Omega ^*({{\mathcal {R}}}^{{\text {op}}}))_{-\lambda }} \oplus {\text {Id}}_{(\Omega ^*({{\mathcal {R}}}^{{\text {op}}}))_{-\lambda }}^{\oplus (-\langle h_i,-\lambda \rangle )} \Rightarrow F_i E_i|_{(\Omega ^*({{\mathcal {R}}}^{{\text {op}}}))_{-\lambda }}\) from Lemma 4.9 applied to the weight \(-\lambda \) and the \(\mathcal {H}eis'_{-k}\)-module category \(\Omega ^*({{\mathcal {R}}}^{{\text {op}}})\). Hence, it is an isomorphism by the previous lemma. \(\square \)
4.4 Heisenberg to Kac–Moody
Now we can prove the main theorem of the section. Recall that \({{\mathcal {R}}}\) is a locally finite Abelian or Schurian module category over \(\mathcal {H}eis_k\). Let \(E_i\) and \(F_i\) be the eigenfunctors from Sect. 4.1, and recall the various diagrams representing natural transformations between these functors introduced there. Let I be the spectrum of \({{\mathcal {R}}}\) as in Sect. 4.2, and \({{\mathfrak {U}}}(\mathfrak {g})\) be the corresponding Kac–Moody 2-category as in Sect. 3.3. We also need the weight space decomposition of \({{\mathcal {R}}}\) from (4.14). As in [10], there is some freedom in the following theorem as it involves a choice of normalization; for the sake of clarity, we have fixed a particular one.
Theorem 4.11
Associated to \({{\mathcal {R}}}\), there is a unique 2-representation \(\mathbf{R} :{{\mathfrak {U}}}(\mathfrak {g})\rightarrow \mathfrak {Cat}_\Bbbk \) defined on objects by \(\lambda \mapsto {{\mathcal {R}}}_\lambda \), on generating 1-morphisms by \(E_i 1_\lambda \mapsto E_i|_{{{\mathcal {R}}}_\lambda }\) and \(F_i 1_\lambda \mapsto F_i|_{{{\mathcal {R}}}_\lambda }\), and on generating 2-morphisms by


in the degenerate case, or


in the quantum case.
Proof
We need to verify the defining relations (3.45)–(3.48) and (3.56)–(3.58).
The quiver Hecke algebra relations (3.45)–(3.47) follow from the calculations performed in [10]. Note also that our formulae look different from the ones in [10] in the quantum case due to the fact that we are working with a different normalization for the quadratic relation in the Hecke algebra. In fact, it is perfectly reasonable to check all of the relations (3.45)–(3.47) from scratch without referring to [10] at all; the diagrammatic formalism now in place makes this particularly convenient. To give the flavor of the calculation, we check the quadratic relation (3.46) in the quantum case. One first uses (4.8) to check that

Then, we place the right-hand side of the expression just displayed on top of the formula for the crossing from the statement of the theorem, to obtain a natural transformation \(\theta \). This is easily seen to be zero in the case \(j=i\) as required. We are left with four cases: \(j^-=i\ne j^+\), \(j^- \ne i = j^+\), \(j^-=i=j^+\) and \(j^- \ne i \ne j^+\). According to (3.46), we need to show that \(\theta \) equals  where \(f=-q^{-1}i^{-1}(q^{-1}x_2-q x_1)\), \(qi^{-1}(qx_2-q^{-1}x_1)\), \(-i^{-2}(qx_2-q^{-1}x_1)(q^{-1}x_2-qx_1)\) or 1 in these four cases. Note moreover that
where \(f=-q^{-1}i^{-1}(q^{-1}x_2-q x_1)\), \(qi^{-1}(qx_2-q^{-1}x_1)\), \(-i^{-2}(qx_2-q^{-1}x_1)(q^{-1}x_2-qx_1)\) or 1 in these four cases. Note moreover that
Hence, we have that \(f=gab\) where
To complete the analysis, we just have to use Lemmas 4.1–4.2 to see that

which is what we wanted as \(f=gab\).
The adjunction relation (3.48) is immediate.
Finally, we need to check the inversion relation. This depends on Lemmas 4.8–4.10. As usual we just go through the details in the quantum case. First, we observe using (4.8) that

Using this, we can compute the images of the morphisms in (3.56)–(3.58). The first is equal to the morphism from Lemma 4.8 composed on the right by another invertible morphism, hence, it is invertible. Similarly, the second is equal to the morphism from Lemma 4.9 composed on the right by an invertible diagonal matrix. Finally, the last one is equal to the morphism from Lemma 4.10 composed on the left by an invertible diagonal matrix. This completes the proof. \(\square \)
Remark 4.12
In the setup of Theorem 4.11, the images of the generating 2-morphisms  and
and  are uniquely determined by the images of the other generators thanks to Lemma 3.4. It is not easy to find explicit formulae for these in practice. Nevertheless, we do understand how to apply \(\mathbf{R} \) to dotted bubbles, although it is easier for this to go in the other direction; see (5.37) and (5.38) below.
are uniquely determined by the images of the other generators thanks to Lemma 3.4. It is not easy to find explicit formulae for these in practice. Nevertheless, we do understand how to apply \(\mathbf{R} \) to dotted bubbles, although it is easier for this to go in the other direction; see (5.37) and (5.38) below.
5 Generalized cyclotomic quotients
The Heisenberg category \(\mathcal {H}eis_k\) (resp., the Kac–Moody 2-category \({{\mathfrak {U}}}(\mathfrak {g})\)) has some universal cyclic module categories (resp., 2-representations) known as generalized cyclotomic quotients (GCQs for short). In this section, we construct an explicit isomorphism between Heisenberg and Kac–Moody GCQs, and use this to prove a converse to Theorem 4.11.
5.1 Kac–Moody 2-representations
Let \({{\mathfrak {U}}}(\mathfrak {g})\) be the Kac–Moody 2-category as in Sect. 3.3. Its 2-representation theory has been developed rather fully in the literature. We begin the section by reviewing some of the basic facts established in [17, 34]; see also [8] which extended some of the results to the Schurian setting. Actually, as discussed in the introduction, the history here is a little convoluted, since many of these results were first established in the setting of (degenerate) affine Hecke algebras. However, with hindsight, the proofs are most naturally explained in terms of the representation theory of the nil-Hecke algebra.
Suppose that we are given a locally finite Abelian or Schurian 2-representation \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) of \({{\mathfrak {U}}}(\mathfrak {g})\). Let
which is again a locally finite Abelian or Schurian category. The functors \(E_i|_{{{\mathcal {R}}}_\lambda }\) and \(F_i|_{{{\mathcal {R}}}_\lambda }\) for all \(\lambda \) define endofunctors \(E_i\) and \(F_i\) of \({{\mathcal {R}}}\). The rightwards and leftwards cups and caps in \({{\mathfrak {U}}}(\mathfrak {g})\) define canonical adjunctions \((E_i, F_i)\) and \((F_i, E_i)\) for all \(i \in I\). In particular, \(E_i\) and \(F_i\) are sweet endofunctors of \({{\mathcal {R}}}\). There are also divided power functors \(E_i^{(r)}, F_i^{(r)}\) such that \(E_i^r \cong (E_i^{(r)})^{\oplus r!}\) and \(F_i^r \cong (E_i^{(r)})^{\oplus r!}\). These are constructed using the action of the nil-Hecke algebra on the functors \(E_i^r\) and \(F_i^r\). The divided power functors induce endomorphisms \(e_i^{(r)} := [E_i^{(r)}]\) and \(f_i^{(r)} := [F_i^{(r)}]\) of the Grothendieck group
as defined in Sect. 2.2, making \(K_0({{\mathcal {R}}})\) into an integrable module over the Kostant \({{\mathbb {Z}}}\)-form for the universal enveloping algebra of \(U(\mathfrak {g})\) with (5.2) as its weight space decomposition. This assertion is a consequence of the categorical Serre relations proved in [34, Proposition 4.2] (see also [26, Corollary 7]); the integrability is [8, Lemma 3.6].
We will assume from now on that the 2-representation \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) is nilpotent, meaning that the following hold:
-
For each \(\lambda \in X\) and \(V \in {{\mathcal {R}}}_\lambda \), we have that \(E_i V=F_iV=\mathbf{0 }\) for all but finitely many \(i \in I\).
-
The endomorphisms
 are nilpotent for all \(i \in I\), \(\lambda \in X\) and finitely generated \(V \in {{\mathcal {R}}}_\lambda \); equivalently, all of the endomorphisms
are nilpotent for all \(i \in I\), \(\lambda \in X\) and finitely generated \(V \in {{\mathcal {R}}}_\lambda \); equivalently, all of the endomorphisms  are nilpotent.
are nilpotent.
The first property implies that
are well-defined endofunctors of \({{\mathcal {R}}}\). The canonical adjunctions \((E_i, F_i)\) and \((F_i, E_i)\) for all i induce adjunctions (E, F) and (F, E), hence, these are sweet endofunctors too. By the second property, it makes sense to define \({\varepsilon }_i(V)\) and \(\phi _i(V)\) to be the nilpotency degrees of the endomorphisms  and
and  , respectively, for any finitely generated \(V \in {{\mathcal {R}}}_\lambda \) and \(i \in I\). In other words, the minimal polynomials of these endomorphisms are \(u^{{\varepsilon }_i(V)}\) and \(u^{\phi _i(V)}\), respectively.
, respectively, for any finitely generated \(V \in {{\mathcal {R}}}_\lambda \) and \(i \in I\). In other words, the minimal polynomials of these endomorphisms are \(u^{{\varepsilon }_i(V)}\) and \(u^{\phi _i(V)}\), respectively.
Like in Sect. 4.2, for any \(\lambda \in X\) and \(V \in {{\mathcal {R}}}_\lambda \), we let \(Z_V := Z({{\text {End}}}_{{\mathcal {R}}}(V))\). Then, assuming that V is finitely generated so that all but finitely many bubbles act as zero due to the assumption of nilpotency, we define

for each \(i \in I\). The following are the Kac–Moody counterparts of Lemmas 4.3–4.4; see also [41, Lemma 3.8].
Lemma 5.1
Suppose that \(i \in I\) and V is a finitely generated object of \({{\mathcal {R}}}_\lambda \) for \(\lambda \in X\).
-
(1)
If \(f(u) \in Z_V[u]\) is a monic polynomial such that
 , then \(g(u) := \mathbb {O}_{V,i}(u) f(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg f(u)+\langle h_i,\lambda \rangle \) such that
, then \(g(u) := \mathbb {O}_{V,i}(u) f(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg f(u)+\langle h_i,\lambda \rangle \) such that  .
. -
(2)
If \(g(u) \in Z_V[u]\) is a monic polynomial such that
 , then \(f(u) := \mathbb {O}_{V,i}(u)^{-1} g(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg g(u)-\langle h_i,\lambda \rangle \) such that
, then \(f(u) := \mathbb {O}_{V,i}(u)^{-1} g(u)\) is a monic polynomial in \(Z_V[u]\) of degree \(\deg g(u)-\langle h_i,\lambda \rangle \) such that  .
.
Proof
Mimic the proof of Lemma 4.3 using Lemma 3.5. \(\square \)
Lemma 5.2
Let \(L \in {{\mathcal {R}}}_\lambda \) be an irreducible object. For \(i \in I\), we have that
In particular, \(\phi _i(L)-{\varepsilon }_i(L)= \langle h_i,\lambda \rangle \).
Proof
We first apply Lemma 5.1(1) with \(f(u) = u^{{\varepsilon }_i(L)}\) to deduce that \(\mathbb {O}_{V,i}(u) u^{{\varepsilon }_i(L)}\) is a monic polynomial of degree \({\varepsilon }_i(L)+\langle h_i,\lambda \rangle \) divisible by \(u^{\phi _i(L)}\). Hence, \(\phi _i(L) \le {\varepsilon }_i(L)+\langle h_i,\lambda \rangle \). Then we apply Lemma 5.1(2) with \(g(u) = u^{\phi _i(L)}\) to deduce that \(\mathbb {O}_{V,i}(u)^{-1} u^{\phi _i(L)}\) is monic of degree \(\phi _i(L)-\langle h_i,\lambda \rangle \) divisible by \(u^{{\varepsilon }_i(L)}\). Hence, \({\varepsilon }_i(L) \le \phi _i(L)-\langle h_i,\lambda \rangle \). We deduce that both inequalities are equalities and the lemma follows. \(\square \)
Corollary 5.3
If \(V \in {{\mathcal {R}}}_\lambda \) is any finitely generated object, all coefficients of \(\mathbb {O}_{V,i}(u)\) apart from the leading one are nilpotent.
Proof
Lemma 5.2 shows that the natural transformations defined by the bubbles  for \(r \ge -\langle h_i,\lambda \rangle \) are zero on all irreducible objects \(L \in {{\mathcal {R}}}_\lambda \). Hence, they define elements of the Jacobson radical of \({{\text {End}}}_{{\mathcal {R}}}(V)\). \(\square \)
for \(r \ge -\langle h_i,\lambda \rangle \) are zero on all irreducible objects \(L \in {{\mathcal {R}}}_\lambda \). Hence, they define elements of the Jacobson radical of \({{\text {End}}}_{{\mathcal {R}}}(V)\). \(\square \)
The final fundamental result to be mentioned here reveals some remarkable combinatorics which motivated several of our earlier notational choices. Still assuming nilpotency, there is an associated crystal \((\mathbf{B} ,{\tilde{e}}_i, {\tilde{f}}_i, {\varepsilon }_i, \phi _i, {\text {wt}})\) in the general sense of Kashiwara; more precisely, it is what is called a classical crystal in [24]. This follows by [17, Proposition 5.20] in the locally finite Abelian setting or [8, Theorem 4.31] in the Schurian case; many of the ideas here go back to the work of Grojnowski [22]. In more detail, the underlying set \(\mathbf{B} \) is the set of isomorphism classes of irreducible objects in \({{\mathcal {R}}}\). The crystal operators \({\tilde{e}}_i, {\tilde{f}}_i:\mathbf{B} \rightarrow \mathbf{B} \sqcup \{\varnothing \}\) are defined on an irreducible object \(L \in {{\mathcal {R}}}_\lambda \) as follows:
-
if \(E_i L \ne 0\) then \({\tilde{e}}_i(L)\) is \({\text {hd}}(E_i L) \cong {\text {soc}}(E_i L)\) (which is irreducible), else \(E_i L = \varnothing \);
-
if \(F_i L \ne 0\) then \({\tilde{f}}_i(L)\) is \({\text {hd}}(F_i L) \cong {\text {soc}}(F_i L)\) (which is irreducible), else \(F_i L = \varnothing \).
The weight function \({{\text {wt}}}:\mathbf{B} \rightarrow X\) is defined by \({{\text {wt}}}(L) := \lambda \) for \(L \in {{\mathcal {R}}}_\lambda \). The functions \({\varepsilon }_i, \phi _i:\mathbf{B} \rightarrow {{\mathbb {N}}}\) take \(L \in \mathbf{B} \) to the nilpotency degrees of the endomorphisms  and
and  as above. Part of what it means to say that this is a crystal datum gives that \({\varepsilon }_i(L) = \max \{n \in {{\mathbb {N}}}\,|\,E_i^{n} L \ne 0\}\) and \(\phi _i(L) = \max \{n \in {{\mathbb {N}}}\,|\,F_i^{n} L \ne 0\}\). Moreover, it is known that the endomorphism algebras of \(E_i L\) and \(F_i L\) are isomorphic to \(\Bbbk [u] / (u^{{\varepsilon }_i(L)})\) and \(\Bbbk [u] / (u^{\phi _i(L)})\), respectively.
as above. Part of what it means to say that this is a crystal datum gives that \({\varepsilon }_i(L) = \max \{n \in {{\mathbb {N}}}\,|\,E_i^{n} L \ne 0\}\) and \(\phi _i(L) = \max \{n \in {{\mathbb {N}}}\,|\,F_i^{n} L \ne 0\}\). Moreover, it is known that the endomorphism algebras of \(E_i L\) and \(F_i L\) are isomorphic to \(\Bbbk [u] / (u^{{\varepsilon }_i(L)})\) and \(\Bbbk [u] / (u^{\phi _i(L)})\), respectively.
Remark 5.4
The 2-representations \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) constructed in Theorem 4.11 are nilpotent. Moreover, the functors \(E_i, F_i\) and functions \({\varepsilon }_i, \phi _i\) and \({{\text {wt}}}\) as introduced in Sects. 4.1 and 4.2 are the same as in the present subsection. Consequently, all of the results summarized here can be applied to the study of locally finite Abelian or Schurian \(\mathcal {H}eis_k\)-module categories. In particular, the description of the endomorphism algebras of \(E_i L\) and \(F_i L\) just mentioned implies that the homomorphisms (4.1) are actually isomorphisms for irreducible V.
5.2 Kac–Moody GCQs
The next three subsections are concerned with GCQs. These first appeared on the Kac–Moody side in [39, Proposition 5.6]; see also [8, \(\S \)4.2]. We will only need them under the assumption of nilpotency, although it can also be useful to consider these categories more generally; e.g., see [41]. Let \({{\mathfrak {U}}}(\mathfrak {g})\) be the Kac–Moody 2-category as in the previous subsection. The data needed to define a (nilpotent) GCQ of \({{\mathfrak {U}}}(\mathfrak {g})\) is as follows:
-
a finite-dimensional, commutative, local \(\Bbbk \)-algebra Z with maximal ideal J;
-
dominant weights \(\mu ,\nu \in X^+\);
-
monic polynomials \(\mu _i(u) \in u^{\langle h_i, \mu \rangle }+J[u]\), \(\nu _i(u) \in u^{\langle h_i, \nu \rangle }+J[u]\) for all \(i \in I\).
In the important special case that \(Z = \Bbbk \), the polynomials \(\mu _i, \nu _i\) provide no additional data beyond that of the dominant weights \(\mu ,\nu \) since we necessarily have that \(\mu _i(u) = u^{\langle h_i, \mu \rangle }\) and \(\nu _i(u) = u^{\langle h_i, \nu \rangle }\). Let \(\kappa := \nu - \mu \in X\) and
We also need notation for the coefficients of \(\mathbb {O}_i(u)\) and its inverse defined from the expansions
Associated to the weight \(\kappa \), there is a universal 2-representation \(({{\mathcal {R}}}(\kappa )_\lambda )_{\lambda \in X}\) defined by setting \({{\mathcal {R}}}(\kappa )_\lambda := \mathcal {H}om_{{{\mathfrak {U}}}(\mathfrak {g})}(\kappa ,\lambda )\); the 1- and 2-morphisms in \({{\mathfrak {U}}}(\mathfrak {g})\) act by horizontally composing on the left in the obvious way. Extending scalars, we obtain from this a Z-linear 2-representation \(({{\mathcal {R}}}(\kappa )_\lambda \otimes _\Bbbk Z)_{\lambda \in X}\). Let \(({\mathcal {I}}_Z(\mu |\nu )_\lambda )_{\lambda \in X}\) be the sub-2-representation generated by the 2-morphisms

Equivalently, by [8, Lemma 4.14], \(({\mathcal {I}}_Z(\mu |\nu )_\nu )_{\lambda \in X}\) is generated by the 2-morphisms

The generalized cyclotomic quotient \((\mathcal {H}_Z(\mu |\nu )_\lambda )_{\lambda \in X}\) is the quotient 2-representation. Thus, for \(\lambda \in X\), we have that
This is the Z-linear category with objects that are 1-morphisms \(G 1_\kappa :\kappa \rightarrow \lambda \) in \({{\mathfrak {U}}}(\mathfrak {g})\), and morphism space \({\text {Hom}}_{\mathcal {H}_Z(\mu |\nu )_\lambda }(G 1_\kappa , G'1_\kappa )\) that is the quotient of \({\text {Hom}}_{{{\mathfrak {U}}}(\mathfrak {g})}(G 1_\kappa ,G'1_\kappa ) \otimes _\Bbbk Z\) by the Z-submodule spanned by all string diagrams from \(G 1_\kappa \) to \(G'1_\kappa \) which have one of the above generating 2-morphisms appearing on its right-hand boundary. Note in particular by [8, Lemma 4.14] again that

in \({{\text {End}}}_{\mathcal {H}_Z(\mu |\nu )_\kappa }(1_\kappa )\). It is often convenient to put all of the categories \(\mathcal {H}_Z(\mu |\nu )_\lambda \) together into a single Z-linear category
We denote objects in this category simply by words in the monoid \(\langle E_i, F_i\rangle _{i \in I}\) generated by the symbols \(E_i, F_i\,(i \in I)\), such a word G standing for the 1-morphism \(G 1_\kappa \). If \(G = G_d\cdots G_1\) with each \(G_r \in \{E_i, F_i\,|\,i \in I\}\), we let
Then the object G belongs to \(\mathcal {H}_Z(\mu |\nu )_{\lambda }\) for \(\lambda = \kappa +{{\text {wt}}}(G)\).
Certain morphism spaces in \(\mathcal {H}_Z(\mu |\nu )\) can be described quite explicitly. To prepare for this, recall that there is a basis theorem for 2-morphism spaces in \({{\mathfrak {U}}}(\mathfrak {g})\). This was formulated originally as the nondegeneracy condition by Khovanov and Lauda in [27, \(\S \)3.2.3]. It was proved by them in finite type A, and it was proved in general in [41]; see also [18] for a completely different approach.
Lemma 5.5
The quotient of the Z-algebra \({{\text {End}}}_{{{\mathfrak {U}}}(\mathfrak {g})}(1_\kappa ) \otimes _\Bbbk Z\) by the ideal V generated by  is isomorphic to Z.
is isomorphic to Z.
Proof
By the nondegeneracy condition, \({{\text {End}}}_{{{\mathfrak {U}}}(\mathfrak {g})}(1_\kappa )\) is a polynomial algebra generated freely by the dotted bubbles  for \(i \in I\) and \(r \ge - \langle h_i, \kappa \rangle \). Since \(\mu _i(u)\) is monic of degree \(\langle h_i, \mu \rangle \), factoring out the ideal generated by
for \(i \in I\) and \(r \ge - \langle h_i, \kappa \rangle \). Since \(\mu _i(u)\) is monic of degree \(\langle h_i, \mu \rangle \), factoring out the ideal generated by  for \(s \ge 0\) reduces to the free polynomial algebra on generators
for \(s \ge 0\) reduces to the free polynomial algebra on generators  for \(i \in I\) and \(- \langle h_i, \kappa \rangle \le r < \langle h_i, \mu \rangle \). Then we tensor over \(\Bbbk \) with Z and factor out the ideal generated by the remaining elements
for \(i \in I\) and \(- \langle h_i, \kappa \rangle \le r < \langle h_i, \mu \rangle \). Then we tensor over \(\Bbbk \) with Z and factor out the ideal generated by the remaining elements  , leaving the algebra Z as the final quotient. \(\square \)
, leaving the algebra Z as the final quotient. \(\square \)
Let \(QH_d\) be the quiver Hecke algebra. This is the locally unital \(\Bbbk \)-algebra with local unit provided by the system \(\{1_{\varvec{i}}\,|\,\varvec{i}= (i_1,\dots ,i_d) \in I^d\}\) of mutually orthogonal idempotents, and generators
These generators are subject to the “local” relations represented by (3.45)–(3.47), interpreting \(y_r 1_{\varvec{i}}\) (resp., \(\tau _s 1_{\varvec{i}}\)) as the string diagram with d upwards-oriented strings colored \(i_1,\dots ,i_d\) from right to left with a dot on the rth one (resp., a crossing of the sth and \((s+1)\)th ones). The cyclotomic quiver Hecke algebra \(H_d^\mu (Z)\) is the quotient of the Z-algebra \(QH_d \otimes _\Bbbk Z\) by the two-sided ideal U generated by \(\left\{ \mu _{i_1}(y_1 1_{\varvec{i}})\,\big |\,\varvec{i}\in I^d\right\} \); we interpret \(H^\mu _0(Z)\) simply as the algebra Z. Consider the diagram

The top map \(\imath _d\) here is the obvious Z-algebra homomorphism sending \(1_{\varvec{i}} \otimes \beta \) to the endomorphism of \(E_{\varvec{i}} 1_\kappa := E_{i_d}\cdots E_{i_1}1_\kappa \) induced by \(\beta :1_\kappa \Rightarrow 1_\kappa \), and \(y_r 1_{\varvec{i}} \otimes 1\) and \(\tau _s 1_{\varvec{i}} \otimes 1\) to the 2-morphisms represented by the string diagrams of \(y_r 1_{\varvec{i}}\) and \(\tau _s 1_{\varvec{i}}\), respectively. The nondegeneracy condition implies that \(\imath _d\) is actually an isomorphism. The right-hand map \(\pi \) is the natural quotient map. The left-hand map \(\pi _1{\bar{\otimes }}\pi _2\) is the product of the natural quotient map \(\pi _1:QH_d \otimes _\Bbbk Z \twoheadrightarrow H_d^\mu (Z)\) with kernel U and the Z-algebra homomorphism \(\pi _2:{{\text {End}}}_{{{\mathfrak {U}}}(\mathfrak {g})}(1_\kappa )\otimes _\Bbbk Z \twoheadrightarrow Z\) with kernel V arising from Lemma 5.5. The proof of the following lemma is similar to the proof of [6, Lemma 8.3].
Lemma 5.6
There is a unique isomorphism \(\jmath _d\) making the diagram (5.13) commute.
Proof
Let \(A := QH_d \otimes _\Bbbk Z\) and \(B := {{\text {End}}}_{{{\mathfrak {U}}}(\mathfrak {g})}(1_\kappa )\otimes _\Bbbk Z\). As \(\imath _d\) is an isomorphism, it suffices to show that \(\imath _d(\ker \pi _1 {\bar{\otimes }} \pi _2) = \ker \pi \). Note that \(\ker \pi _1 {\bar{\otimes }} \pi _2 = A \otimes V + U \otimes B\). It is obvious that \(\pi \circ \imath _d\) sends generators of \(A \otimes V\) and \(U \otimes B\) to zero, hence, \(\imath _d(\ker \pi _1 {\bar{\otimes }} \pi _2) \subseteq \ker \pi \). It remains to show that \(\imath _d^{-1}(\ker \pi ) \subseteq \ker \pi _1 {\bar{\otimes }} \pi _2\). By definition \(\ker \pi \) consists of Z-linear combinations of 2-morphisms \(\theta :E_{\varvec{i}} 1_\kappa \Rightarrow E_{\varvec{j}} 1_\kappa \) of the form

where \(\rho \) is one of the generating 2-morphisms (5.7) for \({\mathcal {I}}_Z(\mu |\nu )\) and \(\sigma ,\tau ,\lambda \) are any other 2-morphisms in \({{\mathfrak {U}}}(\mathfrak {g})\) so that the compositions make sense. We must show for such \(\theta \) that \(\imath _d^{-1}(\theta ) \in A \otimes V + U\otimes B\). If  for \(-\langle h_i,\kappa \rangle \le r < \langle h_i, \mu \rangle \), the inverse image \(\imath _d^{-1}(\theta )\) obviously lies in \(A \otimes V\). Assume instead that
for \(-\langle h_i,\kappa \rangle \le r < \langle h_i, \mu \rangle \), the inverse image \(\imath _d^{-1}(\theta )\) obviously lies in \(A \otimes V\). Assume instead that  . To compute \(\imath _d^{-1}(\theta )\), we first “straighten” the diagram \(\theta \). Thus, proceeding by induction on the number of crossings, we use the relations in \({{\mathfrak {U}}}(\mathfrak {g})\) to slide dotted bubbles to the right-hand edge and to eliminate all other cups or caps from the diagram, always keeping the generator \(\rho \) fixed on the right boundary. This process reduces \(\theta \) to a Z-linear combination of morphisms of the following two types:
. To compute \(\imath _d^{-1}(\theta )\), we first “straighten” the diagram \(\theta \). Thus, proceeding by induction on the number of crossings, we use the relations in \({{\mathfrak {U}}}(\mathfrak {g})\) to slide dotted bubbles to the right-hand edge and to eliminate all other cups or caps from the diagram, always keeping the generator \(\rho \) fixed on the right boundary. This process reduces \(\theta \) to a Z-linear combination of morphisms of the following two types:
-
(I)
 for \(\sigma ',\tau '\in \imath _d(A \otimes 1)\) and \(\delta \in \imath _d(1 \otimes B)\);
for \(\sigma ',\tau '\in \imath _d(A \otimes 1)\) and \(\delta \in \imath _d(1 \otimes B)\); -
(II)
 for \(\lambda '\in \imath _d(A \otimes 1), \delta \in \imath _d(1 \otimes B)\) and \(s \ge 0\).
for \(\lambda '\in \imath _d(A \otimes 1), \delta \in \imath _d(1 \otimes B)\) and \(s \ge 0\).
These morphisms arise when \(\rho \) ends up on a propagating strand (type I) or on a dotted bubble (type II) after straightening. It remains to observe that the image under \(\imath _d^{-1}\) of a type I morphism lies in \(U \otimes B\), and the image of a type II morphism lies in \(A \otimes V\). \(\square \)
Corollary 5.7
For \(d \ge 0\), we have that \( \dim \left( \bigoplus _{\varvec{i},\varvec{j}\in I^d} {\text {Hom}}_{\mathcal {H}_Z(\mu |\nu )}(E_{\varvec{i}}, E_{\varvec{j}})\right) = \ell ^d d! \dim Z \) where \(\ell := \sum _{i \in I} \langle h_i, \mu \rangle \).
Proof
It is well known that \(\dim H^\mu _d(Z) = \ell ^d d! \dim Z\). For example, this follows by a Shapovalov form calculation given the categorification theorem of [23]. \(\square \)
Corollary 5.8
\(\mathcal {H}_Z(\mu |\nu )\) is a finite-dimensional category, i.e., all of its morphism spaces are finite-dimensional vector spaces over \(\Bbbk \).
Proof
Using the biadjunction of \(E_i\) and \(F_i\), it suffices to show that \({\text {Hom}}_{\mathcal {H}_Z(\mu |\nu )}(\varnothing , G)\) is finite-dimensional for any word G. This space is clearly zero unless G has an equal number of E-type letters as F-type letters. Also Corollary 5.7 establishes the result if \(G=F_{j_1}\cdots F_{j_d} E_{i_d}\cdots E_{i_1}\), i.e., all the F-type letters are to the left of the E-type letters. The general case then follows by induction on the length, using the isomorphisms (3.56)–(3.58) to establish the induction step. \(\square \)
Remark 5.9
In the remainder of the article, we really only need to appeal to fact that \(\ell ^d d! \dim Z\) is an upper bound for the dimension in Corollary 5.7. This follows from the existence of a surjective homomorphism \(\jmath _d\) as in (5.13), which follows as above from the surjectivity of the homomorphism \(\imath _d\). The latter assertion is easily proved without needing to appeal to the nondegeneracy condition.
It is often useful to work in the larger category \(\mathcal {H}om_\Bbbk (\mathcal {H}_Z(\mu |\nu )^{{{\text {op}}}}, \mathcal {V}ec_{{\text {fd}}})\) of \(\Bbbk \)-linear functors and natural transformations. This can be thought of in elementary algebraic terms by replacing \(\mathcal {H}_Z(\mu |\nu )\) with the locally unital algebra
Multiplication in \(H_Z(\mu |\nu )\) is induced by composition in the category \(\mathcal {H}_Z(\mu |\nu )\), and its local unit \(\left\{ 1_G\,\big |\,G \in \langle E_i, F_i\rangle _{i \in I}\right\} \) arises from the identity morphisms of the objects of \(\mathcal {H}_Z(\mu |\nu )\). Then \(\mathcal {H}om_\Bbbk (H_{{\mathbb {Z}}}(\mu |\nu )^{{{\text {op}}}}, \mathcal {V}ec_{{\text {fd}}})\) is isomorphic to the category \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )\) of locally finite-dimensional right modules over this algebra. In view of Corollary 5.8, \(H_Z(\mu |\nu )\) is locally finite-dimensional, hence, \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )\) is a Schurian category. Similarly to (5.14), we define \(H_Z(\mu |\nu )_\lambda \) from the category \(\mathcal {H}_Z(\mu |\nu )_\lambda \) for each \(\lambda \in X\); then (5.11) translates into the algebra decomposition
The categorical action of \({{\mathfrak {U}}}(\mathfrak {g})\) on \(\left( \mathcal {H}_Z(\mu |\nu )\right) _{\lambda \in X}\) extends to make \(\left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )_\lambda \right) _{\lambda \in X}\) into a Schurian 2-representation. One way to see this is explained in [8, Construction 4.26], where the extensions of the categorification functors \(E_i\) and \(F_i\) to arbitrary \(H_Z(\mu |\nu )\)-modules are realized by tensoring with certain bimodules, and the generating 2-morphisms of \({{\mathfrak {U}}}(\mathfrak {g})\) act via explicit bimodule homomorphisms.
Let \(P:= 1_\varnothing H_Z(\mu |\nu )\) be the finitely generated projective \(H_Z(\mu |\nu )\)-module associated to the empty word. By Lemma 5.6 with \(d=0\), we have that \({{\text {End}}}_{H_Z(\mu |\nu )}(P) \cong Z\). As Z is local, it follows that P is a projective indecomposable module. Then for any word \(G \in \langle E_i, F_i\rangle _{i \in I}\) the module GP obtained by applying the functor G is identified with the right ideal \(1_G H_Z(\mu |\nu )\). These modules for all G give a projective generating family for the Schurian category \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )\) such that
Remark 5.10
In the special case that \(\nu = 0\), the GCQ \(H_Z(\mu |\nu )\) is Morita equivalent to the usual cyclotomic quotient, that is, the locally unital algebra \(\bigoplus _{d \ge 0} H^\mu _d(Z)\); see [35, Theorem 4.25]. Recall by [23] that finitely generated projective modules over this algebra gives a categorification of the Weyl \({{\mathbb {Z}}}\)-form of the integrable lowest weight module \(V(-\mu )\) of \({{\mathfrak {U}}}(\mathfrak {g})\). In general, finitely generated projective \(H_Z(\mu |\nu )\)-modules can be used to categorify the tensor product \(V(\mu |\nu ) := V(-\mu )\otimes V(\nu )\) of the integrable lowest weight module \(V(-\mu )\) and the integrable highest weight module \(V(\nu )\); see [39]. This result is not needed below.
5.3 Heisenberg GCQs
On the Heisenberg side, GCQs have been defined in the degenerate case in the introduction of [4], and in the quantum case in [13, \(\S \)9]. As usual, we will discuss both cases simultaneously according to the value of \(z \in \Bbbk \). The required data is as follows:
-
a finite-dimensional, commutative, local \(\Bbbk \)-algebra Z with maximal ideal J;
-
monic polynomials \(m(u), n(u) \in Z[u]\), assuming in addition in the quantum case that \(m(0), n(0) \in Z^\times \).
Let \(k :=\deg n(u)-\deg m(u)\) and
To this data, we are going to associate a left tensor ideal \({\mathcal {I}}_Z(m|n)\) of the strict Z-linear monoidal category \(\mathcal {H}eis_k \otimes _\Bbbk Z\). The precise definition of \({\mathcal {I}}_Z(m|n)\) is slightly different in the degenerate and quantum cases; it will be explained in the next two paragraphs. Then the generalized cyclotomic quotient is the quotient category
which is itself naturally a Z-linear \(\mathcal {H}eis_k\)-module category. This quotient category has objects that are words in the monoid \(\langle E, F\rangle \), and for two such words \(G, G'\) the morphism space \({\text {Hom}}_{\mathcal {H}_Z(m|n)}(G, G')\) is the quotient of \({\text {Hom}}_{\mathcal {H}eis_k}(G,G')\otimes _\Bbbk Z\) by the Z-submodule defined by the ideal \({\mathcal {I}}_Z(m|n)\). In both cases, we will have that

in \({{\text {End}}}_{\mathcal {H}_Z(m|n)}(\mathbb {1})\).
Here is the definition of the left tensor ideal \({\mathcal {I}}_Z(m|n)\) in the degenerate case. Define \(\mathbb {O}^{(r)}, {\widetilde{\mathbb {O}}}^{(r)} \in Z\) from the coefficients of the formal Laurent series \(\mathbb {O}(u), \mathbb {O}(u)^{-1}\) so that
this notation being consistent with (3.12) and (3.13). Then \({\mathcal {I}}_Z(m|n)\) is generated by

Equivalently, by [4, Lemma 1.8], it is generated by

The same lemma implies that (5.19) holds.
Lemma 5.11
In the degenerate case, the quotient of the Z-algebra \({{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1}) \otimes _\Bbbk Z\) by the ideal V generated by  is isomorphic to Z.
is isomorphic to Z.
Proof
The basis theorem proved in [14, Theorem 6.4] implies that \({{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1})\) is a polynomial algebra generated freely by  for \(r \ge -k\). Given this, the lemma follows similarly to Lemma 5.5. \(\square \)
for \(r \ge -k\). Given this, the lemma follows similarly to Lemma 5.5. \(\square \)
In order to define the left tensor ideal \({\mathcal {I}}_Z(m|n)\) in the quantum case, there is a minor additional complication involving some choices of square roots: we assume henceforth that we are given distinguished square roots \(\sqrt{c}\) of each \(c \in \Bbbk ^\times \) such that \(\sqrt{1/c} = 1/\sqrt{c}\). The need for this is an artifact of the choice of normalization of the quantum Heisenberg category; see Remark 3.2. Given these square roots, we get also distinguished square roots \(\sqrt{c}\) of all \(c \in Z^\times \) lifting the chosen square root of the image of c in \(\Bbbk = Z / J\). Then we define \(\mathbb {O}^{(r)}, {\widetilde{\mathbb {O}}}^{(r)} \in Z\) so that
this notation being consistent with (3.35)–(3.36) for \(t = \sqrt{m(0)/n(0)}\). Then \({\mathcal {I}}_Z(m|n)\) is generated by

Equivalently, by [13, Lemma 9.2], it is generated by

and also (5.19) holds. Recalling from (3.23) that \(\mathcal {H}eis_k\) is defined over the algebra \(\mathbb {K}= \Bbbk [t,t^{-1}]\) in the quantum case, and that  by the defining relations, the presence of the generator
by the defining relations, the presence of the generator  in the definition of \({\mathcal {I}}_Z(m|n)\) has the effect of forcing the parameter t to act on any morphism in \(\mathcal {H}_Z(m|n)\) by multiplication by the scalar \(\sqrt{m(0)/n(0)} \in Z^\times \). This is necessary for some choice of the square root due to the last part of Lemma 4.3.
in the definition of \({\mathcal {I}}_Z(m|n)\) has the effect of forcing the parameter t to act on any morphism in \(\mathcal {H}_Z(m|n)\) by multiplication by the scalar \(\sqrt{m(0)/n(0)} \in Z^\times \). This is necessary for some choice of the square root due to the last part of Lemma 4.3.
Lemma 5.12
In the quantum case, the quotient of the Z-algebra \({{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1}) \otimes _\Bbbk Z\) by the ideal V generated by  is isomorphic to Z.
is isomorphic to Z.
Proof
By the basis theorem from [13, Theorem 10.1], \({{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1})\) is a free polynomial algebra over \(\mathbb {K}\) on generators  for \(-k< r < \deg m(u)\),
for \(-k< r < \deg m(u)\),  for \(s <0\), and
for \(s <0\), and  for \(s \ge \deg m(u)\). Since m(u) is monic, factoring out the ideal generated by
for \(s \ge \deg m(u)\). Since m(u) is monic, factoring out the ideal generated by  for \(s \ge 0\) leaves us with the free polynomial algebra over \(\mathbb {K}\) on generators
for \(s \ge 0\) leaves us with the free polynomial algebra over \(\mathbb {K}\) on generators  for \(-k< r < \deg m(u)\) and
for \(-k< r < \deg m(u)\) and  for \(s <0\). Then, since m(0) is a unit, factoring out the ideal generated by for \(s < 0\) leaves us with the free polynomial algebra over \(\mathbb {K}\) on generators
for \(s <0\). Then, since m(0) is a unit, factoring out the ideal generated by for \(s < 0\) leaves us with the free polynomial algebra over \(\mathbb {K}\) on generators  for \(-k< r < \deg m(u)\). Finally we tensor over \(\Bbbk \) with Z and factor out the ideal generated by the remaining elements
for \(-k< r < \deg m(u)\). Finally we tensor over \(\Bbbk \) with Z and factor out the ideal generated by the remaining elements  for \(-k \le r < \deg m(u)\). The first of these with \(r=-k\) substitutes \(t \in \mathbb {K}\) by \(\sqrt{m(0)/n(0)} \in Z\), leaving a free polynomial algebra over Z on generators
for \(-k \le r < \deg m(u)\). The first of these with \(r=-k\) substitutes \(t \in \mathbb {K}\) by \(\sqrt{m(0)/n(0)} \in Z\), leaving a free polynomial algebra over Z on generators  for \(-k< r < \deg m(u)\). Then the remaining relations for \(-k< r < \deg m(u)\) evaluate these generators to elements of Z. \(\square \)
for \(-k< r < \deg m(u)\). Then the remaining relations for \(-k< r < \deg m(u)\) evaluate these generators to elements of Z. \(\square \)
Now we proceed like in the previous subsection. Let \(AH_d\) be the affine Hecke algebra, degenerate or quantum according to the value of z. This is the \(\Bbbk \)-algebra with generators \(\{x_1,\dots ,x_d, s_1,\dots ,s_{d-1}\}\) (dots and crossings) in the degenerate case or \(\{x_1^{\pm 1}, \dots , x_d^{\pm 1}, \tau _1^{\pm 1}, \dots , \tau _{d-1}^{\pm 1}\}\) (invertible dots and positive/negative crossings) in the quantum case subject to the “local” relations represented by (3.3) or (3.26) and (3.27), respectively. The cyclotomic Hecke algebra \(H_d^m(Z)\) is the quotient of the Z-algebra \(AH_d \otimes _\Bbbk Z\) by the two-sided ideal U generated by \(m(x_1)\); we interpret \(H^m_0(Z)\) simply as the algebra Z. Consider the diagram

The top map \(\imath _d\) is the evident Z-algebra homomorphism. The basis theorem proved in [14, Theorem 6.4] or [13, Theorem 10.1] implies that this is actually an isomorphism. The right-hand map \(\pi \) is the natural quotient map. The left-hand map \(\pi _1{\bar{\otimes }}\pi _2\) is the product of the natural quotient map \(\pi _1:AH_d \otimes _\Bbbk Z \twoheadrightarrow H_d^m(Z)\) with kernel U and the Z-algebra homomorphism \(\pi _2:{{\text {End}}}_{\mathcal {H}eis_k}(\mathbb {1})\otimes _\Bbbk Z \twoheadrightarrow Z\) with kernel V arising from Lemmas 5.11 and 5.12.
Lemma 5.13
There is a unique isomorphism \(\jmath _d\) making the diagram (5.26) commute.
Proof
This is similar to the proof of Lemma 5.6, using Lemmas 5.11 and 5.12 in place of Lemma 5.5. \(\square \)
Corollary 5.14
\(\dim {{\text {End}}}_{\mathcal {H}_Z(a|b)}(E^d) = \ell ^d d! \dim Z\) where \(\ell := \deg m(u)\).
Proof
This is the dimension of the level \(\ell \) cyclotomic Hecke algebra \(H_d^m(Z)\). \(\square \)
Corollary 5.15
\(\mathcal {H}_Z(m|n)\) is a finite-dimensional category.
Proof
This follows by an argument similar to Corollary 5.8, using (3.9) and (3.10) in the degenerate case, or the analogous inversion relations in the quantum case. \(\square \)
As we did in (5.14), we switch from now on to using algebraic language by viewing the finite-dimensional category \(\mathcal {H}_Z(m|n)\) instead as the locally finite-dimensional locally unital algebra
with local unit \(\{1_G\,|\,G \in \langle E, F \rangle \}\) and multiplication induced by composition. Then we can consider the Schurian category \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\). The categorical action of \(\mathcal {H}eis_k\) on \(\mathcal {H}_Z(m|n)\) extends canonically to make \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) into a Schurian \(\mathcal {H}eis_k\)-module category.
Let \(P := 1_\varnothing H_Z(m|n)\). As \({{\text {End}}}_{H_Z(m|n)}(P) \cong Z\), this is a projective indecomposable module. Then for any \(G \in \langle E, F \rangle \) the projective module GP is identified with the right ideal \(1_G H_Z(m|n)\). These modules for all G give a projective generating family for \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) such that
Remark 5.16
Like in Remark 5.10, in the case that \(n(u) = 1\), the GCQ \(H_Z(m|n)\) is Morita equivalent to the usual cyclotomic quotient, that is, the locally unital algebra \(\bigoplus _{d \ge 0} H^m_d(Z)\). This is proved in the degenerate case in [4, Theorem 1.7]; the proof in the quantum case is similar.
5.4 Isomorphisms between GCQs
Fix a finite-dimensional, commutative, local \(\Bbbk \)-algebra Z with maximal ideal J and monic polynomials \(m(u), n(u) \in Z[u]\), and let \(k := \deg n(u)-\deg m(u)\). Then define the Heisenberg GCQ \(H_Z(m|n)\) as in (5.27). Let \({{\bar{m}}}(u), {{\bar{n}}}(u) \in \Bbbk [u]\) be the reductions of m(u), n(u) modulo J. Let I be the union of the trajectories of the roots of \({{\bar{m}}}(u)\) and \({{\bar{n}}}(u)\) under the automorphisms \(i \mapsto i^\pm \) defined in the introduction. This gives us the data needed to define the Kac–Moody algebra \(\mathfrak {g}\) with root lattice X. Let \(\mu ,\nu \in X^+\) be the dominant weights defined by declaring that \(\langle h_i, \mu \rangle \) and \(\langle h_i,\nu \rangle \) are the multiplicities of \(i\in I\) as a root of \({{\bar{m}}}(u)\) and \({{\bar{n}}}(u)\), respectively, and let \(\kappa := \nu -\mu \). Then we apply Corollary 2.4 to the polynomials m(u), n(u) to deduce that there are unique monic polynomials \(\mu _i(u) \in u^{\langle h_i, \mu \rangle } + J[u], \nu _i(u) \in u^{\langle h_i, \nu \rangle } + J[u]\) such that
in the degenerate case (here \(\mu _i(u), \nu _i(u)\) are the polynomials \(m_i(u), n_i(u)\) produced by Corollary 2.4), or
in the quantum case (this time \(\mu _i(u), \nu _i(u)\) are \(i^{-\langle h_i,\mu \rangle } m_i(iu), i^{-\langle h_i,\nu \rangle } n_i(iu)\)). These polynomials give us the data needed for the Kac–Moody GCQ \(H_Z(\mu |\nu )\) according to (5.14). In this subsection, we are going to show that \(H_Z(\mu |\nu ) \cong H_Z(m|n)\). In order to do this, we apply the general machinery from Section 4 to analyze the Schurian \(\mathcal {H}eis_k\)-module category \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\).
Lemma 5.17
The spectrum of the \(\mathcal {H}eis_k\)-module category \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) is the set I generated by the roots of the polynomials m(u) and n(u) as above.
Proof
From (5.29) and (5.30), we get the CRT decomposition
Moreover, the image of \((u-i)\) in the ith summand of this decomposition is nilpotent. From the \(d=1\) case of Lemma 5.13, we see that there is an isomorphism

So from (5.31), we get induced a decomposition of the module EP such that \((u-i)\) acts nilpotently on the ith summand. It follows that this summand is simply the generalized i-eigenspace \(E_i P\) as defined in Sect. 4.1. This shows that \(EP = \bigoplus _{i \in I} E_i P\) with \({{\text {End}}}_{H_Z(m|n)}(E_i P) \cong Z[u] / (\mu _i(u))\). Consequently, \(E_i P\) is non-zero if and only if \(i \in I\) and \(\langle h_i, \mu \rangle > 0\). A similar discussion applies to FP: we have that \(FP = \bigoplus _{i \in I} F_i P\) with \({{\text {End}}}_{H_Z(m|n)}(F_i P) \cong Z[u] / (\nu _i(u))\). Consequently, \(F_i P\) is non-zero if and only if \(i \in I\) and \(\langle h_i, \nu \rangle > 0\). In view of Lemma 4.6, we deduce that the spectrum of \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) contains the set I.
Conversely, we must show that I is contained in the spectrum of \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\). To prove this, we say that \(V \in {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) belongs to I if \(E V = \bigoplus _{i \in I} E_i V\) and \(FV = \bigoplus _{i \in I} F_i V\). We must show that every \(V \in {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) belongs to I. As the modules GP for \(G \in \langle E, F \rangle \) give a projective generating family, and these functors are exact, it suffices to show that all GP belong to I. To prove this, we proceed by induction on the length of the word G. The base case \(G = \varnothing \) follows from the previous paragraph. To prove the induction step, it suffices to establish the following: if L is an irreducible \(H_Z(m|n)\)-module belonging to I then the modules EL and FL also belong to I. To see this, let K be an irreducible subquotient of either EL or FL. Since L belongs to I, all roots of the minimal polynomials \(m_L(u)\) and \(n_L(u)\) belong to I. We must show that all roots of \(m_K(u)\) and \(n_K(u)\) also belong to I. In the case that K is a subquotient of EL, we argue as follows. All roots of \(m_K(u)\) belong to I due to a well-known observation about the affine Hecke algebra \(AH_2\); see [14, Lemma 6.1] or [13, Lemma 9.3]. To deduce that all roots of \(n_K(u)\) belong to I, use the fact that \(n_K(u) = \frac{n_L(u) m_K(u)}{m_L(u)} \times \)(a rational function in \(\Bbbk (u)\) with zeros and poles in I) thanks to Lemmas 4.4 and 4.5. The argument in the case that K is a subquotient of FL is similar. \(\square \)
With Lemma 5.17 in hand, we see that the endofunctors E and F of \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) decompose into eigenfunctors as \(E = \bigoplus _{i \in I} E_i\) and \(F = \bigoplus _{i \in I} F_i\) as in (4.12). Applying (4.14), we also have the weight decomposition
Applying Theorem 4.11, \(\left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n\right) _\lambda )_{\lambda \in X}\) is a nilpotent 2-representation of \({{\mathfrak {U}}}(\mathfrak {g})\). Let P be the projective indecomposable module \(1_\varnothing H_{m|n}\) and recall that \(\kappa = \nu -\mu \).
Lemma 5.18
The module P belongs to \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\kappa \). Moreover, under the categorical action of \({{\mathfrak {U}}}(\mathfrak {g})\) just defined, we have isomorphisms


Finally, the generating function from (5.4) satisfies \(\mathbb {O}_{P,i}(u) = \nu _i(u)/\mu _i(u)\).
Proof
For the first statement, it suffices to show that the unique irreducible quotient L of P belongs to \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\kappa \). By (5.19) and the definition (5.17), we have that \(\mathbb {O}_P(u) = n(u)/m(u)\), where \(\mathbb {O}_P(u)\) is the generating function defined by (4.10). Hence, \(\mathbb {O}_L(u) = {{\bar{n}}}(u) / {{\bar{m}}}(u)\). Using the observation immediately following (4.13) together with (5.29) and (5.30), it follows that \(\langle h_i, {{\text {wt}}}(L) \rangle = \langle h_i, \nu \rangle - \langle h_i, \mu \rangle = \langle h_i, \kappa \rangle .\) Thus, \({{\text {wt}}}(L) = \kappa \) as required.
To establish (5.33), the argument from the first paragraph of the proof of Lemma 5.17 shows that there is an isomorphism

So we get (5.33) using the definition of the action of  from the statement of Theorem 4.11. The proof of (5.34) is similar.
from the statement of Theorem 4.11. The proof of (5.34) is similar.
Finally, we must compute \(\mathbb {O}_{P,i}(u) \in u^{\langle h_i,\kappa \rangle }+ u^{\langle h_i,\kappa \rangle -1}Z[u^{-1}]\). Applying Lemma 5.1(1) with \(f(u) = \mu _i(u)\), we see that \(g(u) := \mathbb {O}_{P,i}(u) \mu _i(u)\) is a monic polynomial in Z[u] of degree \(\langle h_i, \nu \rangle \) such that  . Then by (5.34), it follows that the image of \(g(u) - \nu _i(u)\) is zero in \(Z[u] / (\nu _i(u))\). Since \(g(u)-\nu _i(u)\) is a polynomial of degree \(\langle h_i,\nu \rangle -1\) and \(1, u, u^2,\dots ,u^{\langle h_i,\nu \rangle -1}\) are linearly independent over Z in this algebra, it follows that \(g(u) = \nu _i(u)\). Now we have shown that \(\mathbb {O}_{P,i}(u) \mu _i(u)=\nu _i(u)\), and the result follows. \(\square \)
. Then by (5.34), it follows that the image of \(g(u) - \nu _i(u)\) is zero in \(Z[u] / (\nu _i(u))\). Since \(g(u)-\nu _i(u)\) is a polynomial of degree \(\langle h_i,\nu \rangle -1\) and \(1, u, u^2,\dots ,u^{\langle h_i,\nu \rangle -1}\) are linearly independent over Z in this algebra, it follows that \(g(u) = \nu _i(u)\). Now we have shown that \(\mathbb {O}_{P,i}(u) \mu _i(u)=\nu _i(u)\), and the result follows. \(\square \)
Finally, we need to pass to an idempotent expansion of the locally unital algebra \(H_Z(m|n)\), i.e., we must refine its local unit. Take \(G = G_d \cdots G_1 \in \langle E,F\rangle \). As \(E = \bigoplus _{i \in I} E_i\) and \(F = \bigoplus _{i \in I} F_i\), there is a decomposition
of the endofunctor G, where \(G_{\varvec{i}} := (G_d)_{i_d}\cdots (G_1)_{i_1}\) for \(\varvec{i}= (i_1,\dots ,i_d) \in I^d\). Recalling that \(G P = 1_G H_Z(m|n)\), we deduce that the idempotent \(1_G \in H_Z(m|n)\) decomposes as \(1_G = \sum _{\varvec{i}\in I^d} 1_{G_{\varvec{i}}}\) for mutually orthogonal idempotents \(1_{G_{\varvec{i}}}\) such that \(1_{G_{\varvec{i}}} H_Z(m|n)=G_{\varvec{i}} P\). In this way, we have defined a refinement of the original local unit for the algebra \(H_Z(m|n)\), with the new local unit being indexed by the same set \(\langle E_i, F_i\rangle _{i \in I}\) as the local unit of \(H_Z(\mu |\nu )\). Note moreover for \(G \in \langle E_i, F_i\rangle _{i \in I}\) that GP belongs to \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\lambda \) for \(\lambda = \kappa + {{\text {wt}}}(G)\). So the weight space decomposition of \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\) from (5.32) is consistent with the algebra decomposition
This should be compared with the decomposition (5.15) of the algebra \(H_Z(\mu |\nu )\).
Theorem 5.19
With notation as above, there is a unique isomorphism of locally unital Z-algebras \(\theta :H_Z(\mu |\nu ){\mathop {\rightarrow }\limits ^{\sim }} H_Z(m|n)\) defined on generators of the algebra \(H_Z(\mu |\nu )\) involving upwards dots or crossings or rightwards cups or caps by the formulae in the statement of Theorem 4.11, and with \(\theta (1_G) = 1_G\) for each \(G \in \langle E_i, F_i\rangle _{i \in I}\).
Proof
As the projective module P belongs to \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\kappa \), the categorical action of \({{\mathfrak {U}}}(\mathfrak {g})\) on the family \(\left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\lambda \right) _{\lambda \in X}\) induces a unique Z-linear morphism of 2-representations
sending \(1_\kappa \mapsto P\). Lemma 5.18 shows that the generators of \({\mathcal {I}}_Z(\mu |\nu )\) from (5.7) map to zero, hence, this factors through the quotient to give a Z-linear morphism of 2-representations \(\left( \mathcal {H}_Z(\mu |\nu )_\lambda \right) _{\lambda \in X} \rightarrow \left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\lambda \right) _{\lambda \in X}.\) Thus, we have constructed a Z-linear functor
sending G to GP for each \(G \in \langle E_i, F_i\rangle _{i \in I}\). Using (5.14) and (5.28), it follows that \(\Theta \) induces a Z-algebra homomorphism \(\theta :H_Z(\mu |\nu ) \rightarrow H_Z(m|n)\) sending \(1_G \mapsto 1_G\) for each \(G \in \langle E_i, F_i \rangle _{i \in I}\). By its definition, this may be computed explicitly on generators of \(H_Z(\mu |\nu )\) involving upwards dots or crossings or rightwards cups or caps using the formulae from Theorem 4.11; as noted in Remark 4.12, we have not given explicit formulae for leftwards cups or caps, but these are not needed.
To show \(\theta \) is an isomorphism, we show equivalently that the functor \(\Theta \) is fully faithful, i.e., it defines isomorphisms \(\Theta _{G,G'}:{\text {Hom}}_{\mathcal {H}_Z(\mu |\nu )}(G, G') {\mathop {\rightarrow }\limits ^{\sim }} {\text {Hom}}_{H_Z(m|n)}(GP, G'P)\) for all \(G, G' \in \langle E_i, F_i\rangle _{i \in I}\). We first treat the case that G and \(G'\) both belong to \(\langle E_i\rangle _{i \in I}\). We may assume that both G and \(G'\) have the same length \(d \ge 0\), since otherwise both morphism spaces are zero. Then the Z-linear map \(\Theta _{G,G'}\) is surjective. To see this, since every morphism in \({\text {Hom}}_{H_Z(m|n)}(GP, G'P)\) is a Z-linear combination of morphisms obtained by composing dots and crossings of the form (4.6), we just need to show that all of the latter morphisms are in the image. This follows on inverting the formulae in Theorem 4.11 (we will write the inverse formulae explicitly explicitly in Theorem 5.22 below). Then to see that \(\Theta _{G,G'}\) is injective we use the equality of dimensions which follows on comparing Corollaries 5.7 and 5.14.
To establish the fully faithfulness for more general words \(G, G' \in \langle E_i, F_i\rangle _{i \in I}\), the idea is to reduce to the special case just treated. We proceed by induction on the sum of the lengths of the words G and \(G'\). Given morphisms \(H,H' \in {\text {Add}}(\mathcal {H}_Z(\mu |\nu ))\), i.e., finite direct sums of words in \(\langle E_i, F_i\rangle _{i \in I}\), and an isomorphism \(\alpha \in {\text {Hom}}_{\mathcal {H}_Z(\mu |\nu )}(H', H)\) defined by some 2-morphism in \({{\mathfrak {U}}}(\mathfrak {g})\), we can apply \(\Theta \) to obtain an isomorphism \(\beta \in {\text {Hom}}_{H_Z(m|n)}(H' P, H P)\) such that the following diagram commutes:

The vertical arrows in this diagram are isomorphisms, so we deduce that \(\Theta _{H,G'}\) is an isomorphism if and only if \(\Theta _{H',G'}\) is an isomorphism. Using this observation for isomorphisms \(\alpha \) obtained from the isomorphisms (3.56)–(3.58), one reduces to proving the fully faithfulness in the situation that all letters of the form \(F_i\,(i \in I)\) in G appear to the left of all letters of the form \(E_i \,(i \in I)\); this argument also requires the induction hypothesis since shorter words may arise when (3.57) and (3.58) are used. Next, we note for any \(H \in \langle E_i, F_i\rangle _{i \in I}\) that the following diagram commutes:

where \(\alpha :H \rightarrow E_i F_i H\) is the morphism in \(\mathcal {H}_Z(\mu |\nu )\) defined by the unit of the adjunction \((F_i, E_i)\) and \(\beta :HP \rightarrow E_i F_i HP\) is its image under \(\Theta \). The compositions down the left edge and down the right edge of this diagram are adjunction isomorphisms, so we deduce that \(\Theta _{F_i H, G'}\) is an isomorphism if and only if \(\Theta _{H, E_i G'}\) is an isomorphism. Using this observation, we reduce the proof of fully faithfulness to the situation that \(G \in \langle E_i\rangle _{i \in I}\). Then we repeat the process to reduce further to the case that all letters of the form \(F_i\,(i \in I)\) in \(G'\) appear to the left of all letters of the form \(E_i\,(i \in I)\). Finally, using the other adjunction \((E_i, F_i)\) we move all the letters \(F_i\) from \(G'\) to G, putting us into the situation treated in the previous paragraph. \(\square \)
Corollary 5.20
Let \(\theta ^*:{\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\rightarrow {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )\) be the restriction functor arising from the isomorphism \(\theta \). This defines a strongly equivariant isomorphism between \(\left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)_\lambda \right) _{\lambda \in X}\), that is, the 2-representation obtained by applying Theorem 4.11 to the Heisenberg GCQ \({\text {mod}}_{{\text {lfd}}}\text {-}H_Z(m|n)\), and \(\left( {\text {mod}}_{{\text {lfd}}}\text {-}H_Z(\mu |\nu )_\lambda \right) _{\lambda \in X}\), that is, the 2-representation arising from the Kac–Moody GCQ.
Remark 5.21
Bearing in mind Remarks 5.10 and 5.16, Theorem 5.19 can be viewed as a substantial generalization of the isomorphism theorem from [10]. The original isomorphism \(H_d^\mu (Z) {\mathop {\rightarrow }\limits ^{\sim }} H_d^m(Z)\) from [10] may be recovered from Theorem 5.19 using also Lemmas 5.6 and 5.13; actually, one just needs the special case \(n(u)=1,\nu =0\) of the theorem.
5.5 Kac–Moody to Heisenberg
Now we can prove the converse to Theorem 4.11. As usual we discuss the degenerate case \(z=0\) and the quantum case \(z \ne 0\) simultaneously. Let I be a subset of \(\Bbbk \) closed under the automorphisms \(i \mapsto i^{\pm }\) defined in the introduction, assuming \(0 \notin I\) in the quantum case. Let \({{\mathfrak {U}}}(\mathfrak {g})\) be the Kac–Moody 2-category associated to this data. The dotted arrows in the statement of the following theorem should be interpreted in the same way as was explained after (4.9). Now these dotted arrows can be labelled by any power series in \(\Bbbk [\![y_1,\dots ,y_n]\!]\), and make sense due to the assumed nilpotency.
Theorem 5.22
Assume that \(({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) is a nilpotent 2-representation of \({{\mathfrak {U}}}(\mathfrak {g})\) that is either locally finite Abelian or Schurian. Let \({{\mathcal {R}}}\) be defined from this as in (5.1). Assume in addition that \({{\mathcal {R}}}\) is of central charge \(k \in {{\mathbb {Z}}}\), i.e., \({{\mathcal {R}}}_\lambda \ne \mathbf{0} \Rightarrow \sum _{i \in I} \langle h_i, \lambda \rangle = k\). Then there is a unique way to make \({{\mathcal {R}}}\) into a \(\mathcal {H}eis_k\)-module category so that E and F act as the endofunctors (5.3), and the generating morphisms in \(\mathcal {H}eis_k\) map to natural transformations according to


in the degenerate case, or


in the quantum case with the action of \(t \in \mathbb {K}\) chosen so that \(t_L = \sqrt{\prod _{i \in I} (-i)^{-\langle h_i,\lambda \rangle }}\) for all irreducible \(L \in {{\mathcal {R}}}_\lambda \) and \(\lambda \in X\). We also have tha

in the degenerate case, and

in the quantum case.
Proof
Note to start with that the formulae for dots, crossings and rightwards cups and caps in the statement of the theorem are equivalent to the ones in Theorem 4.11. We have simply rearranged them to make the Heisenberg morphisms the subjects.
We first explain the proof in the (easier) degenerate case. The formulae in the theorem give us well-defined natural transformations  ,
,  ,
,  and
and  . We just need to verify that these natural transformations satisfy the relations (3.3) and (3.4) and the inversion relations (3.9) and (3.10). As every object of \({{\mathcal {R}}}\) is a direct limit of finitely generated objects, and every finitely generated object is a finite direct sum of indecomposable objects, it suffices to check the relations on an indecomposable, finitely generated \(V \in {{\mathcal {R}}}_\kappa \) and \(\kappa \in X\). Let \(Z := Z_V = Z({{\text {End}}}_{{\mathcal {R}}}(V))\), which is a finite-dimensional, commutative, local \(\Bbbk \)-algebra. Let \(\mu \in X^+\) be defined so that \(\langle h_i, \mu \rangle \) is the nilpotency degree of the endomorphism
. We just need to verify that these natural transformations satisfy the relations (3.3) and (3.4) and the inversion relations (3.9) and (3.10). As every object of \({{\mathcal {R}}}\) is a direct limit of finitely generated objects, and every finitely generated object is a finite direct sum of indecomposable objects, it suffices to check the relations on an indecomposable, finitely generated \(V \in {{\mathcal {R}}}_\kappa \) and \(\kappa \in X\). Let \(Z := Z_V = Z({{\text {End}}}_{{\mathcal {R}}}(V))\), which is a finite-dimensional, commutative, local \(\Bbbk \)-algebra. Let \(\mu \in X^+\) be defined so that \(\langle h_i, \mu \rangle \) is the nilpotency degree of the endomorphism  . Let \(\mu _i(u) := u^{\langle h_i, \mu \rangle }\). Let \(\nu := \kappa +\mu \) and \(\nu _i(u) := \mathbb {O}_{V, i}(u) \mu _i(u) \in Z[u]\), which is a polynomial of degree \(\langle h_i, \nu \rangle \). In other words, \(\mathbb {O}_i(u) := \nu _i(u) / \mu _i(u)\) is \(\mathbb {O}_{V,i}(u)\). Defining \(\mathbb {O}_i^{(r)}\) as in (5.6), the relations (5.7) are satisfied in the action of \({{\mathfrak {U}}}(\mathfrak {g})\) on V. These are the defining relations of the Kac–Moody GCQ \(\mathcal {H}_Z(\mu |\nu )\), so we get induced a unique Z-linear morphism of 2-representations \(\left( \mathcal {H}_Z(\mu |\nu )\right) _{\lambda \in X} \rightarrow ({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) sending \(1_\kappa \mapsto V\). This gives us a Z-linear functor \(\mathcal {H}_Z(\mu |\nu ) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\). Hence, using the isomorphism of Theorem 5.19, we get a Z-linear functor \(\mathcal {H}_Z(m|n) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\) for \(m(u), n(u) \in Z[u]\) defined as in (5.29). The assumption that \({{\mathcal {R}}}\) is of central charge k means that \(\mathcal {H}_Z(m|n)\) is a \(\mathcal {H}eis_k\)-module category. The evaluations on V of the natural transformations arising in the relations to be checked are the images under this functor of corresponding morphisms in \(\mathcal {H}_Z(m|n)\). Since the relations hold for the latter this does the job. It just remains to prove (5.37). Again it suffices to check that this holds when evaluated on the chosen object V, that is, we must show that \(\mathbb {O}_V(u) = \prod _{i \in I} \mathbb {O}_{V,i}(u-i)\). We know already that \(\mathbb {O}_{V,i}(u) = \nu _i(u) / \mu _i(u)\), so by the definition (5.29) we have that \(\prod _{i \in I} \mathbb {O}_{V,i}(u-i) = n(u) / m(u)\). This equals \(\mathbb {O}_V(u)\) due to (5.17) and (5.19).
. Let \(\mu _i(u) := u^{\langle h_i, \mu \rangle }\). Let \(\nu := \kappa +\mu \) and \(\nu _i(u) := \mathbb {O}_{V, i}(u) \mu _i(u) \in Z[u]\), which is a polynomial of degree \(\langle h_i, \nu \rangle \). In other words, \(\mathbb {O}_i(u) := \nu _i(u) / \mu _i(u)\) is \(\mathbb {O}_{V,i}(u)\). Defining \(\mathbb {O}_i^{(r)}\) as in (5.6), the relations (5.7) are satisfied in the action of \({{\mathfrak {U}}}(\mathfrak {g})\) on V. These are the defining relations of the Kac–Moody GCQ \(\mathcal {H}_Z(\mu |\nu )\), so we get induced a unique Z-linear morphism of 2-representations \(\left( \mathcal {H}_Z(\mu |\nu )\right) _{\lambda \in X} \rightarrow ({{\mathcal {R}}}_\lambda )_{\lambda \in X}\) sending \(1_\kappa \mapsto V\). This gives us a Z-linear functor \(\mathcal {H}_Z(\mu |\nu ) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\). Hence, using the isomorphism of Theorem 5.19, we get a Z-linear functor \(\mathcal {H}_Z(m|n) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\) for \(m(u), n(u) \in Z[u]\) defined as in (5.29). The assumption that \({{\mathcal {R}}}\) is of central charge k means that \(\mathcal {H}_Z(m|n)\) is a \(\mathcal {H}eis_k\)-module category. The evaluations on V of the natural transformations arising in the relations to be checked are the images under this functor of corresponding morphisms in \(\mathcal {H}_Z(m|n)\). Since the relations hold for the latter this does the job. It just remains to prove (5.37). Again it suffices to check that this holds when evaluated on the chosen object V, that is, we must show that \(\mathbb {O}_V(u) = \prod _{i \in I} \mathbb {O}_{V,i}(u-i)\). We know already that \(\mathbb {O}_{V,i}(u) = \nu _i(u) / \mu _i(u)\), so by the definition (5.29) we have that \(\prod _{i \in I} \mathbb {O}_{V,i}(u-i) = n(u) / m(u)\). This equals \(\mathbb {O}_V(u)\) due to (5.17) and (5.19).
Now consider the quantum case. The formulas in the statement of the theorem give us natural transformations  ,
,  ,
,  , the first two of which are clearly invertible. As \(\mathcal {H}eis_k\) is a \(\mathbb {K}\)-linear category rather than a \(\Bbbk \)-linear category, we also need to define an invertible natural transformation \(t:{{\mathcal {R}}}\rightarrow {{\mathcal {R}}}\) such that \(t_{EV} = E t_V\) and \(t_{FV} = F t_V\) for each \(V \in {{\mathcal {R}}}\). Before we do this in general, consider the situation for an irreducible object \(L \in {{\mathcal {R}}}_\lambda \). The minimal polynomials of
, the first two of which are clearly invertible. As \(\mathcal {H}eis_k\) is a \(\mathbb {K}\)-linear category rather than a \(\Bbbk \)-linear category, we also need to define an invertible natural transformation \(t:{{\mathcal {R}}}\rightarrow {{\mathcal {R}}}\) such that \(t_{EV} = E t_V\) and \(t_{FV} = F t_V\) for each \(V \in {{\mathcal {R}}}\). Before we do this in general, consider the situation for an irreducible object \(L \in {{\mathcal {R}}}_\lambda \). The minimal polynomials of  and
and  are \(u^{{\varepsilon }_i(L)}\) and \(u^{\phi _i(L)}\), so in a \(\mathcal {H}eis_k\)-action consistent with these formulas, we have that \(m_L(u) = \prod _{i \in I} (u-i)^{{\varepsilon }_i(L)}\) and \(n_L(u) = \prod _{i \in I} (u-i)^{\phi _i(L)}\). In view of Lemma 4.4, using also that \(\langle h_i, \lambda \rangle = \phi _i(L)-{\varepsilon }_i(L)\) by Lemma 5.2, it follows that \(t_L^2 = \prod _{i \in I} (-i)^{-\langle h_i, \lambda \rangle }\). In the statement of the theorem, we have stipulated that \(t_L = \sqrt{\prod _{i \in I} (-i)^{-\langle h_i, \lambda \rangle }}\), thereby making the same fixed choice of square root as in the definition of GCQs in Sect. 5.3. In general, it suffices to define the natural transformation t on objects V that are finitely generated and indecomposable; then we can define \(t_V\) on an arbitrary \(V \in {{\mathcal {R}}}\) by taking direct sums and limits. Fixing such an object \(V \in {{\mathcal {R}}}_\kappa \), define \(Z, \mu , \nu , \mu _i(u)\) and \(\nu _i(u)\) as in the previous paragraph. Then, as before, we get a Z-linear functor \(\mathcal {H}_Z(\mu |\nu ) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\). Composing with the isomorphism from Theorem 5.19, this gives us a Z-linear functor \(\mathcal {H}_Z(m|n) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\) where \(m(u), n(u) \in Z[u]\) are defined as in (5.30). On \(\mathcal {H}_Z(m|n)\), we know that t acts as
are \(u^{{\varepsilon }_i(L)}\) and \(u^{\phi _i(L)}\), so in a \(\mathcal {H}eis_k\)-action consistent with these formulas, we have that \(m_L(u) = \prod _{i \in I} (u-i)^{{\varepsilon }_i(L)}\) and \(n_L(u) = \prod _{i \in I} (u-i)^{\phi _i(L)}\). In view of Lemma 4.4, using also that \(\langle h_i, \lambda \rangle = \phi _i(L)-{\varepsilon }_i(L)\) by Lemma 5.2, it follows that \(t_L^2 = \prod _{i \in I} (-i)^{-\langle h_i, \lambda \rangle }\). In the statement of the theorem, we have stipulated that \(t_L = \sqrt{\prod _{i \in I} (-i)^{-\langle h_i, \lambda \rangle }}\), thereby making the same fixed choice of square root as in the definition of GCQs in Sect. 5.3. In general, it suffices to define the natural transformation t on objects V that are finitely generated and indecomposable; then we can define \(t_V\) on an arbitrary \(V \in {{\mathcal {R}}}\) by taking direct sums and limits. Fixing such an object \(V \in {{\mathcal {R}}}_\kappa \), define \(Z, \mu , \nu , \mu _i(u)\) and \(\nu _i(u)\) as in the previous paragraph. Then, as before, we get a Z-linear functor \(\mathcal {H}_Z(\mu |\nu ) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\). Composing with the isomorphism from Theorem 5.19, this gives us a Z-linear functor \(\mathcal {H}_Z(m|n) \rightarrow {{\mathcal {R}}}\), \(\varnothing \mapsto V\) where \(m(u), n(u) \in Z[u]\) are defined as in (5.30). On \(\mathcal {H}_Z(m|n)\), we know that t acts as
Modulo the unique maximal ideal J of Z, this expression equals \(\sqrt{\prod _{i \in I} (-i)^{-\langle h_i, \kappa \rangle }}\), which is the desired action of t on irreducible quotients of V. So we can use this formula to define the morphism \(t_V:V \rightarrow V\), and have the data needed to define the natural transformation t. We still need to check that \(t_{EV} = E t_V\) and \(t_{FV} = F t_V\) and to verify the other defining relations of \(\mathcal {H}eis_k\), namely, (3.27) and (3.28), the inversion relation (3.33) and (3.34), and the additional relation explained immediately after (3.34). But these all follow as in the previous paragraph because they are true for the action of \(\mathcal {H}eis_k\) on \(\mathcal {H}_Z(m|n)\). Finally, to prove (5.38), we argue in the same way as explained at the end of the previous paragraph, using (5.30) instead of (5.29). \(\square \)
Remark 5.23
Like in Remark 4.12, the actions of the leftwards cups and caps in \(\mathcal {H}eis_k\) are uniquely determined by the actions of the other generators due now to [14, Lemma 5.2] or [13, Lemma 4.3], but it is not easy to find explicit formulae.
Notes
In the quantum case there is one additional relation recorded just after (3.34).
In [12, \(\S \)2.1], essentially finite Abelian categories were called “Schurian categories” but we will use the latter terminology for a slightly different notion.
In [8] the terminology “locally Schurian” was used instead of “Schurian.”
In [13], one also finds \((-)\)-bubbles which will not be needed here.
References
Ariki, S.: On the decomposition numbers of the Hecke algebra of G(m,1, n). J. Math. Kyoto Univ. 36, 789–808 (1996)
Beliakova, A., Habiro, K., Lauda, A., Webster, B.: Cyclicity for categorified quantum groups. J. Algebra 452, 118–132 (2016)
Brundan, J.: On the definition of Kac–Moody 2-category. Math. Ann. 364, 353–372 (2016)
Brundan, J.: On the definition of Heisenberg category. Algebr. Comb. 1, 523–544 (2018)
Brundan, J.: Representations of the oriented skein category. arXiv:1712.08953
Brundan, J., Comes, J., Kujawa, J.: A basis theorem for the degenerate affine oriented Brauer–Clifford supercategory. Can. J. Math. 71, 1061–1101 (2019)
Brundan, J., Comes, J., Nash, D., Reynolds, A.: A basis theorem for the affine oriented Brauer category and its cyclotomic quotients. Quantum Topol. 8, 75–112 (2017)
Brundan, J., Davidson, N.: Categorical actions and crystals. Contemp. Math. 684, 116–159 (2017)
Brundan, J., Kleshchev, A.: Representations of shifted Yangians and finite W-algebras. Mem. Am. Math. Soc. 196(918), viii+107 (2008)
Brundan, J., Kleshchev, A.: Blocks of cyclotomic Hecke algebras and Khovanov–Lauda algebras. Invent. Math. 178, 451–484 (2009)
Brundan, J., Kleshchev, A.: Graded decomposition numbers for cyclotomic Hecke algebras. Adv. Math. 222, 1883–1942 (2009)
Brundan, J., Losev, I., Webster, B.: Tensor product categorifications and the super Kazhdan–Lusztig conjecture. Int. Math. Res. Not. 20, 6329–6410 (2017)
Brundan, J., Savage, A., Webster, B.: On the definition of quantum Heisenberg category. Algebra Number Theory 14, 275–321 (2020)
Brundan, J., Savage, A. Webster, B.: The degenerate Heisenberg category and its Grothendieck ring. arXiv:1812.03255v2
Brundan, J., Stroppel, C.: Semi-infinite highest weight categories. arXiv:1808.08022v2
Cheng, S.-J., Wang, W.: Brundan–Kazhdan–Lusztig and super duality conjectures. Publ. Res. Inst. Math. Sci. 44, 1219–1272 (2008)
Chuang, J., Rouquier, R.: Derived equivalences for symmetric groups and \(_2\)-categorification. Ann. Math. 167, 245–298 (2008)
Dupont, B.: Rewriting modulo isotopies in Khovanov–Lauda–Rouquier’s categorification of quantum groups. arXiv:1907.09901
Entova-Aizenbud, I.: Categorical actions and multiplicities in the Deligne category \( {\operatorname{Re}}\!\operatorname{p}(GL_t)\). J. Algebra 504, 391–431 (2018)
Etingof, P., Gelaki, S., Nikshych, D., Ostrik, V.: Tensor Categories. American Mathematical Society, Providence (2015)
Ginzburg, V., Guay, N., Opdam, E., Rouquier, R.: On the category \({\cal{O}}\) for rational Cherednik algebras. Invent. Math. 154, 617–651 (2003)
Grojnowski, I.: Affine \(_p\) controls the representation theory of the symmetric group and related Hecke algebras. arXiv:math.RT/9907129
Kang, S.-J., Kashiwara, M.: Categorification of highest weight modules via Khovanov–Lauda–Rouquier algebras. Invent. Math. 190, 699–742 (2012)
Kang, S.-J., Kashiwara, M., Misra, K., Miwa, T., Nakashima, T., Nakayashiki, A.: Perfect crystals of quantum affine Lie algebras. Duke Math. J. 68, 499–607 (1992)
Khovanov, M.: Heisenberg algebra and a graphical calculus. Fundam. Math. 225, 169–210 (2014)
Khovanov, M., Lauda, A.: A diagrammatic approach to categorification of quantum groups II. Trans. Am. Math. Soc. 363, 2685–2700 (2011)
Khovanov, M., Lauda, A.: A categorification of quantum \((n)\). Quantum Topol. 1, 1–92 (2010)
Licata, A., Savage, A.: Hecke algebras, finite general linear groups, and Heisenberg categorification. Quantum Topol. 4, 125–185 (2013)
Macdonald, I.G.: Symmetric Functions and Hall Polynomials, Oxford Mathematical Monographs, 2nd edn. OUP, Oxford (1995)
Mackaay, M., Savage, A.: Degenerate cyclotomic Hecke algebras and higher level Heisenberg categorification. J. Algebra 505, 150–193 (2018)
Nandakumar, V., Zhao, G.: Categorification via blocks of modular representations II. arXiv:2005.08248
Queffelec, H., Savage, A., Yacobi, O.: An equivalence between truncations of categorified quantum groups and Heisenberg categories. J. Éc. Polytech. Math. 5, 197–238 (2018)
Riche, S., Williamson, G.: Tilting modules and the \(p\)-canonical basis. Astérisque no. 397, ix+184 pp. (2018)
Rouquier, R.: \(2\)-Kac–Moody algebras. arXiv:0812.5023v1
Rouquier, R.: Quiver Hecke algebras and 2-Lie algebras. Algebra Colloq. 19, 359–410 (2012)
Shan, P.: Crystals of Fock spaces and cyclotomic rational double affine Hecke algebras. Ann. Sci. ÉÍ c. Norm. Sup. 44, 147–182 (2010)
Turaev, V., Virelizier, A.: Monoidal Categories and Topological Field Theory, Progress in Mathematics, vol. 322. Springer, Berlin (2017)
Virk, R.: Derived equivalences and \(\mathfrak{sl}_2\)-categorifications for \(U_q(\mathfrak{gl}_n)\). J. Algebra 346, 82–100 (2011)
Webster, B.: Canonical bases and higher representation theory. Compos. Math. 151, 121–166 (2015)
Webster, B.: Knot invariants and higher representation theory. Mem. Am. Math. Soc. 250(1191), v+141 (2017)
Webster, B.: Unfurling Khovanov–Lauda–Rouquier algebras. arXiv:1603.06311v2
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J.B. supported in part by NSF Grant DMS-1700905. A.S. supported by Discovery Grant RGPIN-2017-03854 from the Natural Sciences and Engineering Research Council of Canada. B.W. supported by Discovery Grant RGPIN-2018-03974 from the Natural Sciences and Engineering Research Council of Canada. This research was also supported by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Research and Innovation.
Rights and permissions
About this article
Cite this article
Brundan, J., Savage, A. & Webster, B. Heisenberg and Kac–Moody categorification. Sel. Math. New Ser. 26, 74 (2020). https://doi.org/10.1007/s00029-020-00602-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-020-00602-5





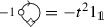 where
where  is the last entry of the inverse of the matrix (
is the last entry of the inverse of the matrix ( where
where  is the last entry of the inverse of the matrix (
is the last entry of the inverse of the matrix ( where
where  , while for (
, while for ( where
where  .
. , then
, then  .
. , then
, then 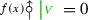 .
. are nilpotent for all
are nilpotent for all  are nilpotent.
are nilpotent. , then
, then  .
. , then
, then  .
. for
for  for
for