Bicommutant categories from fusion categories

Abstract

Bicommutant categories are higher categorical analogs of von Neumann algebras that were recently introduced by the first author. In this article, we prove that every unitary fusion category gives an example of a bicommutant category. This theorem categorifies the well-known result according to which a finite dimensional $*$-algebra that can be faithfully represented on a Hilbert space is in fact a von Neumann algebra.

1 Introduction

Bicommutant categories were introduced by the first author in the recent preprint [14], as a categorification of the notion of a von Neumann algebra.

Recall that a von Neumann algebra is a subalgebra of the algebra of bounded operators on a Hilbert space which is equal to its bicommutant:

$$\begin{aligned} \qquad \qquad \qquad A\subset B(H)\,\,\quad \mathrm {s.t.}\quad A=A''\qquad \qquad \mathrm {(von\,Neumann\,algebra).} \end{aligned}$$

Bicommutant categories are defined similarly. They are tensor categories equipped with a tensor functor to the category ${{\mathrm{Bim}}}(R)$ of all separable bimodules over a hyperfinite factor, such that the natural comparison functor from the category to its bicommutant is an equivalence of categories:

$$\begin{aligned} \qquad \qquad \qquad \mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)\,\quad \mathrm {s.t.}\quad \mathcal {C}\mathop {\rightarrow }\limits ^{\simeq }\mathcal {C}'' \qquad \qquad \mathrm {(bicommutant\,category).} \end{aligned}$$

The main result of this paper is that every unitary fusion category gives an example of a bicommutant category. The fusion categories themselves are not bicommutant categories, as they do not admit infinite direct sums: In a fusion category, every object is a finite direct sum of simple objects. In other words, every object is of the form $\bigoplus _i c_i\otimes V_i$ for some finite dimensional vector spaces $V_i\in \mathsf {Vec}$ and simple objects $c_i\in \mathcal {C}$. In order to make $\mathcal {C}$ into a bicommutant category, we need to allow the $V_i$ to be arbitrary separable Hilbert spaces. The resulting category is denoted as $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ (this is an instance of balanced tensor product of linear categories [33]). Our main result is as follows:

Theorem A

If $\mathcal {C}$ is a unitary fusion category, then $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ is a bicommutant category.

By a result of Popa [27], every unitary fusion category $\mathcal {C}$ can be embedded in ${{\mathrm{Bim}}}(R)$ (see Theorem 3.5). We prove that its bicommutant $\mathcal {C}''$ is equivalent to $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$, and that the latter is a bicommutant category.

As a special case of the above theorem, if G is a finite group and $\omega$ is a cocycle representing a class $[\omega ]\in H^3(G,U(1))$, then the tensor category $\mathsf{Hilb}^\omega [G]$ of G-graded Hilbert spaces with associator twisted by $\omega$ is a bicommutant category. That result was conjectured in [14, §6] as part of a bigger conjecture about categories of representations of twisted loop groups.

We summarize the categorical analogy in the table below. Going left to right is “categorification,” and going down is passing to the infinite dimensional case:

An algebra A	A tensor category $\mathcal {C}$
A finite dimensional algebra	A fusion category
The center of an algebra Z(A)	The Drinfeld center $\mathcal {Z}(\mathcal {C})$
The commutant (or centralizer) $Z_B(A)$ of A in B	The commutant $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ of $\mathcal {C}$ in $\mathcal {D}$
The algebra B(H) of bounded operators	The category ${{\mathrm{Bim}}}(R)$ of all bimodules
On a Hilbert space	On a hyperfinite factor R
The commutant $A':=Z_{B(H)}(A)$	The commutant $\mathcal {C}':=\mathcal {Z}_{{{\mathrm{Bim}}}(R)}(\mathcal {C})$
A von Neumann algebra $A=A''$	A bicommutant category $\mathcal {C}\cong \mathcal {C}''$

We have omitted one technical point in the above discussion. Von Neumann algebras are not just algebras; they are $*$-algebras (all the other structures such as the norm and the various topologies can be deduced from the $*$-algebra structure, but the $*$-algebra cannot be deduced from the algebra structure). Similarly, bicommutant categories are equipped with two involutions which mimic the involutions that are naturally present on ${{\mathrm{Bim}}}(R)$. One of the involutions acts at the level of morphisms (the adjoint of a linear map), and the other acts at the level of objects (the complex conjugate of a bimodule). We call such categories bi-involutive tensor categories (see Definition 2.5). Thus, we add the following line to the above table:

$*$-algebra A

Bi-involutive tensor category $\mathcal {C}$

2 Preliminaries

2.1 Involutions on tensor categories

A linear dagger category is a linear category $\mathcal {C}$ over the complex numbers, equipped with an anti-linear map $\mathcal {C}(x,y)\rightarrow \mathcal {C}(y,x):f\mapsto f^*$ for every $x,y\in \mathcal {C}$ called the adjoint of a morphism. It satisfies $f^{**}=f$ and $(f\circ g)^*=g^*\circ f^*$, from which it follows that ${{\mathrm{id}}}_x^*={{\mathrm{id}}}_x$. An invertible morphism of a dagger category is called unitary if $f^*=f^{-1}$.

A functor $F:\mathcal {C}\rightarrow \mathcal {D}$ between dagger categories is a dagger functor if $F(f)^*=F(f^*)$.

Definition 2.1

([31, §7]) A dagger tensor category is a linear dagger category $\mathcal {C}$ equipped with a monoidal structure whose associators $\alpha _{x,y,z}:(x\otimes y)\otimes z\rightarrow x\otimes (y\otimes z)$ and unitors $\lambda _x:1\otimes x\rightarrow x$ and $\rho _x:x\otimes 1\rightarrow x$ are unitary, and which satisfies the compatibility condition $(f\otimes g)^* =f^*\otimes g^*$.

The last condition can be rephrased as saying that the monoidal product $\otimes :\mathcal {C}\otimes _{\mathsf {Vec}} \mathcal {C}\rightarrow \mathcal {C}$ is a dagger functor. From now on, we shall abuse notation, and omit all associators and unitors from our formulas. We trust the reader to insert them wherever needed.

Definition 2.2

Let $\mathcal {C}$ and $\mathcal {D}$ be dagger tensor categories. A dagger tensor functor $F: \mathcal {C}\rightarrow \mathcal {D}$ is a dagger functor equipped with a unitary natural transformation $\mu _{x,y}:F(x)\otimes F(y)\rightarrow F(x\otimes y)$ and a unitary isomorphism $i:1_\mathcal {D}\rightarrow F(1_\mathcal {C})$ such that the following identities hold for all $x,y,z\in \mathcal {C}$:

$$\begin{aligned} \mu _{x,y\otimes z}\circ ({{\mathrm{id}}}_{F(x)}\otimes \mu _{y,z})&= \mu _{x\otimes y, z}\circ (\mu _{x,y}\otimes {{\mathrm{id}}}_{F(z)})\\ \mu _{1,x}\circ (i\otimes {{\mathrm{id}}}_{F(x)})&={{\mathrm{id}}}_{F(x)} \qquad \,\,\, \mu _{x,1}\circ ({{\mathrm{id}}}_{F(x)}\otimes i) = {{\mathrm{id}}}_{F(x)}. \end{aligned}$$

We shall be interested in dagger tensor categories which are equipped with a second involution, this time at the level of objects (compare [15, Def. 1.3]):

Definition 2.3

A bi-involutive tensor category is a dagger tensor category $\mathcal {C}$ with a covariant anti-linear dagger functor $\overline{\,\cdot \,}:\mathcal {C}\rightarrow \mathcal {C}$ called the conjugate. This functor should be involutive, meaning that for every $x\in \mathcal {C}$, we are given a unitary natural isomorphisms $\varphi _x:x\rightarrow \overline{\overline{x}}$ satisfying $\varphi _{\overline{x}}=\overline{\varphi _{x}}$. It should be anti-compatible with the tensor structure, meaning that we have unitary natural isomorphisms

$$\begin{aligned} \nu _{x,y}:\overline{x} \otimes \overline{y} \mathop {\longrightarrow }\limits ^{\simeq }\overline{y \otimes x} \end{aligned}$$

and a unitary $j:1\rightarrow \overline{1}$ satisfying $\nu _{x,z\otimes y}\circ ({{\mathrm{id}}}_{\overline{x}}\otimes \nu _{y,z})=\nu _{y\otimes x, z}\circ (\nu _{x,y}\otimes {{\mathrm{id}}}_{\overline{z}})$ and $\nu _{1,x}\circ (j\otimes {{\mathrm{id}}}_{\overline{x}})={{\mathrm{id}}}_{\overline{x}}=\nu _{x,1}\circ ({{\mathrm{id}}}_{\overline{x}}\otimes j)$. Finally, we require the compatibility conditions $\varphi _1=\overline{j}\circ j$ and $\varphi _{x \otimes y}=\overline{\nu _{y,x}}\circ \nu _{\overline{x},\overline{y}}\circ (\varphi _x\otimes \varphi _y)$ between the above pieces of data.

Remark 2.4

It is interesting to note that the map j can be recovered from the other data as $j= \lambda _{\overline{1}}\circ (\varphi ^{-1}_1\otimes {{\mathrm{id}}}_{\overline{1}})\circ \nu _{\overline{1}1}^{-1}\circ \overline{\lambda _{\overline{1}}}^{-1}\circ \varphi _1$. We believe that the notion of bi-involutive category as presented above is equivalent to its variant without j (and without the axioms that involve j). Nevertheless, we find it more pleasant to include this piece of data in the definition.

Note that in the category of Hilbert spaces, the isomorphism $\varphi _H:H\rightarrow \overline{\overline{H}}$ is an identity arrow. Whenever that is the case, we have $\overline{j}=j^{-1}$ and $\overline{\nu _{y,x}}=\nu _{\overline{x},\overline{y}}^{-1}$.

Definition 2.5

Let $\mathcal {C}$ and $\mathcal {D}$ be bi-involutive tensor categories. A bi-involutive tensor functor is a dagger tensor functor $F:\mathcal {C}\rightarrow \mathcal {D}$, equipped with a unitary natural transformation $\upsilon _x:F(\overline{x})\rightarrow \overline{F(x)}$ satisfying the three conditions $\upsilon _{\overline{x}}= \overline{\upsilon _{x}}^{-1}\circ \varphi _{F(x)}\circ F(\varphi _x)^{-1}$,  $\upsilon _{1_\mathcal {C}}= \overline{i}\circ j_\mathcal {D}\circ i^{-1}\circ F(j_\mathcal {C})^{-1}$, and $\upsilon _{x\otimes y}= \overline{\mu _{x,y}}\circ \nu _{F(y),F(x)}\circ (\upsilon _y\otimes \upsilon _x)\circ \mu _{\overline{y},\overline{x}}^{-1}\circ F(\nu _{y,x})^{-1}$.

2.2 Unitary fusion categories

A tensor category $\mathcal {C}$ is rigid if for every object $x\in \mathcal {C}$, there exists an object $x^\vee \in \mathcal {C}$, called the dual of x, and maps $\mathrm {ev}_x : x^\vee \otimes x \rightarrow 1$ and $\mathrm {coev}_x : 1 \rightarrow x \otimes x^\vee$ satisfying the zigzag axioms

$$\begin{aligned} ({{\mathrm{id}}}_x \otimes \, \mathrm {ev}_x) \circ (\mathrm {coev}_x \otimes {{\mathrm{id}}}_x) = {{\mathrm{id}}}_x \quad \mathrm {and}\quad (\mathrm {ev}_x \otimes {{\mathrm{id}}}_{x^\vee }) \circ ({{\mathrm{id}}}_{x^\vee } \otimes \, \mathrm {coev}_x) = {{\mathrm{id}}}_{x^\vee } \end{aligned}$$

(1)

(those equations determine $x^\vee$ up to unique isomorphism). Moreover, for every $x \in \mathcal {C}$, there should exist an object ${}^\vee x \in \mathcal {C}$ such that $({}^\vee x)^\vee \cong x$. The dual of a morphism $f:x\rightarrow y$ is given by

$$\begin{aligned} f^\vee :=(\mathrm {ev}_y\otimes {{\mathrm{id}}}_{x^\vee })\circ ({{\mathrm{id}}}_{y^\vee }\otimes f \otimes {{\mathrm{id}}}_{x^\vee })\circ ({{\mathrm{id}}}_{y^\vee }\otimes \,\mathrm {coev}_x) :y^\vee \rightarrow x^\vee . \end{aligned}$$

Let $\mathsf {Vec}$ denote the category of finite dimensional vector spaces. A category is semisimple if it is equivalent to a direct sum of copies of $\mathsf {Vec}$, possibly infinitely many. Equivalently, it is semisimple if it admits finite direct sums (including the zero sum), and every object is a direct sum of finitely many (possibly zero) simple objects.

Definition 2.6

A fusion category is a tensor category which is rigid, semisimple, with simple unit, and finitely many isomorphism classes of simple objects.

Let $\mathsf {Hilb}$ denote the dagger category of Hilbert spaces and bounded linear maps. A C*-category is a dagger category $\mathcal {C}$ for which there exists a faithful dagger functor $\mathcal {C}\rightarrow \mathsf {Hilb}$ whose image is norm-closed at the level of hom-spaces. Equivalently [10, Prop. 1.14], a C*-category is a dagger category such that for every arrow $f:x\rightarrow y$, there exists an arrow $g:x\rightarrow x$ with $f^*\circ f=g^*\circ g$,¹ and such that the norms

$$\begin{aligned} \Vert f\Vert ^2:=\sup \big \{|\lambda | : f^*{\circ } f-\lambda {\cdot } {{\mathrm{id}}}\,\,\, \mathrm {is\,\,not\,\,invertible}\big \} \end{aligned}$$

are complete and satisfy $\Vert f\circ g\Vert \le \Vert f\Vert \Vert g\Vert$ and $\Vert f^*\circ f\Vert =\Vert f\Vert ^2$. A C*-tensor category is a dagger tensor category whose underlying dagger category is a C*-category.

Definition 2.7

A unitary fusion category is a dagger tensor category whose underlying dagger category is a C*-category, and whose underlying tensor category is a fusion category.

By [35, Thm. 4.7] and [2, §4] , every rigid C*-tensor category with simple unit (in particular, every unitary fusion category) can be equipped with a canonical bi-involutive structure. The conjugation $\overline{\,\cdot \,}$ is characterized at the level of objects (up to unique unitary isomorphisms) by the data of structure morphisms $\mathrm {ev}_x : \overline{x} \otimes x \rightarrow 1$ and $\mathrm {coev}_x : 1 \rightarrow x \otimes \overline{x}$, subject to the two zigzag axioms (1) and the balancing condition

$$\begin{aligned} \qquad \quad \mathrm {coev}_x^*\circ (f\otimes {{\mathrm{id}}}_{\overline{x}})\circ \mathrm {coev}_x= \mathrm {ev}_x\circ ({{\mathrm{id}}}_{\overline{x}}\otimes f)\circ \mathrm {ev}_x^* \quad \forall \,\,f:x\rightarrow x. \end{aligned}$$

The conjugation applied to a morphism $f:x\rightarrow y$ is given by $\overline{f}:=(f^*)^\vee :\overline{x}\rightarrow \overline{y}$. The coherences between the conjugation and the tensor structure are given by $j=\mathrm {coev}_1$ and $\nu _{x,y}=(\mathrm {ev}_x\otimes {{\mathrm{id}}}_{\overline{y\otimes x}})\circ ({{\mathrm{id}}}_{\overline{x}}\otimes \mathrm {ev}_y\otimes {{\mathrm{id}}}_{x\otimes \overline{y\otimes x}})\circ ({{\mathrm{id}}}_{\overline{x}\otimes \overline{y}}\otimes \mathrm {coev}_{y\otimes x})$. The last piece of data is provided by the isomorphisms

$$\begin{aligned} \varphi _x:=({{\mathrm{id}}}_{\overline{\overline{x}}}\,\otimes \, \mathrm {ev}_x)\circ (\mathrm {ev}_{\overline{x}}^*\otimes {{\mathrm{id}}}_x):x\rightarrow \overline{\overline{x}}. \end{aligned}$$

Finally, the maps $\varphi _x:x\rightarrow \overline{\overline{x}}$ equip such a category with a canonical pivotal structure, which is furthermore spherical.

Note that a unitary fusion category is a fusion category with an additional structure. A fusion category could therefore, in principle, have more than one unitary structures. The question of uniqueness is best formulated in the following way (see [9, §5] for related work).

Question 2.8

Let $F:\mathcal {C}\mathop {\rightarrow }\limits ^{\simeq }\mathcal {D}$ be a tensor equivalence between two unitary fusion categories. Is any such F naturally equivalent to a dagger tensor functor?

Given a fusion category $\mathcal {C}$, we define a new category $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ as follows. Its objects are formal expressions $\bigoplus _i x_i\otimes H_i$ (finite direct sums) with $x_i\in \mathcal {C}$ and $H_i\in \mathsf{Hilb}$, and the morphisms are given by

$$\begin{aligned} {{\mathrm{Hom}}}_{\,\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}}\Big (\bigoplus _i x_i\otimes H_i, \bigoplus _j y_j\otimes K_j\Big )\,:=\,\, \bigoplus _{i,j} \mathcal {C}(x_i,y_j)\otimes _\mathbb {C}\mathsf{Hilb}(H_i,K_j). \end{aligned}$$

As we saw, if $\mathcal {C}$ is a unitary fusion category, then it is equipped with a canonical bi-involutive structure. Combining it with the corresponding structure on $\mathsf{Hilb}$ yields a bi-involutive structure on $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$. The adjoint of a morphism $\sum f_{ij}\otimes g_{ij}:\bigoplus x_i\otimes H_i\rightarrow \bigoplus y_j\otimes K_j$ is $\sum f_{ij}^*\otimes g_{ij}^*$, and the conjugate of an object $\bigoplus x_i\otimes H_i$ is $\bigoplus \overline{x_i}\otimes \overline{H_i}$. The structure data $\varphi$, $\nu$, j are inherited from those of $\mathcal {C}$ and of $\mathsf{Hilb}$.

2.3 The commutant of a category

Given an algebra B and a subalgebra $A\subset B$, the commutant of A inside B, also called the centralizer, is the algebra

$$\begin{aligned} Z_B(A):=\{b\in B\,|\,ab=ba\,\, \forall a\in A\}. \end{aligned}$$

In this section, we introduce higher categorical variants of the above notion, where the algebras A and B are replaced by tensor categories, dagger tensor categories, and finally bi-involutive tensor categories.

Definition 2.9

([20]) Let $\mathcal {C}$ and $\mathcal {D}$ be tensor categories, and let $F=(F,\mu ,i): \mathcal {C}\rightarrow \mathcal {D}$ be a tensor functor. The commutant $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ of $\mathcal {C}$ in $\mathcal {D}$ is the category whose objects are pairs $(X, e_X)$ with $X\in \mathcal {D}$ an object, and $e_X=(e_{X,y}:X\otimes F(y)\mathop {\rightarrow }\limits ^{\scriptscriptstyle \simeq }F(y)\otimes X)_{y\in \mathcal {C}}$ a half-braiding. The components $e_{X,y}$ of the half-braiding must satisfy the following “hexagon” axiom:

Note that by setting $y=z=1_\mathcal {C}$ in the above diagram, it follows that $e_{X,1_\mathcal {C}}={{\mathrm{id}}}_X$.

A morphism $(X,e_X)\rightarrow (Y, e_Y)$ in $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ is a morphism $f:X\rightarrow Y$ in $\mathcal {D}$ such that $({{\mathrm{id}}}_{F(z)}\otimes f)\circ e_{X,z} = e_{Y,z}\circ (f\otimes {{\mathrm{id}}}_{F(y)})$. The tensor product of two objects $(X,e_X)$, $(Y, e_Y)$ of $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ is given by $(X,e_X)\otimes (Y, e_Y) = (X\otimes Y,e_{X\otimes Y})$, with

$$\begin{aligned} e_{X\otimes Y,z}=(e_{X,z}\otimes {{\mathrm{id}}}_Y)\circ ({{\mathrm{id}}}_X\otimes e_{Y,z}), \end{aligned}$$

and the associators and unitors of $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ are inherited from those of $\mathcal {D}$.

Remark 2.10

The Drinfeld center $\mathcal {Z}(\mathcal {C})$ is the commutant of $\mathcal {C}$ in itself.

If $\mathcal {C}$ and $\mathcal {D}$ are dagger tensor categories and $F: \mathcal {C}\rightarrow \mathcal {D}$ is a dagger tensor functor, then we may consider the full subcategory

$$\begin{aligned} \mathcal {Z}_\mathcal {D}^*(\mathcal {C})\,\subset \, \mathcal {Z}_\mathcal {D}(\mathcal {C}) \end{aligned}$$

whose objects are pairs $(X, e_X)$ as above, where the maps $e_{X,y}: X \otimes F(y)\rightarrow F(y)\otimes X$ are unitary. We call $\mathcal {Z}_\mathcal {D}^*(\mathcal {C})$ the unitary commutant of $\mathcal {C}$ in $\mathcal {D}$ (compare [21, Def. 6.1]). Unlike $\mathcal {Z}_\mathcal {D}(\mathcal {C})$, the unitary commutant is a dagger category, and its $*$-operation is inherited from $\mathcal {D}$.

Remark 2.11

The inclusion $\mathcal {Z}_\mathcal {D}^*(\mathcal {C})\hookrightarrow \mathcal {Z}_\mathcal {D}(\mathcal {C})$ is in general not an equivalence. The easiest counterexample is given by $\mathcal {C}=\mathsf {Vec}[G]$ for G some infinite group, and $\mathcal {D}=\mathsf {Vec}$. Then, $\mathcal {Z}^*_\mathcal {D}(\mathcal {C})$ is the category of unitary representations of G, whereas $\mathcal {Z}_\mathcal {D}(\mathcal {C})$ is the category of all representations of G. See [22, Thm. 6.4] and [9, Proposition 5.24] for some positive results when $\mathcal {C}$ is a fusion category.

If $\mathcal {C}$ and $\mathcal {D}$ are bi-involutive tensor categories, and $F: \mathcal {C}\rightarrow \mathcal {D}$ is a bi-involutive tensor functor, then the unitary commutant $\mathcal {Z}^*_\mathcal {D}(\mathcal {C})$ of $\mathcal {C}$ in $\mathcal {D}$ is also naturally equipped with the structure of a bi-involutive tensor category. The conjugate of $(X,e_X)\in \mathcal {Z}^*_\mathcal {D}(\mathcal {C})$ is the pair $(\overline{X},e_{\overline{X}})$ consisting of the object $\overline{X}\in \mathcal {D}$ and the half-braiding

The coherence isomorphisms $\varphi$, j, and $\nu$ are inherited from $\mathcal {D}$.

We will be especially interested in the case when $\mathcal {D}={{\mathrm{Bim}}}(R)$, the tensor category of bimodules over some hyperfinite von Neumann factor R. The monoidal product on that category is based on the operation of Connes fusion, which we describe next.

2.4 $L^2$-spaces and Connes fusion

Let R be a von Neumann algebra, with predual $R_*$ and positive part $R_*^+\subset R_*$. The $L^2$-space of R (also known as standard form of R), denoted as $L^2R$, is the Hilbert space generated by symbols $\sqrt{\phi }$ for $\phi \in R_*^+$, under the inner product

$$\begin{aligned} \langle \sqrt{\phi },\sqrt{\psi }\rangle = \underset{t\rightarrow i/2}{\mathrm {anal.\,cont.}}\, \phi ([D\phi :D\psi ]_t), \end{aligned}$$

where $[D\phi :D\psi ]_t\in R$ is Connes’ non-commutative Radon–Nikodym derivative.² The Hilbert space $L^2R$ is an R–R-bimodule, with the two actions of R are determined by the formula

$$\begin{aligned} \langle a\sqrt{\phi }\, b,\sqrt{\psi }\rangle = \underset{t\rightarrow i/2}{\mathrm {anal.\,cont.}}\, \phi \big ([D\phi :D\psi ]_t \sigma _t^\psi (b) a\big ), \end{aligned}$$

where $\sigma _t^\psi$ is the modular flow. Finally, the modular conjugation $J:L^2R\rightarrow L^2R$ is given by $J(\lambda \sqrt{\phi })=\overline{\lambda }\sqrt{\phi }$ for $\lambda \in \mathbb {C}$. General references about $L^2R$ include [11, 12, 18].

Given a right module H and a left module K, their fusion $H\boxtimes _R K$ is the Hilbert space generated by symbols $\alpha [\xi ]\beta$, for $\alpha :L^2R\rightarrow H$ a right R-linear map, $\xi \in L^2R$, and $\beta :L^2R\rightarrow K$ a left R-linear map, under the inner product

$$\begin{aligned} \big \langle \alpha _1[\xi _1]\beta _1, \alpha _2[\xi _2]\beta _2\big \rangle \,=\, \big \langle \ell ^{-1}(\alpha _2^*\circ \alpha _1)\xi _1 r^{-1}(\beta _2^*\circ \beta _1),\xi _2\big \rangle _{L^2R}. \end{aligned}$$

Here, $\ell$ and r denote the left and right actions of R on its $L^2$ space, defined by $\ell (a)(\xi )=a\xi$ and $r(a)(\xi )=\xi a$, respectively.

There exist two alternative descriptions of $H\boxtimes _R K$, as generated by symbols $\alpha [\xi$ for $\alpha :L^2R\rightarrow H$ a right R-linear map and $\xi \in K$ a vector, and generated by symbols $\xi ]\beta$ for $\beta :L^2R\rightarrow K$ a left R-linear map and $\xi \in H$ a vector. The isomorphisms between the above models are given by

$$\begin{aligned} \alpha [\xi ]\beta \,\,\mapsto \,\,\alpha (\xi )]\beta \quad \mathrm {and}\quad \alpha [\xi ]\beta \,\,\mapsto \,\,\alpha [\beta (\xi ). \end{aligned}$$

General references about Connes fusion include [24, 30] and [4, Appendix B. $\delta$].

The two actions of R on $L^2R$ are each other’s commutants. That property characterizes the bimodules which are invertible with respect to Connes fusion:

Lemma 2.12

([30, Prop. 3.1]) Let A and B be von Neumann algebras, and let H be an A–B-bimodules such that A and B are each other’s commutants on H (in particular, they act faithfully on H). Then, H is an invertible A–B-bimodule.

Connes fusion has the following useful faithfulness property:

Lemma 2.13

Let R be a von Neumann algebra, and let H be a faithful right module. Then, for any left modules $K_1$ and $K_2$, the map

$$\begin{aligned} H\boxtimes _R -: {{\mathrm{Hom}}}_R(K_1,K_2)\rightarrow {{\mathrm{Hom}}}(H\boxtimes _R K_1,H\boxtimes _R K_2) \end{aligned}$$

(2)

is injective.

Proof

Let $R'$ be the commutant of R on H. By Lemma 2.12, H is an invertible $R'$–R-bimodule. The map (2) can then be factored as the composite of the bijection ${{\mathrm{Hom}}}_R(K_1,K_2)\cong {{\mathrm{Hom}}}_{R'}(H\boxtimes K_1,H\boxtimes K_2)$ with the inclusion

$$\begin{aligned} {{\mathrm{Hom}}}_{R'}(H\boxtimes K_1,H\boxtimes K_2)\subset {{\mathrm{Hom}}}(H\boxtimes K_1,H\boxtimes K_2). \end{aligned}$$

$\square$

The operation of fusion makes the category ${{\mathrm{Bim}}}(R)$ of R–R-bimodules³ into a tensor category, with unit object $L^2R$. The associator is given by

$$\begin{aligned} (H\boxtimes _R K) \boxtimes _R L \rightarrow H\boxtimes _R (K \boxtimes _R L)\,\,:\,\, (\alpha [\xi )]\beta \mapsto \alpha [(\xi ]\beta ), \end{aligned}$$

for $\alpha :L^2R\rightarrow H$ a right R-linear map, $\xi \in K$, and $\beta :L^2R\rightarrow L$ a left R-linear map, and the two unitors are given by

$$\begin{aligned} H\boxtimes _R L^2R\rightarrow H: \alpha [\xi \mapsto \alpha (\xi ) \quad \mathrm {and}\quad L^2R\boxtimes _R H\rightarrow H: \alpha [\xi \mapsto \ell ^{-1}(\alpha )\xi . \end{aligned}$$

The category ${{\mathrm{Bim}}}(R)$ is a dagger tensor category, with adjoints of morphisms defined at the level of the underlying Hilbert spaces. It is even a bi-involutive tensor category. Given a bimodule $H\in {{\mathrm{Bim}}}(R)$, the underlying Hilbert space of $\overline{H}$ is the complex conjugate of H (with scalar multiplication $\lambda \overline{\xi }=\overline{\overline{\lambda }\xi }$), and the two actions of R are given by $a\overline{\xi }b=\overline{b^*\xi a^*}$. The transformation $\varphi$ is the identity. The map $j:L^2R\rightarrow \overline{L^2R}$ is given by $j(\xi )=\overline{J(\xi )}$, with J the modular conjugation (note that j is linear, and J is anti-linear), and the coherence $\nu :\overline{H} \boxtimes _R \overline{K} \rightarrow \overline{K \boxtimes _R H}$ is given by

$$\begin{aligned} \nu (\alpha [\xi ]\beta )=\overline{(\overline{\beta }\circ j)[J(\xi )](\overline{\alpha }\circ j)} \end{aligned}$$

for $\alpha :L^2R\rightarrow \overline{H}$, $\xi \in L^2R$, and $\beta :L^2R\rightarrow \overline{K}$. The latter is equivalently given by $\nu (\alpha [\xi )=\overline{J(\xi )](\overline{\alpha }\circ j)}$, or $\nu (\xi ]\beta )=\overline{(\overline{\beta }\circ j)[J(\xi )}$.

Remark 2.14

Let ${{\mathrm{Bim}}}^\circ (R)\subset {{\mathrm{Bim}}}(R)$ be the full subcategory of dualizable bimodules (equivalently, the bimodules with finite statistical dimension [2, § 5 and Cor. 7.14]). Then, by [2, Cor. 6.12] , the canonical conjugation on ${{\mathrm{Bim}}}^\circ (R)$ (described in Sect. 2.2) is the restriction of the conjugation on ${{\mathrm{Bim}}}(R)$ described above.

2.5 Graphical calculus

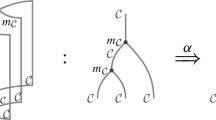
Throughout this paper, we will use the string diagram calculus familiar from tensor categories: Objects are denoted by strands, and morphisms are denoted by coupons [17, 31] . For example, the following string diagram

represents a morphism $v\otimes w\rightarrow x\otimes y\otimes z$.

Given a dualizable object $x\in \mathcal {C}$ in a C*-tensor category, the canonical evaluation and coevaluations maps $\mathrm {ev}_x : \overline{x} \otimes x \rightarrow 1$ and $\mathrm {coev}_x : 1 \rightarrow x \otimes \overline{x}$, and their adjoints $\mathrm {ev}_x^* : 1\rightarrow \overline{x} \otimes x$ and $\mathrm {coev}_x^* : x \otimes \overline{x}\rightarrow 1$ are denoted graphically as follows:

They satisfy:

along with the equations $\overline{\mathrm {ev}_x}=j\circ \mathrm {ev}_x \circ ({{\mathrm{id}}}_{\overline{x}}\otimes \varphi _x^{-1})\circ \nu _{x,\overline{x}}^{-1}$ and $\overline{\mathrm {coev}_x}=\nu _{\overline{x},x}\circ (\varphi _x\otimes {{\mathrm{id}}}_{\overline{x}})\circ \mathrm {coev}_x\circ j^{-1}$ which, after omitting the coherences j, $\nu$, and $\varphi$, can be conveniently abbreviated

$$\begin{aligned} \overline{\mathrm {ev}_x}=\mathrm {ev}_x \qquad \qquad \text {and}\qquad \qquad \overline{\mathrm {coev}_x}=\mathrm {coev}_x. \end{aligned}$$

The dimension of a dualizable object $x\in \mathcal {C}$ is given by

$$\begin{aligned} d_x:=\mathrm {coev}_x^*\circ \mathrm {coev}_x=\mathrm {ev}_x\circ \mathrm {ev}_x^*\,\in \,{\mathbb R}_{\ge 0}. \end{aligned}$$

Given dualizable objects $x,y,z\in \mathcal {C}$, Frobenius reciprocity (or pivotality) provides canonical isomorphisms

The sesquilinear pairing o, for $f,g\in \mathrm {Hom}(1,x\otimes y\otimes z)$, equips this vector space with the structure of a finite dimensional Hilbert space. The dual (or complex conjugate) Hilbert space is then given by any one of the following canonically isomorphic vector spaces:

Let $e_i\in \mathrm {Hom}(1,x\otimes y\otimes z)$ and $e^i\in \mathrm {Hom}(1,\overline{z}\otimes \overline{y}\otimes \overline{x})$ be dual bases, and consider the canonical element

$$\begin{aligned} \sqrt{d_xd_yd_z}\,\cdot \,\sum _i e_i\otimes e^i. \end{aligned}$$

We will be making great use of string diagrams where pairs of trivalent nodes are labeled by the above canonical element. These will be denoted by pairs of circular colored nodes, as follows:

(3)

Remark 2.15

The element .

When occurring in a bigger diagram, it might happen that we need to use the above canonical elements in more that one place. In that case, we will use multiple colors to indicate the various pairs of nodes (often, the coupling can also be inferred from the string labels). The remaining coupons will be sometimes denoted by little squares. For example:

(4)

When $x,y,z\in \mathcal {C}$ are irreducible objects, we will write $N_{x,y}^z$ for the dimension of $\mathrm {Hom}( x\otimes y,z)$. Let us also fix a set ${{\mathrm{Irr}}}(\mathcal {C})\subset {{\mathrm{Ob}}}(\mathcal {C})$ of representatives of the isomorphism classes of irreducible objects.

The following lemma lists the most important relations satisfied in the above graphical calculus. To our knowledge, the following relations have not appeared in this exact form in the literature, but they are certainly well known to experts:

Lemma 2.16

The following relations hold:

Proof

By definition, the dual basis $e_i\in \mathrm {Hom}(z,x\otimes y)$ and $e^i\in \mathrm {Hom}(x\otimes y,z)$ satisfy

By “undoing the trace,” it follows that, for $e_i$ and $e^j$ as above,

$$\begin{aligned} e^j \circ e_i = d_z^{-1}\delta _{i,j}\cdot {{\mathrm{id}}}_z. \end{aligned}$$

(5)

The two Bigon relations are immediate consequences of the above equation:

$$\begin{aligned} \sqrt{d_xd_yd_z}\cdot \sum _i e^i\circ e_i&= \sqrt{d_xd_yd_z}\cdot \sum _i d_z^{-1}\cdot {{\mathrm{id}}}_z= \sqrt{d_xd_yd_z^{-1}}\,N_{x,y}^z\cdot {{\mathrm{id}}}_z\\ d_xd_yd_z\sum _{i,j} (e^j\circ e_i)\otimes e_j\otimes e^i&=\, d_xd_y\sum _{i,j} \delta _{i,j} {{\mathrm{id}}}_z\otimes e_j\otimes e^i\\&= \sqrt{d_xd_yd_z^{-1}}\sqrt{d_xd_yd_z}\sum _i {{\mathrm{id}}}_z\otimes e_i\otimes e^i. \end{aligned}$$

In order to prove the fusion relation

$$\begin{aligned} \sum _{z,j} \sqrt{d_z}\sqrt{d_xd_yd_z}\cdot e_j \circ e^j=\sqrt{d_xd_y}\cdot {{\mathrm{id}}}_{x\otimes y}\,, \end{aligned}$$

it is enough to argue that it holds after precomposition with an arbitrary basis element $e_i\in \mathrm {Hom}(z',x\otimes y)$ and object $z'\in {{\mathrm{Irr}}}(\mathcal {C})$. So we must show that the equation $\sum _{z,j} d_z\cdot e_j \circ e^j\circ e_i = e_i$ holds. This is again a consequence of Eq. (5):

$$\begin{aligned} \sum _{z,j} d_z\cdot e_j \circ e^j\circ e_i =\sum _{z,j} d_z\cdot e_j\circ ( d_z^{-1}\delta _{z,z'}\delta _{i,j}\cdot {{\mathrm{id}}}_z)\,=\,e_i. \end{aligned}$$

To prove the I $=$ H relation, we rewrite it as

and note that both sides are of the form $\sqrt{d_xd_yd_zd_w}\,\sum f_a\otimes f^a$ for $\{f_a\}$ a basis of $\mathrm {Hom}(x\otimes w, y\otimes z)$ and $\{f^a\}$ the dual basis of $\mathrm {Hom}(\overline{w}\otimes \overline{x}, \overline{z}\otimes \overline{y})$ with respect to the pairing

To see that and are indeed dual bases, we use the relation (5) twice:

The verification that and are dual bases is entirely similar.$\square$

Let us now assume that $\mathcal {C}$ is furthermore a fusion category, and let $\dim (\mathcal {C}):=\sum _{x\in {{\mathrm{Irr}}}(\mathcal {C})}\, d_x^2$ be its global dimension. We then have the following result.

Lemma 2.17

The following relation holds:

(6)

Proof

Recall that $d_a=d_{\overline{a}}$. For every $x\in {{\mathrm{Irr}}}(\mathcal {C})$, we have

$$\begin{aligned} \sum _{a, b} d_a d_b N_{a,b}^x = \sum _{a} d_a\big (\sum _{b} N_{\overline{a}, x}^b d_b \big ) = \sum _{a} d_a(d_ad_x) = d_x\;\!\dim (\mathcal {C}). \end{aligned}$$

Using the two Bigon relations, the left-hand side of (6) then simplifies to

$$\begin{aligned} \sum _{a,b}d_ad_bd_x^{-1}N_{a,b}^x\,\delta _{x,y} \cdot {{\mathrm{id}}}_x\otimes {{\mathrm{id}}}_{\overline{x}} \,=\, \dim (\mathcal {C})\,\delta _{x,y}\cdot {{\mathrm{id}}}_x\otimes {{\mathrm{id}}}_{\overline{x}}. \end{aligned}$$

$\square$

There is an alternative proof of Lemma 2.17 which proceeds as follows. We use the I $=$ H relation to rewrite the left-hand side of (6) as

We then note that the only terms which contribute to the sum are the ones with $b = 1$, and so we are left with

2.6 Cyclic fusion

Given rings $R_i$ and bimodules ${}_{R_{i-1}}(M_i)_{R_i}$ for $i\in \{1,\ldots ,n\}$ (indices modulo n), we may define the cyclic tensor product

$$\begin{aligned} \Big [ M_1 \otimes _{R_1} M_2 \otimes _{R_2} \cdots \otimes _{R_{n-1}} M_n \otimes _{R_n} - \Big ]_{\mathrm{cyclic}}:=\, \big (M_1 \otimes _{\mathbb Z} M_2 \otimes _{\mathbb Z} \cdots \otimes _{\mathbb Z} M_n\big )\big /\sim \, \end{aligned}$$

(7)

where $\sim$ is the equivalence relation generated by

The cyclic Connes fusion, first introduced in [1, Appendix A], is the analog of the above construction for Connes fusion.

Unlike the cyclic tensor product, the cyclic fusion is not always defined. Let us explain by an analogy why it is not always defined, and when we can expect it to be defined. If one takes the point of view that a bimodule between rings is something that categorifies the notion of a linear map, then the expression (7) categorifies the number

$$\begin{aligned} tr(f_1\circ f_2\circ \cdots \circ f_n). \end{aligned}$$

Now, we like to think of bimodules between von Neumann algebras as categorifying the notion of a bounded linear map between infinite dimensional Hilbert spaces. Given bounded linear maps $f_i:H_{i-1}\rightarrow H_i$, $i\in \{1,\ldots ,n\}$ (indices modulo n), then the above trace is not always defined. It is however defined if at least two of the maps are Hilbert–Schmidt.

For bimodules between von Neumann algebras, we propose the following as a categorification of the Hilbert–Schmidt condition:

Definition 2.18

A bimodule ${}_AH_B$ between von Neumann algebras is coarse if the action of the algebraic tensor product $A\odot B^{\text {op}}$ extends to the spatial tensor product $A\,{\bar{\otimes }}\, B^{\text {op}}$. Equivalently, a bimodule is coarse if it is a direct summand of a bimodule of the form

$$\begin{aligned} {}_A(H_1)\otimes _{\mathbb {C}} (H_2)_B \end{aligned}$$

(8)

(and if A or B are factors, then any coarse bimodule is of the form (8)).

Coarse bimodules form an ideal in the sense that if ${}_AH_B$ is coarse and ${}_BK_C$ is any bimodule, then ${}_AH\boxtimes _BK_C$ is coarse.

Definition 2.19

Let $R_i$ be von Neumann algebras, and let ${}_{R_{i-1}}(H_i)_{R_i}$, $i\in \{1,\ldots ,n\}$, be bimodules (indices modulo n). Assume that at least two of the $H_i$ are coarse. Then, we define the cyclic fusion by:

$$\begin{aligned}&\Big [ H_1 \boxtimes _{R_1} H_2 \boxtimes _{R_2} \cdots \boxtimes _{R_{n-1}} H_n \boxtimes _{R_n} - \Big ]_{\mathrm{cyclic}}\\&\quad :=\Big (H_{a+1} \boxtimes _{R_{a+1}} \cdots \boxtimes _{R_{b-1}} H_b\Big ) \boxtimes _{R_a^{\text {op}}{\bar{\otimes }} R_b} \Big (H_{b+1} \boxtimes _{R_{b+1}} \cdots \boxtimes _{R_{a-1}} H_a\Big ) \end{aligned}$$

(cyclic numbering), where the indices a and b are chosen so that at least one of the $\{H_{a+1},\ldots ,H_b\}$ is coarse, and at least one of the $\{H_{b+1},\ldots ,H_a\}$ is coarse.

Remark 2.20

A priori, the above description depends on the choice of locations a and b used to “cut the circle”:

In [1, Appendix A], it was shown that when all the $H_i$ are coarse (and as long as there are at least two of them), the cyclic fusion is well defined up to canonical unitary isomorphism. It is also well defined in the presence of non-coarse bimodules: Let the $H_{i_1},\ldots ,H_{i_k}$ be coarse, and let the other bimodules be non-coarse. Then, we may define the cyclic fusion in terms of the operation described in [1, Appendix A] as

Inspired by [29], we propose the following graphical calculus for morphisms between cyclic fusions. The Hilbert space $[ H_1 \boxtimes _{R_1} \cdots \boxtimes _{R_{n-1}} H_n \boxtimes _{R_n} - ]_{\mathrm{cyclic}}$ corresponds to an arrangement of parallel strands (labeled by the various Hilbert spaces) on the surface of a cylinder. A string diagram on the cylinder represents a morphism:

We draw thick strands for the coarse bimodules and thin strands for the bimodules which are not coarse. For a morphism to be well defined, any horizontal plane intersecting the cylinder should cross at least two thick strands (and if the plane crosses through the middle of a coupon which is connected to at least one thick strand, then this coupon counts as one thick strand).

Later on in this paper, we will combine the above cylinder graphical calculus with the colored dots notation from (3).

3 Bicommutant categories

Let R be a hyperfinite factor, and let ${{\mathrm{Bim}}}(R)$ be the category of R–R-bimodules whose underlying Hilbert space is separable. The latter is a bi-involutive tensor category under the operation of Connes fusion, as discussed in Sect. 2.4.

Recall that a bi-involutive tensor functor between two bi-involutive tensor categories $\mathcal {C}$ and $\mathcal {D}$ is a quadruple $(F,\mu ,i,\upsilon )$, where $F:\mathcal {C}\rightarrow \mathcal {D}$ is a functor, and

$$\begin{aligned} \mu _{x,y}:F(x)\otimes _{\scriptscriptstyle \mathcal {D}} F(y)\rightarrow F(x\otimes _{\scriptscriptstyle \mathcal {C}} y),\quad i:1_\mathcal {D}\rightarrow F(1_\mathcal {C}),\quad \upsilon _x:F({\overline{x}}^{\scriptscriptstyle \mathcal {C}})\rightarrow \overline{F(x)}^{\scriptscriptstyle \mathcal {D}} \end{aligned}$$

are unitary isomorphisms.

Notation 3.1

Given a bi-involutive tensor category $\mathcal {C}$ and a bi-involutive tensor functor $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$, we will write

$$\begin{aligned} \mathcal {C}' := \mathcal {Z}^*_{{{\mathrm{Bim}}}(R)}(\mathcal {C}) \end{aligned}$$

for the unitary commutant of $\mathcal {C}$ in ${{\mathrm{Bim}}}(R)$.

There is an obvious bi-involutive tensor functor $\mathcal {C}'\rightarrow {{\mathrm{Bim}}}(R)$ given by forgetting the half-braiding. It therefore makes sense to consider the commutant of the commutant. There is also an “inclusion” functor $\iota :\mathcal {C}\rightarrow \mathcal {C}''$ from the category to its bicommutant. It sends an object $X\in \mathcal {C}$ to the object $(X,e'_X)\in \mathcal {C}''$ with half-braiding given by $e'_{X,(Y,e_Y)}:=e_{Y,X}^{-1}$ for $(Y,e_Y)\in \mathcal {C}'$. The coherence data $\mu$, i, $\upsilon$ for $\iota$ are all identity morphisms.

Definition 3.2

A bicommutant category is a bi-involutive tensor category $\mathcal {C}$ for which there exists a hyperfinite factor R and a bi-involutive tensor functor $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$, such that the “inclusion” functor $\iota :\mathcal {C}\rightarrow \mathcal {C}''$ is an equivalence.

If a bi-involutive tensor functor $\alpha :\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ is such that the corresponding “inclusion” functor $\iota$ is an equivalence, then we say that $\alpha$ exhibits $\mathcal {C}$ as a bicommutant category.

3.1 Representing tensor categories in ${{\mathrm{Bim}}}(R)$

A representation of a $*$-algebra A on a Hilbert space H is a $*$-algebra homomorphism $A\rightarrow B(H)$. By analogy, we define a representation of a bi-involutive tensor category $\mathcal {C}$ to be a bi-involutive tensor functor $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$, for some von Neumann algebra R. One can alternatively describe this as an action of $\mathcal {C}$ on the category $\mathrm {Mod}(R)$ of left R-modules.

Definition 3.3

A morphism between two representations $\alpha _1:\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R_1)$ and $\alpha _2:\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R_2)$ of $\mathcal {C}$ consists of an $R_2$–$R_1$-bimodule $\Phi$, along with unitary natural isomorphisms

$$\begin{aligned} \phi _X: \Phi \boxtimes _{R_1} \alpha _1(X) \rightarrow \alpha _2(X)\boxtimes _{R_2} \Phi \end{aligned}$$

for every $X\in \mathcal {C}$, subject to the coherence condition

A morphism $(\Phi ,\phi )$ between two representations is an equivalence if the bimodule $\Phi$ is invertible, or equivalently if the induced map $\mathrm {Mod}(R_1)\rightarrow \mathrm {Mod}(R_2)$ is an equivalence of categories.

A representation $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ is called fully faithful if non-isomorphic objects of $\mathcal {C}$ remain non-isomorphic in ${{\mathrm{Bim}}}(R)$, and if simple objects of $\mathcal {C}$ remain simple in ${{\mathrm{Bim}}}(R)$ (this agrees with the usual notion of fully faithfulness from category theory). In the next theorem, we will see that if we restrict the von Neumann algebra R to be a hyperfinite factor which is not of type $\mathrm I$, then every unitary fusion category admits a fully faithful representation in ${{\mathrm{Bim}}}(R)$. We begin with the following well-known lemma:

Lemma 3.4

Let R be a hyperfinite factor which is not of type $\mathrm{I}$, and let $R_{\mathrm{II}_1}$ be a hyperfinite $\mathrm{II}_1$-factor. Then, $R\,{\bar{\otimes }}\, R_{\mathrm{II}_1}\cong R$.

Proof

If R is either of type $\mathrm{II}_1$ or $\mathrm{II}_\infty$, then the result follows from the uniqueness of the hyperfinite $\mathrm{II}_1$ and $\mathrm{II}_\infty$ factors [23, Thm. XIV]. We may therefore assume that R is of type $\mathrm{III}$.

Let $\sigma :\mathbb {R}\rightarrow \mathrm {Aut}(R)$ be the modular flow of R. The flow of weights [5] is the dual action of $\mathbb {R}$ on the von Neumann algebra $S(R):=Z(R\rtimes _\sigma \mathbb {R})$.⁴ By the work of Connes [3], Haagerup [13], and Krieger [19] (see also [32, Chapt. XVIII] ), the map $R\mapsto S(R)$ establishes a bijective correspondence between isomorphism classes of hyperfinite type $\mathrm{III}$ factors, and isomorphism types of ergodic actions of $\mathbb {R}$ on abelian von Neumann algebras, provided one excludes the standard action of $\mathbb {R}$ on $L^\infty (\mathbb {R})$. (The latter is the flow of weights of the hyperfinite $\mathrm{II}_1$ and $\mathrm{II}_\infty$ factors.)

Given abelian von Neumann algebras $Z_1$ and $Z_2$ with actions of $\mathbb {R}$, we write $Z_1\wedge _\mathbb {R}Z_2:=(Z_1\,{\bar{\otimes }}\,Z_2)^{\mathbb {R}_\mathrm{diag}}$ for the fixed-point algebra with respect to $\mathbb {R}_\mathrm{diag}:=\{(t,-t):t\in \mathbb {R}\}\subset \mathbb {R}^2$, along with the residual $\mathbb {R}^2/\mathbb {R}_\mathrm{diag}$ action. The algebra $L^\infty (\mathbb {R})$ with its standard $\mathbb {R}$ action is a unit for that operation: $Z\wedge _\mathbb {R}L^\infty (\mathbb {R}) = Z$. Now, by [5, Cor. II.6.8], given two factors $M_1$ and $M_2$, there is a canonical isomorphism $S(M_1\,{\bar{\otimes }}\,M_2) \cong S(M_1) \wedge _\mathbb {R}S(M_2)$.⁵ It follows that

$$\begin{aligned} S(R\,{\bar{\otimes }}\, R_{\mathrm{II}_1}) \,\cong \, S(R) \wedge _\mathbb {R}S(R_{\mathrm{II}_1}) \,\cong \, S(R) \wedge _\mathbb {R}L^\infty (\mathbb {R}) \,\cong \, S(R). \end{aligned}$$

Using the Connes–Haagerup–Krieger classification theorem of hyperfinite type $\mathrm{III}$ factors, it follows that $R\,{\bar{\otimes }}\, R_{\mathrm{II}_1}\cong R$. $\square$

Theorem 3.5

Let R be a hyperfinite factor which is not of type $\mathrm{I}$. Then, every unitary fusion category $\mathcal {C}$ admits a fully faithful representation $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$.

Proof

Let $R_{\mathrm{II}_1}$ be a hyperfinite $\mathrm{II}_1$ factor. By the work of Popa [27, Thm. 3.1] (see also [8, Thm. 4.1]), there exists a fully faithful representation

$$\begin{aligned} \mathcal {C}\hookrightarrow {{\mathrm{Bim}}}(R_{\mathrm{II}_1}). \end{aligned}$$

Let now R be an arbitrary hyperfinite factor which is not of type $\mathrm{I}$. By Lemma 3.4, we have $R\,{\bar{\otimes }}\, R_{\mathrm{II}_1}\cong R$. We may therefore compose the above embedding with the map

$\square$

The above result raises the question of uniqueness. We believe that the following conjecture should follow straightforwardly from Popa’s uniqueness theorems for hyperfinite finite depth subfactors of types $\mathrm{II}_1$ [25, 26] and $\mathrm{III}_1$ [28]. However, we do not attempt to prove it here as it would take us too far afield.

Conjecture 3.6

Let $\mathcal {C}$ be a unitary fusion category, and let R be a hyperfinite factor which is either of type $\mathrm{II}_1$ or $\mathrm{III}_1$. Then, any two fully faithful representations $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ are equivalent in the sense of Definition 3.3.

4 The commutant of a fusion category

Throughout this section, we fix a factor R (not necessarily hyperfinite), a unitary fusion category $\mathcal {C}$, and a representation $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$. To simplify the notation, we will assume that the representation is fully faithful and identify $\mathcal {C}$ with its image in ${{\mathrm{Bim}}}(R)$, but the fully faithfulness condition is actually not required for the results of this section. It will however be needed later on, in Sect. 5.

4.1 Constructing objects in $\mathcal {C}'$

The goal of this section is to construct a functor

$$\begin{aligned} \quad \underline{\Delta }:{{\mathrm{Bim}}}(R)\rightarrow \mathcal {C}' \qquad \underline{\Delta }(\Lambda )=(\Delta (\Lambda ),e_{\Delta (\Lambda )}). \end{aligned}$$

For simplicity of notation, we will denote the underlying object $\Delta (\Lambda )$ of $\underline{\Delta }(\Lambda )$ simply by $\Delta$. It is given by

$$\begin{aligned} \Delta \, := \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x\boxtimes \Lambda \boxtimes \overline{x}\,. \end{aligned}$$

(9)

Note that this object does not depend, up to canonical unitary isomorphism, on the choice of representatives of the simple objects of $\mathcal {C}$.

For $a\in \mathcal {C}$, an irreducible object, the half-braiding $e_{\Delta ,a}:\Delta \boxtimes a\rightarrow a\boxtimes \Delta$, is given by

(10)

where the projection $\Delta \boxtimes a\rightarrow x\boxtimes \Lambda \boxtimes \overline{x}\boxtimes a$ and inclusion $a\boxtimes y\boxtimes \Lambda \boxtimes \overline{y}\rightarrow a\boxtimes \Delta$ are implicit in the notation. The half-braiding is natural with respect to morphisms $a\rightarrow a'$ between simple objects, and we extend it by additivity to all objects.

Proposition 4.1

$e_{\Delta }=(e_{\Delta ,a}:\Delta \boxtimes a\rightarrow a\boxtimes \Delta )_{a\in \mathcal {C}}$ is a unitary half-braiding.

Proof

The maps $e_{\Delta ,a}$ are natural in a by construction. To see that $e_{\Delta ,a}$ is unitary, we use the Bigon and Fusion relations:

The verification that $e_{\Delta ,a}\circ e_{\Delta ,a}^*={{\mathrm{id}}}_{a\boxtimes \Delta }$ is similar.

It remains to verify the “hexagon” axiom $e_{\Delta ,a\boxtimes b} = ({{\mathrm{id}}}_{a}\boxtimes e_{\Delta ,b}) \circ (e_{\Delta ,a}\boxtimes {{\mathrm{id}}}_{b}$). We do this with the help of the Fusion and I = H relations:

$\square$

Proposition 4.2

The assignment $\Lambda \mapsto (\Delta , e_\Delta )$ defines a functor ${{\mathrm{Bim}}}(R)\rightarrow \mathcal {C}'$.

Proof

Given a morphism $f: \Lambda _1 \rightarrow \Lambda _2$ in ${{\mathrm{Bim}}}(R)$, we let

$$\begin{aligned} \Delta (f) :=\, \sum {{\mathrm{id}}}_x\boxtimes f \boxtimes {{\mathrm{id}}}_{\overline{x}}\,:\,\Delta (\Lambda _1)\rightarrow \Delta (\Lambda _2). \end{aligned}$$

In order to check that this is a morphism in $\mathcal {C}'$, we need to verify that $e_{\Delta (\Lambda _2),a}\circ (\Delta (f)\boxtimes {{\mathrm{id}}}_a)=({{\mathrm{id}}}_a\boxtimes \Delta (f))\circ e_{\Delta (\Lambda _1),a}$. This is straightforward using the definition (10) of the half-braiding:

$\square$

Remark 4.3

The construction of $\underline{\Delta }(\Lambda )=(\Delta (\Lambda ),e_{\Delta (\Lambda )})$ works under the greater generality of a rigid C*-tensor category (in particular semisimple) represented in ${{\mathrm{Bim}}}(R)$, not necessarily fully faithfully. The half-braiding (10) is unitary by Proposition 4.1, and thus bounded.

4.2 The endomorphism algebra

In this section, we fix a bimodule $\Lambda \in {{\mathrm{Bim}}}(R)$. Our goal is to compute the endomorphism algebra of $\underline{\Delta }(\Lambda )$. As in the previous section, we will write $\Delta$ for the underlying object of $\underline{\Delta }(\Lambda )$.

Theorem 4.4

The map that sends

$$\begin{aligned} f\,=\,\,\big (f_a: \Lambda \boxtimes a \rightarrow a\boxtimes \Lambda \big )_{a\in {{\mathrm{Irr}}}(\mathcal {C})} \end{aligned}$$

to

induces a vector space isomorphism

$$\begin{aligned} \bigoplus _{a\in {{\mathrm{Irr}}}(\mathcal {C})} {{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}(\Lambda \boxtimes a, a\boxtimes \Lambda ) \,\,\cong \,\, {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda )). \end{aligned}$$

Under the above isomorphism, the left-hand side acquires the following $*$-algebra structure: The $*$-operation is given by

(11)

and the product is given by

(12)

Remark 4.5

The map $f_{\overline{a}}:\Lambda \boxtimes \overline{a} \rightarrow \overline{a}\boxtimes \Lambda$, which appears in the right-hand side of (11) requires the choice of an isomorphism between $\overline{a}$ and the unique element of ${{\mathrm{Irr}}}(\mathcal {C})$ to which it is isomorphic. It is important to note that, because $\overline{a}$ appears in both the domain and the codomain, the map $f_{\overline{a}}$ does not depend on that choice.

Remark 4.6

If we take $\Lambda =\bigoplus _{x\in {{\mathrm{Irr}}}(C)} x$, then the two Eqs. (11) and (12) are exactly the ones describing Ocneanu’s tube algebra [7, 16].

Proof of Theorem 4.4

We begin by checking, using the I = H relation, that the formula $({{\mathrm{id}}}_b\boxtimes T_f)\circ e_{\Delta ,b}=e_{\Delta ,b}\circ (T_f\boxtimes {{\mathrm{id}}}_b)$ holds:

This ensures that $T_f\in {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$.

We now show that the map $\bigoplus _{a\in Irr(\mathcal {C})} {{\mathrm{Hom}}}(\Lambda \boxtimes a, a\boxtimes \Lambda ) \rightarrow {{\mathrm{End}}}_{\mathcal {C}'}(\Delta )$ given by $f\mapsto T_f$ is an isomorphism. For that, we define a map the other way as follows. It sends $T\in {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$ to the element $f_T =(f_{T,a}: \Lambda \boxtimes a \rightarrow a \boxtimes \Lambda )$ given by

We now check that these two maps are each other’s inverses. The equation $f_{T_f}=f$ is an easy consequence of Lemma 2.17:

For the other direction, we need to check that $T_{f_T}=T$ holds for every $T\in {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$:

Here, we have used the I = H relation, followed by the fact that T commutes with (a scalar multiple of) the half-braiding, and finally Lemma 2.17.

At last, we check that the isomorphism $\bigoplus _{a\in {{\mathrm{Irr}}}(\mathcal {C})} {{\mathrm{Hom}}}(\Lambda \boxtimes a, a\boxtimes \Lambda ) \cong {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$ is compatible with the $*$-operation (11) and the multiplication (12):

Here, the last line’s middle equality follows from the I = H relation. $\square$

Remark 4.7

The map $f\mapsto T_f:\bigoplus _{a\in {{\mathrm{Irr}}}(\mathcal {C})} {{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}(\Lambda \boxtimes a, a\boxtimes \Lambda )\rightarrow {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$ makes sense in the greater generality of a rigid C*-tensor category represented in ${{\mathrm{Bim}}}(R)$. In particular, the operator $T_f$ is always bounded (this follows from being unitary, and hence bounded).

5 Absorbing objects

A tensor category $\mathcal {C}$ has no zero-divisors if for every nonzero object X and every objects $Y_1, Y_2$, the maps

$$\begin{aligned} {{\mathrm{Hom}}}(Y_1,Y_2)\rightarrow {{\mathrm{Hom}}}(X\otimes Y_1,X\otimes Y_2) \quad \text {and}\quad {{\mathrm{Hom}}}(Y_1,Y_2)\rightarrow {{\mathrm{Hom}}}(Y_1\otimes X,Y_2\otimes X) \end{aligned}$$

are injective. Note that for categories with involutions, it is enough to check that one of the above maps is injective.

Example 5.1

The tensor category ${{\mathrm{Bim}}}(R)$ has no zero-divisors. Indeed, since R is a factor, every nonzero module is faithful, and the claim follows from Lemma 2.13.

Example 5.2

Fusion categories have no zero-divisors. To see that, consider an object X and a morphism $f:Y_1\rightarrow Y_2$ such that ${{\mathrm{id}}}_X\otimes f=0$. We need to show that $X\not \cong 0$ implies $f=0$. Since X is nonzero, ${{\mathrm{ev}}}_X$ is an epimorphism (indeed a projection onto a direct summand). The morphism ${{\mathrm{ev}}}_X\otimes {{\mathrm{id}}}_{Y_1}$ is then also an epimorphism, and we may reason as follows:

$$\begin{aligned} f\circ (\underbrace{{{\mathrm{ev}}}_X\otimes {{\mathrm{id}}}_{Y_1}}_{\text {epi.}}) = {{\mathrm{ev}}}_X\otimes f = ({{\mathrm{ev}}}_X\otimes 1_{Y_2})\circ ({{\mathrm{id}}}_{X^\vee }\otimes \underbrace{{{\mathrm{id}}}_X\otimes f}_{=0})=0 \;\;\Rightarrow \;\; f=0. \end{aligned}$$

Definition 5.3

Let $\mathcal {C}$ be a tensor category with no zero-divisors. A nonzero object X is called

• right absorbing if for every nonzero object $Y\in \mathcal {C}$, we have $X\otimes Y\cong X$,

• left absorbing if for every nonzero object $Y\in \mathcal {C}$, we have $Y\otimes X\cong X$, and

• absorbing if X is both right and left absorbing.

Clearly, if $\mathcal {C}$ admits an absorbing object, then such an object is unique up to (non-canonical) isomorphism. Note also that if a category has both right absorbing and left absorbing objects, then any such object is in fact absorbing.

If $\mathcal {C}$ is equipped with a conjugation, then X is right absorbing if and only if $\overline{X}$ is left absorbing. In this case, any right absorbing object is automatically absorbing, and isomorphic to its conjugate. By taking $Y=1\oplus 1$, we can also readily see that any absorbing object satisfies $X\oplus X \cong X$.

Let $\mathsf {Hilb}$ be the category of separable Hilbert spaces.

Example 5.4

The Hilbert space $\ell ^2(\mathbb N)$ is absorbing in $\mathsf {Hilb}$.

Example 5.5

If $\mathcal {C}$ is a unitary fusion category, then the object

$$\begin{aligned} \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x\otimes \ell ^2(\mathbb N) \end{aligned}$$

of $\mathcal {C}\otimes _{\mathsf {Vec}}\mathsf {Hilb}$ is absorbing. Indeed, for any simple objects y and z of $\mathcal {C}$, there exists an x such that z occurs as a summand of $x\otimes y$. The object $y\otimes (\bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x)$ therefore contains each simple object at least once. It follows that $y\otimes (\bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x\otimes \ell ^2(\mathbb N))$ contains each simple object infinitely many times. The same remains true when y gets replaced by an arbitrary nonzero object of $\mathcal {C}\otimes _{\mathsf {Vec}}\mathsf {Hilb}$.

Example 5.6

Let G be an infinite countable group, and let $\mathsf{Rep}(G)$ denote the category of unitary representation of G whose underlying Hilbert spaces is separable. Then,

$$\begin{aligned} \ell ^2(G)\otimes \ell ^2(\mathbb N) \end{aligned}$$

is absorbing in $\mathsf{Rep}(G)$. Indeed, if V is a unitary representation with orthonormal basis $\{v_i\}_{i\in I}$, then $e_g\otimes e_i \mapsto (g\cdot v_i)\otimes e_g$ defines a unitary isomorphism $\ell ^2(G)\otimes \ell ^2(I)\rightarrow V\otimes \ell ^2(G)$. It follows that $V\otimes \ell ^2(G)\otimes \ell ^2(\mathbb N)\cong \ell ^2(G)\otimes \ell ^2(I\times \mathbb {N})\cong \ell ^2(G)\otimes \ell ^2(\mathbb N)$.

Let R be a separable factor, and let ${{\mathrm{Bim}}}(R)$ be the category of R–R-bimodules whose underlying Hilbert space is separable. Let also $\mathrm {Mod}(R)$ be the category of left R-modules whose underlying Hilbert space is separable. We say that $H\in \mathrm {Mod}(R)$ is infinite if it is nonzero and satisfies $H\oplus H\cong H$. It is well known that an infinite module exists and is unique up to isomorphism.

Example 5.7

The bimodule

$$\begin{aligned} {_{R}L^2(R)}\otimes \ell ^2(\mathbb {N}) \otimes L^2(R)_R \end{aligned}$$

is absorbing in ${{\mathrm{Bim}}}(R)$. To see that, let $_{R}H_R \in {{\mathrm{Bim}}}(R)$ be any nonzero bimodule. The following two modules are infinite, and therefore isomorphic: $_{R} H \boxtimes _R L^2(R) \otimes \ell ^2(\mathbb {N})$ and ${_{R}L^2(R)} \otimes \ell ^2(\mathbb {N})$. It follows that $_{R} H \boxtimes _R L^2(R) \otimes \ell ^2(\mathbb {N})\otimes L^2(R)_R \,\cong \, {_{R}L^2(R)} \otimes \ell ^2(\mathbb {N})\otimes L^2(R)_R$.

Remark 5.8

If we had taken ${{\mathrm{Bim}}}(R)$ to be the category of all bimodules, with no restriction on cardinality, then it would not admit an absorbing object (and similarly for the previous examples).

Absorbing objects are useful because they control half-braidings:

Proposition 5.9

Let $\Omega$ be an absorbing object of $\mathcal {C}$, and let $(X,e_X)$ be an object of $\mathcal {C}'$. Then, $e_X$ is completely determined by its value on $\Omega$.

Proof

Let Y be a nonzero object of $\mathcal {C}$. Since $e_X$ is a half-braiding, we have a commutative diagram

Fix an isomorphism $\phi :Y\boxtimes \Omega \rightarrow \Omega$. The following square is commutative

and so we get an equation

$$\begin{aligned} e_{X,Y}\boxtimes {{\mathrm{id}}}_\Omega =({{\mathrm{id}}}_Y\boxtimes e_{X,\Omega }^{-1})\circ (\phi ^{-1} \boxtimes {{\mathrm{id}}}_X)\circ e_{X,\Omega }\circ ({{\mathrm{id}}}_X \boxtimes \phi ). \end{aligned}$$

In particular, we see that $e_{X,Y}\boxtimes {{\mathrm{id}}}_\Omega$ is completely determined by $e_{X,\Omega }$. Since ${{\mathrm{Bim}}}(R)$ has no zero-divisors, $e_{X,Y}$ is completely determined by $e_{X,Y}\boxtimes {{\mathrm{id}}}_\Omega$. Putting those two facts together, we see that $e_{X,Y}$ is completely determined by $e_{X,\Omega }$. $\square$

5.1 The absorbing object of $\mathcal {C}'$

We now return to our usual setup, which is that of a separable factor R equipped with a fully faithful representation $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ of some unitary fusion category $\mathcal {C}$. Our next goal is to show that $\mathcal {C}'$ admits absorbing objects. Recall the construction

$$\begin{aligned} \quad \underline{\Delta }:{{\mathrm{Bim}}}(R)\rightarrow \mathcal {C}' \qquad \underline{\Delta }(\Lambda )=(\Delta (\Lambda ),e_{\Delta (\Lambda )}) \end{aligned}$$

from Sect. 4.1.

Theorem 5.10

The functor $\underline{\Delta }$ sends absorbing objects to absorbing objects. In particular, the category $\mathcal {C}'$ admits absorbing objects.

The proof of this theorem will depend on Theorem 5.12, proved in next section, according to which the endomorphism algebra of $\underline{\Delta }(\Lambda )$ is a factor whenever $\Lambda$ is absorbing in ${{\mathrm{Bim}}}(R)$. We begin with the following technical lemma:

Lemma 5.11

Suppose that $\underline{\Omega }=(\Omega , e_\Omega )\in \mathcal {C}'$ is such that $\Omega$ is absorbing in ${{\mathrm{Bim}}}(R)$, and such that $\underline{\Omega }\oplus \underline{\Omega }\;\!\cong \;\! \underline{\Omega }$ in $\mathcal {C}'$. Then, $\underline{\Omega }$ is (non-canonically) isomorphic to $\underline{\Delta }(\Omega )$.

Proof

Let $\varphi :\Omega \rightarrow \Delta (\Omega )$ be the map given by

By the fusion relation, this map is compatible with the half-braidings:

and therefore defines a morphism $\varphi :\underline{\Omega }\rightarrow \underline{\Delta }(\Omega )$ in $\mathcal {C}'$.

The coevaluation map $\mathrm {coev}_x:L^2R\rightarrow x\boxtimes \overline{x}$ is, up to a constant, the inclusion of a direct summand. So $\varphi$ is manifestly injective. By polar decomposition in $\mathcal {C}'$, the map $\varphi$ therefore induces a unitary isomorphism between $\underline{\Omega }$ and a certain subobject of $\underline{\Delta }(\Omega )$.

Now, the subobjects of $\underline{\Delta }(\Omega )$ are in one-to-one correspondence with the projections in $M:={{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Omega ))$, which is a factor by Theorem 5.12. Let $p\in M$ be the projection corresponding to $\underline{\Omega }$. Since $\underline{\Omega }\oplus \underline{\Omega }\cong \underline{\Omega }$ and $\underline{\Omega }\ne 0$, that projection is infinite (its range is an infinite module). So there is a partial isometry $u\in M$ with $p=uu^*$ and $u^*u=1$. The latter provides an isomorphism $u:\underline{\Delta }(\Omega )\rightarrow \underline{\Omega }$ in $\mathcal {C}'$. $\square$

Proof of Theorem 5.10

Let $\Lambda$ be an absorbing object of ${{\mathrm{Bim}}}(R)$, and let X be an arbitrary nonzero object of $\mathcal {C}'$. We wish to show that $\underline{\Omega }:=\underline{\Delta }(\Lambda )\boxtimes X$ is isomorphic to $\underline{\Delta }(\Lambda )$. Let $\Omega$ denote the underlying object of $\underline{\Omega }$. If we could show that $\underline{\Omega }$ satisfies the hypotheses of Lemma 5.11, then we could reason as follows:

$$\begin{aligned} \underline{\Delta }(\Lambda )\boxtimes X\,=\,\,\underline{\Omega }\,\,\cong \,\,\underline{\Delta }(\Omega ) \,\,\cong \,\, \underline{\Delta }(\Lambda ), \end{aligned}$$

where the last isomorphism holds because $\Omega$ and $\Lambda$ are both absorbing in ${{\mathrm{Bim}}}(R)$.

So let us show that $\underline{\Omega }$ satisfies the hypotheses of Lemma 5.11. Since $\Lambda$ is absorbing in ${{\mathrm{Bim}}}(R)$, the object $\Omega =\bigoplus _x x\boxtimes \Lambda \boxtimes \overline{x}\boxtimes X$ is clearly absorbing in ${{\mathrm{Bim}}}(R)$. And since $\Lambda \oplus \Lambda \cong \Lambda$ in ${{\mathrm{Bim}}}(R)$ and $\Lambda \mapsto \underline{\Delta }(\Lambda )\boxtimes X$ is a linear functor, the same holds true for $\underline{\Omega }$, namely $\underline{\Omega }\oplus \underline{\Omega }\;\!\cong \;\! \underline{\Omega }$.$\square$

5.2 The endomorphism algebra is a factor

The goal of this section is to prove that when $\Lambda$ is absorbing, the endomorphism algebra of $\underline{\Delta }(\Lambda )$ is a factor (a von Neumann algebra with trivial center). We emphasize the fact that, for the above result to hold, it is essential that the representation $\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ be fully faithful (this is used in the last paragraph of the proof of Theorem 5.13).

Theorem 5.12

If $\Lambda$ is absorbing in ${{\mathrm{Bim}}}(R)$, then ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$ is a factor.

It will be easier to prove the following stronger result:

Theorem 5.13

If $\Lambda$ is absorbing, then ${{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda )$ has trivial commutant in ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$. In other words, the inclusion

$$\begin{aligned} {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda )\subset {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda )) \end{aligned}$$

(13)

is an irreducible subfactor.

Proof

The absorbing object is unique up to isomorphism. So without loss of generality, we may take $\Lambda$ to be the one from example 5.7, namely $\Lambda ={_{R}L^2(R)}\otimes \ell ^2(\mathbb {N}) \otimes L^2(R)_R.$ Let

$$\begin{aligned} \Lambda _0:={_{R}L^2R} \otimes L^2R_R. \end{aligned}$$

Writing H for $\ell ^2(\mathbb {N})$, we have

$$\begin{aligned} {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda )\,&\cong \, {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _0)\,{\bar{\otimes }}\,B(H)\quad \text {and}&{{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))\,&\cong \,{{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _0))\,{\bar{\otimes }}\,B(H), \end{aligned}$$

and so $Z_{{{\mathrm{End}}}(\underline{\Delta }(\Lambda ))}({{\mathrm{End}}}(\Lambda ))\cong Z_{{{\mathrm{End}}}(\underline{\Delta }(\Lambda _0))}({{\mathrm{End}}}(\Lambda _0))$. It is therefore equivalent to prove the statement of the theorem for $\Lambda _0$ instead of $\Lambda$. Recall from Theorem 4.4 that

$$\begin{aligned} {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _0)) \,\,\cong \,\, \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} {{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _0\boxtimes x, x\boxtimes \Lambda _0), \end{aligned}$$

with product as in (12).

Let $f=(f_x: \Lambda _0 \boxtimes x \rightarrow x\boxtimes \Lambda _0)_{x\in {{\mathrm{Irr}}}(\mathcal {C})}$ be an element that commutes with every $g\in {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _0)=R^{\text {op}}\,{\bar{\otimes }}\,R$:

(14)

The bimodule $\Lambda _0$ is of the form (8), and thus coarse. The action of the algebraic tensor product $R\odot R^{\text {op}}$ (the one which equips it with the structure of an R–R-bimodule) therefore extends to an action of the spatial tensor product $R\,{\bar{\otimes }}\, R^{\text {op}}$. We may therefore treat $\Lambda _0$ as a left $(R\,{\bar{\otimes }}\, R^{\text {op}})$-module. Writing 1 for $L^2(R)$, we then have canonical isomorphisms

$$\begin{aligned} {}_R(x\boxtimes _R\Lambda _0)_R&\,\cong \, {}_{R{\bar{\otimes }} R^\mathrm {op}}((x\otimes 1)\boxtimes _{R{\bar{\otimes }} R^\mathrm {op}}\Lambda _0) \\ {}_R(\Lambda _0\boxtimes _R x)_R&\,\cong \, {}_{R{\bar{\otimes }} R^\mathrm {op}} ((1\otimes x)\boxtimes _{R{\bar{\otimes }} R^\mathrm {op}}\Lambda _0). \end{aligned}$$

Under those identifications, Eq. (14) becomes:

(15)

where , and we have used the string diagram notation for bicategories reviewed in [2, §2] .

Note that $\Lambda _0 = L^2(R{\bar{\otimes }} R^\mathrm {op})$. We may therefore identify $(x\otimes 1)\boxtimes _{R{\bar{\otimes }} R^\mathrm {op}}\Lambda _0$ with $x\otimes 1$, and $(1\otimes x)\boxtimes _{R{\bar{\otimes }} R^\mathrm {op}}\Lambda _0$ with $1\otimes x$. The maps $f_x$ can then be viewed as left $(R\,{\bar{\otimes }}\, R^{\text {op}})$-module maps:

$$\begin{aligned} f_x: 1\otimes x \rightarrow x\otimes 1. \end{aligned}$$

The operators ${{\mathrm{id}}}_{1\otimes x}\boxtimes g$ and ${{\mathrm{id}}}_{x\otimes 1}\boxtimes g$ which appear on the two sides of (15) are nothing else than the right actions of $g\in R\,{\bar{\otimes }}\, R^{\text {op}}$ on $1\otimes x$ and on $x\otimes 1$, and so Eq. (15) is just the statement that $f_x$ is a right $(R\,{\bar{\otimes }}\, R^{\text {op}})$-module map. Each $f_x$ is therefore both a left $(R\,{\bar{\otimes }}\, R^{\text {op}})$-module and a right $(R\,{\bar{\otimes }}\, R^{\text {op}})$-module map.

But $1\otimes x$ and $x\otimes 1$ are irreducible $(R\,{\bar{\otimes }}\, R^{\text {op}})$–$(R\,{\bar{\otimes }}\, R^{\text {op}})$-bimodules, and $1\otimes x\not \cong x\otimes 1$ unless $x=1$. The maps $f_x$ can therefore only be nonzero when $x=1$, in which case it must be a scalar. $\square$

Let us now assume that $\Lambda$ is a coarse bimodule, and that it is given to us as the tensor product of a left R-modules with a right R-module:

$$\begin{aligned} \Lambda ={}_RH\otimes _{\mathbb {C}} K_R\,. \end{aligned}$$

Then, we have ${{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda )={{\mathrm{End}}}({}_RH)\,{\bar{\otimes }}\,{{\mathrm{End}}}(K_R)$, and the subfactor (13) is of the form

$$\begin{aligned} {{\mathrm{End}}}({}_RH)\,{\bar{\otimes }}\,{{\mathrm{End}}}(K_R)\,\subset \, {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda )). \end{aligned}$$

Proposition 5.14

The algebras ${{\mathrm{End}}}({}_RH)$ and ${{\mathrm{End}}}(K_R)$ are each other’s relative commutants in ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$.

Proof

We will only prove that $Z_{{{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))}({{\mathrm{End}}}({}_RH))={{\mathrm{End}}}(K_R)$. The other claim is symmetric and can be proved in a completely analogous way.

Let $b\in {{\mathrm{End}}}({}_RH)$ be an endomorphism of H, and let f be an element of ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$. Let $f_a:\Lambda \boxtimes a\rightarrow a \boxtimes \Lambda$ be the maps which correspond to $f\in {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$ under the bijection established in Theorem 4.4. The statement that b and f commute is then equivalent to the statement that for every $a\in {{\mathrm{Irr}}}(\mathcal {C})$, the following equality holds in ${{\mathrm{Hom}}}(H\otimes _{\mathbb C}K\boxtimes _R a,a\boxtimes _R H\otimes _{\mathbb C}K)$:

Treating K as a left $R^{{{\mathrm{op}}}}$-module and letting $R'$ be the commutant of R on H (so that H is an R–$R'{}^{{{\mathrm{op}}}}$-bimodule), we may “fold” the above diagram (as we did to get (15)):

where . It follows that $f_a$ is not just in

$$\begin{aligned}&{{\mathrm{Hom}}}_{R\,{\bar{\otimes }}\, R^{\text {op}}}\big ( (1\otimes a)\boxtimes _{R\,{\bar{\otimes }}\, R^{\text {op}}}(H\otimes K), (a\otimes 1)\boxtimes _{R\,{\bar{\otimes }}\, R^{\text {op}}}(H\otimes K) \big )\\&\quad =\,{{\mathrm{Hom}}}_{R}(L^2R\boxtimes _R H,a\boxtimes _RH)\,{\bar{\otimes }}\, {{\mathrm{Hom}}}_{R^{{{\mathrm{op}}}}}(a\boxtimes _{R^{{{\mathrm{op}}}}} K,L^2R\boxtimes _{R^{{{\mathrm{op}}}}}K), \end{aligned}$$

but actually in

$$\begin{aligned} {{\mathrm{Hom}}}_{R,R'{}^{{{\mathrm{op}}}}}\big (L^2R\boxtimes _R H,a\boxtimes _RH\big ) \,{\bar{\otimes }}\, {{\mathrm{Hom}}}_{R^{{{\mathrm{op}}}}}\big (a\boxtimes _{R^{{{\mathrm{op}}}}} K,L^2R\boxtimes _{R^{{{\mathrm{op}}}}}K\big ). \end{aligned}$$

But H is an invertible R–$R'{}^{{{\mathrm{op}}}}$-bimodule, and so

$$\begin{aligned} {{\mathrm{Hom}}}_{R,R'{}^{{{\mathrm{op}}}}}(L^2R\boxtimes _R H,a\boxtimes _RH) ={{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}(1,a). \end{aligned}$$

It follows that $f_a=0$ unless $a=1$, in which case $f\in {{\mathrm{Hom}}}_{R^{{{\mathrm{op}}}}}\big (K,K\big )={{\mathrm{End}}}(K_R)$. $\square$

Remark 5.15

Proposition 5.14 implies Theorems 5.12 and 5.13. It shows that, among other things, these two theorems hold in the greater generality of $\Lambda$ a coarse bimodule (as opposed to merely absorbing).

5.3 Algebras acting on cyclic fusions

Let $\Lambda _1$ and $\Lambda _2$ be coarse bimodules. In Sect. 4.2, we computed the endomorphism algebra of $\underline{\Delta }(\Lambda _1)=(\Delta (\Lambda _1),e_{\Lambda _1})\in \mathcal {C}'$. Our next task is to compute the commutant of ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _1))$ on the cyclic fusion

$$\begin{aligned} \qquad \Big [ \Delta (\Lambda _1) \boxtimes \Lambda _2 \boxtimes - \Big ]_{\text {cyclic}} = \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} \Big [ x \boxtimes \Lambda _1 \boxtimes \overline{x} \boxtimes \Lambda _2 \boxtimes - \Big ]_{\text {cyclic}} \end{aligned}$$

We first note that there is a commuting action of ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _2))$ on that same Hilbert space:

Here, we have used Theorem 4.4 in order to write a generic element of ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _1))$ as a sum of operators of the form , and similarly for ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _2))$. We have then used the I = H relation to show that the resulting operators commute. We have also secretly used the existence of a canonical isomorphism

$$\begin{aligned} \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} \overline{x}\boxtimes \Lambda _2 \boxtimes x \,\,\cong \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x\boxtimes \Lambda _2 \boxtimes \overline{x}. \end{aligned}$$

(16)

(At first sight, this looks like is might depend on the choice of isomorphisms between each $\overline{x}$ and the corresponding object of ${{\mathrm{Irr}}}(\mathcal {C})$. But as each $\overline{x}$ appears next to an x, the isomorphism (16) is independent of those choices.)

Lemma 5.16

Let $\Lambda _1$ and $\Lambda _2$ be coarse bimodules. Then, $N_1={{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _1)$ and $N_2={{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _2)$ are each other’s commutants on $\big [ \Lambda _1 \boxtimes _R \Lambda _2 \boxtimes _R - \big ]_{\mathrm{cyclic}}$.

Proof

The algebra $N_1$ is the commutant of $R\,{\bar{\otimes }}\,R^{\text {op}}$ on $\Lambda _1$. By Lemma 2.12, the latter is therefore invertible as an $N_1$-$(R^{\text {op}}\,{\bar{\otimes }}\,R)$-bimodule. Similarly, $\Lambda _2$ is invertible as an $(R^{\text {op}}\,{\bar{\otimes }}\,R)$-$N_2$-bimodule. It follows that

$$\begin{aligned} \big [ \Lambda _1 \boxtimes _R \Lambda _2 \boxtimes _R - \big ]_{\text {cyclic}}=\,\Lambda _1 \boxtimes _{R^{\text {op}}\,{\bar{\otimes }}\,R} \Lambda _2 \end{aligned}$$

is an invertible $N_1$–$N_2^{\text {op}}$-bimodule. $\square$

Proposition 5.17

Let $\Lambda _1$ and $\Lambda _2$ be coarse bimodules. Then, $M_1={{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _1))$ and $M_2={{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _2))$ are each other’s commutants on $H=\bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} \big [ x \boxtimes \Lambda _1 \boxtimes \overline{x} \boxtimes \Lambda _2 \boxtimes - \big ]_{\mathrm{cyclic}}$.

Proof

Let f be in $M_2'$. Since f commutes with ${{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _2)\subset M_2$, it follows from Lemma 5.16 that $f\in {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Delta (\Lambda _1))$. We therefore have the following situation:

(17)

It remains to show that f commutes with the half-braiding. Write $\Lambda _2$ as ${}_R(H_2)\otimes _{\mathbb {C}} (H_1)_R$, for some right/left R-modules $H_1$ and $H_2$. We then have a canonical isomorphism

$$\begin{aligned} \big [ x \boxtimes \Lambda _1 \boxtimes \overline{x} \boxtimes \Lambda _2 \boxtimes - \big ]_{\text {cyclic}} =\, H_1\boxtimes x \boxtimes \Lambda _1 \boxtimes \overline{x} \boxtimes H_2. \end{aligned}$$

Taking g of the form

for R-module maps $v:H_2\rightarrow a\boxtimes H_2$ and $u:H_1\boxtimes a\rightarrow H_1$, Eq. (17) becomes:

This being true for any u and v, it follows that

Finally, fusing with $H_1$ and $H_2$ are faithful operations by Lemma 2.13, and so the above equation implies $e_{\Delta (\Lambda _1),a}\circ (f\boxtimes {{\mathrm{id}}}_a)=({{\mathrm{id}}}_a\boxtimes f)\circ e_{\Delta (\Lambda _1),a}$, as desired.$\square$

6 Proof of the main theorem

Let $\mathcal {C}$ be a unitary fusion category, and let $\alpha :\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ be a fully faithful representation. Then, $\alpha$ extends to a functor

$$\begin{aligned} \alpha ^{\mathsf{Hilb}}\,:\,\,\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}\,&\,\rightarrow \,\,\,{{\mathrm{Bim}}}(R) \\ \textstyle \bigoplus x_i\otimes H_i\,&\mapsto \, \textstyle \bigoplus \alpha (x_i)\otimes H_i. \end{aligned}$$

Here, the first “$-\otimes H_i$” is formal (as defined in Sect. 2.2), whereas the second one is evaluated in ${{\mathrm{Bim}}}(R)$.

Lemma 6.1

The restriction functor $(\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb})'\rightarrow \mathcal {C}'$ is an equivalence.

Proof

Given an object $(X,e_X)\in \mathcal {C}'$, we can extend the half-braiding $e_X=(e_{X,y}:X\otimes y\rightarrow y\otimes X)_{y\in \mathcal {C}}$ to arbitrary objects $Y=\bigoplus y_i\otimes H_i$ of $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ by

The half-braiding $e_{X,Y}$ is completely determined from the $e_{X,y_i}$ by naturality, and so the functor $(\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb})'\rightarrow \mathcal {C}'$ is a bijection on objects. To finish the argument, we note that again by naturality, given two objects $(X_1,e_{X_1})$ and $(X_2,e_{X_2})$ in $\mathcal {C}'$, a map $f:X_1\rightarrow X_2$ is a morphism $(X_1,e_{X_1})\rightarrow (X_2,e_{X_2})$ in $\mathcal {C}'$ if and only if it is a morphism between the corresponding objects of $(\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb})'$. $\square$

Theorem

(Theorem A) Let $\mathcal {C}$ be a unitary fusion category, and let $\alpha :\mathcal {C}\rightarrow {{\mathrm{Bim}}}(R)$ be a fully faithful representation. Then, $\alpha ^{\mathsf{Hilb}}$ exhibits $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ as a bicommutant category.

Proof

We will show that $\mathcal {C}''$ is equivalent to $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$. The result will then follow since $\mathcal {C}''=(\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb})''$ by Lemma 6.1. We first note that the “inclusion” functor $\iota :\mathcal {C}\rightarrow \mathcal {C}''$ (described in Sect. 3)

extends to a functor

$$\begin{aligned} \iota ^{\mathsf{Hilb}}\,:\,\,\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}\,&\,\rightarrow \,\,\,\mathcal {C}'' \\ \textstyle \bigoplus x_i\otimes H_i\,&\mapsto \, \textstyle \bigoplus \iota (x_i)\otimes H_i \end{aligned}$$

where the first “$-\otimes H_i$” is formal, and the second is evaluated in $\mathcal {C}''$.

• The functor $\iota ^{\mathsf{Hilb}}$ is fully faithful:

The functor is fully faithful on simple objects, since their images remain simple in $\mathcal {C}''$. Indeed, they remain simple in ${{\mathrm{Bim}}}(R)$, and therefore also in $\mathcal {C}''$. For finite sums of simple objects, fully faithfulness follows by additivity. For the remaining objects, we have

$$\begin{aligned} {{\mathrm{Hom}}}_{\mathcal {C}''} \Big ({\textstyle \bigoplus _i}\, \iota (x_i)\otimes H_i, {\textstyle \bigoplus _j}\, \iota (y_j)\otimes K_j\Big )&= \bigoplus _{ij} {{\mathrm{Hom}}}_{\mathcal {C}''}\!\big (\iota (x_i),\iota (y_j)\big )\otimes _\mathbb {C}\mathsf{Hilb}(H_i,K_j) \\&= \bigoplus _{ij} {{\mathrm{Hom}}}_{\mathcal {C}}(x_i,y_j)\otimes _\mathbb {C}\mathsf{Hilb}(H_i,K_j)\\&={{\mathrm{Hom}}}_{\,\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}} \Big ({\textstyle \bigoplus _i}\, x_i\otimes H_i, {\textstyle \bigoplus _j}\, y_j\otimes K_j\Big ), \end{aligned}$$

where we have used the finite dimensionality of ${{\mathrm{Hom}}}_{\mathcal {C}''}(\iota (x_i),\iota (y_j))$ in the first equality.

• The functor $\iota ^{\mathsf{Hilb}}$ is essentially surjective:

Let $\underline{\Omega }\in \mathcal {C}'$ be an absorbing object. The proof splits into three steps:

• 1. If $(X,e_X)$ is an object of $\mathcal {C}''$, then its underlying bimodule X lies in $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$ (the essential image of $\iota ^{\mathsf{Hilb}}$).

• 2. Let $(X,e_X^{\scriptscriptstyle (1)})$ and $(X,e_X^{\scriptscriptstyle (2)})\in \mathcal {C}''$ be two objects with same underlying bimodule X. Then, $e_{X,\underline{\Omega }}^{\scriptscriptstyle (1)}=e_{X,\underline{\Omega }}^{\scriptscriptstyle (2)}$.

• 3. Given an object $(X,e_X)\in \mathcal {C}''$, then $e_X=\big (e_{X,\underline{Y}}:X\boxtimes Y\rightarrow Y\boxtimes X\big )_{\underline{Y}=(Y,e_Y)\in \mathcal {C}'}$ is uniquely determined by $e_{X,\underline{\Omega }}$.

These are proven in Propositions 6.2, 6.4, and 5.9, respectively.$\square$

Proposition 6.2

The underlying bimodule of an object of $\mathcal {C}''$ lies in $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$.

Proof

Let $\Lambda _0:={}_RL^2(R)\otimes L^2(R)_R$, and let $(\Delta _0,e_{\Delta _0}):=\underline{\Delta }(\Lambda _0)$. Given an object $(X,e_X)$ of $\mathcal {C}''$, the half-braiding $e_X$ yields a bimodule map

$$\begin{aligned} e\,:=\,e_{X,\underline{\Delta }(\Lambda _0)}: X\boxtimes _R \Delta _0\rightarrow \Delta _0\boxtimes _R X \end{aligned}$$

which, after rewriting

$$\begin{aligned} X\boxtimes _R \Delta _0 \,&= X\boxtimes _R\Big (\bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y\boxtimes _R \Lambda _0\boxtimes _R \overline{y} \Big )\\&= \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} X\boxtimes _R y\boxtimes _R L^2R\otimes L^2R\boxtimes _R \overline{y}\\&= \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} \big (X\boxtimes _R y\big )\otimes \overline{y}\quad \,\,\, \text {and}\\ \Delta _0\boxtimes _R X\,&= \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y\otimes \big (\overline{y}\boxtimes _R X\big ), \end{aligned}$$

becomes a map

$$\begin{aligned} e\,:\,\, \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} \big (X\boxtimes _R y\big )\otimes \overline{y} \,\rightarrow \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y\otimes \big (\overline{y}\boxtimes _R X\big ). \end{aligned}$$

The Hilbert spaces $(X\boxtimes _R y)\otimes \overline{y}$ and $y\otimes (\overline{y}\boxtimes _R X)$ each have four actions of R, two left actions, and two right actions:

In order to keep track of all these copies of R, we denote them $R_1$, $R_2$, $R_3$, $R_4$, respectively.

The map e is a morphism in ${{\mathrm{Bim}}}(R)$, meaning that it is an $R_1$–$R_4$-bimodule map. This map also has the property of being natural with respect to endomorphisms of $\underline{\Delta }(\Lambda _0)$. Restricting attention to

$$\begin{aligned} {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(\Lambda _0)= R^{\text {op}}\,{\bar{\otimes }}\,R\,\subset \, {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _0)), \end{aligned}$$

this translates into the property of e being an $R_3$–$R_2$-bimodule map (or rather an $R_2^{{{\mathrm{op}}}}$–$R_3^{{{\mathrm{op}}}}$-bimodule map). All in all, we learn that there is an isomorphism of quadri-modules:

$$\begin{aligned} \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} \big (X\boxtimes _R y\big )\otimes \overline{y} \,\,\,\cong \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y\otimes \big (\overline{y}\boxtimes _R X\big ). \end{aligned}$$

Now, applying ${{\mathrm{Hom}}}_{R_3,R_4}(L^2R, -)$ to the above isomorphism, we get an $R_1$–$R_2$-bimodule isomorphism:

$$\begin{aligned} X \,&\cong \, {{\mathrm{Hom}}}_{R_3,R_4}\Big (L^2R, \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} (X\boxtimes y) \otimes \overline{y}\Big ) \\&\cong \, {{\mathrm{Hom}}}_{R_3,R_4}\Big (L^2R, \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y \otimes (\overline{y}\boxtimes X)\Big ) \cong \bigoplus _{y\in {{\mathrm{Irr}}}(\mathcal {C})} y\otimes {{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}\big (L^2R, \overline{y}\boxtimes X\big ). \end{aligned}$$

Finally, ${{\mathrm{Hom}}}_{{{\mathrm{Bim}}}(R)}(L^2R, \overline{y}\boxtimes X)$ is just some Hilbert space (because $L^2R$ is irreducible), and so the above isomorphism exhibits X as an element of $\mathcal {C}\otimes _\mathsf{Vec}\mathsf{Hilb}$.

Let $\mathcal {C}'_{abs} \subset \mathcal {C}'$ be the full subcategory of absorbing objects of $\mathcal {C}'$. This is a non-unital tensor category, and it makes sense to talk about half-braidings with $\mathcal {C}'_{abs}$ (the axioms of a half-braiding never mention unit objects).

Lemma 6.3

Let $\underline{\Omega }=(\Omega ,e_\Omega )\in \mathcal {C}'$ be an absorbing object, let X be a right R-module, and let $u:X\boxtimes \Omega \rightarrow X\boxtimes \Omega$ be a right module map that commutes with ${{\mathrm{id}}}_X\otimes {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Omega })$. Then, $u=v\boxtimes {{\mathrm{id}}}_{\Omega }$ for some right module map $v:X\rightarrow X$.

Proof

By Theorem 5.10, we can write $\underline{\Omega }$ as $\underline{\Delta }(\Lambda )$ for some absorbing bimodule $\Lambda$. In particular, we then have $\Omega =\bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} x\boxtimes \Lambda \boxtimes \overline{x}$. Letting $\Lambda _2:={}_RL^2R\otimes _{\mathbb C} X_R$, we can then identify $X\boxtimes \Omega$ with

$$\begin{aligned} \bigoplus _{x\in {{\mathrm{Irr}}}(\mathcal {C})} \big [ x \boxtimes \Lambda \boxtimes \overline{x} \boxtimes \Lambda _2 \boxtimes - \big ]_{\text {cyclic}} \end{aligned}$$

By Proposition 5.17, since u commutes with ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda ))$, it lies in ${{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Delta }(\Lambda _2))$. Now, we also know that u commutes with $R^{{{\mathrm{op}}}}={{\mathrm{End}}}({}_RL^2R)$. By Proposition 5.14, it therefore comes from some element of ${{\mathrm{End}}}(X_R)$, which we may call v. In other words, $u=v\boxtimes {{\mathrm{id}}}_{\Omega }$.$\square$

Proposition 6.4

An object $X\in {{\mathrm{Bim}}}(R)$ admits at most one half-braiding with $\mathcal {C}'_{abs}$.

Proof

Let $e^{\scriptscriptstyle (1)}_X$ and $e^{\scriptscriptstyle (2)}_X$ be two half-braidings. Given an object $\underline{\Omega }\in \mathcal {C}'_{abs}$, with underlying bimodule $\Omega \in {{\mathrm{Bim}}}(R)$, we need to show that the two maps $e_1:=e^{\scriptscriptstyle (1)}_{X,\underline{\Omega }}$ and $e_2:=e^{\scriptscriptstyle (2)}_{X,\underline{\Omega }}$ are equal. Let $u:=e_2^{-1}\circ e_1$. The maps $e_1$ and $e_2$ are natural with respect to endomorphisms of $\underline{\Omega }$, and so u commutes with ${{\mathrm{id}}}_X\otimes {{\mathrm{End}}}_{\mathcal {C}'}(\underline{\Omega })$. By Lemma 6.3, we may therefore write it as $u=v\boxtimes {{\mathrm{id}}}_{\Omega }$ for some $v\in {{\mathrm{End}}}_{{{\mathrm{Bim}}}(R)}(X)$. All in all, we get a commutative diagram

Fix an isomorphism $\phi : \underline{\Omega }\boxtimes \underline{\Omega } \rightarrow \underline{\Omega }$ in $\mathcal {C}'$, and let us denote by the same letter the corresponding isomorphism $\Omega \boxtimes \Omega \rightarrow \Omega$. By combining the “hexagon” axiom with the statement that the half-braiding is natural with respect to $\phi$, we get the following commutative diagrams (as in the proof of Proposition 5.9):

(18)

and

(19)

Horizontally precomposing (19) with

yields the following diagram

The latter is almost identical to (18), but for the top right arrow. All maps in sight being isomorphisms, it follows that ${{\mathrm{id}}}_\Omega \boxtimes e_1={{\mathrm{id}}}_\Omega \boxtimes e_2$. At last, by Lemma 2.13, we conclude that $e_1=e_2$.$\square$