Efficient Representation of Lattice Path Matroids

Abstract

Efficient deterministic algorithms to construct representations of lattice path matroids over finite fields are presented. They are built on known constructions of hierarchical secret sharing schemes, a recent characterization of hierarchical matroid ports, and the existence of isolating weight functions for lattice path matroids whose values are polynomial on the size of the ground set.

1 Introduction

Every linear code determines a matroid, namely the one that is represented by any of its generator matrices. Several properties of the code are derived from that matroid. For example, the weight enumerator of the code is derived from the Tutte polynomial of the matroid [19]. Another example is the correspondence between maximum distance separable linear codes and representations of uniform matroids. Determining over which fields uniform matroids are represented is equivalent to solving the main conjecture for maximum distance separable codes. Detailed information on that conjecture is given in [26, Problem 6.5.19]. Important advances for solving it have been presented in [1, 2].

Additional connections follow from applications of linear codes other than plain error detection and correction, as network coding [15] or locally repairable codes [13, 30]. Among them, secret sharing has attracted most attention, and it is the main motivation for our results. Vector secret sharing schemes [9] are ideal and linear, so they are among the most efficient secret sharing schemes. The access structures of vector secret sharing schemes coincide with the ports of representable matroids. Every representation of a matroid over a finite field provides a vector secret sharing scheme for each of its ports. The efficiency of those schemes is determined by the size of the field.

Given a family of representable matroids, some basic questions are motivated by those applications. Over which (finite) fields can they be represented? Which is the minimum size of those fields? Are there efficient algorithms to find a representation for every member of the family?

This paper deals with efficient deterministic constructions of representations of matroids over finite fields. Specifically, deterministic algorithms that provide, for each member in a given family of representable matroids, a representation over some finite field $\textbf{F}_q$. Both the running time and the size $\log q$ of the elements in the finite field must be polynomial in the number of elements in the ground set.

The existence of such algorithms is well known for uniform and graphic matroids, and it has been proved for matroids with two clonal classes [3]. Efficient deterministic representations for other families of matroids are derived from constructions of several classes of vector secret sharing schemes, namely hierarchical [9, 14, 31], compartmented [12], and uniform multipartite [11] schemes. Some results on deterministic algorithms for transversal matroids are given in [21, 24], but no efficient algorithms are known for that class.

For other families of matroids, only efficient randomized algorithms are known. This is the case for transversal matroids. The output of those algorithms is correct with high probability, but there is no efficient way to check whether or not this is the case.

In this paper, we present efficient deterministic algorithms for lattice path matroids, a family of transversal matroids introduced in [8]. Even though the existence of such algorithms has not been explicitly stated before, it directly follows from previous works in secret sharing. Namely, the constructions of hierarchical vector secret sharing schemes in [9, 14, 31] and a recent characterization of the matroids determined by those schemes, which were proved to coincide with lattice path matroids [25]. In addition to pointing out and explaining that connection, the main contribution in this paper is a simpler and more general description of those constructions. Specifically, using isolating weight functions in a similar way as in [21], a general method to find representations of transversal matroids is presented. It is efficient if the values of the isolating weight functions are polynomial in the size of the ground set. The existence of such functions is proved for lattice path matroids. The application to other families of transversal matroids remains an open question.

Our algorithms provide two kinds of representations of lattice path matroids. The first one works for large algebraic extensions of relatively small prime fields and it corresponds to the constructions of hierarchical secret sharing schemes in [9, 14]. The second one deals with large prime fields. Another such construction was proposed in [31], but it applies only to nested matroids.

2 Preliminaries

The main concepts and known results together with the terminology and notation that are used in the paper are explained in this section. After presenting the basics on polymatroids and matroids, we discuss the connection between transversal matroids and Boolean polymatroids, which is used later to describe the two existing characterizations [17, 25] of hierarchical matroid ports, that is, the access structures of ideal hierarchical secret sharing schemes. In addition, we review some facts and open questions on ideal multipartite secret sharing schemes and multi-uniform matroids that are the initial point of this work. Polymatroids play a fundamental role in that topic.

2.1 Polymatroids, Matroids, and Matroid Ports

The reader is referred to [26] for a textbook on matroid theory. Most of the time, we use here the terminology and notation from it. More information about polymatroids, matroid ports, and their application to secret sharing is found in [22].

A set function $f :2^{E} \rightarrow \textbf{R}$ on a finite set $E$ is monotone if $f(X) \le f(Y)$ whenever $X \subseteq Y \subseteq E$, and it is submodular if $f(X) + f(Y) - f(X \cup Y) - f(X \cap Y) \ge 0$ for all $X,Y \subseteq E$. A polymatroid is a pair $(E,f)$ formed by a ground set $E$ and a rank function f. The former is a finite set and the latter is a monotone, submodular set function on $E$ with $f(\emptyset ) = 0$. Integer polymatroids are those with integer-valued rank functions. From now on, only integer polymatroids are considered.

An integer polymatroid $M= (E,r)$ with $r(\{x\}) \le 1$ for each $x \in E$ is a matroid. The independent sets of the matroid $M$ are the subsets of the ground set with $r(X) = |X|$. A basis is a maximal independent set and a circuit is a minimal dependent set. All bases have $r(E)$ elements, and that value is called the rank of the matroid.

For an element $p_o$ in the ground set $E$, the port of the matroid $M$ at $p_o$ is formed by the sets $X \subseteq E \setminus \{p_o\}$, such that $r(X \cup \{p_o\}) = r(X)$. Observe that the minimal sets in the matroid port are the ones, such that $X \cup \{p_o\}$ is a circuit. A matroid is connected if every two different elements in the ground set lie in a common circuit. As a consequence of [26, Theorem 4.3.3], a connected matroid is determined by any of its ports.

Given a matrix A over a field $K$ with columns indexed by a set $E$ and a set $X \subseteq E$, let r(X) be the rank of the submatrix formed by the columns corresponding to the elements in X. Then, $M= (E,r)$ is a matroid. In that situation, $M$ is representable over $K$, or $K$-representable, and the matrix A is a representation of $M$ over $K$.

While representations of matroids are collections of vectors (the columns of a matrix), some polymatroids can be represented by collections of vector subspaces. A polymatroid (E, f) is $K$-representable if there exists a collection $(V_x)_{x \in E}$ of subspaces of a $K$-vector space V, such that $f(X) = \dim \sum _{x \in X} V_x$ for every $X \subseteq E$.

2.2 Transversal Matroids and Boolean Polymatroids

We discuss next some basic facts about transversal matroids, Boolean polymatroids, and lattice path matroids. The reader is referred to [6,7,8, 23, 26] for additional information on those topics.

For an integer polymatroid $(S,f)$, consider the family formed by the subsets $X \subseteq S$, such that $|Y| \le f(Y)$ for every $Y \subseteq X$. By [26, Corollary 11.1.2], that is the family of independent sets of a matroid, which is called the matroid induced by the polymatroid $(S,f)$.

Let G be a bipartite graph with vertices in the parts $J$ and $S$. For a set X of vertices, N(X) denotes the set of neighbors of the vertices in X. If $B \subseteq S$, we notate $G_B$ for the subgraph of G induced by $J\cup B$. The biadjacency matrix of the bipartite graph G is a (0, 1)-matrix whose rows and columns are indexed by the sets $J$ and $S$, respectively, and the entries equal to 1 mark the edges of G.

The graph G determines two sequences of sets. Namely, $(C_x \,:\, x \in S)$ with $C_x = N(\{x\}) \subseteq J$ and $(A_j \,:\, j \in J)$ with $A_j = N(\{j\}) \subseteq S$. Observe that the sets in those sequences may not be distinct.

A set $X \subseteq S$ is a partial transversal of the sequence $(A_j :\, j \in J)$ if there is an injective map $\varphi :X \rightarrow J$, such that $x \in A_j$ if $\varphi (x) = j$. Those partial transversals are the independent sets of a transversal matroid $M$ with ground set $S$. Observe that $X \subseteq S$ is an independent set of $M$ if and only if there is a matching in G covering all vertices in X. The sequence $(A_j :\, j \in J)$ of subsets of $S$ and, equivalently, the graph G provide a presentation of the transversal matroid $M$. A transversal matroid may admit different presentations, but there exist presentations such that the size of $J$ equals the rank of the matroid [6, Theorem 2.6]. From now on, we always assume that this is the case, that is, we assume that there is a matching in G with $|J|$ edges. In that situation, $B \subseteq S$ is a basis of $M$ if and only if the subgraph $G_B$ has a perfect matching.

The sequence $(C_x :\, x \in S)$ of subsets of $J$ determines a Boolean polymatroid with ground set $S$. Namely, the polymatroid $(S,f)$ with $f(X) = |N(X)| = \left| \bigcup _{x \in X} C_x \right|$ for every $X \subseteq S$. By Hall’s marriage theorem, $X \subseteq S$ is an independent set of the transversal matroid $M$ determined by G if and only if $|Y| \le |N(Y)| = f(Y)$ for every $Y \subseteq X$. Therefore, a matroid is transversal if and only if it is induced by a Boolean polymatroid.

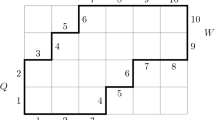
Lattice path matroids, which were introduced in [8], are a special class of transversal matroids. As a consequence of [6, Lemma 4.7], the following definition is equivalent to the one in [8]. For positive integers m, n, with $m \le n$, we notate $[m,n] = \{m, m+1, \ldots , n\}$ and $[n] = [1,n]$.

Proposition 2.1

Let G be a bipartite graph with parts $J= [r]$ and $S= [n]$. Then, the following conditions are equivalent.

• 1. There are sequences $(a_1, \ldots , a_r)$ and $(b_1, \ldots , b_r)$ in $S$ with $1 = a_1 \le a_2 \le \cdots \le a_r$ and $b_1 \le b_2 \le \cdots \le b_r = n$, such that $a_j \le b_j$ and $A_j = [a_j,b_j]$ for every $j \in J$.

• 2. There are sequences $(c_1, \ldots , c_n)$ and $(d_1, \ldots , d_n)$ in $J$ with $1 = c_1 \le c_2 \le \cdots \le c_n$ and $d_1 \le d_2 \le \cdots \le d_n = r$, such that $c_x \le d_x$ and $C_x = [c_x,d_x]$ for every $x \in S$.

Definition 2.2

A lattice path matroid is a transversal matroid that admits a presentation with the conditions of Proposition 2.1. It is a nested matroid (also called generalized Catalan matroid) in the particular case that it admits such a presentation with $b_1 = n$ or, equivalently, $c_n = 1$.

2.3 Vector Secret Sharing Schemes

The reader is referred to [4] for a comprehensive survey on secret sharing. In a secret sharing scheme, a secret value is distributed into shares among some players in such a way that only some qualified sets of players are able to recover the secret from their shares. The qualified sets form the access structure, which is a monotone family of sets of players. That is, every set containing a qualified set is qualified. A secret sharing scheme is perfect if the shares from an unqualified set do not provide any information on the secret value, and it is ideal if, in addition, each share has the same size as the secret value, which is the optimal case. Brickell and Davenport [10] proved that the access structure of every ideal secret sharing scheme is a matroid port.

Vector secret sharing schemes are ideal schemes determined by linear codes. A linear code of length n over a finite field $K$ is a vector subspace $C \subseteq K^n$. The rows of a generator matrix form a basis of C. Such a linear code C determines a vector secret sharing scheme as follows. Given a secret value $s \in K$, choose uniformly at random a code word $c = (c_1, c_2,\ldots , c_n) \in C$ with $c_1 = s$, and distribute the shares $c_2, \ldots , c_n$ among the $n-1$ players in the scheme. A set X is qualified if and only if the first column of the generator matrix is a linear combination of the columns corresponding to the players in X. Let $M$ be the $K$-representable matroid associated to the linear code C, that is, the matroid represented by the generator matrix. The access structure of the secret sharing scheme is the port of $M$ at the element in the ground set corresponding to the first column. Therefore, the access structures of vector secret sharing schemes are the ports of representable matroids. Each representation of a matroid over a finite field provides vector secret sharing schemes for its ports and, conversely, a representation of a matroid over a finite field is obtained from a vector secret sharing scheme for any of its ports.

2.4 Matroids with Large Clonal Classes

Two elements in the ground set of a matroid are clones if the map that interchanges them and let all other elements fixed is an automorphism of the matroid. The equivalence classes of that equivalence relation are the clonal classes of the matroid, For example, uniform matroids are those having only one clonal class.

In a secret sharing scheme, players x and y are clones if, for every set A of players with $x,y \notin A$, the set $A \cup \{x\}$ is qualified if and only if so is $A \cup \{y\}$. That is, they play the same role in the scheme. If the access structure is a matroid port, two players are clones if and only if they are clones in the matroid.

Definition 2.3

A matroid $M$ is $\Pi$-uniform for some partition $\Pi = (S_i \,:\, i \in P)$ of the ground set if all elements in the same part are clones. That is, each $S_i$ is a subset of a clonal class. If $|P| = m$, we say that $M$ is m-uniform.

For a partition $\Pi$ of the set of players, $\Pi$-uniform access structures are defined analogously. A secret sharing scheme is said to be multipartite if its access structure is m-uniform, specially when m is much smaller than the number of players. Ideal multipartite schemes have been studied by several authors [5, 9, 12, 14, 16, 17, 27, 29, 31, 32]. Their access structures are ports of m-uniform matroids, which are called m-partite in the works on secret sharing. The main examples are compartmented and hierarchical secret sharing schemes.

Let $M= (S,r)$ be a $\Pi$-uniform matroid with $\Pi = (S_i \,:\, i \in P)$. Associated to $M$, consider the integer polymatroid $(P,g)$ with

$$\begin{aligned} g(I) = r \left( \bigcup _{i \in I} S_i \right) \end{aligned}$$

for every $I\subseteq P$. The matroid $M$ is determined by the integer polymatroid $(P,g)$ and the partition $\Pi$. Indeed, consider the map $\pi :S\rightarrow P$ with $\pi (x) = i$ if $x \in S_i$ and the polymatroid $(S,f)$ with $f(X) = g(\pi (X))$ for each $X \subseteq S$. Then, $M$ is the matroid induced by the polymatroid (S, f). The following result was proved in [16, Theorem 6.1].

Proposition 2.4

Consider a $\Pi$-uniform matroid $M= (S,r)$ with $\Pi = (S_i \,:\, i \in P)$ and its associated polymatroid $(P,g)$. There exists an integer $q(M)$, such that $M$ is $K$-representable if the field $K$ has at least $q(M)$ elements and $(P,g)$ is $K$-representable.

Nevertheless, no efficient deterministic methods are known to find representations of matroids with large clonal classes from representations of the associated polymatroids, which lead to the open problem posed in [16, Open Problem 6.9] and [18, Section VII]. Preliminary versions of that problem are found in [9, 31, 32]. Solutions for some classes of multi-uniform matroids are given in [3, 9, 11, 12, 14, 31].

2.5 Hierarchical Secret Sharing and Lattice Path Matroids

In an access structure, a player x is hierarchically inferior to a player y if, for every set A of players with $x,y \notin A$, the set $A \cup \{y\}$ is qualified if so is the set $A \cup \{x\}$. In that situation, we write $x \preceq y$. Observe that x, y are clones if and only if $x \preceq y$ and $y \preceq x$. An access structure is hierarchical if that preorder in the set of players is total. Hierarchical secret sharing schemes are those having a hierarchical access structure.

Efficient deterministic constructions of vector secret sharing schemes were presented in [9, 31] for the so-called hierarchical threshold access structures. The construction in [9] was generalized in [14] to all hierarchical matroid ports, which had been previously characterized in [17] in terms of multi-uniform matroids induced by Boolean polymatroids. An alternative characterization has been recently found [25], which is summarized in the following. If $M$ is a lattice path matroid on the ground set $S= [n]$, then the ports of $M$ at each of the elements $p_o = 1$ and $p_o = n$ are hierarchical access structures. Conversely, every hierarchical matroid port is of that form. In particular, hierarchical threshold access structures are the ports of nested matroids. Moreover, the hierarchical order is compatible with the order in the ground set. Specifically, in the port of $M$ at $p_o = 1$, a player x is hierarchically inferior to a player y if $1 < y \le x \le n$, while the hierarchical order is reversed in the port of $M$ at $p_o = n$.

Proposition 2.1 clarifies the connection between those two characterizations of hierarchical matroid ports. While the characterization in [17] uses the Boolean polymatroid determined by the sets $C_x$, the one in [25] focuses on the lattice path matroid determined by the sets $A_j$.

Therefore, the constructions from [9, 31] and the ones from [14] provide efficient deterministic algorithms to find representations over finite fields for nested matroids and, respectively, lattice path matroids. The method in [9, 14] provides representations over algebraic field extensions of large degree, while the one in [31], which applies only to nested matroids, it is based on Birkhoff interpolation and yields representations over large prime fields. In the following sections, we give an alternative description of the former and we present a new construction over prime fields that applies to all lattice path matroids.

3 Representations of Transversal Matroids

It is well known that representations for a transversal matroid $M$ are obtained by modifying the biadjacency matrix of a presentation G. Indeed, for each edge (j, x) of G, replace the corresponding entry (equal to 1) in the biadjacency matrix with a variable $\alpha _{j,x}$. Take an arbitrary field K and assume that the entries of the matrix are polynomials over $K$ in the variables $\alpha _{j,x}$. Clearly, the determinant of the square submatrix formed by the columns corresponding to a set $B \subseteq S$ with $|B| = r$ is a non-zero polynomial if B is a basis of $M$ and it is zero otherwise. At this point, representations for $M$ are obtained by assigning values to the variables $\alpha _{j,x}$. One possibility is considering that $\alpha _{j,x}$ are algebraically independent elements over $K$ in some extension field. In addition, for every sufficiently large field $K$, it is possible to substitute the variables $\alpha _{j,x}$ by elements in $K$ in such a way that the value of every polynomial corresponding to a basis of $M$ is non-zero. Nevertheless, it is not clear how to efficiently choose those elements. We describe next two methods to assign values to the variables $\alpha _{j,x}$ from a weight function on the edges of the graph.

Definition 3.1

A weight function with non-negative integer values on the edges of G is isolating if, for every basis B of the transversal matroid $M$, among the perfect matchings of $G_B$, there is only one with minimum weight.

Every bipartite graph admits an isolating weight function. Indeed, enumerate the edges $\{e_0, e_1.\ldots , e_{m-1}\}$ and take $w(e_k) = 2^k$. Nevertheless, the methods that are described in the following provide efficient representations for a family of transversal matroids only if the values of the isolating weight functions are polynomial in the size of the ground set.

Proposition 3.2

([28], Theorems 3.2 and 4.1) If p is a prime number, there is a deterministic algorithm to find an irreducible polynomial over $\textbf{F}_p$ of degree s. Its running time is $O(p^{1/2} s^4)$ ignoring powers of $\log s$ and $\log p$. If $q = p^d$, there is a deterministic algorithm to find an irreducible polynomial over $\textbf{F}_{q}$ of degree s that runs in time $O(p^{1/2} s^3 + s^4 d^2)$ ignoring powers of $\log s$ and $\log p$.

Proposition 3.3

Consider a transversal matroid $M$ with rank r over n elements, a presentation G of $M$, an isolating weight function w on the edges of G, and integers s, t with $t = \max w(j,x)$ and s larger than the maximum weight of a matching in G.

• 1. There exists a deterministic algorithm that, for every prime number p, provides a representation of $M$ over the finite field with $p^{s}$ elements. The running time is polynomial in n, p, and s.

• 2. There exists a deterministic algorithm that, for each prime number $p > 2^{rt} \, r^{r/2}$, provides a representation of $M$ over $\textbf{F}_p$. The running time of the algorithm is polynomial in $\log p$ and n.

Proof

Take a variable $\alpha$ and put $\alpha _{j,x} = \alpha ^{w(j,x)}$ for every edge (j, x) of G. Take an arbitrary field $K$ and assume that the entries of the matrix are polynomials over $K$ in the variable $\alpha$. Then, the determinant of the submatrix corresponding to a basis B is a non-zero polynomial. Indeed, the coefficient of the minimum degree equals either 1 or $-1$, because it corresponds to the unique perfect matching in $G_B$ with minimum weight. For each basis, the degree of that polynomial is at most the maximum weight of a perfect matching, and hence less than s.

Consider an arbitrary prime number p and $q = p^s$, and take $K= \textbf{F}_p$. Using the algorithm given by Shoup [28], find an irreducible polynomial $f(\alpha )$ over $\textbf{F}_{p}$ of degree s. As we mentioned in Proposition 3.2, that can be done in time $O(p^{1/2} s^4)$ ignoring the powers of $\log s$ and $\log p$. Then, the quotient ring $\textbf{F}_p[\alpha ]/(f(\alpha ))$ is isomorphic to the field $\textbf{F}_q$, an algebraic extension of $\textbf{F}_p$. The class of $\alpha$ in that quotient ring is an element in $\textbf{F}_q$ whose minimal polynomial over $\textbf{F}_{p}$ is of degree s. By identifying the entries of the matrix with elements in $\textbf{F}_q$, a representation of the matroid $M$ over that field is obtained.

To construct a representation over a prime field, assume that K is the field of real numbers, and hence, the entries of the matrix are assumed to be real polynomials in the variable $\alpha$. Those polynomials have integer coefficients, because they are either zero or a power of $\alpha$. Therefore, for every basis B, the determinant of the corresponding submatrix is a non-zero polynomial $h_B(\alpha )$ with integer coefficients. Moreover, $h_B(2) \ne 0$, because the coefficient of the minimum degree term is $\pm 1$. Put $\alpha = 2$ and let A be the the resulting integer matrix. Observe that $0 \le a_{j,x} \le 2^t$ for every entry of that matrix. For a basis B, the corresponding submatrix $A_B$ satisfies

$$\begin{aligned} |\det A_B| \le 2^{rt}\, r^{r/2} \end{aligned}$$

by Hadamard’s inequality. Therefore, that determinant is not a multiple of p for any prime number p larger than $2^{rt}\, r^{r/2}$, and hence, the matrix A provides a representation of $M$ over the prime field $\textbf{F}_p$. $\square$

The most computationally expensive step in the first algorithm is to find an irreducible polynomial over $\textbf{F}_{p}$ of degree s. Since p can be the same for all matroids in the family, the computation time depends almost exclusively on the value of s, and hence on the maximum weight of the perfect matchings in the subgraphs $G_B$. In addition, the value of s determines the size of the finite field $\textbf{F}_q$, and hence the efficiency of the representations and their applications as, for example, secret sharing schemes. It is well known that the arithmetic operations in $\textbf{F}_q$ can be performed in time polynomial in $\log q$ using a representation of the field given by an irreducible polynomial, that is, by identifying $\textbf{F}_q$ with $\textbf{F}_p[\alpha ]/(f(\alpha ))$.

The size of the representations given by the second construction is $n r \log p$, and hence, it provides representations of size $O(n r( r t + (r/2)\log r))$, where t is the maximum weight of the edges.

4 Efficient Representations of Lattice Path Matroids

In this section, we consider only transversal matroids of rank r with a representation G with $J= [r]$ and $S= [n]$. For a set $B\subseteq S$, we notate $B = (x_1, \ldots , x_r)$ to indicate that its elements are arranged in increasing order.

We present in Proposition 4.2 a sufficient condition for the existence of isolating weight functions with polynomial weights. By combining it with Proposition 3.3, efficient representations for lattice path matroids are obtained. The following technical result is a consequence of the rearrangement inequality.

Lemma 4.1

Let $(p_1, \ldots , p_r)$ and $(q_1, \ldots , q_r)$ be sequences of real numbers, such that the first one is non-decreasing and the second one is non-increasing. Then

$$\begin{aligned} p_1 q_1 + \cdots + p_r q_r \le p_1 q_{\sigma 1} + \cdots + p_r q_{\sigma r} \le p_1 q_{r} + \cdots + p_r q_{1} \end{aligned}$$

for every permutation $\sigma$. Moreover, each of those bounds is attained only by one permutation if each sequence has distinct terms.

Proposition 4.2

Let $M$ be a transversal matroid, such that, for each basis $B = (x_{1}, \ldots , x_{r})$, all pairs $(j,x_j)$ with $j \in J$ are edges of G. Then, G admits an isolating weight function with maximum weight at most $(r-1)(n-1)$. In addition, for each basis B, the maximum weight of the perfect matchings in $G_B$ is less than $r (r-1)(n-1)/2$.

Proof

For $j \in [r]$ and $x \in [n]$, take $p_j = j - 1$ and $q_x = n - x$. For every edge (j, x), take the weight $w(j,x) = p_j q_x$. This is an isolating weight function, because, by Lemma 4.1, the perfect matching formed by the edges $(j, x_{j})$ is the only one in $G_B$ with minimum weight. Finally, by Lemma 4.1 again, the weight of a perfect matching in $G_B$ is at most

$$\begin{aligned} (r-1)(n-1) + (r -2)(n-2) + \cdots + 1 \cdot (n-r+1) \end{aligned}$$

(1)

and hence less than $r (r-1)(n-1)/2$. Smaller upper bounds can be obtained from (1), but they are not better than $O(r^2 n)$. $\square$

By the following two propositions, lattice path matroids are the only transversal matroids satisfying the sufficient condition in Proposition 4.2.

Proposition 4.3

Let $M$ be a lattice path matroid and let G be a presentation of $M$ in the conditions of Proposition 2.1. If $B = (x_{1}, \ldots , x_{r})$ is a basis of $M$, then $(j, x_{j})$ is an edge of G for every $j \in J$.

Proof

Suppose that there is a basis B without that property. Let P be a perfect matching in $G_B$ with the maximum number of edges of the form $(j,x_j)$ and take the minimum $k \in J$, such that $(k,x_k)$ is not in P. Since P is a perfect matching, $k \le r-1$, and there exist $\ell _1, \ell _2 \in [k+1,r]$, such that $(\ell _1,x_{k})$ and $(k,x_{\ell _2})$ are edges in P. Then

$$\begin{aligned} a_{k} \le a_{\ell _1} \le x_{k} < x_{\ell _2} \le b_{k} \le b_{\ell _1}, \end{aligned}$$

which implies that $(k,x_{k})$ and $(\ell _1,x_{\ell _2})$ are edges of G. Then

$$\begin{aligned} P' = (P \setminus \{(k, x_{\ell _2}), (\ell _1,x_k)\}) \cup \{(k,x_k),(\ell _1, x_{\ell _2})\} \end{aligned}$$

is a perfect matching in $G_B$ with more edges of the form $(j,x_j)$ than P. $\square$

Proposition 4.4

Let $M$ be a transversal matroid without loops that admits a presentation G, such that, for every basis $B = (x_{1}, \ldots , x_{r})$ and for every $j \in J$, the pair $(j, x_{j})$ is an edge. Then, $M$ is a lattice path matroid.

Proof

Let $B_1 = (a_1, \ldots , a_r)$ and $B_2 = (b_1, \ldots , b_r)$ be the first and last bases of $M$ in the lexicographic order. We are going to prove that the sequence of sets $([a_j,b_j] \,:\, j \in J)$ is a presentation of $M$, and hence, it is a lattice path matroid. For two distinct bases $B,B'$, we notate $B \ll B'$ if B precedes $B'$ in the lexicographic order. We prove first that $x_j \in [a_j,b_j]$ for each $j \in [r]$ if $(x_1, \ldots , x_r)$ is a basis. Suppose that there is a basis with $x_j < a_j$ for some $j \in [r]$. Take B the first such basis in the lexicographic order and the minimum $j \in [r]$ with $x_j < a_j$. Since $B_1 \ll B$, the minimum $k \in [r]$ with $x_{k} > a_{k}$ satisfies $k < j$. Then, $B' = (B \setminus \{x_{k}\}) \cup \{a_{k}\}$ is another basis in the same situation with $B' \ll B$, a contradiction. Symmetrically, $x_j \le b_j$ for each $j \in [r]$. We prove next that (j, x) is an edge if $x \in [a_j,b_j]$. Since x is not a loop, there is an edge (k, x). If $k > j$ and $x \ne b_j$, consider the basis $B = (a_1, \ldots , a_{j-1}, b_j, \ldots , b_r)$. Then, $(B \setminus \{b_k\}) \cup \{x\}$ is a basis and x is its jth element, which implies that (j, x) is an edge. Symmetrically, the same happens if $k < j$ and $x \ne a_j$. $\square$

The following result is a direct consequence of Propositions 3.3, 4.2, and 4.3.

Proposition 4.5

Given a presentation of a lattice path matroid $M$ with rank r on n elements in the conditions of Proposition 2.1, there are two efficient constructions of representations for $M$, which are described in the following.

• 1. There is an efficient deterministic algorithm to find a representation of $M$ over the finite field with $q = p^s$ elements, where $s = r(r-1)(n-1)/2$ and p is an arbitrarily chosen prime number. The running time of the algorithm is polynomial in p and the size n of the ground set.

• 2. For every prime number $p > 2^{r(r-1)(n-1)} r^{r/2}$, there is an efficient deterministic algorithm to find a representation of $M$ over $\textbf{F}_p$. The running time of the algorithm is polynomial in $\log p$ and the size n of the ground set.

The construction of hierarchical threshold secret sharing schemes in [31], which uses Birkhoff interpolation, provides another efficient deterministic algorithm to find representations of nested matroids over prime fields $\textbf{F}_p$ with

$$\begin{aligned} p > (r-1)! \; 2^{-r+2} (r - 1)^{(r-1)/2} n^{(r-1)(r-2)/2}. \end{aligned}$$

The second construction in Proposition 4.5 yields less efficient representations, but it applies to all lattice path matroids.

We present next an improvement to the first algorithm in Proposition 4.5 for lattice path matroids with a relatively small number of clonal classes. It is equivalent to the constructions of hierarchical vector secret sharing schemes in [9, 14].

Take $J= [r]$, $S= [n]$, and integers $t_i$ with $1 = t_1< t_2< \cdots< t_m < t_{m+1}= n + 1$. Consider the partition $\Pi = (S_i :\, i \in [m])$ of S with $S_i = [t_i, t_{i+1} - 1]$. For every $x \in S$, put $\pi (x) = i$ if $x \in S_i$. Consider a bipartite graph G in the conditions of Proposition 2.1, such that, for each $i \in [m]$, all vertices in $S_i$ have the same neighbors. Then, G is a presentation of a $\Pi$-uniform lattice path matroid $M$. Observe that the port of $M$ at the element $1 \in S$ is a hierarchical access structure in which all players in the same part are hierarchically equivalent.

As we did before, we replace the non-zero entries of the biadjacency matrix of G with polynomials in the variable $\alpha$ over some finite field. Take a prime power q such that $q > |S_i| = t_{i+1} - t_i$ for every $i \in [m]$. For each $i \in [m]$, take $t_{i+1} - t_i$ distinct non-zero elements $(\beta _{x} \,:\, x \in S_i)$ in the finite field $\textbf{F}_q$. For $j \in J$ and $x \in S$, take $p_j = j-1$ and $q_x = m - \pi (x)$, and consider on the edges of G the weight function $w(j,x) = p_j q_x$. Finally, consider the matrix H that is obtained by replacing the entry in the biadjacency matrix of G corresponding to the edge (j, x) with $\beta _x^{j-1} \alpha ^{w(j,x)}$.

We prove next that, for every basis B of $M$, the determinant of the submatrix $H_B$ formed by the corresponding columns is a non-zero polynomial. Even though the chosen weight function is not isolating, we can check that the coefficient of the minimum degree term is non-zero. Indeed, let $B = (x_1, \ldots , x_r)$ be a basis of $M$. By Lemma 4.1, the perfect matching $((j,x_j) \,:\, j \in J)$ has minimum weight, but there are other perfect matchings in $G_B$ with the same weight, namely the ones of the form $((j,x_{\sigma j}) \,:\, j \in J)$, where $\sigma$ is any permutation such that $\pi (x_{\sigma j}) = \pi (x_j)$ for every $j \in J$. The entries corresponding to the edges of $G_B$ involved in those perfect matchings lie on square submatrices on the diagonal of $H_B$, one for each $i \in [m]$ with $B \cap S_i \ne \emptyset$. The determinant of each of those submatrices is of the form $\alpha ^{\ell _i} \Delta _i$, where $\Delta _i$ is the determinant of a Vandermonde-like matrix, and hence non-zero. Therefore, the coefficient of the minimum degree term of $\det H_B$ is equal to $\prod _i \Delta _i \ne 0$. Observe that the weight of a perfect matching in any subgraph $G_B$ is less than $r(r-1)(m-1)/2$. At this point, the following result has been proved.

Proposition 4.6

There exists a deterministic algorithm that, given an m-uniform lattice path matroid $M$ with the conditions above, provides a representation of $M$ over a finite field with $q^s$ elements, where q is a prime power larger than the number of elements in each part and $s = r(r-1)(m-1)/2$. The running time of the algorithm is polynomial in q and the size n of the ground set.

This algorithm improves on the first one in Proposition 4.5 if the number of parts m is small in relation to the size of the ground set. Even though q cannot be arbitrarily small, the degree s of the extension can be much smaller and, as we discussed before, this is the main parameter to be taken into account.

Every bi-uniform matroid (that is, $m=2$) is a lattice path matroid, and hence, the algorithm in Proposition 4.6 provides representations with $s = r(r-1)/2$. Nevertheless, the algorithm proposed in [3] is in general more efficient, because the degree of the extension is $s = d (d-1)/2$, where $d = r(S_1) + r(S_2) - r$.